景德镇市2016学年第三次质量检测试卷九年级数学及答案
景德镇市中考数学三模试卷

景德镇市中考数学三模试卷姓名:________ 班级:________ 成绩:________一、选择题(满分30分) (共10题;共30分)1. (3分)﹣3的倒数是()A . 3B . ﹣3C .D .2. (3分)(2017·天门) 下列运算正确的是()A . (π﹣3)0=1B . =±3C . 2﹣1=﹣2D . (﹣a2)3=a63. (3分)(2016·菏泽) 以下微信图标不是轴对称图形的是()A .B .C .D .4. (3分) (2016九上·威海期中) 一次函数y=kx﹣k,y随x的增大而减小,那么反比例函数y= 满足()A . 当x>0时,y>0B . 在每个象限内,y随x的增大而减小C . 图象分布在第一、三象限D . 图象分布在第二、四象限5. (3分)(2016·巴彦) 三棱柱的三视图如图所示,△EFG中,EF=6cm,∠EFG=45°,则AB的长为()A . 6cmB . 3 cmC . 3cmD . 6 cm6. (3分)方程+2=的解为()A . x1=4,x2=1B . x1=, x2=C . x=4D . x1=4,x2=-17. (3分)在△ABC中,∠A、∠B、∠C的对边分别为a、b、c,且a=5,b=12,c=16,下面四个式中错误的有()①sinA= ;②cosA= ;③tanA= ;④sinB= .A . 1个B . 2个C . 3个D . 4个8. (3分) (2019九上·潮南期末) 如图,在⊙O中,弦AB与CD交于点E,BE=DE,∠B=40°,则∠A的度数是()A . 20°B . 30°C . 40°D . 80°9. (3分)将抛物线y=2x2-12x+16绕它的顶点旋转180°,所得抛物线的解析式是().A . y=-2x2-12x+16B . y=-2x2+12x-16C . y=-2x2+12x-19D . y=-2x2+12x-2010. (3分)在矩形ABCD中,AB=3,AD=4,P是AD上的动点,PE⊥AC于E,PF⊥BD于F,则PE+PF的值为()A .B . 2C .D . 1二、填空题(满分30分) (共10题;共30分)11. (3分)(2017·重庆) “渝新欧”国际铁路联运大通道全长11000千米,成为服务“一带一路”的大动脉之一,将数11000用科学记数法表示为________.12. (3分) (2017八下·弥勒期末) 计算: +6 =________.13. (3分)(2013·百色) 函数y= 中,自变量x的取值范围是________.14. (3分)(2018·江城模拟) 分解因式:ax4﹣9ay2=________.15. (3分)不等式组的解集为﹣1<x<2,则a=________ ,b=________16. (3分)如图,已知圆锥的底面直径为4,母线长为6,则它的全面积为________.17. (3分) (2017八下·吴中期中) 四边形ABCD中,对角线AC、BD相交于点O,给出下列四个条件:①AD∥BC;②AD=BC;③OA=OC;④OB=OD从中任选两个条件,能使四边形ABCD为平行四边形的选法有________种.18. (3分) (2015八下·嵊州期中) 如图,Rt△ABC中,∠B=90°,AC=10cm,BC=8cm,现有两个动点P、Q 分别从点A和点B同时出发,其中点P以1cm/s的速度,沿AB向终点B移动;点Q以2cm/s的速度沿BC向终点C 移动,其中一点到终点,另一点也随之停止.连结PQ,若经x秒后P,Q两点之间的距离为4 ,那么x的值为________.19. (3分) (2019八下·绍兴期中) 如图,平行四边形ABCD中,AE平分∠BAD,交BC于点E,且AB=AE,延长AB与DE的延长线交于点F.下列结论中:①△ABC≌△AED;②△ABE是等边三角形;③AD=AF;④S△ABE=S△CDE;⑤S△ABE=S△CEF .其中正确的是________.20. (3分) (2017九下·江阴期中) 如图,一条笔直的公路l穿过草原,公路边有一消防站A,距离公路5千米的地方有一居民点B,A、B的直线距离是10 千米.一天,居民点B着火,消防员受命欲前往救火.若消防车在公路上的最快速度是80千米/小时,而在草地上的最快速度是40千米/小时,则消防车在出发后最快经过________小时可到达居民点B.(友情提醒:消防车可从公路的任意位置进入草地行驶.)三、解答题(满分60分) (共7题;共60分)21. (7分)先化简,再求值:()÷(x+1),其中x=tan60°+1.22. (7.0分)(2018·广东模拟) 如图,一条公路的转弯处是一段圆弧(1)用直尺和圆规作出所在圆的圆心O;要求保留作图痕迹,不写作法(2)若的中点C到弦AB的距离为,求所在圆的半径.23. (8.0分) (2017七下·乌海期末) 某校为了开设武术、舞蹈、剪纸等三项活动课程以提升学生的体艺素养,随机抽取了部分学生对这三项活动的兴趣情况进行了调查(每人从中只能选一项),并将调查结果绘制成如图两幅统计图,请你结合图中信息解答问题:(1)将条形统计图补充完整;(2)本次抽样调查的样本容量是________;(3)扇形图中舞蹈类所占的圆心角度数为________ 度;(4)已知该校有2000名学生,请你根据样本估计全校学生中喜欢剪纸的人数是________24. (8.0分)如图,在△ABC中,∠B=60°,△ABC的角平分线AD、CE相交于点O,(1)求∠AOC的度数;(2)求证:AE+CD=AC;(3)求证:OE=OD.25. (10分) (2019七下·方城期中) 学校准备购进一批节能灯,已知1只A型节能灯和3只B型节能灯共需26元;3只A型节能灯和2只B型节能灯共需29元.(1)求一只A型节能灯和一只B型节能灯的售价各是多少元;(2)学校准备购进这两种型号的节能灯共50只,并且A型节能灯的数量不多于B型节能灯数量的3倍,设购进A型节能灯m只.①请用含m的代数式表示总费用;②请设计出最省钱的购买方案,并说明理由.26. (10分) (2017八上·义乌期中) 如图1,已知∠DAC=90°,△ABC是等边三角形,点P为射线AD上任意一点(点P与点A不重合),连结CP,将线段CP绕点C顺时针旋转60°得到线段CQ,连结QB并延长交直线AD 于点E.(1)如图1,猜想∠QEP=________°;(2)如图2,3,若当∠DAC是锐角或钝角时,其它条件不变,猜想∠QEP的度数,选取一种情况加以证明;(3)如图3,若∠DAC=135°,∠ACP=15°,且AC=4,求BQ的长.27. (10.0分)(2018·宿迁) 如图,AB、AC分别是⊙O的直径和弦,OD⊥AC于点D,过点A作⊙O的切线与OD的延长线交于点P,PC、AB的延长线交于点F.(1)求证:PC是⊙O的切线;(2)若∠ABC=60°,A B=10,求线段CF的长,参考答案一、选择题(满分30分) (共10题;共30分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、二、填空题(满分30分) (共10题;共30分)11-1、12-1、13-1、14-1、15-1、16-1、17-1、18-1、19-1、20-1、三、解答题(满分60分) (共7题;共60分)21-1、22-1、22-2、23-1、23-2、23-3、23-4、24-1、24-2、24-3、25-1、25-2、26-1、26-2、26-3、27-1、27-2、。
景德镇市中考数学三模考试试卷

景德镇市中考数学三模考试试卷姓名:________ 班级:________ 成绩:________一、选择题 (共16题;共40分)1. (3分)(2018·金华模拟) 的相反数是A . 3B .C .D .2. (2分)下列四个立体图形中,左视图为矩形的是()A . ①③B . ①④C . ②③D . ③④3. (3分)(2017·重庆) 估计 +1的值在()A . 2和3之间B . 3和4之间C . 4和5之间D . 5和6之间4. (2分) (2016七下·青山期中) 如图,把一张对面互相平行的纸条折成如图所示那样,EF是折痕,若∠EFB=32°,则下列结论正确的有()1)∠C′EF=32° (2)∠AEC=116° (3)∠BGE=64°(4)∠BFD=116°.A . 1个B . 2个C . 3个D . 4个5. (3分) (2019九上·襄阳期末) 用一枚质地均匀的硬币做抛掷试验,前10次掷的结果都是正面向上,如果下一次掷得的正面向上的概率为P(A),则()A . P(A)=1B . P(A)=C . P(A)>D . P(A)<6. (3分)(2018·台州) 计算,结果正确的是()A . 1B .C .D .7. (3分)下列命题中,真命题是()A . 对角线相等的四边形是等腰梯形B . 对角线互相垂直平分的四边形是正方形C . 对角线互相垂直的四边形是菱形D . 四个角相等的四边形是矩形8. (3分)(2016·竞秀模拟) 下列计算正确的是()A . (﹣ab3)2=a2b3B . (x+3)2=x2+9C . (﹣4)0=1D . (﹣1)﹣3=19. (3分) (2017八下·兴化月考) 顺次连接一个四边形的各边中点,得到了一个矩形,则下列四边形①平行四边形;②菱形;③对角线互相垂直的四边形;④对角线相等的四边形,满足条件的是()A . ①③④B . ②③C . ①②④D . ①②③10. (3分)(2017·扬州) 一元二次方程x2﹣7x﹣2=0的实数根的情况是()A . 有两个不相等的实数根B . 有两个相等的实数根C . 没有实数根D . 不能确定11. (2分) (2020八上·奉化期末) 在平面直角坐标系中,若点P与点Q的横坐标相同,而纵坐标不同,则直线PQ与x轴的关系是()A . 平行B . 垂直C . 重合D . 以上都不对12. (2分)矩形的长为x,宽为y,面积为12,则y与x之间的函数关系用图象表示大致为()A .B .C .D .13. (2分) (2020九上·醴陵期末) 若=,则下列各式不成立的是()A . =B . =C . =D . =14. (2分)若正比例函数y=kx的图象经过点(1,2),则k的值为()A . -B . -2C .D . 215. (2分)(2017·松江模拟) 已知在Rt△ABC中,∠C=90°,如果BC=2,∠A=α,则AC的长为()A . 2sinαB . 2cosαC . 2tanαD . 2cotα16. (2分) (2016九上·太原期末) 从一块正方形铁皮的四角上各剪去一个边长为3cm的小正方形,制成一个无盖的盒子,若盒子的容积为300cm3 ,则铁皮的边长为()A . 16cmB . 14cmC . 13cmD . 11cm二、填空题 (共3题;共10分)17. (3分)(2017·南岸模拟) ﹣(2﹣)0+(﹣)﹣1=________.18. (3分)(2016·上海) 如果a= ,b=﹣3,那么代数式2a+b的值为________.19. (4分)如图,以O为位似中心,作出四边形ABCD的位似图形,使新图形与原图形的相似比为2:1,并以O为原点,写出新图形各点的坐标.三、解答题 (共7题;共58分)20. (9.0分) (2017七上·黄陂期中) 红红有5张写着以下数字的卡片,请你按要求抽出卡片,完成下列各问题:(1)从中取出2张卡片,使这2张卡片上数字乘积最大,最大值是________(2)从中取出2张卡片,使这2张卡片上数字相除的商最小,最小值是________(3)从中取出除0以外的其他4张卡片,将这4个数字进行加、减、乘、除或乘方等混合运算,使运算结果为24(注:每个数字只能用一次,如:23×[1-(-2)],请另外写出两种符合要求的运算式子:________ ________21. (9分)(2017·张家界) 如图,在正方形ABCD中,AD=2 ,把边BC绕点B逆时针旋转30°得到线段BP,连接AP并延长交CD于点E,连接PC,则三角形PCE的面积为________.22. (9分) (2017七下·大庆期末) 某车间有28名工人,生产某种型号的螺栓和螺母。
江西省景德镇市2016届九年级上期末数学试卷含答案解析

中位数是(
)
A.b B.c C. D.
3.某几何体的主视图和左视图完全一样均如图所示,则该几何体的俯视图不可能是 ()
A.
B.
C.
D.
4.关于 x 的一元一次不等式 x▱ b<0 恰有两个正整数解,则 b 的值可能是( ) A.1 B.2.5 C.2 D.3.5
5.如图,△ABC 中,AE 交 BC 于点 D,∠C=∠E,AD=3,BD=5,DC=2,则 DE 的长等于 ()
2015-2016 学年江西省景德镇市九年级(上)期末数学试卷
一、选择题(本大题共 6 小题,每小题 3 分,共 18 分)每题只有一个正确的选项
1.下列各数中,为有理数的是(
)
A.π B. C.3.14 D.
2.已知 5 个正数 a,b,c,d,e,且 a<b<c<d<e,则新一组数据 0,a,b,c,d,e 的
22.小敏将笔记本电脑水平放置在桌子上,显示屏 OB 与底板 OA 所在水平线的夹角为 120°,感觉最舒适(如图 1),侧面示意图为图 2.使用时为了散热,她在底板下垫入散热 架 ACO′后,电脑转到 AO′B′位置(如图 3),侧面示意图为图 4.已知 OA=OB=24cm, O′C⊥OA 于点 C,O′C=12cm. (1)求∠CAO′的度数; (2)显示屏的顶部 B′比原来升高了多少?
A. B. C. D.
6.如图是二次函数 y=ax2+bx+c 的图象,下列结论:
2016年初中毕业学业考试第三次模拟试题答案
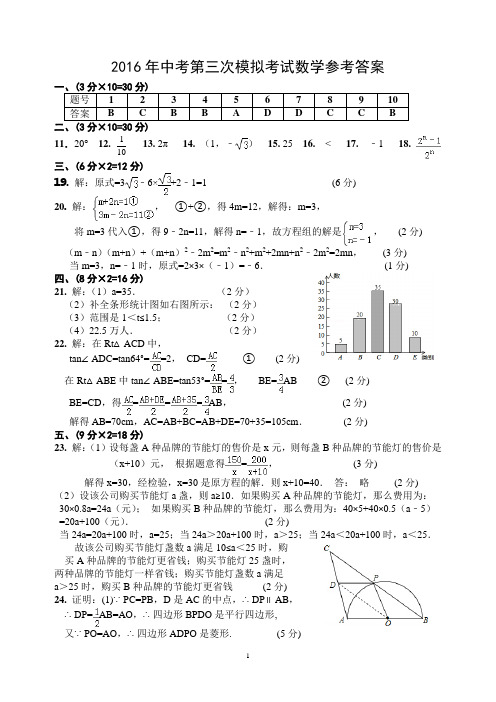
2016年中考第三次模拟考试数学参考答案题号 1 2 3 4 5 6 7 8 9 10答案 B C B B A D D C C B113. 2π14. (1,﹣)15. 25 16. < 17. ﹣1 18. 11.20°12.10三、(6分×2=12分)19.解:原式=3﹣6×+2﹣1=1 (6分)20.解:,①+②,得4m=12,解得:m=3,将m=3代入①,得9﹣2n=11,解得n=﹣1,故方程组的解是,(2分) (m﹣n)(m+n)+(m+n)2﹣2m2=m2﹣n2+m2+2mn+n2﹣2m2=2mn,(3分)当m=3,n=﹣1时,原式=2×3×(﹣1)=﹣6.(1分)四、(8分×2=16分)21. 解:(1)a=35.(2分)(2)补全条形统计图如右图所示:(2分)(3)范围是1<t≤1.5;(2分)(4)22.5万人.(2分)22. 解:在Rt△ACD中,tan∠ADC=tan64°==2,CD=①(2分)在Rt△ABE中tan∠ABE=tan53°==,BE=AB ②(2分)BE=CD,得===AB,(2分)解得AB=70cm,AC=AB+BC=AB+DE=70+35=105cm.(2分)五、(9分×2=18分)23. 解:(1)设每盏A种品牌的节能灯的售价是x元,则每盏B种品牌的节能灯的售价是(x+10)元,根据题意得=,(3分) 解得x=30,经检验,x=30是原方程的解.则x+10=40.答:略(2分) (2)设该公司购买节能灯a盏,则a≥10.如果购买A种品牌的节能灯,那么费用为:30×0.8a=24a(元);如果购买B种品牌的节能灯,那么费用为:40×5+40×0.5(a﹣5)=20a+100(元).(2分)当24a=20a+100时,a=25;当24a>20a+100时,a>25;当24a<20a+100时,a<25.故该公司购买节能灯盏数a满足10≤a<25时,购买A种品牌的节能灯更省钱;购买节能灯25盏时,两种品牌的节能灯一样省钱;购买节能灯盏数a满足a>25时,购买B种品牌的节能灯更省钱(2分)24. 证明:(1)∵PC=PB,D是AC的中点,∴DP∥AB,∴DP=AB=AO,∴四边形BPDO是平行四边形,又∵PO=AO,∴四边形ADPO是菱形. (5分)(2)∵DP ∥AB ,DP=AB=OB ,∠CPD=∠PBO ,在△CDP 与△POB 中,∴△CDP ≌△POB (4分)六、(10分×2=20分)25. 解:(1)∵△ADP 沿点A 旋转至△ABP ′,∴根据旋转的性质可知,△APD ≌△AP ′B ,∴AP=AP ′,∠PAD=∠P ′AB ,∵∠PAD+∠PAB=90°,∴∠P ′AB+∠PAB=90°,即∠PAP ′=90°,∴△APP ′是等腰直角三角形; (3分)(2)△BPP ′是直角三角形, 由(1)知∠PAP ′=90°,AP=AP ′=1,∴PP ′=,∵P ′B=PD=,PB=2,∴P ′B 2=PP ′2+PB 2,∴∠P ′PB=90°,∴△BPP ′是直角三角形. ∵△APP ′是等腰直角三角形,∴∠APP ′=45°,∴∠BPQ=180°﹣90°﹣45°=45°; (4分)(3)作BE ⊥AQ ,垂足为E ,∵∠BPQ=45°,PB=2,∴PE=BE=2,∴AE=2+1=3,∴AB== (3分)26. (1)∵y=﹣x+3与x 轴交于点A ,与y 轴交于点B ,∴当y=0时,x=3,即A 点坐标为(3,0),当x=0时,y=3,即B 点坐标为(0,3),将A (3,0),B (0,3)代入y=﹣x 2+bx+c ,得,解得∴抛物线的解析式为y=﹣x 2+2x+3; (3分)(2)∵OA=OB=3,∠BOA=90°,∴∠QAP=45°.如图①所示:∠PQA=90°时,设运动时间为t 秒,则QA=,PA=3﹣t .在Rt △PQA 中,,即:,解得:t=1;如图②所示:∠QPA=90°时,设运动时间为t 秒,则QA=,PA=3﹣t .在Rt △PQA 中,,即:,解得:t=. 综上所述,当t=1或t=时,△PQA 是直角三角形; (3分)(3)如图④所示:过点M 作ME ⊥y 轴于点E, 设运动时间为t 秒,则OP=t ,BQ=(3﹣t ). ∵y=﹣x 2+2x+3=﹣(x ﹣1)2+4,∴点M 的坐标为(1,4).又∵B 点坐标为(0,3)∴ME=BE=1,∴∠EBM=45°,∠QBM=90°MB==.当△BOP ∽△QBM时,即:,整理得:t 2﹣3t+3=0,△=32﹣4×1×3<0,无解:当△BOP ∽△MBQ 时,即:,解得t=. ∴当t=时,以B ,Q ,M 为顶点的三角形与 以O ,B ,P 为顶点的三角形相似. (4分)E。
景德镇市2016学年中考第三次质量检测数学试卷及答案

景德镇市2016学年第三次质量检测试卷九年级数学命题人:马小宇(景德镇二中)、余建华 审校人:刘倩 说 明:1.本卷共六大题,全卷共24题,满分120分,考试时间为120分钟2.本卷分为试题卷和答题卷,答案要求写在答题卷上,不得在试题卷上作答,否则不给分一、选择题(本大题共6小题,每小题3分,共18分)每题只有一个正确的选项 1.2,0,3中,大小在-1和2之间的数是:( ▲ )A ..-2 C .0 D .3 2.算式63)(5.010)-⋅⨯的结果用科学计数法表达正确的是( ▲ )A .31510⨯B .41510⨯C .31.510⨯D .41.510⨯ 3.如图是由6个相同的小立方块搭成的几何体,则下列说法正确的是( ▲ ) A .主视图的面积最大 B .俯视图的面积最大 C .左视图的面积最大 D .三个视图面积一样大4.关于x 的一元二次方程24sin 20x x α-⋅+=有两个等根,则锐角α的度数是( ▲ ) A .30° B .45° C .60° D .90°5.如图,⊙O 是△ABC 的内切圆,切点分别是D 、E 、F ,已知∠A=100°,∠C=30°,则 ∠DFE 的度数是( ▲ ) A .55° B .60° C .65° D .70°6.如图,在△ABC 中,点O 是△ABC 的角平分线的交点,过点O 作EF ∥BC 分别交AB 、AC 于点E 、F ,已知BC=a (a 是常数),设△ABC 的周长为y ,△AEF 的周长为x ,在下列图象中,大致表示y 与x 之间的函数关系的是( ▲ )A .B .C .D .二、填空题(本大题共6个小题,每小题3分,共18分) 7.分解因式:32a ab -= ▲ ; 8.分式方程211x x=-的解x= ▲ ; 9.在一次体检中,测得某小组5名同学的身高分别是:170,162,155, 160,168(单位:厘米),则这组数据的极差是 ▲ 厘米; 10.如图,Rt △ABC 中,∠ABC=90°,DE 垂直平分AC ,垂足为O , AD∥BC ,且AB=5,BC=12,则AD 的长为 ▲ ;第3题图第5题图第6题图ABC·OE F 第10题图11.如图,点A ,B 的坐标分别为(1,4) 和(4,4),抛物线2()y a x m n =++ 的顶点在线段AB 上,与x 轴交于C , D 两点(C 在D 的左侧),点C 的横 坐标最小值为-3,则点D 的横坐标 的最大值为 ▲ ;12.如图在Rt △ACB 中,C 为直角顶点, ∠ABC=25°,O 为斜边中点.将OA绕着点O 逆时针旋转θ°(0180θ<<)至OP ,当△BCP 恰为轴对称图形时,θ的值为 ▲ .三、解答题(本大题共5小题,每小题各6分,共30分)13. 解不等式组:110334(1)1x x +⎧-≥⎪⎨⎪+->⎩ .14.为了抓住景德镇瓷博会的商机,某商场决定购进甲、乙两种纪念品.若购进甲种纪念品1件,乙种纪念品2件,需要160元;购进甲种纪念品2件,乙种纪念品3件,需 要280元.问购进甲、乙两种纪念品每件各需要多少元?15.如图,已知在四边形ABCD 中,∠ADB=∠ACB ,延长 AD 、BC 相交于点E .求证:AC ·DE=BD ·CE .16.如图(甲、乙),AB 为半圆⊙1O 的直径,1AO 为半圆⊙2O 的直径,仅用无刻度的直 尺完成下列作图:(1)如图甲,C 为半圆⊙1O 上一点,请在半圆⊙1O 找个点D ,使得D 恰为 AC 的中点;(2)如图乙,E 为半圆⊙2O 上一点,请在半圆⊙2O 找个点F ,使得F 恰为 AE 的中点.17.中考前各校初三学生都要进行体育测试,某次中考体育测试设有A 、B 两处考点,甲、 乙、丙三名学生各自随机选择其中的一处进行中考体育测试,请用表格或树状图分析: (1)求甲、乙、丙三名学生在同一处进行体育测试的概率;(2)求甲、乙、丙三名学生中至少有两人在B 处进行体育测试的概率.甲图 乙图第12题图第11题图四、(本大题共4小题,每小题各8分,共32分) 18.为增强学生的身体素质,教育行政部门规定学生每天参加户外活动的平均时间不少于1 小时.为了解学生参加户外活动的情况,对部分学生参加户外活动的时间进行抽样调 查,并将调查结果绘制作成如下两幅不完整的统计图,请你根据图中提供的信息解答 下列问题:(1)一共调查了多少名学生; (2)请补全条形统计图;(3)若该校共有6000名学生, 根据以上调查结果估计 该校全体学生每天参与 户外活动所用的总时间.19.某厂家新开发的一种摩托车如图所示,它的大灯A 射出的光线AB 、AC 与地面MN 的 夹角分别为8°和10°,大灯A 离地面距离1m .(1)该车大灯照亮地面的宽度BC 约是多少(不考虑其它因素)?(2)一般正常人从发现危险到做出刹车动作的反应时间是0.2s ,从发现危险到摩托车完全停下所行驶的距离叫做最小安全距离,某人以60km /h 的速度驾驶该车,从60km /h 到摩托车停止的刹车距离是143m ,请判断该车大灯的设计是否能满足最小安全距离的要求,请说明理由. 参考数据:7sin 850︒≈,1tan 87︒≈,4sin1023︒≈,5tan1028︒≈.20.如图在平面直角坐标系中,直线l :124y x =+与y 轴交于点A ,与x 轴交于点B ,反比例函数2ky x=与直线l 交于点C ,且AB=2AC . (1)求反比例函数的解析式;(2)根据函数图象,直接写出120y y <<的x 的取值范围.21.小段同学看到一则材料,甲开汽车,乙骑自行车从M 地出发沿一条公路匀速前往N 地,设乙行驶的时间为t (h ),甲乙两人之间的距离为y (km ), y 与t 的函数关系如图1所示,小段思考后发现了图1的部分正确信息,乙先出发1h , 甲出发20分钟后与乙相遇,…,请你帮助小段同学解决以下问题: (1)分别求出线段BC ,CD 所在直线的函数表达式; (2)当15<y <25时,求t 的取值范围;(3)分别求出甲、乙行驶的路程S 甲、S 乙与时间t 的函数表达式,并在图2所给的直角坐标系中分别画出它们的图象.五、(本大题共1小题,每小题10分,共10分)22.定义{a ,b ,c }为函数2y ax bx c =++的“特征数”. (1)“特征数”为{-1,2,3}的函数解析式为 ▲ ,将“特征数”为{0,1,1}的函数向下平移两个单位以后得到的函数解析式为 ▲ ; (2)我们把横、纵坐标均为整数的点称为“整点”,试问:在上述两空填写的函数图象围成的封闭图形(包含边界)内共有多少个整点?请给出详细的运算过程; (3)定义“特征数”的运算:①{1a ,1b ,1c }+{2a ,2b ,2c }={12a a +,12b b +,12c c +};②λ·{1a ,1b ,1c }={1a λ,1b λ,1c λ}(其中λ为任意常数).试问:“特征数”为{﹣1,2,3}+λ·{0,1,﹣1}的函数是否过定点?如果过定点,请计算出该定点坐标;如果不存在,请说明你的理由. 六、(本大题共1小题,每小题12分,共12分)23.如图1,ABCD 为正方形,直线MN 分别过AD 边与BC 边的中点,点P 为直线MN上任意一点,连接PB 、PC 分别与AD 边交于E 、F 两点,PC 与BD 交于点K ,连接AK 与PB 交于点G .●探索发现 当点P 落在AD 边上时,如图2,试探究PB 与AK 的位置关系以及PB 、PK 、AK 三者的数量关系(直接写出无需证明);●延伸拓展 当点P 落在正方形外,如图1,以上两个结论是否仍然成立?如果成立请给出证明,如果不成立请说明你的理由;●应用推广 如图3,在等腰Rt △ABD 中,其中∠BAD=90°,腰长为3,M 、N 分别为AD 边与BD 边的中点,K 为线段DN 中点,F 为AD 边上靠近于D 的三等分点.连接KF 并延长与直线MN 交于点P ,连接PB 分别与AD 、AK 交于点E 、G .试求四边形EFKG 的周长及面积.C D 图1C D 图2 G M A B D P K F E N 图3景德镇市2016学年第三次质量检测试卷九年级数学答案一、选择题(本大题共6小题,每小题3分,共18分)二、填空题(本大题共6个小题,每小题3分,共18分) 7.a (a +b )(a -b ) 8. ﹣1 9. 15 10.16924; 11. 8 12.50°,65°,80° 三、解答题(本大题共5小题,每小题各6分,共30分) 13.解:122x <≤. 14.解:设甲商品x 元/件,乙商品y 元/件,根据题意, 得:216023280x y x y +=⎧⎨+=⎩,解得:8040x y =⎧⎨=⎩.答:购进甲种纪念品每件各需要80元,购进乙种纪念品每件各需要40元.15.证明:∵∠ADB=∠ACB ,∴∠EDB=∠ECA . 又∠E=∠E ,∴△ECA ∽△EDB . ∴AC CEBD DE=,即AC ·DE=BD ·CE .16.解:17.解:(1)画树状图为:共有8种等可能的结果数,其中甲、乙、丙三名学生在同一处进行体育测试的结果数为2,所以甲、乙、丙三名学生在同一处进行体育测试的概率2184P ==; (2)甲、乙、丙三名学生至少有两人在B 处进行体育测试的结果数为4,甲图 乙图所以甲、乙、丙三名学生至少有两人在B 处进行体育测试的概率4182P ==. 四、(本大题共4小题,每小题各8分,共32分) 18.解:(1)调查的总人数是:10÷20%=50(人);(2)参加户外活动时间是1.5小时的人数是:50-10-20-8=12(人); (3)该校户外活动的平均时间是:0.510120 1.512281.1850⨯+⨯+⨯+⨯=(小时).该校全体学生每天参与户外互动所用的总时间:6000×1.18=7080(小时).19.解:(1)过A 作AD ⊥MN 于点D ,在Rt △ACD 中,5tan 28AD ACD CD ∠==,CD=5.6(m ), 在Rt △ABD 中,1tan 7AD ABD BD ∠==,BD=7(m ), ∴BC=7-5.6=1.4(m ).答:该车大灯照亮地面的宽度BC 是1.4m ;(2)该车大灯的设计不能满足最小安全距离的要求.理由如下: ∵以5060//3km h m s =的速度驾驶,最小安全距离为:50140.2833⨯+=(m ), 而大灯能照到的最远距离是BD=7m ,∴该车大灯的设计不能满足最小安全距离的要求.20.解:(1)如图,过点C 作CH ⊥y 轴,垂足为H . 把x=0代入124y x =+,得:y=4,把y=0代入124y x =+,得:x=﹣2, ∴A 点坐标为(0,4),B 点坐标为(﹣2,0),MN B C A D∴OB=2,OA=4.∵OB ∥CH ,∴△ABO ∽△ACH , ∴2OA OB AB AH CH AC ===,即422AH CH==, 解得AH=2,CH=1,∴OH=6,∴点C 坐标为(1,6). 把点C 坐标代入反比例函数解析式,得:k=6, ∴反比例函数的解析式为:6y x=. (2)∵点C 坐标为(1,6),∴由图象可知,120y y <<时的x 范围是:0<x <1.21.解:(1)设线段BC 所在直线的函数解析式为:11y k t b =+, 将点B (43,0),点C (2,30)代入解析式,得: 1111114450360230k k b b k b ⎧=+=⎧⎪⇒⎨⎨=-⎩⎪+=⎩ . 故线段BC 所在直线的函数解析式为:y=45t -60(423t ≤≤). 设线段CD 所在直线的函数解析式为:22y k t b =+, 将点C (2,30),点D (4,0)代入解析式,得: 222222230154060k b k k b b +==-⎧⎧⇒⎨⎨+==⎩⎩ . 故线段CD 所在直线的函数解析式为:y=﹣15t +60(24t <≤).(2)乙骑车的速度为30÷(4-2)=15(km/h ),∴线段OA 所在的直线的函数表达式为y=15t (0≤t ≤1), ∴点A 的纵坐标为15.当15<y <25时,即15<45t -60<25或15<﹣15t +60<25,解得:51739t <<或733t <<. 故当15<y <25时,t 的取值范围为51739t <<或733t <<. (3)甲开车的速度:15÷(413-)+15=60(km/h ), ∴60(1)6060S t t =-=-甲(1≤t ≤2),15S t =乙(0≤t ≤4).所画图形如图:五、(本大题共1小题,每小题10分,共10分) 22.解:(1)223y x x =-++,1y x =-; (2)联立直线与二次函数方程2223401y x x x x y x ⎧=-++⇒--=⎨=-⎩1122A B x x +⇒==, 估算21,23A B x x -<<-<<.横坐标为﹣1的整点有(﹣1,0)(﹣1横坐标为0的整点有(0,3)(0,2)(0横坐标为1的整点有(1,4)(1,3)(1 横坐标为2的整点有(2,3)(2,2)(2合计,共16个整点;(3)依据定义,{﹣1,2,3}+λ·{0,1,﹣1}={-1,2+λ,3-λ},∴该函数解析式为:22(2)3(23)(1)y x x x x x λλλ=-+++-=-+++-, 令x -1=0,即x=1,解得:y=4,∴该函数始终过定点(1,4).六、(本大题共1小题,每小题12分,共12分)23.解:●探索发现 PB ⊥AK ,PB=PK +AK ; ●延伸拓展 以上两个结论仍然成立,理由如下: ∵点P 在MN 上,根据对称性易得∠1=∠2且PB=PC , 又∠ABK=∠CBK=45°,BA=BC ,BK=BK , ∴△ABK ≌△CBK ,于是∠2=∠3且AK=CK , ∴∠1=∠3. 又∠1+∠4=90°,∴∠3+∠4=90°,即PB ⊥AK .∴PB=PC=PK +CK=PK +AK .C D 图1●应用推广过点B 作AD 的平行线交PK 延长线与点C ,连接CD . ∵FD ∥BD ,∴△FDK ∽△CBK .又DK ︰BK=1︰3,∴FD ︰BC=1︰3. 而FD ︰AD=1︰3,于是BC=AD . 又BC ∥AD 且AB ⊥AD 且AB=AD , ∴四边形ABCD 为正方形.由上一问可知:PB=PK +AK ,即(PE +BE )=(PF +FK )+AK ,又PE=PF , ∴BE= FK +AK .在Rt △EAB 中,AE=1,AB=3,根据勾股定理BE =又AG ⊥BE (上一问结论),易证Rt △AGE ∽Rt △BGA ,且相似比为1:3,设EG=t ,AG=3t ,BG=9t ,∴BE=10t =∴四边形EFKG 的周长=EF +FK +GK +EG=EF +(FK +AK )-AG +EG=EF +BE -AG +EG=1+10t -3t +t=1+8t=1+过点K 作AD 垂线,垂足为H ,易知HK ∥AB 且DK :DB=1:4, ∴1344KH AB ==. 111312322242EFKG AFK AEG S S S AF KH AG EG t t∆∆=-=⋅⋅-⋅⋅=⋅⋅-⋅⋅ 3334205=-=.GM AB DPKF E N图3 CH。
江西省景德镇市中考数学三模试卷

.
(2)如果小明将“求助”留在第二题使用,请用树状图或者列表来分析小明顺利通关的概
率.
(3)从概率的角度分析,你建议小明在第几题使用“求助”.(直接写出答案)
四、(本大题共 2 小题,每小题各 8 分,共 24 分)
18.(8 分)如图 1,是全国最大的瓷碗造型建筑坐落于江西景德镇,整体造型概念来自“宋
1.D; 2.A; 3.C; 4.B; 5.C; 6.B;
二、填空题(本大题共 6 个小题,每小题 3 分,共 18 分)
7.5.24×106; 8.2; 9.20; 10.
; 11.
; 12.
;
三、解答题(本大题共 5 小题,每小题各 6 分,共 30 分)
13.
; 14. 相似的是( )
A.∠DAC=∠ABC C.AC2=BC•CD
B.AC 是∠BCD 的平分线 D. =
第1页(共8页)
6.(3 分)如图,在直角坐标系中,直线
分别与 x 轴、y 轴交于点 M、N,点 A、
B 分别在 y 轴、x 轴上,且∠ABO=30°,AB=4,将△ABO 绕原点 O 顺时针旋转 180°, 在旋转过程中,当 AB 与直线 MN 平行时点 A 的坐标为( )
第3页(共8页)
17.(6 分)小明参加某个智力竞答节目,答对最后两道单选题就顺利通关.第一道单选题
有 3 个选项,第二道单选题有 4 个选项,这两道题小明都不会,不过小明还有一个“求
助”没有用(使用“求助”可以让主持人去掉其中一题的一个错误选项).
(1)如果小明第一题不使用“求助”,那么小明答对第一道题的概率是
A.(1, )
B.( ,1)
C.( ,﹣1) D.(1, )
江西省景德镇市中考数学三模考试试卷

江西省景德镇市中考数学三模考试试卷姓名:________ 班级:________ 成绩:________一、选择题(每小题2分,共12分) (共6题;共12分)1. (2分) (2022七上·滨江期末) 计算下列各式,值最小的是()A .B .C .D .2. (2分)(2019·荆门模拟) 由6个大小相同的正方体搭成的几何体如图所示,则关于它的视图说法正确的是()A . 正视图的面积最大B . 左视图的面积最大C . 俯视图的面积最大D . 三个视图的面积一样大3. (2分)下列何者是0.000 815的科学记号()A . 8.15×10-3B . 8.15×10-4C . 815×10-3D . 815×10-64. (2分)下列多项式中不能用平方差公式分解的是()A . a2-b2B . -x2-y2C . 49x2-y2z2D . 16m4n2-25p25. (2分)(2018·台湾) 如图1的矩形ABCD中,有一点E在AD上,今以BE为折线将A点往右折,如图2所示,再作过A点且与CD垂直的直线,交CD于F点,如图3所示,若AB=6 ,BC=13,∠BEA=60°,则图3中AF的长度为何?()A . 2B . 4C . 2D . 46. (2分)已知P为⊙O外一点,PA,PB为⊙O的切线,A、B为切点,∠P=70°,C为⊙O上一个动点,且不与A、B重合,则∠BCA=()A . 35°、145°B . 110°、70°C . 55°、125°D . 110°二、填空题(每小题3分,共24分) (共8题;共24分)7. (3分)(2014·河南) 计算:﹣|﹣2|=________.8. (3分) (2019七上·宁波期中) 小明组织同学去看电影《我和我的祖国》,电影票原价每张元,活动期间打八折,他们共花了1200元,则电影票共买了________张.(用含的代数式表示)9. (3分) (2018九上·长春开学考) 关于的一元二次方程有实数解,那么实数的取值范围是________.10. (3分) (2017八上·武汉期中) 如图,自行车的三角形支架,这是利用三角形具有________性.11. (3分) (2019九上·南海期末) 如图,现有测试距离为5m的一张视力表,表上一个E的高AB为2cm,要制作测试距离为3m的视力表,其对应位置的E的高CD为________cm.12. (3分)(2018·绍兴) 等腰三角形ABC中,顶角A为40°,点P在以A为圆心,BC长为半径的圆上,且BP=BA,则∠PBC的度数为________。
景德镇市2018学年第三次质量检测试卷九年级数学标准答案

景德镇市2018学年第三次质量检测试卷九年级数学答案一、选择题(本大题共6小题,每小题3分,共18分)二、填空题(本大题共6个小题,每小题3分,共18分) 7.a (a +b )(a -b ) 8. ﹣1 9. 15 10.16924; 11. 8 12.50°,65°,80° 三、解答题(本大题共5小题,每小题各6分,共30分) 13.解:122x <≤. 14.解:设甲商品x 元/件,乙商品y 元/件,根据题意,得:216023280x y x y +=⎧⎨+=⎩,解得:8040x y =⎧⎨=⎩.答:购进甲种纪念品每件各需要80元,购进乙种纪念品每件各需要40元.15.证明:∵∠ADB=∠ACB ,∴∠EDB=∠ECA . 又∠E=∠E ,∴△ECA ∽△EDB . ∴AC CEBD DE=,即AC ·DE=BD ·CE .16.解:17.解:(1)画树状图为:共有8种等可能的结果数,其中甲、乙、丙三名学生在同一处进行体育测试的结果数为2,甲图 乙图所以甲、乙、丙三名学生在同一处进行体育测试的概率2184P ==; (2)甲、乙、丙三名学生至少有两人在B 处进行体育测试的结果数为4, 所以甲、乙、丙三名学生至少有两人在B 处进行体育测试的概率4182P ==. 四、(本大题共4小题,每小题各8分,共32分) 18.解:(1)调查的总人数是:10÷20%=50(人);(2)参加户外活动时间是1.5小时的人数是:50-10-20-8=12(人); (3)该校户外活动的平均时间是:0.510120 1.512281.1850⨯+⨯+⨯+⨯=(小时).该校全体学生每天参与户外互动所用的总时间:6000×1.18=7080(小时).19.解:(1)过A 作AD ⊥MN 于点D ,在Rt △ACD 中,5tan 28AD ACD CD ∠==,CD=5.6(m ), 在Rt △ABD 中,1tan 7AD ABD BD ∠==,BD=7(m ), ∴BC=7-5.6=1.4(m ).答:该车大灯照亮地面的宽度BC 是1.4m ;(2)该车大灯的设计不能满足最小安全距离的要求.理由如下: ∵以5060//3km h m s =的速度驾驶,最小安全距离为:50140.2833⨯+=(m ), 而大灯能照到的最远距离是BD=7m ,∴该车大灯的设计不能满足最小安全距离的要求.20.解:(1)如图,过点C 作CH ⊥y 轴,垂足为H .M N B C A D把x=0代入124y x =+,得:y=4,把y=0代入124y x =+,得:x=﹣2, ∴A 点坐标为(0,4),B 点坐标为(﹣2,0), ∴OB=2,OA=4.∵OB ∥CH ,∴△ABO ∽△ACH , ∴2OA OB AB AH CH AC ===,即422AH CH==, 解得AH=2,CH=1,∴OH=6,∴点C 坐标为(1,6). 把点C 坐标代入反比例函数解析式,得:k=6, ∴反比例函数的解析式为:6y x=. (2)∵点C 坐标为(1,6),∴由图象可知,120y y <<时的x 范围是:0<x <1.21.解:(1)设线段BC 所在直线的函数解析式为:11y k t b =+, 将点B (43,0),点C (2,30)代入解析式,得: 1111114450360230k k b b k b ⎧=+=⎧⎪⇒⎨⎨=-⎩⎪+=⎩ . 故线段BC 所在直线的函数解析式为:y=45t -60(423t ≤≤). 设线段CD 所在直线的函数解析式为:22y k t b =+, 将点C (2,30),点D (4,0)代入解析式,得: 222222230154060k b k k b b +==-⎧⎧⇒⎨⎨+==⎩⎩ . 故线段CD 所在直线的函数解析式为:y=﹣15t +60(24t <≤).(2)乙骑车的速度为30÷(4-2)=15(km/h ),∴线段OA 所在的直线的函数表达式为y=15t (0≤t ≤1), ∴点A 的纵坐标为15.当15<y <25时,即15<45t -60<25或15<﹣15t +60<25,解得:1719t <<或733t <<.故当5<y <25时,t 的取值范围为1719t <<或733t <<. (3)甲开车的速度:15÷(413-)+15=60(km/h ), ∴60(1)6060S t t =-=-甲(1≤t ≤2),15S t =乙(0≤t ≤4).所画图形如图:五、(本大题共1小题,每小题10分,共10分) 22.解:(1)223y x x =-++,1y x =-; (2)联立直线与二次函数方程2223401y x x x x y x ⎧=-++⇒--=⎨=-⎩A B x x ⇒==, 估算21,23A B x x -<<-<<.横坐标为﹣1的整点有(﹣1,0)(﹣1横坐标为0的整点有(0,3)(0,2)(0 横坐标为1的整点有(1,4)(1,3)(1 横坐标为2的整点有(2,3)(2,2)(2合计,共16个整点;(3)依据定义,{﹣1,2,3}+λ·{0,1,﹣1}={-1,2+λ,3-λ},∴该函数解析式为:22(2)3(23)(1)y x x x x x λλλ=-+++-=-+++-, 令x -1=0,即x=1,解得:y=4,∴该函数始终过定点(1,4).六、(本大题共1小题,每小题12分,共12分) 23.解:●探索发现 PB ⊥AK ,PB=PK +AK ;●延伸拓展 以上两个结论仍然成立,理由如下:D∵点P 在MN 上,根据对称性易得∠1=∠2且PB=PC , 又∠ABK=∠CBK=45°,BA=BC ,BK=BK , ∴△ABK ≌△CBK ,于是∠2=∠3且AK=CK , ∴∠1=∠3. 又∠1+∠4=90°,∴∠3+∠4=90°,即PB ⊥AK . ∴PB=PC=PK +CK=PK +AK . ●应用推广 过点B 作AD 的平行线交PK 延长线与点C ,连接CD. ∵FD ∥BD ,∴△FDK ∽△CBK .又DK ︰BK=1︰3,∴FD ︰BC=1︰3. 而FD ︰AD=1︰3,于是BC=AD . 又BC ∥AD 且AB ⊥AD 且AB=AD , ∴四边形ABCD 为正方形.由上一问可知:PB=PK +AK ,即(PE +BE )=(PF +FK )+AK ,又PE=PF , ∴BE= FK +AK . 在Rt △EAB 中,AE=1,AB=3,根据勾股定理BE =又AG ⊥BE (上一问结论),易证Rt △AGE ∽Rt △BGA ,且相似比为1:3,设EG=t ,AG=3t ,BG=9t ,∴BE=10t =∴四边形EFKG 的周长=EF +FK +GK +EG=EF +(FK +AK )-AG +EG=EF +BE -AG +EG=1+10t -3t +t=1+8t=1+. 过点K 作AD 垂线,垂足为H ,易知HK ∥AB 且DK :DB=1:4, ∴1344KH AB ==. 111312322242EFKG AFK AEG S S S AF KH AG EG t t∆∆=-=⋅⋅-⋅⋅=⋅⋅-⋅⋅ 3334205=-=. GM AB DP KF E N图3CH。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
景德镇市2016学年第三次质量检测试卷九年级数学命题人:马小宇(景德镇二中)、余建华 审校人:刘倩 说 明:1.本卷共六大题,全卷共24题,满分120分,考试时间为120分钟2.本卷分为试题卷和答题卷,答案要求写在答题卷上,不得在试题卷上作答,否则不给分一、选择题(本大题共6小题,每小题3分,共18分)每题只有一个正确的选项 1.2,0,3中,大小在-1和2之间的数是:( ▲ )A ..-2 C .0 D .3 2.算式63)(5.010)-⋅⨯的结果用科学计数法表达正确的是( ▲ )A .31510⨯B .41510⨯C .31.510⨯D .41.510⨯ 3.如图是由6个相同的小立方块搭成的几何体,则下列说法正确的是( ▲ ) A .主视图的面积最大 B .俯视图的面积最大 C .左视图的面积最大 D .三个视图面积一样大4.关于x 的一元二次方程24sin 20x x α-⋅+=有两个等根,则锐角α的度数是( ▲ ) A .30° B .45° C .60° D .90°5.如图,⊙O 是△ABC 的内切圆,切点分别是D 、E 、F ,已知∠A=100°,∠C=30°,则 ∠DFE 的度数是( ▲ ) A .55° B .60° C .65° D .70°6.如图,在△ABC 中,点O 是△ABC 的角平分线的交点,过点O 作EF ∥BC 分别交AB 、AC 于点E 、F ,已知BC=a (a 是常数),设△ABC 的周长为y ,△AEF 的周长为x ,在下列图象中,大致表示y 与x 之间的函数关系的是( ▲ )A .B .C .D .二、填空题(本大题共6个小题,每小题3分,共18分) 7.分解因式:32a ab -= ▲ ; 8.分式方程211x x=-的解x= ▲ ; 9.在一次体检中,测得某小组5名同学的身高分别是:170,162,155, 160,168(单位:厘米),则这组数据的极差是 ▲ 厘米; 10.如图,Rt △ABC 中,∠ABC=90°,DE 垂直平分AC ,垂足为O , AD ∥BC ,且AB=5,BC=12,则AD的长为 ▲ ; 11.如图,点A ,B 的坐标分别为(1,4)第3题图第5题图第6题图ABC·OE F 第10题图和(4,4),抛物线2()y a x m n =++ 的顶点在线段AB 上,与x 轴交于C , D 两点(C 在D 的左侧),点C 的横 坐标最小值为-3,则点D 的横坐标 的最大值为 ▲ ;12.如图在Rt △ACB 中,C 为直角顶点, ∠ABC=25°,O 为斜边中点.将OA绕着点O 逆时针旋转θ°(0180θ<<)至OP ,当△BCP 恰为轴对称图形时,θ的值为 ▲ .三、解答题(本大题共5小题,每小题各6分,共30分)13. 解不等式组:110334(1)1x x +⎧-≥⎪⎨⎪+->⎩ .14.为了抓住景德镇瓷博会的商机,某商场决定购进甲、乙两种纪念品.若购进甲种纪念品1件,乙种纪念品2件,需要160元;购进甲种纪念品2件,乙种纪念品3件,需 要280元.问购进甲、乙两种纪念品每件各需要多少元?15.如图,已知在四边形ABCD 中,∠ADB=∠ACB ,延长 AD 、BC 相交于点E .求证:AC ·DE=BD ·CE .16.如图(甲、乙),AB 为半圆⊙1O 的直径,1AO 为半圆⊙2O 的直径,仅用无刻度的直 尺完成下列作图:(1)如图甲,C 为半圆⊙1O 上一点,请在半圆⊙1O 找个点D ,使得D 恰为AC 的中点; (2)如图乙,E 为半圆⊙2O 上一点,请在半圆⊙2O 找个点F ,使得F 恰为AE 的中点.17.中考前各校初三学生都要进行体育测试,某次中考体育测试设有A 、B 两处考点,甲、 乙、丙三名学生各自随机选择其中的一处进行中考体育测试,请用表格或树状图分析: (1)求甲、乙、丙三名学生在同一处进行体育测试的概率;(2)求甲、乙、丙三名学生中至少有两人在B 处进行体育测试的概率. 四、(本大题共4小题,每小题各8分,共32分)甲图 乙图18.为增强学生的身体素质,教育行政部门规定学生每天参加户外活动的平均时间不少于1 小时.为了解学生参加户外活动的情况,对部分学生参加户外活动的时间进行抽样调 查,并将调查结果绘制作成如下两幅不完整的统计图,请你根据图中提供的信息解答 下列问题:(1)一共调查了多少名学生; (2)请补全条形统计图;(3)若该校共有6000名学生, 根据以上调查结果估计 该校全体学生每天参与 户外活动所用的总时间.19.某厂家新开发的一种摩托车如图所示,它的大灯A 射出的光线AB 、AC 与地面MN 的 夹角分别为8°和10°,大灯A 离地面距离1m .(1)该车大灯照亮地面的宽度BC 约是多少(不考虑其它因素)?(2)一般正常人从发现危险到做出刹车动作的反应时间是0.2s ,从发现危险到摩托车完全停下所行驶的距离叫做最小安全距离,某人以60km /h 的速度驾驶该车,从60km /h 到摩托车停止的刹车距离是143m ,请判断该车大灯的设计是否能满足最小安全距离的要求,请说明理由. 参考数据:7sin 850︒≈,1tan 87︒≈,4sin1023︒≈,5tan1028︒≈.20.如图在平面直角坐标系中,直线l :124y x =+与y 轴交于点A ,与x 轴交于点B ,反比例函数2ky x=与直线l 交于点C ,且AB=2AC . (1)求反比例函数的解析式;(2)根据函数图象,直接写出120y y <<的x 的取值范围.21.小段同学看到一则材料,甲开汽车,乙骑自行车从M 地出发沿一条公路匀速前往N 地,设乙行驶的时间为t (h ),甲乙两人之间的距离为y (km ), y 与t 的函数关系如图1所示,小段思考后发现了图1的部分正确信息,乙先出发1h , 甲出发20分钟后与乙相遇,…,请你帮助小段同学解决以下问题: (1)分别求出线段BC ,CD 所在直线的函数表达式; (2)当15<y <25时,求t 的取值范围;(3)分别求出甲、乙行驶的路程S 甲、S 乙与时间t 的函数表达式,并在图2所给的直角坐标系中分别画出它们的图象.五、(本大题共1小题,每小题10分,共10分)22.定义{a ,b ,c }为函数2y ax bx c =++的“特征数”. (1)“特征数”为{-1,2,3}的函数解析式为 ▲ ,将“特征数”为{0,1,1}的函数向下平移两个单位以后得到的函数解析式为 ▲ ; (2)我们把横、纵坐标均为整数的点称为“整点”,试问:在上述两空填写的函数图象围成的封闭图形(包含边界)内共有多少个整点?请给出详细的运算过程; (3)定义“特征数”的运算:①{1a ,1b ,1c }+{2a ,2b ,2c }={12a a +,12b b +,12c c +};②λ·{1a ,1b ,1c }={1a λ,1b λ,1c λ}(其中λ为任意常数).试问:“特征数”为{﹣1,2,3}+λ·{0,1,﹣1}的函数是否过定点?如果过定点,请计算出该定点坐标;如果不存在,请说明你的理由. 六、(本大题共1小题,每小题12分,共12分)23.如图1,ABCD 为正方形,直线MN 分别过AD 边与BC 边的中点,点P 为直线MN上任意一点,连接PB 、PC 分别与AD 边交于E 、F 两点,PC 与BD 交于点K ,连接AK 与PB 交于点G .●探索发现 当点P 落在AD 边上时,如图2,试探究PB 与AK 的位置关系以及PB 、PK 、AK 三者的数量关系(直接写出无需证明);●延伸拓展 当点P 落在正方形外,如图1,以上两个结论是否仍然成立?如果成立请给出证明,如果不成立请说明你的理由;●应用推广 如图3,在等腰Rt △ABD 中,其中∠BAD=90°,腰长为3,M 、N 分别为AD 边与BD 边的中点,K 为线段DN 中点,F 为AD 边上靠近于D 的三等分点.连接KF 并延长与直线MN 交于点P ,连接PB 分别与AD 、AK 交于点E 、G .试求四边形EFKG 的周长及面积.景德镇市2016学年第三次质量检测试卷九年级数学答案C D 图1C D 图2 G M A B D P K F E N 图3一、选择题(本大题共6小题,每小题3分,共18分)二、填空题(本大题共6个小题,每小题3分,共18分) 7.a (a +b )(a -b ) 8. ﹣1 9. 15 10.16924; 11. 8 12.50°,65°,80° 三、解答题(本大题共5小题,每小题各6分,共30分) 13.解:122x <≤. 14.解:设甲商品x 元/件,乙商品y 元/件,根据题意, 得:216023280x y x y +=⎧⎨+=⎩,解得:8040x y =⎧⎨=⎩.答:购进甲种纪念品每件各需要80元,购进乙种纪念品每件各需要40元.15.证明:∵∠ADB=∠ACB ,∴∠EDB=∠ECA . 又∠E=∠E ,∴△ECA ∽△EDB . ∴AC CEBD DE=,即AC ·DE=BD ·CE .16.解:17.解:(1)画树状图为:共有8种等可能的结果数,其中甲、乙、丙三名学生在同一处进行体育测试的结果数为2,所以甲、乙、丙三名学生在同一处进行体育测试的概率2184P ==; (2)甲、乙、丙三名学生至少有两人在B 处进行体育测试的结果数为4, 所以甲、乙、丙三名学生至少有两人在B 处进行体育测试的概率4182P ==. 四、(本大题共4小题,每小题各8分,共32分)甲图 乙图18.解:(1)调查的总人数是:10÷20%=50(人);(2)参加户外活动时间是1.5小时的人数是:50-10-20-8=12(人); (3)该校户外活动的平均时间是:0.510120 1.512281.1850⨯+⨯+⨯+⨯=(小时).该校全体学生每天参与户外互动所用的总时间:6000×1.18=7080(小时).19.解:(1)过A 作AD ⊥MN 于点D ,在Rt △ACD 中,5tan 28AD ACD CD ∠==,CD=5.6(m ), 在Rt △ABD 中,1tan 7AD ABD BD ∠==,BD=7(m ), ∴BC=7-5.6=1.4(m ).答:该车大灯照亮地面的宽度BC 是1.4m ;(2)该车大灯的设计不能满足最小安全距离的要求.理由如下: ∵以5060//3km h m s =的速度驾驶,最小安全距离为:50140.2833⨯+=(m ), 而大灯能照到的最远距离是BD=7m ,∴该车大灯的设计不能满足最小安全距离的要求.20.解:(1)如图,过点C 作CH ⊥y 轴,垂足为H . 把x=0代入124y x =+,得:y=4,把y=0代入124y x =+,得:x=﹣2, ∴A 点坐标为(0,4),B 点坐标为(﹣2,0),∴OB=2,OA=4.∵OB ∥CH ,∴△ABO ∽△ACH ,MN B C A D∴2OA OB AB AH CH AC ===,即422AH CH==, 解得AH=2,CH=1,∴OH=6,∴点C 坐标为(1,6). 把点C 坐标代入反比例函数解析式,得:k=6, ∴反比例函数的解析式为:6y x=. (2)∵点C 坐标为(1,6),∴由图象可知,120y y <<时的x 范围是:0<x <1.21.解:(1)设线段BC 所在直线的函数解析式为:11y k t b =+, 将点B (43,0),点C (2,30)代入解析式,得: 1111114450360230k k b b k b ⎧=+=⎧⎪⇒⎨⎨=-⎩⎪+=⎩ . 故线段BC 所在直线的函数解析式为:y=45t -60(423t ≤≤). 设线段CD 所在直线的函数解析式为:22y k t b =+, 将点C (2,30),点D (4,0)代入解析式,得: 222222230154060k b k k b b +==-⎧⎧⇒⎨⎨+==⎩⎩ . 故线段CD 所在直线的函数解析式为:y=﹣15t +60(24t <≤).(2)乙骑车的速度为30÷(4-2)=15(km/h ),∴线段OA 所在的直线的函数表达式为y=15t (0≤t ≤1), ∴点A 的纵坐标为15.当15<y <25时,即15<45t -60<25或15<﹣15t +60<25,解得:51739t <<或733t <<. 故当15<y <25时,t 的取值范围为51739t <<或733t <<. (3)甲开车的速度:15÷(413-)+15=60(km/h ), ∴60(1)6060S t t =-=-甲(1≤t ≤2),15S t =乙(0≤t ≤4).所画图形如图:五、(本大题共1小题,每小题10分,共10分) 22.解:(1)223y x x =-++,1y x =-; (2)联立直线与二次函数方程2223401y x x x x y x ⎧=-++⇒--=⎨=-⎩1122A B x x +⇒==, 估算21,23A B x x -<<-<<.横坐标为﹣1的整点有(﹣1,0)(﹣1横坐标为0的整点有(0,3)(0,2)(0横坐标为1的整点有(1,4)(1,3)(1 横坐标为2的整点有(2,3)(2,2)(2合计,共16个整点;(3)依据定义,{﹣1,2,3}+λ·{0,1,﹣1}={-1,2+λ,3-λ},∴该函数解析式为:22(2)3(23)(1)y x x x x x λλλ=-+++-=-+++-, 令x -1=0,即x=1,解得:y=4,∴该函数始终过定点(1,4).六、(本大题共1小题,每小题12分,共12分)23.解:●探索发现 PB ⊥AK ,PB=PK +AK ; ●延伸拓展 以上两个结论仍然成立,理由如下: ∵点P 在MN 上,根据对称性易得∠1=∠2且PB=PC , 又∠ABK=∠CBK=45°,BA=BC ,BK=BK , ∴△ABK ≌△CBK ,于是∠2=∠3且AK=CK , ∴∠1=∠3. 又∠1+∠4=90°,∴∠3+∠4=90°,即PB ⊥AK .∴PB=PC=PK +CK=PK +AK .C D 图1●应用推广过点B 作AD 的平行线交PK 延长线与点C ,连接CD . ∵FD ∥BD ,∴△FDK ∽△CBK .又DK ︰BK=1︰3,∴FD ︰BC=1︰3. 而FD ︰AD=1︰3,于是BC=AD . 又BC ∥AD 且AB ⊥AD 且AB=AD , ∴四边形ABCD 为正方形.由上一问可知:PB=PK +AK ,即(PE +BE )=(PF +FK )+AK ,又PE=PF , ∴BE= FK +AK .在Rt △EAB 中,AE=1,AB=3,根据勾股定理BE =又AG ⊥BE (上一问结论),易证Rt △AGE ∽Rt △BGA ,且相似比为1:3,设EG=t ,AG=3t ,BG=9t ,∴BE=10t =∴四边形EFKG 的周长=EF +FK +GK +EG=EF +(FK +AK )-AG +EG=EF +BE -AG +EG=1+10t -3t +t=1+8t=1+过点K 作AD 垂线,垂足为H ,易知HK ∥AB 且DK :DB=1:4, ∴1344KH AB ==. 111312322242EFKG AFK AEG S S S AF KH AG EG t t∆∆=-=⋅⋅-⋅⋅=⋅⋅-⋅⋅ 3334205=-=.GM AB DPKF E N图3 CH。
