河北省唐山市丰南区2018届九年级数学下学期期中试题答案
河北省唐山市丰南区2018届九年级数学第二次模拟试题答
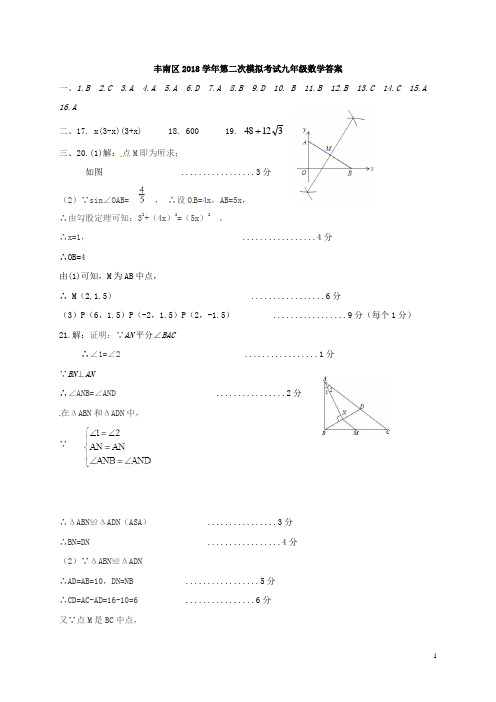
丰南区2018学年第二次模拟考试九年级数学答案一、1.B 2.C 3.A 4.A 5.A 6.D 7.A 8.B 9.D 10. B 11.B 12.B 13.C 14.C 15.A16.A二、17. x(3-x)(3+x) 18. 600 19. 31248三、20.(1)解:点M 即为所求;如图 .................3分(2)∵sin ∠OAB= , ∴设O B=4x ,AB=5x ,∴由勾股定理可知:32+(4x )2=(5x )2 ,∴x=1, .................4分∴OB=4由(1)可知,M 为AB 中点,∴ M (2,1.5) .................6分(3)P (6,1.5)P (-2,1.5)P (2,-1.5) .................9分(每个1分)21.解:证明:∵AN 平分∠BAC∴∠1=∠2 .................1分∵BN ⊥AN∴∠ANB=∠AND ................2分在ΔABN 和ΔADN 中,∵∴ΔABN ≌ΔADN (ASA ) ................3分∴BN=DN .................4分(2)∵ΔABN ≌ΔADN∴AD=AB=10,DN=NB .................5分∴CD=AC-AD=16-10=6 ................6分又∵点M 是BC 中点,22. 解:(1)第二条边:2a+3 第三条边:38-a-(2a+3)=35-3a ................2分(2) 由三边关系可知⎩⎨⎧+〉-+-〉++3233533532a a a a a a ................3分解得:8315〈〈a ................4分∵a ≠2a+3 ∴分两种情况:①a=35-3a a=438 不符合三边关系 舍去 ................5分 ②2a+3=35-3a a=526 符合三边关系 ................6分 ∴a=526 (3)不能为直角三角形 ................7分.理由:∵8315〈〈a 且a 为整数 ∴a=6或7当a=6时,三边为:6、15、17,22217156≠+,不是直角三角形; ................8分当a=7时,三边为:7、17、14,22217147≠+,不是直角三角形. ................9分 23. 解:(1)对比甲乙的直方图可得:乙在整理数据时漏了一个数据,它在169.5--174.5内;(答案不唯一) ................2分(2)120°; ................4分(3)160或161;(160,161,160.5也给分) ................6分(4) ................7分分 分在甲地游玩的时间是1-0.5=0.5(h ). ................2分(2)妈妈驾车速度:20×3=60(km/h )设直线BC 解析式为y=20x+b 1,把点B (1,10)代入得b 1=-10∴y=20x-10 ................3分代入得b 2=-80∴y=60x-80 ................4分解⎩⎨⎧-=-=80601020x y x y 得:⎩⎨⎧==2575.1y x ∴交点F (1.75,25). ................5分答:小明出发1.75小时(105分钟)被妈妈追上,此时离家25km . ................6分 (3)设从家到乙地的路程为skm.分 解得:s=30答:从家到乙地的路程为30km. (方法不唯一) ................10分25.解:∵BD 是矩形ABCD 的对角线,∠ABD =30°∴∠ADB=60°,由平移可得,B'C'=BC=AD ,∠D'B'C'=∠DBC=∠ADB=60°,∴AD ∥B'C' ................1分 ∴四边形AB'C'D 是平行四边形, ................2分∵B'为BD 中点,∴Rt △ABD 中,AB'=错误!未找到引用源。
河北省唐山市九年级下学期期中数学试卷

河北省唐山市九年级下学期期中数学试卷姓名:________ 班级:________ 成绩:________一、选择题 (共6题;共12分)1. (2分) (2016高一下·锦屏期末) 如果a是有理数,则下列判断中正确的是()A . -a是负数B . |a|是正数C . |a|不是负数D . -|a|不是负数2. (2分) (2020九下·凤县月考) 计算: ()A .B .C . 2D . -23. (2分)(2017·平南模拟) 一个几何体如图所示,则该几何体的三视图正确的是()A .B .C .D .4. (2分)等腰三角形的周长为13cm,其中一边长为3cm,则该等腰三角形的底边为()A . 7cmB . 8cmC . 7cm或3cmD . 3cm5. (2分)在Rt△ABC中,∠C=90°,AB=4,S△ABC=,则tanA+tanB=()A .B .C .D . 46. (2分)(2017·黑龙江模拟) 如图,为了测量某棵树的高度,小明用长为2m的竹竿作测量工具,移动竹竿,使竹竿顶端的影子与树的顶端的影子恰好落在地面的同一点.此时竹竿与这一点相距5m,与树相距10m,则树的高度为()A . 5mB . 6mC . 7mD . 8m二、填空题 (共10题;共11分)7. (1分)(2011·嘉兴) 当x________时,分式有意义.8. (1分)(2020·百色模拟) 因式分解:2ax2﹣4axy+2ay2=________.9. (1分) (2016七上·凤庆期中) 用科学记数法表示:2014应记为________.10. (1分)(2017·邵阳模拟) 甲乙两人8次射击的成绩如图所示(单位:环)根据图中的信息判断,这8次射击中成绩比较稳定的是________(填“甲”或“乙”)11. (2分)如图,∠BAC=90°,AB=AC,CE⊥AD于E,BF⊥AD于F,若AF=8cm,EF=5cm,则BF=________,CE=________.12. (1分)已知y1=﹣x+3,y2=3x﹣4,当x________时,y1>y2 .13. (1分) (2017九上·徐州开学考) 如果2是一元二次方程x2+bx+2=0的一个根,那么常数b的值为________.14. (1分)(2018·玉林) 如图,正六边形ABCDEF的边长是6+4 ,点O1 , O2分别是△ABF,△CDE的内心,则O1O2=________.15. (1分) (2019七上·浦东期末) 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,AB=5,且AC在直线1上,将△ABC绕点A顺时针旋转到位置①,可得到点P1 ,将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2 ,将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3 ,…,按此规律继续旋转,得到点P2018为止,则AP2018=________.16. (1分)(2019·永州) 如图,直线y=4﹣x与双曲线y 交于A , B两点,过B作直线BC⊥y轴,垂足为C ,则以OA为直径的圆与直线BC的交点坐标是________.三、解答题 (共11题;共115分)17. (5分)(2017·西华模拟) 先化简,再求值:(﹣)÷ ,其中x=2sin30°+2 cos45°.18. (20分) (2019八上·北京期中) 分式计算:(1)(2)(3)(4)先化简,再求值:,其中m=1.19. (11分) (2019九上·泰州月考) 已知△ABC中,a、b、c分别为∠A、∠B、∠C的对边,方程是关于x的一元二次方程.(1)判断方程的根的情况为________(填序号);①方程有两个相等的实数根;②方程有两个不相等的实数根;③方程无实数根;④无法判断(2)如图,若△ABC内接于半径为2的⊙O,直径BD⊥AC于点E,且∠DAC=60°,求方程的根;(3)若是方程的一个根,△ABC的三边a、b、c的长均为整数,试求a、b、c的值.20. (8分)(2019·金台模拟) 在“书香校园”活动中,某校为了解学生家庭藏书情况,随机抽取本校部分学生进行调查,并绘制成部分统计图表如下:类别家庭藏书m本学生人数A0≤m≤2520B26≤m≤100aC101≤m≤20050D m≥20166根据以上信息,解答下列问题:(1)该调查的样本容量为________,a=________;(2)在扇形统计图中,“A”对应扇形的圆心角为________°;(3)若该校有2000名学生,请估计全校学生中家庭藏书200本以上的人数.21. (6分) (2016九上·苏州期末) 某商场为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“30元”的字样.规定:顾客在本商场同一日内,每消费满200元,就可以在箱子里先后摸出两个球(第一次摸出后不放回).商场根据两小球所标金额的和返还相应价格的购物券,可以重新在本商场消费.某顾客刚好消费200元.(1)该顾客至少可得到________元购物券;(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于30元的概率.22. (10分) (2018八上·姜堰期中) 如图,E、F分别是等边三角形ABC的边AB、AC上的点,且BE=AF,CE 与BF交于点P.(1)求证:CE=BF;(2)求∠BPC的度数.23. (5分)(2017·河北模拟) 如图,已知:长江路西段与黄河路的夹角为150°,长江路东段与淮河路的夹角为135°,黄河路全长AC=20km,从A地道B地必须先走黄河路经C点后再走淮河路才能到达,城市道路改造后,直接打通长江路(即修建AB路段).问:打通长江路后从A地道B地可少走多少路程?(参考数据:≈1.4,≈1.7)24. (15分)(2017·全椒模拟) 如图,⊙O的直径AD长为6,AB是弦,∠A=30°,CD∥AB,且CD= .(1)求∠C的度数;(2)求证:BC是⊙O的切线;(3)求阴影部分面积.25. (15分) (2017八下·桂林期末) 我国是一个严重缺水的国家.为了加强公民的节水意识,某市制定了如下用水收费标准:每户每月的用水不超过6吨时,水价为每吨2元,超过6吨时,超过的部分按每吨3元收费.该市某户居民5月份用水x吨,应交水费y元.(1)若0<x≤6,请写出y与x的函数关系式.(2)若x>6,请写出y与x的函数关系式.(3)如果该户居民这个月交水费27元,那么这个月该户用了多少吨水?26. (10分) (2017八上·安庆期末) 解答题(1)如图1,以△ABC的边AB、AC为边分别向外作正方形ABDE和正方形ACFG,连接EG,试判断△ABC与△AEG面积之间的关系,并说明理由.(2)园林小路,曲径通幽,如图2所示,小路由白色的正方形理石和黑色的三角形理石铺成.已知中间的所有正方形的面积之和是a平方米,内圈的所有三角形的面积之和是b平方米,这条小路一共占地多少平方米.27. (10分)(2017·威海) 已知:AB为⊙O的直径,AB=2,弦DE=1,直线AD与BE相交于点C,弦DE在⊙O 上运动且保持长度不变,⊙O的切线DF交BC于点F.(1)如图1,若DE∥AB,求证:CF=EF;(2)如图2,当点E运动至与点B重合时,试判断CF与BF是否相等,并说明理由.参考答案一、选择题 (共6题;共12分)1-1、2-1、3-1、4-1、5-1、6-1、二、填空题 (共10题;共11分)7-1、8-1、9-1、10-1、11-1、12-1、13-1、14-1、15-1、16-1、三、解答题 (共11题;共115分)17-1、18-1、18-2、18-3、18-4、19-1、19-2、19-3、20-1、20-2、20-3、21-1、21-2、22-1、22-2、23-1、24-1、24-2、24-3、25-1、25-2、25-3、26-1、26-2、27-1、27-2、。
河北省唐山市丰南区九级数学下学期期中试题答案

河北省唐山市丰南区2018届九年级数学下学期期中试题答案 (仅供参考,试卷如有问题,请各位老师自行解决,答案不唯一的酌情给分)一、1.C 2.D 3.D 4.D 5.C 6.D 7.C 8.B 9.C 10. D 11.C 12.B 13.C 14.C 15.B16.C二、17. 9 18. 8 19. 41 三、20.(1)解:如图......................................2分 ∵AD BC CE AB ⋅=⋅2121 ∴AD CE 2= .............................................3分 ∴21=CE AD ............................................4分 (2)解:①点A 在第二象限 ...............................5分 理由:∵a 没有平方根∴00〉-〈a a .........................................6分∴点A 在第二象限②由题意可知c a 3=-∴3a c =或3a c =-.........................................7分∴3328324c b c c b c ⨯-+=⎧⎨--=-⎩ 解得,3,3,1a b c === ∴B (3,1) .............8分 或3(3)28324c b c c b c ⨯--+=⎧⎨---=-⎩解得,6,6,2a b c ===- ∴B (6,-2)............9分 (1) 证明:∵AB=A C ∴∠B=∠C . .....................1分∵AD+EC=AB AD+BD=AB ∴BD =EC .....................2分在△DBE 和△ECF 中∵BE =CF ∠B =∠C BD =EC ,∴△DBE ≌△ECF (SAS ). ....................3分∴DE=EF . .....................4分∴DEF 是等腰三角形.(2)解:∵∠A=40°,∠B=∠C , ∴∠B=∠C=70°......................5分∴∠BDE+∠DEB=110°.∵△DBE ≌△ECF .∴∠FEC =∠BDE , .....................6分∴∠FEC+∠DEB=110°,∴∠DEF=70°. .....................7分(3)当∠A 为60度时,△DEF 是等边三角形 .....................9分21.(1)-5或1 .....................2分(2)8cm 或4cm .....................4分(3)120°或60° .....................6分(4)由题意可知:若三边长为17、17、8,此时8+17>17,周长为42; .....................8分若三边长为17、8、8,此时8+8<17,无法围成三角形,此情况舍去. .....................9分22.解:(1)5028.010===c b a .....................3分(2)略 .....................4分(3)(5×10+6×18+7×14+8×8)÷50=6.4(本) .....................6分(4)样本中,学生课外阅读7本及以上的人数占0.28+0.16=0.44 .....................7分 估计全校约有1200×0.44=528人课外阅读7本及以上. .....................9分23.解:(1)由题意得:x=1时y=2;x=2时,y=6代入得:.....................2分⎩⎨⎧=+=+6242b a b a .....................3分 解得:⎩⎨⎧==11b a∴x x y +=2 .....................4分(2)由题意得:g=31x-150-(x 2+x ) .....................5分g=-x 2 +30x-150 .....................6分(3)∵g=-x 2 +30x-150;∴g=-x 2 +30x-150=-(x-15)2 +75, .....................8分∴a=-1<0,抛物线开口向下,g有最大值.∴当x=15时,g最大值=75. .....................9分即设施开放15个月后,游乐场的纯收益达到最大为75万元. .....................10分25.(1)∵A(-1,0),B(0,3),∠AOB=90°∴tan∠BAO=3∴∠BAO=60° ....................2分(2)S1=S2, ....................3分理由如下:依题意有:OA=A′O,∠BAO=60°,∴△A′AO是等边三角形,∴∠AOA′=∠BA′O=60°, ....................4分∴A′B′∥x轴,∴点A′、B′到x轴的距离相等 .........5分∵∠ABO=∠A′OB=90°-60°=30°∴A′O=A′B=AA′ ....................6分∵等边△A′AO的三条高都相等∴点O到AB的距离等于点B′到x轴的距离∴S1=S2(等底等高的三角形面积相等).................7分(3)S1与S2的关系没变,仍然有S1=S2, .................8分理由如下:过点B作BC⊥A′O于C,过点B′作B′D⊥x轴于D,∴∠BCO=∠B′DO=90° .................9分依题意有:∠BOD=∠A′OB′=90°,∴∠1+∠A′OD=∠2+∠A′OD=90°∴∠1=∠2又∵B′O=BO∴△BOC≌△B′OD(AAS) .................10分∴BC=B′D又∵AO=A′O∴S1=S2(等底等高的三角形面积相等) .................11分∥,26.解:(1)∵OA BC∴OAD ADB ∠=∠,∴tan tan 2ADB OAD ∠=∠=. 在Rt ABD △中,∵6AB OC ==, ∴63tan 2AB DB ADB ===∠.∴1CD CB BD =-=,(1,6)D . .................2分 ∵抛物线21:(0)M y ax bx a =+≠过A ,D 两点,∴1640,6,a b a b +=⎧⎨+=⎩解得2,8.a b =-⎧⎨=⎩∴抛物线1M 的表达式为228y x x =-+. .................3分(2)∵222282(4)2(2)8y x x x x x =-+=--=--+. ∴抛物线的对称轴为2x =. .................4分 设点(2,)P y ,∵(4,0)A ,(0,6)C ,∴2224652AC =+=,2222(42)4AP y y =-+=+, 22222(6)4(6)CP y y =+-=+-. ∵90CPA ∠=︒,∴222AC AP CP =+,即225244(6)y y =+++-, .................5分 整理得2640y y --=.解得1313y =+,2313y =-, .................6分故1(2,313)P +,2(2,313)P -. .................7分(2)由题意知,抛物线2M 的表达式为228y x x m =-+-, ①∵(1,6)D ,∴(1,6)D m '-,设直线AE 的表达式为y mx n =+, 则40,4,m n n +=⎧⎨=⎩解得1,4,m n =-⎧⎨=⎩∴直线AE 的表达式为4y x =-+. .................8分 ∵点(1,6)D m '-在直线AE 上, ∴146m -+=-,解得3m =. ................9分 ②由①知,当抛物线经过点(1,3)时,m 的值为3; 当x m =时,设直线与抛物线交于点(,4)P m m -+,则2428m m m m -+=-+-, 解得22m =+或22m =-(舍去); .................10分 当抛物线228y x x m =-+-与直线AE 只有一个交点时, 联立228,4,y x x m y x ⎧=-+-⎨=-+⎩ 消去y ,整理得32940x x m -++=, 由818(4)0m ∆=-+=,解得498m =. (11)分 综上可知,所求m 的取值范围为49228m <..................12分。
冀教版九年级数学下期中综合检测试卷有答案

九年级数学下册期中综合检测(时间:90分钟满分:120分)一、选择题(第1~10小题各3分,第11~16小题各2分,共42分)1.圆的直径为13 cm,如果圆心与直线的距离是d,那么()A.当d=8 cm时,直线与圆相交B.当d=4.5 cm时,直线与圆相离C.当d=6.5 cm时,直线与圆相切D.当d=13 cm时,直线与圆相切2.抛物线y=2x2-5x+6的对称轴是()A.x=B.x=C.x=-D.x=-3.在△ABC中,∠C=90°,AC=BC=4 cm,点D是AB边的中点,以点C为圆心,4 cm长为半径作圆,则点A,B,C,D四点中在圆内的有()A.1个B.2个C.3个D.4个4.一次函数y=ax+b与二次函数y=ax2+bx+c在同一坐标系中的图像可能是()ABCD5.已知抛物线y=-x2+mx+n的顶点坐标是(-1,-3),则m和n的值分别是()A.2,4B.-2,-4C.2,-4D.-2,06.对于函数y=-x2-2x+2使得y随x的增大而增大的x的取值范围是()A.x≥-1B.x≥0C.x≤0D.x≤-17.在Rt△ABC中,∠C=90°,AB=10,AC=6,以C为圆心作☉C和AB相切,则☉C的半径为()A.8B.4C.9.6D.4.88.若(2, 5),(4, 5)是抛物线y=ax2+bx+c上的两点,则它的对称轴是()A.x=-1B.x=1C.x=2D.x=39.如图所示,PA切☉O于点A,PO交☉O于点B,若PA=6,BP=4,则☉O的半径为()A.2B.C.D.5(第9题图)10.如图所示,PA,PB是☉O的两条切线,切点是A,B.如果OP=4,OA=2,那么∠AOB等于()(第10题图)A.90°B.100°C.110°D.120°11.便民商店经营一种商品,在销售过程中,发现一周利润y(元)与每件销售价x(元)之间的关系满足y=-2(x-20)2+1558,由于某种原因,价格只能是15≤x≤22,那么一周可获得最大利润是()A.20元B.1508元C.1550元D.1558元12.若二次函数y=x2-6x+c的图像过A(-1,y1),B(2,y2),C(3+,y3),则y1,y2,y3的大小关系是()A.y1>y2>y3B.y1>y3>y2C.y2>y1>y3D.y3>y1>y213.如图所示,正六边形ABCDEF内接于☉O,则∠ADB的度数是()A.60°B.45°C.30°D.22.5°(第13题图)(第14题图)14.已知二次函数y=ax2+bx+c的图像如图所示,则下列结论:①ac>0;②a-b+c<0;③x<0时,y <0;④ax2 + bx + c=0(a≠0)有两个大于-1的实数根.其中错误的有()A.①②B.③④C.①③D.②④15.对于任意实数t,抛物线y=x2+(2-t)x+t总经过一个固定的点,这个点是()A.(1, 0)B.(-1, 0)C.(-1, 3)D. (1, 3)16.若二次函数y=ax2+bx+c(a≠0)的图像与x轴有两个交点,坐标分别为(x1,0),(x2,0),且x1<x2,若图像上有一点M(x0,y0)在x轴下方,则下列判断正确的是()A.a>0B.b2-4ac≥0C.x1<x0<x2D.a(x0-x2)(x0-x2)<0二、填空题(第17~18小题各3分,第19小题4分,共10分)17.函数y=2x2-4x-1写成y=a(x-h)2+k的形式是,其图像的顶点坐标是,对称轴是.18.如图所示,已知AB为☉O的直径,PA,PC是☉O的切线,A,C为切点,∠BAC=30°,则∠P的度数为.19.将抛物线y=2(x-3)2+3向右平移2个单位长度后,再向下平移5个单位长度,所得抛物线的顶点坐标为.三、解答题(共68分)20.(9分)如图所示,AB是☉O的直径,AC是弦,CD是☉O的切线,C为切点,AD⊥CD于点D.求证:(1)∠AOC=2∠ACD;(2)AC2=AB·AD.(第20题图)(第21题图)21.(9分)已知二次函数y=x2+mx+n的图像经过点P(-3,1),对称轴是经过(-1,0)且平行于y轴的直线.(1)求m,n的值;(2)如图所示,一次函数y=kx+b的图像经过点P,与x轴相交于点A,与二次函数的图像相交于另一点B,点B在点P的右侧,PA∶PB=1∶5,求一次函数的表达式.22.(9分)水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤.通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤.为了保证每天至少售出260斤,张阿姨决定降价销售.(1)若将这种水果每斤的售价降低x元,求每天的销售量是多少斤(用含x的代数式表示);(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?23.(9分)[2016·天津中考]在☉O中,AB为直径,C为☉O上一点.(1)如图①所示,过点C作☉O的切线,与AB的延长线相交于点P,若∠CAB=27°,求∠P的大小;(2)如图②所示,D为上一点,且OD经过AC的中点E,连接DC并延长,与AB的延长线相交于点P,若∠CAB=10°,求∠P的大小.24.(10分)如图所示,一位篮球运动员在距篮圈水平距离4米处跳起投篮,球运行的路线是抛物线,当球运行的水平距离为2.5 m时,达到最大高度3.5 m,然后准确落入篮圈.已知篮圈中心到地面的高度为3.05 m.(1)建立如图所示的直角坐标系,求抛物线的解析式;(2)已知该运动员身高1.8 m,在这次跳投中,球在头顶上方0.25 m处出手,则球出手时,他跳离地面的高度是多少?25.(10分)如图所示,在△ABC中,∠C= 90°,以AB上一点O为圆心,OA长为半径的圆与BC相切于点D,分别交AC,AB于点E,F.(1)若AC=6,AB= 10,求☉O的半径;(2)连接OE,ED,DF,EF.若四边形BDEF是平行四边形,试判断四边形OFDE的形状,并说明理由.26.(12分)某公司生产的一种健身产品在市场上受到普遍欢迎,每年可在国内、国外市场上全部售完.该公司的年产量为6千件,若在国内市场销售,平均每件产品的利润y1(元)与国内销售数量x(千件)的关系为:y1=若在国外销售,平均每件产品的利润y2(元)与国外的销售数量t(千件)的关系为:y2=(1)用x的代数式表示t为t=;当0<x≤4时,y2与x的函数解析式为y2=;当4≤x<时,y2=100.(2)求每年该公司销售这种健身产品的总利润w(千元)与国内销售数量x(千件)的函数解析式,并指出x的取值范围.(3)该公司每年国内、国外的销售量各为多少时,可使公司每年的总利润最大?最大值为多少?【答案与解析】1.C(解析:当d<r时,则直线与圆相交;当d=r时,则直线与圆相切;当d>r时,则直线与圆相离.已知圆的直径为13 cm,则半径为6.5 cm,当d=6.5 cm时,直线与圆相切,当d<6.5 cm时,直线与圆相交,当d>6.5 cm时,直线与圆相离,故A,B,D错误,C正确.)2.A(解析:对称轴为x=-=-= .)3.B(解析:以C为圆心、4 cm长为半径作圆.∵∠C=90°,AC=BC=4 cm,∴A,B到圆心C的距离等于半径,∴点A,B在圆上;∵在直角三角形ABC中,D是AB的中点,AC=BC=4 cm,∴AB=4 cm,∴CD=AB=2 cm,∵2<4,∴点D在☉C内,那么在圆内只有点C和点D两个点.)4.C(解析:当a<0时,二次函数图像开口向下,一次函数图像经过第二、四象限,此时C,D符合,又由C,D中图像可知二次函数图像的对称轴在y轴左侧,所以-<0,即b<0,只有C符合.同理可讨论当a>0时的情况.)5.B(解析:抛物线y=-x2+mx+n的顶点坐标是,所以=-1,=-3,解得m=-2,n=-4.)6.D(解析:由题意知函数图像开口向下,所以在对称轴左侧y随x的增大而增大,由对称轴为x=-1,知所求x的取值范围是x≤-1.)7.D(解析:在Rt△ABC中,∠C=90°,AB=10,AC=6,所以BC=8.过点C作CD⊥AB,交AB于点D,则CD=4.8,因为☉C和AB相切,所以CD 即为☉C的半径,所以☉C的半径为4.8.)8.D(解析:因为已知两点的纵坐标相同,所以横坐标应关于对称轴对称,从而抛物线的对称轴为x=3.)9.B(解析:连接OA,∵PA切☉O于点A,∴∠OAP=90°,∴PA2+OA2=OP2.∵PA=6,BP=4,∴36+OA2=(OB+4)2,解得OA=.)10.D(解析:由题意易得PA===2,△APO≌△BPO,∴∠AOP=∠BOP.∵sin∠AOP=AP∶OP=2∶4=∶2,∴∠AOP=60°.∴∠AOB=120°.)11.D(解析:∵y=-2(x-20)2+1558,a=-2<0,∴抛物线开口向下,函数有最大值,∴x=20时,y最大=1558(元).∵x=20在15≤x≤22范围内,∴y的最大值为1558元.)12.B(解析:由题意知A(-1,y1),B(2,y2)在对称轴x=3的左侧,且y随x的增大而减小,因为-1<2,所以y2<y1,根据二次函数图像的对称性可知C(3+,y3)中,|3+-3|=,-1<<2,所以y1>y3>y2.)13.C(解析:∵正六边形ABCDEF内接于☉O,∴弧AB的度数等于360°÷6=60°,∴∠ADB=30°.)14.C(解析:①由图像可知二次函数y=ax2+bx+c(a≠0)的图像开口向下,∴a<0,∵与y轴的交点在x轴上方,∴c>0,∴ac<0,①错误;②∵当x=-1时,y=a-b+c,而由图像知当x=-1时,y<0,∴a-b+c<0,②正确;③根据图像可知当x<-1时,抛物线在x轴的下方,∴当x<-1时,y<0,③错误;④从图像可知抛物线与x轴的交点的横坐标都大于-1,∴方程ax2+bx+c=0(a≠0)有两个大于-1的实数根,④正确.故错误的有①③.)15.D(解析:当x=1时,y=1+(2-t)+t=3,故抛物线经过固定点(1,3).)16.D(解析:二次函数图像的开口方向可能向上,也可能向下,所以选项A错误.若二次函数y=ax2+bx+c(a≠0)与x轴有两个不同的交点,则b2-4ac>0,所以选项B错误.符合条件的点M(x0,y0)有多种可能,当a>0时,x1<x0<x2;当a<0时,有两种情况:一种是x0<x1<x2,另一种是x1<x2<x0,所以选项C错误.而当a>0时,x1<x0<x2,所以a(x0-x1)(x0-x2)<0;当a<0时,无论x0<x1<x2,还是x1<x2<x0,a(x0-x1)(x0-x2)都小于0,所以选项D正确.)17.y=2(x-1)2-3(1,-3)x=1(解析:配方可得y=2(x-1)2-3,所以顶点坐标为(1,-3),对称轴为x=1.)18.60°(解析:∵PA是☉O的切线,AB为☉O的直径,∴PA⊥AB,∴∠BAP=90°.∵∠BAC=30°,∴∠CAP=90°-∠BAC=60°.又∵PA,PC分别切☉O于点A,C,∴PA=PC,∴△PAC为等边三角形,∴∠P=60°.)19.(5,-2)(解析:y=2(x-3)2+3向右平移2个单位长度,再向下平移5个单位长度,得到抛物线y=2(x-5)2-2,所以顶点坐标为(5,-2).)20.证明:(1)∵CD是☉O的切线,C为切点,∴∠OCD=90°,即∠ACD+∠ACO=90°.①∵OC=OA,∴∠ACO=∠CAO,∴∠AOC=180°-2∠ACO,即∠AOC+∠ACO=90°.②由①②,得∠ACD-∠AOC=0,即∠AOC=2∠ACD.(2)如图所示,连接BC.∵AB是☉O的直径,∴∠ACB=90°.在Rt△ACD与Rt△ABC中,∵∠AOC=2∠B,∠AOC=2∠ACD(由(1)知),∴∠B=∠ACD,∴ Rt△ACD∽Rt△ABC,∴ =,即AC2=AB·AD.(第20题图)(第21题图)21.解:(1)∵二次函数图像的对称轴是经过(-1,0)且平行于y轴的直线,∴-=-1,解得m=2,此时二次函数的解析式为y=x2+2x+n,∵二次函数图像过点P(-3,1),∴将点P代入得1=9-6+n,解得n=-2.故n=-2,m=2.(2)由(1)知二次函数的解析式为y=x2+2x-2.如图所示,过P作PC⊥x轴于点C,过B作BD⊥x轴于点D,则PC∥BD,易证△APC∽△ABD,∴===,∵PC=1,∴BD=6,∴y B=6.∵点B在二次函数图像上,设B点横坐标为x,∴x2+2x-2=6,解得x1=2,x2=-4(舍去),∴B点坐标为(2 ,6),将点B,P代入一次函数得解得∴一次函数的表达式是y=x+4.22.解:(1)设每斤的售价降低x元,则每天销售量为×20+100=(100+200x)斤,为了保证每天至少售出260斤,即100+200x≥260,∴x≥0.8,∴每天的销售量是100+200x(0.8≤x<2)斤.(2)设张阿姨需将每斤的售价降低y元(0.8≤y<2),其利润为W元,根据题意得W=(100+200y)(4-2-y)=-200y2+300y+200,若W=300,即-200y2+300y+200=300,解得y1=1,y2=(舍去),∴张阿姨需将每斤的售价降低1元.23.解:(1)如图所示,连接OC.∵☉O与PC相切于点C,∴OC⊥PC,即∠OCP=90°,∵∠CAB=27°,∴∠COB=2∠CAB=54°.在Rt△OPC 中,∠P+∠COP=90°,∴∠P=90°-∠COP=36°.(2)∵E为AC的中点,OD为☉O的半径,∴OD⊥AC,即∠AEO=90°,在Rt△AOE中,由∠EAO=10°,得∠AOE=90°-∠EAO=80°,∴∠ACD=∠AOD=40°.∵∠ACD是△ACP的一个外角,∴∠P=∠ACD-∠CAP=30°. 24.解:(1)由题意可设抛物线的解析式为y=ax2+c,由图像可知抛物线过点(0,3.5),(1.5,3.05),所以解得所以抛物线的解析式为y=-0.2x2+3.5.(2)设球出手时,他跳离地面的高度为h m,则球出手时,球的高度为h+1.8+0.25=(h+2.05)m,由(1)知y=-0.2x2+3.5,∴h+2.05=-0.2×(-2.5)2+3.5,∴h=0.2(m).25.解:(1)如图所示,连接OD,设☉O的半径为r.∵BC切☉O于点D,∴OD⊥BC.∵∠C=90°,∴OD∥AC,易得△OBD∽△ABC,∴= ,即 =,解得r =,∴☉O的半径为.(2)四边形OFDE是菱形.如图所示,∵四边形BDEF是平行四边形,∴∠DEF=∠B,DE∥BF.∵∠DEF=∠DOB,∴∠B=∠DOB.由(1)知∠ODB=90°,∴∠DOB+∠B=90°,∴∠DOB=60°.∵DE∥AB,∴∠ODE=60°.∵OD=OE,∴△ODE是等边三角形,∴OD=DE.∵OD=OF,∴DE=OF.∴四边形OFDE是平行四边形.∵OE=OF,∴平行四边形OFDE是菱形.26.解:(1)6-x5x+806(2)当0<x≤2时,w=(15x+90)x+(5x+80)(6-x)=10x2+40x+480;当2<x≤4时,w=(-5x+130)x+(5x+80)(6-x)=-10x2+80x+480;当4<x<6时,w=(-5x+130)x+100(6-x)=-5x2+30x+600.综上所述,w=(3)当0<x≤2时,w=10x2+40x+480=10(x+2)2+440,当x=2时,w最大=600;当2<x≤4时,w=-10x2+80x+480=-10(x-4)2+640,当x=4时,w最大=640.当4<x<6时,w=-5x2+30x+600=-5(x-3)2+645;当4<x<6时,w<640.综上可知当x=4时,w最大=640.所以国内销售4千件,国外销售2千件时,利润最大,最大利润为64万元(或640千元).。
唐山市九年级下学期数学期中考试试卷

唐山市九年级下学期数学期中考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共5题;共10分)1. (2分) (2019七上·朝阳期末) 若一个整数12500…0用科学记数法表示为1.25×1010 ,则原数中“0”的个数为()A . 5B . 8C . 9D . 102. (2分)(2019·下城模拟) 若数组2,2,x,3,4的平均数为3,则这组数中的()A . x=3B . 中位数为3C . 众数为3D . 中位数为x3. (2分)如图,一段公路的转弯处是一段圆弧(),则的展直长度为()A . 3πB . 6πC . 9πD . 12π4. (2分)(2011·苏州) 如图,巳知A点坐标为(5,0),直线y=x+b(b>0)与y轴交于点B,连接AB,∠α=75°,则b的值为()A . 3B .C . 4D .5. (2分)如图所示的抛物线是二次函数y=ax2+bx+c(a≠0)的图象,则下列结论:①abc>0;②b+2a=0;③抛物线与x轴的另一个交点为(4,0);④a+c>b;⑤3a+c<0.其中正确的结论有()A . 5个B . 4个C . 3个D . 2个二、填空题 (共11题;共14分)6. (1分) (2016七上·港南期中) ﹣4的相反数是________,倒数是________,绝对值是________.7. (2分)计算:(﹣3)5×(﹣3)7=________;5m÷5n=________;( 23 )m=________;(a2b)m=________.8. (1分) (2016九上·海门期末) 分解因式:(a+b)2﹣4ab=________.9. (2分) (2020八上·新乡期末) 若分式的值为0,则的值为________.10. (1分)(2017·滨湖模拟) 若圆锥底面圆的直径和母线长均为4cm,则它的侧面展开图的面积等于________ cm2 .11. (1分) (2017八下·龙海期中) =________.12. (1分)如图,一个转盘被分成7个相同的扇形,颜色分为红、黄、绿三种,指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,当作指向右边的扇形),则指针指向红色的概率为________.13. (1分)(2017·安徽模拟) 如图,抛物线y1=(x﹣2)2﹣1与直线y2=x﹣1交于A、B两点,则当y2≥y1时,x的取值范围为________.14. (1分) (2015八下·津南期中) 已知菱形的两条对角线长为8和6,那么这个菱形面积是________,菱形的高________.15. (1分)(2016·徐州) 如图,⊙O是△ABC的内切圆,若∠ABC=70°,∠ACB=40°,则∠BOC=________°.16. (2分)(2019·西安模拟) 如图,已知正方形ABCD的边长为2,以点A为圆心,1为半径作圆,E是⊙A 上的任意一点,将点E绕点D按逆时针方向旋转90°得到点F,则线段AF的长的最小值________.三、解答题 (共10题;共105分)17. (10分)计算(1)(2)(3) 1﹣(4).18. (10分) (2015九下·深圳期中) 解分式方程:.19. (12分)(2019·五华模拟) 为了庆祝“五四”青年节,我市某中学举行了书法比赛,赛后随机抽查部分参赛同学成绩(满分为100分),并制作成图表如下分数段频数频率60≤x<70300.1570≤x<80m0.4580≤x<9060n90≤x≤100200.1请根据以上图表提供的信息,解答下列问题:(1)这次随机抽查了________学生;表中的数m=________,n=________;(2)请在图中补全频数分布直方图;(3)若绘制扇形统计图,分数段60≤x<70所对应扇形的圆心角的度数是________;(4)全校共有600名学生参加比赛,估计该校成绩不低于80分的学生有多少人?20. (2分) (2016九上·泰顺期中) 将背面相同,正面分别标有数字1,2,3,4的四张卡片洗匀后,背面朝上放在桌面上.(1)从中随机抽取一张卡片,求该卡片正面上的数字是偶数的概率;(2)先从中随机抽取一张卡片(不放回),将该卡片正面上的数字作为十位上的数字;再随机抽取一张,将该卡片正面上的数字作为个位上的数字,则组成的两位数恰好是4的倍数的概率是多少?请用树状图或列表法加以说明.21. (10分)(2018·普宁模拟) 如图,已知矩形ABCD(AB<AD).(1)请用直尺和圆规按下列步骤作图,保留作图痕迹;①以点A为圆心,以AD的长为半径画弧交边BC于点E,连接AE;②作∠DAE的平分线交CD于点F;③连接EF;(2)在(1)作出的图形中,若AB=8,AD=10,则tan∠FEC的值为________.22. (5分)(2017·新野模拟) 如图,AB为一斜坡,其坡角为19.5°,紧挨着斜坡AB底部A处有一高楼,一数学活动小组量得斜坡长AB=15m,在坡顶B处测得楼顶D处的仰角为45°,其中测量员小刚的身高BC=1.7米,求楼高AD.(参考数据:sin19.5°≈ ,tan19.5°≈ ,最终结果精确到0.1m).23. (10分) (2019八上·海珠期末) 在Rt△ABC中,∠B=90°,AB=8,CB=5,动点M从C点开始沿CB 运动,动点N从B点开始沿BA运动,同时出发,两点均以1个单位/秒的速度匀速运动(当M运动到B点即同时停止),运动时间为t秒.(1) AN=________;CM=________.(用含t的代数式表示)(2)连接CN,AM交于点P.①当t为何值时,△CPM和△APN的面积相等?请说明理由.②当t=3时,试求∠APN的度数.24. (15分) (2017九上·上城期中) 如图,以已知线段为弦作⊙ ,使其经过已知点.(1)利用直尺和圆规作圆(保留作图痕迹,不必写出作法).(2)若,,求过A 、B、C三点的圆的半径.25. (20分)(2019·金华) 如图,在平面直角坐标系中,正方形OABC的边长为4,边OA,OC分别在x轴,y 轴的正半轴上,把正方形OABC的内部及边上,横,纵坐标均为整数的点称为好点,点P为抛物线y=-(x-m)2+m+2的顶点。
河北省唐山市九年级下学期期中数学试卷

河北省唐山市九年级下学期期中数学试卷姓名:________ 班级:________ 成绩:________一、选择题 (共6题;共12分)1. (2分) (2018九上·铜梁期末) 图中所有的小正方形都全等,已有4个正方形被涂黑,现将①②③④中某一个涂黑使得它与原来4个小正方形组成的图形既是轴对称图形又是中心对称图形,则要被涂黑的正方形是()A . ①B . ②C . ③D . ④2. (2分)(2019·黄埔模拟) 一个几何体的三视图如图所示,这个几何体是()A . 圆锥B . 圆柱C . 球D . 三棱柱3. (2分) (2020七下·青岛期中) 下列计算正确的是()A .B .C .D .4. (2分) (2016八上·永登期中) 已知点A(4,﹣3),则它到y轴的距离为()A . ﹣3B . ﹣4C . 3D . 45. (2分)(2012·沈阳) 气象台预报“本市明天降水概率是30%”,对此消息下列说法正确的是()A . 本市明天将有30%的地区降水B . 本市明天将有30%的时间降水C . 本市明天有可能降水D . 本市明天肯定不降水6. (2分)一列火车自2013年全国铁路第10次大提速后,速度提高了26千米/小时,现在该列火车从甲站到乙站所用的时间比原来减少了1个小时。
已知甲、乙两个车站的路程是312千米,设火车提速前的速度为x千米/小时,根据题意所列方程正确的是()A .B .C .D .二、填空题 (共10题;共12分)7. (1分) (2022七上·滨江期末) 计算: ________(结果用科学记数法表示).8. (3分) (2016七上·金华期中) 代数式10﹣|2x﹣5|所能取到的最________(填大或小)值是________,此时x=________.9. (1分) (2017八下·郾城期末) 在2017年的理化生实验考试中某校6名学生的实验成绩统计如图,这组数据的众数是________分.10. (1分)化简:=________ .11. (1分) (2019八下·海安期中) 将直线y=2x﹣4的图象向上平移3个单位长度后,所得的直线的解析式是________.12. (1分)(2018·苍南模拟) 如图,要在宽AB为20米的瓯海大道两边安装路灯,路灯的灯臂CD与灯柱BC成120°角,灯罩的轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线(即O为AB的中点)时照明效果最佳,若CD= 米,则路灯的灯柱BC高度应该设计为________米(计算结果保留根号).13. (1分)在平面直角坐标系中,若一条平行于x轴的直线y=2分别交双曲线y=﹣和y= 于A、B两点,P是x轴上的任意一点,则△ABP的面积等于________.14. (1分)(2019·长春) 如图,直线MN∥PQ,点A、B分别在MN、PQ上,∠MAB=33°。
河北省唐山市九年级下学期数学期中考试试卷

河北省唐山市九年级下学期数学期中考试试卷姓名:________班级:________成绩:________一、 单选题 (共 10 题;共 20 分)1. (2 分) (2014·杭州) 已知边长为 a 的正方形的面积为 8,则下列说法中,错误的是( )A . a 是无理数B . a 是方程 x2﹣8=0 的一个解C . a 是 8 的算术平方根D . a 满足不等式组2. (2 分) (2019·常州) 若代数式 A.有意义,则实数 的取值范围是( )B.C.D.3. (2 分) 把多项式分解因式,下列结果正确的是 ( )A.B.C.D.4. (2 分) 方程A.B.C.或D.的解是5. (2 分) (2017·徐州) 如图,在平面直角坐标系 xOy 中,函数 y=kx+b(k≠0)与 y= (m≠0)的图象相交于点 A(2,3),B(﹣6,﹣1),则不等式 kx+b> 的解集为( )第 1 页 共 14 页A . x<﹣6 B . ﹣6<x<0 或 x>2 C . x>2 D . x<﹣6 或 0<x<2 6. (2 分) (2016 九上·长春期中) 下列图形中只是中心对称图形的是( )A. B.C.D. 7. (2 分) (2018·临河模拟) 如图,已知点 A(0,1),B(0,-1),以点 A 为圆心,AB 为半径作圆,交 轴 的正半轴于点 C,则∠BAC 等于 ( )A . 90° B . 120° C . 60° D . 30° 8. (2 分) (2019·白银) 如图,足球图片正中的黑色正五边形的内角和是( ).第 2 页 共 14 页A . 180° B . 360° C . 540° D . 720° 9. (2 分) (2019 七上·辽阳月考) 一个正方体的展开图如图所示,每一个面上都写有一个自然数并且相对 两个面所写的两个数之和相等,那么 a+b﹣2c=( )A . 40 B . 38 C . 36 D . 34 10. (2 分) (2016·包头) 如图,直线 y= x+4 与 x 轴、y 轴分别交于点 A 和点 B,点 C、D 分别为线段 AB、 OB 的中点,点 P 为 OA 上一动点,PC+PD 值最小时点 P 的坐标为( )A . (﹣3,0) B . (﹣6,0)C . (﹣ ,0) D . (﹣ ,0)二、 填空题 (共 8 题;共 8 分)第 3 页 共 14 页11. (1 分) (2019·南通)5G 信号的传播速度为 300000000m/s,将 300000000 用科学记数法表示为________.12. (1 分) (2019·扬中模拟) 某次数学测试,某班一个学习小组的六位同学的成绩如下:84、75、75、92、86、99,则这六位同学成绩的中位数是________.13. (1 分) (2019·安徽) 命题“如果 a+b=0,那么 a,b 互为相反数”的逆命题为________.14. (1 分) (2018·常州) 如图,在▱ABCD 中,∠A=70°,DC=DB,则∠CDB=________.15. (1 分) (2017·高淳模拟) 如图,点 A,B,C 在⊙O 上,∠ACB 的度数是 20°, 的半径是________.的长为 π,则⊙O16. (1 分) (2018·青海) 如图,用一个半径为 20cm,面积为 不计接头损耗 ,则圆锥的底面半径 r 为________cm.的扇形铁皮,制作一个无底的圆锥17.(1 分)函数 y=kx+b 的图象平行于直线 y=﹣2x,且与 y 轴交于点(0,3),则此一次函数的解析式为________. 18. (1 分) 一副三角板叠在一起如图放置,最小锐角的顶点 D 恰好放在等腰直角三角形的斜边上,AC 与 DM, DN 分别交于点 E、F,把△DEF 绕点 D 旋转到一定位置,使得 DE=DF,则∠BDN 的度数是________ .三、 解答题 (共 10 题;共 94 分)第 4 页 共 14 页19. (10 分) (2017·深圳模拟) 计算:|2﹣ |+( ﹣2016)0+2cos30°+( ) ﹣1 .20. (10 分) 解不等式:﹣2≤2x﹣ .21. (10 分) (2017 八上·温州月考) 如图,已知点 D,E 分别在边 AC,AB 上,AE = AD,BE = CD,边 BD,CE 交于点 O,求证: (1) ∠B=∠C. (2) OE=OD. 22. (6 分) (2017·兖州模拟) 某学校为了增强学生体质,决定开设以下体育课外活动项目:A 篮球、B 乒乓 球、C 跳绳、D 踢毽子,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成 了两幅不完整的统计图,请回答下列问题:(1) 这次被调查的学生共有________人; (2) 请你将条形统计图补充完成; (3) 在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓 球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答). 23. (11 分) (2019 八上·皇姑期末) 某校为了解学生的安全意识情况,在全校范围内随机抽取部分学生进 行问卷调查,根据调查结果,把学生的安全意识分成“淡薄”、“一般”、“较强”、“很强”四个层次,并绘制 如下两幅尚不完整的统计图.第 5 页 共 14 页根据以上信息,解答下列问题:(1) 该校有名同学,现要对安全意识为“淡薄”、“一般”的学生加强安全教育,根据调查结果,估计全校需要加强对安全教育的学生约有多少名?(2) 请直接将条形统计图补充完整.24. (10 分) (2018·衢州模拟) 在 Rt△ABC 中,∠ACB=90°,BE 平分∠ABC,D 是边 AB 上一点,以 BD 为直径的⊙O 经过点 E,且交 BC 于点 F.(1) 求证:AC 是⊙O 的切线; (2) 若 BF=6,⊙O 的半径为 5,求 CE 的长. 25. (6 分) (2018·夷陵模拟) A、B 两辆汽车同时从相距 330 千米的甲、乙两地相向而行,s(千米)表示 汽车与甲地的距离,t(分)表示汽车行驶的时间,如图,L1 , L2 分别表示两辆汽车的 s 与 t 的关系?(1) L1 表示哪辆汽车到甲地的距离与行驶时间的关系? (2) 汽车 B 的速度是多少? (3) 求 L1,L2 分别表示的两辆汽车的 s 与 t 的关系式. (4) 2 小时后,两车相距多少千米? (5) 行驶多长时间后,A、B 两车相遇?第 6 页 共 14 页26. (10 分) 如图所示,画出△ABC 三边的高.27. (10 分) (2018·菏泽) 如图,在平面直角坐标系中,抛物线 y=ax2+bx﹣5 交 y 轴于点 A,交 x 轴于点 B (﹣5,0)和点 C(1,0),过点 A 作 AD∥x 轴交抛物线于点 D.(1) 求此抛物线的表达式; (2) 点 E 是抛物线上一点,且点 E 关于 x 轴的对称点在直线 AD 上,求△EAD 的面积; (3) 若点 P 是直线 AB 下方的抛物线上一动点,当点 P 运动到某一位置时,△ABP 的面积最大,求出此时点 P 的坐标和△ABP 的最大面积. 28. (11 分) (2017 八下·东营期末) 如图 1,在矩形纸片 ABCD 中,AB=3cm,AD=5cm,折叠纸片使 B 点落在边 AD 上的 E 处,折痕为 PQ.过点 E 作 EF//AB 交 PQ 于 F,连接 BF,(1) 求证:四边形 BFEP 为菱形; (2) 当 E 在 AD 边上移动时,折痕的端点 P,Q 也随着移动. ①当点 Q 与点 C 重合时,(如图 2),求菱形 BFEP 的边长; ②如限定 P,Q 分别在 BA,BC 上移动,求出点 E 在边 AD 上移动的最大距离.第 7 页 共 14 页一、 单选题 (共 10 题;共 20 分)1-1、 2-1、 3-1、 4-1、 5-1、 6-1、 7-1、 8-1、 9-1、 10-1、二、 填空题 (共 8 题;共 8 分)11-1、 12-1、 13-1、 14-1、 15-1、 16-1、 17-1、 18-1、三、 解答题 (共 10 题;共 94 分)参考答案第 8 页 共 14 页19-1、20-1、 21-1、 21-2、 22-1、22-2、22-3、 23-1、第 9 页 共 14 页23-2、24-1、第 10 页 共 14 页24-2、25-1、25-2、25-3、25-4、25-5、26-1、27-1、27-2、27-3、28-1、28-2、。
学2018届九年级下学期期中考试数学试题(附答案)

2017—2018学年第二学期初三数学期中考试试卷考试时间为120分钟.试卷满分130分一、选择题(本大题共10小题,每题3分,共计30分.) 1.-3的相反数是( ) A .3 B .-3C .13D .-132.函数yx 的取值范围是( )A .2x ≠B .2x ≥C .2x ≤D .2x >3.下列计算结果正确的是( ) A.277a a a += B.236a a a ?C.34a aa ? D.()22ab ab =4.下面四个手机应用图标中,属于中心对称图形的是( )A .B .C .D .5. 如果反比例函数1k y x-=的图象经过点(1,-2),那么k 的值是( ) A .-2B .-1C .2D .16.对于一组统计数据3,3,6,5,3.下列说法错误的是( )A .众数是3B .平均数是4C .中位数是6D .方差是1.6 7. 如图所示,所给的三视图表示的几何体是( )A .圆锥B .四棱锥C .三棱锥D .三棱柱8. 如图,O ⊙中,弦AB ,CD 相交于点P ,∠A=42°,∠APD=77°,则∠B 的大小是( ) A. 35°B. 34°C. 43°D.44°9.如图,在R t △ABC 中,∠ABC=90°,AB=3,BC=4,∠BAC ,∠ACB 的平分线相交于点E ,过点E 作EF ∥AC 交AC 于点F ,则EF 的长为( ) A .52 B .154 C . 103 D .53第8题图 第9题图 第10题图 10.已知正方形MNOK 和正六边形ABCDEF 边长均为1,把正方形放在正六边形中,使OK 边与AB 边重合,如图所示.按下列步骤操作:将正方形在正六边形中绕点B 顺时针旋转,使KM 边与BC 边重合,完成第一次旋转;再绕点C 顺时针旋转,使MN 边与CD 边重合,完成第二次旋转;……在这样连续6次旋转的过程中,点B ,M 间的距离不可能是( )A .0.5B .0.6C .0.7D .0.8 二、填空题(本大题共8小题,每题2分,共计16分.) 11.分解因式:ab ﹣a 2= .12.某公司在埃及新投产一座鸡饲料厂,年生产饲料可饲养57000000只肉鸡,这个数据用科学记数法可表示为 .13. 命题“全等三角形的面积相等”的逆命题是 命题.(填入“真”或“假”) 14.已知圆锥的底半径为3cm ,母线长为6cm ,则圆锥的侧面积是 cm 2.15.如图, A B C '''∆是ABC ∆在点O 为位似中心经过位似变换得到的,若A B C '''∆的面积与ABC ∆的面积比是4:9,则:OB OB '为 .16. 如图,菱形ABCD 的对角线相交于点O ,AC =2,BD =点B 与点O 重合,折痕为EF ,则五边形AEFCD 的周长为 .17. 如图,半径为6cm 的⊙O 中,C 、D 为直径AB 的三等分点,点E 、F 分别在AB 两侧的半圆上,∠BCE=∠BDF=60°,连接AE 、BF ,则图中两个阴影部分的面积为 m 2.第15题图 第16题图 第17题图18. 已知四边形ABCD 中A (-2,1+m )、B (-2,2+m )、C (0,2+m )、D (0,1+m ),有一抛物线2(1)y x =+与该四边形ABCD 的边(包括四个顶点)恰好有3个交点,则m 的值是 .三、解答题(本大题共10小题,共计84分.解答需写出必要的文字说明或演算步骤.) 19.计算与化简(本题共有2小题,每小题4分,共8分)(1101()20172--; (2)2()(2)x y x y x +--.20.(本题共有2小题,每小题4分,共8分)(1)解不等式组: ⎪⎩⎪⎨⎧-≥-->+1312112x x x ; (2)解方程:x 2+3x ﹣2=0 .21.(本题满分8分)如图,已知:△ABC 中,AB=AC ,M 是BC 的中点,D 、E 分别是AB 、AC 边上的点,且BD=CE .求证:MD=ME .22.(本题满分8分)在“宏扬传统文化,打造书香校园”活动中,学校计划开展四项活动:“A﹣国学诵读”、“B﹣演讲”、“C﹣课本剧”、“D﹣书法”,要求每位同学必须且只能参加其中一项活动,学校为了了解学生的意愿,随机调查了部分学生,结果统计如下:(1)如图,希望参加活动C占20%,希望参加活动B占15%,则被调查的总人数为人,扇形统计图中,希望参加活动D所占圆心角为度,根据题中信息补全条形统计图.(2)学校现有800名学生,请根据图中信息,估算全校学生希望参加活动A有多少人?23.(本小题满分8分) 某超市为了答谢顾客,凡在本超市购物的顾客,均可凭购物小票参与抽奖活动,奖品是三种瓶装饮料,它们分别是:绿茶、红茶和可乐,抽奖规则如下:①如图,是一个材质均匀可自由转动的转盘,转盘被等分成五个扇形区域,每个区域上分别写有“可”、“绿”、“乐”、“茶”、“红”字样;②参与一次抽奖活动的顾客可进行两次“有效随机转动”(当转动转盘,转盘停止后,可获得指针所指区域的字样,我们称这次转动为一次“有效随机转动”);③假设顾客转动转盘,转盘停止后,指针指向两区域的边界,顾客可以再转动转盘,直到转动为一次“有效随机转动”;④当顾客完成一次抽奖活动后,记下两次指针所指区域的两个字,只要这两个字和奖品名称的两个字相同(与字的顺序无关),便可获得相应奖品一瓶;不相同时,不能获得任何奖品.根据以上规则,回答下列问题:(1)求一次“有效随机转动”可获得“乐”字的概率;(2)有一名顾客凭本超市的购物小票,参与了一次抽奖活动,请你用列表或树状图等方法,求该顾客经过两次“有效随机转动”后,获得一瓶可乐的概率.24. (本小题满分6分)如图1,点M ,N 把线段AB 分割成AM ,MN 和BN ,若以AM ,MN ,BN 为边的三角形是一个直角三角形,则称点M ,N 是线段AB 的勾股分割点(1)已知点M ,N 是线段AB 的勾股分割点,若AM=3,MN=4,则BN 的长为 ; (2)已知点C 是线段AB 上的一定点,其位置如图2所示,请在BC 上画一点D ,使C ,D 是线段AB 的勾股分割点(要求尺规作图,不写画法,保留作图痕迹,画出一种情形即可)图1 图225.(本小题满分8分)定义:数学活动课上,李老师给出如下定义:如果一个三角形有一边上的中线等于这条边的一半,那么称三角形为“智慧三角形”.DFCEBAOBA理解:⑴如图1,已知B A ,是⊙O 上两点,请在圆上找出满足条件的点C ,使A B C ∆为“智慧三角形”(画出点C 的位置,保留作图痕迹);⑵如图2,在正方形ABCD 中,E 是BC 的中点,F 是CD 上一点,且CD CF 41=,试判断AEF ∆是否为“智慧三角形”,并说明理由;运用:⑶如图3,在平面直角坐标系xOy 中,⊙O 的半径为1,点Q 是直线3=y 上的一点,若在⊙O 上存在一点P ,使得OPQ ∆为“智慧三角形”,其面积的最小值为 .26.(本小题满分10分)为满足社区居民健身的需要,市政府准备采购若干套健身器材免费提供给社区,经考察,劲松公司有,A B 两种型号的健身器可供选择.(1)劲松公司2015年每套A 型健身器的售价为2.5万元,经过连续两年降价,2017年每套售价为1.6 万元,求每套A 型健身器年平均下降率n ;图1 图2(2)2017年市政府经过招标,决定年内采购并安装劲松公司,A B 两种型号的健身器材共80套,采购专项费总计不超过112万元,采购合同规定:每套A 型健身器售价为1.6万元,每套B 型健身器售价为()1.51n - 万元. ①A 型健身器最多可购买多少套?②安装完成后,若每套A 型和B 型健身器一年的养护费分别是购买价的005 和0015 .市政府计划支出10 万元进行养护.27. (本小题满分10分) 如图,已知抛物线y =12x 2+的直线y=−x+b 交抛物线于另一点C (-5,6),点D C 不重合),作DE ∥AC ,交该抛物线于点E , (1)求m,n,b 的值; (2)求tan ∠ACB ;(3)探究在点D 运动过程中,是否存在∠不存在,请说明理由.28. (本小题满分10分) 如图1,在△ABC 中,∠A=30°,点P 从点A 出发以2cm /s 的速度沿折线A ﹣C ﹣B 运动,点Q 从点A 出发以a (cm /s )的速度沿AB 运动,P ,Q 两点同时出发,当某一点运动到点B 时,两点同时停止运动.设运动时间为x (s ),△APQ 的面积为y (cm 2),y 关于x 的函数图象由C 1,C 2两段组成,如图2所示.(1)求a 的值;(2)求图2中图象C 2段的函数表达式;(3)当点P 运动到线段BC 上某一段时△APQ 的面积,大于当点P 在线段AC 上任意一点时△APQ 的面积,求x 的取值范围.C 1C 2初三数学答案一、选择题(本大题共10题,每小题3分,共计30分)1、A2、B3、C4、B5、B6、C7、C8、A9、D 10、A二、填空题(本大题共8小题,每小题2分,共计16分)11、a(b-a) 12、5.7×10713、假14、18π15、2:316、7 17、18、-1三、解答题(本大题共10小题,共计84分.)19.(本题满分8分)(1) =2+2-1=3(化简3分各1分+1分) (2)=2x2+y2(公式2分+去括号1分+1分)20. (本题满分8分)(1) 由(1)得x>-1 (1分) 由(2)得x≤2(3分)∴-1<x≤2 (4分)(2)∵b2﹣4ac=32﹣4×1×(﹣2)=17(2分),∴x x==4分)21.(本题满分8分)⑴证明:△ABC中,∵AB=AC,∴∠DBM=∠ECM,(2分)∵M是BC的中点,∴BM=CM,(4分)在△BDM和△CEM中,,∴△BDM≌△CEM(SAS),(7分)∴MD=ME.(8分)22.(本小题满分8分)⑴60 (2分)72 (4分)⑵B 9人 D 12人图中一个空1分(6分)⑶360(8分)23. (本小题满分8分)解:(1)∵转盘被等分成五个扇形区域,每个区域上分别写有“可”、“绿”、“乐”、“茶”、“红”字样;∴一次“有效随机转动”可获得“乐”字的概率为:;(2分)(2)画树状图得:(4分)∵共有25种等可能的结果,该顾客经过两次“有效随机转动”后,获得一瓶可乐的有2种情况,(7分)∴该顾客经过两次“有效随机转动”后,获得一瓶可乐的概率为:.(8分)24. (本小题满分6分)(1)2分 5(2)尺规作图过点C作AB的垂线(4分)作DF的中垂线(6分)25. (本小题满分8分)2分5分6分8分(326. (本小题满分10分)解:2.5(1-n)2=1.6(1分)解得:n 1=0.2=20%, n 2=1.8(不合题意,舍去). (2分) 答:每套A 型健身器材年平均下降率n 为20%; (3分) (2)①设A 型健身器材可购买m 套,则B 型健身器材可购买(80﹣m )套, (4分) 依题意得:1.6m+1.5×(1﹣20%)×(80﹣m )≤112, (5分) 整理,得1.6m+96﹣1.2m ≤1.2,解得m ≤40, (6分) 即A 型健身器材最多可购买40套; (7分) ②设总的养护费用是y 元,则y=1.6×5%m+1.5×(1﹣20%)×15%×(80﹣m ),(8分) ∴y=﹣0.1m+14.4.∵﹣0.1<0, ∴y 随m 的增大而减小,∴m=40时,y 最小.∵m=40时,y 最小值=﹣01×40+14.4=10.4(万元).又∵10万元<10.4万元,∴该计划支出不能满足养护的需要27. (本小题满分10分)解:(1)∵直线y=−x+b 经过点C(−5,6) ∴b =1 (1分) ∵B 在x 轴上,且在直线y=−x+b 上 ∴B(1,0) ∵抛物线y =12x 2+mx +n 过B(1,0)、C(−5,6)∴ m=1,n=−32………………………3分(2)作CF ⊥x 轴于F ,作AG ⊥BC 于G ∴F(−5,0)∵抛物线y =12x 2+mx +n 与x 轴交于A 、B∴A(−3,0) B(1,0)∴CF=BF=6,AF=2,AB=4∴∠CBF=45°∴BG=AG=2 2 ∴CG=4 2∴tan ∠ACB=12………………………6分(3) ∵DE ∥AC ∴∠BDE=∠BCA ∵∠DEA=45° ∠DBA=45° ∴∠BAE=∠BDE=∠BCA ………………………8分 ∴tan ∠BAE=12设E (t,12 t 2+t −32 ) ∴tan ∠BAE =−12 t 2−t +32 t+3 =12∴t=0 ∴E(0,− 32 ) ∴AE= 32 5 ………………………10分28. (本小题满分10分)(1)a=1 (2分)(2)如图2,作PD ⊥AB 于D ,由图象可知,PB =5×2﹣2x =10﹣2x ,PD =PB •sin B =(10﹣2x )•sin B ,∴y =12×AQ ×PD =12x ×(10﹣2x )•sin B , ∵当x =4时,y =43,∴12×4×(10﹣2×4)•sin B =43, 解得,sin B =13,( 4分) ∴y =12x ×(10﹣2x )×13,即21533y x x =-+ ; (6分,酌情给分) (3)22115233x x x =-+,解得,x 1=0,x 2=2,(7分) 由图象可知,当x =2时,212y x =有最大值,最大值是12×22=2,21533x x -+=2解得x 1=3,x 2=2,(9分)∴当2<x <3时,点P 运动到线段BC 上某一段时△APQ 的面积,大于当点P 在线段AC 上任意一点时△APQ 的面积.(10分,酌情给分)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
河北省唐山市丰南区2018届九年级数学下学期期中试题答案 (仅供参考,试卷如有问题,请各位老师自行解决,答案不唯一的酌情给分)
一、1.C 2.D 3.D 4.D 5.C 6.D 7.C 8.B 9.C 10. D 11.C 12.B 13.C 14.C 15.B
16.C
二、17. 9 18. 8 19. 41
三、20.(1)解:如图 (2)
分 ∵AD BC CE AB ⋅=⋅2
121 ∴AD CE 2= .............................................3分 ∴2
1=CE AD ............................................4分 (2)解:①点A 在第二象限 ...............................5分 理由:∵a 没有平方根
∴00〉-〈a a .........................................6分
∴点A 在第二象限 ②由题意可知c a 3=-
∴3a c =或3a c =-.........................................7分
∴3328324
c b c c b c ⨯-+=⎧⎨--=-⎩ 解得,3,3,1a b c === ∴B (3,1) .............8分 或3(3)28324c b c c b c ⨯--+=⎧⎨---=-⎩
解得,6,6,2a b c ===- ∴B (6,-2)............9分 (1) 证明:∵AB=A C ∴∠B=∠C . .....................1分
∵AD+EC=AB AD+BD=AB ∴BD =EC .....................2分
在△DBE 和△ECF 中
∵BE =CF ∠B =∠C BD =EC ,
∴△DBE ≌△ECF (SAS ). ....................3分
∴DE=EF . .....................4分
∴DEF 是等腰三角形.
(2)解:∵∠A=40°,∠B=∠C , ∴∠B=∠C=70°......................5分
∴∠BDE+∠DEB=110°.
∵△DBE ≌△ECF .∴∠FEC =∠BDE , .....................6分
∴∠FEC+∠DEB=110°,
∴∠DEF=70°. .....................7分
(3)当∠A 为60度时,△DEF 是等边三角形 .....................9分
21.(1)-5或1 .....................2分
(2)8cm 或4cm .....................4分
(3)120°或60° .....................6分
(4)由题意可知:
若三边长为17、17、8,此时8+17>17,周长为42; .....................8分
若三边长为17、8、8,此时8+8<17,无法围成三角形,此情况舍去. .....................9分
22.解:(1)5028.010===c b a .....................3分
(2)略 .....................4分
(3)(5×10+6×18+7×14+8×8)÷50=6.4(本) .....................6分
(4)样本中,学生课外阅读7本及以上的人数占0.28+0.16=0.44 .....................7分 估计全校约有1200×0.44=528人课外阅读7本及以上. .....................9分
23.解:(1)由题意得:x=1时y=2;x=2时,y=6代入得:.....................2分
⎩
⎨⎧=+=+6242b a b a .....................3分 解得:⎩⎨⎧==1
1b a
∴x x y +=2 .....................4分
(2)由题意得:
g=31x-150-(x 2
+x ) .....................5分
g=-x 2 +30x-150 .....................6分
(3)∵g=-x 2 +30x-150;
∴g=-x 2 +30x-150=-(x-15)2 +75, .....................8分
∴a=-1<0,抛物线开口向下,g有最大值.
∴当x=15时,g最大值=75. .....................9分
即设施开放15个月后,游乐场的纯收益达到最大为75万元. .....................10分25.(1)∵A(-1,0),B(0,3),∠AOB=90°
∴tan∠BAO=3∴∠BAO=60° ....................2分
(2)S1=S2, ....................3分
理由如下:
依题意有:OA=A′O,∠BAO=60°,
∴△A′AO是等边三角形,
∴∠AOA′=∠BA′O=60°, ....................4分
∴A′B′∥x轴,∴点A′、B′到x轴的距离相等 .........5分
∵∠ABO=∠A′OB=90°-60°=30°
∴A′O=A′B=AA′ ....................6分
∵等边△A′AO的三条高都相等
∴点O到AB的距离等于点B′到x轴的距离
∴S1=S2(等底等高的三角形面积相等).................7分
(3)S1与S2的关系没变,仍然有S1=S2, .................8分
理由如下:
过点B作BC⊥A′O于C,过点B′作B′D⊥x轴于D,
∴∠BCO=∠B′DO=90° .................9分
依题意有:∠BOD=∠A′OB′=90°,∴∠1+∠A′OD=∠2+∠A′OD=90°∴∠1=∠2
又∵B′O=BO
∴△BOC≌△B′OD(AAS) .................10分
∴BC=B′D
又∵AO=A′O
∴S1=S2(等底等高的三角形面积相等) .................11分
∥,
26.解:(1)∵OA BC
∴OAD ADB ∠=∠,
∴tan tan 2ADB OAD ∠=∠=. 在Rt ABD △中,∵6AB OC ==, ∴6
3tan 2AB
DB ADB ===∠.
∴1CD CB BD =-=,(1,6)D . .................2分 ∵抛物线21:(0)M y ax bx a =+≠过A ,D 两点,
∴1640,
6,a b a b +=⎧⎨+=⎩解得2,8.
a b =-⎧⎨=⎩
∴抛物线1M 的表达式为2
28y x x =-+. .................3分
(2)∵222282(4)2(2)8y x x x x x =-+=--=--+. ∴抛物线的对称轴为2x =. .................4分 设点(2,)P y ,
∵(4,0)A ,(0,6)C ,
∴2224652AC =+=,2222(42)4AP y y =-+=+, 22222(6)4(6)CP y y =+-=+-. ∵90CPA ∠=︒,
∴222AC AP CP =+,即225244(6)y y =+++-, .................5分 整理得2640y y --=.
解得13y =,23y =, .................6分
故1(2,3P ,2(2,3P . .................7分
(2)由题意知,抛物线2M 的表达式为228y x x m =-+-, ①∵(1,6)D ,
∴(1,6)D m '-,
设直线AE 的表达式为y mx n =+, 则40,4,m n n +=⎧⎨=⎩解得1,
4,
m n =-⎧⎨=⎩
∴直线AE 的表达式为4y x =-+. .................8分 ∵点(1,6)D m '-在直线AE 上, ∴146m -+=-,解得3m =. ................9分 ②由①知,当抛物线经过点(1,3)时,m 的值为3; 当x m =时,设直线与抛物线交于点(,4)P m m -+,
则2
428
m m m m
-+=-+-,
解得2
m=或2
m=(舍去); .................10分当抛物线2
28
y x x m
=-+-与直线AE只有一个交点时,
联立
2
28,
4,
y x x m y x
⎧=-+-⎨
=-+
⎩
消去y,整理得3
2940
x x m
-++=,
由818(4)0
m
∆=-+=,解得
49
8
m=. .................11分
综上可知,所求m的取值范围为
49
2
8
m<. .................12分。
