第一课时 函数的单调性
第一课时 函数的单调性

)
解析:函数 f(x)=2x2-mx+5 的图象是开口方向朝上,以直线 x= 若函数 f(x)在(-≦,-2]上单调递减,则-2≤ 所以 f(1)=7-m≤15.故选 C.
m ,即 m≥-8, 4
高中·数学
自我检测
1.(单调性的定义)已知函数 f(x)的定义域为 D,在区间 M 上单调递增,则( (A)M=D (C)M⊆ D 是增函数知3≤-a-1,即a≤-4.
(2)由题意得-a-1=3,a=-4. 答案:(1)(-∞,-4] (2)-4 误区警示 函数的单调区间与函数在某一区间上单调是两个不同的概
念,其中后者的区间是函数单调区间的子集.
高中·数学
变式探究:若本题改为函数f(x)=-x2-2(a+1)x+3在区间(1,2)上是单调函
象翻到x轴上方就得到f(x)=|x2+2x-3|的图象,如图所示.
由图象易得,函数的递增区间是[-3,-1],[1,+≦); 函数的递减区间是(-≦,-3],[-1,1].
高中·数学
题型三 函数单调性的应用 【例3】 已知函数f(x)=-x2-2(a+1)x+3. (1)函数f(x)在区间(-∞,3]上是增函数,则实数a的取值范围是 (2)函数f(x)的单调递增区间是(-∞,3],则实数a的值为 解析:f(x)=-x2-2(a+1)x+3=-(x+a+1)2+(a+1)2+3. 因此函数的单调递增区间为(-≦,-a-1]. . ;
.
高中·数学
点击进入 课时作业
f(x)=
2x 在(1,+∞)上是减函数. x 1
2 ,设 x1>x2>1, x 1
数学课件:函数的单调性

如果函数在某区间的两端点取值 相等,则函数在该区间内可能存 在拐点或极值点。
常见函数的单调性
一次函数
二次函数
指数函数
对数函数
一次函数在其定义域内是单 调的,其单调性取决于一次 项系数的正负。一次项系数 大于0时,函数单调递增; 一次项系数小于0时,函数 单调递减。
二次函数的单调性取决于二 次项系数和一次项系数的正 负。当二次项系数大于0时 ,函数开口向上,对称轴左 侧函数单调递减,右侧函数 单调递增;当二次项系数小 于0时,函数开口向下,对 称轴左侧函数单调递增,右 侧函数单调递减。
要点二
详细描述
在函数中,如果函数在某个区间内单调递增或递减,那么 我们可以根据这个性质来确定参数的取值范围。例如,如 果函数$f(x)$在区间$[a, b]$上单调递增,那么对于任意的 $x_1, x_2 in [a, b]$,如果$x_1 < x_2$,则有$f(x_1) < f(x_2)$。因此,如果函数在某个区间内单调递增,那么参 数必须满足一定的条件才能使函数在这个区间内单调递增 。
函数单调性的几何解释
单调性的几何解释
在平面坐标系中,如果函数图像在某区间内是上升或下降的,则该函数在此区间 内是单调递增或单调递减的。
单调性的判定方法
通过观察函数图像或利用导数来判断函数的单调性。如果函数图像在某区间内是 上升或下降的,或者导数大于0或小于0,则该函数在此区间内是单调递增或单调 递减的。
02
判断函数单调性的方法
导数与函数单调性
导数大于0,函数单 调递增;导数小于0 ,函数单调递减。
导数等于0的点可能 是函数的极值点或拐 点。
导数的符号变化点可 能是函数的拐点或极 值点。
函数的单调性第一课时
y 1-
0
2
1 -
-
3 2
2
x
(1)根据函数说出函数的单调区间以及 函数在各单调区间内的单调性;
(2)写出函数的定义域和值域
2.研究一次函数y=kx+b的图像,指出 当k取何值时函数是减函数。
3.2.1 函数的单调性
课堂小结:
一、函数单调性的定义 二、判断函数单调性的两种方法:
(1)图像法 (2)定义法:4个步骤
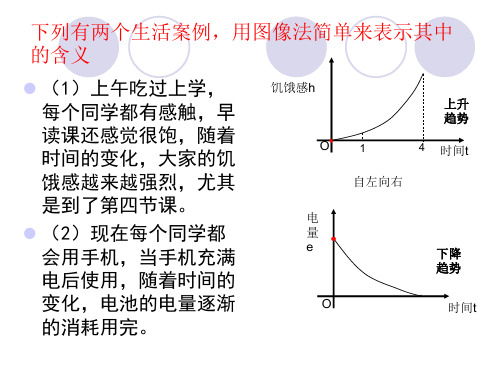
下列有两个生活案例,用图像法简单来表示其中 的含义
(1)上午吃过上学, 每个同学都有感触,早 读课还感觉很饱,随着 时间的变化,大家的饥 饿感越来越强烈,尤其 是到了第四节课。
(2)现在每个同学都 会用手机,当手机充满 电后使用,随着时间的 变化,电池的电量逐渐 的消耗用完。
饥饿感h O
上升 趋势
观察函数图像
.
解:由图像可以看出,函数的增区间为(0,40),减区间为(40,60).
练习:下图是定义在闭区间[-5,5]上的函数y=f(x)的图 象,根据图象说出y=f(x)的单调区间,以及在每一单调 区间上, y=f(x)是增函数还是减函数。
正确答案: 增区间为:[-2,1],[3,5] 减区间为:[-5,-2],[1,3]
单调区间的说明:
如果函数f(x)在区间(a,b)内是增函数(或减 函数),那么称函数f(x)在区间(a,b)内具有 单调性。区间(a,b)叫做函数f(x)的单调区间。
注意一点:函数f(x)的单调区间不仅是开区 间,也可以是闭区间、半开半闭区间。
3.2.1 函数的单调性 动脑思考 探索新知
函数单调性的判定方法
其图像为一条直线
列表:
1
x01 y -2 2
5.3.1函数的单调性(第一课时)课件(人教版)

利用导数判断含参函数的单调性
例
2:函数
f
(
x
)
1 = ax
2-(
a+1)
x
+lnx
,a>0,试讨论函数
f(
x
)
的单调性.
2
解:函数的定义域为(0,+∞),
1 ax2-(a+1)x+1 (ax-1)(x-1)
f′(x)=ax-(a+1)+ =
=
,
x
x
x
1
1
1
1,
①当 0<a<1 时, >1,∴x∈(0,1)和( ,+∞)时,f′(x)>0;x∈ a 时,f′(x)<0,
a
a
1
1
0,
,1
∴函数 f(x)在 a 和(1,+∞)上单调递增,在 a 上单调递减,
利用导数判断含参函数的单调性
综上所述,
1
1
,+∞
1,
当 0<a<1 时,函数 f(x)在(0,1)和 a
上单调递增,在 a 上单调递减;
当 a=1 时,函数 f(x)在(0,+∞)上单调递增;
1
1
0,
,1
当 a>1 时,函数 f(x)在 a 和(1,+∞)上单调递增,在 a 上单调递减.
RART 02
函数的单调性与导数
函数的单调性
思考:视察下面一些函数的图象,探讨函数的单调性与导数的正负的关系.
y y=x
O
x
(1)
y
y=x2
O
x
(2)
y
y=x3
O
x
y y=x-1
O
x
(3)
第一课时 函数的单调性

(2)函数的单调区间
如果函数y=f(x)在区间D上是单调递增或单调递减,那么就说函数y=f(x)在 这一区间具有(严格的)单调性,区间D叫做y=f(x单)的调_区__间_______.
A.已知区间I,若对任意的x1,x2∈I,当x1<x2时,f(x1)<f(x2),则y=f(x) 在I上是增函数 B.函数y=x2在R上是增函数
由x1,x2∈(1,+∞),得x1>1,x2>1,
所以 x21-1>0,x22-1>0,x1+x2>0. 又 x1<x2,所以 x1-x2<0,
于是((xx11- 2-x12) )( (xx221- +1x) 2)<0,即 f(x1)>f(x2), 因此,函数 f(x)=x2-1 1在(1,+∞)上单调递减.
训练 2 (1)已知函数 f(x)=25x-+x1,,xx<≥1,1,则 f(x)的单调递减区间是_(_-__∞__,__1_)___.
解析 当x≥1时,f(x)是增函数,当x<1时,f(x)是减函数,所以f(x)的单
调递减区间为(-∞,1).
(2)画出函数y=|x|(x-2)的图象,并指出函数的单调区间.
训练 1 求证:函数 f(x)=-x1-1 在区间(-∞,0)上单调递增.
证明 ∀x1,x2∈(-∞,0),且x1<x2<0,
因为 f(x1)-f(x2)=-x11-1--x12-1 =x12-x11=x1x-1xx2 2,
高中数学必修一(人教版)《3.2.1 第一课时 函数的单调性》课件

(1)已知f(x)的定义域为[a,b]且为增函数,若f(m)>f(n),则m,n满足什么
关系?
a≤m≤b, 提示:a≤n≤b,
m>n
⇔f(m)>f(n).
(2)影响二次函数 y=ax2+bx+c(a≠0)的单调性的因素有哪些? 提示:a 的正负及-2ba的大小.
【学透用活】 [典例3] (1)已知函数f(x)=-x2-2(a+1)x+3. ①若函数f(x)在区间(-∞,3]上是增函数,则实数a的取值范围是________; ②若函数f(x)的单调递增区间是(-∞,3],则实数a的值为________. (2) 若 函数 f(x) = x2 + ax + b 在 区间 [1,2] 上不 单 调 , 则 实 数 a 的取 值 范 围为 ________.
答案:(-∞,1),(1,+∞)
2.将本例中“y=-x2+2|x|+3”改为“y=|-x2+2x+3|”,如何求解? 解:函数y=|-x2+2x+3|的图象如图所示.
由图象可知其单调递增区间为[-1,1],[3,+∞);单调递减区间为 (-∞,-1),(1,3).
题型三 函数单调性的应用
[探究发现]
(3)若f(x)是R上的减函数,则f(-3)>f(2).
()
(4)若函数f(x)在区间(1,2]和(2,3)上均单调递增,则函数f(x)在区间(1,3)上也单
调递增.
()
答案:(1)× (2)× (3)√ (4)×
2.函数y=f(x)的图象如图所示,其增区间是 A.[-4,4] B.[-4,-3]∪[1,4] C.[-3,1] D.[-3,4] 解析:由图可知,函数y=f(x)的单调递增区间为[-3,1],选C. 答案:C
[方法技巧] 1.图象法求函数单调区间的步骤 (1)作图:作出函数的图象. (2)结论:上升图象对应单调递增区间,下降图象对应单调递减区间. 2.常见函数的单调区间 (1)y=ax+b,a>0 时,单调递增区间为(-∞,+∞);a<0 时,单调递减区 间为(-∞,+∞). (2)y=ax,a>0 时,单调递减区间为(-∞,0)和(0,+∞);a<0 时,单调递 增区间为(-∞,0)和(0,+∞). (3)y=a(x-m)2+n,a>0 时,单调递减区间为(-∞,m],单调递增区间为 (m,+∞);a<0 时,单调递增区间为(-∞,m],单调递减区间为(m,+∞).
5.3.1函数的单调性第一课时

学 习 目 标
01
通过具体函数的图象,发现函数的单调性与导数
的正负之间的关系,体会数形结合思想;(直观
想象)
02
能根据函数导数的正负判断函数的单调性,并会
求函数的单调区间,体会算法思想(数学运算)
单调性是函数的重要性质,它不仅反映了函数变化的趋势,还是研究函数极值与
最大(小)值的基础性问题。虽然可以通过函数图象的升降观察函数的单调性,但
当 ∈ 0, 时,ℎ′ > 0,
函数ℎ 的图像是“上升”的,函数ℎ 在 0, 内单调递增
当 ∈ , 时,ℎ′ < 0,
函数ℎ 的图像是“下降”的,函数ℎ 在 , 内单调递减
ℎ()
追问1
我们看到,函数ℎ 的单调性与ℎ′ 的正负有内在联系。
对于高台跳水问题是否有以下结论?
当1 < < 4时,′() > 0;
当 > 4或 < 1时,′() < 0;
当 = 4或 = 1时, ′ = 0;
试画出函数()图象的大致形状。
y
解答
在区间 (1, 4) 内, f (x)>0,
o 1
4
x
y
则在这区间内函数是增函数;
在区间 (-∞, 1)与(4, +∞) 内,f (x)<0,
A
B
D
)
C
D
02
函数 = ()的图像是下列四个图像之一,其导函数 = ′ 图
象如下右图所示,则该函数图象可能是(
B
)
例4、函数 = ()的图象如下右图所示,则 ′ < 0的
解集是( B )
教学课件:第一课时-函数的单调性

几何解释
在函数图像上,任意两点$x_1 <
x_2$,如果函数值$f(x_1)
<
f(x_2)$,则该函数图像在区间$I$
上呈上升趋势。
单调减函数
定义
如果对于任意$x_1 < x_2$,都有$f(x_1) > f(x_2)$,则称函数$f(x)$在区间$I$ 上单调递减。
几何解释
在函数图像上,任意两点$x_1 < x_2$,如果函数值$f(x_1) > f(x_2)$,则该函 数图像在区间$I$上呈下降趋势。
图像法
通过观察函数的图像来判断函数的单调性。如果图像在某区间内呈上升趋势,则函数在该 区间内单调递增;如果图像在某区间内呈下降趋势,则函数在该区间内单调递减。
03 函数的单调性性质
单调函数的连续性
总结词
单调函数在其定义域内是连续的,即 函数图像在定义域内没有间断点。
详细描述
单调函数在其定义域内的每一点都是 连续的,这意味着函数值在定义域内 不会突然跳跃或中断。单调函数的图 像是一条连续的曲线。
单调函数的可导性
总结词
单调函数在其定义域内是可导的,即函数图像在定义域内没 有拐点。
详细描述
单调函数在其定义域内的每一点都是可导的,这意味着函数 值的变化率是恒定的。单调函数的导数要么恒大于等于零, 要么恒小于等于零。
单调函数的极值
总结词
单调函数在其定义域内没有极值点,即函数在单调区间内没有局部最大值或局部 最小值。
详细描述
由于单调函数的图像是一条连续的上升或下降曲线,因此在单调区间内,函数值 要么单调递增,要么单调递减,没有局部最大值或局部最小值。极值点只出现在 函数的拐点或定义域的边界上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.3 函数的基本性质
1.3.1 单调性与最大(小)值
第一课时函数的单调性
【选题明细表】
基础巩固
1.下列命题正确的是( D )
(A)定义在(a,b)上的函数f(x),若存在x1、x2∈(a,b),当x1<x2时,有f(x1)<f(x2),那么f(x)在(a,b)上为增函数
(B)定义在(a,b)上的函数f(x),若有无穷多对x1、x2∈(a,b),当x1<x2时,有f(x1)<f(x2),那么f(x)在(a,b)上为增函数
(C)若函数f(x)在区间I1上为减函数,在区间I2上也为减函数,那么f(x)在区间I1∪I2上就一定是减函数
(D)若函数f(x)是区间I上的增函数,且f(x1)<f(x2)(x1、x2∈I),则x1<x2
解析:选项A中并不是对任意x1、x2都成立;选项B中虽然有无穷多对,但也不能代表“所有”“任意”;选项C中以f(x)=为例,虽然在
(-∞,0)和(0,+∞)上均为减函数,但在整个定义域上却不具有单调性.故选D.
2.如果函数f(x)在区间[a,b]上是增函数,对于任意的x1、x2∈
[a,b](其中x1<x2),下列结论不正确的是( C )
(A)>0
(B)(x1-x2)[f(x1)-f(x2)]>0
(C)f(a)<f(x1)<f(x2)<f(b)
(D)f(x2)-f(x1)>0
解析:因为x1<x2,f(x)在[a,b]上是增函数,
所以f(x1)<f(x2),x1-x2<0,f(x1)-f(x2)<0,
故选项A、B、D正确.
对选项C:因为a≤x1<x2≤b且f(x)在[a,b]上是增函数,
所以f(a)≤f(x1)<f(x2)≤f(b),故选C.
3.下列函数中,在(-∞,0]内为增函数的是( C )
(A)y=x2-2 (B)y=
(C)y=1+2x (D)y=-(x+2)2
解析:选项A、B在(-∞,0)上为减函数,选项D在(-2,0]上为减函数,只有选项C满足在(-∞,0]内为增函数.故选C.
4.若函数f(x)=(2a-1)x+b是R上的减函数,则( D )
(A)[,+∞) (B)(-∞,]
(C)(-,+∞) (D)(-∞,)
解析:由一次函数的性质得2a-1<0,即a<,
故选D.
5.已知y=x2+2(a-2)x+5在区间(4,+∞)上是增函数,则a的取值范围是( B )
(A)(-∞,-2] (B)[-2,+∞)
(C)[-6,+∞) (D)(-∞,-6]
解析:由题意得-≤4得a≥-2.故选B.
6.若函数f(x)在R上单调递增,则f(x2-2x)与f(-1)的大小关系为( A )
(A)f(x2-2x)≥f(-1) (B)f(x2-2x)≤f(-1)
(C)f(x2-2x)=f(-1) (D)不能确定
解析:因为x2-2x=(x-1)2-1≥-1,
又函数f(x)在R上单调递增,
所以f(x2-2x)≥f(-1).故选A.
7.已知函数f(x)=则f(x)的单调递减区间是. 解析:当x≥1时,f(x)是增函数;当x<1时,f(x)是减函数,所以f(x)的单调递减区间为(-∞,1).
答案:(-∞,1)
8.函数f(x)=|2x-1|的单调减区间为,单调增区间
为.
解析:函数f(x)=|2x-1|=2|x-|的图象如图所示,由图可知函数f(x)的单调递增区间为[,+∞),
单调递减区间为(-∞,].
答案:(-∞,] [,+∞)
9.(2015蒙自一中质检)已知函数f(x)=.
(1)求f(x)的定义域和值域;
(2)判断函数f(x)在区间(2,5)上的单调性,并用定义来证明所得结论.
解:(1)f(x)===1+,
定义域为{x|x≠1},值域为{y|y≠1}.
(2)由函数解析式可知该函数在(2,5)上是减函数,下面证明此结论. 证明:任取x1,x2∈(2,5),
设x1<x2,
则f(x1)-f(x2)=-=.
因为2<x1<x2<5,
所以x2-x1>0,x1-1>0,x2-1>0,
所以f(x1)>f(x2).
故函数在(2,5)上为减函数.
能力提升
10.已知函数f(x)=4x2-kx-8在[1,4]上具有单调性,则实数k的取值范围是( C )
(A)(-∞,4]∪[16,+∞) (B)[4,16]
(C)(-∞,8]∪[32,+∞) (D)[8,32]
解析:由f(x)在[1,4]上具有单调性,
得-≤1或-≥4,
得k≤8或k≥32.
故选C.
11.已知函数f(x)在区间[-1,1]上是单调函数且f(0)<f(1),则满足f(x)<f()的实数x的取值范围为.
解析:由题意知函数f(x)在区间[-1,1]上是单调增函数,所以不等式f(x)<f()等价于
即-1≤x<.
答案:[-1,)
12.已知定义在区间(0,+∞)上的函数f(x)满足f()=f(x 1)-f(x2),且当x>1时,f(x)<0.
(1)求f(1)的值;
(2)判断f(x)的单调性;
(3)若f(3)=-1,解不等式f(|x|)<-2.
解:(1)令x1=x2>0,
代入得f(1)=f(x1)-f(x1)=0,
故f(1)=0.
(2)任取x1,x2∈(0,+∞),
且x 1>x2,则>1,
由于当x>1时,f(x)<0,
所以f()<0,即f(x1)-f(x2)<0.
因此f(x1)<f(x2),
故函数f(x)在区间(0,+∞)上是单调递减函数.
(3)由f()=f(x1)-f(x2)得
f()=f(9)-f(3),
而f(3)=-1,
所以f(9)=-2.
由于函数f(x)在区间(0,+∞)上是单调递减函数,
且f(|x|)<-2=f(9),
所以|x|>9,解得x>9或x<-9.
探究创新
13.已知函数f(x)=满足对任意x1≠x2,都有<0成立,则实数a的取值范围是.
解析:由<0对任意x1≠x2都成立,得f(x)是减函数,则得a≤0.
答案:(-∞,0]。
