平行四边形的性质及判定测试题2014新版
平行四边形判定专项练习30题

平行四边形的判定专项练习30 题(有答案)1.如图,四边形ABCD 中, AD ∥BC, ED∥ BF , AF=CE ,求证: ABCD 是平行四边形.2.如图,四边形ABCD 中,∠ BAC=90 °, AB=11 ﹣ x, BC=5 , CD=x ﹣ 5, AD=x ﹣ 3, AC=4 .求证:四边形ABCD 为平行四边形.3.已知四边形ABCD 的对角线AC 与 BD 交于点 O,现给出四个条件:① OA=OC ;② AB=CD ;③∠ BAD= ∠DCB ;④ AD ∥ BC.请你从中选择两个,推出四边形ABCD 为平行四边形,并写出你的推理过程.( 1)从以上 4 个条件中任意选取 2 个条件,能推出四边形ABCD 是平行四边形的有(用序号表示)_________.( 2)从( 1)中选出一种情况,写出你的推理过程.4.如图,已知:点 B 、 E、 F、D 在一条直线上,DF=BE , AE=CF .请从下列三个条件中选择一个合适的条件,添加到已知条件中,使四边形ABCD 是平行四边形,并说明理由,供选择的三个条件(请从其中选择一个):①AB=DC ;② BC=AD ;③ ∠ AED= ∠ CFB .5.如图,在 ?ABCD 中, AC 交 BD 于点 O,点 E,点 F 分别是 OA ,OC 的中点,请判断线段 BE , DF 的位置关系和数量关系,并说明你的结论.6.如图所示,以△ABC 的三边为边在 BC 的同侧分别作三个等边三角形△ ABD 、△ BCE、△ ACF ,猜想:四边形ADEF 是什么四边形,试证明你的结论.7.如图,已知BE ⊥ AD , CF⊥ AD ,且 BE=CF .求证:( 1)AD 是△ ABC 的中线;( 2)请连接BF、 CE,试判断四边形BECF 是何种特殊四边形,并说明理由.8.如图,矩形 ABCD 的两条对角线 AC 和 BD 相交于点 O, E、 F 是 BD 上的两点,且∠ AEB= ∠CFD .求证:四边形AECF 是平行四边形.9.如图:在四边形ABCD 中, AD ∥BC , AB=CD ,E 是 BC 上一点, DE=AB .求证:四边形ABED 是平行四边形.10.如图,已知AB ∥DC, E 是 BC 的中点, AE , DC 的延长线交于点F;(1)求证:△ ABE ≌△ FCE ;(2)连接 AC , BF.则四边形 ABFC 是什么特殊的四边形?请说明理由.11.等边△ ABC 中,点 D 在 BC 上,点 E 在 AB 上,且 CD=BE ,以 AD 为边作等边△ADF ,如图.求证:四边形CDFE 是平行四边形.12.如图,分别以 Rt△ ABC 的直角边 AC 及斜边 AB 向外作等边△ ACD 、等边△ ABE .若∠ BAC=30 °, EF⊥ AB ,垂足为 F,连结 DF.求证:( 1)△ ABC ≌△ EAF ;( 2)四边形ADFE 是平行四边形.13.已知:如图,在△ ABC 中,中线 BE ,CD 交于点 O, F, G 分别是 OB ,OC 的中点.求证:四边形 DFGE 是平行四边形.14.如图所示:在四边形A、C 同时出发,点 P以(1)几秒钟后,四边形(2)几秒钟后,四边形ABCD 中, AD ∥BC、 BC=18cm , CD=15cm ,AD=10cm , AB=12cm ,动点 P、Q 分别从2cm/秒的速度由 A 向 D 运动,点 Q 以 3cm/秒的速度由 C 向 B 运动.ABQP 为平行四边形?并求出此时四边形ABQP 的周长PDCQ 为平行四边形?并求出此时四边形PDCQ 的周长.15.求证:顺次连接四边形各边中点所得的四边形是平行四边形.16.△ ABC 中,中线 BE 、 CF 相交于 O, M 是 BO 的中点, N 是 CO 的中点,求证:四边形 MNEF 是平行四边形.17.如图, AD=DB , AE=EC ,FG∥ AB , AG ∥BC .(1)证明:△ AGE ≌△ CFE;(2)说明四边形 ABFG 是平行四边形;(3)研究图中的线段 DE, BF , FC 之间有怎样的位置关系和数量关系.18.如图,△ ABC 和△ ADE 都是等边三角形,点 D 在 BC 边上, AB 边上有一点F,且 BF=DC ,连接 EF、 EB .(1)求证:△ ABE ≌△ ACD ;(2)求证:四边形 EFCD 是平行四边形.19.已知在△ ABC 中, D、 E 分别是 AB 、AC 的中点,点 F 在 DE 的延长线上,且 EF=DE ,图中有几个平行四边形?请说明你的理由.20.如图,在△ ABC 中,AD 是中线,点 E 是 AD 的中点,过 A 点作 BC 的平行线交CE 的延长线于点F,连接 BF.求证:四边形AFBD 是平行四边形.21.如图:在四边形 ABCD 中, AD ∥ BC, E 是 BC 的中点, BC=2AD .找出图中所有的平行四边形,并选择一个说明它是平行四边形的理由.22.求证:两组对角分别相等的四边形是平行四边形.23.已知:如图,A、 B、 C、D 在同一条直线上,且AB=CD , AE ∥ DF,AE=DF .求证:四边形EBFC 是平行四边形.24.如图,在△ ABC 中, D 是 BC 边的中点, E、 F 分别在 AD 及其延长线上, CE∥ BF ,连接 BE、 CF.图中的四边形BFCE 是平行四边形吗?为什么?25.已知点 E、 F、 G、H 分别为四边形ABCD 四边的中点,试问四边形EFGH 的形状并说明理由.26.如图,已知四边形 ABCD 中 AD=BC ,点 A 、 B、 E 在同一条直线上,且∠ B=∠ EAD ,试说明四边形 ABCD 是平行四边形.27.如图, AD ∥ BC, ED∥ BF ,且 AE=CF ,求证:四边形ABCD 是平行四边形.28.已知:△ ABC 的中线 BD、 CE 交于点 O, F、 G 分别是 OB 、 OC 的中点.求证:四边形DEFG 是平行四边形.29.如图,△ACD 、△ ABE 、△ BCF 均为直线 BC 同侧的等边三角形.当 AB ≠AC 时,求证:四边形 ADFE 为平行四边形.30.已知:在四边形ABCD 中, AD ∥ BC,且 AB=DC=5 , AC=4 , BC=3 .求证:四边形ABCD 为平行四边形.平行四边形的判定30 题参考答案:1.∵ AD ∥BC ,∴∠ DAE= ∠ BCF ,∵ED∥ BF,∴∠ DEF= ∠ BFE,∴∠ AED= ∠ CFB ,又∵ AF=CE ,∴AE=CF ,在△ADE 和△ CBF 中:∵∠ DAE= ∠ BCF ,∠AED= ∠CFB ,AE=CF ,∴△ ADE ≌△ CBF (AAS ),∴AD=CB ,即: AD ∥ CB,AD=CB ,∴四边形 ABCD 是平行四边形,2.∵∠ BAC=90 °, AB=11 ﹣ x, BC=5 , AC=4 .222∴( 11﹣ x) +4 =5 ,解得: x1=8, x2=14 >11(舍去),当x=8 时, BC=AD=5 ,AB=CD=3 ,∴四边形 ABCD 为平行四边形.3.( 1)解:能推出四边形 ABCD 是平行四边形的有①④ 、③④ ;故答案是:①④、③④;( 2)以①④为例进行证明.如图,在四边形ABCD 中, OA=OC , AD ∥ BC .证明:∵ AD ∥ BC,∴∠ DAO= ∠ BCO.∴在△ AOD 与△COB 中,,∴四边形ABCD 是平行四边形.5. BE=DF , BE∥ DF因为 ABCD 是平行四边形,所以 OA=OC , OB=OD ,因为 E, F 分别是 OA ,OC 的中点,所以 OE=OF ,所以BFDE 是平行四边形,所以 BE=DF , BE ∥ DF6.四边形ADEF 是平行四边形.连接 ED 、EF,∵△ ABD 、△BCE 、△ACF 分别是等边三角形,∴AB=BD , BC=BE ,∠ DBA= ∠EBC=60 °.∴∠ DBE= ∠ ABC .∴△ ABC ≌△ DBE .同理可证△ ABC ≌△ FEC,∴AB=EF , AC=DE .∵AB=AD , AC=AF ,∴AD=EF , DE=AF .∴四边形 ADEF 是平行四边形7.( 1)∵ BE ⊥ AD ,CF⊥ AD ,∴∠ BED= ∠ CFD.∵∠ BDE= ∠ CDF, BE=CF ,∴△ BED ≌△ CFD.∴BD=CD .∴AD 是△ ABC 的中线.(2)四边形 BECF 是平行四边形,由( 1)得: BD=CD , ED=FD .∴四边形 BECF 是平行四边形8.∵四边形ABCD 是矩形∴ AB ∥CD , AB=CD ,∴△ AOD ≌△ COB ( ASA ),∴AD=BC ,∴在四边形ABCD 中, AD BC ,∴四边形 ABCD 为平行四边形.∴∠ ABE= ∠ CDF,又∵∠ AEB= ∠ CFD,∴△ ABE ≌△ CDF,∴BE=DF ,又∵四边形ABCD 是矩形,∴OA=OC , OB=OD ,∴OB ﹣BE=OD ﹣ DF,∴OE=OF ,∴四边形AECF 是平行四边形4.选择①,9.∵ AD ∥ BC, AB=CD ,∵ DF=BE ,AE=CF , AB=CD ,∴四边形ABCD 是等腰梯形,∴△ ABE ≌△ CDF (sss),∴∠ B=∠ C,∴∠ DEC= ∠B ,∴AB ∥DE,∴四边形 ABED 是平行四边形.10.( 1)证明:∵ AB ∥ DC ,∴∠ 1=∠ 2,∠ FCE= ∠EBA ,∵E 为 BC 中点,∴CE=BE ,∵在△ ABE 和△ FCE 中,∠ 1=∠ 2,∠ FCE= ∠EBA ,CE=BE ,∴△ ABE ≌△ FCE;(2)四边形ABFC 是平行四边形;理由:由( 1)知:△ ABE ≌△ FCE,∴ EF=AE ,∵CE=BE ,∴四边形 ABFC 是平行四边形11.连接 BF ,∵△ ADF 和△ ABC 是等边三角形,∴AF=AD=DF , AB=AC=BC ,∠ABC= ∠ACD= ∠CAB= ∠ FAD=60 °,∴∠ FAD ﹣∠ EAD= ∠ CAB ﹣∠ EAD ,∴∠ FAB= ∠CAD ,在△FAB 和△DAC 中,∴△ FAB ≌△ DAC ( SAS),∴BF=DC ,∠ ABF= ∠ ACD=60 °,∵ BE=CD ,∴BF=BE ,∴△ BFE 是等边三角形,∴EF=BE=CD ,在△ACD 和△CBE 中∵,∴△ ACD ≌△ CBE ( SAS),∴AD=CE=DF ,∵EF=CD ,∴四边形 CDFE 是平行四边形.∴∠ FEA= ∠ BAC ,在△ ABC 和△EAF 中,,∴△ ABC ≌△ EAF ( AAS );(2)∵∠BAC=30 °,∠DAC=60 °,∴∠ DAB=90 °,即 DA ⊥ AB ,∵EF⊥AB ,∴ AD ∥EF,∵△ABC ≌△EAF ,∴ EF=AC=AD ,∴四边形 ADFE 是平行四边形13.在△ ABC 中,∵AD=BD , AE=CE ,∴DE∥BC 且 DE=BC .在△ OBC 中,∵ OF=FB , OG=GC ,∴FG∥ BC 且 FG= BC .∴DE ∥ FG, DE=FG .∴四边形 DFGE 为平行四边形14.(1)x 秒后,四边形 ABQP 为平行四边形.则 2x=18﹣3x,解得 x=3.6 .3.6 秒钟后,四边形 ABQP 为平行四边形,此时四边形ABQP 的周长是 3.6×2×2+12 ×2=38.4cm .(2)y 秒后,四边形 PDCQ 为平行四边形. 10﹣ 2y=3y ,解得 y=2.2 秒钟后,四边形 PDCQ 为平行四边形,此时四边形 PDCQ 的周长是 3.6×2×2+15×2=43.2cm .15.:连接 BD ,∵E、F 为 AD ,AB 中点,∴ FE BD .又∵ G、H 为 BC,CD 中点,∴GH BD ,故GH FE.同理可证, EH FG.∴四边形FGHE 是平行四边形16.∵ BE ,CF 是△ ABC 的中线,∴EF∥ BC 且 EF= BC,∴MN ∥BC 且 MN= BC,∴EF∥MN 且 EF=MN ,∴四边形 MNEF 是平行四边形.17.( 1)证明:∵ AG∥ BC (已知)∴∠ G=∠ EFC(两直线平行,内错角相等)∵∠AEG= ∠FEC(对顶角相等),又AE=EC (已知)∴△ AGE ≌△ CFE( AAS );( 2)说明:∵ FG∥ AB ,AG ∥ BC (已知)∴四边形 ABFG 是平行四边形(平行四边形的定义);∵EF=BF ,BF=DC ,∴ EF=DC ,∴四边形 EFCD 是平行四边形19.平行四边形ADCF 和平行四边形DBCF .理由:( 1)∵ D 、E 分别是 AB 、 AC 边的中点,∴DE∥BC,.又∵ EF=DE ,∴DF=BC ,∴四边形DBCF 是平行四边形;( 2)在四边形 ADCF 中,( 3)解:线段 DE ,BF,FC 之间的位置关系是DE ∥ BF,∵ EF=DE ,DE ∥FC ,数量关系是 DE=BF=FC ,又∵ E 是 AC 边的中点,理由:由( 1)可知△ AGE ≌△ CFE∴ EA=EC ,∴ AG=FC , FE=EG (全等三角形的对应边相等),∴四边形 ADCF 是平行四边形∴ E 是 FG 的中点,又∵ AD=DB (已知)20.∵ E 为 AD 中点,∴ DE 为三角形 ABC 的中位线,∴ AE=DE ,∴ DE= BC,DE ∥ BC,∵AF ∥BC,∴∠ AFE= ∠ DCE ,即 DE∥ BF, DE ∥ FC,在△AEF 和△CED 中由( 2)可知四边形 ABFG 是平行四边形∴ AG=BF ,∵,∴ BF=FC= BC ,∴△ AEF ≌△ CED( AAS ),∴ DE=BF=FC ,∴ AF=DC ,即线段 DE , BF, FC 之间的位置关系是 DE∥BF ,∵ AD 是△ ABC 的中线,DE ∥FC ,数量关系是 DE=BF=FC .∴ BD=DC ,∴ AF=BD ,即 AF∥ BD ,AF=BD ,故四边形 AFBD 是平行四边形21.图中有两个平行四边形: ?ABED 、 ?AECD .18.( 1)∵△ ABC 和△ ADE 都是等边三角形,∵,∴ AE=AD , AB=AC ,∠ EAD= ∠ BAC=60 °,∴∠ EAD ﹣∠ BAD= ∠ BAC ﹣∠ BAD ,∴ AD=BE ,∵ AD ∥ BC ,即:∠ EAB= ∠ DAC ,∴四边形 ABED 是平行四边形.∴△ ABE ≌△ ACD ( SAS);22.已知:四边形ABCD ,∠ A= ∠C,∠ B= ∠D ,( 2)证明:∵△ ABE ≌△ ACD ,∴ BE=DC ,∠ EBA= ∠ DCA ,又∵ BF=DC ,∴ BE=BF .∵△ ABC 是等边三角形,求证:四边形 ABCD 是平行四边形,∴∠ DCA=60 °,证明:∵∠ A= ∠ C,∠ B=∠ D,∴△ BEF 为等边三角形.∠ A+ ∠ B+∠ C+∠ D=360 °,∴∠ EFB=60 °, EF=BF∴ 2∠A+2 ∠B=360 °,∵△ ABC 是等边三角形,∴∠ A+ ∠ B=180 °,23.∵ AE ∥ DF,∴∠ A=∠D,在△ABE 和△ DCF 中∴△ ABE ≌△ DCF (SAS),∴EB=FC ,∠ ABE= ∠DCF ,∵∠ ABE+ ∠EBC=180 °,∠ DCF+ ∠ FCB=180 °,∴∠ EBC= ∠FCB ,∴BE ∥FC,∵ BE=FC ,∴四边形 EBFC 是平行四边形24.∵ CE∥ BF , BD=CD ,∴△ BDF ≌△ CDE ,∴BF=CE ,∴四边形 BFCE 是平行四边形.25.四边形 EFGH 是平行四边形证明:连接 AC 、 BD∵ E、 F、 G、H 分别为四边形ABCD 四边的中点∴ EH= BD ,FG= BD , HG= AC , EF= AC∴EH=FG , EF=HG∴四边形 EFGH 是平行四边形.26.∵∠ B=∠ EAD ,∴AD ∥BC,∵ AD=BC ,∴四边形 ABCD 是平行四边形.27.∵ AD ∥BC,∴∠ EAD= ∠ FCB ,又ED∥ BF,∴∠FED= ∠ EFB,∠ AED=180 °﹣∠ FED ,∠ CFB=180 °﹣∠ EFB,∴∠ AED= ∠ CFB,又已知 AE=CF ,∴△ AED ≌△ CFB ,∴AD=BC ,∴四边形ABCD 是平行四边形.28.∵AD ∥BC ,∴∠ EAD= ∠ FCB,又ED∥ BF,∴∠FED= ∠ EFB ,∠ AED=180 °﹣∠ FED,∠ CFB=180 °﹣∠ EFB ,∴∠ AED= ∠ CFB,又已知 AE=CF ,∴△AED ≌△CFB ,∴ AD=BC ,∴四边形 ABCD 是平行四边形.29.∵△ ABE 、△ BCF 为等边三角形,∴AB=BE=AE ,BC=CF=FB ,∠ ABE= ∠CBF=60 °.∴∠ FBE= ∠ CBA ,在△FBE 和△CBA 中,,∴△ FBE ≌△ CBA ( SAS).∴EF=AC .又∵△ ADC 为等边三角形,∴CD=AD=AC .∴EF=AD .同理可得 AE=DF .∴四边形 AEFD 是平行四边形30.∵ AB=5 , AC=4 , BC=3222∴ AB =AC +BC∴∠ BCA=90 °∵AD ∥BC∴∠ DAC= ∠BCA=90 °∵DC=5 ,AC=4 ,222∴AD =DC ﹣AC =9∴ AD=BC=3∴四边形ABCD 为平行四边形.。
2013-2014新人教版八年级下平行四边形的判定测试题

平行四边形判定测试题2014-4-3一、选择题1.(2013•泸州)四边形ABCD 中,对角线AC 、BD 相交于点O ,下列条件不能判定这个四边形是平行四④两条对角线相等. 以上四种条件中,可以判定四边形ABCD 是平行四边形的有( )A .1个B .2个C .3个D .4个3.(2013·泰安)如图,在平行四边形ABCD 中,AB=4,∠BAD 的平分线与BC 的延长线交于点E ,与DC 交于点F ,且点F 为边DC 的中点,DG ⊥AE ,垂足为G ,若DG=1,则AE 的边长为( )A .2B .4C .4D .84.(2013•荆门)四边形ABCD 中,对角线AC 、BD 相交于点O ,给出下列四个条件:①AD ∥BC ;②AD=BC ;③OA=OC ;④OB=OD(A)AB ∥CD ,AD=BC (B)AB=AD ,CB=CD(C)AB=CD ,AD=BC (D)∠B=∠C ,∠A=∠D6.(2013•钦州)如图,图1、图2、图3分别表示甲、乙、丙三人由甲A 地到B 地的路线图(箭头表示行条件,这个条件可以是( )①AF=CF ;②AE=CF ;③∠BAE=∠FCD ;④∠BEA=∠FCEA .①或②B .②或③C .③或④D .①或③或④8.下列条件中,能判定四边形是平行四边形的条件是( ) A.一组对边平行,另一组对边相等 B.一组对边平行,一组对角相等 C.一组对边平行,一组邻角互补 D.一组对边相等,一组邻角相等9.如图,已知□ABCD 的对角线交点是O ,直线EF 过O 点,且平行于BC ,直线GH 过且平行于AB ,则图中共有( )个平行四边形.A.5B.6C.7D.1010..以下结论正确的是( )A.对角线相等,且一组对角也相等的四边形是平行四边形B.一边长为5cm ,两条对角线分别是4cm 和6cm 的四边形是平行四边形 1题图 3题图 6题图 7题图 9题图C.一组对边平行,且一组对角相等的四边形是平行四边形D.对角线相等的四边形是平行四边形11.如图,在△ABC 中,DE ∥AB ,FD ∥BC ,EF ∥AC ,则下列说法中正确的有( )个。
(完整版)平行四边形的性质及判定测试题

平行四边形的性质及判定测试题班级 _____学号 _____ 姓名 ______ 成绩 ____一、填空:(每空4分,共32分)1、 在平行四边形 ABCD 中,已知AB 、BC 、CD 三条边的长度分别为(x+3),( x-4 )和16,则这个四边形 的周长是 _____________ 。
2、 如图,在平行四边形 ABCD 中,EF 〃AD,GH 〃AB,EF 、GH 相交于点0,则图中共有________ 个平行四边形. _3、 平行四边形 ABCD 中,/ A = 45°, BC = 2 ,则AB 与CD 之间的距离是 ______________ ;若 AB = 3,四边形ABCD 的面积是 ________ , △ ABD 的面积是 _____ .4、 在平行四边形 ABCD 中,AB 1, BC 3, ABC 与 BCD 的平分线分别交 AD 于E 、F ,则EF 的长为5、 平行四边形的两个邻角的平分线相交所成的角是 _____________ °6、 ________________________________________________________________ 若口ABCD 与口ABEF 有公共边 AB ,那么四边形 DCEF 是 _________________________________________________7、 _________________________________________________________________________________________________ 在厶ABC 中,AB=6cm , AC=8cm , BC=10cm , D 、E 、F 分别是各边中点, 则厶DEF 的周长= ______________ △ DEF 的面积是 ______ .& A,B,C,D 在同一个平面内,从① AB//CD ②AB=CD ③BC// AD ④BC=A [这四个条件中任意选两个, 能使四边形ABCD 是平行四边形的选法有 ___________________ 种、解答题:(共56 分)1、已知如图,O 为平行四边形 ABCD 的对角线AC 的中点,EF 经过点O ,且与AB 交于E ,与CD 交于F 。
平行四边形的判定测试题
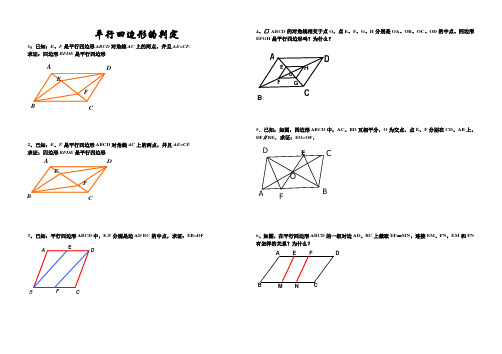
平行四边形的判定1:已知:E 、F 是平行四边形ABCD 对角线AC 上的两点,并且AE =CF . 求证:四边形BFDE 是平行四边形2、已知:E 、F 是平行四边形ABCD 对角线AC 上的两点,并且AE=CF . 求证:四边形BFDE 是平行四边形3、已知:平行四边形ABCD 中,E.F 分别是边AD BC 的中点,求证:EB=DF4、□ ABCD 的对角线相交于点O ,点E 、F 、G 、H 分别是OA 、OB 、OC 、OD 的中点。
四边形EFGH 是平行四边形吗?为什么?5.已知:如图,四边形ABCD 中,AC 、BD 互相平分,O 为交点,点E 、F 分别在CD 、AB 上,DF ∥BE .求证:EO=OF .6、如图,在平行四边形ABCD 的一组对边AD 、BC 上截取EF =MN ,连接EM 、FN ,EM 和FN 有怎样的关系?为什么?CDFBABCDEFOA BCDE F M NDA B C E F D A B C E F G E F D O H C B A巨型的性质7:□ABCD 的对角线AC 与BD 相交于点O ,(1)若AC=BD ,则□ABCD 是 形; (2)若∠ABC 是直角,则□ABCD 是形; 8:9.已知△ABC 是Rt △,∠ABC=900, BD 是斜边AC 上的中线(1)若BD=3㎝ 求AC(2) 若∠C=30°,AB =5㎝,求AC 与BD10.已知菱形的周长是12cm ,那么它的边长是______. 菱形ABCD 中∠BAD =60度,则∠ABD =_______.11、如图,将矩形ABCD 沿AE折叠,使点D 落在BC 边上的F 点处。
(1)若∠BAF =60°,求∠EAF 的度数;(2)若AB =6cm ,AD =10cm ,求线段CE 的长12、将长方形ABCD 的纸片,沿EF 折成如图所示;已知∠EFG=55º,求∠FGE13、练习3如图,矩形ABCD 沿BE 折叠,使点C 落在AD 边上的F 点处,如果∠ABF=60º,求∠CBEC BACCDA。
(完整版)平行四边形性质和判定习题(答案详细)(可编辑修改word版)
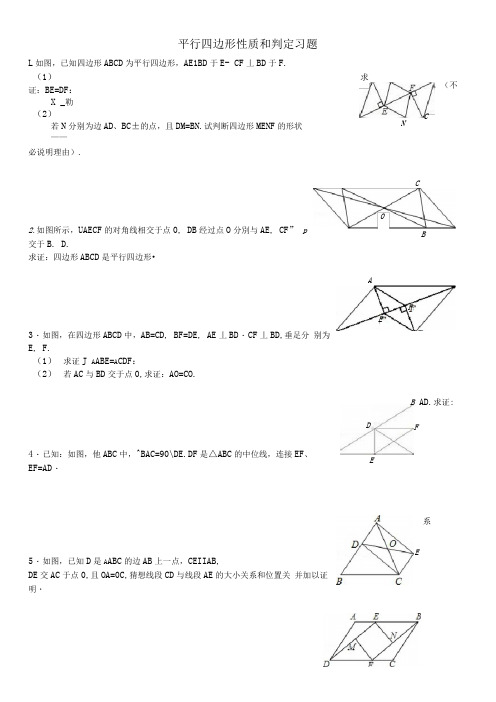
平行四边形性质和判定习题L如图,已知四边形ABCD为平行四边形,AE1BD于E- CF丄BD于F.(1)求证:BE=DF:X _勒(2)若N分别为边AD、BC±的点,且DM=BN.试判断四边形MENF的形状——必说明理由).2.如图所示,UAECF的对角线相交于点0, DB经过点O分別与AE, CF” p交于B. D.求证:四边形ABCD是平行四边形•3・如图,在四边形ABCD中,AB=CD, BF=DE, AE丄BD・CF丄BD,垂足分别为E, F.(1)求证J A ABE=A CDF:(2)若AC与BD交于点0,求证:AO=CO.4・已知:如图,他ABC中,^BAC=90\DE.DF是△ABC的中位线,连接EF、EF=AD・5・如图,已知D是A ABC的边AB上一点,CEIIAB,DE交AC于点0,且OA=0C,猜想线段CD与线段AE的大小关系和位置关并加以证明・B AD.求证:。
(不CNCBAFED FE系E6・如图,已知,UABCD中,AE=CF, M、N分别是DE、BF的中点.求证:四边形MFNE是平行四边形•7・如图,平行四边形ABCD, E 、F 两点在对角线BD 上,且BE=DF,连接AE. EG CF, FA ・求证:四边形AECF 是平行四边形•& 在UABCD 中,分别以AD 、BC 为边向内作等边△ADE 和等边△BCF,连接BE. DF ・求证:四边形BEDF 是平 行四边形・DBIIAC,且DB 丄AC. E 是AC 的中点,求证:BC=DE ・2如图,在梯形ABCD 中,ADIIBC, AD=24cm. BC=30cm,点P 自点A 向D 以IcmZs 的速度运动,到D 点Q 自点C 向B 以2cm/s 的速度运动,到B点即停止,直线PQ 截梯形为两个四边形•问当P. Q同时10. 已知脣 点即停止. 出发,几秒后其中一个四边形为平行四边形?IL 如图:已知D 、E 、F 分别是A ABC 各边的中点, 求证:AE 仃DF 互相平分.如图所示, 9・ED13.如图,已知四边形ABCD中,点E, F. G, H分别是AB、CD、AC. BD的中点,并且点E、F、G、H有在同一条直线上.求证:EF和GH互相平分・14.如图J oABCD 中,MNIIAC.试说明MQ=NP.15.已知:如图所示「平行四边形ABCD的对角线AC, BD柑交于点6 EF经过点0并且分别和AB. CD相交于点E, F,点G, H分别为OA, 0C的中点.求证:四边形EHFG是平行四边形.-46 如制已知的ABCD中,E、F是对角线BD上的两点,BE=DF,点G、H分别在BA和DC的延长线上,且AG=CH. 连接GE、EH、HF、FG.(1)求证:四边形GEHF是平行四边形;(2)若点G、H分别在线段BA和DC上,尖余条件不变,则(1)中的结论是否成立?(不用说明理由)17.如图,在A ABC中,D是AC的中点,E是线段BC延长线一点,过点A作BE的平行线与线段ED的延长线交于点F,连接AE、CF.(1)求证J AF=CE:(2)如果AC=EF,且ZACB=135\试判断四边形AFCE是什么样的四边形,并证明你的结论・18,如图平行四边形ABCD 中.mBC=6(几 点E 、F 分別在CD.BC 的延长线上,AE||BD ・ EEhBB 垂足为点F, DF=2 (1) 求证:D 是EC 中点; (2) 求FC 的长.19.如图,已知A ABC 是等边三角形,点D 、F 分别在线段BC 、AB 匕 厶EFB=60。
(完整版)平行四边形的性质和判定练习题.doc

初 2017 级寒假培训(八) A 层----平行四边形的性质与判定班级: 姓名:1.定 :两 互相平行的四 形叫做平行四 形,平行四 形 ABCD 作: □ ABCD几何 言:AB // CD , AD // BC , 四边形 ABCD 是平行四边形AD2.性 :平行四 形的 平行且相等, 角相等, 角互 , 角 互相平分;几何 言:∵四 形 ABCD 是平行四 形O∴ AD ∥ BC, _________ ( 平行); AD=BC ,__________( 相等);BCBAC BCD , _________( 角相等); BACABC 180 ⋯( 角互 ) ;OA OC ,( 角 互相平分) 。
平行四边形的判定:判定 1.两 分 平行的四 形是平行四 形 判定 2.两 分 相等的四 形是平行四 形 判定 3.两 角分 相等的四 形是平行四 形 判定 4. 角 互相平分的四 形是平行四 形 判定 5. 一 平行且相等的四 形是平行四 形; 几何 言判定 1.AB // CD , AD // BC , 四边形 ABCD 是平行四边形判定 2. AB DC , AD BC , 四边形 ABCD 是平行四边形判定 3. ABCADC , BADBCD , 四边形 ABCD 是平行四边形 判定 4. AO CO, BO DO , 四边形 ABCD 是平行四边形 判定 5.AB // CD , AB CD ,四边形 ABCD 是平行四边形夯 基 :1. 如 ,将 □ ABCD 的一 BC 延 至 E ,若∠ A =110°, ∠ 1=________.ADABADB E1 D C BCCE242. 如 ,在 □ ABCD 中, A 120,D =°.3. 在平行四 形ABCD 中, AB6cm , BC 8cm , 平行四 形ABCD 的周cm .4. 如 ,在 □ ABCD 中,已知 AD 8CM , AB 6CM , ,DE 平分 ADC 交 BC 于点 E ,则 BE 等于()A.2CMB.4CMC.6CM D .8CM5.平行四边形中一边的长为10cm,那么它的两条对角线的长度可以是()A.4cm和 6cmB.20cm和30cmC.6cm和8cmD.8cm和12cm6.在□ABCD中,对角线 AC,BD相交于点 O,若 BD与 AC的和为 18cm,CD: DA=2:3,AOB的周长为 13cm,那么 BC的长为()A. 6cmB. 9cm C .3cm D .12cm7.如图, ?ABCD 中, AC 、 BD 为对角线, BC=6 , BC 边上的高为4,则阴影部分的面积为.8. 在下面给出的条件中,能判定四边形ABCD是平行四边形的是()A. AB BC, AD CDB.AB // CD, AD BCC.AB // CD , B DD. AB, C D9. 一个四边形的三个相邻内角度数依次如下,那么其中是平行四边形的是()A.88 ,108 ,88B.88 ,104 ,108 C .88 ,92 ,92 D.108 ,72 ,10810.点 A, B,C, D 在同一平面内,从①AB∥CD,② AB=CD,③ BC∥ AD,④ BC=AD 这四个条件中任选两个,能使四边形ABCD是平行四边形的选法有()种A. 3 B.4 C.5 D. 6 ADB C8.如图,在平行四边形 ABCD 中,若 AB=6 ,AD=10 ,?ABC 的平分线交 AD 于点 E,交 CD 的延长线于点 F,求 DF 的长.9. 已知:如图a,ABCD 的对角线 AC 、 BD 相交于点 O , EF 过点 O 与 AB 、 CD 分别相交于点 E 、 F .(1)求证:OE OF , AE CF , BE DF .(2)若上题中的条件都不变,将EF 转动到图 b 的位置,那么结论是否成立?若将EF向两方延长与平行四边形的两对边的延长线分别相交(图 c 和图 d),结论是否成立,说明你的理由.10.已知如图, O 为平行四边形 ABCD的对角线 AC 的中点, EF 经过点 O,且与 AB 交于 E,与 CD 交于 F,求证:四边形 AECF是平行四边形。
(完整版)平行四边形的性质习题(有答案)

平行四边形的性质测试题一、选择题(每题 3 分共 30 分)1.下边的性质中,平行四边形不必定具备的是()A.对角互补B.邻角互补C.对角相等D.内角和为 360°2.在中,∠ A:∠ B:∠ C:∠ D 的值能够是()A .1:2:3:4B .1:2:1:2C .1:1:2:2 D.1: 2:2:13.平行四边形的对角线和它的边能够构成全等三角形()A.3对B.4 对 C .5对D. 6 对A D 4.以下图,在中,对角线 AC、BD交于点 O,?以下式子中一O 定建立的是()B CA.AC⊥ BD B . OA=OC C. AC=BD D .AO=OD5.以下图,在中, AD=5,AB=3,AE均分∠ BAD交BC A D边于点 E,则线段 BE、 EC的长度分别为()BE C A .2和3 B.3和2 C .4和1 D .1和46.的两条对角线订交于点 O,已知 AB=8cm,BC=6cm,△AOB的周长是 18cm,那么△ AOD的周长是()A .14cmB .15cmC .16cmD .17cm7.平行四边形的一边等于14,它的对角线可能的取值是()A .8cm和 16cmB .10cm和 16cmC . 12cm和 16cmD . 20cm和 22cm 8.如图,在中,以下各式不必定正确的选项是()A.∠ 1+∠ 2=180° B .∠ 2+∠ 3=180C.∠ 3+∠ 4=180°D.∠ 2+∠4=180°9.如图,在中,∠ ACD=70°,AE⊥ BD于点E,则∠ ABE等于()A、20°B、25° C 、 30° D 、35°10.如图,在△ MBN中, BM=6,点 A、C、D 分别在 MB、NB、MN上,四边形 ABCD为平行四边形,∠NDC=∠ MDA,那么的周长是()二、填空题(每题 3 分共 18 分)11.在中,∠ A:∠ B=4:5,则∠ C=______.12.在中, AB:BC=1:2,周长为 18cm,则 AB=______cm,AD=_______cm.13.在中,∠A=30°,则∠ B=______,∠C=______,∠D=________.14.如图,已知:点 O是的对角线的交点, ?AC=?48mm,?BD=18mm,AD=16mm,那么△ OBC的周长等于 _______mm.15.如图,在中,E、F是对角线BD上两点,要使△ ADF≌△ CBE,还需增添一个条件是 ________.16.如图,在中,EF∥ AD,MN∥ AB,那么图中共有_______?个平行四边形.三、解答题17.已知:如图,在中,E、F是对角线AC?上的两点,AE=CF.BE与DF的大小有什么关系,并说明原因。
平行四边形性质与判定练习题

平行四边形性质与判定练习题1. 平行四边形的定义平行四边形是指有四条边对两对相邻边均平行的四边形。
2. 平行四边形的性质根据平行四边形的定义,我们可以得出以下性质:- 对边相等:平行四边形的对边相等,即两对相邻边的长度相等。
- 对角线互相平分:平行四边形的两条对角线互相平分,即把平行四边形分成四个相等的三角形。
- 对角线长的一半为高:平行四边形的两条对角线交点到任意边的距离等于对角线的一半,即为平行四边形的高。
3. 判定平行四边形的条件可以利用以下条件来判定一个四边形是否为平行四边形:- 边对边平行:四边形的对边必须互相平行。
- 对角线相等:四边形的对角线必须相等。
4. 练题请回答以下平行四边形的判定练题:1. 判断四边形ABCD是否为平行四边形:- A(2, 3), B(4, 7), C(8, 5), D(6, 1)- AB = 5, BC = 3, CD = 5, DA = 3- AC ≠ BD2. 判断四边形EFGH是否为平行四边形:- E(-1, -3), F(3, -3), G(5, 1), H(1, 1)- EF = 4, FG = 5, GH = 5, HE = 4- EG = FH, EF ≠ GH3. 判断四边形IJKL是否为平行四边形:- I(-2, 1), J(-2, 4), K(2, 4), L(2, 1)- IJ = KL = 3, JK = LI = 5- IJ ≠ KL, JK = LI根据以上判定条件,我们可以得出:- 题目1的四边形ABCD不是平行四边形;- 题目2的四边形EFGH不是平行四边形;- 题目3的四边形IJKL是平行四边形。
以上是关于平行四边形性质与判定的练习题。
希望能帮助你更好地理解平行四边形和判定条件。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A
B C
D
E
平行四边形测试题
一、选择题
1. 在以下平行四边形的性质中,错误的是 ( )
A. 对边平行
B. 对角相等
C. 对边相等
D. 对角线互相垂直 2. 在平行四边形ABCD 中,∠A=65°,则∠D 的度数是 ( )
A. 105°
B. 115°
C. 125°
D. 65°
3.下列给出的条件中,能判定四边形ABCD 是平行四边形的是 ( ). A.AB ∥CD ,AD=BC B.AB=AD ,CB=CD C.AB=CD ,AD=BC D.∠B=∠C ,∠A=∠D 4.关于四边形ABCD :①两组对边分别相等;②一组对边平行且相等;③一组对边平行且另一组对边相等;④两条对角线相等. 以上四种条件中,可以判定四边形ABCD 是平行四边形的有…( ) A .1个
B .2个
C .3个
D .4个
5、下列说法正确的是( ).
A 平行四边形的对角互补,邻角相等
B 平行四边形的对角线相等
C 两组对边分别平行的图形是平行四边形
D 平行四边形的对边平行且相等
6、如图,在□ABCD 中,已知AD =8㎝, AB =6㎝, DE 平分∠ADC 交BC 边于点E ,则BE 等于( ) A.2cm B.4cm C.6cm D.8cm
7. 在□ABCD 中,对角线AC 、BD 相交于点O ,若AC=6,BD=8,则边AB 的取值范围( ) A 1<AB<7 B 2<AB<4 C 6<AB<8 D 3<AB<4 8、在平面直角坐标系中,□ABCD 的顶点,A ,B ,D 的坐标分别是(0,0
(5,0),(2,3),则顶点C 的坐标是( )
A (3,7) B(5,3) C(7,3) D (8,2)
6.(2010 江津)四边形ABCD 的对角线互相平分,要使它成为矩形,那么需要添加的条件是( )
A .A
B CD = B .AD B
C = C .AB BC =
D .AC BD =
7. (2010 四川成都)已知四边形ABCD ,有以下四个条件:①//AB CD ;②AB CD =;③//BC AD ;④BC AD =.从这四个条件中任选两个,能使四边形ABCD 成为平行四边形的选法种数共有( )
A .6种
B .5种
C .4种
D .3种
A
二、填空题
1、已知平行四边形的周长是100cm, AB:BC=4 : 1,则AB 的长是________________.
2、在平行四边形中,若一个角为其邻角的2倍,则这个平行四边形各内角的度数分别是 。
3、如下图1,在平行四边形ABCD 中, BC=2AB, CA ⊥AB,则∠B=______度,∠CAD=______度.
4、在四边形ABCD 中,AD ∥BC ,分别添加下列一个条件,①AB ∥CD,②AB=DC,③AD=BC, ④∠A=∠C ,⑤∠B=∠C,能使四边形ABCD 成为平行四边形的条件的序号是 。
5、如图2,在□ABCD 中,EF ∥AD, GH ∥AB,EF 、GH 相交于点O,则图中共有 个
平行四边形.
6、用边长分别为2cm ,3cm ,4cm 的两个全等三角形拼成四边形,共能拼成 个四边形, 个为平行四边形。
7、延长△ABC 的中线AD 至E ,使DE=AD ,连接BE ,CE ,则AB_____CE ,AC_______BE 。
9.如图:在□ABCD 中,AC 、BD 为对角线,BC=6,BC 边上的高为4, 则阴影部分的面积为________
10.已知平行四边形的面积是144,
相邻两边上的高分别为8和9,则它的
周长是____________ 个全部·。
