2012数学新题分类汇编:算法初步与复数(高考真题 模拟新题)
2012年算法初步理科数学高考题汇编

2012年算法初步理科数学高考题汇编2012年高考真题理科数学解析汇编:算法初步一、选择题1.(2012年高考(天津理))阅读右边的程序框图,运行相应的程序,当输入的值为时,输出的值为()A.B.C.D.2.(2012年高考(新课标理))如果执行右边的程序框图,输入正整数和实数,输出,则()A.为的和B.为的算术平均数C.和分别是中最大的数和最小的数D.和分别是中最小的数和最大的数3.(2012年高考(陕西理))右图是用模拟方法估计圆周率的程序框图,表示估计结果,则图中空白框内应填入()D.4.(2012年高考(山东理))执行下面的程序图,如果输入,那么输出的的值为()A.2B.3C.4D.55.(2012年高考(辽宁理))执行如图所示的程序框图,则输出的S的值是()A.1B.C.D.46.(2012年高考(北京理))执行如图所示的程序框图,输出的S值为()A.2B.4C.8D.167.(2012年高考(安徽理))如图所示,程序框图(算法流程图)的输出结果是()A.B.C.D.二、填空题8.(2012年高考(浙江理))若程序框图如图所示,则该程序运行后输出的值是______________.9.(2012年高考(江西理))下图为某算法的程序框图,则程序运行后输出的结果是______________.10.(2012年高考(江苏))下图是一个算法流程图,则输出的k的值是____.11.(2012年高考(湖南理))如果执行如图3所示的程序框图,输入,n=3,则输出的数S=____.12.(2012年高考(湖北理))阅读如图所示的程序框图,运行相应的程序,输出的结果__________.13.(2012年高考(广东理))(算法)执行如图2所示的程序框图,若输入的值为8,则输出的值为______.14.(2012年高考(福建理))阅读右图所示的程序框图,运行相应地程序,输出的值等于_____________________.2012年高考真题理科数学解析汇编:算法初步参考答案一、选择题1.【答案】C【命题意图】本试题主要考查了算法框图的读取,并能根据已给的算法程序进行运算.【解析】根据图给的算法程序可知:第一次,第二次,则输出.2.【解析】选3.解析:点落在单位圆内或圆上,随机产生1000个数,,故选D.4.【解析】当时,第一次,第二次,第三次,此时不满足,输出,选B.5.【答案】D【解析】根据程序框图可计算得由此可知S的值呈周期出现,其周期为4,输出时因此输出的值与时相同,故选D【点评】本题主要考查程序框图中的循环结构、数列的周期性以及运算求解能力,属于中档题.此类题目需要通过计算确定出周期(如果数值较少也可直接算出结果),再根据周期确定最后的结果.6.【答案】C【解析】,循环结束,输出的为8,故选C【考点定位】本小题主要考查程序框图,涉及到判断循环结束的时刻,以及简单整数指数幂的计算.7.【解析】选二、填空题8.【答案】【解析】T,i关系如下图:T1i23456二、填空题9.3【解析】本题考查算法程序框图的应用以及运算求解的能力.由程序框图可知:第一次:T=0,k=1,成立,a=1,T=T+a=1,k=2,2第二次:不成立,a=0,T=T+a=1,k=3,3第三次:不成立,a=0,T=T+a=1,k=4,4第四次:成立,a=1,T=T+a=2,k=5,满足判断条件,继续循环;第五次:成立,a=1,T=T+a=2,k=6,6【点评】对于循环结构的算法框图问题,要观察什么时候刚好退出循环,,直到循环终止为止.体现考纲中要求理解输出语句,了解算法的含义与思想.来年需要注意判断条件的求解,程序的输出功能等.10.【答案】5.【考点】程序框图.【分析】根据流程图所示的顺序,程序的运行过程中变量值变化如下表: 是否继续循环k循环前00第一圈是10第二圈是2-2第三圈是3-2第四圈是40第五圈是54第六圈否输出5∴最终输出结果k=5.11.【答案】【解析】输入,n=3,,执行过程如下:;;,所以输出的是.【点评】本题考查算法流程图,要明白循环结构中的内容,一般解法是逐步执行,一步步将执行结果写出,特别是程序框图的执行次数不能出错.12.考点分析:本题考查程序框图.解析:程序在运行过程中各变量的值如下表示:第一圈循环:当n=1时,得s=1,a=3.第二圈循环:当n=2时,得s=4,a=5第三圈循环:当n=3时,得s=9,a=7,此时n=3,不再循环,所以解s=9.13.解析:8.第一次循环,,,;第二次循环,,,;第三次循环,,,.此时退出循环,输出的值为8.14.【答案】【解析】,输出【考点定位】该题主要考查算法的基本思想、结构和功能,把握算法的基本思想是解好此类问题的根本.。
2012年高考数学 高考试题+模拟新题分类汇编专题L 算法初步与复数 文
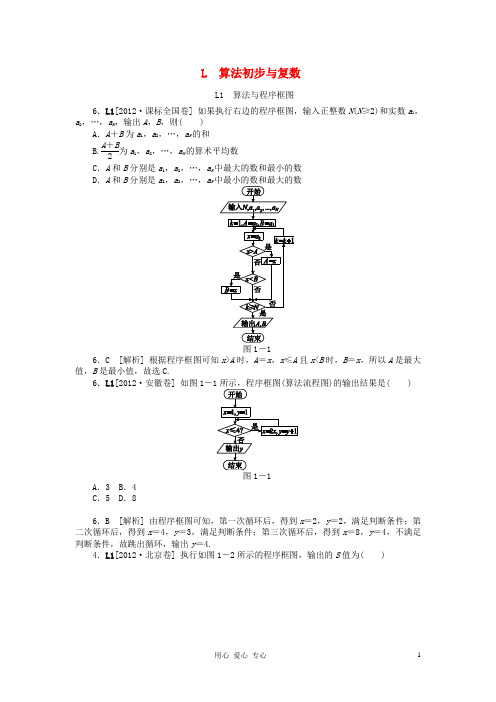
L 算法初步与复数L1 算法与程序框图6.L1[2012·课标全国卷] 如果执行右边的程序框图,输入正整数N(N≥2)和实数a1,a2,…,a N,输出A,B,则( )A.A+B为a1,a2,…,a N的和B.A+B2为a1,a2,…,a N的算术平均数C.A和B分别是a1,a2,…,a N中最大的数和最小的数D.A和B分别是a1,a2,…,a N中最小的数和最大的数6.C [解析] 根据程序框图可知x>A时,A=x,x≤A且x<B时,B=x,所以A是最大值,B是最小值,故选C.6.L1[2012·安徽卷] 如图1-)的输出结果是( )图1-1A.3 B.4C.5 D.86.B [解析] 由程序框图可知,第一次循环后,得到x=2,y=2,满足判断条件;第二次循环后,得到x=4,y=3,满足判断条件;第三次循环后,得到x=8,y=4,不满足判断条件,故跳出循环,输出y=4.4.L1[2012·北京卷] 执行如图1-2所示的程序框图,输出的S值为( )A.2 B.4C.8 D.164.C [解析] 本题考查了循环结构的流程图,简单的整数指数幂计算等基础知识.根据循环k=0,S=1;k=1,S=2;k=2,S=8,当k=3,时,输出S=8.6.L1[2012·福建卷] 阅读如图1-1所示的程序框图,运行相应的程序,输出的s值等于( )A.-3 B.-10 C.0 D.-26.A [解析] 第一次循环由于k=1<4,所以s=2-1=1,k=2;第二次循环k=2<4,所以s=2-2=0,k=3;第三次循环k=3<4,所以s=0-3=-3,k=4,结束循环,所以输出s=-3.16.L1[2012·福建卷] 某地区规划道路建设,考虑道路铺设方案,方案设计图中,点表示城市,两点之间连线表示两城市间可铺设道路,连线上数据表示两城市间铺设道路的费用.要求从任一城市都能到达其余各城市,并且铺设道路的总费用最小,例如:在三个城市道路设计中,若城市间可铺设道路的线路图如图1-2①,则最优设计方案如图1-2②,此时铺设道路的最小总费用为10.2现给出该地区可铺设道路的线路图如图1-2③,则铺设道路的最小总费用为________.16.16 [解析] 根据题意先选择中间最优线路,中间有三条,分别是A→F→G→D、E→F→B、E→G→C,费用最低的是A→F→G→D为3+1+2=6;再选择A→F→G→D线路到点E的最低费用线路是:A→E费用为2;再选择A→F→G→D到C、B的最低费用,则选择:G→C→B,费用最低为3+5=8,所以铺设道路的最小费用为:6+2+8=16.9.L1[2012·广东卷] 执行如图1-2所示的程序框图,若输入n的值为6,则输出s 的值为( )图1-2A.105 B.16C.15 D.19.C [解析] 第一次循环结果是:s=1,i=3;第二次循环结果是:s=3,i=5;第三次循环结果是:s=15,i=7,此时i>n,结束循环,输出s=15.所以选择C.16.L1[2012·湖北卷] 阅读如图1-5所示的程序框图,运行相应的程序,输出的结果s=________.16.[答案] 9[解析] 因为已知a=1,s=0,n=1,所以第一次运行后:s=s+a=1,a=a+2=3,n=1<3成立,满足判断条件;第二次运行后:n=n+1=2,s=s+a=1+3=4,a=a+2=5,n=2<3成立,满足判断条件;第三次运行后:n=n+1=3,s=s+a=4+5=9,a=a+2=7,n=3<3不成立,不满足判断条件,输出s的值(s=9).14.L1[2012·湖南卷] 如果执行如图1-4所示的程序框图,输入x=4.5,则输出的数i图1-414.4 [解析] 本题考查程序框图和循环结构,意在考查考生的逻辑推理能力和对循环结构的理解能力;具体的解题思路和过程:依次循环,达到条件退出.当i=1时x=3.5,当i=2时x=2.5,当i=3时x=1.5,当i=4时x=0.5,此时退出循环,故i=4.[易错点] 本题易错一:循环条件弄错,多计一次,或者少计一次,得到错误结果. 4.L1[2012·江苏卷] 图1-1是一个算法流程图,则输出的k 的值是________.4.5 [解析] 本题为对循环结构的流程图的含义的考查.解题突破口为从循环终止条件入手,再一一代入即可.将k =1,2,3,…,分别代入可得k =5.15.L1[2012·江西卷] 图1-5是某算法的程序框图,则程序运行后输出的结果是________.15.3 [解析] 当k =1时,此时sin π2=1>sin0=0成立,因此 a =1,T =0+1=1,k=1+1=2,k <6成立,再次循环;因sin π=0>sin π2=1不成立,因此a =0,T =1+0=1,k =2+1=3,此时k <6成立,再次循环;因sin 3π2=-1> sin π=0不成立,因此a =0,T=1+0=1,k =3+1=4,此时k <6成立,再次循环;因sin2π=0>sin 3π2=-1成立,因此a =1,T =1+1=2,k =4+1=5,此时k <6成立,再次循环;因sin 5π2=1> sin2π=0成立,因此a =1,T =2+1=3,k =5+1=6,此时k <6不成立,退出循环,此时T =3.10.L1[2012·辽宁卷] 执行如图1-2所示的程序框图,则输出的S 值是( )图1-2A .4 B.32 C.23D .-110.D [解析] 本小题主要考查程序框图的应用.解题的突破口为分析i 与6的关系.当i =1时,S =22-4=-1;当i =2时,S =22--1=23;当i =3时,S =22-23=32;当i =4时,S =22-32=4;当i =5时,S =22-4=-1;当i =6时程序终止,故而输出的结果为-1.7.L1[2012·山东卷] 执行如图1-1所示的程序框图,如果输入a =4,那么输出的n 的值为()A .2B .3C .4D .57.B [解析] 本题考查算法与程序框图,考查数据处理能力,容易题.当n =0时,P =1,Q =3,P <Q 成立,执行循环;当n =1时,P =5,Q =7,P <Q 成立,执行循环;当n =2时,P =21,Q =15,P <Q 不成立,但是n =2+1=3后,再输出.5.L1[2012·陕西卷] 图1-2是计算某年级500名学生期末考试(满分为100分)及格率q 的程序框图,则图中空白框内应填入( )A .q =N MB .q =M NC .q =NM +ND .q =MM +N5.D [解析] 从框图中可以看出M代表及格的人数,N代表不及格的人数,M+N代表总人数,故填入的应为及格率q=MM+N.3.L1[2012·天津卷] 阅读如图1-1所示的程序框图,运行相应的程序,则输出S的值为( )A.8 B.18C.26 D.80图1-13.C [解析] 当n=1时,S=2;当n=2时,S=2+32-3=8;当n=3时,S=8+33-32=26;当n=4时输出S=26.13.L1[2012·浙江卷] 若某程序框图如图1-4所示,则该程序运行后输出的值是________.13.1120 [解析] 当i =1时,T =11=1,而i =1+1=2,不满足条件i >5;接下来,当i =2时,T =12,而i =2+1=3,不满足条件i >5;接下来,当i =3时,T =123=16,而i =3+1=4,不满足条件i >5;接下来,当i =4时,T =164=124,而i =4+1=5,不满足条件i >5;接下来,当i =5时,T =1245=1120,而i =5+1=6,满足条件i >5;此时输出T =1120,故应填1120.L2 基本算法语句 L3 算法案例 L4 复数的基本概念与运算2.L4[2012·浙江卷] 已知i 是虚数单位,则3+i1-i=( )A .1-2iB .2-iC .2+iD .1+2i2.D [解析] 本题主要考查复数的四则运算,检测学生对基础知识的掌握情况. 3+i 1-i =3+i 1+i 1-i 1+i =2+4i2=1+2i ,故应选D. 1.L4[2012·天津卷] i 是虚数单位,复数5+3i4-i=( )A .1-iB .-1+iC .1+iD .-1-i1.C [解析] 5+3i 4-i =5+3i 4+i 4-i 4+i =5×4-3+3×4+5i42+12=1+i. 15.L4[2012·上海卷] 若1+2i 是关于x 的实系数方程x 2+bx +c =0的一个复数根,则( )A .b =2,c =3B .b =2,c =-1C .b =-2,c =-1D .b =-2,c =315.D [解析] 考查复数的概念和一元二次方程中根与系数的关系(即韦达定理),可利用方程的两根是共轭复数解题.由韦达定理可知:-b =(1+2i)+(1-2i)=2,∴b =-2, c =(1+2i)(1-2i)=1+2=3,∴c =3,所以选D.此题还可以直接把复数根1+2i 代入方程中,利用复数相等求解.1.L4[2012·上海卷] 计算:3-i1+i=________(i 为虚数单位)1.1-2i [解析] 考查复数的除法运算,是基础题,复数的除法运算实质就是分母实数化运算.原式=3-i 1-i 1-i 2=1-2i. 4.A2、L4[2012·陕西卷] 设a ,b ∈R ,i 是虚数单位,则“ab =0”是“复数a +bi为纯虚数”的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件4.B [解析] 本小题主要考查充要条件的概念以及复数的相关知识,解题的突破口为弄清什么是纯虚数,然后根据充要条件的定义去判断.a +b i =a -b i ,若a +bi 为纯虚数,a=0且b ≠0,所以ab =0不一定有a +b i 为纯虚数,但a +bi 为纯虚数,一定有ab =0,故“ab=0”是“复数a +bi为纯虚数”的必要不充分条件,故选B.1.L4[2012·山东卷] 若复数z 满足z (2-i)=11+7i(i 为虚数单位),则z 为( ) A .3+5i B .3-5i C .-3+5i D .-3-5i1.A [解析] 本题考查复数的概念及运算,考查运算能力,容易题.设z =a +b i(a ,b ∈R ),由题意得(a +b i)(2-i)=(2a +b )+(2b -a )i =11+7i ,即 ⎩⎪⎨⎪⎧ 2a +b =11,2b -a =7, 解之得⎩⎪⎨⎪⎧a =3,b =5.3.L4[2012·辽宁卷] 复数11+i=( )A.12-12iB.12+12i C .1-i D .1+i3.A [解析] 解题的突破口为分子分母同乘以分母的共轭复数.因为11+i =1-i 1+i 1-i =1-i 2=12-i 2,所以答案选A.2.L4[2012·课标全国卷] 复数z =-3+i2+i的共轭复数是( )A .2+iB .2-iC .-1+iD .-1-i2.D [解析] 因为z =-3+i 2+i =-3+i 2-i 2+i 2-i =-1+i ,所以z =-1-i.故选D.1.L4[2012·江西卷] 若复数z =1+i(i 为虚数单位),z 是z 的共轭复数,则z 2+z2的虚部为( )A .0B .-1C .1D .-21.A [解析] ∵z =1+i ,∴z 2=(1+i)2=2i ,z =1-i ,z 2=(1-i)2=-2i ,∴z 2+z 2=0,故选A.3.L4[2012·江苏卷] 设a ,b ∈R ,a +b i =11-7i1-2i(i 为虚数单位),则a +b 的值为________.3.8 [解析] 本题考查复数的四则运算.解题突破口为将所给等式右边的分子、分母同时乘以分母的共轭复数即可.因为11-7i 1-2i =11-7i 1+2i 5=5+3i ,所以a =5,b =3.2.L4[2012·湖南卷] 复数z =i(i +1)(i 为虚数单位)的共轭复数是( ) A .-1-i B .-1+i C .1-i D .1+i2.A [解析] 本题考查复数的乘法运算和复数的共轭复数,意在考查考生对复数的简单运算和共轭复数的掌握.复数z =i(i +1)=i 2+i =-1+i ,其共轭复数为z =-1-i ,所以选A.[易错点] 本题易错一:把i 2等于1,导致错选C ;易错二:忘记共轭复数的定义.12.L4[2012·湖北卷] 若3+b i1-i=a +b i(a ,b 为实数,i 为虚数单位),则a +b =________.12.[答案] 3[解析] 由3+b i1-i=a +b i ,得3+b i =(a +b i)(1-i)=a +b +(b -a )i ,即a +b -3-a i=0.所以⎩⎪⎨⎪⎧a +b -3=0,-a =0, 解得⎩⎪⎨⎪⎧a =0,b =3,所以a +b =3.1.L4[2012·广东卷] 设i 为虚数单位,则复数3+4ii=( )A .-4-3iB .-4+3iC .4+3iD .4-3i1.D [解析] 因为3+4i i =3+4i i i·i =3i -4-1=4-3i ,所以选择D.1.L4[2012·福建卷] 复数(2+i)2等于( ) A .3+4i B .5+4i C .3+2i D .5+2i1.A [解析] 利用复数乘法运算求解,(2+i)2=4+4i +i 2=3+4i ,所以选择A.2.L4[2012·北京卷] 在复平面内,复数10i3+i对应的点的坐标为( )A .(1,3)B .(3,1)C .(-1,3)D .(3,-1)2.A [解析] 本题考查复数代数形式的除法运算和复数几何意义.10i3+i=10i 3-i 3+i 3-i =1+3i ,所以它对应点的坐标为(1,3).1.L4[2012·安徽卷] 复数z 满足(z -i)i =2+i ,则z =( ) A .-1-i B .1-i C .-1+3i D .1-2i1.B [解析] 由()z -i i =2+i ,得z -i =2+ii=1-2i ,所以z =1-i.L5 单元综合2012模拟题1.[2012·保定八校联考] 图K44-1为一个算法的程序框图,则其输出结果是()A .0B .2012C .2011D .11. A [解析] p =0,n =1,p =1,n =2,p =1,n =3,p =0,n =4,p =0,n =5,p =1,n =6,…,周期为4的循环变化,可知p =0,n =2012,是;p =0,n =2013;否,输出p =0.2.[2012·银川一中检测] 运行下面的程序,如果输入的n 是6,那么输出的p 是( )INPUT “n=”;n k =1 p =1WHILE k<=n p =p*k k =k +1WEND PRINT p ENDA .120B .720C .1440D .50402.B [解析] 如果输入的n 是6,k =1,p =1;k =2,p =2;k =3,p =6;k =4,p =24;k =5,p =120;k =6,p =720;输出720.3.[2012·南阳质量评估] 执行下面的程序框图,若p =4,则输出的S 等于________.K44-53. 1516 [解析] 因p =4,n =0,S =0;n =1,S =12;n =2,S =12+122;n =3,S =12+122+123;n =4,S =12+122+123+124=1516;不满足n <p ,输出S =1516.4.[2012·江西师大附中月考] 设复数z 1=1-3i ,z 2=3-2i ,则z 1z 2在复平面内对应的点在( )A .第一象限B .第二象限C .第三象限D .第四象限4.D [解析] ∵z 1z 2=1-3i 3-2i =1-3i 3+2i 3-2i 3+2i =9-7i 13,∴z 1z 2在复平面内对应的点在第四象限.5.[2012·湖南师大附中月考] 已知x1+i=1-y i ,其中x 、y 是实数,i 是虚数单位,则x +y i 等于( )A .1+2iB .1-2iC .2+iD .2-i5.C [解析] x 1+i =1-y i ⇒x =(1-y i)(1+i)⇒x =(1+y )+(1-y )i ⇒⎩⎪⎨⎪⎧ 1-y =0,x =1+y ⇒⎩⎪⎨⎪⎧ x =2,y =1,故x +y i =2+i.。
2012年高考试题+模拟新题分类汇编专题文科L 算法初步与复数(高考真题+模拟新题).pdf

13.人 琴 俱 亡 1.疏通文义,明确文言实词、虚词在文中的意思。
2.诵读文章,梳理文中的故事情节。
3.体会人物的心情和个性特点,感受兄弟亲情。
●重点: 1.掌握常见的文言实词与虚词。
2.体会用独特的悼念方式表达深厚的兄弟情谊,感受凄美的爱的感情熏陶。
1.下面是某同学制作的知识卡片,请你帮着补充完整。
刘义庆(403—444),字 季伯 , 南朝宋 时文学家。
《宋书》本传说他“性简素,寡嗜欲”,爱好文学。
刘宋宗室,袭封临川王赠任荆州刺史等官职,在政八年,政绩颇佳。
刘义庆自幼才华出众,爱好文学。
所著《世说新语》是记述汉末以来士大夫阶层轶事琐事的一部书,文学史上称“ 轶事小说 ”。
? 2.给下列加点字注音。
笃( dǔ ) 舆( yú ) 径( jìng ) 弦( xián ) 不调( tiáo )掷地( zhì )恸( tòng )卒( zú ) 3.解释下面句中加点的词。
子敬俱病笃:都;病重。
何以都不闻消息:为什么。
便索舆来奔丧: 轿子。
弦既不调:已经。
语时了不悲:完全。
子敬素好琴:一向。
因恸绝良久:于是。
月余亦卒:死。
? 4.参照课文注释,翻译下列句子。
(1)语时了不悲。
说话时完全不悲伤。
? (2)便索舆来奔丧,都不哭。
就要轿子来,去看望丧事,一路上都没有哭。
5.通读课文,根据下面图示填空。
问题一:一读,标节奏,读通文章,读准字音和节奏。
用“/”号标出停顿。
王 子 猷、子 敬/俱 病 笃,而 子 敬/先 亡。
子 猷/问 左 右:“何 以/都 不 闻 消 息?此 已 丧 矣。
”语 时/了 不 悲。
便 索 舆/来 奔 丧,都 不 哭。
子 敬/素 好 琴 ,便 径 入/坐 灵 床 上,取 子 敬 琴/弹,弦/既 不 调,掷 地/云:“子 敬/子 敬,人 琴/俱 亡。
” 因/恸 绝 良 久,月 余/亦 卒。
2012年高考文科数学试题分类汇编--复数(修改版)

数系的扩充与复数的引入学问要点梳理学问点一:复数的基本概念1.虚数单位:(1)它的平方等于,即;(2)与-1的关系: 就是-1的一个平方根,即方程的一个根,方程的另一个根是;(3)实数可以与它进行四则运算,进行四则运算时,原有加、乘运算律仍旧成立;(4)的周期性:,,,().2. 概念形如()的数叫复数,记作:();其中:叫复数的实部,叫复数的虚部.说明:这里简单忽视,但却是列方程求复数的重要依据.3.复数的分类()4.复数集全体复数所成的集合叫做复数集,用字母表示;复数集与其它数集之间的关系:5.复数与实数、虚数、纯虚、0的关系:对于复数(),当且仅当时,复数是实数;当且仅当时,复数叫做虚数;当且仅当且时,复数叫做纯虚数;当且仅当时,复数就是实数0.6.复数相等的充要条件两个复数相等的定义:假如两个复数的实部和虚部分别相等,那么我们就说这两个复数相等.即:假如,那么.特殊地: . 说明:(1)(2)一个复数一旦实部、虚部确定,那么这个复数就唯一确定;反之一样.(3)复数相等的充要条件是将复数转化为实数解决问题的基础.(4)一般地,两个复数只能说相等或不相等,而不能比较大小.假如两个复数都是实数,就可以比较大小;也只有当两个复数全是实数时才能比较大小.6.共轭复数:两个复数的实部相等,而且虚部相反,那么这两个复数叫做共轭复数.复数的共轭复数记作:().学问点二:复数的代数表示法及其四则运算1.复数的代数形式: 把复数表示成的形式,叫做复数的代数形式.2.四则运算设,(a,b,c,d∈R)留意:复数除法通常上下同乘分母的共轭复数.学问点三:复数的几何意义1.复平面、实轴、虚轴:复数()可用点表示,这个建立了直角坐标系来表示复数的平面叫做复平面,也叫高斯平面,轴叫做实轴,轴叫做虚轴.实轴上的点都表示实数.除了原点外,虚轴上的点都表示纯虚数.复数集C和复平面内全部的点所成的集合是一一对应关系,即复数复平面内的点每一个复数有复平面内唯一的一个点和它对应;反过来,复平面内的每一个点,有唯一的一个复数和它对应,这就是复数的一种几何意义,也就是复数的另一种表示方法,即几何表示方法.2.复数的几何表示(1)坐标表示:在复平面内以点表示复数();(2)向量表示:以原点为起点,点为终点的向量表示复数. 向量的长度叫做复数的模,记作.即.理解:(1)向量与点以及复数一一对应;(2)两个复数不全是实数时不能比较大小,但它们的模可以比较大小.3.复数加减法的几何意义:假如复数、分别对应于向量、,那么以、为两边作平行四边形,对角线表示的向量就是的和所对应的向量.对角线表示的向量就是两个复数的差所对应的向量.2012高考真题1.【2012安徽1】复数z 满意i i i z +=-2)(,则 z = ( ) (A ) i --1 (B ) i -1 (C ) i 31+- (D )i 21-2.【2012新课标2】复数z =-3+i2+i的共轭复数是 ( ) (A )2+i (B )2-i (C )-1+i (D )-1-i3.【2012山东1】若复数z 满意(2)117i(i z i -=+为虚数单位),则z 为( ) (A)3+5i (B)3-5i (C)-3+5i (D)-3-5i4.【2012浙江2】已知i 是虚数单位,则31ii+-=( ) A 1-2i B 2-i C 2+i D 1+2i5.【2012上海15】若12+i 是关于x 的实系数方程20x bx c ++=的一个复数根,则( )A 、2,3b c ==B 、2,1b c ==-C 、2,1b c =-=-D 、2,3b c =-= 6.【2012陕西4】设,a b R ∈,i 是虚数单位,则“0ab =”是“复数ba i+为纯虚数”的( ) A.充分不必要条件 B. 必要不充分条件C. 充分必要条件 D. 既不充分也不必要条件 7.【2012辽宁3】复数11i=+( ) (A) 1122i - (B)1122i + (C) 1i - (D) 1i +8.【2012江西1】若复数i z +=1 (i 为虚数单位) z -是z 的共轭复数 , 则2z +z -²的虚部为( ) A 0 B -1 C 1 D -29.【2012湖南2】复数z=i (i+1)(i 为虚数单位)的共轭复数是( )A.-1-iB.-1+iC.1-iD.1+i 10.【2012湖北12】.若=a+bi (a ,b 为实数,i 为虚数单位),则a+b=____________.11.【2012广东1】设i 为虚数单位,则复数34ii+=( ) A. 43i -- B. 43i -+ C. 43i + D. 43i - 12.【2102福建1】复数(2+i )2等于( ) A.3+4i B.5+4i C.3+2i D.5+2i13.【2102北京2】在复平面内,复数103ii+对应的点的坐标为( ) A . (1 ,3) B .(3,1) C .(-1,3) D .(3 ,-1) 14.【2012天津1】i 是虚数单位,复数534i i+-=( )(A )1-i (B )-1+I (C )1+I (D )-1-i 15.【2012江苏3】设a b ∈R ,,117ii 12ia b -+=-(i 为虚数单位),则a b +的值为 . 16.【2012上海1】计算:31ii -=+ (i 为虚数单位) (2011课标)(2)复数512ii=-( )(A )2i - (B )12i - (C ) 2i -+ (D )12i -+ (2011全国理)(1)复数212ii+-的共轭复数是 ( ) (A )35i - (B )35i (C )i - (D )i(2010课标)(3)已知复数23(13)iz i +=-,则Z = ( ) (A)14 (B )12(C )1 (D )2。
2012高考试题分类汇编13复数

2012高考试题分类汇编:13:复数1.【2012高考安徽文1】复数z 满足i i i z +=-2)(,则 z =(A ) i --1 (B ) i -1(C ) i 31+- (D )i 21-【答案】B 【解析】2()21i z i i i z i i i+-=+⇔=+=-。
2.【2012高考新课标文2】复数z =-3+i 2+i 的共轭复数是(A )2+i (B )2-i (C )-1+i (D )-1-i【答案】D 【解析】i i i i i i i i z +-=+--+-+-=++-=1555)2)(2()2)(3(23,所以其共轭复数为i z --=1,选D. 3.【2012高考山东文1】若复数z 满足(2)117i(i z i -=+为虚数单位),则z 为(A)3+5i (B)3-5i (C)-3+5i (D)-3-5i【答案】A 【解析】i i i i i i i i z 5352515)2)(2()2)(711(2711+=+=+-++=-+=.故选A. 4.【2012高考浙江文2】已知i 是虚数单位,则31i i +-= A 1-2i B 2-i C 2+i D 1+2i【答案】D【解析】31i i +-(3)(1)2412(1)(1)2i i i i i i +++===+-+.5.【2012高考上海文15】若1i 是关于x 的实系数方程20x bx c ++=的一个复数根,则( )A 、2,3b c ==B 、2,1b c ==-C 、2,1b c =-=-D 、2,3b c =-=【答案】D【解析】因为i 21+是实系数方程的一个复数根,所以i 21-也是方程的根,则b i i -==-++22121,c i i ==-+3)21)(21(,所以解得2-=b ,3=c ,选D.6.【2012高考陕西文4】设,a b R ∈,i 是虚数单位,则“0ab =”是“复数b a i +为纯虚数”的( )A.充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件【答案】B.【解析】00=⇔=a ab 或0=b ,而复数bi a ib a -=+是纯虚数00≠=⇔b a 且,ib a ab +⇐=∴0是纯虚数,故选B. 7.【2012高考辽宁文3】复数11i=+ (A) 1122i - (B)1122i + (C) 1i - (D) 1i + 【答案】A 【解析】11111(1)(1)222i i i i i i --===-++-,故选A 【点评】本题主要考查复数代数形式的运算,属于容易题。
全国各地市2012届高三模拟试题分类解析汇编:13:复数与算法

全国各地市2012年模拟试题分类解析汇编:复数与算法【江西省泰和中学2012届高三12月周考】复数32i i -+的实部为( )A .i B .-I C .1 D .-1【答案】C 【解析】因为312i i i -=-+,所以实部为1.【2012唐山市高三上学期期末统一考试文】复数1(1)(1)i i -+= ( )A .2iB .-2iC .2D .-2【答案】 A【解析】本题主要考查复数的四则运算. 属于基础知识、基本运算的考查.1(1)(1)22(1)(1)2i i i i ii i i i i -+---+====⋅【2012江西师大附中高三下学期开学考卷文】设复数113iz =-,232iz =-,则21z z 在复平面内对应的点在( )A .第一象限B .第二象限C .第三象限D .第四象限 【答案】D【解析】本题主要考查复数的四则运算运算以及复平面的概念. 属于基础知识、基本运算的考查.∵1213i 13i 32i 9732323213z i z ii i--+-===--+,∴21z z 在复平面内对应的点在第四象限。
【2012三明市普通高中高三上学期联考文】已知i 是虚数单位,则(1)i i -= A .1i -- B .1i -+C .1i +D .1i -【答案】C【解析】本题主要考查复数的四则运算运算以及虚数单位的概念. 属于基础知识、基本运算 的考查.2(1)(1)1i i i i i i-=-=--=+【2012年石家庄市高中毕业班教学质检1文】阅读如图所示的程序框图,输出的S 值为 A .0 B .21+C .221+D .12-【答案】B【解析】本题主要考查算法的流程图、特殊角的三角函数值的计算. 属于基础知识、基本运算的考查.流程图的功能是计算2345678sinsin in sin insininsin4444444491011in sin sin 444s s s s πππππππππππ++++++++++2345678sin sin insinin sininsin44444444s s s ππππππππ+++++++=91011insinsin1444s πππ++=+【2012唐山市高三上学期期末统一考试文】执行右面的程序框图,如果输出的是341a =,那么判断框( ) A .4?k < B .5?k < C .6?k <D .7?k <【答案】 C【解析】本题主要考查算法流程图. 属于基础知识、基本运算的考查.1,1;2,5;3,21;4,85;5,341,6k a k a k a k a k a k ===========6<6不成立,输出341【2012黄冈市高三上学期期末考试文】复数121ii ++(i 是虚数单位)的虚部是( )A .1B .3C .12 D .32【答案】 C 【解析】本题主要考查复数的四则运算运算以及虚部的概念. 属于基础知识、基本运算的考查. 12(12)(1)1111(1)(1)222i i i i iii i ++--+===-+++-,虚部是12【2012金华十校高三上学期期末联考文】复数31x iz i +=-(,x R i ∈是虚数单位)是实数,则x 的值为 ( )A .3B .-3C .0D【答案】 B【解析】本题主要考查复数的概念与复数的四则运算. 属于基础知识、基本运算的考查. 3(3)(1)(3)(3)331(1)(1)222x i x i i x x ix x z iii i +++-++-+====+--+是实数,∴3032xx +=⇒=-【2012金华十校高三上学期期末联考文】执行如图 的程序框图,输出的S 和n 的值分别是( ) A .11,3 B .11,4 C .9,3 D .9,4 【答案】 D【解析】本题主要考查算法流程图的理解. 属于基础知识、基本运算的考查.0,0,1,S T n T S ===≤成立,继续执行循环体; 3,1,2,S T n T S ===≤成立,继续执行循环体; 6,4,3,S T n T S ===≤成立,继续执行循环体; 9,11,4,S T n T S ===≤不成立,输出9,4S n ==.【2012武昌区高三年级元月调研文】复数21ii +的共轭复数为 ( )A .1i +B .1i -C .1i -+D .1i --【答案】B【解析】本题主要考查复数的四则运算运算以及共轭复数的概念. 属于基础知识、基本运算 的考查.因为22(1)2211(1)(1)2ii i i iii i -+===+++-,所以复数21ii +的共轭复数为1i -.【2012武昌区高三年级元月调研文】执行右边的程序框图,那么输出的S 的值是 ( ) A .2 450 B .2 550 C .5 050 D .4 900 【答案】A【解析】本题主要考查算法框图的识图,属于基础知识、基本能力的考查. 从框图可以看出,它是要求输出98以内偶数的和,(098)5002498504924502+⨯++++==⨯=【2012年西安市高三年级第一次质检文】复数的实部是A.-1B. 1C.OD. -2 【答案】A【解析】本题主要复数的概念、复数的四则运算 . 属于基础知识、基本运算的考查.2(1)1i i i +=--,所以复数的实部为-1【2012年西安市高三年级第一次质检文】 执行如图所示的程序框图,输出的s值为A. -3B.C. D. 2【答案】D【解析】本题主要考查算法流程图. 属于基础知识、基本运算的考查.10,4,011,3i i i s =<=+== 11131,4,112,1213i i i s -=<=+===-+ 1122,4,211,3112i i i s --=<=+===--+ 313,4,314,231i i i s --=<=+===-+4,4,i i =<不成立,输出S=2【2012粤西北九校联考理】执行如图的程序框图,若输出的n =5,则输入整数p 的最小值是(A .6 B.7 C.8 D.15 (第7题图)【答案】C【解析】执行如图的程序框图:,5;15,4,7,3;3,2;1,1=========n s n s n s n s n 输出,则P=8【2012宁德质检理】运行如右所示的程序框图,输入下列四个函数,则可以输出的函 数是( )A .2()f x x =B .()cos 2f x x =C .()xf x e=D .()sin f x x π=【答案】D【解析】只有()sin f x x π=满足()0f x =有解,且()(2)f x f x =+成立; 成立。
2012新题分类汇编:算法初步与复数(高考真题+模拟新题)

九、算法初步与复数(高考真题+模拟新题)课标文数12.L1[2011·安徽卷] 如图1-3所示,程序框图(算法流程图)的输出结果是________.图1-3课标文数12.L1[2011·安徽卷] 【答案】 15【解析】 第一次进入循环体有T =0+0,第二次有:T =0+1,第三次有T =0+1+2,…第k +1次有T =0+1+2+…+k =k (k +1)2,若T =105,解得k =14,继续执行循环,这时k =15,T >105,所以输出的k 的值是15.课标理数11.L1[2011·安徽卷] 如图1-3所示,程序框图(算法流程图)的输出结果是________.图1-3 课标理数11.L1[2011·安徽卷] 15 【解析】 第一次进入循环体有T =0+0,第二次有:T =0+1,第三次有T =0+1+2,…,第k +1次有T =0+1+2+…+k =k (k +1)2,若T =105,解得k =14,继续执行循环,这时k =15,T >105,所以输出的k 的值是15.课标理数4.L1[2011·北京卷] D 【解析】 第(i =0)一步,i =0+1=1,s =2-12+1=13;第(i =1)二步,i =1+1=2,s =13-113+1=-12;第(i =2)三步,i =2+1=3,s =-12-1-12+1=-3;第(i =3)四步,i =3+1=4,s =-3-1-3+1=2;第(i =4)五步,i =4<4不成立,输出s =2,故选D.课标文数6.L1[2011·北京卷] 执行如图1-2所示的程序框图,若输入A 的值为2,则输出的P 值为( )图1-2A .2B .3C .4D .5课标文数6.L1[2011·北京卷] C 【解析】 第一步,P =1+1=2,S =1+12=32;第二步,P =2+1=3,S =32+13=116;第三步,P =3+1=4,S =116+14=2512>2,输出P =4,故选C.课标理数1.A1,L4[2011·福建卷] i 是虚数单位,若集合S ={-1,0,1},则( )A .i ∈SB .i 2∈SC .i 3∈S D.2i∈S课标理数1.A1、L4[2011·福建卷] B 【解析】 由i 2=-1,而-1∈S ,故选B.课标文数5.L1[2011·福建卷] 阅读图1-1所示的程序框图,运行相应的程序,输出的结果是( )图1-1A .3B .11C .38D .123 课标文数5.L1[2011·福建卷] B 【解析】 该程序框图是当型的循环结构,由程序框图可知,第一次循环,a =12+2=3;第二次循环,a =32+2=11; 当a =11时,a <10不成立,输出a =11,故选B.课标理数13.L1[2011·湖南卷] 若执行如图1-3所示的框图,输入x 1=1,x 2=2,x 3=3,x =2,则输出的数等于________.图1-3课标理数13.L1[2011·湖南卷] 23【解析】 由累加的赋值符号S =S +(x i -x )2得到S =(1-2)2+(2-2)2+(3-2)2=2,而最后输出的结果为S =1i S =13×2=23.课标文数11.L1[2011·湖南卷] 若执行如图1-2所示的框图,输入x 1=1,x 2=2,x 3=4,x 4=8,则输出的数等于________.图1-2课标文数11.L1[2011·湖南卷]154【解析】 由累加的赋值符号x =x +x i 得到x =x 1+x 2+x 3+x 4=1+2+4+8=15,而最后输出的结果为x =14x =14×15=154.课标理数13.L1[2011·江西卷] 图1-6是某算法的程序框图,则程序运行后输出的结果是________.图1-6课标理数13.L1[2011·江西卷] 【答案】 10【解析】 第一次,s =0+(-1)1+1=0,n =2,第二次,s =0+(-1)2+2=3,n =3,第三次,s =3+(-1)3+3=5,n =4,第四次,s =5+(-1)4+4=10>9,终止循环,输出结果10.课标文数13.L1[2011·江西卷] 图1-6是某算法的程序框图,则程序运行后输出的结果是________.图1-6 课标文数13.L1[2011·江西卷] 27 【解析】 第一次:s =(0+1)×1=1,n =1+1=2,第二次:s =(1+2)×2=6,n =3,第三次:s =(6+3)×3=27,n =4,而n =4>3,退出循环,输出s =27.故填27.课标理数3.L1[2011·课标全国卷] 执行如图1-1所示的程序框图,如果输入的N 是6,那么输出的p是()图1-1A .120B .720C .1440D .5040 课标理数3.L1[2011·课标全国卷] B 【解析】 k =1时,p =1; k =2时,p =1×2=2; k =3时,p =2×3=6; k =4时,p =6×4=24; k =5时,p =24×5=120; k =6时,p =120×6=720.课标文数9.L1[2011·辽宁卷] 执行下面的程序框图,如果输入的n 是4,则输出的p 是()图1-5A .8B .5C .3D .2课标文数9.L1[2011·辽宁卷] C【解析】由于n=4,所以当k=1时,p=1,s=1,t=1;当k=2时,p=2,s=1,t=2;当k=3时,p=3,s=2,t=3,此时k=4,输出p,此时p=3,故选C.课标文数5.L1[2011·课标全国卷] 执行下面的程序框图,如果输入的N是6,那么输出的p是()图1-1A.120 B.720 C.1440 D.5040课标文数5.L1[2011·课标全国卷] B【解析】k=1时,p=1;k=2时,p=1×2=2;k=3时,p=2×3=6;k=4时,p=6×4=24;k=5时,p=24×5=120;k=6时,p=120×6=720.课标理数13.L1[2011·山东卷] 执行图1-3所示的程序框图,输入l=2,m=3,n=5,则输出的y的值是________.图1-3课标理数13.L1[2011·山东卷] 68【解析】把l=2,m=3,n=5代入y=70l+21m+15n得y=278,此时y=278>105,第一次循环y=278-105=173,此时y=173>105,再循环,y=173-105=68,输出68,结束循环.课标文数14.L1[2011·山东卷] 执行图1-4所示的程序框图,输入l=2,m=3,n=5,则输出的y的值是________.图1-4[来源:Z_xx_]课标文数14.L1[2011·山东卷] 68 【解析】 把l =2,m =3,n =5代入y =70l +21m +15n 得y =278,此时y =278>105,第一次循环y =278-105=173,此时y =173>105,再循环,y =173-105=68,输出68,结束循环.课标理数8.L1[2011·陕西卷] 图1-3中,x 1,x 2,x 3为某次考试三个评阅人对同一道题的独立评分,p 为该题的最终得分.当x 1=6,x 2=9,p =8.5时,x 3等于( )图1-3A .11B .10C .8D .7 课标理数8.L1[2011·陕西卷] C 【解析】 由题目中所给的数据p =8.5,x 1=6,x 2=9,则若满足条件|x 3-x 1|s <|x 3-x 2|时,不成立,故应不满足条件|x 3-x 1|<|x 3-x 2|,此时满足x 2+x 32=8.5,则x 3=8,并且代入也符合题意,故选C.课标文数7.L1[2011·陕西卷] 如下框图,当x 1=6,x 2=9,p =8.5时,x 3等于( )图1-4A .7B .8C .10D .11课标文数7.L1[2011·陕西卷] B 【解析】 因为x 1=6,x 2=9,p =8.5,p =x 1+x 22或p =x 2+x 32,当x 1=6,x 2=9,p =x 1+x 22=7.5,不合题意,故p =x 2+x 32=8.5,x 2=9,得x 3=8,故答案为B.课标数学4.L1[2011·江苏卷] 根据如图所示的伪代码,当输入a ,b 分别为2,3时,最后输出的m 的值为________.Read a ,b If a >b Then m ←a Else m ←b End If Print m课标数学4.L1[2011·江苏卷] 3【解析】 因为a =2<b =3,所以m =3.课标理数3.L1[2011·天津卷] 阅读程序框图1-1,运行相应的程序,则输出i 的值为( )图1-1A .3B .4C .5D .6 课标理数3.L1[2011·天津卷] B 【解析】 i =1时,a =1×1+1=2; [来源:学|科|网] i =2时,a =2×2+1=5; i =3时,a =3×5+1=16;i =4时,a =4×16+1=65>50,∴输出i =4,故选B.图1-2课标文数3.L1[2011·天津卷] 阅读图1-2所示的程序框图,运行相应的程序,若输入x 的值为-4,则输出y 的值为( )A .0.5B .1C .2D .4 课标文数3.L1[2011·天津卷] C 【解析】 当x =-4时,x =|x -3|=7;当x =7时,x =|x -3|=4;当x =4时,x =|x -3|=1<3,∴y =2.课标理数12.L1[2011·浙江卷] 若某程序框图如图1-4所示,则该程序运行后输出的k 的值是________.图1-4课标理数12.L1[2011·浙江卷] 5【解析】 k =3时,a =43=64,b =34=84,a <b ; k =4时,a =44=256,b =44=256,a =b ; k =5时,a =45=256×4,b =54=625,a >b .图1-5课标文数14.L1[2011·浙江卷] 某程序框图如图1-5所示,则该程序运行后输出的k 的值是________.课标文数14.L1[2011·浙江卷] 5 【解析】 k =3时,a =43=64,b =34=84,a <b ; k =4时,a =44=256,b =44=256,a =b ; k =5时,a =45=256×4,b =54=625,a >b . 课标理数11.L2[2011·福建卷] 运行如图1-4所示的程序,输出的结果是________. a =1b =2a =a +b PRINT a END图1-4课标理数11.L2[2011·福建卷] 【答案】 3【解析】 由已知,输入a =1,b =2,把a +b 的值赋给a ,输出a =3.课标理数16.L3[2011·湖南卷] 对于n ∈N *,将n 表示为n =a 0×2k +a 1×2k -1+a 2×2k -2+…+a k -1×21+a k ×20,当i =0时,a i =1,当1≤i ≤k 时,a i 为0或1.记I (n )为上述表示中a i 为0的个数(例如:1=1×20,4=1×22+0×21+0×20,故I (1)=0,I (4)=2),则(1)I (12)=________; (2)∑127n =12I(n)=________. 课标理数16.L3[2011·湖南卷] (1)2 (2)1093【解析】 (1)本题实考二进制与十进制间的互化:因为I (12)=1×23+1×22+0×21+0×20,根据题目给出的定义可得到: I (12)=2;(2) n =11272I (n )=2I (1)+2I (2)+2I (3)+…+2I (127)利用二进制与十进制间的互化,列举得:I (1)=1(2)共一个,则S 1=2I (1)=20=1;I (2)=10(2),I (3)=11(2)共2个, 则S 2=2I (2)+2I (3)=21+20=3;I (4)=100(2),I (5)=101(2),I (6)=110(2),I (7)=111(2)共4个,则S 3=2I (4)+…+2I (7)=9; I (8)=1000(2),I (9)=1001(2),…,I (15)=1111(2) 共8个,则S 4=2I (8)+…+2I (15)=27;……I (64)=100000(2),…,I (127)=1111111(2)共64个,则S 7=2I (64)+…+2I (127)=729; 故∑n =11272I (n )=2I (1)+2I (2)+2I (3)+…+2I (127)=S 1+S 2+S 3+S 4+S 5+S 6+S 7=1+3+9+27+81+243+729=1093.课标文数1.L4[2011·安徽卷] 设i 是虚数单位,复数1+a i2-i为纯虚数,则实数a 为( )A .2B .-2C .-12 D.12课标文数1.L4[2011·安徽卷] A 【解析】 法一:1+a i 2-i =(1+a i )·(2+i )(2-i )(2+i )=2-a +(2a +1)i5为纯虚数,所以⎩⎪⎨⎪⎧2-a =0,2a +1≠0,解得a =2. 法二:1+a i 2-i =i (a -i )2-i为纯虚数,所以a =2.答案为A.课标理数1.L4[2011·安徽卷] 设i 是虚数单位,复数1+a i2-i为纯虚数,则实数a 为( )A .2B .-2C .-12 D.12课标理数1.L4[2011·安徽卷] A 【解析】 法一:1+a i 2-i =(1+a i )·(2+i )(2-i )(2+i )=2-a +(2a +1)i5为纯虚数,所以⎩⎪⎨⎪⎧2-a =0,2a +1≠0, 解得a =2. 法二:1+a i 2-i =i ()a -i 2-i为纯虚数,所以a =2.答案为A.课标理数2.L4[2011·北京卷] 复数i -21+2i=( )A .iB .-IC .-45-35iD .-45+35i课标理数2.L4[2011·北京卷] A 【解析】 i -21+2i =(i -2)(1-2i )(1+2i )(1-2i )=5i5=i ,故选A.课标文数2.L4[2011·北京卷] 复数i -21+2i =( )A .iB .-IC .-45-35iD .-45+35i课标文数2.L4[2011·北京卷] A 【解析】 i -21+2i =(i -2)(1-2i )(1+2i )(1-2i )=5i5=i ,故选A.大纲理数1.L4[2011·全国卷] 复数z =1+i ,z 为z 的共轭复数,则z z -z -1=( ) A .-2i B .-I C .i D .2i大纲理数1.L4[2011·全国卷] B 【解析】 ∵z =1-i ,∴z z -z -1=(1+i)(1-i)-(1+i)-1=-i ,故选B.课标文数2.L4[2011·福建卷] i 是虚数单位,1+i 3等于( ) A .i B .-i C .1+i D .1-i 课标文数2.L4[2011·福建卷] D 【解析】 由1+i 3=1+i 2·i =1-i ,故选D.课标理数1.L4[2011·广东卷] 设复数z 满足(1+i)z =2,其中i 为虚数单位,则z =( )[来源:学科网]A .1+iB .1-IC .2+2iD .2-2i课标理数1.L4[2011·广东卷] B 【解析】 z =21+i =2(1-i )(1+i )(1-i )=2(1-i )2=1-i ,故选B.课标文数1.L4[2011·广东卷] 设复数z 满足i z =1,其中i 为虚数单位,则z =( ) A .-i B .i C .-1 D .1课标文数1.L4[2011·广东卷] A 【解析】 由i z =1得z =1i =ii2=-i ,所以选A.课标理数1.L4[2011·湖北卷] i 为虚数单位,则⎝ ⎛⎭⎪⎫1+i 1-i 2011=( )A .-iB .-1C .iD .1课标理数1.L4[2011·湖北卷] A 【解析】 因为1+i 1-i =()1+i 2()1-i ()1+i =i ,所以⎝ ⎛⎭⎪⎫1+i 1-i 2011=i 502×4+3=i 3=-i.课标理数1.L4[2011·湖南卷] 若a ,b ∈R ,i 为虚数单位,且(a +i)i =b +i ,则( ) A .a =1,b =1 B .a =-1,b =1 C .a =-1,b =-1 D .a =1,b =-1 课标理数1.L4[2011·湖南卷] D 【解析】 由(a +i)i =b +i 得-1+a i =b +i ,根据复数相等的充要条件,得a =1,b =-1,故选D.课标文数2.L4[2011·湖南卷] 若a ,b ∈R ,i 为虚数单位,且(a +i)i =b +i ,则( ) A .a =1,b =1 B .a =-1,b =1 C .a =1,b =-1 D .a =-1,b =-1 课标文数2.L4[2011·湖南卷] C 【解析】 由(a +i)i =b +i 得-1+a i =b +i ,根据复数的相等,a =1,b =-1,故选C.课标理数1.L4[2011·江西卷] 若z =1+2ii,则复数z =( )A .-2-iB .-2+IC .2-iD .2+i课标理数1.L4[2011·江西卷] D 【解析】 z =1+2i i =i (1+2i )i 2=-(i -2)=2-i ,故z =2+i.故选D.课标文数1.L4[2011·江西卷] 若(x -i)i =y +2i ,x ,y ∈R ,则复数x +y i =( ) A .-2+i B .2+I C .1-2i D .1+2i 课标文数1.L4[2011·江西卷] B 【解析】 由题设得x i +1=y +2i ,∴x =2,y =1,即x +y i =2+i.故选B.课标理数1.L4[2011·课标全国卷] 复数2+i1-2i的共轭复数是( )A .-35i B.35I C .-i D .i课标理数 1.L4[2011·课标全国卷] C 【解析】 2+i 1-2i =(2+i )(1+2i )(1-2i )(1+2i )=5i5=i ,所以其共轭复数为-i.故选C.图1-1课标文数2.L4[2011·辽宁卷] i 为虚数单位,1i +1i 3+1i 5+1i7=( )A .0B .2iC .-2iD .4i课标文数2.L4[2011·辽宁卷] A 【解析】 1i +1i 3+1i 5+1i7=-i +i -i +i =0,故选A.课标文数2.L4[2011·课标全国卷] 复数5i1-2i=( )A .2-iB .1-2iC .-2+iD .-1+2i课标文数2.L4[2011·课标全国卷] C 【解析】 5i 1-2i =5i (1+2i )(1-2i )(1+2i )=5i -105=-2+i. 课标理数2.L4[2011·山东卷] 复数z =2-i 2+i(i 为虚数单位)在复平面内对应的点所在象限为( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限课标理数2.L4[2011·山东卷] D 【解析】 z =2-i 2+i =(2-i )2(2+i )(2-i )=3-4i 4+1=35-45i ,又点⎝⎛⎭⎫35,-45在第四象限,所以该复数在复平面内对应的点也在第四象限.课标文数2.L4[2011·山东卷] 复数z =2-i 2+i(i 为虚数单位)在复平面内对应的点所在象限为( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限课标文数2.L4[2011·山东卷] D 【解析】 z =2-i 2+i =(2-i )2(2+i )(2-i )=3-4i 4+1=35-45i ,又点⎝⎛⎭⎫35,-45在第四象限,所以该复数在复平面内对应的点也在第四象限.课标文数8.A1,L4[2011·陕西卷] 设集合M ={y |y =|cos 2x -sin 2x |,x ∈R },N =⎩⎨⎧⎭⎬⎫x ⎪⎪⎪⎪⎪⎪x i <1,i 为虚数单位,x ∈R ,则M ∩N 为( ) A .(0,1) B .(0,1] C .[0,1) D .[0,1]课标文数8.A1,L4[2011·陕西卷] C 【解析】 对M ,由基本不等式得y =|cos 2x -sin 2x |=|cos2x |,故0≤y ≤1.对N ,⎪⎪⎪⎪x i <1,即|-x i|<1,所以-1<x <1,故M ∩N =[0,1),故答案为C.课标数学1.A1[2011·江苏卷] 已知集合A ={-1,1,2,4},B ={-1,0,2}, 则A ∩B =________.课标数学1.A1[2011·江苏卷] {-1,2} 【解析】 因为集合A ,B 的公共元素为-1,2,故A ∩B ={-1,2}.课标数学3.L4[2011·江苏卷] 设复数z 满足i(z +1)=-3+2i(i 为虚数单位),则z 的实部是________.课标数学3.L4[2011·江苏卷] 1 【解析】 因为z +1=-3+2i i =-3i +2i 2i 2=2+3i ,所以z =1+3i ,故实部为1.大纲理数2.L4[2011·四川卷] 复数-i +1i=( ) A .-2i B.12i C .0 D .2i 大纲理数2.L4[2011·四川卷] A 【解析】 -i +1i=-i -i =-2i ,所以选A. 课标理数1.L4[2011·天津卷] i 是虚数单位,复数1-3i 1-i=( ) A .2+i B .2-I C .-1+2i D .-1-2i课标理数1.L4[2011·天津卷] B 【解析】 1-3i 1-i =(1-3i )(1+i )(1-i )(1+i )=4-2i 2=2-i.课标文数1.L4[2011·天津卷] i 是虚数单位,复数1-3i 1-i=( ) A .2-i B .2+I C .-1-2i D .-1+2i课标文数1.L4[2011·天津卷] A 【解析】 1-3i 1-i =(1-3i )(1+i )(1-i )(1+i )=4-2i 2=2-i. 课标理数2.L4[2011·浙江卷] 把复数z 的共轭复数记作z ,i 为虚数单位.若z =1+i ,则(1+z )·z =( )A .3-iB .3+iC .1+3iD .3课标理数2.L4[2011·浙江卷] A 【解析】 ∵z =1+i,∴z =1-i ,∴(1+z )·z =(2+i)(1-i)=3-i.课标文数2.L4[2011·浙江卷] 若复数z =1+i ,i 为虚数单位,则(1+z )·z =( )A .1+3iB .3+3iC .3-iD .3课标文数2.L4[2011·浙江卷] A 【解析】 ∵z =1+i ,∴(1+z )·z =(2+i)(1+i)=1+3i.大纲理数1.L4[2011·重庆卷] 复数i 2+i 3+i 41-i=( ) A .-12-12i B .-12+12i C.12-12i D.12+12i 大纲理数1.L4[2011·重庆卷] C 【解析】 i 2+i 3+i 41-i =-1-i +11-i =-i 1-i =-i (1+i )(1-i )(1+i )=-i -12=12-12i.故选C. [2011·南昌期末] 若框图(如图K48-2)所给的程序运行结果为S =20,那么判断框中应填入的关于k 的条件是( )[来源:学科网][2011·东莞期末] 已知(x +i)(1-i)=y ,则实数x ,y 分别为( )A .x =-1,y =1B .x =-1,y =2C .x =1,y =1D .x =1,y =2[2011·北京高考样卷] 若a -i i=b +2i ,其中a ,b ∈R ,i 是虚数单位,则a -b 的值为( )A.-1 B.-3 C.3 D.1。
高考数学 (真题 模拟新题分类汇编) 算法初步与复数 理

算法初步与复数L1算法与程序框图图1-15.L1[2013·新课标全国卷Ⅰ] 执行如图1-1所示的程序框图,如果输入的t∈[-1,3],则输出的s属于( )A.[-3,4]B.[-5,2]C.[-4,3]D.[-2,5]5.A [解析] 由框图可知,当t∈[-1,1)时,s=3t,故此时s∈[-3,3);当t∈[1,3]时,s=4t-t2=-(t-2)2+4,故此时s∈[3,4],综上,s∈[-3,4].5.L1、L2[2013·安徽卷] 某班级有50名学生,其中有30名男生和20名女生,随机询问了该班五名男生和五名女生在某次数学测验中的成绩,五名男生的成绩分别为86,94,88,92,90,五名女生的成绩分别为88,93,93,88,93.下列说法一定正确的是( ) A.这种抽样方法是一种分层抽样B.这种抽样方法是一种系统抽样C.这五名男生成绩的方差大于这五名女生成绩的方差D.该班男生成绩的平均数小于该班女生成绩的平均数5.C [解析] 分层抽样是按照比例的抽样,由于男女生人数不同,抽取的人数相同;系统抽样是按照一定规则的分段抽样,故题中抽样方法即不是分层抽样也不是系统抽样.又五名男生的成绩的平均数为90,方差为8,五名女生成绩的平均数是91,方差为6,但该班所有男生成绩的平均数未必小于该班所有女生成绩的平均数.故选项C中的结论正确,选项D 中的结论不正确.2.L1[2013·安徽卷] 如图1-1所示,程序框图(算法流程图)的输出结果是( )图1-1A.16B.2524C.34D.11122.D [解析] 依次运算的结果是s =12,n =4;s =12+14,n =6;s =12+14+16,n =8,此时输出s ,故输出结果是12+14+16=1112.4.L1[2013·北京卷] 执行如图1-1所示的程序框图,输出的S 的值为()图1-1A .1 B.23 C.1321 D.6109874.C [解析] 执行第一次循环时S =12+12×1+1=23,i =1;第二次循环S =232+12×23+1=1321,i =2,此时退出循环,故选C.6.L1[2013·福建卷] 阅读如图1-2所示的程序框图,若输入的k =10,则该算法的功能是( )图1-2A.计算数列{2n-1}的前10项和B.计算数列{2n-1}的前9项和C.计算数列{2n-1}的前10项和D.计算数列{2n-1}的前9项和6.A [解析] S=0,i=1→S=1,i=2→S=1+2,i=3→S=1+2+22,i=4→…→S =1+2+22+…+29,i=11>10,故选A.17.L1[2013·广东卷] 某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图1-4所示,其中茎为十位数,叶为个位数.(1)根据茎叶图计算样本均值:(2)日加工零件个数大于样本均值的工人为优秀工人,根据茎叶图推断该车间12名工人中有几名优秀工人?(3)从该车间12名工人中,任取2人,求恰有1名优秀工人的概率.图1-417.解:18.L1[2013·广东卷] 如图1-5(1),在等腰直角三角形ABC中,∠A=90°,BC=6,D,E分别是AC,AB上的点,CD=BE=2,O为BC的中点,将△ADE沿DE折起,得到如图1-5(2)所示的四棱锥A′-BCDE,其中A′O= 3.(1)证明:A′O⊥平面BCDE;(2)求二面角A′-CD-B的平面角的余弦值.图1-518.解:19.L1[2013·广东卷] 设数列{a n }的前n 项和为S n ,已知a 1=1,2S n n =a n +1-13n 2-n -23,n∈N *.(1)求a 2的值;(2)求数列{a n }的通项公式;(3)证明:对一切正整数n ,有1a 1+1a 2+…+1a n <74.19.解:20.L1[2013·广东卷] 已知抛物线C 的顶点为原点,其焦点F(0,c)(c>0)到直线l :x -y -2=0的距离为322,设P 为直线l 上的点,过点P 作抛物线C 的两条切线PA ,PB ,其中A ,B 为切点.(1)求抛物线C 的方程;(2)当点P(x 0,y 0)为直线l 上的定点时,求直线AB 的方程; (3)当点P 在直线l 上移动时,求|AF|·|BF|的最小值.20.解:21.L1[2013·广东卷] 设函数f(x)=(x -1)e x -kx 2(k∈R ). (1)当k =1时,求函数f(x)的单调区间;(2)当k∈⎝ ⎛⎦⎥⎤12,1时,求函数f(x)在[0,k]上的最大值M. 21.解:16.L1[2013·广东卷] 已知函数f(x)=2cos ⎝ ⎛⎭⎪⎫x -π12,x ∈R . (1)求f ⎝ ⎛⎭⎪⎫-π6的值;(2)若cos θ=35,θ∈⎝ ⎛⎭⎪⎫3π2,2π,求f ⎝⎛⎭⎪⎫2θ+π3.16.解:11.L1[2013·广东卷] 执行如图1-2所示的程序框图,若输入n 的值为4,则输出s 的值为________.图1-211.7 [解析] 1≤4,s =1+0=1,i =2;2≤4,s =1+1=2,i =3;3≤4,s =2+2=4,i =4;4≤4,s =4+3=7,i =5;5>4,故输出s =7.12.L1[2013·湖北卷] 阅读如图1-4所示的程序框图,运行相应的程序,输出的结果i =________.图1-412.5 [解析] 逐次运算结果是a =5,i =2;a =16,i =3;a =8,i =4;a =4,i =5,满足条件,输出i =5.13.L1[2013·湖南卷] 执行如图1-3所示的程序框图,如果输入a =1,b =2,则输出的a 的值为________.图1-313.9 [解析] 根据程序框图所给流程依次可得,a=1,b=2,①a=3,②a=5,③a=7,④a=9,满足条件输出a=9.5.L1[2013·江苏卷] 如图1-1是一个算法的流程图,则输出的n的值是________.图1-15.3 [解析] 逐一代入可得当a=26>20时,n=37.L1[2013·江西卷] 阅读如图1-1所示的程序框图,如果输出i=5,那么在空白矩形框中应填入的语句为( )图1-1A.S=2*i-2 B.S=2*i-1C.S=2*i D.S=2*i+47.C [解析] 依次检验可知选C.13.L1[2013·山东卷]图1-3执行如图1-3所示的程序框图,若输入的ε的值为0.25,则输出的n的值为________.13.3 [解析] 第一次执行循环体时,F1=3,F0=2,n=1+1=2,1F1=13>0.25;第二次执行循环体时,F1=2+3=5,F0=3,n=2+1=3,1F1=15<0.25,满足条件,输出n=3.18.L1,K6[2013·四川卷] 某算法的程序框图如图1-6所示,其中输入的变量x在1,2,3,…,24这24个整数中等可能随机产生.图1-6(1)分别求出按程序框图正确编程运行时输出y的值为i的概率P i(i=1,2,3);(2)甲、乙两同学依据自己对程序框图的理解,各自编写程序重复运行n次后,统计记录了输出y的值为i(i=1,2,3)的频数.以下是甲、乙所作频数统计表的部分数据.甲的频数统计表(部分)乙的频数统计表(部分)当n =2 100时,根据表中的数据,分别写出甲、乙所编程序各自输出y 的值为i(i =1,2,3)的频率(用分数表示),并判断两位同学中哪一位所编写程序符合算法要求的可能性较大;(3)按程序框图正确编写的程序运行3次,求输出y 的值为2的次数ξ的分布列及数学期望.18.解:(1)变量x 是在1,2,3,…,24这24个整数中随机产生的一个数,共有24种可能.当x 从1,3,5,7,9,11,13,15,17,19,21,23这12个数中产生时,输出y 的值为1,故P 1=12;当x 从2,4,8,10,14,16,20,22这8个数中产生时,输出y 的值为2,故P 2=13;当x 从6,12,18,24这4个数中产生时,输出y 的值为3,故P 3=16,所以,输出y 的值为1的概率为12,输出y 的值为2的概率为13,输出y 的值为3的概率为16. (2)当n =2 100时,甲、乙所编程序各自输出y 的值为i(i =1,2,3)的频率如下:(3)随机变量ξ可能的取值为0,1,2,3.P(ξ=0)=C 03×⎝ ⎛⎭⎪⎫130×⎝ ⎛⎭⎪⎫233=827,P(ξ=1)=C 13×⎝ ⎛⎭⎪⎫131×⎝ ⎛⎭⎪⎫232=49,P(ξ=2)=C 23×⎝ ⎛⎭⎪⎫132×⎝ ⎛⎭⎪⎫231=29,P(ξ=3)=C 33×⎝ ⎛⎭⎪⎫133×⎝ ⎛⎭⎪⎫230=127,故ξ的分布列为所以,E ξ=0×827+1×49+2×29+3×127=1.即ξ的数学期望为1.3.L1[2013·天津卷] 阅读如图1-1所示的程序框图,运行相应的程序,若输入x 的值为1,则输出S 的值为( )图1-1A .64B .73C .512D .5853.B [解析] 当x =1时,S =0+1=1;当x =2时,S =1+23=9;当x =4时,S =9+43=73满足题意输出.图1-16.L1[2013·新课标全国卷Ⅱ] 执行如图1-1所示的程序框图,如果输入的N =10,那么输出的S =( )A .1+12+13+…+110B .1+12!+13!+ (110)C .1+12+13+…+111D .1+12!+13!+ (111)6.B [解析] k =1,T =1,S =1;k =2,T =12,S =1+12;k =3,T =12×3,S =1+12+12×3;k =4,T =12×3×4,S =1+12!+13!+14!,…,10>10不成立,继续循环.答案为B.5.L1[2013·浙江卷] 某程序框图如图1-1所示,若该程序运行后输出的值是95,则( )图1-1A .a =4B .a =5C .a =6D .a =75.A [解析] S =1+11×2+12×3+…+1k (k +1)=1+1-12+12-13+…+1k -1k +1=1+1-1k +1=2-1k +1=95,故k =4,k =k +1=5,满足k>a 时,即5>a 时,输出S ,所以a =4,选择A.8.L1,L2[2013·重庆卷] 执行如图1-4所示的程序框图,如果输出s =3,那么判断框内应填入的条件是( )图1-4A .k ≤6B .k ≤7C .k ≤8D .k ≤98.B [解析] 第一次输入得s =log 23,k =3;第二次得s =log 23·log 34=2,k =4;第三次得s =2log 45,k =5;第四次得s =2log 45·log 56=2 log 46,k =6;第五次得s =2log 46·log 67=2log 47,k =7;第六次得s =2log 47·log 78=2log 48=2log 4432=3,k =8,输出,故选B.L2 基本算法语句5.L1、L2[2013·安徽卷] 某班级有50名学生,其中有30名男生和20名女生,随机询问了该班五名男生和五名女生在某次数学测验中的成绩,五名男生的成绩分别为86,94,88,92,90,五名女生的成绩分别为88,93,93,88,93.下列说法一定正确的是( )A .这种抽样方法是一种分层抽样B .这种抽样方法是一种系统抽样C .这五名男生成绩的方差大于这五名女生成绩的方差D .该班男生成绩的平均数小于该班女生成绩的平均数5.C [解析] 分层抽样是按照比例的抽样,由于男女生人数不同,抽取的人数相同;系统抽样是按照一定规则的分段抽样,故题中抽样方法即不是分层抽样也不是系统抽样.又五名男生的成绩的平均数为90,方差为8,五名女生成绩的平均数是91,方差为6,但该班所有男生成绩的平均数未必小于该班所有女生成绩的平均数.故选项C 中的结论正确,选项D 中的结论不正确.2.L2[2013·陕西卷] 根据下列算法语句,当输入x 为60时,输出y 的值为( )输入x ;If x ≤50 Then y =0.5*xElsey =25+0.6*(x -50) End If 输出y.A .25B .30C .31D .612.C [解析] 算法语言给出的是分段函数y =⎩⎪⎨⎪⎧0.5x ,x≤50,25+0.6(x -50),x>50,输入x =60时,y =25+0.6(60-50)=31.8.L1,L2[2013·重庆卷] 执行如图1-4所示的程序框图,如果输出s =3,那么判断框内应填入的条件是( )图1-4A .k ≤6B .k ≤7C .k ≤8D .k ≤98.B [解析] 第一次输入得s =log 23,k =3;第二次得s =log 23·log 34=2,k =4;第三次得s =2log 45,k =5;第四次得s =2log 45·log 56=2 log 46,k =6;第五次得s =2log 46·log 67=2log 47,k =7;第六次得s =2log 47·log 78=2log 48=2log 4432=3,k =8,输出,故选B.L3 算法案例L4 复数的基本概念与运算2.L4[2013·新课标全国卷Ⅰ] 若复数z 满足(3-4i)z =|4+3i|,则z 的虚部为( ) A .-4 B .-45 C .4 D.452.D [解析] z =|4+3i|3-4i =53-4i =5(3+4i )25=35+45i ,故z 的虚部是45.1.L4[2013·安徽卷] 设i 是虚数单位,z 是复数z 的共轭复数,若z·zi +2=2z ,则z=( )A .1+iB .1-iC .-1+iD .-1-i1.A [解析] 设z =a +bi(a ,b∈R ),则z =a -bi ,所以z·zi +2=2z ,即2+(a 2+b 2)i=2a +2bi ,根据复数相等的充要条件得2=2a ,a 2+b 2=2b ,解得a =1,b =1,故z =1+i.2.L4[2013·北京卷] 在复平面内,复数(2-i)2对应的点位于( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限2.D [解析] (2-i)2=4-4i +i 2=3-4i ,对应的复平面内点的坐标为(3,-4),所以选D.1.L4[2013·福建卷] 已知复数z 的共轭复数z =1+2i(i 为虚数单位),则z 在复平面内对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限1.D [解析] z =1-2i ,对应的点为P(1,-2),故选D.3.L4[2013·广东卷] 若复数iz =2+4i ,则在复平面内,z 对应的点的坐标是( ) A .(2,4) B .(2,-4) C .(4,-2) D .(4,2)3.C [解析] 设复数z =a +bi ,a ,b∈R ,则iz =i(a +bi)=-b +ai =2+4i ,解得b =-2,a =4.故在复平面内,z 对应的点的坐标是(4,-2),选C.1.L4[2013·湖北卷] 在复平面内,复数z =2i1+i(i 为虚数单位)的共轭复数对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限1.D [解析] z =2i 1+i =2i (1-i )(1+i )(1-i )=i(1-i)=1+i ,z =1-i ,z 对应的点在第四象限,选D.1.L4[2013·湖南卷] 复数z =i ·(1+i)(i 为虚数单位)在复平面上对应的点位于( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限1.B [解析] 由题z =i ·(1+i)=i +i 2=-1+i ,在复平面上对应的点坐标为(-1,1),即位于第二象限,选B.2.L4[2013·江苏卷] 设z =(2-i)2(i 为虚数单位),则复数z 的模为________.2.5 [解析] 因为z =(2-i)2=4-4i +i 2=3-4i ,所以复数z 的模为5.1.A1,L4[2013·江西卷] 已知集合M ={1,2,zi},i 为虚数单位,N ={3,4},M∩N ={4},则复数z =( )A .-2iB .2iC .-4iD .4i1.C [解析] zi =4z =-4i ,故选C.1.L4[2013·辽宁卷] 复数z =1i -1的模为( )A.12B.22C. 2 D .2 1.B [解析] 复数z =1i -1=-1+i 2,所以|z|=-1+i 2=22,故选B.2.L4[2013·全国卷] (1+3i)3=( )A .-8B .8C .-8iD .8i2.A [解析] (1+3i)3=13+3×12(3i)+3×1×(3i)2+(3i)3=1+33i -9-33i =-8.1.L4[2013·山东卷] 复数z 满足(z -3)(2-i)=5(i 为虚数单位),则z 的共轭复数z 为( )A .2+iB .2-iC .5+iD .5-i1.D [解析] 设z =a +bi ,(a ,b∈R ),由题意得(a +bi -3)(2-i)=(2a +b -6)+(2b-a +3)i =5,即⎩⎪⎨⎪⎧2a +b -6=5,2b -a +3=0,解之得⎩⎪⎨⎪⎧a =5,b =1,∴z =5-i.6.L4[2013·陕西卷] 设z 1,z 2是复数,则下列命题中的假.命题是( ) A .若|z 1-z 2|=0,则z 1=z 2 B .若z 1=z 2,则z 1=z 2C .若|z 1|=|z 2|,则z 1·z 1=z 2·z 2D .若|z 1|=|z 2|,则z 21=z 226.D [解析] 设z 1=a +bi ,z 2=c +di(a ,b ,c ,d∈R ),若|z 1-z 2|=0,则z 1-z 2=(a -c)+(b -d)i =0a =c ,b =d ,故A 正确.若z 1=z 2,则a =c ,b =-d ,所以z 1=z 2,故B 正确.若|z 1|=|z 2|,则a 2+b 2=c 2+d 2,所以z 1·z 1=z 2·z 2,故C 正确.又z 21=(a 2-b 2)+2abi ,z 22=(c 2-d 2)+2cdi ,由a 2+b 2=c 2+d 2不能推出z 21=z 22成立,故D 错.2.L4[2013·四川卷] 如图1-1所示,在复平面内,点A 表示复数z ,则图1-1中表示z 的共轭复数的点是( )图1-1A .AB .BC .CD .D2.B [解析] 复数与共轭复数的几何关系是其表示的点关于x 轴对称.9.L4[2013·天津卷] 已知a ,b∈R ,i 是虚数单位,若(a +i)(1+i)=bi ,则a +bi =________.9.1+2i [解析] (a +i)(1+i)=a -1+(a +1)i =bi ,∴⎩⎪⎨⎪⎧a -1=0,a +1=b ,解得a =1,b =2.故a +bi =1+2i. 2.L4[2013·新课标全国卷Ⅱ] 设复数z 满足(1-i)z =2i ,则z =( ) A .-1+i B .-1-i C .1+i D .1-i2.A [解析] (1-i)z =2i ,则z =2i1-i =i(1+i)=-1+i.故选A.1.L4[2013·浙江卷] 已知i 是虚数单位,则(-1+i)(2-i)=( )A.-3+i B.-1+3iC.-3+3i D.-1+i1.B [解析] (-1+i)(2-i)=-2+i+2i+1=-1+3i,故选择B.11.L4[2013·重庆卷] 已知复数z=5i1+2i(i是虚数单位),则|z|=________.11. 5 [解析] 因为z=5i(1-2i)(1+2i)(1-2i)=2+i,所以|z|=22+12= 5.L5单元综合1.[2013·杭州质检] k的值是( )A.4 B.5C.6 D.71.B [解析] 由题意,得n=5,k=0⇒n=16,k=1⇒n=8,k=2⇒n=4,k=3⇒n=2,k=4⇒n=1,k=5⇒终止当n=2时,执行最后一次循环;当n=1时,循环终止,这是关键.输出k=5.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课标文数12.L1[2011·安徽卷] 如图1-3所示,程序框图(算法流程图)的输出结果是________.图1-3课标文数12.L1[2011·安徽卷] 【答案】 15 【解析】 第一次进入循环体有T =0+0,第二次有:T =0+1,第三次有T =0+1+2,…第k +1次有T =0+1+2+…+k =k (k +1)2,若T =105,解得k =14,继续执行循环,这时k=15,T >105,所以输出的k 的值是15.课标理数11.L1[2011·安徽卷] 如图1-3所示,程序框图(算法流程图)的输出结果是________.图1-3课标理数11.L1[2011·安徽卷] 15 【解析】 第一次进入循环体有T =0+0,第二次有:T =0+1,第三次有T =0+1+2,…,第k +1次有T =0+1+2+…+k =k (k +1)2,若T =105,解得k =14,继续执行循环,这时k =15,T >105,所以输出的k 的值是15.课标理数4.L1[2011·北京卷] D 【解析】 第(i =0)一步,i =0+1=1,s =2-12+1=13;第(i =1)二步,i =1+1=2,s =13-113+1=-12;第(i =2)三步,i =2+1=3,s =-12-1-12+1=-3;第(i =3)四步,i =3+1=4,s =-3-1-3+1=2;第(i =4)五步,i =4<4不成立,输出s =2,故选D.课标文数6.L1[2011·北京卷] 执行如图1-2所示的程序框图,若输入A 的值为2,则输出的P 值为()图1-2A .2B .3C .4D .5课标文数6.L1[2011·北京卷] C 【解析】 第一步,P =1+1=2,S =1+12=32;第二步,P =2+1=3,S =32+13=116;第三步,P =3+1=4,S =116+14=2512>2,输出P =4,故选C.课标理数1.A1,L4[2011·福建卷] i 是虚数单位,若集合S ={-1,0,1},则( )A .i ∈SB .i 2∈SC .i 3∈S D.2i∈S课标理数1.A1、L4[2011·福建卷] B 【解析】 由i 2=-1,而-1∈S ,故选B.课标文数5.L1[2011·福建卷] 阅读图1-1所示的程序框图,运行相应的程序,输出的结果是( )图1-1A .3B .11C .38D .123 课标文数5.L1[2011·福建卷] B 【解析】 该程序框图是当型的循环结构,由程序框图可知,第一次循环,a =12+2=3;第二次循环,a =32+2=11; 当a =11时,a <10不成立,输出a =11,故选B.课标理数13.L1[2011·湖南卷] 若执行如图1-3所示的框图,输入x 1=1,x 2=2,x 3=3,x =2,则输出的数等于________.图1-3课标理数13.L1[2011·湖南卷] 23【解析】 由累加的赋值符号S =S +(x i -x )2得到S=(1-2)2+(2-2)2+(3-2)2=2,而最后输出的结果为S =1i S =13×2=23.课标文数11.L1[2011·湖南卷] 若执行如图1-2所示的框图,输入x 1=1,x 2=2,x 3=4,x 4=8,则输出的数等于________.图1-2课标文数11.L1[2011·湖南卷]154【解析】 由累加的赋值符号x =x +x i 得到x =x 1+x 2+x 3+x 4=1+2+4+8=15,而最后输出的结果为x =14x =14×15=154.课标理数13.L1[2011·江西卷] 图1-6是某算法的程序框图,则程序运行后输出的结果是________.图1-6 课标理数13.L1[2011·江西卷] 【答案】 10【解析】 第一次,s =0+(-1)1+1=0,n =2,第二次,s =0+(-1)2+2=3,n =3,第三次,s =3+(-1)3+3=5,n =4,第四次,s =5+(-1)4+4=10>9,终止循环,输出结果10.课标文数13.L1[2011·江西卷] 图1-6是某算法的程序框图,则程序运行后输出的结果是________.图1-6课标文数13.L1[2011·江西卷] 27 【解析】 第一次:s =(0+1)×1=1,n =1+1=2,第二次:s =(1+2)×2=6,n =3,第三次:s =(6+3)×3=27,n =4,而n =4>3,退出循环,输出s =27.故填27.课标理数3.L1[2011·课标全国卷] 执行如图1-1所示的程序框图,如果输入的N 是6,那么输出的p 是( )图1-1A .120B .720[来源:]C .1440D .5040 课标理数3.L1[2011·课标全国卷] B 【解析】 k =1时,p =1; k =2时,p =1×2=2; k =3时,p =2×3=6; k =4时,p =6×4=24; k =5时,p =24×5=120; k =6时,p =120×6=720.课标文数9.L1[2011·辽宁卷] 执行下面的程序框图,如果输入的n是4,则输出的p是()图1-5A.8 B.5 C.3 D.2课标文数9.L1[2011·辽宁卷] C【解析】由于n=4,所以当k=1时,p=1,s=1,t =1;当k=2时,p=2,s=1,t=2;当k=3时,p=3,s=2,t=3,此时k=4,输出p,此时p=3,故选C.课标文数5.L1[2011·课标全国卷] 执行下面的程序框图,如果输入的N是6,那么输出的p是()图1-1A.120 B.720C.1440 D.5040课标文数5.L1[2011·课标全国卷] B【解析】k=1时,p=1;k=2时,p=1×2=2;k=3时,p=2×3=6;k=4时,p=6×4=24;k=5时,p=24×5=120;k=6时,p=120×6=720.课标理数13.L1[2011·山东卷] 执行图1-3所示的程序框图,输入l=2,m=3,n=5,则输出的y的值是________.图1-3课标理数13.L1[2011·山东卷] 68【解析】把l=2,m=3,n=5代入y=70l+21m+15n得y=278,此时y=278>105,第一次循环y=278-105=173,此时y=173>105,再循环,y=173-105=68,输出68,结束循环.课标文数14.L1[2011·山东卷] 执行图1-4所示的程序框图,输入l=2,m=3,n=5,则输出的y的值是________.图1-4[来源:Z_xx_]课标文数14.L1[2011·山东卷] 68【解析】把l=2,m=3,n=5代入y=70l+21m+15n得y=278,此时y=278>105,第一次循环y=278-105=173,此时y=173>105,再循环,y=173-105=68,输出68,结束循环.课标理数8.L1[2011·陕西卷] 图1-3中,x1,x2,x3为某次考试三个评阅人对同一道题的独立评分,p为该题的最终得分.当x1=6,x2=9,p=8.5时,x3等于()图1-3A .11B .10C .8D .7 课标理数8.L1[2011·陕西卷] C 【解析】 由题目中所给的数据p =8.5,x 1=6,x 2=9,则若满足条件|x 3-x 1|s <|x 3-x 2|时,不成立,故应不满足条件|x 3-x 1|<|x 3-x 2|,此时满足x 2+x 32=8.5,则x 3=8,并且代入也符合题意,故选C.课标文数7.L1[2011·陕西卷] 如下框图,当x 1=6,x 2=9,p =8.5时,x 3等于( )图1-4A .7B .8C .10D .11课标文数7.L1[2011·陕西卷] B 【解析】 因为x 1=6,x 2=9,p =8.5,p =x 1+x 22或p=x 2+x 32,当x 1=6,x 2=9,p =x 1+x 22=7.5,不合题意,故p =x 2+x 32=8.5,x 2=9,得x 3=8,故答案为B.课标数学4.L1[2011·江苏卷] 根据如图所示的伪代码,当输入a ,b 分别为2,3时,最后输出的m 的值为________.Read a ,b If a >b Then m ←a Else m ←b End If Print m课标数学4.L1[2011·江苏卷] 3 【解析】 因为a =2<b =3,所以m =3.课标理数3.L1[2011·天津卷] 阅读程序框图1-1,运行相应的程序,则输出i的值为()图1-1A.3 B.4 C.5 D.6课标理数3.L1[2011·天津卷] B【解析】i=1时,a=1×1+1=2;[来源:学|科|网] i=2时,a=2×2+1=5;i=3时,a=3×5+1=16;i=4时,a=4×16+1=65>50,∴输出i=4,故选B.图1-2课标文数3.L1[2011·天津卷] 阅读图1-2所示的程序框图,运行相应的程序,若输入x 的值为-4,则输出y的值为()A.0.5 B.1C.2 D.4课标文数3.L1[2011·天津卷] C【解析】当x=-4时,x=|x-3|=7;当x=7时,x =|x-3|=4;当x=4时,x=|x-3|=1<3,∴y=2.课标理数12.L1[2011·浙江卷] 若某程序框图如图1-4所示,则该程序运行后输出的k 的值是________.图1-4课标理数12.L1[2011·浙江卷] 5【解析】k=3时,a=43=64,b=34=84,a<b;k=4时,a=44=256,b=44=256,a=b;k=5时,a=45=256×4,b=54=625,a>b.[来源:学§科§网Z§X§X§K]图1-5课标文数14.L1[2011·浙江卷] 某程序框图如图1-5所示,则该程序运行后输出的k的值是________.课标文数14.L1[2011·浙江卷] 5【解析】k=3时,a=43=64,b=34=84,a<b;k=4时,a=44=256,b=44=256,a=b;k=5时,a=45=256×4,b=54=625,a>b.课标理数11.L2[2011·福建卷] 运行如图1-4所示的程序,输出的结果是________.a=1b=2a=a+bPRINT aEND图1-4课标理数11.L2[2011·福建卷] 【答案】 3【解析】由已知,输入a=1,b=2,把a+b的值赋给a,输出a=3.课标理数16.L3[2011·湖南卷] 对于n ∈N *,将n 表示为n =a 0×2k +a 1×2k -1+a 2×2k -2+…+a k -1×21+a k ×20,当i =0时,a i =1,当1≤i ≤k 时,a i 为0或1.记I (n )为上述表示中a i 为0的个数(例如:1=1×20,4=1×22+0×21+0×20,故I (1)=0,I (4)=2),则(1)I (12)=________; (2)∑127n =12I(n)=________. 课标理数16.L3[2011·湖南卷] (1)2 (2)1093【解析】 (1)本题实考二进制与十进制间的互化:因为I (12)=1×23+1×22+0×21+0×20,根据题目给出的定义可得到: I (12)=2;(2)∑n =11272I (n )=2I (1)+2I (2)+2I (3)+…+2I (127)利用二进制与十进制间的互化,列举得: I (1)=1(2)共一个,则S 1=2I (1)=20=1; I (2)=10(2),I (3)=11(2)共2个, 则S 2=2I (2)+2I (3)=21+20=3;I (4)=100(2),I (5)=101(2),I (6)=110(2),I (7)=111(2)共4个,则S 3=2I (4)+…+2I (7)=9; I (8)=1000(2),I (9)=1001(2),…,I (15)=1111(2) 共8个, 则S 4=2I (8)+…+2I (15)=27; ……I (64)=100000(2),…,I (127)=1111111(2)共64个,则S 7=2I (64)+…+2I (127)=729; 故∑n =11272I (n )=2I (1)+2I (2)+2I (3)+…+2I (127)=S 1+S 2+S 3+S 4+S 5+S 6+S 7=1+3+9+27+81+243+729=1093.课标文数1.L4[2011·安徽卷] 设i 是虚数单位,复数1+a i2-i为纯虚数,则实数a 为( )A .2B .-2C .-12 D.12课标文数1.L4[2011·安徽卷] A 【解析】 法一:1+a i 2-i =(1+a i )·(2+i )(2-i )(2+i )=2-a +(2a +1)i5为纯虚数,所以⎩⎪⎨⎪⎧2-a =0,2a +1≠0,解得a =2.法二:1+a i 2-i =i (a -i )2-i为纯虚数,所以a =2.答案为A.课标理数1.L4[2011·安徽卷] 设i 是虚数单位,复数1+a i2-i为纯虚数,则实数a 为( )A .2B .-2C .-12 D.12课标理数1.L4[2011·安徽卷] A 【解析】 法一:1+a i 2-i =(1+a i )·(2+i )(2-i )(2+i )=2-a +(2a +1)i5为纯虚数,所以⎩⎪⎨⎪⎧2-a =0,2a +1≠0, 解得a =2.法二:1+a i 2-i =i ()a -i 2-i为纯虚数,所以a =2.答案为A.课标理数2.L4[2011·北京卷] 复数i -21+2i=( )A .iB .-iC .-45-35iD .-45+35i课标理数2.L4[2011·北京卷] A 【解析】 i -21+2i =(i -2)(1-2i )(1+2i )(1-2i )=5i5=i ,故选A.课标文数2.L4[2011·北京卷] 复数i -21+2i=( )A .iB .-iC .-45-35iD .-45+35i课标文数2.L4[2011·北京卷] A 【解析】 i -21+2i =(i -2)(1-2i )(1+2i )(1-2i )=5i5=i ,故选A.大纲理数1.L4[2011·全国卷] 复数z =1+i ,z 为z 的共轭复数,则z z -z -1=( ) A .-2i B .-i C .i D .2i大纲理数1.L4[2011·全国卷] B 【解析】 ∵z =1-i ,∴z z -z -1=(1+i)(1-i)-(1+i)-1=-i ,故选B.课标文数2.L4[2011·福建卷] i 是虚数单位,1+i 3等于( ) A .i B .-i C .1+i D .1-i 课标文数2.L4[2011·福建卷] D 【解析】 由1+i 3=1+i 2·i =1-i ,故选D.课标理数1.L4[2011·广东卷] 设复数z 满足(1+i)z =2,其中i 为虚数单位,则z =( )[来源:学科网]A .1+iB .1-iC .2+2iD .2-2i课标理数1.L4[2011·广东卷] B 【解析】 z =21+i =2(1-i )(1+i )(1-i )=2(1-i )2=1-i ,故选B.课标文数1.L4[2011·广东卷] 设复数z 满足i z =1,其中i 为虚数单位,则z =( ) A .-i B .i C .-1 D .1课标文数1.L4[2011·广东卷] A 【解析】 由i z =1得z =1i =ii2=-i ,所以选A.[来源:]课标理数1.L4[2011·湖北卷] i 为虚数单位,则⎝ ⎛⎭⎪⎫1+i 1-i 2011=( )A .-iB .-1C .iD .1课标理数 1.L4[2011·湖北卷] A 【解析】 因为1+i 1-i =()1+i 2()1-i ()1+i =i ,所以⎝ ⎛⎭⎪⎫1+i 1-i 2011=i 502×4+3=i 3=-i.课标理数1.L4[2011·湖南卷] 若a ,b ∈R ,i 为虚数单位,且(a +i)i =b +i ,则( ) A .a =1,b =1 B .a =-1,b =1 C .a =-1,b =-1 D .a =1,b =-1 课标理数1.L4[2011·湖南卷] D 【解析】 由(a +i)i =b +i 得-1+a i =b +i ,根据复数相等的充要条件,得a =1,b =-1,故选D.课标文数2.L4[2011·湖南卷] 若a ,b ∈R ,i 为虚数单位,且(a +i)i =b +i ,则( ) A .a =1,b =1 B .a =-1,b =1 C .a =1,b =-1 D .a =-1,b =-1 课标文数2.L4[2011·湖南卷] C 【解析】 由(a +i)i =b +i 得-1+a i =b +i ,根据复数的相等,a =1,b =-1,故选C.课标理数1.L4[2011·江西卷] 若z =1+2ii,则复数z =( )A .-2-iB .-2+iC .2-iD .2+i课标理数1.L4[2011·江西卷] D 【解析】 z =1+2i i =i (1+2i )i 2=-(i -2)=2-i ,故z =2+i.故选D.[来源:] 课标文数1.L4[2011·江西卷] 若(x -i)i =y +2i ,x ,y ∈R ,则复数x +y i =( ) A .-2+i B .2+i C .1-2i D .1+2i 课标文数1.L4[2011·江西卷] B 【解析】 由题设得x i +1=y +2i ,∴x =2,y =1,即x +y i =2+i.故选B.课标理数1.L4[2011·课标全国卷] 复数2+i1-2i的共轭复数是( )A .-35i B.35iC .-iD .i课标理数1.L4[2011·课标全国卷] C 【解析】 2+i 1-2i =(2+i )(1+2i )(1-2i )(1+2i )=5i5=i ,所以其共轭复数为-i.故选C.图1-1课标文数2.L4[2011·辽宁卷] i 为虚数单位,1i +1i 3+1i 5+1i7=( )A .0B .2iC .-2iD .4i课标文数2.L4[2011·辽宁卷] A 【解析】 1i +1i 3+1i 5+1i7=-i +i -i +i =0,故选A.课标文数2.L4[2011·课标全国卷] 复数5i1-2i=( )A .2-iB .1-2iC .-2+iD .-1+2i课标文数2.L4[2011·课标全国卷] C 【解析】 5i1-2i =5i (1+2i )(1-2i )(1+2i )=5i -105=-2+i.[来源:学科网ZXXK]课标理数2.L4[2011·山东卷] 复数z =2-i2+i(i 为虚数单位)在复平面内对应的点所在象限为( )A .第一象限B .第二象限C .第三象限D .第四象限[来源:学科网]课标理数2.L4[2011·山东卷] D 【解析】 z =2-i 2+i =(2-i )2(2+i )(2-i )=3-4i 4+1=35-45i ,又点⎝⎛⎭⎫35,-45在第四象限,所以该复数在复平面内对应的点也在第四象限.课标文数2.L4[2011·山东卷] 复数z =2-i2+i(i 为虚数单位)在复平面内对应的点所在象限为( )A .第一象限B .第二象限C .第三象限D .第四象限课标文数2.L4[2011·山东卷] D 【解析】 z =2-i 2+i =(2-i )2(2+i )(2-i )=3-4i 4+1=35-45i ,又点⎝⎛⎭⎫35,-45在第四象限,所以该复数在复平面内对应的点也在第四象限.课标文数8.A1,L4[2011·陕西卷] 设集合M ={y |y =|cos 2x -sin 2x |,x ∈R },N =⎩⎨⎧⎭⎬⎫x ⎪⎪⎪⎪⎪⎪x i <1,i 为虚数单位,x ∈R ,则M ∩N 为( ) A .(0,1) B .(0,1] C .[0,1) D .[0,1] 课标文数8.A1,L4[2011·陕西卷] C 【解析】 对M ,由基本不等式得y =|cos 2x -sin 2x |=|cos2x |,故0≤y ≤1.对N ,⎪⎪⎪⎪x i <1,即|-x i|<1,所以-1<x <1,故M ∩N =[0,1),故答案为C.课标数学 1.A1[2011·江苏卷] 已知集合A ={-1,1,2,4},B ={-1,0,2}, 则A ∩B =________.课标数学1.A1[2011·江苏卷] {-1,2} 【解析】 因为集合A ,B 的公共元素为-1,2,故A ∩B ={-1,2}.课标数学3.L4[2011·江苏卷] 设复数z 满足i(z +1)=-3+2i(i 为虚数单位),则z 的实部是________.课标数学3.L4[2011·江苏卷] 1 【解析】 因为z +1=-3+2i i =-3i +2i 2i 2=2+3i ,所以z =1+3i ,故实部为1.大纲理数2.L4[2011·四川卷] 复数-i +1i=( )A .-2i B.12i C .0 D .2i大纲理数2.L4[2011·四川卷] A 【解析】 -i +1i=-i -i =-2i ,所以选A.课标理数1.L4[2011·天津卷] i 是虚数单位,复数1-3i1-i=( )A .2+iB .2-iC .-1+2iD .-1-2i课标理数1.L4[2011·天津卷] B 【解析】 1-3i 1-i =(1-3i )(1+i )(1-i )(1+i )=4-2i2=2-i.课标文数1.L4[2011·天津卷] i 是虚数单位,复数1-3i1-i=( )A .2-iB .2+iC .-1-2iD .-1+2i课标文数1.L4[2011·天津卷] A 【解析】 1-3i 1-i =(1-3i )(1+i )(1-i )(1+i )=4-2i2=2-i.课标理数2.L4[2011·浙江卷] 把复数z 的共轭复数记作z ,i 为虚数单位.若z =1+i ,则(1+z )·z =( )A .3-iB .3+iC .1+3iD .3课标理数2.L4[2011·浙江卷] A 【解析】 ∵z =1+i ,∴z =1-i ,∴(1+z )·z =(2+i)(1-i)=3-i.课标文数2.L4[2011·浙江卷] 若复数z =1+i ,i 为虚数单位,则(1+z )·z =( ) A .1+3i B .3+3i C .3-i D .3课标文数2.L4[2011·浙江卷] A 【解析】 ∵z =1+i ,∴(1+z )·z =(2+i)(1+i)=1+3i.大纲理数1.L4[2011·重庆卷] 复数i 2+i 3+i 41-i=( )A .-12-12iB .-12+12iC.12-12iD.12+12i 大纲理数1.L4[2011·重庆卷] C 【解析】 i 2+i 3+i 41-i =-1-i +11-i =-i 1-i =-i (1+i )(1-i )(1+i )=-i -12=12-12i.故选C.[2011·南昌期末] 若框图(如图K48-2)所给的程序运行结果为S =20,那么判断框中应填入的关于k 的条件是( )[来源:学科网][2011·东莞期末] 已知(x +i)(1-i)=y ,则实数x ,y 分别为( ) A .x =-1,y =1 B .x =-1,y =2 C .x =1,y =1 D .x =1,y =2[2011·北京高考样卷] 若a -ii=b +2i ,其中a ,b ∈R ,i 是虚数单位,则a -b 的值为( )A .-1B.-3 C.3 D.1。
