matlab教程2
合集下载
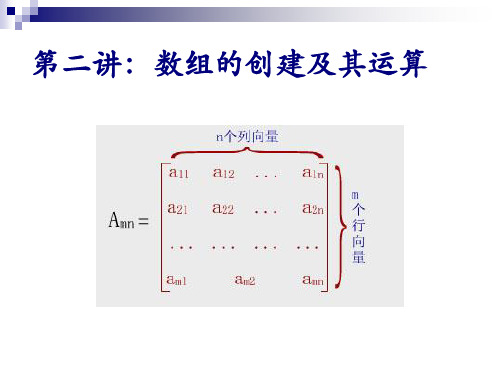
matlab2_matlab教程

x1+2x2+3x3=1 2x1+3x2+4x3=2 a=[1 2 3;2 3 4];b=[1;2]; x=a\b x= 1.00 0 x=
x1 1 2 3 1 x2 = 2 3 4 2 x3
a
x = b
x=pinv(a)b
0.83 0.33
0
-0.17
六、微分方程求解
微分方程求解的仿真算法有多种,常用 的有Euler(欧拉法)、Runge Kutta(龙 格-库塔法。 Euler法称一步法,用于一阶微分方程
a=[1 2 3;4 5 6;7 8 9]; b=[2 4 6;1 3 5;7 9 10]; a.*b ans = 2 8 18 4 15 30 49 72 90
a=[1 2 3;4 5 6;7 8 9]; b=[2 4 6;1 3 5;7 9 10];
a*b ans = 25 55 85
37 85 133
二、数据的保存与获取
把matlab工作空间中一些有用的数 据长久保存下来的方法是生成mat数 据文件。 save —— 将工作空间中所有的变 量存到matlab.mat文件中。 默认文件名
save data——将工作空间中所
有的变量存到data.mat文件中。
save data a b ——将工作空间 中a和b变量存到data.mat文件中。
rand —— 随机矩阵
eye —— 单位矩阵
zeros ——全部元素都为0的矩阵
ones ——全部元素都为1的矩阵
还有伴随矩阵、稀疏矩阵、魔方 矩阵、对角矩阵、范德蒙等矩阵的创 建,就不一一介绍了。
注意:matlab严格区分大小写字母,因
此a与A是两个不同的变量。 matlab函数名必须小写。
matlab使用教程2-2

第2章 Matlab语言程序设计 章 语言程序设计
写二进制文件: 用fwrite写二进制文件: 写二进制文件 COUNT=fwrite(Fid, A, precision) 例: Fid=fopen(‘test.dat’, ‘w’); cnt=fwrite(Fid, A, ‘float’) fclose(Fid); 读取ASCII数据文件: 数据文件: 用fscanf读取 读取 数据文件 [A, COUNT]=fscanf(Fid, format, size) format用以控制读取的数据格式,由%加上格式符组成, 用以控制读取的数据格式, 加上格式符组成, 用以控制读取的数据格式 常见的格式符有: 常见的格式符有:d, i, o,u, x, e, f, s, c。 。 例:fscanf(Fid, ‘%s’); fscant(Fid, ‘%6.2f’); fscanf(Fid, “%5d’);
第2章 Matlab语言程序设计 章 语言程序设计
d) 其它与流程控制有关的语句
if
if
break语句循环结构 语句循环结构 语句
continue 语句循环结构 语句循环结构
第2章 Matlab语言程序设计 章 语言程序设计
pause 指令使程序运行停止,等待用户按任意键继续; 指令使程序运行停止 等待用户按任意键继续; 使程序运行停止, input 指令提示用户从键盘输入数值、字符串或表达 指令提示用户从键盘输入数值 提示用户从键盘输入数值、 并接受输入; 式,并接受输入; disp指令在屏幕上显示字符串; 指令在屏幕上显示字符串 指令在屏幕上显示字符串 echo on指令显示其后所有执行文件的指令; 指令显示其后所有执行文件的指令 指令显示其后所有执行文件的指令; echo off指令关闭其后所有执行文件的指令显示。 指令关闭其后所有执行文件的指令显示 指令关闭其后所有执行文件的指令显示。
MATLAB课件-第二讲
A(r,c)
访问A的由r指定行和c指定列上元素构 成的子数组;r,c可取多行或列
A(r, :)
访问A的r指定行上全部元素构成的子 数组;此处冒号表示全部列
A(:,c)
访问A的c指定列上全部元素的子数 组;此处冒号表示全部行
【例1】单下标的使用 >>a=zeros(2, 5); >>a(:)=-1:8
【例4】>> diag (diag(D)) %外面diag含义为利用一维数组生 成对角阵
ans= 100 010 001
【例5】>>命令栏输入:magic(3) ans =
816 357 492 说明:magic(3)生成一3x3魔方矩阵,即该矩阵横、竖、斜 各列元素总和相等
2.4 数组操作
常见的数组操作函数
命令 permute repmat
reshape
flipud
fliplr
rot90
含义
重排数组的维度次序
按指定的“行数、列数”铺放模块数组,以形成更大 的数组
在总元素数不变的前提下,改变数组的“行数、列 数” 以数组“水平中线”为对称轴,交换上下对称位置上 的数组元素
以数组“垂直中线”为对称轴,交换左右对称位置上 的数组元素
>>a([1 3 5 5 3 1])
ans = 0 5 10 10 5 0
>>a(6)
??? Index exceeds matrix dimensions. 索引超出矩阵维度。 下标值超出了数组的维数,导致错误
>>a(2.1)
??? Subscript indices must either be real positive integers or logicals.
二MATLAB基本操作

在逻辑操作中,所有输入元素的非零值都当 作1处理,例如: x=[23 -5 ;0 0.001] ~x ans=0 0
10
§2.4 逻辑和关系运算
二. 关系操作符 MATLAB提供了六种关系操作符,这些
操作符与逻辑运算配合使用,可使程序 设计更加灵活。 例如:if and(a==1,b>5)
……
end 则当a=1且b>5时执行指定的语句。
例如:a=[1 2 3; 4 5 6; 7 8 9] 又如:b=[1:3; 4:6; 7:9]
c=[1: 6 : 0.5] 注意:关于:的使用相当灵活,大家可随
着学习的不断深入对:的使用逐步加深 灵活。
§2.2 矩阵基础
(2)从外部数据文件读取 load score.dat
(3) 利用matlab内部函数产生矩阵 例如:b=eye(3); 单位阵 c= ones(2,5); 全一阵 d=zeros(3,2); 全零阵 e=rand(2,3); 随机阵
这样很容易产生元素等值的矩阵: c3=8×ones(8,9);
§2.3 矩阵产生和操作
MATLAB提供的rand和randn可分别产 生均匀分布和正态分布的随机数。 例如要产生[0,1]之间均匀分布的随机向 量R(100×1),可输入R=rand(100,1) 如果要产生[-a,a](a为正数)之间均匀分 布的随机数则应输入
§2.5操作符和特殊字符
7. xor 功能:异或操作。 格式:C=xor(A,B) C=xor(A,B)完成阵列A和B对应元素的 异或操作。 如: A=[0 0 pi eps]
B=[0 -2 4 1.2] C=xor(A,B) C=0 1 0 1
§2.7 基本数学函数
一.三角函数
10
§2.4 逻辑和关系运算
二. 关系操作符 MATLAB提供了六种关系操作符,这些
操作符与逻辑运算配合使用,可使程序 设计更加灵活。 例如:if and(a==1,b>5)
……
end 则当a=1且b>5时执行指定的语句。
例如:a=[1 2 3; 4 5 6; 7 8 9] 又如:b=[1:3; 4:6; 7:9]
c=[1: 6 : 0.5] 注意:关于:的使用相当灵活,大家可随
着学习的不断深入对:的使用逐步加深 灵活。
§2.2 矩阵基础
(2)从外部数据文件读取 load score.dat
(3) 利用matlab内部函数产生矩阵 例如:b=eye(3); 单位阵 c= ones(2,5); 全一阵 d=zeros(3,2); 全零阵 e=rand(2,3); 随机阵
这样很容易产生元素等值的矩阵: c3=8×ones(8,9);
§2.3 矩阵产生和操作
MATLAB提供的rand和randn可分别产 生均匀分布和正态分布的随机数。 例如要产生[0,1]之间均匀分布的随机向 量R(100×1),可输入R=rand(100,1) 如果要产生[-a,a](a为正数)之间均匀分 布的随机数则应输入
§2.5操作符和特殊字符
7. xor 功能:异或操作。 格式:C=xor(A,B) C=xor(A,B)完成阵列A和B对应元素的 异或操作。 如: A=[0 0 pi eps]
B=[0 -2 4 1.2] C=xor(A,B) C=0 1 0 1
§2.7 基本数学函数
一.三角函数
MATLAB-2基础入门

format 只改变变量的输出格式, 但不会影响变量的值!
数值显示格式设置
缺省显示格式:简洁的短(short g)格式 窗口命令及语法格式:format 显示格式 关键字 如:format long %15位数字显示
21
各种 format 格式
格式
format
format short format long
为便于学习,以算例方式叙述,并通过 算例归纳一些MATLAB最基本的规则和语法结 构。
【例】
求 [12 2 (7 4)] 32 的算术运算结果。 本例演示:最初步的命令输入形式和必需的 操作步骤。
(1)用键盘在MATLAB命令窗中输入以下内容
>> (12+2*(7-4))/3^2
(2)在上述表达式输入完成后,按 [Enter] 键,该命令被执行,并显示如下结果。
29
Matalab7.1的workspace窗口
Matalab6.5的workspace窗口
32
工作空间浏览器主要功能及其操作方法
四、历史指令窗(Command History)
历史窗口:
首先记录每次启动时间;并记录在命令窗口输入 命令,此次运行期间,输入的所有命令被记录为 一组,并以此次启动时间为标志。
>>radius=5.2; %圆的半径 >>area=pi*5.2^2, circle_len=2*pi*5.2 area = 84.9487 circle_len = 32.6726
以上两例,命令行中用到了等号“=” 。 计算结果不再赋给“ans”,而是赋给 用户指定的变量y、area、circle_len 。 无论是预定义变量还是用户自定义变量 都被存储在系统的工作空间内,即系统 定义的一个存储窗口变量的内存空间。 Who、whos命令用来显示工作空间的 变量 clear命令用来清除工作空间的变量。
数值显示格式设置
缺省显示格式:简洁的短(short g)格式 窗口命令及语法格式:format 显示格式 关键字 如:format long %15位数字显示
21
各种 format 格式
格式
format
format short format long
为便于学习,以算例方式叙述,并通过 算例归纳一些MATLAB最基本的规则和语法结 构。
【例】
求 [12 2 (7 4)] 32 的算术运算结果。 本例演示:最初步的命令输入形式和必需的 操作步骤。
(1)用键盘在MATLAB命令窗中输入以下内容
>> (12+2*(7-4))/3^2
(2)在上述表达式输入完成后,按 [Enter] 键,该命令被执行,并显示如下结果。
29
Matalab7.1的workspace窗口
Matalab6.5的workspace窗口
32
工作空间浏览器主要功能及其操作方法
四、历史指令窗(Command History)
历史窗口:
首先记录每次启动时间;并记录在命令窗口输入 命令,此次运行期间,输入的所有命令被记录为 一组,并以此次启动时间为标志。
>>radius=5.2; %圆的半径 >>area=pi*5.2^2, circle_len=2*pi*5.2 area = 84.9487 circle_len = 32.6726
以上两例,命令行中用到了等号“=” 。 计算结果不再赋给“ans”,而是赋给 用户指定的变量y、area、circle_len 。 无论是预定义变量还是用户自定义变量 都被存储在系统的工作空间内,即系统 定义的一个存储窗口变量的内存空间。 Who、whos命令用来显示工作空间的 变量 clear命令用来清除工作空间的变量。
MATLAB基础教程第2章

第二章 数组、矩阵及其运算
2.1 数组的创建和寻访
例2-2 一维数组的生成与访问
命令:X=rand(1,5) 命令:X(3) 命令:X([1 2 5]) 命令:X(1:3) 命令:X(3:end) 命令:X(3:-1:1) 命令:X(find(X>0.5)) 命令:X([1 2 3 4 4 3 2 1])
第二章 数组、矩阵及其运算
2.2 矩阵的运算
例2-6 矩阵的乘法(接着上面的例子) A*B 3*A
注意:矩阵相乘时要求A的列数等于B的行数
第二章 数组、矩阵及其运算
2.2 矩阵的运算
A/B(矩阵右除)表示的是方程X*B=A的解 A\B(矩阵左除)表示的是方程A*X=B的解
例2-7 矩阵的除法( 见教材P.23)
第二章 数组、矩阵及其运算
2.3 数组的运算
1、数组的基本运算
例2-8 ( 见教材P.25)
第二章 数组、矩阵及其运算
2.3 数组的运算
数组运算和矩阵运算指令对照表
数组运算 指令 A.’ A=s A+s,A-s s.*A s./A,A.\s A.^n A+B,A-B A.*B A./B B.\A 含义 非共轭转置,相当于conj(A’) 把标量s赋给A中每个元素 标量s分别于A的元素之和(差) 标量s分别于A的元素之积 S分别被A的元素除 A的每个元素自乘n次 对应元素相加(减) 对应元素相加(乘) A的元素被B的对应元素相除 (与上相同) A^n A+B,A-B A*B A /B B\A 方阵A自乘n次 矩阵和(差) 同内维矩阵相乘 A右除B A左除B S*A 标量s分别于A的元素之积 A’ 指令 共轭转置 矩阵运算 含义
第二章 数组、矩阵及其运算
第2章 MATLAB基本操作

6. 逻辑操作符 功能: 功能:逻辑操作运算。 格式: 格式:A&B A|B ~A 注意逻辑操作有相应的M文件 文件: 注意逻辑操作有相应的 文件:A&B等效 等效 ),A|B等效于 等效于or(A,B), 于and(A,B), ( , ), 等效于 , , ~A等效为 等效为not(A)。 等效为 。
2.关系操作符 关系操作符 关系运算符包括: 关系运算符包括:< 、< = 、〉、> = 、= = 、 ~= 3.测试用的逻辑函数 测试用的逻辑函数 1)all函数测定矩阵中是否全为非零元素 2)any函数测试出矩阵中是否有非零值 3) find函数可找出矩阵中的非零元素及其下 标 4) exist函数在装入数据之前对数据文件作 检测
利用取整和求余函数,可得到整数或精确到小数点后的第 几位。例如: x1=10-round(20*rand(2,5)) %产生[-10 10]之间的随机数(取整) x1 = -4 4 -1 -4 7 -7 -2 0
2 −7
x2=10-round(2000*rand(2,5))/100 %产生[−10 10]之间的随机 数(精确到0.01) x2 = -8.0000 -2.9000 -3.2000 -6.4300 -6.3600 3.1600 4.2100 -0.6800 3.1800 -4.5400
5.函数 函数 内部函数、工具箱函数、自定义函数。 1)函数的嵌套 x=sqrt(log(z)) 函数的嵌套 2)多输入函数 theta=atan2(y,x) 多输入函数 3)多输出函数 [v,d] = eig(a) 多输出函数 [y,I] = max(x) 6.表达式 表达式 a=(1+sqrt(10))/2 b=abs(3+5i) c=sin(exp(-2.3))
matlab7.0 自学教程第二章(1)

A(:)=[1,4,7,2,5,8,3,6,9]'
A=[1, 2, 3, 4, 5]; 3) 逻辑1标识法 L=logical([1, 0, 1, 0, 1]) 【例2.2-6】数组标识与寻访 A(L) ans=[1,3,5] A=zeros(2,6) A(2,1:2:5)=[-1,-3,-5] A =0 0 0 0 0 0 A =1 3 5 7 9 11 0 0 0 0 0 0 -1 4 -3 8 -5 12 A(:)=1:12 B=A([1,2,2,2],[1,3,5] ) A =1 3 5 7 9 11 B =1 5 9 2 4 6 8 10 12 -1 -3 -5 A(2,4) -1 -3 -5 ans = 8 -1 -3 -5 A(8) L=A<3 ans = 8 A([1,2,5,6]') L = A(:,[1,3]) 1 0 0 0 0 0 ans = ans =1 5 1 0 1 0 1 0 1 2 6 A(L)=NaN 2 A(:,4:end) A= 5 ans =7 9 11 NaN 3 5 7 9 11 6 8 10 12 NaN 4 NaN 8 NaN 12
plot(t,Sx,'.k','MarkerSize',12) xlabel('x'),ylabel('Sx'),grid on
syms t x ft=t^2*cos(t) sx=int(ft,t,0,x) ft = t^2*cos(t) sx = x^2*sin(x) - 2*sin(x) + 2*x*cos(x)
函数 f (.) 的数组运算规则
函数数组运算规则的定义 x11 x12 … x1n
x21 x22 … x2n
