江西省南昌市十所省重点中学命制2016届高三第二次模拟突破冲刺数学(理)试题(九)
江西省南昌市十所省重点中学命制2016届高三第二次模拟突破冲刺数学(理)试题(一) 含答案

南昌市十所省重点中学2016年二模突破冲刺交流试卷(01)高三数学(理)一.选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一是符合题目要求的.1.已知复数z 满足(2)5i z i +=(其中i 是虚数单位,满足21i=-),则复数z 的共轭复数在复平面中对应的点在第几象限( ) A 。
第一象限 B 。
第二象限 C 。
第三象限D.第四象限2.要得到函数sin 44y x π⎛⎫=- ⎪⎝⎭的图象,只需要将函数sin 4y x =的图象( ) A 向左平移π16个单位 B 向右平移π16个单位 C 向左平移π4个单位 D 向右平移π4个单位3.设x R ∈ ,则“31x +< "是“220x x +-> "的( )A 充分而不必要条件B 必要而不充分条件C 充要条件D 既不充分也不必要条件4.先后掷骰子两次,落在水平桌面后,记正面朝上的点数分别为x ,y ,设事件A 为“x +y 为偶数”, 事件B 为“x y ≠”,则概率()P B A =( )A .12B .14C . 13D .235.如果双曲线22221(0,0)x y a b a b-=>>的一条渐近线与直线310x y -+=平行,则双曲线的离心率为( ) A .B .C . 2D . 36. 将图1中的等腰直角三角形ABC 沿斜边BC 的中线折起得到空间四面体ABCD(如图2),则在空间四面体ABCD 中,AD 与BC 的位置关系是( )A .相交且垂直B .相交但不垂直C .异面且垂直D .异面但不垂直7.已知向量()()2016,2,,2016-==k b k a的夹角为钝角,则函数()201622++=k k k f 的最小值为( )A. 2013 B 。
2014 C. 2015 D 。
20168。
已知函数()()sin f x x ωϕ=A +(A ,ω,ϕ均为正的常数)的最小正周期为π,当23x π=时,函数()f x 取得最小值,则下列结论正确的是( )A (1)(1)(0)f f f <-<B (0)(1)(1)f f f <<- C(1)(0)(1)f f f -<<D(1)(0)(1)f f f <<-9。
江西省南昌市十所省重点中学命制2016届高三数学第二次模拟突破冲刺试题 理(三)

南昌市十所省重点中学2016年二模突破冲刺交流试卷(03)高三数学(理)(考试时间:120分钟试卷满分:150分)第I 卷选择题(共60分)一.选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 设复数iz --=12,则在复平面内z i ⋅对应的点坐标为 A .()1,1 B .()1,1- C .()1,1-- D . ()1,1-2. 已知两个集合(){}2ln 2++-==x x y x A ,⎭⎬⎫⎩⎨⎧≤-+=212x e e xB 则=⋂B AA.⎪⎭⎫⎢⎣⎡-2,21 B . ⎥⎦⎤ ⎝⎛--21,1 C .()e ,1- D .()e ,23.随机变量~(0,1)N ξ,则()12P ξ≤≤=A.0.0215 B. 0.1359 C. 0.1574 D. 0.2718(参考数据:()0.6826P μσξμσ-≤≤+=,(22)0.9544P μσξμσ-≤≤+=,(33)0.9974P μσξμσ-≤≤+=) 4.从9,8,7,6,5,4,3,2,1中不放回地依次取2个数,事件=A “第一次取到的是奇数” =B “第二次取到的是奇数”,则 ()=A B P A.51 B . 103 C .52 D .21,已知正方体1D 上. 当三棱C.2429.若正数,a b 满足:121=+b a 则2112-+-b a 的最小值为( ) A.2 B. 2 C. 22 D. 110.如图,圆O 与x 轴的正半轴的交点为A ,点B ,C 在圆O 上,点B 的坐标为(1,2)-,点C 位于第一象限,AOC α∠=.若BC =,则2s i n sc o s2αα.A.B - CD 11. 已知P B A ,,是双曲线12222=-by ax 上的不同三点,且AB 连线经过坐标原点,若直线PB PA ,的斜率乘积32=⋅PB PA k k ,则该双曲线的离心率=eA . 25B . 315C . 210D . 212.已知函数()()21ln ,2+==x x g e x f x,对()+∞∈∃∈∀,0,b R a ,使得()()b g a f =,则a b -的最小值为 A . 22ln 1+B . 22ln 1- C . 12-e D .1-e二、填空题:本大题共4小题,每小题5分。
江西省南昌市十所省重点中学命制高三数学第二次模拟突
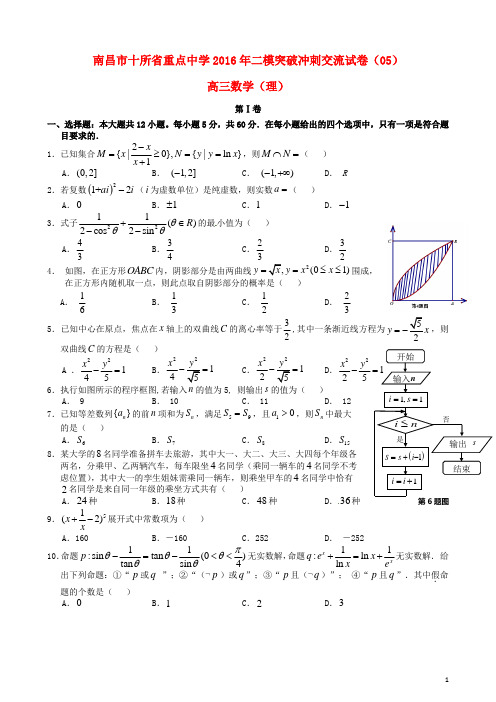
是否输入 1,1i s ==输出 s 结束开始i n≤第6题图n()1s i s +-=1i i =+南昌市十所省重点中学2016年二模突破冲刺交流试卷(05)高三数学(理)第Ⅰ卷一、选择题:本大题共12小题。
每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知集合2{|0},{|ln }1xM x N y y x x -=≥==+,则M N ⋂=( )A .(0,2]B . (1,2]-C . (1,)-+∞D . R2.若复数()21+2ai i -(i 为虚数单位)是纯虚数,则实数a =( )A .0B .1±C .1D .1-3.式子2211()2cos 2sin R θθθ+∈--的最小值为( ) A .43 B .34 C .23 D .324. 如图,在正方形OABC 内,阴影部分是由两曲线2,(01)y x y x x ==≤≤围成,在正方形内随机取一点,则此点取自阴影部分的概率是( )A .16 B .13C .12 D . 235.已知中心在原点,焦点在x 轴上的双曲线C 的离心率等于32,其中一条渐近线方程为5y x =-,则双曲线C 的方程是( )A .22145x y -=B .22145x -=C .22125x -=D .22125x y -= 6.执行如图所示的程序框图,若输入的值为5, 则输出s 的值为( )A . 9B . 10C . 11D . 127.已知等差数列{}n a 的前n 项和为n S ,满足59S S =,且10a >,则n S 中最大 的是( ) A .6S B .7S C .8S D .15S8.某大学的8名同学准备拼车去旅游,其中大一、大二、大三、大四每个年级各 两名,分乘甲、乙两辆汽车,每车限坐4名同学(乘同一辆车的4名同学不考 虑位置),其中大一的孪生姐妹需乘同一辆车,则乘坐甲车的4名同学中恰有 2名同学是来自同一年级的乘坐方式共有( )A .24种B .18种C .48种D .36种9.51(2)x x+-展开式中常数项为( )A .160B .-160C .252D . -25210.命题11:sin tan (0tan sin 4p πθθθθθ-=-<<无实数解,命题11:ln ln xx q e x x e+=+无实数解. 给出下列命题:①“p 或q ”;②“(¬p )或q ”;③“p 且(¬q )”; ④“p 且q ”.其中假.命题的个数是( ) A .0B .1C .2D .311则几何体的体积为( ) A .16B .13C .1D .4312.若)(x f 是定义在(0,)+∞的函数,且()0f x >.满足2()()0f x xf x '+>,则下列不等式正确的是( )A .2016(2016)2015(2015)f f >B . 2016(2016)2015(2015)f f < C.332015(2015)2016(2016)f f <D . 332015(2015)2016(2016)f f > 第2413.已知向量1(,2a =r 14.x ,y 15.已知边长为2316.在ABC ∆中,角三、解答题:解答应写出文字说明,证明过程或演算步骤.17.已知函数()21f x x =+,数列{}n a 满足*()()n a f n n N =∈,数列{}n b 的前n 项和为n T ,且12b =,12()n n T b n N +=-∈.(1)分别求{},{}n n a b 的通项公式;(2) 定义[]()x x x =+,[]x 为实数x 的整数部分,()x 为小数部分,且0()1x ≤<.记n c =()nna b ,求数列{}n c 的前n 项和n S .第11题18.某校课改实行选修走班制,现有甲,乙,丙,丁四位学生准备选修物理,化学,生物三个科目.每位学生只选修一个科目,且选修其中任何一个科目是等可能的. (1)恰有2人选修物理的概率; (2)选修科目个数ξ的分布列及期望.19.如图,在四棱锥P ABCD -中,底面ABCD 是菱形,且120ABC ∠=︒.点E 是棱PC 的中点,平面ABE 与棱PD 交于点F . (1)求证://AB EF ;(2)若2PA PD AD ===,且平面PAD ⊥平面ABCD ,求平面PAF 与平面AFE 所成的锐二面角的余弦值.20.已知抛物线C 的标准方程为22(0)y px p =>,M 为抛物线C 上一动点,(,0)(0)A a a ≠为其对称轴上一点,直线MA 与抛物线C 的另一个交点为N .当A 为抛物线C 的焦点且直线MA 与其对称轴垂直时,△MON 的面积为18.(1)求抛物线C 的标准方程; (2)记11t AM AN=+,若t 值与M 点位置无关,则称此时的点A 为“稳定点”,试求出所有“稳定点”,若没有,请说明理由.21.已知函数()ln(1)xf x x =+..AE DC BO第22题图(1)当0x >时,证明:2()2x f x +<; (2)当1x >-,且0x ≠时,不等式(1)()1kx f x x +>+成立,求实数的值.请考生在第(22)、(23)、(24)三题中任选一题做答.注意:只能做所选定的题目.如果多做,则按所做的第一个题目计分,做答时请用2B 铅笔在答题卡上将所选题号后的方框涂黑. 22.选修4—1:几何证明选讲如图,AB 是圆O 的直径,点C 在圆O 上,延长BC 到D 使BC CD =,过C 作圆O 的切线交AD 于E . 若6AB =,2ED =. (1)求证:CE AD ⊥; (2)求BC 的长.23.选修4—4:坐标系与参数方程已知曲线C 的参数方程为2cos 2sin x ty t⎧=⎪⎨=⎪⎩(t 为参数),C 在点()1,1处的切线为l ,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系. (1)求l 的极坐标方程; (2)过点13(4M -任作一直线交曲线C 于,A B 两点,求||AB 的最小值.24.选修4—5:不等式选讲:设函数4()||||(0)f x x x a a a=-++>. (1)证明:()4f x ≥;(2)若(2)5f <,求a 的取值范围.是否输入 1,1i s ==输出 s 结束开始i n≤n ()1s i s +-=1i i =+参考答案 第Ⅰ卷一、选择题:本大题共12小题。
江西省南昌市十所省重点中学命制2016届高三数学第二次模拟突破冲刺试题理(四)

XX 市十所省重点中学2021年二模突破冲刺交流试卷〔 04〕高三数学〔理〕一、选择题 〔本大题共 12 小题,每题 5 分,共 60 分 . 在每题给出的四个选项中,只有一项为哪一项符合题意的〕 .1、复数z10 2i 〔其中i 是虚数单位〕,那么 z =( )3 iA 、22B、 23C、 32D 、 332、集合Ax x 21 0 , Bx x 20 ,那么AB 〔〕xA .,2B . 0,1C. 2,2 D. ,13、抛物线 x 2 =4y上一点 P 到焦点的距离为 3,那么点 P 到 y 轴的距离为()A .22B. 1C. 2D . 34、某小区有 1000 户,各户每月的用电量近似服从正态分布N(300 ,l01) ,那么用电 量在 320 度以上的户数估计约为 ( )〔参考数据 :假设随机变量 服从正态分布 N 〔μ ,σ2〕,那么=68.26% , = 95.44%,=99.74%.〕A .17B.23 C .34D. 46 .yx y(a,b 为正数〕 的最大值为5、设变量x, y 满足约束条件x y 0,且目标函数 z1,那么abab2x y 10的最小值为〔〕 .A 、2B 、 4C 、 2 D、 2 26、函数f (x)=2cos( x+) 图象的一个对称中心为(2 , 0) ,且f (1)> f (3),要得到函数f(x) 的图象3可将函数 y=2cos x 的图象 ( )3A.向左平移 1 个单位长度B.向左平移 个单位长度26C.向右平移 1个单位长度D .向右平移个单位长度267、执行如下图的程序框图,那么输出的b 值为 ( )A . 8B.30C.92 D. 968、一个正三棱柱的主〔正〕视图是长为2 3,宽为 4的矩形 , 那么它的外接球的外表积等于 ( )A. 64B. 48C.32 D.1612 34第7题图第8题图9、F是双曲线x2y20,b0)的左焦点,过点F作双曲线的一条渐近线的垂线, 垂足为A,交另一22 1(aa b条渐近线于点 B ,如果3FA FB ,那么此双曲线的离心率为( )A、2B、 3C、 2D、310、在△ ABC中,内角 A, B, C的对边分别为a, b, c,角 B 为锐角,且 2 sinAs inC=sin 2B,那么的取值X围为〔〕A、1,3B、2,3C、1,322D 2 ,32211、如图,在直角坐标平面中正方形OACB的边长为1,点 P 为扇形yOAB的弧AB上任意一点, D为 OA的中点,E 为 OB的中点,OP xAE yBD x, y R ,B C设 a x, y ,那么 a OC 的最大值为〔〕E PA、2B、—2C、3D、 2 2DO Ax 12、定义在R上的函数y f x 1的图像关于1,0 对称,且当 x,0 时, f x xf ' x 0 〔其中 f ' x 是 f x 的导函数〕,假设 a (30.3 )f 30.3,22 34第7题图第8题图9、F是双曲线x2y20,b0)的左焦点,过点F作双曲线的一条渐近线的垂线, 垂足为A,交另一22 1(aa b条渐近线于点 B ,如果3FA FB ,那么此双曲线的离心率为( )A、2B、 3C、 2D、310、在△ ABC中,内角 A, B, C的对边分别为a, b, c,角 B 为锐角,且 2 sinAs inC=sin 2B,那么的取值X围为〔〕A、1,3B、2,3C、1,322D 2 ,32211、如图,在直角坐标平面中正方形OACB的边长为1,点 P 为扇形yOAB的弧AB上任意一点, D为 OA的中点,E 为 OB的中点,OP xAE yBD x, y R ,B C设 a x, y ,那么 a OC 的最大值为〔〕E PA、2B、—2C、3D、 2 2DO Ax12、定义在R上的函数y f x 1的图像关于1,0 对称,且当 x,0 时, f x xf ' x 0 〔其中 f ' x 是 f x 的导函数〕,假设 a (30.3 )f 30.3,22 34第7题图第8题图9、F是双曲线x2y20,b0)的左焦点,过点F作双曲线的一条渐近线的垂线, 垂足为A,交另一22 1(aa b条渐近线于点 B ,如果3FA FB ,那么此双曲线的离心率为( )A、2B、 3C、 2D、310、在△ ABC中,内角 A, B, C的对边分别为a, b, c,角 B 为锐角,且 2 sinAs inC=sin 2B,那么的取值X围为〔〕A、1,3B、2,3C、1,322D 2 ,32211、如图,在直角坐标平面中正方形OACB的边长为1,点 P 为扇形yOAB的弧AB上任意一点, D为 OA的中点,E 为 OB的中点,OP xAE yBD x, y R ,B C设 a x, y ,那么 a OC 的最大值为〔〕E PA、2B、—2C、3D、 2 2DO Ax12、定义在R上的函数y f x 1的图像关于1,0 对称,且当 x,0 时, f x xf ' x 0 〔其中 f ' x 是 f x 的导函数〕,假设 a (30.3 )f 30.3,22 34第7题图第8题图9、F是双曲线x2y20,b0)的左焦点,过点F作双曲线的一条渐近线的垂线, 垂足为A,交另一22 1(aa b条渐近线于点 B ,如果3FA FB ,那么此双曲线的离心率为( )A、2B、 3C、 2D、310、在△ ABC中,内角 A, B, C的对边分别为a, b, c,角 B 为锐角,且 2 sinAs inC=sin 2B,那么的取值X围为〔〕A、1,3B、2,3C、1,322D 2 ,32211、如图,在直角坐标平面中正方形OACB的边长为1,点 P 为扇形yOAB的弧AB上任意一点, D为 OA的中点,E 为 OB的中点,OP xAE yBD x, y R ,B C设 a x, y ,那么 a OC 的最大值为〔〕E PA、2B、—2C、3D、 2 2DO Ax12、定义在R上的函数y f x 1的图像关于1,0 对称,且当 x,0 时, f x xf ' x 0 〔其中 f ' x 是 f x 的导函数〕,假设 a (30.3 )f 30.3,22 34第7题图第8题图9、F是双曲线x2y20,b0)的左焦点,过点F作双曲线的一条渐近线的垂线, 垂足为A,交另一22 1(aa b条渐近线于点 B ,如果3FA FB ,那么此双曲线的离心率为( )A、2B、 3C、 2D、310、在△ ABC中,内角 A, B, C的对边分别为a, b, c,角 B 为锐角,且 2 sinAs inC=sin 2B,那么的取值X围为〔〕A、1,3B、2,3C、1,322D 2 ,32211、如图,在直角坐标平面中正方形OACB的边长为1,点 P 为扇形yOAB的弧AB上任意一点, D为 OA的中点,E 为 OB的中点,OP xAE yBD x, y R ,B C设 a x, y ,那么 a OC 的最大值为〔〕E PA、2B、—2C、3D、 2 2DO Ax12、定义在R上的函数y f x 1的图像关于1,0 对称,且当 x,0 时, f x xf ' x 0 〔其中 f ' x 是 f x 的导函数〕,假设 a (30.3 )f 30.3,22 34第7题图第8题图9、F是双曲线x2y20,b0)的左焦点,过点F作双曲线的一条渐近线的垂线, 垂足为A,交另一22 1(aa b条渐近线于点 B ,如果3FA FB ,那么此双曲线的离心率为( )A、2B、 3C、 2D、310、在△ ABC中,内角 A, B, C的对边分别为a, b, c,角 B 为锐角,且 2 sinAs inC=sin 2B,那么的取值X围为〔〕A、1,3B、2,3C、1,322D 2 ,32211、如图,在直角坐标平面中正方形OACB的边长为1,点 P 为扇形yOAB的弧AB上任意一点, D为 OA的中点,E 为 OB的中点,OP xAE yBD x, y R ,B C设 a x, y ,那么 a OC 的最大值为〔〕E PA、2B、—2C、3D、 2 2DO Ax12、定义在R上的函数y f x 1的图像关于1,0 对称,且当 x,0 时, f x xf ' x 0 〔其中 f ' x 是 f x 的导函数〕,假设 a (30.3 )f 30.3,22 34第7题图第8题图9、F是双曲线x2y20,b0)的左焦点,过点F作双曲线的一条渐近线的垂线, 垂足为A,交另一22 1(aa b条渐近线于点 B ,如果3FA FB ,那么此双曲线的离心率为( )A、2B、 3C、 2D、310、在△ ABC中,内角 A, B, C的对边分别为a, b, c,角 B 为锐角,且 2 sinAs inC=sin 2B,那么的取值X围为〔〕A、1,3B、2,3C、1,322D 2 ,32211、如图,在直角坐标平面中正方形OACB的边长为1,点 P 为扇形yOAB的弧AB上任意一点, D为 OA的中点,E 为 OB的中点,OP xAE yBD x, y R ,B C设 a x, y ,那么 a OC 的最大值为〔〕E PA、2B、—2C、3D、 2 2DO Ax12、定义在R上的函数y f x 1的图像关于1,0 对称,且当 x,0 时, f x xf ' x 0 〔其中 f ' x 是 f x 的导函数〕,假设 a (30.3 )f 30.3,22 34第7题图第8题图9、F是双曲线x2y20,b0)的左焦点,过点F作双曲线的一条渐近线的垂线, 垂足为A,交另一22 1(aa b条渐近线于点 B ,如果3FA FB ,那么此双曲线的离心率为( )A、2B、 3C、 2D、310、在△ ABC中,内角 A, B, C的对边分别为a, b, c,角 B 为锐角,且 2 sinAs inC=sin 2B,那么的取值X围为〔〕A、1,3B、2,3C、1,322D 2 ,32211、如图,在直角坐标平面中正方形OACB的边长为1,点 P 为扇形yOAB的弧AB上任意一点, D为 OA的中点,E 为 OB的中点,OP xAE yBD x, y R ,B C设 a x, y ,那么 a OC 的最大值为〔〕E PA、2B、—2C、3D、 2 2DO Ax12、定义在R上的函数y f x 1的图像关于1,0 对称,且当 x,0 时, f x xf ' x 0 〔其中 f ' x 是 f x 的导函数〕,假设 a (30.3 )f 30.3,2。
江西省南昌市十所省重点中学命制2016届高三第二次模拟突破冲刺数学(理)试题(七) 含答案

南昌市十所省重点中学2016年二模突破冲刺交流试卷(07)高三数学(理)第Ⅰ卷一.选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 若复数满足(34)|43|i z i -⋅=+,i 是虚数单位,则z 的虚部为( )A.4- B 。
45C 。
4D 。
45- 2。
设集合{||1|3}P x x =+≤,1{|(),(2,1)}3xQ y y x ==∈-,则PQ =( )A 。
1(4,)9- B.1(,2]9C 。
1(,2]3D 。
1(,2)33.已知命题p :∀x 1,x 2∈R,(f (x 2)-f (x 1))(x 2-x 1)≥0,则⌝p 是( ) A 、∃x 1,x 2∈R ,(f (x 2)-f (x 1))(x 2-x 1)≤0 B 、∀x 1,x 2∈R ,(f (x 2)-f (x 1))(x 2-x 1)≤0 C 、 ∃x 1,x 2∈R ,(f (x 2)-f (x 1))(x 2-x 1)<0 D 、∀x 1,x 2∈R,(f (x 2)-f (x 1))(x 2-x 1)<04。
若),(ππα2∈,)4sin(2cos 3απα-=,则α2sin 的值为( ) A . 1817-B .1817 C .181-D .1815。
在如图所示的程序框图中,若输出的值是3,则输入x 的取值范围是( )A .(4, 10]B .(2,+∞)C .(2, 4]D .(4,+∞)6. 有关以下命题:①用相关指数2R 来刻画回归效果,2R 越小,说明模型的拟合效果越好;②已知随机变量ξ服从正态分布2(2,)N σ,(4)0.79,P ξ≤=则(2)0.21P ξ≤-=;③采用系统抽样法从某班按学号抽取5名同学参加活动,学号为5,16,27,38,49的同学均被选出,则该班学生人数可能为60;其中正确的命题的个数为( )A 。
3个 B. 2个 C. 1个 D. 0个 7.一个三棱锥的三视图如图所示,则该三棱锥的表面积为( ) A 。
江西省南昌市十所省重点中学命制2016届高三第二次模拟突破冲刺数学(理)试题(二)资料

第11题图(2)′图(1)左视图主视图4南昌市十所省重点中学2016年二模突破冲刺交流试卷(02)高三数学(理)第Ⅰ卷(选择题部分,共60分)一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1、已知集合{}22530A x x x =--≤,{}2B x Z x =∈≤,则A B ⋂中的元素个数为( )(A)2 (B)3 (C)4 (D)52、若复数z 满足11z i ii -=-+(),则z 的实部为( )(A)121(C)1(D)123、《张丘建算经》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有女不善织,日减功迟,初日织五尺,末日织一尺,今三十织迄,问织几何.”其意思为:有个女子不善于织布,每天比前一天少织同样多的布,第一天织五尺,最后一天织一尺,三十天织完,问三十天共织布( ) (A)30尺 (B)90尺 (C)150尺 (D)180尺 4、已知抛物线()02:2>=p px y C 的焦点为,F P 为C 上一点,若,4=PF 点P 到y 轴的距离等于等于3,则点F 的坐标为( )(A) (1,0)- (B)(1,0) (C)(2,0) (D)(2,0)- 5、执行如图所示的程序框图,如果输入的50t =,则输出的n =( )(A)5 (B)6 (C)7 (D)86、现有5人参加抽奖活动,每人依次从装有5张奖票(其中3张为中奖票) 的箱子中不放回地随机抽取一张,直到3张中奖票都被抽出时活动结束, 则活动恰好在第4人抽完后结束的概率为( )(A)101 (B)51 (C)103 (D)52 7、()622--x x 的展开式中2x 的系数等于( )(A)-48 (B)48 (C)234 (D)4328、设,x y 满足010,3220y ax y x y ≥⎧⎪+-≤⎨⎪--≤⎩若2210y x x z +-=的最小值为12-,则实数a 的取值范围是( ) (A)21-≤a (B)23-<a (C)21≥a (D)23<a 9、某几何体的主视图和左视图如图(1),它的俯视图的直观图是矩形1111O A B C 如图(2),其中116O A =,112O C =,则该几何体的侧面积为( )(A)48 (B)64 (C)96 (D)12810、已知函数()()()e e b ax x xf x -++-=2,当0>x 时,()0≤x f ,则实数a(A)0>a (B)10≤<a (C)1≥a (D)1≤a 11、已知,,A B C 在球O 的球面上,1,2AB BC ==, 60=∠ABC ,直线OA 与截面ABC 所成的角为 30,则球O 的表面积为( )(A)π4 (B)π16 (C)π34 (D)163π12、已知()()R x x f y ∈=的导函数为()x f '.若()()32x x f x f =--,且当0≥x 时,()23x x f >',则不等式()()13312+->--x x x f x f 的解集是( ) (A)1(,)2-+∞ (B)1(,)2+∞ (C)1(,)2-∞- (D)1(,)2-∞第Ⅱ卷(非选择题部分,共90分)本卷包括必考题和选考题两部分,第13题~第21题为必考题,每个试题考生都必须做答,第22题~第24题为选考题,考生根据要求做答.二、填空题:本大题共4小题,每小题5分.13、已知θ为第四象限角,sin 3cos 1θθ+=,则tan θ= .14、对于同一平面的单位向量,,a b c ,若a 与b 的夹角为 60,则()(2)a b a c -⋅-的最大值是 .15、已知A ,B 为双曲线()0,01:2222>>=-b a by a x C 右支上两点,O 为坐标原点,若OAB ∆是边长为c 的等边三角形,且222b a c +=,则双曲线C 的渐近线方程为 . 16、已知数列}{n a 的前n 项和为,,,046,21>==n n S S S S 且22122,+-n n n S S S ,成等比数列,12221-2,++n n n S S S ,成等差数列,则2016a 等于 .三、解答题:解答应写出文字说明,证明过程和演算步骤. 17、(本小题满分12分)如图,平面四边形ABCD 中,AB =AD =CD =,30CBD ∠=,120BCD ∠=,求(Ⅰ)ADB ∠;(Ⅱ)ADC ∆的面积S .18、(本小题满分12分)从某企业生产的某种产品中抽取100件,测量这些产品的质量指标值,由测量结果得到如图所示的频率分布直方图,质量指标值落在区间[)55,65(Ⅰ)求这些产品质量指标值落在区间[]75,85内的频率;(Ⅱ)若将频率视为概率,从该企业生产的这种产品中随机抽取3件,记这3件产品中质量指标值位于区间[)45,75内的产 品件数为X ,求X 的分布列与数学期望.AB DC19、(本小题满分12分)如图,四棱柱1111ABCD A BC D -的底面ABCD 是菱形,AC BD O =,1AO ⊥底面ABCD ,21==AA AB .(Ⅰ)证明:平面1ACO ⊥平面11BB D (Ⅱ)若60BAD ∠=,求二面角B -20、(本小题满分12分)以椭圆2222:1(0)x y C a b a b +=>>的离心率为36,以其四个顶点为顶点的四边形的面积等于32.(Ⅰ)求椭圆C 的标准方程;(Ⅱ)过原点且斜率不为0的直线l 与椭圆C 交于P ,Q 两点,A 是椭圆C 的右顶点,直线AP ,AQ 分别与y 轴交于点M ,N ,问:以MN 为直径的圆是否恒过x 轴上的定点?若恒过x 轴上的定点,请求出该定点的坐标;若不恒过x 轴上的定点,请说明理由.21、(本小题满分12分)已知函数()(1)()x f x a x e a =--.(常数R a ∈且0a ≠).(Ⅰ)证明:当0>a 时,函数()x f 有且只有一个极值点; (Ⅱ)若函数()x f 存在两个极值点12,x x ,证明:()2140e x f <<且()2240e x f <<.请考生在第(22)、(23)、(24)三题中任选一题作答。
江西省南昌市十所省重点中学命制2016届高三数学第二次模拟突破冲刺试题(六)理

XX 市十所省重点中学2021年二模突破冲刺交流试卷〔 06〕高三数学〔理〕第 I 卷一.选择题:本大题共 12 小题,每题 5 分,在每题给出的四个选项中,只有一项为哪一项符合题目要求的.1.复数(12i)2〔其中i 为虚数单位〕的虚部为〔〕A .4B.4C. 4iD .4i2.集合A{ y | y( 1 )x 21, xR} ,那么满足ABB 的集合 B 可以是〔〕2A .{0,1}B . { x | 1 x1}C .{ x | 0x1}D. { x | x 0}223.以下有关命题说法正确的选项是〔〕A .命题p :“ x R ,sinx + cosx =2 〞,那么 p 是真命题B .1〞是“ x 25x 60〞的必要不充分条件“ xC .命题“xR ,使得x 2 x 1 ( 0〞的否认是:“ x R ,x 2x1 0〞D .“a 1 〞是“() log0,1)在 (0,) 上为增函数〞的充要条件f x a x aa4.tan( ) 1 ,那么 sin cos 的值为〔〕2 sincos4A . 1/2B . 2C . 2 2D .-2 5.阅读以下程序框图,运行相应程序,那么输出的 S 值为( )n=n+12n1否是开场n=1,S=1n ≥ 3输出 S完毕S=S ·cos9A .1B.1C.1D.18816321(log 1 0.5)x1(log 1 0.5) y,那么实数x, y 的关系是〔6.x 3( y) 3〕3 3A .x y 0B .x y 0C . x y 0D .x y 07.F 1, F 2分别是椭圆x 2 y 2 1(a b 0) 的左、右焦点, A 是椭圆上位于第一象限内的一点,Oa2b2为坐标原点,OA OF 2| OF 2 |2,假设椭圆的离心率等于2,那么直线 OA 的方程是()2A .y1 x. 2 . 3.y xyxyxD2B 2C 232121319.如图正方体ABCD A 1BC D的棱长为 1,点E 在线段BB和线段A B上移动,1 111 1 1 EAB(0, ) ,过直线 AE, AD 的平面 ADFE 将正方体分成两局部, 记A 12棱 BC 所在局部的体积为 V( ),那么函数 V V ( ),(0, )2 的大致图像是〔 〕y y A 111 1 2x2xOO4242yAy B111 1 2x 2xOO4242CDD1C1B 1FDCEB10.圆C :x 2 y 2 2x 4y 10 上存在两点关于直线 l :x my 10 对称,经过点 M (m,m) 作圆的两条切线,切点分别为 P ,Q ,那么 |PQ|A . 3B .23C . 13D .12 131311.某几何体的三视图如下图,其中俯视图为扇形,那么一个质点从扇形的圆心起始,绕几何体的侧面运动一周回到起点,其最短路径为 A.4+4B. 6 33C.4+2D. 63,点 A, B 是函数 f ( x) 图像上不同两点,那AOB 〔 O 为坐标原点〕的取值X围是〔〕A. (0, )B.(0, ]C.(0, )D. (0,]4433第二卷本卷包括必考题和选考题两局部.第13 题 ~第 21 题为必考题,每个试题考生都必须作答,第22- 第 242题为选考题,考生根据要求作答.二.填空题:本大题共 4 小题,每题 5 分.13.在(2 x34)9的展开式中,不含x 的各项系数之和为___.yx+ y-1≤0,1)214.不等式组x- y+1≥0,表示的平面区域内的点都在圆x2( y r 2 (r 0) 内,那么r的最小y≥02值是 _______.15.0a, 设函数 f ( x)2021x12021x a, a的最大值为 P,最小值为 Q,那么 P+Q x sin x220211的值为 _______.16.在ABC中, D为AB的一个三等分点,且AB3AD, AC AD,CB 3那么 cos B =.三、解答题:解容许写出文字说明,证明过程或演算步骤.17.〔本小题总分值12 分〕b n为单调递增的等差数列,b3b826,b5b6 168 ,设数列 a n满足2a1 22 a223 a32n a n2b n( Ⅰ) 求数列b n的通项;( Ⅱ) 求数列a n的前 n 项和 S n.18.〔本小题总分值12 分〕某市对贫困家庭自主创业给予小额贷款补贴,每户贷款额为 2 万元,贷款期限有 6 个月、 12 个月、 18 个月、 24 个月、 36 个月五种,这五种贷款期限政府分别需要补助200 元、 300 元、 300 元、 400 元、 400 元,从2021 年享受此项政策的困难户中抽取了100 户进展了调查统计,选取贷款期限的频数如下表:贷款期限 6 个月12 个月18 个月24 个月36个月频数2040201010以上表各种贷款期限的频率作为2021年贫困家庭选择各种贷款期限的概率.〔Ⅰ〕某小区2021年共有 3 户准备享受此项政策,计算其中恰有两户选择贷款期限为12 个月的概率;〔Ⅱ〕设给某享受此项政策的困难户补贴为元,写出的分布列,假设预计2021年全市有 3.6 万户享受此项政策,估计2021年该市共要补贴多少万元.19.〔本小题总分值12 分〕如图四棱锥P ABCD 的底面是一等腰梯形,其中AD // BC ,其中AD 3BC6,AB DC22 ,又平面PAD平面 ABCD , PA PD5,点O是P线段 AD 的中点,经过直线 OB 且与直线 PA 平行的平面 OBM 与直线 PC 相交于点 M .M〔Ⅰ〕确定实数t ,使得 PM tMC;DC〔Ⅱ〕求平面PAD 与平面 OBM 夹角的余弦值.20.〔本小题总分值12 分〕椭圆 C1x 2y26,焦距为 4 2 ,抛物线 C2: x2 2 py( p 0) 的焦点F :22 1(a b 0) 的离心率为3a b是椭圆 C1的顶点.〔Ⅰ〕求 C1与 C2的标准方程;〔Ⅱ〕 C1上不同于F的两点P, Q 满足 FP FQ 0 ,且直线 PQ 与 C2相切,求FPQ的面积.21.〔本小题总分值12 分〕函数 f ( x) a x x2x ln a a 0, a 1 .〔Ⅰ〕求函数f ( x) 的单调区间;〔Ⅱ〕假设存在x1, x21,1,使得f ( x1 ) f ( x2 ) e 1e是自然对数的底数〕,XX数a的取值X围.〔请考生在第 22,23,24 题中任选一题做答,如果多做,那么按所做的第一题计分,做答时请写清题号 .22.〔本小题总分值10 分〕选修 4— 1:几何证明选讲如图, O 为等腰三角形ABC 内一点,圆 O 与ABC 的底边 BC 交于M、 N 两点与底边上的高AD 交于点 G,与AB、AC分别相切于E、F两点.AGEFOBCMDN〔Ⅰ〕证明:EF / / BC ;〔Ⅱ〕假设AG等于O 的半径,且AE MN 2 3 ,求四边形 EBCF 的面积.23.〔本小题总分值10 分〕选修4--4 :坐标系与参数方程在直角坐标系xOy 中,以原点O为极点,以x 轴正半轴为极轴,曲线C的极坐标方程为sin2( Ⅱ ) 过点 P(0, 2) 作斜率为l 直线l与曲线 C交于 A, B 两点,试求11|PA|的值.|PB|24.〔本小题总分值10 分〕选修4— 5 :不等式选讲函数 f ( x) | x 1| | x 1| .〔Ⅰ〕解不等式 f ( x)3 ;〔Ⅱ〕假设 f ( x) 的最小值为m,设 a 0 , b 0 ,且 a b m ,求12的最小值.a b5参考答案一.选择题:本大题共12 小题,每题5 分,在每题给同的四个选项中,只有一项为哪一项符合题目要求的.题号123456789101112答案A C D B B D B C C D D A 二.填空题:本大题共 4 小题,每题 5 分.13.- 1; 14. 5 ;15. 4030 ;16.76 .218三、解答题:解容许写出文字说明,证明过程或演算步骤.17.解: (Ⅰ )解法 1:设 b n的公差为d,那么b n为单调递增的等差数列d0 且b6b5,,, 1 分b3b826b5b6 26解得b512,,, 4 分由得b614b5b6168b5b6168d b6b52,,, 5 分b n b5( n5)d122(n5)2n2b n2n 2 ,,, 6 分解法 2:设b n的公差为 d,那么b n为单调递增的等差数列d0,,, 1 分b3b8262b19d26解得b14,,, 5 分由得b5b6168b14d b15d168d2b n b1(n1) d42( n1)2n2b n2n2,,, 6 分〔Ⅱ〕 2b n22n24n 1,,,7 分由 2a 22 a 23 a2n 1a2n a2b n①123n 1n得 2a22 a23 a2n 1 a2b n 1②,,,8 分123n 1① - ②得2n a n4n 14n 3 4n, n 2a n 3 2n n 2,,9 分b18 不符合上式a n 8n1,,,10 分又 a1232n n2当 n 2 时,S n8322232n8 3 22 1 2n 1 3 2n 14122n 1,,,11 分S18 符合上式S n34, n N *,,,12 分18.解:〔 I 〕由一困难户选择贷款期限为12 个月的概率是0.4,所以小区2021年准备享受此项政策的 3 户恰有两户选择贷款期限为12 个月的概率是P1 C31 0.42 0.60.288;,,,,,,,,,,,,,,,,,,,,, 5 分〔Ⅱ〕 P(200)0.2 , P(300) 0.6, P(400)0.2 ,,,,8 分所以的分布列是:200300400P0. 20. 60. 2E 300 〔元〕,,,,,,,,,,,,,,,,,,,,,,,,12 分所以估计 2021年该市共要补贴 1080 万元.19 .解:〔 I 〕连接 AC ,设 AC OB N ,那么平面PAC平面P OBMMN ,因为 PA // 平面 OBM ,所以 MN // PA ,因此 tPMAN,MMCNCD又 BC // AD ,所以 △ ONA △ BNC ,CAN所以 t PM AO 35 分MC NC CB; ,,,,,,2O〔Ⅱ〕因为 PA PD ,所以 PO AD ,又平面 PAD 平面 ABCD ,所以 PO 平面 ABCD ,NB设线段 BC 的中点为 E ,由 ABCD 是等腰梯形,所以OE AD ,如图以点 O 为原点, OA, OE, OP 所在直线分别为x 轴、 y 轴、zA轴,建立空间直角坐标系.因为 OP PA 2 OA 24,OEAB 2 (OA EB )22所以A(3,0,0), B(1,2,0), C ( 1,2,0), D ( 3,0,0) ,P(0,0, 4) ,,,, 7 分zP平面 PAD 的法向量m(0,1,0) ,设平面OBM 的法向量 n(x, y, z) ,MD由 n OB x 2y 0 ,由〔1〕得 n PA3x 4z 0 ,C令 x1,得 y1, z 3 ,即 n (1, 1 , 3) ,,,, 10 分OEy2 42 412B所以 cosm, n2,A1 92911x4 16所以平面 PAD 与平面 OBM 夹角的余弦值是229.,,,,,,,,, 12 分2920.解:〔 I 〕设椭圆 的焦距为 ,依题意有,,解得,,故椭圆的标准方程为. ,,,,,,3 分又抛物线:开口向上,故是椭圆 的上顶点,,故抛物线的标准方程为.,,,,,,5 分〔 II 〕显然,直线的斜率存在.设直线的方程为,设,,那么,,所以估计 2021年该市共要补贴 1080 万元.19 .解:〔 I 〕连接 AC ,设 AC OB N ,那么平面PAC平面P OBMMN ,因为 PA // 平面 OBM ,所以 MN // PA ,因此 tPMAN,MMCNCD又 BC // AD ,所以 △ ONA △ BNC ,CAN所以 t PM AO 35 分MC NC CB; ,,,,,,2O〔Ⅱ〕因为 PA PD ,所以 PO AD ,又平面 PAD 平面 ABCD ,所以 PO 平面 ABCD ,NB设线段 BC 的中点为 E ,由 ABCD 是等腰梯形,所以OE AD ,如图以点 O 为原点, OA, OE, OP 所在直线分别为x 轴、 y 轴、zA轴,建立空间直角坐标系.因为 OP PA 2 OA 24,OEAB 2 (OA EB )22所以A(3,0,0), B(1,2,0), C ( 1,2,0), D ( 3,0,0) ,P(0,0, 4) ,,,, 7 分zP平面 PAD 的法向量m(0,1,0) ,设平面OBM 的法向量 n(x, y, z) ,MD由 n OB x 2y 0 ,由〔1〕得 n PA3x 4z 0 ,C令 x1,得 y1, z 3 ,即 n (1, 1 , 3) ,,,, 10 分OEy2 42 412B所以 cosm, n2,A1 92911x4 16所以平面 PAD 与平面 OBM 夹角的余弦值是229.,,,,,,,,, 12 分2920.解:〔 I 〕设椭圆 的焦距为 ,依题意有,,解得,,故椭圆的标准方程为. ,,,,,,3 分又抛物线:开口向上,故是椭圆 的上顶点,,故抛物线的标准方程为.,,,,,,5 分〔 II 〕显然,直线的斜率存在.设直线的方程为,设,,那么,,所以估计 2021年该市共要补贴 1080 万元.19 .解:〔 I 〕连接 AC ,设 AC OB N ,那么平面PAC平面P OBMMN ,因为 PA // 平面 OBM ,所以 MN // PA ,因此 tPMAN,MMCNCD又 BC // AD ,所以 △ ONA △ BNC ,CAN所以 t PM AO 35 分MC NC CB; ,,,,,,2O〔Ⅱ〕因为 PA PD ,所以 PO AD ,又平面 PAD 平面 ABCD ,所以 PO 平面 ABCD ,NB设线段 BC 的中点为 E ,由 ABCD 是等腰梯形,所以OE AD ,如图以点 O 为原点, OA, OE, OP 所在直线分别为x 轴、 y 轴、zA轴,建立空间直角坐标系.因为 OP PA 2 OA 24,OEAB 2 (OA EB )22所以A(3,0,0), B(1,2,0), C ( 1,2,0), D ( 3,0,0) ,P(0,0, 4) ,,,, 7 分zP平面 PAD 的法向量m(0,1,0) ,设平面OBM 的法向量 n(x, y, z) ,MD由 n OB x 2y 0 ,由〔1〕得 n PA3x 4z 0 ,C令 x1,得 y1, z 3 ,即 n (1, 1 , 3) ,,,, 10 分OEy2 42 412B所以 cosm, n2,A1 92911x4 16所以平面 PAD 与平面 OBM 夹角的余弦值是229.,,,,,,,,, 12 分2920.解:〔 I 〕设椭圆 的焦距为 ,依题意有,,解得,,故椭圆的标准方程为. ,,,,,,3 分又抛物线:开口向上,故是椭圆 的上顶点,,故抛物线的标准方程为.,,,,,,5 分〔 II 〕显然,直线的斜率存在.设直线的方程为,设,,那么,,所以估计 2021年该市共要补贴 1080 万元.19 .解:〔 I 〕连接 AC ,设 AC OB N ,那么平面PAC平面P OBMMN ,因为 PA // 平面 OBM ,所以 MN // PA ,因此 tPMAN,MMCNCD又 BC // AD ,所以 △ ONA △ BNC ,CAN所以 t PM AO 35 分MC NC CB; ,,,,,,2O〔Ⅱ〕因为 PA PD ,所以 PO AD ,又平面 PAD 平面 ABCD ,所以 PO 平面 ABCD ,NB设线段 BC 的中点为 E ,由 ABCD 是等腰梯形,所以OE AD ,如图以点 O 为原点, OA, OE, OP 所在直线分别为x 轴、 y 轴、zA轴,建立空间直角坐标系.因为 OP PA 2 OA 24,OEAB 2 (OA EB )22所以A(3,0,0), B(1,2,0), C ( 1,2,0), D ( 3,0,0) ,P(0,0, 4) ,,,, 7 分zP平面 PAD 的法向量m(0,1,0) ,设平面OBM 的法向量 n(x, y, z) ,MD由 n OB x 2y 0 ,由〔1〕得 n PA3x 4z 0 ,C令 x1,得 y1, z 3 ,即 n (1, 1 , 3) ,,,, 10 分OEy2 42 412B所以 cosm, n2,A1 92911x4 16所以平面 PAD 与平面 OBM 夹角的余弦值是229.,,,,,,,,, 12 分2920.解:〔 I 〕设椭圆 的焦距为 ,依题意有,,解得,,故椭圆的标准方程为. ,,,,,,3 分又抛物线:开口向上,故是椭圆 的上顶点,,故抛物线的标准方程为.,,,,,,5 分〔 II 〕显然,直线的斜率存在.设直线的方程为,设,,那么,,。
江西省南昌市十所省重点中学命制2016届高三数学第二次模拟突破冲刺试题(七)理

...3x y a 0 8. 设x, y 满足约束条件x y 0 , 假设目标函数z x y 的最大2x y值为 2 ,那么实数 a 的值为〔 〕A. 2B.C.1D.29.等差数列a n 的公差d,且 a 1 ,a 3 , a 13成等比数列,假设a 1 1 ,S n 为数列 a n 的前n 项和,那么2S n16的最小值为〔〕a n 3A .4B. 3C.23 2D . 2过双曲线x2y 2b10.1(a 0,b 0) 的右焦点F 作直线 yA , 交双曲线的左支x 的垂线,垂足为a2b 2a于 B 点,假设FB2FA ,那么该双曲线的离心率为〔〕A.3B.2C.5 D.711. 我国南北朝数学家何承天创造的“调日法〞是程序化寻求准确分数来表示数值的算法, 其理论依据是:设实数 x 的缺乏近似值和过剩近似值分别为b 和d(a,b,c, dN ) ,那么bd是 x 的更为准确的不aca c16 是足近似值或过剩近似值。
我们知道3.14159,假设令3149 ,那么第一次用“调日法〞后得311610 155的更为准确的过剩近似值,即,假设每次都取最简分数, 那么第四次用“调日法〞后可得 的510近似分数为〔 〕226378 109A.7B.20C.25D. 3512. 函数fx2x , gx x cosx sin x ,当 x3 ,3 时,方程f xg x 根的个数是〔〕A 、8B、 6C、 4D、 2第二卷二、填空题 : 本大题共4 小题, 每题5 分, 共 20 分 , 请将答案填在答题卡的相应位置.13.x16展 开式的 常数项 是 540 ,那么由 曲线y x 2和 y x a 围 成的 封闭图形的面积为ax________.14. ABC 的三个内角为 3cos A sinA7 C 的最大值为________.A,B,C ,假设tan,那么 2cos B sin22D AC B ,那么三棱锥 D AC B 的外接球的外表积为________.16.设函数y x3x2,x e,的图象上存在两点P, Q ,使得POQ 是以O为直角顶点的直角三角形a ln x,x e〔其中 O 为坐标原点〕,且斜边的中点恰好在y 轴上,那么实数 a 的取值X围是.三、解答题:本大题共 5 个题,共 60分,解容许写出文字说明、证明过程或演算步骤.17.数列{ a n}的前 n 项和为S n,且S n2a n1,设b2(log2a1),n N *.n n(1〕求数列{ a n}的通项公式;(2〕求数列{ b n a n}的前 n 项和T n;18.如图,四边形ABCD 与BDEF均为菱形,DABDBF 60 ,且 FA FC .〔Ⅰ〕求证:AC平面BDEF;〔Ⅱ〕求证:FC ∥平面EAD;〔Ⅲ〕求二面角A FC B 的余弦值.19.某研究小组在电脑上进展人工降雨模拟试验,准备用A、 B、 C 三种人工降雨方式分别对甲、乙、丙三地实施人工降雨,其试验数据统计如下方式实施地点大雨中雨小雨模拟实验总次数A甲4次6次2次12次B乙 3 次 6 次 3 次12 次C丙 2 次 2 次8 次12 次假定对甲、乙、丙三地实施的人工降雨彼此互不影响,请你根据人工降雨模拟试验的统计数据(I)求甲、乙、丙三地都恰为中雨的概率;( Ⅱ ) 考虑到旱情和水土流失,如果甲地恰需中雨即到达理想状态,乙地必须是大雨才到达理想状态,丙地只能是小雨或中雨即到达理想状态,记“甲、乙、丙三地中到达理想状态的个数〞为随机变量ξ ,求随机变量ξ的分布列和数学期望Eξ.20.椭圆: x2y21〔a b 0〕的右焦点为 (2 2 , 0) ,且椭圆上一点 M 到其两焦点F1, F2 a2b2的距离之和为 4 3 .〔Ⅰ〕求椭圆的标准方程;〔Ⅱ〕设直线l : y x m( m R)与椭圆交于不同两点A,B,且 AB 3 2 .假设点 P( x0 , 2) 满足PA PB ,求 x0的值.21.a R ,函数 f ( x)( x a) | x 1|。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
南昌市十所省重点中学2016年二模突破冲刺交流试卷(09)高三数学(理)一、选择题(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1、已知集合{}R y y x M =∈=,{}2R y y x N =∈=,则M N = ( ) A .R B .∅ C .[)0,+∞ D .()0,+∞2、221i i ⎛⎫= ⎪-⎝⎭( )A .2i -B .4i -C .2iD .4i3、设数列{a n }满足a 1+2a 2=3,且对任意的n ∈N *,点列{P n (n ,a n )}恒满足1n n P P + =(1,2),则数列{a n }的前n 项和S n 为( ).A .3()4n n -B .4()3n n -C .2()3n n -D .1()2n n -4、在一组样本数据(x 1,y 1),(x 2,y 2),…,(x n ,y n )(n ≥2,x 1,x 2,…,x n 不全相等)的散点图中,若所有样本点(x i ,y i )(i =1,2,…,n )都在直线y =—12x +1上,则这组样本数据的样本相关系数为 ( )A .-1B .0 C.—12D .15、已知圆222410x y x y +-++=和两坐标轴的公共点分别为A ,B ,C ,则C ∆AB 的面积为( )A .4B .2 C. D6、执行如图所示的程序框图,输出20152016s =,那么判断框内应填( )A .2015?k ≤B .2016?k ≤C .2015?k ≥D .2016?k ≥7、已知不等式组110x y x y y +≤⎧⎪-≥-⎨⎪≥⎩所表示的平面区域为D ,若直线3y kx =-与平面区域D 有公共点,则k 的取值范围是( )A .[]3,3-B .11,,33⎛⎤⎡⎫-∞-+∞ ⎪⎥⎢⎝⎦⎣⎭C .(][),33,-∞-+∞D .11,33⎡⎤-⎢⎥⎣⎦8、(421x x ⎛⎫+ ⎪⎝⎭的展开式中x 的系数是( )A .1B .2C .3D .12 9、已知函数2sin y x =的定义域为[],a b ,值域为[]2,1-,则b a -的值不可能是( )A .53π B .76π C .π D .56π10.已知一个空间几何体的三视图如图所示,根据图中标出的尺寸(单位:cm ),可得这个几何体的体积是( )3cmA .2B .4C .6D . 12 11、如图所示,圆O 为正三角形C AB 的内切圆,P 为圆O 上一点,向量C x y AP =AB+A,则x y +的取值范围为( )A .1,12⎡⎤⎢⎥⎣⎦B .1,13⎡⎤⎢⎥⎣⎦C .1,14⎡⎤⎢⎥⎣⎦D .11,32⎡⎤⎢⎥⎣⎦12、下图展示了一个由区间()0,1到实数集R 的映射过程:区间()0,1中的实数m 对应数轴上的点M (点A 对应实数0,点B 对应实数1),如图①;将线段AB 围成一个圆,使两端点A 、B 恰好重合,如图②;再将这个圆放在平面直角坐标系中,使其圆心在y 轴上,点A 的坐标为()0,1,在图形变化过程中,图①中线段AM 的长度对应于图③中的弧D A M 的长度,如图③,图③中直线AM 与x 轴交于点(),0n N ,则m 的象就是n ,记作()f m n =.给出下列命题:①114f ⎛⎫= ⎪⎝⎭;②102f ⎛⎫= ⎪⎝⎭;③()f x 是奇函数;④()f x 在定义域上单调递增,则所有真命题的序号是( )A .①②B .②③C .①④D .②④二、填空题(本大题共4小题,每小题5分,共20分.)13、若命题“R x ∃∈,使得22390x ax -+<成立”为假命题,则实数a 的取值范围是 .14、中心在原点,对称轴为坐标轴的双曲线C 的两条渐近线与圆()2221x y -+=都相切,则双曲线C 的离心率是 .15、如图,空间四边形CD AB 中,C D 45∠A =,cos C ∠A B =,C AD A =C 6B =.若点E 在线段C A 上运动,则DEB +E的最小值为 .16、设函数()()()222ln 2f x x a x a=-+-,其中0x >,R a ∈,存在0x 使得()045f x ≤成立,则实数a 的值为三、解答题(解答应写出文字说明、证明过程或演算步骤)17.(理)设数列{}n a 的前n 项和为n S ,已知13a =,133n n S S +=+ *()n N ∈, (1)求数列{}n a 的通项公式; (2)若1n n nn b a a +=-,求数列{}n b 的前n 项和为n T ,*n N ∈.18.(12分)为了解春季昼夜温差大小与某种子发芽多少之间的关系,现在4月份的30天都记录了每天昼夜温差与每天每100颗种子浸泡后的发芽数,从中随机挑选了5天进行分析研究,得到如下表格:(1)请根据4月7日、15日和21日的三天数据,求出y 关于x 的线性回归方程y ^=b ^x +a ^; (2)若某天种子发芽率不低于14,则称该天种子发芽情况为“长势喜人”。
根据表中5天的数据,以频率为概率,估计4月份的整体种子发芽情况。
若在4月份中随机挑选3天,记“长势喜人”的天数为X ,求X 的分布列及数学期望。
⎝ ⎛⎭⎪⎫参考公式:b ^=∑ni =1x i y i-n x - y -∑n i =1x 2i-n x -2,a ^=y --b ^ x -19.(本题满分为12分)如图,已知四棱锥P ABCD -的底面为菱形,120BCD ∠= ,2AB PC ==,AP BP ==.(Ⅰ)求证:AB PC ⊥;(Ⅱ)求二面角B PC D --的余弦值.20、在直角坐标系xOy 中,设点A (-1,0),B (1,0),Q 为△ABC 的外心.已知CG →+2OG →=0,QG ∥AB . (1)求点C 的轨迹Γ的方程;(2)设经过F (0,2)的直线交轨迹Γ于点E ,H ,直线EH 与直线l :y =322交于点M ,点P 是直线y=2上异于点F 的任意一点.若直线PE ,PH ,PM 的斜率分别为k 1,k 2,k 3,问是否存在实数t ,使得1k 1+1k 2=tk 3?若存在,求t 的值;若不存在,请说明理由.21、已知函数()()222ln 2f x x x x ax =-++.(1)当1a =-时,求()f x 在点()()1,1f 处的切线方程;(2)当0a >时,设函数()()2g x f x x =--,且函数()g x 有且仅有一个零点,若2e x e -<<,()g x m ≤,求m 的取值范围.ADCBP请考生在第22、23、24题中任选一题作答,如果多做,则按所做的第一题计分.作答时请写清题号.22. (本小题满分10分) 选修4-1:几何证明选讲如图,△ABC 中,∠ACB =90°,D 是AC 上一点,以AD 为直径作⊙O 交AB 于点G .(1)证明:B 、C 、D 、G 四点共圆;(2)过点C 作⊙O 的切线CP ,切点为P ,连接OP ,作PH ⊥AD 于H ,若CH =165,OH =95,求CD ·CA的值.23. (本小题满分10分) 选修4-4:坐标系与参数方程已知极坐标系的极点在直角坐标系的原点处,极轴与x 轴非负半轴重合,直线l 的参数方程为:⎩⎨⎧x =-1+32ty =12t(t 为参数),曲线C 的极坐标方程为:ρ=4cos θ.(1)写出曲线C 的直角坐标方程和直线l 的普通方程; (2)设直线l 与曲线C 相交于P ,Q 两点,求|PQ |的值.24. (本小题满分10分) 选修4-5:不等式选讲已知函数()|1|2|1|f x m x x =---+.(1)当5m =时,求不等式()2f x >的解集;(2)若二次函数223y x x =++与函数()y f x =的图象恒有公共点,求实数m 的取值范围.数学(理)参考答案一、选择题(本大题共12小题,每小题5分,共60分).二、填空题(本大题共4小题,每题5分,共20分)13. ⎡-⎣14.3或215.716.15三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.)17. (12分)解:(1)133n nS S+=+,当2n≥时,133n nS S-=+,两式相减,得:13n na a+=(2n≥)又13a=,代入133n nS S+=+得29a=3nna∴=()n N+∈………………………………6分(2)1nn nnba a+=-133n nn+=-123nn= ………………………………7分231123()23333n nnT=+++2341111231()3233333n n nn nT+-=++++23412111111()32333333n n nnT+∴=++++-…………………………10分解得:36243n nnT+=-……………………………………12分18. (12分)解:(1)由数据得,另3天的平均数x-=12,y-=27,3 x-y-=972,3 x-2=432,∑3i=1x i y i=977,∑3i=1x2i=434,所以b^=977-972434-432=52,………………………3分a^=27-52×12=-3,所以y关于x的线性回归方程为y^=52x-3. ………………………6分(2)依题意得,选出的5天中,“长势喜人”的天数为3天.所以某一天为“长势喜人”的概率为3=5P(长势喜人) ………………………8分 X 的所有可能取值为0,1,2,3.0303238=C ()()55125P =(X=0)12132336=C ()()55125P =(X=1) 21232354=C ()()55125P =(X=2)30332327=C ()()P =(X=3)(3)5X B ,,355EX ∴=⨯= ………………………………………12分19. (12分)解析:(Ⅰ)证明:取AB 的中点O ,连接,PO CO AC ,. ∵AP BP =,∴PO AB ⊥又四边形ABCD 是菱形,且120BCD ∠=︒, ∴ACB V 是等边三角形,∴CO AB ⊥ 又CO PO O =I ,∴AB PCO ⊥平面,又PC PCO ⊂平面,∴AB PC ⊥ ……………………………………6分(Ⅱ)由2AB PC ==,AP BP ==,易求得1PO =,OC =∴222OP OC PC +=,OP OC ⊥以O 为坐标原点,以OC ,OB ,OP 分别为x 轴,y 轴,z 轴建立空间直坐标系O xyz -,则(0,1,0)B ,C ,(0,0,1)P ,2,0)D -,∴1,0)BC =- ,1)PC =- ,(0,2,0)DC =设平面DCP 的一个法向量为1(1,,)n y z = ,则1n PC ⊥ ,1n DC ⊥,∴11020n PC z n DC y ⎧⋅==⎪⎨⋅==⎪⎩,∴z =0y =,∴1(1n = …………………………8分 设平面BCP 的一个法向量为2(1,,)n b c = ,则2n PC ⊥ ,2n BC ⊥,∴220n PC c n BC b ⎧⋅==⎪⎨⋅==⎪⎩,∴c =b =,∴2(1n = …………………10分∴121212cos ,||||n n n n n n ⋅<>===⋅∵二面角B PC D --为钝角,∴二面角B PC D --的余弦值为7-………………12分 20. (12分)解: (1)设C (x ,y ),∵CG →+2OG →=0,∴G (x 3,y 3),设Q (x 1,y 1),∵Q 为△ABC 的外心, ∴Q 在线段AB 的中垂线上, ∴x 1=0,又QG ∥AB ,∴y 1=y ′3,∴Q (0,y3),根据|QA |=|QC |,得x 2+y 23=1(y ≠0). ……………………………5分(2)当直线EF 的斜率不存在时,t =2.设直线EF 的斜率为k ,则直线EH 的方程为y =kx +2, 点M 坐标为(22k ,322). 把直线方程代入椭圆方程3x 2+y 2=3并整理,得(k 2+3)x 2+22kx -1=0, ……………………………7分 设E (x 1,y 1),F (x 2,y 2),P (a ,2)(a ≠0),则有x 1+x 2=-22k k 2+3,x 1x 2=-1k 2+3,…………………………………8分所以1k 1=x 1-a y 1-2=x 1-a kx 1,1k 2=x 2-a kx 2,1k 3=1k-2a .又因为1k 1+1k 2=x 1-a kx 1+x 2-a kx 2=2k -22a ,…………………………………12分故存在常数t =2符合题意.21. (12分)解答:(1)当a=﹣1时,f (x )=(x 2﹣2x )•lnx ﹣x 2+2,定义域(0,+∞), ∴f′(x )=(2x ﹣2)•lnx+(x ﹣2)﹣2x .……………………………………2分 ∴f′(1)=﹣3, 又f (1)=1,∴f (x )在(1,f (1))处的切线方程3x+y ﹣4=0;…………………………4分 (2)g (x )=f (x )﹣x ﹣2=0, 则(x 2﹣2x )•lnx+ax 2+2=x+2,即a=,…………………………6分令h (x )=,则h′(x )=,令t (x )=1﹣x ﹣2lnx ,则t′(x )=,∵x >0,∴t′(x )<0,∴t (x )在(0,+∞)上是减函数,…………………………8分 又∵t (1)=h′(1)=0,∴当0<x <1时,h′(x )>0,当x >1时,h′(x )<0, ∴h (x )在(0,1)上单调递增,在(1,+∞)上单调递减, ∴h (x )max =h (1)=1,∴当函数g (x )有且仅有一个零点时a=1,当a=1时,g (x )=(x 2﹣2x )•lnx+x 2﹣x ,若e ﹣2<x <e ,g (x )≤m ,只需证明g (x )max ≤m , ∴g′(x )=(x ﹣1)(3+2lnx ), 令g′(x )=0,得x=1或32x e -=又∵e ﹣2<x <e , ∴函数g (x )在(e ﹣2,32e -)上单调递增,在(32e-,1)上单调递减,在(1,e )上单调递增,又g (32e -)=﹣e ﹣3+232e-,g (e )=2e 2﹣3e ,∵g (32e -)=﹣e ﹣3+232e -<232e -<2e <2e (32e-)=g (e ),∴g (32e-)<g (e ),∴m≥2e 2﹣3e .…………………………………………………………12分请考生从22、23、24题中任选一题作答(相应方框填涂);如果多做,则按所做的第一题计分; 如果不填涂,则按22题计分。
