5.2.2平行线的判定练习课课件
合集下载
七级数学人教版下 5.2.2 平行线的判定 优秀课件 (共25张PPT)

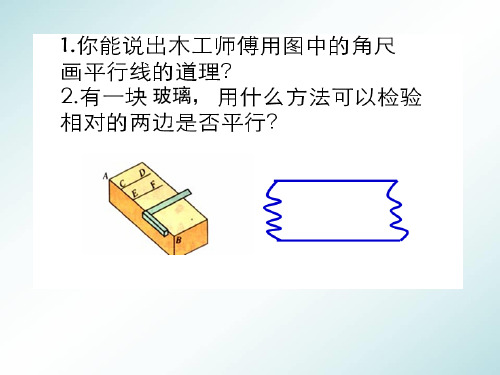
还记得如何用三角板和直尺画平行线吗? 一放、二靠、三推、四画。
图1,2中的直线平行吗?你是怎么判断的?
1
2
1、画图过程中直尺起到了什么作用? ∠1和∠2是什么位置关系 的角? 2、在三角板移动的过程中,∠1和∠2的大小发生变化了吗? 3、要判断a//b你有办法了吗?
a
A.
1
b 2
怎样使得两根木条保持平行呢?
a
1
2
∴b ∥ c(同位角相等,两直线平行)
结论:在同一平面内,垂直于同一条直线的两条直线互相( 平行 )
平行线的判定示意图
判定
同位角相等 内错角相等 同旁内角互补
两直线平行 位置关系
数量关系
1、快乐总和宽厚的人相伴,财富总与诚信的人相伴,聪明总与高尚的人相伴,魅力总与幽默的人相伴,健康总与阔达的人相伴。 2、人生就有许多这样的奇迹,看似比登天还难的事,有时轻而易举就可以做到,其中的差别就在于非凡的信念。
7、人往往有时候为了争夺名利,有时驱车去争,有时驱马去夺,想方设法,不遗余力。压力挑战,这一切消极的东西都是我进取成功的催化剂。 8、真想干总会有办法,不想干总会有理由;面对困难,智者想尽千方百计,愚者说尽千言万语;老实人不一定可靠,但可靠的必定是老实人;时间,抓起来是黄金,抓不起来是流水。 9、成功的道路上,肯定会有失败;对于失败,我们要正确地看待和对待,不怕失败者,则必成功;怕失败者,则一无是处,会更失败。1、快乐总和宽厚的人相伴,财富总与诚信的人相伴,聪明总与高尚的人相伴,魅力总与幽默的人相伴,健康总与阔达的人相伴。
用判定定理1应 该注意:
①找出同位角; ②说明这两个同位角相等; ③得出“平行”的结论。
想一想
2.如果∠2 =∠5, ∠1 =∠2 能判定哪两条直线平行? ∠3 =∠4
5.2.2平行线的判定课件20151月

9.如图,根据下列条件可判断哪 两条直线平行,并说明理由。 (1)∠1=∠2 (2)∠3=∠A
A
D
1 4
C
2
3
(3)∠A+∠2+∠4=180°
B
10.如图所示,已知∠1=∠2,AC 平分∠DAB,试说明DC∥AB.
证明:
D
2
C
∵ AC平分∠DAB (已知)
∴∠1=∠3 ∵ ∠1=∠2 (角平分线的定义) (已知)
A E B
第2题
D F C
4.如图1所示,下列条件中,能判断AB∥CD的是( ) A.∠BAD=∠BCD B.∠1=∠2; C.∠3=∠4 D.∠BAC=∠ACD
A
A
1 2
D F C
D
4
E B
(1) (2) 5.如图2所示,如果∠D=∠EFC,那么( ) A.AD∥BC B.EF∥BC C.AB∥DC
练2:
2.如图,已知∠A与∠D互补, 可以判定哪两条直线平行? ∠B与哪个角互补,可以判 定直线AD∥BC? A 解:
D
C
B
1) ∵ ∠A与∠D互补(已知) ∴AB∥DC(同旁内角互补,两直线平行) 2) ∵∠B与∠A互补(已知) ∴ AD∥BC(同旁内角互补,两直线平行)
练3:结合图形回答问题:
例:在同一平面内,两条直线垂直于同一条直 线,这两条直线平行吗?为什么?
答:垂直于同一条直线的两条直线平行. c b 理由:如图, ∵ b⊥a,c⊥a(已知) a
1 2
∴∠1=∠2=90°(垂直定义)
∴b∥c(同位角相等,两直线平行)
自我测试
D E
1.如果∠A=∠3,那么AD ∥ BE , 2 1 3 ( 同位角相等,两直线平行.) 2.如果∠2=∠E,那么BD ∥ CE , A B ( 内错角相等,两直线平行.) 3.如果∠A+∠ABE=1800,那么 AD ∥ BE , ( 同旁内角互补,两直线平行.) 4.如果∠2=∠D ,那么DA∥EB ( 内错角相等,两直线平行.) 5.如果∠DBC+∠C =1800,那么DB∥EC (∥EF
人教版七年级数学下册5.2.2第1课时 平行线的判定 课件(共21张PPT) (1)

几何语言:
∵ ∠3=∠2(已知),
∴ a∥b(内错角相等,两直线平行).
1
a
3
2 b
考 点 2 利用内错角相等判定两直线平行
完成下面证明:如图所示,CB平分∠ACD,∠1=∠3.
求证:AB∥CD.
证明:∵CB平分∠ACD, ∴∠1 = ∠2( 角平分线的定义_______). ∵∠1 = ∠3, ∴∠2 = ∠ 3 .
两直线平行
数量关系
位置关系
课后作业
1.从课后习题中选取; 2.完成练习册本课时的习题。
∴AB∥CD( 内错角相等,两直线平行_).
知识点3:利用同旁内角互补判定两条直线平行
如图,如果1+2 = 180° ,你能判定 a / / b 吗?
解:能, ∵1+2=180°(已知), 1+3=180°(邻补角的性质),
c
3
a
1
∴2=3(同角的补角相等) .
2
b
∴a//b(同位角相等,两直线平行) .
两条直线平行?请说明理由?
解: AB∥CD.
理由如下:
D
3C
∵ AC平分∠DAB(已知),
1
∴ ∠1=∠2(角平分线定义).
2
A
B
又∵ ∠1= ∠3(已知) ,
∴ ∠2=∠3(等量代换).
∴ AB∥CD(内错角相等,两直线平行).
四 课堂小结
判定
平行线的判 定示意图
同位角相等 内错角相等 同旁内角互补
证明:∵∠1+∠A=180º ( 已知 ), ∠1=∠2 (对顶角相等 ),
ቤተ መጻሕፍቲ ባይዱ
B
2 13
D
《平行线的判定》精品ppt课件

A
B
C
D
E
F
பைடு நூலகம்
1
3
2
∠1 +∠2=180°(已知), ∠2 +∠3=180°(邻补角互补),
∠1 =∠3(同角的补角相等).
AB∥CD
(同位角相等,两直线平行).
∵ ∠4+∠7=180 °(已知) ∠4+∠1=180°(邻补角的定义)
∴ ∠7=∠1(同角的补角相等)
∴ AB∥CD(内错角相等, 两直线平行)
思考:
下图中,如果∠1=∠7,能得出AB∥CD吗? 写出你的推理过程
∵∠1=∠7 ∠1=∠3
∴ ∠7=∠3
∴ AB∥CD
B
1
A
C
D
F
3
7
E
( )
已知
( )
对顶角相等
( )
等量代换
( )
C.∠4+∠5=180° D.∠2+∠4=180°
B
达标检测 反思目标
2.如图,BE是AB的延长线。由∠CBE=∠A可以判定____∥___根据是________________________由∠CBE=∠C可以判定___∥____根据是___________________________
解:根据∠OEB+∠EOD=180°得到 AB∥CD
上交作业:课本15—16 页 第4、7 题
课后作业
·
A
B
P
还记得如何用三角板和直尺画平行线吗?
一放、二靠、三推、四画。
从画图过程,三角板起到什么作用?
C
D
1
2
两条直线被第三条直线所截, 如果同位角相等,那么这两条直线平行.
B
C
D
E
F
பைடு நூலகம்
1
3
2
∠1 +∠2=180°(已知), ∠2 +∠3=180°(邻补角互补),
∠1 =∠3(同角的补角相等).
AB∥CD
(同位角相等,两直线平行).
∵ ∠4+∠7=180 °(已知) ∠4+∠1=180°(邻补角的定义)
∴ ∠7=∠1(同角的补角相等)
∴ AB∥CD(内错角相等, 两直线平行)
思考:
下图中,如果∠1=∠7,能得出AB∥CD吗? 写出你的推理过程
∵∠1=∠7 ∠1=∠3
∴ ∠7=∠3
∴ AB∥CD
B
1
A
C
D
F
3
7
E
( )
已知
( )
对顶角相等
( )
等量代换
( )
C.∠4+∠5=180° D.∠2+∠4=180°
B
达标检测 反思目标
2.如图,BE是AB的延长线。由∠CBE=∠A可以判定____∥___根据是________________________由∠CBE=∠C可以判定___∥____根据是___________________________
解:根据∠OEB+∠EOD=180°得到 AB∥CD
上交作业:课本15—16 页 第4、7 题
课后作业
·
A
B
P
还记得如何用三角板和直尺画平行线吗?
一放、二靠、三推、四画。
从画图过程,三角板起到什么作用?
C
D
1
2
两条直线被第三条直线所截, 如果同位角相等,那么这两条直线平行.
七年级数学5.2.2平行线的判定PPT课件
如图:B= D=45°, C=135°,
问图中有哪些直线平行?
A
D
答:AB//CD,AD//BC B
C
∵ B=45°(已知)
C=135°(已知) B+ C=180° AB//CD(同旁内角互补,两直线平行) 同理:AD//BC
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
纸条,
(点阵中相邻的四个点构成正方形).
E
G
A
B
C
D
F
H
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
画平行线的事 实
同位角相等, 两直线平行。
同旁内角互补, 两直线平行。
内错角相等, 两直线平行。
判定方法3 两条直线被第三条直线所截,如果 同旁内角互补,那么这两条直线平行
简单说成:同旁内角互补,两直线平行
1a
几何语言: ∵∠1+∠4=1800(已知)
3
4
2b
∴a∥b(同旁内角互补,两直线平行)
想一想 经营者提供商品或者服务有欺诈行为的,应当按照消费者的要求增加赔偿其受到的损失,增加赔偿的金额为消费者购买商品的价款或接受服务的费用
简记为“垂直于同一直线的两直线平行”。
∵ a⊥b,a⊥c(已知) ∴ b//c(垂直于同一直线的两条直线平行)
a
1
c
2
b
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
七年级数学下册《5.2.2平行线的判定》课件

书 香
知道了...... 学会了......
1、课本P125 练习1、2 2、同步练习10.2(一)
如图:
(1) 和 是直线AB,BC被直线AC所截而得 到的 ____同__旁__内__角______
(2) 和 是直线AB,AC被直线BD 所截而得
到的_____同__位___角___________
是内错角。
与________
A
E1
D
3
2
B
4
F
C
(3) 与 是直线AB和直线AF被直线ED所截而
得到的___内__错___角。
A
E
2
B
(4)
1
D
3
4
F
C
识别同位角、内错角、同旁 内角步骤: 先抽取;看三线;找截线; 再判断。
和______是直线AB和直线AF被直线BC所截而得
的__同__位____角。
点?
A
E
21
34
B
65
D
图中还有其它同旁内角吗?C
7
8
F
讨论:
你能用什么符号来表示这三类角? 同位角: 内错角: 同旁内角:
两手的拇指和食指如何组合得 到同位角、内错角、同旁内角?
练一练
1、如图,找出图中的同位角、内错角、同旁内角
14
23
同位角: 65 7 8 内错角:
同旁内角:
2、如图:(1)________________是同位角。
E
2
1
34
B
6
5
7 F8
D
1.同位角
如图,∠4和∠8与截线及两条被截直线在位置上有什么特
5.2.2平行线的判定(课件)七年级数学下册(人教版)

CD
AB
A
D
1
B
C
人教版数学七年级下册
谢谢聆听
∴∠1=∠2(同角的补角相等)
∴a∥b(同位角相等,两直线平行)
1
3 4
a
2
b
探究新知
人教版数学七年级下册
判定两条直线平行的方法:
判定方法3:两条直线被第三条直线所截,如果同旁内角互补,
那么这两条直线平行.
1
a
3 4
简单说成:同旁内角互补,两直线平行.
2
符号语言表示:∵∠2+∠4=180°(已知)
人教版数学七年级下册
课后作业
人教版数学七年级下册
2.如图:
如果∠1=∠D,那么______∥________;
AD
BC
如果∠1=∠B,那么______∥________;
CD
AB
如果∠A+∠B=180°,那么______∥________;
BC
AD
如果∠A+∠D=180°,那么______∥________.
人教版数学七年级下册
2.如图:
AD
BC
如果∠B=∠1,则可得____//___
同位角相等,两直线平行
根据是_____________________
AB
CD
如果∠D=∠1,则可得到____//___
B
内错角相等,两直线平行
根据是_______________________
A
1
D
C
巩固练习
人教版数学七年级下册
但是,由于直线无限延伸,检验它们是否相交有困难,
所以难以直接根据两条直线是否相交来判定是否平行,那么
AB
A
D
1
B
C
人教版数学七年级下册
谢谢聆听
∴∠1=∠2(同角的补角相等)
∴a∥b(同位角相等,两直线平行)
1
3 4
a
2
b
探究新知
人教版数学七年级下册
判定两条直线平行的方法:
判定方法3:两条直线被第三条直线所截,如果同旁内角互补,
那么这两条直线平行.
1
a
3 4
简单说成:同旁内角互补,两直线平行.
2
符号语言表示:∵∠2+∠4=180°(已知)
人教版数学七年级下册
课后作业
人教版数学七年级下册
2.如图:
如果∠1=∠D,那么______∥________;
AD
BC
如果∠1=∠B,那么______∥________;
CD
AB
如果∠A+∠B=180°,那么______∥________;
BC
AD
如果∠A+∠D=180°,那么______∥________.
人教版数学七年级下册
2.如图:
AD
BC
如果∠B=∠1,则可得____//___
同位角相等,两直线平行
根据是_____________________
AB
CD
如果∠D=∠1,则可得到____//___
B
内错角相等,两直线平行
根据是_______________________
A
1
D
C
巩固练习
人教版数学七年级下册
但是,由于直线无限延伸,检验它们是否相交有困难,
所以难以直接根据两条直线是否相交来判定是否平行,那么
5.2.2 平行线的判定(1)课件1(人教版)

(内错角相等,两直线平行)
练习:
5.如图, 如何判断这块玻璃板的上下两边 平行?
(方法三)
解:如图,画截线a,
1
度量∠1,∠2
2
a
若∠1+∠2 =180°,
则玻璃板的上下两边平行
(同旁内角互补,两直线平行)
练习: 2.如图,已知∠A与∠D互补,
D
C
可以判定哪两条直线平行?
∠B与哪个角互补,可以判
5.如图, 如何判断这块玻璃板的上下两边
平行?
(方法一)
1
解:如图,画截线a, 度量∠1,∠2 若∠1=∠2 ,
2 a
则玻璃板的上下两边平行
(同位角相等,两直线平行)
练习:
5.如图, 如何判断这块玻璃板的上下两边 平行?
(方法二) 解:如图,画截线a,
度量∠1,∠2 若∠1=∠2 ,
1
2 a
则玻璃板的上下两边平行
定直线AD∥BC?
解:
A
B
1) ∵ ∠A与∠D互补(已知)
∴AB∥DC(同旁内角互补,两直线平行)
2) ∠B与∠A互补时
可判定AD∥BC(同旁内角互补,两直线平行)
七嘴八舌说一说
c
如图:(1)由1= 2, 可推出a//b吗?为什么?
3 答:可以推出a//b。 根据同位角相等,两直线平行
(2)由3= 2,可推出a//b吗? 如何推出?写出你的推理过程
解: 1=3(已知) 3= 2(对顶角相等)
1= 2 a//b(同位角相等,两直线平行)
a
2
b
问题探究、发现定理
5.2.2 平行线的判定(1)
复习回顾:
一、判断:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A
C
E
1
G
3
H
2
解∵ ∠1=∠2=55° ∠2=∠3(对顶角相等) ∴∠3= 55°(等量代换)
B
D
F
∴∠1=∠3 (等量代换)
∴AB∥CD(同位角相等,两直线平行)
例题
例4 已知:如图,∠1=∠C,∠2=∠B, 求证:MN∥EF. 证明: ∵ ∠1=∠C (已知)
M 2 E B F C
A
1
N
∴ MN∥BC (内错角相等,两直线平行)
1如图,∠D =∠A,∠B =∠FCB, 求证:ED∥CF.
.
例1 如下图,已知∠1=120°, ∠C=60° 2 1 判断直线AB与CD是否平行 A 答: AB∥CD
理由:∵ ∠1=120°( 已知 ) C
B D
∴ ∠2=180°—∠1 =60° ( 邻补角定义 ) 又∵ ∠C=60°( 已知 ) ∴ ∠2= ∠C( 等量代换
C
B
练习1:如图,直线EF与∠ABC的一边BA,相交 于D, ∠B+ ∠ADE=180°,EF与BC平行吗? 为什么? A E F 答: EF与BC平行 D 理由: ∵ ∠B+ ∠ADE=180( 已知 )
∠ADE= ∠BDF( 对顶角相等 ) B
∴ ∠BDF+ ∠B=180°( 等量代换 ) ∴ EF∥BC( 同旁内角互补,两直线平行 )
)
∴AB∥CD( 同位角相等,两直线平行 )
例2 如图,已知∠1= ∠3,AC平分 ∠DAB你能判断那两条直线平行?请说 明理由? D 3 答: AB∥CD 理由: ∵ AC平分∠DAB(已知 ) 1 2 A ∴ ∠1=∠2(角平分线定义 )) 又∵ ∠1= ∠3(已知 ) ∴ ∠2=∠3( 等量代换) ∴ AB∥CD( 内错角相等,两直线平+∠D=180°, 那么BC平行DE吗?为什么?
A B C E D
答:BC∥DE 理由:∵ ∠B=∠C ( 已知 ) ∠B+ ∠D=180°( 已知 )
∴ ∠C+ ∠D=180°( 等量代换 ) ∴BC∥DE( 同旁内角互补,两直线平行 )
例2 已知:如图,ABC、CDE都是直线, 且∠1=∠2,∠1=∠C, A 求证:AC∥FD. 证明: ∵ ∠1 = ∠2, ∠1 = ∠C (已知) ∴ ∠2=∠C (等量代换) ∴ AC∥FD (同位角相等,两直线平行)
∵ ∠2=∠B (已知)
∴ EF∥BC (同位角相等,两直线平行) ∴ MN∥EF (平行于同一直线的两条直线平行)
考考你
7、如图,AF、CE、BD交于点B,且BE平分 ∠DBF,且∠1= ∠C,问BD与AC平行吗? 为什么? A
D E 1 B F C
C D
B
1
F
2
E
、如右图,∠1=∠2=55°∠3等 于多少度?直线AB,CD平行吗? E 说明你的理由。
A
1
C
G
3
H
2
解∵ ∠1=∠2=55° ∠2=∠3(对顶角相等) ∴∠3= 55°(等量代换)
B
D
F
∴∠1=∠3 (等量代换)
∴AB∥CD(同位角相等,两直线平行)
10、如右图,∠1=∠2=55°∠3 等于多少度?直线AB,CD平行 吗?说明你的理由。
