中心对称 课件1北师大版八年级
合集下载
初中数学《中心对称》精品ppt北师大版1
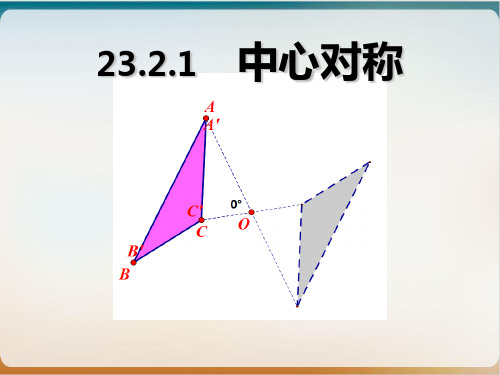
23.2.1 中心对称
观察下面两组图形中的左右两部分,它们是通过怎 样的变换得到的?
图1 平移
图2 轴对称
轴对称:对称轴、翻折180°、重合
观察下面两组图形中的左右两部分,它们是通过怎 样的变换得到的?
O
O
图1
图2
旋转中心
旋转三要素 旋转方向
旋转角度
演示
显示弧
A
α
M
α = 180.00°
B'
拖动点M控制旋转角度
A'
画对称中心
如图,已知△ABC 与△DEF 中心对称,点 A 和点 D 是对称点, 画出对称中心 O.
F
E
A
O
D
B
C
这节课你学到了什么?
中心对称的概念
把一个图形绕着某一个点旋转180°,如果它能够与另一个图 形重合,那么就说这两个图形关于这个点对称或中心对称 这个点叫做对称中心. 能重合的对应点叫做关于对称中心的对称点.
连接各组对称点,你有什么发现?这两个三角形有什么关系?
(1)OA=OA′、OB=OB′、 OC=OC′ (2)△ABC≌△A′B′C′
中心对称的性质
① 对称点所连线段都经过对称中心,而且被对称 中心所平分. ② 两个图形全等
A
B' C' CO B
A'
中心对称与轴对称
轴对称
有一条对称轴——直线
图形沿对称轴对折 (翻折180°)后重合 对称点的连线被 对称轴垂直平分
图形沿对称轴对折(翻ቤተ መጻሕፍቲ ባይዱ 180°)后重合
有一个对称中心——点
图形绕对称中心旋转 180°后重合
对称点的连线被对 称轴垂直平分
观察下面两组图形中的左右两部分,它们是通过怎 样的变换得到的?
图1 平移
图2 轴对称
轴对称:对称轴、翻折180°、重合
观察下面两组图形中的左右两部分,它们是通过怎 样的变换得到的?
O
O
图1
图2
旋转中心
旋转三要素 旋转方向
旋转角度
演示
显示弧
A
α
M
α = 180.00°
B'
拖动点M控制旋转角度
A'
画对称中心
如图,已知△ABC 与△DEF 中心对称,点 A 和点 D 是对称点, 画出对称中心 O.
F
E
A
O
D
B
C
这节课你学到了什么?
中心对称的概念
把一个图形绕着某一个点旋转180°,如果它能够与另一个图 形重合,那么就说这两个图形关于这个点对称或中心对称 这个点叫做对称中心. 能重合的对应点叫做关于对称中心的对称点.
连接各组对称点,你有什么发现?这两个三角形有什么关系?
(1)OA=OA′、OB=OB′、 OC=OC′ (2)△ABC≌△A′B′C′
中心对称的性质
① 对称点所连线段都经过对称中心,而且被对称 中心所平分. ② 两个图形全等
A
B' C' CO B
A'
中心对称与轴对称
轴对称
有一条对称轴——直线
图形沿对称轴对折 (翻折180°)后重合 对称点的连线被 对称轴垂直平分
图形沿对称轴对折(翻ቤተ መጻሕፍቲ ባይዱ 180°)后重合
有一个对称中心——点
图形绕对称中心旋转 180°后重合
对称点的连线被对 称轴垂直平分
北师大版八年级下册数学 3.3 中心对称教学课件 (共16张PPT)
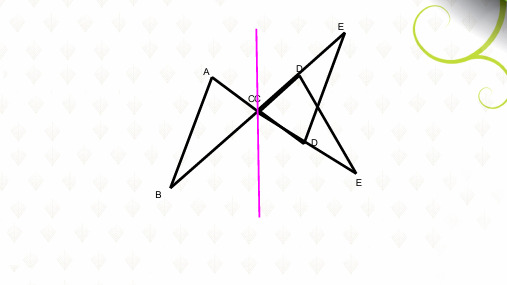
E
A
D
CC
D
E B
3.3.中心对称
观察
观察下面的2组图形,看一看各组中2个图形的形状、大小是否 相同? 怎样将一个图形旋转得到另一个图形?
O
180°
重合
B180°Fra bibliotek(2)
C
重合
认识新朋友
B
180° C
把一个图形绕着某一个点旋转180°,如果 它能够与另一个图形重合,那么就说这两个图形
关于这个点对称或中心对称,
这个点叫做对称中心
这两个图形在旋转中能重合的对应点叫做关于中心的对称点.
O
B
(2) C
两只小鱼关于 成中心 对称,
对称中心是 .
△OCD和△OAB关于
对
称,对称中心
是
.
点C和
点B和
是关于O的对称点; 是关于O的对称点
探归究纳
点O是AA′的中点。
C
△ABC≌△A′B′C′
A
B
● B′ O
A′
中心对称的性质
C′
1、探中究心一对:称观的察两个两图个形图是形全你等发形。现了什么?
探2、究中二心:对分称别的两连个接图对形称,点对称AA点′所,连B线B′段,都经CC过′对,称你中又心发,而现且
被对称中心所平分。
了什么?
议一议 中心对称与轴对称有什么区别?
又有什么联系?
L
A
A/
轴对称
A
中心对称O
有一条对称轴---直线
的段△A'AB′'B′C′. (不要求写画法)
A C
B
A′ O
A′ 点A′即为所求的点
随堂练如习图,D是△ABC的边AC上 一点,画出△EFG,使它与△ ABC
A
D
CC
D
E B
3.3.中心对称
观察
观察下面的2组图形,看一看各组中2个图形的形状、大小是否 相同? 怎样将一个图形旋转得到另一个图形?
O
180°
重合
B180°Fra bibliotek(2)
C
重合
认识新朋友
B
180° C
把一个图形绕着某一个点旋转180°,如果 它能够与另一个图形重合,那么就说这两个图形
关于这个点对称或中心对称,
这个点叫做对称中心
这两个图形在旋转中能重合的对应点叫做关于中心的对称点.
O
B
(2) C
两只小鱼关于 成中心 对称,
对称中心是 .
△OCD和△OAB关于
对
称,对称中心
是
.
点C和
点B和
是关于O的对称点; 是关于O的对称点
探归究纳
点O是AA′的中点。
C
△ABC≌△A′B′C′
A
B
● B′ O
A′
中心对称的性质
C′
1、探中究心一对:称观的察两个两图个形图是形全你等发形。现了什么?
探2、究中二心:对分称别的两连个接图对形称,点对称AA点′所,连B线B′段,都经CC过′对,称你中又心发,而现且
被对称中心所平分。
了什么?
议一议 中心对称与轴对称有什么区别?
又有什么联系?
L
A
A/
轴对称
A
中心对称O
有一条对称轴---直线
的段△A'AB′'B′C′. (不要求写画法)
A C
B
A′ O
A′ 点A′即为所求的点
随堂练如习图,D是△ABC的边AC上 一点,画出△EFG,使它与△ ABC
八年级下册数学课件(北师版)中心对称

3.下列多边形中,是轴对称图形而不是中心对称图形的
是④ . ① 平行四边形 ② 矩形 ③ 菱形 ④ 等腰梯形
注意: 等边三角形不是中心对称图形! 是轴对称图形
O
注意:
平行四边形不是轴对称图形! 是中心对称图形
A
D
O
B
C
1条
无
等边三角形
3条
无
平行四边形
无
对角线交点
矩形
2条
对角线交点
菱形
2条
对角线交点
正方形
4条
Байду номын сангаас
对角线交点
等腰梯形
1条
无
1.下列图形中既是轴对称图形又是中心对称图形的
是 ③. ①角 ②正三角形 ③线段 ④ 平行四边形
2.下列多边形中,是中心对称图形而不是轴对称图形的
是① . ① 平行四边形 ② 矩形 ③ 菱形 ④ 正方形
如果将中心对称图形对称的部分看成两个 图形,则它们成中心对称.
我们平时见过的几何图形中,有哪些 是中心对称图形?并指出对称中心.
怎样的多边形是中心对称图形? 偶数边的 正多边形
常见的轴对称图形与中心对称图形
对
图
称
形性
轴对称图形
图形
对称轴条数
中心对称图形
图形
对称中心
线段
2条
中点
角
1条
无
等腰三角形
作图
(1)如图,选择点O为对称中心,画出点A关 于点O的对称点A′;
A
O
A′
画法:连接AO并延长到A′,使OA′=OA,得到 点A的对称点A′.
点A′即为所求的点.
(2)如图,选择点O为对称中心,画出与 △ABC关于点O对称的△A′B′C′.
是④ . ① 平行四边形 ② 矩形 ③ 菱形 ④ 等腰梯形
注意: 等边三角形不是中心对称图形! 是轴对称图形
O
注意:
平行四边形不是轴对称图形! 是中心对称图形
A
D
O
B
C
1条
无
等边三角形
3条
无
平行四边形
无
对角线交点
矩形
2条
对角线交点
菱形
2条
对角线交点
正方形
4条
Байду номын сангаас
对角线交点
等腰梯形
1条
无
1.下列图形中既是轴对称图形又是中心对称图形的
是 ③. ①角 ②正三角形 ③线段 ④ 平行四边形
2.下列多边形中,是中心对称图形而不是轴对称图形的
是① . ① 平行四边形 ② 矩形 ③ 菱形 ④ 正方形
如果将中心对称图形对称的部分看成两个 图形,则它们成中心对称.
我们平时见过的几何图形中,有哪些 是中心对称图形?并指出对称中心.
怎样的多边形是中心对称图形? 偶数边的 正多边形
常见的轴对称图形与中心对称图形
对
图
称
形性
轴对称图形
图形
对称轴条数
中心对称图形
图形
对称中心
线段
2条
中点
角
1条
无
等腰三角形
作图
(1)如图,选择点O为对称中心,画出点A关 于点O的对称点A′;
A
O
A′
画法:连接AO并延长到A′,使OA′=OA,得到 点A的对称点A′.
点A′即为所求的点.
(2)如图,选择点O为对称中心,画出与 △ABC关于点O对称的△A′B′C′.
4.7 中心对称图形 课件 1(北师大版八年级上)

学科网,zxxk.fenghuangxueyi
中 心 对 称 图 形
a 1.什么是轴对称? l 它有哪些性质? P 2.什么是旋转对 称? M’ M P’
N’
N
下列旋转对称图形旋转几度能与自 身重合?
60° 120° 180° 240° 300° 120° 240°
72° 144° 216° 288°
学科网,zxxk.fenghuangxueyi
A
O
D C
B
B
A C D A B’ C’ O B E
把一个图形绕着某一 点旋转180 ,如果它 能够和另一个图形重 合,那么,我们就说 这两个图形成中心对 C 称,这个点叫做对称 中心,这两个图形中 的对应点,叫做关于 中心的对称点.
A’
C’ A B’ O
在成中心对称的 两个图形中,连结对 A’ B 称点的线段都经过对 C 称中心,并且被对称 ∵⊿ABC 与⊿A’B’C’ 中心平分。 关于点O称中心对称 反过来,如果两 ∴O在AA上, 个图形的对应点连成 且 OA=OA’ 的线段都经过某一点, ∵ O 在 AA 上, 并且被平分,那么这 且 OA=OA’ 两个图形一定关于这 ∴ 点 A 与点 A’ 关于点 一点成中心对称 O称中心对称
怎样的两个图形叫做关于某直线成轴对称? 成轴对称的两个图形有什么性质?
轴 对 称
中心对称
有一个对称中心:点 图形绕中心旋转180° 旋转后与另一图形重 合 两个图形是全等形
定 1 一条轴对称:直线 图形沿轴对折, 义 三 2 即翻转180° 要 3 翻转后与另一图形 点 重合 两个图形是全等形 1 性
90° 180° 270°
180°
一个图形绕着中心点 旋转180后能与自身 重合,我们就把这种 图形叫做中心对称图 形,这个中心点叫做 对称中心。
中 心 对 称 图 形
a 1.什么是轴对称? l 它有哪些性质? P 2.什么是旋转对 称? M’ M P’
N’
N
下列旋转对称图形旋转几度能与自 身重合?
60° 120° 180° 240° 300° 120° 240°
72° 144° 216° 288°
学科网,zxxk.fenghuangxueyi
A
O
D C
B
B
A C D A B’ C’ O B E
把一个图形绕着某一 点旋转180 ,如果它 能够和另一个图形重 合,那么,我们就说 这两个图形成中心对 C 称,这个点叫做对称 中心,这两个图形中 的对应点,叫做关于 中心的对称点.
A’
C’ A B’ O
在成中心对称的 两个图形中,连结对 A’ B 称点的线段都经过对 C 称中心,并且被对称 ∵⊿ABC 与⊿A’B’C’ 中心平分。 关于点O称中心对称 反过来,如果两 ∴O在AA上, 个图形的对应点连成 且 OA=OA’ 的线段都经过某一点, ∵ O 在 AA 上, 并且被平分,那么这 且 OA=OA’ 两个图形一定关于这 ∴ 点 A 与点 A’ 关于点 一点成中心对称 O称中心对称
怎样的两个图形叫做关于某直线成轴对称? 成轴对称的两个图形有什么性质?
轴 对 称
中心对称
有一个对称中心:点 图形绕中心旋转180° 旋转后与另一图形重 合 两个图形是全等形
定 1 一条轴对称:直线 图形沿轴对折, 义 三 2 即翻转180° 要 3 翻转后与另一图形 点 重合 两个图形是全等形 1 性
90° 180° 270°
180°
一个图形绕着中心点 旋转180后能与自身 重合,我们就把这种 图形叫做中心对称图 形,这个中心点叫做 对称中心。
八年级数学下册《3.3 中心对称》课件1 (新版)北师大版

第八页,共13页。
2、已知△ABC(如图),画出△A`B`C` , 使△A`B`C`与△ABC关于(guānyú)点C成中 心对称.
A
B
C
第九页,共13页。
3、已知四边形ABCD(如图),画出四边形 A`B`C` D`使四边形A`B`C`D`与四边形ABCD关 于(guānyú)CD中点O成中心对称.
C′
A
如图.
O
B △ABC与△A′B′C′是关于
(guānyú)点O成中心对称的
B′
两个三角形,点O是对称中
心, 对应点A和A`、B和B`、
C和C`是关于(guānyú)中心
A′
C
O的对称点.
中心对称与中心对称图形有何区别与联系呢?
第六页,共13页。
如图,△ABC与△A′B′C′是关于点O成中心对
A
D
O B
C
第十页,共13页。
4、如图所示的图形是由两个半圆(bànyuán)组 成的图形.已知点B是AC的中点,画出此图形关 于点B成中心对称的图形.
A
B
C
第十一页,共13页。
5、如图,△ABC与△A′B′C′是关于(guānyú) 某点成中心对称的两个三角形, 你能找出对 称中心O吗?
C′
A
我们就说这两个图形关于这个点成中心对称.
3、中心对称的性质
性质1 关于中心对称的两个图形是全等形.
性质2 关于中心对称的两个图形,对称点的连线都经过 对称中心,并且被对称中心平分.
第十三页,共13页。
∴AA`、BB`、CC`经过点O,且 OA=OA`,OB=OB`,OC=OC`
第七页,共13页。
中心对称(zhōnɡ xīn 1、已知Ad点uì和Oc点hē,nɡ画)作出点图A关于(guānyú)点O的对称点
中心对称课件数学北师大版八年级下册

感悟新知
解题秘方:紧扣中心对称与相关定义判断 .
知1-练
解:从图中易看出旋转中心为点 A,故点 A 为对称中 心;点A, B, C, D 绕点 A 旋转 180°后的位置分别 在点 A, G,H, E 处,故点 A, B, C, D 关于点 A 的对称点分别是点 A, G,H, E.
感悟新知
知1-练
能在每个图形的内部或边上.
▲▲
▲▲
感悟新知
2. 中心对称与轴对称的关系
知1-讲
项目
中心对称
轴对称
有一个对称中心
有一条对称轴
区分
图形绕对称中心旋转 180°
图形沿对称轴折叠
旋转后与另一个图形 折叠后与另一个图形
重合
重合
相同点
都是两个图形之间的关系,并且变换前后的 两个图形全等
感悟新知
知1-练
例1 如图 3-3-1,两个五角星关于某一点成中心对称,指出 哪一点是对称中心,并指出图中点 A, B, C, D 的 对称点 .
感悟新知
知3-练
解:A 是轴对称图形,不是中心对称图形,故本 选项不合题意; B 既是轴对称图形,又是中心对 称图形 , 故本选项符合题意; C 不是轴对称图形 , 是中心对称图形,故本选项不合题意; D 不是轴 对称图形,是中心对称图形 , 故本选项不合题意 . 答案:B
感悟新知
3-1. [中考·黑龙江龙东地区] 下列新能源汽车标志知3-练 图案中,既是轴对称图形,又是中心对称图形的 是( A )
知3-讲
项目 区分
中心对称
(1)是针对两个图形而言 的; (2)是指两个图形的 (位 置)关系; (3)对称点在两个图形上
中心对称图形
初中数学课件-中心对称课件北师大版1

解法2:
初中数学课件-中心对称课件北师大版 1(精 品课件 )
C
O B′
A′
B A
C′
初中数学课件-中心对称课件北师大版 1(精 品课件 )
2.已知A,B,O三点不共线,AA'关于O对称,BB'关于O 对称,那么线段AB与A'B'的关系是_相__等__且__平__行___.
初中数学课件-中心对称课件北师大版 1(精 品课件 )
初中数学课件-中心对称课件北师大版 1(精 品课件 )
三、中心对称的作图
问题1. 已知A点和O点,画出点A关于点O的对称点A'.
初中数学课件-中心对称课件北师大版 1(精 品课件 )
(1) ×
(2) √
(3) √
初中数学课件-中心对称课件北师大版 1(精 品课件 )
2.等边三角形是中心对称图形吗? 不是
O
初中数学课件-中心对称课件北师大版 1(精 品课件 )
初中数学课件-中心对称课件北师大版 1(精 品课件 )
3.如图是一块平行四边形草地,要在上面修建一条小 路,使得草地被小路分成面积相等的两部分,修路的方 法有几种?
初中数学课件-中心对称课件北师大版 1(精 品课件 )
初中数学课件-中心对称课件北师大版 1(精 品课件 )
问题3. 如图,选择点O为对称中心,画出与△ABC 关于点O对称的△A′B′C′.
C
A
B′
O
B
A′
C′
只需做出三个关键点A,B,C的对称点,顺次连接即可.
初中数学课件-中心对称课件北师大版 1(精 品课件 )
A
O
A'
(1)连接AO, (2)延长AO至A',使OA'=OA,
中心对称-课件1北师大版八年级

k
中心对称
观察发现1
中心对称的概念
想一想 中心对称与轴对称的联系与区别
A
C1
B1
B
轴对称
O
C
A1
中心对称
1 有一条对称轴——直线 有一个对称中心——点
2 图形沿轴对折(翻转180°) 图形绕中心旋转180°
3 翻转后和另一个图形重合 旋转后和另一个图形重合
中心对称的性质
A
O
B C
C1 B1
A1
注意: 等边三角形不是中心对称图形! 是轴对称图形! 是中心对称图形
A
D
O
B
C
作图
(2)如图,选择点O为对称中心,画出与 △ABC关于点O对称的△A′B′C′.
分析:确定一个三角形需要几个点?作一个三角形关于某 点成中心对称的三角形,需要作几个点的对称点呢?
画法:1. 连接AO并延长到A′,使 B’ OA ′=OA,得到点A的对称点A′.
A’
2. 同样画B、C的对称点 B′、C′.
A
C1
B1
O
B
C
A1
(1)关于中心对称的两个图形是全等形;
(2)关于中心对称的两个图形,对称点所连 线段都经过对称中心,而且被对称中心平分.
作图
(1)如图,选择点O为对称中心,画出点A关 于点O的对称点A′;
A
O
A′
画法:连接AO并延长到A′,使OA′=OA,得 到点A的对称点A′.
点A′即为所求的点.
菱形
2条
对角线交点
正方形
4条
对角线交点
等腰梯形
1条
无
填空题:
巩固练习
1.下列图形中既是轴对称图形又是中心对称图
中心对称
观察发现1
中心对称的概念
想一想 中心对称与轴对称的联系与区别
A
C1
B1
B
轴对称
O
C
A1
中心对称
1 有一条对称轴——直线 有一个对称中心——点
2 图形沿轴对折(翻转180°) 图形绕中心旋转180°
3 翻转后和另一个图形重合 旋转后和另一个图形重合
中心对称的性质
A
O
B C
C1 B1
A1
注意: 等边三角形不是中心对称图形! 是轴对称图形! 是中心对称图形
A
D
O
B
C
作图
(2)如图,选择点O为对称中心,画出与 △ABC关于点O对称的△A′B′C′.
分析:确定一个三角形需要几个点?作一个三角形关于某 点成中心对称的三角形,需要作几个点的对称点呢?
画法:1. 连接AO并延长到A′,使 B’ OA ′=OA,得到点A的对称点A′.
A’
2. 同样画B、C的对称点 B′、C′.
A
C1
B1
O
B
C
A1
(1)关于中心对称的两个图形是全等形;
(2)关于中心对称的两个图形,对称点所连 线段都经过对称中心,而且被对称中心平分.
作图
(1)如图,选择点O为对称中心,画出点A关 于点O的对称点A′;
A
O
A′
画法:连接AO并延长到A′,使OA′=OA,得 到点A的对称点A′.
点A′即为所求的点.
菱形
2条
对角线交点
正方形
4条
对角线交点
等腰梯形
1条
无
填空题:
巩固练习
1.下列图形中既是轴对称图形又是中心对称图
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
菱形
2条
对角线交点
正方形
4条
对角线交点
等腰梯形
1条
无
填空题:
巩固练习
1.下列图形中既是轴对称图形又是中心对称图
形的是 ③ .
①角 ②正三角形 ③线段 ④ 平行四边形
2.下列多边形中,是中心对称图形而不是轴 对称图形的是 ① . ① 平行四边形 ② 矩形 ③ 菱形 ④ 正方形 3.下列多边形中,是轴对称图形而不是中心对 称图形的是 ④ . ① 平行四边形 ② 矩形 ③ 菱形 ④ 等腰梯形
k
中心对称
观察发现1
中心对称的概念
想一想 中心对称与轴对称的联系与区别
A
C1
B1
Bห้องสมุดไป่ตู้
轴对称
O
C
A1
中心对称
1 有一条对称轴——直线 有一个对称中心——点
2 图形沿轴对折(翻转180°) 图形绕中心旋转180°
3 翻转后和另一个图形重合 旋转后和另一个图形重合
中心对称的性质
A
O
B C
C1 B1
A1
B
(5)
至少旋转多少度与自身重合?
中心对称图形的概念
想一想 中心对称与中心对称图形的联系与区别
区别:
中心对称指两个全等图形的相互位置关系, 中心对称图形指一个图形本身成中心对称.
联系:
如果将中心对称图形的两个图形看成一个整 体,则它们是中心对称图形.
如果将中心对称图形对称的部分看成两个图 形,则它们成中心对称.
作图
(2)如图,选择点O为对称中心,画出与 △ABC关于点O对称的△A′B′C′.
分析:确定一个三角形需要几个点?作一个三角形关于某 点成中心对称的三角形,需要作几个点的对称点呢?
画法:1. 连接AO并延长到A′,使 B' OA ′=OA,得到点A的对称点 A′.
A'
2. 同样画B、C的对称点 B′、C′.
想一想
我们平时见过的几何图形中,有哪些是 中心对称图形?并指出对称中心.
怎样的多边形是中心对称图形?
偶数边的 正多边形
常见的轴对称图形与中心对称图形
对
图
称
形
性
轴对称图形
图形
对称轴条数
中心对称图形
图形
对称中心
线段
2条
中点
角
1条
无
等腰三角形
1条
无
等边三角形
3条
无
平行四边形
无
对角线交点
矩形
2条
对角线交点
A
C1
B1
O
B
C
A1
(1)关于中心对称的两个图形是全等形;
(2)关于中心对称的两个图形,对称点所连 线段都经过对称中心,而且被对称中心平分.
作图
(1)如图,选择点O为对称中心,画出点A关 于点O的对称点A′;
A
O
A′
画法:连接AO并延长到 A′,使OA′=OA,得 到点A的对称点 A′.
点A′即为所求的点.
注意: 等边三角形不是中心对称图形! 是轴对称图形
O
注意:
平行四边形不是轴对称图形! 是中心对称图形
A
D
O
B
C
3. 顺次连接A′、B′、C′各点.
C'
△A′B′C′即为所求的三角形.
举例
巩固练习
画一个与已知四边形ABCD成中心对称的图形. (1)以顶点A为对称中心; (2)以BC边的中点为对称中心.
N
F
B
A G
E
C
. B
M
O
A
C
D
D
观察发现2
下列图形旋转多少度与自身重合?
(1) (2)
(3)
(4)
A
O
