余角与补角(教案)
21余角与补角教案
教学目标:
1.掌握余角和补角的概念及性质,并能运用它们解决一些简单的实际问题。
2.掌握对顶角的定义与性质的应用
教学重点、难点:
余角与补角的性质,对顶角的定义与性质 教学过程:
2 1
一.复习、引入
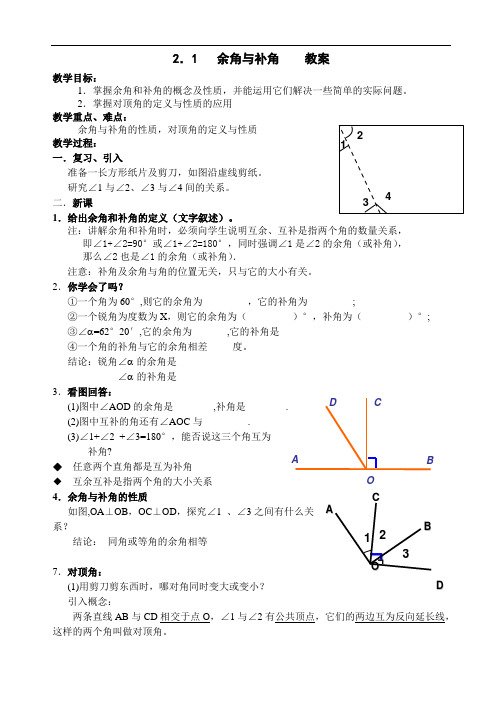
准备一长方形纸片及剪刀,如图沿虚线剪纸。
研究∠1 与∠2、∠3 与∠4 间的关系。 二.新课
结论:锐角∠ 的余角是__________
∠ 的补角是__________
3.看图回答: (1)图中∠AOD 的余角是________,补角是________.
D
C
(2)图中互补的角还有∠AOC 与_________.
(3)∠1+∠2 +∠3=180°,能否说这三个角互为
补角?
◆ 任意两个直角都是互为补角
①一个角为 60°,则它的余角为_________,它的补角为_________;
②一个锐角为度数为 X,则它的余角为(_________)°,补角为(_________)°;
③∠=62°20′,它的余角为_______,它的补角是_____________
④一个角的补角与它的余角相差_____度。
性质
同角或等角的余角相等
同角或等角的补角相等
ห้องสมุดไป่ตู้
2.对顶角定义及其性质
四.作业: 1、课本 62 页 问题解决 1 2、《学考精练》第 29~30 页。 五、教学后记:
34
1.给出余角和补角的定义(文字叙述)。 注:讲解余角和补角时,必须向学生说明互余、互补是指两个角的数量关系, 即∠1+∠2=90°或∠1+∠2=180°,同时强调∠1 是∠2 的余角(或补角), 那么∠2 也是∠1 的余角(或补角).
数学教案-余角和补角

数学教案-余角和补角一、教学目标1.了解并掌握余角和补角的概念;2.能够应用余角和补角的性质解决实际问题;3.发展学生的逻辑思维和分析问题的能力。
二、教学重点1.余角和补角的定义;2.通过余角和补角的性质解决问题。
三、教学内容1. 余角的定义和性质余角是指两个角的角度之和为90度的关系。
对于一个角A,它的余角是指与角A的度数之和为90度的另一个角。
余角的度数等于90减去角A的度数。
2. 补角的定义和性质补角是指两个角的角度之和为180度的关系。
对于一个角A,它的补角是指与角A的度数之和为180度的另一个角。
补角的度数等于180减去角A的度数。
3. 应用余角和补角解决问题通过理解和掌握余角和补角的性质,我们可以应用它们来解决一些实际问题。
例如,如果知道一个角的度数,就可以求出它的余角和补角的度数。
又或者,通过已知两个角互为余角或补角的关系,可以求出它们的度数。
四、教学步骤第一步:引入介绍余角和补角的概念,引导学生思考两个角度数之和为90度和180度的关系。
第二步:讲解余角和补角的定义详细讲解余角和补角的定义,示范通过已知一个角度数求其余角和补角的过程,让学生理解概念。
第三步:探究余角和补角的性质让学生自己观察、探索余角和补角的性质,比如余角的度数等于90减去原角的度数,补角的度数等于180减去原角的度数。
第四步:练习提供一些练习题,让学生通过计算求解角的余角和补角,并检查答案。
第五步:应用解决问题给出一些实际问题,要求学生应用余角和补角的概念和性质来解决,培养学生的应用能力和分析问题的能力。
第六步:总结与评价对本节课的内容进行总结,检查学生对余角和补角的掌握情况,并评价学生的学习效果。
五、教学评估通过课堂上的练习和实际问题的解决,评估学生对余角和补角的理解和应用能力。
六、拓展教学对于学习较快的学生,可以引导他们进一步探究余角和补角的性质以及求解更复杂的问题。
同时,可以引导学生应用余角和补角的概念解决其他几何问题。
余角和补角教学设计3篇

余角和补角教学设计3篇余角和补角教学设计3篇作为一名优秀的教育工作者,常常需要准备教学设计,借助教学设计可以提高教学效率和教学质量。
我们该怎么去写教学设计呢?下面是小编收集整理的余角和补角教学设计,供大家参考借鉴,希望可以帮助到有需要的朋友。
余角和补角教学设计1教学目标1、知识目标:结合具体图形认识一个角的余角和补角,掌握余角和补角的性质2、能力目标:通过观察、猜想、推理、归纳、交流等活动,发展学生空间观念,提高学生的抽象概括能力,培养学生简单的逻辑推理能力和知识运用能力。
3、情感目标:体会观察、归纳、推理对数学知识获取的重要作用,并通过看一看,想一想,猜一猜,说一说,画一画等活动发挥学生的主动作用。
重点、难点、关键1、重点:认识角的互余、互补关系及其性质。
2、难点:通过简单的推理,归纳出余角、补角的性质。
3、关键:了解推理的意义和推理过程,是掌握性质的关键。
数学准备量角器、三角板、多媒体设备。
教学过程一、设情引入(1)(2)提问:怎样把角铁(1)变成角架(2)?教师展开模型角架(2),学生观察发现:要把角铁(1)变成角架(2),需在角架(1)上截出一个缺口。
如果要把角铁(1)弯成120°的角,你知道截去的缺口是多少度吗?要求截去的缺口是多少度,实质上是求什么呢?通过今天的学习,你将会解决这些问题。
二、探究新知 1、余角和补角的概念猜一猜,量一量,图中哪两个角的和是多少?1(答:∠1+∠2=90°,∠4+∠5=90°)象这样,如果两个角的和等于90°,那么这两个角就称为互为余角,其中一个角就叫做另一个角的余角。
类似地,如下图,∠α+∠β=180°。
象这样,如果两个角的和等于180°,那么这两个就叫做互为补角,其中一个角就叫做另一个角的补角。
想一想:(1)锐角的余角是什么角?锐角的补角是什么角?直角和余角吗?钝角呢?(2)如果∠1+∠2+∠3=90°,那么∠1、∠2、∠3互余,对吗?如果∠3+∠4=180°,那么∠3与∠4互余吗?(3)说说图中哪两个角互为余角?哪两个角互为补角(多媒体出示)2、余角和补角的性质思考:(1)如果∠1与∠2互余,∠2与∠3互余,那么∠1与∠3有什么关系?由此你可得到什么结论?(2)如果∠1与∠2互余,∠3与∠4互余,且∠1=∠3,那么∠2与∠4有什么关系?由此你可得到什么结论?学生分组讨论、交流,然后共同归纳出:由(1)可得:同角的余角相等;由(2)可得:等角的余角相等。
余角和补角的教案

余角和补角的教案教案:余角和补角一、教学内容本节课的教学内容来自小学数学教材第七章《几何图形》的第三节,主要讲述余角和补角的概念及计算方法。
教材通过具体的图形和实例,引导学生理解余角和补角的含义,学会如何找出两个角的余角和补角,并能够运用到实际问题中。
二、教学目标1. 学生能够理解余角和补角的概念,掌握它们的计算方法。
2. 学生能够通过观察和操作,找出两个角的余角和补角。
3. 学生能够运用余角和补角的知识解决实际问题。
三、教学难点与重点重点:余角和补角的概念及计算方法。
难点:如何找出两个角的余角和补角,以及如何运用到实际问题中。
四、教具与学具准备教具:黑板、粉笔、直尺、量角器。
学具:练习本、铅笔、橡皮。
五、教学过程1. 情景引入:老师:同学们,你们知道什么是余角和补角吗?今天我们就来学习这个知识点。
2. 知识讲解:老师:我们来看一下余角和补角的定义。
余角是指两个角的和等于90度的两个角,而补角是指两个角的和等于180度的两个角。
3. 例题讲解:老师:现在我们来做一些练习题。
题目一是找出两个角的余角和补角。
题目二是运用余角和补角的知识解决实际问题。
4. 随堂练习:学生们独立完成练习题,老师巡回指导。
老师:通过本节课的学习,我们知道了什么是余角和补角,以及如何计算它们的度数。
希望大家能够运用这个知识解决实际问题,并在日常生活中运用到。
六、板书设计余角:两个角的和等于90度补角:两个角的和等于180度七、作业设计1. 题目一:找出两个角的余角和补角。
答案:角A的余角是60度,补角是150度。
2. 题目二:运用余角和补角的知识解决实际问题。
答案:如果一个角是45度,那么它的余角是45度,补角是135度。
八、课后反思及拓展延伸老师:通过本节课的教学,我发现学生们对余角和补角的概念掌握得比较好,但在解决实际问题时,有些学生还是有些困难。
在今后的教学中,我将继续通过实例和练习题,帮助学生们更好地理解和运用余角和补角的知识。
余角和补角的教案

余角和补角的教案一、教学内容本节课选自《初中数学》七年级下册第四章《角的性质与分类》,具体内容为4.3节“余角和补角”。
通过本章学习,学生已经掌握了角的分类和性质,本节将在此基础上,引导学生深入理解余角和补角的概念,并能运用其解决实际问题。
二、教学目标1. 知识与技能:学生能够理解并掌握余角和补角的概念,能够准确找出余角和补角,并运用其进行计算。
2. 过程与方法:培养学生运用数学知识解决实际问题的能力,提高学生的逻辑思维能力和空间想象能力。
3. 情感态度与价值观:激发学生学习数学的兴趣,培养学生的团队协作意识和探究精神。
三、教学难点与重点重点:余角和补角的概念及其运用。
难点:找出角的余角和补角,并能熟练进行计算。
四、教具与学具准备三角板、量角器、直尺、圆规等。
五、教学过程1. 实践情景引入教师展示一组图片(如剪刀、钟表等),引导学生观察并找出其中的角,为新课的学习做好铺垫。
2. 新课导入(1)教师引导学生复习角的性质和分类。
(2)教师提出问题:“如果两个角的和等于90度,那么这两个角有什么关系?”引导学生思考。
(3)教师给出余角的概念,并引导学生找出角的余角。
(4)教师通过例题讲解,让学生掌握找出余角的方法。
3. 例题讲解(1)找出下列角的余角:① 30°② 45°③ 60°(2)如果一个角的余角比这个角小30度,求这个角的度数。
4. 随堂练习(1)找出下列角的余角:① 20°② 35°③ 55°(2)已知一个角的度数,求它的余角。
5. 补角的引入(1)教师提出问题:“如果两个角的和等于180度,那么这两个角有什么关系?”引导学生思考。
(2)教师给出补角的概念,并引导学生找出角的补角。
6. 例题讲解(1)找出下列角的补角:① 90°② 60°③ 120°(2)已知一个角的补角,求这个角的度数。
7. 随堂练习(1)找出下列角的补角:① 30°② 45°③ 75°(2)已知一个角的度数,求它的补角。
余角与补角教案

余角与补角教案教案标题:余角与补角教案教学目标:1. 理解余角和补角的概念;2. 掌握计算余角和补角的方法;3. 能够应用余角和补角的概念解决几何问题。
教学准备:1. 教师准备:教材《数学》教科书、黑板、白板、彩色粉笔、投影仪等;2. 学生准备:学生书、笔、纸等。
教学过程:步骤一:导入(5分钟)1. 引入余角和补角的概念:请学生回顾角的定义,并提问:什么是余角?什么是补角?2. 学生回答后,教师进行解释和概念的明确化,确保学生对余角和补角的概念有基本的理解。
步骤二:概念讲解(15分钟)1. 教师通过示意图和实例,详细解释余角和补角的概念,强调它们与原角之间的关系;2. 教师提供多个例题,引导学生观察并总结计算余角和补角的方法;3. 学生积极参与讨论,教师及时纠正和引导。
步骤三:练习与巩固(20分钟)1. 学生个别或小组完成教材上的练习题,巩固计算余角和补角的方法;2. 教师巡回指导,解答学生遇到的问题,并对学生的答案进行评价。
步骤四:拓展应用(15分钟)1. 教师设计一些与实际生活或几何问题相关的练习题,要求学生运用余角和补角的概念解答;2. 学生个别或小组完成拓展应用题,教师鼓励学生思考和讨论,提供必要的提示。
步骤五:归纳总结(5分钟)1. 教师引导学生总结本节课所学的内容,强调余角和补角的重要性;2. 学生回答问题,教师进行总结和补充。
步骤六:作业布置(5分钟)1. 教师布置适量的作业,要求学生巩固和拓展所学内容;2. 强调作业的重要性和批改的及时性。
教学反思:本节课通过引入概念、讲解、练习和应用等环节,使学生逐步理解和掌握余角和补角的概念和计算方法。
通过拓展应用,培养学生运用所学知识解决实际问题的能力。
同时,注重学生的参与和思考,提高课堂的互动性和学生的学习兴趣。
在教学过程中,教师要注意及时纠正学生的错误,鼓励学生提问和讨论,激发他们的学习动力。
余角和补角教案

余角和补角教案一、教学目标1.了解余角和补角的概念及性质;2.掌握求解余角和补角的方法;3.能够应用余角和补角解决相关问题。
二、教学重点1.掌握余角和补角的定义和性质;2.能够灵活运用余角和补角求解问题。
三、教学内容1. 余角和补角的定义余角和补角是与一个角相加等于90度的两个角。
当两个角的和为90度时,它们互为余角;当两个角的和为180度时,它们互为补角。
2. 余角和补角的性质•余角和补角的和等于90度或180度;•余角和补角互为对立角;•余角和补角具有交换律和结合律。
3. 求解余角和补角的方法求解余角:给定角A,它的余角记作A’,则有A + A’ = 90度。
求解补角:给定角A,它的补角记作A’‘,则有A + A’’ = 180度。
4. 余角和补角的应用余角和补角在几何图形的计算中有广泛的应用,特别是在计算角的大小和角的性质时。
四、教学步骤Step 1:引入知识(5分钟)通过举例介绍余角和补角的概念,引出余角和补角的定义和性质。
Step 2:讲解求解余角和补角的方法(10分钟)详细讲解如何求解余角和补角,并通过示例演示,让学生掌握求解的具体步骤。
Step 3:练习与讨论(15分钟)给学生提供一些练习题,让他们通过求解余角和补角的方法解答,并进行讨论,加深对概念和性质的理解。
Step 4:拓展应用(15分钟)引导学生通过余角和补角的概念和性质,应用于解决几何图形相关问题,并帮助学生理解角的特性和计算方法。
Step 5:归纳总结(5分钟)对余角和补角的定义、性质和求解方法进行归纳总结,让学生更好地理解和记忆。
五、教学资源准备1.教学课件;2.打印的练习题。
六、教学评估方式1.针对练习题进行课堂讨论和答疑;2.布置相关作业,检查学生对余角和补角的理解和应用。
七、教学延伸1.深入学习角的性质和计算方法,探究其他角的概念;2.继续进行相关的几何图形计算和问题求解。
通过本节课的学习,学生能够准确理解和应用余角和补角的概念,掌握求解的具体方法,并能够应用余角和补角解决相关问题。
余角和补角教案

余角和补角教案余角和补角教案余角和补角教案1教学目标:1、知识与技能:⑴、在具体的现实情境中,认识一个角的余角和补角,掌握余角和补角的性质。
⑵、了解方位角,能确定具体物体的方位。
2、过程与方法:进一步提高学生的抽象概括能力,发展空间观念和知识运用能力,学会简单的逻辑推理,并能对问题的结论进行合理的猜想。
3、情感态度与价值观:体会观察、归纳、推理对数学知识中获取数学猜想和论证的重要作用,初步数学中推理的严谨性和结论的确定性,能在独立思考和小组交流中获益。
重、难点及关键:1、重点:认识角的互余、互补关系及其性质,确定方位是本节课的重点。
2、难点:通过简单的推理,归纳出余角、补角的性质,并能用规范的语言描述性质是难点。
3、关键:了解推理的意义和推理过程是掌握性质的关键。
教学过程:一、引入新课:让学生观察意大利著名建筑比萨斜塔。
比萨斜塔建于1173年,工程曾间断了两次很长的时间,历经约二百年才完工。
设计为垂直建造,但是在工程开始后不久便由于地基不均匀和土层松软而倾斜。
二、新课讲解:1、探究互为余角的定义:如果两个角的和是90(直角),那么这两个角叫做互为余角,其中一个角是另一个角的余角。
即:1是2的余角或2是1的余角。
2、练习⑴:图中给出的各角,那些互为余角?3、探究互为补角的定义:如果两个角的和是180(平角),那么这两个角叫做互为补角,其中一个角是另一个角的补角。
即:3是4的补角或4是3的补角。
4、练习⑵:(1)图中给出的各角,那些互为补角?(2)填下列表:a的余角 a的补角53245776223x结论:同一个锐角的补角比它的余角大90。
(3)填空:①70的余角是,补角是。
②a(90)的它的余角是,它的补角是。
重要提醒:ⅰ(如何表示一个角的余角和补角)锐角a的余角是(90a )a的补角是(180a )ⅱ互余和互补是两个角的数量关系,与它们的位置无关。
5、讲解例题:例1:若一个角的补角等于它的余角4倍,求这个角的度数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
答:
A
余角与补角(教案)
1、教学目标
知识与技能:经历观察,操作,推理,交流等过程,进一步发展空间观念,推理能力和有条理的表达能力。
过程与方法:在具体的情景中了解余角、补角和对顶角及其性质,并能运用这些性质解决一些生活中的实际问题。
情感、态度与价值观:通过学生喜欢的台球运动,抽象到角的有关的几何图形,在愉悦的情景中,领悟数学与现实生活的紧密联系,培养学以致用的价值趋向。
2、教学重难点
重点:余角、补角、对顶角的性质及应用。
难点:余角、补角的性质。
3、教具:三角板,直尺,黄鳝夹子
4、课时设计:共一课时,第一课时
5、教学过程
情景再现:角的定义,两种。
讲解台球运动,过度到直角。
再到今天的新课。
作直角ABC,射线BD分∠ABC
则∠ABD+∠DBC=900
在数学中.“如果两个角的和是直角,那么称这两个角互为余角”
作平角MNP,射线NQ分∠MNP
则∠MNQ+∠QNP=1800
在数学中.“如果两个角的和是平角,那么称这两个角互为补角”
★注:余角,补角的定义中,只说了度量数量的关系,没有说位子上的要求.
如图:ON⊥DE, ∠AON=∠NOB
想一想
(1),那些角互为余角, 那些角互为补角.
(2), ∠AOD和∠BOE有什么关系?为什么?
(3), ∠AOE和∠BOD有什么关系?为什么?
学生分组学习.
老师和同学一起得出结果.
同角或等角的余角相等, 同角或等角的补角相等.
展示教具, 黄鳝夹子
老师操作角的大小,学生观察.然后给出对顶角的定义.
一个角的反向延长线所组成的角与其本身称为对顶角.
证明对顶角相等.有学生证明.
因为∠AOD+∠AOC=1800,∠COB+∠AOC=1800
所以∠AOD =∠COB
6,巩固练习
请同学们找出图中那些角互余,那些角互补,那些角是对顶角.
7,作业习题2.1 1.3题问题解决1.2题. 2.3.4排的同学加黑板上的补充题8板书设计.
9课后反思:
(1)学生回答不规范,老师应规范哈语言
(2)引入要连贯
(3)多强调,余角补角的互为性,应成对出现。
B自我评析:本堂课从效果上面看还是成功的,教学目标也达到了。
但还是有写地方不足,时间没有把握好。
学生分组学习的时间给长了,但是没有办法,有大部分的学生的基础很差。
要照顾哈。
另外就是在老师没有强调余角补角只要满足度量数量关系,不要求位置关系前只有一个学生想到了。
从这点看,本班的学生的思维不够活跃。
