第五版传热学课件第五章
合集下载
传热学—第五章
4-6 对流换热准则关系式的实验获取方法由于对流换热问题的复杂性，实验研究是解决换热问题的主要方法。
在工程上大量使用的对流换热准则关系式都是通过实验获得的。
这里对实验研究的方法做一个简单的介绍。
我们从无量纲微分方程组推出了一般化的准则关系式()Pr Re,θf Nu x '=。
但这是一个原则性的式子，要得到某种类型的对流换热问题在给定范围内的具体的准则关系式，在多数情况下还必须通过实验的办法来确定。
如何去进行实验?如何测量实验数据?以及如何整理实验数据而得出准则关系式？这里用流体流过平板的换热问题为例进行简单的讨论。
图4－12给出了平板在风洞中进行换热实验的示意图。
相关的物理量标识在图中。
为了得出该换热问题的准则关系式，必须测量的物理量有：流体来流速度u ∞,来流温度t ∞,平板表面温度t w ,平板的长度L 和宽度B ，以及平板的加热量Q （通过测量电加热器的电流I 和电压V 而得出）。
当我们获得这些物理量之后就能够热平衡关系式求出对流换热系数，即由()LBt t V I Qw ∞-=⋅=α得到()[]LB t t IVw ∞-=α。
由于我们是在寻找准则关系式，必须在不同的工况下获得不同的换热系数值。
所以在某一实验工况下测量上述物理量，并计算出换热系数与该工况对应，然后改变工况又得出对应的另一个换热系数值。
如此进行N 次，就可以得到一组对应数据如下：Nu u u u N ∞∞∞∞⇔⇔⇔⇔αααα321321 将它们无量纲化可以得出νλανλανανλαL u L NuL u L Nu L u L Nu L u L Nu N NN N∞∞∞∞=⇔==⇔==⇔==⇔=ReRe Re Re 321333222111。
如果认为准则关系式有mnmc c Nu Re PrRe 1==这样的形式。
这是一种先验的处理办法，但是，这给拟合准则关系式带来较大的方便。
对此式两边取对数有，Re 1g m gc gNu +=，从而使关系式变为线性关系式，如mx a y +=的形式。
传热学-第五章3-4-PPT
温度：
t 数量级为 1
边界层厚度：δ数量级Δ
18
X方向壁面特征长度：l 数量级为1
二维对流换热，其微 分方程组已导出：
u v 0 x y
（u
u x
v
u y
)
Fx
p x
( 2u
x 2
2u y 2
)
（u
v x
v
v ) y
Fy
p y
(
2v x 2
2v y 2
)
c p u
t x
v
t y
2t x 2
u
t x
v
t y
a
2t y 2
应的定解条件，则 可以求解
dp dx
u
du dx
若 du 0，则 dp 0
dx
dx
23
例如：对于主流场均速 u 、均温 t ，并给定恒定
壁温的情况下的流体纵掠平板换热，即边界条件为
y 0 u 0, v 0, t tw
y u u, t t
求解上述方程组(层流边界层对流换热微分方程组) 可得局部表面传热系数 hx 的表达式
t与 相似，随着 x 增加而增厚,它反映了流
体热量传递的渗透深度。
流动边界层与热边界层的状况决定了热量传 递过程和边界层内的温度分布
10
层流：温度呈抛物线分布
湍流：温度呈幂函数分布 湍流边界层贴壁处的温度梯度明显大于层流
T y
w,t
T y
w, L
故：湍流换热比层流换热强！
11
与 t 的关系：分别反映流体分子和流体微
a
Pr
——普朗特数，反映流体物性对换热 的影响
式中ν 、a 的单位都是 m2 / s，故Pr数是无因次数。
传热学第五版课件完整版_图文
接触热阻的定义：
接触热阻的影响因素： 粗糙度
挤压压力 硬度匹配情形 空隙中介质的性质
减小接触热阻的措施： 表面尽量平整 增加挤压压力
两表面一软一硬 涂导热姆
第七节 二维稳态导热
应用领域：房间墙角，地下埋管，矩形保温层，短肋片
二维稳态导热微分方程： 二维稳态导热问题的研究手段：
解析法 数值法 形状因子法
第i层与第i+1层之间接触面的温度：
二、第三类边界条件
常物性时导热微分方程组如下：
根据第一类边界条件时的结果: （此时壁温tw1和tw2为未知） 与以上两个边界条件共三式变形后 相加,可消去tw1和tw2，得：
单层平壁的热流密度：
多层平壁的热流密度：
第二节 通过复合平壁的导热
应用领域：空心砖，空斗墙
并解出其通解为 ：
代入边界条件求出c1和c2，并代入通解，得出特解 ：
等截面直肋的温度分布：
肋端过余温度：
肋片散热量：
当考虑肋端散热时，计算肋片散热量时可采用假想肋高 代替实际肋高 l
一维温度场假定的检验 ：
请同学们思考一个问题:
肋高越大，肋的散热面积越大，因而采用 增加肋高的方法可以增加肋的散热量。这 种方法在实际换热器设计中是否可行？若 可行，是否会有某些局限性？
一、等截面直肋的导热
一维简化的假设条件： 肋片的高度l远大于肋片的厚度δ， 因而厚度方向温差很小，
负内热源的处理方法—— 将y方向的对流散热量 等效转化为负内热源
断面周长： 断面面积：
进行负内热源处理后等截面直肋导热微分方程组如下：
（假定肋端绝热）
定义 ：
令
—— 过余温度
：
使导热微分方程齐次化 ：
接触热阻的影响因素： 粗糙度
挤压压力 硬度匹配情形 空隙中介质的性质
减小接触热阻的措施： 表面尽量平整 增加挤压压力
两表面一软一硬 涂导热姆
第七节 二维稳态导热
应用领域：房间墙角，地下埋管，矩形保温层，短肋片
二维稳态导热微分方程： 二维稳态导热问题的研究手段：
解析法 数值法 形状因子法
第i层与第i+1层之间接触面的温度：
二、第三类边界条件
常物性时导热微分方程组如下：
根据第一类边界条件时的结果: （此时壁温tw1和tw2为未知） 与以上两个边界条件共三式变形后 相加,可消去tw1和tw2，得：
单层平壁的热流密度：
多层平壁的热流密度：
第二节 通过复合平壁的导热
应用领域：空心砖，空斗墙
并解出其通解为 ：
代入边界条件求出c1和c2，并代入通解，得出特解 ：
等截面直肋的温度分布：
肋端过余温度：
肋片散热量：
当考虑肋端散热时，计算肋片散热量时可采用假想肋高 代替实际肋高 l
一维温度场假定的检验 ：
请同学们思考一个问题:
肋高越大，肋的散热面积越大，因而采用 增加肋高的方法可以增加肋的散热量。这 种方法在实际换热器设计中是否可行？若 可行，是否会有某些局限性？
一、等截面直肋的导热
一维简化的假设条件： 肋片的高度l远大于肋片的厚度δ， 因而厚度方向温差很小，
负内热源的处理方法—— 将y方向的对流散热量 等效转化为负内热源
断面周长： 断面面积：
进行负内热源处理后等截面直肋导热微分方程组如下：
（假定肋端绝热）
定义 ：
令
—— 过余温度
：
使导热微分方程齐次化 ：
传热学课件第5章
传热学C Heat Transfer
第五章 对流换热原理
传热学C Heat Transfer
§5-1 对流换热概述
一、对流换热的定义和机理
对流换热：流体流过固体壁面时所发生的热 量传递过程。
机理：既有热对流，也有导热，不是基本的热量传 热方式。
传热学C Heat Transfer
二、牛顿冷却公式
hx— 壁面x处局 系部 W 数 （ m 表 2C ) 面
由以上得：
hx
tw
t
t y
y0,x
它揭示了对流换热问题的 本质
传热学C Heat Transfer
五、局部对流换热系数与边界层的关系
传热学C Heat Transfer
平均对流传热系数：
h 1 At
AhxtxdAx
对于长度为 l 的平板：
1. 定义：当流体流过固体壁面时, 由于流体粘性的作用,使得在固 体壁面附近存在速度发生剧烈 变化的薄层称为流动边界层或 速度边界层。
2. 速度边界层厚度d 的规定：速度等于99%主流 速度。
传热学C Heat Transfer
3. 特点：通常情况下，边界层厚度d是比壁面尺度l 小一个数量级以上的小量。 d << l
传热学C Heat Transfer
例如，对于外掠平板的对流换热现象，可以得到雷
诺数Ｒｅ、普朗特数Ｐｒ和努赛尔数Ｎｕ。如果是
两个相似的外掠平板的对流换热现象，则必有：
R'eR"e Pr ' Pr" N'uN"u
根据相似的这种性质，在实验中就只需测量各准 则所包括的量，避免了测量的盲目性，解决了实验 中测量那些量的问题。
Gr gtL3 2
第五章 对流换热原理
传热学C Heat Transfer
§5-1 对流换热概述
一、对流换热的定义和机理
对流换热：流体流过固体壁面时所发生的热 量传递过程。
机理：既有热对流，也有导热，不是基本的热量传 热方式。
传热学C Heat Transfer
二、牛顿冷却公式
hx— 壁面x处局 系部 W 数 （ m 表 2C ) 面
由以上得：
hx
tw
t
t y
y0,x
它揭示了对流换热问题的 本质
传热学C Heat Transfer
五、局部对流换热系数与边界层的关系
传热学C Heat Transfer
平均对流传热系数：
h 1 At
AhxtxdAx
对于长度为 l 的平板：
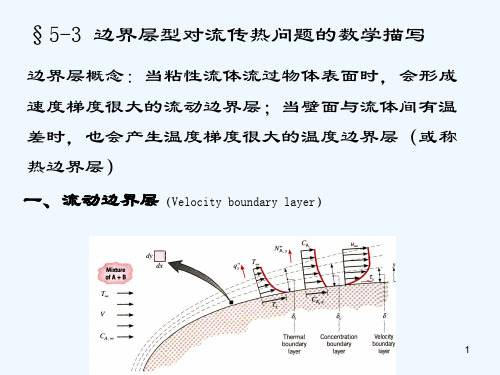
1. 定义：当流体流过固体壁面时, 由于流体粘性的作用,使得在固 体壁面附近存在速度发生剧烈 变化的薄层称为流动边界层或 速度边界层。
2. 速度边界层厚度d 的规定：速度等于99%主流 速度。
传热学C Heat Transfer
3. 特点：通常情况下，边界层厚度d是比壁面尺度l 小一个数量级以上的小量。 d << l
传热学C Heat Transfer
例如，对于外掠平板的对流换热现象，可以得到雷
诺数Ｒｅ、普朗特数Ｐｒ和努赛尔数Ｎｕ。如果是
两个相似的外掠平板的对流换热现象，则必有：
R'eR"e Pr ' Pr" N'uN"u
根据相似的这种性质，在实验中就只需测量各准 则所包括的量，避免了测量的盲目性，解决了实验 中测量那些量的问题。
Gr gtL3 2
传热学第5章
如何确定表面传热系数的大小是对流换热计算的核 心问题，也是本章讨论的主要内容。
2. 对流换热的影响因素
对流换热是流体的导热和对流两种基本传热方式共 同作用的结果，因此，凡是影响流体导热和对流的因 素都将对对流换热产生影响。主要有以下五个方面：
2
(1)流动的起因：影响流体的速度分布与温度分布。 强迫对流换热 自然对流换热
17
5.3 边界层概念
1.速度边界层（流 动边界层） 速度发生明显变 化的流体薄层。
流动边界层厚度 :
紊流核心
u 0.99u l
流场的划分: 主流区：y> 理想流体 边界层区: 0 y
u y 速度梯度存在于粘性力的作用区。
18
边界层的流态： 层流边界层、过渡区、紊流边界层
单位时间从y方向净进入微元体的质量所携带的能
12
单位时间内微元体热力学能的增加为
dU h 于是根据微元体的能量守恒 d ut vt 2t 2t 可得 2 2 dxdy c p x y dxdy x y t cp dxdy t 2t 2t t t u v cp u v t x2 y 2 x y x y
上面两式建立了对流换热表面传热系数与温度场 之间的关系。而流体的温度场又和速度场密切相关， 所以对流换热的数学模型应该包括描写速度场和温度 场的微分方程。
9
1）连续性微分方程（质量守恒） u v dy 0 x y 2）动量微分方程（动量守恒） 压力差 0 惯性力
y
微元体
dx
x
2u 2u u u u p x方向: u x v y Fx x x 2 y 2 Du p 体积力 粘性力 2 Fx u d x 2v 2v v v v p v 2 2 y方向: u Fy x y y x y
传热学课件第五章辐射换热理论
E E d
0
d
在相同的温度下以黑体的辐射力最大 ,
用Eb表示,则实际物体的辐射力E为
E = ε Eb
式中：ε 为物体的发射率（或黑度）；
Eb为同温度下黑体的辐射力,W/m2。
二 、有效辐射 物体表面除了因本身的温度特性向外 界发出本身辐射外 ,其它物体投射到物体表 面上的投射辐射还有部分被反射。本身辐 射和反射辐射之和称为有效辐射,记为J,单 位为w/m2,即 J = E + ρ G 式中,E称为发射辐射或本身 辐射,ρ G为反射辐射,G称为该 表面接受到的投入辐射。 有效辐射在辐射换热的分析和计算中 非常重要。
Fb ( 01T ) 0.07025%, Fb ( 02T ) 8.88%
则 F b ( 1T 2T ) Fb ( 0 2T ) Fb ( 0 1T ) 8.88% 0.07025% 8.81%
结果分析:在灯丝发出的辐射能中，可见光只 占8.81％，其余91.19％属于不可见的红外辐射， 并转化为热能，散失到周围环境中，钨丝灯作为光 源其效率是很低的。
进行辐射换热计算时，需要计算物体辐射能 力的大小。对于黑体辐射可从普朗克定律积分得 出 Eb ＝σ bT4 W/m2 式中：σ b为黑体辐射常数，σ b＝5.67×10－8W/ （m2·K4）；T为黑体热力学温度，K。 上式也可 4 写为 T Eb c0 2 W/m 100 式中：c0为黑体辐射系数，c0＝5.67。 上式表明黑体的辐射力与热力学温度的四次 方成正比，故又称为四次方定律。
首页
重点与难点
重点：
1. 热辐射的特点、热辐射表面的性质。 2. 辐射力、黑体、灰体、有效辐射等基本 概念。 3. 热辐射基本定律。 4. 气体辐射的特点。
0
d
在相同的温度下以黑体的辐射力最大 ,
用Eb表示,则实际物体的辐射力E为
E = ε Eb
式中：ε 为物体的发射率（或黑度）；
Eb为同温度下黑体的辐射力,W/m2。
二 、有效辐射 物体表面除了因本身的温度特性向外 界发出本身辐射外 ,其它物体投射到物体表 面上的投射辐射还有部分被反射。本身辐 射和反射辐射之和称为有效辐射,记为J,单 位为w/m2,即 J = E + ρ G 式中,E称为发射辐射或本身 辐射,ρ G为反射辐射,G称为该 表面接受到的投入辐射。 有效辐射在辐射换热的分析和计算中 非常重要。
Fb ( 01T ) 0.07025%, Fb ( 02T ) 8.88%
则 F b ( 1T 2T ) Fb ( 0 2T ) Fb ( 0 1T ) 8.88% 0.07025% 8.81%
结果分析:在灯丝发出的辐射能中，可见光只 占8.81％，其余91.19％属于不可见的红外辐射， 并转化为热能，散失到周围环境中，钨丝灯作为光 源其效率是很低的。
进行辐射换热计算时，需要计算物体辐射能 力的大小。对于黑体辐射可从普朗克定律积分得 出 Eb ＝σ bT4 W/m2 式中：σ b为黑体辐射常数，σ b＝5.67×10－8W/ （m2·K4）；T为黑体热力学温度，K。 上式也可 4 写为 T Eb c0 2 W/m 100 式中：c0为黑体辐射系数，c0＝5.67。 上式表明黑体的辐射力与热力学温度的四次 方成正比，故又称为四次方定律。
首页
重点与难点
重点：
1. 热辐射的特点、热辐射表面的性质。 2. 辐射力、黑体、灰体、有效辐射等基本 概念。 3. 热辐射基本定律。 4. 气体辐射的特点。
传热学第五版课件完整版PPT课件
d 2t qV 0 2 dx
7.物性参数λ 、 ρ 、c均为常数，一维稳态温度场，无内热源：
d 2t 0 2 dx
第四节
通解
导热过程的单值性条件
特解
作用：用来对某一特定的导热过程进行进一步的具体说明
四种单值性条件：
几 何 条 件 时 间 条 件 物 理 条 件 边 界 条 件
δ,l,d……
q z
t z
第二节
导热系数
每种物质的导热系数可通过实验确定 常用物质可查表获取
一 般 规 律
固相>液相>气相 金属>非金属 晶体>无定形态 纯物质>有杂质物质 纯金属>合金
导热系数的主要影响因素：温度、压力
气体的导热系数：
随温度升高而增大（由于分子运动速度和比定容热容增大），
压力对其影响不大（密度增大但自由程减小）
第三节
导热微分方程式
研究目标：确定物体内的温度场
研究基础： 导热微分方程式＝能量守恒定律＋傅立叶定律 研究对象： 右 图 中 的 六 面 微 元 体
根据能量守恒定律： 导入和导出微元体的净热量＋微元体中内热源的发热量 ＝微元体热能（内能）的增加
在一定时间dτ内: 导入微元体的净热量： 导出微元体的净热量：
t t t t c qV x x y y z z
——导热微分方程式
在几种特殊条件下对导热微分方程式的简化：
1.物性参数λ 、 ρ 、c均为常数：
q z dz q z q z dz z
q y
代入上式
再将傅立叶定律代入，得出： 三个方向导入与导出微元体的净热量：
《传热学》第5章_对流传热的理论基础
9
第5章 对流传热的理论基础
在dτ范围内，在x方向上由流体净带出微元体的热量为：
u t H x dx H x c p u t dxdyd x x
同样的道理，在dτ范围内，在y方向上由流体净带出微元体的热量为： t v H y dy H y c p v y t y dxdyd 在单位时间内，由于流体的流动而带出微元体的净热量为：
(3)一般没有第三类边界条件(如果流体通过一层薄壁与另一种流体发生 热交换,则另一种流体的表面传热系数可以作为所求解问题的边界条件)
方程组中包含四个未知数，虽然可以求解,但是由于复杂性和非线性，
导致求解方程组难度很大，两个关键人物：普朗特提出边界层概念、 波尔豪森提出热边界层概念,从而使得 对流传热得到了实质性的发展。
15
第5章 对流传热的理论基础
层流层向湍流层过渡的距离xc由临界雷诺数决定：
Rec u xc / v
范围在2×105到3×106范围之间，一般情况下，取边界雷诺数5×105。 3. 流动边界层内的动量方程 当流体外掠物体流动时,层流边界层内粘性流体的稳态动量方程可写为：
u u 1 dp 2u u v v 2 x y dx y
与二维的Navier-Stokes方程相比，层流边界层的运动微分方程特点是： 1. 在u方程中略去了主流方向的二阶导数项； 2. 略去了关于速度v的动量方程 3. 认为边界层中p / y 0，因而上式中利用dp / dx 代替 p / x
说明：该公式仅适用于边界层类型的流动，且流体不脱离固体表面时
描述：规定达到主流速度的99%处的距离y为流动边界层的厚度,记为δ
方法：数量级分析法
14
第5章 对流传热的理论基础
第5章 对流传热的理论基础
在dτ范围内，在x方向上由流体净带出微元体的热量为：
u t H x dx H x c p u t dxdyd x x
同样的道理，在dτ范围内，在y方向上由流体净带出微元体的热量为： t v H y dy H y c p v y t y dxdyd 在单位时间内，由于流体的流动而带出微元体的净热量为：
(3)一般没有第三类边界条件(如果流体通过一层薄壁与另一种流体发生 热交换,则另一种流体的表面传热系数可以作为所求解问题的边界条件)
方程组中包含四个未知数，虽然可以求解,但是由于复杂性和非线性，
导致求解方程组难度很大，两个关键人物：普朗特提出边界层概念、 波尔豪森提出热边界层概念,从而使得 对流传热得到了实质性的发展。
15
第5章 对流传热的理论基础
层流层向湍流层过渡的距离xc由临界雷诺数决定：
Rec u xc / v
范围在2×105到3×106范围之间，一般情况下，取边界雷诺数5×105。 3. 流动边界层内的动量方程 当流体外掠物体流动时,层流边界层内粘性流体的稳态动量方程可写为：
u u 1 dp 2u u v v 2 x y dx y
与二维的Navier-Stokes方程相比，层流边界层的运动微分方程特点是： 1. 在u方程中略去了主流方向的二阶导数项； 2. 略去了关于速度v的动量方程 3. 认为边界层中p / y 0，因而上式中利用dp / dx 代替 p / x
说明：该公式仅适用于边界层类型的流动，且流体不脱离固体表面时
描述：规定达到主流速度的99%处的距离y为流动边界层的厚度,记为δ
方法：数量级分析法
14
第5章 对流传热的理论基础
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
对流换热情况分类
第二节 对流换热微分方程组
对流换热问题总的求解步骤（二维不可压缩牛顿型流体）
已知条件
动量方程
速度场
能量方程
温度场
过程方程
hx
h
一、对流换热过程微分方程式
推导依据：流体在贴壁处处于无滑移状态，贴壁流体层仅有导热发生
t q x 根据傅立叶导热定律： y w, x
对流换热微分方程组量级分析过程
1.连续方程： u v 0 x y
1 1
2.x方向动量方程：
?
v ~ 0
2u 2u u u p u x v y x x 2 y 2
2.微元体所受的外力：（x,y两方向）
Xdxdy 体积力 Ydxdy
x yx x y dxdy 表面力 y xy dxdy y x
将上式在x,y两个方向代入牛顿第二定律，得到Navier-Stokes方程：
各方向流进和流出微元体的质量流量：
M x udy x方向 M x M x dx M x x dx M y vdx M y y方向 M y dy M y y dy 将以上四式代入质量守恒定律： M x M y M x dx M y dy
u x yx u u x方向： u x v y X x y y xy v v v y方向： u x v y Y y x
对于不可压缩流体：
努谢尔特准则Nu x
准则方程的意义—— 把微分方程所反映的众多因素间的规律用少数几个准则来概括， 从而减少变量个数，以便于进行对流换热问题的分析、实验研究 和数据处理。
第三节 边界层换热微分方程组
研究目的—— 简化对流换热微分方程组
一、流动边界层
1.定义：
Ludwig Prandtl (1875-1953)
距离壁面
u 0.99u
处以内的流体层
2.流动边界层的5个特点：
（1）边界层的厚度较之定型尺寸为极小量 （2）边界层内速度梯度很大
l
u u y x
第一节 对流换热概述
常见对流换热设备： 壳管式 换热器 蒸汽锅炉水循环系统
采暖散热器
冷凝器
连续肋片管束
环肋片管束
影响对流换热的因素
一、流动的起因和流动状态
起因
自然对流 受迫对流 混合对流
层流
流动状态 紊流
二、流体的热物理性质 （比热容、导热系数、密度、黏度、体积膨胀系数等）
比热容和密度大，单位体积流体能携带更多能量 导热系数大，流体内部导热能力强 黏度小，流体流动顺畅
u x p 2 u v x 表面法向应力 表面切向应力 yx xy v y x y p 2 y
将其代入Navier-Stokes方程，并采用连续方程化简，得到：
2u 2u u u u p x方向： u x v y X x x 2 y 2 2v 2v v v v p y方向： u x v y Y y x 2 y 2
惯性力
对稳态流动：
体积力
压强梯度
黏滞力
u v 0
当只有重力场作用时：
X g x
Y g y
四、能量微分方程式
推导依据—— 内能增量＝导热热量＋对流热量
1.导热热量：
t x dy x t y dx y 2t x dx 2 dxdy x方向导入的净热量： x x x x
p dp du u x dx dx
1 1 11 t 1
1 ? 1
1 t2
~0
2 t
小量，可除去
四、外掠平板层流换热边界层微分方程式分析解简述
对外掠平板层流：
u const
压力梯度项：
p dp du u 0 x dx dx
（3）边界层流态分为层流和紊流，紊流边界层紧靠壁处仍是层流，称层流底层
判断流态的准则——临界雷诺数
Re c
u xc
5 105
（4）流场分为主流区和边界层区，主流可忽略黏性，边界层考虑流体黏性
（5）边界层法线方向压力梯度很小，边界层与主流区压力相同
p 0 y
根据伯努利方程：
p dp du u x dx dx
11 1
? 2
1 2
p ~ 0 y
流动边界层第五个特点
所有项全为小量，可将此方程全部除去 4.能量方程：
2t 2t t t c p u v 2 2 x x y y
（量级分析方法的结论）
3.不同流动模型下边界层的描述：
管内受迫流动
受迫横向 外掠圆管
沿热竖壁 自然对流
二、热边界层
1.定义：
距离壁面
t
0.99 f 处以内的流体层
其中：
t tf
2.与流动边界层的关系——取决于黏性系数与热扩散率的相对大小 普朗特准则 Pr
a
三、数量级分析与边界层微分方程
x tu x方向对流入的净热量： x dx c p dxdy x x x y tv y方向对流入的净热量： y y dy c p dxdy y y t 3.内能增量： c dxdy p
数量级分析方法—— 将方程中各量和各项目量级的相对大小进行比较，舍去量级小的 量和项目，从而简化方程，使其可以求解 分析对象——二维稳态受迫层流，且忽略重力作用 分析基础——各基本参数的量级
~ 0 , y ~ 0 , t ~ 0 t ~ 0
u ~ 01, u ~ 01, t ~ 01, t ~ 01, l ~ 01, x ~ 01,
根据傅立叶定律： y方向导入的净热量：
y 2t y y dy 2 dxdy y y
2.对流热量：
由左方进入微元体的焓值：
x c p tudy y c p tvdx
由下方进入微元体的焓值：
根据牛顿冷却定律：
qx hx t w t f x hx t x
对流换热过程方程：
hx
y y , 其中＝t t w t x w, x x w, x
t
二、连续性方程
推导依据——质量守恒定律
第五章 对流换热分析
研究对象——流体与固体壁面之间的传热过程 研究目的——确定牛顿冷却定律 q h t w t f 中的h
局部对流表面传热系数hx
对流表面 传热系数
平均对流表面传热系数 h
Isaac Newton(1642-1727)
h dA
x A
A
确定对流表面传热系数的四种方法 分析法 类比法 数值法 实验法
冷凝器
锅炉
四、换热表面几何因素 （壁面尺寸、粗糙度、形状及与流体的相对位置)
定型尺寸——换热中有决定意义的尺寸，以此特征 尺寸作为分析计算的依据，能准确反映物体形状对 换热的影响
对流表面传热系数h的多参数函数
h f u, t w , t f , , c p , , , , l
外掠平板层流换热边界层微分方程组：
t hx y t x w, x u v 0 x y u u 2u u v x y y 2 t t 2t u v a x y y 2
4个方程,4个未知数(h,u,v,t)， 理论上存在唯一解， 可通过数学方法进行求解
求解结果
hx 0.332 Re1x 2 Pr1 3 局部表面传热系数： x
或可写成：Nux 0.332 Re1x 2 Pr1 3 ——准则方程
其中：
c p ——无量纲物性 普朗特准则 Pr a
t hx 5个方程,5个未知数(h,u,v,t,p)， y t x w, x 理论上存在唯一解 u v x y 0 2u u u p 2u 但由于方程组 u u x v y X x x 2 y 2 过于复杂，实 2v v v v p 2 v 际不可求解， u x v y Y y x 2 y 2 必须进一步进 2t t t t 2t 行简化 c p u v x 2 x y y 2
1 1 11 1
1
1 1 ? 1 2
~02
小பைடு நூலகம்，可除去
3.y方向动量方程：
2v 2v v v p u v 2 2 x x y y y
得出：
u v 0 x y
三、动量微分方程式(N•S方程)
推导依据——牛顿第二定律F＝ma
1.微元体的质量×加速度： dxdy
DU d
DU d
在两个方向的分量分别为：
Du x, y, u u x u y u u u u v d x y x y Dv x, y, v v x v y v v v u v d x y x y