12利用辅助线在基本平面立体表面求点的投影
12利用辅助线在基本平面立体表面求点的投影
12利用辅助线在基本平面立体表面求点的投影平面几何辅助线ps辅助线几何辅助线秘籍街头篮球辅助线ps辅助线快捷键智能辅助线辅助线街头篮球大操场辅助线ai辅助线
3.1 平面立体的投影
教学目的：
1.熟练掌握棱柱、棱锥、棱台等平面立体的投影特点 及画法。能根据它们的两个投影画出第三投影。 2.熟练运用积聚性和辅助线法在基本平面体的表面上 取点，并能判别其可见性。
3.1 平面立体的投影
2.棱锥表面上点的投影 凡属于特殊位置表面上的点，可利用投影的积聚性直接求得其投影;而属于 一般位置表面上的点可通过在该面上作辅助线的方法求得其投影。 如图3-3（b）所示，已知棱面△SAB上点M的V面投影m′和棱面△SAC上点N的 H面投影n，求作M、N两点的其余投影。 由于点N所在棱面△SAC为侧垂面，可借助该平面在W 面上的积聚投影求得 n″，再由n和n″求得（n′）。由于点N所属棱面△SAC的V面投影不可见，所以 （n′）为不可见。 点M所在平面△SAB为一般位置平面，如图3-3（a）所示，过锥顶S和点M 引 一直线SI，作出SI的有关投影，根据点在直线上的从属性质求得点的相应投影。 具体作图时，过m′引s′1′，由s′1′求作H面投影s1，再由m′引投影连线交 于s1上点m，最后由m和m′求得m″。 另一种作法是过点M引MII线平行于AB，也可求得点M的m和m″，具体作法如 图3-3所示。由于点M 所属棱面△SAB在H面和W面上的投影是可见的，所以点m和 m″也是可见的。
图3-1 由基本体组成的形体
表面由平面所围成的实体，称为平面立体。平面立体上两相邻平面的交线 称为棱线。平面立体分棱柱和棱锥两种。
由于平面立体表面是平面，画平面立体的三视图，可归结为画出各平面间 的交线（棱线）和各顶点的投影。然后判别可见性，将可见的棱线投影画成粗 实线，不可见的棱线投影画成细虚线。
3-1-立体表面上点投影解析
步骤：1、过m’点作m’e’//a’b’；
s"
m
a"(c") b"
2、求出E在H面的投影e，作em//ab,得到点M在H面投影m；
3、根据“高平齐，宽相等”，由m’和m求出m”。
三、圆柱体表面上点的投影
例：已知圆柱面上M点和N点 的正面投影，求水平投影和侧面 投影。
分析：点在圆柱面上，利用水平
投影积聚性，可以求出点M和点 N的水平投影。
由于棱柱的表面都是平面，所以在棱柱的表面上取点 与在平面上取点的方法相同。
a′ b′
a”
b”
AB DC
d′ c′ a(d)
d”
c”
b(c)
平面的投影可见，点的投影可见； 平面积聚成直线，点的投影可见
如何判断可 见性？
例：已知六棱柱ABCD侧表面上点M的V面投影m’， 求该点的H面投影m和W面投影m″。
1.培养学生 正确分析和 解决问题的 能力； 2.培养学生 理论联系实 践、举一反 三的能力。
1.激发学生 良好的合作 意识； 2.培养学生 具有耐心细 致的工作作 风和严肃认 真的工作态 度。
1.让学生在 实践中找到 学习乐趣， 提高学习兴 趣； 2.培养学生 自学的能力。
重点难点
重点
1.根据已知点 的投影绘制其 余点的投影； 2.正确利用辅 助线或辅助圆 绘制立体表面 上点的投影。
n’ (n”)
(m’)
m”
不可 见
m n
M N
练习
已知下列各平面立体的两视图，补画第三视图，并 作出立体表面上点M、N的另外两个投影。
练习2
n’ (m’)
m”
n”
m n
小结
机械制图第一,二章检测试题 (2)
机械制图第一，二章检测试题（1）一、填空。
（每空1分，共计30分）1．机械制图国家标准对于图纸幅面、标题栏和明细栏的内容、格式及尺寸均有规定。
A3图纸的长边尺寸是，短边尺寸是，标题栏一般应位于图纸的，文字方向为方向。
2．图样中与相应要素的线性尺寸之比，称为比例。
3．图样中书写的汉字应写成，字体的代表字体的号数，要做到字体工整、、、排列整齐。
4．绘制机械图样有9种基本线型。
其中可见轮廓线用绘制，轴线、对称中心线用绘制，细点画线、细实线的宽度为粗实线的。
5．一个标注完整的尺寸由、和三个要素组成。
尺寸界线表示尺寸的范围，用细实线绘制，也可以利用轮廓线、轴线或对称中心线代替，但是尺寸线只能用绘制。
标注尺寸时，应严格执行国家标准，做到、、、。
6．线性尺寸的数字一般应注写在尺寸线的，也允许注写在尺寸线的，标注角度时，角度的数字一律写成方向。
7．圆和大于半圆的圆弧应当标注直径尺寸，并在直径前加符号“”，半圆和小于半圆的圆弧应标注半径尺寸，并在半径前加符号“”。
如果是球面的直径或半径时，应在直径符号或半径符号前加注符号“”，对于铆钉的头部、轴的端部以及手柄的端部等，在不致引起误解的情况下可以省略这个符号。
8．机械制图中，“C2”表示倒角时，其中“C”表示，“ 2”。
相同要素均布者，需标注出均布符号，标注尺寸时，应尽可能使用符号或缩写词代替汉字。
二、在画图线接头处的时候，应该注意哪些问题。
在下列题目中填写“应”或“不应”。
（每处1分，共计7分）1．圆心是两点画线的线段交点。
2．虚线与虚线相交处有间隙。
3．虚线与粗实线相交处有间隙。
4．虚线与点画线相交处有间隙。
5．细虚线为粗实线的延长线时留有间隙。
6．点画线两端超出圆弧2-5毫米。
7．较小的圆的中心线以细实线代替。
三．校核尺寸注法。
本题左边图中尺寸注法有错误，请你仔细查看，并在右边图中正确地标注尺寸（每处2分，共计20）四、画出尺寸数字和箭头。
画出箭头并填入尺寸数值，尺寸数值从图中量取，并取整数。
基本形体的三视图面上的点和线PPT学习教案
2 圆锥体
S
圆锥的形成
锥顶
直角三角形绕 其直角边旋转
圆锥面 而成
底面 轴线
过圆锥面上任一点可作一条直线通过锥 顶，该点的运动轨迹为一圆周---维圆
第30页/共52#34;
S
s
对V面的 轮廓线
对W面的 轮廓线
第31页/共52页
轮廓线投影 的对应关系
圆锥面投影 可见性判断
主俯视图长对正 主左视图高平齐 俯左视图宽相等
高
长
宽
宽
三等关系
长对正 高平齐 宽相等
第3页/共52页
3、三视图之间的方位对应关系
上
上
左 下
右后
前
下
后 上
后
左
右
前
左
右
下 前
主视图反映：上、下 、左、右 俯视图反映：前、后 、左、右 左视图反映：上、下 、前、后
第4页/共52页
二、平面立体
1 棱柱
2 棱锥
映实形。侧棱面SAC
为侧垂面，另两个侧
棱面为一般位置平面
a
。
第16页/共52页
棱锥面上取点，辅助线法
3、
S
s
s
Ⅱ
2
2
3
M
Ⅰ
m 1 (3)
1
C
B
b n a
c b(c)
a
N
A
b
m s3
c
1
n2
a
第17页/共52页
s’
s” 截头三棱锥的画法
e’k’ fn’ ’ m’
a’
c’
b’
c
n
am s e
32工程制图6版答案-第2章 投影基础10
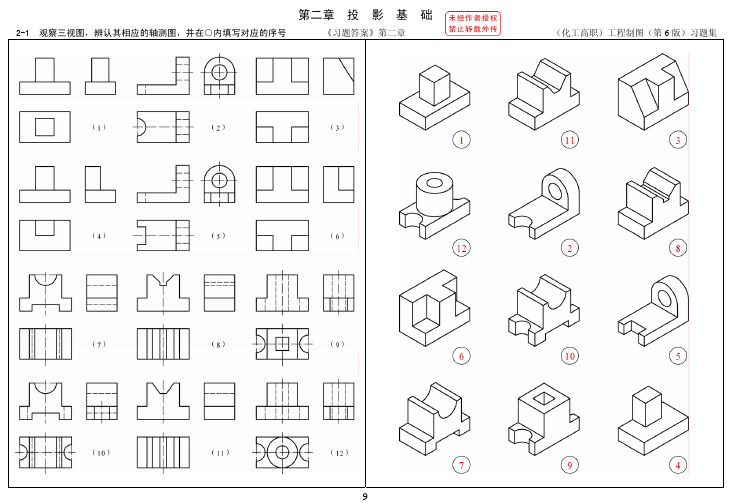
点 A 在（V 面）；点 B 在（H 面）；点 C 在（Y 轴）
13
2-6 直线的投影
2-6-1 判断 AB 直线的空间位置。
《习题答案》第二章
2-6-2 判断 AB 直线的空间位置。
2-6-3 判断 EF 直线的空间位置。
（化工高职）工程制图（第 6 版）习题集
2-6-4 已知点 K 在 V 面上，补全直线的三面 投影。
《习题答案》第二章
（化工高职）工程制图（第 6 版）习题集
2-5-2 根据轴测图及其尺寸，按 1∶1 的比例画出三视图。
2-5-3 作点 A（15，27，30）、点 B（30，0， 23）的三面投影。
2-5-4 已知点的两面投影，求作第三投影。
2-5-5 判别 A、B、C 三点的空间位置。
2-5-6 已知点 B 在点 A 的右 22mm、下 20mm、前 12mm 处，求作点 B 的三面投影。
水平 面
正垂 面
侧平 面
2-7-4 补画六边形的第三面投影，判别其空间位置，并标出平 2-7-5 补画八边形的第三面投影，判别其空间位置，并标出平 2-7-6 补画七边形的第三面投影，判别其空间位置，并标出平
面与投影面的倾角。
面与投影面的倾角。
面与投影面的倾角。
铅垂 面
正垂 面
15
侧垂 面
2-8 平面内直线和点的投影
2-8-1 E、F 两点在已知平面内，求它们的另一投影。
《习题答案》第二章
2-8-2 直线 MN 在已知平面内，求它们的另一投影。
（化工高职）工程制图（第 6 版）习题集
2-8-3 完成四边形 ABCD 的正面投影。
2-8-4 已知点 K 属于△ABC 平面，完成△ABC 的正面投影。
立体表面上点的投影PPT课件
当立体表面沿某个方向移动时，其上的点也会相应地移动，导致投 影点的位置发生变化。
缩放
当立体表面按比例放大或缩小时，其上的点也会相应地放大或缩小 ，导致投影点的位置发生变化。
THANKS
感谢观看
投影的平移
总结词
平移是移动投影中心到新的位置，但不改变投影平面的方向。
详细描述
在投影变换中，平移是指将投影中心移动到新的位置，但不改变投影平面的方向。通过平移，可以改 变投影中心的位置，使得立体表面上的点在投影平面上呈现不同的位置。平移操作不会改变点在立体 表面上的位置和方向，只是改变了投影中心的位置。
05
CATALOGUE
立体表面上的点与投影的关系
点与投影的对应关系
投影线与投影面
每个点在立体表面上有且仅有一 条投影线，该线与投影面相交于 一点，该点即为该点在投影面上 的投影。
唯一性
一个点在投影面上的投影位置唯 一确定，反之亦然，即每个投影 点都对应立体表面上的一个点。
点与投影的度量关系
距离关系
04
详细描述
投影与原点连线与曲面相切，并且投 影与原点之间的连线与曲面内的任意 一条线段都垂直。
06
详细描述
投影与原点连线长度保持不变，即投影与原点 之间的距离等于原点到曲面的垂直距离。
点在多个面上的投影
总结词
确定点在多个面上的投影位 置
详细描述
当一个点位于多个平面的交 线上时，其投影将位于这些 平面的交线上，并且与原点
具有相同的距离。
总结词
投影与原点连线垂直于所有平面
详细描述
投影与原点连线垂直于所有相关平面，并 且投影与原点之间的连线与所有平面内的 任意一条线段都垂直。
3-2 平面立体-平面立体三视图及表面上点的投影
底面//H
锥顶S到底面的垂线垂足是四边形的中心
§3-2 平面立体三视图及表面上点的投影
一、平面立体三视图
3、正四棱锥——绘制三视图
步骤： 选主视图 绘制作图基准线 逐个形体绘制 检查、描深
画基准线 画底面 画左右棱锥面 画前后棱锥面 检查、描深
§3-2 平面立体三视图及表面上点的投影
S
C A B
画基ቤተ መጻሕፍቲ ባይዱ线 画底面ABC 画SAC面 画SAB、SBC面 检查、描深
§3-2 平面立体三视图及表面上点的投影
一、平面立体三视图
§3-2 平面立体三视图及表面上点的投影
二、平面立体表面上点、线的投影
1、正三棱柱上点线的投影
m'
C A B
M
m"
k'
n'
k"
(n ")
K
N
C1
m
n
画基准线 画顶、底 画前后棱面 画其他棱面 检查、描深
§3-2 平面立体三视图及表面上点的投影
一、平面立体三视图
2、正三棱柱——投影分析 由5个表面围成
按图示姿态：
顶面、底面 //H 后棱面 //V
两个前棱面 ⊥H
§3-2 平面立体三视图及表面上点的投影
一、平面立体三视图
2、正三棱柱——绘制三视图
一、平面立体三视图
4、正三棱锥——投影分析 由4个表面围成
按图示姿态：
底面 //H
S
后棱锥面
⊥W
C A B
锥顶S到底面的垂线垂足是三角形的中心
辅助圆法求圆锥表面点的投影
2. 曲面立体表面的截交线 ⑴ 圆柱 由于圆柱表面的投影具有积聚性，圆柱面在与轴线垂 直的投影面上有积聚性，端面在与轴线平行的投影面 上有积聚性，故可直接用积聚性求圆柱表面的截交线。 根据截平面与圆柱轴线的相对位置不同，所得到的截
1.2.3切割体的投影
用平面切割立体，则该切割面称为截平面，截平面与 立体表面的交线称为截交线，由截交线所围成的平面 称为截断面，如图1-16所示。
棱柱表面是由平面围成的，棱线为平行于轴线的直线， 故截平面与平面立体表面相交，所得截交线的形状是 平面多边形，截平面与棱线的交点为多边形的顶点， 多边形的边是平面立体表面与截平面的交线。
分类 立体图 三视图 截交线形状
截平面垂直 于轴线
圆
截平面倾斜 于轴线 （θ＞α）
椭圆
图1-16 截平面与截交线
由于立体的形状各不相同，以及截平面和立体的相对
位置不同，所以截交线的形状也各不相同。但截交线 都具有以下两个基本通性： ⑴ 公有性 截交线是截平面与立体表面的共有线，截交 线上的点是截平面与立体表面的共有点。 ⑵ 封闭性 由于立体表面是封闭的，所以截交线是封闭 的平面直线（或曲线），截断面是封闭的平面图形。 1. 平面立体的截交线 ⑴ 棱柱
⑵ 棱锥 棱锥的表面由平面所围成，棱线为直线，故截平面与 棱锥相交，所得到的截交线的形状是平面多边形，棱 线与截平面的交点是多边形的顶点，多边形的边是棱
锥表面与截平面的交线，如图1-16所示。 综上所述，求平面立体被切割后的投影主要是求截交 线的投影，而求截交线的实质就是求两平面的交线， 可以根据截交线的共有性和封闭性，利用棱线法，将 线的投影转化为点的投影，具体步骤如下： ① 空间及投影分析。首先，分析截平面与切割体的相 对位置，以便确定截交线的形状；其次，分析截平面 与投影面的相对位置，以便确定截交线的投影特性。 ② 画出截交线的投影。求出截平面与被截棱线的交点， 并判断可见性，然后依次连接各顶点成多边形。 ③ 完善各轮廓投影。
《机械制图》全部电子教案
机械制图电子教案[课题编号]4-2①[课题名称]绘图工具及其使用基本作图法[教材版本]王幼龙主编、中等职业教育国家规划教材--机械制图（机械类），第3版，北京：高等教育出版社，2007。
王幼龙主编、中等职业教育国家规划教材配套教学用书--机械制图习题集（机械类），第3版，北京：高等教育出版社，2007。
[教学目标与要求]一、知识与技能1、了解常用的绘图工具及其用法；2、通过学习与练习，能基本掌握常用绘图工具的使用方法；3、熟练掌握用三角板、圆规等分线段、圆周和作正多边形等基本作图方法。
二、学习方法与素质养成通过练习，能较熟练使用绘图工具，掌握基本作图方法，为后续学习打好基础。
[教学重点]三角板、圆规的使用方法；等分圆周和作多边形。
[教学难点]图板和丁字尺及三角板的配合使用。
[分析学生]1、部分绘图工具，学生在学几何时已会使用，等分线段也容易理解。
2、运用常用的绘图工具，从学习一开始要注意正确的方法，并通过不断练习达到运用自如。
3、学习时学生可能会认为简单易学，产生马虎现象。
要引导学生正确运用绘图工具的方法，通过练习熟练地绘制图线。
[教学设计思路]教学方法：讲演结合、讲练结合、归纳法。
[教学资源]机械制图网络课程，圆规、三角板、直尺、图板、丁字尺、曲线板。
[教学安排]2学时（90分钟）。
教学步骤：讲课与演示交叉进行，讲课与练习交叉进行，最后进行归纳。
[教学过程]一、复习回顾（5～10分钟）1、标注尺寸的基本规则和注意事项；角度尺寸的标注；倾斜尺寸注法等。
2、讲评作业共性问题。
3、提问教材P.23 思考题4、5题。
4、预习提问，集中问题。
二、导入新课简述本节课的作用和重要性，导入本节课教学目标和要求。
绘图离不开工具，今天要介绍绘图工具及其使用，重点放在使用上。
绘图速度的快慢、图画质量的高低，在很大程度上决定于是否能采用正确的绘图方法和按正确的工作程序，自如地运用各种绘图工具绘制几何图形。
三、新课教学（70～80分钟）1、绘图工具及其使用教师讲解并演示常用绘图工具，除实物演示，还应充分运用网络课程演示。
机械制图 第四章 立体及其表面交线的投影
作图步骤：
例：求作截平面平行圆锥轴线的截交线的投影 可在圆锥面上作辅助圆，或作辅助素线法 例：求作截平面斜切圆锥的截交线的投影
3. 切割球体
平面从任何方向截切球体所产生的截交线均为 圆。 截平面平行投影面时，截交线在该投影面上的 投影反映实形。 例：半球开槽的三面投影图
四. 综合举例
【例1】：求作顶针上的表面交线
求作顶针的表面交线
A
Ⅰ Ⅰ
Ⅴ Ⅴ B 求连杆头的表面交线
(a) 两平面立体 相交
(b) 平面立体与 曲面立体相 交
(c) 两曲面立体 相交
其相贯线可看成由平面立体上 有关表面分别切割另一基本体所产 生的截交线所围而成。
立体相交的三种情形
相贯线为两回转 体相交的表面交 线——本节讨论
(a) 两外圆柱面 相交（柱柱相贯）
特例：当截平面与圆柱轴线成450斜切时，截交 线的侧面投影为圆。
综合举例：
【例1】：联轴节的三面投影
【例2】：联轴套的三面投影
【例3】：轴销的三面投影
2. 切割圆锥体
可产生直线、圆、椭圆、双曲线和抛物线等 五种不同性质的截交线。
记忆口诀：
截在锥顶两直线，切去锥顶是椭圆； 保留锥顶双曲线；平行锥面抛物线。
【例2】：求作连杆头表面交线的投影
§4-3 立体相交表面交线的投影
一、概述 两个基本体相交（又叫相贯），在相交表面所产 生的交线，叫立体相交表面交线，又叫相贯线。 相贯线的基本性质：
是两相交回转体表面的共有线、分界线。 一般是闭合的空间曲线，特殊情况下是平面曲线 或直线。
可见，求作相贯线实质上是求作两相交回转体表 面上共有点的问题。 常用两种方法：
基本几何体的投影及尺寸标注
第十四讲§3—1 基本几何体的投影及尺寸标注课题:1、平面立体的投影及表面取点2、曲面立体的投影及表面取点课堂类型:讲授教学目的:1、讲解平面立体和曲面立体的种类及其三视图画法2、讲解在平面立体和圆柱体表面取点、取线的作图方法教学要求:1、能够熟练掌握平面立体和圆柱体的三视图画法2、能够熟练运用利用点所在的面的积聚性法和辅助线法在平面立体和圆柱体表面取点、取线教学重点:1、平面立体和曲面立体的种类及其三视图画法。
2、在平面立体和圆柱体表面取点、取线的作图方法教学难点:在圆柱体表面取点、取线的作图方法教具:基本体模型:三棱柱、四棱柱、五棱柱、六棱柱、三棱锥、四棱锥、圆柱体等教学方法:用教学模型辅助讲解。
教学过程:一、复习旧课结合作业复习直线和平面投影变换的作图方法和步骤。
二、引入新课题机器上的零件,不论形状多么复杂,都可以看作是由基本几何体按照不同的方式组合而成的。
基本几何体——表面规则而单一的几何体。
按其表面性质,可以分为平面立体和曲面立体两类。
1、平面立体——立体表面全部由平面所围成的立体,如棱柱和棱锥等。
(出示模型给学生看)。
2、曲面立体——立体表面全部由曲面或曲面和平面所围成的立体,如圆柱、圆锥、圆球等。
(出示模型给学生看)。
曲面立体也称为回转体。
三、教学内容(一)平面立体的投影及表面取点1、棱柱棱柱由两个底面和棱面组成,棱面与棱面的交线称为棱线,棱线互相平行。
棱线与底面垂直的棱柱称为正棱柱。
本节仅讨论正棱柱的投影。
(1)棱柱的投影以正六棱柱为例。
如图3-1(a)所示为一正六棱柱,由上、下两个底面(正六边形)和六个棱面(长方形)组成。
设将其放置成上、下底面与水平投影面平行,并有两个棱面平行于正投影面面。
上、下两底面均为水平面,它们的水平投影重合并反映实形,正面及侧面投影积聚为两条相互平行的直线。
六个棱面中的前、后两个为正平面,它们的正面投影反映实形,水平投影及侧面投影积聚为一直线。
《机械制图》教案——第三章 立体投影及表面交线
第三章基本立体的投影、截交线、相贯线§1立体的投影1．1平面立体的投影本节教学目标：掌握平面立体的投影特性和作图方法；掌握拉伸体的形成、投影及画法；熟悉平面立体表面中特殊位置的点、线的三面投影及画法。
重点：平面立体的投影特性及表面取点、取线的投影。
难点：平面立体表面中特殊位置处点、线的投影。
引入：通过对前面知识的学习已经知道，很多的机械零件都是由一些简单的基本形体组成，比如螺栓，我们可以将它分成正六棱柱、圆柱体和圆锥台三部分。
如果我们要绘制此螺栓的三视图，同学们都应该知道必须要绘制正六棱柱、圆柱体和圆锥台的三视图。
任何一个复杂的物体都可以看成由基本体组成，按组成基本体表面的性质进行分类，基本体可分为平面体和曲面体。
平面立体侧表面的交线称为棱线若平面立体所有棱线互相平行，称为棱柱。
若平面立体所有棱线交于一点，称为棱锥。
1.1.1棱柱的投影1. 以正六棱柱为例，分析平面立体的结构，（1）正六棱柱共有几个表面？有何关系？（2）正六棱柱共有几条侧棱？有何关系？提问：1）不同位置的投影有什么不同？2）应怎样放置最合理？提示：使尽可能多的表面和棱线处于特殊位置。
2.投影特性分析（1）投影分析：上、下两个底面——平行的两个侧面——其余的几个侧面（2）三面投影图分析（3）绘图步骤：1）建立投影面系；2）根据三等原则绘制三面投影；3）区分可见性。
3. 棱柱体的投影特性（重点：学生应掌握）（1）当棱柱的底面平行于某一投影面时，棱柱的投影在该面上为与底面相等的正多边形。
（2）另两面投影为几个相邻的矩形线框。
4. 棱柱表面取点、线重点：所取的点、线属于棱柱的哪个面上？进而再求三面投影。
***若点所在平面的投影可见，点的投影可见；若平面的投影积聚成直线，点的投影也可见。
例：例：已知四棱柱，试完成其Ｖ、Ｈ投影。
（图7-1）图7-1四棱柱的投影1.1.2棱锥的投影棱锥的投影是棱锥各顶点同面投影连线的集合。
1. 棱锥的定义2. 棱锥的形体分析（1）投影分析：下底面——顶点——其余的几个侧面（2）三面投影图分析（3）绘图步骤：1）建立投影面系；2）根据三等原则绘制三面投影；3）区分可见性。
《机械制图习题集》习题答案——第2章
由于棱
锥体的棱面 无积聚性， 表面取点要 利用辅助线 法。
2-2 回转体的投影及表面取点
完成回转体的投影，并作出表面上各点的三面投影。
（1
）
a'
a"
b'
(b")
(b) a
回转体表面取点， 根据已知点的可见性 判断点所处的位置， 按投影关系，找出各 点的投影。
（2 ）
(c') 1'
a'
b'
1" c" a"
4、完成相贯体的三视图。
1'
5'(6') 3'(4') 2' 7'(8')
1"
5" 6"
4"
3"
8"
7" 2"
4 86 21
75 3
圆锥体与圆
柱形孔正交。因 圆锥面的投影无 积聚性，利用辅 助平面求一般位 置的点。
5、完成相贯体的三视图。
1'
5'(6') 3'(4') 7'(8') 2'
1"
6"
b"
c
a
b
圆锥面的投
影无积聚性，表 面取点利用辅助 素线或辅助纬圆 法求解。底面上 的点可利用投影 关系直接求出。
（3 ）
a'
b'
a" (b")
1a
圆锥台的表面
2 b
投影无积聚性，表 面上取点利用辅助
纬圆法。
（4 ）
平面立体及其表面上点和线的投影
第 12 页
（一）利用“从属性法”和“积聚性法”作图
（a） 图3-4 正三棱锥的投影
第7 页
平面立体及其轴测投影
第8 页
（3）投影分析。图3-4（b）所示为正
三棱锥的投影图，它具有如下特点。
➢ H面投影：为等边三角形，它反映正三
棱锥的底面实形，3个侧面的投影表现为
类似形，顶点投影重合于等边三角形的垂
心。
（b）
➢ V面投影：为两个三角形，即左、右两
图3-4 正三棱锥的投影
面的投影，且反映两底面实形；六边形的 6个顶点是6条棱边（铅垂线）的积聚投影。 ➢ V面投影：为3个矩形线框。其中，中间 的矩形线框为前、后侧面的重合投影；左 侧矩形为左侧前、后侧面的重合投影，右 侧矩形为右侧前、后侧面的重合投影，它 们均为类似形；上、下两底面的投影积聚 为直线段。 ➢ W面投影：为两个矩形线框，分别是左、 右4个铅垂侧面的重合投影（不反映实 形）。
判断立体表面上点、线可见性的原则是：如果点、线所在表面 的投影可见，则点、线的同面投影可见；否则，不可见。
求立体表面上点和线的投影问题，一般是指已知立体的三面投 影和其表面上某一点的一面投影，求该点或线的其他两面投影。这 类问题的求解方法有从属性法、积聚性法和辅助线法。
第 11 页
平面立体及其轴测投影
个侧棱面的类似形。
通过上述分析可以得出以下结
➢ W面投影：为一个三角形。其中，后侧 论：
棱面SAC积聚为最后方的一直线段，左、
（1）三棱锥在与其底面平行
右侧棱面的投影仍为三角形，且相互重合。
的投影面中的投影反映底面实形， 即投影为多边形或三角形的组合图
形；
（2）另外两面投影为并列的
2.2立体表面上的点、直线、平面的投影
第二节
3.一般位置平面
立体表面上点、直线、平面的投影
对V，H，W面都倾斜， 不在同一直线上的三 点构成的平面。 投影特性 一般位置平 面的投影特 性：三面投 影仍为平面 图形，且面 积缩小。其 投影为和原 来形状类似 的图形。 （类似性）
a′ c′
b′ A
a″ B b b″ c″
C a c
第二节
Z
b●
bx X
12
bz
b
●
作图步骤： 1）在a′左方12 mm ， 上方8 mm 处确定b′；
a
8
az O
a
by YW ay
ax
a
2）作b′b⊥OX 轴，且在a 前 10 mm 处确定b ；
10
ay by
YH
b
●
3）按投影关系求得b″。
第二节
立体表面上点、直线、平面的投影
当空间两点位于对投影面的同一条投影线上时，这两点在该投影面上的 投影重合，称这两点为对该投影面的重影点。
W
V
●
a
●
az
O
W a
YW
X
ax
A
●
O
X
ax a
H
●
ay
a●
H
ay
Y
ay
YH
向下翻
第二节
立体表面上点、直线、平面的投影
1）、V、H两投影都反映横标，且投影连 线 垂直X轴；aa⊥OX轴。 2）、V、W两投影都反映高标，且投影 连线垂直Z轴；aa⊥OZ轴。 3）、H、W两投影都反映纵标，投影连 线是一条折线。
注意: 点的各个投影一定要写在它所属的投影面区域内。
第二节
机械制图第三章 几何体表面点、线、平面的投影
第三章 几何体表面点、线、平面的投影
图3-2 点的投影
第三章 几何体表面点、线、平面的投影
例3-1 已知点的两面投影，求作第三面投影(图3-3)。 解 分析：因为空间点的每一面投影都反映了两个坐标值，所以 只要已知点的两面投影，就等于知道了点的三个坐标值，因而点 的第三面投影也能确定。 根据点的投影规律，过已知点的两面投 影图按箭头指示方向分别作出相应的投影线，两垂线的交点即为 所求，如图3-3a、b、c所示。
第三章 几何体表面点、线、平面的投影
表3-3 投影面的平行面
第三章 几何体表面点、线、平面的投影
表3-3 投影面的平行面
第三章 几何体表面点、线、平面的投影
3.投影面垂直面 投影面垂直面是指垂直于一个投影面，且与另外两个投影面倾斜 的平面形。 1)铅垂面。 2)正垂面。 3)侧垂面。
第三章 几何体表面点、线、平面的投影
第三章 几何体表面点、线、平面的投影
(1)真实性 当直线AB平行于投影面时，它在该投影面上的投影ab 的长度与空间线段AB相等，这种性质称为真实性，如图3-10b所示。 (2)收缩性 当直线AB倾斜于投影面时，它在该投影面上的投影ab 的长度比空间线段AB的长度短。 (3)积聚性 当直线AB垂直于投影面时，它在该投影面上的投影a(b) 重合成一点。
第三章 几何体表面点、线、平面的投影
图3-19 正棱柱表面上点的投影
第三章 几何体表面点、线、平面的投影
二、辅助直线法 1.作图方法、步骤分析 1)判断点在物体的哪个表面上，并分析该表面的空间位置和点在 该表面上的具体部位。 2)如该表面为一般位置面，则可用辅助直线法求作点的投影。
第三章 几何体表面点、线、平面的投影
第三章 几何体表面点、线、平面的投影
科学出版社机械工程图学习题集1~10章答案
编辑ppt
4-2.过点S作一直线与EF相交于D点,使点D距H 面为20MM。
41
编辑ppt
4-3.过点M作一正平线MN与AB相交于N点。
42
编辑ppt
4-4 判断直线MN是否属于给定平面。
43
答＿否＿
编辑ppt
4-5 直线AD属于已知平面,求直线的另一投影。
44
编辑ppt
4-6 已知三角形ABC和三角形DEF共面,试 补出三角形DEF的另一投影。
29
编辑ppt
3-19 已知等腰直角三角形ABC为一正平面,又知斜 边AC的正面投影和点C的水平投影,求其三面投影。
30
编辑ppt
2-20 已知DEF为一正垂面和水平投影，并知 与H面的倾角α=45°,求该平面的另两个投影。
31
编辑ppt
3-21 已知等边三角形ABC为一侧平面，又知其AC 的侧面投影和点C的正面投影，求其三面投影。
9
编辑ppt
第三章 投影法与 几何元素的投影
10
编辑ppt
3-1 已知点A(25,15,25)、B(35,25,20)、 C(15,30,30)的坐标试作其三面投影图。
11
编辑ppt
3-2 已知各点的两投影,补画第三投影。
12
编辑ppt
3-3从立体图中1:1量取点A、B的各坐标,画 出其三面投影图。
编辑ppt
机械工程识图习题（答案）
1
1-10章
编辑ppt
第一章制图基本知识
2
编辑ppt
尺寸标注练习
1-2(1).图中画好的尺寸线上标注尺寸数字,大小从图中量取(1:1)
3
编辑ppt
尺寸标注练习
画法几何及机械制图第三章 立体的投影
3-1 平面立体及其表面取点
以若干个多边形平面所围成的立体叫做平面立体。 工程中常见的平面立体是棱柱（主要是直棱柱）及棱锥 （常以棱台的形式出现）。 一、棱柱 1.投影 用前一章的知识，研究平面立体上各个多边形的投 影，即研究各多边形的边及顶点的投影，综合起来，就 是平面立体的投影。2Fra bibliotek图3-1
11
2.四棱台上挖方槽 从图3-7（a)的立体图上观察到，所谓开槽，实质上 是三个平面P、Q、R截切立体的结果。 该题给出四棱台的三面投影及正面投影上给出槽形， 试补作槽的另外两个投影。
12
图3-7
13
3-2 回转体及其表面取点
由曲面或曲面与平面所围成的立体叫做曲面立体， 而本节只论述曲面立体中的回转体，即圆柱、圆锥、圆 球等。
19
图3-10
20
3.表面上取点 (1)辅助素线法 从圆锥面的形成可知，圆锥面可理解成若干直素线 所包围的面，这些素线都通过锥顶。在图3-11的立体图 上，圆锥面上有一点M，它在素线SA上，按线上的点的 作图方法，根据已知的正面投影m′，求出另两投影m及 m″。此法在解决处于转向轮廓线上的点最为方便，见图 3-11的投影图。图中另有一点N，已知其水平投影n，求 另外两投影n′及n″，其作法相同。
17
图3-9
18
二、圆锥 1.形成 圆锥是由一圆锥面和一底平面所围成。圆锥面的形 成，是一条与轴线斜交的直母线绕轴线作圆周运动，回 转的轨迹即是圆锥面。母线在回转过程中的任一位置称 为素线，母线与轴线的夹角α始终不变，α＜90°，称为 半锥角，见图3-10（a)。 2.投影分析 图3-10（b)是圆锥的三面投影图。圆锥面和底面的 水平投影重合，中心线的交点是圆锥轴线及锥顶S的投 影。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
利用辅助线在基本平面立体表面求点的投影。
3.1 平面立体的投影
立体包含基本体和组合体。柱、锥、圆球、圆环等几何体是组成机件的基本 形体，简称基本体。基本体组合后的立体称组合体。当立体带有切口、切槽等结 构时，又称切割体。切割体和相贯体（两相交的立体）均是组合体。如图3-1所 示是由基本体组成的机件。本章着重研究基本体、切割体及相贯体的形体特色和 三视图的画法。
3.1 平面立体的投影
图3-3 正三棱锥的投影
3.1 平面立体的投影
3.棱锥台 棱锥台可看成由平行于棱底面的平面截去锥顶一部分而形成的。由正棱锥截 得的棱台叫正棱台，其顶面与底面为互相平行的相似多边形，侧平面为等腰梯形。 图3-4（b）为四棱锥台投影图。四棱台的顶面和底面为水平面，H面投影为 两矩形线框，反映实形。V面W 面投影分别积聚为横向直线段。左右侧面为正垂 面，V面投影积聚成两条斜线，H面和W面的ห้องสมุดไป่ตู้影为等腰梯形，是类似形。前后侧 面及四条侧棱的投影，分析方法相同。
上的积聚性投影abcd上。再根据m′和m求出W面投影，由于ABCD面的W面投影为可 见，故m″也为可见。
图3-2 正六棱柱的投影
3.1 平面立体的投影
3.1.2 棱锥 棱锥的底面为多边形，各侧面为若干具有公共顶点的三角形。从棱锥顶点到 底面的距离叫做锥高。当棱锥底面为正多边形，各侧面是全等的等腰三角形时， 称为正棱锥。 1.棱锥的投影 如图3-3（a）所示为一个正三棱锥的三面投影直观图。该三棱锥的底面为等 边三角形，三个侧面为全等的等腰三角形，图中将其放置成底面平行于H面，并 有一个侧面垂直于W面。 如图3-3（b）为该三棱锥的投影图。由于锥底面△ABC为水平面，所以，它 的H面投影△abc反映了底面的实形，V面和W面分别积聚成平行X轴和Y轴的直线段 a′b′c′和a″（c″）b″。锥体的后侧面△SAC为侧垂面，它的W面投影积聚为 一段斜线s″a″（c″），它的V面和H面投影为类似形△s′a′c′和△sac，前 者为不可见，后者为可见。左、右两个侧面为一般位置平面，在三个投影面上的 投影均是类似形。 画棱锥投影时，一般先画底面的各个投影，然后定锥顶S的各个投影，同时 将它与底面各顶点的同名投影连接起来，即可完成。
3.1 平面立体的投影
2.棱锥表面上点的投影 凡属于特殊位置表面上的点，可利用投影的积聚性直接求得其投影;而属于 一般位置表面上的点可通过在该面上作辅助线的方法求得其投影。 如图3-3（b）所示，已知棱面△SAB上点M的V面投影m′和棱面△SAC上点N的 H面投影n，求作M、N两点的其余投影。 由于点N所在棱面△SAC为侧垂面，可借助该平面在W 面上的积聚投影求得 n″，再由n和n″求得（n′）。由于点N所属棱面△SAC的V面投影不可见，所以 （n′）为不可见。 点M所在平面△SAB为一般位置平面，如图3-3（a）所示，过锥顶S和点M 引 一直线SI，作出SI的有关投影，根据点在直线上的从属性质求得点的相应投影。 具体作图时，过m′引s′1′，由s′1′求作H面投影s1，再由m′引投影连线交 于s1上点m，最后由m和m′求得m″。 另一种作法是过点M引MII线平行于AB，也可求得点M的m和m″，具体作法如 图3-3所示。由于点M 所属棱面△SAB在H面和W面上的投影是可见的，所以点m和 m″也是可见的。
3.1 平面立体的投影
为了便于画图和看图，在绘制平面立体的三视图时，应尽可能地将它的一些 棱面或棱线放置于与投影面平行或垂直的位置。
3.1.1 棱柱 常见的棱柱为直棱柱，它的顶面和底面是两个全等且互相平行的多边形，称 为特征面，各侧面为矩形，侧棱垂直于底面。顶面和底面为正多边形的直棱柱， 称为正棱柱。 1.棱柱的投影 如图3-2（a）所示，正六棱柱的顶面和底面为正六边形的水平面，前后两个 矩形侧面为正平面，其他侧面为矩形的铅垂面。 如图3-2（b）所示，水平投影的正六边形线框是六棱柱顶面和底面的重合投 影，因为此投影反映六棱柱特征面的实形，故称为特征视图。六边形的边和顶点 是六个侧面和六条侧棱的积聚投影。 正面投影的三个矩形线框是六棱柱六个侧面的投影，中间的矩形线框为前、 后侧面的重合投影，反映真实性。左、右两矩形线框为其余四个侧面的重合投 影，是类似形。而正面投影中上下两条图线是顶面和底面的积聚投影，另外四条 图线是六条侧棱的投影。 2.棱柱表面上点的投影 由于直棱柱的表面都处于特殊位置，所以棱柱表面上点的投影均可利用平面
图3-4 四棱锥台的投影
3.1 平面立体的投影
教学目的：
1.熟练掌握棱柱、棱锥、棱台等平面立体的投影特点 及画法。能根据它们的两个投影画出第三投影。 2.熟练运用积聚性和辅助线法在基本平面体的表面上 取点，并能判别其可见性。
教学重点：
1.掌握棱柱、棱锥、棱台等平面立体的投影。 2.利用积聚性和辅助直线法在基本平面体表面求点的 投影。
图3-1 由基本体组成的形体
表面由平面所围成的实体，称为平面立体。平面立体上两相邻平面的交线 称为棱线。平面立体分棱柱和棱锥两种。
由于平面立体表面是平面，画平面立体的三视图，可归结为画出各平面间 的交线（棱线）和各顶点的投影。然后判别可见性，将可见的棱线投影画成粗 实线，不可见的棱线投影画成细虚线。
3.1 平面立体的投影
投影的积聚性来作图。 在判别可见性时，若平面处于可见位置，则该面上点的同面投影也是可见的;
反之，为不可见。在平面积聚投影上的点的投影，可以不必判别其可见性。 如图3-2（b）所示，已知六棱柱ABCD侧面上点M的V面投影m′，求该点的H面
投影m和W面投影m″。 由于点M所属棱柱面ABCD为铅垂面，因此点M的H面投影m，必在该侧面在H面