结构动力学-8z
合集下载
结构动力学

第2章 单自由度系统
§2.4 简谐荷载的强迫振动
2.4.1 无阻尼系统
1、运动方程
mx kx F0 sin t
2、解的形式
x x x
设:
x A sin t
(m 2 k ) A F0
第2章 单自由度系统
解得:
A
A
(m 2 k )
F0 k xst (1 2 2 ) (1 2 )
已知
结构
荷载
响应
荷载
已知或未知
结构
已知
第1章 绪论
§1.2 研究对象
1、结构——弹性恢复力 fk(x) 2、外力——时变特性 fp(t)
§1.3 研究内容
1、结构动力特性——固有频率、振型、阻尼 2、结构响应——位移、速度、加速度
第1章 绪论
§1.4 研究方法
1、时域法——解析法、逐步积分法 2、频域法——谱分析法
k m
①简支梁问题
m l
第2章 单自由度系统
1 k
l3 48 EI
k
48EI l3
48EI ml 3
第2章 单自由度系统
②悬臂梁问题 弯曲变形
x
l 3EI
3
m
k
3EI l3
k
剪切变形
l3 12EI
k
12EI l3
弯曲变形 剪切变形
第2章 单自由度系统
2 i i ,max m xi ki xi2,maxi
第2章 单自由度系统
m x
i 2 i i ,max
2 2 J max m2 xmax
1 2 2 m1l 2 max m2l 2 max 3 1 2 m1l 2 m2l 2 max 3
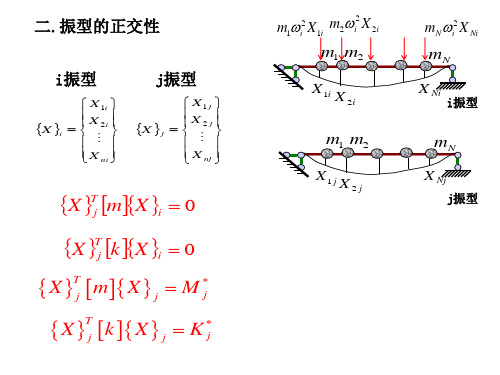
结构动力学-8z振型的正交性
cN1
cN 2
cNN
--阻尼矩阵
mn
f Dn
yn (t)
m2 m f D 2
1
f D1
y2 (t) y1(t)
cij --当质点j有单位速度 ( y j 1) ,其余质点速度为0时, 质点i上的阻尼力.
若下式成立
X
T i
cX
j
0
C
* j
i j i j
则将 c称作正交阻尼矩阵, c*j 称作振型j的广义阻尼系数.
0.151 0.0591
0
c 0.0591 0.151 0.0591 km
0
0.0591 0.0919
m
EI1
k m2 m
EI1
k
m
EI1
k
解.
1
1
21
(a0
a112 )
2
1
2 2
(a0
a1
2 2
)
a0 0.0328 k / m
a1 0.0591 m / k
3
1
23
(a0
( m* r k* )X * 0
m*r k* 0
---频率方程
K
* 2
K
* n
X X 1X 2 X n ---振型矩阵
振型方程
kX 1 12mX 1
kX 2
2 2
mX
2
kX n
2 n
mX
n
k X mX 2 ---振型方程
12
2
2 2
---频率矩阵
2 n
X T kX X T mX 2
X T kX X T mX 2
Di2
结构动力学

中国矿业大学
中国矿业大学
中国矿业大学
中国矿业大学
中国矿业大学
例题:
中国矿业大学
中国矿业大学
中国矿业大学
中国矿业大学
14-4 单自由度结构在简谐荷载作用下的强迫振动
所谓强迫振动,是指结构在动力荷载即外来干扰力 作用下产生的振动
惯性力:FI my 恢复力:Fe k11 y 阻尼力:FR y 干扰力:F (t ) FI FR Fe F (t ) 0 my y k11 y F (t )
2
式中: k
2
2
中国矿业大学
14-4 单自由度结构在简谐荷载作用下的强迫振动
F (t ) F sin t F 2 y y sin t y m y C1 sin t C2 cos t
2
中国矿业大学
14-4 单自由度结构在简谐荷载作用下的强迫振动
2 2
2C2 sin t C1 sin t C2 cos t
2 2
F sin t m
中国矿业大学
14-4 单自由度结构在简谐荷载作用下的强迫振动
即: F C1 2 2C2+C1 2- sin t= m
C -2C -C cos t
中国矿业大学
P(t) P t o
P(t) P t o
a ) 简谐荷载
b) 周期撞击荷载
P(t) P t o 图14 -2 冲击荷载 t2
o P
P(t)
t
图14-3 突加常值荷载
中国矿业大学
中国矿业大学
14-1 概述 3、动力自由度 自由度: 结构在弹性变形过程中确定全部质点位置所需的独立 参数的数目。 (1)集中质量法 (2)广义坐标法
中国矿业大学
中国矿业大学
中国矿业大学
中国矿业大学
例题:
中国矿业大学
中国矿业大学
中国矿业大学
中国矿业大学
14-4 单自由度结构在简谐荷载作用下的强迫振动
所谓强迫振动,是指结构在动力荷载即外来干扰力 作用下产生的振动
惯性力:FI my 恢复力:Fe k11 y 阻尼力:FR y 干扰力:F (t ) FI FR Fe F (t ) 0 my y k11 y F (t )
2
式中: k
2
2
中国矿业大学
14-4 单自由度结构在简谐荷载作用下的强迫振动
F (t ) F sin t F 2 y y sin t y m y C1 sin t C2 cos t
2
中国矿业大学
14-4 单自由度结构在简谐荷载作用下的强迫振动
2 2
2C2 sin t C1 sin t C2 cos t
2 2
F sin t m
中国矿业大学
14-4 单自由度结构在简谐荷载作用下的强迫振动
即: F C1 2 2C2+C1 2- sin t= m
C -2C -C cos t
中国矿业大学
P(t) P t o
P(t) P t o
a ) 简谐荷载
b) 周期撞击荷载
P(t) P t o 图14 -2 冲击荷载 t2
o P
P(t)
t
图14-3 突加常值荷载
中国矿业大学
中国矿业大学
14-1 概述 3、动力自由度 自由度: 结构在弹性变形过程中确定全部质点位置所需的独立 参数的数目。 (1)集中质量法 (2)广义坐标法
结构动力学8

{u}——有限元节点系位移向量。当采用时域逐步积分法进 行分析,阻尼矩阵[C]可以采用Rayleigh阻尼阵。
8.4.2 基本分析过程
结构有限元模型的运动方程:
& & [M ]{u&}+ [C ]{u}+ [K ]{u} = {p(t )}
有限元模型的节点系运动方程与前面介绍的框架结构的 运动方程在形式上完全相同,不同之处仅在于单元刚 度矩阵和质量阵的形成上。本节介绍的形成单元刚度 阵和质量阵的方法更具通用性。 前面所介绍的结构动力方程的解法,例如振型叠加法、 Fourier变换方法、时域逐步积分法等均可以用于结构 有限元模型的动力反应问题分析。
i=1
4
ψi的定义是ui发生单位位移, 而其余自由度不动, 即完全约束时, 梁单元的位移(线位移),因此,ψi(x)满足如下边界条件:
i = 1 : ψ 1 (0) = 1, ψ 1' (0) = ψ 1 ( L) = ψ 1' ( L) = 0
' ' i = 2 : ψ 2 (0) = 1, ψ 2 (0) = ψ 2 ( L) = ψ 2 ( L) = 0 ' ' i = 3 : ψ 3 ( L) = 1, ψ 3 (0) = ψ 3 (0) = ψ 3 ( L) = 0 ' ' i = 4 : ψ 4 ( L) = 1, ψ 4 (0) = ψ 4 (0) = ψ 4 ( L) = 0
8.4.1 有限元离散化
采用有限元法离散时,首先将一根梁分成有限段,称为 有限单元。每一个单元的尺寸可以是任意的,可以完 全相同,也可以完全不相同。这些单元仅仅在单元间 的节点上连续(连接)。 在这个简单的例子中,节点就是单元的端点,在每一个 节点上有两个自由度,横向位移和转角。 在有限元法中节点的位移(包括横向位移和转角)被选 为广义坐标。而运动方程就是用这些有直接物理意义 的量(位移和转角)来形成的。
8.4.2 基本分析过程
结构有限元模型的运动方程:
& & [M ]{u&}+ [C ]{u}+ [K ]{u} = {p(t )}
有限元模型的节点系运动方程与前面介绍的框架结构的 运动方程在形式上完全相同,不同之处仅在于单元刚 度矩阵和质量阵的形成上。本节介绍的形成单元刚度 阵和质量阵的方法更具通用性。 前面所介绍的结构动力方程的解法,例如振型叠加法、 Fourier变换方法、时域逐步积分法等均可以用于结构 有限元模型的动力反应问题分析。
i=1
4
ψi的定义是ui发生单位位移, 而其余自由度不动, 即完全约束时, 梁单元的位移(线位移),因此,ψi(x)满足如下边界条件:
i = 1 : ψ 1 (0) = 1, ψ 1' (0) = ψ 1 ( L) = ψ 1' ( L) = 0
' ' i = 2 : ψ 2 (0) = 1, ψ 2 (0) = ψ 2 ( L) = ψ 2 ( L) = 0 ' ' i = 3 : ψ 3 ( L) = 1, ψ 3 (0) = ψ 3 (0) = ψ 3 ( L) = 0 ' ' i = 4 : ψ 4 ( L) = 1, ψ 4 (0) = ψ 4 (0) = ψ 4 ( L) = 0
8.4.1 有限元离散化
采用有限元法离散时,首先将一根梁分成有限段,称为 有限单元。每一个单元的尺寸可以是任意的,可以完 全相同,也可以完全不相同。这些单元仅仅在单元间 的节点上连续(连接)。 在这个简单的例子中,节点就是单元的端点,在每一个 节点上有两个自由度,横向位移和转角。 在有限元法中节点的位移(包括横向位移和转角)被选 为广义坐标。而运动方程就是用这些有直接物理意义 的量(位移和转角)来形成的。
结构动力学课件—dyanmics-of-structures-ch8知识资料18页PPT

If it is assumed that damping stresses are developed in proportion to the strain velocity, a uniaxial stressstrain relation of the form Using this equation, the basic relations may be expressed as follows:
The potential energy
kinetic energy
CHAPTER 8. GENERALIZED SDOF SYSTEMS
Generalized SDOF:
CHAPTER 8. GENERALIZED SDOF SYSTEMS
84 SELECTION OF THE RAYLEIGH VIBRATION SHAPE
CHAPTER 8. GENERALIZED SDOF SYSTEMS
谢谢!
CHAPTER 8. GENERABiblioteka IZED SDOF SYSTEMS
Example E82.
CHAPTER 8. GENERALIZED SDOF SYSTEMS
82 GENERALIZED PROPERTIES: DISTRIBUTED FLEXIBILITY
CHAPTER 8. GENERALIZED SDOF SYSTEMS
CHAPTER 8. GENERALIZED SDOF SYSTEMS
CHAPTER 8. GENERALIZED SDOF SYSTEMS
CHAPTER 8. GENERALIZED SDOF SYSTEMS
Example E83.
CHAPTER 8. GENERALIZED SDOF SYSTEMS
The potential energy
kinetic energy
CHAPTER 8. GENERALIZED SDOF SYSTEMS
Generalized SDOF:
CHAPTER 8. GENERALIZED SDOF SYSTEMS
84 SELECTION OF THE RAYLEIGH VIBRATION SHAPE
CHAPTER 8. GENERALIZED SDOF SYSTEMS
谢谢!
CHAPTER 8. GENERABiblioteka IZED SDOF SYSTEMS
Example E82.
CHAPTER 8. GENERALIZED SDOF SYSTEMS
82 GENERALIZED PROPERTIES: DISTRIBUTED FLEXIBILITY
CHAPTER 8. GENERALIZED SDOF SYSTEMS
CHAPTER 8. GENERALIZED SDOF SYSTEMS
CHAPTER 8. GENERALIZED SDOF SYSTEMS
CHAPTER 8. GENERALIZED SDOF SYSTEMS
Example E83.
CHAPTER 8. GENERALIZED SDOF SYSTEMS
结构动力学

一、绪论
1.1 阪神地震
首先请大家看日本阪 神地震录像,希望能从 中体会到学习结构动力 学的重要性。 更希望大家能学好结 构动力学(三要素),且作用
结果使受荷物体质量的加速度(惯性力与外荷比)不
可忽视,这种荷载称动力荷载,简称动荷。
自重、缓慢变化的荷载,其惯性力与外荷比很小, 分析时仍视作静荷载。 静荷只与作用位臵有关,而动荷是坐标和时间的函 数。
二、体系的运动方程建立
2.1 建立运动方程的基本步骤 2.2 运动方程建立举例
2.3 体系运动方程的一般形式
2.4 应注意的几个问题
2.5 刚度法、柔度法列方程的步骤
2.6 运动方程建立总结
2.1 建立运动方程的基本步骤
作为本科学习,这里只讨论用达朗泊尔原理通过列 平衡方程得到运动方程的“直接平衡法”。以下讨论 列平衡方程称刚度法 中一律认为系统的阻尼是等效粘滞阻尼。 直接平衡法列方程的一般步骤为: 1) 确定体系的自由度——质量独立位移数; 2) 建立坐标系,确定未知位移(坐标正向为正); 3) 根据阻尼理论确定质量所受的阻尼力; 4) 根据达朗泊尔原理在质量上假想作用有惯性力 (注意:惯性力是实际的,但它不作用在质量上); 5) 取质量为隔离体并作受力图; 6) 根据达朗泊尔原理列每一质量的瞬时动力平衡方 程,此方程就是运动(微分)方程。
1.6 建立结构运动方程的一般方法
3) 利用哈密顿原理来建立运动方程——变分法 分析力学中学过哈密顿原理。通过建立系统动能、 势能和耗能(分别记作 T、EP、V),获得如下哈密 顿泛函
H (T E P V )dt
t1
t2
根据哈密顿原理,可由令哈密顿泛函的一阶变分等于 零来建立“动平衡方程”——运动方程。 当没有耗能时,所得到的是无阻尼的方程。否则, 是有阻尼情况。 用哈密顿原理时和上两方法不同,不再考虑惯性力、 阻尼例和弹性恢复力等,它们通过能量变分来得到。
结构动力学-8-精品文档
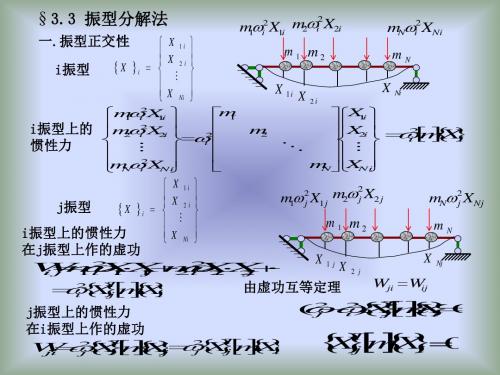
例:已知图示体系的第一振型, 试求第二振型.
m
EI
2.23 X1 ; 1
解:
T 1
l EI l
y1
m y2
X m0 12 X m X 2 . 23 1 0 2 X 02 m 22
2 . 23 mX 2 mX 0 12 22
2 k X m X i i i
2i
T T 2 X k X X m X i j i j i
X k X 0 i
T j
m22 j X2 j m12 X j 1j
m 1 m2
1 j
mN2 j XNj
m
EI
l EI l
y1
m y2
2 . 23 0 . 897 X ; X 1 2 1 1
m m 2 m
T 1
18 12 7 EI k 1 7 18 48 l3 7 7
i振型上的惯性力 在j振型上作的虚功
mN
X
Nj
X 2 2 W m X X m X X ij 1i 1 i 1 j 2i 2 i 2 j
2 X m X i j i T
X
2 j
由虚功互等定理
j振型上的惯性力 在i振型上作的虚功
2 j T i
2 (2 X m X 0 j i) j i T
Wji W ij
X m X W X m X i ji j
2 j T j
T X m X 0 j i
振型对质量的正交性的物理意义
哈尔滨工业大学结构动力学课件第八次课
12 EI
9 11 33 12
3
Y ( F M Y ) M Y Y F M Y kY F
1
..
..
..
书后习题
拉格朗日方法
通常当质点较多,约束比较复杂时,适合用能量分析 方法,例如Lagrange第2类方程。
拉格拉日方程, L T U ,
对于 m 个质点的质点系, 共约束是 r 个, 那么广义 坐标系 n=3m-r 个,也就是有 n 个自由度数。
刚体在空间运动有六个 DOF
有限单元法将连续体离散成若干有限单元构成
3.1.2 多自由度系统振动微分方程的建立。 可用牛顿力学与分析力学的任何一种方法均 可,常用的牛顿法、达朗贝尔原理、Lagrange 第二 类方程、有限元方法等。 牛顿法:
dt qi
M q Kq 0
..
无阻尼受迫振动
d T 对于有耗散力的方程为
dt qi qi 有阻尼受迫振动
U Qi d T dt qU qi i Q
qi
i
d T dt qi
.. .. ..
m
y2 F1 m1 y1 21 F2 m2 y 2 22 F3 m3 y3 23 11 l 3 2 2 3 3 2 1 1 2 3 12 EI 3 3 .. 7 .. l 16 l .. l y F 31 22 3 F1 m1 y111 31 2 9 m2 y 2 1332 F3 m3 y3 33 33 y12 EI1 m1 y1 11 F2 m2 F 12 EI 1 12 EI
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
X1i
X2i
m m 1 2
X1 j X2 j
mN
X Nj
j振型
{X} [m]{X}i = 0
T j
{X}T [k]{X}i = 0 j
X} j [ m]{ X} j = M* { j
T
X} j [ k]{ X} j = K* { j
T
三.广义质量、广义刚度、振型矩阵、振型的规范化 广义质量、广义刚度、振型矩阵、 1.广义质量、 1.广义质量、广义刚度 广义质量
* K1
* K2
* M1 = O * Kn
* M2
2 ω1 2 ω2 O O * 2 Mn ωn
[K ] = [M ][ω ]
* * 2
3.振型的规范化 3.振型的规范化 归一化振型 标准化振型
[k]{X}j = ω2[m]{X}j j
{X}T [k]{X}j = ω2{X}T [m]{X}j j j j
{X}T [k]{X}j j ω2 = j {X}T [m]{X}j j
K* = {X}j [k]{X}j j
T
=
K* j M* j
---广义刚度 ---广义刚度 ---广义质量 ---广义质量
* * 2
{X}1 =
{X}
0 i
=
采用标准化振型时
[K ] = [M ][ω ]
Ki* = ωi2
[K ] = [ω ]
* 2
四.坐标的耦联与解耦、正则坐标 坐标的耦联与解耦、 1.坐标的耦联 1.坐标的耦联
mnω Xn
2mnຫໍສະໝຸດ Xn& & MY + KY = 0
刚度耦联、阻尼耦联、 刚度耦联、阻尼耦联、质量耦联
[X ]T [k][X ] = [X ]T [m][X ][ω2 ]
* K1 [X ]T [k][X ] = * K2
= K* O * Kn
[ ]
---广义刚度 ---广义刚度 矩阵
* M1 [X ]T [m][X ] = * K1
M* = {X}j [m]{X}j j
T
2.振型矩阵 2.振型矩阵
[X ] = [{X}1{X}2 L{X}n ]
---振型矩阵 ---振型矩阵
[X ]T [k][X ] = [X ]T [m][X ][ω2 ]
{X}T [k]{X} 1 1 {X}T [k]{X}1 2 = L
&& M Xq + KXq = 0
&& X T M Xq + X T KXq = 0
2.耦联坐标的解耦(利用振型矩阵关于K 2.耦联坐标的解耦(利用振型矩阵关于K、M的正交性) 耦联坐标的解耦 的正交性)
& + X T KXq = 0 X M & Xq
T
& & M q+K q =0
* *
--- n个单自由度方程 坐标 称为正则坐标
T
qj (0) =
{ X} j [ m]{ y(0)}
T
M* j & { X} j [ m]{ y(0)}
T
同理
& qj (0) =
M* j
q j (t ) = q j (0) cos ωt +
* K1 =
T {X}1 [k]{X}2 {X}T [k]{X}2 2
L
O * Kn
L L L L L L
* K2
[X ] = [{X}1{X}2 L{X}n ]
振型方程
---振型矩阵 ---振型矩阵
[k]{X}1 = ω12[m]{X}1 2 [k]{X}2 = ω2 [m]{X}2
q
{X}T [k]{X}j j ω2 = j {X}T [m]{X}j j
=
K* j M* j
由原体系的初始条件确定正则体系的初始条件: 由原体系的初始条件确定正则体系的初始条件:
{ y(0)} = ∑{ X}i qi (0)
i=1
n
{X}T [m] 左乘 j
{ X} j [ m]{ y(0)} = M*qj (0) j
m2ω X2
2
m2 m1
X2 X1
mω2 X1 1
2.耦联坐标的解耦(利用振型矩阵关于K、M的正交性) 2.耦联坐标的解耦(利用振型矩阵关于K 耦联坐标的解耦 的正交性)
X = { X}1 { X}2 L X}n {
---振型矩阵已知 ---振型矩阵已知
设:
&& && Y = Xq, Y = Xq
1 {X}1 = 1.618
k
k
m
使确定其标准化振型。 使确定其标准化振型。
M
0* 1
EI1 = ∞
m = [ 1.618] 1 0
1 M
0* i
0 1 .618 = 3.6179m m 1
1 1 1 3.6179m .618
LL 2 [k]{X}n = ωn [m]{X}n
[k][ X ] = [m][ X ][ω2 ]
---振型方程 ---振型方程
[ω ]
2
2 ω1 =
2 ω2
---频率矩阵 ---频率矩阵 O 2 ωn
[X ]T [k][X ] = [X ]T [m][X ][ω2 ]
{X}T [m]{X}i i
= Mi* =1
求 {X}i0的标准化振型 {X}i : 0 设:{X}i =α{X}i
Mi* = {X}i [m]{X}i =α2{X}i
T 0T
[m]{X}i0 = 1
α 2 = 1/ Mi0*
{X}i
= α{X}i =
0
1
Mi
{X}i0 0*
m
EI1 = ∞
例.已知图示体系的基本振型为
二.振型的正交性 i振型
{X}i
X1i X = 2i M Xni
m2ωi2 X2i mω X1i 1
2 i
mNωi2 X Ni
m m 1 2
mN
XNi
i振型
j振型
{X}j
X1 j X 2j = M Xnj
* M2
= M* O * Mn
[
]
---广义质量 ---广义质量 矩阵
* K2
* M1 = O * Kn
* M2
2 ω1 2 ω2 O O * 2 Mn ωn
