贾俊平2009年统计学第4章数据的概括性度量
精选人大版,贾俊平,第五版,统计学第4章数据的概括性度量资料

R
. =
最高组上限
-
最低组下限
2. 平均差
1. 离散程度的测度值之一
2. 各变量值与其均值离差绝对值的平均数
3. 能全面反映一组数据的离散程度
4. 数学性质较差,实际中应用较少
5. 计算公式为
未分组数据 组距分组数据
N
Xi X
M D i1 N K X i X Fi
M D i1 K
QD = QU - QL =3–2 =1
4.2.3 数值型数据:方差和标准差 1.极差
1. 一组数据的最大值与最小值之差
2. 离散程度的最简单测度值
3. 易受极端值影响
4. 未考虑数据的分布 5. 计算公式为
7 8 9 10
7 8 9 10
未分组数据 R = max(Xi) - min(Xi)
组距分组数据
QU位置=3×50/4=37.5
350 30
QU 125
4 10
5 128.75(个)
4.1.3 数值型数据:平均值 1.集中趋势的测度值之一 2.最常用的测度值 3.一组数据的均衡点所在 4.易受极端值的影响 5.用于数值型数据,不能用于定类数据和定
序数据
均值(计算公式)
M0
125
(14
14 10 8) (14
10)
5
123(个)
4.1.2 顺序数据:中位数和分位数 1.中位数
集中趋势的测度值之一 排序后处于中间位置上的值 不受极端值的影响 主要用于定序数据,也可用数值型数据,但不能
用于定类数据
各变量值与中位数的离差绝对值之和最小,即
25% 25% 25% 25%
贾俊平《统计学》考研真题(含复试)与典型习题详解(数据的概括性度量)【圣才出品】

2.统计学期中考试非常简单,为了评估简单程度,教师记录了 9 名学生交上考试试卷
的时间如下(分钟)
33 29
45 60 42 19 52 38 36[东北财经大学
2012 研]
(1)这些数据的极差为( )。
A.3.00
B.-3.00
C.41.00
D.-41.00
【答案】C
【解析】数据按从小到大排序结果如下:
A.0.38
B.0.40
C.0.54
D.2.48
【答案】A
【解析】离散系数也称为变异系数,它是一组数据的标准差与其相应的平均数之比。其
计算公式为: vs
s x
。得到 vs
22.85 0.38 。 12.45
9.已知某工厂生产的某零件的平均厚度是 2 厘米,标准差是 0.25 厘米。如果已知该 厂生产的零件厚度为正态分布,可以判断厚度在 1.5 厘米到 2.5 厘米之间的零件大约占 ( )。[浙江工商大学 2011 研]
圣才电子书 十万种考研考证电子书、题库视频学习平台
5.随机变量 X 的方差为 2,随机变量 Y=2X,那么 y 的方差是( )。[中央财经大学 2011 研]
A.1 B.2 C.4 D.8 【答案】D
【解析】Var(cX ) c2Var(X ) 22 2 8
7.设 X1,X2,…,X n 为随机样本,则哪个统计量能较好地反映样本值的分散程度( )。
[中山大学 2012 研] A.样本平均 B.样本中位数 C.样子书
【答案】C
十万种考研考证电子书、题库视频学习平台
【解析】集中趋势是指 一 组 数 据 向 某 一 中 心 值 靠 拢 的 程 度 ,它 反 映 了 一 组 数 据 中 心
统计学第四章习题答案 贾俊平
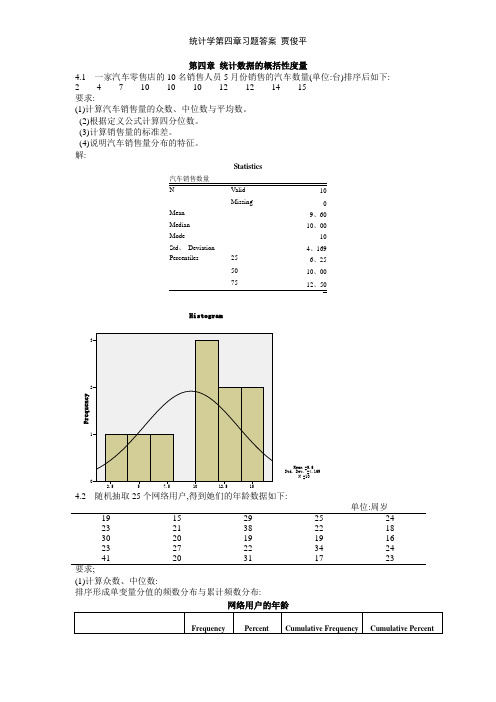
第四章 统计数据的概括性度量4.1 一家汽车零售店的10名销售人员5月份销售的汽车数量(单位:台)排序后如下: 2 4 7 10 10 10 12 12 14 15 要求:(1)计算汽车销售量的众数、中位数与平均数。
(2)根据定义公式计算四分位数。
(3)计算销售量的标准差。
(4)说明汽车销售量分布的特征。
解:Statistics汽车销售数量 10 Missing0 Mean 9、60 Median 10、00Mode10 Std 、 Deviation 4、169 Percentiles25 6、25 50 10、00 75单位:周岁19 15 29 25 24 23 21 38 22 18 30 20 19 19 16 23 27 22 34 24 41 20 3117 23要求;(1)计算众数、中位数:排序形成单变量分值的频数分布与累计频数分布:网络用户的年龄(2)根据定义公式计算四分位数。
Q1位置=25/4=6、25,因此Q1=19,Q3位置=3×25/4=18、75,因此Q3=27,或者,由于25与27都只有一个,因此Q3也可等于25+0、75×2=26、5。
(3)计算平均数与标准差;Mean=24、00;Std、Deviation=6、652(4)计算偏态系数与峰态系数:Skewness=1、080;Kurtosis=0、773(5)对网民年龄的分布特征进行综合分析:分布,均值=24、标准差=6、652、呈右偏分布。
如需瞧清楚分布形态,需要进行分组。
1、确定组数:()lg 25lg() 1.398111 5.64lg(2)lg 20.30103n K =+=+=+=,取k=6 2、确定组距:组距=( 最大值 - 最小值)÷ 组数=(41-15)÷6=4、3,取53、分组频数表网络用户的年龄 (Binned)分组后的直方图::一种就是所有颐客都进入一个等待队列:另—种就是顾客在三千业务窗口处列队3排等待。
统计学第四章习题答案 贾俊平

第四章统计数据的概括性度量4.1 一家汽车零售店的10名销售人员5月份销售的汽车数量(单位:台)排序后如下:2 4 710 10 10 12 12 14 15要求:(1)计算汽车销售量的众数、中位数和平均数.(2)根据定义公式计算四分位数。
(3)计算销售量的标准差。
(4)说明汽车销售量分布的特征。
解:Statistics10Missing0Mean9.60Median10.00Mode10Std。
Deviation4。
169Percentiles25 6.255010.0075单位:周岁19152925242321382218302019191623272234244120311723要求;(1)计算众数、中位数:排序形成单变量分值的频数分布和累计频数分布:网络用户的年龄(2)根据定义公式计算四分位数。
Q1位置=25/4=6。
25,因此Q1=19,Q3位置=3×25/4=18.75,因此Q3=27,或者,由于25和27都只有一个,因此Q3也可等于25+0.75×2=26.5.(3)计算平均数和标准差;Mean=24.00;Std. Deviation=6.652(4)计算偏态系数和峰态系数:Skewness=1.080;Kurtosis=0.773(5)对网民年龄的分布特征进行综合分析:分布,均值=24、标准差=6.652、呈右偏分布。
如需看清楚分布形态,需要进行分组。
1、确定组数:()lg 25lg() 1.398111 5.64lg(2)lg 20.30103n K =+=+=+=,取k =6 2、确定组距:组距=( 最大值 — 最小值)÷ 组数=(41-15)÷6=4。
3,取53、分组频数表网络用户的年龄 (B in ned)分组后的直方图::一种是所有颐客都进入一个等待队列:另—种是顾客在三千业务窗口处列队3排等待。
为比较哪种排队方式使顾客等待的时间更短.两种排队方式各随机抽取9名顾客。
统计学第五版(贾俊平)课后习题答案

300~ 350 400
30 -13520652.3 1036628411.8
400~ 450 42 500
533326.9 12442517.1
500~ 550 600
18
33765928.7 4164351991.6
600以上 650 11 122527587.627364086138.8 合计 — 120 38534964.451087441648.4
7.8已知:总体服从正态分布,但未知,为小样本,,。 根据样本数据计算得:,。 总体均值的95%的置信区间为: ,即(7.11,12.89)。
7.9已知:总体服从正态分布,但未知,为小样本,,。 根据样本数据计算得:,。 从家里到单位平均距离的95%的置信区间为: ,即(7.18,11.57)。
7.10(1)已知: ,,,。 由于为大样本,所以零件平均长度的95%的置信区间为: ,即(148.87,150.13)。 (2)在上面的估计中,使用了统计中的中心极限定理。该定理表明: 从均值为、方差为的总体中,抽取容量为的随机样本,当充分大时(通 常要求),样本均值的抽样分布近似服从均值为、方差为的正态分布。
7.13已知:总体服从正态分布,但未知,为小样本,,。 根据样本数据计算得:,。 网络公司员工平均每周加班时间的90%的置信区间为: ,即(10.36,16.76)。
7.14(1)已知:,,,。 总体总比例的99%的置信区间为: ,即(0.32,0.70); (2)已知:,,,。 总体总比例的95%的置信区间为: ,即(0.78,0.86); (3)已知:,,,。 总体总比例的90%的置信区间为: ,即(0.46,0.50)。
500~600 550 18 9900
600以上 650 11 7150
贾俊平《统计学》(第7版)考研真题与典型题详解-第4章 数据的概括性度量【圣才出品】

第4章数据的概括性度量一、单项选择题1.一组数据的峰度系数为3.5,则该数据的统计分布应具有的特征是()。
[中央财经大学2018研]A.扁平分布B.尖峰分布C.左偏分布D.右偏分布【答案】B【解析】峰度系数用来度量数据在中心的聚集程度。
在正态分布情况下,峰度系数值是3。
大于3的峰度系数说明观察量更集中,有比正态分布更短的尾部;小于3的峰度系数说明观测量不那么集中,有比正态分布更长的尾部,类似于矩形的均匀分布。
2.某企业男性职工占80%,月平均工资为450元,女性职工占20%,月平均工资为400元,该企业全部职工的平均工资为()。
[中央财经大学2015研] A.425元B.430元C.435元D.440元【答案】D【解析】企业全部职工的平均工资=男性职工比例×男性月平均工资+女性职工比例×女性月平均工资=80%×450+20%×400=440(元)。
3.15位同学的某门课程考试成绩中,70分出现3次,80分出现4次,85分出现6次,90分出现2次,则他们成绩的众数为()。
[华中农业大学2015研] A.80B.85C.81.3D.90【答案】B【解析】众数是一组数据中出现次数最多的变量值。
题中,85分出现次数最多,故成绩的众数为85分。
4.一组样本的变异系数(CV)等于10,样本均值为5,则样本方差为()。
[厦门大学2014研]A.2B.4C.0.5D.2500【答案】D【解析】变异系数是一组数据的标准差与其相应的平均数之比,因而样本标准差=样本均值×变异系数=5×10=50,样本方差=50×50=2500。
5.现抽取了10个同学,每个同学的月生活费数据排序后为:660,750,780,850,960,1080,1250,1500,1630,2000。
则中位数的位置为()。
[重庆大学2013研]A.5.5B.5C.4D.6【答案】A【解析】中位数是将样本排序后处于中间位置的数据,总共有10个样本,因此中位数的位次=(1+10)/2=5.5。
统计学第4章数据的概括性度量

https://
REPORTING
• 引言 • 集中趋势的度量 • 离散程度的度量 • 偏态与峰态的度量 • 数据分布形态的图形表示 • Excel在概括性度量中的应用
目录
PART 01
引言
REPORTING
WENKU DESIGN
概括性度量的定义
方差和标准差能够全面反映数据的离散程度,且计算相对简单。其中标
准差具有与原始数据相同的量纲,更便于比较不同数据集之间的离散程
度。
PART 04
偏态与峰态的度量
REPORTING
WENKU DESIGN
偏态及其度量
偏态定义
偏态是指数据分布的不对称性。 在统计学中,偏态通常通过计算 偏态系数来衡量。
特点
算术平均数对极端值敏感,当数 据集中存在极端异常值时,算术
平均数可能会受到较大影响。
中位数
定义
计算公式
中位数是一组数据按照大小顺序排列后, 位于中间位置的数值,用于反映数据集中 趋势的一个统计指标。
中位数 = 第(n+1)/2项数据(n为数据个数 )适用Fra bibliotek围特点
适用于数值型数据,且数据分布呈偏态或 存在极端异常值的情况。
偏态与峰态度量
包括偏态系数和峰态系数 等,用于描述数据分布的 形态特点。
PART 02
集中趋势的度量
REPORTING
WENKU DESIGN
算术平均数
定义
算术平均数是一组数据的总和 除以数据的个数,用于反映数 据集中趋势的一个统计指标。
计算公式
算术平均数 = 数据总和 / 数据 个数
适用范围
适用于数值型数据,且数据之 间没有极端异常值的情况。
统计学第四章习题答案 贾俊平

第四章统计数据的概括性度量4.1 一家汽车零售店的10名销售人员5月份销售的汽车数量(单位:台)排序后如下:2 4 7 10 10 10 12 12 14 15要求:(1)计算汽车销售量的众数、中位数和平均数。
(2)根据定义公式计算四分位数。
(3)计算销售量的标准差。
(4)说明汽车销售量分布的特征。
解:Statistics10Missing 0Mean 9.60Median 10.00Mode 10Std. Deviation 4.169Percentiles 25 6.2550 10.0075单位:周岁19 15 29 25 2423 21 38 22 1830 20 19 19 1623 27 22 34 2441 20 31 17 23要求;(1)计算众数、中位数:排序形成单变量分值的频数分布和累计频数分布:网络用户的年龄(2)根据定义公式计算四分位数。
Q1位置=25/4=6.25,因此Q1=19,Q3位置=3×25/4=18.75,因此Q3=27,或者,由于25和27都只有一个,因此Q3也可等于25+0.75×2=26.5。
(3)计算平均数和标准差;Mean=24.00;Std. Deviation=6.652(4)计算偏态系数和峰态系数:Skewness=1.080;Kurtosis=0.773(5)对网民年龄的分布特征进行综合分析:分布,均值=24、标准差=6.652、呈右偏分布。
如需看清楚分布形态,需要进行分组。
1 k=6 2)÷6=4.3,取53、分组频数表网络用户的年龄 (Binned)分组后的直方图:种是所有颐客都进入一个等待队列:另—种是顾客在三千业务窗口处列队3排等待。
为比较哪种排队方式使顾客等待的时间更短.两种排队方式各随机抽取9名顾客。
得到第一种排队方式的平均等待时间为7.2分钟,标准差为1.97分钟。
第二种排队方式的等待时间(单位:分钟)如下:5.5 6.6 6.7 6.8 7.1 7.3 7.4 7.8 7.8要求:(1)画出第二种排队方式等待时间的茎叶图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
统计学
STATISTICS (第四版)
众数
(不惟一性)
无众数 原始数据: 一个众数 原始数据:
10 6
5 5
9 12 9 8
6 5
8 5
多于一个众数 原始数据: 25 28 28 36 42 42
4 - 10
统计学
STATISTICS (第四版)
分类数据的众数
(例题分析)
百分比 (%)
4 - 24
统计学
STATISTICS (第四版)
数值型数据的四分位数
(9个数据的算例)
1500 750 780 1080 850 960 2000 1250 1630 750 780 850 960 1080 1250 1500 1630 2000
【例】:9个家庭的人均月收入数据
原始数据: 排 序: 位 置:
1
2
方法3
9 1 2 1 Q位置 3 2
3
4
5
6
7
8
9
QL 850
4 - 25
QU 1500
统计学
STATISTICS (第四版)
数值型数据的四分位数
(9个数据的算例)
1500 750 780 1080 850 960 2000 1250 1630 750 780 850 960 1080 1250 1500 1630 2000
【例】:10个家庭的人均月收入数据
排 位 序: 置:
1 2
3
4
5
6
7
8
9
10
n 1 10 1 位置 5.5 2 2
960 1080 中位数 1020 2
4 - 18
统计学
STATISTICS (第四版)
四分位数
(quartile)
1. 排序后处于25%和75%位置上的值
不同品牌饮料的频数分布 饮料品牌 频数 比例
解:这里的变量为“饮 料品牌”,这是个分类 变量,不同类型的饮料 就是变量值 所调查的50人中,购 买可口可乐的人数最多 ,为15人,占被调查总 人数的30%,因此众数 为“可口可乐”这一品 牌,即
Mo=可口可乐
可口可乐 旭日升冰茶 百事可乐 汇源果汁 露露 合计
方法1:定义算法
方法2:较准确算法
4 - 20
统计学
STATISTICS (第四版)
四分位数
(位置的确定)
Q位置 n 1 2 1 2
方法3:
其中[ ]表示中位数的位置取整。这样计算出的四分位数的 位置,要么是整数,要么在两个数之间0.5的位置上 方法4: Excel给出的四分位数位置的确定方法
STATISTICS (第四版)
数值型数据的四分位数
(9个数据的算例)
1500 750 780 1080 850 960 2000 1250 1630 750 780 850 960 1080 1250 1500 1630 2000
【例】:9个家庭的人均月收入数据(4种方法计算)
原始数据: 排 序: 位 置:
4 - 2
统计学
STATISTICS (第四版)
哪名运动员的发挥更稳定?
最会的比赛结果是,中国运动员郭文珺凭借决赛的稳 定发挥,以总成绩492.3环夺得金牌,预赛排在第1名 的俄罗斯运动员纳塔利娅· 帕杰林娜以总成绩498.1环 获得银牌,预赛排在第4名的格鲁吉亚运动员妮诺· 萨 卢克瓦泽以总成绩487.4环的成绩获得铜牌,而预赛 排在第3名的蒙古运动员卓格巴德拉赫· 蒙赫珠勒仅以 479.6环的成绩名列第8名 由此可见,在射击比赛中,运动员能否取得好的成绩 ,发挥的稳定性至关重要。那么,怎样评价一名运动 员的发挥是否稳定呢?通过本章内容的学习就能很容 易回答这样的问题
4. 低层次数据的测度值适用于高层次的测量数据,但高 层次数据的测度值并不适用于低层次的测量数据
4 - 7
统计学
STATISTICS (第四版)
分类数据:众数
4 - 8
统计学
STATISTICS (第四版)
众数
(mode)
1. 一组数据中出现次数最多的变量值
2. 适合于数据量较多时使用 3. 不受极端值的影响 4. 一组数据可能没有众数或有几个众数 5. 主要用于分类数据,也可用于顺序数据和 数值型数据
x
N
i
统计学
STATISTICS (第四版)
加权平均数-分组数据
(Weighted mean)
设各组的组中值为:M1 ,M2 ,… ,Mk 相应的频数为: f1 , f2 ,… ,fk 样本加权平均
M 1 f1 M 2 f 2 M k f k x f1 f 2 f k M 1 f1 M 2 f 2 M k f k f1 f 2 f k
1
2
方法1
3
4
5
6
7
8
9
9 QL 位置 2.25 4
3 9 QU 位置 6.75 4
QL 780 (850 780) 0.25 QU 1250 (1500 1250) 0.75 1437.5 797.5
4 - 23
统计学
STATISTICS (第四版)
4 - 16
从累计频数看, 中位数在“一般”这 一组别中 中位数为
Me=一般
统计学
STATISTICS (第四版)
数值型数据的中位数
(9个数据的算例)
9个家庭的人均月收入数据
1500 750 780 1080 850 960 2000 1250 1630 750 780 850 960 1080 1250 1500 1630 2000
【例】
原始数据: 排 序: 位 置:
1
2
3
4
5
6
7
8
9
n 1 9 1 位置 5 2 2 中位数 1080
4 - 17
统计学
STATISTICS (第四版)
数值型数据的中位数
(10个数据的算例)
660 750 780 850 960 1080 1250 1500 1630 2000
4 - 11
15 11 9 6 9 50
0.30 0.22 0.18 0.12 0.18 1
30 22 18 12 18 100
统计学
STATISTICS (第四版)
顺序数据的众数
(例题分析)
甲城市 户数 (户) 百分比 (%)
甲城市家庭对住房状况评价的频数分布 回答类别
解:这里的数据为顺 序数据。变量为“回 答类别” 甲城市中对住房 表示不满意的户数最 多 , 为 108户 , 因 此 众数为“不满意”这 一类别,即
统计学
STATISTICS (第四版)
第 4 章 数据的概括性度量
作者:中国人民大学统计学院 4 - 1
贾俊平
统计学
STATISTICS (第四版)
哪名运动员的发挥更稳定?
在奥运会女子10米气手枪比赛中,每个运动员首先进行 每组10抢共4组的预赛,然后根据预赛总成绩确定进入决 赛的8名运动员。决赛时8名运动员再进行10枪射击,再 将预赛成绩加上决赛成绩确定最后的名次 在2008年8月10日举行的第29届北京奥运会女子10米气 手枪决赛中,进入决赛的8名运动员的预赛成绩和最后10 枪的决赛成绩如下表
QL位置
4 - 21
n3 3n 1 QU位置 4 4
如果位置不是整数,则按比例分摊位置两侧数值的差值
统计学
STATISTICS (第四版)
顺序数据的四分位数
(例题分析)
解:QL位置= (300)/4 =75 QU位置 =(3×300)/4 =225 不 从累计频数看, QL 在“ 甲城市
50%
Me
50%
2. 不受极端值的影响 3. 主要用于顺序数据,也可用数值型数据,但不能 用于分类数据
4 - 14
统计学
STATISTICS (第四版)
中位数
(位置和数值的确定)
n 1 位置确定 中位数位置 2
x n 1 2 Me 1 x n x n 1 2 2 2 n为奇数
4 - 3
统计学
STATISTICS (第四版)
第 4 章 数据的概括性度量
4.1 集中趋势的度量 4.2 离散程度的度量 4.3 偏态与峰态的度量
4 - 4
统计学
STATISTICS (第四版)
学习目标
1. 2. 3. 4. 5. 6.
4 - 5
集中趋势各测度值的计算方法 集中趋势各测度值的特点及应用场合 离散程度各测度值的计算方法 离散程度各测度值的特点及应用场合 偏态与峰态的测度方法 用Excel计算描述统计量并进行分析
平均数
(mean)
1. 也称为均值,一组数据相加后除以数据的个数得 到的结果 2. 集中趋势的最常用测度值 x 3. 一组数据的均衡点所在 4. 体现了数据的必然性特征 5. 易受极端值的影响 6. 有简单平均数和加权平均数之分 7. 根据总体数据计算的,称为平均数,记为;根据 样本数据计算的,称为样本平均数,记为x
非常不满意 不满意 一般 满意 非常满意
合计
4 - 12
24 108 93 45 30
300
8 36 31 15 10
100.0
Mo=不满意
统计学
STATISTICS (第四版)
顺序数据:中位数和分位数
