立体几何练习题六
立体几何练习题

E立体几何练习题1.在直四棱住1111D C B A ABCD -中,12AA =,底面是边长为1的正方形,E 、F 、G 分别是棱B B 1、D D 1、DA 的中点.(Ⅰ)求证:平面E AD 1//平面BGF ; (Ⅱ)求证:1D E ⊥面AEC .2.如图,正方体1111D C B A ABCD -的棱长为2,E 为AB 的中点. (1)求证: 1BDD AC 平面⊥(2)求点B 到平面EC A 1的距离.3.如图所示,在三棱柱111ABC A B C -中,1AA ⊥平面,90ABCACB ∠=,2AB =1BC =1AA =. (Ⅰ)求三棱锥111A AB C -的体积;(Ⅱ)若D 是棱1CC 的中点,棱AB 的中点为E , 证明:11//C AB DE 平面4.如图,在棱长均为2的三棱柱ABC DEF -中,设侧面四边形FEBC 的两对角线相交于O ,若BF ⊥平面AEC ,AB AE =.(1) 求证:AO ⊥平面FEBC ; (2) 求三棱锥B DEF -的体积.FEABD CG 1C 1A1B 1D 1B 1C ED CBA1D 1A5.如图,在体积为1的三棱柱111C B A ABC -中,侧棱⊥1AA 底面ABC ,AB AC ⊥, 11==AA AC ,E 为线段AB 上的动点.(Ⅰ)求证: CA 1C CA 11⊥C 1E ;(2)线段AB 上是否存在一点E ,使四面体E-AB 1C 1的体积为61若存在,请确定点E 的位置;若不存在,请说明理由.6.已知三棱柱ABC —A 1B 1C 1的直观图和三视图如图所示,其主视图BB 1A 1A 和侧视图A 1ACC 1均为矩形,其中AA 1=4。
俯视图ΔA 1B 1C 1中,B 1C 1=4,A 1C 1=3,A 1B 1=5,D 是AB 的中点。
(1)求证:AC ⊥BC 1; (2)求证:AC 1∥平面CDB 1;(3)求异面直线AC 1与B 1C 所成角的余弦值。
立体几何第六讲面面垂直练习题(含答案)
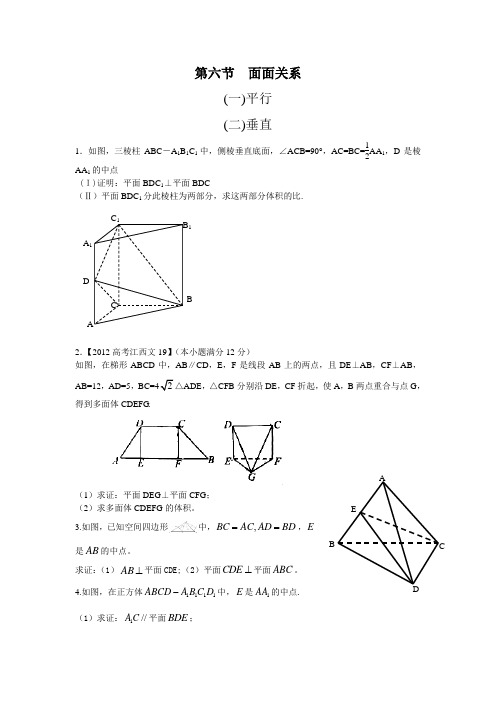
第六节 面面关系(一)平行 (二)垂直1.如图,三棱柱ABC -A 1B 1C 1中,侧棱垂直底面,∠ACB=90°,AC=BC=12AA 1,D 是棱AA 1的中点(I)证明:平面BDC 1⊥平面BDC(Ⅱ)平面BDC 1分此棱柱为两部分,求这两部分体积的比.2.【2012高考江西文19】(本小题满分12分)如图,在梯形ABCD 中,AB ∥CD ,E ,F 是线段AB 上的两点,且DE ⊥AB ,CF ⊥AB ,AB=12,AD=5,BC=42△ADE ,△CFB 分别沿DE ,CF 折起,使A ,B 两点重合与点G ,得到多面体CDEFG .(1)求证:平面DEG ⊥平面CFG ; (2)求多面体CDEFG 的体积。
3.如图,已知空间四边形中,,BC AC AD BD ==,E是AB 的中点。
求证:(1)⊥AB 平面CDE;(2)平面CDE ⊥平面ABC 。
4.如图,在正方体1111ABCD A B C D -中,E 是1AA 的中点. (1)求证:1//A C 平面BDE ;B 1C BADC 1A 1AEDBCA AC⊥平面BDE.(2)求证:平面15.已知四棱锥P—ABCD,底面ABCD是菱形,∠PDDAB,60平面ABCD,PD=AD,=⊥︒点E为AB中点,点F为PD中点.(1)证明平面PED⊥平面PAB;(2)求二面角P—AB—F的平面角的余弦值第六节 面面关系答案(一)平行 (二)垂直1.【命题意图】本题主要考查空间线线、线面、面面垂直的判定与性质及几何体的体积计算,考查空间想象能力、逻辑推理能力,是简单题.【解析】(Ⅰ)由题设知BC ⊥1CC ,BC ⊥AC ,1CC AC C ⋂=,∴BC ⊥面11ACC A , 又∵1DC ⊂面11ACC A ,∴1DC BC ⊥,由题设知01145A DC ADC ∠=∠=,∴1CDC ∠=090,即1DC DC ⊥,又∵DC BC C ⋂=, ∴1DC ⊥面BDC , ∵1DC ⊂面1BDC , ∴面BDC ⊥面1BDC ;(Ⅱ)设棱锥1B DACC -的体积为1V ,AC =1,由题意得,1V =1121132+⨯⨯⨯=12,由三棱柱111ABC A B C -的体积V =1,∴11():V V V -=1:1, ∴平面1BDC 分此棱柱为两部分体积之比为1:1.2.【解析】(1)由已知可得AE=3,BF=4,则折叠完后EG=3,GF=4,又因为EF=5,所以可得EG GF ⊥又因为CF EGF ⊥底面,可得CF EG ⊥,即EG CFG ⊥面所以平面DEG ⊥平面CFG . (2)过G 作GO 垂直于EF ,GO 即为四棱锥G-EFCD 的高,所以所求体积为11125520335DECF S GO ⋅=⨯⨯⨯=正方形3.证明:(1)BC AC CE AB AE BE =⎫⇒⊥⎬=⎭同理,AD BD DE AB AE BE =⎫⇒⊥⎬=⎭又∵CE DE E ⋂= ∴AB ⊥平面CDE (2)由(1)有AB ⊥平面CDE又∵AB ⊆平面ABC , ∴平面CDE ⊥平面ABC 4.证明:(1)设AC BD O ⋂=,∵E 、O 分别是1AA 、AC 的中点,∴1A C ∥EO又1AC ⊄平面BDE ,EO ⊂平面BDE ,∴1A C ∥平面BDE (2)∵1AA ⊥平面ABCD ,BD ⊂平面ABCD ,1AA BD ⊥ 又BD AC ⊥,1AC AA A⋂=,∴BD ⊥平面1A AC ,BD ⊂平面BDE ,∴平面BDE ⊥平面1A AC5.(1)证明:连接BD.ADB DAB AD AB ∆∴︒=∠=,60, 为等边三角形.E 是AB 中点,.DE AB ⊥∴⊥PD 面ABCD ,AB ⊂面ABCD ,.PD AB ⊥∴⊂DE 面PED ,PD ⊂面PED ,⊥∴=AB D PD DE , 面PED. ⊂AB 面PAB ,⊥∴PED 面面PAB.(2)解:⊥AB 平面PED ,PE ⊂面PED ,.PE AB ⊥∴ 连接EF ,⊂EF PED ,.EF AB ⊥∴PEF ∠∴为二面角P —AB —F 的平面角. 设AD=2,那么PF=FD=1,DE=3. 在,1,2,7,===∆PF EF PE PEF 中,147572212)7(cos 22=⨯-+=∠∴PEF 即二面角P —AB —F 的平面角的余弦值为.1475立体几何练习题1.设α、β、γ为两两不重合的平面,l 、m 、n 为两两不重合的直线,给出下列四个命题: 若α⊥γ,β⊥γ,则α∥β;②若m ⊂α,n ⊂α,m ∥β,n ∥β,则α∥β;③若α∥β,l ⊂α,则l ∥β;④若α∩β=l ,β∩γ=m ,γ∩α=n ,l ∥γ,则m ∥n . 其中真命题的个数是( ) A .1 B .2 C .3 D .42.正方体ABCD ﹣A 1B 1C 1D 1中,BD 1与平面ABCD 所成角的余弦值为() A .B .CD .3.三棱柱ABC ﹣A 1B 1C 1中,AA 1=2且AA 1⊥平面ABC ,△ABC 是 边长为的正三角形,该三棱柱的六个顶点都在一个球面上,则这个球的体积为() A . 8πB .C .D . 8π4.三个平面两两垂直,它们的三条交线交于点O ,空间一点P 到三个平面的距离分别为3、4、5,则OP 长为()A . 5B . 2C . 3D . 55.如图,四棱锥S ﹣ABCD 的底面为正方形,SD ⊥底面ABCD ,则下列结论中不正确的是() A . AC⊥SB B .AB∥平面SCDC . SA 与平面SBD 所成的角等于SC 与平面SBD 所成的角 D . AB 与SC 所成的角等于DC 与SA 所成的角6.如图,四棱锥P ﹣ABCD 的底面为正方形,PD ⊥底面ABCD ,PD=AD=1,设点CG 到平面PAB 的距离为d 1,点B 到平面PAC 的距离为d 2,则有( ) A . 1<d 1<d 2 B . d 1<d 2<1C . d 1<1<d 2D . d 2<d 1<17.在锐角的二面角βα--EF ,A EF ∈,AG α⊂, 45=∠GAE ,若AG 与β所成角为 30,则二面角βα--EF 为__________. 8.给出下列四个命题:(1)若平面α上有不共线的三点到平面β的距离相等,则βα//; (2)两条异面直线在同一平面内的射影可能是两条平行直线;(3)两条异面直线中的一条平行于平面α,则另一条必定不平行于平面α; (4)b ,a 为异面直线,则过a 且与b 平行的平面有且仅有一个. 其中正确命题的序号是_______________________9.已知正方体 1111ABCD A B C D -中,点E 是棱 11A B 的中点,则直线AE 与平而 11BDD B 所成角的正弦值是_________.EFA Gαβ10.已知直三棱柱111ABC A B C -中,090ABC ∠=,122AC AA ==,2AB =,M 为1BB 的中点,则1B 与平面ACM 的距离为______11.边长分别为a 、b 的矩形,按图中所示虚线剪裁后,可将两个小矩形拼接成一个正四棱锥的底面,其余恰好拼接成该正四棱锥的4个侧面,则ba的取值范围是 . 12.已知矩形ABCD 的长4AB =,宽3AD =,将其沿对角线BD 折起,得到四面体A BCD -,如图所示, 给出下列结论:①四面体A BCD -体积的最大值为725; ②四面体A BCD -外接球的表面积恒为定值;③若E F 、分别为棱AC BD 、的中点,则恒有EF AC ⊥且EF BD ⊥; ④当二面角A BD C --为直二面角时,直线AB CD 、所成角的余弦值为1625; ⑤当二面角A BD C --的大小为60︒时,棱AC 的长为145. 其中正确的结论有 (请写出所有正确结论的序号). 13.如图,在直三棱柱ABC ﹣A 1B 1C 1中,∠BAC=90°,AB=BB 1,直线B 1C 与平面ABC 成30°角.(I )求证:平面B 1AC⊥平面ABB 1A 1;(II )求直线A 1C 与平面B 1AC 所成角的正弦值.14.如图,在三棱锥P ﹣ABC 中,D ,E ,F 分别为棱PC ,AC ,AB 的中点.已知PA⊥AC,PA=AB=6,BC=8,DF=5. (1)若PB⊥BC,证明平面BDE⊥平面ABC . (2)求直线BD 与平面ABC 所成角的正切值.15.如图,长方体ABCD ﹣A 1B 1C 1D 1中,AB=AD=1,AA 1=2,点P 为DD 1的中点. (1)求证:直线BD 1∥平面PAC ;4343AB CD4334DCBA(2)求证:平面PAC⊥平面BDD1B1;(3)求CP与平面BDD1B1所成的角大小.16.如图,四棱锥P﹣ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上(1)求证:AC⊥平面PDB(2)当PD=AB且E为PB的中点时,求AE与平面PDB所成的角的大小.17.在四棱锥P﹣ABCD中,底面ABCD为平行四边形,∠ADC=45°,AD=AC=1,O为AC中点,PO⊥平面ABCD,PO=2,M为PD中点.(Ⅰ)求证:PB∥平面ACM;(Ⅱ)求证:AD⊥平面PAC;(Ⅲ)求二面角M﹣AC﹣D的正切值.18.如图所示,在四棱锥P﹣ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE.(1)证明:BD⊥平面PAC;(2)若PA=1,AD=2,求二面角B﹣PC﹣A的正切值.19.如图,直三棱柱ABC﹣A1B1C1中,CA⊥CB,AA1=AC=CB=2,D是AB的中点.(1)求证:BC1∥平面A1CD;(2)求证:A1C⊥AB1;(3)若点E在线段BB1上,且二面角E﹣CD﹣B的正切值是,求此时三棱锥C﹣A1DE的体积.20.如图,四棱锥S﹣ABCD的底面是正方形,每条侧棱的长都是底面边长的倍,P为侧棱SD上的点.(1)求证:AC⊥SD;(2)若SD⊥平面PAC,求二面角P﹣AC﹣D的大小;(3)在(2)的条件下,侧棱SC上是否存在一点E,使得BE∥平面PAC.若存在,求SE:EC的值;若不存在,试说明理由.试卷答案1.B:解:若α⊥γ,β⊥γ,则α与β可能平行也可能相交,故①错误;由于m,n不一定相交,故α∥β不一定成立,故②错误;由面面平行的性质定理,易得③正确;由线面平行的性质定理,我们易得④正确;故选B2.D考点:棱柱的结构特征.专题:空间角.分析:找出BD1与平面ABCD所成的角,计算余弦值.解答:解:连接BD,;∵DD1⊥平面ABCD,∴BD是BD1在平面ABCD的射影,∴∠DBD1是BD1与平面ABCD所成的角;设AB=1,则BD=,BD1=,∴cos∠DBD1===;故选:D.点评:本题以正方体为载体考查了直线与平面所成的角,是基础题.3.C考点:球的体积和表面积.专题:计算题;空间位置关系与距离.分析:根据题意,正三棱柱的底面中心的连线的中点就是外接球的球心,求出球的半径即可求出球的体积.解答:解:由题意可知:正三棱柱的底面中心的连线的中点就是外接球的球心,因为△ABC是边长为的正三角形,所以底面中心到顶点的距离为:1;因为AA1=2且AA1⊥平面ABC,所以外接球的半径为:r==.所以外接球的体积为:V=πr3=π×()3=.故选:C.点评:本题给出正三棱柱有一个外接球,在已知底面边长的情况下求球的体积.着重考查了正三棱柱的性质、正三角形的计算和球的体积公式等知识,属于中档题.4.D考点:平面与平面垂直的性质.专题:计算题;空间位置关系与距离.分析:构造棱长分别为a,b,c的长方体,P到三个平面的距离即为长方体的共顶点的三条棱的长,OP为长方体的对角线,求出OP即可.解答:构造棱长分别为a,b,c的长方体,P到三个平面的距离即为长方体的共顶点的三条棱的长,则a2+b2+c2=32+42+52=50因为OP为长方体的对角线.所以OP=5.故选:D.点评:本题考查点、线、面间的距离计算,考查计算能力,是基础题.5.D考点:直线与平面垂直的性质.专题:综合题;探究型.分析:根据SD⊥底面ABCD,底面ABCD为正方形,以及三垂线定理,易证AC⊥SB,根据线面平行的判定定理易证AB∥平面SCD,根据直线与平面所成角的定义,可以找出∠ASO是SA与平面SBD所成的角,∠CSO是SC与平面SBD所成的角,根据三角形全等,证得这两个角相等;异面直线所成的角,利用线线平行即可求得结果.解答:解:∵SD⊥底面ABCD,底面ABCD为正方形,∴连接BD,则BD⊥AC,根据三垂线定理,可得AC⊥SB,故A正确;∵AB∥CD,AB⊄平面SCD,CD⊂平面SCD,∴AB∥平面SCD,故B正确;∵SD⊥底面ABCD,∠ASO是SA与平面SBD所成的角,∠DSO是SC与平面SBD所成的,而△SAO≌△CSO,∴∠ASO=∠CSO,即SA与平面SBD所成的角等于SC与平面SBD所成的角,故C正确;∵AB∥CD,∴AB与SC所成的角是∠SCD,DC与SA所成的角是∠SAB,而这两个角显然不相等,故D不正确;故选D.点评:此题是个中档题.考查线面垂直的性质定理和线面平行的判定定理,以及直线与平面所成的角,异面直线所成的角等问题,综合性强.6.D考点:点、线、面间的距离计算.专题:综合题;空间位置关系与距离;空间角.分析:过C做平面PAB的垂线,垂足为E,连接BE,则三角形CEB为直角三角形,根据斜边大于直角边,再根据面PAC和面PAB与底面所成的二面角,能够推导出d2<d1<1.解答:解:过C做平面PAB的垂线,垂足为E,连接BE,则三角形CEB为直角三角形,其中∠CEB=90°,根据斜边大于直角边,得CE<CB,即d2<1.同理,d1<1.再根据面PAC和面PAB与底面所成的二面角可知,前者大于后者,所以d2<d1.所以d2<d1<1.故选D.点评:本题考查空间距离的求法,解题时要认真审题,仔细解答,注意空间角的灵活运用.7.48.(2)(4)10.111.1 (,) 212.②③④13.考点:平面与平面垂直的判定;直线与平面所成的角.专题:证明题.分析:(I)欲证平面B1AC⊥平面ABB1A1,关键是寻找线面垂直,而AC⊥平面ABB1A1,又AC⊂平面B1AC,满足面面垂直的判定定理;(II)过A1做A1M⊥B1A1,垂足为M,连接CM,∠A1CM为直线A1C与平面B1AC所成的角,然后在三角形A1CM 中求出此角的正弦值即可.解答:解:(I)证明:由直三棱柱性质,B1B⊥平面ABC,∴B1B⊥AC,又BA⊥AC,B1B∩BA=B,∴AC⊥平面ABB1A1,又AC⊂平面B1AC,∴平面B1AC⊥平面ABB1A1.(II)解:过A1做A1M⊥B1A1,垂足为M,连接CM,∵平面B1AC⊥平面ABB1A,且平面B1AC∩平面ABB1A1=B1A,∴A1M⊥平面B1AC.∴∠A1CM为直线A1C与平面B1AC所成的角,∵直线B1C与平面ABC成30°角,∴∠B1CB=30°.设AB=BB1=a,可得B1C=2a,BC=,∴直线A1C与平面B1AC所成角的正弦值为点评:本题主要考查了平面与平面垂直的判定,以及直线与平面所成的角,考查空间想象能力、运算能力和推理论证能力.14.考点:直线与平面所成的角;平面与平面垂直的判定.专题:空间位置关系与距离;空间角.分析:(1)由已知得DE⊥AC,DE2+EF2=DF2,从而DE⊥平面ABC,由此能证明平面BDE⊥平面ABC.(2)由DE⊥平面ABC,得∠DBE是直线BD与平面ABC所成的角,由此能求出直线BD与平面ABC所成角的正切值.解答:(1)证明:∵在三棱锥P﹣ABC中,D,E,F分别为棱PC,AC,AB的中点.PA⊥AC,PA=AB=6,BC=8,DF=5,∴DE⊥AC,DE=3,EF=4,DF=5,∴DE2+EF2=DF2,∴DE⊥EF,又EF∩AC=F,∴DE⊥平面ABC,又DE⊂平面BDE,∴平面BDE⊥平面ABC.(2)∵DE⊥平面ABC,∴PA⊥平面ABC,∴PA⊥AB,∵PB⊥BC,∴AB⊥BC,∴AC==10,∴,由DE⊥平面ABC,得∠DBE是直线BD与平面ABC所成的角,tan∠DBE==.∴直线BD与平面ABC所成角的正切值为.点评:本题考查平面与平面垂直的证明,考查直线与平面所成角的正切值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.15.考点:直线与平面平行的判定;平面与平面垂直的判定;直线与平面所成的角.专题:证明题.分析:(1)设AC和BD交于点O,由三角形的中位线的性质可得PO∥BD1,从而证明直线BD1∥平面PAC.(2)证明AC⊥BD,DD1⊥AC,可证AC⊥面BDD1B1,进而证得平面PAC⊥平面BDD1B1 .(3)CP在平面BDD1B1内的射影为OP,故∠CPO是CP与平面BDD1B1所成的角,在Rt△CPO中,利用边角关系求得∠CPO的大小.解答:(1)证明:设AC和BD交于点O,连PO,由P,O分别是DD1,BD的中点,故PO∥BD1,∵PO⊂平面PAC,BD1⊄平面PAC,所以,直线BD1∥平面PAC.(2)长方体ABCD﹣A1B1C1D1中,AB=AD=1,底面ABCD是正方形,则AC⊥BD,又DD1⊥面ABCD,则DD1⊥AC.∵BD⊂平面BDD1B1,D1D⊂平面BDD1B1,BD∩D1D=D,∴AC⊥面BDD1B1.∵AC⊂平面PAC,∴平面PAC⊥平面BDD1B1 .(3)由(2)已证:AC⊥面BDD1B1,∴CP在平面BDD1B1内的射影为OP,∴∠CPO是CP与平面BDD1B1所成的角.依题意得,,在Rt△CPO中,,∴∠CPO=30°∴CP与平面BDD1B1所成的角为30°.点评:本题考查证明线面平行、面面垂直的方法,求直线和平面所称的角的大小,找出直线和平面所成的角是解题的难点,属于中档题.16.考点:直线与平面所成的角;直线与平面垂直的判定.专题:综合题;空间位置关系与距离;空间角.分析:(1)根据题意证明AC⊥BD,PD⊥AC,可得AC⊥平面PDB;(2)设AC∩BD=O,连接OE,根据线面所成角的定义可知∠AEO为AE与平面PDB所的角,在Rt△AOE中求出此角即可.解答:(1)证明:∵四边形ABCD是正方形,∴AC⊥BD,∵PD⊥底面ABCD,∴PD⊥AC,又BD∩PD=D∴AC⊥平面PDB,(3分)(2)设AC∩BD=O,连接OE,由(1)知AC⊥平面PDB于O,∴∠AEO为AE与平面PDB所的角,(5分)又O,E分别为DB、PB的中点,∴OE∥PD,OE=PD,在Rt△AOE中,OE=PD=AB=AO,∴∠AEO=45°,(7分)即AE与平面PDB所成的角的大小为45°.(8分)点评:本题主要考查了直线与平面垂直的判定,以及直线与平面所成的角,考查空间想象能力、运算能力和推理论证能力,属于中档题.17.考点:与二面角有关的立体几何综合题;直线与平面平行的判定;直线与平面垂直的判定.专题:计算题.分析:(Ⅰ)连接OM,BD,由M,O分别为PD和AC中点,知OM∥PB,由此能够证明PB∥平面ACM.(Ⅱ)由PO⊥平面ABCD,知PO⊥AD,由∠ADC=45°,AD=AC=1,知AC⊥AD,由此能够证明AD⊥平面PAC.(Ⅲ)取DO中点N,连接MN,由MN∥PO,知MN⊥平面ABCD.过点N作NE⊥AC于E,由E为AO中点,连接ME,由三垂线定理知∠MEN即为所求,由此能求出二面角M﹣AC﹣D的正切值.解答:(Ⅰ)证明:连接OM,BD,∵M,O分别为PD和AC中点,∴OM∥PB,∵OM⊂平面ACM,PB⊄ACM平面,∴PB∥平面ACM….(4分)(Ⅱ)证明:由已知得PO⊥平面ABCD∴PO⊥AD,∵∠ADC=45°,AD=AC=1,∴AC⊥AD,∵AC∩PO=O,AC,PO⊂平面PAC,∴AD⊥平面PAC.…..(8分)(Ⅲ)解:取DO中点N,连接MN,则MN∥PO,∴MN⊥平面ABCD过点N作NE⊥AC于E,则E为AO中点,连接ME,由三垂线定理可知∠MEN即为二面角M﹣AC﹣D的平面角,∵MN=1,NE=∴tan∠MEN=2…..(13分)点评:本题考查直线与平面平行、直线现平面垂直的证明,考查二面角的正切值的求法,解题时要认真审题,仔细解答,注意三垂直线定理的合理运用.18.考点:二面角的平面角及求法;直线与平面垂直的判定.专题:空间位置关系与距离;空间角;立体几何.分析:(1)由题设条件及图知,可先由线面垂直的性质证出PA⊥BD与PC⊥BD,再由线面垂直的判定定理证明线面垂直即可;(2)由图可令AC与BD的交点为O,连接OE,证明出∠BEO为二面角B﹣PC﹣A的平面角,然后在其所在的三角形中解三角形即可求出二面角的正切值.解答:(1)∵PA⊥平面ABCD∴PA⊥BD∵PC⊥平面BDE∴PC⊥BD,又PA∩PC=P∴BD⊥平面PAC(2)设AC与BD交点为O,连OE∵PC⊥平面BDE∴PC⊥平面BOE∴PC⊥BE∴∠BEO为二面角B﹣PC﹣A的平面角∵BD⊥平面PAC∴BD⊥AC∴四边形ABCD为正方形,又PA=1,AD=2,可得BD=AC=2,PC=3∴OC=在△PAC∽△OEC中,又BD⊥OE,∴∴二面角B﹣PC﹣A的平面角的正切值为3点评:本题考查二面角的平面角的求法及线面垂直的判定定理与性质定理,属于立体几何中的基本题型,二面角的平面角的求法过程,作,证,求三步是求二面角的通用步骤,要熟练掌握19.考点:棱柱、棱锥、棱台的体积;空间中直线与直线之间的位置关系;直线与平面平行的判定.专题:综合题;空间位置关系与距离;空间角.分析:(1)连接AC1交A1C于点F,由三角形中位线定理得BC1∥DF,由此能证明BC1∥平面A1CD.(2)利用线面垂直的判定定理证明A1C⊥平面AB1C1,即可证明A1C⊥AB1;(3)证明∠BDE为二面角E﹣CD﹣B的平面角,点E为BB1的中点,确定DE⊥A1D,再求三棱锥C﹣A1DE 的体积.解答:(1)证明:连结AC1,交A1C于点F,则F为AC1中点,又D是AB中点,连结DF,则BC1∥DF,因为DF⊂平面A1CD,BC1⊄平面A1CD,所以BC1∥平面A1CD.…(3分)(2)证明:直三棱柱ABC﹣A1B1C1中,因为AA1=AC,所以AC1⊥A1C…(4分)因为CA⊥CB,B1C1∥BC,所以B1C1⊥平面ACC1A1,所以B1C1⊥A1C…(6分)因为B1C1∩AC1=C1,所以A1C⊥平面AB1C1所以A1C⊥AB1…(8分)(3)在直三棱柱ABC﹣A1B1C1中,AA1⊥CD,因为AC=CB,D为AB的中点,所以CD⊥AB,CD⊥平面ABB1A1.所以CD⊥DE,CD⊥DB,所以∠BDE为二面角E﹣CD﹣B的平面角.在Rt△DEB中,.由AA1=AC=CB=2,CA⊥CB,所以,.所以,得BE=1.所以点E为BB1的中点.…(11分)又因为,,,A1E=3,故,故有DE⊥A1D所以…(14分)点评:本题主要考查直线与平面平行、垂直等位置关系,考查线面平行、二面角的概念、求法、三棱锥C﹣A1DE的体积等知识,考查空间想象能力和逻辑推理能力,是中档题.20.考点:直线与平面平行的判定;直线与平面垂直的判定;与二面角有关的立体几何综合题.专题:计算题;证明题;压轴题.分析:(1)连BD,设AC交于BD于O,由题意知SO⊥平面ABCD.以O为坐标原点,分别为x轴、y轴、z轴正方向,建立坐标系O﹣xyz,设底面边长为a,求出高SO,从而得到点S与点C 和D的坐标,求出向量与,计算它们的数量积,从而证明出OC⊥SD,则AC⊥SD;(2)根据题意先求出平面PAC的一个法向量和平面DAC的一个法向量,设所求二面角为θ,则,从而求出二面角的大小;(3)在棱SC上存在一点E使BE∥平面PAC,根据(Ⅱ)知是平面PAC的一个法向量,设,求出,根据可求出t的值,从而即当SE:EC=2:1时,,而BE不在平面PAC内,故BE∥平面PAC解答:证明:(1)连BD,设AC交于BD于O,由题意知SO⊥平面ABCD.以O为坐标原点,分别为x轴、y轴、z轴正方向,建立坐标系O﹣xyz如图.设底面边长为a,则高.于是,,,,故OC⊥SD从而AC⊥SD(2)由题设知,平面PAC的一个法向量,平面DAC的一个法向量.设所求二面角为θ,则,所求二面角的大小为30°.(3)在棱SC上存在一点E使BE∥平面PAC.由(Ⅱ)知是平面PAC的一个法向量,且设,则而即当SE:EC=2:1时,而BE不在平面PAC内,故BE∥平面PAC点评:本题主要考查了直线与平面平行的判定,以及空间两直线的位置关系的判定和二面角的求法,涉及到的知识点比较多,知识性技巧性都很强.。
人教A版高一数学必修第二册第八章《立体几何初步》单元练习题卷含答案解析 (22)

高一数学必修第二册第八章《立体几何初步》单元练习题卷6(共22题)一、选择题(共10题)1.下列命题中正确的有( )①一个棱柱至少有5个平面;②正棱锥的侧面都是全等的等腰三角形;③有两个面平行且相似,其他各面都是梯形的多面体是棱台;④正方形的直观图是正方形.A.1B.2C.3D.42.若a和b是异面直线,a和c是平行直线,则b和c的位置关系是( )A.平行B.异面C.异面或相交D.相交、平行或异面3.已知矩形ABCD的顶点都在球心为O,半径为R的球面上,AB=6,BC=2√3,且四棱锥O−ABCD的体积为8√3,则R等于( )A.4B.2√3C.4√79D.√134.已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( )A.πB.3π4C.π2D.π45.已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( )A.πB.3π4C.π2D.π46.一个三棱锥是正三棱锥的充要条件是( )A.底面是正三角形,三个侧面是全等的等腰三角形B.各个面都是正三角形C.三个侧面是全等的等腰三角形D.顶点在底面上的射影为重心7.某三棱锥的三视图如图所示,则该三棱锥的体积为( )A.43B.83C.4D.88.如图所示的平面中阴影部分绕中间轴旋转一周,形成的几何体形状为( )A.一个球体B.一个球体中间挖去一个圆柱C.一个圆柱D.一个球体中间挖去一个长方体9.若平面α∥平面β,点A,C∈α,B,D∈β,则直线AC∥BD的充要条件是( )A.AB∥CD B.AD∥CBC.AB与CD相交D.A,B,C,D共面10.一个几何体的三视图如图所示,则该几何体的体积为( )A.210B.208C.206D.204二、填空题(共6题)11.点A在平面α内,点B不在平面α内,点A,B都在直线l上,用集合的语言表述上述语句.12.在斜二测画法中,位于平面直角坐标系中的点M(4,4)在直观图中的对应点是Mʹ,则点Mʹ的坐标为.13.已知某球体的表面积为36π,则该球体的体积是.14.由斜二测画法得到以下结论:①三角形的直观图是三角形;②平行四边形的直观图是平行四边形;③正方形的直观图是正方形;④菱形的直观图是菱形.其中正确结论的序号是.15.立体图形直观图的画法步骤:(1)画轴:与平面图形的直观图画法相比多了一个轴,直观图中与之对应的是轴.(2)画底面:平面表示水平平面,平面和表示竖直平面,按照平面图形的画法,画底面的直观图.(3)画侧棱:已知图形中平行于z轴(或在z轴上)的线段,在其直观图中和都不变.(4)成图:去掉辅助线,将被遮挡的部分改为.16.思考辨析,判断正误.两个平面同时与第三个平面相交,若两交线平行,则这两个平面平行.三、解答题(共6题)17.如图,在正方体ABCD−A1B1C1D1中,设A1C∩平面ABC1D1=E.能否判断点E在平面A1BCD1内?并说明理由.18.已知三棱锥A−BCD的两条棱AB=CD=6,其余各棱长均为5,求三棱锥的内切球半径.19.简单组合体的结构特征请描述如图所示的几何体是如何形成的.20.圆台的母线长为2a,母线与轴的夹角为30∘,下底面半径是上底面半径的2倍,求两底面的半径及两底面面积之和.21.请回答下列问题:(1) 已知:l⫋α,D∈α,A∈l,B∈l,C∈l,D∉l.求证:直线AD,BD,CD共面于α.(2) 将一个苹果切3刀,最多可以切成x块,最少可切成y块,求x+y的值.22.已知P是平面ABC外一点,PA⊥平面ABC,AC⊥BC,求证:PC⊥BC.答案一、选择题(共10题)1. 【答案】B【解析】①因为底面最少为三角形,故3个侧面,2个底面,共5个面,故①正确;②正棱锥的底面是正多边形,顶点在底面上的射影是底面正多边形的中心,射影侧面都是全等的等腰三角形,故②正确;③不正确,因为不能保证各侧棱的延长线交与一点;④正方形的直观图是平行四边形,所以④不正确;正确的命题只有①②.故选:B.【知识点】直观图、棱台的结构特征、棱锥的结构特征、棱柱的结构特征2. 【答案】C【解析】考虑正方体ABCD−AʹBʹCʹDʹ中,直线AB看做直线a,直线BʹCʹ看做直线b,即直线a和直线b是异面直线,若直线CD看做直线c,可得a,c平行,则b,c异面;若直线AʹBʹ看做直线c,可得a,c平行,则b,c相交.若b,c平行,由a,c平行,可得a,b平行,这与a,b异面矛盾,故b,c不平行.故选:C.【知识点】直线与直线的位置关系3. 【答案】A【解析】设球心O到平面ABCD的距离为ℎ,由题意可知V O−ABCD=13S矩形ABCD⋅ℎ=13×6×2√3⋅ℎ=8√3,解得ℎ=2,又矩形ABCD所在的截面圆的半径为1 2√AB2+BC2=12√62+(2√3)2=2√3,从而球的半径R=√22+(2√3)2=4.【知识点】球的结构特征、棱锥的表面积与体积4. 【答案】B【解析】因为圆柱的高为 1,它的两个底面的圆周在直径为 2 的同一个球的球面上, 所以该圆柱底面圆周半径 r =√12−(12)2=√32, 所以该圆柱的体积:V =Sℎ=π×(√32)2×1=3π4.故选:B .【知识点】圆柱的表面积与体积5. 【答案】B【解析】设圆柱的底面半径为 r ,则 r 2+(12)2=12,解得 r =√32, 所以 V 圆柱=π×(√32)2×1=3π4.【知识点】球的表面积与体积、圆柱的表面积与体积6. 【答案】A【解析】C 项,如图,橙色的 4 条棱相等,蓝色的 2 条棱相等,三个侧面是全等的等腰三角形,但不是正三棱锥.【知识点】充分条件与必要条件、棱锥的结构特征7. 【答案】A【知识点】棱锥的表面积与体积、由三视图还原空间几何体8. 【答案】B【知识点】圆柱的表面积与体积、球的表面积与体积9. 【答案】D【解析】当 AC ∥BD 时,A ,B ,C ,D 一定共面;当 A ,B ,C ,D 共面时,平面ABDC ∩α=AC ,平面ABDC ∩β=BD ,由 α∥β 得 AC ∥BD .【知识点】直线与平面平行关系的判定、直线与平面平行关系的性质10. 【答案】D【解析】由已知中的三视图可得:该几何体是由一个正方体切去一个三棱锥所得的组合体,正方体的边长为6,切去一个三棱锥的底面是直角边长分别为6,6的等腰直角三角形,高为2,故该几何体的体积为V=63−13×12×6×6×2=204.【知识点】三视图、棱锥的表面积与体积、棱柱的表面积与体积二、填空题(共6题)11. 【答案】A∈α,B∉α,A∈l,B∈l【知识点】平面的概念与基本性质12. 【答案】(4,2)【解析】由直观图画法“横不变,纵折半”可得点Mʹ的坐标为(4,2).【知识点】直观图13. 【答案】36π【解析】S=4πr2=36π⇒r=3,所以V=43πr3=36π.【知识点】球的表面积与体积14. 【答案】①②【知识点】直观图15. 【答案】z;zʹ;xʹOʹyʹ;yʹOʹzʹ;xʹOʹzʹ;平行性;长度;虚线【知识点】直观图16. 【答案】×【知识点】平面与平面平行关系的判定三、解答题(共6题)17. 【答案】可以判断点E在平面A1BCD1内.理由如下:如图,因为A1C∩平面ABC1D1=E,所以E∈A1C,E∈平面ABC1D1.因为 A 1C ⊂平面A 1BCD 1, 所以 E ∈平面A 1BCD 1.【知识点】平面的概念与基本性质18. 【答案】解法一:易知内切球球心 O 到各面的距离相等.设点 E ,F 为 CD ,AB 的中点,则点 O 在 EF 上且点 O 为 EF 的中点. 在 △ABE 中,AB =6,AE =BE =4, 所以 OH =3√78,即三棱锥的内切球半径为 3√78. 解法二:设球心 O 到各面的距离为 R , 则 4×13S △BCD ×R =V A−BCD .而 S △BCD =12×6×4=12,V A−BCD =2V C−ABE =6√7,所以 4×13×12R =6√7,即 R =3√78, 即三棱锥的内切球半径为 3√78.【知识点】棱锥的结构特征19. 【答案】 ① 是由一个圆锥和一个圆台拼接而成的组合体;② 是由一个长方体截去一个三棱锥后得到的几何体; ③ 是由一个圆柱挖去一个三棱锥后得到的几何体.【知识点】组合体20. 【答案】设圆台上底面半径为 r ,则下底面半径为 2r .将圆台还原为圆锥,如图,则有 ∠ABO =30∘. 在 Rt △BOʹAʹ 中,r BAʹ=sin30∘=12,所以 BAʹ=2r .在 Rt △BOA 中,2rBA =sin30∘=12, 所以 BA =4r .又 BA −BAʹ=AAʹ,即 4r −2r =2a , 所以 r =a ,所以两底面面积之和 S =πr 2+π(2r )2=5πr 2=5πa 2,所以圆台上底面半径为 a ,下底面半径为 2a ,两底面面积之和为 5πa 2. 【知识点】圆台的结构特征21. 【答案】(1) 因为l⫋α,A∈l,B∈l,C∈l,所以A,B,C∈α又D∈α,D∉l,所以AD⫋α,BD⫋α,CD⫋α,则直线AD,BD,CD共面.(2) x=8,y=3,x+y=11.【知识点】平面的概念与基本性质22. 【答案】如图,因为PA⊥平面ABC,PC是平面ABC的斜线,所以AC是PC在平面ABC上的射影,又BC⊂平面ABC,且AC⊥BC,所以由三垂线定理得PC⊥BC.【知识点】直线与平面垂直关系的性质。
立体几何练习题及解答

立体几何练习题及解答《立体几何练习题及解答》练习一:体积计算题目:一个正方体箱子的边长为3cm,请计算该正方体箱子的体积。
解答:正方体的体积计算公式为边长的立方,即V = a³,其中a为正方体的边长。
代入已知条件,正方体箱子的边长a = 3cm。
则体积V = 3³ = 27cm³。
所以该正方体箱子的体积为27cm³。
练习二:表面积计算题目:一个长方体的长为5cm,宽为3cm,高为4cm,请计算该长方体的表面积。
解答:长方体的表面积计算公式为2ab + 2bc + 2ac,其中a、b、c分别为长方体的三个边长。
代入已知条件,长方体的长a = 5cm,宽b = 3cm,高c = 4cm。
则表面积S = 2(5×3) + 2(3×4) + 2(5×4) = 30 + 24 + 40 = 94cm²。
所以该长方体的表面积为94cm²。
练习三:棱柱的体积计算题目:一个棱柱的底面为边长为5cm的正方形,高为8cm,请计算该棱柱的体积。
解答:棱柱的体积计算公式为底面积乘以高,即V = S × h,其中S为底面积,h为高度。
代入已知条件,棱柱的底面为正方形,边长a = 5cm,高度h = 8cm。
底面积S = a² = 5×5 = 25cm²。
则体积V = S × h = 25 × 8 = 200cm³。
所以该棱柱的体积为200cm³。
练习四:金字塔的体积计算题目:一个金字塔的底边是边长为6cm的正方形,高为10cm,请计算该金字塔的体积。
解答:金字塔的体积计算公式为底面积乘以高再除以3,即V = S ×h ÷ 3,其中S为底面积,h为高度。
代入已知条件,金字塔的底边为正方形,边长a = 6cm,高度h =10cm。
底面积S = a² = 6×6 = 36cm²。
专题6:立体几何中点到面的距离求法基础练习题
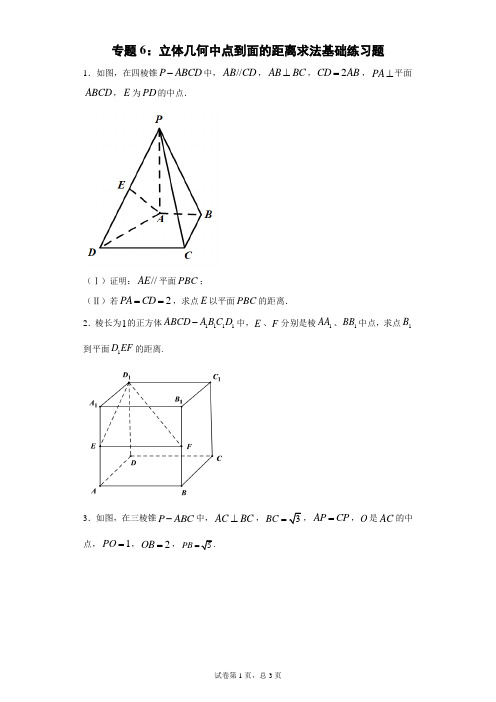
因为 为 的中点,所以 ,
又 平面 , 平面 ,所以 平面 .
因为 ,所以 .
又 ,所以四边形 是平行四边形,所以 ,
因为 平面 , 平面 ,所以 平面 ;
因为 ,且 平面 , 平面 ,
所以平面 平面 ;
因为 平面 ,所以 平面 .
(Ⅱ)因为 是 的中点,
所以点 到平面 的距离是点 到平面 距离的 .
设C到平面 的距离为 ,则 .
【点睛】
本题主要考查了线面平行的判定定理的应用,以及空间向量的在求点到平面距离中的应用,属于基础题.
7.(1)证明见解析;(2) .
【分析】
(1)利用线面平行的判定定理证明即可.
(2)利用面面垂直的判定定理证出面 面 ,过 作 , 的长即为 到面 的距离,根据 即可求解.
【详解】
(1)证明:连接 ,设 ,连 ,
则 是三角形 的中位线,
面 .
(2) 面 面 面 ,
过 作 ,
垂足为 ,易知 面 ,
则 的长即为 到面 的距离, 与 中,
, ,
可知 ,所以 .
【点睛】
本题考考查了线面平行的判定定理、面面垂直的性质定理、求点到面的距离,考察了逻辑推理能力,属于基础题.
8.(1)证明见解析;(2) .
因为 平面 , , ,
所以 平面 .所以 .
所以 .
在 中, , ,
所以 .
设点 到平面 的距离为 ,
则 ,解得 .
所以点 到平面 的距离是 .
【点睛】
本题主要考查证明线面平行,考查等体积法求点到面的距离,属于常考题型.
2.
【分析】
利用等体积法列方程,解方程求得点 到平面 的距离.
立体几何练习题及解析

立体几何练习题及解析一、选择题1. 下列哪个是正方体?A. 圆柱体B. 球体C. 锥体D. 正四面体解析:正确答案为D。
正四面体是一个具有四个等边三角形面的多面体,也是一种立体几何体。
2. 以下哪个是圆锥体?A. 立方体B. 正方形C. 圆柱体D. 球体解析:正确答案为C。
圆柱体的两个底面都是同心圆,且高度与底面的半径相等。
3. 以下哪个不是球体的属性?A. 没有棱B. 没有边C. 没有顶点D. 没有底面解析:正确答案为D。
球体没有底面,它是由无数个相同半径的小球面组成的。
二、填空题1. 立方体有多少个面?解析:立方体有6个面。
2. 锥体有多少个顶点?解析:锥体有1个顶点。
3. 正四面体有多少个边?解析:正四面体有6个边。
三、计算题1. 一个圆柱体的底面半径为5 cm,高度为8 cm,计算其体积和表面积。
解析:圆柱体的体积公式为V = πr²h,表面积公式为S = 2πrh + 2πr²。
将底面半径r = 5 cm,高度h = 8 cm代入公式计算得:V = π(5)²(8) = 200π cm³S = 2π(5)(8) + 2π(5)² = 80π + 50π = 130π cm²2. 一个球体的半径为10 cm,计算其体积和表面积。
解析:球体的体积公式为V = (4/3)πr³,表面积公式为S = 4πr²。
将半径r = 10 cm代入公式计算得:V = (4/3)π(10)³ = 4000π/3 cm³S = 4π(10)² = 400π cm²3. 一个正方体的边长为6 cm,计算其体积和表面积。
解析:正方体的体积公式为V = a³,表面积公式为S = 6a²。
将边长a = 6 cm代入公式计算得:V = 6³ = 216 cm³S = 6(6)² = 216 cm²四、解答题1. 画出一个平行六面体,其中底面是边长为4 cm的正方形,高度为6 cm。
空间立体几何练习题(含答案)
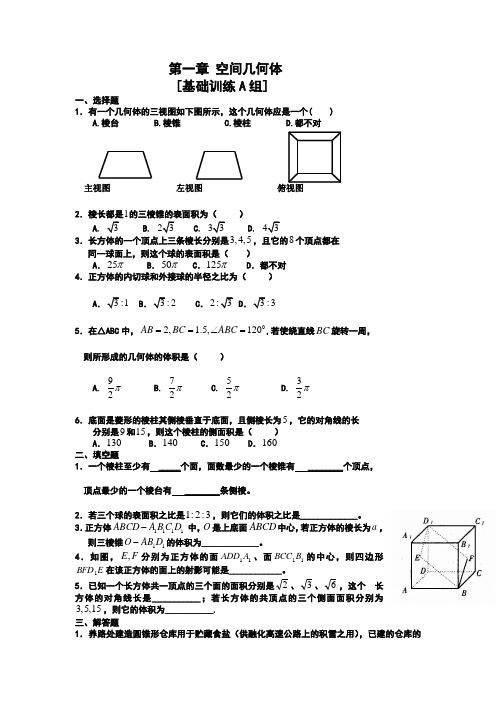
第一章 空间几何体 [基础训练A 组]一、选择题1.有一个几何体的三视图如下图所示,这个几何体应是一个( )A.棱台B.棱锥C.棱柱D.都不对2.棱长都是1的三棱锥的表面积为( )3.长方体的一个顶点上三条棱长分别是3,4,5,且它的8个顶点都在 同一球面上,则这个球的表面积是( )A .25πB .50πC .125πD .都不对 4.正方体的内切球和外接球的半径之比为( )AB2 C.5.在△ABC 中,02, 1.5,120AB BC ABC ==∠=,若使绕直线BC 旋转一周, 则所形成的几何体的体积是( )A.92π B. 72π C. 52π D. 32π 6.底面是菱形的棱柱其侧棱垂直于底面,且侧棱长为5,它的对角线的长 分别是9和15,则这个棱柱的侧面积是( ) A .130 B .140 C .150 D .160 二、填空题1.一个棱柱至少有 _____个面,面数最少的一个棱锥有 ________个顶点, 顶点最少的一个棱台有 ________条侧棱。
2.若三个球的表面积之比是1:2:3,则它们的体积之比是_____________。
3.正方体1111ABCD A BC D - 中,O 是上底面ABCD 中心,若正方体的棱长为a , 则三棱锥11O AB D -的体积为_____________。
4.如图,,E F 分别为正方体的面11A ADD 、面11B BCC 的中心,则四边形E BFD 1在该正方体的面上的射影可能是____________。
5.已知一个长方体共一顶点的三个面的面积分别是2、3、6,这个 长方体的对角线长是___________;若长方体的共顶点的三个侧面面积分别为3,5,15,则它的体积为___________. 三、解答题1.养路处建造圆锥形仓库用于贮藏食盐(供融化高速公路上的积雪之用),已建的仓库的主视图 左视图 俯视图C 底面直径为12M ,高4M ,养路处拟建一个更大的圆锥形仓库,以存放更多食盐,现有两种方案:一是新建的仓库的底面直径比原来大4M (高不变);二是高度增加4M (底面直径不变)。
立体几何练习题

立体几何题型一、平行与垂直的证明例1.如图,在四棱锥P —ABCD 中,底面ABCD 是正方形,侧棱PD ⊥底面ABCD ,PD =DC ,E 是PC 的中点,作EF ⊥PB 交PB 于点F . (1)证明PA //平面EDB ;(2)证明PB ⊥平面EFD例2.四棱锥S A B C D -中,底面ABCD 为平行四边形,侧面SB C ⊥底面ABCD ,已知45A B C ∠=︒,2A B =,BC =SA SB ==(Ⅰ)证明:SA B C ⊥;(Ⅱ)求直线SD 与平面SBC 所成角的大小. 变式:已知四棱锥P -ABCD 的底面为直角梯形,AB ∥DC ,⊥=∠PA DAB ,90底面ABCD ,且PA =AD =DC =21AB =1,M 是PB 的中点.(Ⅰ)证明:面PAD ⊥面PCD ; (Ⅱ)求AC 与PB 所成的角;(Ⅲ)求面AMC 与面BMC 所成二面角的大小.ACDBCASOE A DCBNM EP题型二、空间角与距离例3.如图,在四棱锥O A B C D -中,底面A B C D 四边长为1的 菱形,4A B C π∠=, OA ABCD ⊥底面, 2O A =,M 为O A 的中点。
(Ⅰ)求异面直线AB 与MD 所成角的大小; (Ⅱ)求点B 到平面OCD 的距离。
例4. 如图,四面体ABCD 中,O 、E 分别BD 、BC 的中点,CA =CB =CD =BD =2 (Ⅰ)求证:AO ⊥平面BCD ;(Ⅱ)求异面直线AB 与CD 所成角的大小; (Ⅲ)求点E 到平面的距离. 变式:如图,正三棱锥O A B C -的三条侧棱O A 、O B 、O C 两两垂直,且长度均为2.E 、F 分别是A B 、A C 的中点,H 是E F 的中点,过E F 的平面与侧棱O A 、O B 、O C 或其延长线分别相交于1A 、1B 、1C ,已知132O A =.(1)求证:11B C ⊥面O A H ; (2)求二面角111O A BC --的大小.1C 1A题型三、探索性问题例5.在四棱锥P-ABCD 中,底面ABCD 是矩形,侧棱PA 垂直于底面,E 、F 分别是AB 、PC 的中点.(1)求证://EF 平面PAD ;(2)当平面PCD 与平面ABCD 成多大二面角时,⊥EF 平面PCD ?变式:如图,在三棱锥A -BCD 中,侧面ABD 、ACD 是全等的直角三角形,AD 是公共的斜边,且AD ,BD =CD =1,另一个侧面是正三角形 (1)求证:AD ⊥BC(2)求二面角B -AC -D 的大小(3)在直线AC 上是否存在一点E ,使ED 与面BCD 成30︒角?若存在,确定E 的位置;若不存在,说明理由.DC题型四、折叠、展开问题例6.已知正方形A B C D E 、F 分别是A B 、C D 的中点,将AD E 沿D E 折起,如图所示,记二面角A D E C --的大小为(0)θθπ<< (1) 证明//B F 平面ADE ;(2)若A C D 为正三角形,试判断点A 在平面B C D E 内的射影G 是否在直线E F 上,证明你的结论,并求角θ的余弦值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
立体几何练习题六
一、选择题(计60分)
1、条件甲:直线a、b是异面直线;条件乙:两条直线a 、b无公共点,则甲是乙的()
A.充分非必要条件B.必要非充分条件
C.充要条件D.既非充分又非必要条件2、若球的大圆的面积扩大为原来的3倍,则它的体积扩大为原来的()
A.3倍B.27倍C.33倍D.33倍
3、如果直线a∥平面α,那么直线a与平面α内的()
A、一条直线不相交
B、两条相交直线不相交
C、无数条直线不相交
D、任意一条直线都不相交
4、已知P是三角形ABC所在平面外的一点,且P到三角形三个顶点的距离相等,那么P在平面ABC内的射影一定是三角形ABC 的( )
A、垂心
B、外心 C 、内心D、重心
5、侧棱长为2a的正三棱锥其底面周长为9a,则棱锥的高为
()
A、a
B、2a
C、2
D、27a
6、已知一个凸多面体面数为8,各面多边形的内角总和为16π,则它的棱数为( )
A 、24
B 、32
C 、18
D 、16
7、正方形ABCD 与正方形ABEF 成90° 的二面角,则异面直线AC 与BF 所成的角为 ( ) A 、45° B 、60° C 、30° D 、90° 8、在正方体ABCD —A 'B 'C 'D '中,BC '与截面BB 'D 'D 所成的角为( )
A .3π
B .4π
C .6π
D .arctan2
9、有一个三棱锥,如果它的底面是直角三角形,那么它的三个 侧面( )
A 、一定都是直角三角形
B 、至多只能有一个直角三角形
C 、至多只能有两个直角三角形
D 、可能都是直角三角形
10、已知球面上的三点A ,B ,C ,且6
A B
c m =,8BC cm =,10AC cm =,
球的半径为13cm ,则球心到平面ABC 的距离是( ) A 、11cm B 、12cm C 、13cm D 、14cm 11、方程x 3
-6x 2
+9x-10=0的实根个数是 ( )
A 、3
B 、2
C 、1
D 、0
12、一个透明密闭的正方体容器中,恰好盛有该容器一半容积的水,
任意转动这个正方体,则水面在容器中的形状可以是(1)三角形
(2)菱形(3)矩形(4)正方形(5)正六边形其中正确的是 ( )
A 、(1)(2)(3)(4)(5)
B 、(2)(3)(4)
C 、(2)(3)(4)(5)
D 、(3)(4)
二、填空题(计16分)
13、正方形ABCD中,AB=10㎝,PA垂直于ABCD所在的平面且
PA=5㎝,则P到DC的距离为____________;
14、函数f(x)= x3-6x2+9x(0<x<5)的单调增区间为___________;
15、已知正方体的八个顶点中,有四个点恰好为正四面体的顶点,
则该正四面体与正方体的体积之比是_______________;
16、将边长为2,锐角为600的菱形ABCD沿较短对角线BD折成
四面体ABCD,点E、F分别为AC、BD的中点,则下列命
题中正确的是______(将正确的命题序号全填上)
①EF∥AB ②EF是异面直线AC与BD的公
垂线
③当四面体ABCD的体积最大时,AC=6④AC垂直于截面
BDE
三、解答题(74分)
17、等腰直角三角形ABC中,∠C=90°,平面ABC外一点P在
平面ABC内的射影是AB边的中点,若PC=AB=24,求:
(1)PC与平面ABC所成的角
(2)P点到直线AC,BC的距离。
(12分)
P
A
C
18、若正四棱锥所有棱长与底面边长均相等,
求①斜高与棱锥高之比
②相邻两个侧面所成二面角的大小。
(12分)
19、在立体图形V-ABC中,∠VAB=∠VAC=∠ABC=90°,①平面
VAB与平面VBC有何种位置关系?请说明理由。
②若1VA=4,试求A点到平面VBC的距离(12分)BC=BA=
2
V
B
A
C
A 1
B 1
A
D
20、如图,直三棱柱ABC-A 1B 1C 1的底面ABC 为等腰直角三角形,
90A C B ∠=︒,AC=1,C
点到AB 1的距离为CE=
2
3,D 为AB 的中
点. (12分)
(1)求证:AB 1⊥平面CED ; (2)求异面直线AB 1与CD 之间的距离;
(3)求二面角B 1—AC —B 的平面角.
21、已知实数a ≠0,函数f(x)=ax(x-2)2
(x ∈R)有极大值32。
(1)求实数a 的值;
(2)求函数f(x)的单调区间。
(12分)
22、如图所示,正方形的边长为3a ,E 、F 、G 、H 是正方形边AB 、
CD 的三等分点,将正方形沿EH 、FG 对折成一个三棱柱 AEF-DHG 求:(14分)
①异面直线EA 与FD 所成的角
②求二面角F-HD-G 大小 ③求棱锥A-DHF 的体积
2004—2005学年第二学期第二次月考
数学答题卷
一、选择题(60分)
二、填空题 13、5
5
; 14、(0,1)和(3,5);15、1∶3; 16、②③④
三、解答题
A
E
F
B
D
H
G
C
E
A
F
H
G
D
17、(1)600
;(2)6
14
;
18、(1)
3
∶
2
;(2)π-arccos 3
1;
19、(1)垂直 ;(2)5
58
;
20、(1)略 ;(2)2
1 ;(3)arctan
2
;
21、(1)a=27 ;(2)x ∈(-∞,3
2)和x ∈(2,+∞)单调第增;
x ∈(3
2,2)单调递减
22、(1)arccos
20
10 ;(2)arctan2
3
;(3)
4
3a 3。
