2.4一维射影变换
第二章 射影变换-第四节 一维射影变换课件ppt课件
一、一维射影变换
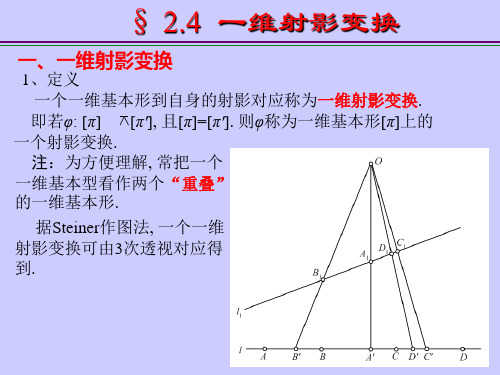
1、定义 一个一维基本形到自身的射影对应称为一维射影变换. [π'], 且[π]=[π']. 则φ称为一维基本形[π]上的 即若φ: [π] 一个射影变换. 注:为方便理解, 常把一个 一维基本型看作两个“重叠” 的一维基本形. 据Steiner作图法, 一个一维 射影变换可由3次透视对应得 到.
a11 a12 0,
a21 a22
0
(2.10)
其中对应点的坐标是关于一维基本形[π]上的同一坐标系取得的.
(ad bc 0)
§ 2.4 一维射影变换
一、一维射影变换
1、定义 2、代数表示 (1). 坐标表示 (2). 参数表示 定理2.16 一维基本形上的一个变换为射影变换其对应元素 的参数λ,λ' 满足一个双线性方程 a 'b c 'd 0 (ad bc 0) (2.13) 证 “=>”. 见教材, 略. “<=”. 设一维基本形(P)上的一个变换φ使得任一对对应元素的 参数λ,λ' 满足双线性方程(2.13). 显然φ是一个双射,只要证φ保交比. 设λi ,λi' (i=1,2,3,4)为任意四对对应元素的参数. 则 b1 d b3 d (ad bc)(1 3 ) 1 '3 ' . a1 c a3 c (a1 c)(a3 c) 同法可以求出λ2'–λ4', λ2'–λ3', λ1'–λ4', 得到 (1 '3 ' )(2 '4 ' ) (1 3 )(2 4 ) . (2 '3 ' )(1 '4 ' ) (2 3 )(1 4 )
高等几何第二章2013

§ 2.1 交比
一、点列中四点的交比 1. 定义
2. 性质 3. 特殊情况 定理2.3 共线四点的交比值出现0, 1, 三者之一这四点中有 某二点相同. 证明 根据定理2.1,令P1=P2或P2=P3或P3=P4或P4=P1直接验证. 此时, 上述6个不同的交比值又只有3组:0, 1, .
§ 2.1 交比
一、点列中四点的交比 1. 定义
4. 调和比 5. 交比的计算 (1) 由坐标求交比 例2 已知P1(3,1,1), P2(7,5,1), Q1(6,4,1), Q2(9,7,1). 求(P1 P2, Q1 Q2). 解 第一步. 验证四点共线. 第二步. 以P1, P2为基点, 参数表示Q1, Q2. 令 iQi P i P2 . i=1,2. 1 对于i=1, 利用P.34例1.3, 有1 3. 对于i=2, 同理求得 2 3. 于是, 2. 性质 3. 特殊情况
而 于是
1 ( p1 p2 , p3 p4 ) ( P P2 , P3 P4 ). 1 2
§ 2.1 交比
二、线束中四直线的交比
1. 线束的参数表示 则 2. 定义 3. 交比为射影不变量
定理2.6 设线束S(p)中四直线pi被直线s截于四点Pi(i=1,2,3,4).
( p1 p2 , p3 p4 ) ( P P2 , P3 P4 ). 1
( PP2 , P P4 ) k , 1 3
(k 0,1, )
和其中三点的坐标. 则第四点的坐标可唯一确定.
§ 2.1 交比
一、点列中四点的交比 1. 定义
4. 调和比 5. 交比的计算 (2) 由交比求坐标 例3 已知P1, P2分别是x轴、y轴上的无穷远点, P3是斜率为1的 方向上的无穷远点, 且(P1P2,P3P4)=r. 求P4的坐标. 解:由题设知P1, P2, P3的坐标分别为(1,0,0), (0,1,0), (1,1,0). 设
高等几何讲义 第三章 射影变换____§1 一维射影变换

的乘积.
➢ 注意:定理6的证明表明,虽然射影对应可传递, 但透视一般是不可传递的.
高 等 几 何 ( Higher Geometry )
1 1
u1 u2
t1 t2
v1 v2
1 2
u1 u2
1 2
v1 v2
t1 t2
x vI x/ v/ II
高 等 几 何 ( Higher Geometry )
§1 一维射影变换
令
u1 u2
t1 t2
v1 v2
t1 t2
,则
/1 /2
v21 u21
v12, u12
从而
u21 u12 /2
v21 v12 /1
c
证明:如图,设
p
(ab/)(a/b),q
(bc/)(b/c),
b a
s
t
q
r (ca/)(c/a), s (ac/)(ba/), p r
t (bc/)(ca/),d /. d
因 {a/, p, s, b} a {a/, b/, c/, d} c {t, q, c/, b}a,/ b/ / c/
§1 一维射影变换
且设 I 上的动点 x 对应 II 上
的点 x/,则 (u/v/; t/x/) (uv; tx).
u
t
设各点射影坐标分别为 u(u1,
u2)、v(v1, v2)、t(t1, t2)、 x(1,
u/
t/
2)、x/(/1, /2),则得
第四节射影对应代数表示

1. 射影对应 设
l (A, B, C, ……)
l ( A, B, C , )
(1) 几何表示 (2) 代数表示
(I )
(AB,CX)=(A’B’,C’X ’)
xa )( x xb ) ( xc xa )( x xb ) ( xc ; )( x xa ) ( xc xb )( x xa ) ( xc xb
(实)
标准型在解题中有重要且巧妙的应用。
习题选解 例1 设A1A2A3为坐标三点形, O(1, 1, 1). A2O×A1A3=A, P是
A2A3上的动点, PO×A1A2=Q, QA×A2A3=P‘. 若P, P’的齐次坐标分
别为(0,λ,1), (0,λ',1). 求(P)到(P')的射影变换的方程和不变元素. 解. 由题设各点的坐标,可得
( II )
x xb x xb k ; x xa x xa
( III )
xx x x 0
( 0) ;
a b ax b ( IV ) x ( 0) ; cx d c d a11 x1 a12 x2 a11 a12 x1 (V ) ( 0) 。 a21 a22 2 a 21 x1 a 22 x 2 x
( XY , PQ) ( XY , P Q)
( XYP) ( XYP ) ( XYQ) ( XYQ) ( XYP ) ( XYQ) ( XYP ) ( XYQ)
( XY , PP) ( XY , QQ)
( XY , PP' ) k (常数)。
2 x n 1 3 , x1 0, 例3 设数列的递推公式为 xn x n 1 6
高等几何讲义 第三章 射影变换____§1 一维射影变换

高 等 几 何 ( Higher Geometry )
§1 一维射影变换
➢ 例1 设 abcd 为平行四边形,过顶点 a 作直线
ae 与对角线 bd 平行.证明:直线 ab、ad
与直线 ac、ae 成调和共轭.
证明:因 ae 与 bd 平行,故 a
设二者交点为无穷远点 p.
o
p e
d
记(ac)(bd) o.则
的线性变换:
T:
//12 aa1211
a12 a22
12,det(aij)
0.
(3.1)
证明:不妨设两个一维基本形 I 与 II 均为点列.
在 I 上取定三点 u、v、t,使其在 II 上的对应点依
Hale Waihona Puke 次为 II 的坐标系 / [u/, v/; t/] 中的基点和单位点.
高 等 几 何 ( Higher Geometry )
高 等 几 何 ( Higher Geometry )
高 等 几 何 ( Higher Geometry )
§1 一维射影变换
➢ 同类一维基本形间的透视:
若两个点列是同一线束的 若两个线束是同一点列的
截影,则称这两个点列是 投影,则称这两个线束是
透视的.
透视的.
线束的心称为透视中心. 点列的底称为透视轴.
§1 一维射影变换
且设 I 上的动点 x 对应 II 上
的点 x/,则 (u/v/; t/x/) (uv; tx).
u
t
设各点射影坐标分别为 u(u1,
u2)、v(v1, v2)、t(t1, t2)、 x(1,
u/
t/
2)、x/(/1, /2),则得
11 0 0 11
一维射影变换
§ 6.1 一维基本形的射影对应
例3. 如果三点形ABC的边CB, CA, AB分别通过在同 一直线上的三点P, Q, R, 又顶点B, C各在一条定直线上. 求证:顶点A也在一条定直线上. 证明 显然,
(B,B1,B2,…) 于是, R(B,B1,B2,…)
(P )
(C,C1,C2,…) Q(C,C1,C2,…)
§ 6.1 一维基本形的射影对应
(4) Steiner作图法 已知两点列间射影对应的三对相异 的对应元素, 求作任一元素的对应元素.
(5) 思考:将(4)中 “点列” 改为 “一维基本形”. (6) 定理2.2 两个一维基本形间的射影对应可由已知相 异的三对对应元素唯一确定.
§ 6.1 一维基本形的射影对应
§ 6.1 一维基本形的射影对应
(3). 线束↔线束. 对应直线交点共线.
S (a, b, c,...)
(s)
S ' (a' , b' , c' ,...)
透视轴
注
(1)透视关系具有对称性,但它不具有传递性. (2) 透视对应是一个保交比的双射. (3) 连续两次透视对应的结果不一定仍是透视对应 .
§ 6.1 一维基本形的射影对应
一、透视对应(中心射影)
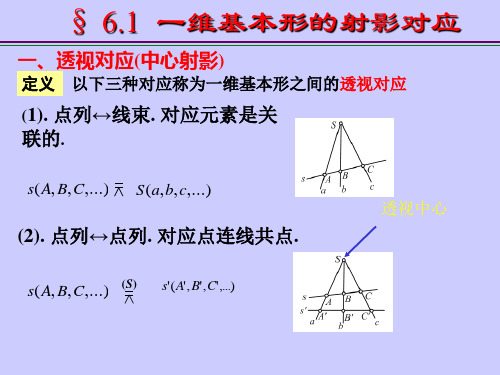
定义 以下三种对应称为一维基本形之间的透视对应
(1). 点列↔线束. 对应元素是关 联的.
s( A, B, C ,...) S (a, b, c,...)
透视中心
(2). 点列↔点列. 对应点连线共点.
s( A, B, C ,...)
(S)
s' ( A' , B' , C' ,...)
A恰为上述两射影点列对应直线 的交点.
射影变换、仿射变换、欧式变换、相似变换、等距变换
射影变换、仿射变换、欧式变换、相似变换、等距变换射影变换组成了⼀个群,这个群被称为射影变换群。
仿射变换是射影变换的⼦群。
欧式变换(旋转+平移+等⽐缩放)是仿射变换的⼦群。
相似变换和等距变换则是欧式变换的⼦群。
0.射影变换定义由有限次中⼼射影的积定义的两条直线间的⼀⼀对应变换称为⼀维射影变换。
由有限次中⼼射影的积定义的两个平⾯之间的⼀⼀对应变换称为⼆维射影变换。
性质——交⽐不变性如果平⾯上点场的点建⽴了⼀个⼀⼀对应,并且满⾜:(1)任何共线三点的象仍是共线三点;(2)共线四点的交⽐不变。
则这个⼀⼀对应叫做点场的射影变换,简称射影变换。
矩阵表⽰⽤H表⽰,H为3×3的可逆实矩阵,虽然有9个未知数,但只有8个⾃由度(只与具体⽐率有关),其中h31与h32不为0是它与仿射变换的本质区别,它使得仿射变换的⾮线性效应。
可以把⼀个H分解为:H=SAP,其中S为相似变换,A为仿射变换,P为射影变换。
变换前后共点,共线,交⽐,相切,拐点,切线的不连续性和岐点保持不变。
注:n×n可逆实矩阵称为⼀般线性群GL(n),当把相差⾮零纯量因⼦的矩阵都视为等同时,便得到射影映射群,记为PL(n),在平⾯射影变换时为PL(3)。
射影变换矩阵表⽰:H = { h11, h12, h13h21, h22, h23h31, h32, h33 }其中当最后⼀⾏为(0,0,1)时的变换为仿射变换,在仿射的前提下,当左上⾓2×2矩阵正交时为欧式变换,左上⾓矩阵⾏列式为1时为定向欧式变换。
1、等距变换:它相当于是平移变换和旋转变换的复合,⽤R表⽰变换矩阵,R为3×3矩阵,R={{r11,r12,tx},{r21,r22,ty},{0,0,1}}左上⾓2×2矩阵为旋转部分,tx和ty为平移因⼦,它有三个⾃由度,即旋转,x⽅向平移,y⽅向平移。
等距变换前后长度,⾯积,线线之间的⾓度都不变。
2.相似变换它相当于是等距变换和均匀缩放的⼀个复合,⽤S表⽰变换矩阵,S为3×3矩阵,S={{s*r11,s*r12,tx},{s*r21,s*r22,ty},{0,0,1}}左上⾓2×2矩阵为旋转部分,tx和ty为平移因⼦,它有4个⾃由度,即旋转,x⽅向平移,y⽅向平移和缩放因⼦s。
射影变换
射影变换4.1 点列和线束点列和线束定义.两个矢量),,(321a a a 和),,(321b b b 表示不同的点当且仅当这两个矢量线性无关. 在两点A ),,(321a a a 与B ),,(321b b b 的连线上任意一点),,(321x x x X 满足0321321321=b b b a a a x x x即,三点A ),,(321a a a ,B ),,(321b b b 与),,(321x x x X 共线的充分必要条件是0321321321=b b b a a a x x x以B A ,为基点的点列中,任何一点X 都可以表示为B A X μλ+=,用齐次坐标可以表示为B A B A X λλμ'+=+=;以m l ,为基线的线束中,任何一直线p 都可以表示为m l p μλ+=,用齐次坐标可以表示为m l m l p λλμ'+=+=.练习4-11.已知A 和B 的齐次坐标分别为)1,1,5(和)1,0,1(-,求直线AB 上一点C ,使1)(-=ABC ,若B A C λ+=,求出λ.解利用非齐次坐标),(y x 与齐次坐标),,(321x x x 之间的关系31x x x =,32x xy =.这时,)1,5(),(=y x A ,)0,1(),(-=y x B ,再利用BC AC ABC =)(.115-=+-x x ,解得2=x,101-=--y y ,解得21=y .即)21,2(=C ,C 点的齐次坐标为)1,21,2(. 因为B A C 2121+=,所以 1=λ. 注意:以B A ,为基点的点列中,任何一点X 都可以表示为B A X μλ+=,用齐次坐标可以表示为B A B A X λλμ'+=+=. 2.试证明:三点),,(321x x x ,),,(321y y y ,),,(321z z z 共线的充分必要条件为0321321321=z z z y y y x x x 证明三点),,(321x x x ,),,(321y y y ,),,(321z z z 共线的充分必要条件为λ=--=--=--333322221111y z x z y z x z y z x z所以0332211321332211321321321=-------=y z y z y z y y y x z x z x z z z z y y y x x x4.已知直线0143=++y x 与02=+y x ,求过两直线的交点与点)0,1,2(的直线方程.解两直线0143=++y x 与02=+y x 的交点为)5,1,3(112143321--=x x x 于是点)5,1,3(--与点)0,1,2(的直线方程为05105012513321321=+-=--x x x x x x即05105321=+-x x x .4.2 点列和线束的交比定义4.2设D C B A ,,,为点列上共线的四点,则这四点的交比为ADBC BDAC CD AB ⋅⋅=),(.定理 4.1取A 和B 为基点,将D C B A ,,,四点的坐标依次表示为a ,b ,b a 1λ+,b a 2λ+,则四点的交比为21),(λλ=CD AB . 定理4.2若D C B A ,,,四点的坐标为)4,3,2,1(21=+i P P i λ,21,P P 点列上两个基点,则),(),(432124142313λλλλλλλλλλλλ=----=CD AB定理4.3将某两点互换,同时互换其余两点,则交比不变.即),(),(),(),(BA DC AB CD DC BA CD AB ===定理4.4只在一对点中互换,交比转为其倒数.即),(1),(CD AB DC AB =,),(1),(CD AB CD BA =定理4.5交换中间两点,则交比为1与原值的差,即),(1),(CD AB BD AC -= 定义4.3当1),(-=CD AB 时,称D C ,调和分割线段AB .调和分割的关系是对等的.因为1),(),(-==CD AB AB CD ,所以,B A ,也调和分割线段CD ,有时也称D C B A ,,,为调和点列.定义4.4称21λλ为四直线d c b a ,,,的交比,记为),(cd ab .即 =),(cd ab 21λλ.注意:用齐次坐标之间的关系定义交比,点列的交比与线束的交比在形式上完全一致.定理4.6设四直线d c b a ,,,,若b a c 1λ+=,b a d 2λ+=,则=),(cd ab 21λλ. 定理4.7若四直线q p a 1μ+=,q p b 2μ+=,q p c 3μ+=,q p d 4μ+=,则 424132314321),(),(μμμμμμμμμμμμ----==cd ab .这个比值也称为数4321,μμμμ的交比.定理4.8两个点列经过中心投影,交比不变.练习4-21. 设E D C B A ,,,,是同一直线上的五点,求证1),)(,)(,(=EC AB DE AB CD AB .证明由交比定义ADBC BDAC CD AB ⋅⋅=),(,1),)(,)(,(=⋅⋅⋅⋅⋅⋅⋅⋅=ACBE BCAE AE BD BE AD AD BC BD AC EC AB DE AB CD AB .2.设C B A ,,三点的坐标分别为)1,1,1(,)1,1,1(-,)1,0,1(,且2),(=CD AB ,求点D 的坐标.解)1,1,1(=A ,)1,1,1(-=B ,则C B A ==+)1,0,1(2121,于是12=λ.设B A D 1λ+=,由2),(21==λλCD AB 可知,21=λ,所以)3,1,3(2-=+=B A D .注意:以B A ,为基点的点列中,任何一点X 都可以表示为B A X μλ+=,用齐次坐标可以表示为B A B A X λλμ'+=+=. 3.求四点)1,1,2(-A ,)1,1,1(-B ,)0,0,1(C ,)5,5,1(-D 的交比),(CD AB .解利用定理 4.1,取A 和B 为基点,将D C B A ,,,四点的坐标依次表示为a ,b ,b a 1λ+,b a 2λ+,则四点的交比为21),(λλ=CD AB . 这里B AC +=,于是11=λ, B AD 32-=,于是232-=λ,由21),(λλ=CD AB 可知,32),(21-==λλCD AB . 注意:以B A ,为基点的点列中,任何一点X 都可以表示为B A X μλ+=,用齐次坐标可以表示为B A B A X λλμ'+=+=. 7.试证:02321=+-x x x ,023321=-+x x x ,0721=-x x ,0531=-x x 所表示的四直线共点,并求这四直线的交比.解直线0721=-x x 与0531=-x x 的交点为)5,7,1(15017321=--x x x 点)5,7,1(满足四直线,所以,此四直线共点. 四直线与x 轴的交点分别为211-=x ,322=x ,03=x ,514=x ,所以,21),(4321=l l l l .4.3 完全四点形和完全四线形完全四点形和完全四线形定义.定理4.6完全四点形通过每一个对角点有一组调和线束,即通过这个对角点的两边和对角三角形的两边.定理4.10完全四线形的每一条对角线上有一组调和点列,即这条直线上的两个顶点及对角三角形的两个顶点.练习4-32.设XYZ 是完全四点形ABCD 的对边三点形,XY 分别交BD AC ,于M L ,,不用笛沙格定理,证明CM BL YZ ,,共点.证明由四点形ABCD ,根据定理可知,在AC 边上的四点L Y C A ,,,调和共轭, 即1),(-=YL AC .在四点形YBZL 中,LB 与YZ 交于N ,MN 与YL 交于C ',由定理可得),(-='YL CA 所以,点C 应与点C '重合,即CM BL YZ ,,共点.4.4 一维基本图形的射影对应两个点列成射影对应的定义. 两个线束成射影对应的定义. 点列与线束成射影对应的定义.定理4.11 设两个一维基本图形成射影对应,则对应四元素的交比相等. 定理4.12 若两个一维基本图形对应四个元素的交比相等,则必成射影对应. 定理 4.13 如果已知两个一维图形的任意三对对应元素,那么可以确定唯一一个射影对应.练习4-45. 若三角形ABC 的三边AB 、BC 、C A 分别通过共线的三点P ,Q ,R ,二顶点B 与C 各在定直线上,求证顶点A 也在一条直线上.证明根据图形(见第4题图)可知,题图)(第2Λ),,,(21ΛB B B ),,,(21ΛC C C ,则Λ),,,(21ΛB B B P ),,,(21ΛC C C R在这两个射影线束中,PR是自对应元素,所 以Λ),,,(21ΛB B B P ),,,(21ΛC C C R两透视对应的线束对应直线的交点Λ,,,21A A A 共线. 4.5 透视对应定义4.8点列和线束成射影对应,如果对应直线过对应点,这种特殊的射影对应称为透视对应,这时也这两个一维图形处于透视状态.定义4.9两个点列和同一个线束成透视对应,也就是说两个点列成中心射影对应,则称这两个点列成透视对应.定义4.10两个线束和同一个点列成透视对应,则称这两个线束成透视对应. 定理4.14两个射影对应的点列成透视的充要条件是:两个点列的公共点自对应. 定理4.15两个射影对应的线束成透视的充要条件是:两个线束的公共点自对应. 定理4.16(巴卜斯定理)设C B A ,,是直线l 上互异的三点,C B A ''',,是l '上互异的三点,那么三个交点C B C B L '⨯'=,B A B A N '⨯'=,A C A C M '⨯'=共线.定理4.17对于两个不共底的且不成透视对应的射影对应点列,用两次透视对应,可把第一个点列变成第二个点列.也就是说,射影对应是两个透视对应的复合.定理4.18设一个点列与一个线束成射影对应而不成透视对应,那么用三次透视就可以彼此转换.即,这时的射影对应是三个透视对应的复合.题图)(第5A1.如图四边形ABCD 被EF 分成两个四边形AFED 和FBCE ,求证三个四边形ABCD ,AFED ,FBCE 的对角线交点H G K ,,共线.证明因为D ,E ,C 直线l 上互异的三点,A ,F ,B 是直线m 上互异 的三点,由定理4.16(巴卜斯定理),三个交点AE DF G⨯=,AC DB K ⨯=, FC EB H ⨯=共线.4.6 对合对应对合对应定义.定理4.19两个重叠的一维图形(点列、线束)q p μ+,q p μ'+成为对合对应的充分必要条件是:对应元素的参数μ和μ'满足0)(=+'++'d b a μμμμ其中02≠-b ad .定理4.20不重合的两对对应元素,确定唯一一个对合对应.1.求参数为21→,20→的两对对应元素所确定的对合对应. 解利用定理 4.19,这里两对对应元素的参数μ和μ'分别为21,1='=μμ和2,0='=μμ,设0)(=+'++'d b a μμμμ为所求的对合对应,把两对对应参数值代入得)题图(第1DAFBCEGKHlm⎪⎩⎪⎨⎧=+=++0202321d b d b a 解得2:1:1::-=d b a ,因此,这两对对应元素所确定的对合对应为02=-'++'μμμμ.。
第三章射影变换
第三章 射影变换与射影坐标本章首先引入射影不变量——交比。
然后在此基础上,讨论了一维基本形之间的射影对应与射影变换,以及二维射影对应和射影变换,还定义了一维和二维射影坐标。
§1 交比与调和比点列中四点的交比与调和比定义1.1 共线的四个不同点A ,B ,C ,D 的交比等于单比(ABC )与单比(ABD )的比,记作:(AB ,CD ),即(AB ,CD )=)()(ABD ABC其中A ,B 叫基点偶,C ,D 叫分点偶。
交比又称交叉比和复比。
由交比和单比的定义,我们可AD BC BDAC BDAD BC ACABD ABC CD AB ⋅⋅===)()()(, 其中AC ,BC ,AD ,BD 是有向线段的数量。
我们不难得出:(1) 点偶C ,D 不分离点偶A ,B 时,交比(AB ,CD )﹥0; (2) 点偶C ,D 分离点偶A ,B 时,交比(AB ,CD )﹤0; (3) 当C ,D 重合时,(AB ,CD )=1; (4) 当A ,C 重合时,(AB ,CD )=0。
定理1.1 基点偶与分点偶交换,交比值不改变,即 (AB ,CD )=(CD ,AB ) 证明 由定义1.1,(CD ,AB )=),(CD AB BCAD BDAC CB DA DB CA =⋅⋅=⋅⋅ 定理1.2 基点偶的两个字母交换或分点偶的两个字母交换,交比的值变成原来的交比值的倒数,即(BA ,CD )=(AB ,DC )=),(1CD AB证明(AB ,DC )=),(1)()(1)()(CD AB ABD ABC ABC ABD == 又(BA ,CD )=(CD ,BA )=),(1),(1CD AB AB CD =推论 同时交换每个点偶里的字母,交比的值不改变,即 (AB ,CD )=(BA ,DC ) 定理1.3 交换中间的两个字母或两端的两个字母,交比的值等于1减去原来的交比值,即(AC ,BD )=(DB ,CA )=1-(AB ,CD )证明(AC ,BD )AD CB CD AB ⋅⋅=AD CB BD CB BC AC ⋅++=))(( AD CB BDAC CB BD CB AC ⋅⋅+++=)(AD CB BD AC ⋅⋅+=1=1+)(ADBC BDAC ⋅⋅-=1-(AB ,CD )共线四点1,2,3,4一共有4!=24中不种的排列,所以有24个交比,根据交比的运算性质,它们只有6个不同的交比值,即(12,34)=(34,12)=(21,43)=(43,21)=m(21,34)=(34,21)=(12,43)=(43,12)=m1(13,24)=(24,13)=(31,42)=(42,31)=1-m(13,42)=(42,13)=(31,24)=(24,31)=m-11(14,23)=(23,14)=(41,32)=(32,41)=1-m 1(14,32)=(32,14)=(41,23)=(23,41)=1-m m例1 已知(P 1P 2,P 3P 4)=3,求(P 4P 3,P 2P 1)和(P 1P 3,P 2P 4)的值解 (P 4P 3,P 2P 1)= (P 2P 1 ,P 4P 3)=(P 1P 2,P 3P 4)=3 (P 1P 3,P 2P 4)=1-(P 1P 2,P 3P 4)=1-3=-2下面研究交比的代数表示定理1.4 一直线上的无穷远点分其上任何两点的单比等于1。
射影几何中对合问题的研究
第37卷第3期2020年6月晋中学院学报Journal of Jinzhong UniversityVol .37 No .3Jun . 2020射影几何中对合问题的研究晋琚(晋中学院数学学院,山西晋中030619)摘要:在一维射影变换的基础上对射影几何中对合的相关问题进行了研究,并对对合的 一些题型进行了整理求解.关键词:射影几何;射影变换;对合;二重元素中图分类号= 0185文献标志码:A文章编号= 1683-1808(2020)03-0009-031维射影变换1.1定义定义1 .1两个重叠的一维基本形的射影对应叫做一维射影变换.[1]4 1.2代数表示定理1.1两个点列间射应变换的代数表达式为非奇线性对应,X —-P •土\PXl'= 〇11*1+°12*2. A或者(p #〇). A =px 2 =1.3对应点参数满足的方程定理1.2两个重叠的一维基本形4 +AB j +A 间的射影变换对应点参数满足的条件为aAA ’+ 6A + cA ’+ d = 0 其中 acf - 6c # 0.1.4决定的条件定理1.3已知三对对应元素则可以唯一决定一个射影变换.(因为三对对应元素就可以确定:c :d , 决定了这个变换)1.5二重元素(自对应元素)两个不同实的自对应元素,称为双曲型的射影变换.两个相同实的自对应元素,称为抛物型的射影变换.一对共轭虚的自对应元素,称为椭圆型的射影变换.2对合 2.1定义定义2.1在一维射影变换中,如果对于任何元素,无论看作第一基本形还是第二基本形,它的对应元 素是一样的,那么这种非恒等的射影变换叫做对合.[2]11 2.2代数表示定理2.1对合的代数表达式为a n 如〇21 〇22#0.[收稿日期]2020-01-22[作者简介]晋裙(1981-),女,山西洪洞人,晋中学院数学学院,讲师,硕士,研究方向:代数._ a i l %+a i2证明:射影变换为对合o x —且an,,A =#0.an ai2 di \ dna 11x ,- anx - a 12= 0a 21xr x + 〇22x - anx r - a l 2= 0«两式相减得且牝2.3对应点参数满足的方程定理2.2两个重叠的一维基本形4+ABM +A 'B 成为对合的充要条件是对应点的参数A 与A '满足以 下方程:aAA' + 6(A+A') + d = 0 其中 a <f - 62# 0 •(1)证明:“4”设P 和(?为一对对合对应点,并设P = A + pB ,Q = A + qB由于对合是射影变换,有apq + bp + cq + d = 0 (PQ )①aqp + bq + cp + d - 0 (Q —>■ P )(2)①-②得(p - q)(b - c ) = 0 .③④由于P 和0是不同点,所以p # g .于是有i # c因此,对合的对应点参数满足aAA ,+ 6(A +A 〇 + d = 0 其中 ad - 6V 0 .若⑴式成立,设P —(?,P ',则参数/得apq + b(p + q ) + d 二 Q aqp '+ b(q + p ') + d - 0 ②-④得(aq + b)(p - p ') - 0 .由于叫+ 6为不定值,所以p = p ,.所以P — 0,(?—尸,此时射影变换为对合•2.4决定的条件定理2.3已知两对对应元素则可以唯一决定一个对合.证明:由于对合对应点参数满足方程:aAA ,+ 6(A +A ,)+ d = 0 其中 ad - 6V 0 .已知两对对应点参数Pl ->• qi >P 2 -*• qi ^apiqi + b{pi + 91) + = 0ap^qi + b (p 2 + qi ) + d — 0可以求得a : 6: d 确定对合方程.2.5二重元素(自对应元素)两个不同实的自对应元素,称为双曲型的对合.一对共轭虚的自对应元素,称为椭圆型的对合.注:在对合方程aAA ' + 6(A +A ') + d = 0 其中 a <f - 62 # 0中,设 A =A ,,得 aA 2 + 26A +d = 0.由于A =462-4ai # 0,所以A >0时,两个不同实的自对应元素称为双曲型的对合;A <0时,一对 共轭虚的自对应元素称为椭圆型的对合.A # 0,无抛物型的对合.2.6双曲型对合的一个性质定理2.4双曲型对合的任何一对对应元素p -p ',与其两个二重元素调和共轭,即.10 •证明:由对合对应知(PP,EF) = -1又所以3对合相关题型求解p x i -(PP',EF) = (FP,EF) = l/(PF,EF).(PF,EF)2= 1.(PP,EF)¥=l.(PP,EF) = -1.x \+2x 2例1求对合的自对应点坐标.[3]px2,= — x2解:1)首先排除自对应点为无穷远点,因为(1,0)—(1,0)时,必有你 2)将对合表达式化为非齐次坐标形式.x + 2x =-------—,Ax -I0,此题衂=4 # 0•令,得 2»2 - - 1 = 0,解得= 1 或=化为齐次形式,自对应点为(1,1)(-1,2).例2已知对合的两对对应元素参数为3 — 2,5 — 1,试求此对合方程,并求二重元素.解:将3 — 2,5 — 1代入oAA ,+ 6(A +A ') + d = 0 其中 W - 62# 0 得6a + 5b + d - 0 5a + 6b + d - 0推得a :6:<i =::= -1 : (-1) : 11 = 1 : 1 : (-11).6 1155 6所以此对合方程为AA ; + A + A ; - 11 =0.令A ,有 A2+A - 11,解得 A 1>2 = -1 ± 2V T .所以二重元素的参数为-1 ± 2V ^~ .参考文献[1] 梅向明,刘增贤.高等几何[M ].北京:高等教育出版社,2008.[2] 朱德祥,朱维宗.高等几何[M ].北京:高等教育出版社,2015.[3] 梅向明,刘增贤.高等几何学习指导与习题选解[M ].北京:高等教育出版社,2003.(编辑郭继荣)• 11 •。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课件作者:南京师大数科院周兴和
§ 2.5 一维基本形的对合
一பைடு நூலகம்定义
定义2.11. 两个成射影对应的重叠的一维基本形中, 若对任意一 个元素, 无论把它看着属于第一基本形的元素或是第二基本形的 元素, 其对应元素相同, 则称这种非恒同 非恒同的射影变换为一个对合 对合. 非恒同 对合 定义2.11'. 设f 为一维基本形[π]上的一个非恒同 非恒同的射影变换. 若 非恒同 对任意的x∈[π], 都有f(x)=f–1(x), 则f 称为[π]上的一个对合 对合. 对合 注 (1). 对合非恒同. (2). 对合是特殊的射影变换.
§ 2.4 一维射影变换
一、一维射影变换
1、定义 2、代数表示 (1). 坐标表示 ρx1 ' = a11 x1 + a12 x2 ρx2 ' = a21 x1 + a22 x2 (2). 参数表示 定义. 定义 形如 axx'+bx + cx'+ d = 0 的方程称为关于x, x'的双线性方程 双线性方程. 双线性方程
将实数轴添加无穷远点, 并令在 f 下, 无穷远点与自己对应, 则 f 是点列上的射影变换, 具有如下性质: 无论将x作为第一 x' = f ( x) = − x. l(P) 或第二基本形的元素, ∀x ∈ R, 视x ∈ l'(P') −1 x' = f ( x) = − x. 其对应元素相同.
对合的定义
铛!铛!铛! ……
The class has already begun!
§ 2.4 一维射影变换
一、一维射影变换
1、定义 一个一维基本形到自身的射影对应称为一维射影变换 一维射影变换. 一维射影变换 [π'], 且[π]=[π']. 则φ称为一维基本形[π]上的 即若φ: [π] 一个射影变换. 注:为方便理解, 常把一个 一维基本型看作两个“重叠” “重叠” 的一维基本形. 据Steiner作图法, 一个一维 射影变换可由3次透视对应得 到.
§ 2.4 一维射影变换
一、一维射影变换
1、定义 2、代数表示 (1). 坐标表示 (2). 参数表示 定理2.16 一维基本形上的一个变换为射影变换 的参数λ,λ' 满足一个双线性方程 aλλ '+bλ + cλ '+ d = 0 (ad − bc ≠ 0) 其对应元素
(2.13)
注1、(2.13)对于线束的射影变换同样适用. 注2、(2.13)对于一般射影对应适用. 只要将λ, λ'作为对应元素 对于各自基本形中取定基元素的参数. 因此, (2.13)可以作为一维 一维 射影对应的参数定义. 射影对应的参数定义
§ 2.4 一维射影变换
例1. 设A1A2A3为坐标三点形, O(1, 1, 1). A2O×A1A3=A, P是A2A3 上的动点, PO×A1A2=Q, QA×A2A3=P'. 若P, P'的齐次坐标分别为 (0,λ,1), (0,λ',1). 求(P)到(P')的射影变换的方程和不变元素. 解. 显然, P=A3+λA2, P'=A3+λ'A2. 所以, 只要 求出λ, λ'的关系式. A2 (0,1,0) ⇒ A2O:x1 − x3 = 0 ⇒ A(1,0,1). O(1,1,1)
§ 2.4 一维射影变换
例3. 2003级期中试题:已知P, P'为点列l(P)上非抛物型射影变 级期中试题: 级期中试题 换φ的两对相异的对应点, E为φ一个不变点, 求作φ的另一个不变 点F. 解. 作法 (1). 过E任作异于l的 直线m. (2). 在m上任取异于E 的相异二点V, V'. (3). 连结PV, P'V'交于点P''. (4). 连结QV, Q'V'交于点Q''. (5). 连结P''Q''交l于点于F为所求. 证明. 见上例.
双曲型 相异实根 相异实不变元 > 0 ∆ = 0 ⇒ (2.14)有两个 相同实根 ⇒ (2.13)有两个 相同实不变元 称为 抛物型 < 0 椭圆型 共轭虚根 共轭虚不变元
§ 2.4 一维射影变换
二、一维射影变换的分类
1、分类 2、性质 (1). 双曲型、椭圆型射影变换 定理2.18 对于双曲、椭圆型射影变换, 任一对相异的对应元素 与两个不变元素的交比为定值, 称为双曲、椭圆型射影变换的特征 特征 不变量. 不变量 证明. 设X, Y为两个不变元素, P≠P'为任一对相异的对应元素. 设 X, Y, P, P'的坐标依次为x, y, x+y, x+µy. 则这四点的参数依次为0, ∞, 1, µ. 于是
( EP' , PR) = −1.
法二. 代数法. 设E, P', P, R的参数依次为λ1, λ2,λ3,λ4. 由抛物型射影变换的性质, 有 1 1 − = k. P → P': λ3 − λ1 λ2 − λ1 1 1 − = k. P' → R : 由此二式,得 λ2 − λ1 λ4 − λ1 2 1 1 = + . 变形可得(EP', PR)=–1. λ2 − λ1 λ3 − λ1 λ4 − λ1 思考:仿照上例,设计一个作图题.
0
定理2.17 在实复射影平面上, 任一个一维射影变换至少有一 个不变元素. 非恒同的一维射影变换至多有两个相异的不变元素. 证明. 在(2.13)中, 令λ=λ'. 则有一维射影变换的不变元素方程 不变元素方程
aλ2 + (b + c)λ + d = 0,
(ad − bc ≠ 0)
(2.14)
立刻可得结论. 据此可得一维射影变换的分类:
l ( P, P ' E , F )
从而,
(P'')
l ' (V , V ' E , F ' ) l (Q, Q' E , F ) l (Q, Q' E , F )
l ' (V , V ' E , F ' ) l ( P, P ' E , F )
(Q'')
于是, (PP', EF)=(QQ', EF). 从而E, F为两个不变点. 另法. 由作图, 有 (V) (V') ( P, Q, E , F ) ( P' ' , Q' ' , F ' , F ) ( P' , Q' , E , F ) 所以, E, F为两个不变点. 2003级期中试题:已知点列上非抛物型射影变换φ的两对相 级期中试题: 级期中试题 异的对应点及其一个不变点, 求作φ的另一个不变点.
1 1 1 1 − − = 0 令λ = λ ' 不变元方程: 2 = 0 ⇒ λ = ∞, 不变元为A2 . λ ' λ λλ ' λ
(如图)
§ 2.4 一维射影变换
例2. 设P, P', Q, Q'为点列l(P)上射影变换的两对对应点, E是不 变点, V, V'是过E的直线l'上任意两点. PV×P'V'=P'', QV×Q'V'=Q''. 求证:P''Q''×l=F为另一个不变点. 证明. 设P''Q''×l'=F'. 则有
P(0, λ ,1), O(1,1,1) ⇒ PO : (1 − λ ) x1 − x2 + λx3 = 0.
P' (0, λ ' ,1), A(1,0,1) ⇒ P' A : λ ' x1 + x2 − λ ' x3 = 0.
PO 1 − λ −1 λ P ' A 共点于Q ⇔ λ ' 1 − λ ' = 0 ⇔ 变换式:λ − λ '−1 = 0. ⇒ 0 0 1 A1 A2
§ 2.5 一维基本形的对合
今日作业 P.72: 1, 2(3), 4
See you this evening!
§ 2.4 一维射影变换
例4. 设点列l(P)上射影变换为抛物型的, E是不变点, P, P'为一 对相异的对应点. 当把P'看成第一点列的点时, 其对应点为R. 求证: (EP', PR)=–1. 证明. 利用上例作图. 因为E是唯一不变点, 所以必有P''Q''×l=E. 考察完全四点形VV'P''Q'', 立即可得
§ 2.4 一维射影变换
二、一维射影变换的分类
1、分类 设有射影变换 ϕ : aλλ '+bλ + cλ '+ d = 0, (ad − bc ≠ 0) (2.13) 若存在λ0 ∈ R, 使aλ2 + (b + c)λ0 + d = 0, 则称A+λ B为φ的一个不变元素 不变元素. 0 不变元素
§ 2.5 一维基本形的对合
一、定义
考察函数 f : R → R, f ( x) = − x, 有下列性质 (i). f 为一个双射; f 2 = f f = I . 即∀x ∈ R, f 2 ( x) = f ( f ( x)) = f (− x) = −(− x) = x. (ii).
f = f −1. 即
0 ↔ 0 ⇒ aλλ '+bλ + cλ '+ d = 0 ⇒ d = 0. 1 1 1 ∞ ↔ ∞ ⇒ a+b +c +d = 0 ⇒ a = 0. λ' λ λλ ' b 1↔ µ ⇒ b + cµ = 0 ⇒ µ = − . c 1 c 从而, ( XY , PP ' ) = = − = 常数. µ b
