高等几何讲义 第三章 射影变换____§1 一维射影变换
第二章 射影变换-第四节 一维射影变换课件ppt课件
一、一维射影变换
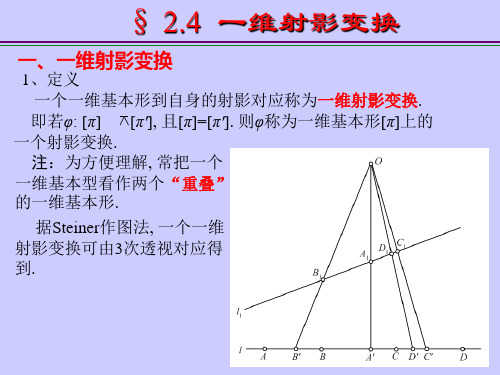
1、定义 一个一维基本形到自身的射影对应称为一维射影变换. [π'], 且[π]=[π']. 则φ称为一维基本形[π]上的 即若φ: [π] 一个射影变换. 注:为方便理解, 常把一个 一维基本型看作两个“重叠” 的一维基本形. 据Steiner作图法, 一个一维 射影变换可由3次透视对应得 到.
a11 a12 0,
a21 a22
0
(2.10)
其中对应点的坐标是关于一维基本形[π]上的同一坐标系取得的.
(ad bc 0)
§ 2.4 一维射影变换
一、一维射影变换
1、定义 2、代数表示 (1). 坐标表示 (2). 参数表示 定理2.16 一维基本形上的一个变换为射影变换其对应元素 的参数λ,λ' 满足一个双线性方程 a 'b c 'd 0 (ad bc 0) (2.13) 证 “=>”. 见教材, 略. “<=”. 设一维基本形(P)上的一个变换φ使得任一对对应元素的 参数λ,λ' 满足双线性方程(2.13). 显然φ是一个双射,只要证φ保交比. 设λi ,λi' (i=1,2,3,4)为任意四对对应元素的参数. 则 b1 d b3 d (ad bc)(1 3 ) 1 '3 ' . a1 c a3 c (a1 c)(a3 c) 同法可以求出λ2'–λ4', λ2'–λ3', λ1'–λ4', 得到 (1 '3 ' )(2 '4 ' ) (1 3 )(2 4 ) . (2 '3 ' )(1 '4 ' ) (2 3 )(1 4 )
几何空间选论(第三讲 射影几何与射影空间)

第三讲射影几何与射影空间一、射影几何的起源与确立射影几何是研究图形的射影性质,即经过射影变换后,依然保持图形性质不变的几何学分支。
射影几何也叫投影几何学,通过它可以把欧氏几何、仿射几何等联系起来。
射影几何的某些内容在公元前就已经出现了,基于绘图学和建筑学的需要,古希腊几何学家就开始研究透视法,也就是投影和截影。
早在公元前200年左右,阿波罗尼奥斯就曾把二次曲线作为正圆锥面的截线来研究。
在4世纪帕普斯的著作中,出现了帕普斯定理。
但射影几何直到十九世纪才形成独立体系,趋于完备。
1.达·芬奇(1452—1519)射影几何的最早起源是绘画。
达·芬奇是一位思想深邃,学识渊博,多才多艺的画家、发明家、哲学家、音乐家、医学家、建筑和军事工程师。
他广泛地研究与绘画有关的光学、数学、地质学、生物学等多种学科。
在《绘画专论》一书中,他对透视法作了详尽的论述。
他的代表作《最后的晚餐》是基督教传说中最重要的故事。
这幅画就是严格采用透视法的。
在数学方面,他巧妙地用圆柱滚动一周的方法解决了化圆为方的难题,另外他还研究过等腰梯形、圆内接多边形的作图,四面体的重心等。
此外,达·芬奇还发现了液体压力的概念,提出了连通器原理。
达·芬奇在生理解剖学上也取得了巨大的成就,被认为是近代生理解剖学的始祖。
他绘制了比较详细的人体解剖图。
在建筑方面,达·芬奇也表现出了卓越的才华。
他设计过桥梁、教堂、城市街道和城市建筑。
达·芬奇的研究和发明还涉及到了军事领域。
他发明了簧轮枪、子母弹、三管大炮、坦克车、浮动雪鞋、潜水服及潜水艇、双层船壳战舰、滑翔机、直升飞机和旋转浮桥等。
看过《达·芬奇密码》的人大概都知道达·芬奇密码筒。
达·芬奇设计的这种密码筒造型古典,内涵着文艺复兴特质,设计优雅。
要打开密码筒,必须解开一个5位数的密码,密码筒上有5个转盘,每个转盘上都有26个字母,可能作为密码的排列组合多达11881376种。
高等几何讲义 第三章 射影变换____§1 一维射影变换

的乘积.
➢ 注意:定理6的证明表明,虽然射影对应可传递, 但透视一般是不可传递的.
高 等 几 何 ( Higher Geometry )
1 1
u1 u2
t1 t2
v1 v2
1 2
u1 u2
1 2
v1 v2
t1 t2
x vI x/ v/ II
高 等 几 何 ( Higher Geometry )
§1 一维射影变换
令
u1 u2
t1 t2
v1 v2
t1 t2
,则
/1 /2
v21 u21
v12, u12
从而
u21 u12 /2
v21 v12 /1
c
证明:如图,设
p
(ab/)(a/b),q
(bc/)(b/c),
b a
s
t
q
r (ca/)(c/a), s (ac/)(ba/), p r
t (bc/)(ca/),d /. d
因 {a/, p, s, b} a {a/, b/, c/, d} c {t, q, c/, b}a,/ b/ / c/
§1 一维射影变换
且设 I 上的动点 x 对应 II 上
的点 x/,则 (u/v/; t/x/) (uv; tx).
u
t
设各点射影坐标分别为 u(u1,
u2)、v(v1, v2)、t(t1, t2)、 x(1,
u/
t/
2)、x/(/1, /2),则得
高等几何3.3—3.4节

注 上述定义、定理表明线束的交比与点列的交比 具有完全相同的形式.
5
云南师范大学
3.3 线束的交比
二、线束交比的几何意义
1. 斜率表示 如图, 在以S(x0,y0)为束心的线束 中,取定二直线x=x0, y=y0. 则直线的 (负)斜率k可以作为参数来表示线束. 由定理3. 8,可得
对于通常线束中以ki为斜率的四直线pi (i=1,2,3,4), 有
定理3.9的证明(留作练习)
15
云南师范大学
3.4 一维射影对应
二、一维射影几何基本定理:
定理3.10 设两个一维基本图形成射影对应, 则对应四元素的交比相等。
证明思路分析:由于四元素的交比等于对应 参数的交比,因此,若设两个一维几何图 形的对应参数分别为:
1、2、3、4, 1、2、3、4, 则证明:(12,3 4)=(12,3 4).
上式也可写为: x1 ' a11 a12 x1 , x2 ' a21 a22 x2 或
X ' AX ,
| A | 0.
22
云南师范大学
3.4 一维射影对应
例1. 求射影对应式, 使l上的点(1, 0), (2, 1), (4, 1)依次 对应于l'上的点(1, 0), (–1, 1), (1, 1). 解. 设所求对应式为
17
云南师范大学
3.4 一维射影对应
二、一维射影几何基本定理:
定理3.11 若两个一维基本图形对应四元素的 交比相等,则必成射影对应。 (证明见教材P.34-35)
定理3.10和定理3.11 说明:两个一维基本图 形成射影的充要条件是:对应元素的交比 相等。同时,这两个定理说明了:交比是 射影不变量。
一维射影变换
§ 6.1 一维基本形的射影对应
例3. 如果三点形ABC的边CB, CA, AB分别通过在同 一直线上的三点P, Q, R, 又顶点B, C各在一条定直线上. 求证:顶点A也在一条定直线上. 证明 显然,
(B,B1,B2,…) 于是, R(B,B1,B2,…)
(P )
(C,C1,C2,…) Q(C,C1,C2,…)
§ 6.1 一维基本形的射影对应
(4) Steiner作图法 已知两点列间射影对应的三对相异 的对应元素, 求作任一元素的对应元素.
(5) 思考:将(4)中 “点列” 改为 “一维基本形”. (6) 定理2.2 两个一维基本形间的射影对应可由已知相 异的三对对应元素唯一确定.
§ 6.1 一维基本形的射影对应
§ 6.1 一维基本形的射影对应
(3). 线束↔线束. 对应直线交点共线.
S (a, b, c,...)
(s)
S ' (a' , b' , c' ,...)
透视轴
注
(1)透视关系具有对称性,但它不具有传递性. (2) 透视对应是一个保交比的双射. (3) 连续两次透视对应的结果不一定仍是透视对应 .
§ 6.1 一维基本形的射影对应
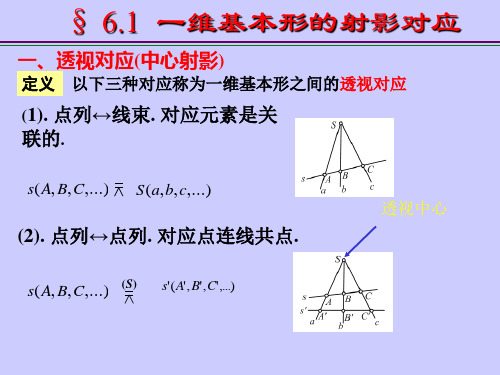
一、透视对应(中心射影)
定义 以下三种对应称为一维基本形之间的透视对应
(1). 点列↔线束. 对应元素是关 联的.
s( A, B, C ,...) S (a, b, c,...)
透视中心
(2). 点列↔点列. 对应点连线共点.
s( A, B, C ,...)
(S)
s' ( A' , B' , C' ,...)
A恰为上述两射影点列对应直线 的交点.
第三章一维射影几何学

O
a s, b s, c s a s 1 b s d s a s 2 b s
1 2 B,C D 1 A 2
A a
A
C
D
C B
B D b d a 2b
所以,点列上任意一点M的坐标可表为:
(a1 ub1 , a 2 b2 , a3 b3 )
的形式,当时,
0 可表为
(a1 b1 , a 2 b2 , a3 b3 )
的形式.为
M 1 , M 2 点列的基点
u
AC BD 定义:设A、B、C、D为共线的四点,把 定义为这四点 AD BC
sin Q3 cos Q1 sin Q1 cos Q3 sin Q4 cos Q2 sin Q2 cos Q4 sin Q4 cos Q1 sin Q1 cos Q4 sin Q3 cos Q2 cos Q3 sin Q2 sin Q3 Q1 sin Q4 Q2 sin Q4 Q1 sin Q3 Q2
第三章 一维射影几何学
§3.1 点列与线束
维的概念:平面内的点与直线都有两个坐标,平面内的点几 何学和线几何学都是二维的。 定义1 点列:动点在一条直线上移动产生的图形称为点列。那 条定直线称为点列的底,设 M 1 a1 a2 a2 ,M 2 b1 b2 b2
M 为定直线上二点, x1 , x2 , x3 为点列的动点,则:
1, ,0
四点中也只当某两点重合时,六个交比值才能有等于
第二种情况
1
AC AD BC BD
射影变换
射影变换4.1 点列和线束点列和线束定义.两个矢量),,(321a a a 和),,(321b b b 表示不同的点当且仅当这两个矢量线性无关. 在两点A ),,(321a a a 与B ),,(321b b b 的连线上任意一点),,(321x x x X 满足0321321321=b b b a a a x x x即,三点A ),,(321a a a ,B ),,(321b b b 与),,(321x x x X 共线的充分必要条件是0321321321=b b b a a a x x x以B A ,为基点的点列中,任何一点X 都可以表示为B A X μλ+=,用齐次坐标可以表示为B A B A X λλμ'+=+=;以m l ,为基线的线束中,任何一直线p 都可以表示为m l p μλ+=,用齐次坐标可以表示为m l m l p λλμ'+=+=.练习4-11.已知A 和B 的齐次坐标分别为)1,1,5(和)1,0,1(-,求直线AB 上一点C ,使1)(-=ABC ,若B A C λ+=,求出λ.解利用非齐次坐标),(y x 与齐次坐标),,(321x x x 之间的关系31x x x =,32x xy =.这时,)1,5(),(=y x A ,)0,1(),(-=y x B ,再利用BC AC ABC =)(.115-=+-x x ,解得2=x,101-=--y y ,解得21=y .即)21,2(=C ,C 点的齐次坐标为)1,21,2(. 因为B A C 2121+=,所以 1=λ. 注意:以B A ,为基点的点列中,任何一点X 都可以表示为B A X μλ+=,用齐次坐标可以表示为B A B A X λλμ'+=+=. 2.试证明:三点),,(321x x x ,),,(321y y y ,),,(321z z z 共线的充分必要条件为0321321321=z z z y y y x x x 证明三点),,(321x x x ,),,(321y y y ,),,(321z z z 共线的充分必要条件为λ=--=--=--333322221111y z x z y z x z y z x z所以0332211321332211321321321=-------=y z y z y z y y y x z x z x z z z z y y y x x x4.已知直线0143=++y x 与02=+y x ,求过两直线的交点与点)0,1,2(的直线方程.解两直线0143=++y x 与02=+y x 的交点为)5,1,3(112143321--=x x x 于是点)5,1,3(--与点)0,1,2(的直线方程为05105012513321321=+-=--x x x x x x即05105321=+-x x x .4.2 点列和线束的交比定义4.2设D C B A ,,,为点列上共线的四点,则这四点的交比为ADBC BDAC CD AB ⋅⋅=),(.定理 4.1取A 和B 为基点,将D C B A ,,,四点的坐标依次表示为a ,b ,b a 1λ+,b a 2λ+,则四点的交比为21),(λλ=CD AB . 定理4.2若D C B A ,,,四点的坐标为)4,3,2,1(21=+i P P i λ,21,P P 点列上两个基点,则),(),(432124142313λλλλλλλλλλλλ=----=CD AB定理4.3将某两点互换,同时互换其余两点,则交比不变.即),(),(),(),(BA DC AB CD DC BA CD AB ===定理4.4只在一对点中互换,交比转为其倒数.即),(1),(CD AB DC AB =,),(1),(CD AB CD BA =定理4.5交换中间两点,则交比为1与原值的差,即),(1),(CD AB BD AC -= 定义4.3当1),(-=CD AB 时,称D C ,调和分割线段AB .调和分割的关系是对等的.因为1),(),(-==CD AB AB CD ,所以,B A ,也调和分割线段CD ,有时也称D C B A ,,,为调和点列.定义4.4称21λλ为四直线d c b a ,,,的交比,记为),(cd ab .即 =),(cd ab 21λλ.注意:用齐次坐标之间的关系定义交比,点列的交比与线束的交比在形式上完全一致.定理4.6设四直线d c b a ,,,,若b a c 1λ+=,b a d 2λ+=,则=),(cd ab 21λλ. 定理4.7若四直线q p a 1μ+=,q p b 2μ+=,q p c 3μ+=,q p d 4μ+=,则 424132314321),(),(μμμμμμμμμμμμ----==cd ab .这个比值也称为数4321,μμμμ的交比.定理4.8两个点列经过中心投影,交比不变.练习4-21. 设E D C B A ,,,,是同一直线上的五点,求证1),)(,)(,(=EC AB DE AB CD AB .证明由交比定义ADBC BDAC CD AB ⋅⋅=),(,1),)(,)(,(=⋅⋅⋅⋅⋅⋅⋅⋅=ACBE BCAE AE BD BE AD AD BC BD AC EC AB DE AB CD AB .2.设C B A ,,三点的坐标分别为)1,1,1(,)1,1,1(-,)1,0,1(,且2),(=CD AB ,求点D 的坐标.解)1,1,1(=A ,)1,1,1(-=B ,则C B A ==+)1,0,1(2121,于是12=λ.设B A D 1λ+=,由2),(21==λλCD AB 可知,21=λ,所以)3,1,3(2-=+=B A D .注意:以B A ,为基点的点列中,任何一点X 都可以表示为B A X μλ+=,用齐次坐标可以表示为B A B A X λλμ'+=+=. 3.求四点)1,1,2(-A ,)1,1,1(-B ,)0,0,1(C ,)5,5,1(-D 的交比),(CD AB .解利用定理 4.1,取A 和B 为基点,将D C B A ,,,四点的坐标依次表示为a ,b ,b a 1λ+,b a 2λ+,则四点的交比为21),(λλ=CD AB . 这里B AC +=,于是11=λ, B AD 32-=,于是232-=λ,由21),(λλ=CD AB 可知,32),(21-==λλCD AB . 注意:以B A ,为基点的点列中,任何一点X 都可以表示为B A X μλ+=,用齐次坐标可以表示为B A B A X λλμ'+=+=. 7.试证:02321=+-x x x ,023321=-+x x x ,0721=-x x ,0531=-x x 所表示的四直线共点,并求这四直线的交比.解直线0721=-x x 与0531=-x x 的交点为)5,7,1(15017321=--x x x 点)5,7,1(满足四直线,所以,此四直线共点. 四直线与x 轴的交点分别为211-=x ,322=x ,03=x ,514=x ,所以,21),(4321=l l l l .4.3 完全四点形和完全四线形完全四点形和完全四线形定义.定理4.6完全四点形通过每一个对角点有一组调和线束,即通过这个对角点的两边和对角三角形的两边.定理4.10完全四线形的每一条对角线上有一组调和点列,即这条直线上的两个顶点及对角三角形的两个顶点.练习4-32.设XYZ 是完全四点形ABCD 的对边三点形,XY 分别交BD AC ,于M L ,,不用笛沙格定理,证明CM BL YZ ,,共点.证明由四点形ABCD ,根据定理可知,在AC 边上的四点L Y C A ,,,调和共轭, 即1),(-=YL AC .在四点形YBZL 中,LB 与YZ 交于N ,MN 与YL 交于C ',由定理可得),(-='YL CA 所以,点C 应与点C '重合,即CM BL YZ ,,共点.4.4 一维基本图形的射影对应两个点列成射影对应的定义. 两个线束成射影对应的定义. 点列与线束成射影对应的定义.定理4.11 设两个一维基本图形成射影对应,则对应四元素的交比相等. 定理4.12 若两个一维基本图形对应四个元素的交比相等,则必成射影对应. 定理 4.13 如果已知两个一维图形的任意三对对应元素,那么可以确定唯一一个射影对应.练习4-45. 若三角形ABC 的三边AB 、BC 、C A 分别通过共线的三点P ,Q ,R ,二顶点B 与C 各在定直线上,求证顶点A 也在一条直线上.证明根据图形(见第4题图)可知,题图)(第2Λ),,,(21ΛB B B ),,,(21ΛC C C ,则Λ),,,(21ΛB B B P ),,,(21ΛC C C R在这两个射影线束中,PR是自对应元素,所 以Λ),,,(21ΛB B B P ),,,(21ΛC C C R两透视对应的线束对应直线的交点Λ,,,21A A A 共线. 4.5 透视对应定义4.8点列和线束成射影对应,如果对应直线过对应点,这种特殊的射影对应称为透视对应,这时也这两个一维图形处于透视状态.定义4.9两个点列和同一个线束成透视对应,也就是说两个点列成中心射影对应,则称这两个点列成透视对应.定义4.10两个线束和同一个点列成透视对应,则称这两个线束成透视对应. 定理4.14两个射影对应的点列成透视的充要条件是:两个点列的公共点自对应. 定理4.15两个射影对应的线束成透视的充要条件是:两个线束的公共点自对应. 定理4.16(巴卜斯定理)设C B A ,,是直线l 上互异的三点,C B A ''',,是l '上互异的三点,那么三个交点C B C B L '⨯'=,B A B A N '⨯'=,A C A C M '⨯'=共线.定理4.17对于两个不共底的且不成透视对应的射影对应点列,用两次透视对应,可把第一个点列变成第二个点列.也就是说,射影对应是两个透视对应的复合.定理4.18设一个点列与一个线束成射影对应而不成透视对应,那么用三次透视就可以彼此转换.即,这时的射影对应是三个透视对应的复合.题图)(第5A1.如图四边形ABCD 被EF 分成两个四边形AFED 和FBCE ,求证三个四边形ABCD ,AFED ,FBCE 的对角线交点H G K ,,共线.证明因为D ,E ,C 直线l 上互异的三点,A ,F ,B 是直线m 上互异 的三点,由定理4.16(巴卜斯定理),三个交点AE DF G⨯=,AC DB K ⨯=, FC EB H ⨯=共线.4.6 对合对应对合对应定义.定理4.19两个重叠的一维图形(点列、线束)q p μ+,q p μ'+成为对合对应的充分必要条件是:对应元素的参数μ和μ'满足0)(=+'++'d b a μμμμ其中02≠-b ad .定理4.20不重合的两对对应元素,确定唯一一个对合对应.1.求参数为21→,20→的两对对应元素所确定的对合对应. 解利用定理 4.19,这里两对对应元素的参数μ和μ'分别为21,1='=μμ和2,0='=μμ,设0)(=+'++'d b a μμμμ为所求的对合对应,把两对对应参数值代入得)题图(第1DAFBCEGKHlm⎪⎩⎪⎨⎧=+=++0202321d b d b a 解得2:1:1::-=d b a ,因此,这两对对应元素所确定的对合对应为02=-'++'μμμμ.。
一维射影几何学
一、点列中四点的交比
例1(习题3.4):求四点(2,1,-1),(1,-1,1), (1,0,0),(1,5,-5)顺这次序的交比。
解:取(2,1,-1),(1,-1,1)为基点,将其余两点表为它 们的线性组合。易求 (1,0,0) ∝ (2,1,-1)+ (1,-1,1),
(1,5,-5)∝ (2,1,-1)- 3/2(1,-1,1),
( ABC ) ( AB, CD) . ( ABD)
8
西南大 学
一、点列中四点的交比 定理3.1. 设取A,B为基底,将这四点的齐次坐标顺次 表为a, b, a 1b, a 2b 则 ( AB, CD) 1 . (3.2)
2
3.2 点列的交比
证明思路分析:由于交比是简比的比,而简比又是分 割比的相反数,可以先将这四点的齐次坐标化为非齐 次坐标,再用A,B的非齐次坐标线性表示C,D的非齐次 坐标,利用定比分割公式,易求点C、D分割A、B的 分割比分别是: b b
3
本章内容
3.1
一、一维基本图形
点列和线束
(1) 点列(同一直线上点 的集合)
(1)' 线束(平面上过同一 点的直线的集合)
记号 l(A,B,C,…) 或 l(P) 底 元素
记号 L(a,b,c,…) 或 L(p) 束心 元素
4
3.1 一、一维基本图形
西南大 学
点列和线束
(2)点列和线束统称为一维几何图形(流 形),它们互为对偶图形。 (3)取定直线l上的两点A(a)、B(b)[a= (a , a b= (b , b , b )],则l上任一点M(x)可表为:
1
3
a3
2
3
a3
( ABC ) 1 因此, ( AB, CD) . ( ABD) 2
一维射影变换
一维基本形的射影变换
2、一维射影变换的性质
(1). 双曲型、椭圆型射影变换
定理. 对于双曲、椭圆型射影变换,任一对相异的对应元 素与两个不变元素的交比为定值,该定值称为双曲、椭圆型射 影变换的特征不变量.
证明 设X, Y为两个不变元素, PP'为任一对相异的对应元 素. 设X, Y, P, P'的坐标依次为x, y, x+y, x+y. 则这四元素的参 数依次为0, , 1, . 于是 0 0 a ' b c ' d 0 d 0. 1 1 1 ab c d 0 a 0. ' ' b 1 b c 0 . c 1 c ( XY , PP ') 常数。 从而, b
a a
( ) ( ) 2 0, a a
1 c 于是 k a 是常数。
c c
一维基本形的射影变换
例1 设A, B, C为相异的共线点且有 (A, B, C, P, Q, R) (B, C, A, Q, R, X). 求证:X=P. 证明. 因为 A B 所以 (AB, CP) = (BC, AQ) =(CA, BR) = (AB, CX) . 从而有X=P. B C C A P Q Q R R X
1、一维射影变换的分类 设有射影变换 a ' b c ' d 0 (ad bc 0) (*) 若存在 0 R, 使a02+(b+c)0+d=0, 则称A+0B为的一个不变元素. 定理. 在实-复射影平面上, 任一个一维射影变换至少有一个 不变元素. 非恒同的一维射影变换至多有两个相异的不变元素.
高等几何(第三、四章)
➢由于交比经中心射影后不变,故交比在透 视对应下保持不变。
➢透视关系是对称的,但不具有传递性。 ➢定义2.3.透视对应链即为射影对应。
射影对应具有传递性。
2.2 一维基本形的射影对应
➢定义2.3.透视对应链即为射影对应。 射影对应具有传递性。
➢定理2.1 两个点列间的一一对应是射影对 应的充要条件是:任何四个对应点的交比相 等。 必要性显然; 下面证明充分性;
P3
m2 m2
m3 m1
P1
m3 m2
m1 m1
P2 ,
P4
m2 m4 m2 m1
P1
m4 m2
m1 m1
P2 ,
P3
P1
m3 m2
m1 m1
m2 m2
m1 m3
P2 ,
P4
P1
m4 m2
m1 m1
m2 m2
m1 m4
P2 ,
m3 m1 m2 m1
(P1P2 , P3P4 )
设一个对应T保持任何四对对应点的交比不变,我们证明 T可由两个透视对应结合而成。
怎样才算证明了T可由两个透视对应结合而成?
要证明T的任何一对对应点均可由两个透视对应结合得 到。
设 D, D’是T的任何一对对应点,我们证明D’可由D经过 两次透视对应得到。
题目条件是T保持任何四对对应点的交比不变,现在只 有一对对应点,无法用此条件,故我们设出三对对应点:
B
ac
b
C
ca b
§2 一维射影变换
➢点列与线束统称为一维基本形,本节研究一维基 本形间的一种对应关系。
➢本节讲授的顺序与课本有所不同,我们的思路是 从三个不同的角度去刻画一维射影对应,这三个 角度分别为几何直观、本质性质以及代数的角度.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高 等 几 何 ( Higher Geometry )
§1 一维射影变换
➢ 例1 设 abcd 为平行四边形,过顶点 a 作直线
ae 与对角线 bd 平行.证明:直线 ab、ad
与直线 ac、ae 成调和共轭.
证明:因 ae 与 bd 平行,故 a
设二者交点为无穷远点 p.
o
p e
d
记(ac)(bd) o.则
的线性变换:
T:
//12 aa1211
a12 a22
12,det(aij)
0.
(3.1)
证明:不妨设两个一维基本形 I 与 II 均为点列.
在 I 上取定三点 u、v、t,使其在 II 上的对应点依
Hale Waihona Puke 次为 II 的坐标系 / [u/, v/; t/] 中的基点和单位点.
高 等 几 何 ( Higher Geometry )
高 等 几 何 ( Higher Geometry )
高 等 几 何 ( Higher Geometry )
§1 一维射影变换
➢ 同类一维基本形间的透视:
若两个点列是同一线束的 若两个线束是同一点列的
截影,则称这两个点列是 投影,则称这两个线束是
透视的.
透视的.
线束的心称为透视中心. 点列的底称为透视轴.
§1 一维射影变换
且设 I 上的动点 x 对应 II 上
的点 x/,则 (u/v/; t/x/) (uv; tx).
u
t
设各点射影坐标分别为 u(u1,
u2)、v(v1, v2)、t(t1, t2)、 x(1,
u/
t/
2)、x/(/1, /2),则得
11 0 0 11
/1 /2
1 0
/1 /2
0 1
1 1
u1 u2
t1 t2
v1 v2
1 2
u1 u2
1 2
v1 v2
t1 t2
x vI x/ v/ II
高 等 几 何 ( Higher Geometry )
§1 一维射影变换
令
u1 u2
t1 t2
v1 v2
t1 t2
,则
/1 /2
v21 u21
v12, u12
从而
u21 u12 /2
v21 v12 /1
透视点列的等价定义是它 透视线束的等价定义是它
们的对应点连线共点. 们的对应直线交点共
x
线.x/
x
d/
a/ b/
c/
/
a bc d
高 等 几 何 ( Higher Geometry )
/ / / /
§1 一维射影变换 ➢记号:用“ ”表示透视.
如前面三图中的透视分别记为:
{, , , } {a, b, c, },
,
若记 a11 v2,a12 v1,a21 u2,a22 u1,
则得所求射影变换式为
T:
//12 aa1211
a12 a22
12,det(aij)
0.
反之,也可证明(3.1)必为射影对应.
➢ 在 (3.1) 中令 1/2,/ /1//2,a a21,b
a11,c a22,d a12,则可得
➢ 解法一:(非齐次坐标法) 设对应式为 a/ b
c/ d = 0,则
由 0 1 得
c d 0,
由10得
b d 0,
由 2 2 得
4a 2b 2c d 0.
高 等 几 何 ( Higher Geometry )
§1 一维射影变换
由以上三式联立求解,得
a: b: c: d 3 : 4 : 4: 4,
这表明在边 ab上,a、b与 u、z 成调和共轭.
高 等 几 何 ( Higher Geometry )
§1 一维射影变换
➢2. 一维基本形之间的射影对应
➢ 一维基本形 I 与 II 之间的一一对应 T: III,若保 持交比不变,则称为射影对应.
➢ 关于射影对应的表达式,有 ➢ 定理3 两个一维基本形之间的射影对应是非退化
只需证二点列情形.
a bc d
若{a, b, c, d, } x {a/, b/, c/, d/, },则
{a, b, c, d, } x{a, b, c, d, } {a/, b/, c/, d/, }, 故 (ab; cd) (xa, xb; xc, xd) (a/b/; c/d/). ➢ 注意:{xa, xb, xc, }可简写为 x{a, b, c, }.
故所求射影对应为 3/ 4 4/ 4 0.
➢ 解法二:(齐次坐标法) 设对应式为
//12 aa1211
a12 a22
12,det(aij)
0.
由 (0, 1) (1, 1) 得
1 1
a12 a22,
由 (1, 1) (0, 1) 得
0
2
a11 a21
a12 a22,
由 (2, 1) ( 2, 1) 得
{ a, b, c, } x {a/, b/, c/, },
{, , , } { /, /, /, },
写在记号“ ”上方的文字表示透视中心或透视 轴.
高 等 几 何 ( Higher Geometry )
§1 一维射影变换 x
➢ 定理2 透视保持交比不变.
d/
a/ b/
c/
/
证明:由定理1及对偶原理,
23 2a11 a12
3 2a21 a22.
高 等 几 何 ( Higher Geometry )
§1 一维射影变换
将以上三组方程中的第一个联立,可解得
➢ 例2 求证:完全四点形的一边
x
上的二顶点,两条对角线与此
边的二交点,四点成调和共
d
轭.(可作结论使用)
m
证明:如图,由完全四点形的
对角线上的调和共轭性质, a
有 (yz; mn) 1.
c yn ub z
又以点 x 为中心,有 {u, z, a, b} {y, z, m, n}, 故(uz; ab) (yz; mn) 1.
高 等 几 何 ( Higher Geometry )
§1 一维射影变换
➢ 推论1 采用非齐次坐标,两个一维基本形之间的
射影对应式为
a/ b c/ d 0,ad bc 0.
➢ 推论2 三对对应元素决定两个一维基本形之间的
射影对应.
➢ 例3 求射影对应,使直线 上坐标为0、1、2的
三点依次对应于 /上坐标为 1、0、2的三点.
b
c
a{b, d, c, e} {b, d, o, p}, 故 (ab, ad; ac, ae) (bd; op).
因平行四边形对角线互相平分,故 (bd; op) 1. 所以 (ab, ad; ac, ae) 1.
高 等 几 何 ( Higher Geometry )
§1 一维射影变换
