一维射影变换剖析
高等几何5.1节
0.
注：上面的推导即求解教材习题5.1.
12
云南师范大学
5.1 一维射影坐标系
三、射影坐标的特例
1.仿射坐标
取A1为直线上的无穷远点P，取A2为原点O，则
( A1 A2 , EP) ( P A2 , EP)
( PE , A2 P ) ( PEA2 ) A2 P OP A2 E OE
kx kx2 x x1
k 1
kx2 x
0
8
云南师范大学
5.1 一维射影坐标系
二、笛氏坐标与射影坐标的转换
kx kx2 由 ， x x1
k 1 kx2 x 0
知，同一点的笛氏坐标x和射影坐标λ 之间有一个 行列式不为0的双一次关系式,因此，它们之间的 关系是射影对应（见3.4节）即有： x . 于是由定理3.1知，四点的交比既等于它们笛氏坐 标的交比，也等于它们射影坐标的交比。
a2
p
a1 e
6
云南师范大学
5.1 一维射影坐标系
一、一维射影坐标系
2.线束的射影坐标系
说明: (1)设 0，则[u1 , u2 ]与[u1 , u2 ]代表同一线.
2 (0, 0)不代表任何线, u2 0与 相对应.
x1 sin(a1, e) sin(a2 , p) (3) (a1a2 , ep ) x2 sin(a1, p)sin(a2 , e)
4
云南师范大学
5.1 一维射影坐标系
一、一维射影坐标系 1.点列的射影坐标系 说明：
（1）对于任意的数 0，坐标( x1, x2 )和( x1, x2 )代表同一点;
第二章 射影变换-第四节 一维射影变换课件ppt课件
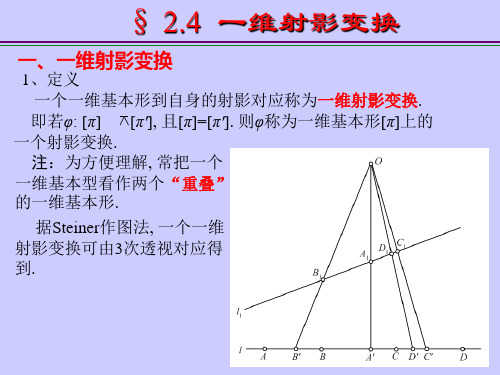
一、一维射影变换
1、定义 一个一维基本形到自身的射影对应称为一维射影变换. [π'], 且[π]=[π']. 则φ称为一维基本形[π]上的 即若φ: [π] 一个射影变换. 注：为方便理解, 常把一个 一维基本型看作两个“重叠” 的一维基本形. 据Steiner作图法, 一个一维 射影变换可由3次透视对应得 到.
a11 a12 0,
a21 a22
0
(2.10)
其中对应点的坐标是关于一维基本形[π]上的同一坐标系取得的.
(ad bc 0)
§ 2.4 一维射影变换
一、一维射影变换
1、定义 2、代数表示 (1). 坐标表示 (2). 参数表示 定理2.16 一维基本形上的一个变换为射影变换其对应元素 的参数λ,λ' 满足一个双线性方程 a 'b c 'd 0 (ad bc 0) (2.13) 证 “=>”. 见教材, 略. “<=”. 设一维基本形(P)上的一个变换φ使得任一对对应元素的 参数λ,λ' 满足双线性方程(2.13). 显然φ是一个双射,只要证φ保交比. 设λi ,λi' (i=1,2,3,4)为任意四对对应元素的参数. 则 b1 d b3 d (ad bc)(1 3 ) 1 '3 ' . a1 c a3 c (a1 c)(a3 c) 同法可以求出λ2'–λ4', λ2'–λ3', λ1'–λ4', 得到 (1 '3 ' )(2 '4 ' ) (1 3 )(2 4 ) . (2 '3 ' )(1 '4 ' ) (2 3 )(1 4 )
高等几何讲义 第三章 射影变换____§1 一维射影变换
的乘积．
➢ 注意：定理6的证明表明，虽然射影对应可传递， 但透视一般是不可传递的．
高 等 几 何 ( Higher Geometry )
1 1
u1 u2
t1 t2
v1 v2
1 2
u1 u2
1 2
v1 v2
t1 t2
x vI x/ v/ II
高 等 几 何 ( Higher Geometry )
§1 一维射影变换
令
u1 u2
t1 t2
v1 v2
t1 t2
，则
/1 /2
v21 u21
v12， u12
从而
u21 u12 /2
v21 v12 /1
c
证明：如图，设
p
(ab/)(a/b)，q
(bc/)(b/c)，
b a
s
t
q
r (ca/)(c/a)， s (ac/)(ba/)， p r
t (bc/)(ca/)，d /． d
因 {a/, p, s, b} a {a/, b/, c/, d} c {t, q, c/, b}a，/ b/ / c/
§1 一维射影变换
且设 I 上的动点 x 对应 II 上
的点 x/，则 (u/v/; t/x/) (uv; tx)．
u
t
设各点射影坐标分别为 u(u1,
u2)、v(v1, v2)、t(t1, t2)、 x(1,
u/
t/
2)、x/(/1, /2)，则得
第四节射影对应代数表示
1. 射影对应 设
l (A, B, C, ……)
l ( A, B, C , )
(1) 几何表示 (2) 代数表示
(I )
（AB，CX）=（A’B’，C’X ’）
xa )( x xb ) ( xc xa )( x xb ) ( xc ; )( x xa ) ( xc xb )( x xa ) ( xc xb
（实）
标准型在解题中有重要且巧妙的应用。
习题选解 例1 设A1A2A3为坐标三点形, O(1, 1, 1). A2O×A1A3=A, P是
A2A3上的动点, PO×A1A2=Q, QA×A2A3=P‘. 若P, P’的齐次坐标分
别为(0,λ,1), (0,λ',1). 求(P)到(P')的射影变换的方程和不变元素. 解. 由题设各点的坐标，可得
( II )
x xb x xb k ; x xa x xa
( III )
xx x x 0
( 0) ;
a b ax b ( IV ) x ( 0) ; cx d c d a11 x1 a12 x2 a11 a12 x1 (V ) ( 0) 。 a21 a22 2 a 21 x1 a 22 x 2 x
( XY , PQ) ( XY , P Q)
( XYP) ( XYP ) ( XYQ) ( XYQ) ( XYP ) ( XYQ) ( XYP ) ( XYQ)
( XY , PP) ( XY , QQ)
( XY , PP' ) k （常数）。
2 x n 1 3 , x1 0, 例3 设数列的递推公式为 xn x n 1 6
高等几何讲义 第三章 射影变换____§1 一维射影变换
高 等 几 何 ( Higher Geometry )
§1 一维射影变换
➢ 例1 设 abcd 为平行四边形，过顶点 a 作直线
ae 与对角线 bd 平行．证明：直线 ab、ad
与直线 ac、ae 成调和共轭．
证明：因 ae 与 bd 平行，故 a
设二者交点为无穷远点 p．
o
p e
d
记(ac)(bd) o．则
的线性变换：
T:
//12 aa1211
a12 a22
12，det(aij)
0．
(3.1)
证明：不妨设两个一维基本形 I 与 II 均为点列．
在 I 上取定三点 u、v、t，使其在 II 上的对应点依
Hale Waihona Puke 次为 II 的坐标系 / [u/, v/; t/] 中的基点和单位点．
高 等 几 何 ( Higher Geometry )
高 等 几 何 ( Higher Geometry )
高 等 几 何 ( Higher Geometry )
§1 一维射影变换
➢ 同类一维基本形间的透视：
若两个点列是同一线束的 若两个线束是同一点列的
截影，则称这两个点列是 投影，则称这两个线束是
透视的．
透视的．
线束的心称为透视中心． 点列的底称为透视轴．
§1 一维射影变换
且设 I 上的动点 x 对应 II 上
的点 x/，则 (u/v/; t/x/) (uv; tx)．
u
t
设各点射影坐标分别为 u(u1,
u2)、v(v1, v2)、t(t1, t2)、 x(1,
u/
t/
2)、x/(/1, /2)，则得
11 0 0 11
高等几何3.3—3.4节
注 上述定义、定理表明线束的交比与点列的交比 具有完全相同的形式.
5
云南师范大学
3.3 线束的交比
二、线束交比的几何意义
1. 斜率表示 如图, 在以S(x0,y0)为束心的线束 中，取定二直线x=x0, y=y0. 则直线的 (负)斜率k可以作为参数来表示线束. 由定理3. 8，可得
对于通常线束中以ki为斜率的四直线pi (i=1,2,3,4), 有
定理3.9的证明（留作练习）
15
云南师范大学
3.4 一维射影对应
二、一维射影几何基本定理：
定理3.10 设两个一维基本图形成射影对应， 则对应四元素的交比相等。
证明思路分析：由于四元素的交比等于对应 参数的交比，因此，若设两个一维几何图 形的对应参数分别为：
1、2、3、4， 1、2、3、4， 则证明：（12，3 4）=（12，3 4）.
上式也可写为： x1 ' a11 a12 x1 , x2 ' a21 a22 x2 或
X ' AX ,
| A | 0.
22
云南师范大学
3.4 一维射影对应
例1. 求射影对应式, 使l上的点(1, 0), (2, 1), (4, 1)依次 对应于l'上的点(1, 0), (–1, 1), (1, 1). 解. 设所求对应式为
17
云南师范大学
3.4 一维射影对应
二、一维射影几何基本定理：
定理3.11 若两个一维基本图形对应四元素的 交比相等，则必成射影对应。 （证明见教材P.34-35）
定理3.10和定理3.11 说明：两个一维基本图 形成射影的充要条件是：对应元素的交比 相等。同时，这两个定理说明了：交比是 射影不变量。
一维射影变换
§ 6.1 一维基本形的射影对应
例3. 如果三点形ABC的边CB, CA, AB分别通过在同 一直线上的三点P, Q, R, 又顶点B, C各在一条定直线上. 求证：顶点A也在一条定直线上. 证明 显然,
(B,B1,B2,…) 于是, R(B,B1,B2,…)
(P )
(C,C1,C2,…) Q(C,C1,C2,…)
§ 6.1 一维基本形的射影对应
(4) Steiner作图法 已知两点列间射影对应的三对相异 的对应元素, 求作任一元素的对应元素.
(5) 思考：将(4)中 “点列” 改为 “一维基本形”. (6) 定理2.2 两个一维基本形间的射影对应可由已知相 异的三对对应元素唯一确定.
§ 6.1 一维基本形的射影对应
§ 6.1 一维基本形的射影对应
(3). 线束↔线束. 对应直线交点共线.
S (a, b, c,...)
(s)
S ' (a' , b' , c' ,...)
透视轴
注
(1)透视关系具有对称性，但它不具有传递性. (2) 透视对应是一个保交比的双射. (3) 连续两次透视对应的结果不一定仍是透视对应 .
§ 6.1 一维基本形的射影对应
一、透视对应(中心射影)
定义 以下三种对应称为一维基本形之间的透视对应
(1). 点列↔线束. 对应元素是关 联的.
s( A, B, C ,...) S (a, b, c,...)
透视中心
(2). 点列↔点列. 对应点连线共点.
s( A, B, C ,...)
(S)
s' ( A' , B' , C' ,...)
A恰为上述两射影点列对应直线 的交点.
第三章一维射影几何学
k 3 k1 k 4 k 2 k 4 k1 k 3 k 2
O
tg Q 2 tg Q 2
A x
ab, cd
tg Q 3 tg Q 1 tg Q 4 tg Q 4 tg Q 1 tg Q 3
2
2
5 8
作业：
P5 4
1，4，5，6
§3.3线束的交比
设a,b,c,d为一线束中的四直线，取a和b作为基线，把它们的齐次坐 标依次表示为 a , b , c a 1b , d a 2 b （a,b既代表直线，又代表它 们的坐标向量）
设以一直线S截此四线于点A，B，C，D，则这四点的坐标顺序为：
AC BD
交比可由简比求得
AD BD
ABC ABD
定理1 ：设取A和B为基点，将这四点的齐次坐标顺序表达为：
a , b , a 1b , a 2 b
则
AB CD
1 2
定理2： 设点列上四点A、B、C、D的齐次坐标为P+ i q i 1, 2, 3, 4
s in a c s in
bd
例1：试证一角的两边与其内外角平分线的交比等于-1。 证明：如图，设角的两边为a,b，内外角平分线分别为c,d.
a b , cd
sin a c sin sin a d
sin Q 3 sin Q 1 c o s Q 3 c o s Q1
sin Q 4 sin Q 2 cos Q 4 cos Q 2
一维射影几何学
一、点列中四点的交比
例1（习题3.4）：求四点(2,1,-1),(1,-1,1), (1,0,0),(1,5,-5)顺这次序的交比。
解：取(2,1,-1),(1,-1,1)为基点，将其余两点表为它 们的线性组合。易求 (1,0,0) ∝ (2,1,-1)+ (1,-1,1)，
(1,5,-5)∝ (2,1,-1)- 3/2(1,-1,1)，
( ABC ) ( AB, CD) . ( ABD)
8
西南大 学
一、点列中四点的交比 定理3.1. 设取A,B为基底，将这四点的齐次坐标顺次 表为a, b, a 1b, a 2b 则 ( AB, CD) 1 . (3.2)
2
3.2 点列的交比
证明思路分析：由于交比是简比的比，而简比又是分 割比的相反数，可以先将这四点的齐次坐标化为非齐 次坐标，再用A,B的非齐次坐标线性表示C,D的非齐次 坐标，利用定比分割公式，易求点C、D分割A、B的 分割比分别是： b b
3
本章内容
3.1
一、一维基本图形
点列和线束
(1) 点列(同一直线上点 的集合)
(1)' 线束(平面上过同一 点的直线的集合)
记号 l(A,B,C,…) 或 l(P) 底 元素
记号 L(a,b,c,…) 或 L(p) 束心 元素
4
3.1 一、一维基本图形
西南大 学
点列和线束
（2）点列和线束统称为一维几何图形（流 形），它们互为对偶图形。 （3）取定直线l上的两点A(a)、B(b)[a= (a , a b= (b , b , b )],则l上任一点M（x）可表为：
1
3
a3
2
3
a3
( ABC ) 1 因此， ( AB, CD) . ( ABD) 2
第三章射影变换
第三章 射影变换与射影坐标本章首先引入射影不变量——交比。
然后在此基础上，讨论了一维基本形之间的射影对应与射影变换，以及二维射影对应和射影变换，还定义了一维和二维射影坐标。
§1 交比与调和比点列中四点的交比与调和比定义1.1 共线的四个不同点A ，B ，C ，D 的交比等于单比（ABC ）与单比（ABD ）的比，记作：（AB ，CD ），即（AB ，CD ）=)()(ABD ABC其中A ，B 叫基点偶，C ，D 叫分点偶。
交比又称交叉比和复比。
由交比和单比的定义，我们可AD BC BDAC BDAD BC ACABD ABC CD AB ⋅⋅===)()()(， 其中AC ，BC ，AD ，BD 是有向线段的数量。
我们不难得出：（1） 点偶C ，D 不分离点偶A ，B 时，交比（AB ，CD ）﹥0； （2） 点偶C ，D 分离点偶A ，B 时，交比（AB ，CD ）﹤0； （3） 当C ，D 重合时，（AB ，CD ）=1； （4） 当A ，C 重合时，（AB ，CD ）=0。
定理1.1 基点偶与分点偶交换，交比值不改变，即 （AB ，CD ）=（CD ，AB ） 证明 由定义1.1，（CD ，AB ）=),(CD AB BCAD BDAC CB DA DB CA =⋅⋅=⋅⋅ 定理1.2 基点偶的两个字母交换或分点偶的两个字母交换，交比的值变成原来的交比值的倒数，即（BA ，CD ）=（AB ，DC ）=),(1CD AB证明（AB ，DC ）=),(1)()(1)()(CD AB ABD ABC ABC ABD == 又（BA ，CD ）=（CD ，BA ）=),(1),(1CD AB AB CD =推论 同时交换每个点偶里的字母，交比的值不改变，即 （AB ，CD ）=（BA ，DC ） 定理1.3 交换中间的两个字母或两端的两个字母，交比的值等于1减去原来的交比值，即（AC ，BD ）=（DB ，CA ）=1－（AB ，CD ）证明（AC ，BD ）AD CB CD AB ⋅⋅=AD CB BD CB BC AC ⋅++=))(( AD CB BDAC CB BD CB AC ⋅⋅+++=)(AD CB BD AC ⋅⋅+=1=1+)(ADBC BDAC ⋅⋅-=1－（AB ，CD ）共线四点1，2，3，4一共有4！=24中不种的排列，所以有24个交比，根据交比的运算性质，它们只有6个不同的交比值，即（12，34）=（34，12）=（21，43）=（43，21）=m（21，34）=（34，21）=（12，43）=（43，12）=m1（13，24）=（24，13）=（31，42）=（42，31）=1－m（13，42）=（42，13）=（31，24）=（24，31）=m-11（14，23）=（23，14）=（41，32）=（32，41）=1－m 1（14，32）=（32，14）=（41，23）=（23，41）=1-m m例1 已知（P 1P 2，P 3P 4）=3，求（P 4P 3，P 2P 1）和（P 1P 3，P 2P 4）的值解 （P 4P 3，P 2P 1）= （P 2P 1 ，P 4P 3）=（P 1P 2，P 3P 4）=3 （P 1P 3，P 2P 4）=1－（P 1P 2，P 3P 4）=1－3=－2下面研究交比的代数表示定理1.4 一直线上的无穷远点分其上任何两点的单比等于1。
高等几何2.4
相异实不变元素 共轭虚不变元素
例 判别下列一维射影变换的类型:
双曲型 椭圆型
⇒ 射影变换 (1)有两个 相同实不变元素 称为 抛物型
(1) 2 4 3 5 0; (2) 6 6 0;
椭圆型
双曲型
抛物型
(3) 5 4 0.
a 2 (b c) d 0,
(ad bc 0)
(2)
定理2 在复数范围内, 任一个一维射影变换至少有一个不变 元素. 非恒同的一维射影变换至多有两个相异的不变元素.
§ 2.4 一维射影变换
2. 一维射影变换的分类
a 2 (b c) d 0
(2)
相异实根 0 (b c) 2 4ad 0 (2)有两个 相同实根 0 共轭虚根
§ 2.4 一维射影变换
2. 代数表示 (1). 坐标表示
a11 a21 a12 0, a22 a11 x1 a12 x2 x1 齐次坐标 a21 x1 a22 x2 表示: x2
0
其中对应点的坐标是在同一坐标系下取得的.
a x a12 非齐次坐标 x 11 , a21 x a22 表示：
§ 2.4 一维射影变换
3. 双曲型、椭圆型射影变换的性质 定理3 对于双曲型或椭圆型射影变换, 任一对相异的对应元 素与两个不变元素的交比为常数, 称为双曲型或椭圆型射影变换 的特征不变量.
c ( XY , PP) 常数. b
§ 2.4 一维射影变换
二、一维射影变换的分类
1. 一维射影变换的不变元素 设一维射影变换 的参数方程为 a b c d 0, (ad bc 0) (1) 若存在 0 ,使 2 a0 (b c)0 d 0, 则称 A+0B 为 的一个不变元素, 称 0 为不变元素参数. 在(1)中, 令'= , 得一维射影变换的不变元素参数的方程
射影变换
P P* x
无穷远点 P P0 x 0 分别相当于拓广直线上的 原点 单位点 PP x 1 1
从而，可以利用交比定义射影直线上一种非齐次射影坐标.
§ 2.1 交比
一、点列中四点的交比
例5 (P.47, 例2.3)一直线依次交三点形P1P2P3的三边P2P3, P3P1, P1P2于Q1, Q2, Q3.在此三边上另取点Q1', Q2', Q3', 使
第二章 射影变换
本章地位 平面射影几何的核心内容之一
在一维、二维射影空间以及齐 次坐标的基础上，系统学习一 维、二维射影变换及其一些特 殊情形，对一些射影性质进行 初步研究.
本章内容
§ 2.1 交比
交比 、定义 定义2.1. 设P1, P2, P3, P4为点列l(P)中四点, 且P1 ≠ P2，其齐次 坐标依次为a, b, a+λ1b, a+λ2b. 则记(P1P2,P3P4)表示这四点构成的 一个交比. 定义为 1 (P P , P P ) . 1 2 3 4 (2.1) 2 称P1, P2为基点对， P3, P4为分点对. 定理2.1. 设点列l(P)中四点Pi的齐次坐标为a+λib(i=1,2,3,4). 则
§ 2.1 交比
今日作业 P.53: 1; 4
再见！
课件作者：南师大数科院周兴和
此即P.45, 式(2.4). 不必背诵，但是要熟练掌握变化规律！
§ 2.1 交比
一、点列中四点的交比 1、定义
2、性质 3、特殊情况 定理2.3 共线四点的交比值出现0, 1, ∞三者之一这四点中有 某二点相同. 证明 可根据定理2.1，令P1=P2或P2=P3或P3=P4或P4 = P1进行验 证即可. 此时, 上述6个不同的交比值又只有3组：0, 1, ∞.
一维射影变换
一维基本形的射影变换
2、一维射影变换的性质
(1). 双曲型、椭圆型射影变换
定理. 对于双曲、椭圆型射影变换，任一对相异的对应元 素与两个不变元素的交比为定值，该定值称为双曲、椭圆型射 影变换的特征不变量.
证明 设X, Y为两个不变元素, PP'为任一对相异的对应元 素. 设X, Y, P, P'的坐标依次为x, y, x+y, x+y. 则这四元素的参 数依次为0, , 1, . 于是 0 0 a ' b c ' d 0 d 0. 1 1 1 ab c d 0 a 0. ' ' b 1 b c 0 . c 1 c ( XY , PP ') 常数。 从而, b
a a
( ) ( ) 2 0, a a
1 c 于是 k a 是常数。
c c
一维基本形的射影变换
例1 设A, B, C为相异的共线点且有 (A, B, C, P, Q, R) (B, C, A, Q, R, X). 求证：X=P. 证明. 因为 A B 所以 (AB, CP) = (BC, AQ) =(CA, BR) = (AB, CX) . 从而有X=P. B C C A P Q Q R R X
1、一维射影变换的分类 设有射影变换 a ' b c ' d 0 (ad bc 0) (*) 若存在 0 R, 使a02+(b+c)0+d=0, 则称A+0B为的一个不变元素. 定理. 在实-复射影平面上, 任一个一维射影变换至少有一个 不变元素. 非恒同的一维射影变换至多有两个相异的不变元素.
第二章 射影变换-第五节 一维基本形的对合课件ppt课件
课件作者：南京师大数科院周兴和
§ 2.5 一维基本形的对合
一、定义
定义2.11. 两个成射影对应的重叠的一维基本形中, 若对任意一 个元素, 无论把它看着属于第一基本形的元素或是第二基本形的 元素, 其对应元素相同, 则称这种非恒同的射影变换为一个对合. 定义2.11'. 设f 为一维基本形[π]上的一个非恒同的射影变换. 若 对任意的x∈[π], 都有f(x)=f–1(x), 则f 称为[π]上的一个对合. 注 (1). 对合非恒同. (2). 对合是特殊的射影变换.
§ 2.5 一维基本形的对合
一、定义 二、代数表示
1、参数形式
定理2.20 一维基本形[π]上的一个变换f 为对合f 的任一对对 应元素的参数λ,λ' 满足双线性方程 a 'b( ' ) d 0. (ad b2 0) (2.15) 注 (1). 这里指取定基元素A≠B, 对应元素为A+λB↔A+λ'B.
(2). 从对应式可见λ,λ'的地位完全平等. 故无论将一个已知元 素的参数λ0代入到λ的位置求 λ'(求f 下的像), 还是代入到λ'的求λ (求f –1下的像), 其结果相同. 这恰为对合的本质特征, 故可作为对 合的参数定义.
§ 2.5 一维基本形的对合
一、定义 二、代数表示
1、参数形式 2、坐标形式
将实数轴添加无穷远点, 并令在 f 下, 无穷远点与自己对应, 则 f 是点列上的射影变换, 具有如下性质： 无论将x作为第一 x' f ( x) x. l(P) 或第二基本形的元素， x R, 视x l'(P') 1 x' f ( x) x. 其对应元素相同.
第二章 射影变换-第五节 一维基本形的对合课件ppt课件
( AB, DP) ( BA, CP)
注：若未指定R, 则当A在平面上 变动时, 可得到l(P)上以X, Y为不变 元素的任意多的对应点偶.
§ 2.5 一维基本形的对合
例5 (P.79, Ex. 5)设A, B, C, D是共线点且(AB, DP)=(AB, PC). 求 证：P有两种可能位置且与A, B调和共轭. 证明. 因为
( AB, DP) ( AB, PC)
定理2.23 任一对合必有两个相异的不变元素, 即任一对合不 是双曲型即是椭圆型, 不存在抛物型对合. 定理2.24 一维射影变换f 成为对合f 有两个相异的不变元素, 且任一对相异的对应元素被两个不变元素调和分离. 即假设f : (P)→(P')为对合, 且E, F为其两个不变元素. 则对f 的 任意一对对应元P, P'(P≠P'), 均有(PP', EF)=–1.
例2 设 ( A, B, C, D, E, F ) ( B, C, D, A, E, F ). 求证：E, F为由A↔C; B↔D所决定的对合的不变元素. 证明. 由题设, 有
A
B C
C D
D A
E E
F F
B
( A, C, B, E )
所以,
' P P 1 1,P 2P 3
( B, D, C, E )ቤተ መጻሕፍቲ ባይዱ
(C, A, D, E ).
' P P 3 3
( AC, BE) (CA, DE).
' ' ' P P , P 1 1 2P 3 ( AC, BF) (CA, DF ).
同理, 由对合的几何条件, E, F为由A↔C; B↔D所决定的对合的不变元素. 由本例可见, 几何条件中, 也可以包含不变元素！
高等几何(第三、四章)
➢由于交比经中心射影后不变，故交比在透 视对应下保持不变。
➢透视关系是对称的，但不具有传递性。 ➢定义2.3.透视对应链即为射影对应。
射影对应具有传递性。
2.2 一维基本形的射影对应
➢定义2.3.透视对应链即为射影对应。 射影对应具有传递性。
➢定理2.1 两个点列间的一一对应是射影对 应的充要条件是：任何四个对应点的交比相 等。 必要性显然； 下面证明充分性；
P3
m2 m2
m3 m1
P1
m3 m2
m1 m1
P2 ,
P4
m2 m4 m2 m1
P1
m4 m2
m1 m1
P2 ,
P3
P1
m3 m2
m1 m1
m2 m2
m1 m3
P2 ,
P4
P1
m4 m2
m1 m1
m2 m2
m1 m4
P2 ,
m3 m1 m2 m1
(P1P2 , P3P4 )
设一个对应T保持任何四对对应点的交比不变,我们证明 T可由两个透视对应结合而成。
怎样才算证明了T可由两个透视对应结合而成？
要证明T的任何一对对应点均可由两个透视对应结合得 到。
设 D, D’是T的任何一对对应点，我们证明D’可由D经过 两次透视对应得到。
题目条件是T保持任何四对对应点的交比不变，现在只 有一对对应点，无法用此条件，故我们设出三对对应点：
B
ac
b
C
ca b
§2 一维射影变换
➢点列与线束统称为一维基本形，本节研究一维基 本形间的一种对应关系。
➢本节讲授的顺序与课本有所不同，我们的思路是 从三个不同的角度去刻画一维射影对应，这三个 角度分别为几何直观、本质性质以及代数的角度.
第4章射影变换学习辅导(1)
第4章 射影变换学习辅导(1)学习方法引荐本章内容是在仿射变换的基础上，进一步研究射影变换和在射影变换下的不变问题.首先对点列和线束引入基本射影不变量——交比.即从介绍交比概念，引入共线四点的交比和调和比，共点四线形的交比和调和比.在此基础上讨论两个同类一维基本形的射影对应，射影变换及其特殊情况—对合，主要研究点列到点列的射影对应.在本章内容中，交比是重要的概念，它是射影变换的基本不变量.一维基本形的射影对应（变换）是平面射影几何的基础.作为调和比的几何背景本章还介绍了完全四点形及对偶图形完全四线形的调和性，这两个图形的调和性也是射影几何的重要不变性，它们在射影几何中也具有重要地位. 学习本章时要抓住以下几点：1.点列与线束的交比与调和比；2.完全四点形和完全四线形的调和性质；3.一维基本形的射影对应；4.一维基本形的对合.它们的基本内容包括如下：1.点列与线束的交比和调和比（1）点列的四点的交比.我们知道，单比是仿射变换的基本不变量，但对于中心投影来说，单比不是不变量.这样就发生如何建立中心投影的基本不变量的问题，这个基本不变量就是交比.交比是两个单比的比，它有许多基本性质，见教材中的定理.由这些定理知，共线四点A ，B ，C ，D 共有24种排列，即有24个交比，分为6类，每类的四个交比值相等.当（AB ，CD ）=－1时，CD 调和分割线段AB ，由调和分割的关系是对等的，因此A ，B ，C ，D 称为调和点列.（AB ，CD ）=（CD ，AB ）=－1（2）交比的代数表示设点P 1，P 2，P 的坐标分别为（x 1，y 1），（x 2，y 2），（x 3，y 3），单比（P 1P 2P ）=μ，则 μμ--=121x x x μμ--=121y y y （1） P 的齐次坐标（21x x μ-，21y y μ-，μ-1），当μ=1时，（1）式无意义.但当μ→1时，可得到P 1，P 2所在直线上的无穷远点.所以（P 1P 2P ∞）=1即一直线上的无穷远点分其上任何两点的单比等于1，也就是（P 1P 2，P 3P ∞）=（P 1P 2P 3）如果四点P 1，P 2，P 3，P 4中，P 1或P 2为无穷远点，则上式可作为交比的定义. 设四个不同的共线点P 1（A+λ1B ），P 2（A+λ2B ），P 3 (A+λ3B )，P 4 (A+λ4B )，则))(())((),(413242314321λλλλλλλλ----=P P P P 其中λi （i =1，2，3，4）彼此不相等.设四个不同的共线点的三点及其交比k （k ≠1，k ≠0）为已知，则第四点必唯一确定.（3）线束的四直线的交比与调和比与点列的四点的交比类似，线束中四直线的的交比是利用三条直线的单比定义的.（AB ，CD ）=)()(ABD ABC 应该注意，四直线的交比值与直线μ的取法无关.如果线束S 的四直线A ，B ，C ，D 被任何一条直线S 截于四点A ，B ，C ，D ，则（AB ，CD ）=（AB ，CD ）由这个结论可以推出与点列交比性质相类似的关于线束交比的性质，因此也可知四条直线所构成的24个交比值分为6类，每类的四个交比值相等.交比经中心投影后不变，即交比为射影性质.2.完全四点形与完全四线形调和性利用完全四点形的性质，可以解决“已知共线三点，求作第四调和点”的作图方法. 设S ，S '是完全四点形ABCD 的一对对边，它们的交点是对边点X ，X 与其它二对边点的连线是l ，l '，图4-1.则必有（SS '，ll '）=－1XS l 'D l S 'M Q CY LA B E图4-1设S ，S '是完全四线形ABCD 的一对对顶点，它们的连线是对顶线x ，x 与其它两对顶线交点T ，T'，图4-2.则（SS '，TT'）=－1.TS yA x DT' CA S '图4-23.一维基本形的射影对应（1）透视对应如果一个点列和一个线束的元素之间建立了一一对应且对应元素是结合的，则这个对应叫做透视对应，点列和线束叫做透视的.显然，点列与线束的透视关系具有对称性.点列与点列或线束与线束的透视关系都具有对称性.交比在透视对应下不变.（2）射影对应两个一维基本图形之间的射影对应的性质：①是一一对应的②A ∧B 则B ∧A③具有传递性，即若A ∧B ，B ∧C ，则A ∧C两个点列间的一一对应是射影对应⇔任何四点的交比与其对应四点的交比相等.已知两个一维图形的三对对应元素，那么可以确定唯一一个射影对应.两个点列间的射影对应是透视对应⇔它们底的交点自对应.两个线束间的射影对应是透视对应⇔它们顶点的连线自对应.4.一维基本形的对合对合是射影变换的一种特殊的情况，在对合里每对对应元素的每个元素归入哪个基本形都可以.射影变换成为对合对应的充分必要条件.重点、难点解析1.交比和调和比仿射变换（对应）是对平行射影而言的，单比是仿射几何中最重要的概念，它又是仿射变换的基本不变量.在研究中心射影时，我们引进了无穷远元素.可以证明，在中心射影下，共线三点的单比不是不变量.由此引入交比概念，首先研究共线四点的交比（1）关于交比的定义定义（4.2）把交比定义为两个单比的比，即共线四点A ，B ，C ，D 的交比定义为两个单比（ABC ）和（ABD ）的比，表为(AB ,CD )=)()(ABD ABC . 交比也称复比，即两个单比之比的意思.这种定义可称为几何定义.交比还有另一种定义，即代数法定义：设四个不同的共线点A ，B ，C ，D 的坐标顺次为A ，B ，A+λ1B ，A+λ2B ，则 (AB ，CD )=21λλ 以上两种定义方法是不同的.用第一种方法定义(AB ，CD )=)()(ABD ABC =ADBC BD AC ⋅⋅，所用坐标的非齐坐标，AC ，BD ，BC ，AD 都指有向线段的代数长度；第二种定义方法(AB ，CD )=21λλ,用齐次坐标.例如，共线四点A （2，1，-1），B （1，-1，1），C （1，0，0），D （1，5，-5），求（AB ，CD ）时，可把A 和B 作为基础点对，则C =A + B ，λ1=1，D = 2A -3B ，λ2 =32-所求交比 21λλ=32- 注意，第二种定义方法采用齐次点坐标，可以不限制这四个点中是否有无穷远点.所以，定义(AB ，CD )=)()(ABD ABC =ADBC BD AC ⋅⋅，还属于欧氏平面上的定义，不能解决无穷远点的问题，在射影平面，应使用(AB ，CD )=21λλ的定义方法. 关于交比的定义，要注意以下问题：① A ，B ，C ，D 四点必须共线，而且要考虑顺序，顺序不同则交比不同；② AC ，BD ，BC ，AD 都是有向线段的代数长，因而交比（AB ，CD ）是个数值.（2）交比的性质由于A ，B ，C ，D 四个点的编排顺序不同，所得的交比也不同，共线四点可以组成24种编排顺序，因而可以有24个交比值.由交比的性质原理可知，对于每个排列，还有另三种排列，它们的交比等于已知排列的交比，因此，这24种排列所产生的交比值，实际上只有6类，并且在24个排列中，只要求出1个交比值，就可求出其它23个交比值.例如，已知（AB ，CD ）=3，则可知（DC ，BA ）=（BA ，DC ）=（AB ，CD ）=3.而（AC ，BD ）=1－（AB ，CD ）= －2（3）几个特殊的交比共线四点A ，B ，C ，D 中，设A ，B ，C 是固定点，第四点D 沿直线移动.可以证明，点D 在直线上的每个位置都对应一个确定的交比（AB ，CD ）的值.点D 的不同位置对应不同的交比值，不然的话，假设点D 和D '在两个不同的位置，且有（AB ，CD ）=（AB ，CD '） 则)()()()(D AB ABC ABD ABC '=， 因而（ABD ）=（ABD '）这只有在D = D '时，等式才成立，因此，（AB ，CD ）的每个值，对应点D 的一个确定的位置.当这四个点中有无穷远点时，还可以用其他方法证明这个结论.证明如下：设已知三点的坐标是A ＋1λB ，A ＋2λB ，A ＋3λB 则由k =----))(())((41324231λλλλλλλλ （其中k 为定值，且k ≠0，1） 可以求出4λ，确定第四点.因此第四点A ＋4λB 唯一确定.下面讨论交比的几个特殊情况①D 与C 重合时，则有（AB ，CD ）= 1②当D 与B 重合时，则有（AB ，CD ）=（AB ，CB ）=ABBC BB AC ⋅⋅ = 0 ③当D 与A 重合时，（AB ，CD ）=（AB ，CA ）= ∞=⋅⋅AA BC BA AC ④D 为无穷远点时，则有（AB ，CD ）=（AB ，CD ∞）==∞)()(ABD ABC （ABC ） 可以看出，若第四点为无穷远点，则其交比等于前三个点的单比（ABC ），利用这个性质若无穷远点不在第四个点的位置，可以交换到第四个点的位置，以求其交比.（4）点列中四点的调和比调和比是交比的重要特例.当（AB ，CD ）=－1时，称为C ，D 调和分割A ，B .或称点偶A ，B 与点偶C ，D 调和共轭.D 叫做A ，B ，C 的第四调和点.应当注意，在调和分割中，两对点的关系是完全对等的.点列中四点A ，B ，C ，D 所组成的交比可以有六个交比值，在一般情况下，这六个交比值是不等的，但当且仅当这四个点适当地编排顺序，可以组成调和共轭的两对点偶时，（注意排除两点重合和虚点不考虑），那么这六个交比值才有相同的.（5）线束的交比和调和比①由定义知，四直线A ，B ，C ，D 的交比为)()(ABD ABC =ADBC BD AC ⋅⋅，注意这个定义中数目的排列.②要注意定理4.7：如果线束S 的四线A ，B ，C ，D 被任何一条直线S 截于四点A ，B ，C ，D ，则（AB ，CD ）=（AB ，CD ）的证明.在上述定理中，若点S ，A ，B ，C ，D 都是有穷远元素时，或者，当S 为无穷远点或S 为无穷远直线时（即A ，B ，C ，D 都是无穷远点），此定理仍成立.即（AB ，CD ）的值与直线S 的取法无关，所以仍可取（AB ，CD ）=（AB ，CD ） ③定理4.7是一个非常重要的定理，由于定理可以证明“两点列同时截一线束，则此点列上对应四点的交比相等.”还可以推广证明投影于同一点列的两线束的四条对应直线的交比相等.可以知道，此定理使点列和线束的问题沟通了，为研究交比是中心射影下的不变量打下基础，同时点列和线束的问题可以对偶地进行研究.（6）有关交比的作图问题① 有关交比的作图可以根据共线四点的交比的定义，借助初等几何作图来完成，需要用相应例题来理解.② 第四调和点的作图● 用“一角两条边和这个角内外平分线调和共轭”作第四调和点.● 利用相似三角形作第四调和点.（7）利用交比的调和共轭解初等几何问题交比和调和共轭是几何学中的重要概念，它们在几何的研究中有重要的作用，运用这些概念和有关性质，可以解决一些初等几何问题主要在以下三个方面：①角平分线的调和性.②利用交比证明有关圆的问题.③与图有关的调和共轭问题.2.完全四点形和完全四线形的调和性完全四点形和完全四线形是射影几何中的重要图形，由于这两个图形具有调和性，而交比又是射影变换的不变量，所以对完全四点形的性质的研究在射影几何中占有重要地位. 值得注意的是，在前面调和比是用交比来定义的，而交比之定义为单比之比，所以定义调和比此时用了变量概念.对完全四点形的性质的研究，可以使我们完全不用度量概念，而使用下列方法来定义调和比或调和共轭.即“一直线S 上的点偶A ，B 与C ，D ，A ，B 是一个完全四点形的对边点，C ，D 是通过第三个对边点的两条对边与S 的交点，则A ，B 与C ，D 成调和共轭”.这种定义是综合地纯射影的定义，这种定义方法只与直线和直线相交的作图有关，与度量无关.由于完全四点形的调和性是射影性质，所以它的对偶图形完全四线形也有调和性. 学习本单元内容时还应注意以下问题：（1）注意完全四点形与中学所熟悉的四边形的区别.四边形指简单四边形，由顶点依次连接而成，顶点数等于边数，均为4，如图4-3.ABCD 为简单四边形.而完全四点形是平面内无三点共线的四点及其两两连线所构成的图形，如图4-4.完全四点形ABCD 有四个顶点A ，B ，C ，D ，有六条边（即任何两顶点的连线都是边），通过同一顶点的边叫邻边，不通过同一顶点的边叫对边，因此有三对对边：AB 与CD ；AC 与BD ；AD 与BC ，对边交点叫对边点，共三个，即AB ×CD =X ，AC ×BD =Y ，AD ×BC =Z.三个对边点组成对边三点形XYZ.BCD A Y CDX ZA B图4-3 图4-4完全四点形的一对对边被通过这两个边交点的对边三点形的两边调和分割.完全四线形的一对对顶点被连接这两个点的对角三角形的两边调和分割.（2）利用完全四点形的调和性作第四调和点我们知道，一直线l上的点偶P1，P2，Q1，Q2成为调和共轭的充要条件是：“P1和P2是一个完全四点形的对边点，Q1和Q2是通过第三个对边点的两条对边与l的交点”，根据这个道理，可以通过完全四点形的作图来作第四调和点.如图4-5，已知直线l上有三点P1，P2，P3，求作点P4，使（P1P2，P3P4）=-1.作法如下：过P1P2若任作一直线交于点A，在P2A上任取一点B，连B P3，过P1A于点C，再连P2C，P1B，交于点D.连AD与L交于P4，则P4为所求第四调和点.ACBDlP1P4P2P3图4-5应当指出，以上作图是只用一根直尺完成的.而且过P1，P2的直线是任意作的，但P4点是唯一的，这由笛沙格定理保证.在图4-5中，根据定理，若P4为P1P2中点，则P为l上无穷远点，于是利用直尺可以作出CB// P1P2，反之，如果知道CB// P1P2，也可以用一根直尺求P1P2中点.（3）应用完全四点形的调和性解初等几何问题.利用完全四点形的调和性，可以比较简捷地解决一些初等几何中的共点和共线问题.例如，三角形三个顶角的外角平分线交其对边的三点共线.3.一维基本形的射影对应（1）什么叫一维基本形基本形，指以点、直线、平面为元素所形成的某些无穷集合，一维基本形指点列和线束.什么叫一维呢？关于维的概念，要注意几何学的维与空间的维是有区别的.几何学中的维数，指几何元素活动的自由度，也就是几何元素的坐标或参数必不可少的数目，这个数就是几何学的维数.此如平面内的点和直线应该有两个坐标，但在点列中以A，B为基点的任一点坐标可以表为A，B的坐标的线性组合，即C = A + λB，其中λ为参数，所以点列中的点可以用一个独立参数表示（对于线束也有类似结论）.也就是说，点列的每个点（或线束中的每一直线）都可以用一个独立参数表示，点列和线束就叫一维图形.点列和线束就是一维几何研究的对象.关于空间的维数，是指把直线，平面或空间都看成四点构成，空间的维数是点活动的自由度，所以直线叫一维空间.平面叫二维空间，我们生活的空间叫三维空间.由于几何学研究的元素不限于点，所以几何学中的维与所处空间的维不同.比如，平面上的直线几何应该叫二维几何学，这是由于把直线看作基本元素，平面上决定直线需要两个比值，即必不可少的参数为2.（2）一维基本形的透视对应与射影对应的关系①在前几章所讨论的透视仿射对应是对平行射影而言，本章所论的透视对应则对中心投影而言，透视对应包括点列和线束之间的透视对应；点列与点列之间的透视对应.在定义中可以将点列换成线束，或把线束换成点列.所以点列与线束的透视对应具有对称性.由透视对应的定义还可以看出，透视对应保持四元素的交比不变.但透视关系不满足传递性.需要注意，透视对应一定是射影对应，但射影不一定成透视对应，因此，透视对应与射影对应是特殊与一般的关系.②射影对应必是一一对应，且具有传递性、对称性、反身性，即具有等价关系.③透视对应在什么条件下才成为射影对应呢？由定理知，两个点列间的射影对应是透视对应的充要条件是它们的底的交点自对应也就是它们的公共元素自对应.两个点列成射影对应时，把它们的公共点看作是第一个点列的点时，它在第二个点列上的对应点，一般情况下不是它本身，只有当两个点列成透视对应时，其公共元素才自对应.④应该注意，如果一维射影对应使无穷远点对应无穷远点，则该对应一定是仿射对应，要证明这个结论，只需证明这种对应保持单比不变.由于射影对应保持交比不变.所以，仿射对应可看作特殊的射影对应.4.一维基本形的对合（1）关于对合概念对合对应是重要的，特殊的射影变换.在两个重叠的射影对应的一维基本形中，第一个基本形的元素P 对应第二个基本形的元素P'，但如果把P'看作第一个基本形的元素，那么它在第二个基本形里不一定对应P.但如果这个对应为对合对应，则根据对合定义“在两个重叠而且射影对应的一维基本形里，如果对于任何元素，无论看作属于第一个基本形或第二基本形，它的对应元素是一样的，那么这种非恒等的射影变换叫做对合（对应）”.那么P'就一定对应P.若两个重叠一维基形成射影对应，可假设两个重叠点列成射影对应，在什么条件下才成为对合呢？实际上只要有一对对应元素符合对合条件，则这种射影变换一定是对合.（2）对合的代数表示和确定对合是特殊的射影变换，从对合的代数表示，也可以看出射影变换成为对合的条件，即在射影变换式0=+'++'d c b a λλλλ，0≠-bc ad 中，若是对合，则有B = C ，反之也成立.上式说明射影变换范围比对合大.我们知道，三对对应元素决定唯一一个射影变换，如果是对合，则只要有不重合的两对对应点便可决定唯一一个对合对应.判定一个射影变换是否为对合对应，也可用如下事实：对合对应存在两个二重元素，射影变换是对合的充要条件是任何一对对应元素与两个二重元素调和共轭.例如，求由两个二重点1，2所确定的对合方程，可有两种解法.解法1 设对合方程为0)(=+'++'d b a λλλλ将1，2代入，得A +2B +D = 04A +4B +D = 0代入对合方程，得2λλ'-3（λ+λ'）+ 4 = 0解法2 利用（12，x x '）= -1其中x ，x '为一对对合点的坐标 则12121-=-'-'--x x x x 即2xx '－3（x+x '）+ 4 = 0典型例题例1 填空题（1）两线束间的射影对应是透视对应的充分必要条件为 .（2）两点列间射影对应由 对对应点唯一确定.（3）共线四点的交比是 不变量.（4）两个点列经过中心投影， 不变.（5）不重合的 对应元素，可以确定唯一一个对合对应.解 （1）由定理知，两线束间的射影对应是透视对应的充分必要条件是：两个线束的公共线自对应.（2）已知射影对应被其三对对应点所唯一确定，因此两个点列间的三对对应点可以决定唯一一个射影对应.（3）共线四点的交比是射影不变量.（4）两个点列经过中心投影，交比不变.（5）不重合的两对对应元素，可以确定唯一一个对合对应.例2 单选题（1）若（AB ,CD ）=r ，则（DB ，AC ）=（ ）A .r 1B .r-11 C .r r -1 D .r 11- （2）设A ，B ，A +λ1B ，A +λ2B 是四条不同的有穷远共点直线l 1，l 2，l 3，l 4的齐次坐标，则（l 1l 2，l 3l 4）=（ ）A .λ1B .λ2C .21λλ D .λ1λ2 （3）设1，2，3，4是四个不同的共线点，如果（12，34）=（23，41）则（13，24）=（ ）A .－1B .1C .0D .∞解 由交比的运算定理，（1）选D ；（2）选C （3）选A例3 求证P 1（3，1），P 2（7，5）与P 3（6，4），P 4（9，7）成调和共轭.分析 可以采用非齐次坐标与齐次坐标两种方法进行证明解法1(P 1P 2，P 3P 4)=))(())((14232413x x x x x x x x ----=)76)(39()79)(36(----=-1 解法2 将P 1，P 2，P 3，P 4写成齐次坐标，则P 1（3，1，1），P 2（7，5，1），P 3（6，4，1），P 4（9，7，1）可以写作P 3（24，16，4），P 4（-18，-14，-2）于是 P 3 =P 1 +3P 2 P 4 =P 1 -3P 2∴(P 1P 2，P 3P 4)=33-=-1 例4 求证：一角的两条边与这个角的内外角平分线调和共轭.证法1 利用共点直线成调和共轭的定义进行证明.如图4-6所示，角的两边为A ，B ，其内外角平分线分别为l 1，l 2(AB ，l 1l 2)=)()(21abl abl （ABl 1）=1（ABl 2）= -1∴ (AB ，l 1l 2) = -1A B图4-6证法2 用代数法设取原点在三角形SAB 内部，A ×B 分别在A ，B 直线上.设SA 的法线方程为0=α，设SB 的法线方程为0=β，为了求内角分线l 1和外角分线l 2方程，利用角平分线的几何特性，设P （x ，y ）为角平分线l 1上的任一点，则它们到A ，B 的距离相离，即α=β或βα=或βα-=取l 1为βα=即0=-βα，即11=λl 2为βα-=即0=+βα，即12-=λ∴( AB ，l 1l 2)=121-=λλ 证法3 根据定理，如图4-7，若用直线l 1 // l 2求截角的两边A ，B 分别交A ，B 于A ，B ，交l 1于T 1，交l 2于T ∞，则由l 1和l 2互相垂直，可知S T 1⊥l 1，又l 1为角平分线，由初等几何定理，可知△SAB 为等腰三角形，且有A T 1=T 1B ，即T 1为AB 中点，根据定理知(AB ，T 1T ∞)=-1(AB ，l 1l 2 )=-1SA T 1 Bl A l 1 B图4-7例5 若A ，B ，C ，D 为共线四点，且（AB ，CD ）=-1，CD 中点为O ，求证O C 2=O A ·O B 证明 (AB ，CD )=1-=⋅⋅ADBC BD AC 即AC ·BD +BC ·AD = 0把AC ，BD ，BC ，AD 都以0为原点表示，则有（O C -O A ）（O D -O B ）+（O D -O A ）（O C -O B ）= 0整理得 2（O A ·O B +O C ·O D ）=(O A +O B )(O C +O D )而 O D =-O C∴ 2(O A ·O B -O C 2)=(O A +O B )(O D -O C )=0即 O C 2=O A ·O B例6 设三直线 1111c y b x a p ++=2222c y b x a p ++=3333c y b x a p ++=求证以p 1= 0，p 2= 0，p 3= 0为三边的三角形的重心由方程312212311312332)()()(p b a b a p b a b a p b a b a -=-=-给出.3B O p 3 C图4-8分析 如图4-8，ΔABC 三边AB ，AC ，BC 的方程分别为p 1= 0，p 2= 0，p 3= 0.设BC 边上中线A O 的方程q 3=0.过A 点作BC 的平行线l 3，则l 3的斜率为333b a k l -=. 由于l 3过p 1和p 2的交点A ，所以l 3可由p 1和p 2线性表示，即l 3的方程为0)(222111=+++++c y b x a c y b x a λl 3的斜率为2121b b a a λλ++-∴ 332121b a b b a a -=++-λλ 32321313b a a b b a a b --=λ ∴ l 3的方程为023********=--+p b a a b b a a b p 由于l 3与BC 平行，所以l 3与BC 交于无穷远点L ∞，又D 为BC 中点，（BC ，D L ∞）= -1两条直线截同一线束，所得对应四点的交比不变，可得（p 1p 2，q 3l 3）=-1∴ q 3的方程为023********=--+p b a a b a b b a p 同理q 1的方程为03131321212=--+p b a a b a b b a p 则q 1与q 3的交点为312212131313232)()()(p b a b a p b a a b p b a a b -=-=- 例7 已知A ，B ，C 三直线交于点P ，试用直尺作出第四条直线和它们成调和共轭. 作法：如图4-9. A ，B ，C 三直线交于点P ，任作不通过P 点的直线l ，l 与直线A ，B ，C 分别交于A ，B ，C 三点，在P A 上任取一点M ，连B M 交P C 于N.连A N 交P B 于K ，连MK 交l 于P ，则有（AB ，CD ）=-1.连P D ，即为所求第四调和线D ，即（AB ，CD ）= -1PM B C DA N KlA CB D如图4-9例8 已知三点形ABC 及平面上一点P （P 不在ABC 的任一边上）.A P ，B P ，C P 与对边交于A '，B '，C '，且BC 与B 'C '交于A 1，CA 与C 'A '交于B 1，AB 与A 'B '交于C 1. 如图4-10.求证：（1）（BC ，AA '）= -1，（CA ，B 1B '）= -1（2）A 1，B 1，C 1三点共线.证明（1）由完全四点形C 'AB 'P 的调和性，可知（BC ，A 1A '）= -1又（B ，C ，A 1，A '）∧（A ，C ，B '，B 1）∴（CA ，B 1B '）=（AC ，B 'B 1）=（BC ，A 1A '）= -1（2）由三点形ABC 和A 'B 'C '的对应点连线共点P ，由笛沙格定理可知，对应边交点A 1，B 1，C 1共线.PC '图4-10例9 巴卜斯命题：设A 1，B 1，C 1与A 2，B 2，C 2为同一平面内两直线上的两组共线点，B 1C 2与B 2C 1交于L ，C 1A 2与C 2A 1交于M ，A 1B 2与A 2B 1交于N.如图4-11.求证L ，M ，N 共线.证明A 1B 1N D C 1M ELA 2B 2C 2 O图4-11∵（B 1，D ，N ，A 2）∧（O ，C 2，B 2，A 2）∧（B 1，C 2，L ，E ）∴（B 1，D ，N ，A 2）∧（B 1，C 2，L ，E ）由于两点列底的交点B 1自对应，有（B 1，D ，N ，A 2）∧（B 1，C 2，L ，E ）因此DC 2，NL ，A 2E 三直线共点M.即L ，M ，N 共线. □例10 如果三角形中一个角平分线过对边中点，那么这个三角形是等腰三角形. 证明 如图4-12，由于M 为AB 中点，C N ∞为外角平分线，则有（AB ，C N ∞）= -1∴（AB M ）= -1，（AB N ∞）= 1即 1-=BMAM 1=MB AM 而 1==BCAC MB AM 从而，AC =BC .□C N ∞A MB N ∞图4-12自测练习1.填空题（1）两点列间的射影对应是透视对应的充分必要条件是 .（2）共线四点的调和比为 .（3）四个共线点A ，B ，C ，D ，如果（AB ，CD ）=r ，则（DA ，BC ）= .（4）一维基本形的射影变换的不变元素的个数 .（5）射影变换有 对对应元素满足对合对应的要求，则一定是对合.2.单选题（1）A ，B ，C ，D 为共线四点，且（CD ，BA ）= k ，则（BD ，AC ）=（ ）.A .k 1 B .k 11- C .kk -1 D .k （2）（ ）对不同的对应元素，确定唯一一个射影对应.A .1B .2C .3D .4（3）两个一维基本形成射影对应，则对应四元素的交比（ ）.A .相等B .不等C .1D .-1（4）线束S 的四直线A ，B ，C ，D 被任何一条直线S 截于四点A ，B ，C ，D ，若（AB ，CD ）=k ，则（AB ，CD ）=（ ）A .k1 B .1-k C .k 11-D .k 3.A ，B ，C ，D 为共线四点，如图4-13所示，相邻两点距离相等，计算这四点形成的各交比值.A B C D· · · ·图4-134.设A ，B ，C ，D ，E 为直线上五点，求证：（AB ，CD ）·(AB ，DE )·(AB ，EC ) = 15.已知点A =（1，1，1），B =（1，-1，1），C =（1，O ，1）且（AB ，CD ）= 2，求C 点坐标.6.若直线l 1，l 2，l 3，l 4的方程为（1）012=+-y x ，023=-+y x ，07=-y x ，015=-x（2）0=-y x ，02=+y x ，0=+y x ，03=-y x求（l 1l 2，l 3l 4）.7.设P 1，P 2分别是坐标轴上的无穷远点，P 3是斜率为1的直线上的无穷远点，又（P 1P 2，P 3P 4）= m ，求P 4的坐标.8.设A ，B ，C ，D ，E 为共线五点，且（AD ，BC ）=-1，（CE ，AB ）=-1.求证4AC ·ED =3AD ·EC .9.设ΔABC 的三条高线为AD ，BE ，CF 交于M 点，EF 和CB 交于点G .求证（BC ，DG ）=-1.当AB =AC 时，还可以得到什么结果？10.设XYZ 是完全四点形ABCD 的对边三点形，XZ 分别交AC ，BD 于L ，M ，不用笛沙格定理证明YZ ，B L ，C M 共点（图4-14）.LZM图4-1411.求以下重叠一维基本形的射影变换自对应点的参数（坐标）.（1）066=+'+-'x x x x（2）01=+'+x x12.求两对对应元素，其参数211→，20→所确定的对合对应.参考答案1.（1）它们的底自对应，（2）1，（3）1-r r ， （4）不能大于2，（5）一对2.（1）B ，（2）C ，（3）A ，（4）D3.34，43，31-，3-，41，44.用交比定义证明即可.5.由A =（1，1，1），B =（1，-1，1）则D =（1，0，1）=A +B ，于是λ2=1设C =A +λ1B ，由（AB ，CD ）=21λλ=2可知λ1=2， 所以C =A +2B =（3，-1，3）6.（1）l 1，l 2，l 3，l 4与x 轴的交点分别为211-=x ，322=x ，03=x ，514=x ∴ （l 1l 2，l 3l 4）=21 （2）l 1，l 2，l 3，l 4都过原点∴ （l 1l 2，l 3l 4）=-57.设P 1，P 2，P 3，P 4分别是直线上l 1，l 2，l 3，l 4上的无穷远点，其中l 1：x = 0l 2：y = 0l 3：y = x ，即x -y = 0l 4：x +λy = 0则（l 1l 2，l 3l 4）=（P 1P 2，P 3P 4）= m以l 1，l 2为基线.由l 3：x -y = 0，得λ1=-1l 4：x +λy = 0，得λ2=λ∵（l 1l 2，l 3l 4）= m ∴21λλ=λ1-= m 代入l 4的方程中得y=mx∴P 4点的坐标为（1，m ，0）.8.证明 设A ，B ，C 的坐标分别为A ，B ，A +B ，设D 为A +λ1B ，E 为A +λ2B ， 由（AD ，BC ）=-1，可知（AB ，DC ）=1-（-1）=2又（CE ，AB ）=-1，可知（AB ，CE ）=-1则λ1=2，λ2=-1∴（CD ，AE ）=43 （CD ，AE ）=CE DA DE CA ⋅⋅=43 即4AC ·ED =3AD ·EC .□9.如图，由完全四点AF M E 的调和性，可知（BC ，DG ）=-1当AB =AC 时，D 为BC 中点，所以G 为BC 直线上的无穷远点，因此EF ∥CB10.证明 由四点形ABCD ，根据定理，可知在AC 边上的四点A ，C ，Y ，L 调和分割即（AC ，XL ）=-1.在四点形Y B ZL 中，L B 与YZ 交于N ，MN 与YL 交于C ，由定理可得（AC '，YL ）=-1 ∴点C 应与点C '重合，即YZ ，B L ，C M 共点.□11.（1）0652=+-λλλ1=3，λ2=2（2）012=+'+λλ0120=+'++'λλλλ01112='++'⋅λλλλ 自对应元素为λ=λ'，将其代入上式得两自对应元素为λ1=∞，λ2=31-. 12.设0)(=+'++'d b a λλλλ为所求对合对应，则 ⎪⎩⎪⎨⎧=+=++0202321d b d b a 所以 A : B : D =1 : 1 : -2即 02=-'++'λλλλ为所确定的对合对应.[文档可能无法思考全面，请浏览后下载，另外祝您生活愉快，工作顺利，万事如意!]。
射影变换
P3P4 )
(1 (2
3 )(2 3 )(1
4 ) 4 )
.
(2.2)
§ 2.1 交比
证明定理2.1. 以P1, P2,为基点，参数表示P3, P4. 设
a+λ1b=a', a+λ2b=b'.
从中解出a,
b,
得
a
a' 2
b' 1
,
2 1
b b'a' .
2 1
于是， P1, P2, P3, P4的坐标可表示为 a', b', 2 3 a' 3 1 b', 2 4 a' 4 1 b' 2 1 2 1 2 1 2 1
中的两个著名定理：Menelaus定理、Ceva定理.
§ 2.1 交比
一、点列中四点的交比
二、线束中四直线的交比
1、线束的参数表示
设a, b为线束S(p)中取定的相异二直线. 则对于任意的p∈S(p),
其坐标可表示为
a b
R.
称a, b为基线, λ为参数.
这里a, b, p均表示直线的齐次坐标. 注1 参数λ的几何意义？不易说清楚！容易看出
解：设 P3 P1 1P2, P4 P1 2P2. 则显然2 1, 由
(P1P2 , P3P4 )
1 2
1
1
2.
可得 1 2, 从而P3的坐标为(3,–1,3).
§ 2.1 交比
一、点列中四点的交比 1、定义 2、性质 3、特殊情况
4、调和比 5、交比的计算 (1). 由坐标求交比 (2). 由交比求坐标
即
a', b', a' 3 1 b', a' 4 1 b'.
第二章射影映射资料
第二章 射影映射本章将阐明一维射影变换、射影映射和二维射影变换的几何意义；研究它们各有哪些类型；并对其中比较重要的几种特殊类型进行较深入的讨论。
§1透视透视是一个很简单但又最基本的射影映射。
一般非透视的射影变换、射影映射可以用透视来表示。
定义 如果一个点列与一个线束的元素之间建立了一一对应且对应元素是结合的,则这个对应叫做透视对应,点列与线束叫做透视的,或配景。
图2.1记成(,,,)(,,,,)y z u v a ξηζϕψ⋅⋅⋅∧⋅⋅⋅定义 点ξ和ξ’的对应点的连线交于一点s,也就是这两个点列与同一线束s 成透视,则这两个点列叫做透视点列,点s 叫做透视中心，记作(,,)(,,,)Sa b c a b c ξξ∧''''⋅⋅⋅⋅⋅⋅=或()()a a ξξ''∧图2.2对偶定义：线束s 和s ’的对应直线的交点在一直线α上,也就是这两个线束与同一点列透视,则这两个线束叫做透视线束。
直线α叫做透视轴。
记作(,,,)(,,,)s s αηζϕηζϕ∧''''⋅⋅⋅⋅⋅⋅=或()()s s αηη∧''=图2.3.两个点列射影的,记作()()a a ξξ''∧；两个线束射影的,记作()()s s ηη''∧看图2.2,如果,,,ηζϕψ是线束s 的四条直线,分别与ξ和ξ’交于a,b,c,d 和a ’,b ’,c ’, d ’,则有R(a,b ；c,d)=R(,;,ηζϕψ)=R(a ’,b ’；c ’,d ’)所以透视对应保持交比不变,又因透视是一一对应,所以透视是射影对应(斯丹纳定义)。
图2.1 图2.2 图2.3显然,透视对应把点ξξ'⨯映射为自身。
定理1 直线ξ到ξ’的透视是射影对应,它把公共点ξξ'⨯映射为自身。
反过来,又有 定理2 直线ξ到ξ’的一个射影对应,如果把公共点ξξ'⨯映射为自身,那么这个射影对应是透视。
射影变换基础
1 T
1
1 1 1
1
k2 1 1 A2 B2 k . A2 B2 k1
k2 (k is a scalar) k1
MA B M so
1 1 1
1 1 1
1
k . A B2 ,
1 2
1 2
A B and A B2 are similar matrices
根据相似矩阵的性质，这两个矩阵具有相同 的特征值。再假定B1也为可逆矩阵，则相 应的特征值不为0，因此根据特征值两两相 除(消去标量k),则得到两个不变量。可见同 一平面两个非退化二次曲线有两个绝对不 变量，当存在退化情况时，有一个特征值 为0，因此只有一个不变量。
1 T
1
1 T
1
if A1 is invertable matrix , A1 M MA I , then k2 .B2 ( M ) B1 M k1 A2 .MA B M , so MA B M
1 1 1 1 1 1 1 1 1 T 1
( M ) A1 M .MA B M
• 由有限次中心射影的积定义的两条直线间 的一一对应变换称为一维射影变换.
二维（高维）射影变换
Def3.2 由有限次中心射影的积定义的两个平面之间的一一对 应变换称为二维射影变换.
交比不变量
• Def 3.3 (交比）若A,B,C,D为直线L上任意四 点，则下式定义的R称为交比(cross ratio)
' ' ' '
线束的射影变换
• 平面上两个线束的射影变换及线束的交比。 如下图所示，平面上有两个线束O,O’，若 它们所有对应线的交点共线，则称这两个 线束的对应为中心射影。类似点列的射影 变换，有限次中心射影的积称为线束间的 射影变换。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
一、一维射影坐标系
定义. 在射影直线 l 上取定一个有序三点组 P*、P0、E，则
称 [P*, P0, E] 为射影坐标系。直线 l 上任意一点 P 的非齐次射影
坐标规定为
x (P*P0 , EP).
其中P0 叫原点，E叫单位点.
在这坐标系下， P0的非齐次射影坐标为0，E的非齐次射
一维基本形的射影变换
例1 设A, B, C为相异的共线点且有
(A, B, C, P, Q, R)
(B, C, A, Q, R, X).
求证：X=P.
证明. 因为
ABCPQR
所以
BCAQRX
(AB, CP) = (BC, AQ) =(CA, BR) = (AB, CX) . 从而有X=P.
一维基本形的射影变换
的参数,' 满足一个双线性方程
a ' b c ' d 0
(ad bc 0)
(*)
即在一维基本形[]上取定基元素AB, 则对应元素为A+B A+'B.
一维基本形的射影变换
三、一维射影变换的分类与性质
1、一维射影变换的分类
设有射影变换
a ' b c ' d 0
(ad bc 0)
(*)
影坐标为1， P*没有非齐次射影坐标。
如果把P*看成是无穷远点，则非齐次射影坐标就变成非
齐次仿射坐标，此时 x (P*P0 ,
EP)
(PEP0 )
P0 P P0 E
.
如果把P*看成是无穷远点，且P0E=1，则非齐次射影坐标
就变成非齐次笛卡儿坐标，此时 x=P0P。
有了非齐次射影坐标系，就可定义齐次射影坐标系，P0
例2 设P, P'与 Q, Q'为点列l(P)上射影变换的两对对应点, E 是不变点, V, V'是过E的直线l'上任意两点. PVP'V'=P'', QVQ'V'=Q''. 求证：P''Q''l=F为另一个不变点.
证明. 如图有
(P,Q, E, F) (V) (P '',Q '', F ', F) (V') (P ',Q ', E, F)
证明. 代数法. 设E, P', P, R的参数依次为1, 2, 3, 4. 由抛
物型射影变换的性质, 有
P P':
1
1
k.
3 1 2 1
P' R: 1 1 k.
2 1 4 1
由此二式，得 2 11.
2 1 3 1 4 1
经过直接计算, 得(EP', PR) = –1.
k
k
令射影变换式为 a b c d 0. 因为α是自对应元的参数，
所以是方程 2 (b c) d 0 的重根，因此有
2 d , 2 b c .
a
a
代入射影对应式得 (2 c ) c 2 0, 即
aa
(
c a
)
(
c a
)
2
0,
于是
1 c
k
a
是常数。
' '
1
b c 0 b .
( XY , PP ')
1
c b
常数。
c
一维基本形的射影变换
(2). 抛物型射影变换
定理. 抛物型射影变换的不变元参数与任一对相异的对应
元素的参数, '满足
1 1 k.
'
证明. 要证明的式子等价于 ( 1) ( 1) 2 0.
立刻可得结论. 据此可得一维射影变换的分类：
0
相异实根
相异实不变元 双曲型
0 (*)有两个相同实根 (*)有两个相同实不变元 称为抛物型
0
共轭虚根
共轭虚不变元 椭圆型
一维基本形的射影变换
2、一维射影变换的性质
(1). 双曲型、椭圆型射影变换
定理. 对于双曲、椭圆型射影变换，任一对相异的对应元 素与两个不变元素的交比为定值，该定值称为双曲、椭圆型射 影变换的特征不变量.
所以, E, F为两个不变点.
思考. 已知P, P'; Q, Q'为点列l(P)上双曲
型射影变换的两对相 异的对应点， E为一 个不变点, 如何作的
另一个不变点F？
一维基本形的射影变换
例3. 设点列l(P)上射影变换为抛物型的, E是不变点, P, P'为 一对相异的对应点, 且(P')=R. 求证：(EP', PR)= –1.
定理. 在一维非齐次射影坐标系下，交比的表达式为
(P1P2 ,
P3P4 )
( x1 ( x1
x3 )(x2 x4 )(x2
x4 ) x3 )
.
注记. 交比的这个表达式与它在一维非齐次笛卡儿坐标系 下的表达式一样。
一维基本形的射变换
2、一维射影变换的代数表示 (1). 坐标表示 a. 非齐次坐标表示 x ' ax b , ad cb cx d
若存在 0 R, 使a02+(b+c)0+d=0, 则称A+0B为的一个不变元素.
定理. 在实-复射影平面上, 任一个一维射影变换至少有一个 不变元素. 非恒同的一维射影变换至多有两个相异的不变元素.
证明 在(*)中, 令='. 则有一维射影变换的不变元素方程
a2 (b c) d 0,
(ad bc 0)
证明 设X, Y为两个不变元素, PP'为任一对相异的对应元
素. 设X, Y, P, P'的坐标依次为x, y, x+y, x+y. 则这四元素的参 数依次为0, , 1, . 于是
0 0 a ' b c ' d 0 d 0.
从而,
a b 1 c 1 d 1 0 a 0.
其中对应点的坐标是关于一维基本形[]上的同一坐标系取得的.
b. 齐次坐标表示
x1 x2
' '
a11x1 a21x1
a12 x2 a22 x2
a11 a12 0, a21 a22
0
其中对应点的坐标是关于一维基本形[]上的同一坐标系取得的.
一维基本形的射影变换
(2). 参数表示
定理 . 一维基本形上的一个变换为射影变换其对应元素
的齐次射影坐标为(0,1)，E的齐次射影坐标为(1,1)，并规定P*
的齐次坐标系为(1,0)。
一维基本形的射影变换
二、一维射影变换
1、一维射影变换的定义
定义. 一个一维基本形到自身的射影对应称为一维射影变
换. 即若 : [] [']，且[]=[']，则称为一维基本形[]
上的一个一维射影变换。
一维射影变换是特殊的射影对应. 一个一维射影变换可由不超过3次透视对应得到.