重庆数学中考26题专题训练

合集下载

重庆中考数学26题专项.doc

中考26题第二小问专项讲解第一大类:线段最大值一、基本题型：_ _丄2 3 9例1：如图，抛物线J = _7X +T X + 2与兀轴交于A.B两点，与y轴交于C点, P为抛物线上BC±方的一点。

1、过点P作y轴的平行线交BC于M,求PM的最大值。

2、过点P作X轴的平行线交BC于M,求PM的最大值。

二、变式题型1：过点P作y轴的平行线交BC于M,作PN丄BC于N。

3、求PN的最大值，PM+PN的最大值。

4、求APMN周长的最大值。

5、求APMN面积的最大值。

三、变式题型2：P为抛物线上E C上方的一点。

D为E C延长线上的一点且C D = B C 6、求APBC面积的最大值。

7、求APDC面积的最大值。

例2：如图，抛物线与y = -yx2+|x + 2兀轴交于4, B两点，与y轴交于C点,P为抛物线的顶点。

1、M是BC上的一点，求PM + AM最小时M点的坐标。

2、D为点C关于x轴的对称点，M是BC±的一点，求DM+PM最小时M点的坐标。

3、M是BC上的一点，N是AC上的一点，求° OMN周长的最小值及M点的坐标。

4、M. N为直线B C±的动点，N在下方且MN = V5 ,最小值。

5、M. N为直线BC上的动点，N在下方且MN = V5 , D在抛物线上且在D与C对称。

求四边形PMND周长的最小值。

6、M为对称轴上的一点，MN丄y轴于N, D在抛物线上且在D与C对称。

求DM + MN + N A的最小值。

7、M为对称轴上的一点，MN丄y轴于N, D在抛物线上且在D与C对称。

求DM + MN + N B的最小值。

8、M为对称轴上的一点，N为y轴上一点，D在抛物线上且在D与C对称。

求OM + MN + N D第二大类: 线段和的最小值9、M为EC上的一点，求PM + 討的最小值。

求PM + MN + AN 的10、D在抛物线上且在D与C对称，在BC±找一点N, M是x轴上的一点。

2021年重庆中考数学第26题几何证明专题训练

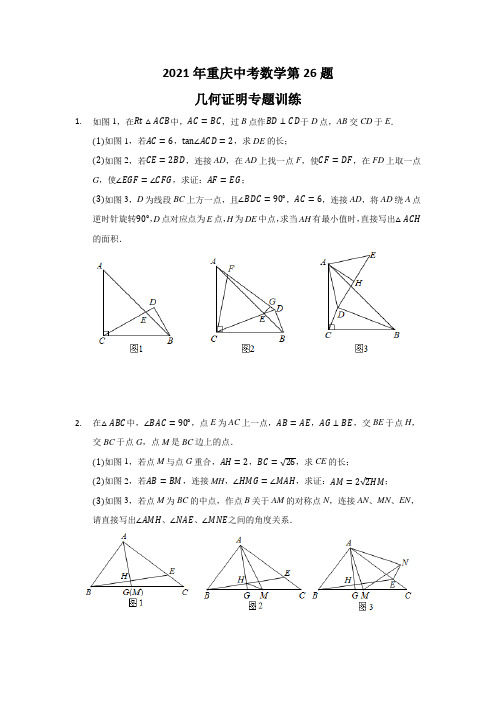
2021年重庆中考数学第26题几何证明专题训练1.如图1，在Rt△ACB中，AC=BC，过B点作BD⊥CD于D点，AB交CD于E．(1)如图1，若AC=6，tan∠ACD=2，求DE的长；(2)如图2，若CE=2BD，连接AD，在AD上找一点F，使CF=DF，在FD上取一点G，使∠EGF=∠CFG，求证：AF=EG；(3)如图3，D为线段BC上方一点，且∠BDC=90°，AC=6，连接AD，将AD绕A点逆时针旋转90°，D点对应点为E点，H为DE中点，求当AH有最小值时，直接写出△ACH 的面积．2.在△ABC中，∠BAC=90°，点E为AC上一点，AB=AE，AG⊥BE，交BE于点H，交BC于点G，点M是BC边上的点．(1)如图1，若点M与点G重合，AH=2，BC=√26，求CE的长；(2)如图2，若AB=BM，连接MH，∠HMG=∠MAH，求证：AM=2√2HM；(3)如图3，若点M为BC的中点，作点B关于AM的对称点N，连接AN、MN、EN，请直接写出∠AMH、∠NAE、∠MNE之间的角度关系．3.如图，在△ABC和△DEF中，AB=AC，DE=DF，∠BAC=∠EDF=120°，线段BC与EF相交于点O．(1)若点O恰好是线段BC与线段EF的中点．①如图1，当点D在线段BC上，A、F、O、E四点在同一条直线上时，已知BC=4√3，DE=√3，求AD的长；②如图2，连接AD，CF相交于点G，连接OG，BG，当BG⊥OG时，求证：BG=√3CG．2(2)若点D与点A重合，CF//AB，H、K分别为OC、AF的中点，连接HK，直接写出HKAE−OF 的值．AC，连接4.在△ABC和△AEF中，∠AFE=∠ABC=90°，∠AEF=∠ACB=30°，AE=12 EC，点G是EC中点，将△AEF绕点A顺时针旋转．(1)如图1，若E恰好在线段AC上，AB=2，连接FG，求FG的长度；(2)如图2，若点F恰好落在射线CE上，连接BG，证明：GB=√3AB+GC；2GC最大时，直接写出直线AB，(3)如图3，若AB=3，在△AEF旋转过程中，当GB−12AC，BG所围成三角形的面积．5.如图，四边形ABCD为正方形，△AEF为等腰直角三角形，∠AEF=90°，连接FC，G为FC的中点，连接GD，ED．(1)如图①，E在AB上，直接写出ED，GD的数量关系．(2)将图①中的△AEF绕点A逆时针旋转，其它条件不变，如图②，(1)中的结论是否成立？说明理由．(3)若AB=5，AE=1，将图①中的△AEF绕点A逆时针旋转一周，当E，F，C三点共线时，直接写出ED的长．6.如图1，在四边形ABCD中，AC交BD于点E，△ADE为等边三角形．(1)若点E为BD的中点，AD=4，CD=5，求△BCE的面积；(2)如图2，若BC=CD，点F为CD的中点，求证：AB=2AF；(3)如图3，若AB//CD，∠BAD=90°，点P为四边形ABCD内一点，且∠APD=90°，连接BP，取BP的中点Q，连接CQ.当AB=6√2，AD=4√2，tan∠ABC=2时，求CQ+√10BQ的最小值．107.已知△ABC中，∠ACB=90°，AC=2BC．(1)如图①，若AB=BD，AB⊥BD，求证：CD=√2AB；(2)如图②，若AB=AD，AB⊥AD，BC=1，求CD的长；(3)如图③，若AD=BD，AD⊥BD，AB=2√5，求CD的长．8.在△ABC中，∠ABM=45°，AM⊥BM，垂足为M，点C是BM延长线上一点，连接AC．(1)如图1，若AB=3√2，BC=5，求AC的长；(2)如图2，点D是线段AM上一点，MD=MC，点E是△ABC外一点，EC=AC，连接ED并延长交BC于点F，且点F是线段BC的中点，求证：∠BDF=∠CEF．9.在平行四边形ABCD中，对角线AC、BD交于点O，过点A作AE⊥BC于E，过点C作CF⊥CD交AE于点F，连接OF.以OF为直角边作Rt△OFG，其中∠OFG=90°，连接AG．(1)如图1，若∠EAB=30°，OA=2√3，AB=6，则求CE的长度；(2)如图2，若CF=CD，∠FGO=45°，求证：EC=√2AG+2EF；(3)如图3，动点P从点A运动到点D(不与点A、点D重合)，连接FP，过点P作FP的垂线，又过点D作AD的垂线交FP的垂线于点Q，点A′是点A关于FP的对称点，连接A′Q.若AE=2EC，FG=2OF，EF=1，AG=√5，则在动点P的运动过程中，直接写出A′Q的最小值．10.在正方形ABCD中，E为边CD上一点(不与点C、D重合)，垂直于BE的一条直线MN分别交BC、BE、AD于点M、P、N，正方形ABCD的边长为6．(1)如图1，当点M和点C重合时，若AN=4，求线段PM的长度；(2)如图2，当点M在边BC上时，判断线段AN、MB、EC之间的数量关系，并说明理由；(3)如图3，当垂足P在正方形ABCD的对角线AC上运动时，连接NB，将△BPN沿着BN翻折，点P落在点P′处，AB的中点为Q，直接写出P′Q的最小值．11.如图1，在正方形ABCD中，P是对角线BD上的一点，点E在AD的延长线上，且PA=PE，PE交CD于F．(1)求∠CPE的度数；(2)如图2，把正方形ABCD改为菱形ABCD，其他条件不变，当∠ABC=120°时，连接CE，试探究线段AP与线段CE的数量关系，并说明理由．12. 如图，在菱形ABCD 中，∠ABC =60°，分别过点B 作BC 的垂线，过点D 作CD 的垂线，两垂线相交于点E ．(1)如图1，若AD =4，连接AE ，BD ，求三角形ADE 的面积；(2)如图2，点F 是DE 延长线上的一点，点G 为EB 延长线上的一点，且EF =BG ，连接BF ，DG ，DG 交FB 的延长线于点H ，连接AH ，试猜想线段AH ，BH ，HD 的数量关系并证明你的结论；(3)如图3，在(2)的条件下，在AH 上取得一点P ，使得HP =3AP ，已知Q 为直线ED 上一点，连接BQ ，连接QP ，当BQ +QP 最小时，直接写出S △QDC S 菱形ABCD 的值．13. 如图，已知△ABC 中，∠ABC =45°，CD 是边AB 上的高线，E 是AC 上一点，连接BE ，交CD 于点F ．(1)如图1，若∠ABE =15°，BC =√3+1，求DF 的长；(2)如图2，若BF =AC ，过点D 作DG ⊥BE 于点G ，求证：BE =CE +2DG ；(3)如图3，若R 为射线BA 上的一个动点，以BR 为斜边向外作等腰直角△BRH ，M 为RH 的中点.在(2)的条件下，将△CEF 绕点C 旋转，得到△CE′F′，E ，F 的对应点分别为E′，F′，直线MF′与直线AB 交于点P ，tan∠ACD =13，直接写出当MF′取最小值时RMPF′的值．14. 如图△ABC 为等腰直角三角形，∠A =90°，D 、E 分别为AB 、AC 边上的点，连接DE ，以DE 为直角边向上作等腰直角三角形DEF ，连接BE 、BF ．(1)如图1，当CE =AD 时，求证：BF ⊥BD ；(2)如图2，H 为BE 的中点，过点D 作DG ⊥BC 于点G ，连接GH.求证：BF =2HG ；(3)如图3，BE 与DF 交于点R ，延长BF 交AC 于点P ，∠APB 的角平分线交BE 于点Q.若点E 为AC 上靠近点A 的三等分点，且tan∠AED =67，请直接写出BR QR 的值．15. 如图，△ABC 是等边三角形，△BDE 是顶角为120°的等腰三角形，BD =DE ，连接CD ，AE ．(1)如图1，连接AD ，若∠ABE =60°，AB =BE =√3，求CD 的长；(2)如图2，若点F 是AE 的中点，连接CF ，DF.求证：CD =2DF ；(3)如图3，在(2)的条件下，若AB =2√3，BD =2，将△BDE 绕点B 旋转，点H 是△AFC 内部的一点，当DF 最大时，请直接写出2HA +HF +√5HC 的最小值的平方．16.如图，点B，C，D在同一条直线上，△BCF和△ACD都是等腰直角三角形.连接AB，DF，延长DF交AB于点E．(1)如图1，若AD=BD，DE是△ABD的平分线，BC=1，求CD的长度；(2)如图2，连接CE，求证：DE=√2CE+AE；(3)如图3，改变△BCF的大小，始终保持点F在线段AC上(点F与点A，C不重合).将ED绕点E顺时针旋转90°得到EP.取AD的中点O，连接OP.当AC=2时，直接写出OP 长度的最大值．17.如图，已知△ABC为等腰直角三角形，AB=AC且∠CAB=90°，E为BC上一点，且BE=AC，过E作EF⊥BC且EF=EC，连接CF．(1)如图1，已知AB=2，连接AE、AF，求△AEF的面积；(2)如图2所示，D为AB上一点，连接DB，作∠DBH=45°交EF于H点，求证：CD=HF+√2CE；(3)已知△ABC面积为8+4√2，D为射线AC上一点，作∠DBH=45°，交射线EF于H，连接DH，点M为DH的中点，当CM有最小值时，请直接写出△CMD的面积．18.如图，Rt△ABC中，∠ABC=90°，AB=BC，点E是边BC上的一个动点，点D是射线AC上的一个动点；连接DE，以DE为斜边，在DE右侧作等腰Rt△DFE，再过点D 作DH⊥BC，交射线BC于点H．(1)如图1，若点F恰好落在线段AE上，且∠DEH=60°，CD=3√2，求出DF的长；(2)如图2，若点D在AC延长线上，此时，过F作FG⊥BC于点G，FG与AC边的交点记为M，当AE=DE时，求证：FM+√2MD=AB；(3)如图3，若AB=4√10，点D在AC延长线上运动，点E也随之运动，且始终满足AE=DE，作点E关于DF的对称点E′，连接CF、FE′、DE′，当CF取得最小值时，请直接写出此时四边形CFE′D的面积．19.如图1，在Rt△ABC中，∠BAC=90°，AB=AC，点D是BC边上一动点，连接AD，把AD绕点A顺时针旋转90°，得到AE，连接DE．(1)如图1所示，若BC=4，在D点运动过程中，当tan∠BDE=8时，求线段CD的长；11(2)如图2所示，点F是线段DE的中点，连接BF并延长交CA延长线于点M，连接DM，交AB于点N，连接CF，AF，当点N在线段CF上时，求证：AD+BF=CF；(3)如图3，若AB=2√3，将△ABC绕点A顺时针旋转得△AB′C′，连接CC′，P为线段CC′上一点，且CC′=√3PC′，连接BP，将BP绕点B顺时针旋转60°得到BQ，连接PQ，K 为PQ的中点，连接CK，请直接写出线段CK的最大值．20.在△ABC中，AC=BC，D为△ABC外一点，连接CD．(1)如图1，若∠ACB=60°，CD//AB，连接BD交AC于点E，且CD=2AB=2，求S△BCE．EC，(2)如图2，CE=CD，∠ECB=∠DCA，ED交AB于点F，FG垂直平分EC，且FG=12BF．M，N分别为AF，CD中点，连接MN，求证：MN=12(3)如图3，若∠ACB=90°，CD//AB，将AD绕着A点顺时针旋转60°得到AD′，连接DD′，BD′，且AC=√6，求BD′的最小值．21.已知，等腰直角△ABC中，AC=BC，∠ACB=90°，D为AB边上的一点，连接CD，以CD为斜边向右侧作直角△CDE，连接AE并延长交BC的延长线于点F．(1)如图1，当∠CDE=30°，AD=1，BD=3时，求线段DE的长；(2)如图2，当CE=DE时，求证：点E为线段AF的中点；(3)如图3，当点D与点A重合，AB=4时，过E作EG⊥BA交直线BA于点G，EH⊥BC交直线BC于点H，连接GH，求GH长度的最大值．22.如图，在锐角△ABC中，∠ACB=45°，点D是边BC上一动点，连接AD，将线段AD绕点A逆时针旋转90°得到线段AE，连接DE交AC于点F．(1)如图1，若∠ADC=60°，求证：DF=AF+EF；(2)如图2，在点D运动的过程中，当∠ADC是锐角时，点M在线段DC上，且AM=AD，连接ME，猜想线段ME，MD，AC之间存在的数量关系，并证明你猜想的结论；(3)在点D运动的过程中，当∠ADC是钝角时，点N是线段DE上一动点，连接CN，若AF=m，请直接用含m的代数式表示2CN+√2NE的最小值．CF=3523.如图1，在Rt△ABC与Rt△ABD中，∠ACB=∠ADB=90°，∠BAC=60°，CE⊥AB交AB于点E，AE=AD，点F在线段BD上，连接AF．(1)若AC=4，求线段BD的长；(2)如图2，若∠DAF=60°，点M为线段BF的中点，连接CM，证明：2CM=BF+√3AC；(3)如图3，在(2)的条件下，将△ADF绕点A旋转得△AD′F′，连接BF′，点M为线段BF′的中点，连接D′M，当D′M长度取最小时，在线段AB上有一动点N，连接MN，将线段MN绕点M逆时针旋转60°至MN′，连接D′N′，若AC=4，请直接写出(2MN′−√2D′N′)的最小值．。

2020年重庆中考几何第26题专题训练一(含答案解析)

2020年中考几何题专题训练一答案解析\1、已知：在△ABC中，BC＝2AC，∠DBC＝∠ACB，BD＝BC，CD交线段AB于点E．（1）如图1，当∠ACB＝90°时，则线段DE、CE之间的数量关系为；（2）如图2，当∠ACB＝120°时，求证：DE＝3CE；（3）如图3，在（2）的条件下，点F是BC边的中点，连接DF，DF与AB交于G，△DKG和△DBG 关于直线DG对称（点B的对称点是点K，延长DK交AB于点H．若BH＝10，求CE的长．2、（2016春•重庆校级期中）在△ABC中，AB＝AC，D为射线BC上一点，DB＝DA，E为射线AD上一点，且AE＝CD，连接BE．（1）如图1，若∠ADB＝120°，AC＝2，求DE的长；（2）如图2，若BE＝2CD，连接CE并延长交AB于点F，求证：CF＝3EF；（3）如图3，若BE⊥AD，垂足为点E，猜想AE，BE，BD之间的数量关系，直接写出关系式．3、（2019秋•江岸区校级月考）在菱形ABCD中，∠ABC＝60°（1）如图1，P是边BD延长线上一点，以AP为边向右作等边△APE，连接BE、CE．①求证：CE⊥AD；②若AB＝，BE＝，求AE的长；（2）如图2，P是边CD上一点，点D关于AP的对称点为E，连接BE并延长交AP的延长线于点F，连接DE、DF．若BE＝11，DE＝5，求△ADF的面积．4、（2016秋•南岗区校级月考）已知：如图，在等边△ABC中，点D是AC上任意一点，点E在BC延长线上，连接DB，使得BD＝DE．（1）如图1，求证：AD＝CE；（2）如图2，取BD的中点F，连接AE、AF．求证：∠CAE＝∠BAF；（3）如图3，在（2）的条件下，过点F作AE的垂线，垂足为H，若AH＝．求EH的长．5、已知，在Rt△ABC中，∠C＝90°，AC＝BC，点D在边BC上，连接AD，作DE⊥AD，且DE＝AD，连接BE、AE，DE与AB交于点H，（1）如图1所示，求证：∠C＝∠ABE；（2）如图2，把射线AD沿AB折叠，分别交BE、DE的延长线于点F、点G．若∠AEB＝75°，求证：HG＝2DH；（3）在（2）的条件下，若BE＝3，求DH的长？6、如图，在△ABC中，∠ABC＝90°，AB＝BC，点D是△ABC内部一点，连接AD，BD和CD．（1）如图1，若∠BDC＝90°，BD＝1，CD＝2，求AC的长．（2）如图2，若CD平分∠ACB，∠BDC＝90°，过点B作BE∥AC交AD的延长线于点E，求证：AD ＝DE．（3）如图3，若CD＝CB，∠BCD＝30°，取线段AC的中点F，连接DF，求证：∠AFD＝45°7、（2013•洪山区模拟）如图1，直角梯形ABCD中，BC＝CD，AB∥CD，∠ABC＝90°，点P为边AD上一点，BC＝PB．（1）求证：∠CBP＝2∠DCP；（2）如图2，若∠ABP的平分线交CP的延长线于点E，连接DE，求证：BE+DE＝CE；（3）在（2）的条件下，若AB＝1，BC＝2，请直接写出线段CE的长度．8、（2016秋•松北区期末）如图，在△ABC中，∠ACB＝60°，点D在射线BC上，AB＝AD．（1）如图1，求证：BC+CD＝AC；（2）如图2，取AB的中点F，延长CA至点E，连接BE、DE、EF，使得∠ABE＝∠CAD，EF＝AE，求证：∠BEF＝2∠ABD；（3）如图3，在（2）的条件下，FG⊥BE于点G，FG＝4，EF＝，求△AED的面积．9、（2016•九龙坡区校级一模）已知，Rt△ABC中，∠ACB＝90°，∠CAB＝30°，分别以AB、AC为边，向Rt△ABC外作等边△ABD和等边△ACE（1）如图1，连接BE、CD，若BC＝2，求BE的长；（2）如图2，连接DE交AB于点F，作BH⊥AD于H，连接FH．求证：BH＝2FH；（3）如图3，取AB、CD得中点M、N，连接M、N，试探求MN和AE的数量关系，并直接写出结论．10、重庆八中初2020级九上期末11、重庆实验外国语学校初2020级九上期末12、重庆双福育才中学初2020级九上期末2020年中考几何题专题训练一答案解析\1、已知：在△ABC中，BC＝2AC，∠DBC＝∠ACB，BD＝BC，CD交线段AB于点E．（1）如图1，当∠ACB＝90°时，则线段DE、CE之间的数量关系为DE＝2CE；（2）如图2，当∠ACB＝120°时，求证：DE＝3CE；（3）如图3，在（2）的条件下，点F是BC边的中点，连接DF，DF与AB交于G，△DKG和△DBG 关于直线DG对称（点B的对称点是点K，延长DK交AB于点H．若BH＝10，求CE的长．（1）解：∵∠DBC＝∠ACB＝90°，∴∠DBC+∠ACB＝180°，∴AC∥BD，∴∠DBE＝∠CAE又∵∠DEB＝∠AEC，∴△DBE∽△CAE，∴＝，又∵BD＝BC＝2AC，∴DE＝2CE；故答案为：DE＝2CE．（2）证明：如图2，∵∠DBC＝∠ACB＝120°，BD＝BC，∴∠D＝∠BCD＝30°，∴∠ACD＝90°，过点B作BM⊥DC于M，则DM＝MC，BM＝BC，∵AC＝BC，∴BM＝AC，∵在△BME和△ACE中∴△BME≌△ACE（AAS），∴ME＝CE＝CM，∴DE＝3EC；（3）解：如图，过点B作BM′⊥DC于点M′，过点F作FN⊥DB交DB的延长线于点N，设BF＝a，∵∠DBF＝120°，∴∠FBN＝60°，∴FN＝a，BN＝a，∵DB＝BC＝2BF＝2a，∴DN＝DB+BN＝a，∴DF＝＝＝a，∵AC＝BC，BF＝BC，∴BF＝AC，∴△BDF≌△BCA（SAS），∴∠BDF＝∠CBA，又∵∠BFG＝∠DFB，∴△FBG∽△FDB，∴＝＝，∴BF2＝FG×FD，∴a2＝a×FG，∴FG＝a，∴DG＝DF﹣FG＝a，BG＝＝a，∵△DKG和△DBG关于直线DG对称，∴∠GDH＝∠BDF，∴∠ABC＝∠GDH，又∵∠BGF＝∠DGH，∴△BGF∽△DGH，∴＝，∴GH＝＝a，∵BH＝BG+GH＝a＝10，∴a＝2；∴BC＝2a＝4，CM′＝BC cos30°＝2，∴DC＝2CM′＝4，∵DE＝3EC，∴EC＝DC＝．2、（2016春•重庆校级期中）在△ABC中，AB＝AC，D为射线BC上一点，DB＝DA，E为射线AD上一点，且AE＝CD，连接BE．（1）如图1，若∠ADB＝120°，AC＝2，求DE的长；（2）如图2，若BE＝2CD，连接CE并延长交AB于点F，求证：CF＝3EF；（3）如图3，若BE⊥AD，垂足为点E，猜想AE，BE，BD之间的数量关系，直接写出关系式．（1）解：∵DA＝DB，∠ADB＝120°，∴∠ABC＝∠BAD＝30°，∵AB＝AC，∴∠ABC＝∠C＝30°，∴∠CAD＝90°，在RtACD中，tan30°＝，∴AD＝2×＝2，AE＝CD＝2AD＝4 ∴DE＝AE﹣AD＝CD﹣AD＝4﹣2＝2；（2）证明：如图，过A作AG∥BC，∵DB＝DA，AB＝AC，∴∠BAD＝∠ABC，∠ABC＝∠ACB，∴∠BAD＝∠ACB，∵AE＝CD，在△ABE和△CAD中∴△ABE≌△CAD（SAS），∴BE＝AD，∵BE＝2CD，∴AD＝2CD＝2AE，∴AE＝DE，∵AG∥BC，∴∠G＝∠DCE，∠GAE＝∠CDE，在△AGE和△DCE中∴△AGE≌△DCE（AAS），∴GE＝CE，AG＝CD＝AE，∴△AGE为等腰三角形，∴∠GAF＝∠ABC＝∠BAD，∴F为GE的中点，∴CE＝EG＝2EF，∴CF＝3EF；（3）如图3，取BE中点M，延长AM至N，使MN＝AM，连接BN，EN，∴四边形ABNE是平行四边形，∴AE∥BN，∴∠NBC＝∠D，BN＝AE＝CD，∵AB＝AC，DB＝DA，∴∠ABC＝∠ACB＝∠BAD，∴∠BAC＝∠D＝∠NBC，∵∠ABN＝∠NBC+∠ABC，∠ACD＝∠BAC+∠ABC，∴∠ABN＝∠ACD，在△ABN和△ACD中∴△ABN≌△ACD（SAS），∴BD＝AD＝AN＝2AM，∵BE⊥AD，∴AE2+ME2＝AM2，∴AE2+（BE）2＝（AN）2，∴AE2+BE2＝BD2．3、（2019秋•江岸区校级月考）在菱形ABCD中，∠ABC＝60°（1）如图1，P是边BD延长线上一点，以AP为边向右作等边△APE，连接BE、CE．①求证：CE⊥AD；②若AB＝，BE＝，求AE的长；（2）如图2，P是边CD上一点，点D关于AP的对称点为E，连接BE并延长交AP的延长线于点F，连接DE、DF．若BE＝11，DE＝5，求△ADF的面积．（1）①证明：在菱形ABCD中，∠ABC＝60°，∴∠ADC＝60°，且AB＝BC＝DA＝DC，∴△ADC和△ABC是等边三角形，∴AB＝AC，∠BAC＝∠CAD＝60°，又∵△APE是等边三角形，∴AE＝AP，∠EAP＝60°，∴∠BAC+∠CAP＝∠PAE+∠CAP，即∠BAP＝∠CAE，∴△BAP≌△CAE（SAS），∴∠ACE＝∠ABP＝∠ABC＝30°，∵∠CAD＝60°，∴∠ACE+∠CAD＝90°，∴CE⊥AD；②解：如图1，设AC与BD交于点O，由①知，∠ACE＝30°，且∠ACB＝60°，∴∠ACE+∠ACB＝∠BCE＝90°，∵在Rt△BCE中，BC＝AB＝，BE＝，∴CE＝＝4，由①知，△BAP≌△CAE，∴BP＝CE＝4，在Rt△BOC中，∠ACB＝60°，∴BO＝BC＝，CO＝AO＝BC＝，∴OP＝BP﹣BO＝，∴在Rt△AOP中，AP＝＝＝，∴AE＝AP＝；（2）解：如图2，连接AE，过点A作AH⊥BF于点H，∵点D关于AP的对称点为E，∴AP垂直平分DE，∴AD＝AE，FD＝FE，∴∠EAF＝∠DAF＝∠EAD，∠DFA＝∠EFA＝∠DFE，又∵在菱形ABCD中，AB＝AD，∴AB＝AE，∴AH垂直平分BE，∴EH＝BH＝BE＝，∠BAH＝∠EAH＝∠BAE，∴∠HAF＝∠EAH+∠EAF＝∠BAD，∵∠ABC＝60°，∴∠BAD＝180°﹣∠ABC＝120°，∴∠HAF＝60°，∴∠AFH＝90°﹣∠HAF＝30°，∴∠DFE＝60°，∴△DEF为等边三角形，∴EF＝DE＝5，∴HF＝HE+EF＝+5＝，在Rt△AHF中，∠AFH＝30°，∴AH＝HF＝，∴S△AEF＝EF•AH＝×5×＝，∵AD＝AE，FD＝FE，AF＝AF，∴△ADF≌△AEF（SSS），∴△ADF的面积为．4、（2016秋•南岗区校级月考）已知：如图，在等边△ABC中，点D是AC上任意一点，点E在BC延长线上，连接DB，使得BD＝DE．（1）如图1，求证：AD＝CE；（2）如图2，取BD的中点F，连接AE、AF．求证：∠CAE＝∠BAF；（3）如图3，在（2）的条件下，过点F作AE的垂线，垂足为H，若AH＝．求EH的长．解：（1）如图1，作DF∥AB，∵DF∥AB，∴，∵AC＝BC，∴CF＝CD，∴BF＝AD，∵DF∥AB，∴∠DFC＝60°，∴∠BFD＝120°，∵BD＝DE，∴∠E＝∠DBE，在△BDF和△EDC中，，∴△BDF≌△EDC，（AAS）∴BF＝CE，∴AD＝CE，（2）如图2，过点B作BG∥AC交AF的延长线于G，∴∠G＝∠DAF，∠CBG＝∠ACB＝60°，∴∠ABG＝∠ABC+∠CBG＝120°＝∠ACE，∵点F是BD中点，∴BF＝DF，在△BFG和△DFA中，，∴△BFG≌△DFA，∴BG＝AD，由（1）知，AD＝CE，∴BG＝CE，在△ABG和△ACE中，，∴△ABG≌△ACE，∴∠BAF＝CAE；（3）由（2）知，∠BAF＝∠CAE，∴∠FAE＝∠FAC+∠CAE＝∠FAC+∠BAF＝∠BAC＝60°，∵FH⊥AE，∴∠AHF＝90°，∴∠AFH＝90°﹣∠FAE＝30°，在Rt△AFH中，AH＝，∴AF＝2，由（2）知，△BFG≌△DFA，∴GF＝AF＝2，由（2）知，△ABG≌△ACE，∴AE＝AG＝2AF＝4，∴EH＝AE﹣AH＝4﹣＝3．5、已知，在Rt△ABC中，∠C＝90°，AC＝BC，点D在边BC上，连接AD，作DE⊥AD，且DE＝AD，连接BE、AE，DE与AB交于点H，（1）如图1所示，求证：∠C＝∠ABE；（2）如图2，把射线AD沿AB折叠，分别交BE、DE的延长线于点F、点G．若∠AEB＝75°，求证：HG＝2DH；（3）在（2）的条件下，若BE＝3，求DH的长？证明：（1）如图1，过点E作EM⊥BC于M，∵∠ACB＝90°，AD⊥DE∴∠ACB＝∠ADE＝90°∵∠ADB＝∠ACB+∠DAC＝∠ADE+∠EDB∴∠DAC＝∠EDB，且∠ACD＝∠EMD＝90°，AD＝DE ∴△ACD≌△DME（AAS）∴AC＝DM，CD＝EM∵AC＝BC，∴BC＝DM∴CD＝BM∴BM＝EM，且EM⊥BM∴∠EBM＝45°∵∠C＝90°，AC＝BC∴∠ABC＝∠BAC＝45°∴∠ABE＝180°﹣∠ABC﹣∠EBM＝90°∴∠C＝∠ABE（2）如图2，过点E作EM⊥BC于M，∵∠C＝90°，AC＝BC，∠ADE＝90°，AD＝DE∴∠CAB＝∠DAE＝∠AED＝45°由（1）可知∠EBM＝45°，∴∠CBE＝135°，∵∠DAE+∠AEB+∠DBE+∠ADB＝360°，且∠AEB＝75°，∴∠ADB＝105°∴∠ACD+∠CAD＝∠ADB＝105°∴∠CAD＝15°∴∠DAB＝30°∵把射线AD沿AB折叠，分别交BE、DE的延长线于点F、点G．∴∠DAB＝∠BAG＝30°∴∠DAG＝60°，且∠ADE＝90°∴∠G＝30°＝∠BAG∴AH＝HG∵∠ADE＝90°，∠DAH＝30°∴AH＝2DH∴HG＝2DH（3）作EN平分∠DEB交BC于点N，∵EM＝BM，∠EMB＝90°∴BE＝EM，且BE＝3，∴EM＝∵∠AEB＝75°，∠AED＝45°∴∠DEN＝30°∵EN平分∠DEB∴∠DEN＝15°∵∠EDM＝∠CAD＝15°∴∠DEN＝∠EDB＝15°，∴DN＝EN，∠ENM＝30°，且EM⊥BM∴NE＝2EM＝3，NM＝EM＝在Rt△DEM中，DE＝＝3+3＝AD∵∠DAH＝30°，∠ADH＝90°∴AD＝DH＝3+3∴DH＝3+6、如图，在△ABC中，∠ABC＝90°，AB＝BC，点D是△ABC内部一点，连接AD，BD和CD．（1）如图1，若∠BDC＝90°，BD＝1，CD＝2，求AC的长．（2）如图2，若CD平分∠ACB，∠BDC＝90°，过点B作BE∥AC交AD的延长线于点E，求证：AD ＝DE．（3）如图3，若CD＝CB，∠BCD＝30°，取线段AC的中点F，连接DF，求证：∠AFD＝45°解：（1）如图1，∵∠BDC＝90°，BD＝1，CD＝2，∴BC＝＝＝，∵AB＝BC＝，由勾股定理得：AC＝＝＝；（2）如图2，延长BD交AC于P，∵DC平分∠ACB，∴∠BCD＝∠ACD，∵∠BDC＝90°，∴∠BDC＝∠PDC＝90°，∵CD＝CD，∴△BDC≌△PDC，∴BD＝PD，∵BE∥AC，∴∠E＝∠EAC，∠EBD＝∠DPA，∴△BDE≌△PDA，∴AD＝DE；（3）如图3，以BD为边作等边三角形BDE，连接BF、CE，∴BD＝DE＝BE，∵AB＝BC，F是AC的中点，∴BF⊥AC，∴∠AFB＝90°，∵∠ABC＝90°，∴BF＝AF，∵CD＝BC，∠BCD＝30°，∴∠CBD＝∠CDB＝75°，∵CE＝CE，∴△CEB≌△CED，∴∠BCE＝∠DCE＝15°，∵∠CBD＝75°，∠DBE＝60°，∴∠CBE＝75°﹣60°＝15°，∵∠ABC＝90°，∴∠ABD＝90°﹣75°＝15°，∴∠ABD＝∠CBE，∴△ABD≌△CBE，∴∠BAD＝∠BCE＝15°，∴∠ABD＝∠BAD＝15°，∴AD＝BD，∵DF＝DF，∴△ADF≌△BDF，∴∠AFD＝∠BFD＝∠AFB＝×90°＝45°．7、（2013•洪山区模拟）如图1，直角梯形ABCD中，BC＝CD，AB∥CD，∠ABC＝90°，点P为边AD上一点，BC＝PB．（1）求证：∠CBP＝2∠DCP；（2）如图2，若∠ABP的平分线交CP的延长线于点E，连接DE，求证：BE+DE＝CE；（3）在（2）的条件下，若AB＝1，BC＝2，请直接写出线段CE的长度．解：（1）取CP的中点F，连接BF，如图1，∵BC＝BP，BF是底边上的中点，∴∠CBF＝∠PBF＝∠CBP，BF⊥PC，∴∠CBF+∠BCF＝90°，∵∠BCF+∠DCP＝90°，∴∠DCP＝∠CBF，∴∠CBP＝2∠DCP；（2）过得C作CG⊥CE交EB的延长线于点G，连接BD，如图2，∵BC＝CD，∠BCD＝90°，∴∠CBD＝45°，∵∠EBF＝∠EBP+∠PBF＝∠ABP+∠CBP＝45°，∴∠BEF＝180°﹣∠EBF﹣∠BFE＝45°，∴△CEG是等腰直角三角形，∴EG＝CE，CG＝CE，∵∠ECG＝90°＝∠BCD，∴∠BCG＝∠DCE，在△CBD和△CDE中∴△CBD≌△CDE（SAS），∴BG＝DE，∴DE+BE＝BG+BE＝EG＝CE；（3）CE＝，理由如下；取CD的中点M，连接MF，设MF的延长线交直线AB与B′，如图2，∵F是PC的中点，∴FM∥AD，∵AB∥CD，∴四边形AB′MD是平行四边形，∴AB′＝DM＝1＝AB，∴B′与B重合，即B、F、M在一条直线上，∴BM⊥CE，∵∠CBF＝∠MBC，∴△BFC∽△BCM，∴＝，即＝，∴BF＝2CF，∵∠BEF＝45°，∠BFE＝90°，∴EF＝BF＝2CF，∵CF＝PF，∴CF＝PF＝PE，CE＝3CF，∵S△BCM＝CF•BM＝BC•CM，∴CF＝＝＝，∴CE＝3CF＝．8、（2016秋•松北区期末）如图，在△ABC中，∠ACB＝60°，点D在射线BC上，AB＝AD．（1）如图1，求证：BC+CD＝AC；（2）如图2，取AB的中点F，延长CA至点E，连接BE、DE、EF，使得∠ABE＝∠CAD，EF＝AE，求证：∠BEF＝2∠ABD；（3）如图3，在（2）的条件下，FG⊥BE于点G，FG＝4，EF＝，求△AED的面积．（1）证明：延长DB至E，使BE＝CD，连接AE，∵AB＝AD，∴∠ABD＝∠ADB，∵∠ABE+∠ABD＝180°，∠ADC+∠ADB＝180°，∴∠ABE＝∠ADC，在△ABE和△ADC中，，∴△ABE≌△ADC，∴∠C＝∠E＝60°，∴△AEC为等边三角形，∴AC＝CE，∵BC+BE＝CE，∴BC+CD＝AC；（2）证明：∵AB＝AD，∴∠ABD＝∠ADB，∵∠CAD+∠ADB＝∠ACB＝60°，∠CAD＝∠ABE，∴∠ABE+∠ABD＝∠CAD+∠ADB＝60°，∴△BEC为等边三角形，过点A作AN∥BC交EB于N，∴△ENA为等边三角形，∠NAB＝∠ABD，∴AN＝AE，∴BN＝AC，∴∠NAB＝∠ADC，在△BNA和△ACD中，，∴△BNA≌△ACD，∴AN＝CD，∴CD＝AE，延长EF至M使得EF＝FM，连接BM，∴△AEF≌△BMF，∴AE＝BM，AE∥BM，∴BM＝CD，∠MBC＝∠ECB＝60°，∴∠EBM＝∠EBC+∠MBC＝120°，又∵∠ECD＝∠EBM＝120°，∴△BEM≌△CED，∴∠BEF＝∠CED，∵EF＝AE，∴∠EFA＝∠EAF，∴∠BEF+∠EBF＝∠ACB+∠ABD，∴∠BEF+60°﹣∠ABD＝∠ABD+60°，∴∠BEF＝2∠ABD∠CED＝2∠ABD；（3）解：由（2）得，△EMD是等边三角形，∴，过点A作AP⊥DE于P，由（2）可证△EFG≌△EAP，∴AP＝FG＝4，∴S△AED＝DE×AP＝××4＝37．9、（2016•九龙坡区校级一模）已知，Rt△ABC中，∠ACB＝90°，∠CAB＝30°，分别以AB、AC为边，向Rt△ABC外作等边△ABD和等边△ACE（1）如图1，连接BE、CD，若BC＝2，求BE的长；（2）如图2，连接DE交AB于点F，作BH⊥AD于H，连接FH．求证：BH＝2FH；（3）如图3，取AB、CD得中点M、N，连接M、N，试探求MN和AE的数量关系，并直接写出结论．解：（1）如图1，Rt△ABC中，∠CAB＝30°，BC＝2，∴AB＝4，AC＝2，∵△ACE是等边三角形，∴AE＝AC＝2，∠EAC＝60°，∴∠EAB＝60°+30°＝90°，在Rt△EAB中，EB＝＝＝2；（2）如图2，过E作EG∥BD，交BA的延长线于G，∴∠EGA＝∠ABD，∵△ABD是等边三角形，∴∠ABD＝60°，∴∠EGA＝60°，Rt△AEG中，设AG＝x，∴EG＝2x，AE＝x，∴AC＝AE＝BH＝x，∵∠BDH＝60°，∴BD＝2x，∴EG＝BD＝2x，∵∠EFG＝∠BFD，∴△EFG≌△DFB，∴EF＝DF，等边△ABD中，∵BH⊥AD，∴AH＝DH，∴FH是△AED的中位线，∴FH＝AE＝BH，∴BH＝2FH；（3）如图3，连接BN，并延长交AD于H，∵∠CBA＝60°＝∠BAD，∴BC∥AD，∴∠BCN＝∠NDH，∵CN＝ND，∠CNB＝∠DNH，∴△CNB≌△DNH，∴BN＝NH，BC＝DH，∵M是AB的中点，∴MN是△ABH的中位线，∴MN＝AH，设BC＝x，则DH＝x，AB＝AD＝2x，∴AH＝x，∴MN＝x，Rt△ACB中，AC＝2x，∴AE＝2x，∴＝＝，∴AE＝4MN．10、重庆八中初2020级九上期末11、重庆实验外国语学校初2020级九上期末12、重庆双福育才中学初2020级九上期末。

2020重庆中考复习数学第26题专题训练六(含答案解析)

2020重庆中考复习数学第26题专题训练六　1、如图1，在△ABC中，∠BAC＝90°，AC＝2AB，D是线段AC中点，E是线段AD上一点，过点D作DF⊥BE交BE的延长钱于点F，连接AF，过点A作AG⊥AF于点A，交BF于点G（1）若∠ABE＝∠C，BC＝2，求AE的长；（2）若点E为AD中点，求证：GE﹣FE＝FD；（3）如图2，连接BD，点N为BD中点，连接GN，若AD＝GF，请直接写出NG、GE、EA的数量关系．4、已知△ABC中，点D为BC的中点，BD＝AB，AD⊥BC．（1）如图1，求∠BAD的度数；（2）如图2，点E为BC上一点，点F为AC上一点，连接AE、BF交于点G，若∠AGF＝60°，求证：BE＝CF；（3）如图3，在（2）的条件下，点G为BF的中点，点H为AG上一点，延长BH交AC于点K，AK ＝HK，BM⊥AE交AE延长线于点M，BG＝9，HM＝10，求线段AG的长．5、已知△ABC中，∠B＝60°，点D是AB边上的动点，过点D作DE∥BC交AC于点E，将△ADE沿DE折叠，点A对应点为F点．（1）如图1，当点F恰好落在BC边上，求证：△BDF是等边三角形；（2）如图2，当点F恰好落在△ABC内，且DF的延长线恰好经过点C，CF＝EF，求∠A的大小；（3）如图3，当点F恰好落在△ABC外，DF交BC于点G，连接BF，若BF⊥AB，AB＝9，求BG 的长．6、如图，在△ABC中，AB＝AC，∠BAC＝90°，D为BC边的中点，点E在直线BC上（不与点D重合），连接AE，过点C作直线AE的垂线，垂足为点F，交直线AD于点G，连接EG．（1）如图（1），当点E在线段BD上时，易证DE＝DG，请直接写出三条线段BE，AB，EG之间的数量关系是　；（2）如图（2），当点E在线段BC的延长线上时，请写出三条线段BE、AB、EG之间的数量关系，并证明你的结论；（3）若线段BC＝2，当△AEG为等腰三角形时，请直接写出的值．7、如图，在△ABC中，∠BAC＝90°，将△ABC沿AD翻折，点B恰好与点C重合，点E在AC边上，连接BE．（1）如图①，若点F是BE的中点，连接DF，且AF＝5，AE＝6，求DF的长；（2）如图②，若AF⊥BE于点F，并延长AF交BC于点G，当点E是AC的中点时，连接EG，求证：AG+EG＝BE；（3）在（2）的条件下，连接DF，请直接写出∠DFG的度数．8、如图，在Rt△ABC中，AC＝BC，∠ACB＝90°，点D、E分别在AC、BC上，BD与AE交于点O，且CD＝CE，若点F是BD的中点，连接CF，交AE于点G．（1）求证：CF⊥AE；（2）如图2，过点F作FM⊥BC，交AE的延长线于点M，垂足为H，连接CM，若CG＝GM．①求证：CF＝CM；②求的值．9、（1）【问题发现】如图1，在Rt△ABC中，AB＝AC＝4，∠BAC＝90°，点D为AC的中点，过点A作BD的垂线，垂足为E，延长AE交BC于点F，求△ABF的面积．小明发现，过点C作AC的垂线，交AF的延长线于点G，构造出全等三角形，经过推理和计算，能够得到BF与CF的数量关系，从而使问题得到解决，请直接填空：＝　2，△ABF的面积为　．（2）【类比探究】如图2，将（1）中的条件“点D为AC的中点”改为“点D为边AC上的一点，且满足CD＝2AD”，其他条件不变，试求△ABF的面积，并写出推理过程．（3）【拓展迁移】如图3，在△ABC中，AB＝AC＝4，∠BAC＝120°，点D为AC上一点，且满足CD ＝2AD，E为BD上一点，∠AEB＝60°，延长AE交BC于F，请直接写出△ABF的面积．2020重庆中考复习数学第26题专题训练六参考答案　1、如图1，在△ABC中，∠BAC＝90°，AC＝2AB，D是线段AC中点，E是线段AD上一点，过点D作DF⊥BE交BE的延长钱于点F，连接AF，过点A作AG⊥AF于点A，交BF于点G（1）若∠ABE＝∠C，BC＝2，求AE的长；（2）若点E为AD中点，求证：GE﹣FE＝FD；（3）如图2，连接BD，点N为BD中点，连接GN，若AD＝GF，请直接写出NG、GE、EA的数量关系．解：（1）∵△ABC中，∠BAC＝90°，AC＝2AB，BC＝2，∴由勾股定理可得AB＝2，AC＝4，∵∠ABE＝∠C，∠BAE＝∠CAB＝90°，∴△BAE∽△CAB，∴AB2＝AE×AC，即22＝AE×4，解得AE＝1，（2）证明：如图1，过A作AH⊥BF于H，则∠AHE＝90°，∵DF⊥BE，∠BAC＝90°，∠AEB＝∠FED，∴∠ABG＝∠ADF，∵AG⊥AF，∠BAC＝90°，∴∠BAG＝∠DAF，∵AC＝2AB，D是线段AC中点，∴AB＝AD，在△ABG和△ADF中，，∴△ABG≌△ADF（ASA），∴AG＝AF，∴△AGF是等腰直角三角形，∴AH＝GF＝GH，∵点E为AD中点，∴AE＝DE，在△AEH和△DEF中，，∴△AEH≌△DEF（AAS），∴EH＝EF，AH＝DF＝GH，∵GE﹣HE＝GH，∴GE﹣FE＝FD；（3）NG、GE、EA的数量关系为：NG+GE＝2AE．理由：如图2，连接AN，NF，由（2）可得，△AGF是等腰直角三角形，∵AB＝AD，∠BAD＝90°，N是BD的中点，∴∠DAN＝45°＝∠ADN，∴△ADN是等腰直角三角形，∵AD＝GF，∴等腰Rt△AGF与等腰Rt△ADN全等，∴AG＝AF＝AN＝ND，∵Rt△BDF中，N是BD的中点，∴NF＝ND＝BN，∴AN＝NF＝AF，即△ANF是等边三角形，∴∠NAF＝∠ANF＝60°，∵∠DAN＝45°，△ABG≌△ADF，∴∠DAF＝15°＝∠BAG，∵∠ABN＝∠BAN＝45°，∴∠GAN＝30°，∵∠AGF＝45°，∴∠ABE＝30°，∴Rt△ABE中，BE＝2AE，∵∠ABN＝45°，∴∠GBN＝15°，由NF＝ND＝NB，可得∠FND＝2∠GBN＝30°，在△ANG和△NDF中，，∴△ANG≌△NDF（SAS），∴GN＝FD＝BG，∵BG+GE＝BE＝2AE，∴NG+GE＝2AE．MDEFBACG解：　（1）由E 为CR 中点可得AG 平分BAC ，过G 作GH AB ，则有GH=CG=1，故BG=2（2）延长FD 交AG 于点M ，易证：()BFD AMD AAS ，所以BF=AM再证：()BFC CEA AAS ，所以BF=CE=AM ，CF=AE∴CF-CE=AE-AM ，即EM=EF ∴EFM 为等腰直角三角形　∴222EFFMDF（3）结论为：622BDEF4、（2017秋?许昌月考）已知△ABC中，点D为BC的中点，BD＝AB，AD⊥BC．（1）如图1，求∠BAD的度数；（2）如图2，点E为BC上一点，点F为AC上一点，连接AE、BF交于点G，若∠AGF＝60°，求证：BE＝CF；（3）如图3，在（2）的条件下，点G为BF的中点，点H为AG上一点，延长BH交AC于点K，AK ＝HK，BM⊥AE交AE延长线于点M，BG＝9，HM＝10，求线段AG的长．解：（1）∵点D为BC的中点，AD⊥BC，∴AB＝AC，BD＝CD＝BC，∵BD＝AB，∴AB＝BC＝AC，∴△ABC是等边三角形，∴∠BAC＝60°，∵AD⊥BC，∴∠BAD＝∠BAC＝30°；（2）由（1）知，△ABC是等边三角形，∴AB＝BC，∠ABC＝∠C＝60°，∴∠ABF+∠CBF＝60°，∵∠AGF＝60°，∴∠BAE+∠ABF＝60°，∴∠BAE＝∠CBF，在△ABE和△BCF中，，∴△ABE≌△BCF（ASA），∴BE＝CF，（3）如图，过F作FN⊥AE于N，过F作FD⊥BM，交BM的延长线于D，∵AM⊥BM，∴GM∥DF，∵BG＝GF，∴BM＝DM，∵∠AGF＝60°，∴∠BGM＝60°，∵BM⊥AE，∴∠BMG＝90°，∴∠GBM＝30°，在Rt△BMG中，MG＝BG＝，BM＝DM＝FN＝，∵AK＝HK，∴∠HAK＝∠AHK＝∠BHM，∵∠ANF＝∠HMB＝90°，∴△ANF≌△HMB，∴AN＝HM＝10，Rt△FGN中，∠NFG＝∠GBM＝30°，∴GN＝GF＝，∴AG＝AN+NG＝10+＝14.5．5、（2019秋?中山市期末）已知△ABC中，∠B＝60°，点D是AB边上的动点，过点D作DE∥BC交AC于点E，将△ADE沿DE折叠，点A对应点为F点．（1）如图1，当点F恰好落在BC边上，求证：△BDF是等边三角形；（2）如图2，当点F恰好落在△ABC内，且DF的延长线恰好经过点C，CF＝EF，求∠A的大小；（3）如图3，当点F恰好落在△ABC外，DF交BC于点G，连接BF，若BF⊥AB，AB＝9，求BG 的长．（1）证明：如图1，∵∠B＝60°，DE∥BC，∴∠ADE＝∠B＝60°，∵△ADE沿DE折叠，点A对应点为F点，∴∠ADE＝∠FDE＝60°，∴∠BDF＝60°，∴∠DFB＝60°＝∠B＝∠BDF，∴△BDF是等边三角形；（2）解：∵∠B＝60°，DE∥BC，∴∠ADE＝∠B＝60°，∵△ADE沿DE折叠，点A对应点为F点，∴∠ADE＝∠FDE＝60°，∠A＝∠DFE，∴∠ADC＝120°，∵CF＝EF，∴∠FEC＝∠FCE，设∠FEC＝∠FCE＝x，则∠A＝∠DFE＝∠FEC+∠FCE＝2x，在△ADC中，∠A+∠ACD+∠ADC＝180°，即2x+x+120°＝180°，解得：x＝20°，∴∠A＝2x＝40°；（3）解：同（1）得：∠BDF＝60°，△BDG是等边三角形，∠ADE＝∠B＝60°，∴BG＝BD，由折叠的性质得：AD＝FD，∵BF⊥AB，∴∠BFD＝90°﹣60°＝30°，∴FD＝2BD，∴AD＝2BD，∵AD+BD＝AB，∴2BD+BD＝9，∴BD＝3，∴BG＝BD＝3．6、（2018?连山区一模）如图，在△ABC中，AB＝AC，∠BAC＝90°，D为BC边的中点，点E在直线BC上（不与点D重合），连接AE，过点C作直线AE的垂线，垂足为点F，交直线AD于点G，连接EG．（1）如图（1），当点E在线段BD上时，易证DE＝DG，请直接写出三条线段BE，AB，EG之间的数量关系是　AB﹣EG＝BE；（2）如图（2），当点E在线段BC的延长线上时，请写出三条线段BE、AB、EG之间的数量关系，并证明你的结论；（3）若线段BC＝2，当△AEG为等腰三角形时，请直接写出的值．解：（1）如图1中，结论：AB﹣EG＝BE理由：∵AB＝AC，∠BAC＝90°，BD＝DC，∴AD⊥BC，∠ABC＝∠ACB＝45°，AD＝BD＝DC，∴BD＝AB，∵CF⊥AE，∴∠AFG＝∠CDG＝90°，∵∠AGF＝∠CGD，∴∠FAG＝∠GCD，∵∠ADE＝∠CDG，∴△ADE≌△CDG，∴DE＝DG，∴DE＝EG，∵BE+ED＝BD，∴BE+EG＝AB，∴AB﹣EG＝BE．（2）如图2中，结论：AB+EG＝BE．理由：同法可证：△ADE≌△CDG，∴DE＝DG，∴DE＝EG，∵BE﹣ED＝BD，∴BE+﹣EG＝AB，∴AB+EG＝BE．（3）①如图2中，当GA＝GE时，DG＝DE＝2﹣2，EG＝4﹣2，此时：＝＝﹣1．②如图3中，当GA＝GE时，设BD＝AD＝CD＝a，则AB＝AC＝CE＝a，DG＝DE＝a+a，EG＝a+2a，∴＝＝1+．③当点E与点C重合时，EG＝AB，可得EG：AB＝1，综上所述，的值为﹣1或1+或1．7、（2018?站前区校级一模）如图，在△ABC中，∠BAC＝90°，将△ABC沿AD翻折，点B恰好与点C重合，点E在AC边上，连接BE．（1）如图①，若点F是BE的中点，连接DF，且AF＝5，AE＝6，求DF的长；（2）如图②，若AF⊥BE于点F，并延长AF交BC于点G，当点E是AC的中点时，连接EG，求证：AG+EG＝BE；（3）在（2）的条件下，连接DF，请直接写出∠DFG的度数．解：（1）∵将△ABC沿AD翻折，点B恰好与点C重合，∴AB＝AC，BD＝CD，∠ADB＝∠ADC＝90°，且∠BAC＝90°，∴△ABC是等腰直角三角形，∵点F是BE的中点，AF＝5，∠BAC＝90°，∴BE＝10，∴AB＝＝＝8，∴AC＝8，∴EC＝2，∵BD＝CD，BF＝EF，∴DF＝EC＝1，（2）如图②，过点C作CH⊥AC交AG的延长线于点H，∵AB＝AC，∠BAC＝90°，BD＝CD，∴∠ABC＝∠BAD＝∠DAC＝∠ACB＝45°，∵∠BEA+∠CAH＝90°，∠CAH+∠H＝90°，∴∠H＝∠BEA，且AB＝AC，∠AFB＝∠ACH＝90°，∴△ABE≌△CAH（AAS）∴BE＝AH，AE＝CH，∠CAH＝∠ABE，∵AE＝CE，∴CE＝CH，∵∠ACH＝90°，∠ACB＝45°，∴∠ACB＝∠GCH，且CE＝CH，CG＝CG，∴△CEG≌△CHG（SAS）∴EG＝GH，∵BE＝AH＝AG+GH，∴AG+EG＝BE；（3）如图②，连接NG，∵∠ABC＝∠BAD＝∠DAC＝∠ACB＝45°，∴AD＝BD＝CD，∵∠BAN＝∠ACG＝45°，AB＝AC，∠ABE＝∠CAH，∴△ABN≌△CAG（ASA）∴AN＝CG，∴AD﹣AN＝CD﹣CG，∴DN＝DG，∴∠DNG＝45°∵∠NDG＝∠NFG＝90°，∴点N，点F，点G，点D四点共圆，∴∠DFG＝∠DNG＝45°．8、如图，在Rt△ABC中，AC＝BC，∠ACB＝90°，点D、E分别在AC、BC上，BD与AE交于点O，且CD＝CE，若点F是BD的中点，连接CF，交AE于点G．（1）求证：CF⊥AE；（2）如图2，过点F作FM⊥BC，交AE的延长线于点M，垂足为H，连接CM，若CG＝GM．①求证：CF＝CM；②求的值．（1）证明：如图1中，∵AC＝BC，∠ACE＝∠BCD＝90°，CE＝CD，∴△ACE≌△BCD（SAS），∴∠CAE＝∠CBD，∵DF＝FB，∴CF＝FD＝FB，∴∠FCB＝∠FBC，∴∠FCB＝∠CAE，∵∠CAB+∠AEC＝90°，∴∠AEC+∠FCB＝90°，∴∠CGE＝90°，∴CF⊥AE．（2）①证明：如图2中，∵FM⊥BC，∴∠FHC＝∠CGE＝∠MGF＝90°，∴∠ECG+∠CEG＝90°，∠ECG+∠CFH＝90°，∴∠CEG＝∠CFH，∵CG＝GM，∴△CGE≌△MGF（AAS），∴CE＝FM，EG＝GF，∵CD＝CE，∴CD＝FM，∵∠FHB＝∠ACB＝90°，∴CD∥FM，∴四边形CDFM是平行四边形，∴CM＝DF，∵CF＝DF＝FB，∴CM＝CF．②连接EF，BM．设FG＝EG＝a，∵CM＝BF，CM∥BF，∴FG∥BM，∴＝，∵△CAE≌△CBD，∴∠CAE＝∠CBD，∵∠CAB＝∠CBA，∴∠OAB＝∠OBA，∴OA＝OB，∴＝，易知OG＝GF＝EG＝a，EF＝EM＝a，∴OM＝2a+a，∴＝＝．9、（2015?新乡二模）（1）【问题发现】如图1，在Rt△ABC中，AB＝AC＝4，∠BAC＝90°，点D为AC的中点，过点A作BD的垂线，垂足为E，延长AE交BC于点F，求△ABF的面积．小明发现，过点C作AC的垂线，交AF的延长线于点G，构造出全等三角形，经过推理和计算，能够得到BF与CF的数量关系，从而使问题得到解决，请直接填空：＝　2，△ABF的面积为　．（2）【类比探究】如图2，将（1）中的条件“点D为AC的中点”改为“点D为边AC上的一点，且满足CD＝2AD”，其他条件不变，试求△ABF的面积，并写出推理过程．（3）【拓展迁移】如图3，在△ABC中，AB＝AC＝4，∠BAC＝120°，点D为AC上一点，且满足CD ＝2AD，E为BD上一点，∠AEB＝60°，延长AE交BC于F，请直接写出△ABF的面积．解：（1）如图1，过点C作AC的垂线，交AF的延长线于点G．∵∠BAC＝90°，∴∠ABD+∠ADB＝90°，∵AE⊥BD，∴∠DAE+∠ADB＝90°，∴∠CAG＝∠ABD，在△ACG和△BAD中，，∴△ACG≌△BAD（ASA），∴CG＝AD＝AC＝，∵BA∥CG，∴△CFG∽△BFA，∴＝＝，即BF＝BC，BF：CF＝2，∴△ABF的面积＝××4×4＝；故答案为2，．（2）如图2，过点C作AC的垂线，交AF的延长线于点H．∵∠BAC＝90°∴∠ABD+∠ADB＝90°，∵AE⊥BD，∴∠DAE+∠ADB＝90°，∴∠CAG＝∠ABD，在△ACG和△BAD中，，∴△ACH≌△BAD（ASA），∴CH＝AD＝AC＝AB，∵BA∥CH，∴△CFH∽△BFA，∴＝＝，即BF＝BC，∴△ABF的面积＝××4×4＝6；（3）如图3中，作CH⊥BC交AF的延长线于H，AK⊥BC于K．∵AB＝AC，∠BAC＝120°，∴∠ABC＝∠ACB＝30°，∵∠BCH＝90°，∴∠ACH＝∠BAD＝120°，∵∠ABD+∠ADB＝180°﹣120°＝60°，∠AEB＝∠EAD+∠ADE＝60°，∴∠ABD＝∠CAH，∴△BAD≌△ACH（ASA），∴CH＝AD∵AK⊥BC，∴BK＝CK，在Rt△ACK中，∵AC＝4，∠ACK＝30°，∴AK＝AC＝2，CK＝BK＝2，∵AK∥CH，AD＝CH＝，∴FK：FC＝AK：CH＝2：＝3：2，∴BF：BC＝4：5，∴S△ABF＝?S△ABC＝××4×2＝．。

2020重庆中考复习数学第26题专题训练六(含答案解析)

2020重庆中考复习数学第26题专题训练六1、如图1，在△ABC中，∠BAC＝90°，AC＝2AB，D是线段AC中点，E是线段AD上一点，过点D作DF⊥BE交BE的延长钱于点F，连接AF，过点A作AG⊥AF于点A，交BF于点G（1）若∠ABE＝∠C，BC＝2，求AE的长；（2）若点E为AD中点，求证：GE﹣FE＝FD；（3）如图2，连接BD，点N为BD中点，连接GN，若AD＝GF，请直接写出NG、GE、EA的数量关系．4、已知△ABC中，点D为BC的中点，BD＝AB，AD⊥BC．（1）如图1，求∠BAD的度数；（2）如图2，点E为BC上一点，点F为AC上一点，连接AE、BF交于点G，若∠AGF＝60°，求证：BE＝CF；（3）如图3，在（2）的条件下，点G为BF的中点，点H为AG上一点，延长BH交AC于点K，AK ＝HK，BM⊥AE交AE延长线于点M，BG＝9，HM＝10，求线段AG的长．5、已知△ABC中，∠B＝60°，点D是AB边上的动点，过点D作DE∥BC交AC于点E，将△ADE沿DE折叠，点A对应点为F点．（1）如图1，当点F恰好落在BC边上，求证：△BDF是等边三角形；（2）如图2，当点F恰好落在△ABC内，且DF的延长线恰好经过点C，CF＝EF，求∠A的大小；（3）如图3，当点F恰好落在△ABC外，DF交BC于点G，连接BF，若BF⊥AB，AB＝9，求BG 的长．6、如图，在△ABC中，AB＝AC，∠BAC＝90°，D为BC边的中点，点E在直线BC上（不与点D重合），连接AE，过点C作直线AE的垂线，垂足为点F，交直线AD于点G，连接EG．（1）如图（1），当点E在线段BD上时，易证DE＝DG，请直接写出三条线段BE，AB，EG之间的数量关系是；（2）如图（2），当点E在线段BC的延长线上时，请写出三条线段BE、AB、EG之间的数量关系，并证明你的结论；（3）若线段BC＝2，当△AEG为等腰三角形时，请直接写出的值．7、如图，在△ABC中，∠BAC＝90°，将△ABC沿AD翻折，点B恰好与点C重合，点E在AC边上，连接BE．（1）如图①，若点F是BE的中点，连接DF，且AF＝5，AE＝6，求DF的长；（2）如图②，若AF⊥BE于点F，并延长AF交BC于点G，当点E是AC的中点时，连接EG，求证：AG+EG＝BE；（3）在（2）的条件下，连接DF，请直接写出∠DFG的度数．8、如图，在Rt△ABC中，AC＝BC，∠ACB＝90°，点D、E分别在AC、BC上，BD与AE交于点O，且CD＝CE，若点F是BD的中点，连接CF，交AE于点G．（1）求证：CF⊥AE；（2）如图2，过点F作FM⊥BC，交AE的延长线于点M，垂足为H，连接CM，若CG＝GM．①求证：CF＝CM；②求的值．9、（1）【问题发现】如图1，在Rt△ABC中，AB＝AC＝4，∠BAC＝90°，点D为AC的中点，过点A作BD的垂线，垂足为E，延长AE交BC于点F，求△ABF的面积．小明发现，过点C作AC的垂线，交AF的延长线于点G，构造出全等三角形，经过推理和计算，能够得到BF与CF的数量关系，从而使问题得到解决，请直接填空：＝ 2，△ABF的面积为．（2）【类比探究】如图2，将（1）中的条件“点D为AC的中点”改为“点D为边AC上的一点，且满足CD＝2AD”，其他条件不变，试求△ABF的面积，并写出推理过程．（3）【拓展迁移】如图3，在△ABC中，AB＝AC＝4，∠BAC＝120°，点D为AC上一点，且满足CD ＝2AD，E为BD上一点，∠AEB＝60°，延长AE交BC于F，请直接写出△ABF的面积．2020重庆中考复习数学第26题专题训练六参考答案1、如图1，在△ABC中，∠BAC＝90°，AC＝2AB，D是线段AC中点，E是线段AD上一点，过点D作DF⊥BE交BE的延长钱于点F，连接AF，过点A作AG⊥AF于点A，交BF于点G（1）若∠ABE＝∠C，BC＝2，求AE的长；（2）若点E为AD中点，求证：GE﹣FE＝FD；（3）如图2，连接BD，点N为BD中点，连接GN，若AD＝GF，请直接写出NG、GE、EA的数量关系．解：（1）∵△ABC中，∠BAC＝90°，AC＝2AB，BC＝2，∴由勾股定理可得AB＝2，AC＝4，∵∠ABE＝∠C，∠BAE＝∠CAB＝90°，∴△BAE∽△CAB，∴AB2＝AE×AC，即22＝AE×4，解得AE＝1，（2）证明：如图1，过A作AH⊥BF于H，则∠AHE＝90°，∵DF⊥BE，∠BAC＝90°，∠AEB＝∠FED，∴∠ABG＝∠ADF，∵AG⊥AF，∠BAC＝90°，∴∠BAG＝∠DAF，∵AC＝2AB，D是线段AC中点，∴AB＝AD，在△ABG和△ADF中，，∴△ABG≌△ADF（ASA），∴AG＝AF，∴△AGF是等腰直角三角形，∴AH＝GF＝GH，∵点E为AD中点，∴AE＝DE，在△AEH和△DEF中，，∴△AEH≌△DEF（AAS），∴EH＝EF，AH＝DF＝GH，∵GE﹣HE＝GH，∴GE﹣FE＝FD；（3）NG、GE、EA的数量关系为：NG+GE＝2AE．理由：如图2，连接AN，NF，由（2）可得，△AGF是等腰直角三角形，∵AB＝AD，∠BAD＝90°，N是BD的中点，∴∠DAN＝45°＝∠ADN，∴△ADN是等腰直角三角形，∵AD＝GF，∴等腰Rt△AGF与等腰Rt△ADN全等，∴AG＝AF＝AN＝ND，∵Rt△BDF中，N是BD的中点，∴NF＝ND＝BN，∴AN＝NF＝AF，即△ANF是等边三角形，∴∠NAF＝∠ANF＝60°，∵∠DAN＝45°，△ABG≌△ADF，∴∠DAF＝15°＝∠BAG，∵∠ABN＝∠BAN＝45°，∴∠GAN＝30°，∵∠AGF＝45°，∴∠ABE＝30°，∴Rt△ABE中，BE＝2AE，∵∠ABN＝45°，∴∠GBN＝15°，由NF＝ND＝NB，可得∠FND＝2∠GBN＝30°，在△ANG和△NDF中，，∴△ANG≌△NDF（SAS），∴GN＝FD＝BG，∵BG+GE＝BE＝2AE，∴NG+GE＝2AE．G解：（1）由E 为CR 中点可得AG平分BAC ∠，过G 作GH AB ⊥，则有GH=CG=1，故（2）延长FD 交AG 于点M，易证:()BFD AMD AAS ∆≅∆，所以BF=AM 再证：()BFC CEA AAS∆≅∆，所以BF=CE=AM，CF=AE ∴CF-CE=AE-AM，即EM=EF ∴EFM ∆为等腰直角三角形∴2EF FM ==（3）结论为：2BD EF +=4、（2017秋•许昌月考）已知△ABC中，点D为BC的中点，BD＝AB，AD⊥BC．（1）如图1，求∠BAD的度数；（2）如图2，点E为BC上一点，点F为AC上一点，连接AE、BF交于点G，若∠AGF＝60°，求证：BE＝CF；（3）如图3，在（2）的条件下，点G为BF的中点，点H为AG上一点，延长BH交AC于点K，AK ＝HK，BM⊥AE交AE延长线于点M，BG＝9，HM＝10，求线段AG的长．解：（1）∵点D为BC的中点，AD⊥BC，∴AB＝AC，BD＝CD＝BC，∵BD＝AB，∴AB＝BC＝AC，∴△ABC是等边三角形，∴∠BAC＝60°，∵AD⊥BC，∴∠BAD＝∠BAC＝30°；（2）由（1）知，△ABC是等边三角形，∴AB＝BC，∠ABC＝∠C＝60°，∴∠ABF+∠CBF＝60°，∵∠AGF＝60°，∴∠BAE+∠ABF＝60°，∴∠BAE＝∠CBF，在△ABE和△BCF中，，∴△ABE≌△BCF（ASA），∴BE＝CF，（3）如图，过F作FN⊥AE于N，过F作FD⊥BM，交BM的延长线于D，∵AM⊥BM，∴GM∥DF，∵BG＝GF，∴BM＝DM，∵∠AGF＝60°，∴∠BGM＝60°，∵BM⊥AE，∴∠BMG＝90°，∴∠GBM＝30°，在Rt△BMG中，MG＝BG＝，BM＝DM＝FN＝，∵AK＝HK，∴∠HAK＝∠AHK＝∠BHM，∵∠ANF＝∠HMB＝90°，∴△ANF≌△HMB，∴AN＝HM＝10，Rt△FGN中，∠NFG＝∠GBM＝30°，∴GN＝GF＝，∴AG＝AN+NG＝10+＝14.5．5、（2019秋•中山市期末）已知△ABC中，∠B＝60°，点D是AB边上的动点，过点D作DE∥BC交AC于点E，将△ADE沿DE折叠，点A对应点为F点．（1）如图1，当点F恰好落在BC边上，求证：△BDF是等边三角形；（2）如图2，当点F恰好落在△ABC内，且DF的延长线恰好经过点C，CF＝EF，求∠A的大小；（3）如图3，当点F恰好落在△ABC外，DF交BC于点G，连接BF，若BF⊥AB，AB＝9，求BG 的长．（1）证明：如图1，∵∠B＝60°，DE∥BC，∴∠ADE＝∠B＝60°，∵△ADE沿DE折叠，点A对应点为F点，∴∠ADE＝∠FDE＝60°，∴∠BDF＝60°，∴∠DFB＝60°＝∠B＝∠BDF，∴△BDF是等边三角形；（2）解：∵∠B＝60°，DE∥BC，∴∠ADE＝∠B＝60°，∵△ADE沿DE折叠，点A对应点为F点，∴∠ADE＝∠FDE＝60°，∠A＝∠DFE，∴∠ADC＝120°，∵CF＝EF，∴∠FEC＝∠FCE，设∠FEC＝∠FCE＝x，则∠A＝∠DFE＝∠FEC+∠FCE＝2x，在△ADC中，∠A+∠ACD+∠ADC＝180°，即2x+x+120°＝180°，解得：x＝20°，∴∠A＝2x＝40°；（3）解：同（1）得：∠BDF＝60°，△BDG是等边三角形，∠ADE＝∠B＝60°，∴BG＝BD，由折叠的性质得：AD＝FD，∵BF⊥AB，∴∠BFD＝90°﹣60°＝30°，∴FD＝2BD，∴AD＝2BD，∵AD+BD＝AB，∴2BD+BD＝9，∴BD＝3，∴BG＝BD＝3．6、（2018•连山区一模）如图，在△ABC中，AB＝AC，∠BAC＝90°，D为BC边的中点，点E在直线BC上（不与点D重合），连接AE，过点C作直线AE的垂线，垂足为点F，交直线AD于点G，连接EG．（1）如图（1），当点E在线段BD上时，易证DE＝DG，请直接写出三条线段BE，AB，EG之间的数量关系是 AB﹣EG＝BE；（2）如图（2），当点E在线段BC的延长线上时，请写出三条线段BE、AB、EG之间的数量关系，并证明你的结论；（3）若线段BC＝2，当△AEG为等腰三角形时，请直接写出的值．解：（1）如图1中，结论：AB﹣EG＝BE理由：∵AB＝AC，∠BAC＝90°，BD＝DC，∴AD⊥BC，∠ABC＝∠ACB＝45°，AD＝BD＝DC，∴BD＝AB，∵CF⊥AE，∴∠AFG＝∠CDG＝90°，∵∠AGF＝∠CGD，∴∠F AG＝∠GCD，∵∠ADE＝∠CDG，∴△ADE≌△CDG，∴DE＝DG，∴DE＝EG，∵BE+ED＝BD，∴BE+EG＝AB，∴AB﹣EG＝BE．（2）如图2中，结论：AB+EG＝BE．理由：同法可证：△ADE≌△CDG，∴DE＝DG，∴DE＝EG，∵BE﹣ED＝BD，∴BE+﹣EG＝AB，∴AB+EG＝BE．（3）①如图2中，当GA＝GE时，DG＝DE＝2﹣2，EG＝4﹣2，此时：＝＝﹣1．②如图3中，当GA＝GE时，设BD＝AD＝CD＝a，则AB＝AC＝CE＝a，DG＝DE＝a+a，EG＝a+2a，∴＝＝1+．③当点E与点C重合时，EG＝AB，可得EG：AB＝1，综上所述，的值为﹣1或1+或1．7、（2018•站前区校级一模）如图，在△ABC中，∠BAC＝90°，将△ABC沿AD翻折，点B恰好与点C重合，点E在AC边上，连接BE．（1）如图①，若点F是BE的中点，连接DF，且AF＝5，AE＝6，求DF的长；（2）如图②，若AF⊥BE于点F，并延长AF交BC于点G，当点E是AC的中点时，连接EG，求证：AG+EG＝BE；（3）在（2）的条件下，连接DF，请直接写出∠DFG的度数．解：（1）∵将△ABC沿AD翻折，点B恰好与点C重合，∴AB＝AC，BD＝CD，∠ADB＝∠ADC＝90°，且∠BAC＝90°，∴△ABC是等腰直角三角形，∵点F是BE的中点，AF＝5，∠BAC＝90°，∴BE＝10，∴AB＝＝＝8，∴AC＝8，∴EC＝2，∵BD＝CD，BF＝EF，∴DF＝EC＝1，（2）如图②，过点C作CH⊥AC交AG的延长线于点H，∵AB＝AC，∠BAC＝90°，BD＝CD，∴∠ABC＝∠BAD＝∠DAC＝∠ACB＝45°，∵∠BEA+∠CAH＝90°，∠CAH+∠H＝90°，∴∠H＝∠BEA，且AB＝AC，∠AFB＝∠ACH＝90°，∴△ABE≌△CAH（AAS）∴BE＝AH，AE＝CH，∠CAH＝∠ABE，∵AE＝CE，∴CE＝CH，∵∠ACH＝90°，∠ACB＝45°，∴∠ACB＝∠GCH，且CE＝CH，CG＝CG，∴△CEG≌△CHG（SAS）∴EG＝GH，∵BE＝AH＝AG+GH，∴AG+EG＝BE；（3）如图②，连接NG，∵∠ABC＝∠BAD＝∠DAC＝∠ACB＝45°，∴AD＝BD＝CD，∵∠BAN＝∠ACG＝45°，AB＝AC，∠ABE＝∠CAH，∴△ABN≌△CAG（ASA）∴AN＝CG，∴AD﹣AN＝CD﹣CG，∴DN＝DG，∴∠DNG＝45°∵∠NDG＝∠NFG＝90°，∴点N，点F，点G，点D四点共圆，∴∠DFG＝∠DNG＝45°．8、如图，在Rt△ABC中，AC＝BC，∠ACB＝90°，点D、E分别在AC、BC上，BD与AE交于点O，且CD＝CE，若点F是BD的中点，连接CF，交AE于点G．（1）求证：CF⊥AE；（2）如图2，过点F作FM⊥BC，交AE的延长线于点M，垂足为H，连接CM，若CG＝GM．①求证：CF＝CM；②求的值．（1）证明：如图1中，∵AC＝BC，∠ACE＝∠BCD＝90°，CE＝CD，∴△ACE≌△BCD（SAS），∴∠CAE＝∠CBD，∵DF＝FB，∴CF＝FD＝FB，∴∠FCB＝∠FBC，∴∠FCB＝∠CAE，∵∠CAB+∠AEC＝90°，∴∠AEC+∠FCB＝90°，∴∠CGE＝90°，∴CF⊥AE．（2）①证明：如图2中，∵FM⊥BC，∴∠FHC＝∠CGE＝∠MGF＝90°，∴∠ECG+∠CEG＝90°，∠ECG+∠CFH＝90°， ∴∠CEG＝∠CFH，∵CG＝GM，∴△CGE≌△MGF（AAS），∴CE＝FM，EG＝GF，∵CD＝CE，∴CD＝FM，∵∠FHB＝∠ACB＝90°，∴CD∥FM，∴四边形CDFM是平行四边形，∴CM＝DF，∵CF＝DF＝FB，∴CM＝CF．②连接EF，BM．设FG＝EG＝a，∵CM＝BF，CM∥BF，∴FG∥BM，∴＝，∵△CAE≌△CBD，∴∠CAE＝∠CBD，∵∠CAB＝∠CBA，∴∠OAB＝∠OBA，∴OA＝OB，∴＝，易知OG＝GF＝EG＝a，EF＝EM＝a，∴OM＝2a+a，∴＝＝．9、（2015•新乡二模）（1）【问题发现】如图1，在Rt△ABC中，AB＝AC＝4，∠BAC＝90°，点D为AC的中点，过点A作BD的垂线，垂足为E，延长AE交BC于点F，求△ABF的面积．小明发现，过点C作AC的垂线，交AF的延长线于点G，构造出全等三角形，经过推理和计算，能够得到BF与CF的数量关系，从而使问题得到解决，请直接填空：＝ 2，△ABF的面积为．（2）【类比探究】如图2，将（1）中的条件“点D为AC的中点”改为“点D为边AC上的一点，且满足CD＝2AD”，其他条件不变，试求△ABF的面积，并写出推理过程．（3）【拓展迁移】如图3，在△ABC中，AB＝AC＝4，∠BAC＝120°，点D为AC上一点，且满足CD ＝2AD，E为BD上一点，∠AEB＝60°，延长AE交BC于F，请直接写出△ABF的面积．解：（1）如图1，过点C作AC的垂线，交AF的延长线于点G．∵∠BAC＝90°，∴∠ABD+∠ADB＝90°，∵AE⊥BD，∴∠DAE+∠ADB＝90°，∴∠CAG＝∠ABD，在△ACG和△BAD中，，∴△ACG≌△BAD（ASA），∴CG＝AD＝AC＝，∵BA∥CG，∴△CFG∽△BF A，∴＝＝，即BF＝BC，BF：CF＝2，∴△ABF的面积＝××4×4＝；故答案为2，．（2）如图2，过点C作AC的垂线，交AF的延长线于点H．∵∠BAC＝90°∴∠ABD+∠ADB＝90°，∵AE⊥BD，∴∠DAE+∠ADB＝90°，∴∠CAG＝∠ABD，在△ACG和△BAD中，，∴△ACH≌△BAD（ASA），∴CH＝AD＝AC＝AB，∵BA∥CH，∴△CFH∽△BF A，∴＝＝，即BF＝BC，∴△ABF的面积＝××4×4＝6；（3）如图3中，作CH⊥BC交AF的延长线于H，AK⊥BC于K．∵AB＝AC，∠BAC＝120°，∴∠ABC＝∠ACB＝30°，∵∠BCH＝90°，∴∠ACH＝∠BAD＝120°，∵∠ABD+∠ADB＝180°﹣120°＝60°，∠AEB＝∠EAD+∠ADE＝60°， ∴∠ABD＝∠CAH，∴△BAD≌△ACH（ASA），∴CH＝AD∵AK⊥BC，∴BK＝CK，在Rt△ACK中，∵AC＝4，∠ACK＝30°，∴AK＝AC＝2，CK＝BK＝2，∵AK∥CH，AD＝CH＝，∴FK：FC＝AK：CH＝2：＝3：2，∴BF：BC＝4：5，∴S△ABF＝•S△ABC＝××4×2＝．。

中考数学复习专题训练精选试题及答案

中考数学复习专题训练精选试题及答案一、选择题1. 以下哪一个数是最小的无理数？A. √2B. πC. 3.14D. √9答案：A2. 若一个等差数列的首项是2，公差是3，则第8项是多少？A. 17B. 18C. 19D. 20答案：A3. 一个二次函数的图像开口向上，顶点坐标为（3，-4），则该二次函数的一般式为：A. y = x² + 6x - 13B. y = x² - 6x + 13C. y = -x² + 6x - 13D. y = -x² - 6x + 13答案：B4. 在三角形ABC中，a = 5，b = 7，C = 60°，则边c 的长度等于：A. 6B. 8C. 10D. 12答案：C二、填空题1. 已知a = 3，b = 4，则a² + b² = _______。

答案：252. 已知一个等差数列的前5项和为35，首项为7，求公差d = _______。

答案：23. 在梯形ABCD中，AB // CD，AB = 6，CD = 8，AD = BC = 5，求梯形的高h = _______。

答案：34. 若函数f(x) = x² - 2x + 1的最小值为m，求m =_______。

答案：0三、解答题1. 已知一元二次方程x² - 4x - 12 = 0，求解该方程。

解：首先，将方程因式分解为(x - 6)(x + 2) = 0。

然后，解得x = 6或x = -2。

答案：x = 6或x = -22. 已知一个长方体的长为a，宽为b，高为c，且a、b、c成等差数列。

若长方体的体积为V，求V的表达式。

解：由题意可知，a + c = 2b，所以c = 2b - a。

长方体的体积V = abc = ab(2b - a)。

答案：V = ab(2b - a)3. 已知三角形ABC，AB = AC，∠BAC = 40°，BC = 6，求三角形ABC的周长。

重庆中考第26题专题专训(教师版)

重庆中考数学第26题专题专训1．如图1，在平面直角坐标系中，抛物线y=﹣x2﹣x﹣2与x轴交于A，B两点（点A 在点B的左侧），交y轴于点C．（1）求直线AC的解析式；（2）点P是直线AC上方抛物线上的一动点，过点P作PD⊥AC，垂足为D，当线段PD的长度最大时，点Q从点P出发，先以每秒1个单位的速度沿适当的路径运动到y轴上的点M处，再沿MC以每秒3个单位的速度运动到点C停止，当点Q在整个运动中所用时间t最少时，求点M的坐标；（3）如图2，将△BOC沿直线BC平移，平移后B，O，C三点的对应点分别是B′，O′，C′，点S是坐标平面内一点，若以A，C，O′，S为顶点的四边形是菱形，请直接写出所有符合条件的点S的坐标．解：（1）当y=0时，﹣x2﹣x﹣2=0，解这个方程，得：x1=﹣6，x2=﹣1，∴点A（﹣6，0），B（﹣1，0），当x=0时，y=﹣2，∴C（0，﹣2），设直线AC的解析式为：y=ax+b（a≠0），将点A（﹣6，0），C（0，﹣2）代入得：，∴，∴直线AC的解析式为：y=﹣x﹣2；（3分）（2）如图1，过点P作PE∥y轴交直线AC于点E，设P（a，﹣），则点E（a，﹣﹣2），∴PE=（﹣）﹣（﹣﹣2）=﹣﹣2a，∵AO=6，OC=2，∴AC===2，∵∠PDE=∠AOC=90°，∠PED=∠ACO，∴△PDE∽△AOC，∴=，∴PD=PE==﹣﹣，对称轴是：a=﹣3，∵﹣，∴当a=﹣3时，PD的长度最大，此时点P的坐标为（﹣3，2），如图1所示，在x轴上取点F（1，0），连接CF并延长，∴CF===3，∴sin∠OCF==，点M是y轴上一点，过点M作MH⊥CF于点H，由△CHM∽△COF，可知：=，∵t==PM+MH，如图2，当P、M、H在同一直线上时，t的值最小，此时，过P作PK⊥y轴于K，由△PKM∽△COF，可知：=2，∴KM=，∴M（0，），（7分）（3）如图3，当四边形ACSO'是菱形时，过S作SG⊥y轴于G，延长O'C'交x轴于H，∵四边形ACSO'是菱形，∴AO'=AC=SC，AO'∥SC，∴∠AMC=∠BCS，∴∠AO'H+∠MC'O'=∠BCO+∠OCS，∵∠MC'O'=∠BCO，∴∠AO'H=∠OCS，∵∠AHO'=∠CGS，∴△O'AH≌△CSG，∴AH=SG，O'H=CG，Rt△OCB中，sin∠OCB==，∴sin∠BC'H==，设BH=x，则BC'=3x，∴C'H=2x，∴AH=SG=5﹣x，∵O'C'=OC=2，∴C'H=OG=2x，由勾股定理得：AC2=O'A2，∴AO2+OC2=O'H2+AH2，∴=（5﹣x）2+（2+2x）2，解得：x=，当x=时，SG=5﹣x=，OG=2x=，当x=＜0时，不符合题意，舍去，SG=5﹣x=，OG=2x=，此时S的坐标为：或；②如图4，过S作SH⊥AO于H，延长O'B'到y轴交于G，∵SE∥CF，EC∥SF，∴四边形SECF是平行四边形，∴∠ESF=∠ECF，∵四边形ASO'C是菱形，∴∠ASO'=∠ACO'，∴∠ASH=∠O'CG，同理得：△ASH≌△O'CG，∴AH=O'G，SH=CG，sin∠GCB'==，设GB'=x，则CB'=3x，CG=2x，∴O'G=1+x，由勾股定理得：AC2=O'C2，∴62+（2）2=（2x）2+（x+1）2解得：x=，当x=时，SH=CG=2x=，OH=6﹣AH=6﹣O'G=5﹣x=，当x=＜0时，不符合题意，舍去，此时，点S的坐标为：（，）；③如图5，AC为对角线时，同理可得S（，）④如图6，过S作SE⊥x轴于E，延长B'O'交y轴于H，延长O'C'交x轴于G，设GB'=x，则CB'=3x，CG=2x，∴O'G=O'H=1+x，∵∠HO'D=∠O'DA=∠EAS，易得△SEA≌△CHO'，同理可得S（，）；⑤如图7，过S作SH⊥x轴于H，过O'作O'E⊥SH于E，延长C'O'交x轴于G，设OG=x，则BG=1+x，∵O'B'∥BG，∴，∴，∴C'G=2（1+x），∴O'G=C'G﹣C'O'=2x，∴AG=1+x，同理得：62+（2）2=（1+x）2+（2x）2，解得：x1=，x2=（舍），可得S；综上所述，S的坐标为：或或（，）或（，）或（，）．（12分）2．在平面直角坐标系中，已知抛物线322+--=x x y 的图象交x 轴于A 、B 两点（点A 在点B 左侧），交y 轴于点C ．（1）求直线AC 的解析式；（2）抛物线的对称轴交直线AC 于点E ，直线AC 上方的抛物线上有一动点P ，当△PEC 面积最大时，线段CE 在直线AC 上平移，记线段CE 平移后为E C ''，求E C P ''∆的周长最小值；（3）抛物线的顶点为D ，连接AD ，将线段AD 沿直线AC 平移，记线段AD 平移后为D A ''，过点D '作x 轴的垂线交x 轴于点G ，当G D A ''∆ 为等腰三角形时，求A A '的长度．解：（1）抛物线y=﹣x 2﹣2x+3，∴A （﹣3，0），B （1，0），C （0，3），∴直线AC 的解析式 y=x+3；（2）∵对称轴为x=﹣1，∴E （﹣1，2），设P （m ，﹣m 2﹣2m+3）， ∴S △PEC =﹣m 2﹣m=﹣（m+）2+，∴当m=﹣时，S △PEC 的有最大值，即：P（﹣，），将线段PC平移，使得C与E重合，得到线段P'E，∴P'（﹣，），P''（﹣，），∴△PC'E'的周长的最小值为PP''+CE=+（3）∵抛物线y=﹣x2﹣2x+3，∴D（﹣1，4），设A'（﹣3+n，n），D'（﹣1+n，4+n），则G（﹣1+n，0），∴AA'=|n|，∴A'D'2=20，A'G2=n2+4，D'G2=n2+8n+16，∵△A′D′G为等腰三角形，①当A'D'=A'G时，∴20=n2+4，∴n=±4，∴AA'=4②当A'D'=D'G时，∴20=n2+8n+16，∴n=±2﹣4，∴AA'=2±4③当D'G=A'G时，∴n2+4=n2+8n+16，∴n=﹣，∴AA'=，即：AA′的长度为4或2或．3.如图，在平面直角坐标系中，抛物线y=﹣x2+x+3与x轴交于A，B两点（点A在点B左侧），与y轴交于点C，连接BC，过点A作AD∥BC交y轴于点D．（1）求平行线AD、BC之间的距离；（2）如图1，点P为线段BC上方抛物线上的一动点，当△PCB的面积最大时，Q从点P出发，先沿适当的路径运动到直线BC上点M处，再沿垂直于直线BC的方向运动到直线AD上的点N处，最后沿适当的路径运动到点B处停止．当点Q的运动路径最短时，求点M的坐标及点Q经过的最短路径的长；（3）如图2，将抛物线以每秒个单位长度的速度沿射线AD方向平移，抛物线上的点A、C平移后的对应点分别记作A′、C′，当△A′C′B是以C′B为底边的等腰三角形时，将等腰△A′C′B 绕点D逆时针旋转一周，记旋转中的△A′C′B为△A″C″B′，若直线A″C″与y轴交于点K，直线A″C″与直线AD交于点I，当△DKI是以KI为底边的等腰三角形时，求出DK2的值．解：（1）如图1中，作AH⊥BC于H．对于抛物线y=﹣x2+x+3，令y=0，得到﹣x2+x+3=0，解得x=﹣或3，∴A（﹣，0），B（3，0），令x=0，得到y=3，∴C（0，3），∴OA=，OB=3，AB=4，OC=3，BC==3，=•AB•CO=•BC•AH，∵S△ABC∴AH==，∵AD∥BC，∴AD与BC之间的距离为．（2）如图2中，设P（m，﹣m2+m+3），S△PBC =S△POB+S△PCO﹣S△BOC=×3×（﹣m2+m+3）+×3×m﹣×3×3=﹣（m﹣）2+，∵﹣＜0，∴m=时，△PBC的面积最大，此时P（，），作B关于直线AD的对称点B′交AD于K，连接PK交BC于M，作MN⊥AD于N，连接BN，则PM+MN+BN 的值最小．∵直线BC的解析式为y=﹣x+3，AD∥BC，∴直线AD的解析式为y=﹣x﹣1，∵BB′⊥BC，∴直线BB′的解析式为y=x﹣6，由，解得，∴K（，﹣），∴直线PK的解析式为y=﹣x+，由，解得，∴M（，），∴点Q经过的最短路径的长=PM+MN+BN=MN+（PM+MK）=MN+PK，∵MN=，PK==，∴点Q经过的最短路径的长为+．4. 抛物线y=﹣x2﹣x+与x轴交于点A，B（点A在点B的左边），与y轴交于点C，点D 是该抛物线的顶点．（1）如图1，连接CD，求线段CD的长；（2）如图2，点P是直线AC上方抛物线上一点，PF⊥x轴于点F，PF与线段AC交于点E；将线段OB沿x轴左右平移，线段OB的对应线段是O1B1，当PE+EC的值最大时，求四边形PO1B1C周长的最小值，并求出对应的点O1的坐标；（3）如图3，点H是线段AB的中点，连接CH，将△OBC沿直线CH翻折至△O2B2C的位置，再将△O 2B2C绕点B2旋转一周，在旋转过程中，点O2，C的对应点分别是点O3，C1，直线O3C1分别与直线AC，x轴交于点M，N．那么，在△O2B2C的整个旋转过程中，是否存在恰当的位置，使△AMN是以MN为腰的等腰三角形？若存在，请直接写出所有符合条件的线段O2M的长；若不存在，请说明理由．解：（1）如图1，过点D作DK⊥y轴于K，当x=0时，y=，∴C（0，），y=﹣x2﹣x+=﹣（x+）2+，∴D（﹣，），∴DK=，CK=﹣=，∴CD===；（4分）（2）在y=﹣x2﹣x+中，令y=0，则﹣x2﹣x+=0，解得：x1=﹣3，x2=，∴A（﹣3，0），B（，0），∵C（0，），易得直线AC的解析式为：y=，设E（x，），P（x，﹣x2﹣x+），∴PF=﹣x2﹣x+，EF=，Rt△ACO中，AO=3，OC=，∴AC=2，∴∠CAO=30°，∴AE=2EF=，∴PE+EC=（﹣x2﹣x+）﹣（x+）+（AC﹣AE），=﹣﹣x+[2﹣（）]，=﹣﹣x﹣x，=﹣（x+2）2+，（5分）∴当PE+EC的值最大时，x=﹣2，此时P（﹣2，），（6分）∴PC=2，∵O1B1=OB=，∴要使四边形PO1B1C周长的最小，即PO1+B1C的值最小，如图2，将点P向右平移个单位长度得点P1（﹣，），连接P1B1，则PO1=P1B1，再作点P1关于x轴的对称点P2（﹣，﹣），则P1B1=P2B1，∴PO1+B1C=P2B1+B1C，∴连接P2C与x轴的交点即为使PO1+B1C的值最小时的点B1，∴B1（﹣，0），将B1向左平移个单位长度即得点O1，此时PO1+B1C=P2C==，对应的点O1的坐标为（﹣，0），（7分）∴四边形PO1B1C周长的最小值为+3；（8分）（3）O2M的长度为或或2+或2．（12分）理由是：如图3，∵H是AB的中点，∴OH=，∵OC=，∴CH=BC=2，∴∠HCO=∠BCO=30°，∵∠ACO=60°，∴将CO沿CH对折后落在直线AC上，即O2在AC上，∴∠B2CA=∠CAB=30°，∴B2C∥AB，∴B2（﹣2，），①如图4，AN=MN，∴∠MAN=∠AMN=30°=∠O2B2O3，由旋转得：∠CB2C1=∠O2B2O3=30°，B2C=B2C1，∴∠B2CC1=∠B2C1C=75°，过C1作C1E⊥B2C于E，∵B2C=B2C1=2，∴=B2O2，B2E=，∵∠O2MB2=∠B2MO3=75°=∠B2CC1，∠B2O2M=∠C1EC=90°，∴△C1EC≌△B2O2M，∴O2M=CE=B2C﹣B2E=2﹣；②如图5，AM=MN，此时M与C重合，O2M=O2C=，③如图6，AM=MN，∵B2C=B2C1=2=B2H，即N和H、C1重合，∴∠CAO=∠AHM=∠MHO2=30°，∴O2M=AO2=；④如图7，AN=MN，过C1作C1E⊥AC于E，∴∠NMA=∠NAM=30°，∵∠O3C1B2=30°=∠O3MA，∴C1B2∥AC，∴∠C1B2O2=∠AO2B2=90°，∵∠C1EC=90°，∴四边形C 1EO 2B 2是矩形， ∴EO 2=C 1B 2=2，，∴EM=，∴O 2M=EO 2+EM=2+，综上所述，O 2M 的长是或或2+或2．5. 如图，在平面直角坐标系中，点A 在抛物线y=﹣x 2+4x 上，且横坐标为1，点B 与点A 关于抛物线的对称轴对称，直线AB 与y 轴交于点C ，点D 为抛物线的顶点，点E 的坐标为（1，1）．（1）求线段AB 的长；（2）点P 为线段AB 上方抛物线上的任意一点，过点P 作AB 的垂线交AB 于点H ，点F 为y 轴上一点，当△PBE 的面积最大时，求PH+HF+FO 的最小值；（3）在（2）中，PH+HF+FO 取得最小值时，将△CFH 绕点C 顺时针旋转60°后得到△CF′H′，过点F'作CF′的垂线与直线AB 交于点Q ，点R 为抛物线对称轴上的一点，在平面直角坐标系中是否存在点S ，使以点D ，Q ，R ，S 为顶点的四边形为菱形，若存在，请直接写出点S 的坐标，若不存在，请说明理由．解：（1）由题意A （1，3），B （3，3）， ∴AB=2．（2）如图1中，设P （m ，﹣m 2+4m ），作PN ∥y 轴J 交BE 于N ． ∵直线BE 的解析式为y=x ， ∴N （m ，m ），∴S△PEB=×2×（﹣m2+3m）=﹣m2+3m，∴当m=时，△PEB的面积最大，此时P（，），H（，3），∴PH=﹣3=，作直线OG交AB于G，使得∠COG=30°，作HK⊥OG于K交OC于F，∵FK=OF，∴PH+HF+FO=PH+FH+FK=PH+HK，此时PH+HF+OF的值最小，∵•HG•OC=•OG•HK，∴HK==+，∴PH+HF+OF的最小值为+．（3）如图2中，由题意CH=，CF=，QF=，CQ=1，∴Q（﹣1，3），D（2，4），DQ=，①当DQ为菱形的边时，S1（﹣1，3﹣），S2（﹣1，3+），②当DQ为对角线时，可得S3（﹣1，8），③当DR为对角线时，可得S4（5，3）综上所述，满足条件的点S坐标为（﹣1，3﹣）或（﹣1，3+）或（﹣1，8）或（5，3）．6．如图1，在平面直角坐标系中，抛物线y=与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，抛物线的顶点为点D，过点B作BC的垂线，交对称轴于点E．（1）求证：点E与点D关于x轴对称；（2）点P为第四象限内的抛物线上的一动点，当△PAE的面积最大时，在对称轴上找一点M，在y轴上找一点N，使得OM+MN+NP最小，求此时点M的坐标及OM+MN+NP的最小值；（3）如图2，平移抛物线，使抛物线的顶点D在射线AD上移动，点D平移后的对应点为D′，点A的对应点A′，设抛物线的对称轴与x轴交于点F，将△FBC沿BC翻折，使点F落在点F′处，在平面内找一点G，若以F′、G、D′、A′为顶点的四边形为菱形，求平移的距离．（1）证明：如图1中，令y=0，得到x2﹣x﹣3=0，解得x=﹣或3，∴A（﹣，0），B（3，0），令x=0，可得y=﹣3，∴C（0，﹣3），∵y=x2﹣x﹣3=（x﹣）2﹣4，∴顶点D（，﹣4），设对称轴与x轴交于F，则BF=2，∵△EFB∽△BOC，∴=，∴=，∴EF=4，∴E（，4），∴E、D关于x轴对称．（2）过点P作PQ∥y轴，交直线AE于点Q．=x+2，∵yAE∴设P（a，a2﹣a﹣3），Q（a，a+2），（0＜a＜3），7．如图1，在平面直角坐标系中，抛物线2y x x=--与x轴交于A、B两点(点A在点B 的左侧)，与y轴交于点C．(1)求直线AC的解析式；(2)如图2，点E(a，b)是对称轴右侧抛物线上一点，过点E垂直于y轴的直线与AC交于点D(m，n)．点P是x轴上的一点，点Q是该抛物线对称轴上的一点，当a m+最大时，求点E的坐标，并直接写出23EQ PQ PB++的最小值；(3)如图3，在(2)的条件下，连结OD，将△AOD沿x轴翻折得到△AOM，再将△AOM沿射线CB 的方向以每秒3个单位的速度沿平移，记平移后的△AOM为△A O M'''，同时抛物线以每秒1个单位的速度沿x轴正方向平移，点B的对应点为B'．△A B M'''能否为等腰三角形？若能，请求出所有符合条件的点M'的坐标；若不能，请说明理由．8．如图1，在平面直角坐标系中，抛物线423412++-=x x y 与x 轴交于A 、B 两点（点A 在点B左侧），与y 轴交于点C ．（1）求抛物线的对称轴及△ABC 的周长；（2）点D 是线段AC 的中点，过点D 作BC 的平行线，分别与x 轴、抛物线交于点E 、F ，点P为直线BC 上方抛物线上的一动点，连接PD 交线段BC 于点G ，当四边形PGEF 面积最大时，点Q 从点P 出发沿适当的路径运动到x 轴上的点M 处，再沿射线DF 方向运动5个单位到点N 处，最后回到直线BC 上的点H 处停止，当点Q 的运动路径最短时，求点Q 的最短运动路径长及点H 的坐标；（3）如图2，将△AOC 绕点O 顺时针旋转至△A 1OC 1的位置，点A 、C 的对应点分别为点A 1、C 1，且点A 1落在线段AC 上，再将△A 1OC 1沿y 轴平移得△A 2O 1C 2，其中直线O 1C 2与x 轴交于点K ，点T 是抛物线对称轴上的动点，连接KT 、O 1T ，△O 1KT 能否成为以O 1K 为直角边的等腰直角三角形?若能，请直接写出所有符合条件的点T 的坐标；若不能，请说明理由．9.如图,在平面直角坐标系中,抛物线y=-x2-3x+4交x轴于A、D两点(点A在点B的左例), 交y轴于点C,顶点为点D,连接BC,作直线AC.(1)求点D 的坐标和直线BC 的解析式；(2)若点P 为BC 上方抛物线上的一个动点,连接PC 、PB,过P 作PE ⊥y 轴于点E,当△PBC 面积最大时,将△PEC 绕平面内一点逆时针方向旋转90°后得到△111C E P .点P 、E 、C 的对应点分别是点1P 、1E 、1C ,当点C 1C 落在线段AC 上时,连接PP 1,求A C C P PP 111122++的最小值，并求出此时点1C 的坐标；(3)在(2)的条件下,将△111C E P 沿射线AC 以每秒2个单位长度的速度平移,记平移后的△111C E P 为△222C E P 点1P 、1E 、1C 的对应点分别是点2P、2E ,C 2,设平移时间为秒,当△CD P 2为等腰三角形时,求t 的值.10.如图，在平面直角坐标系中，抛物线)0≠(++=2a c bx ax y 交x 轴于A 、B 两点，交y 轴于点C ， AO=CO=4，BO=6，点D 是第四象限抛物线上一点，且点F 的纵坐标为-4.(1)求抛物线的解析式和直线CF 的解析式；(2)如图1，点P 是直线CF 上方抛物线上一点，点E 在直线CF 上，点E 的横坐标为3，当△PCF 的面积最大时,在y 轴有一动点M ，在x 轴有一动点N ，当PM+MN+NE 的值最小时，求出PM+MN+NE 的最小值.(3)如图2，点D 为线段BO 的中点，连接CD ，将CDO ∆绕着点D 顺时针旋转α度得到对应''C DO ∆ ()0180α︒<<︒.设直线'C D 和直线''C O 分别与直线BC 交于H 、G 两点,当三角形C ′HG 是等腰三角形时，直接写出腰的长度.11.如图1，在平面直角坐标系中，抛物线c bx x y ++-=2的图像与x 轴交于点A 和点B （5,0），与y 轴交于点C ，点D （1,8）是抛物线上一点.（1）求抛物线和直线AD 的解析式；（2）点Q 是抛物线一象限内一动点，过点Q 作QN ∥AD 交BC 于N ，QG ⊥AB 交BC 与点M ，交AB 于点G （如图1），当QNM ∆的周长最大时，求QNM ∆周长的最大值；此时，在直线BC 上有两动点P 、H ，且PH=22（P 在H 的右边），K （2,0），当HK PQ -最大时求点P 的坐标（3）直线AD 与y 轴交于点F ，点E 是点C 关于对称轴的对称点，点P 是线段AE 上的一动点，将AFP ∆沿着FP 所在的直线翻折得到FP A '∆（点A 的对应点为点A '）（如图2），当FP A '∆与AED ∆重叠部分为直角三角形时，求AP 的长.(第26题1) (第26题2) (第26题备用图)12．如图1,在平面直角坐标系中,抛物线()032≠-+=a bx ax y 过点()0,2-A 和点()0,23B ，且与y 轴交于点C ，抛物线的顶点为点D ，过点B 作BC 的垂线，交对称轴于点E.(1)求抛物线的解析式和点D 的坐标；(2)点P 为第四象限内的抛物线上的一动点，当△PAE 的面积最大时，在x 轴上找一点M ，使△MPC 周长最小，求此时点M 的坐标；(3)如图2,将线段AD 在射线AD 上移动,点D 平移后的对应点为D ′,点A 的对应点为A ′,设抛物线的对称轴与x 轴交于点F ,若以F 、D ′、A ′为顶点的三角形为等腰三角形，求平移的距离。

2020重庆中考复习数学第26题专题训练五(含答案解析)

2020重庆中考复习数学第26题专题训练五1、如图，在△ABC中，∠ACB＝90°，AC＝BC，E为AC边的一点，F为AB边上一点，连接CF，交BE于点D且∠ACF＝∠CBE，CG平分∠ACB交BD于点G，（1）求证：CF＝BG；（2）延长CG交AB于H，连接AG，过点C作CP∥AG交BE的延长线于点P，求证：PB＝CP+CF；（3）在（2）问的条件下，当∠GAC＝2∠FCH时，若S△AEG＝3，BG＝6，求AC的长．2、[问题背景]如图1所示，在△ABC中，AB＝BC，∠ABC＝90°，点D为直线BC上的一个动点（不与B、C重合），连结AD，将线段AD绕点D按顺时针方向旋转90°，使点A旋转到点E，连结EC．[问题初探]如果点D在线段BC上运动，通过观察、交流，小明形成了以下的解题思路：过点E作EF⊥BC 交直线BC于F，如图2所示，通过证明△DEF≌△，可推证△CEF是三角形，从而求得∠DCE＝．[继续探究]如果点D在线段CB的延长线上运动，如图3所示，求出∠DCE的度数．[拓展延伸]连接BE，当点D在直线BC上运动时，若AB＝，请直接写出BE的最小值．3、（2019秋•锦江区校级期末）在Rt△ABC中，∠ACB＝90°，∠A＝30°，BD是△ABC的角平分线．（1）如图1，求证：AD＝2DC．（2）如图2，作∠CBD的角平分线交线段CD于点M，若CM＝1，求△DBM的面积；（3）如图3，过点D作DE⊥AB于点E，点N是线段AC上一点（不与C、D重合），以BN为一边，在BN的下方作∠BNG＝60°，NG交DE延长线于点G，试探究线段ND，DG与AD之间的数量关系，并说明理由．4、（2019•镇平县三模）如图1，已知直角三角形ABC，∠ACB＝90°，∠BAC＝30°，点D是AC边上一点，过D作DE⊥AB于点E，连接BD，点F是BD中点，连接EF，CF．（1）发现问题：线段EF，CF之间的数量关系为；∠EFC的度数为；（2）拓展与探究：若将△AED绕点A按顺时针方向旋转α角（0°＜α＜30°），如图2所示，（1）中的结论还成立吗？请说明理由；（3）拓展与运用：如图3所示，若△AED绕点A旋转的过程中，当点D落到AB边上时，AB边上另有一点G，AD＝DG＝GB，BC＝3，连接EG，请直接写出EG的长度．5、（2017春•西城区校级期末）如图1，在等腰△ABC中，AB＝AC，∠BAC＝a，点P是线段AB的中点，点E是线段CB延长线上一点，且PE＝PC，将线段PC绕点P顺时针旋转α得到PD，连接BD．（1）如图2，若α＝60°，其他条件不变，先补全图形，然后探究线段BD和BC之间的数量关系，并说明理由．（2）如图3，若α＝90°，其他条件不变，探究线段BP、BD和BC之间的等量关系，并说明理由．6、【发现问题】如图1，已知△ABC，以点A为直角顶点、AB为腰向△ABC外作等腰直角△ABE．请你以A为直角顶点、AC为腰，向△ABC外作等腰直角△ACD（不写作法，保留作图痕迹）．连接BD、CE．那么BD与CE的数量关系是BD＝CE．【拓展探究】如图2，已知△ABC，以AB、AC为边向外作正方形AEFB和正方形ACGD，连接BD、CE，试判断BD与CE之间的数量关系，并说明理由．【解决问题】如图3，有一个四边形场地ABCD，∠ADC＝60°，BC＝15，AB＝8，AD＝CD，求BD的最大值．7、（1）如图1，点C为线段AB外一个动点，已知AB＝a，AC＝b．当点C位于BA的延长线上时，线段BC取得最大值，则最大值为（用含a，b的式子表示）；（2）如图2，点C为线段AB外一个动点，若AB＝10，AC＝3，分别以AC，BC为边，作等边三角形ACD和等边三角形BCE，连接AE，DB．①求证：AE＝DB；②请直接写出线段AE的最大值；（3）如图3，AB＝6，点M为线段AB外一个动点，且AM＝2，MB＝MN，∠BMN＝90°，请直接写出线段AN的最大值．8、【初步探索】（1）如图1：在四边形ABC中，AB＝AD，∠B＝∠ADC＝90°，E、F分别是BC、CD上的点，且EF ＝BE+FD，探究图中∠BAE、∠F AD、∠EAF之间的数量关系．小王同学探究此问题的方法是：延长FD到点G，使DG＝BE．连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是；【灵活运用】（2）如图2，若在四边形ABCD中，AB＝AD，∠B+∠D＝180°．E、F分别是BC、CD上的点，且EF＝BE+FD，上述结论是否仍然成立，并说明理由；【拓展延伸】（3）如图3，已知在四边形ABCD中，∠ABC+∠ADC＝180°AB＝AD，若点E在CB的延长线上，点F在CD的延长线上，如图3所示，仍然满足EF＝BE+FD，请写出∠EAF与∠DAB的数量关系，并给出证明过程．9、（2018•大东区一模）如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，点O为AB中点，点P为直线BC上的动点（不与点B、点C重合），连接OC、OP，将线段OP绕点P逆时针旋转60°，得到线段PQ，连接BQ．（1）如图1，当点P在线段BC上时，请直接写出线段BQ与CP的数量关系．（2）如图2，当点P在CB延长线上时，（1）中结论是否成立？若成立，请加以证明；若不成立，请说明理由；（3）如图3，当点P在BC延长线上时，若∠BPO＝45°，AC＝，请直接写出BQ的长．10、模型发现：同学们知道，三角形的两边之和大于第三边，即如图1，在△ABC中，AB+AC＞BC．对于图1，若把点C看作是线段AB外一动点，且AB＝c，AC＝b，则线段BC的长会因为点C的位置的不同而发生变化．因为AB、AC的长度固定，所以当∠BAC越大时，BC边越长．特别的，当点C位于时，线段BC的长取得最大值，且最大值为（用含b，c的式子表示）（直接填空）.模型应用：点C为线段AB外一动点，且AB＝3，AC＝2，如图2所示，分别以AC，BC为边，作等边三角形ACD 和等边三角形BCE，连接BD，AE．（1）求证：BD＝AE．（2）线段AE长的最大值为．模型拓展：如图3，在平面直角坐标系中，点A是y轴正半轴上的一动点，点B是x轴正半轴上的一动点，且AB ＝8．若AC⊥AB，AC＝3，试求OC长的最大值．11、已知：△ABC中，∠ACB＝90°，AC＝BC．（1）如图1，点D在BC的延长线上，连AD，过B作BE⊥AD于E，交AC于点F．求证：AD＝BF；（2）如图2，点D在线段BC上，连AD，过A作AE⊥AD，且AE＝AD，连BE交AC于F，连DE，问BD与CF有何数量关系，并加以证明；（3）如图3，点D在CB延长线上，AE＝AD且AE⊥AD，连接BE、AC的延长线交BE于点M，若AC ＝3MC，请直接写出的值．12、已知在△ABC中，AB＝AC，射线BM、BN在∠ABC内部，分别交线段AC于点G、H．（1）如图1，若∠ABC＝60°，∠MBN＝30°，作AE⊥BN于点D，分别交BC、BM于点E、F．①求证：∠1＝∠2；②如图2，若BF＝2AF，连接CF，求证：BF⊥CF；（2）如图3，点E为BC上一点，AE交BM于点F，连接CF，若∠BFE＝∠BAC＝2∠CFE，求的值．13、已知，△ABC中，AB＝AC，∠BAC＝90°，E为边AC任意一点，连接BE．（1）如图1，若∠ABE＝15°，O为BE中点，连接AO，且AO＝1，求BC的长；（2）如图2，F也为AC上一点，且满足AE＝CF，过A作AD⊥BE交BE于点H，交BC于点D，连接DF交BE于点G，连接AG；①若AG平分∠CAD，求证：AH＝AC；②如图3，当G落在△ABC外时，若将△EFG沿EF边翻折，点G刚好落在AB边上点P，直接写出AG与EF的数量关系．14、如图所示，Rt△ABC中，∠ACB＝90°，E为AC中点，作ED⊥AC交AB于D，连接CD；（1）如图1，求证：AB＝2CD；（2）如图2，作CF⊥AB交AB于F，点G为CF上一点，点H为DE延长线上一点，分别连接AH、GH，若∠AHG＝2∠B，求证：AH＝GH；（3）如图3，在（2）的条件下，连接DG，且有DE＝BF，∠EDG＝90°，若AC＝6，求AH的长度．15、【问题情境】一节数学课后，老师布置了一道课后练习题：如图：已知在Rt△ABC中，AC＝BC，∠ACB＝90°，CD⊥AB于点D，点E、F分别在A和BC上，∠1＝∠2，FG⊥AB于点G，求证：△CDE≌△EGF．（1）阅读理解，完成解答本题证明的思路可用下列框图表示：根据上述思路，请你完整地书写这道练习题的证明过程；（2）特殊位置，证明结论若CE平分∠ACD，其余条件不变，求证：AE＝BF；（3）知识迁移，探究发现如图，已知在Rt△ABC中，AC＝BC，∠ACB＝90°，CD⊥AB于点D，若点E是DB的中点，点F在直线CB上且满足EC＝EF，请直接写出AE与BF的数量关系．（不必写解答过程）16、在正方形ABCD和等腰直角△BGF中，∠BGF＝90°，P是DF的中点，连接PG、PC．（1）如图1，当点G在BC边上时，延长GP交DC于点E．求证：PG＝PC；（2）如图2，当点F在AB的延长线上时，（1）中的结论是否成立？请证明你的结论；（3）如图3，若四边形ABCD为菱形，且∠ABC＝60°，△BGF为等边三角形，点F在CB的延长线上时，线段PC、PG又有怎样的数量关系，请直接写出你的结论，并画出论证过程中需要添加的辅助线．17、在△ABC中，∠BAC＝60°，点D、E分别在边AC、AB上，AD＝AE，连接CE、BD相交于点F，且∠BEC＝∠ADF，连接AF．（1）如图1，连接ED，求证：∠ABD＝∠CED；（2）如图2，求证：EF+FD＝AF；（3）如图3，取BC的中点G，连接AG交BD于点H，若∠GAC＝3∠ABD，BH＝7，求△ABH的面积．18、点D，E分别在△ABC的边AC，BD上，BD，CE交于点F，连接AF，∠F AE＝∠F AD，FE＝FD．（1）如图1，若∠AEF＝∠ADF，求证：AE＝AD；（2）如图2，若∠AEF≠∠ADF，FB平分∠ABC，求∠BAC的度数；（3）在（2）的条件下，如图3，点G在BE上，∠CFG＝∠AFB若AG＝6，△ABC的周长为20，求BC长．2020重庆中考复习数学第26题专题训练五参考答案1、（2019秋•天桥区期末）如图，在△ABC中，∠ACB＝90°，AC＝BC，E为AC边的一点，F为AB边上一点，连接CF，交BE于点D且∠ACF＝∠CBE，CG平分∠ACB交BD于点G，（1）求证：CF＝BG；（2）延长CG交AB于H，连接AG，过点C作CP∥AG交BE的延长线于点P，求证：PB＝CP+CF；（3）在（2）问的条件下，当∠GAC＝2∠FCH时，若S△AEG＝3，BG＝6，求AC的长．证明：（1）如图1，∵∠ACB＝90°，AC＝BC，∴∠A＝45°，∵CG平分∠ACB，∴∠ACG＝∠BCG＝45°，∴∠A＝∠BCG，在△BCG和△CAF中，∵，∴△BCG≌△CAF（ASA），∴CF＝BG；（2）如图2，∵PC∥AG，∴∠PCA＝∠CAG，∵AC＝BC，∠ACG＝∠BCG，CG＝CG，∴△ACG≌△BCG，∴∠CAG＝∠CBE，∵∠PCG＝∠PCA+∠ACG＝∠CAG+45°＝∠CBE+45°，∠PGC＝∠GCB+∠CBE＝∠CBE+45°，∴∠PCG＝∠PGC，∴PC＝PG，∵PB＝BG+PG，BG＝CF，∴PB＝CF+CP；（3）解法一：如图3，过E作EM⊥AG，交AG于M，∵S△AEG＝AG•EM＝3，由（2）得：△ACG≌△BCG，∴BG＝AG＝6，∴×6×EM＝3，EM＝，设∠FCH＝x°，则∠GAC＝2x°，∴∠ACF＝∠EBC＝∠GAC＝2x°，∵∠ACH＝45°，∴2x+x＝45，x＝15，∴∠ACF＝∠GAC＝30°，在Rt△AEM中，AE＝2EM＝2，AM＝＝3，∴M是AG的中点，∴AE＝EG＝2，∴BE＝BG+EG＝6+2，在Rt△ECB中，∠EBC＝30°，∴CE＝BE＝3+，∴AC＝AE+EC＝2+3+＝3+3．解法二：同理得：∠CAG＝30°，AG＝BG＝6，如图4，过G作GM⊥AC于M，在Rt△AGM中，GM＝3，AM＝＝＝3，∵∠ACG＝45°，∠MGC＝90°，∴GM＝CM＝3，∴AC＝AM+CM＝3+3．2、（2019秋•淮安期末）[问题背景]如图1所示，在△ABC中，AB＝BC，∠ABC＝90°，点D为直线BC上的一个动点（不与B、C重合），连结AD，将线段AD绕点D按顺时针方向旋转90°，使点A旋转到点E，连结EC．[问题初探]如果点D在线段BC上运动，通过观察、交流，小明形成了以下的解题思路：过点E作EF⊥BC 交直线BC于F，如图2所示，通过证明△DEF≌△ADB，可推证△CEF是等腰直角三角形，从而求得∠DCE＝135°．[继续探究]如果点D在线段CB的延长线上运动，如图3所示，求出∠DCE的度数．[拓展延伸]连接BE，当点D在直线BC上运动时，若AB＝，请直接写出BE的最小值．解：[问题初探]如图2，过点E作EF⊥BC交直线BC于F，∴∠DFE＝90°＝∠ABD，∴∠EDF+∠DEF＝90°，由旋转知，AD＝DE，∠ADE＝90°，∴∠ADB+∠EDF＝90°，∴∠ADB＝∠DEF，∴△ABD≌△DFE（AAS），∴BD＝EF，DF＝AB，∵AB＝BC，∴BC＝DF，∴BD＝CF，∴EF＝CF，∴△CEG是等腰直角三角形，∴∠ECF＝45°，∴∠DCE＝135°，故答案为：ADB，等腰直角，135；[继续探究]如图3，过点E作EF⊥BC于F，∴∠DFE＝90°＝∠ABD，∴∠EDF+∠DEF＝90°，由旋转知，AD＝DE，∠ADE＝90°，∴∠ADB+∠EDF＝90°，∴∠ADB＝∠DEF，∴△ABD≌△DFE（AAS），∴BD＝EF，DF＝AB，∵AB＝BC，∴BC＝DF，∴BD＝CF，∴EF＝CF，∴△CEG是等腰直角三角形，∴∠ECF＝45°，∴∠DCE＝45°；[拓展延伸]如图4，在△ABC中，∠ABC＝90°，AB＝BC＝，∴∠ACB＝45°当点D在射线BC上时，由[问题初探]知，∠BCM＝135°，∴∠ACM＝∠BCM﹣∠ACB＝90°，当点D在线段CB的延长线上时，由[继续探究]知，∠BCE＝45°，∴∠ACN＝∠ACB+∠BCM＝90°，∴点E是过点C垂直于AC的直线上的点，∴当BE⊥MN时，BE最小，∵∠BCE＝45°，∴∠CBE＝45°＝∠BCE，∴BE＝CE，∴BE最小＝BC＝，即：BE的最小值为．3、（2019秋•锦江区校级期末）在Rt△ABC中，∠ACB＝90°，∠A＝30°，BD是△ABC的角平分线．（1）如图1，求证：AD＝2DC．（2）如图2，作∠CBD的角平分线交线段CD于点M，若CM＝1，求△DBM的面积；（3）如图3，过点D作DE⊥AB于点E，点N是线段AC上一点（不与C、D重合），以BN为一边，在BN的下方作∠BNG＝60°，NG交DE延长线于点G，试探究线段ND，DG与AD之间的数量关系，并说明理由．证明：（1）如图1，过点D作DE⊥AB，∵BD是△ABC的角平分线，DE⊥AB，∠ACB＝90°，∴DC＝DE，∵∠A＝30°，DE⊥AB，∴AD＝2DE，∴AD＝2DC；（2）如图2，过点M作ME∥BD，∵∠ACB＝90°，∠A＝30°，∴∠ABC＝60°，∵BD是△ABC的角平分线，∴∠ABD＝∠DBC＝30°，∵BM平分∠CBD，∴∠CBM＝15°＝∠DBM，∵ME∥BD，∴∠MEC＝∠CBD＝30°，∠EMB＝∠DBM＝∠MBE，∴ME＝BE，∵∠MEC＝30°，∠C＝90°∴CE＝MC＝，ME＝2MC＝2＝BE，∴BC＝+2，∵∠CBD＝30°，∠C＝90°，∴BC＝CD，∴CD＝1+，∴DM＝，∴△DBM的面积＝××（+2）＝1+；（3）若点N在CD上时，AD＝DG+DN，理由如下：如图3所示：延长ED使得DW＝DN，连接NW，∵∠ACB＝90°，∠A＝30°，BD是△ABC的角平分线，DE⊥AB于点E，∴∠ADE＝∠BDE＝60°，AD＝BD，∵DN＝DW，且∠WDN＝60°∴△WDN是等边三角形，∴NW＝DN，∠W＝∠WND＝∠BNG＝∠BDN＝60°，∴∠WNG＝∠BND，在△WGN和△DBN中，∴△WGN≌△DBN（SAS），∴BD＝WG＝DG+DN，∴AD＝DG+DN．（3）若点N在AD上时，AD＝DG﹣DN，理由如下：如图4，延长BD至H，使得DH＝DN，连接HN，由（1）得DA＝DB，∠A＝30°．∵DE⊥AB于点E．∴∠2＝∠3＝60°．∴∠4＝∠5＝60°．∴△NDH是等边三角形．∴NH＝ND，∠H＝∠6＝60°．∴∠H＝∠2．∵∠BNG＝60°，∴∠BNG+∠7＝∠6+∠7．即∠DNG＝∠HNB．在△DNG和△HNB中，∴△DNG≌△HNB（ASA）．∴DG＝HB．∵HB＝HD+DB＝ND+AD，∴DG＝ND+AD．∴AD＝DG﹣ND．4、（2019•镇平县三模）如图1，已知直角三角形ABC，∠ACB＝90°，∠BAC＝30°，点D是AC边上一点，过D作DE⊥AB于点E，连接BD，点F是BD中点，连接EF，CF．（1）发现问题：线段EF，CF之间的数量关系为EF＝CF；∠EFC的度数为120°；（2）拓展与探究：若将△AED绕点A按顺时针方向旋转α角（0°＜α＜30°），如图2所示，（1）中的结论还成立吗？请说明理由；（3）拓展与运用：如图3所示，若△AED绕点A旋转的过程中，当点D落到AB边上时，AB边上另有一点G，AD＝DG＝GB，BC＝3，连接EG，请直接写出EG的长度．解：（1）如图1中，∵DE⊥AB，∴∠BED＝90°，∵∠BCD＝90°，BF＝DF，∴FE＝FB＝FD＝CF，∴∠FBE＝∠FEB，∠FBC＝∠FCB，∴∠EFC＝∠EFD+∠CFD＝∠FBE+∠FEB+∠FBC+∠FCB＝2（∠FBE+∠FBC）＝2∠ABC＝120°，故答案为：EF＝CF，120°．（2）结论成立．理由：如图2中，取AB的中点M，AD的中点N，连接MC，MF，ED，EN，FN．∵BM＝MA，BF＝FD，∴MF∥AD，MF＝AD，∵AN＝ND，∴MF＝AN，MF∥AN，∴四边形MFNA是平行四边形，∴NF＝AM，∠FMA＝∠ANF，在Rt△ADE中，∵AN＝ND，∠AED＝90°，∴EN＝AD＝AN＝ND，同理CM＝AB＝AM＝MB，在△AEN和△ACM中，∠AEN＝∠EAN，∠MCA＝∠MAC，∵∠MAC＝∠EAN，∴∠AMC＝∠ANE，又∵∠FMA＝∠ANF，∴∠ENF＝∠FMC，在△MFC和△NEF中，，∴△MFC≌△NEF（SAS），∴FE＝FC，∠NFE＝∠MCF，∵NF∥AB，∴∠NFD＝∠ABD，∵∠ACB＝90°，∠BAC＝30°，∴∠ABC＝60°，△BMC是等边三角形，∠MCB＝60°∴∠EFC＝∠EFN+∠NFD+∠DFC＝∠MCF+∠ABD+∠FBC+∠FCB＝∠ABC+∠MCB＝60°+60°＝120°．（3）如图3中，作EH⊥AB于H．在Rt△ABC中，∵∠BAC＝30°，BC＝3，∴AB＝2BC＝6，在Rt△AED中，∠DAE＝30°，AD＝2，∴DE＝AD＝1，在Rt△DEH中，∵∠EDH＝60°，DE＝1，∴EH＝ED•sin60°＝，DH＝ED•cos60°＝，在Rt△EHG中，EG＝＝．5、（2017春•西城区校级期末）如图1，在等腰△ABC中，AB＝AC，∠BAC＝a，点P是线段AB的中点，点E是线段CB延长线上一点，且PE＝PC，将线段PC绕点P顺时针旋转α得到PD，连接BD．（1）如图2，若α＝60°，其他条件不变，先补全图形，然后探究线段BD和BC之间的数量关系，并说明理由．（2）如图3，若α＝90°，其他条件不变，探究线段BP、BD和BC之间的等量关系，并说明理由．解：（1）BC＝2BD，理由：如图2，连接CD，由旋转可得，CP＝DP，∠CPD＝60°，∴△CDP是等边三角形，∴∠CDP＝60°＝∠PCD，又∵P是AB的中点，AB＝AC，∠A＝60°，∴等边三角形ABC中，∠PCB＝30°，CP⊥AB，∴∠BCD＝30°，即BC平分∠PCD，∴BC垂直平分PD，∴∠BDC＝∠BPC＝90°，∴Rt△BCD中，BC＝2BD．（2）如图3，取BC中点F，连接PF，∵∠A＝90°，AB＝AC，∴△ABC是等腰直角三角形，∵P是AB的中点，F是BC的中点，∴PF是△ABC的中位线，∴PF∥AC，∴∠PFB＝∠ACB＝45°，∠BPF＝∠A＝90°，∴△BPF是等腰直角三角形，∴BF＝BP，BP＝PF，∵∠DPC＝∠BPF＝90°，∴∠BPD＝∠FPC，又∵PD＝PC，∴△BDP≌△FCP，∴BD＝CF，∵BC＝BF+FC，∴BC＝BD+BP．6、（2019春•碑林区校级月考）【发现问题】如图1，已知△ABC，以点A为直角顶点、AB为腰向△ABC外作等腰直角△ABE．请你以A 为直角顶点、AC为腰，向△ABC外作等腰直角△ACD（不写作法，保留作图痕迹）．连接BD、CE．那么BD与CE的数量关系是BD＝CE．【拓展探究】如图2，已知△ABC，以AB、AC为边向外作正方形AEFB和正方形ACGD，连接BD、CE，试判断BD与CE之间的数量关系，并说明理由．【解决问题】如图3，有一个四边形场地ABCD，∠ADC＝60°，BC＝15，AB＝8，AD＝CD，求BD的最大值．【发现问题】解：延长CA到M，作∠MAC的平分线AN，在AN上截取AD＝AC，连接CD，即可得到等腰直角△ACD；连接BD、CE，如图1所示：∵△ABE与△ACD都是等腰直角三角形，∴AB＝AE，AD＝AC，∠BAE＝∠CAD＝90°，∴∠BAD＝∠EAC，在△BAD和△EAC中，，∴△BAD≌△EAC（SAS），∴BD＝CE，【拓展探究】解：BD＝CE；理由如下：∵四边形AEFB与四边形ACGD都是正方形，∴AB＝AE，AD＝AC，∠BAE＝∠CAD＝90°，∴∠BAD＝∠EAC，在△BAD和△EAC中，，∴△BAD≌△EAC（SAS），∴BD＝CE；【解决问题】解：以AB为边向外作等边三角形ABE，连接CE，如图3所示：则∠BAE＝60°，BE＝AB＝AE＝8，∵AD＝CD，∠ADC＝60°，∴△ACD是等边三角形，∴∠CAD＝60°，AC＝AD，∴∠CAD+∠BAC＝∠BAE+∠BAC，即∠BAD＝∠EAC，在△BAD和△EAC中，，∴△BAD≌△EAC（SAS），∴BD＝CE；当C、B、E三点共线时，CE最大＝BC+BE＝15+8＝23，∴BD的最大值为23．7、（2018春•铁西区期中）（1）如图1，点C为线段AB外一个动点，已知AB＝a，AC＝b．当点C位于BA的延长线上时，线段BC取得最大值，则最大值为a+b（用含a，b的式子表示）；（2）如图2，点C为线段AB外一个动点，若AB＝10，AC＝3，分别以AC，BC为边，作等边三角形ACD和等边三角形BCE，连接AE，DB．①求证：AE＝DB；②请直接写出线段AE的最大值；（3）如图3，AB＝6，点M为线段AB外一个动点，且AM＝2，MB＝MN，∠BMN＝90°，请直接写出线段AN的最大值．（1）解：∵点C为线段AB外一动点，且AC＝b，AB＝a，∴当点C位于BA的延长线上时，线段BC的长取得最大值，且最大值为AC+AB＝a+b，（2）①证明：如图2中，∵△ACD与△BCE是等边三角形，∴CD＝AC，CB＝CE，∠ACD＝∠BCE＝60°，∴∠DCB＝∠ACE，在△CAD与△EAB中，，∴△CAD≌△EAB（SAS），∴AE＝BD．②∵线段AE长的最大值＝线段BD的最大值，由（1）知，当线段BD的长取得最大值时，点D在BA的延长线上，∴最大值为AD+AB＝3+10＝13；（3）如图3中，连接BN，∵将△AMN绕着点M顺时针旋转90°得到△PBM，连接AP，则△APM是等腰直角三角形，∴MA＝MP＝2，BP＝AN，∴P A＝2，∵AB＝6，∴线段AN长的最大值＝线段BP长的最大值，∴当P在线段BA的延长线时，线段BP取得最大值最大值＝AB+AP＝6+2．8、（2019秋•武冈市期中）【初步探索】（1）如图1：在四边形ABC中，AB＝AD，∠B＝∠ADC＝90°，E、F分别是BC、CD上的点，且EF ＝BE+FD，探究图中∠BAE、∠F AD、∠EAF之间的数量关系．小王同学探究此问题的方法是：延长FD到点G，使DG＝BE．连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是∠BAE+∠F AD＝∠EAF；【灵活运用】（2）如图2，若在四边形ABCD中，AB＝AD，∠B+∠D＝180°．E、F分别是BC、CD上的点，且EF＝BE+FD，上述结论是否仍然成立，并说明理由；【拓展延伸】（3）如图3，已知在四边形ABCD中，∠ABC+∠ADC＝180°AB＝AD，若点E在CB的延长线上，点F在CD的延长线上，如图3所示，仍然满足EF＝BE+FD，请写出∠EAF与∠DAB的数量关系，并给出证明过程．解：（1）∠BAE+∠F AD＝∠EAF．理由：如图1，延长FD到点G，使DG＝BE，连接AG，根据SAS可判定△ABE≌△ADG，进而得出∠BAE＝∠DAG，AE＝AG，再根据SSS可判定△AEF≌△AGF，可得出∠EAF＝∠GAF＝∠DAG+∠DAF＝∠BAE+∠DAF．故答案为：∠BAE+∠F AD＝∠EAF；（2）仍成立，理由：如图2，延长FD到点G，使DG＝BE，连接AG，∵∠B+∠ADF＝180°，∠ADG+∠ADF＝180°，∴∠B＝∠ADG，又∵AB＝AD，∴△ABE≌△ADG（SAS），∴∠BAE＝∠DAG，AE＝AG，∵EF＝BE+FD＝DG+FD＝GF，AF＝AF，∴△AEF≌△AGF（SSS），∴∠EAF＝∠GAF＝∠DAG+∠DAF＝∠BAE+∠DAF；（3）∠EAF＝180°﹣∠DAB．证明：如图3，在DC延长线上取一点G，使得DG＝BE，连接AG，∵∠ABC+∠ADC＝180°，∠ABC+∠ABE＝180°，∴∠ADC＝∠ABE，又∵AB＝AD，∴△ADG≌△ABE（SAS），∴AG＝AE，∠DAG＝∠BAE，∵EF＝BE+FD＝DG+FD＝GF，AF＝AF，∴△AEF≌△AGF（SSS），∴∠F AE＝∠F AG，∵∠F AE+∠F AG+∠GAE＝360°，∴2∠F AE+（∠GAB+∠BAE）＝360°，∴2∠F AE+（∠GAB+∠DAG）＝360°，即2∠F AE+∠DAB＝360°，∴∠EAF＝180°﹣∠DAB．9、（2018•大东区一模）如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，点O为AB中点，点P为直线BC上的动点（不与点B、点C重合），连接OC、OP，将线段OP绕点P逆时针旋转60°，得到线段PQ，连接BQ．（1）如图1，当点P在线段BC上时，请直接写出线段BQ与CP的数量关系．（2）如图2，当点P在CB延长线上时，（1）中结论是否成立？若成立，请加以证明；若不成立，请说明理由；（3）如图3，当点P在BC延长线上时，若∠BPO＝45°，AC＝，请直接写出BQ的长．解：（1）CP＝BQ，理由：如图1，连接OQ，由旋转知，PQ＝OP，∠OPQ＝60°⊅∴△POQ是等边三角形，∴OP＝OQ，∠POQ＝60°，在Rt△ABC中，O是AB中点，∴OC＝OA＝OB，∴∠BOC＝2∠A＝60°＝∠POQ，∴∠COP＝∠BOQ，在△COP和△BOQ中，，∴△COP≌△BOQ（SAS），∴CP＝BQ，（2）CP＝BQ，理由：如图2，连接OQ，由旋转知，PQ＝OP，∠OPQ＝60°∴△POQ是等边三角形，∴OP＝OQ，∠POQ＝60°，在Rt△ABC中，O是AB中点，∴OC＝OA＝OB，∴∠BOC＝2∠A＝60°＝∠POQ，∴∠COP＝∠BOQ，在△COP和△BOQ中，，∴△COP≌△BOQ（SAS），∴CP＝BQ，（3）如图3，在Rt△ABC中，∠A＝30°，AC＝，∴BC＝AC•tan∠A＝，过点O作OH⊥BC，∴∠OHB＝90°＝∠BCA，∴OH∥AB，∵O是AB中点，∴CH＝BC＝，OH＝AC＝，∵∠BPQ＝45°，∠OHP＝90°，∴∠BPQ＝∠PQH，∴PH＝OH＝，∴CP＝PH﹣CH＝﹣＝，连接BQ，同（1）的方法得，BQ＝CP＝．10、（2018秋•东海县期末）模型发现：同学们知道，三角形的两边之和大于第三边，即如图1，在△ABC中，AB+AC＞BC．对于图1，若把点C看作是线段AB外一动点，且AB＝c，AC＝b，则线段BC的长会因为点C的位置的不同而发生变化．因为AB、AC的长度固定，所以当∠BAC越大时，BC边越长．特别的，当点C位于线段BA的延长线上时，线段BC的长取得最大值，且最大值为b+c（用含b，c的式子表示）（直接填空）模型应用：点C为线段AB外一动点，且AB＝3，AC＝2，如图2所示，分别以AC，BC为边，作等边三角形ACD 和等边三角形BCE，连接BD，AE．（1）求证：BD＝AE．（2）线段AE长的最大值为5．模型拓展：如图3，在平面直角坐标系中，点A是y轴正半轴上的一动点，点B是x轴正半轴上的一动点，且AB ＝8．若AC⊥AB，AC＝3，试求OC长的最大值．解：当点C位于线段BA的延长线上时，线段BC的长取得最大值，最大值为b+c，故答案为：线段BA的延长线上；b+c；模型应用：（1）证明：∵△ACD、△BCE都是等边三角形，∴CD＝CA＝AD，CB＝CE，∠ACD＝60°，∠BCE＝60°，∴∠DCB＝∠ACE，在△DCB和△ACE中，，∴△DCB≌△ACE（SAS）∴BD＝AE；（2）当点D位于线段BA的延长线上时，线段BD的长取得最大值，最大值为AB+AD＝AB+AC＝3+2＝5，∵AE＝BD，∴线段AE长的最大值为5，模型拓展：取AB的中点G，连接OG、CG，在Rt△AOB中，G为AB的中点，∴OG＝AB＝4，在Rt△CAG中，CG＝＝＝5，当点O、G、C在同一条直线上时，OC最大，最大值为4+5＝9．11、已知：△ABC中，∠ACB＝90°，AC＝BC．（1）如图1，点D在BC的延长线上，连AD，过B作BE⊥AD于E，交AC于点F．求证：AD＝BF；（2）如图2，点D在线段BC上，连AD，过A作AE⊥AD，且AE＝AD，连BE交AC于F，连DE，问BD与CF有何数量关系，并加以证明；（3）如图3，点D在CB延长线上，AE＝AD且AE⊥AD，连接BE、AC的延长线交BE于点M，若AC ＝3MC，请直接写出的值．（1）证明：如图1中，∵BE⊥AD于E，∴∠AEF＝∠BCF＝90°，∵∠AFE＝∠CFB，∴∠DAC＝∠CBF，∵BC＝CA，∴△BCF≌△ACD，∴BF＝AD．（2）结论：BD＝2CF．理由：如图2中，作EH⊥AC于H．∵∠AHE＝∠ACD＝∠DAE＝90°，∴∠DAC+∠ADC＝90°，∠DAC+∠EAH＝90°，∴∠DAC＝∠AEH，∵AD＝AE，∴△ACD≌△EHA，∴CD＝AH，EH＝AC＝BC，∵CB＝CA，∴BD＝CH，∵∠EHF＝∠BCF＝90°，∠EFH＝∠BFC，EH＝BC，∴△EHF≌△BCF，∴FH＝CF，∴BD＝CH＝2CF．（3）如图3中，同法可证BD＝2CM．∵AC＝3CM，设CM＝a，则AC＝CB＝3a，BD＝2a，∴＝＝．12、（2019秋•松北区期末）已知在△ABC中，AB＝AC，射线BM、BN在∠ABC内部，分别交线段AC于点G、H．（1）如图1，若∠ABC＝60°，∠MBN＝30°，作AE⊥BN于点D，分别交BC、BM于点E、F．①求证：∠1＝∠2；②如图2，若BF＝2AF，连接CF，求证：BF⊥CF；（2）如图3，点E为BC上一点，AE交BM于点F，连接CF，若∠BFE＝∠BAC＝2∠CFE，求的值．（1）①证明：如图1中，∵AB＝AC，∠ABC＝60°∴△ABC是等边三角形，∴∠BAC＝60°，∵AD⊥BN，∴∠ADB＝90°，∵∠MBN＝30°，∠BFD＝60°＝∠1+∠BAF＝∠2+∠BAF，∴∠1＝∠2②证明：如图2中，在Rt△BFD中，∵∠FBD＝30°，∴BF＝2DF，∵BF＝2AF，∴BF＝AD，∵∠BAE＝∠FBC，AB＝BC，∴△BFC≌△ADB，∴∠BFC＝∠ADB＝90°，∴BF⊥CF（2）在BF上截取BK＝AF，连接AK．∵∠BFE＝∠2+∠BAF，∠CFE＝∠4+∠1，∴∠CFB＝∠2+∠4+∠BAC，∵∠BFE＝∠BAC＝2∠EFC，∴∠1+∠4＝∠2+∠4∴∠1＝∠2，∵AB＝AC，∴△ABK≌CAF，∴∠3＝∠4，S△ABK＝S△AFC，∵∠1+∠3＝∠2+∠3＝∠CFE＝∠AKB，∠BAC＝2∠CEF，∴∠KAF＝∠1+∠3＝∠AKF，∴AF＝FK＝BK，∴S△ABK＝S△AFK，∴＝2．13、（2017春•合肥期末）已知，△ABC中，AB＝AC，∠BAC＝90°，E为边AC任意一点，连接BE．（1）如图1，若∠ABE＝15°，O为BE中点，连接AO，且AO＝1，求BC的长；（2）如图2，F也为AC上一点，且满足AE＝CF，过A作AD⊥BE交BE于点H，交BC于点D，连接DF交BE于点G，连接AG；①若AG平分∠CAD，求证：AH＝AC；②如图3，当G落在△ABC外时，若将△EFG沿EF边翻折，点G刚好落在AB边上点P，直接写出AG与EF的数量关系．（1）解：如图1中，在AB上取一点M，使得BM＝ME，连接ME．在Rt△ABE中，∵OB＝OE，∴BE＝2OA＝2，∵MB＝ME，∴∠MBE＝∠MEB＝15°，∴∠AME＝∠MBE+∠MEB＝30°，设AE＝x，则ME＝BM＝2x，AM＝x，∵AB2+AE2＝BE2，∴（2x+x）2+x2＝22，∴x＝（负根已经舍弃），∴AB＝AC＝（2+）•，∴BC＝AB＝+1．方法二：作EH⊥BC于H，求出BH，CH即可解决问题．（2）证明：如图2中，作CP⊥AC，交AD的延长线于P，GM⊥AC于M．∵BE⊥AP，∴∠AHB＝90°，∴∠ABH+∠BAH＝90°，∵∠BAH+∠P AC＝90°，∴∠ABE＝∠P AC，在△ABE和△CAP中，，∴△ABE≌△CAP，∴AE＝CP＝CF，∠AEB＝∠P，在△DCF和△DCP中，，∴△DCF≌△DCP，∴∠DFC＝∠P，∴∠GFE＝∠GEF，∴GE＝GF，∵GM⊥EF，∴FM＝ME，∵AE＝CF，∴AF＝CE，∴AM＝CM，在△GAH和△GAM中，，∴△AGH≌△AGM，∴AH＝AM＝CM＝AC（3）解：结论：AG＝EF．理由：如图3中，作CM⊥AC交AD的延长线于M，连接PG交AC于点O．由（2）可知△ACM≌△BAE，△CDF≌△CDM，∴∠AEB＝∠M＝∠GEF，∠M＝∠CFD＝∠GFE，AE＝CM＝CF，∴∠GEF＝∠GFE，∴GE＝GF，∵△EFP是由△EFG翻折得到，∴EG＝EP＝GF＝PF，∴四边形EGFP是菱形，∴PG⊥AC，OE＝OF，∵AE＝CF，∴AO＝OC，∵AB∥OP，∴BP＝PC，∵PF∥BE，∴EF＝CF＝AE，∵PB＝PC，AO＝OC，∴PO＝OG＝AB，∴AB＝PG，AB∥PG，∴四边形ABPG是平行四边形，∴AG∥BC，∴∠GAO＝∠ACB＝45°，设EO＝OF＝a，则OA＝OG＝3a，AG＝3a，∴＝＝，∴AG＝EF14、（2017春•南岗区校级月考）如图所示，Rt△ABC中，∠ACB＝90°，E为AC中点，作ED⊥AC交AB于D，连接CD；（1）如图1，求证：AB＝2CD；（2）如图2，作CF⊥AB交AB于F，点G为CF上一点，点H为DE延长线上一点，分别连接AH、GH，若∠AHG＝2∠B，求证：AH＝GH；（3）如图3，在（2）的条件下，连接DG，且有DE＝BF，∠EDG＝90°，若AC＝6，求AH的长度．解：（1）∵E为AC中点，作ED⊥AC交AB于D，∴AD＝CD，∵∠ACB＝90°，∴BC∥DE，∴AD＝BD，∴CD＝BD，∴AB＝2CD；（2）如图2，连接CH，∵点E是AC的中点，∴AE＝CE，∵DE⊥AC，∴CH＝AH，∴∠ACH＝∠CAH，∵∠ACB＝90°，∴∠B+∠BAC＝90°，∵CF⊥AB，∴∠BAC+∠ACF＝90°，∴∠ACF＝∠B，∴∠HCG＝∠ACH+∠ACF＝∠CAH+∠B，∠AHG＝2∠B∴在四边形AHGF中，∠AFG+∠FGH+∠AHG+∠F AH＝360°，∴∠FGH＝360°﹣（∠AFG+∠AHG+∠F AH）＝360°﹣（90°+2∠B+∠CAH+∠BAC）＝360°﹣（90°+2∠B+∠CAH+90°﹣∠B）＝360°﹣（180°+∠B+∠CAH）＝180°﹣（∠B+∠CAH），∵∠CGH＝180°﹣∠FGH＝∠B+∠CAH＝∠HCG，∴CH＝GH，∵CH＝AH，∴AH＝GH；（3）如图3，由（1）知，DE∥BC，∴∠B＝∠ADE，在△BFC和△DEA中，，∴△BFC≌△DEA，∴BC＝AD，∵AD＝BD＝CD，∴BC＝BD＝CD，∴△BCD是等边三角形，∴∠B＝60°，在Rt△ABC中，AC＝6，∴BC＝2，AB＝4，∵CF⊥BD，∴DF＝，CF＝3，∵∠BAC＝30°，∴∠ADE＝60°，∵∠EDG＝90°，∠FDG＝30°，在Rt△DFG中，DF＝，∴FG＝1，DG＝2，∴CG＝CF﹣FG＝2过点H作HN⊥CF，由（2）知，CH＝GH，∴NG＝CG＝1，∴FN＝NG+FG＝2，过点H作HM⊥AB，∴∠FMH＝∠NFM＝∠HNF＝90°，∴四边形NFMH是矩形，∴HM＝FN＝2，在Rt△DMH中，∠ADE＝60°，HM＝2，∴DH＝，在Rt△HDG中，根据勾股定理得，HG＝＝．15、【问题情境】一节数学课后，老师布置了一道课后练习题：如图：已知在Rt△ABC中，AC＝BC，∠ACB＝90°，CD⊥AB于点D，点E、F分别在A和BC上，∠1＝∠2，FG⊥AB于点G，求证：△CDE≌△EGF．（1）阅读理解，完成解答本题证明的思路可用下列框图表示：根据上述思路，请你完整地书写这道练习题的证明过程；（2）特殊位置，证明结论若CE平分∠ACD，其余条件不变，求证：AE＝BF；（3）知识迁移，探究发现如图，已知在Rt△ABC中，AC＝BC，∠ACB＝90°，CD⊥AB于点D，若点E是DB的中点，点F在直线CB上且满足EC＝EF，请直接写出AE与BF的数量关系．（不必写解答过程）（1）证明：∵AC＝BC，∠ACB＝90°，∴∠A＝∠B＝45°，∵CD⊥AB，∴∠CDB＝90°，∴∠DCB＝45°，∵∠ECF＝∠DCB+∠1＝45°+∠1，∠EFC＝∠B+∠2＝45°+∠2，∠1＝∠2，∴∠ECF＝∠EFC，∴CE＝EF，∵CD⊥AB，FG⊥AB，∴∠CDE＝∠EGF＝90°，在△CDE和△EGF中，，∴△CDE≌△EGF（AAS）；（2）证明：由（1）得：CE＝EF，∠A＝∠B，∵CE平分∠ACD，∴∠ACE＝∠1，∵∠1＝∠2，∴∠ACE＝∠2，在△ACE和△BEF中，，∴△ACE≌△BEF（AAS），∴AE＝BF；（3）AE＝BF，作EH⊥BC与H，如图3所示：设DE＝x，根据题意得：BE＝DE＝x，AD＝BD＝2x，CD＝AD＝2x，AE＝3x，根据勾股定理得：BC＝AC＝2x，∵∠ABC＝45°，EH⊥BC，∴BH＝x，∴CH＝BC﹣BH＝x，∵EC＝EF，∴FH＝CH＝x，∴BF＝x﹣x＝x，∴＝，∴AE＝．。

重庆中考26题专题训练

1. 已知：如图，在平面直角坐标系xOy中，矩形OABC的边OA在y轴的正半轴上，OC在x轴的正半轴上，OA=2，OC=3．过原点O作∠AOC的平分线交AB于点D，连接DC，过点D作DE⊥DC，交OA于点E．（1）求过点E、D、C的抛物线的解析式；（2）将∠EDC绕点D按顺时针方向旋转后，角的一边与y轴的正半轴交于点F，另一边与线段OC交于点G．如果DF与（1）中的抛物线交于另一点M，点M的横坐标为65，那么EF=2GO是否成立？若成立，请给予证明；若不成立，请说明理由；（3）对于（2）中的点G，在位于第一象限内的该抛物线上是否存在点Q，使得直线GQ与AB的交点P与点C、G构成的△PCG是等腰三角形？若存在，请求出点Q的坐标；若不存在，请说明理由．2. 已知：如图，抛物线)0(22≠+-=a c ax ax y 与y 轴交于点C （0，4），与x 轴交于点A 、B ，点A 的坐标为（4，0）。

（1）求该抛物线的解析式；（2）点Q 是线段AB 上的动点，过点Q 作QE ∥AC ，交BC 于点E ，连接CQ 。

当△CQE 的面积最大时，求点Q 的坐标；（3）若平行于x 轴的动直线l 与该抛物线交于点P ，与直线AC 交于点F ，点D 的坐标为（2，0）。

问：是否存在这样的直线l ，使得△ODF 是等腰三角形？若存在，请求出点P 的坐标；若不存在，请说明理由。

Y XE C A D Q B O 28题图3.如图28-1所示，一张三角形纸片ABC ，∠ACB=90°,AC=8,BC=6.沿斜边AB 的中线CD 把这张纸片剪成11AC D ∆和22BC D ∆两个三角形（如图28-2所示）.将纸片11AC D ∆沿直线2D B （AB ）方向平移（点12,,,A D D B 始终在同一直线上），当点1D 于点B 重合时，停止平移.在平移过程中，11C D 与2BC 交于点E,1AC 与222C D BC 、分别交于点F 、P.(1) 当11AC D ∆平移到如图28-3所示的位置时，猜想图中的1D E 与2D F 的数量关系，并证明你的猜想； (2) 设平移距离21D D 为x ，11AC D ∆与22BC D ∆重叠部分面积为y ，请写出y 与x 的函数关系式，以及自变量的取值范围；(3) 对于（2）中的结论是否存在这样的x 的值；若不存在，请说明理由.CB D A 28-1图P E F A D 1B C 1D 2C 228-3图 C 2D 2C 1B D 1A 28-2图4.如图1，在平面直角坐标系中有一个Rt △OAC ，点A （6，8），点C （6，0），将其沿直线AC 翻折，翻折后图形为△BAC ．动点P 从点O 出发，沿折线O →A →B 的方向以每秒2个单位的速度向B 运动，同时动点Q 从点B 出发，在线段BO 上以每秒1个单位的速度向点O 运动，当其中一个点到达终点时，另一点也随之停止运动．设运动的时间为t （秒）．（1）设△OPQ 的面积为S ，求S 与t 之间的函数关系式，并写出自变量t 的取值范围；（2）如图2，固定△OAC ，将△ACB 绕点C 逆时针旋转，旋转后得到的三角形为△''CB A ，设''B A 与AC 交于点D ，当∠'BCB =∠CAB 时，求线段CD 的长；（3）如图3，在△ACB 绕点C 逆时针旋转的过程中，若设C A '所在直线与OA 所在直线的交点为E ，是否存在点E 使△ACE 为等腰三角形，若存在，求出点E 的坐标，若不存在，请说明理由.图1 图2 图3备用图42251015BEB'A'OCAxyx642251015DB'A'OCBAyxy42251015OCBAx422451015Q POCBAy5.如图1，抛物线24y x x c =-+交x 轴于点A 和(1,0),B -交y 轴于点C ，且抛物线的对称轴交x 轴于点D ． (1)求这个抛物线的解析式；(2)若点E 在抛物线上，且位于第四象限，当四边形ADCE 面积最大时，求点E 的坐标；(3)如图2，在抛物线上是否存在这样的点P ，使PAB ∆中的内角．．中有一边与x 轴所夹锐角．．的正切值为12？若存在，求出点P 的坐标，若不存在，请说明理由.6. 如图1，矩形OABC 的顶点O 为原点，点E 在AB 上，把CBE ∆沿CE 折叠，使点B 落在OA 边上的点D 处，点A D 、坐标分别为(10,0)和(6,0)，抛物线215y x bx c =++过点C B 、. (1)求C B 、两点的坐标及该抛物线的解析式；(2)如图2，长、宽一定的矩形PQRS 的宽1PQ =，点P 沿(1)中的抛物线滑动，在滑动过程中x PQ //轴，且RS 在PQ 的下方，当P 点横坐标为-1时，点S 距离x 轴511个单位，当矩形PQRS 在滑动过程中被x 轴分成上下．．两部分的面积比为2:3时，求点P 的坐标；(3)如图3，动点M N 、同时从点O 出发，点M 以每秒3个单位长度的速度沿折线ODC 按C D O →→的路线运动，点N 以每秒8个单位长度的速度沿折线OCD 按D C O →→的路线运动，当M N 、两点相遇时，它们都停止运动．设M N 、同时从点O 出发t 秒时，OMN ∆的面积为S ．①求出S 与t 的函数关系式，并写出t 的取值范围：②设0S 是①中函数S 的最大值，那么0S = .。

2023重庆中考数学b卷压轴题26题

2023重庆中考数学b卷压轴题26题题目：已知二次函数y=x²-2x-3一、对题目进行分析，这道题主要考察二次函数的性质和图像，需要理解二次函数的表达式，掌握其对称轴和开口方向等信息。

二、解题步骤：1. 根据二次函数表达式，我们可以得到对称轴为直线x=1，开口向上。

2. 在B卷压轴题中，通常需要考生进行一些复杂的计算和推理。

首先，我们需要找到函数图像与x轴的交点，这可以通过令y=0来求解。

解方程x²-2x-3=0，得到x₁=3，x₂=-1。

也就是说，函数图像与x轴有两个交点(-1,0)和(3,0)。

3. 将已知的两个交点坐标代入图像中，可以得到图像大致呈抛物线形状，开口向上，与x轴有两个交点(-1,0)和(3,0)。

对称轴为直线x=1。

4. 接下来，我们需要根据题目要求，求出函数图像与直线y=4的交点坐标。

将直线y=4代入二次函数表达式中，得到一元二次方程x²-2x-7=0。

解得，该方程的两个解分别为x₃=5和x₄=-2。

也就是说，图像与直线y=4有两个交点(5,4)和(-2,4)。

5. 最后，根据题目要求，求出图像与直线y=-2的交点与对称轴的间距。

由于题目中未给出具体的坐标值，因此需要进行一些简单的代数计算。

综上，通过以上步骤的推理和计算，我们可以得出以下结论：当x=1时，y=2当x=-2时，y=-5当x=5时，y=4因此，函数图像与直线y=-2的交点坐标为(5,4)，该点与对称轴的距离为4。

三、总结：这道题考察了二次函数的性质和图像，需要考生具备一定的数学基础和推理能力。

解题的关键在于理解二次函数的表达式，掌握其对称轴和开口方向等信息，并能够进行一些复杂的计算和推理。

同时，考生还需要注意题目中的细节和要求，确保解题的准确性和完整性。

2021重庆中考26题专题复习及答案2

重庆中考26题专题复习1、如图1，已知直角三角形ABC，∠ACB＝90°，∠BAC＝30°，点D是AC边上一点，过D作DE⊥AB于点E，连接BD，点F是BD中点，连接EF，CF．（1）发现问题：线段EF，CF之间的数量关系为EF＝CF；∠EFC的度数为120°；（2）拓展与探究：若将△AED绕点A按顺时针方向旋转α角（0°＜α＜30°），如图2所示，（1）中的结论还成立吗？请说明理由；（3）拓展与运用：如图3所示，若△AED绕点A旋转的过程中，当点D落到AB边上时，AB边上另有一点G，AD＝DG＝GB，BC＝3，连接EG，请直接写出EG的长度．解：（1）如图1中，∵DE⊥AB，∴∠BED＝90°，∵∠BCD＝90°，BF＝DF，∴FE＝FB＝FD＝CF，∴∠FBE＝∠FEB，∠FBC＝∠FCB，∴∠EFC＝∠EFD+∠CFD＝∠FBE+∠FEB+∠FBC+∠FCB＝2（∠FBE+∠FBC）＝2∠ABC＝120°，故答案为：EF＝CF，120°．（2）结论成立．理由：如图2中，取AB的中点M，AD的中点N，连接MC，MF，ED，EN，FN．∵BM＝MA，BF＝FD，∴MF∥AD，MF＝AD，∵AN＝ND，∴MF＝AN，MF∥AN，∴四边形MFNA是平行四边形，∴NF＝AM，∠FMA＝∠ANF，在Rt△ADE中，∵AN＝ND，∠AED＝90°，∴EN＝AD＝AN＝ND，同理CM＝AB＝AM＝MB，在△AEN和△ACM中，∠AEN＝∠EAN，∠MCA＝∠MAC，∵∠MAC＝∠EAN，∴∠AMC＝∠ANE，又∵∠FMA＝∠ANF，∴∠ENF＝∠FMC，在△MFC和△NEF中，，∴△MFC≌△NEF（SAS），∴FE＝FC，∠NFE＝∠MCF，∵NF∥AB，∴∠NFD＝∠ABD，∵∠ACB＝90°，∠BAC＝30°，∴∠ABC＝60°，△BMC是等边三角形，∠MCB＝60°∴∠EFC＝∠EFN+∠NFD+∠DFC＝∠MCF+∠ABD+∠FBC+∠FCB＝∠ABC+∠MCB＝60°+60°＝120°．（3）如图3中，作EH⊥AB于H．在Rt△ABC中，∵∠BAC＝30°，BC＝3，∴AB＝2BC＝6，在Rt△AED中，∠DAE＝30°，AD＝2，∴DE＝AD＝1，在Rt△DEH中，∵∠EDH＝60°，DE＝1，∴EH＝ED•sin60°＝，DH＝ED•cos60°＝，在Rt△EHG中，EG＝＝．2、如图1，在等腰△ABC中，AB＝AC，∠BAC＝a，点P是线段AB的中点，点E是线段CB延长线上一点，且PE＝PC，将线段PC绕点P顺时针旋转α得到PD，连接BD．（1）如图2，若α＝60°，其他条件不变，先补全图形，然后探究线段BD和BC之间的数量关系，并说明理由．（2）如图3，若α＝90°，其他条件不变，探究线段BP、BD和BC之间的等量关系，并说明理由．解：（1）BC＝2BD，理由：如图2，连接CD，由旋转可得，CP＝DP，∠CPD＝60°，∴△CDP是等边三角形，∴∠CDP＝60°＝∠PCD，又∵P是AB的中点，AB＝AC，∠A＝60°，∴等边三角形ABC中，∠PCB＝30°，CP⊥AB，∴∠BCD＝30°，即BC平分∠PCD，∴BC垂直平分PD，∴∠BDC＝∠BPC＝90°，∴Rt△BCD中，BC＝2BD．（2）如图3，取BC中点F，连接PF，∵∠A＝90°，AB＝AC，∴△ABC是等腰直角三角形，∵P是AB的中点，F是BC的中点，∴PF是△ABC的中位线，∴PF∥AC，∴∠PFB＝∠ACB＝45°，∠BPF＝∠A＝90°，∴△BPF是等腰直角三角形，∴BF＝BP，BP＝PF，∵∠DPC＝∠BPF＝90°，∴∠BPD＝∠FPC，又∵PD＝PC，∴△BDP≌△FCP，∴BD＝CF，∵BC＝BF+FC，∴BC＝BD+BP．3、【发现问题】如图1，已知△ABC，以点A为直角顶点、AB为腰向△ABC外作等腰直角△ABE．请你以A为直角顶点、AC为腰，向△ABC外作等腰直角△ACD（不写作法，保留作图痕迹）．连接BD、CE．那么BD与CE的数量关系是BD＝CE．【拓展探究】如图2，已知△ABC，以AB、AC为边向外作正方形AEFB和正方形ACGD，连接BD、CE，试判断BD与CE之间的数量关系，并说明理由．【解决问题】如图3，有一个四边形场地ABCD，∠ADC＝60°，BC＝15，AB＝8，AD＝CD，求BD的最大值．【发现问题】解：延长CA到M，作∠MAC的平分线AN，在AN上截取AD＝AC，连接CD，即可得到等腰直角△ACD；连接BD、CE，如图1所示：∵△ABE与△ACD都是等腰直角三角形，∴AB＝AE，AD＝AC，∠BAE＝∠CAD＝90°，∴∠BAD＝∠EAC，在△BAD和△EAC中，，∴△BAD≌△EAC（SAS），∴BD＝CE，【拓展探究】解：BD＝CE；理由如下：∵四边形AEFB与四边形ACGD都是正方形，∴AB＝AE，AD＝AC，∠BAE＝∠CAD＝90°，∴∠BAD＝∠EAC，在△BAD和△EAC中，，∴△BAD≌△EAC（SAS），∴BD＝CE；【解决问题】解：以AB为边向外作等边三角形ABE，连接CE，如图3所示：则∠BAE＝60°，BE＝AB＝AE＝8，∵AD＝CD，∠ADC＝60°，∴△ACD是等边三角形，∴∠CAD＝60°，AC＝AD，∴∠CAD+∠BAC＝∠BAE+∠BAC，即∠BAD＝∠EAC，在△BAD和△EAC中，，∴△BAD≌△EAC（SAS），∴BD＝CE；当C、B、E三点共线时，CE最大＝BC+BE＝15+8＝23，∴BD的最大值为23．。

2021重庆中考26题专题复习及答案5

重庆中考数学26题专题复习1、已知，△ABC中，AB＝AC，∠BAC＝90°，E为边AC任意一点，连接BE．（1）如图1，若∠ABE＝15°，O为BE中点，连接AO，且AO＝1，求BC的长；（2）如图2，F也为AC上一点，且满足AE＝CF，过A作AD⊥BE交BE于点H，交BC 于点D，连接DF交BE于点G，连接AG；①若AG平分∠CAD，求证：AH＝AC；①如图3，当G落在△ABC外时，若将△EFG沿EF边翻折，点G刚好落在AB边上点P，直接写出AG与EF的数量关系．（1）解：如图1中，在AB上取一点M，使得BM＝ME，连接ME．在Rt△ABE中，∵OB＝OE，∴BE＝2OA＝2，∵MB＝ME，∴∠MBE＝∠MEB＝15°，∴∠AME＝∠MBE+∠MEB＝30°，设AE＝x，则ME＝BM＝2x，AM＝x，∵AB2+AE2＝BE2，∴（2x+x）2+x2＝22，∴x＝（负根已经舍弃），∴AB＝AC＝（2+）•，∴BC＝AB＝+1．方法二：作EH⊥BC于H，求出BH，CH即可解决问题．（2）证明：如图2中，作CP⊥AC，交AD的延长线于P，GM⊥AC于M．∵BE⊥AP，∴∠AHB＝90°，∴∠ABH+∠BAH＝90°，∵∠BAH+∠P AC＝90°，∴∠ABE＝∠P AC，在△ABE和△CAP中，，∴△ABE≌△CAP，∴AE＝CP＝CF，∠AEB＝∠P，在△DCF和△DCP中，，∴△DCF≌△DCP，∴∠DFC＝∠P，∴∠GFE＝∠GEF，∴GE＝GF，∵GM⊥EF，∴FM＝ME，∵AE＝CF，∴AF＝CE，∴AM＝CM，在△GAH和△GAM中，，∴△AGH≌△AGM，∴AH＝AM＝CM＝AC（3）解：结论：AG＝EF．理由：如图3中，作CM⊥AC交AD的延长线于M，连接PG交AC于点O．由（2）可知△ACM≌△BAE，△CDF≌△CDM，∴∠AEB＝∠M＝∠GEF，∠M＝∠CFD＝∠GFE，AE＝CM＝CF，∴∠GEF＝∠GFE，∴GE＝GF，∵△EFP是由△EFG翻折得到，∴EG＝EP＝GF＝PF，∴四边形EGFP是菱形，∴PG⊥AC，OE＝OF，∵AE＝CF，∴AO＝OC，∵AB∥OP，∴BP＝PC，∵PF∥BE，∴EF＝CF＝AE，∵PB＝PC，AO＝OC，∴PO＝OG＝AB，∴AB＝PG，AB∥PG，∴四边形ABPG是平行四边形，∴AG∥BC，∴∠GAO＝∠ACB＝45°，设EO＝OF＝a，则OA＝OG＝3a，AG＝3a，∴＝＝，∴AG＝EF2、如图所示，Rt△ABC中，∠ACB＝90°，E为AC中点，作ED⊥AC交AB于D，连接CD；（1）如图1，求证：AB＝2CD；（2）如图2，作CF⊥AB交AB于F，点G为CF上一点，点H为DE延长线上一点，分别连接AH、GH，若∠AHG＝2∠B，求证：AH＝GH；（3）如图3，在（2）的条件下，连接DG，且有DE＝BF，∠EDG＝90°，若AC＝6，求AH的长度．解：（1）∵E为AC中点，作ED⊥AC交AB于D，∴AD＝CD，∵∠ACB＝90°，∴BC∥DE，∴AD＝BD，∴CD＝BD，∴AB＝2CD；（2）如图2，连接CH，∵点E是AC的中点，∴AE＝CE，∵DE⊥AC，∴CH＝AH，∴∠ACH＝∠CAH，∵∠ACB＝90°，∴∠B+∠BAC＝90°，∵CF⊥AB，∴∠BAC+∠ACF＝90°，∴∠ACF＝∠B，∴∠HCG＝∠ACH+∠ACF＝∠CAH+∠B，∠AHG＝2∠B∴在四边形AHGF中，∠AFG+∠FGH+∠AHG+∠F AH＝360°，∴∠FGH＝360°﹣（∠AFG+∠AHG+∠F AH）＝360°﹣（90°+2∠B+∠CAH+∠BAC）＝360°﹣（90°+2∠B+∠CAH+90°﹣∠B）＝360°﹣（180°+∠B+∠CAH）＝180°﹣（∠B+∠CAH），∵∠CGH＝180°﹣∠FGH＝∠B+∠CAH＝∠HCG，∴CH＝GH，∵CH＝AH，∴AH＝GH；（3）如图3，由（1）知，DE∥BC，∴∠B＝∠ADE，在△BFC和△DEA中，，∴△BFC≌△DEA，∴BC＝AD，∵AD＝BD＝CD，∴BC＝BD＝CD，∴△BCD是等边三角形，∴∠B＝60°，在Rt△ABC中，AC＝6，∴BC＝2，AB＝4，∵CF⊥BD，∴DF＝，CF＝3，∵∠BAC＝30°，∴∠ADE＝60°，∵∠EDG＝90°，∠FDG＝30°，在Rt△DFG中，DF＝，∴FG＝1，DG＝2，∴CG＝CF﹣FG＝2过点H作HN⊥CF，由（2）知，CH＝GH，∴NG＝CG＝1，∴FN＝NG+FG＝2，过点H作HM⊥AB，∴∠FMH＝∠NFM＝∠HNF＝90°，∴四边形NFMH是矩形，∴HM＝FN＝2，在Rt△DMH中，∠ADE＝60°，HM＝2，∴DH＝，在Rt△HDG中，根据勾股定理得，HG＝＝．3、一节数学课后，老师布置了一道课后练习题：如图：已知在Rt△ABC中，AC＝BC，∠ACB＝90°，CD⊥AB于点D，点E、F分别在A和BC上，∠1＝∠2，FG⊥AB于点G，求证：△CDE≌△EGF．（1）阅读理解，完成解答本题证明的思路可用下列框图表示：根据上述思路，请你完整地书写这道练习题的证明过程；（2）特殊位置，证明结论若CE平分∠ACD，其余条件不变，求证：AE＝BF；（3）知识迁移，探究发现如图，已知在Rt△ABC中，AC＝BC，∠ACB＝90°，CD⊥AB于点D，若点E是DB的中点，点F在直线CB上且满足EC＝EF，请直接写出AE与BF的数量关系．（不必写解答过程）（1）证明：∵AC＝BC，∠ACB＝90°，∴∠A＝∠B＝45°，∵CD⊥AB，∴∠CDB＝90°，∴∠DCB＝45°，∵∠ECF＝∠DCB+∠1＝45°+∠1，∠EFC＝∠B+∠2＝45°+∠2，∠1＝∠2，∴∠ECF＝∠EFC，∴CE＝EF，∵CD⊥AB，FG⊥AB，∴∠CDE＝∠EGF＝90°，在△CDE和△EGF中，，∴△CDE≌△EGF（AAS）；（2）证明：由（1）得：CE＝EF，∠A＝∠B，∵CE平分∠ACD，∴∠ACE＝∠1，∵∠1＝∠2，∴∠ACE＝∠2，在△ACE和△BEF中，，∴△ACE≌△BEF（AAS），∴AE＝BF；（3）AE＝BF，作EH⊥BC与H，如图3所示：设DE＝x，根据题意得：BE＝DE＝x，AD＝BD＝2x，CD＝AD＝2x，AE＝3x，根据勾股定理得：BC＝AC＝2x，∵∠ABC＝45°，EH⊥BC，∴BH＝x，∴CH＝BC﹣BH＝x，∵EC＝EF，∴FH＝CH＝x，∴BF＝x﹣x＝x，∴＝，∴AE＝．。

2018年重庆中考数学第26题专题训练

（1）求抛物线的解析式并直接写出点D 的坐标；
（2）点P为直线x=1右方抛物线上的一点（点P不与点B重合），记A、B、C、P四点所构成的四边形面积为，若，求点P的坐标；
（3）点Q是线段BD上的动点，将△DEQ沿边EQ翻折得到△ ，是否存在点Q使得△ 与△BEQ的重叠部分图形为直角三角形，若存在，请求出BQ的长，若不存在，请说明理由．
8.如图1，已知抛物线与轴交于两点（点在点的左侧），与轴交于点，点是点关于抛物线对称轴的对称点，连接，过点作轴于点，过点作交的延长线于点 .
（1）求线段的长度；
（2）如图2，试在线段上找一点，在线段上找一点P，且点为直线上方抛物线上的一点，求当的周长最小时，面积的最大值是多少；
设点Q是线段AC上的动点，作QD⊥x轴交抛物线于点D，求线段QD长度的最大值。
4.如图，已知抛物线y=x2+bx+c的图象与x轴的一个交点为B（5，0），另一个交点为A，且与y轴交于点C（0，5）．
（1）求直线BC与抛物线的解析式；
（2）若点M是抛物线在x轴下方图象上的一动点，过点M作MN∥y轴交直线BC于点N，求MN的最大值；
1.如图，抛物线y=﹣x2﹣2x+3 的图象与x轴交于A、B两点（点A在点B的左边），与y轴交于点C，点D为抛物线的顶点．
（1）求Aபைடு நூலகம்B、C的坐标；
（2）点M为线段AB上一点（点M不与点A、B重合），过点M作x轴的垂线，与直线AC交于点E，与抛物线交于点P，过点P作PQ∥AB交抛物线于点Q，过点Q作QN⊥x轴于点N．若点P在点Q左边，当矩形PQMN的周长最大时，求△AEM的面积；
（3）如图2，以AC为对角线作正方形AMCN，将正方形AMCN在平面内平移得正方形A′M′C′N′．当正方形A′M′C′N′有顶点在△ABC的边AC上（不含端点）时，正方形A′M′C′N′与△ABC重叠部分得到的多边形能否为轴对称图形，如果能，求出此时重叠部分面积S的值，或重叠部分面积S的取值范围；如果不能，请说明理由．

2020年重庆中考26题二次函数综合

二次函数二次函数压轴题总结：（凡解析几何问题，均是以几何性质探路，代数书写竣工。

）已知、 y=322--x x （以下几种分类的函数解析式就是这个）1、和最小，差最大在对称轴上找一点P ，使得PB+PC 的和最小，求出P 点坐标在对称轴上找一点P ，使得PB-PC 的差最大，求出P 点坐标解决方案：识别模型，A 、若为过河问题模型，根据“异侧和最小，同侧差最大，根据问题同侧异侧相互转化”；B 、若有绝对值符号或不隶属于过河问题，可将问题形式平方，构建函数，转化为求函数最值问题（若表达式中含有根式等形式，可考虑用换元法求最值）。

2、求面积最大连接AC,在第四象限抛物线上找一点P ，使得ACP ∆面积最大，求出P 坐标解决方案：熟悉基本图形的面积公式【或根据拼图思想，采用割补法求面积（注意不重不漏）。

】，根据问题，灵活选择面积公式，务必使表达式简单，变量的最值好求，讲变量的最值问题转化为：”定值+变量的最值“3、讨论直角三角连接AC,在对称轴上找一点P ，使得ACP ∆为直角三角形，求出P 坐标或者在抛物线上求点P ，使△ACP 是以AC 为直角边的直角三角形．解决方案：此类问题是分类讨论思想能力的考察，由于直角三角形的”直角边“”和“斜边”不确定而展开讨论。

在不忘三角形满足三边关系的条件下，勿忘“等腰直角三角形”。

4、讨论等腰三角连接AC,在对称轴上找一点P ，使得ACP ∆为等腰三角形，求出P 坐标解决方案：分析同上4，在能组成△的大前提下，根据谁作为腰，谁作为底边展开讨论。

5、讨论平行四边形 1、点E 在抛物线的对称轴上，点F 在抛物线上，且以B ，A ，F ，E 四点为顶点的四边形为平行四边形，求点F 的坐标解决方案：从平行四边形的性质入手，已知三点求另外一点，分析其位置情况（分别以3点中任一已知两点的线段为平行四边形的边或其对角线来展开所有的情况的讨论）。

6、相似三角形问抛物线上是否存在一动点D ，使得△ABD ∽△ABC 。

2019重庆中考第26题二次函数综合问题探索举例(含解题思路提示)

P若A(m,n)，则C(-n,m)OA=OC1x 2019重庆中考26题二次函数综合问题探索举例二次函数综合问题，是重庆历届中考必考题，在解答此类问题时，除二次函数、一次函数等必备的知识外，还涉及到如下一些知识：1.两点的所有连线中，线段最短，简单说成：两点之间，线段最短（新人教版七上基础知识）2.连接直线外一点与直线上各点的所有线段中，垂线段最短.简单说成：垂线段最短. （新人教版七下基础知识）3.两点P 1(x 1,y 1)，P 2(x 2,y 2)的距离公式：P 1P 2 =212212)y y ()x x (-+- （新人教版八下拓展知识）特别：当P 1P 2∥y 轴时，P 1P 2 =12y y -. 当P 1P 2∥x 轴时，P 1P 2 =12x x -.4.两直线y=k 1x+b 1，y=k 2x+b 2平行的条件：k 1=k 2，且b 1≠b 2. （新人教版八下拓展知识）5.两直线y=k 1x+b 1，y=k 2x+b 2垂直的条件：k 1k 2=-1. （新人教版八下拓展知识）如图，直线y=k 1x ，y=k 2x 垂直的条件是：k 1k 2=-1.6.常见图形的计算、性质、判定等.答图1图1典例探索例1.（2019重庆B 卷）在平面直角坐标系中，抛物线y=32x 23x 432++-与x 轴交于A ，B 两点（点A 在点B 左侧），与y 轴交于点C ，顶点为D ，对称轴与x 轴交于点Q.（1）如图1，连接AC ，BC.若点P 为直线BC 上方抛物线上一动点，过点P 作PE ∥y 轴交BC 于点E ，作PF ⊥BC 于点F ，过点B 作BG ∥AC 交y 轴于点G.点H ，K 分别在对称轴和y 轴上运动，连接PH ，HK.当△PEF 的周长最大时，求PH+HK+23KG 的最小值及点H 的坐标. （2）如图2，将抛物线沿射线AC 方向平移，当抛物线经过原点O 时停止平移，此时抛物线顶点记为D /，N 为直线DQ 上一点，连接点D /，C ，N ，△D /CN 能否构成等腰三角形？若能，直接写出满足条件的点N 的坐标；若不能，请说明理由.思路：点坐标→PH+HK+23KG 的最小值→H 的坐标. （2）由条件→新抛物线→设出N 的坐标求得D /N ，D /C ，CN →建立方程求出N 的坐标.提示：（1）易求A(-2,0)，B(4,0)，C(0,32)，D(1,439)，△PEF ∽△BOC. ∴当PE 最大时，△PEF 的周长最大.易求直线BC 的解析式为y=32x 23+- 设P(x, 32x 23x 432++-)，则E(x, 32x 23+-) ∴PE=32x 23x 432++--(32x 23+-)=x 3x 432+- ∴当x=2时，PE 有最大值. ∴P(2, 32)，此时，如图将直线OG 绕点G 逆时针旋转60 °得到直线l ，过点P 作PM ⊥l 于点M ，过点K 作KM /⊥l 于M /.则PH+HK+23KG= PH+HK+KM /≥PM ，易知∠POB=60°.POM 在一直线上.易得PM=10，H(1,3)（2）易得直线AC 的解析式为y=32x 3+，过D 作AC 的平行线，易求此直线的解析式为y=435x 3+，所以可设D /(m, 435m 3+)，平移后的抛物线y 1=435m 3)m x (432++--.将（0，0）代入解得m 1=-1（舍），m 2=5.所以D /(5,4325). 设N(1,n)，又C(0,32)，D /(5,4325). 所以NC 2=1+(n-32)2，D /C 2=22)324325(5-+=161267，D /N 2=22)n 4325()15-+-（. 分NC 2= D /C 2；D /C 2= D /N 2；NC 2= D /N 2.列出关于n 的方程求解.答案N 1(1,4139338+)，N 2(1, 4139338-)，N 3(1,41011325+)，N 4(1, 41011325-)，N 5(1,1363641). 例2.（2019重庆A 卷）如图，在平面直角坐标系中，抛物线y=x 2-2x-3与x 轴交于点A ，B（点A 在点B 的左侧）交y 轴于点C ，点D 为抛物线的顶点，对称轴与x 轴交于点E. （1）连结BD ，点M 是线段BD 上一动点（点M 不与端点B ，D 重合），过点M 作MN ⊥BD 交抛物线于点N （点N 在对称轴的右侧），过点N 作NH ⊥x 轴，垂足为H ，交BD 于点F ，点P 是线段OC 上一动点，当MN 取得最大值时，求HF+FP+31PC 的最小值；（2）在（1）中，当MN 取得最大值，HF+FP+31PC 取得最小值时，把点P 向上平移22个单位得到点Q ，连接AQ ，把△AOQ 绕点O 顺时针旋转一定的角度α(0°<α<360°)，得到△A /OQ /，其中边A /Q /交坐标轴于点G ，在旋转过程中，是否存在一点G ，使得∠Q /=∠Q /OG ？若存在，请直接写出所有满足条件的点Q /的坐标；若不存在，请说明理由.思路：（1）MN 取得最大值→FN 最大→点F 坐标及HF 的值→HF+FP+31PC 的最小值. （2）由P 的坐标→Q 点坐标→注意∠Q /=∠AQO 构成直角三角形，求出Q /的坐标.提示：（1）易得A(-1,0)，B(3,0)，C(0,-3)，D(1,-4)，E(1,0).直线BD 的解析式为y=2x-6. 易得△MNF ∽△EBD ，所以要MN 取最大值，只要FN 设N(x, x 2-2x-3)，F(x,2x-6). 则FN=-x 2+4x-3，∴当x=2时，FN 最大，此时MN 最大，F(2,-2)，HF=2. ∴当FP+31PC 最小时，HF+FP+31PC 最小. 如图，以PC 为斜边，31PC 的长为直角边，作Rt △CRP ，其中PR=31PC 因此，当点F ，P ，R 在一条直线上时，FP+31PC 最小.此时，过F 作y 为S ，则△CPR ∽△FPS.又易得FS=2. S(0,-2) SP=22，FP=223，PC=CS-PS=222-，所以PR=31PC=622-.答案3247+（2）由（1）知SP=22，将P 向上平移22个单位得到的Q 点即为S 点，所以OQ=2. 如图，过Q /作Q /T ⊥x 轴于T.在Rt △OQ /T 中，易得∠Q /OT 的正切为一定值.结合勾股定理及方程思想求出两直角边.552)，(552,554-).例3.（2019重庆中考考试说明题型示例）在平面直角坐标系中，抛物线y=22x 23x 422-+与x 轴交于A 、B 两点（点A 在点B 左侧），与y 轴交于点C.（1）如图甲所示，点D 是抛物线第二象限上一点，且满足22x x A D =-，过点D 作AC 的平行线，分别与x 轴、射线CB 交于点F 、E ，点P 为直线AC 下方抛物线上的一动点，连接PD 交线段AC 于点Q ，当四边形PQEF 面积最大时，在y 轴上找一点M ，x 轴上找一点N ，使得PM+MN-53NB 取得最小值；（2）如图乙所示，将△BOC 沿直线AC 平移得到△B /O /C /，再将△B /O /C /沿B /C /翻折得到△B /O //C /，连接C /B ，O //B ，则△C /BO //能否构成等腰三角形？若能，请直接写出所有符合条件的点O //的坐标；若不能，请说明理由.思路：（1）四边形PQEF 面积最大→△PDF 的面积最大→P 点坐标→PM+MN-53NB 最小值. （2）由条件表达出C /，B ，O //的坐标→求得C /B ，O //B ，O //C /→建立方程求出O //的坐标. 提示：（1）易得A(24-,0)，B(2,0)，C(0,22-)，又点D 是抛物线第二象限上一点，且满足22x x A D =-，∴D(26-,27).易得直线AC 的解析式y=22x 21--，∴直线DF 的解析式为y=24x 21+-，易得直线CB 的解析式为y=22x 2-. ∴易得F(28,0)，E(2512,2514). ∵四边形PQEF 面积=△PDF 的面积－△DQE 的面积.而平行线得，△DQE 的面积=△DAE 的面积.而△DAE 的面积为定值，∴当△PDF 的面积最大时，四边形PQEF 面积最大. 过P 作PT ⊥x 轴，交DF 于点T ，则当PT 最大时，△PDF 的面积最大. 设P(x, 22x 23x 422-+)，则T(x, 24x 21+-).PT=24x 21+--(22x 23x 422-+)=26x 2x 422+--， ∴当x=22-时，PT 最大，此时P(22-,23-). △PDF 的面积最大，四边形PQEF 面积最大.如图，作点P 关于y 轴的对称点P /(22,23-).过点B 作直线l : y=243x 43-(针对53NB) 过P /作直线l ////PM+MN-53NB 5即为所求的最小值.易求直线l /的解析式为y=32x 34--，∴W(52,523-)，∴P /W=23.答案23.（2）易得直线AC 的解析式为y=22x 21--，直线OO /的解析式为y=x 21-，直线BB /解析式为y=22x 21+-.直线BC 的解析式为y=22x 2- . AC ⊥BC.设O /(t, t 21-)，则C /(t, 22t 21--)，B /(2t +,t 21-)，则直线B /C /的解析式为y=22t 25x 2--，所以O /O //与B /C /的交点坐标为(524t (+,522t 21--)，所以O //(528t +,524t 21--). ∴C /B 2=22)22t 21()2t (++-=10t 452+. O //C / 2=O /C / 2=OC 2=8. O //B 2=22)524t 21()2528t (++-+=2t 22t 452++.若C /B=O //C /.则10t 452+=8，此无解，舍去.若C /B=O //B.则10t 452+=2t 22t 452++，解得t=22.∴O //(5281,529-). 若O //B= O //C /.则2t 22t 452++=8，解得t 1=538224+-，t 2=538224--∴O //(538224+,53822+-)，O //(538224-,53822--). 答案O //(5281,529-)或O //(538224+,53822+-)或O //(538224-,53822--).图1图2答图如下例 4.（2019重庆中考考试说明参考试卷）如图所示，在平面直角坐标系中，抛物线y=3x 332x 332--与x 轴交于A 、B 两点（点A 在点B 的左侧），与y 轴交于点C ，对称轴与x 轴交于点D ，点E(4,n)在抛物线上.（1）点P 为直线CE 下方抛物线上的一点，连接PC ，PE.当△PCE 的面积最大时，连接CD ，CB ，点K 是线段CB 的中点，点M 是CP 上的一点，点N 是CD 上的一点，求KM+MN+NK 的最小值；（2）点G 是线段CE 的中点，将抛物线y=3x 332x 332--沿x 轴正方向平移得到新抛物线y /，y /经过点D ，y /的顶点为点F. 在新抛物线y /的对称轴上，是否存在一点Q ，使得△FGQ为等腰三角形？若存在，请直接写出点Q 的坐标，若不存在，请说明理由.思路：（1）△PCE 的面积最大→P 点坐标→KM+MN+NK 的最小值.（2）由条件→新抛物线→设Q 点坐标→求出FG ，GQ ，FQ →建立方程求出Q 点的坐标. 提示：（1）易得A(-1,0)，B(3,0)，C(0,3-)，D(1,0)，E(4,335).则易得直线CE 的解析式为y=3x 332-.过P 作x 轴的垂线交直线CE 于T ，则当PT 最大时，△PCE 的面积最大. 设P(x, 3x 332x 332--)， T(x, 3x 332-).PT=3x 332--(3x 332x 332--)=x 334x 332+-. ∴当x=2时，PT 最大，△PCE 的面积最大，此时P(2, 3-). 由OC=3，OB=3，易得∠OCB=60°.又易得DB=DC=2.CP ∥x 轴，K 关于CD 对称的点就是点O. 设K 关于CP 对称的点K /.连接OK /交CP 于M ，交DC 于N.则此时的M 、N 使得KM+MN+NK 最小.答案KM+MN+NK 最小值是3. （2）易得F(3,334-)，G(2,33)，设Q(3,t).则FG 2=328. GQ 2=2)33t (1-+=34t 332t 2+-. QF 2=2)334t (+=316t 338t 2++. 若GQ=FG ，则34t 332t 2+-=328，解得t=32或t=334-(此时Q 与F 重合，舍). 若GQ=QF ，则34t 332t 2+-=316t 338t 2++，解得t=532-. 若QF=FG ，则316t 338t 2++=328，解得t=321234+-或t=. 答案Q(3, 32)或(3, 532-)或(3, 321234+-)或(3, 321234--).例5.（2019重庆巴蜀三诊）如图1，抛物线x 63y 2+-=A 、B 两点（点A 在点B 的右侧），与y 轴相交于点C ，对称轴与x 轴相交于点H ，与AC 相交于点T. （1）点P 是线段AC 上方抛物线上一点，过点PQ ∥AC 交抛物线的对称轴于点Q ，当△AQH 面积最大时，点M 、N 在y 轴上（点M 在点N 的上方），MN=3，点G 在直线AC 上，求PM+NG+21GA 的最小值. （2）点E 为BC 中点，EF ⊥x 轴于F ，连接EH ，将△EFH 沿EH 翻折得△EF /H ，如图2所示，再将△EF /H 沿直线BC 平移，记平移中的△EF /H 为△E /F //H /，在平移过程中，直线E /H /与x 轴交于点R ，则是否存在这样的点R ，使得△RF /H /为等腰三角形，若存在，求出R 点坐标.思路：（1）△AQH 面积最大→△APT 面积最大→P 的坐标→PM+NG+21GA 的最小值. （2）由条件表达出F /，H /，R 的坐标→求出F /H /，F /R ，H /R →建立方程求出R 的坐标.提示：（1）由题意得B(-2,0)，A(6,0)，C(0,32)，设AC 与对称轴交于T ，连接AQ ，PT ，PA.如图.∵S △AQH =S △ATH + S △AQT 而S △ATH 为定值338. ∴△AQH 的面积最大，即△AQT 的面积最大. 又PQ ∥AC ，∴S △AQT =S △APT . 过点P 作PR ∥y 轴交AC 于R. 易求得AC 的解析式为y=32x 33+-设P(m, 32m 332m 632++-)，则R(m, 32m 33+-)S △APT =4)m 3m 63(212⨯+-⨯=m 32m 332+-.∴当m=3时面积最大，此时P(3,235). 过点G 作GE ⊥x 轴交x 轴于E ，作x 轴关于直线AC 的对称直线l ，E 的对称点为E /，将PM 沿y 轴向下平移3个单位至P /N ，作点P /关于y 轴的对称点P //，作P //S ⊥l 于点S.如图所示，则有PM+NG+21GA=P //N+NG+GE //≥P //S.易求P //S=4315 （2）易得△ABC ，△BOC ，△EFH 均为含30E(-1,3)，F(-1,0)，H(2,0)，F /(21,233). 易得直线BC 的解析式为y=32x 3+，直线HH /的解析式为y=32x 3-，直线EH 的解析式为y=332x 33+-. 将△EF /H 沿直线BC 平移，设在水平方向上记平移|t|个单位.则平移后的△E /F //H /中易得E /(t-1,3t 3+)，H /(t+2,t 3)，易得直线E /H /的解析式为y=332t 334x 33++-. ∴R(4t+2,0). ∴(F /H /)2=22)233t 3()212t (-+-+=4t 2-6t+9.(H /R)2=22)t 30()]2t ()2t 4[(-++-+=12t 2. (F /R)2=22)2330()212t 4(-+-+=16t 2+12t+9.图1若F /H /= H /R ，4t 2-6t+9=12t 2.解得t=43或t=23-，此时R(5,0)（此时F /、H /、R 共线，舍）或R(-4,0). 若F /H /= F /R ，4t 2-6t+9=16t 2+12t+9，解得t=0或t=23-，此时R(2,0)（此时H /、R 重合，舍）或R(-4,0). 若H /R= F /R ，12t 2=16t 2+12t+9.解得t 1=t 2=23-，此时R(-4,0).答案R(-4,0). 例6.（2019重庆南开测试四）如图，在平面直角坐标系中，抛物线3x 49x 43y 2++-=与x 轴交于A ，B 两点（点A 在点B 左侧），与y 轴交于点C ；连接BC.点P 为线段BC 上方抛物线上的一动点，连接OP 交BC 于点Q.（1）如图1，当OQ PQ值最大时，点E 为线段AB 上一点，在线段BC 上有两动点M ，N （M在N 上方），且MN=1，求PM+MN+NE-53BE 的最小值；（2）如图2，连接AC ，将△AOC 沿射线CB 方向平移，点A ，C ，O 平移后的对应点分别记作A 1，C 1，O 1，当C 1B=O 1B 时，连接A 1B ，O 1B ，将△A 1O 1B 绕点O 1沿顺时针方向旋转90°后得△A 2O 1B 1，在直线x=21上是否存在点K ，使得△A 2B 1K 为等腰三角形？若存在，直接写出点K 的坐标；若不存在，请说明理由.思路：（1）OQ PQ值最大→P 点坐标→PM+MN+NE-53BE 的最小值.（2）由条件表达出A 2，B 1，K 的坐标→求出A 2B 1，B 1K ，A 2K →建立方程求出K 的坐标. 提示：（1）易得A(-1,0)，B(4,0)，C(0,3).直线BC 的解析式为y=3x 43+-. 过点P 作PH ∥y 轴交BC 于H.令P(a,3a 49a 432++-)，则H(a, 3a 43+-)，∴PH=a 3a 432+-.易得△PQH ∽△OQC ，∴OQ PQ =O CPH=3a3a 432+-=a a 412+-∴当a=2时，OQPQ最大，此时P(2,29)将P 沿MN 方向平移1个单位（即向右平移54，向下平移53）得P /(514,1093).过点A 作AJ ∥CB.过点E 作EK ⊥AJ 于K ，过点P /作P /K /⊥AJ 于K /.则 PM+MN+NE-53BE= PM+MN+NE-53(AB-AE)= PM+MN+NE+53AE-53AB =P /N+NE+EK-2≥P /K /-2=2527-=517. 注：MN=1，EK=53AE ，53AB=3，易得直线AJ 的解析式为y=43x 43--，直线P /K /的解析式为y=61x 34+，∴K /(2511-,5021-），P /K /=527. 答案最小值为517. （2）易得直线AA 1的解析式为y=43x 43--，直线OO 1的解析式为y=x 43-，又直线BC 的解析式为y=3x 43+-.设A 1(t-1,t 43-)，则C 1(t,3t 43+-)，O 1(t, t 43-).又B(4,0)， ∴当C 1B=O 1B 时，22)3t 43()4t (+-+-=22)t 43()4t (-+-，解得：t=2. ∴A 1(1,23-)，O 1(2, 23-)，∴A 2(2,21-)，B 1(27,27-) 设K(21,y)，则A 2K 2=22)y 21()212(--+-=25y y 2++，A 2B 12=45， B 1K 2=22)y 27()2127(--+-=485y 7y 2++. 若A 2K= A 2B 1，25y y 2++=445，解得y=25或y=27-. 若A 2B 1=B 1K ，445=485y 7y 2++，解得y=-2或y=-5. 若A 2K= B 1K ，25y y 2++=485y 7y 2++，解得y=825- 答案K 1(21,25)(此时K 1、A 2、B 1在一直线上，舍去)， K 2(21,27-)，K 3(21,-2)，K 4(21,-5)，K 5(21,825-). 反思：重庆中考二次函数的综合题，一般设计两个问：第（1）问，通常是线段（均可转化为线段）取最值时，求几条线段和差的最值. 第（2）问，通常是在图形变换下，出现特殊情况时，直接写出坐标.看视较难，其实还是有一定的解题思路:（1）把动点产生的最值问题，转化为动线段的最值，确定其动点取最值时的坐标，再把几条线段和差转化为几何图形的有关最值，或把几条线段和差转化为代数问题求最值.（2）在经历图形变换后，需要求出相关线段的长度，利用方程思想求出其中未知数的值，写出坐标.车到山前必有路，船到桥头自然直，山穷水尽疑无路，柳暗花明又一村.只要不断向前做，定会发现新思路.。

重庆数学中考26题专题训练

重庆中考数学26题专项.doc

2021年重庆中考数学第26题几何证明专题训练

2020年重庆中考几何第26题专题训练一(含答案解析)

2020重庆中考复习数学第26题专题训练六(含答案解析)

2020重庆中考复习数学第26题专题训练六(含答案解析)

最新2018重庆中考数学第26题专题训练

中考数学复习专题训练精选试题及答案

最新重庆中考数学第26题专题训练

重庆中考第26题专题专训(教师版)

2020重庆中考复习数学第26题专题训练五(含答案解析)

重庆中考26题专题训练

2023重庆中考数学b卷压轴题26题

2021重庆中考26题专题复习及答案2

2021重庆中考26题专题复习及答案5

2018年重庆中考数学第26题专题训练

2020年重庆中考26题二次函数综合

2019重庆中考第26题二次函数综合问题探索举例(含解题思路提示)