2019重庆中考数学第24题专题训练二(含部分答案)
2019重庆中考数学第24题专题训练十二
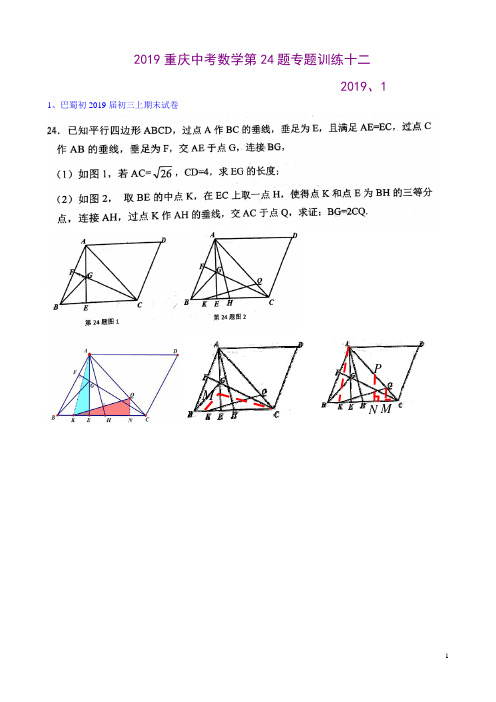
2019重庆中考数学第24题专题训练十二2019、1 1、巴蜀初2019届初三上期末试卷PM2、重庆市南岸区11中、二外、珊瑚2018-2019学年度上期三校期末联考九年级数学4、2018-2019学年重庆实验外国语学校九年级数学定时练习试题如图△ABC,以AC为斜边向下作等腰直角△ADC,直角边AD交BC于点EBC=+DC的长;(1)如图1,若∠ACB=30°,∠B=45°,BC=2(2)如图2,若等腰R△ADC的直角顶点D恰好落在线段BC的垂直平分线上,过点A作AF⊥BC于点F,连接DF,求证:AB=.图1 图26、如图,△ABC中,∠BAC=5°,点D是AB边上一点,且CB=CD,过点B作BH⊥CD于H,交AC于E(1)若CH=4,DH=2,求△BCD的面积;(2)求证:∠BEC=∠A+12∠BCD;(3)用等式表示AE与BD之间的数量关系;并证明。
7、如图,在△DAC中,DADC,E是AC上的一点,CD=CE连接DE(1)若AC=16,CD=10,求DE的长;(2)若∠ACG=∠DAC,且GC=GF=CH且CH⊥GF,垂足为P,求证CF.8、如图1,在五边形 ABCDE 中∠,E=90°,BC=DE 连接AC,AD,且⊥AB=AD,AC BC (1)求证:AC=AE; (2)如图2,若∠ABC=∠CAD,AF 为BE 边上的中线,求证:AF ⊥CDABB图1 图2方法一:方法二:N方法三:9、如图①,在等腰Rt△ABC中,∠ACB=90°,点D在AC上(且不与点A,C重合),以AD为直角边向外作等腰Rt△ADE,使∠ADE=90°,连接CE,再以CE、CB为邻边作平行四边形CBFE(1)已知,求线段CF的长;(2)将Rt△ADE绕点A逆时针旋转角a(90°<a<180°),如图②,连接CD、CE,再以CE、CB为邻边作平行四边形CBFE,设线段AB、CE交于点G,求证:CF=CD.10、已知,在△ABC中,∠ABC=45,高线AD、BE相交于点G,(1)如图,若∠CAD=30°,GE=2,求DG的长(2)如图2,连接DE,过点D作DF⊥DE交BE于点F,连接AF,过点D作DH⊥AF于点H交BE于点M求证:AF=2DM11、如图在ABC中,过点A作AE⊥BC交BC于E,D为△BC外一点且AD⊥DC,AD交BC 于F,连接、D,已知AE=BE,AD= DC.(1) AB=,,求DC长度;(2)求证:∠CBD+∠ACE=45B CADM12、八中2019级周考1513、如图,平行四边形ABCD 中,过点B 作BE⊥CD 于点E,点F 是AD 上一点,连接BF、CF,交BE 于点G.. (1)若CF 平分∠BCD,∠A=60°,BC=,求线段CG 的长。
2019重庆中考数学第24题专题训练---矩形(含答案)

2019重庆中考数学第24题专题训练---矩形1、沙坪坝区2017—2018学年度第二学期期末调研测试八年级数学试题如图,在矩形ABCD 中,点E 为AD 上一点,连接BE 、CE ,∠ABE =45°. (1)如图1,若32BE,BC =4,求EC 的长.(2)如图2,点P 是EC 的中点,连接BP 并延长交CD 于F ,H 为AD 上一点,连接HF ,且∠DHF =∠CBF ,求证:BP=PF+FH .2、重庆市南开(融侨)中学初2019级暑假作业数学综合练习 已知,如图所示,在矩形ABCD 中,点E 为BC 边上,∠AEF=90°.(1)如图1,已知点F 在CD 边上,AD=AE,AD=5,AB=4,求DF 的长; (2)如图2,已知AE=EF,点G 为AF 的中点,求证:2.AB BE BG +=FCDFG图1 图23、重庆第二外国语学校初2019级初三年级第二学月质量检测如图,在矩形ABCD 中,点E 为BC 边上一点,过点E 作EF ⊥DE 于点E. (1)如图1,已知F 在AB 上,AD=DE,AD=10, CD=6, 求BF 的长; (2)如图2,已知DE=EF ,点G 为DF 的中点,求证:2.CD EC CG +=4、已知:在矩形ABCD 中,点H 是对角线AC 与BD 交点,点E 是AB 上的一点,连接HE,连接CE 交BD于F.(1) 如图1,若HE ⊥AC.且BC=3,AB=4,求△BEH 的面积; (2) 如图2,若∠AEB=∠BEC,求证:F 是BH 的中点.5、重庆巴蜀中学2019届初三下半期如图1,在矩形ABCD 中,AC 为矩形的对角线,点E 为AD 边上一点,连接BE. (1)若045EBC ∠=,且BE=CB ,AB=2,求AC 的长;(2)如图2,过B 作BF ⊥BE,使得BF=CD,连接CF 交BE 于点G,,当G 为CF 的中点时,求证:AE=2BG.6、重庆南开(融侨)中学初2018届初三下入学在矩形ABCD 中,点F 在AD 延长线上,且DF=DC,M 为AB 边上一点,N 为MD 的中点,点E 在直线CF 上,且BN=NE.(1)如图1,若AB=BC=6,13BM AB =,E 为线段FC 上的点,求NE 的长;(2)如图2.若AB<BC,E 为线段FC 延长线上的点,连结BE,求证:2.BE NE =7、重庆一中初2018级17—18学年度下期第一次定时作业如图1:在矩形ABCD中,AC为对角线,延长CD至点E使CE=CA,连接AE,F为AB上一点,且BF=DE,连接FC.(1)若DE=1,CF=22,求CD的长;(2)如图2,点G为线段AE的中点,连接BG交AC于H,若∠BHC+∠ABG=60°,求证:AF+CE=3AC.8、重庆巴蜀中学初2018级17—18学年度下期第一次月考在矩形ABCD中,对角线AC、BD交于点O,E为OB上一点,连接CE,G为CE中点.(1)如图1,连接AE,OG,若∠DAC=60°,BE=2,AB=53,求OG的长;(2)如图2,点F为线段OC上一点,连接BF,BG,若∠COB=∠OBG=∠CBF,求证:BE+CF=OA.2019重庆中考数学第24题专题训练---矩形答案1、沙坪坝区2017—2018学年度第二学期期末调研测试八年级数学试题如图,在矩形ABCD 中,点E 为AD 上一点,连接BE 、CE ,∠ABE =45°. (1)如图1,若32BE,BC =4,求EC 的长.(2)如图2,点P 是EC 的中点,连接BP 并延长交CD 于F ,H 为AD 上一点,连接HF ,且∠DHF =∠CBF ,求证:BP=PF+FH .解:(1)∵矩形ABCD ,∴∠A =∠D =90° 又∵∠ABE =45° ∴AB =AE设AB =AE =x 在Rt △ABE 中,∠A =90° 222AB AE BE += 即(22233x x += 解得:13x = 23x =-(舍) ∴AB =AE =3∵矩形ABCD ∴ AB =CD =3, BC =AD =4 ∴ED =AD -AE =4-3=1 在Rt △CDE 中,∠D =90° 22223110CE CD ED =++ (2)如答图,延长BF 交AD 的延长线于G ∵AG ∥BC , ∴∠G =∠PBC 又∵P 为CE 的中点, ∴EP =CP 在△EPG 和△CPB 中 G PBCEPG CPB EP CP ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△EPG ≌△CPB (AAS ) ∴BP =GP∵∠DHF =∠CBF ,∠CBF=∠G ∴∠DHF=∠G ∴FH =FG ∴GP =PF +FG =PF +FH2、重庆市南开(融侨)中学初2019级暑假作业数学综合练习 已知,如图所示,在矩形ABCD 中,点E 为BC 边上,∠AEF=90°. (1)如图1,已知点F 在CD 边上,AD=AE,AD=5,AB=4,求DF 的长; (2)如图2,已知AE=EF,点G 为AF 的中点,求证:2.AB BE BG +=ABCDEFABCDFEGH图1 图23、重庆第二外国语学校初2019级初三年级第二学月质量检测如图,在矩形ABCD 中,点E 为BC 边上一点,过点E 作EF ⊥DE 于点E. (1)如图1,已知F 在AB 上,AD=DE,AD=10, CD=6, 求BF 的长;(2)如图2,已知DE=EF ,点G 为DF 的中点,求证:.CD EC +=解答:M4、已知:在矩形ABCD中,点H是对角线AC与BD交点,点E是AB上的一点,连接HE,连接CE交BD 于F.(3)如图1,若HE⊥AC.且BC=3,AB=4,求△BEH的面积;(4)如图2,若∠AEB=∠BEC,求证:F是BH的中点.解答:M5、重庆巴蜀中学2019届初三下半期如图1,在矩形ABCD 中,AC 为矩形的对角线,点E 为AD 边上一点,连接BE. (1)若045EBC ∠=,且BE=CB ,AB=2,求AC 的长;(2)如图2,过B 作BF ⊥BE,使得BF=CD,连接CF 交BE 于点G,,当G 为CF 的中点时,求证:AE=2BG.解法一:解法二:解法三:解法四:6、重庆南开(融侨)中学初2018届初三下入学在矩形ABCD 中,点F 在AD 延长线上,且DF=DC,M 为AB 边上一点,N 为MD 的中点,点E 在直线CF 上,且BN=NE.(1)如图1,若AB=BC=6,13BM AB =,E 为线段FC 上的点,求NE 的长; (2)如图2.若AB<BC,E 为线段FC 延长线上的点,连结BE,求证:2.BE NE =如图1:在矩形ABCD中,AC为对角线,延长CD至点E使CE=CA,连接AE,F为AB上一点,且BF=DE,连接FC.(1)若DE=1,CF=22,求CD的长;(2)如图2,点G为线段AE的中点,连接BG交AC于H,若∠BHC+∠ABG=60°,求证:AF+CE=3AC. 解答:在矩形ABCD中,对角线AC、BD交于点O,E为OB上一点,连接CE,G为CE中点. (3)如图1,连接AE,OG,若∠DAC=60°,BE=2,AB=53,求OG的长;(4)如图2,点F为线段OC上一点,连接BF,BG,若∠COB=∠OBG=∠CBF,求证:BE+CF=OA.。
2019重庆中考数学第24题专题训练---- 平行四边形(含大部分题目答案)
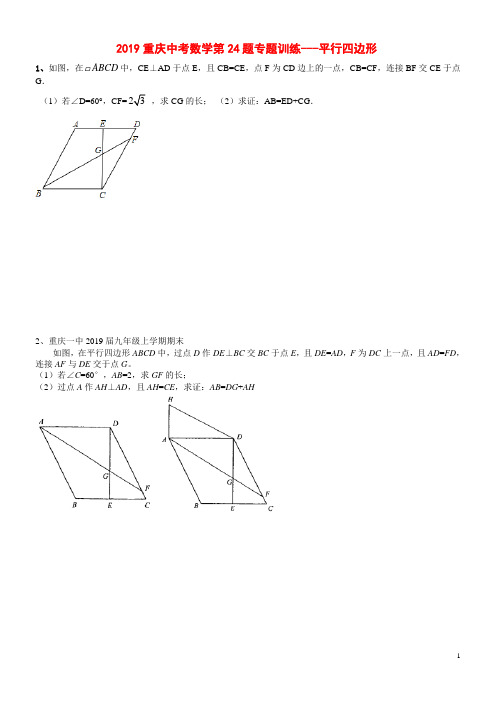
6、重庆市沙坪坝区 2019 届九年级上学期期末
A E
D
G
F
A
D
G
E
F
B
C
第 24 题图 1
B
C
第 24 题图 2
3
7、已知,在平行四边形 ABCD 中,AE⊥BC,且 E 为 BC 的中点,AE=2BE,P 为 BC 上一点,连接 DP,作 EF⊥DP 于点 F,连接 AF. (1)若 AD=4,求 AE 的长; (2)求证: 2 AF+EF=DF.
G.点 H 在 BC 的延长线上,且 CH=AG, 连接 EH.
(1)若 BC 12 2 ,AB=13,求 AF 的长; (2)求证:EB=EH.
9
19、重庆市 2018 年初中学业水平暨高中招生考试数学( A 卷)
A
F
D
O
H
G
B
E
C
10
2019 重庆中考数学第 24 题专题训练---平行四边形答案
连接 AF 与 DE 交于点 G。 (1)若∠C=60°,AB=2,求 GF 的长; (2)过点 A 作 AH⊥AD,且 AH=CE,求证:AB=DG+AH
1
3、如图,已知 ABCD 中,DE⊥BC 于点 E,DH⊥AB 于点 H,AF 平分∠BAD,分别交 DC、DE、DH 于点 F、G、M,
(1)若∠F=60°,∠C=45°,BC= 2 6 ,请求出 AB 的长;(2)求证:CD=BF+DF.
F
E
D
A
B
G
C
6
13、重庆一中初 2019 级 17-18 学年度下期期末
已知在平行四边形 ABCD 中,过点 D 作 DE BC 于点 E ,且 AD DE .连接 AC 交 DE 于点 F ,作 DG AC 于点 G . (1)如图 1,若 EF 1 , AF 13 ,求 DG 的长;
2019重庆中考数学第24题专题训练十一

2019重庆中考数学第24题专题训练十一
2018、12
1、重庆实验外国语学校2018-2019学年度度上期2020级八年级第二次月考(2018年12月中旬)
2、2018-2019学年重庆实验外国语学校九年级数学定时练习试题
如图△ABC,以AC为斜边向下作等腰直角△ADC,直角边AD交BC于点E
BC=+求线段DC的长;
(1)如图1,若∠ACB=30°,∠B=45°,BC=2
(2)如图2,若等腰R△ADC的直角顶点D恰好落在线段BC的垂直平分线上,过点A作AF⊥BC于点F,连接DF,
求证:AB=.
3、重庆第一中学2018-2019学年初2019级初三年级上学期第二次定时作业数学试题
4、2018-2019学年重庆外国语学校初三上第2次月考数学试题
5、重庆八中2019届初三上期第三学月
6、重庆第十一中学珊瑚校区2018-2019学年上学期初2019届初三年级第二次月考。
2019重庆中考数学第24题专题训练---三角形
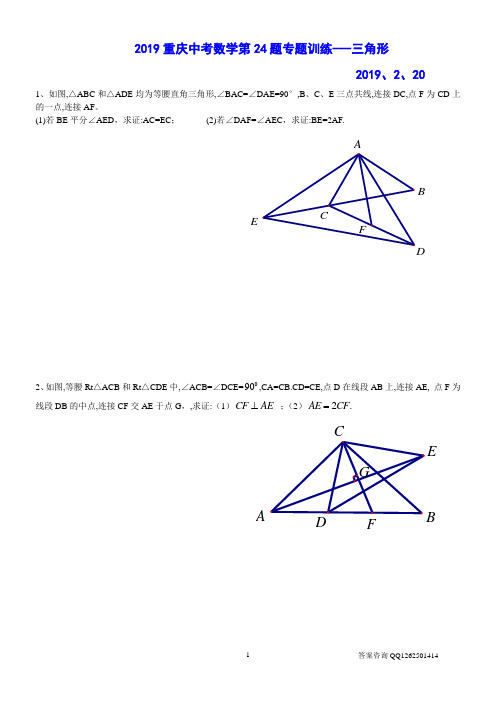
2019重庆中考数学第24题专题训练---三角形2019、2、201、如图,△ABC 和△ADE 均为等腰直角三角形,∠BAC=∠DAE=90°,B 、C 、E 三点共线,连接DC,点F 为CD 上的一点,连接AF 。
(1)若BE 平分∠AED ,求证:AC=EC ; (2)若∠DAF=∠AEC ,求证:BE=2AF.ACBEDF2、如图,等腰Rt △ACB 和Rt △CDE 中,∠ACB=∠DCE=090,CA=CB.CD=CE,点D 在线段AB 上,连接AE, 点F 为线段DB 的中点,连接CF 交AE 于点G ,,求证:(1)CF AE ⊥ ;(2)2.AE CF =GABCDEF3、如图,等腰Rt △ACB 和Rt △CDE 中,∠ACB=∠DCE=090,CA=CB.CD=CE,点D 在线段AB 上,连接AE,过C 作CF ⊥AE 于G ,交AB 于点F,求证:(1)点F 为线段DB 的中点;(2)2.AE CF =GABCDEF4、如图,等腰直角三角形ABC 中,090ACB ∠=,,CE CD ⊥ 且,CE CD = 连接AD ,过C 作CF AD ⊥于F ,交AB 于点G .求证:G 为BE 的中点.FACBDE G5、重庆市巴川中学2018-2019学年度上学期(秋季)初2020届初二年级半期考试 已知在△ABC 中,AB=AC,0120BAC ∠=,,点E 是AD 上一点,AD=CE,060AEC ∠= ,(1)如图1,求证:△ACE ≌△BAD(2)如图2,连接BE 并廷长,交AC 于点H,点E 恰好是BH 的中点,∠BAC 的角平分线交CE 于点F,求证:DE=AE+EF6、八中2019级周考157、重庆八中初2018届初三上期期末考试已知Rt ABC ∆中, CD 是斜边AB 边上的中线,点E 是直角边AC 上一点,连接DE ,.BE (1)如图1,若DE AB ⊥,且3BC =,4AC =,求CDE ∆的,面积;. (2)如图2,若AED BEC ∠=∠,求证:F 是CD 的中点.DF ACBEAC BE图1 图28、如图1,在五边形 ABCDE 中,∠E=90°,BC=DE 连接AC,AD,且AB=AD,AC ⊥BC(1)求证:AC=AE ; (2)如图2,若∠ABC=∠CAD ,AF 为BE 边上的中线,求证:AF ⊥CD.BB图1 图29、如图在ABC中,过点A作AE⊥BC交BC于E,D为△BC外一点且AD⊥DC,AD交BC于F,连接、D,已知AE=BE,AD= DC.(1) AB=22,BC=35,求DC长度;(2)求证:∠CBD+∠ACE=045.AB CED10、在等腰直角△ABC中,AC=BC,∠ACB=90°,CF⊥AB交AB于点F,点D在AC上,连接BD,交CF 于点G,过点C作BD的垂线交BC于点H,交AB于点E:(1)如图1,∠ABD=∠CBD,CG=1,求AB;BH AH.(2)如图2,连接AH、FH,∠AHF=90°,求证:211、如图1,△AOB 中,∠AOB= 90°,AO=BO,点C 在边AB 上,连接CO ,过点O 作CO 的垂线,在垂线上取点D ,使DO=CO,连接BD ,CD.(1)已知AC=2,BC=6,求CD 的长;(2)如图2,取线段BC 的中点E ,连接OE ,AD ,求证:OE ⊥AD 且AD=2OE.AOBDCFAOBDCE图1 图212、如图,△ABC 和△DEC 都是等腰直角三角形,C 为它们的公共直角顶点,连AD ,BE ,F 为线段AD 的中点,连接CF(1)如图1,当D 点在BC 上时,CE=4,BD=2,求CF;(2)如图2,把△DEC 绕C 点顺时针旋转一个锐角,其他条件不变,求证:BE=2CF .13、已知:△AOB 和△COD 均为等腰直角三角形,∠AOB=∠COD=90°.连接AD ,BC ,点H 为BC 中点,连接OH .(1)如图1所示,若AB =8,CD =2,求OH 的长。
2019重庆中考数学第24题专题训练---正方形(含答案)

2019重庆中考数学第24题专题训练---正方形201902121、重庆第一中学2018-2019学年初2019级初三年级上学期第二次定时作业数学试题如图,点M 是正方形ABCD 的边BC 上一点,连接AM ,点E 是线段AM 上一点,CDE ∠的平 分线交AM 延长线于点F .(1)如图1,若点E 为线段AM 的中点,:1:2BM CM =,BE =AB 的长;(2)如图2,若G 为AE 中点,延长DG 至N ,使DG NG =,连接EN ,且EDG ENG ∠=∠,求证:BF DF +=.2、在正方形ABCD 中,点F 是BC 延长线上一点,过点B 作BE ⊥DF 于点E ,交CD 于点G ,连接CE . (1)若正方形ABCD 边长为3,DF =4,求CG 的长; (2)求证:EF+EG =2CE .GEA B CDF3、如图1,在正方形ABCD 中,对角线AC 与BD 交于点,O H 为CD 边上一点,连接BH 交AC 于K ,E 为BH 上一点,连接AE 交BD 于点.F(1)若AE BH ⊥于E ,且6,CK ==求AF 的长; (2)如图2,若=AE BE ,且,BEO EAO ∠=∠求证:.AEH图1 图24、重庆市南开(融侨)中学初2019级暑假作业数学综合练习如图,正方形ABCD 中,CB 的延长线上有一点E,连接AC 、AE. (1)如图1,若AC=4,∠CAE=75°,求△ACE 的面积; (2)如图2,连接BD 交AC 于点O ,在线段AB 上取点F ,使BE=BF ,连接CF ,过点B 作BG ∥CF ,交AE 于点G ,连接OG 、BG.求证:.BG AG +=5、重庆市南岸区11中、二外、珊瑚2018-2019学年度上期三校期末联考九年级数学如图1,以正方形ABCD 边AD 为边作等边三角形ADE ,EF ⊥AD 于点F ,连接BE 交AD 于G . (1)若正方形的边长为2,求AG 的长;(2)如图2,∠EAD 的平分线交BE 于点P ,连接CP ,求证:AP +PC6、在正方形ABCD 中,对角线AC,BD 交于点O,E 为OB 上一点,连接CE,F 为CE 的中点.(1)如图1,连接AE,OF,若 AB=6,求OF 的长;(2)如图2,连接BF,作BG ⊥BF 交CA 的延长线于点G ,求证:.CG BE =7、已知正方形ABCD如图所示,连接其对角线AC,∠BCA的平分线CF交AB于点F,过点B作BM⊥C F于点N,交AC于点M,过点C作CP⊥CF,交AD延长线于点P.(1)若正方形ABCD的边长为4,求△ACP的面积;(2)求证:CP=BM+2FN.8、重庆巴蜀中学初2018届九年级下第二次周考如图1,正方形ABCD中,AE为过顶点A的任意一条射线,过C作CE⊥AE于E.(1)己知AB=6.AE=8,求CE的长;(2)如图2,过D作DF⊥AE于F,求证:DF=EF.图1 图29、重庆一中初2018级初三下期期中如图,在正方形ABCD 中,点M 是边BC 上一点,连接AM ,过点C 作CH ⊥AM 交AM 的延长线于点H ,延长CH 于点M 连接MN 、BN . (1)若AB =4,AH =528,求线段CH 的长度; (2)若∠MAD =∠BMN ,求证:AM =MN +CN .2019重庆中考数学第24题专题训练---正方形答案1、重庆第一中学2018-2019学年初2019级初三年级上学期第二次定时作业数学试题如图,点M 是正方形ABCD 的边BC 上一点,连接AM ,点E 是线段AM 上一点,CDE ∠的平 分线交AM 延长线于点F .(3)如图1,若点E 为线段AM 的中点,:1:2BM CM =,BE =AB 的长;(4)如图2,若G 为AE 中点,延长DG 至N ,使DG NG =,连接EN ,且EDG ENG ∠=∠,求证:BF DF +=.(1):1:2BM CM ==,2BM x CM x ∴=设则∵正方形ABCD 3,90AB x ABC ∴=∠=︒Rt ABM AM ∆在中,∵点E 为线段AM 的中点2AM BM ∴== 2x ∴=36AB x ∴==(2)G AE 为中点AG EG ∴=AGD EGN AG EG AGD EGN DG NG ∆∆=⎧⎪∠=∠⎨⎪=⎩在和中AGD EGN ∴∆≅∆ 4N ∴∠=∠ EDG ENG ∠=∠,34ED EN ∴=∠=∠ DG NG = 90EGD ∴∠=︒AF CDE ∠平分12∴∠=∠123452FDG CDA ∴∠=∠+∠=∠=︒,90A AH AF FD H FAH ⊥∠=︒过作交延长线于即//DG AH ∴45H FDG ∴∠=∠=︒AHF ∴∆为等腰直角三角形,AH AF FH ∴=90DAB HAF ∴∠=∠=︒ DAH BAF ∴∠=∠DAH BAF AH AF DAH BAF AD AB DAH BAF DH BF∆∆=⎧⎪∠=∠⎨⎪=⎩∴∆≅∆∴=在和中BF DF DH DF FH ∴+=+==2、在正方形ABCD 中,点F 是BC 延长线上一点,过点B 作BE ⊥DF 于点E ,交CD 于点G ,连接CE . (1)若正方形ABCD 边长为3,DF =4,求CG 的长; (2)求证:EF+EG =2CE .解答:(1)∵四边形ABCD 是正方形∴∠BCG =∠DCB=∠DCF=90°,BC=DC .∵BE ⊥DF∴∠CBG+∠F=∠CDF+∠F .∴∠CBG=∠CDF . ∴△CBG ≌△CDF .∴BG=DF=4.∴在Rt △BCG 中,222BG BC CG =+∴CG =73422=-. …………………………4分 (2)过点C 作CM ⊥CE 交BE 于点M∵∠BCG=∠MCE =∠DCF =90° ∴∠BCM=∠DCE ,∠MCG=∠ECF ∵BC=DC ,∠CBG=∠CDF∴△CBM ≌△CDE ∴CM=CE∴△CME 是等腰直角三角形∴ME=CE 2 ,即MG+EG=CE 2 又∵△CBG ≌△CDF ∴CG=CF∴△CMG ≌△FCE ∴MG=EF∴EF+EG =2CEGEA B CDFM3、如图1,在正方形ABCD 中,对角线AC 与BD 交于点,O H 为CD 边上一点,连接BH 交AC 于K ,E 为BH 上一点,连接AE 交BD 于点.F(1)若AE BH ⊥于E ,且6,CK ==求AF 的长; (2)如图2,若=AE BE ,且,BEO EAO ∠=∠求证:.AEH图1图2解答:4、重庆市南开(融侨)中学初2019级暑假作业数学综合练习如图,正方形ABCD中,CB的延长线上有一点E,连接AC、AE.(1)如图1,若AC=4,∠CAE=75°,求△ACE的面积;(2)如图2,连接BD交AC于点O,在线段AB上取点F,使BE=BF,连接CF,过点B作BG∥CF,交AE于点G,连接OG、BG.求证:.+=BG AG5、重庆市南岸区11中、二外、珊瑚2018-2019学年度上期三校期末联考九年级数学如图1,以正方形ABCD边AD为边作等边三角形ADE,EF⊥AD于点F,连接BE交AD于G.(1)若正方形的边长为2,求AG的长;(2)如图2,∠EAD的平分线交BE于点P,连接CP,求证解法一:解法二:6、在正方形ABCD 中,对角线AC,BD 交于点O,E 为OB 上一点,连接CE,F 为CE 的中点.(1)如图1,连接AE,OF,若 AB=6,求OF 的长;(2)如图2,连接BF,作BG ⊥BF 交CA 的延长线于点G ,求证:.CG BE =7、已知正方形ABCD 如图所示,连接其对角线AC ,∠BCA 的平分线CF 交AB 于点F ,过点B 作BM⊥C F 于点N ,交AC 于点M ,过点C 作CP⊥CF,交AD 延长线于点P .(1)若正方形ABCD 的边长为4,求△ACP 的面积;(2)求证:CP=BM+2FN .解:∵∠1=∠2=22.5°,又CP⊥CF,∴∠3+∠FCD=∠1+∠FCD=90°∴∠3=∠1=22.5°∴∠P=67.5°又∵四边形ABCD 为正方形,∴∠ACP=45+22.5=67.5°∴∠P=∠ACP∴AP=AC又∵AB=4 ∴AP=42 ∴S △A P C =12AP•CD=82(2)∵在△PDC 和△FBC 中,{ ∠PDC=∠FBCCD=BC∠1=∠3∴△PDC≌△FBC∴CP=CF 在CN 上截取NH=FN ,连接BH∵FN=NH,且BN⊥FH∴BH=BF∴∠4=∠5∴∠4=∠1=∠5=22.5°又∠4+∠BFC=∠1+∠BFC=90°∴∠HBC=∠BAM=45°在△AMB 和△BHC 中,{ ∠1=∠4AB=BC∠HBC=∠BAM,∴△AMB≌△BHC,∴CH=BM∴CF=BM+2FN∴CP=BM+2FN.8、重庆巴蜀中学初2018届九年级下第二次周考如图1,正方形ABCD 中,AE 为过顶点A 的任意一条射线,过C 作CE ⊥AE 于E.(1)己知AB=6.AE=8,求CE 的长;(2)如图2,过D 作DF ⊥AE 于F,求证:DF=EF.图1 图29、重庆一中初2018级初三下期期中如图,在正方形ABCD 中,点M 是边BC 上一点,连接AM ,过点C 作CH ⊥AM 交AM 的延长线于点H ,延长CH 于点M 连接MN 、BN .(1)若AB =4,AH =528,求线段CH 的长度; (2)若∠MAD =∠BMN ,求证:AM =MN +CN .。
2019重庆中考数学第24题专题训练八
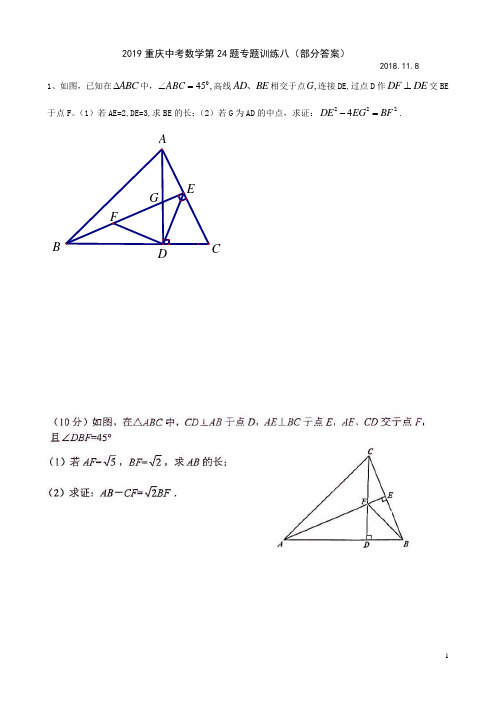
2019重庆中考数学第24题专题训练八(部分答案)2018.11.81、如图,已知在ABC ∆中,045,ABC ∠=高线AD BE 、相交于点,G 连接DE,过点D 作DF DE ⊥交BE 于点F 。
(1)若AE=2,DE=3,求BE 的长;(2)若G 为AD 的中点,求证:2224DE EG BF -=.BDA3、重庆八中初2019级初三上第七次周考如图1、在Rt△ABC中,点D为边AC上一点,DE AB于点E,点M为BD的中点,CM的延长线交AB于点F(1)若∠A=50°,求∠EMC的大小(2)如图2,若△ABC是等腰直角三角形,且EA=EM,AN//EM,求证:CN=NM4、在等腰要三角形ABC中AB=AC,BD是AC边的中线,过点C作CE⊥BC,交BD的延长现于点E,连接AE.(1)如图1,若∠ABC=60º,BE=4,求AE的长;(2)如图2,求证:BE=2AE.BBMN图1 图25、西南大学 附属中学2018--2019学年度上期期中考试八年级数学试题求证:(1);AD DG = (2)1.2AF BE =FDEABC HGDEAM7、如图等腰直角△ABC中,∠ACB= 90°,点D在BA的延长线上,连接CD,过C作CE⊥CD,使CE=CD,连接BE,若点N为BD 的中点,连接CN、BE. (1)求证:AB⊥BE; (2)AE=2CN.M8、如图,等腰直角三角形ABC 中,090ACB ∠=,,CE CD ⊥ 且,CE CD = 连接AD ,过C 作CF AD⊥于F ,交AB 于点G .求证:G 为BE 的中点.FACBDE G9、如图,Rt ABC ∆中,090ACB ∠=,CD AB ⊥于,E ,CD AB DA BC =、的延长线交于.F(1)若.DA = 012,30,AC ABC =∠= 求DE 的长;(2)若2,BC AC =求证:.DA =B。
2019重庆中考数学试卷(含答案)

重庆市2019年初中学业水平暨高中招生考试试卷数 学(全卷共四个大题,满分150分,考试时间120分钟)注意事项:1.认题的答案书写在答题卡上,不得在试题卷上直接作答; 2.作答前认真阅绪答题卡上的注意事项;3.作图(包括作辅助线)请一律用黑色签牛笔完成; 4.考试结束,由监考人员将试题卷和答题卡一并收回.参考公式:抛物线()02≠++=a c bx ax y 的顶点坐标为⎪⎪⎭⎫⎝⎛--a b ac a b 44,22,对称轴为a b 2x -= 一、选择题:(本大题12个小题,每小题4分,共48分)在每个小题的下面,都给出了代号为DC B A 、、、的四个答案,其中只有一个是正确的,请将答题卡...上题号右侧正确答案所对应的方框涂黑. 1.下列各数中,比1-小的数是( )A .2B .1C .0D .-22.如图是由4个相同的小正方体组成的一个立体图形,其主视图是( )A .B .C .D .3.如图,△ABO ∽△CDO ,若6=BO ,3=DO ,2=CD ,则AB 的长是( )A .2B .3C .4D .54.如图,AB 是⊙O 的直径,AC 是⊙O 的切线,A 为切点,BC 与⊙O 交于点D ,连结OD .若︒=∠50C ,则∠AOD 的度数为( ) A.︒40B .︒50C .︒80D .︒1005.下列命题正确的是( )A .有一个角是直角的平行四边形是矩形B .四条边相等的四边形是矩形3题图4题图2题图C.有一组邻边相等的平行四边形是矩形 D.对角线相等的四边形是矩形6.估计()123+623⨯的值应在()A.4和5之间B.5和6之间C.6和7之间D.7和8之间7.《九章算术》中有这样一个题:今有甲乙二人持钱不知其数.甲得乙半而钱五十,乙得甲太半而钱亦五十.问甲、乙持钱各几何?其意思为:今有甲乙二人,不如其钱包里有多少钱,若乙把其一半的钱给甲,则甲的数为50;而甲把其23的钱给乙.则乙的钱数也为50,问甲、乙各有多少钱?设甲的钱数为x,乙的钱数为y,则可建立方程组为()A.15022503x yx y⎧+=⎪⎪⎨⎪+=⎪⎩B.15022503x yx y⎧+=⎪⎪⎨⎪+=⎪⎩C.15022503x yx y⎧+=⎪⎪⎨⎪+=⎪⎩D.15022503x yx y⎧+=⎪⎪⎨⎪+=⎪⎩8.按如图所示的运算程序,能使输出y值为1的是()A.11m n==,B.10m n==,C.12m n==,D.21m n==,9.如图,在平面直角坐标系中,矩形ABCD的顶点A,D分别在x轴、y轴上,对角线BD∥x轴,反比例函数(0,0)ky k xx=>>的图象经过矩形对角线的交点E.若点A(2,0),D(0,4),则k的值为()A.16 B.20 C.32 D.409题图8题图10题图12题图10.为践行“绿水青山就是金山银山”的重要思想,某森林保护区开展了寻找古树活动.如图,在一个坡度(或坡比)i=1:24的山坡AB上发现有一棵占树CD.测得古树底端C到山脚点A的距离AC=26米,在距山脚点A水平距离6米的点E处,测得古树顶端D的仰角∠AED=48°(古树CD与山坡AB的剖面、点E在同一平面上,古树CD与直线AE垂直),则古树CD的高度约为()(参考数据:sin48°≈0.73,cos8°≈0.67,tan48°≈1.11)A.17.0米B.21.9米C.23.3米D.33.3米11.若关于x的一元一次不等式组11(42)42 3122x axx⎧--≤⎪⎪⎨-⎪<+⎪⎩的解集是x≤a,且关于y的分式方程24111y a yy y---=--有非负整数解,则符合条件的所有整数a的和为()A.0 B.1 C.4 D.612.如图,在△ABC中,D是AC边上的中点,连结BD,把△BDC′沿BD翻折,得到△BDC',DC与AB交于点E,连结AC',若AD=AC=2,BD=3则点D到BC的距离为()A.233B.7213C.7D.13二、填空题:(本大题6个小题,每小题4分,共24分)请将每小题的答案直接填在答题卡...中对应的横线上.13.计算:=+1-213-)()(π.14.今年五一节期间,重庆市旅游持续火爆,全市共接待境内外游客超过25600000人次,请把数25600000用科学记数法表示为.15.一个不透明的布袋内装有除颜色外,其余完全相同的3个红球,2个白球,1个黄球,搅匀后,从中随机摸出一个球,记下颜色后放回搅匀,再从中随机摸出一个球,则两次都摸到红球的概率为.16.如图,在菱形ABCD中,对角线AC,BD交于点O,∠ABC=60°,AB=2,分别以点A、点C为圆心,以AO的长为半径画弧分别与菱形的边相交,则图中阴影部分的面积为.(结果保留π)17.某公司快递员甲匀速骑车前往某小区送物件,出发几分钟后,快递员乙发现甲的手机落在公司,无法联系,于是乙匀速骑车去追赶甲.乙刚出发2分钟时,甲也发现自己手机落在公司,立刻按原路原速骑车回公司,2分钟后甲遇到乙,乙把手机给甲后立即原路原速返回公司,甲继续原路原速赶往某小区送物件,甲乙两人相距的路程y(米)与甲出发的时间x(分钟)之间的关系如图所示(乙给甲手机的时间忽略不计).则乙回到公司时,甲距公司的路程是米.16题图17题图20题图18.在精准扶贫的过程中,某驻村服务队结合当地高山地形,决定在该村种植中药材川香、贝母、黄连增加经济收人,经过一段时间,该村已种植的川香、贝母、黄连面积之比4:3:5,是根据中药材市场对川香、贝母、黄连的需求量,将在该村余下土地上继续种植这三种中药材,经测算需将余下土地面积的169种植黄连,则黄连种植总面积将达到这三种中药材种植总面积的4019.为使川香种植总面积与贝母种植总面积之比达到3:4,则该村还需种植贝母的面积与该村种植这三种中药材的总面积之比是 .三、解答题:(本大题7个小题,每小题10分,共70分)解答时每小题必须给出必要的演算过程或推理步骤,画出必要的图形(包括辅助线),请将解答过程书写在答题卡中对应的位置上.19.计算:(1))2(2y x y y x +-+)( (2)292492--÷--+a a a a a )(20.如图,在△ABC 中,AB =AC ,D 是BC 边上的中点,连结AD ,BE 平分∠ABC 交AC 于点E ,过点E作EF ∥BC 交AB 于点F .(1)若∠C =36°,求∠BAD 的度数.(2)若点E 在边AB 上,EF //AC 叫AD 的延长线于点F .求证:FB =FE .21.每年夏季全国各地总有未成年人因溺水而丧失生命,令人痛心秩首.今年某校为确保学生安全,开展了“远离溺水·珍爱生命”的防溺水安全知识竞赛.现从该校七、八年级中各随机抽取10名学生的竞赛成绩(百分制)进行整理、描述和分析(成绩得分用x表示,共分成四组:A.80≤x≤85,B.85≤x≤90,C.90≤x≤95,D.95≤x≤100),下面给出了部分信息:七年级10名学生的竞赛成绩是:90,80,90,86,99,96,96,100,89,82八年级10名学生的竞赛成绩在C组中的数据是:94,90,94八年抽取的学生竞赛成绩扇形统计图七、八年级抽取的学生竞赛成绩统计表年级七年级八年级平均数92 92中位数93 b纵数c100方差52 50.421题图根据以上信息,解答下列问题:(1)直接写出上述图表中a,b,c的值;(2)根据以上数据,你认为该校七、八年级中哪个年级学生掌握防溺水安全知识较好?请说明理由(一条理由即可);(3)该校七、八年级共730人参加了此次竞赛活动,估计参加此次竞赛活动成绩优秀(x≧90)的学生人数是多少?22.《道德经》中的“道生一,一生二,二生三,三生万物”道出了自然数的特征.在数的学习过程中,我们会对其中一些具有某种特性的数进行研究,如学习自然数时,我们研究了奇数、偶数、质数、合数等.现在我们来研究另一种特珠的自然数—“纯数”.定义;对于自然数n,在计算n+(n+1)+(n+2)时,各数位都不产生进位,则称这个自然数n为“纯数”,例如:32是”纯数”,因为计算32+33+34时,各数位都不产生进位;23不是“纯数”,因为计算23+24+25时,个位产生了进位.(1)判断2019和2020是否是“纯数”?请说明理由;(2)求出不大于100的“纯数”的个数.321-=x y 23.在初中阶段的函数学习中,我们经历了“确定函数的表达式——利用函数图象研究其性质一一运用函数解决问题"的学习过程.在画函数图象时,我们通过描点或平移的方法画出了所学的函数图象.同时,我们也学习了绝对值的意义⎩⎨⎧-≥=)0()0(<a a a a a .结合上面经历的学习过程,现在来解决下面的问题在函数b kx y +-=3中,当2=x 时,;4-=y 当0=x 时,.1y -=(1)求这个函数的表达式;(2)在给出的平面直角坐标系中,请用你喜欢的方法面出这个函数的图象井写出这个函数的一条性质; (3)已知函321y -=x 的图象如图所示,结合你所画的函数图象,直接写出不等式3213-≤+-x b kx 的解集.24.某文明小区50平方米和80平方米两种户型的住宅,50平方米住宅套数是80平方米住宅套数的2倍.物管公司月底按每平方米2元收取当月物管费,该小区全部住宅都人住且每户均按时全额缴纳物管费. (1)该小区每月可收取物管费90 000元,问该小区共有多少套80平方米的住宅?(2)为建设“资源节约型社会”,该小区物管公司5月初推出活动一:“垃圾分类送礼物”,50平方米和80平方米的住户分别有40%和20%参加了此次括动.为提离大家的积扱性,6月份准备把活动一升级为活动二:“拉圾分类抵扣物管费”,同时终止活动一.经调査与测算,参加活动一的住户会全部参加活动二,参加活动二的住户会大幅增加,这样,6月份参加活动的50平方米的总户数在5月份参加活动的同户型户数的基础上将增加%2a ,每户物管费将会减少%103a ;6月份参加活动的80平方米的总户数在5月份参加活动的同户型户数的基础上将增加%6a ,每户物管费将会减少%41a .这样,参加活动的这部分住户6月份总共缴纳的物管费比他们按原方式共缴纳的物管费将减少%185a ,求a 的值.25.如图,在平行四边形ABCD 中,点E 在边BC 上,连结AE ,EM ⊥AE ,垂足为E ,交CD 于点M ,AF ⊥BC ,垂足为F ,BH ⊥AE ,垂足为H ,交AF 于点N ,点P 显AD 上一点,连接CP . (1)若DP =2AP =4,CP =17,CD =5,求△ACD 的面积. (2)若AE =BN ,AN =CE ,求证:AD =2CM +2CE .四、解答题:(本大题1个小题,共8分)解答时必须给出必要的演算过程成或推理步骤,画出必要的图形(包括辅助线),请将解作过程书写在答题卡中对应的位置上.26.如图,在平面在角坐标系中,抛物线y=x2-2x-3与x轴交与点A,B(点A在点B的左侧)交y轴于点C,点D为抛物线的顶点,对称轴与x轴交于点E.(1)连结BD,点M是线段BD上一动点(点M不与端点B,D重合),过点M作MN⊥BD交抛物线于点N(点N在对称轴的右侧),过点N作NH⊥x轴,垂足为H,交BD于点F,点P是线段OC上一动点,当MN取得最大值时,求HF+FP+13PC的最小值;(2)在(1)中,当MN取得最大值HF+FP+1/3PC取得小值时,把点P向上平移个22单位得到点Q,连结AQ,把△AOQ绕点O瓶时针旋转一定的角度α(0°<α<360°),得到△AOQ,其中边AQ交坐标轴于点C在旋转过程中,是否存在一点G使得OGQQ''∠=∠?若存在,请直接写出所有满足条件的点Q的坐标;若不存在,请说明理由.2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019重庆中考数学第24题专题训练二
1、如图,00=90,90,ABC DEB ∠∠==,,BA BC BD BE =连接,,AE CD AE 所在直线交CD 于点,F 连
接.BF (1)连接,,AD EC 求证:;AD EC =(2)若,BF AF ⊥求证:F 点为CD 的中点.
C
3、如图,矩形ABCD 中,2BC AB =,点E 是边AD 的中点,点F 是线段AE 上一点(点F 不与点,A E 重合)连接BF ,过点F 作直线BF 的垂线,与线段CE 交于点,G 点H 是线段BG 的中点. (1
)若CE =求矩形ABCD 的面积;
(2)求证:
.BF =
B
4、如图1,在正方形ABCD 中,对角线AC 与BD 交于点,O H 为CD 边上一点,连接BH 交AC 于K ,E 为BH 上一点,连接AE 交
BD 于点.F (1)若AE BH ⊥于E ,且6,CK =
=求AF 的长;
(2
)如图2,若=AE BE ,且,BEO EAO ∠=∠求证:.AE
B
H
B
H
图1 图2
5、如图,在ABC ∆中,0
90BAC ∠=,AB AC =,点D 为形外一点,BD CD ⊥于点D ,CD 交AB 于E , (1)如图1,若0
15ABD ∠=,6,BE =求BC 的长;
(2)如图2,连接AD ,作AF BC ⊥于,F 交CD 于,M 若DA DB =,
求证:.CE =
B
C A
B
C
A
图1
图2
2019重庆中考数学第24题专题训练二答案解析
1、如图,00=90,90,ABC DEB ∠∠==,,BA BC BD BE =连接,,AE CD AE 所在直线交CD 于点,F 连
接.BF (1)连接,,AD EC 求证:;AD EC =(2)若,BF AF ⊥求证:F 点为CD 的中点.
A
C
D
C
3、如图,矩形ABCD 中,2BC AB =,点E 是边AD 的中点,点F 是线段AE 上一点(点F 不与点,A E 重合)连接BF ,过点F 作直线BF 的垂线,与线段CE 交于点,G 点H 是线段BG 的中点.
(1)若CE =求矩形ABCD 的面积;
(2)求证: .BF =
B
4、如图1,在正方形ABCD 中,对角线AC 与BD 交于点,O H 为CD 边上一点,连接BH 交AC 于K ,E 为BH 上一点,连接AE 交
BD 于点.F (1)若AE BH ⊥于E ,且6,CK =
=求AF 的长;
(2)如图2,若=AE BE ,且,BEO EAO ∠=∠
求证:.AE
B
H
图1 图2
5、如图,在ABC ∆中,0
90BAC ∠=,AB AC =,点D 为形外一点,BD CD ⊥于点D ,CD 交AB 于E , (1)如图1,若0
15ABD ∠=,6,BE =求BC 的长;
(2)如图2,连接AD ,作AF BC ⊥于,F 交CD 于,M 若DA DB =,
求证:.CE =
B
C A
B
C
A
图1
图2。
