2012-2013两年理科高考排列组合题汇总
2013届高考数学排列组合.doc
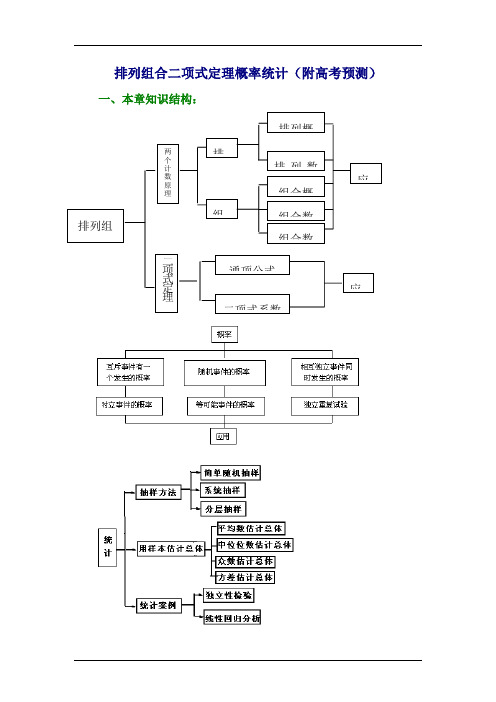
排列组合二项式定理概率统计(附高考预测)一、本章知识结构:二、重点知识回顾 1.排列与组合⑪ 分类计数原理与分步计数原理是关于计数的两个基本原理,两者的区别在于分步计数原理和分步有关,分类计数原理与分类有关.⑫ 排列与组合主要研究从一些不同元素中,任取部分或全部元素进行排列或组合,求共有多少种方法的问题.区别排列问题与组合问题要看是否与顺序有关,与顺序有关的属于排列问题,与顺序无关的属于组合问题.⑬ 排列与组合的主要公式 ①排列数公式:)1()1()!(!+-⋅⋅⋅-=-=m n n n m n n A m n (m ≤n) A n n =n! =n(n ―1)(n ―2) ·…·2·1. ②组合数公式:12)1()1()1()!(!!⨯⨯⋅⋅⋅⨯-⨯+-⋅⋅⋅-=-=m m m n n n m n m n C m n (m ≤n).③组合数性质:①m n n m n C C -=(m ≤n). ②n n n n n n C C C C 2210=+⋅⋅⋅+++③1314202-=⋅⋅⋅++=⋅⋅⋅++n n n n n n C C C C C2.二项式定理 ⑪ 二项式定理(a +b)n =C 0n a n +C 1n a n -1b+…+C r n a n -r b r +…+C n n b n ,其中各项系数就是组合数C r n ,展开式共有n+1项,第r+1项是T r+1 =C r n a n -r b r .⑫ 二项展开式的通项公式二项展开式的第r+1项T r+1=C r n a n -r b r (r=0,1,…n)叫做二项展开式的通项公式。
⑬ 二项式系数的性质①在二项式展开式中,与首末两端“等距离”的两个二项式系数相等,即C r n = C rn n - (r=0,1,2,…,n).②若n 是偶数,则中间项(第12+n 项)的二项公式系数最大,其值为C 2n n;若n 是奇数,则中间两项(第21+n 项和第23+n 项)的二项式系数相等,并且最大,其值为C21-n n= C21+n n.③所有二项式系数和等于2n ,即C 0n +C 1n +C 2n +…+C nn =2n .④奇数项的二项式系数和等于偶数项的二项式系数和,即C 0n +C 2n +…=C 1n +C 3n+…=2n ―1. 3.概率(1)事件与基本事件::S S S ⎧⎪⎧⎨⎨⎪⎩⎩随机事件在条件下,可能发生也可能不发生的事件事件不可能事件:在条件下,一定不会发生的事件确定事件必然事件:在条件下,一定会发生的事件基本事件:试验中不能再分的最简单的“单位”随机事件;一次试验等可能的产生一个基本事件;任意两个基本事件都是互斥的;试验中的任意事件都可以用基本事件或其和的形式来表示.(2)频率与概率:随机事件的频率是指此事件发生的次数与试验总次数的比值.频率往往在概率附近摆动,且随着试验次数的不断增加而变化,摆动幅度会越来越小.随机事件的概率是一个常数,不随具体的实验次数的变化而变化. (3)互斥事件与对立事件:(4)古典概型与几何概型:古典概型:具有“等可能发生的有限个基本事件”的概率模型. 几何概型:每个事件发生的概率只与构成事件区域的长度(面积或体积)成比例.两种概型中每个基本事件出现的可能性都是相等的,但古典概型问题中所有可能出现的基本事件只有有限个,而几何概型问题中所有可能出现的基本事件有无限个.(5)古典概型与几何概型的概率计算公式: 古典概型的概率计算公式:()A P A =包含的基本事件的个数基本事件的总数.几何概型的概率计算公式:()A P A =构成事件的区域长度(面积或体积)试验全部结果构成的区域长度(面积或体积).两种概型概率的求法都是“求比例”,但具体公式中的分子、分母不同.(6)概率基本性质与公式①事件A 的概率()P A 的范围为:0()1P A ≤≤.②互斥事件A 与B 的概率加法公式:()()()P A B P A P B =+ . ③对立事件A 与B 的概率加法公式:()()1P A P B +=.(7) 如果事件A 在一次试验中发生的概率是p ,则它在n 次独立重复试验中恰好发生k 次的概率是p n (k) = C k np k (1―p)n ―k . 实际上,它就是二项式[(1―p)+p]n 的展开式的第k+1项. (8)独立重复试验与二项分布①.一般地,在相同条件下重复做的n 次试验称为n 次独立重复试验.注意这里强调了三点:(1)相同条件;(2)多次重复;(3)各次之间相互独立;②.二项分布的概念:一般地,在n 次独立重复试验中,设事件A 发生的次数为X ,在每次试验中事件A 发生的概率为p ,那么在n 次独立重复试验中,事件A 恰好发生k 次的概率为()(1)(012)k kn k n P X k C p p k n -==-= ,,,,,.此时称随机变量X服从二项分布,记作~()X B n p ,,并称p 为成功概率.4、统计(1)三种抽样方法 ①简单随机抽样简单随机抽样是一种最简单、最基本的抽样方法.抽样中选取个体的方法有两种:放回和不放回.我们在抽样调查中用的是不放回抽取.简单随机抽样的特点:被抽取样本的总体个数有限.从总体中逐个进行抽取,使抽样便于在实践中操作.它是不放回抽取,这使其具有广泛应用性.每一次抽样时,每个个体等可能的被抽到,保证了抽样方法的公平性.实施抽样的方法:抽签法:方法简单,易于理解.随机数表法:要理解好随机数表,即表中每个位置上等可能出现0,1,2,…,9这十个数字的数表.随机数表中各个位置上出现各个数字的等可能性,决定了利用随机数表进行抽样时抽取到总体中各个个体序号的等可能性. ②系统抽样系统抽样适用于总体中的个体数较多的情况.系统抽样与简单随机抽样之间存在着密切联系,即在将总体中的个体均分后的每一段中进行抽样时,采用的是简单随机抽样. 系统抽样的操作步骤:第一步,利用随机的方式将总体中的个体编号;第二步,将总体的编号分段,要确定分段间隔k ,当N n(N为总体中的个体数,n 为样本容量)是整数时,N k n=;当N n不是整数时,通过从总体中剔除一些个体使剩下的个体个数N能被n 整除,这时N k n'=;第三步,在第一段用简单随机抽样确定起始个体编号l ,再按事先确定的规则抽取样本.通常是将l 加上间隔k 得到第2个编号()l k +,将()l k +加上k ,得到第3个编号(2)l k +,这样继续下去,直到获取整个样本. ③分层抽样当总体由明显差别的几部分组成时,为了使抽样更好地反映总体情况,将总体中各个个体按某种特征分成若干个互不重叠的部分,每一部分叫层;在各层中按层在总体中所占比例进行简单随机抽样. 分层抽样的过程可分为四步:第一步,确定样本容量与总体个数的比;第二步,计算出各层需抽取的个体数;第三步,采用简单随机抽样或系统抽样在各层中抽取个体;第四步,将各层中抽取的个体合在一起,就是所要抽取的样本. (2)用样本估计总体样本分布反映了样本在各个范围内取值的概率,我们常常使用频率分布直方图来表示相应样本的频率分布,有时也利用茎叶图来描述其分布,然后用样本的频率分布去估计总体分布,总体一定时,样本容量越大,这种估计也就越精确.①用样本频率分布估计总体频率分布时,通常要对给定一组数据进行列表、作图处理.作频率分布表与频率分布直方图时要注意方法步骤.画样本频率分布直方图的步骤:求全距→决定组距与组数→分组→列频率分布表→画频率分布直方图.②茎叶图刻画数据有两个优点:一是所有的信息都可以从图中得到;二是茎叶图便于记录和表示,但数据位数较多时不够方便.③平均数反映了样本数据的平均水平,而标准差反映了样本数据相对平均数的波动程度,其计算公式为s=.有时也用标准差的平方———方差来代替标准差,两者实质上是一样的.(3)两个变量之间的关系变量与变量之间的关系,除了确定性的函数关系外,还存在大量因变量的取值带有一定随机性的相关关系.在本章中,我们学习了一元线性相关关系,通过建立回归直线方程就可以根据其部分观测值,获得对这两个变量之间的整体关系的了解.分析两个变量的相关关系时,我们可根据样本数据散点图确定两个变量之间是否存在相关关系,还可利用最小二乘估计求出回归直线方程.通常我们使用散点图,首先把样本数据表示的点在直角坐标系中作出,形成散点图.然后从散点图上,我们可以分析出两个变量是否存在相关关系:如果这些点大致分布在通过散点图中心的一条直线附近,那么就说这两个变量之间具有线性相关关系,这条直线叫做回归直线,其对应的方程叫做回归直线方程.在本节要经常与数据打交道,计算量大,因此同学们要学会应用科学计算器.(4)求回归直线方程的步骤:第一步:先把数据制成表,从表中计算出211nni i i i i x y x y x ==∑∑,,,;第二步:计算回归系数的a ,b ,公式为1112211()()()n n ni i i i i i i n ni i i i n x y x y b n x x a y bx =====⎧-⎪⎪=⎪⎨-⎪⎪=-⎪⎩∑∑∑∑∑,;第三步:写出回归直线方程 y bx a =+.(4)独立性检验①22⨯列联表:列出的两个分类变量X 和Y ,它们的取值分别为12{,}x x 和12{,}y y 的样本频数表称为22⨯列联表1构造随机变量22()()()())n ad bc K a b c d a c b d -=++++(其中n a b c d =+++)得到2K 的观察值k 常与以下几个临界值加以比较:如果 2.706k >,就有0090的把握因为两分类变量X 和Y 是有关系;如果 3.841k>就有0095的把握因为两分类变量X和Y是有关系;如果 6.635k>就有0099的把握因为两分类变量X和Y是有关系;如果低于 2.706k≤,就认为没有充分的证据说明变量X和Y是有关系.②三维柱形图:如果列联表1的三维柱形图如下图由各小柱形表示的频数可见,对角线上的频数的积的差的绝对值-较大,说明两分类变量X和Y是有关的,否则的话是无关的.||ad bc图重点:一方面考察对角线频数之差,更重要的一方面是提供了构造随机变量进行独立性检验的思路方法。
高考试题解析分类汇编排列组合

2013高考试题解析分类汇编(理数)排列、组合及二项式定理一、选择题(2013年新课标Ⅱ卷数学(理)已知5)1)(1(x ax ++的展开式中2x 的系数为5,则=a( ) A .4- B .3- C .2- D .1-(2013年山东数学(理)试题用0,1,,9十个数字,可以组成有重复数字的三位数的个数为 ( ) A .243 B .252 C .261 D .279(2013年高考新课标1(理))设m 为正整数,2()m x y +展开式的二项式系数的最大值为a ,21()m x y ++展开式的二项式系数的最大值为b ,若137a b =,则m = ( ) A .5B .6C .7D .8(2013年大纲版数学(理)WORD 版含答案(已校对))()()8411+x y +的展开式中22x y 的系数是( )A .56B .84C .112D .168(2013年福建数学(理)试题满足{},1,0,1,2a b ∈-,且关于x 的方程220ax x b ++=有实数解的有序数对(,)a b 的个数为( )A .14B .13C .12D .10(2013年辽宁数学(理)试题使得()3nx n N n +⎛∈ ⎝的展开式中含有常数项的最小的为( )A .4B .5C .6D .7(2013年四川卷(理))从1,3,5,7,9这五个数中,每次取出两个不同的数分别为,a b ,共可得到lg lg a b -的不同值的个数是( )A .9B .10C .18D .20(2013年陕西卷(理))设函数61,00.,()x x f x x x ⎧⎛⎫-<⎪ ⎪=⎝≥⎭⎨⎪⎩ , 则当x >0时, [()]f f x 表达式的展开式中常数项为( )A .-20B .20C .-15D .15(2013年高考江西卷(理))(x 2-32x)5展开式中的常数项为 ( )A .80B .-80C .40D .-40二、填空题(2013年高考四川卷(理))二项式5()x y +的展开式中,含23x y 的项的系数是_________.(用数字作答)(2013年普通高等学校招生统一考试浙江数学(理)试题(纯WORD 版))将F E D C B A ,,,,,六个字母排成一排,且B A ,均在C 的同侧,则不同的排法共有________种(用数字作答)(2013年普通高等学校招生统一考试重庆数学(理)试题(含答案))从3名骨科.4名脑外科和5名内科医生中选派5人组成一个抗震救灾医疗小组,则骨科.脑外科和内科医生都至少有1人的选派方法种数是___________(用数字作答)(2013年普通高等学校招生统一考试天津数学(理)试题(含答案))6x⎛⎝的二项展开式中的常数项为______.(2013年普通高等学校招生统一考试浙江数学(理)试题(纯WORD 版))设二项式53)1(xx -的展开式中常数项为A ,则=A ________. (2013年高考上海卷(理))设常数a R ∈,若52a x x ⎛⎫+ ⎪⎝⎭的二项展开式中7x 项的系数为10-,则______a =(2013年高考北京卷(理))将序号分别为1,2,3,4,5的5张参观券全部分给4人,每人至少1张,如果分给同一人的2张参观券连号,那么不同的分法种数是_________. 96(2013年安徽数学(理)试题若8x ⎛+ ⎝的展开式中4x 的系数为7,则实数a =______.(2013年大纲版数学(理)6个人排成一行,其中甲、乙两人不相邻的不同排法共有____________种.(用数字作答).。
2012年高考数学试题解析 分项版之专题11 排列组合二项式定理 教师版 文.pdf

2012年高考数学试题解析 分项版之专题11 排列组合二项式定理 教师版 文 一、选择题: 1. (2012年高考重庆卷文科4) 的展开式中的系数为 (A)-270 (B)-90 (C)90 (D)270 2.(2012年高考全国卷文科7)位选手依次演讲,其中选手甲不再第一个也不再最后一个演讲,则不同的演讲次序共有 (A)种 (B)种 (C)种 (D)种 【答案】C 【解析】先排甲,有4种方法,剩余5人全排列有种,所以不同的演讲次序有种,选C. 3.(2012年高考四川卷文科2)的展开式中的系数是( )A、21B、28C、35D、42 4.(2012年高考四川卷文科11)方程中的,且互不相同,在所有这些方程所表示的曲线中,不同的抛物线共有()A、28条B、32条C、36条D、48条 【答案】B 【解析】方程变形得,若表示抛物线,则 所以,分b=-2,1,2,3四种情况: (1)若b=-2, ; (2)若b=2, 二、填空题: 5.(2012年高考全国卷文科13)的展开式中的系数为____________. 【答案】7 【解析】二项展开式的通项为,令,解得,所以,所以的系数为7. 6. (2012年高考上海卷文科8)在的二项式展开式中,常数项等于 . 三、解答题: 7.(2012年高考江苏卷23)(本小题满分10分) 设集合,.记为同时满足下列条件的集合A的个数: ①;②若,则;③若,则. (1)求; (2)求的解析式(用n表示). 【解析】(1)当时,符合条件的集合为:, ∴=4. ( 2 )任取偶数,将除以2 ,若商仍为偶数.再除以2 ,··· 经过次以后.商必为奇数.此时记商为。
于是,其中为奇数, 由条件知.若则为偶数;若,则为奇数, 于是是否属于,由是否属于确定, 设是中所有奇数的集合.因此等于的子集个数, 当为偶数〔 或奇数)时,中奇数的个数是(),。
-高考数学 试题汇编 第一节 排列与组合 理(含解析)

第一节排列与组合两个计数原理与排列问题1.(2012年全国大纲卷,理11,5分)将字母a,a,b,b,c,c排成三行两列,要求每行的字母互不相同,每列的字母也互不相同,则不同的排列方法共有( )(A)12种(B)18种(C)24种(D)36种解析:分两步,第一步先排第1列,有种排法;第二步排第2列有两种排法.所以共有×2=12种排法.答案:A.2.(2012年北京卷,理6,5分)从0,2中选一个数字,从1,3,5中选两个数字,组成无重复数字的三位数,其中奇数的个数为( )(A)24 (B)18(C)12 (D)6解析:第一类:若0、2中选0,则0只能在十位,百位、个位从1,3,5中选有=6种方法,即符合条件的奇数有6个;第二类:若0、2中选2,则2可以在百位或十位,有种方法,其余两位从1,3,5中选有种方法.∴选2时,符合条件的奇数有=12个.综上,由加法计数原理,符合条件的奇数有12+6=18个.答案:B.3.(2010年北京卷,理4)8名学生和2位老师站成一排合影,2位老师不相邻的排法种数为( )(A) (B)(C) (D)解析:解决不相邻问题采用插空法.由于要求2位老师不相邻,故可先排8名学生,共有种排法,然后将2名老师插到9个空中,有种排法,故排法种数为.故选A.答案:A.4.(2010年山东卷,理8)某台小型晚会由6个节目组成,演出顺序有如下要求:节目甲必须排在前两位,节目乙不能排在第一位,节目丙必须排在最后一位,该台晚会节目演出顺序的编排方案共有( )(A)36种 (B)42种(C)48种 (D)54种解析:若甲排在第一位,则除甲、丙外的其余4人可任意排列,有种排法;若甲排在第二位,则乙有种排法,除甲、乙、丙外的其余3人可任意排列,共有种排法,所以一共有+=42(种)不同的编排方案,故选B. 答案:B.两个计数原理与组合问题5.(2012年浙江卷,理6,5分)若从1,2,3,…,9这9个整数中同时取4个不同的数,其和为偶数,则不同的取法共有( )(A)60种 (B)63种 (C)65种 (D)66种解析:和为偶数的取法共有++=1+60+5=66,故选D.答案:D.6.(2012年陕西卷,理8,5分)两人进行乒乓球比赛,先赢3局者获胜,决出胜负为止,则所有可能出现的情形(各人输赢局次的不同视为不同情形)共有( )(A)10种 (B)15种 (C)20种 (D)30种解析:两人打3局:2=2两人打4局:2=2×3=6两人打5局:2=2·=12故决出胜负的所有可能共有2+6+12=20种可能.答案:C.7.(2012年山东卷,理11,5分)现有16张不同的卡片,其中红色、黄色、蓝色、绿色卡片各4张,从中任取3张,要求这3张卡片不能是同一种颜色,且红色卡片至多1张,不同取法的种数为( )(A)232 (B)252 (C)472 (D)484解析:本小题主要考查利用组合数公式解应用题.法一:(直接法)若红色卡片只有1张,则取法有种;若无红色卡片,则取法有-3种,所以满足条件的不同取法的种数为+-3=472种.法二:(间接法)任取3张卡片共有种,其中3张同色的有4种,2张红色的有种,所以满足条件的不同取法的种数为-4-=472种.答案:C.本题难度较大,但思维切入点清晰,既可从条件“不能同色”想到间接法,又可从条件“至多1张”想到分类讨论思想,采用直接法,所以抓住题眼是解决本题的关键.8.(2011年安徽卷,理8)设集合A={1,2,3,4,5,6},B={4,5,6,7,8},则满足S⊆A且S∩B≠的集合S的个数是( )(A)57 (B)56 (C)49 (D)8解析:若集合S满足S⊆A且S∩B≠,则S中的元素至少含有4,5,6中一个,在1,2,3中任意选,由分步计数原理知,有(+++)(++)种选法,故总共有8×7=56(种)选法.故选B.答案:B.9.(2010年全国卷Ⅰ,理6)某校开设A类选修课3门,B类选修课4门,一位同学从中共选3门.若要求两类课程中各至少选一门,则不同的选法共有( )(A)30种(B)35种(C)42种(D)48种解析:法一:分类讨论:要求两类课程中各至少选一门,则不同的选法有:A类2门,B类1门或A类1门,B类2门,即+=30.法二:由正难则反思想:任选3门有种选法,3门全为A类的或B类的有+种选法,所以两类课程中各至少选一门的选法有--=30.故选A.答案:A.10.(2010年湖南卷,理7)在某种信息传输过程中,用4个数字的一个排列(数字允许重复)表示一个信息,不同排列表示不同信息.若所用数字只有0和1,则与信息0110至多有两个对应位置上的数字相同的信息个数为( )(A)10 (B)11 (C)12 (D)15解析:法一:分0个相同、1个相同、2个相同讨论.(1)若0个相同,则信息为:1001,共1个.(2)若1个相同,则信息为:0001,1101,1011,1000.共4个.(3)若2个相同,①若位置一与二相同,则信息为:0101;②若位置一与三相同,则信息为:0011;③若位置一与四相同,则信息为:0000;④若位置二与三相同,则信息为:1111;⑤若位置二与四相同,则信息为:1100;⑥若位置三与四相同,则信息为:1010.共有6个.故与信息0110至多有两个对应位置上的数字相同的信息个数为1+4+6=11.法二:若0个相同,共有1个;若1个相同,共有=4(个);若2个相同,共有=6(个);故共有1+4+6=11(个).故选B.答案:B.11.(2011年北京卷,理12)用数字2,3组成四位数,且数字2,3至少都出现一次,这样的四位数共有 个.(用数字作答)解析:分类讨论:若2出现一次,则四位数有个;若2出现二次,则四位数有个;若2出现3次,则四位数有个,所以共有++=14(个).答案:14排列与组合综合问题12.(2012年新课标全国卷,理2,5分)将2名教师,4名学生分成2个小组,分别安排到甲、乙两地参加社会实践活动,每个小组由1名教师和2名学生组成,不同的安排方案共有( )(A)12种 (B)10种 (C)9种 (D)8种解析:主要考查排列组合的简单应用.法一:先分组再分派,=12, 法二:由位置选元素,先安排甲地,其余去乙地,·=12,故选A.答案:A.13.(2012年辽宁卷,理5,5分)一排9个座位坐了3个三口之家.若每家人坐在一起,则不同的坐法种数为( )(A)3×3! (B)3×(3!)3(C)(3!)4(D)9!解析:9个座位坐3个三口之家,每家人坐在一起,用捆绑法,不同的坐法种数为()=(3!)4.故选C.答案:C.14.(2011年浙江卷,理9)有5本不同的书,其中语文书2本,数学书2本,物理书1本.若将其随机地并排摆放到书架的同一层上,则同一科目的书都不相邻的概率是( )(A)(B)(C)(D)解析:从左到右5个位置可记为1号,2号,3号,4号,5号位置,同一科目不相邻时,①当语文2本在1,5位置,则数学2本在2,4位置,有2×2种排法.②当语文2本在1,4位置,数学2本可在2,5位置或3,5位置,有2×2×2种排法.③当语文2本在1,3位置,数学2本可在2,4位置或2,5位置,有2×2×2种排法.④当语文2本在2,5位置,数学2本可在1,3位置或1,4位置,有2×2×2种排法.⑤当语文2本在2,4位置,数学2本可在1,3位置或1,5位置或3,5位置,有2×2×3种排法.⑥当语文2本在3,5位置,数学2本可在1,4或2,4位置,有2×2×2种排法.∴同一科目不相邻有48种排法,又5本书的总排法共有=120种,∴同一科目不相邻时的概率为=.故选B.答案:B.15.(2012年重庆卷,理15,5分)某艺校在一天的6节课中随机安排语文、数学、外语三门文化课和其它三门艺术课各1节,则在课表上的相邻两节文化课之间最多间隔1节艺术课的概率为(用数字作答).解析:随意排6节课的方法有=720,相邻两节文化课之间至多间隔一节艺术课的对立事件为:相邻两节文化课之间安排3节艺术课或相邻两节文化课之间安排2节艺术课,共有2+=288,所以其概率为1-=.答案:本题考查了两个计数原理,古典概型,考查利用排列组合知识解决实际问题的能力、转化能力,难度适中.16.(2012年湖南卷,理16,5分)设N=2n(n∈N*,n≥2),将N个数x1,x2,…,x N依次放入编号为1,2,…,N的N个位置,得到排列P0=x1x2…x N.将该排列中分别位于奇数与偶数位置的数取出,并按原顺序依次放入对应的前和后个位置,得到排列P1=x1x3…x N-1x2x4…x N,将此操作称为C 变换,将P1分成两段,每段个数,并对每段作C变换,得到P2.当2≤i≤n-2时,将P i分成2i 段,每段个数,并对每段作C变换,得到P i+1,例如,当N=8时,P2=x1x5x3x7x2x6x4x8,此时x7位于P2中的第4个位置.(1)当N=16时,x7位于P2中的第个位置;(2)当N=2n(n≥8)时,x173位于P4中的第个位置.解析:(1)当N=16时,P0=x1x2x3x4…x15x16,P1=x1x3x5…x15x2x4…x16,P2=x1x5x9x13x3x7x11x15x2x6x10x14x4x8x12x16,所以x7位于P2中的第6个位置.(2)当N=2n时,P0=x1x2…x N,P 1=,173为奇数,x173位于P1的第1段;P 2=173=4×43+1,此时x173位于P2的第1段P 3=P3分成8段,每段共2n-3个数,173=8×21+5,此时x173位于P3的第2段,P 4=P4分成16段,每段共2n-4个数,173=16×10+13,此时x173位于P4的第4段,其第4段的数的下标成等差数列,记作{a n},其中a1=13,d=16.所以a n=13+16(n-1)=16n-3.令a n=173,即16n-3=173,n=11.所以x173位于P4的第4段的第11个位置,故x173位于P4中的第3×2n-4+11个位置.答案:6 3×2n-4+1117.(2010年江西卷,理14)将6位志愿者分成4组,其中两个组各2人,另两个组各1人,分赴世博会的四个不同场馆服务,不同的分配方案有种(用数字作答).解析:由题意可知,分成4组共有种分法,故不同的分配方案有=1080(种).答案:1080。
历年高考排列组合试题及其答案

二项式定理历年高考试题荟萃(三))102 分共计24 题, ( 一、填空题本大题共52的系数是________.(用数字作答)(1+2x)的展开式中x、1的展开式中的第5项为常数项,那么、2的值是正整数.已知,则、3 .(的值等于28的展开式中常数项为)+x(1+2)(1。
、4(用数字作答).展开式中含、5的整数次幂的项的系数之和为(用数字作答).28的展开式中常数项为)。
1+2(x()x-、6(用数字作答)的二项展开式中常数项是( 用数字作、7).答.26的展开式中常数项是).(x (+用数字、8)作答.若的二项展开式中、9的系数为,则.(用数字作答)______3n的展开式中含有常数项,x(2则+)若、10.n最小的正整数等于39)+(x.x展开式中的系数是(用、11数字作答).若、12展开式的各项系数之和为32,则n= ,其展开式中的常数项为。
(用数字作答)的展开式中、13的系数为.(用数字作答)55432+ax+a,则a+a+a+a+a若(x-2)x=a=__________.+ax+ax+ax、1450453212314243的系数为(1-x xx(1+2展开式中)).、15; 各项系数之的展开式中常数项为、16和为.(用数字作答)25的系数是x的二项展开式中)(x、17)用数字作答____________.( 36展开式中的常数项为)(x+(1+x )、18_____________.则若x0,>、19+(2.)(2-)-4.(x-)=______________.268k=______________.则120,的系数小于,x的展开式中)是正整数(k)(1+kx已知、20.n的展开式中第m)项的系数记(2x+、21n2,若为bb=b,则=.4m335的系数为)的二项展开式中x(x+、22)用数字作答_____________.(2n的展开式中没有常(1+x+x))(x+已知、23*且2≤n≤8,则n=_____________.数项,n∈N展开式中x的系数为.、24二项式定理历年高考试题荟萃(三)答案)分102 共计, 题24 共本大题( 一、填空题.2,∴系数为x(2)C=解析:40T、132=40.C·2.解:∵的展开式中的第5项为、2,且常数项,∴,得-256.令x=1,则有a+a+a+x+aa+ax+a+a=0,x++:(1解析-x)=aaxax+a514423235010即、352345(a+a+a)+(a+a+a)=0; ①5123405,=2aa+-a-+a=令x-1,则有-aa5302145②a++a)-(+a+(即aaa. )=2531420.联立①②有(a+a+a)(a+a+a)=-∴54021382=256.-=57.×1+2×1:解析57、4.答案:72解析:∵T= 、5r+1(=,.∴r=0,4,8时展开式中的项为整数次幂,所求系数和为++=72.答案:-42解析:的通项、6T=r+1.2)x(1+2∴=,展开式中常数项为42.-=15解析:、87、--r)2(6xTx=r+1.,令12-3xr==0,得r=4,∴T=15.=4.-312rr答案:2解析:∵、9==2.a∴,.)x(2C=T解析答案:7:、10+1rrr=2()C.-n3xx=2.Cx令3n-r=0,则有6n=7r,由展开式中有常7.最小值为n所以,数项.84 T=,∴9-2r=3.∴r=3.∴、11r+184.n=32.2可得展开式中各项系数之和为x=1令:解析5 10、12.∴n=5.而展开式中通项为2r()T(x=r+1.5-r=)5r-15.令5r-15=0,∴xr=3.3T∴常数项为=C=10.54.7展开式中的)由二项式定理得84 (1-、13项为3第·T(-=3.2=84)·,即84.的系数为5=-32.=(-2)令x=0,则a由二项式定理中的赋值法31 解析:,、140令x=1,则a+a+a+a+a+a=-1.∴a+a+a+a+a=-1-a=31.0514232453012的项x解析:展开式中含-6、1530·1·(2x)·m=22·+(-x)·1.21·1(2x)·31+1(-x)··12·(2x)1.402222的系展开式中=x1(-x)=6x-24x+12x2数为∴系数为-6.,-6x展开式中通项为10 32()T(x=r+1.、1625-rr=)其中常数项为,.T==10;令x=1,可得各项系数之和为35=32.2∵:解析40、173·(·)(x22222的系数为∴(-2)1)=10××·x=40x,x40.6展开式中的项)35 (x+答案:、18的系数与常数项的系数之和即为所求,由.T=·(r+1r=)6-3r r=2∴当,x·.时,=15.当r=3=20.,时15+20=35.故原展开式中的常数项为答案:-23 原式、193-4-3=4+4=-23.844,∵=15k解析答案:1:x的系数为k、20+44k=1.∴,Z∈8,k<120,k<15kn的展开式中第m项为)5 记(2x+、21n-m+1m-1==Tab mn-m+1·(·(2x).m-1,则)n-m+1.又∵b=2b,=b∴2·43mn-2×=22·.n-32·.=n=5.解得,.答案:10··x2=10.×=5.、224n展开式中不含)5解析:(x+答案:、23-2-10项即可,xx、x、由n-r(xF=r+1.r=)n-4.时成立n=5可以验证8,≤n≤2∵r.x2 展开式中含x的项、2430·1·(2x)·n=31·+(-x)·1.21·(2x)1·04·=-4x+6x=2x,1(-x)∴展开式中x的系数为2.。
历年高考排列组合试题及其答案

二项式定理历年高考试题荟萃(三)一、填空题 ( 本大题共 24 题, 共计 102 分)1、 (1+2x)5的展开式中x2的系数是________.(用数字作答)2、的展开式中的第5项为常数项,那么正整数的值是 .3、已知,则( 的值等于 .4、(1+2x2)(1+)8的展开式中常数项为。
(用数字作答)5、展开式中含的整数次幂的项的系数之和为(用数字作答).6、(1+2x2)(x-)8的展开式中常数项为。
(用数字作答)7、的二项展开式中常数项是 (用数字作答).8、 (x2+)6的展开式中常数项是 .(用数字作答)9、若的二项展开式中的系数为,则______(用数字作答).10、若(2x3+)n的展开式中含有常数项,则最小的正整数n等于.11、(x+)9展开式中x3的系数是 .(用数字作答)12、若展开式的各项系数之和为32,则n= ,其展开式中的常数项为。
(用数字作答)13、的展开式中的系数为.(用数字作答)14、若(x-2)5=a5x5+a4x4+a3x3+a2x2+a1x+a0,则a1+a2+a3+a4+a5=__________.15、(1+2x)3(1-x)4展开式中x2的系数为 .16、的展开式中常数项为 ; 各项系数之和为.(用数字作答)17、 (x)5的二项展开式中x2的系数是____________.(用数字作答)18、 (1+x3)(x+)6展开式中的常数项为_____________.19、若x>0,则(2+)(2-)-4(x-)=______________.20、已知(1+kx2)6(k是正整数)的展开式中,x8的系数小于120,则k=______________.21、记(2x+)n的展开式中第m项的系数为b m,若b3=2b4,则n= .22、 (x+)5的二项展开式中x3的系数为_____________.(用数字作答)23、已知(1+x+x2)(x+)n的展开式中没有常数项,n∈N*且2≤n≤8,则n=_____________.24、展开式中x的系数为.二项式定理历年高考试题荟萃(三)答案一、填空题 ( 本大题共 24 题, 共计 102 分)1、40解析:T3=C(2x)2,∴系数为22·C=40.2、解:∵的展开式中的第5项为,且常数项,∴,得3、-256解析:(1-x)5=a0+a1x+a2x2+a3x3+a4x4+a5x5.令x=1,则有a0+a1+a2+a3+a4+a5=0,即(a0+a2+a4)+(a1+a3+a5)=0;①令x=-1,则有a0-a1+a2-a3+a4-a5=25,即(a0+a2+a4)-(a1+a3+a5)=25.②联立①②有∴(a0+a2+a4)(a1+a3+a5)=-28=-256.4、57解析:1×1+2×=57.5、答案:72解析:∵T r+1= (=,∴r=0,4,8时展开式中的项为整数次幂,所求系数和为++=72.6、答案:-42解析:的通项T r+1==,∴(1+2x2)展开式中常数项为=-42.7、8、15解析:T r+1=x2(6-r)x-r=x12-3r,令12-3r=0,得r=4,∴T4==15.9、答案:2解析:∵=,∴a=2.10、答案:7解析:T r+1=C(2x3)n-r()r=2Cxx=2Cx令3n-r=0,则有6n=7r,由展开式中有常数项,所以n最小值为7.11、84 T r+1=,∴9-2r=3.∴r=3.∴84.12、5 10 解析:令x=1可得展开式中各项系数之和为2n=32.∴n=5.而展开式中通项为Tr+1=(x2)r()5-r=x5r-15.令5r-15=0,∴r=3.∴常数项为T4=C35=10.13、84 由二项式定理得(1-)7展开式中的第3项为T3=·(-)2=84·,即的系数为84.14、31 解析:由二项式定理中的赋值法,令x=0,则a0=(-2)5=-32.令x=1,则a0+a1+a2+a3+a4+a5=-1.∴a1+a2+a3+a4+a5=-1-a=31.15、-6解析:展开式中含x2的项m=·13·(2x)0··12·(-x)2+·12(2x)1··13·(-x)1+11(2x)2·14(-x)0=6x2-24x2+12x2=展开式中x2的系数为-6x2,∴系数为-6.16、10 32 展开式中通项为T r+1=(x2)5-r()r=,其中常数项为T3==10;令x=1,可得各项系数之和为25=32.17、40解析:∵·(x3)·()2=10×1×(-2)2·x2=40x2,∴x2的系数为40.18、答案:35 (x+)6展开式中的项的系数与常数项的系数之和即为所求,由Tr+1=·()r=·x6-3r,∴当r=2时,=15.当r=3时,=20.故原展开式中的常数项为15+20=35.19、答案:-23 原式=4-33-4+4=-23.20、答案:1解析:x8的系数为k4=15k4,∵15k4<120,k4<8,k∈Z+,∴k=1.21、5 记(2x+)n的展开式中第m项为T m=a n-m+1b m-1=·(2x)n-m+1·()m-1,则b m=·2n-m+1.又∵b3=2b4,∴·2n-2=2×·2n-3=,解得n=5.22、答案:10 ·x4·=5×2=10.23、答案:5解析:(x+)n展开式中不含x0、x-1、x-2项即可,由Fr+1=x n-r()r=x n-4r.∵2≤n≤8,可以验证n=5时成立.24、2 展开式中含x的项n=·13·(2x)0··13·(-x)1+·12(2x)1··14(-x)0=-4x+6x=2x,∴展开式中x的系数为2.。
历年高考数学真题精选45 排列组合

历年高考数学真题精选(按考点分类)专题45 排列组合(学生版)一.选择题(共20小题)1.(2009•全国卷Ⅰ)甲组有5名男同学,3名女同学;乙组有6名男同学、2名女同学.若从甲、乙两组中各选出2名同学,则选出的4人中恰有1名女同学的不同选法共有( )A.150种B.180种C.300种D.345种2.(2010•广东)为了迎接2010年广州亚运会,某大楼安装5个彩灯,它们闪亮的顺序不固定.每个彩灯闪亮只能是红、橙、黄、绿、蓝中的一种颜色,且这5个彩灯闪亮的颜色各不相同,记这5个彩灯有序地闪亮一次为一个闪烁.在每个闪烁中,每秒钟有且只有一个彩灯闪亮,而相邻两个闪烁的时间间隔均为5秒.如果要实现所有不同的闪烁,那么需要的时间至少是()A.1205秒B.1200秒C.1195秒D.1190秒3.(2007•全国卷Ⅱ)5位同学报名参加两个课外活动小组,每位同学限报其中的一个小组,则不同的报名方法共有()A.10种B.20种C.25种D.32种4.(2006•湖南)在数字1,2,3与符号+,-五个元素的所有全排列中,任意两个数字都不相邻的全排列个数是()A.6B.12C.24D.18 5.(2009•陕西)从1,2,3,4,5,6,7这七个数字中任取两个奇数和两个偶数,组成没有重复数字的四位数,其中奇数的个数为()A.432B.288C.216D.108 6.(2014•辽宁)6把椅子排成一排,3人随机就座,任何两人不相邻的坐法种数为() A.144B.120C.72D.24 7.(2012•浙江)若从1,2,3,⋯,9这9个整数中同时取4个不同的数,其和为偶数,则不同的取法共有()A.60种B.63种C.65种D.66种8.(2012•北京)从0、2中选一个数字.从1、3、5中选两个数字,组成无重复数字的三位数.其中奇数的个数为()A .24B .18C .12D .69.(2008•全国卷Ⅰ)将1,2,3填入33⨯的方格中,要求每行、每列都没有重复数字,下面是一种填法,则不同的填写方法共有( )A .6种B .12种C .24种D .48种10.(2010•重庆)某单位安排7位员工在10月1日至7日值班,每天1人,每人值班1天,若7位员工中的甲、乙排在相邻两天,丙不排在10月1日,丁不排在10月7日,则不同的安排方案共有( )A .504种B .960种C .1008种D .1108种11.(2015•上海)组合数122(2m m m nn n C C C n m --++,m ,*)n N ∈恒等于( ) A .2m n C + B .12m n C ++ C .1m n C + D .11m n C ++12.(2010•重庆)某单位拟安排6位员工在今年6月14日至16日(端午节假期)值班,每天安排2人,每人值班1天.若6位员工中的甲不值14日,乙不值16日,则不同的安排方法共有( )A .30种B .36种C .42种D .48种13.(2009•黑龙江)甲、乙两人从4门课程中各选修2门,则甲、乙所选的课程中恰有1门相同的选法有( )A .6种B .12种C .24种D .30种14.(2007•全国卷Ⅰ)甲、乙、丙3位同学选修课程,从4门课程中,甲选修2门,乙、丙各选修3门,则不同的选修方案共有( )A .36种B .48种C .96种D .192种15.(2006•全国卷Ⅰ)设集合{1I =,2,3,4,5}.选择I 的两个非空子集A 和B ,要使B中最小的数大于A 中最大的数,则不同的选择方法共有( )A .50种B .49种C .48种D .47种16.(2017•全国)4个数字1和4个数字2可以组成不同的8位数共有( )A .16个B .70个C .140个D .256个17.(2017•新课标Ⅱ)安排3名志愿者完成4项工作,每人至少完成1项,每项工作由1人完成,则不同的安排方式共有( )A.12种B.18种C.24种D.36种18.(2016•全国)从1,2,3,4,5,6中任取三个不同的数相加,则不同的结果共有( )A.6种B.9种C.10种D.15种19.(2016•新课标Ⅱ)如图,小明从街道的E处出发,先到F处与小红会合,再一起到位于G处的老年公寓参加志愿者活动,则小明到老年公寓可以选择的最短路径条数为( )A.24B.18C.12D.9 20.(2013•全国)3位男同学与2位女同学排成一列,其中女同学相邻的不同排法共有( )A.48种B.36种C.24种D.18种二.填空题(共5小题)21.(2007•陕西)安排3名支教教师去4所学校任教,每校至多2人,则不同的分配方案共有种.(用数字作答)22.(2010•全国大纲版Ⅰ)某学校开设A类选修课3门,B类选修课4门,一位同学从中共选3门,若要求两类课程中各至少选一门,则不同的选法共有种.(用数字作答)23.(2007•重庆)某校要求每位学生从7门课程中选修4门,其中甲、乙两门课程不能都选,则不同的选课方案有种.(以数字作答)24.(2019•上海)首届中国国际进口博览会在上海举行,某高校拟派4人参加连续5天的志愿者活动,其中甲连续参加2天,其他人各参加1天,则不同的安排方法有种(结果用数值表示)25.(2018•新课标Ⅰ)从2位女生,4位男生中选3人参加科技比赛,且至少有1位女生入选,则不同的选法共有种.(用数字填写答案)历年高考数学真题精选(按考点分类)专题45 排列组合(教师版)一.选择题(共20小题)1.(2009•全国卷Ⅰ)甲组有5名男同学,3名女同学;乙组有6名男同学、2名女同学.若从甲、乙两组中各选出2名同学,则选出的4人中恰有1名女同学的不同选法共有( )A.150种B.180种C.300种D.345种【答案】D【解析】分两类(1)甲组中选出一名女生有112536225C C C=种选法;(2)乙组中选出一名女生有211562120C C C=种选法.故共有345种选法.2.(2010•广东)为了迎接2010年广州亚运会,某大楼安装5个彩灯,它们闪亮的顺序不固定.每个彩灯闪亮只能是红、橙、黄、绿、蓝中的一种颜色,且这5个彩灯闪亮的颜色各不相同,记这5个彩灯有序地闪亮一次为一个闪烁.在每个闪烁中,每秒钟有且只有一个彩灯闪亮,而相邻两个闪烁的时间间隔均为5秒.如果要实现所有不同的闪烁,那么需要的时间至少是()A.1205秒B.1200秒C.1195秒D.1190秒【答案】C【解析】由题意知共有5!120=个不同的闪烁,每个闪烁时间为5秒,共5120600⨯=秒;每两个闪烁之间的间隔为5秒,共5(1201)595⨯-=秒.那么需要的时间至少是6005951195+=秒.3.(2007•全国卷Ⅱ)5位同学报名参加两个课外活动小组,每位同学限报其中的一个小组,则不同的报名方法共有()A.10种B.20种C.25种D.32种【答案】D【解析】5位同学报名参加两个课外活动小组,每位同学限报其中的一个小组,则不同的报名方法共有5232=种.4.(2006•湖南)在数字1,2,3与符号+,-五个元素的所有全排列中,任意两个数字都不相邻的全排列个数是( )A .6B .12C .24D .18【答案】B【解析】在数字1,2,3与符号“+”,“ -”五个元素的所有全排列中,先排列1,2,3,有336A =种排法,再将“+”,“ -”两个符号插入, 有222A =种方法,共有12种方法,故选B . 5.(2009•陕西)从1,2,3,4,5,6,7这七个数字中任取两个奇数和两个偶数,组成没有重复数字的四位数,其中奇数的个数为( )A .432B .288C .216D .108【答案】C 【解析】由题意知本题是一个分步计数原理,第一步先从4个奇数中取2个再从3个偶数中取2个共224318C C =种, 第二步再把4个数排列,其中是奇数的共132312A A =种, ∴所求奇数的个数共有1812216⨯=种.6.(2014•辽宁)6把椅子排成一排,3人随机就座,任何两人不相邻的坐法种数为( )A .144B .120C .72D .24【答案】D【解析】使用“插空法“.第一步,三个人先坐成一排,有33A 种,即全排,6种;第二步,由于三个人必须隔开,因此必须先在1号位置与2号位置之间摆放一张凳子,2号位置与3号位置之间摆放一张凳子,剩余一张凳子可以选择三个人的左右共4个空挡,随便摆放即可,即有14C 种办法.根据分步计数原理,6424⨯=. 7.(2012•浙江)若从1,2,3,⋯,9这9个整数中同时取4个不同的数,其和为偶数,则不同的取法共有( )A .60种B .63种C .65种D .66种【答案】D【解析】由题意知本题是一个分类计数问题,要得到四个数字的和是偶数,需要分成三种不同的情况,当取得4个偶数时,有441C =种结果, 当取得4个奇数时,有455C =种结果,当取得2奇2偶时有224561060C C =⨯= ∴共有156066++=种结果8.(2012•北京)从0、2中选一个数字.从1、3、5中选两个数字,组成无重复数字的三位数.其中奇数的个数为( )A .24B .18C .12D .6【答案】B【解析】从0、2中选一个数字0,则0只能排在十位,从1、3、5中选两个数字排在个位与百位,共有236A =种;从0、2中选一个数字2,则2排在十位,从1、3、5中选两个数字排在个位与百位,共有236A =种;2排在百位,从1、3、5中选两个数字排在个位与十位,共有236A =种;故共有23318A =种9.(2008•全国卷Ⅰ)将1,2,3填入33⨯的方格中,要求每行、每列都没有重复数字,下面是一种填法,则不同的填写方法共有( )A .6种B .12种C .24种D .48种【答案】B【解析】填好第一行和第一列,其他的行和列就确定,323212A A ∴= 10.(2010•重庆)某单位安排7位员工在10月1日至7日值班,每天1人,每人值班1天,若7位员工中的甲、乙排在相邻两天,丙不排在10月1日,丁不排在10月7日,则不同的安排方案共有( )A .504种B .960种C .1008种D .1108种【答案】C【解析】分两类:第一类:甲乙相邻排1、2号或6、7号,这时先排甲和乙,有222A ⨯种,然后排丁,有14A 种,剩下其他四个人全排列有44A 种,因此共有2142442384A A A ⨯=种方法 第二类:甲乙相邻排中间,若丙排7号,先排甲和乙,因为相邻且在中间,则有224A ⨯种,然后丙在7号,剩下四个人全排列有44A 种,若丙不排7号,先排甲和乙,因为相邻且在中间,则有224A ⨯种,然后排丙,丙不再1号和7号,有13A 种,接着排丁,丁不排在10月7日,有13A 种,剩下3个人全排列,有33A 种,因此共有242113242333(44)624A A A A A A +=种方法,故共有1008种不同的排法 11.(2015•上海)组合数122(2m m m nn n C C C n m --++,m ,*)n N ∈恒等于( ) A .2m n C +B .12m nC ++ C .1m n C +D .11m n C ++【答案】A 【解析】组合数1211211122m m m m m m m m m m n n n n n n n n n n C C C C C C C C C C ------+++++=+++=+=.12.(2010•重庆)某单位拟安排6位员工在今年6月14日至16日(端午节假期)值班,每天安排2人,每人值班1天.若6位员工中的甲不值14日,乙不值16日,则不同的安排方法共有( )A .30种B .36种C .42种D .48种【答案】C【解析】根据题意,不同的安排方法的数目等于所有排法减去甲值14日或乙值16日的排法数,再加上甲值14日且乙值16日的排法,即221211645443242C C C C C C -⨯+= 13.(2009•黑龙江)甲、乙两人从4门课程中各选修2门,则甲、乙所选的课程中恰有1门相同的选法有( )A .6种B .12种C .24种D .30种【答案】C【解析】根据题意,分两步,①由题意可得,所有两人各选修2门的种数224436C C =, ②两人所选两门都相同的有为246C =种,都不同的种数为246C = 14.(2007•全国卷Ⅰ)甲、乙、丙3位同学选修课程,从4门课程中,甲选修2门,乙、丙各选修3门,则不同的选修方案共有( )A .36种B .48种C .96种D .192种【答案】C【解析】根据题意,甲、乙、丙3位同学选修课程,从4门课程中,甲选修2门,有24C 种,乙、丙各选修3门,有3344C C 种,则不同的选修方案共有23344496C C C =种 15.(2006•全国卷Ⅰ)设集合{1I =,2,3,4,5}.选择I 的两个非空子集A 和B ,要使B中最小的数大于A 中最大的数,则不同的选择方法共有( )A .50种B .49种C .48种D .47种【答案】B【解析】集合A 、B 中没有相同的元素,且都不是空集,从5个元素中选出2个元素,有2510C =种选法,小的给A 集合,大的给B 集合;从5个元素中选出3个元素,有3510C =种选法,再分成1、2两组,较小元素的一组给A 集合,较大元素的一组的给B 集合,共有21020⨯=种方法;从5个元素中选出4个元素,有455C =种选法,再分成1、3;2、2;3、1两组,较小元素的一组给A 集合,较大元素的一组的给B 集合,共有3515⨯=种方法;从5个元素中选出5个元素,有551C =种选法,再分成1、4;2、3;3、2;4、1两组,较小元素的一组给A 集合,较大元素的一组的给B 集合,共有414⨯=种方法;总计为102015449+++=种方法.16.(2017•全国)4个数字1和4个数字2可以组成不同的8位数共有( )A .16个B .70个C .140个D .256个【答案】B【解析】4个数字1和4个数字2可以组成不同的8位数共有:88444470A A A =. 17.(2017•新课标Ⅱ)安排3名志愿者完成4项工作,每人至少完成1项,每项工作由1人完成,则不同的安排方式共有( )A .12种B .18种C .24种D .36种【答案】D【解析】4项工作分成3组,可得:246C =, 安排3名志愿者完成4项工作,每人至少完成1项,每项工作由1人完成,可得:33636A ⨯=种. 18.(2016•全国)从1,2,3,4,5,6中任取三个不同的数相加,则不同的结果共有()A .6种B .9种C .10种D .15种【答案】C【解析】从1,2,3,4,5,6中任取三个不同的数相加,所得的最小值为1236++=,最大值为45615++=,1236++=,1247++=,1251348++=++=,1261352349++=++=++=,136********++=++=++=,14623624511++=++=++=,156********++=++=++=,34613++=,35614++=,45615++=共有:10种不同结果. 19.(2016•新课标Ⅱ)如图,小明从街道的E 处出发,先到F 处与小红会合,再一起到位于G 处的老年公寓参加志愿者活动,则小明到老年公寓可以选择的最短路径条数( )A .24B .18C .12D .9【答案】B【解析】从E 到F ,每条东西向的街道被分成2段,每条南北向的街道被分成2段, 从E 到F 最短的走法,无论怎样走,一定包括4段,其中2段方向相同,另2段方向相同,每种最短走法,即是从4段中选出2段走东向的,选出2段走北向的,故共有22426C C =种走法.同理从F 到G ,最短的走法,有12323C C =种走法. ∴小明到老年公寓可以选择的最短路径条数为6318⨯=种走法.20.(2013•全国)3位男同学与2位女同学排成一列,其中女同学相邻的不同排法共有()A .48种B .36种C .24种D .18种【答案】A 【解析】3位男同学与2位女同学排成一列,其中女同学相邻的不同排法共有:424248A A =种.二.填空题(共5小题)21.(2007•陕西)安排3名支教教师去4所学校任教,每校至多2人,则不同的分配方案共有 种.(用数字作答)【答案】60【解析】分2类:(1)每校最多1人:3424A =; (2)每校至多2人,把3人分两组,再分到学校:223436C A =,共有60种 22.(2010•全国大纲版Ⅰ)某学校开设A 类选修课3门,B 类选修课4门,一位同学从中共选3门,若要求两类课程中各至少选一门,则不同的选法共有 种.(用数字作答)【答案】30【解析】分以下2种情况:(1)A 类选修课选1门,B 类选修课选2门,有1234C C 种不同的选法;(2)A 类选修课选2门,B 类选修课选1门,有2134C C 种不同的选法.所以不同的选法共有12213434181230C C C C +=+=种. 23.(2007•重庆)某校要求每位学生从7门课程中选修4门,其中甲、乙两门课程不能都选,则不同的选课方案有 种.(以数字作答)【答案】25【解析】所有的选法数为47C ,两门都选的方法为2225C C , 故共有选法数为422725351025C C C -=-=. 24.(2019•上海)首届中国国际进口博览会在上海举行,某高校拟派4人参加连续5天的志愿者活动,其中甲连续参加2天,其他人各参加1天,则不同的安排方法有 种(结果用数值表示)【答案】24【解析】在五天里,连续的2天,一共有4种,剩下的3人排列,故有33424A =种 25.(2018•新课标Ⅰ)从2位女生,4位男生中选3人参加科技比赛,且至少有1位女生入选,则不同的选法共有16种.(用数字填写答案)【答案】16【解析】1女2男,有122412C C=,2女1男,有21244C C=根据分类计数原理可得,共有12416+=种,故答案为:16第11页(共11页)。
2013高考数学总复习 10-6排列与组合(理)基础巩固强化练习 新人教A版

10-6排列与组合(理)基础巩固强化1.(2012·某某理,7)从个位数与十位数之和为奇数的两位数中任取一个,其个位数为0的概率是( )A.49B.13C.29D.19 [答案] D[解析] 本题考查计数原理与古典概型,∵两数之和为奇数,则两数一奇一偶,若个位数为奇数,则共有4×5=20个数,若个位数为偶数,共有5×5=25个数,其中个位为0的数共有5个,∴P =520+25=19.2.(2011·某某模拟)甲、乙、丙3位志愿者安排在周一至周五的5天中参加某项志愿者活动,要求每人参加一天且每天至多安排一人,并要求甲安排在另外两位前面.不同的安排方法共有( )A .20种B .30种C .40种D .60种 [答案] A[解析] 分三类:甲在周一,共有A 24种排法; 甲在周二,共有A 23种排法; 甲在周三,共有A 22种排法; ∴A 24+A 23+A 22=20.3.(2012·大纲全国,11)将字母a 、a 、b 、b 、c 、c 排成三行两列,要求每行的字母互不相同,每列的字母也互不相同,则不同的排列方法共有( )A .12种B .18种C .24种D .36种 [答案] A[解析] 先排第一列,因为每列的字母互不相同,因此共有A 33种不同的排法;再排第二列,第二列第一行的字母有2种排法,排好此位置后,其他位置只有一种排法.因此共有2A 33=12种不同的排法.4.(2012·某某豫东、豫北十所名校测试)2011年3月17日上午,日本自卫队选派了两架直升飞机对福岛第一核电站3号机组的燃料池进行了4次注水.如果直升飞机有A 、B 、C 、D 四架供选,飞行员有甲、乙、丙、丁四人供选,且一架直升飞机只安排一名飞行员,则选出两名飞行员驾驶两架直升飞机的不同方法数为( )A .18B .36C .72D .108 [答案] C[解析] 飞机的选法有C 24种,飞行员的选法有C 24种,把飞行员安排到飞机上有A 22,共有C 24×C 24×A 22=72种.5.(2011·某某模拟)如图所示的几何体是由一个正三棱锥P -ABC 与正三棱柱ABC -A 1B 1C 1组合而成,现用3种不同颜色对这个几何体的表面染色(底面A 1B 1C 1不涂色),要求相邻的面均不同色,则不同的染色方案共有( )A .24种B .18种C .16种D .12种 [答案] D[解析] 先涂三棱锥P -ABC 的三个侧面,然后涂三棱柱的三个侧面,共有C 13×C 12×C 11C 12=3×2×1×2=12种不同的涂法.6.(2011·某某模拟)从集合{1,2,3,…,10}中任意选出三个不同的数,使这三个数成等比数列,这样的等比数列的个数为( )A .3B .4C .6D .8 [答案] D[解析] 当公比为2时,等比数列可为1、2、4,2、4、8. 当公比为3时,等比数列可为1、3、9. 当公比为32时,等比数列可为4、6、9.同时,4、2、1,8、4、2,9、3、1和9、6、4也是等比数列,共8个.7.从0,1,2,3,4,5,6,7,8,9这10个数字中任取3个不同的数字构成空间直角坐标系中的点的坐标为(x ,y ,z ),若x +y +z 是3的倍数,则满足条件的点的个数为________.[答案] 252[解析] 当三个数字都能被3整除时,从0,3,6,9中任取三个,构成不同坐标A 34=24个,当三个数字中有一个能被3整除时,另两个的和应能被3整除,这样的两个数共有9组,即:(1,2),(1,5),(1,8),(2,4),(2,7),(4,5),(4,8),(5,7),(7,8),这样的不同坐标有4×9×A33=216个,当三个数字都不能被3整除时,有(1,4,7),(2,5,8)两组,这样的不同坐标有2×A33=12种,∴共有24+216+12=252个.8.有6个大小不同的数按如图的形式随机排列,设第一行的数为M1,第二、三行中的最大数分别为M2、M3,则满足M1<M2<M3的所有排列的个数是________.[答案] 240[解析]设6个数按从小到大顺序依次为a1、a2、a3、a4、a5、a6.据题设条件知M3=a6,可依第二行最大数M2分类讨论.①若M2=a5,有排法C14·C13·A22·A33=144种.②若M2=a4,则a5必在第三行有排法C13·C12·A22A33=72种.③若M2=a3,则a4、a5都在第三行有排法C12·A22A33=24种,据条件知M2不能小于a3.∴满足题设条件的所有不同排列的个数为144+72+24=240个.9.在空间直角坐标系O-xyz中有8个点:P1(1,1,1)、P2(-1,1,1)、…、P7(-1,-1,-1)、P8(1,-1,-1)(每个点的横、纵、竖坐标都是1或-1),以其中4个点为顶点的三棱锥一共有________个(用数字作答).[答案] 58[解析]这8个点构成正方体的8个顶点,此题即转化成以正方体的8个顶点中的4个点为顶点的三棱锥一共有多少个,则共有三棱锥C14C34+(C24C24-2×4-2)+C34C14=58个.[点评] 用间接法求解更简便些,从正方体的8个顶点中任取4个,有不同取法C48种,其中这四点共面的(6个对角面、6个表面)共12个,∴这样的三棱锥有C48-12=58个.10.(2011·某某联考)有3名男生、4名女生,在下列不同条件下,求不同的排列方法总数.(1)选5人排成一排;(2)排成前后两排,前排3人,后排4人;(3)全体排成一排,其中甲不站排头也不站排尾;(4)全体排成一排,女生必须站在一起;(5)全体排成一排,男生互不相邻; (6)女生互不相邻,且顺序一定.[解析] (1)从7人中选5人排列,有A 57=7×6×5×4×3=2520种.(2)分两步完成,先选3人站前排,有A 37种方法,余下4人站后排,有A 44种方法,共有A 37·A 44=5040种.(3)法1:(特殊元素优先法)先排甲,有5种方法,其余6人有A 66种排列方法,共有5×A 66=3600种.法2:(特殊位置优先法)首尾位置可安排另6人中的两人,有A 26种排法,其他有A 55种排法,共有A 26A 55=3600种.(4)(捆绑法)将女生看作一个整体与3名男生一起全排列,有A 44种方法,再将女生全排列,有A 44种方法,共有A 44·A 44=576种.(5)(插空法)先排女生,有A 44种方法,再在女生之间及首尾5个空位中任选3个空位安排男生,有A 35种方法,共有A 44·A 35=1440种.(6)先将男生排好,再将女生插入男生形成的4个空中,由于顺序一定,故只有一种插入方法,∴共有排法A 33=6种.能力拓展提升11.(2012·某某某某市模拟)一个质地均匀的正方体骰子,其六个面上的点数分别为1,2,3,4,5,6,将这颗骰子连续投掷三次,观察向上的点数,则三次点数依次成等比数列的概率为( )A.1108B.1216 C.136D.127[答案] D[解析] 连续抛掷三次骰子可得结果为63=216种,其中依次构成等比数列的情况有 (1)公比为1,共6种.(2)公比为2,只有1种,即1,2,4,. (3)公比为12,只有1种,即4,2,1.∴共有8种,∴P =8216=127.12.(2011·某某某某综合测试)将18个参加青少年科技创新大赛的名额分配给3个学校,要求每校至少有一个名额且各校分配的名额互不相等,则不同的分配方法种数为( )A .96B .114C .128D .136[答案] B[解析]若某一学校的最少人数是1,2,3,4,5,则各有7,5,4,2,1种不同的分组方案.故不同的分配方法种数是(7+5+4+2+1)A33=19×6=114.13.一植物园参观路径如图所示,若要全部参观并且路线不重复,则不同的参观路线种数共有( )A.6种 B.8种C.36种 D.48种[答案] D[解析]如图所示,三个区域按参观的先后次序共有A23种参观方法,对于每一种参观次序,每一个植物园都有2类参观路径,∴共有不同参观路线2×2×2×A23=48种.14.(2012·某某市模拟)将12个参加青少年科技创新大赛的名额分配给3所学校,要求每校至少有一个名额且各校分配的名额互不相等,则不同的分配方法种数为( ) A.36 B.42C.48 D.54[答案] B[解析]由题意,3所学校的分配名额可以分别是1,2,9;1,3,8;1,4,7;1,5,6;2,3,7;2,4,6;3,4,5共7种,然后,每次分配的名额分给3个学校有A33种方法,故不同的分配方法种数为7A 33=42.15.某项公益活动要招募志愿者,某大学拟成立由4名同学组成的志愿者招募宣传队,经过初选,2名男同学,4名女同学成为了候选人,每位候选人当选正式队员的机会是相等的.(1)求当选的4名同学中恰有1名男同学的概率. (2)求当选的4名同学中至少有3名女同学的概率.[解析] 从2男4女共6名同学中选取4人,不同选法共有C 46=15种, (1)恰有1名男同学当选的情况有C 12·C 34=8种, ∴所求概率P =815.(2)当选的4名同学中至少有3名女同学的情况有C 34C 12+C 44=9种,∴所求概率P =915=35.16.(2011·某某模拟)用0,1,2,3,4这五个数字,可以组成多少个满足下列条件的没有重复数字的五位数?(1)被4整除; (2)比21034大的偶数;(3)左起第二、四位是奇数的偶数.[解析] (1)被4整除的数,其特征应是末两位数是4的倍数,可分为两类:当末两位数是20、40、04时,其排列数为3A 33=18,当末两位数是12、24、32时,其排列数为3A 12·A 22=12.故满足条件的五位数共有18+12=30(个).(2)①当末位数字是0时,首位数字可以为2或3或4,满足条件的数共有3×A 33=18个. ②当末位数字是2时,首位数字可以为3或4,满足条件的数共有2×A 33=12个. ③当末位数字是4时,首位数字是3的有A 33=6个,首位数字是2时,有3个,共有9个. 综上知,比21034大的偶数共有18+12+9=39个. (3)方法一:可分为两类: 末位数是0,有A 22·A 22=4(个); 末位数是2或4,有A 22·A 12=4(个); 故共有A 22·A 22+A 22·A 12=8(个).方法二:第二、四位从奇数1,3中取,有A 22个;首位从2,4中取,有A 12个;余下的排在剩下的两位,有A 22个,故共有A 22A 12A 22=8(个).1.从10名大学毕业生中选3人担任村长助理,则甲、乙至少有1人入选,而丙没有入选的不同选法的种数为( )A .85B .56C.49 D.28[答案] C[解析]分两类计算,C22C17+C12C27=49,故选C.2.定义整数集合A与B的运算A*B如下:A*B={(x,y)|x∈A,y∈B,且x+y为偶数},若A={-1,0,1},B={1,2,3,4},则集合A*B中的元素个数为( )A.12 B.6C.4 D.2[答案] B[解析]x=-1时,y=1,3;x=0时,y=2,4;x=1时,y=1,3.故选B.3.若三角形的三边长均为正整数,其中一边长为4,另外两边长分别为b、c,且满足b≤4≤c,则这样的三角形有( )A.10个 B.14个C.15个 D.21个[答案] A[解析]当b=1时,c=4;当b=2时,c=4,5;当b=3时,c=4,5,6;当b=4时,c =4,5,6,7.故共有10个这样的三角形.选A.[点评] 注意三角形两边之和大于第三边,两边之差小于第三边.4.身穿兰、黄两种颜色衣服的各有两人,身穿红色衣服的有一人,现将这五人排成一行,要求穿相同颜色衣服的人不能相邻,则不同的排法共有( )A.48种 B.72种C.78种 D.84种[答案] A[解析]解法一:两种穿相同颜色衣服的人相邻的排法有A33A22A22=24种,只有一种穿相同颜色衣服的人相邻的排法有2(A44A22-24)=48,则穿相同颜色衣服的人不能相邻的排法有A55-24-48=48,故选A.解法二:按穿兰衣服的两人站位分有以下6类:对于①②⑤⑥排上穿黄衣服的两人都只有两类方法.第③类中排上穿黄衣服的两人只有一类方法.第④类中排上穿黄衣服的两人有三类方法.对于上述每一类安排方法,五人的不同站法共有A22A22=4种,∴共有不同排法(4×2+1+3)×4=48种.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2013年全国高考理科数学试题分类汇编10:排列、组合
一、选择题
1 .(2013年普通高等学校招生统一考试山东数学(理)试题(含答案))
用0,1,,9十个数字,
可以组成有重复数字的三位数的个数为 ( )
A.243 B.252 C.261 D.279
【答案】
B
2 .(2013年普通高等学校招生统一考试福建数学(理)试题(纯WORD版))
满足,1,0,1,2ab,
且关于x的方程220axxb有实数解的有序数对(,)ab的个数为 ( )
A.14 B.13 C.12 D.10
【答案】
B
3 .(2013年高考四川卷(理))
从1,3,5,7,9这五个数中,每次取出两个不同的数分别为,ab,
共可得到lglgab的不同值的个数是 ( )
A.9 B.10 C.18 D.20
【答案】
C
二、填空题
4.(2013年上海市春季高考数学试卷(含答案))
36的所有正约数之和可按如下方法得到:因为
22
36=23
,所以36的所有正约数之和为
22222222
(133)(22323)(22323)(122)133)91(
参照上述方法,可求得2000的所有正约数之和为________________________
【答案】
4836
5.(2013年上海市春季高考数学试卷(含答案))
从4名男同学和6名女同学中随机选取3人
参加某社团活动,选出的3人中男女同学都有的概率为________(结果用数值表示).
【答案】
4
5
6.(2013年普通高等学校招生统一考试浙江数学(理)试题(纯WORD版))
将
FEDCBA,,,,,
六个字母排成一排,且BA,均在C的同侧,则不同的排法共有________种(用数字作答)
【答案】
480
7.(2013年普通高等学校招生统一考试重庆数学(理)试题(含答案))
从3名骨科.4名脑外
科和5名内科医生中选派5人组成一个抗震救灾医疗小组,则骨科.脑外科和内科医生
都至少有1人的选派方法种数是___________(用数字作答)
【答案】
590
8.(2013年高考北京卷(理))
将序号分别为1,2,3,4,5的5张参观券全部分给4人,每人至
少1张,如果分给同一人的2张参观券连号,那么不同的分法种数是_________.
【答案】
96
9.(2013年普通高等学校招生统一考试大纲版数学(理)WORD版含答案(已校对))
6
个人排
成一行,其中甲、乙两人不相邻的不同排法共有____________种.(用数字作答).[来
源:Z.xx.k.Com]
【答案】
480
2012高考真题分类汇编:计数原理
1. 【2012高考真题浙江理6】若从1,2,3,…,9这9个整数中同时取4个不同的数,其
和为偶数,则不同的取法共有
A.60种 B.63种 C.65种 D.66种
【答案】D
【解析】从1,2,3,…,9这9个整数中同时取4个不同的数,其和为偶数的取法分为
三类;第一类是取四个偶数,即545C种方法;第一类是取两个奇数,两个偶数,即
602425CC
种方法;第三类是取四个奇数,即144C故有5+60+1=66种方法。故选D。
2. 【2012高考真题新课标理2】将2名教师,4名学生分成2个小组,分别安排到甲、乙
两地参加社会实践活动,
每个小组由1名教师和2名学生组成,不同的安排方案共有( )
()A12种 ()B10种 ()C种 ()D
种
【答案】A
【解析】先安排老师有222A种方法,在安排学生有624C,所以共有12种安排方案,
选A.
3. 【2012高考真题四川理11】方程22aybxc中的,,{3,2,0,1,2,3}abc,且
,,abc
互不相同,在所有这些方程所表示的曲线中,不同的抛物线共有( )
A、60条 B、62条 C、71条 D、80条
【答案】B
【解析】本题可用排除法,,,{3,2,0,1,2,3}abc,6选3全排列为120,这些方程所表
示的曲线要是抛物线,则0a且0b,,要减去40225A,又22或b和33或b时,
方程出现重复,用分步计数原理可计算重复次数为18233,所以不同的抛物线共有
120-40-18=62条.故选B.
4. 【2012高考真题陕西理8】两人进行乒乓球比赛,先赢三局着获胜,决出胜负为止,则
所有可能出现的情形(各人输赢局次的不同视为不同情形)共有( )
A. 10种 B.15种 C. 20种 D. 30种
【答案】C.
【解析】首先分类计算假如甲赢,比分3:0是1种情况;比分3:1共有3种情况,分别是
前3局中(因为第四局肯定要赢),第一或第二或第三局输,其余局数获胜;比分是3:2
共有6种情况,就是说前4局2:2,最后一局获胜,前4局中,用排列方法,从4局中选2
局获胜,有6种情况.甲一共就1+3+6=10种情况获胜.所以加上乙获胜情况,共有10+10=20
种情况.故选C.
5. 【2012高考真题山东理11】现有16张不同的卡片,其中红色、黄色、蓝色、绿色卡片
各4张.从中任取3张,要求这3张卡片不能是同一种颜色,且红色卡片至多1张.不同
取法的种数为
(A)232 (B)252 (C)472 (D)484
【答案】C
【解析】若没有红色卡,则需从黄、蓝、绿三色卡片中选3张,若都不同色则有
64141414CCC
种,若2色相同,则有14414241223CCCC;若红色卡片有1张,则剩余2
张若不同色,有19214142314CCCC种,如同色则有72242314CCC,所以共有
4727219214464
,故选C。
6. 【2012高考真题辽宁理5】一排9个座位坐了3个三口之家,若每家人坐在一起,则不
同的坐法种数为
(A)3×3! (B) 3×(3!)3 (C)(3!)4 (D) 9!
【答案】C
【解析】此排列可分两步进行,先把三个家庭分别排列,每个家庭有3!种排法,三个家庭
共有33!3!3!(3!)种排法;再把三个家庭进行全排列有3!种排法。因此不同的坐法种数
为4(3!),答案为C
【点评】本题主要考查分步计数原理,以及分析问题、解决问题的能力,属于中档题。
7. 【2012高考真题北京理6】从0,2中选一个数字.从1.3.5中选两个数字,组成无重复数
字的三位数.其中奇数的个数为( )
A. 24 B. 18 C. 12 D. 6
【答案】B
【解析】由于题目要求的是奇数,那么对于此三位数可以分成两种情况:奇偶奇;偶奇奇。
如果是第一种奇偶奇的情况,可以从个位开始分析(3种选择),之后十位(2种选择),最后百
位(2种选择),共12种;如果是第二种情况偶奇奇,分析同理:个位(3种情况),十位(2种
情况),百位(不能是0,一种情况),共6种,因此总共12+6=18种情况。
8. 【2012高考真题安徽理10】6位同学在毕业聚会活动中进行纪念品的交换,任意两位
同学之间最多交换一次,进行交换的两位同学互赠一份纪念品,已知6位同学之间共进
行了13次交换,则收到4份纪念品的同学人数为( )
()A1或3 ()B1或4 ()C 2或3 ()D
2或4
【答案】D
【命题立意】本题考查等排列组合的运算问题。
【解析】261315132C.
①设仅有甲与乙,丙没交换纪念品,则收到4份纪念品的同学人数为2人,
②设仅有甲与乙,丙与丁没交换纪念品,则收到4份纪念品的同学人数为4人.
循环不满足条件输出3112x,选C.
9. 【2012高考真题全国卷理11】将字母a,a,b,b,c,c,排成三行两列,要求每行的字母互不相
同,每列的字母也互不相同,则不同的排列方法共有
(A)12种(B)18种(C)24种(D)36种
【答案】A
【解析】第一步先排第一列有633A,在排第二列,当第一列确定时,第二列有两种方法,
如图,所以共有1226种,选A.
10. 【2012高考真题重庆理15】某艺校在一天的6节课中随机安排语文、数学、外语三门
文化课和其他三门艺术课各1节,则在课表上的相邻两节文化课之间最多间隔1节艺术
课的概率为 (用数字作答).
【答案】53
【解析】6节课共有66A种排法.语文、数学、外语三门文化课中间隔1节艺术课有3433AA种
排法,三门文化课中、都相邻有3433AA种排法,三门文化课中有两门相邻有3312122223ACCAC,
故所有的排法有331212222334332ACCACAA,所以相邻两节文化课之间最多间隔1节艺术课的
概率为5326633121222233433AACCACAA
