基于步进电机驱动并联机器人的无震颤滑模控制研究

合集下载

《电气自动化》2011年(第33卷)总目次(总第193—198期)

基于ＡＭ的智能数据采集系统的设计 ……………………………………………………………………………………………………………… 杨柳春（４Ｒ４）无功补偿方式在风力发电系统中的分析与应用 ………………………………………… ………………………………………………………… 陈明忠（８４）双馈式风电机组机网扭振的建模与仿真 ……………………………………………………………………………… 王瑞琳解大王西田张延迟（１５）
级联Ｈ桥五电平变换器系统研究 …………………………………………………………………………………………………………………… 洪春梅（９２）基于以太网的电站监控系统的研究与应用 ……………………………………………………………… 孙晓静谭景文孙晓生刘正铭王春宁（１３）新型模糊ＰＤ复合控制在锅炉汽包水位控制中的应用 ……………………………………… …………………………………………………… 徐毅华（５Ｉ３）工业以太网和ＣＡＮ总线在污水处理系统中的应用 ………………………………………………………………… 王树东孟静静陈仕彬基于ＰＣ控制的电机变频／２Ｌ３频同步切换 ………………………………………………………………………………………………… 刘思闫媛媛（７３）张加胜（１４）
《电气自动化）０１年（３）１２第３卷）总目次
（总第１３— ９９１８期）
第一期
基于模糊神经网络的二自由度内模控制 ……………………………………………………………………………………… 陈高华张井岗永磁直线电机神经滑模控制器设计 ………………………………………………………………………………………………… 马达齐亮数控切割控制软件中割缝补偿算法的实现 …………………………………………………………………………………… 钟溢原唐厚君赵志诚（１）牛玉刚（４）徐青菁（７）

滑模变结构控制理论及其在机器人中的应用研究共3篇

滑模变结构控制理论及其在机器人中的应用研究共3篇滑模变结构控制理论及其在机器人中的应用研究1滑模变结构控制（Sliding Mode Control，SMC）是一种非线性控制方法，具有高精度、强适应性、鲁棒性好等优点，因此被广泛应用于机器人控制领域。

其基本思想是构造一个滑模面，使系统状态到达该面后就会保持在该面上运动，在保证系统稳定性的同时达到控制目的。

本文将阐述滑模变结构控制的理论基础以及在机器人控制中的应用研究。

一、滑模变结构控制的理论基础1. 滑模面滑模面是滑模控制的核心概念，它是一个虚拟平面，将控制系统的状态分为两个区域：滑模面上和滑模面下。

在滑模面上，系统状态变化很小，具有惯性；而在滑模面下，系统状态变化很大，具有灵敏性。

在滑模控制中，系统状态必须追踪滑模面运动，并保持在滑模面上，进而实现控制目的。

2. 滑模控制定律滑模控制定律是滑模变结构控制的核心之一，主要由滑模控制器和滑模面组成。

滑模控制器将系统状态误差与滑模面上的虚拟控制输入之间做差，生成实际控制输入。

而滑模面则是根据控制目的和系统性质，通过手动选择滑模面的形状和大小来合理地设计。

例如，对于已知模型的系统，可使用小扰动理论来设计滑模面；而对于未知模型的系统，可使用自适应滑模控制来自动调节滑模面。

总体来说，滑模控制定律是一种强鲁棒控制方法，在快速响应、鲁棒性和适应性等方面都表现出色。

3. 滑模变结构控制滑模变结构控制是将滑模控制定律与变结构控制相结合形成的一种新型控制方法。

在滑模变结构控制中，滑模面被用来描述整个系统状态，而滑模控制定律则用来保证系统状态追踪滑模面的过程中，系统特征不会发生大的变化。

换句话说，滑模控制定律的目的是在系统状态到达滑模面后，控制系统能够迅速且平稳地滑过该面，进而保持在滑模面上稳定运动。

二、滑模变结构控制在机器人中的应用研究滑模变结构控制广泛应用于机器人控制领域，例如：机器臂控制、移动机器人控制、人形机器人控制等。

滑模控制在并联机器人轨迹跟踪中的应用

ＬｎＩＹａ，ＷＡＮＧｎ，ＣＨＥＮｅｇｈｎＹｏｇＺｈｎ．ｏｇ
（．ｃｏｌｆｃａｉａＥｇｎｅｉ，ｈｎｏｇＵｉｒｉ，ｉａ５０；．ｎｉｅｒｇＭｃｉｅｙＤｐｒ１ＳｈｏｏＭｅｈｎｃｌｎｉｅｒｇＳａｄｎｎｖｓｙＪｎ２０６２Ｅｇｅｉａｈｎｒｅａｔｎｅｔｎ１ｎｎ —
维普资讯
２０年第９０８期
文章编号：０１—２６２０）９—０４１０２５（０８００５—０４
・制与检测・控
滑模控制在并联机器人轨迹跟踪中的应用水
李艳王勇陈正洪，，
ｓｉｎｏｅｃｎｒｌｒｅｅｈｒｒｎｔａｒｏｓｌｇｍｄｏｔｏｌｖｎｔｅｅａｅｉｉｉｌｅｒｒ．Ｔｈｕｓ－ｌｎｏｅｃｎｔｏａｅｕｅｃａｔｒｅｆｃｉｅｄｉｅｅｑａｉｓｉｇｍｄｏｒｌｃｎｒｄｃｈｔｅｆｅｔｖ — ｄｉ
ｍｅｔｈｎｏｇＪａＴｎｎｖｒｉｎ，ＳａｄｎｉｏｏｇＵｉｅｓｔｉａ５０３，Ｃｉａｙ，Ｊｎｎ２０２ｈｎ）
Ａｂｓｒｃ：ＴｈｙｎｍｉｏｅｆａＰｌｎａ－ｔａｔｅｄａｃｍｄｌｏａｒ２ＤＯＦｒｄｄｎｔｃｕａｅｒｌｌｒｂｏｓｅｔｂｌｈｄ．Ｃｏｉｅ— ｅｕｎａｌａｔｔｄｐａａｌｏｔｉｓａｉｅｙｅｓｎｓｄｒｉｈｏｌｅｒｕｃｒａｎｙｏｒｌｌｒｂｏｓｌｉｇｍｏｅｃｎｔｏｌｒｉｏｎｇｔｅｎｎｉａｎｅｔｉｔｆｐａａｌｏｔ，ａｓｉｎｄｏｒｌｓｐｒｐｏｓｄｉｈｓｐａｒｎｅｄｅｅｎｔｉｐｅ、Ｔｈｎｔｅｈｅｓａｌｙｏｈｏｓｄｃｎｒｌｒｉｎｌｅｔｕｒｎｔｅｈｏｓｒｃｉｇｃｔｏ．Ｉｒｒｔｅｕｅｔｂｉｔｆｔｅｐｒｐｏｅｏｔｏｌｓｉｅａａｙｚｄｏｇａａｅｔｅｒｂｕｔｔａｋｎｏｎｒ１ｎｏｄｅｏｒｄｃｃａｔｒｎ，ｑａｉｓｉｎｄｅｃｎｒｌｉｍｐｌｙｅｈｔｅｉｇｕｓ— ｌｇｍｏｏｔｏｓｅｄｉｏｄ．Ｔｈｉｅｓｍｕｌｔｏｅｕｌｓｄｍｏｎｔａｅｔｅｅｆｃｉｅｓｆｔａｉｎｒｓｔｅｓｒｔｈｆｅｔｖｎｅｓｏｈｅ

基于改进滑模-PID策略的步进电机控制技术及试验研究

基于改进滑模-PID策略的步进电机控制技术及试验研究基于改进滑模-PID策略的步进电机控制技术及试验研究摘要：本文基于改进滑模-PID（Proportional-Integral-Derivative）策略，针对步进电机控制技术进行了深入研究。

通过分析步进电机控制的原理和传统PID控制策略的不足之处，提出了一种改进的滑模-PID策略，并设计了相应的控制算法。

通过实验验证，改进的滑模-PID策略相比传统PID控制策略在步进电机控制方面表现出更好的性能。

关键词：步进电机控制技术、滑模控制、PID控制、改进策略、性能评估一、引言步进电机广泛应用于自动控制和运动控制领域，其具有结构简单、成本低、定位精度高等优点。

针对步进电机控制技术的研究，寻求更稳定和高性能的控制策略是一个重要课题。

传统的PID控制策略在步进电机控制方面有一些不足之处，如超调量大、响应时间慢等。

本文在传统PID控制策略的基础上，通过引入滑模控制思想，提出了一种改进的滑模-PID策略，并设计了相应的步进电机控制算法。

二、步进电机控制原理和传统PID控制策略步进电机是一种通电才能工作的开环控制系统，其控制原理基于脉冲信号来驱动电机旋转。

传统PID控制策略是一种反馈控制策略，通过不断调整PID控制器的参数来实现对步进电机的控制。

PID控制器包括比例项、积分项和微分项三个部分，通过给定信号与反馈信号的差值来计算控制器的输出量。

然而，由于步进电机的特殊性，传统PID控制策略在步进电机控制中存在一些问题。

首先，步进电机的惯性较小，反应速度较快，在传统PID控制下容易产生过冲现象。

其次，步进电机的非线性特性，如静摩擦力和动摩擦力的影响，给传统PID控制带来了困难。

最后，步进电机系统参数的变化和外部干扰等因素会影响控制的稳定性和精度。

三、改进的滑模-PID策略及其控制算法为了克服传统PID控制策略的不足，本文提出了一种改进的滑模-PID策略。

滑模控制是一种通过在系统状态空间中构造滑动曲面，使系统状态迅速从初始状态转移到期望状态的控制策略。

动态滑模控制在并联机器人中的应用

立的系统来进行控制，制策略为传统的ＰＤ控制，制效果很不理想．糊控制方法可以在不要求机控Ｉ控模器人模型精确的情况下实现机器人的控制，是模糊控制方法的模糊规则设计比较重要，则设计的好但规
Ａｂｓｒｔｔａｃ：ＤｉｅｔｄｇａｎｔｈｅａａｌｌｏｏｍｅｈａｓｒｃｅａｉｓｔｐｒｌｅｒｂｔｃｎｉｍｗｉｈｔＡＣｅｖｏｍｏｏｄｉｅａｓｒ－ｔｒｒｖ，ｍｏｅｏｄｌｆ
ｃｎｒｌｉｇｓｓｅｏｔｏｌｎｙｔｍｗａｓａｌｓｄ．Ａｎｄｆｄｙａｃｌｎｍｏｅｏｒｌａｇｒｔｍｗａｅｉｎｅｓｅｔｂｉｈｅｋｉｏｎｍｉｓｉｇｄｉｄｃｎｔｏｌｏｉｈｓｄｓｇｄ．
ｔａｉｂｌｔｕｔｅｃｎｔｏｌｒａｄａｇｏｅｆｒｎｅｉｒｃｎｈｅｖｒａｅｓｒｃｕｒｏｒｌ，ｎｏｄｐｒｏｍａｃｎｔａｋｉｇ，ａｄｔｅｈｉｈ— ｃｕａｙｒａｉｅｎｈｇａｃｒｃｅｌｔｍｅ
好，系统抗干扰能力强，系统参数变化不敏感，有良好的跟踪性能．对具
关键词：并联机器人；滑模控制；伺服电机；轨迹跟踪
中图分类号：Ｔ２２Ｐ４
文献标志码：Ａ
文章编号：１０ — ４５２１）１０３— ４０８５７（０００ — ０７０

并联机器人动态滑模轨迹跟踪控制研究动

ｓｌｉｄｌｏｕｒｋａｄｃｍｌｔｇｔｅｄｓｅｒｅｔｒｏｌｉｇｈｉｕａｉｎｒｓｈｉａｏｍｏｅｆｓｒｔｏｐｅｉｈｅｉｄｔｃｏｙｆｌｗｎ．Ｔｅｓｍｌｏｅｕｓｍｕｔｎｐｃａｎｎｒｊａｏｔｓｏｅｅｔｉｔｎｆｓｔｋｎｐｏｒｕｃｓｔｅｃｎｒｌａ．ｈｗｄｔａｌｙａｄａｔｒｉｅＣｍａｅｈｏｔｗｈｓｂｉａｇｃｏｆｏｏｌ
Ｋｅｏｄ：ｙａｃｖｒａｌｓｕｔｒ；ｖｒｅｋｎｍａｉ；－ｙｗｒｓＤｎｍｉａｉｂｅｔｃｕｅＩｅｓｉｅｔｓ６ＤＯＦｐｒｌｌｏｏｓＴａｅｔｒｒｎｃａａｌｂｔ；ｒｊｃｏｙｅｒ
ｔａｋｉｇｒｃｎ
ｈｄｔｂｏｔｌｄａｃｒｅｙｂｃｕｅｏｔＳｎｎｉｅｒｎｒｎｕｌｇＩａｔｈ－Ｏａａ－ｒｏａｅｃｎｒｌｕａｌｅａｓｆｉｏｌａｄｓｏｇｃｐｉ．ｔｉａｔｅ６ＤＦｐｒｏｅｃｔ ’ ｎａｔｏｎｍｓｌ
能力强，具有快速有效跟踪期望轨迹的优良｝能。Ｊ生
关键词：动态滑模变结构；动学反解；自由度并联机器人；迹跟踪运六轨
【ｂｔｃ】ａｌｌｏｏｅｔｐｒｎｐｒｉｒｅｃｄａｐｉｔｎｏｈｏｏａｄｈｖＡｓａｔＰｒｌｂｔａｅｉｏｔｔａｓａｈａｌａｏｅｒｂｔａｅｒａｅｒｓｒｈｍａｔｎｅｒｎｐｃｉｆｔｎｔｅａｖｔｅｉｈｒｉｉ，ｈｄａａｓｏｇｇｄｔ动ｂｒｅａａｉ，ｏａｃｍｌｉｎｏｐｓｉｎｄＳｎｈｗｖｒｉＳｎｇｆｈｉｙｕｄｎｃｃｔｎｕｕａｏｏｉｏａａＯｏ，ｏｅｅ， ’ ｐｙｃｔｆｔｌｎｔ

Stewart并联机器人的非奇异终端滑模控制

Stewart 并联机器人的动力学模型
σ
（4）
式中：s = [s1 ,s 2 ,…,s 6] ；误差矢量 e = q - q d ，e =
T
如图 1 所示，Stewart 并联机器人是一种六自
由度并联机构，其上下 2 个平台通过 6 个可伸缩的
支杆相连。惯性坐标系 ΣO{X,Y,Z} 固定在下平台
作空间的控制能够提供更好的控制性能 [1]。对于
Stewart 并联机器人基于工作空间的控制问题，国
内外研究人员提出了不同的运动控制策略，已提
出的控制策略主要包括积分滑模控制[2]、神经模糊
自适应控制 [3]、自适应 PIDNN 控制 [4]、模态空间控
制[5]、模糊计算力矩控制[6]、自适应滑模控制[7]等。
析和数值仿真实验结果证明所提控制方法的有
式中：
矢量 x = [x1 ,x 2 ,…,x 6] ，
矢量 σ =[σ1 ,σ 2 ,…,σ 6]T 。
T
根据并联机器人系统的控制目的，定义系统
的非奇异终端滑动面 s 为[8]
s = e + ωsig ( ė )
效性。
2
3
于涛等：
Stewart 并联机器人的非奇异终端滑模控制
提出一种基于双幂次趋近律的非奇异终端滑模控制算法。所提控制算
法可以确保机器人系统快速收敛至期望位姿，并且具有良好的控制输入高频抖动抑制能力。首先定义机器人系统的非奇
异终端滑动面；
然后基于机器人系统的拉格朗日动力学模型求得等效控制律，并采用双幂次趋近律设计非线性控制律，从
而得到系统的奇异终端滑模控制律；
人系统的动力学模型，采用等效控制原理和双幂
*辽宁省自然科学基金指导计划项目（201602379）；

基于步进电机的多轴联动控制系统研究

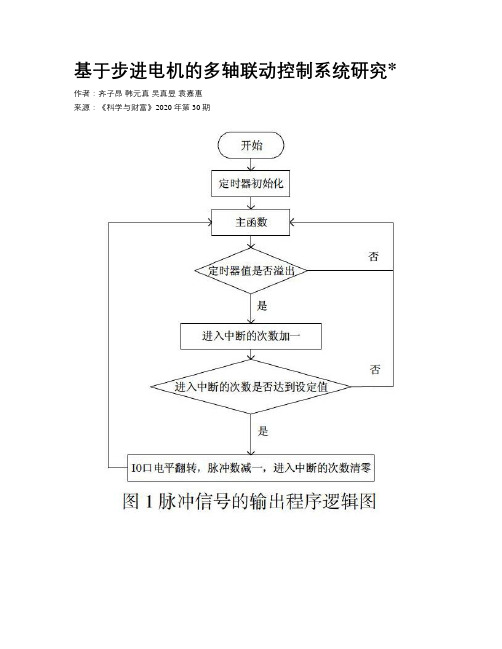
基于步进电机的多轴联动控制系统研究*作者：齐子昂韩元真吴真昱袁嘉惠来源：《科学与财富》2020年第30期摘要：随着社会的进步和人类水平的提高，工厂生产智能化的趋势越来越明显。

而随着工厂生产自动化的不断发展，电机的多轴联动控制也逐渐被人们所注意到，我们一般常见的运动轴可以分为X、Y、Z、Pitch和Yaw轴，而对于多轴联动的控制方法也是多种多样。

本文着重叙述一种基于步进电机的多轴联动控制系统，该系统主要由STM32单片机作为主要处理器，步进电机作为动力装置，再由脉冲信号的脉冲数和脉冲的周期来控制步进电机的转动角度和转动速度，而每个轴的速度和位置数据都通过串口发送至上位机实现数据可视化，而每个轴的运动都是独立的，也就是说多个轴可以同时运动，我们将控制三个电机同时运作，同时朝着目标方向运动，但是考虑到该机构不与其他机构产生碰撞即每两点之间不能简单地按照直线路径，因此需要使用Floyd算法计算出各个点之间的最短路径，大幅度缩短了时间，达到最好的效果。

关键词：多轴联动;串口通信;上位机;Floyd算法;最短路径0 引言为了能将电机运动的时间缩短到最少时间，我们计划采用多轴联动的方式对步进电机进行控制。

对于X、Y、Z、Pitch、Yaw几个运动轴，若只是采取单方向直线运动的话时间无疑将会是非常长的，于是我们将控制三个电机同时运作，同时朝着目标方向运动，同时还要考虑该机构不与其他机构产生碰撞，从而计算出其最短路径，大幅度缩短了时间，达到最好的效果。

STM32单片机为控制系统的核心，处理输入模拟信号和对外部输出控制信号都需要它来实现。

它可以提供控制步进电机运动的脉冲信号，同时还可以将电机的各种状态数据通过串口传输给上位机，将各个运动轴的数据直观的展现出来，同时可以发送控制命令给单片机来控制它的运动。

Floyd算是最常用的求两点间最短路径的方法，应用在很多领域，送货员送货，邮递员送信都需要事先考虑路途长短[1]，在本系统中选择最短路径的方法既可以根据此算法来设计。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

p/) 2 p/)
,
2
2p2 bmI0 cos(
c2np=
J
p/) 2
0
式中: Gi为目标量; G0 为控制量; J为转动部分的转动惯量取 l.04N~m; I0 为相电流取 2.4A; R为相绕组电阻取 l.20; U为相电压取 24V; P为转子齿数取 50; /为极距角取、/5; Lp=L -M=4.0 Xl0 -3 H; bm 为最大磁通取 0.008Wb; J为减速比取 40; D为粘性摩擦系数取 3.0 Xl0 -6 N~m~s/rad0
端各项都小于 00 所以 S~S <00
由上式证明可知7 所取的控制量 u 能够满足滑动
条件7 这意味着该控制算法能形成滑模且稳定收敛0
~~
$ 机床与液压% 2006.No.9
4 机器人控制系统的仿真
图 3 所示的并联机
构驱动电机为二相混合
步进电动机, 其型号为
56ByG250C, 支路模型
位置及运动0 当已知动平台位置 O xp7 yp7 zpO 及运动要求时7 根据该并联机器人机构的运动学分析[31 7 三
个支路 Al Bl Cl \ A2 B2 C2 \ A3 B3 C3 上各主动副的期望角位移分别为:
{Gl =arccosO O yp+a5 -al O a2 O G2 =arccosO O xp+b5 -bl O b2 O G3*=2arctanO O Y1!Y2 -D2 +z2pO
OllO
其中: K>07 S>0 为常数0
证明: 把式 OllO 代入式 Ol0O 可得:
~
SS =S[ dO tO /b0 -KS -O S+D/b0 O sgnO SO 1 =
-KS2 -SIsI-S[ dO tO /b0 -D/b0 sgnO SO 1
Ol2O
考虑到 IdO tO I<D7 K>07 S>07 可得到上式右
AbstractZ Step motorfeaturessmaiiin thevoiume bigin thetorgueand widein therangeofspeed.theparaiieirobotfeatures high rigidity greatioad and high precision.Foranew-type3 -DOFtransiation paraiieirobotmechanismdrived bystep motor asiidingmodecontroiaigorithmwasdesigned thecontroischemewasproposed and themotion controiofthemechanismwasimpiemented bysimuiation.Itisshown fromthesimuiation resuitsthattheparaiieirobotsystemusingtheproposed controiaigorithmdoesnothave thechatteringprobiem.thesystemhasgood robustness and isrobusttotheuncertaintiesand disturbance and hasgood performance in tracking.thehigh -accuracyreaitimecontroioftheparaiieirobotmechanismisimpiemented.
KeywordsZ Paraiieirobot; Siidingmodecontroi; Step motor; transiation
0 引言并联机器人是一类全新的机器人相比串联机器
人它具有刚度大\ 承载能力强\ 误差小\ 精度高\ 自重负荷比小且动力性能好\ 控制容易等一系列优点[l] O
Hurwitz多项式7 即方程 S =0 的根全在负半平面0 为
保证系统的所有状态都能到达滑动模态7 应当满足如
下的条件:
~
SS <0
O9O
把式 O7O\ O8O 代入上式7 得
~
SS
=S[
b0 u
+dO
tO
-~yd
-a2
y"d
-al
~yd
-a0
yd
-
a2 e"-al ~e-a0 e+cl e"+c2 ~e1 <0
~5~
以采用动平台运动控制量的直接控制是难以实现的0 若采用基于动力学模型控制的方法实现动力学解耦7 鉴于该系统动力学模型的高度复杂性7 本文采用各支路分别闭环的控制结构7 通过控制算法的设计7 使系统在实时考虑机器人运动过程中对各支路主动副的作用7 亦称各支路主动副上的干扰作用的情况下7 获得较好的控制性能0
应用7 极大地提高了它们的性能7 其应用也越来越广
泛0 鉴于此7 本设计采用步进电机驱动的并联机器人
支路的模型可以统一用以下传递函数表示0
GO
sO
=s3 +a2
b0 s2 +al
s+a0
O3O
其中的参数 al 7 a2 7 a0 7 b0 由驱动装置和并联机
器人的结构参数决定0 在考虑等效外部干扰的情况
EO2O U -K*S -O S+D/692.3lO *signO SO
Ol5O
以 MAtLAB/Simuiink 构成仿真模型, 根据系统
~4~
$ 机床与液压% 2006.No.9
基于步高国琴! 韩亚锋
" 江苏大学电气信息工程学院! 江苏镇江 2l20l3#
摘要! 步进电机具有体积小\ 转矩大\ 转速范围宽等优点; 并联机器人具有刚度大\ 承载能力强\ 误差小等特点O 本文针对以步进电机驱动的新型三平移并联机器人机构的上述特点设计了滑模控制算法建立了控制系统模型仿真实现了对各支路主动副期望运动轨迹的跟踪O 仿真结果表明Z 该算法解决了滑模控制的震颤问题系统的鲁棒性好且系统抗干扰能力强对系统参数变化不敏感具有良好的跟踪性能实现了对该并联机器人的高精度实时控制O
如图 3 所示0 忽略等效干扰力矩可导出支路的
图 3 机器人支路模型
传递函数:
GO sO =G0 = Gi
LRpc2np
( ) [ ] s3 +
R +D Lp J
s2 +
R~D Lp J
+c2np
(
l
+Kp)
s+LRp~c2np
Ol3O
其中:
Kp=LbpIm0
sin ( cos(
l.2 建立控制模型上述新型三平移并联机器人机构其动平台在空
间的位置和姿态是各关节运动量的复杂非线性函数并且运动过程中各通道间存在着非线性耦合作用所
* 基金项目! 国家自然科学基金资助项目 (50375067> ; 江苏省教育厅资助项目 (03kJD5l0072>
$ 机床与液压% 2006.No.9
下7 机器人支路的模型可以用以下的微分方程表示:
~y+a2 y"+al ~y+a0 y=b0 u +dO tO
O4O
其中: y=G为位置输出7 u 为控制输入0 dO tO 为等效
不确定外部干扰0
设机器人关节运动的期望轨迹\ 速度及其加速度
为[ y"d 7 ~yd 7 yd 1 0 定义轨迹跟踪误差为:
本文所研究的少自由度并联机器人是江苏大学自主研制开发的新型三平移并联机器人机构具有各支路机构简单不存在虚约束且工作空间较大等特点与同类三平移并联机器人机构相比其动力学性能有所改善并且有利于微型化设计O
滑模变结构的一大优点是其滑动模态对加给系统的扰动和系统的参数摄动具有完全的自适应性对外界干扰不敏感同时具有鲁棒性好\ 响应速度快\ 无超调\ 无震荡及综合方法容易实现等优点O 本文将针对上述新型三平移并联机器人机构利用一种无震颤滑模控制算法实现对根据动平台运动要求实时求得的各支路主动副运动轨迹的跟踪O 1 建立三平移并联机器人机构控制模型 l.l 三平移并联机器人机构
机器人关节或支路模型的分散控制系统是目前在实际
过程中应用最为广泛的设计方法之一7 在工业工程中
绝大部分的机器人系统都采用了该类设计方法0
目前在并联机器人控制领域7 对这类实用性比较
强的控制器设计方法已有大量的研究0 由于步进电机
具有良好的点位控制性能7 没有累计误差等优点7 在
控制领域得到了广泛的应用0 而且步进电动机的闭环
O D+zpO O
OlO
其中: Y=yp+l5 -ll 7 L =l3 +l2 sinG3 7 D=O Y2 +z3p + L2 -l24 O O2LO 0 3 变结构控制器的设计
机器人系统的完整的拉格朗日动力学模型可以表
示为如下的形式:
DO g7~gO g"+hO g7~gO ~g+GO ~gO =T
在各支路执行机构分别采用步进电机时7 机器人控制系统的物理结构如图 2 所示0
图 2 步进电机驱动的并联机器人系统控制结构图
图 2 中 Gl \ G2 \ G3*是通过编码器检测的各支路主动副实际角位移0
2 期望角位移求解
上述三平移并联机器人机构7 以动平台上 P点相
对固定平台上坐标原点 O点的位置及运动代表动平台
图 l 三平移并联机器人机构 4R机构位于下静平台上 Al \ A2 \ Bl \ B2 分别位于对应支路上 4R机构中与 3 个 R副轴线平行的两边之中点 C支路与 B支路平行配置 (两组运动副呈平行关系> 4R机构位于支路间 Cl 位于 Bl \ Cl 的连线平行于 A支路的 3 个 R副的轴线 C2 \ C3 位于该支路 4R机构中与 3 个 R副轴线平行的两边之中点O