离散数学试卷及答案(2)
《离散数学》试题及答案 2

《离散数学》试题及答案 2《离散数学》试题及答案2一、填空题1设子集a,b,其中a={1,2,3},b={1,2},则a-b=____________________;?(b)=__________________________.2.设有限集合a,|a|=n,则|?(a×a)|=__________________________.3.设子集a={a,b},b={1,2},则从a至b的所有态射就是_______________________________________,其中双射的就是__________________________.4.已知命题公式g=?(p?q)∧r,则g的主析取范式是_________________________________________________________________________________________.5.设g就是全然二叉树,g存有7个点,其中4个叶点,则g的总度数为__________,分枝点数为________________.6设a、b为两个集合,a={1,2,4},b={3,4},则从a?b=_________________________;a?b=_________________________;a-b=_____________________.7.设r就是子集a上的等价关系,则r所具备的关系的三个特性就是______________________,________________________,______________________________ _.8.设命题公式g=?(p?(q?r)),则使公式g为真的解释有__________________________,_____________________________,__________________________.9.设子集a={1,2,3,4},a上的关系r1={(1,4),(2,3),(3,2)},r1={(2,1),(3,2),(4,3)},则r1?r2=________________________,r2?r1=____________________________,r12=________________________.(a)-10.设有限集a,b,|a|=m,|b|=n,则||?(a?b)|=_____________________________.11设a,b,r是三个集合,其中r是实数集,a={x|-1≤x≤1,x?r},b={x|0≤x<2,x?r},则a-b=__________________________,b-a=__________________________,a∩b=__________________________,.13.设子集a={2,3,4,5,6},r就是a上的相乘,则r以子集形式(列出法)记作__________________________________________________________________.14.设一阶逻辑公式g=?xp(x)??xq(x),则g的前束范式是_______________________________.15.设g就是具备8个顶点的树,则g中减少_________条边就可以把g变为全然图。
离散数学期末试卷及部分答案 (2)

离散数学试题(A 卷及答案)一、证明题(10分)1)(⌝P ∧(⌝Q ∧R))∨(Q ∧R)∨(P ∧R)⇔R证明: 左端⇔(⌝P ∧⌝Q ∧R)∨((Q ∨P)∧R)⇔((⌝P ∧⌝Q)∧R))∨((Q ∨P)∧R)⇔(⌝(P ∨Q)∧R)∨((Q ∨P)∧R)⇔(⌝(P ∨Q)∨(Q ∨P))∧R ⇔(⌝(P ∨Q)∨(P ∨Q))∧R ⇔T ∧R(置换)⇔R2)∃x(A(x)→B(x))⇔ ∀xA(x)→∃xB(x)证明 :∃x(A(x)→B(x))⇔∃x(⌝A(x)∨B(x))⇔∃x ⌝A(x)∨∃xB(x)⇔⌝∀xA(x)∨∃xB(x)⇔∀xA(x)→∃xB(x) 二、求命题公式(P ∨(Q ∧R))→(P ∧Q ∧R)的主析取范式和主合取范式(10分)证明:(P ∨(Q ∧R))→(P ∧Q ∧R)⇔⌝(P ∨(Q ∧R))∨(P ∧Q ∧R))⇔(⌝P ∧(⌝Q ∨⌝R))∨(P ∧Q ∧R) ⇔(⌝P ∧⌝Q)∨(⌝P ∧⌝R))∨(P ∧Q ∧R)⇔(⌝P ∧⌝Q ∧R)∨(⌝P ∧⌝Q ∧⌝R)∨(⌝P ∧Q ∧⌝R))∨(⌝P ∧⌝Q ∧⌝R))∨(P ∧Q ∧R) ⇔m0∨m1∨m2∨m7 ⇔M3∨M4∨M5∨M6三、推理证明题(10分)1) C ∨D, (C ∨D)→ ⌝E, ⌝E →(A ∧⌝B), (A ∧⌝B)→(R ∨S)⇒R ∨S证明:(1) (C ∨D)→⌝E(2) ⌝E →(A ∧⌝B)(3) (C ∨D)→(A ∧⌝B) (4) (A ∧⌝B)→(R ∨S) (5) (C ∨D)→(R ∨S)(6) C ∨D(7) R ∨S2) ∀x(P(x)→Q(y)∧R(x)),∃xP(x)⇒Q(y)∧∃x(P(x)∧R(x))证明(1)∃xP(x) (2)P(a)(3)∀x(P(x)→Q(y)∧R(x)) (4)P(a)→Q(y)∧R(a) (5)Q(y)∧R(a) (6)Q(y) (7)R(a) (8)P(a) (9)P(a)∧R(a) (10)∃x(P(x)∧R(x)) (11)Q(y)∧∃x(P(x)∧R(x))四、设m 是一个取定的正整数,证明:在任取m +1个整数中,至少有两个整数,它们的差是m 的整数倍证明 设1a ,2a ,…,1+m a 为任取的m +1个整数,用m 去除它们所得余数只能是0,1,…,m -1,由抽屉原理可知,1a ,2a ,…,1+m a 这m +1个整数中至少存在两个数s a 和t a ,它们被m 除所得余数相同,因此s a 和t a 的差是m 的整数倍。
《离散数学》试题带答案(二)

《离散数学》试题带答案试卷九试题与答案一、 填空 30% (每空 3分)1、 选择合适的论域和谓词表达集合A=“直角坐标系中,单位元(不包括单位圆周)的点集”则A= 。
2、 集合A={Φ,{Φ}}的幂集P (A) = 。
3、 设A={1,2,3,4},A 上二元关系R={<1,2>,<2,1>,<2,3>,<3,4>}画出R的关系图。
4、 设A={<1,2>,<2 , 4 >,<3 , 3 >} , B={<1,3>,<2,4>,<4,2>},则B A ⋃= 。
B A = 。
5、 设|A|=3,则A 上有 个二元关系。
6、 A={1,2,3}上关系R= 时,R 既是对称的又是反对称的。
7、 偏序集><≤R A ,的哈斯图为,则≤R = 。
8、 设|X|=n ,|Y|=m 则(1)从X 到Y 有 个不同的函数。
(2)当n , m 满足 时,存在双射有 个不同的双射。
9、 2是有理数的真值为 。
10、Q :我将去上海,R :我有时间,公式)()(Q R R Q →∧→的自然语言为 。
11、公式)()(Q P P Q ∧⌝∧→的 主合取范式是 。
12、 若} ,, , {21m S S S S =是集合A 的一个分划,则它应满足 。
二、 选择 20% (每小题 2分)1、 设全集为I ,下列相等的集合是( )。
A 、} |{是偶数或奇数x x A =;B 、)}2( |{y x I y y x B =∧∈∃=;C 、)}12( |{+=∧∈∃=y x I y y x C ;D 、},4,4,3,3,2,2,1,1,0|{ ----=x D 。
2、 设S={N ,Q ,R},下列命题正确的是( )。
A 、S S N N ∈∈∈2 ,2则; B 、S N S Q Q N ⊂∈⊂则 ,; C 、R N R Q Q N ⊂⊂⊂则 ,; D 、S N S N ⋂⊂Φ⊂Φ⊂Φ则 ,。
《离散数学》考试题库及答案(二)
《离散数学》考试题库及答案试卷五试题与答案一、填空15%(每空3分)1、设G 为9阶无向图,每个结点度数不是5就是6,则G 中至少有 个5度结点。
2、n 阶完全图,K n 的点数X (K n ) = 。
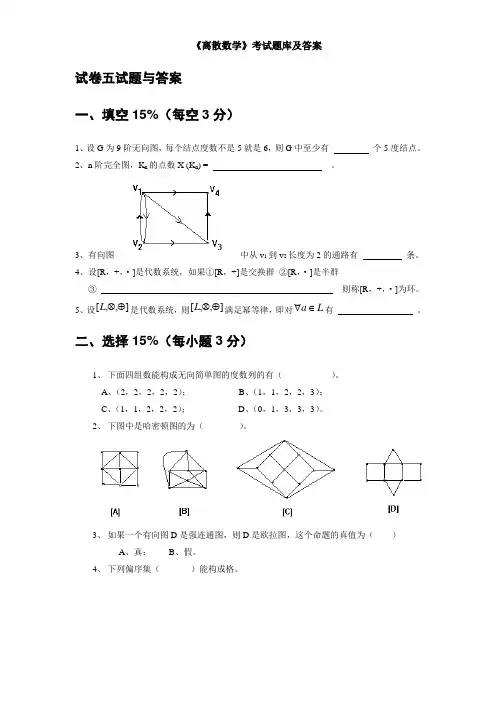
3、有向图 中从v 1到v 2长度为2的通路有 条。
4、设[R ,+,·]是代数系统,如果①[R ,+]是交换群 ②[R ,·]是半群③ 则称[R ,+,·]为环。
5、设],,[⊕⊗L 是代数系统,则],,[⊕⊗L 满足幂等律,即对L a ∈∀有 。
二、选择15%(每小题3分)1、 下面四组数能构成无向简单图的度数列的有( )。
A 、(2,2,2,2,2); B 、(1,1,2,2,3); C 、(1,1,2,2,2); D 、(0,1,3,3,3)。
2、 下图中是哈密顿图的为( )。
3、 如果一个有向图D 是强连通图,则D 是欧拉图,这个命题的真值为( )A 、真;B 、假。
4、 下列偏序集( )能构成格。
5、 设}4,41,3,31,2,21,1{=s ,*为普通乘法,则[S ,*]是()。
A 、代数系统;B 、半群;C 、群;D 、都不是。
三、证明 48%1、(10%)在至少有2个人的人群中,至少有2 个人,他们有相同的朋友数。
2、(8%)若图G 中恰有两个奇数度顶点,则这两个顶点是连通的。
3、(8%)证明在6个结点12条边的连通平面简单图中, 每个面的面数都是3。
4、(10%)证明循环群的同态像必是循环群。
5、(12%)设]1,0,,,,[-+⨯B 是布尔代数,定义运算*为)()(*b a b a b a ⨯+⨯=,求证[B ,*]是阿贝尔群。
四、计算22%1、在二叉树中1) 求带权为2,3,5,7,8的最优二叉树T 。
(5分) 2) 求T 对应的二元前缀码。
(5分)2、 下图所示带权图中最优投递路线并求出投递路线长度(邮局在D 点)。
答案:一、填空(15%)每空3 分1、 6;2、n ;3、2;4、+对·分配且·对+分配均成立;5、a a a a a a =⊕=⊗且。
专升本《离散数学》_试卷_答案

专升本《离散数学》一、(共75题,共150分)1. 集合,则()(2分)A.B.C.D.标准答案:B2. 集合,则下列哪个不是的元素()(2分)A.B.C.D.标准答案:B3. 设,在条件且下与()集合相等。
(2分)A.或B.或C.,或D.,或标准答案:C 4. 集合上的关系,则是()(2分)A.自反的B.对称的C.传递且对称的D.反自反且传递的标准答案:B5. 集合,下列不是到的关系的是()(2分)A.B.C.D.标准答案:A6. ,表示求两数的最小公倍数的运算(表示整数集合),对于运算的零元是()(2分)A.B.C.D.不存在标准答案:D7. 下面各集合都是的子集,()集合在普通加法运算下是封闭的。
(2分)A.B.C.D.标准答案:A8. 设集合,“”为整除关系,则代数系统()(2分)A.是域B.是格,不是布尔代数C.是布尔代数D.不是代数系统标准答案:C9. 在()中,补元是唯一的。
(2分)A.有界格B.有补格C.分配格D.有补分配格。
标准答案:D10. 下列语句中,真命题的是( ) (2分)A.请把门关上B.是素数C.D.太阳从西边升起标准答案:B11. 是自然数集,是小于等于关系,则是()。
(2分)A.有界格B.有补格C.分配格D.有补分配格标准答案:C12. 下列函数中,()是双射(2分)A.B.(除以的余数)C.D.标准答案:D13. 设为集合,,在上有()种不同的关系。
(2分)A.B.C.D.标准答案:D14. 设是个结点、条边和个面的连通平面图,则等于()。
(2分)A.B.C.D.标准答案:A15. 对于独异点,则下列说法正确的是()(2分)A.不一定有单位元B.满足交换律C.一定是半群D.独异点就是群标准答案:C16. 群中,当()时,该群一定是循环群。
(2分)A.B.C.D.标准答案:B17. 设,为普通乘法,则是()(2分)A.代数系统B.半群C.群D.都不是标准答案:D18. 下列各图哪个一定是树()(2分)A.有个结点,条边的连通图B.每对结点之间都有路的图C.有个结点,条边的图D.以上说法都不正确标准答案:A19. 在如下各图中是欧拉图的是()(2分)A.B.C.D.标准答案:B20. 下列等价关系正确的是()(2分)A.B.C.D.标准答案:B21. 下列哪些关系是对称关系()(2分)A.B.C.D.标准答案:A,D22. 的合取范式为()(2分)A.B.C.D.标准答案:B,D23. 关于复合运算,下列说法正确的是()(2分)A.置换的复合不一定是置换B.置换在复合运算下是封闭的C.可数集的无限子集仍是可数集D.以上说法都正确标准答案:B,C24. 为命题,则下述公式中是重言式为()(2分)A.B.C.D.标准答案:B,D25. 令我上街;我去书店看看;我很累则命题“如果我上街,我就去书店看看,除非我很累”可以符号化为()(2分)A.B.C.D.标准答案:A,D26. 若集合,则()(2分)A.且B.但C.但D.且标准答案:A27. 在()下有。
离散数学第二部分测试题-有答案2

离散数学第二部分测试题一、 填空题1.D=}{φ,则幂集}}.{,{)(φφρ=D2. B={1,{2,3}},则幂集=)(B ρ}}}3,2{,1{}},3,2{{},1{,{φ3. 若集合A ,B 的元素个数分别为n B m A ==,,则A 到B 有 nm ⨯2种不同的二元关系。
4. A={φ,a ,{b}},B=}{φ,则{}><><><=⨯φφφφ},{,,,,b a B A5. 设A={1,2,3},则在A 上有 5 个不同的划分。
6.设P ={<1, 2>, <1, 4>, <2, 3>, <4, 4>}和Q ={ <1, 2>, <2, 3>,<4, 2>} 则dom(P ∪Q )= {1,2,4} ,ran(P ∪Q ) = { 2,3,4}7. A I 是集合A 上的恒等关系,A 上的关系R 具有 反对称 性当且仅当1A R R I -⋂⊆8. A I 是集合A 上的恒等关系,A 上的关系R 具有 反自反 性当且仅当Φ=⋂R I A9. 设R 为A 上的关系,R 在A 上具有 传递 当且仅当R R R ⊆ 。
10.设R 为A 上的关系,R 在A 上自反的当且仅当 A I R ⊆ 11.设R 为A 上的关系,R 在A 上对称的当且仅当1R R -=二、 选择题1.集合A={全班同学}上的同龄关系R 为( B )A .对称关系B .等价关系C .偏序关系D .三个都不是 2.在由3个元素组成的集合上,可以有( D )种不同的关系。
A . 3; B .8; C .9 ; D .5123.设集合{}c b a A ,,=,A 上的二元关系{}><><=b b a a R ,,,不具备关系( D )性质A .传递性B .反对称性C .对称性D .自反性三、 计算题1.设集合A={1,2,3},A 上的关系R={<1,1>,<1,2>,<2,2>,<3,2>,<3,3>}(1) 画出R 的关系图; (2) 写出R 的关系矩阵问R 具有关系的哪几些特殊性质(自反、对称、传递等)解 (1)(2)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=110010011M 该关系是自反的但不是反自反的,因为每个顶点都有个环;它是反对称的但不是对称的,因为图中只有单向边;它也是传递的,因为不存在顶点x,y,z ,使得x 到y 有边,y 到z 有边,但x 到z 没边,其中}3,2,1{,,∈z y x 。
离散数学期末考试题(附答案和含解析2)
一.填空题1. 谓词公式)()(x xQ x xP ∃→∀的前束范式是 ∃x ∃y¬P(x)∨Q(y)2。
设全集 E={1,2,3,4,5},A={1,2,3},B={2,5}, 则A ∩B = {2} ,=A {4,5} ,=B A {1,3,4,5} 。
3。
设{}{}b a B c b a A ,,,,==,则=-)()(B A ρρ__{{c },{a ,c},{b,c},{a,b,c}}_,=-)()(A B ρρ__Φ__。
4。
在代数系统(N,+)中,其单位元是0,仅有 单位元0 有逆元。
//x+y=0,x 的逆元= -x ,即x=05.如果连通平面图G 有n 个顶点,e 条边,则G 有__e+2-n __个面。
//点+面-边=23 无向图G 有12条边,G 中有6个3度结点,其余结点的度数均小于3,问G 中至少有 9 个结点?//因为至少,所以 6×3+2n=12×2 解得n=3 总结点m=6+3=9二.选择题1。
与命题公式)(R Q P →→等价的公式是( )(A )R Q P →∨)( (B )R Q P →∧)( (C))(R Q P ∧→ (D ))(R Q P ∨→3。
在图>=<E V G ,中,结点总度数与边数的关系是( C )(A )E v i 2)deg(= (B ) E v i =)deg((C)∑∈=V v i E v 2)deg((D) ∑∈=V v iE v )deg(4. 设D 是有n 个结点的有向完全图,则图D 的边数为( A )(A ))1(-n n (B))1(+n n (C)2/)1(+n n (D)2/)1(-n n5。
无向图G 是欧拉图,当且仅当( C )(A) G 的所有结点的度数都是偶数 (B )G 的所有结点的度数都是奇数(C)G 连通且所有结点的度数都是偶数 (D) G 连通且G 的所有结点度数都是奇数。
离散数学考试题及答案
离散数学考试题及答案一、选择题(每题2分,共20分)1. 在集合论中,下列哪个符号表示属于关系?A. ∈B. ∉C. ⊆D. ∩答案:A2. 对于命题逻辑,下列哪个是真值表的表示方法?A. 真值表B. 逻辑图C. 布尔代数D. 集合论答案:A3. 以下哪个是图论中的基本单位?A. 点B. 线C. 面D. 体答案:A4. 函数f(x) = x^2 + 3x + 2在x=-1处的值是:A. 0C. 4D. 6答案:C5. 在关系数据库中,以下哪个操作用于删除表中的记录?A. SELECTB. INSERTC. UPDATED. DELETE答案:D6. 以下哪个是离散数学中的归纳法证明方法?A. 直接证明法B. 反证法C. 归纳法D. 构造性证明法答案:C7. 在逻辑中,以下哪个是析取命题?A. P ∧ QB. P ∨ QC. ¬PD. P → Q答案:B8. 以下哪个是图的遍历算法?B. BFSC. Dijkstra算法D. Floyd算法答案:B9. 在集合{1, 2, 3}上,以下哪个是幂集?A. {∅, {1}}B. {1, 2}C. {1, 2, 3}D. 所有选项答案:D10. 以下哪个是递归算法的特点?A. 不能自我调用B. 必须有一个终止条件C. 必须有一个基本情况D. 所有选项答案:D二、填空题(每空2分,共20分)1. 在离散数学中,_________ 表示一个命题的否定。
答案:¬P2. 如果集合A和集合B的交集为空集,那么A和B被称为_________。
答案:不相交3. 一个函数f: A → B是_________,如果对于集合B中的每个元素b,集合A中至少有一个元素a与之对应。
答案:满射4. 在图论中,一个没有环的连通图被称为_________。
答案:树5. 一个命题逻辑公式是_________,如果它在所有可能的真值分配下都是真的。
答案:重言式6. 一个关系R在集合A上是_________,如果对于A中的任意两个元素a和b,如果(a, b)属于R,则(b, a)也属于R。
新版离散数学试卷及答案-新版-精选.pdf
题目
1
2
3
4
5
6
7
8
9
10
答案 C D
B、 C C A
DCAD
B
A
三、证明 26%
1、 证:
“
”
a, b, c X 若 < a, b >, < a, c > R 由 R 对 称 性 知
< b, a >, < c, a R ,由 R 传递性得 < b, c > R
“ ” 若 < a, b > R , < a, c > R 有 < b, c > R 任 意 a, b X , 因
求出 R 的传递闭包 t (R) 。
(9 分)
2、如下图所示的赋权图表示某七个城市 v1, v2 , , v7 及预先算出它们之间的一些直接通
信线路造价, 试给出一个设计方案, 使得各城市之间能够通信而且总造价最小。
(9分)
试卷一答案: 一、填空 20% (每小题 2 分)
1、{0 ,1,2,3,4,6} ; 2、( B C ) A ;3、1; 4、( P S R) ( P
试卷二试题与答案
一、填空 20% (每小题 2 分)
1、 P:你努力, Q:你失败。“除非你努力,否则你将失败”的翻译为 ;“虽然你努力了,但还是失败了”的翻译为 。
2、论域 D={1 , 2} ,指定谓词 P
P (1,1) P (1,2) P (2,1) P (2,2)
T
T
F
F
则公式 x yP( y, x) 真值为
C. f : R I , f (x) = [x] ; D . f :I N, f (x) = | x | 。
离散数学试卷及答案二
一、单项选择题(本大题共15小题,每小题1分,共15分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.下列是两个命题变元p,q的小项是()A.p∧┐p∧q B.┐p∨qC.┐p∧q D.┐p∨p∨q2.令p:今天下雪了,q:路滑,则命题“虽然今天下雪了,但是路不滑”可符号化为()A.p→┐q B.p∨┐qC.p∧q D.p∧┐q3.下列语句中是命题的只有()A.1+1=10 B.x+y=10C.sinx+siny<0 D.x mod 3=24.下列等值式不正确的是()A.┐(∀x)A⇔(∃x)┐AB.(∀x)(B→A(x))⇔B→(∀x)A(x)C.(∃x)(A(x)∧B(x))⇔(∃x)A(x)∧(∃x)B(x)D.(∀x)(∀y)(A(x)→B(y))⇔(∃x)A(x)→(∀y)B(y)5.谓词公式(∃x)P(x,y)∧(∀x)(Q(x,z)→(∃x)(∀y)R(x,y,z)中量词∀x的辖域是()A.(∀x)Q(x,z)→(∃x)(∀y)R(x,y,z))B.Q(x,z)→(∀y)R(x,y,z)C.Q(x,z)→(∃x)(∀y)R(x,y,z)D.Q(x,z)6.设R为实数集,函数f:R→R,f(x)=2x,则f是()A.满射函数B.入射函数C.双射函数D.非入射非满射7.设A={a,b,c,d},A上的等价关系R={<a,b>,<b,a>,<c,d>,<d,c>}∪I A,则对应于R的A的划分是()A.{{a},{b,c},{d}} B.{{a,b},{c},{d}}C.{{a},{b},{c},{d}} D.{{a,b},{c,d}}8.设A={Ø},B=P(P(A)),以下正确的式子是()A.{Ø,{Ø}}∈B B.{{Ø,Ø}}∈BC.{{Ø},{{Ø}}}∈B D.{Ø,{{Ø}}}∈B9.设X,Y,Z是集合,一是集合相对补运算,下列等式不正确的是()A.(X-Y)-Z=X-(Y∩Z)B.(X-Y)-Z=(X-Z)-YC.(X-Y)-Z=(X-Z)-(Y-Z)D.(X-Y)-Z=X-(Y∪Z)10.设*是集合A上的二元运算,称Z是A上关于运算*的零元,若()A.,Ax∈∀有x*Z=Z*x=ZB.Z∈A,且A∀有x*Z=Z*x=Zx∈C.Z∈A,且A∀有x*Z=Z*x=xx∈D.Z∈A,且A∃有x*Z=Z*x=Zx∈11.在自然数集N上,下列定义的运算中不可结合的只有()A.a*b=min(a,b)B.a*b=a+bC.a*b=GCD(a,b)(a,b的最大公约数)D.a*b=a(mod b)12.设R为实数集,R+={x|x∈R∧x>0},*是数的乘法运算,<R+,*>是一个群,则下列集合关于数的乘法运算构成该群的子群的是()A.{R+中的有理数} B.{R+中的无理数}C.{R+中的自然数} D.{1,2,3}13.设<A,*, >是环,则下列正确的是()A.<A, >是交换群B.<A,*>是加法群C. 对*是可分配的D.*对 是可分配的14.下列各图不是欧拉图的是()15.设G是连通平面图,G中有6个顶点8条边,则G的面的数目是()A.2个面B.3个面C.4个面D.5个面第二部分非选择题(共85分)二、填空题(本大题共10小题,每空1分,共20分)请在每小题的空格中填上正确答案。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、填空 20% (每小题2分)1、 P :你努力,Q :你失败。
“除非你努力,否则你将失败”的翻译为;“虽然你努力了,但还是失败了”的翻译为 。
2、论域D={1,2},指定谓词P则公式),(x y yP x ∃∀真值为 。
2、 设S={a 1 ,a 2 ,…,a 8},B i 是S 的子集,则由B 31所表达的子集是 。
3、 设A={2,3,4,5,6}上的二元关系}|,{是质数x y x y x R ∨<><=,则R=(列举法)。
R 的关系矩阵M R =。
5、设A={1,2,3},则A 上既不是对称的又不是反对称的关系R= ;A 上既是对称的又是反对称的关系R= 。
6、设代数系统<A ,*>,其中A={a ,b ,c},则幺元是 ;是否有幂等性 ;是否有对称性 。
7、4阶群必是 群或 群。
8、下面偏序格是分配格的是 。
9、n 个结点的无向完全图K n 的边数为 ,欧拉图的充要条件是 。
10、公式R Q P Q P P ⌝∧∨⌝∧∧⌝∨)(())(( 的根树表示为。
二、选择 20% (每小题2分)1、在下述公式中是重言式为( )A .)()(Q P Q P ∨→∧;B .))()(()(P Q Q P Q P →∧→↔↔;C .Q Q P ∧→⌝)(;D .)(Q P P ∨→ 。
2、命题公式 )()(P Q Q P ∨⌝→→⌝ 中极小项的个数为( ),成真赋值的个数为( )。
A .0;B .1;C .2;D .3 。
3、设}}2,1{},1{,{Φ=S ,则 S2 有( )个元素。
A .3;B .6;C .7;D .8 。
4、 设} 3 ,2 ,1 {=S ,定义S S ⨯上的等价关系},,,, | ,,,{c b d a S S d c S S b a d c b a R +=+⨯>∈<⨯>∈<><><<=则由 R 产 生的S S ⨯上一个划分共有( )个分块。
A .4;B .5;C .6;D .9 。
5、设} 3 ,2 ,1 {=S ,S 上关系R 的关系图为则R 具有( )性质。
A .自反性、对称性、传递性;B .反自反性、反对称性;C .反自反性、反对称性、传递性;D .自反性 。
6、设 ,+ 为普通加法和乘法,则( )>+< ,,S 是域。
A .},,3|{Q b a b a x x S ∈+== B .},,2|{Z b a n x x S ∈==C .},12|{Z n n x x S ∈+== D .}0|{≥∧∈=x Z x x S = N 。
7、下面偏序集( )能构成格。
8、在如下的有向图中,从V 1到V 4长度为3 的道路有( )条。
A .1;B .2;C .3;D .4 。
9、在如下各图中( )欧拉图。
10、设R是实数集合,“⨯”为普通乘法,则代数系统<R ,×> 是( )。
A .群;B .独异点;C .半群 。
三、证明 46%1、 设R 是A 上一个二元关系,)},,,(),(|,{R b c R c a A c A b a b a S >∈<>∈<∈∧∈><=且有对于某一个试证明若R是A 上一个等价关系,则S 也是A 上的一个等价关系。
(9分)2、 用逻辑推理证明:所有的舞蹈者都很有风度,王华是个学生且是个舞蹈者。
因此有些学生很有风度。
(11分)3、 若B A f →:是从A 到B 的函数,定义一个函数A B g 2:→ 对任意B b ∈有)})(()(|{)(b x f A x x b g =∧∈=,证明:若f 是A 到B 的满射,则g 是从B 到 A2 的单射。
(10分)4、 若无向图G 中只有两个奇数度结点,则这两个结点一定连通。
(8分)5、 设G 是具有n 个结点的无向简单图,其边数2)2)(1(21+--=n n m ,则G 是Hamilton 图(8分)四、计算 14%1、 设<Z 6,+6>是一个群,这里+6是模6加法,Z 6={[0 ],[1],[2],[3],[4],[5]},试求出<Z 6,+6>的所有子群及其相应左陪集。
(7分)2、 权数1,4,9,16,25,36,49,64,81,100构造一棵最优二叉树。
(7分)一、 填空 20%(每小题2分)1、Q P →⌝;Q P ∧2、T3、},,,,{876540001111131a a a a a B B ==4、R={<2,2>,<2,3>,<2,4>,<2,5>,<2,6>,<3,2>,<3,3>,<3,4>,<3,5>,<3,6>,<4,5>,<4,6>,<5,2>,<5,3>,<5,4>,<5,5>,<5,6>};⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛00000111111100011111111115、R={<1,2>,<1,3>,<2,1>};R={<1,1>,<2,2>,<3,3>}6、a ;否;有7、Klein 四元群;循环群8、 B9、)1(21-n n ;图中无奇度结点且连通 10 、二、选择 20%(每小题 2分)三、 证明 46%1、(9分)(1) S 自反的A a ∈∀,由R 自反,),(),(R a a R a a >∈<∧>∈<∴,S a a >∈∴<,(2) S 对称的传递对称定义R Sa b R R b c R c a S R b c R c a S b a Ab a >∈⇒<>∈<∧>∈<⇒>∈<∧>∈<⇒>∈<∈∀,),(),(),(),(,,(3) S 传递的定义传递S Sc a R R c b R b a R c e R e b R bd R d a Sc b S b a Ac b a >∈⇒<>∈<∧>∈<⇒>∈<∧>∈<∧>∈<∧>∈<⇒>∈<∧>∈<∈∀,),(),(),(),(),(),(,,,,由(1)、(2)、(3)得;S 是等价关系。
2、11分证明:设P(x):x 是个舞蹈者; Q(x) :x 很有风度; S(x):x 是个学生; a :王华 上述句子符号化为:前提:))()((x Q x P x →∀、)()(a P a S ∧ 结论:))()((x Q x S x ∧∃ ……3分①)()(a P a S ∧ P ②))()((x Q x P x →∀ P ③)()(a Q a P → US ② ④)(a P T ①I ⑤).(a Q T ③④I ⑥)(a S T ①I ⑦)()(a Q a S ∧ T ⑤⑥I ⑧)()((x Q x S x ∧∃ EG ⑦……11分3、10分证明 :)(,,2121b b B b b ≠∈∀A a a f ∈∃∴21,满射21212211,),()(,)(,)(a a f a f a f b a f b a f ≠∴≠==是函数由于且使)()()(),()(),()})(()(|{)()},)(()(|{)(21122122112211b g b g b g a b g a b g a b g a b x f A x x b g b x f A x x b g ≠∴∉∉∈∈∴=∧∈==∧∈=但又为单射任意性知由g b b ,,21。
4、8分证明:设G 中两奇数度结点分别为u 和v ,若 u ,v 不连通,则G 至少有两个连通分支G 1、G 2 ,使得u 和v 分别属于G 1和G 2,于是G 1和G 2中各含有1个奇数度结点,这与图论基本定理矛盾,因而u ,v 一定连通。
5、8分证明: 证G 中任何两结点之和不小于n 。
反证法:若存在两结点u ,v 不相邻且1)()(-≤+n v d u d ,令},{1v u V =,则G-V 1是具有n-2个结点的简单图,它的边数)1(2)2)(1(21'--+--≥n n n m ,可得1)3)(2(21'+--≥n n m ,这与G 1=G-V 1为n-2个结点为简单图的题设矛盾,因而G 中任何两个相邻的结点度数和不少于n 。
所以G 为Hamilton 图.四、计算 14%1、 7分解:子群有<{[0]},+6>;<{[0],[3]},+6>;<{[0],[2],[4]},+6>;<{Z 6},+6> {[0]}的左陪集:{[0]},{[1]};{[2]},{[3]};{[4]},{[5]} {[0],[3]}的左陪集:{[0],[3]};{[1],[4]};{[2],[5]} {[0],[2],[4]}的左陪集:{[0],[2],[4]};{[1],[3],[5]} Z 6的左陪集:Z 6 。
2、 7分。
