离散数学试卷及答案(2)
离散数学期末试卷及部分答案 (2)

离散数学试题(A 卷及答案)一、证明题(10分)1)(⌝P ∧(⌝Q ∧R))∨(Q ∧R)∨(P ∧R)⇔R证明: 左端⇔(⌝P ∧⌝Q ∧R)∨((Q ∨P)∧R)⇔((⌝P ∧⌝Q)∧R))∨((Q ∨P)∧R)⇔(⌝(P ∨Q)∧R)∨((Q ∨P)∧R)⇔(⌝(P ∨Q)∨(Q ∨P))∧R ⇔(⌝(P ∨Q)∨(P ∨Q))∧R ⇔T ∧R(置换)⇔R2)∃x(A(x)→B(x))⇔ ∀xA(x)→∃xB(x)证明 :∃x(A(x)→B(x))⇔∃x(⌝A(x)∨B(x))⇔∃x ⌝A(x)∨∃xB(x)⇔⌝∀xA(x)∨∃xB(x)⇔∀xA(x)→∃xB(x) 二、求命题公式(P ∨(Q ∧R))→(P ∧Q ∧R)的主析取范式和主合取范式(10分)证明:(P ∨(Q ∧R))→(P ∧Q ∧R)⇔⌝(P ∨(Q ∧R))∨(P ∧Q ∧R))⇔(⌝P ∧(⌝Q ∨⌝R))∨(P ∧Q ∧R) ⇔(⌝P ∧⌝Q)∨(⌝P ∧⌝R))∨(P ∧Q ∧R)⇔(⌝P ∧⌝Q ∧R)∨(⌝P ∧⌝Q ∧⌝R)∨(⌝P ∧Q ∧⌝R))∨(⌝P ∧⌝Q ∧⌝R))∨(P ∧Q ∧R) ⇔m0∨m1∨m2∨m7 ⇔M3∨M4∨M5∨M6三、推理证明题(10分)1) C ∨D, (C ∨D)→ ⌝E, ⌝E →(A ∧⌝B), (A ∧⌝B)→(R ∨S)⇒R ∨S证明:(1) (C ∨D)→⌝E(2) ⌝E →(A ∧⌝B)(3) (C ∨D)→(A ∧⌝B) (4) (A ∧⌝B)→(R ∨S) (5) (C ∨D)→(R ∨S)(6) C ∨D(7) R ∨S2) ∀x(P(x)→Q(y)∧R(x)),∃xP(x)⇒Q(y)∧∃x(P(x)∧R(x))证明(1)∃xP(x) (2)P(a)(3)∀x(P(x)→Q(y)∧R(x)) (4)P(a)→Q(y)∧R(a) (5)Q(y)∧R(a) (6)Q(y) (7)R(a) (8)P(a) (9)P(a)∧R(a) (10)∃x(P(x)∧R(x)) (11)Q(y)∧∃x(P(x)∧R(x))四、设m 是一个取定的正整数,证明:在任取m +1个整数中,至少有两个整数,它们的差是m 的整数倍证明 设1a ,2a ,…,1+m a 为任取的m +1个整数,用m 去除它们所得余数只能是0,1,…,m -1,由抽屉原理可知,1a ,2a ,…,1+m a 这m +1个整数中至少存在两个数s a 和t a ,它们被m 除所得余数相同,因此s a 和t a 的差是m 的整数倍。
离散数学考试模拟试题及详细参考答案共四套

离散模拟答案11命题符号化(共6小题,每小题3分,共计18分)1.用命题逻辑把下列命题符号化a)假如上午不下雨,我去看电影,否则就在家里读书或看报。
b)我今天进城,除非下雨。
c)仅当你走,我将留下。
2.用谓词逻辑把下列命题符号化a)有些实数不是有理数b)对于所有非零实数x,总存在y使得xy=1。
c) f 是从A到B的函数当且仅当对于每个a∈A存在唯一的b∈B,使得f(a)=b.一、简答题(共6道题,共32分)1.求命题公式(P→(Q→R))↔(R→(Q→P))的主析取范式、主合取范式,并写出所有成真赋值。
(5分)2.设个体域为{1,2,3},求下列命题的真值(4分)a)∀x∃y(x+y=4)b)∃y∀x (x+y=4)3.求∀x(F(x)→G(x))→(∃xF(x)→∃xG(x))的前束范式。
(4分)4.判断下面命题的真假,并说明原因。
(每小题2分,共4分)a)(A⋃B)-C=(A-B) ⋃(A-C)b)若f是从集合A到集合B的入射函数,则|A|≤|B|5.设A是有穷集,|A|=5,问(每小题2分,共4分)a)A上有多少种不同的等价关系?b)从A到A的不同双射函数有多少个?6.设有偏序集<A,≤>,其哈斯图如图1,求子集B={b,d,e}的最小元,最大元、极大元、极小元、上界集合、下界集合、上确界、下确界,(5分)f g图17.已知有限集S={a1,a2,…,a n},N为自然数集合,R为实数集合,求下列集合的基数S;P(S);N,N n;P(N);R,R×R,{o,1}N(写出即可)(6分)二、证明题(共3小题,共计40分)1.使用构造性证明,证明下面推理的有效性。
(每小题5分,共10分)a)A→(B∧C),(E→⌝F)→⌝C, B→(A∧⌝S)⇒B→Eb)∀x(P(x)→⌝Q(x)), ∀x(Q(x)∨R(x)),∃x⌝R(x) ⇒∃x⌝P(x)2.设R1是A上的等价关系,R2是B上的等价关系,A≠∅且B≠∅,关系R满足:<<x1,y1>,<x2,y2>>∈R,当且仅当< x1, x2>∈R1且<y1,y2>∈R2。
《离散数学》试题带答案(二)

《离散数学》试题带答案试卷九试题与答案一、 填空 30% (每空 3分)1、 选择合适的论域和谓词表达集合A=“直角坐标系中,单位元(不包括单位圆周)的点集”则A= 。
2、 集合A={Φ,{Φ}}的幂集P (A) = 。
3、 设A={1,2,3,4},A 上二元关系R={<1,2>,<2,1>,<2,3>,<3,4>}画出R的关系图。
4、 设A={<1,2>,<2 , 4 >,<3 , 3 >} , B={<1,3>,<2,4>,<4,2>},则B A ⋃= 。
B A = 。
5、 设|A|=3,则A 上有 个二元关系。
6、 A={1,2,3}上关系R= 时,R 既是对称的又是反对称的。
7、 偏序集><≤R A ,的哈斯图为,则≤R = 。
8、 设|X|=n ,|Y|=m 则(1)从X 到Y 有 个不同的函数。
(2)当n , m 满足 时,存在双射有 个不同的双射。
9、 2是有理数的真值为 。
10、Q :我将去上海,R :我有时间,公式)()(Q R R Q →∧→的自然语言为 。
11、公式)()(Q P P Q ∧⌝∧→的 主合取范式是 。
12、 若} ,, , {21m S S S S =是集合A 的一个分划,则它应满足 。
二、 选择 20% (每小题 2分)1、 设全集为I ,下列相等的集合是( )。
A 、} |{是偶数或奇数x x A =;B 、)}2( |{y x I y y x B =∧∈∃=;C 、)}12( |{+=∧∈∃=y x I y y x C ;D 、},4,4,3,3,2,2,1,1,0|{ ----=x D 。
2、 设S={N ,Q ,R},下列命题正确的是( )。
A 、S S N N ∈∈∈2 ,2则; B 、S N S Q Q N ⊂∈⊂则 ,; C 、R N R Q Q N ⊂⊂⊂则 ,; D 、S N S N ⋂⊂Φ⊂Φ⊂Φ则 ,。
《离散数学》考试试卷(试卷库20卷)及答案

《离散数学》考试试卷(试卷库20卷)及答案第 1 页/共 4 页《离散数学》考试试卷(试卷库20卷)试题总分: 100 分考试时限:120 分钟、选择题(每题2分,共20分)1. 设论域为全总个体域,M(x):x 是人,Mortal(x):x 是要死的,则“人总是要死的”谓词公式表示为( )(A ))()(x Mortal x M → (B ))()(x Mortal x M ∧(C )))()((x Mortal x M x →?(D )))()((x Mortal x M x ∧?2. 判断下列命题哪个正确?( )(A )若A∪B=A∪C,则B =C (B ){a,b}={b,a}(C )P(A∩B)≠P(A)∩P (B)(P(S)表示S 的幂集)(D )若A 为非空集,则A ≠A∪A 成立3. 集合},2{N n x x A n∈==对( )运算封闭(A )乘法(B )减法(C )加法(D )y x -4. 设≤><,N 是偏序格,其中N 是自然数集合,“≤”是普通的数间“小于等于”关系,则N b a ∈?,有=∨b a ( )(A )a(B )b(C )min(a ,b)(D ) max(a ,b)5. 有向图D=,则41v v 到长度为2的通路有( )条(A )0 (B )1 (C )2 (D )36. 设无向图G 有18条边且每个顶点的度数都是3,则图G 有( )个顶点(A )10 (B )4 (C )8 (D )127. 下面哪一种图不一定是树?()(A )无回路的连通图(B )有n 个结点n-1条边的连通图(C )每对结点间都有通路的图(D )连通但删去一条边则不连通的图 8. 设P :我将去镇上,Q :我有时间。
命题“我将去镇上,仅当我有时间”符号化为()(A )P →Q (B )Q →P (C )P Q (D )Q P ?∨? 9. 下列代数系统中,其中*是加法运算,()不是群。
《离散数学》题库及标准答案

《离散数学》题库及标准答案《离散数学》题库及答案————————————————————————————————作者:————————————————————————————————日期:《离散数学》题库与答案一、选择或填空(数理逻辑部分)1、下列哪些公式为永真蕴含式?( )(1)?Q=>Q→P (2)?Q=>P→Q (3)P=>P→Q (4)?P∧(P∨Q)=>?P答:在第三章里面有公式(1)是附加律,(4)可以由第二章的蕴含等值式求出(注意与吸收律区别)2、下列公式中哪些是永真式?( )(1)(┐P∧Q)→(Q→?R) (2)P→(Q→Q) (3)(P∧Q)→P (4)P→(P∨Q)答:(2),(3),(4)可用蕴含等值式证明3、设有下列公式,请问哪几个是永真蕴涵式?( )(1)P=>P∧Q (2) P∧Q=>P (3) P∧Q=>P∨Q(4)P∧(P→Q)=>Q (5) ?(P→Q)=>P (6) ?P∧(P∨Q)=>?P答:(2)是第三章的化简律,(3)类似附加律,(4)是假言推理,(3),(5),(6)都可以用蕴含等值式来证明出是永真蕴含式4、公式?x((A(x)→B(y,x))∧?z C(y,z))→D(x)中,自由变元是( ),约束变元是( )。
答:x,y, x,z(考察定义在公式?x A和?x A中,称x为指导变元,A为量词的辖域。
在?x A和?x A的辖域中,x的所有出现都称为约束出现,即称x为约束变元,A中不是约束出现的其他变项则称为自由变元。
于是A(x)、B(y,x)和?z C(y,z)中y为自由变元,x和z为约束变元,在D(x)中x为自由变元)5、判断下列语句是不是命题。
若是,给出命题的真值。
( )(1)北京是中华人民共和国的首都。
(2) 陕西师大是一座工厂。
(3) 你喜欢唱歌吗? (4) 若7+8>18,则三角形有4条边。
离散数学练习题2 答案
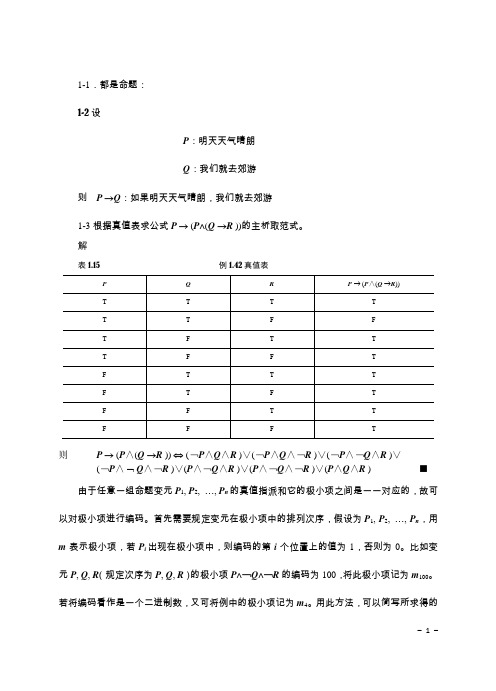
1-1.都是命题:1-2设P:明天天气晴朗Q:我们就去郊游则P →Q:如果明天天气晴朗,我们就去郊游1-3根据真值表求公式P → (P∧(Q →R ))的主析取范式。
解表1.15 例1.42真值表则P → (P∧(Q →R )) ⇔ (﹁P∧Q∧R )∨(﹁P∧Q∧﹁R )∨(﹁P∧﹁Q∧R )∨⌝(﹁P∧Q∧﹁R )∨(P∧﹁Q∧R )∨(P∧﹁Q∧﹁R )∨(P∧Q∧R ) ■由于任意一组命题变元P1, P2, …, P n的真值指派和它的极小项之间是一一对应的,故可以对极小项进行编码。
首先需要规定变元在极小项中的排列次序,假设为P1, P2, …, P n,用m表示极小项,若P i出现在极小项中,则编码的第i个位置上的值为1,否则为0。
比如变元P, Q, R(规定次序为P, Q, R)的极小项P∧﹁Q∧﹁R的编码为100,将此极小项记为m100。
若将编码看作是一个二进制数,又可将例中的极小项记为m4。
用此方法,可以简写所求得的给定公式的主析取范式。
P → (P∧(Q →R )) ⇔m0∨m1∨m2∨m3∨m4∨m5∨m7(规定P, Q, R的次序为P, Q, R)公式P → (P∧(Q →R ))的主析取范式。
解P → (P∧(Q →R ))⇔﹁P∨(P∧(﹁Q∨R ))⇔ (﹁P∨P)∧(﹁P∨﹁Q∨R)⇔ (﹁P∨﹁Q∨R )⇔ (﹁P∨﹁Q∨R )1-4试证明(﹁P →Q )∧(P →R )∧(﹁Q∨S ) ⇒S∨R。
证明(1)﹁P →Q P(2)﹁Q∨S P(3)Q →S T, (2), E16(4)﹁P →S T, (1), (3), I13(5)﹁S →P T, (4), E18(6)P →R P(7)﹁S →R T, (5),(6), I13(8)﹁﹁S∨R T, (7),E16(9)S∨R T, (8), E11-5如果迈克有电冰箱,则或者他卖了洗衣机,或者他向别人借了钱。
离散数学之命题逻辑考试答案2

离散数学之命题逻辑考试1、分析下列语句那些是命题,哪些不是命题。
(每小题1分,正确 “T ”错误写 “F ”,共10分) (1)、北京是中国首都。
(2)、大连是多么美丽啊! (3)、素数只有有限个。
(4)、请勿吸烟! (5)、6+8≥14。
(6)、明天有离散数学课吗? (7)、不存在最大素数。
(8)、9<+Y X 。
(9)、所有素数都是奇数。
(10)实践出真理。
2、设P 表示命题“我学习努力”。
Q 表示命题“我考试通过”。
R 表示命题“我很快乐”。
(每小题2分,共6分) 试用符号表示下列命题:1) 我考试没通过,但我很快乐。
2) 如果我努力学习,那么我考试通过。
3) 如果我学习努力并且考试通过,那么我很快乐。
3、将下列命题符号化:(每小题2分,共14分)1) 我美丽而又快乐。
2) 如果我快乐,那么天就下雨。
3) 电灯不亮,当且仅当灯泡或开关发生故障。
4) 仅当你去,我将留下。
5) 如果老张和老李都不去,他就去。
6) 你不能既吃饭又看电视。
7) 张刚总是在图书馆看书,除非图书馆不开门或张刚生病。
4、给出下列公式的真值表 (每小题5分,共10分)⑴ )(R Q P ∨→⑵ )(Q P ∨⌝⇄)(Q P ⌝∧⌝5、证明下列等价式。
(每小题3分,共12分) 1) P Q P Q P ⇔⌝∧∨∧)()( 2) P Q Q P P ⌝→⌝⇔→→)(3) C B A C B A →⌝∧⇔∨→)()(4) C A D B C D B C B A →→∧⇔∨→∧→∧))(())(())((6、求下列命题公式的主析取范式和主合取范式。
(每小题10分,共20分) 1) )()(Q R Q P →∧→ 2) R Q P →∨⌝)(7、对于下列一组前提,请给出它们的有效结论并证明。
(每小题4分,共8分)a) 如果我努力学习,那么我能通过考试,但我没有通过考试。
b) 统计表有错误,其原因有两个:一个原因是数据有错误;另一个原因是计算有错误。
《离散数学》考试题库及答案(二)

《离散数学》考试题库及答案试卷五试题与答案一、填空15%(每空3分)1、设G 为9阶无向图,每个结点度数不是5就是6,则G 中至少有 个5度结点。
2、n 阶完全图,K n 的点数X (K n ) = 。
3、有向图 中从v 1到v 2长度为2的通路有 条。
4、设[R ,+,·]是代数系统,如果①[R ,+]是交换群 ②[R ,·]是半群③ 则称[R ,+,·]为环。
5、设],,[⊕⊗L 是代数系统,则],,[⊕⊗L 满足幂等律,即对L a ∈∀有 。
二、选择15%(每小题3分)1、 下面四组数能构成无向简单图的度数列的有( )。
A 、(2,2,2,2,2); B 、(1,1,2,2,3); C 、(1,1,2,2,2); D 、(0,1,3,3,3)。
2、 下图中是哈密顿图的为( )。
3、 如果一个有向图D 是强连通图,则D 是欧拉图,这个命题的真值为( )A 、真;B 、假。
4、 下列偏序集( )能构成格。
5、 设}4,41,3,31,2,21,1{=s ,*为普通乘法,则[S ,*]是()。
A 、代数系统;B 、半群;C 、群;D 、都不是。
三、证明 48%1、(10%)在至少有2个人的人群中,至少有2 个人,他们有相同的朋友数。
2、(8%)若图G 中恰有两个奇数度顶点,则这两个顶点是连通的。
3、(8%)证明在6个结点12条边的连通平面简单图中, 每个面的面数都是3。
4、(10%)证明循环群的同态像必是循环群。
5、(12%)设]1,0,,,,[-+⨯B 是布尔代数,定义运算*为)()(*b a b a b a ⨯+⨯=,求证[B ,*]是阿贝尔群。
四、计算22%1、在二叉树中1) 求带权为2,3,5,7,8的最优二叉树T 。
(5分) 2) 求T 对应的二元前缀码。
(5分)2、 下图所示带权图中最优投递路线并求出投递路线长度(邮局在D 点)。
答案:一、填空(15%)每空3 分1、 6;2、n ;3、2;4、+对·分配且·对+分配均成立;5、a a a a a a =⊕=⊗且。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、填空 20% (每小题2分)1、 P :你努力,Q :你失败。
“除非你努力,否则你将失败”的翻译为;“虽然你努力了,但还是失败了”的翻译为 。
2、论域D={1,2},指定谓词P则公式),(x y yP x ∃∀真值为 。
2、 设S={a 1 ,a 2 ,…,a 8},B i 是S 的子集,则由B 31所表达的子集是 。
3、 设A={2,3,4,5,6}上的二元关系}|,{是质数x y x y x R ∨<><=,则R=(列举法)。
R 的关系矩阵M R =。
5、设A={1,2,3},则A 上既不是对称的又不是反对称的关系R= ;A 上既是对称的又是反对称的关系R= 。
6、设代数系统<A ,*>,其中A={a ,b ,c},则幺元是 ;是否有幂等性 ;是否有对称性 。
7、4阶群必是 群或 群。
8、下面偏序格是分配格的是 。
9、n 个结点的无向完全图K n 的边数为 ,欧拉图的充要条件是 。
10、公式R Q P Q P P ⌝∧∨⌝∧∧⌝∨)(())(( 的根树表示为。
二、选择 20% (每小题2分)1、在下述公式中是重言式为( )A .)()(Q P Q P ∨→∧;B .))()(()(P Q Q P Q P →∧→↔↔;C .Q Q P ∧→⌝)(;D .)(Q P P ∨→ 。
2、命题公式 )()(P Q Q P ∨⌝→→⌝ 中极小项的个数为( ),成真赋值的个数为( )。
A .0;B .1;C .2;D .3 。
3、设}}2,1{},1{,{Φ=S ,则 S2 有( )个元素。
A .3;B .6;C .7;D .8 。
4、 设} 3 ,2 ,1 {=S ,定义S S ⨯上的等价关系},,,, | ,,,{c b d a S S d c S S b a d c b a R +=+⨯>∈<⨯>∈<><><<=则由 R 产 生的S S ⨯上一个划分共有( )个分块。
A .4;B .5;C .6;D .9 。
5、设} 3 ,2 ,1 {=S ,S 上关系R 的关系图为则R 具有( )性质。
A .自反性、对称性、传递性;B .反自反性、反对称性;C .反自反性、反对称性、传递性;D .自反性 。
6、设 ,+ 为普通加法和乘法,则( )>+< ,,S 是域。
A .},,3|{Q b a b a x x S ∈+== B .},,2|{Z b a n x x S ∈==C .},12|{Z n n x x S ∈+== D .}0|{≥∧∈=x Z x x S = N 。
7、下面偏序集( )能构成格。
8、在如下的有向图中,从V 1到V 4长度为3 的道路有( )条。
A .1;B .2;C .3;D .4 。
9、在如下各图中( )欧拉图。
10、设R是实数集合,“⨯”为普通乘法,则代数系统<R ,×> 是( )。
A .群;B .独异点;C .半群 。
三、证明 46%1、 设R 是A 上一个二元关系,)},,,(),(|,{R b c R c a A c A b a b a S >∈<>∈<∈∧∈><=且有对于某一个试证明若R是A 上一个等价关系,则S 也是A 上的一个等价关系。
(9分)2、 用逻辑推理证明:所有的舞蹈者都很有风度,王华是个学生且是个舞蹈者。
因此有些学生很有风度。
(11分)3、 若B A f →:是从A 到B 的函数,定义一个函数A B g 2:→ 对任意B b ∈有)})(()(|{)(b x f A x x b g =∧∈=,证明:若f 是A 到B 的满射,则g 是从B 到 A2 的单射。
(10分)4、 若无向图G 中只有两个奇数度结点,则这两个结点一定连通。
(8分)5、 设G 是具有n 个结点的无向简单图,其边数2)2)(1(21+--=n n m ,则G 是Hamilton 图(8分)四、计算 14%1、 设<Z 6,+6>是一个群,这里+6是模6加法,Z 6={[0 ],[1],[2],[3],[4],[5]},试求出<Z 6,+6>的所有子群及其相应左陪集。
(7分)2、 权数1,4,9,16,25,36,49,64,81,100构造一棵最优二叉树。
(7分)一、 填空 20%(每小题2分)1、Q P →⌝;Q P ∧2、T3、},,,,{876540001111131a a a a a B B ==4、R={<2,2>,<2,3>,<2,4>,<2,5>,<2,6>,<3,2>,<3,3>,<3,4>,<3,5>,<3,6>,<4,5>,<4,6>,<5,2>,<5,3>,<5,4>,<5,5>,<5,6>};⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛00000111111100011111111115、R={<1,2>,<1,3>,<2,1>};R={<1,1>,<2,2>,<3,3>}6、a ;否;有7、Klein 四元群;循环群8、 B9、)1(21-n n ;图中无奇度结点且连通 10 、二、选择 20%(每小题 2分)三、 证明 46%1、(9分)(1) S 自反的A a ∈∀,由R 自反,),(),(R a a R a a >∈<∧>∈<∴,S a a >∈∴<,(2) S 对称的传递对称定义R Sa b R R b c R c a S R b c R c a S b a Ab a >∈⇒<>∈<∧>∈<⇒>∈<∧>∈<⇒>∈<∈∀,),(),(),(),(,,(3) S 传递的定义传递S Sc a R R c b R b a R c e R e b R bd R d a Sc b S b a Ac b a >∈⇒<>∈<∧>∈<⇒>∈<∧>∈<∧>∈<∧>∈<⇒>∈<∧>∈<∈∀,),(),(),(),(),(),(,,,,由(1)、(2)、(3)得;S 是等价关系。
2、11分证明:设P(x):x 是个舞蹈者; Q(x) :x 很有风度; S(x):x 是个学生; a :王华 上述句子符号化为:前提:))()((x Q x P x →∀、)()(a P a S ∧ 结论:))()((x Q x S x ∧∃ ……3分①)()(a P a S ∧ P ②))()((x Q x P x →∀ P ③)()(a Q a P → US ② ④)(a P T ①I ⑤).(a Q T ③④I ⑥)(a S T ①I ⑦)()(a Q a S ∧ T ⑤⑥I ⑧)()((x Q x S x ∧∃ EG ⑦……11分3、10分证明 :)(,,2121b b B b b ≠∈∀A a a f ∈∃∴21,满射21212211,),()(,)(,)(a a f a f a f b a f b a f ≠∴≠==是函数由于且使)()()(),()(),()})(()(|{)()},)(()(|{)(21122122112211b g b g b g a b g a b g a b g a b x f A x x b g b x f A x x b g ≠∴∉∉∈∈∴=∧∈==∧∈=但又为单射任意性知由g b b ,,21。
4、8分证明:设G 中两奇数度结点分别为u 和v ,若 u ,v 不连通,则G 至少有两个连通分支G 1、G 2 ,使得u 和v 分别属于G 1和G 2,于是G 1和G 2中各含有1个奇数度结点,这与图论基本定理矛盾,因而u ,v 一定连通。
5、8分证明: 证G 中任何两结点之和不小于n 。
反证法:若存在两结点u ,v 不相邻且1)()(-≤+n v d u d ,令},{1v u V =,则G-V 1是具有n-2个结点的简单图,它的边数)1(2)2)(1(21'--+--≥n n n m ,可得1)3)(2(21'+--≥n n m ,这与G 1=G-V 1为n-2个结点为简单图的题设矛盾,因而G 中任何两个相邻的结点度数和不少于n 。
所以G 为Hamilton 图.四、计算 14%1、 7分解:子群有<{[0]},+6>;<{[0],[3]},+6>;<{[0],[2],[4]},+6>;<{Z 6},+6> {[0]}的左陪集:{[0]},{[1]};{[2]},{[3]};{[4]},{[5]} {[0],[3]}的左陪集:{[0],[3]};{[1],[4]};{[2],[5]} {[0],[2],[4]}的左陪集:{[0],[2],[4]};{[1],[3],[5]} Z 6的左陪集:Z 6 。
2、 7分。
