集美大学第3章 蛮力法
2014集美大学交通运输工程课表
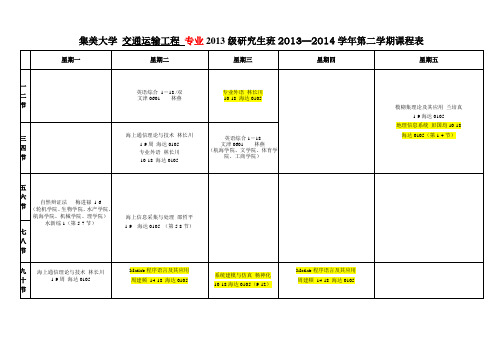
星期一
星期二
星期三
星期四
星期五
一二节
英语综合1-18 /双
文津0601林燕
专业外语林长川
10-18海达0105
模糊集理论及其应用兰培真
1-9海达0105
地理信息系统彭国均10-18
海达0105(第1-4节)
三四节
海上通信理论与技术林长川
1-9周海达0105
专业外语林长川
10-18海达0105
英语综合1-18
文津0601林燕
(航海学院、文学院、体育学院、工商学院)
五六节
自然辩证法梅进禄1-6
(轮机学院、生物学院、水产学院、航海学院、机械学院、理学院)
水新综1(第5-7节)
海上信息采集与处理邵哲平
1-9海达0105(第5-8节林长川
1-9周海达0105
Matlab程序语言及其应用
周建频14-18海达0105
系统建模与仿真杨神化
10-18海达0105(9-12)
Matlab程序语言及其应用
周建频14-18海达0105
集美大学船舶结构力学(48学时)第三章 力法(3)2014(2学时)

216EI v 2 3 11l
M 2 M1 5 R2 ql l 2
因此,有方程:
216 EI M 2 M1 5 v ql 2 3 11l l 2
将此式与上面两方程联立 问题则解决。
题9 求下图 M , v , R 。 1 1 1
据3.6改 (教材52页)
梁的左半段断面惯性矩 为 I 1 ,右半段断面惯性矩 为 I 2 ,可以设想在断面变 化处加上一个柔性系数 A= ∞ 的弹性支座,如图4-27b)所示, 于是就可以按弹性支座上双跨 梁的方法来计算了。
静定基
v AR
EI1
R10
R R12
EI 2
v
静力平衡方程?
R0
A
转角连续方程式?
因此,可列出中间支座断面的 转角连续方程式:
R10
R12
3
l v1 AR1 ( R10 R12 ) 12EI 2 R ql 3
题8
(教材49页例2) 图3-26a所示的具有弹 性支座的多跨梁,试求其断 面弯矩、节点挠度和作用在 弹性支座上的力。
解:1、静定基:
M1
q 1
EI , l
M2
q
E,4I ,4l
M2
3
11l 3 A 216EI
即: 原模型:
A l3 6 EI
静定基:
EI , l EI , l
变协方: 4 4 5 q(2l ) 1 R(2l ) AR 384 EI 48 EI
由此直接解得:
R
v1 AR
可以去掉 中间的弹性支 座代以支反力 R,再利用变 形连续条件列 方程式求解。
R 5ql / 8
大学物理学习指导(第3章)

,'定轴转动时刚体的转动定律
^ 刚体紐定轴转动时,刚体的角加速度与它所受的合外力矩成正比,与刚体的转 动惯量成反比,这称为刚体的转动定律。 31
:
//?
叫
式 ^ 、 7、必须是对同一刚体、同一转轴而言。
8,角动量守恒定律
物体所受的合外力矩等于零,或者不受外力矩的作用,物体的角动量保持不 变。这个结论叫做角动量守恒定律。 I 二加^常矢量
一 转动惯量为/ ^ ^ ^ ^
、
12001^8 ^ 0 1 2 。 一 质 量 为 ^ : 801^8的人,开始时站在转台的中心, ^ 2111时,转台的角速度是多大?
^ 』:2
"; 2 ^ 。 第 页
山# 、理工大学备课紙
年
质量连续分布的刚体 】二 厂2(1^ ^ 厂2一3^
月
日
刚体的转动惯量是刚体作转动时惯性大小的量度。其大小决定于刚体转轴的 位置,刚体本身的形状,质量的大小及其质量分布情况。 6,刚体的角动量 刚体上各质点的角动量之和,即为刚体的角动量。一个刚体绕某一定轴转动, 其角动量为 :加
+ 爐 2 ―威2
由碎块和破盘组成的系统总角动量守恒。
】00 ―】产;十771^^^
^为破盘的角速度。
~ ^ 嫩 、 ^ (^]^!!^^
―
7 ^ ^ 十 卿 0 尺
^ = 0
^0
圆盘余下部分的角动量为
第
页
山系理工大学备课紙
年
I ^ (告魔2 一肌尺2》
月
日
一平面转台绕中心轴转动,每转一周所需时间为纟^ 108,转台对轴的
距轴为「处,取一小段^!厂,其质量01加: 9^^ ,这一小段(!"所受摩擦力矩 习题3-6图 整个杆所受摩擦力矩 1^1 ^2 「2 〃
第三章 蛮力法PPT课件

个定值。设此值为SN ,则不难解
出:SN = N 2 ·(N 2 +1)/2N= N ·(N 2 +1) /2。
.
19
外延法(由巴谢提出)构造奇阶幻方
.
20
H·Coxeter构造幻方的方法
首先在正方形最上面一 行的正中间的小方格内 填写1,然后到它的左 上方的小格内填写下一 个数(注意:我们认为正 方形的同一行或同一行 的头尾是相连的)。如果 走到某个小方格,而该 格已填了数,那末就改 走到原方格的下面一个 方格。
axbyc13穷举查找14穷举查找15穷举查找分配问题n个任务分配给n个人任务j分配给人i的成本是cij16小结蛮力法是一种简单直接地解决问题的方法通常直接基于问题的描述和所涉及的概念定义
算法分析与设计
Analysis and Design of Computer Algorithms
第三章 蛮力法 Brute Force
.
21
习题3.4-10
.
22
直线方程:ax+by=c a=y2-y1 , b=x1-x2, c=x1y2-y1x2
.
12
旅行商问题
穷举查找
.
13
背包问题
穷举查找
.
14
穷举查找
分配问题
N个任务分配给n个人,任务j分配给人i的成本是C[I,j]
.
15
小结
蛮力法是一种简单直接地解决问题的方法,通常 直接基于问题的描述和所涉及的概念定义。
算法 解决问题的实例很少时,它让你花费较少的代
价 可以解决一些小规模的问题 可以作为其他高效算法的衡量标准
.
3
教学内容
0-1背包问题求解方法综述

0-1背包问题求解方法综述算法分析与设计大作业实验题目:0-1背包问题求解方法综述组员:班级:指导老师:0-1背包问题求解方法综述【摘要】:0-1背包问题是一个经典的NP-hard组合优化问题,现实生活中的很多问题都可以以它为模型。
本文首先对背包问题做了阐述,然后用蛮力解法、动态规划算法、贪心算法和回溯解法对背包问题进行求解,分析了0-1背包问题的数学模型,刻划了最优解的结构特征,建立了求最优值的递归关系式。
最后对四种算法从不同角度进行了对比和总结。
【关键词】:0-1背包问题;蛮力解法;动态规划算法;贪心算法;回溯解法。
0.引言0-1背包问题是指给定n个物品,每个物品均有自己的价值vi和重量wi(i=1,2,…,n),再给定一个背包,其容量为W。
要求从n个物品中选出一部分物品装入背包,这部分物品的重量之和不超过背包的容量,且价值之和最大。
单个物品要么装入,要么不装入。
很多问题都可以抽象成该问题模型,如配载问题、物资调运[1]问题等,因此研究该问题具有较高的实际应用价值。
目前,解决0-1背包问题的方法有很多,主要有动态规划法、回溯法、分支限界法、遗传算法、粒子群算法、人工鱼群算法、蚁群算法、模拟退火算法、蜂群算法、禁忌搜索算法等。
其中动态规划、回溯法、分支限界法时间复杂性比较高,计算智能算法可能出现局部收敛,不一定能找出问题的最优解。
文中在动态规划法的基础上进行了改进,提出一种求解0-1背包问题的算法,该算法每一次执行总能得到问题的最优解,是确定性算法,算法的时间复杂性最坏可能为O(2n)。
1.0-1背包问题描述0-1背包问题(KP01)是一个著名的组合优化问题。
它应用在许多实际领域,如项目选择、资源分布、投资决策等。
背包问题得名于如何选择最合适的物品放置于给定背包中。
本文主要研究背包问题中最基础的0/1背包问题的一些解决方法。
为解决背包问题,大量学者在过去的几十年中提出了很多解决方法。
解决背包问题的算法有最优算法和启发式算法[2],最优算法包括穷举法、动态规划法、分支定界法、图论法等,启发式算法包括贪心算法、遗传算法、蚁群算法、粒子算法等一些智能算法。
2020-wfx-第4章 蛮力法-合

程序举例-象棋式
【例4.3】在象棋算式里,不同的棋子代表不同的数,有以 下算式,设计一个算法求这些棋子各代表哪些数字。
兵 炮马 卒
+ 兵 炮车 卒
车 卒 马兵 卒
问题求解
解:采用蛮力法时,设兵、炮、马、卒和车的取值分别为a、b、c、d、
e。则有:
}
4.2.2 简单选择排序和冒泡排序
【问题描述】对于给定的含有n个元素的数组a,对其按元 素值递增排序。
1. 简单选择排序
例如,i=3的一趟简单选择排序过程,其中a[0..2]是有序的,从
a[3..9]中挑选最小元素a[5],将其与a[3]进行交换,从而扩大有序区, 减小无序区。
有序区
1 2 3 6 8 4 10 7 5 9
//比较的两个字符相同时
{ i++; j++;
}
else
//比较的两个字符不相同时
{
i=i-j+1;
//i回退
j=0;
//j从0开始
}
}
if (j==t.length())
//t的字符比较完毕
return i-j;
//t是s的子串,返回位置
else
//t不是s的子串
return -1;
//返回-1
}
for (i=0;i<n;i++)
maxSubSum2(a,n)算法中
{ thisSum=0; for (j=i;j<n;j++) {
只有两重循环, 容易求出T(n)=O(n2)。
thisSum+=a[j]; //maxSum已经包含了a[i..j-1]的最大和
集美大学术科课教案

集美大学术科课教案◆力量素质课教案◆任课教师:专业班级:学生数:周/课次:课的任务1、了解力量素质的概念2、实践学习顺序时间教学内容组织教法开始部分5’ 1 、课堂常规。
2 、宣布本次课教学内容。
准备部分20’1.慢跑400米2.游戏活动:跳绳过关接力3.行进间徒手操a)头部运动b)肩绕环c)体转运动d)俯背运动e)踢腿运动f)弓箭步压腿行进组织形式:学生分为两组,每组出6名同学摇绳,组内每名同学须“S”形依次跳过跳绳,返回时也须依次跳过,并接替一名摇绳的同学,如图所示,返回后下名同学进行。
先全部练习完的组获胜,输的组罚做立卧撑10次。
比赛两次。
顺序时间教学内容组织教法基本部分60’1.力量素质介绍力量素质是指人的机体或机体的某一部分肌肉收缩时克服内外阻力的能力。
力量素质是一切生命活动和体育活动的基础。
力量是生命活动的重要要素,运动肌肉、心肌肌肉、呼吸肌肉的收缩能力,直接构成了人生命活动。
各种体育活动都是由作为运动器官的肌肉以不同的负荷强度、收缩速度和持续时间进行工作而带动了被动运动器官骨骼的移动来完成的,每个人跑、跳、投及攀登爬越等各种体育运动和体力劳动均离不开力量素质。
因此,力量素质是身体最基本的身体素质,是进行一切体育活动和体力劳动的基础。
力量素质影响并促进其它身体素质的发展。
力量素质决定速度素质的提高,耐力素质的增长,柔韧素质的发挥和灵敏素质的表现。
力量素质是掌握动作技术、锻炼方法的基础,同时力量素质的提高对防止运动时受伤起着重复作用。
2.力量素质练习[1]绝对力量[2]相对力量组织教法:先让4-5名同学出来示范一种力量练习,由学生自由制定,其余同学说出这种力量练习锻炼的肌群,示范的同学的动作是否正确。
教师总结,指出错误之处,并引导出力量素质的概念及分类。
并分别解释力量素质类型的概念。
按照运动时肌肉克服阻力的表现形式,把肌肉力量分为绝对肌力、相对肌力、肌肉爆发力和肌肉耐力等几种形式。
解释完后,教师提出几种与力量素质有关的概念:最大深蹲120KG、体重60与80KG的学生卧推分别为60与70KG、立定跳远、连续哑铃摆臂100次,提问学生分别属于哪种力量素质练习。
蛮力法 (2)

11
【例】贴纸问题 有A、B、C、D、E五人,每人额头上都帖了一张黑或白的纸。五人对 坐,每人都可以看到其他人额头上的纸的颜色。五人相互观察后, A说:“我看见有三人额头上帖的是白纸,一人额头上帖的是黑纸” B说:“我看见其他四人额头上帖的都是黑纸” C说:“我看见有一人额头上帖的是白纸,其他三人额头上帖的是黑纸” D说:“我看见其他四人额头上帖的都是白纸” E说:什么也没有说 现在已知额头上帖黑纸的人说的都是谎话,额头上贴白纸的人说的都 是实话,请你编写程序,求出这五个人谁的额头上帖的白纸,谁的额 头上帖的黑纸。
蛮力算法的优缺点:
(1)可以用来解决广阔领域的问题; (2)算法设计思想简单明了; (3)可以解决一些小规模的问题; (4)算法的效率不高,随着问题规模的增大,算法效率急剧下降; (5)问题规模过大时,在时间上,有些蛮力算法不可行。
15
作业1:用蛮力算法求解古堡问题
福尔摩斯到某古堡探险,看到门上写着一个奇怪的算式: ABCDE * ? = EDCBA 他对华生说:“ABCDE应该代表不同的数字,问号也代表某个数字!” 华生:“我猜也是!” 于是,两人沉默了好久,还是没有算出合适的结果来。 请你利用计算机的优势,找到破解的答案。 把 ABCDE 所代表的数字写出来。
蛮力法
1
蛮力法
蛮力法是基于计算机运算速度快这一特性,在解决问题 时采取的一种“懒惰” 策略。这种策略不经过(或者说经过 很少)思考,把问题所有情况或所有过程交给计算机去一 一尝试,从中找出问题的解。 蛮力策略应用:选择排序、冒泡排序、插入排序、顺序 查找、朴素的字符串匹配等。比较常用还有枚举法、盲目
搜索算法等。
2
1 枚举法
枚举法(穷举法)是蛮力策略的一种表现形式,根据问题 中条件将可能情况一一列举出来,逐一尝试从中找出满足 问题条件的解。但有时一一列举出的情况数目很大,则需 要进一步考虑,排除一些明显不合理的情况,尽可能减少 问题可能解的列举数目。 通常从两个方面进行算法设计: 1)找出枚举范围:分析问题所涉及的各种情况。 2)找出约束条件:分析问题的解需要满足的条件,并 用逻辑表达式表示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
abcac
k
j
T[j-k]~T[j-1] = S[i-k]~S[i-1]
i
a b c a b c a c b \0
abcac
k
j
T[0]~T[k-1] = S[i-k]~S[i-1]
T[0]~T[k-1] = T[j-k]~T[j-1]
1
,当j=0时
next[ j] Max{k | 0 k j且' p1...pk1' ' p jk1...p j1'} ,当此集合不空时
2.2 对子集T的每一个元素j
2.2.1 如果weight+wj<C,则 weight=weight+wj;value=value+vj; 2.2.2 否则,转步骤2考察下一个子集;
2.3 如果maxValue<value,则maxValue=value;S=T;
3. 输出子集S中的各元素。
3.2.4 TSP——图问题
3.1.2 关于蛮力法的思考
蛮力法(枚举法、穷举法,暴力法)要求设计者 找出所有可能的情况,然后选择其中一种情况, 若该情况不可行(或不是最优解)则试探下一种 可能的情况。
蛮力法是一种直接解决问题的方法,常常直接基 于问题的描述和所设计的概念定义。
“力”——指计算机的能力,而不是人的智力。 蛮力法常常是最容易应用的方法。
0
,其他情况Biblioteka KMP算法的伪代码描述:
输入:主串S,模式T 算法的时间复杂性T(n)=O(n) 输出:T在S中的位置 1. 在串S和串T中分别设置比较的起始下标i=0, j=0; 2. 重复下述操作, 直到S或T的所有字符均比较完毕:
2.1 如果S[i]等于T[j],则继续比较S和T的下一对字符; 2.2 否则,将下标j回溯到next[j]位置,即j=next[j]; 2.3 如果j等于-1,则将下标i和j分别加1,准备下一趟 比较;
3. 如果T中所有字符均比较完毕,则返回本趟匹配的 开始位置;否则返回0。
3.2.2 选择排序——排序
选择排序开始的时候,扫描整个序列,找到整个序列的最 小记录和序列中的第一个记录交换,从而将最小记录放到 它在有序区的最终位置上,然后再从第二个记录开始扫描 序列,找到n-1个序列中的最小记录,再和第二个记录交 换位置。一般地,第i趟排序从第i个记录开始扫描序列, 在n-i+1(1≤i≤n-1)个记录中找到关键码最小的记录,并 和第i个记录交换作为有序序列的第i个记录。
交换
r1 ≤r2 … … ≤ri-1 ri ri+1 … rmin … rn
有序区 已经位于最终位置
无序区 rmin为无序区的最小记录
算法描述:
void SelectSort(int r[ ], int n) {
for (i=1; i<=n-1; i++) {
index=i; for (j=i+1; j<=n; j++)
问题描述:旅行家要旅行n个城市然后回到出发 城市,要求各个城市经历且仅经历一次,并要求 所走的路程最短。该问题又称为货郎担问题、邮 递员问题、售货员问题,是图问题中最广为人知 的问题。
用蛮力法解决TSP问题,可以找出所有可能的旅 行路线,从中选取路径长度最短的简单回路。
求解: 一个加权连通图中的最短哈密顿回路问题。
60,000,000,000,000,000个可能解。 一个50城市的TSP问题有大约1062个可能解,而一个行
星上也只有1021升水。
蛮力法求解TSP问题,只能解决问题规模很小的实例。
算法的C++语言描述:
int ClosestPoints(int x[ ], int y[ ], int n)
10 54 14 {1, 3, 4} 16 不可行
11 不可行 15 {2, 3, 4} 12 不可行
12 不可行 16 {1, 2, 3, 4} 19 不可行
0/1背包问题算法伪代码描述:
输入:重量{w1, w对2于, …一, 个wn具},有价n个值元{v1素, v的2,集…合, v,n其},子背集数
100,101,102,103,110,111,112, 120,121,122,130,200,201,202, 211,212,220,221,300,301,310。 不难验证只有100,101两个数符合要求。
3.2 各类问题中的蛮力法
3.2.1 串匹配问题——查找
BF算法
KMP算法
下一次开始位置 下一次开始位置
3.1 如果S[i]等于T[j],则继续比较S和T的下一对字符; 3.2 否则,下一趟匹配的开始位置index++,回溯下标 i=index, j=0;
4. 如果T中所有字符均比较完,则返回匹配的开始位 置index;否则返回0。
S=‘aaaaaaaaaaab’
T=‘aaab’
KMP算法
i
本趟开始位置
i 回溯
ii
S 模式T
si
…
tj
回溯
j
j
回溯next[j]
……
BF算法的伪代码描述
输入:主串S(长度为n),模式T(长度为m) 输出:T在S中的位置 1. 初始化主串比较的开始位置index=0; 2. 在串S和串T中设置比较的起始下标i=0, j=0; 3. 重复下述操作, 直到S或T的所有字符均比较完毕:
TSP问题有着简单的表述、重要的应用、以及和其他NP完全 问题的重要关系,它在近100年的时间里强烈地吸引着计算机 科学工作者。
a2
b
5 8
73
c
1
d
序号
1 2 3 4 5 6
路径
a→b→c→d→a a→b→d→c→a a→c→b→d→a a→c→d→b→a a→d→b→c→a a→d→c→b→a
{ int index1, index2; int d, minDist = 1000;
//记载最近点对的下标 //假设最大距离不超过1000
for (int i = 0; i < n - 1; i++) for (int j = i + 1; j < n; j++)
//只考虑i<j的点对
{ d = (x[i]-x[j])* (x[i]-x[j]) + (y[i]-y[j])* (y[i]-y[j]);
序号 1 2 3 4 5 6 7 8
子集 Φ {1} {2} {3} {4}
{1, 2} {1, 3} {1, 4}
重量 价值 序号 子集 重量 价值
0
0
9
{2, 3}
7
52
7 42 10 {2, 4}
8
37
3 12 11 {3, 4}
9
65
4
40 12 {1, 2, 3} 14 不可行
5
25 13 {1, 2, 4} 15 不可行
求an(n为非负整数) 用连续整数检测算法计算GCD(m, n)
蛮力法不是一个最好的算法(巧妙和高效的算法 很少出自蛮力),但当我们想不出更好的办法时,它 也是一种有效的解决问题的方法。
它可能是惟一一种几乎什么问题都能解决的一般 性方法,常用于一些非常基本、但又十分重要的 算法。
3.1.3 蛮力法的优点
第3章 蛮力法
学习要点:
掌握蛮力法的设计思想 应用蛮力法思想,设计求解问题的算法,并分析算
法时间复杂性
3.1 概述
3.1.1 蛮力法的设计思想
蛮力法是指采用遍历(扫描)技术,即采用一定 的策略将待求解问题的所有元素依次处理一次, 从而找出问题的解。
依次处理所有元素是蛮力法的关键,为了避免陷 入重复试探,应保证处理过的元素不再被处理。
求解步骤:
找出枚举范围 找出约束条件
课后作业
P53:2~8,按学号完成相应的题目:
学号尾数mod7=1,完成2 学号尾数mod7=2,完成3 学号尾数mod7=3,完成4 学号尾数mod7=4,完成5 学号尾数mod7=5,完成6 学号尾数mod7=6,完成7 学号尾数mod7=0,完成8
包容量C
量是2n,所以,不论生成子集的算法效率有
输出:装入背包多的高物,品蛮编力法号都会导致一个Ω(2n)的算法.
1. 初始化最大价值maxValue=0;结果子集S=Φ;
2. 对集合{1, 2, …, n}的每一个子集,执行下述操作:
2.1 初始化背包的价值value=0;背包的重量weight=0;
if (d < minDist) {
minDist = d;
index1 = i; index2 = j; }
} cout<<"最近的点对是:"<<index1<<"和"<<index2<<endl;
return minDist;
}
本章小结
蛮力法的设计思想:采用一定的策略将待求解问 题的所有元素依次处理一次,从而找出问题的解 。
在n个物品中找到所有总重量不超过背包容量的子 集,计算每个可能子集的总价值,然后找到价值 最大的子集。
例如,给定4个物品的重量{7, 3, 4, 5},价值{42, 12, 40, 25},和一个容量为10的背包。蛮力法求解 过程为:
w={7, 3, 4, 5} v={42, 12, 40, 25} C=10
逻辑清晰,编写程序简洁 对于一些重要的问题(比如:排序、查找、矩阵
