2018年全国各地中考数学真题汇编:圆填空+选择46题
2018年全国中考数学-甘肃天水中考数学(解析版)

2018年甘肃省天水市初中毕业、升学考试数学(满分150分,考试时间120分钟)一、选择题:本大题共10小题,每小题4分,共40分.不需写出解答过程,请把最后结果填在题后括号内.1.(2018甘肃天水,T1,F4)下列各数中,绝对值最大的数是()A.-2B.3C.0D.-4【答案】D.【解析】因为|−2|=2,|3|=3,|0|=0,|−4|=4,可知0<2<3<4,所以-4的绝对值最大.故选D.【知识点】绝对值2.(2018甘肃天水,T2,F4)近三年,国家投入了用于缓解群众“看病难,看病贵”的问题.将8450亿元用科学记数法表示应为()A.0.845×104亿元B.8.45×103亿元C.8.9.45×104亿元D.84.5×102亿元【答案】B.【解析】8450亿元=8.45×103亿元.【知识点】科学记数法3.(2018甘肃天水,T3,F4)一个几何体的三视图如图所示,则这个几何体是()A.三棱柱B.三棱锥C.圆柱 D 长方体【答案】A.【解析】由俯视图可知几何体的底面是三角形,则几何体是三棱锥或三棱柱,再根据主视图和左视图是长方形,可知该几何体是三棱柱.【知识点】三视图4.(2018甘肃天水,T4,F4)一组数据1,5,7,x 的众数与中位数相等,则这组数据的平均数是()A.6B.5C.4.5D.3.5【答案】C.【解析】当这组数据的众数为1时,则这组数据为1,1,5,7,可知中位数为1.5,不符合题意;当这组数据的众数为5时,则这组数据为1,5,5,7,可知中位数为5,符合题意;当这组数据的众数为7时,则这组数据为1,5,7,7,可知中位数为6,不符合题意.则这组数据的平均数为1+5+5+74=4.5.【知识点】平均数,中位数,众数5.(2018甘肃天水,T5,F4)已知圆锥的底面半径2cm ,母线长为10cm ,则这个圆锥的面积是()A.20πcm 2B.20cm 2C.40πcm 2D.40cm 2【答案】A.【解析】S 圆锥侧=12Rl=12×10×2×π×2=20π(cm 2).【知识点】圆锥侧面积6.(2018甘肃天水,T6,F4)如图所示,点O 是矩形ABCD 对角线AC 的中点,OE ∥AB 交AD 于点E.若OE=3,BC=8,则OB 的长为( )A.4B.5C.√342D.√34【答案】B.【解析】∵四边形ABCD 是矩形,∴∠ABC=90°,AB ∥CD ,AB=CD ,点O 是AC 的中点.∵OE ∥AB ,∴OE ∥CD ,∴OE 是△ACD 的中位线,∴CD=2OE=6,∴AB=6.在Rt △ABC 中,AB=6,BC=8,∴AC=10.∵OB 是Rt △ABC 斜边的中线,∴OB=12AC=5. 【知识点】矩形的性质,中位线的性质7.(2018甘肃天水,T7,F4)如图所示,点A 、B 、C 在⊙O 上.若∠BAC=45°,OB=2,则图中阴影部分的面积为( )A.π-4B.23π-1C.π-2D.23π-2【答案】C.【解析】∵∠BAC=45°,∴∠BOC=90°.则S 扇形BOC =90×π×22360=π, S Rt △BOC =12BO ·CO=12×2×2=2.则阴影部分的面积为S 扇形BOC -S Rt △BOC =π-2.【知识点】扇形面积,圆周角定理8.(2018甘肃天水,T8,F4)在同一平面直角坐标系中,函数y=x+1与函数y=1x 的图像可能是()第8题图【答案】B.【思路分析】首先根据一次函数y=x+1的系数可知其经过的象限,反比例函数y=1x位于的象限,再判断即可.【解题过程】一次函数y=x+1经过一,二,三象限,反比例函数y=1x位于一,三象限,所以B符合题意. 【知识点】反比例函数图像,一次函数图像9.(2018甘肃天水,T9,F4)按一定的规律排列的一组数:12,16,112,120…1a,190,1b…(其中a,b为整数),则a+b的值为()A.182B.172C.242D.200【答案】A.【思路分析】首先根据题意得出分母变化的规律,求出a,b的值,即可得出答案.【解题过程】由题意可知12=11×2,16=12×3,112=13×4,120=14×5…1a=18×9,190=19×10,1b=110×11…可知a=72,b=110,则a+b=182.【知识点】探究规律10.(2018甘肃天水,T10,F4)某学校组织团员举行“伏羲文化旅游节”宣传活动,从学校骑自行车出发。
中考数学真题专项汇编解析—圆与正多边形

中考数学真题专项汇编解析—圆与正多边形一.选择题1.(2022·浙江嘉兴·中考真题)如图,在⊙O中,⊙BOC=130°,点A在BAC上,则⊙BAC的度数为()A.55°B.65°C.75°D.130°【答案】B【分析】利用圆周角直接可得答案.【详解】解:⊙BOC=130°,点A在BAC上,165,2BAC BOC故选B【点睛】本题考查的是圆周角定理的应用,掌握“同圆或等圆中,同弧所对的圆周角是它所对的圆心角的一半”是解本题的关键.2.(2022·山东滨州·中考真题)如图,在O中,弦,AB CD相交于点P,若48,80A APD∠=︒∠=︒,则B的大小为()A.32︒B.42︒C.52︒D.62︒【答案】A【分析】根据三角形的外角的性质可得C A APD ∠+∠=∠,求得32C ∠=︒,再根据同弧所对的圆周角相等,即可得到答案. 【详解】C A APD ∠+∠=∠,48,80A APD ∠=︒∠=︒,32C ∴∠=︒32B C ∴∠=∠=︒故选:A .【点睛】本题考查了圆周角定理及三角形的外角的性质,熟练掌握知识点是解题的关键.3.(2022·江苏连云港·中考真题)如图,有一个半径为2的圆形时钟,其中每个刻度间的弧长均相等,过9点和11点的位置作一条线段,则钟面中阴影部分的面积为( )A .23πB .23πC .43π-D .43π【答案】B【分析】阴影部分的面积等于扇形面积减去三角形面积,分别求出扇形面积和等边三角形的面积即可.【详解】解:如图,过点OC 作OD ⊙AB 于点D ,⊙⊙AOB =2×36012︒=60°, ⊙⊙OAB 是等边三角形,⊙⊙AOD =⊙BOD =30°,OA =OB =AB =2,AD =BD =12AB =1,⊙OD⊙阴影部分的面积为260212236023ππ⋅⨯-⨯B . 【点睛】本题考查了扇形面积、等边三角形的面积计算方法,掌握扇形面积、等边三角形的面积的计算方法是正确解答的关键.4.(2022·湖北武汉·中考真题)如图,在四边形材料ABCD 中,AD BC ∥,90A ∠=︒,9cm AD =,20cm AB =,24cm BC =.现用此材料截出一个面积最大的圆形模板,则此圆的半径是( )A .110cm 13B .8cmC .D .10cm【答案】B【分析】如图所示,延长BA 交CD 延长线于E ,当这个圆为⊙BCE 的内切圆时,此圆的面积最大,据此求解即可.【详解】解:如图所示,延长BA 交CD 延长线于E ,当这个圆为⊙BCE 的内切圆时,此圆的面积最大, ⊙AD BC ∥,⊙BAD =90°, ⊙⊙EAD ⊙⊙EBC ,⊙B =90°, ⊙EA AD EB BC=,即92024EA EA =+, ⊙12cm EA =, ⊙EB =32cm ,⊙40cm EC ,设这个圆的圆心为O ,与EB ,BC ,EC 分别相切于F ,G ,H , ⊙OF =OG =OH ,⊙=EBC EOB COB EOC S S S S ++△△△△,⊙11112222EB BC EB OF BC OG EC OH ⋅=⋅+⋅+⋅, ⊙()2432=243240OF ⨯++⋅, ⊙8cm OF =,⊙此圆的半径为8cm , 故选B .【点睛】本题主要考查了三角形内切圆半径与三角形三边的关系,勾股定理,正确作出辅助线是解题的关键.5.(2022·湖北宜昌·中考真题)如图,四边形ABCD 内接于O ,连接OB ,OD ,BD ,若110C ∠=︒,则OBD ∠=( )A .15︒B .20︒C .25︒D .30【答案】B【分析】根据圆内接四边形的性质求出A ∠,根据圆周角定理可得BOD ∠,再根据OB OD =计算即可.【详解】⊙四边形ABCD 内接于O , ⊙18070A BCD ∠︒-∠︒== ,由圆周角定理得,2140BOD A ∠=∠=︒ , ⊙OB OD =⊙180202BODOBD ODB ︒-∠∠=∠==︒ 故选:B .【点睛】此题考查圆周角定理和圆内接四边形的性质,掌握圆内接四边形的对角互补是解题的关键.6.(2022·四川德阳·中考真题)如图,点E 是ABC 的内心,AE 的延长线和ABC 的外接圆相交于点D ,与BC 相交于点G ,则下列结论:⊙BAD CAD ∠=∠;⊙若60BAC ∠=︒,则120∠=︒BEC ;⊙若点G 为BC 的中点,则90BGD ∠=︒;⊙BD DE =.其中一定正确的个数是( )A .1B .2C .3D .4【答案】D【分析】根据点E 是ABC 的内心,可得BAD CAD ∠=∠,故⊙正确;连接BE ,CE ,可得⊙ABC +⊙ACB =2(⊙CBE +⊙BCE ),从而得到⊙CBE +⊙BCE =60°,进而得到⊙BEC =120°,故⊙正确; BAD CAD ∠=∠,得出BD CD =,再由点G 为BC 的中点,则90BGD ∠=︒成立,故⊙正确;根据点E 是ABC 的内心和三角形的外角的性质,可得()12BED BAC ABC ∠=∠+∠,再由圆周角定理可得()12DBE BAC ABC ∠=∠+∠,从而得到⊙DBE =⊙BED ,故⊙正确;即可求解.【详解】解:⊙点E 是ABC 的内心,⊙BAD CAD ∠=∠,故⊙正确;如图,连接BE ,CE ,⊙点E 是ABC 的内心,⊙⊙ABC =2⊙CBE ,⊙ACB =2⊙BCE , ⊙⊙ABC +⊙ACB =2(⊙CBE +⊙BCE ), ⊙⊙BAC =60°,⊙⊙ABC +⊙ACB =120°,⊙⊙CBE +⊙BCE =60°,⊙⊙BEC =120°,故⊙正确; ⊙点E 是ABC 的内心,⊙BAD CAD ∠=∠,⊙BD CD =,⊙点G 为BC 的中点,⊙线段AD 经过圆心O ,⊙90BGD ∠=︒成立,故⊙正确; ⊙点E 是ABC 的内心,⊙11,22BAD CAD BAC ABE CBE ABC ∠=∠=∠∠=∠=∠, ⊙⊙BED =⊙BAD +⊙ABE ,⊙()12BED BAC ABC ∠=∠+∠, ⊙⊙CBD =⊙CAD ,⊙⊙DBE =⊙CBE +⊙CBD =⊙CBE +⊙CAD ,⊙()12DBE BAC ABC ∠=∠+∠,⊙⊙DBE =⊙BED ,⊙BD DE =,故⊙正确; ⊙正确的有4个.故选:D【点睛】本题主要考查了三角形的内心问题,圆周角定理,三角形的内角和等知识,熟练掌握三角形的内心问题,圆周角定理,三角形的内角和等知识是解题的关键.7.(2022·湖南株洲·中考真题)如图所示,等边ABC 的顶点A 在⊙O 上,边AB 、AC与⊙O分别交于点D、E,点F是劣弧DE上一点,且与D、E不重合,连接DF、∠的度数为()EF,则DFEA.115︒B.118︒C.120︒D.125︒【答案】C【分析】根据等边三角形的性质可得60∠=︒,再根据圆内接四边形的对角互补A即可求得答案.【详解】解:ABC是等边三角形,∴∠=︒-∠=︒,故选C.DFE A∴∠=︒,180120A60【点睛】本题考查了等边三角形的性质及圆内接四边形的性质,熟练掌握圆内接四边形的对角互补是解题的关键.8.(2022·甘肃武威·中考真题)大自然中有许多小动物都是“小数学家”,如图1,蜜蜂的蜂巢结构非常精巧、实用而且节省材料,多名学者通过观测研究发现:蜂巢巢房的横截面大都是正六边形.如图2,一个巢房的横截面为正六边形ABCDEF,若对角线AD的长约为8mm,则正六边形ABCDEF的边长为()A.2mm B.C.D.4mm【答案】D【分析】如图,连接CF与AD交于点O,易证⊙COD为等边三角形,从而CD=OC=OD=12AD,即可得到答案.【详解】连接CF与AD交于点O,⊙ABCDEF为正六边形,⊙⊙COD= 3606=60°,CO=DO,AO=DO=12AD=4mm,⊙⊙COD为等边三角形,⊙CD=CO=DO=4mm,即正六边形ABCDEF的边长为4mm,故选:D.【点睛】本题考查了正多边形与圆的性质,正确把握正六边形的中心角、半径与边长的关系是解题的关键.9.(2022·湖南邵阳·中考真题)如图,⊙O是等边⊙ABC的外接圆,若AB=3,则⊙O的半径是()A .32B C D .52【答案】C【分析】作直径AD ,连接CD ,如图,利用等边三角形的性质得到⊙B =60°,关键圆周角定理得到⊙ACD =90°,⊙D =⊙B =60°,然后利用含30度的直角三角形三边的关系求解.【详解】解:作直径AD ,连接CD ,如图,⊙⊙ABC 为等边三角形,⊙⊙B =60°, ⊙AD 为直径,⊙⊙ACD =90°,⊙⊙D =⊙B =60°,则⊙DAC =30°,⊙CD =12AD , ⊙AD 2=CD 2+AC 2,即AD 2=(12AD )2+32,⊙AD ⊙OA =OB =12AD C .【点睛】本题考查了三角形的外接圆与外心:三角形外接圆的圆心是三角形三条边垂直平分线的交点,叫做三角形的外心.也考查了等边三角形的性质、圆周角定理和含30度的直角三角形三边的关系.10.(2022·四川眉山·中考真题)如图是不倒翁的主视图,不倒翁的圆形脸恰好与帽子边沿PA ,PB 分别相切于点A ,B ,不倒翁的鼻尖正好是圆心O ,若∠=°,则APBOAB28∠的度数为()A.28︒B.50︒C.56︒D.62︒【答案】C【分析】连OB,由AO=OB得,⊙OAB=⊙OBA=28°,⊙AOB=180°-2⊙OAB=124°;因为P A、PB分别相切于点A、B,则⊙OAP=⊙OBP=90°,利用四边形内角和即可求出⊙APB.【详解】连接OB,⊙OA=OB,⊙⊙OAB=⊙OBA=28°,⊙⊙AOB=124°,⊙P A、PB切⊙O于A、B,⊙OA⊙P A,OP⊙AB,⊙⊙OAP+⊙OBP=180°,⊙⊙APB+⊙AOB=180°;⊙⊙APB=56°.故选:C【点睛】本题考查切线的性质,三角形和四边形的内角和定理,切线长定理,等腰三角形的性质等知识,解题的关键是学会添加常用辅助线,构造等腰三角形解决问题.11.(2022·浙江湖州·中考真题)在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点.如图,在6×6的正方形网格图形ABCD中,M,N 分别是AB,BC上的格点,BM=4,BN=2.若点P是这个网格图形中的格点,连接PM,PN,则所有满足⊙MPN=45°的⊙PMN中,边PM的长的最大值是()B.6C.D.A.【答案】C【分析】根据同弧所对的圆周角等于所对圆心角的一半,过点M、N作以点O为圆心,⊙MON=90°的圆,则点P在所作的圆上,观察圆O所经过的格点,找出到点M距离最大的点即可求出.MN,以O 【详解】作线段MN中点Q,作MN的垂直平分线OQ,并使OQ=12为圆心,OM为半径作圆,如图,MN,所以OQ=MQ=NQ,因为OQ为MN垂直平分线且OQ=12⊙⊙OMQ=⊙ONQ=45°,⊙⊙MON=90°,所以弦MN所对的圆O的圆周角为45°,所以点P在圆O上,PM为圆O的弦,通过图像可知,当点P在P'位置时,恰好过格点且P M'经过圆心O,所以此时P M'最大,等于圆O的直径,⊙BM=4,BN=2,⊙MN==⊙MQ=OQ⊙OM=⊙'==C.P M OM2【点睛】此题考查了圆的相关知识,熟练掌握同弧所对的圆周角相等、直径是圆上最大的弦,会灵活用已知圆心角和弦作圆是解题的关键.12.(2022·四川遂宁·中考真题)如图,圆锥底面圆半径为7cm,高为24cm,则它侧面展开图的面积是()A .175π3cm 2B .175π2cm 2C .175πcm 2D .350πcm 2【答案】C【分析】先利用勾股定理计算出AC =25cm ,由于圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长,则可根据扇形的面积公式计算出圆锥的侧面积.【详解】解:在Rt AOC △中,25AC =cm ,⊙它侧面展开图的面积是127251752ππ⨯⨯⨯=cm 2.故选:C【点睛】本题考查了圆锥的计算,理解圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长是解题的关键. 13.(2022·陕西·中考真题)如图,ABC 内接于⊙,46O C ∠=︒,连接OA ,则OAB ∠=( )A .44︒B .45︒C .54︒D .67︒【答案】A【分析】连接OB ,由2⊙C =⊙AOB ,求出⊙AOB ,再根据OA =OB 即可求出⊙OAB .【详解】连接OB ,如图,⊙⊙C =46°,⊙⊙AOB =2⊙C =92°,⊙⊙OAB +⊙OBA =180°-92°=88°,⊙OA =OB ,⊙⊙OAB =⊙OBA ,⊙⊙OAB =⊙OBA =12×88°=44°,故选:A .【点睛】本题主要考查了圆周角定理,根据圆周角定理的出⊙AOB =2⊙C =92°是解答本题的关键.14.(2022·浙江宁波·中考真题)已知圆锥的底面半径为4cm ,母线长为6cm ,则圆锥的侧面积为( )A .236πcmB .224πcmC .216πcmD .212πcm 【答案】B【分析】利用圆锥侧面积计算公式计算即可:S rl π=侧;【详解】4624S rl πππ==⋅⋅=侧2cm ,故选B .【点睛】本题考查了圆锥侧面积的计算公式,比较简单,直接代入公式计算即可. 15.(2022·甘肃武威·中考真题)如图,一条公路(公路的宽度忽略不计)的转弯处是一段圆弧(AB ),点O 是这段弧所在圆的圆心,半径90m OA =,圆心角80AOB ∠=︒,则这段弯路(AB )的长度为( )A .20m πB .30m πC .40m πD .50m π【答案】C 【分析】根据题目中的数据和弧长公式,可以计算出这段弯路(AB )的长度.【详解】解:⊙半径OA =90m ,圆心角⊙AOB =80°,∴这段弯路(AB )的长度为:809040(m)180ππ⨯=,故选C 【点睛】本题考查了弧长的计算,解答本题的关键是明确弧长计算公式.180n r l π=16.(2022·浙江温州·中考真题)如图,,AB AC 是O 的两条弦,⊥OD AB 于点D ,OE AC ⊥于点E ,连结OB ,OC .若130DOE ∠=︒,则BOC ∠的度数为( )A .95︒B .100︒C .105︒D .130︒【答案】B 【分析】根据四边形的内角和等于360°计算可得⊙BAC =50°,再根据圆周角定理得到⊙BOC =2⊙BAC ,进而可以得到答案.【详解】解:⊙OD⊙AB,OE⊙AC,⊙⊙ADO=90°,⊙AEO=90°,⊙⊙DOE=130°,⊙⊙BAC=360°-90°-90°-130°=50°,⊙⊙BOC=2⊙BAC=100°,故选:B.【点睛】本题考查的是圆周角定理,在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.17.(2022·山东泰安·中考真题)如图,点I为的ABC内心,连接AI并延长交ABC 的外接圆于点D,点E为弦AC的中点,连接CD,EI,IC,当2IC=,AI CD=,6 ID=时,IE的长为()5A.5B.4.5C.4D.3.5【答案】C【分析】延长ID到M,使DM=ID,连接CM.想办法求出CM,证明IE是⊙ACM 的中位线即可解决问题.【详解】解:延长ID到M,使DM=ID,连接CM.⊙I是⊙ABC的内心,⊙⊙IAC=⊙IAB,⊙ICA=⊙ICB,⊙⊙DIC=⊙IAC+⊙ICA,⊙DCI=⊙BCD+⊙ICB,⊙⊙DIC=⊙DCI,⊙DI=DC=DM,⊙⊙ICM=90°,⊙CM,⊙AI=2CD=10,⊙AI=IM,⊙AE=EC,⊙IE是⊙ACM的中位线,CM=4,故选:C.⊙IE=12【点睛】本题考查三角形的内心、三角形的外接圆、三角形的中位线定理、直角三角形的判定、勾股定理等知识,解题的关键是学会添加常用辅助线,构造三角形中位线解决问题.18.(2022·浙江丽水·中考真题)某仿古墙上原有一个矩形的门洞,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接于矩形,如图.已知矩形的宽为2m ,高为,则改建后门洞的圆弧长是( )A .5πm 3B .8πm 3C .10πm 3D .5π+2m 3⎛⎫ ⎪⎝⎭【答案】C【分析】利用勾股定理先求得圆弧形的门洞的直径BC ,再利用矩形的性质证得COD ∆是等边三角形,得到60COD ∠=︒,进而求得门洞的圆弧所对的圆心角为36060300︒-︒=︒,利用弧长公式即可求解.【详解】如图,连接AD ,BC ,交于O 点,⊙90BDC ∠=︒ ,⊙BC 是直径,⊙4BC ===, ⊙四边形ABDC 是矩形,⊙122OC OD BC ===,⊙2CD=,⊙OC OD CD==,⊙COD∆是等边三角形,⊙60COD∠=︒,⊙门洞的圆弧所对的圆心角为36060300︒-︒=︒,⊙改建后门洞的圆弧长是11300300410221801803BCπππ︒⨯︒⨯⨯==︒︒(m),故选:C【点睛】本题考查了弧长公式,矩形的性质以及勾股定理的应用,从实际问题转化为数学模型是解题的关键.19.(2022·四川成都·中考真题)如图,正六边形ABCDEF内接于⊙O,若⊙O的周长等于6π,则正六边形的边长为()ABC.3D.【答案】C【分析】连接OB,OC,由⊙O的周长等于6π,可得⊙O的半径,又由圆的内接多边形的性质,即可求得答案.【详解】解:连接OB,OC,⊙⊙O 的周长等于6π, ⊙⊙O 的半径为:3, ⊙⊙BOC 61=⨯360°=60°, ⊙OB =OC ,⊙⊙OBC 是等边三角形,⊙BC =OB =3,⊙它的内接正六边形ABCDEF 的边长为3,故选:C .【点睛】此题考查了正多边形与圆的性质.此题难度适中,注意掌握数形结合思想的应用.20.(2022·四川凉山·中考真题)家具厂利用如图所示直径为1米的圆形材料加工成一种扇形家具部件,已知扇形的圆心角⊙BAC =90°,则扇形部件的面积为( )A .12π米2 B .14π米2C .18π米2D .116π米2【答案】C【分析】连接BC ,先根据圆周角定理可得BC 是O 的直径,从而可得1BC =米,再解直角三角形可得AB AC =【详解】解:如图,连接BC ,90BAC ∠=︒,BC ∴是O 的直径,1BC ∴=米,又AB AC =,45ABC ACB ∴∠=∠=︒,sin AB AC BC ABC ∴==⋅∠,则扇形部件的面积为290123608ππ⨯=(米2),故选:C .【点睛】本题考查了圆周角定理、解直角三角形、扇形的面积公式等知识点,熟练掌握圆周角定理和扇形的面积公式是解题关键. 二.填空题21.(2022·江苏宿迁·中考真题)如图,在正六边形ABCDEF 中,AB =6,点M 在边AF 上,且AM =2.若经过点M 的直线l 将正六边形面积平分,则直线l 被正六边形所截的线段长是_____.【答案】【分析】如图,连接AD ,CF ,交于点O ,作直线MO 交CD 于H ,过O 作OP ⊙AF 于P ,由正六边形是轴对称图形可得:,ABCO DEFO S S 四边形四边形 由正六边形是中心对称图形可得:,,AOMDOHMOFCHOSSSS,OM OH = 可得直线MH 平分正六边形的面积,O 为正六边形的中心,再利用直角三角形的性质可得答案.【详解】解:如图,连接AD ,CF ,交于点O ,作直线MO 交CD 于H ,过O 作OP ⊙AF 于P ,由正六边形是轴对称图形可得:,ABCO DEFO S S 四边形四边形 由正六边形是中心对称图形可得:,,AOMDOHMOFCHOSSSS,OM OH =⊙直线MH 平分正六边形的面积,O 为正六边形的中心,由正六边形的性质可得:AOF 为等边三角形,60,AFO 而6,AB =6,3,ABAF OF OA AP FP226333,OP2,AM则1,MP2213327,OM247.MHOM故答案为:【点睛】本题考查的是正多边形与圆的知识,掌握“正六边形既是轴对称图形也是中心对称图形”是解本题的关键.22.(2022·湖南衡阳·中考真题)如图,用一个半径为6 cm 的定滑轮拉动重物上升,滑轮旋转了120︒,假设绳索粗细不计,且与轮滑之间没有滑动,则重物上升了_________cm .(结果保留π)【答案】4π【分析】利用题意得到重物上升的高度为定滑轮中120°所对应的弧长,然后根据弧长公式计算即可.【详解】解:根据题意,重物的高度为12064180ππ⨯⨯=(cm ). 故答案为:4π.【点睛】本题考查了弧长公式:180n Rl π⋅⋅=(弧长为l ,圆心角度数为n ,圆的半径为R ).23.(2022·浙江杭州·中考真题)如图是以点O 为圆心,AB 为直径的圆形纸片,点C 在⊙O 上,将该圆形纸片沿直线CO 对折,点B 落在⊙O 上的点D 处(不与点A 重合),连接CB ,CD ,AD .设CD 与直径AB 交于点E .若AD =ED ,则⊙B =_________度;BCAD的值等于_________.【答案】36【分析】由等腰三角形的性质得出⊙DAE=⊙DEA,证出⊙BEC=⊙BCE,由折叠的性质得出⊙ECO=⊙BCO,设⊙ECO=⊙OCB=⊙B=x,证出⊙BCE=⊙ECO+⊙BCO=2x,⊙CEB=2x,由三角形内角和定理可得出答案;证明⊙CEO⊙⊙BEC,由相似三角形的性质得出CE BEEO CE=,设EO=x,EC=OC=OB=a,得出a2=x(x+a),求出OE=a,证明⊙BCE⊙⊙DAE,由相似三角形的性质得出BC ECAD AE=,则可得出答案.【详解】解:⊙AD=DE,⊙⊙DAE=⊙DEA,⊙⊙DEA=⊙BEC,⊙DAE=⊙BCE,⊙⊙BEC=⊙BCE,⊙将该圆形纸片沿直线CO对折,⊙⊙ECO=⊙BCO,又⊙OB=OC,⊙⊙OCB=⊙B,设⊙ECO=⊙OCB=⊙B=x,⊙⊙BCE=⊙ECO+⊙BCO=2x,⊙⊙CEB=2x,⊙⊙BEC+⊙BCE+⊙B=180°,⊙x+2x+2x=180°,⊙x=36°,⊙⊙B=36°;⊙⊙ECO=⊙B,⊙CEO=⊙CEB,⊙⊙CEO⊙⊙BEC,⊙CE BEEO CE=,⊙CE2=EO•BE,设EO=x,EC=OC=OB=a,⊙a2=x(x+a),解得,xa(负值舍去),⊙OEa,⊙AE=OA-OE=aa,⊙⊙AED=⊙BEC,⊙DAE=⊙BCE,⊙⊙BCE⊙⊙DAE,⊙BC ECAD AE=,⊙BCAD==36【点睛】本题是圆的综合题,考查了圆周角定理,折叠的性质,等腰三角形的判定与性质,三角形内角和定理,相似三角形的判定与性质,熟练掌握相似三角形的判定与性质是解题的关键.24.(2022·浙江湖州·中考真题)如图,已知AB是⊙O的弦,⊙AOB=120°,OC⊙AB,垂足为C,OC的延长线交⊙O于点D.若⊙APD是AD所对的圆周角,则⊙APD 的度数是______.【答案】30°##30度【分析】根据垂径定理得出⊙AOB=⊙BOD,进而求出⊙AOD=60°,再根据圆周角⊙AOD=30°.定理可得⊙APD=12【详解】⊙OC⊙AB,OD为直径,⊙BD AD,⊙⊙AOB=⊙BOD,⊙⊙AOB=120°,⊙⊙AOD=60°,⊙AOD=30°,⊙⊙APD=12故答案为:30°.【点睛】本题考查了圆周角定理、垂径定理等知识,掌握垂径定理是解答本题的关键.25.(2022·云南·中考真题)某中学开展劳动实习,学生到教具加工厂制作圆锥,他们制作的圆锥,母线长为30cm,底面圆的半径为10 cm,这种圆锥的侧面展开图的圆心角度数是_____. 【答案】120︒【分析】设这种圆锥的侧面展开图的圆心角度数为n ,30210180n =⨯⨯ππ,进行解答即可得.【详解】解: 设这种圆锥的侧面展开图的圆心角度数为n°,30210180n =⨯⨯ππ 120n =︒ 故答案为:120︒. 【点睛】本题考查了圆锥侧面展开图的圆心角,解题的关键是掌握扇形的弧长公式.26.(2022·浙江宁波·中考真题)如图,在⊙ABC 中,AC =2,BC =4,点O 在BC 上,以OB 为半径的圆与AC 相切于点A ,D 是BC 边上的动点,当⊙ACD 为直角三角形时,AD 的长为___________.【答案】32或65【分析】根据切线的性质定理,勾股定理,直角三角形的等面积法解答即可. 【详解】解:连接OA ,⊙当D 点与O 点重合时,⊙CAD 为90°,设圆的半径=r ,⊙OA =r ,OC =4-r ,⊙AC=4,在Rt⊙AOC中,根据勾股定理可得:r2+4=(4-r)2,解得:r=32,即AD=AO=32;⊙当⊙ADC=90°时,过点A作AD⊙BC于点D,⊙12AO•AC=12OC•AD,⊙AD=AO ACOC,⊙AO=32,AC=2,OC=4-r=52,⊙AD=65,综上所述,AD的长为32或65,故答案为:32或65.【点睛】本题主要考查了切线的性质和勾股定理,熟练掌握这些性质定理是解决本题的关键.27.(2022·四川自贡·中考真题)一块圆形玻璃镜面碎成了几块,其中一块如图所示,测得弦AB长20厘米,弓形高CD为2厘米,则镜面半径为____________厘米.【答案】26【分析】令圆O的半径为OB=r,则OC=r-2,根据勾股定理求出OC2+BC2=OB2,进而求出半径.【详解】解:如图,由题意,得OD垂直平分AB,⊙BC=10厘米,令圆O的半径为OB =r ,则OC =r -2,在Rt⊙BOC 中OC 2+BC 2=OB 2,⊙(r -2)2+102=r 2,解得r =26.故答案为:26.【点睛】本题考查垂径定理和勾股定理求线段长,熟练地掌握圆的基本性质是解决问题的关键.28.(2022·浙江温州·中考真题)若扇形的圆心角为120︒,半径为32,则它的弧长为___________. 【答案】π【分析】根据题目中的数据和弧长公式,可以计算出该扇形的弧长. 【详解】解:⊙扇形的圆心角为120°,半径为32,⊙它的弧长为:31202,180ππ⨯=故答案为:π【点睛】本题考查弧长的计算,解答本题的关键是明确弧长的计算公式.180n rl π=29.(2022·新疆·中考真题)如图,⊙O 的半径为2,点A ,B ,C 都在⊙O 上,若30B ∠=︒.则AC 的长为_____(结果用含有π的式子表示)【答案】23π【分析】利用同弧所对的圆心角是圆周角的2倍得到60AOC ∠=︒,再利用弧长公式求解即可.【详解】2AOC B ∠=∠,30B ∠=︒,60AOC ∴∠=︒, ⊙O 的半径为2,60221803AC ππ⨯∴==,故答案为:23π. 【点睛】本题考查了圆周角定理和弧长公式,即180n r l π=,熟练掌握知识点是解题的关键. 30.(2022·四川泸州·中考真题)如图,在Rt ABC △中,90C ∠=︒,6AC =,BC =半径为1的O 在Rt ABC △内平移(O 可以与该三角形的边相切),则点A 到O 上的点的距离的最大值为________.【答案】1【分析】设直线AO 交O 于M 点(M 在O 点右边),当O 与AB 、BC 相切时,AM 即为点A 到O 上的点的最大距离.【详解】设直线AO 交O 于M 点(M 在O 点右边),则点A 到O 上的点的距离的最大值为AM 的长度当O 与AB 、BC 相切时,AM 最长设切点分别为D 、F ,连接OB ,如图⊙90C ∠=︒,6AC =,BC =⊙tan AC BBC==AB ⊙60B ∠=︒⊙O 与AB 、BC 相切 ⊙1302OBD B ∠=∠=︒⊙O 的半径为1⊙1OD OM == ⊙BD⊙AD AB DB =-=⊙OA ⊙1AM OA OM =+=⊙点A 到O 上的点的距离的最大值为1.【点睛】本题考查切线的性质、特殊角度三角函数值、勾股定理,解题的关键是确定点A 到O 上的点的最大距离的图形.31.(2022·浙江嘉兴·中考真题)如图,在廓形AOB 中,点C ,D 在AB 上,将CD 沿弦CD 折叠后恰好与OA ,OB 相切于点E ,F .已知120AOB ∠=︒,6OA =,则EF 的度数为_______;折痕CD的长为_______.【答案】60°##60度【分析】根据对称性作O关于CD的对称点M,则点D、E、F、B都在以M为圆心,半径为6的圆上,再结合切线的性质和垂径定理求解即可.【详解】作O关于CD的对称点M,则ON=MN连接MD、ME、MF、MO,MO交CD于N⊙将CD沿弦CD折叠⊙点D、E、F、B都在以M为圆心,半径为6的圆上⊙将CD沿弦CD折叠后恰好与OA,OB相切于点E,F.⊙ME⊙OA,MF⊙OB⊙90∠=∠=︒MEO MFO⊙120∠=︒AOB⊙四边形MEOF中36060∠=︒-∠-∠-∠=︒EMF AOB MEO MFO即EF 的度数为60°;⊙90MEO MFO ∠=∠=︒,ME MF =⊙MEO MFO ≅(HL ) ⊙1302EMO FMO FME ∠=∠=∠=︒⊙6cos cos30ME OM EMO ===∠︒⊙MN =⊙MO ⊙DC⊙12DN CD == ⊙CD =故答案为:60°;【点睛】本题考查了折叠的性质、切线的性质、垂径定理、勾股定理;熟练掌握折叠的性质作出辅助线是解题的关键.三.解答题32.(2022·四川成都·中考真题)如图,在Rt ABC △中,90ACB ∠=︒,以BC 为直径作⊙O ,交AB 边于点D ,在CD 上取一点E ,使BE CD =,连接DE ,作射线CE 交AB 边于点F .(1)求证:A ACF ∠=∠;(2)若8AC =,4cos 5ACF ∠=,求BF 及DE 的长.【答案】(1)见解析(2)BF =5,4225DE = 【分析】(1)根据Rt ABC △中,90ACB ∠=︒,得到⊙A +⊙B =⊙ACF +⊙BCF =90°,根据BE CD =,得到⊙B =⊙BCF ,推出⊙A =⊙ACF ;(2)根据⊙B =⊙BCF ,⊙A =⊙ACF ,得到AF =CF ,BF =CF ,推出AF =BF =12 AB ,根据4cos cos 5AC ACF A AB ∠===,AC =8,得到AB =10,得到BF =5,根据6BC ,得到3sin 5BC A AB ==,连接CD ,根据BC 是⊙O 的直径,得到⊙BDC =90°,推出⊙B +⊙BCD =90°,推出⊙A =⊙BCD ,得到3sin 5BD BCD BC ∠==,推出185BD =,得到75DF BF BD =-=,根据⊙FDE =⊙BCE ,⊙B =⊙BCE ,得到⊙FDE =⊙B ,推出DE ⊙BC ,得到⊙FDE ⊙⊙FBC ,推出DE DF BC BF =,得到4225DE =. (1)解:⊙Rt ABC △中,90ACB ∠=︒,⊙⊙A +⊙B =⊙ACF +⊙BCF =90°,⊙BE CD =,⊙⊙B =⊙BCF ,⊙⊙A =⊙ACF ;(2)⊙⊙B =⊙BCF ,⊙A =⊙ACF⊙AF =CF ,BF =CF ,⊙AF =BF =12 AB , ⊙4cos cos 5AC ACF A AB ∠===,AC =8, ⊙AB =10,⊙BF =5,⊙6BC , ⊙3sin 5BC A AB ==, 连接CD ,⊙BC 是⊙O 的直径,⊙⊙BDC =90°,⊙⊙B +⊙BCD =90°,⊙⊙A =⊙BCD , ⊙3sin 5BD BCD BC ∠==, ⊙185BD =, ⊙75DF BF BD =-=,⊙⊙FDE =⊙BCE ,⊙B =⊙BCE ,⊙⊙FDE =⊙B ,⊙DE ⊙BC ,⊙⊙FDE ⊙⊙FBC , ⊙DE DF BC BF=, ⊙4225DE =.【点睛】本题主要考查了圆周角,解直角三角形,勾股定理,相似三角形,解决问题的关键是熟练掌握圆周角定理及推论,运用勾股定理和正弦余弦解直角三角形,相似三角形的判定和性质.33.(2022·山东滨州·中考真题)如图,已知AC为O的直径,直线P A与O相切于点A,直线PD经过O上的点B且CBD CAB∠=∠,连接OP交AB于点M.求证:(1)PD是O的切线;(2)2=⋅AM OM PM【答案】(1)见解析(2)见解析【分析】(1)连接OB,由等边对等角及直径所对的圆周角等于90°即可证明;(2)根据直线P A与O相切于点A,得到90∠=︒,根据余角的性质得到OAPOAM APM∠=∠,继而证明OAM APM,根据相似三角形的性质即可得到结论.(1)连接OB,OA OB OC==,OAB OBA OBC OCB∴∠=∠∠=∠,,AC为O的直径,∴∠=∠+∠,ABC OBA OBC∠=∠,CBD CAB∴∠=∠,OBA CBDCBD OBC OBD∴∠+∠=︒=∠,90∴PD是O的切线;(2)直线P A与O相切于点A,∴∠=︒,OAP90⊙PD是O的切线,∴∠=∠=∠=︒,AMO AMP OAP90∴∠+∠=∠+∠=︒,OAM PAM PAM APM90∴∠=∠,OAM APM∴,OAM APMAM OM∴=,PM AM∴2=⋅.AM OM PM【点睛】本题考查了切线的判定和性质,相似三角形的判定和性质,圆周角定理,等腰三角形的性质,熟练掌握知识点是解题的关键.34.(2022·四川泸州·中考真题)如图,点C在以AB为直径的O上,CD平分ACB∠交O于点D,交AB于点E,过点D作O的切线交CO的延长线于点F.(1)求证:FD AB∥;(2)若AC=BC=,求FD的长.【答案】(1)见解析(2)15 8【分析】(1)连接OD,由CD平分⊙ACB,可知AD BD=,得⊙AOD=⊙BOD=90°,由DF是切线可知⊙ODF=90°=⊙AOD,可证结论;(2)过C作CM⊙AB于M,已求出CM、BM、OM的值,再证明⊙DOF⊙⊙MCO,得CM OMOD FD,代入可求.(1)证明:连接OD,如图,⊙CD平分⊙ACB,⊙AD BD=,⊙⊙AOD=⊙BOD=90°,⊙DF是⊙O的切线,⊙⊙ODF=90°⊙⊙ODF=⊙BOD,⊙DF⊙AB.(2)解:过C作CM⊙AB于M,如图,⊙AB 是直径,⊙⊙ACB =90°,⊙AB 2222(25)(5)5BC . ⊙1122AB CM AC BC , 即11525522CM , ⊙CM =2, ⊙2222(5)21BM BC CM , ⊙OM =OB -BM =135122, ⊙DF ⊙AB , ⊙⊙OFD =⊙COM ,又⊙⊙ODF =⊙CMO =90°, ⊙⊙DOF ⊙⊙MCO , ⊙CM OM OD FD, 即32252FD , ⊙FD =158. 【点睛】本题考查了圆的圆心角、弦、弧关系定理、圆周角定理,切线的性质,相似三角形的判定与性质,勾股定理,解题的关键是熟练掌握这些定理,灵活运用相似三角形的性质求解.35.(2022·四川南充·中考真题)如图,AB 为O 的直径,点C 是O 上一点,点D 是O 外一点,BCD BAC ∠=∠,连接OD 交BC 于点E .(1)求证:CD 是O 的切线.(2)若4,sin 5CE OA BAC =∠=,求tan CEO ∠的值.【答案】(1)见解析;(2)3【分析】(1)连接OC ,根据圆周角定理得到⊙ACB =90°,根据OA =OC 推出⊙BCD =⊙ACO ,即可得到⊙BCD +⊙OCB =90°,由此得到结论;(2)过点O 作OF ⊙BC 于F ,设BC =4x ,则AB =5x ,OA =CE =2.5x ,BE =1.5x ,勾股定理求出AC ,根据OF ⊙AC ,得到1BF OB CF OA ==,证得OF 为⊙ABC 的中位线,求出OF 及EF ,即可求出tan CEO ∠的值.(1)证明:连接OC ,⊙AB 为O 的直径,⊙⊙ACB =90°,⊙⊙ACO +⊙OCB =90°,⊙OA =OC ,⊙⊙A =⊙ACO ,⊙BCD BAC ∠=∠,⊙⊙BCD =⊙ACO ,⊙⊙BCD +⊙OCB =90°,⊙OC ⊙CD ,⊙CD 是O 的切线.(2)解:过点O 作OF ⊙BC 于F , ⊙4,sin 5CE OA BAC =∠=,⊙设BC =4x ,则AB =5x ,OA =CE =2.5x ,⊙BE =BC -CE =1.5x ,⊙⊙C =90°,⊙AC 3x =,⊙OA =OB ,OF ⊙AC , ⊙1BF OB CF OA ==, ⊙CF =BF =2x ,EF =CE -CF =0.5x ,⊙OF 为⊙ABC 的中位线,⊙OF =1 1.52AC x =,⊙tan CEO ∠= 1.530.5OF x EF x ==.【点睛】此题考查了圆周角定理,证明直线是圆的切线,锐角三角函数,三角形中位线的判定与性质,平行线分线段成比例,正确引出辅助线是解题的关键. 36.(2022·江苏扬州·中考真题)如图,AB 为O 的弦,OC OA ⊥交AB 于点P ,交过点B 的直线于点C ,且CB CP =.(1)试判断直线BC 与O 的位置关系,并说明理由;(2)若sin 8A OA ==,求CB 的长.【答案】(1)相切,证明见详解(2)6【分析】(1)连接OB ,根据等腰三角形的性质得出A OBA ∠=∠,CPB CBP ∠=∠,从而求出90AOC OBC ∠=∠=︒,再根据切线的判定得出结论;(2)分别作OM AB ⊥交AB 于点M ,ON AB ⊥交AB 于N ,根据sin 8A OA ==求出OP ,AP 的长,利用垂径定理求出AB 的长,进而求出BP 的长,然后在等腰三角形CPB 中求解CB 即可.(1)证明:连接OB ,如图所示:CP CB OA OB ==,,∴A OBA ∠=∠,CPB CBP ∠=∠,APO CPB ∠=∠,APO CBP ∴∠=∠,OC OA ⊥,即90AOP ︒=∠,90A APO OBA CBP OBC ∴∠+∠=︒=∠+∠=∠,OB BC ∴⊥, OB 为半径,经过点O ,∴直线BC 与O 的位置关系是相切.(2)分别作OM AB ⊥交AB 于点M ,ON AB ⊥交AB 于N ,如图所示:AM BM ∴=,CP CB AO CO =⊥,,A APO PCN CPN ∴∠+∠=∠+∠,PN BN =,PCN BCN ∠=∠A PCN BCN ∴∠=∠=∠sin A =,8OA =,sin OM OP A OA AP ∴===4OM AM OP AP ∴====,2AB AM ∴==,111()222PN BN PB AB AP ∴===-=⨯=sin sin BN A BCN CB ∴=∠==,6CB ∴===. 【点睛】本题考查了切线的证明,垂径定理的性质,等腰三角形,勾股定理,三角函数等知识点,熟练掌握相关知识并灵活应用是解决此题的关键,抓住直角三角形边的关系求解线段长度是解题的主线思路.37.(2022·江苏宿迁·中考真题)如图,在网格中,每个小正方形的边长均为1,每个小正方形的顶点称为格点,点A 、B 、C 、D 、M 均为格点.【操作探究】在数学活动课上,佳佳同学在如图⊙的网格中,用无刻度的直尺画了两条互相垂直的线段AB 、CD ,相交于点P 并给出部分说理过程,请你补充完整:解:在网格中取格点E ,构建两个直角三角形,分别是⊙ABC 和⊙CDE . 在Rt ⊙ABC 中,1tan 2BAC ∠=在Rt ⊙CDE 中, ,所以tan tan BAC DCE ∠∠=.所以⊙BAC =⊙DCE .因为⊙ACP + ⊙DCE =⊙ACB =90°,所以⊙ACP +⊙BAC =90°,所以⊙APC =90°,即AB ⊙CD .(1)【拓展应用】如图⊙是以格点O 为圆心,AB 为直径的圆,请你只用无刻度的直尺,在BM 上找出一点P ,使PM =AM ,写出作法,并给出证明:(2)【拓展应用】如图⊙是以格点O 为圆心的圆,请你只用无刻度的直尺,在弦AB 上找出一点P .使2AM =AP ·AB ,写出作法,不用证明.。
2018年全国各地中考数学压轴题汇编:几何综合(西北专版)(解析卷)

2018年全国各地中考数学压轴题汇编(西北专版)几何综合参考答案与试题解析一.选择题(共10小题)1.(2018•陕西)如图,在△ABC中,AC=8,∠ABC=60°,∠C=45°,AD⊥BC,垂足为D,∠ABC的平分线交AD于点E,则AE的长为()A.B.2C.D.3解:∵AD⊥BC,∴∠ADC=∠ADB=90°.在Rt△ADC中,AC=8,∠C=45°,∴AD=CD,∴AD=AC=4.在Rt△ADB中,AD=4,∠ABD=60°,∴BD=AD=.∵BE平分∠ABC,∴∠EBD=30°.在Rt△EBD中,BD=,∠EBD=30°,∴DE=BD=,∴AE=AD﹣DE=.故选:C.2.(2018•兰州)如图,矩形ABCD中,AB=3,BC=4,EF∥DF且BE与DF之间的距离为3,则AE的长是()A.B.C.D.解:如图所示:过点D作DG⊥BE,垂足为G,则GD=3.∵∠A=∠G,∠AEB=∠GED,AB=GD=3,∴△AEB≌△GED.∴AE=EG.设AE=EG=x,则ED=4﹣x,在Rt△DEG中,ED2=GE2+GD2,x2+32=(4﹣x)2,解得:x=.故选:C.3.(2018•陕西)如图,在菱形ABCD中.点E、F、G、H分别是边AB、BC、CD和DA 的中点,连接EF、FG、GH和HE.若EH=2EF,则下列结论正确的是()A.AB=EF B.AB=2EF C.AB=EF D.AB=EF解:连接AC、BD交于O,∵四边形ABCD是菱形,∴AC⊥BD,OA=OC,OB=OD,∵点E、F、G、H分别是边AB、BC、CD和DA的中点,∴EF=AC,EF∥AC,EH=BD,EH∥BD,∴四边形EFGH是矩形,∵EH=2EF,∴OB=2OA,∴AB==OA,∴AB=EF,故选:D.4.(2018•兰州)如图,将▱ABCD沿对角线BD折叠,使点A落在点E处,交BC于点F,若∠ABD=48°,∠CFD=40°,则∠E为()A.102°B.112°C.122°D.92°解:∵AD∥BC,∴∠ADB=∠DBC,由折叠可得∠ADB=∠BDF,∴∠DBC=∠BDF,又∵∠DFC=40°,∴∠DBC=∠BDF=∠ADB=20°,又∵∠ABD=48°,∴△ABD中,∠A=180°﹣20°﹣48°=112°,∴∠E=∠A=112°,故选:B.5.(2018•陕西)如图,△ABC是⊙O的内接三角形,AB=AC,∠BCA=65°,作CD∥AB,并与⊙O相交于点D,连接BD,则∠DBC的大小为()A.15°B.35°C.25°D.45°解:∵AB=AC、∠BCA=65°,∴∠CBA=∠BCA=65°,∠A=50°,∵CD∥AB,∴∠ACD=∠A=50°,又∵∠ABD=∠ACD=50°,∴∠DBC=∠CBA﹣∠ABD=15°,故选:A.6.(2018•白银)如图,点E是正方形ABCD的边DC上一点,把△ADE绕点A顺时针旋转90°到△ABF的位置,若四边形AECF的面积为25,DE=2,则AE的长为()A.5 B.C.7 D.解:∵把△ADE顺时针旋转△ABF的位置,∴四边形AECF的面积等于正方形ABCD的面积等于25,∴AD=DC=5,∵DE=2,∴Rt△ADE中,AE==.故选:D.7.(2018•青海)小桐把一副直角三角尺按如图所示的方式摆放在一起,其中∠E=90°,∠C=90°,∠A=45°,∠D=30°,则∠1+∠2等于()A.150°B.180°C.210°D.270°解:如图:∵∠1=∠D+∠DOA,∠2=∠E+∠EPB,∵∠DOA=∠COP,∠EPB=∠CPO,∴∠1+∠2=∠D+∠E+∠COP+∠CPO=∠D+∠E+180°﹣∠C=30°+90°+180°﹣90°=210°,故选:C.8.(2018•新疆)如图,矩形纸片ABCD中,AB=6cm,BC=8cm.现将其沿AE对折,使得点B落在边AD上的点B1处,折痕与边BC交于点E,则CE的长为()A.6cm B.4cm C.3cm D.2cm解:∵沿AE对折点B落在边AD上的点B1处,∴∠B=∠AB1E=90°,AB=AB1,又∵∠BAD=90°,∴四边形ABEB1是正方形,∴BE=AB=6cm,∴CE=BC﹣BE=8﹣6=2cm.故选:D.9.(2018•白银)如图,⊙A过点O(0,0),C(,0),D(0,1),点B是x轴下方⊙A上的一点,连接BO,BD,则∠OBD的度数是()A.15°B.30°C.45°D.60°解:连接DC,∵C(,0),D(0,1),∴∠DOC=90°,OD=1,OC=,∴∠DCO=30°,∴∠OBD=30°,故选:B.10.(2018•新疆)如图,点P是边长为1的菱形ABCD对角线AC上的一个动点,点M,N分别是AB,BC边上的中点,则MP+PN的最小值是()A.B.1 C.D.2解:如图,作点M关于AC的对称点M′,连接M′N交AC于P,此时MP+NP有最小值,最小值为M′N 的长.∵菱形ABCD关于AC对称,M是AB边上的中点,∴M′是AD的中点,又∵N是BC边上的中点,∴AM′∥BN,AM′=BN,∴四边形ABNM′是平行四边形,∴M′N=AB=1,∴MP+NP=M′N=1,即MP+NP的最小值为1,故选:B.二.填空题(共7小题)11.(2018•陕西)如图,在正五边形ABCDE中,AC与BE相交于点F,则∠AFE的度数为72°.解:∵五边形ABCDE是正五边形,∴∠EAB=∠ABC==108°,∵BA=BC,∴∠BAC=∠BCA=36°,同理∠ABE=36°,∴∠AFE=∠ABF+∠BAF=36°+36°=72°,故答案为:72°.12.(2018•兰州)如图,M、N是正方形ABCD的边CD上的两个动点,满足AM=BN,连接AC交BN于点E,连接DE交AM于点F,连接CF,若正方形的边长为6,则线段CF 的最小值是3﹣3.解:如图,在正方形ABCD中,AD=BC=CD,∠ADC=∠BCD,∠DCE=∠BCE,在Rt△ADM和Rt△BCN中,,∴Rt△ADM≌Rt△BCN(HL),∴∠DAM=∠CBN,在△DCE和△BCE中,,∴△DCE≌△BCE(SAS),∴∠CDE=∠CBE∴∠DCM=∠CDE,∵∠ADF+∠CDE=∠ADC=90°,∴∠DAM+∠ADF=90°,∴∠AFD=180°﹣90°=90°,取AD的中点O,连接OF、OC,则OF=DO=AD=3,在Rt△ODC中,OC==3根据三角形的三边关系,OF+CF>OC,∴当O、F、C三点共线时,CF的长度最小,最小值=OC﹣OF=3﹣3.故答案为:3﹣3.13.(2018•青海)如图,四边形ABCD与四边形EFGH位似,其位似中心为点O,且=,则=.解:∵四边形ABCD与四边形EFGH位似,其位似中心为点O,且=,∴=,则==.故答案为:.14.(2018•陕西)如图,点O是▱ABCD的对称中心,AD>AB,E、F是AB边上的点,且EF=AB;G、H是BC边上的点,且GH=BC,若S1,S2分别表示△EOF和△GOH的面积,则S1与S2之间的等量关系是=.解:∵==,==,∴S1=S△AOB,S2=S△BOC.∵点O是▱ABCD的对称中心,=S△BOC=S▱ABCD,∴S△AOB∴==.即S1与S2之间的等量关系是=.故答案为=.15.(2018•白银)如图,分别以等边三角形的每个顶点为圆心、以边长为半径,在另两个顶点间作一段圆弧,三段圆弧围成的曲边三角形称为勒洛三角形.若等边三角形的边长为a,则勒洛三角形的周长为πa.解:如图.∵△ABC是等边三角形,∴∠A=∠B=∠C=60°,AB=BC=CA=a,∴的长=的长=的长==,∴勒洛三角形的周长为×3=πa.故答案为πa.16.(2018•青海)如图,用一个半径为20cm,面积为150πcm2的扇形铁皮,制作一个无底的圆锥(不计接头损耗),则圆锥的底面半径r为7.5cm.解:解:设铁皮扇形的半径和弧长分别为R、l,圆锥形容器底面半径为r,则由题意得R=20,由Rl=150π得l=15π;由2πr=15π得r=7.5cm.故答案是:7.5cm.17.(2018•新疆)如图,△ABC是⊙O的内接正三角形,⊙O的半径为2,则图中阴影部分的面积是.解:∵△ABC是等边三角形,∴∠C=60°,根据圆周角定理可得∠AOB=2∠C=120°,∴阴影部分的面积是=π,故答案为:三.解答题(共15小题)18.(2018•陕西)如图,已知:在正方形ABCD中,M是BC边上一定点,连接AM.请用尺规作图法,在AM上作一点P,使△DPA∽△ABM.(不写作法,保留作图痕迹)解:如图所示,点P即为所求:∵DP⊥AM,∴∠APD=∠ABM=90°,∵∠BAM+∠PAD=90°,∠PAD+∠ADP=90°,∴∠BAM=∠ADP,∴△DPA∽△ABM.19.(2018•宁夏)已知:AB为⊙O的直径,延长AB到点P,过点P作圆O的切线,切点为C,连接AC,且AC=CP.(1)求∠P的度数;(2)若点D是弧AB的中点,连接CD交AB于点E,且DE•DC=20,求⊙O的面积.(π取3.14)解:(1)连接OC,∵PC为⊙O的切线,∴∠OCP=90°,即∠2+∠P=90°,∵OA=OC,∴∠CAO=∠1,∵AC=CP,∴∠P=∠CAO,又∵∠2是△AOC的一个外角,∴∠2=2∠CAO=2∠P,∴2∠P+∠P=90°,∴∠P=30°;(2)连接AD,∵D为的中点,∴∠ACD=∠DAE,∴△ACD∽△EAD,∴=,即AD2=DC•DE,∵DC•DE=20,∴AD=2,∵=,∴AD=BD,∵AB是⊙O的直径,∴Rt△ADB为等腰直角三角形,∴AB=2,∴OA=AB=,=π•OA2=10π=31.4.∴S⊙O20.(2018•陕西)如图,在Rt△ABC中,∠ACB=90°,以斜边AB上的中线CD为直径作⊙O,分别与AC、BC交于点M、N.(1)过点N作⊙O的切线NE与AB相交于点E,求证:NE⊥AB;(2)连接MD,求证:MD=NB.证明:(1)连接ON,如图,∵CD为斜边AB上的中线,∴CD=AD=DB,∴∠1=∠B,∵OC=ON,∴∠1=∠2,∴∠2=∠B,∴ON∥DB,∵NE为切线,∴ON⊥NE,∴NE⊥AB;(2)连接DN,如图,∵CD为直径,∴∠CMD=∠CND=90°,而∠MCB=90°,∴四边形CMDN为矩形,∴DM=CN,∵DN⊥BC,∠1=∠B,∴CN=BN,∴MD=NB.21.(2018•宁夏)已知点E为正方形ABCD的边AD上一点,连接BE,过点C作CN⊥BE,垂足为M,交AB于点N.(1)求证:△ABE≌△BCN;(2)若N为AB的中点,求tan∠ABE.(1)证明:∵四边形ABCD为正方形∴AB=BC,∠A=∠CBN=90°,∠1+∠2=90°∵CM⊥BE,∴∠2+∠3=90°∴∠1=∠3在△ABE和△BCN中∴△ABE≌△BCN(ASA);(2)∵N为AB中点,∴BN=AB又∵△ABE≌△BCN,∴AE=BN=AB在Rt△ABE中,tan∠ABE═.22.(2018•兰州)如图,在△ABC中,过点C作CD∥AB,E是AC的中点,连接DE并延长,交AB于点F,交CB的延长线于点G,连接AD,CF.(1)求证:四边形AFCD是平行四边形.(2)若GB=3,BC=6,BF=,求AB的长.解:(1)∵E是AC的中点,∴AE=CE,∵AB∥CD,∴∠AFE=∠CDE,在△AEF和△CED中,∵,∴△AEF≌△CED(AAS),∴AF=CD,又AB∥CD,即AF∥CD,∴四边形AFCD是平行四边形;(2)∵AB∥CD,∴△GBF∽△GCD,∴=,即=,解得:CD=,∵四边形AFCD是平行四边形,∴AF=CD=,∴AB=AF+BF=+=6.23.(2018•白银)已知矩形ABCD中,E是AD边上的一个动点,点F,G,H分别是BC,BE,CE的中点.(1)求证:△BGF≌△FHC;(2)设AD=a,当四边形EGFH是正方形时,求矩形ABCD的面积.解:(1)∵点F,G,H分别是BC,BE,CE的中点,∴FH∥BE,FH=BE,FH=BG,∴∠CFH=∠CBG,∵BF=CF,∴△BGF≌△FHC,(2)当四边形EGFH是正方形时,可得:EF⊥GH且EF=GH,∵在△BEC中,点,H分别是BE,CE的中点,∴GH=,且GH∥BC,∴EF⊥BC,∵AD∥BC,AB⊥BC,∴AB=EF=GH=a,∴矩形ABCD的面积=.24.(2018•陕西)问题提出(1)如图①,在△ABC中,∠A=120°,AB=AC=5,则△ABC的外接圆半径R的值为5.问题探究(2)如图②,⊙O的半径为13,弦AB=24,M是AB的中点,P是⊙O上一动点,求PM 的最大值.问题解决(3)如图③所示,AB、AC、是某新区的三条规划路,其中AB=6km,AC=3km,∠BAC=60°,所对的圆心角为60°,新区管委会想在路边建物资总站点P,在AB,AC路边分别建物资分站点E、F,也就是,分别在、线段AB和AC上选取点P、E、F.由于总站工作人员每天都要将物资在各物资站点间按P→E→F→P的路径进行运输,因此,要在各物资站点之间规划道路PE、EF和FP.为了快捷、环保和节约成本.要使得线段PE、EF、FP 之和最短,试求PE+EF+FP的最小值.(各物资站点与所在道路之间的距离、路宽均忽略不计)解:(1)设O是△ABC的外接圆的圆心,∴OA=OB=OC,∵∠A=120°,AB=AC=5,∴△ABO是等边三角形,∴AB=OA=OB=5,(2)当PM⊥AB时,此时PM最大,连接OA,由垂径定理可知:AM=AB=12,∵OA=13,∴由勾股定理可知:OM=5,∴PM=OM+OP=18,(3)设连接AP,OP分别以AB、AC所在直线为对称轴,作出P关于AB的对称点为M,P关于AC的对称点为N,连接MN,交AB于点E,交AC于点F,连接PE、PF,∴AM=AP=AN,∵∠MAB=∠PAB,∠NAC=∠PAC,∴∠BAC=∠PAB+∠PAC=∠MAB+∠NAC=60°,∴∠MAN=120°∴M、P、N在以A为圆心,AP为半径的圆上,设AP=r,易求得:MN=r,∵PE=ME,PF=FN,∴PE+EF+PF=ME+EF+FN=MN=r,∴当AP最小时,PE+EF+PF可取得最小值,∵AP+OP≥OA,∴AP≥OA﹣OP,即点P在OA上时,AP可取得最小值,设AB的中点为Q,∴AQ=AC=3,∵∠BAC=60°,∴AQ=QC=AC=BQ=3,∴∠ABC=∠QCB=30°,∴∠ACB=90°,∴由勾股定理可知:BC=3,∵∠BOC=60°,OB=OC=3,∴△OBC是等边三角形,∴∠OBC=60°,∴∠ABO=90°∴由勾股定理可知:OA=3,∵OP=OB=3,∴AP=r=OA﹣OP=3﹣3,∴PE+EF+PF=MN=r=3﹣9∴PE+EF+PF的最小值为(3﹣9)km.25.(2018•兰州)如图,AB为⊙O的直径,C为⊙O上一点,D为BA延长线上一点,∠ACD=∠B.(1)求证:DC为⊙O的切线;(2)线段DF分别交AC,BC于点E,F且∠CEF=45°,⊙O的半径为5,sinB=,求CF 的长.(1)证明:连接OC,∵AB为⊙O的直径,∴∠ACB=∠BCO+∠OCA=90°,∵OB=OC,∴∠B=∠BCO,∵∠ACD=∠B,∴∠ACD=∠BCO,∴∠ACD+∠OCA=90°,即∠OCD=90°,∴DC为⊙O的切线;(2)解:Rt△ACB中,AB=10,sinB=,∴AC=6,BC=8,∵∠ACD=∠B,∠ADC=∠CDB,∴△CAD∽△BCD,∴,设AD=3x,CD=4x,Rt△OCD中,OC2+CD2=OD2,52+(4x)2=(5+3x)2,x=0(舍)或,∵∠CEF=45°,∠ACB=90°,∴CE=CF,设CF=a,∵∠CEF=∠ACD+∠CDE,∠CFE=∠B+∠BDF,∴∠CDE=∠BDF,∵∠ACD=∠B,∴△CED∽△BFD,∴,∴,a=,∴CF=.26.(2018•青海)如图,在平行四边形ABCD中,E为AB边上的中点,连接DE并延长,交CB的延长线于点F.(1)求证:AD=BF;(2)若平行四边形ABCD的面积为32,试求四边形EBCD的面积.解:(1)∵E是AB边上的中点,∴AE=BE.∵AD∥BC,∴∠ADE=∠F.在△ADE和△BFE中,∠ADE=∠F,∠DEA=∠FEB,AE=BE,∴△ADE≌△BFE.∴AD=BF.(2)过点D作DM⊥AB与M,则DM同时也是平行四边形ABCD的高.=•AB•DM=AB•DM=×32=8,∴S△AED=32﹣8=24.∴S四边形EBCD27.(2018•白银)如图,点O是△ABC的边AB上一点,⊙O与边AC相切于点E,与边BC,AB分别相交于点D,F,且DE=EF.(1)求证:∠C=90°;(2)当BC=3,sinA=时,求AF的长.解:(1)连接OE,BE,∵DE=EF,∴∴∠OBE=∠DBE∵OE=OB,∴∠OEB=∠OBE∴∠OEB=∠DBE,∴OE∥BC∵⊙O与边AC相切于点E,∴OE⊥AC∴BC⊥AC∴∠C=90°(2)在△ABC,∠C=90°,BC=3,sinA=∴AB=5,设⊙O的半径为r,则AO=5﹣r,在Rt△AOE中,sinA===∴r=∴AF=5﹣2×=28.(2018•青海)如图△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上一点,且AP=AC.(2)若PD=,求⊙O的直径.解:(1)证明:连接OA,∵∠B=60°,∴∠AOC=2∠B=120°,又∵OA=OC,∴∠OAC=∠OCA=30°,又∵AP=AC,∴∠P=∠ACP=30°,∴∠OAP=∠AOC﹣∠P=90°,∴OA⊥PA,∴PA是⊙O的切线.(2)在Rt△OAP中,∵∠P=30°,∴PO=2OA=OD+PD,又∵OA=OD,∴PD=OA,∵PD=,∴2OA=2PD=2.∴⊙O的直径为2.29.(2018•新疆)如图,▱ABCD的对角线AC,BD相交于点O.E,F是AC上的两点,并且AE=CF,连接DE,BF.(2)若BD=EF,连接EB,DF,判断四边形EBFD的形状,并说明理由.(1)证明:∵四边形ABCD是平行四边形,∴OA=OC,OB=OD,∵AE=CF,∴OE=OF,在△DEO和△BOF中,∴△DOE≌△BOF.(2)解:结论:四边形EBFD是矩形.理由:∵OD=OB,OE=OF,∴四边形EBFD是平行四边形,∵BD=EF,∴四边形EBFD是矩形.30.(2018•青海)请认真阅读下面的数学小探究系列,完成所提出的问题:(1)探究1:如图1,在等腰直角三角形ABC中,∠ACB=90°,BC=a,将边AB绕点B顺时针旋转90°得到线段BD,连接CD.求证:△BCD的面积为a2.(提示:过点D作BC 边上的高DE,可证△ABC≌△BDE)(2)探究2:如图2,在一般的Rt△ABC中,∠ACB=90°,BC=a,将边AB绕点B顺时针旋转90°得到线段BD,连接CD.请用含a的式子表示△BCD的面积,并说明理由.(3)探究3:如图3,在等腰三角形ABC中,AB=AC,BC=a,将边AB绕点B顺时针旋转90°得到线段BD,连接CD.试探究用含a的式子表示△BCD的面积,要有探究过程.解:(1)如图1,过点D作DE⊥CB交CB的延长线于E,∴∠BED=∠ACB=90°,由旋转知,AB=AD,∠ABD=90°,∴∠ABC+∠DBE=90°,∵∠A+∠ABC=90°,∴∠A=∠DBE,在△ABC和△BDE中,,∴△ABC≌△BDE(AAS)∴BC=DE=a.=BC•DE∵S△BCD=;∴S△BCD(2)△BCD的面积为.理由:如图2,过点D作BC的垂线,与BC的延长线交于点E.∴∠BED=∠ACB=90°,∵线段AB绕点B顺时针旋转90°得到线段BE,∴AB=BD,∠ABD=90°.∴∠ABC+∠DBE=90°.∵∠A+∠ABC=90°.∴∠A=∠DBE.在△ABC和△BDE中,,∴△ABC≌△BDE(AAS)∴BC=DE=a.=BC•DE∵S△BCD=;∴S△BCD(3)如图3,过点A作AF⊥BC与F,过点D作DE⊥BC的延长线于点E,∴∠AFB=∠E=90°,BF=BC=a.∴∠FAB+∠ABF=90°.∵∠ABD=90°,∴∠ABF+∠DBE=90°,∴∠FAB=∠EBD.∵线段BD是由线段AB旋转得到的,∴AB=BD.在△AFB和△BED中,,∴△AFB≌△BED(AAS),∴BF=DE=a.∵S△BCD=BC•DE=•a•a=a2.∴△BCD 的面积为.31.(2018•宁夏)空间任意选定一点O,以点O为端点,作三条互相垂直的射线ox、oy、oz.这三条互相垂直的射线分别称作x轴、y轴、z轴,统称为坐标轴,它们的方向分别为ox(水平向前)、oy(水平向右)、oz(竖直向上)方向,这样的坐标系称为空间直角坐标系.将相邻三个面的面积记为S1、S2、S3,且S1<S2<S3的小长方体称为单位长方体,现将若干个单位长方体在空间直角坐标系内进行码放,要求码放时将单位长方体S1所在的面与x轴垂直,S2所在的面与y轴垂直,S3所在的面与z轴垂直,如图1所示.若将x轴方向表示的量称为几何体码放的排数,y轴方向表示的量称为几何体码放的列数,z轴方向表示的量称为几何体码放的层数;如图2是由若干个单位长方体在空间直角坐标内码放的一个几何体,其中这个几何体共码放了1排2列6层,用有序数组记作(1,2,6),如图3的几何体码放了2排3列4层,用有序数组记作(2,3,4).这样我们就可用每一个有序数组(x,y,z)表示一种几何体的码放方式.(1)如图4是由若干个单位长方体码放的一个几何体的三视图,则这种码放方式的有序数组为(2,3,2),组成这个几何体的单位长方体的个数为12个;(2)对有序数组性质的理解,下列说法正确的是①②⑤;(只填序号)①每一个有序数组(x,y,z)表示一种几何体的码放方式.②有序数组中x、y、z的乘积就表示几何体中单位长方体的个数.③有序数组不同,所表示几何体的单位长方体个数不同.④不同的有序数组所表示的几何体的体积不同.⑤有序数组中x、y、z每两个乘积的2倍可分别确定几何体表面上S1、S2、S3的个数.(3)为了进一步探究有序数组(x,y,z)的几何体的表面积公式S(x,y,z),某同学针对若干个单位长方体进行码放,制作了下列表格:几何体有序数组单位长方体的个数表面上面积为S1的个数表面上面积为S2的个数表面上面积为S3的个数表面积(1,1,1) 1 2 2 2 2S1+2S2+2S3(1,2,1) 2 4 2 4 4S1+2S2+4S3(3,1,1) 3 2 6 6 2S1+6S2+6S3(2,1,2) 4 4 8 4 4S1+8S2+4S3(1,5,1) 5 10 2 10 10S1+2S2+10S3(1,2,3) 6 12 6 4 12S1+6S2+4S3(1,1,7)7 14 14 2 14S1+14S2+2S3(2,2,2)8 8 8 8 8S1+8S2+8S3………………根据以上规律,请写出有序数组(x,y,z)的几何体表面积计算公式S(x,y,z);(用x、y、z、S1、S2、S3表示)(4)当S1=2,S2=3,S3=4时,对由12个单位长方体码放的几何体进行打包,为了节约外包装材料,对12个单位长方体码放的几何体表面积最小的规律进行探究,根据探究的结果请写出使几何体表面积最小的有序数组,并用几何体表面积公式求出这个最小面积.(缝隙不计)解:(1)这种码放方式的有序数组为(2,3,2),组成这个几何体的单位长方体的个数为2×3×2=12个,故答案为(2,3,2),12;(2)正确的有①②⑤.故答案为①②⑤;(3)S(x,y,z)=2yzS1+2xzS2+2xyS3=2(yzS1+xzS2+xyS3).(4)当S1=2,S2=3,S3=4时S(x,y,z)=2(yzS1+xzS2+xyS3)=2(2yz+3xz+4xy)欲使S(x,y,z)的值最小,不难看出x、y、z应满足x≤y≤z(x、y、z为正整数).在由12个单位长方体码放的几何体中,满足条件的有序数组为(1,1,12),(1,2,6),(1,3,4),(2,2,3).而S(1,1,12)=128,S(1,2,6)=100,S(1,3,4)=96,S(2,2,3)=92所以,由12个单位长方体码放的几何体表面积最小的有序数组为:(2,2,3),最小面积为S(2,2,3)=92.。
2018年四川省中考数学真题汇编解析:数与式、方程不等式

2018年全国各地中考数学真题汇编(四川专版)数与式、方程不等式参考答案与试题解析一.选择题(共10小题)1.(2018•绵阳)在一次酒会上,每两人都只碰一次杯,如果一共碰杯55次,则参加酒会的人数为()A.9人B.10人C.11人D.12人解:设参加酒会的人数为x人,根据题意得:x(x﹣1)=55,整理,得:x2﹣x﹣110=0,解得:x1=11,x2=﹣10(不合题意,舍去).答:参加酒会的人数为11人.故选:C.2.(2018•乐山)方程组==x+y﹣4的解是()A.B.C.D.解:由题可得,,消去x,可得2(4﹣y)=3y,解得y=2,把y=2代入2x=3y,可得x=3,∴方程组的解为.故选:D.3.(2018•乐山)估计+1的值,应在()A.1和2之间B.2和3之间C.3和4之间D.4和5之间解:∵≈2.236,∴+1≈3.236,故选:C.4.(2018•南充)不等式x+1≥2x﹣1的解集在数轴上表示为()A.B.C.D.解:移项,得:x﹣2x≥﹣1﹣1,合并同类项,得:﹣x≥﹣2,系数化为1,得:x≤2,将不等式的解集表示在数轴上如下:,故选:B.5.(2018•绵阳)将全体正奇数排成一个三角形数阵:13 57 9 1113 15 17 1923 25 27 29…按照以上排列的规律,第25行第20个数是()A.639 B.637 C.635 D.633解:根据三角形数阵可知,第n行奇数的个数为n个,则前n﹣1行奇数的总个数为1+2+3+…+(n﹣1)=个,则第n行(n≥3)从左向右的第m数为为第+m奇数,即:1+2[+m﹣1]=n2﹣n+2m﹣1n=25,m=20,这个数为639,故选:A.6.(2018•眉山)若α,β是一元二次方程3x2+2x﹣9=0的两根,则+的值是()A.B.﹣C.﹣D.解:∵α、β是一元二次方程3x2+2x﹣9=0的两根,∴α+β=﹣,αβ=﹣3,∴+====﹣.故选:C.7.(2018•乐山)已知实数a、b满足a+b=2,ab=,则a﹣b=()A.1 B.﹣C.±1 D.±解:∵a+b=2,ab=,∴(a+b)2=4=a2+2ab+b2,∴a2+b2=,∴(a﹣b)2=a2﹣2ab+b2=1,∴a﹣b=±1,故选:C.8.(2018•眉山)已知关于x的不等式组仅有三个整数解,则a的取值范围是()A.≤a<1 B.≤a≤1 C.<a≤1 D.a<1解:由x>2a﹣3,由2x>3(x﹣2)+5,解得:2a﹣3<x≤1,由关于x的不等式组仅有三个整数:解得﹣2≤2a﹣3<﹣1,解得≤a<1,故选:A.9.(2018•南充)已知=3,则代数式的值是()A.B.C.D.解:∵=3,∴=3,∴x﹣y=﹣3xy,则原式====,故选:D.10.(2018•眉山)我市某楼盘准备以每平方6000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望,为了加快资金周转,房地产开发商对价格经过连续两次下调后,决定以每平方4860元的均价开盘销售,则平均每次下调的百分率是()A.8% B.9% C.10% D.11%解:设平均每次下调的百分率为x,由题意,得6000(1﹣x)2=4860,解得:x1=0.1,x2=1.9(舍去).答:平均每次下调的百分率为10%.故选:C.二.填空题(共10小题)11.(2018•自贡)分解因式:ax2+2axy+ay2=a(x+y)2.解:原式=a(x2+2xy+y2)…(提取公因式)=a(x+y)2.…(完全平方公式)12.(2018•成都)已知a>0,S1=,S2=﹣S1﹣1,S3=,S4=﹣S3﹣1,S5=,…(即当n为大于1的奇数时,S n=;当n为大于1的偶数时,S n=﹣S n﹣1﹣1),按此规律,S2018=﹣.解:S1=,S2=﹣S1﹣1=﹣﹣1=﹣,S3==﹣,S4=﹣S3﹣1=﹣1=﹣,S5==﹣(a+1),S6=﹣S5﹣1=(a+1)﹣1=a,S7==,…,∴S n的值每6个一循环.∵2018=336×6+2,∴S2018=S2=﹣.故答案为:﹣.13.(2018•自贡)六一儿童节,某幼儿园用100元钱给小朋友买了甲、乙两种不同的玩具共30个,单价分别为2元和4元,则该幼儿园购买了甲、乙两种玩具分别为10、20个.解:设甲玩具购买x个,乙玩具购买y个,由题意,得,解得,甲玩具购买10个,乙玩具购买20个,故答案为:10,20.14.(2018•绵阳)已知a>b>0,且++=0,则=.解:由题意得:2b(b﹣a)+a(b﹣a)+3ab=0,整理得:2()2+﹣1=0,解得=,∵a>b>0,∴=,故答案为.15.(2018•南充)若2n(n≠0)是关于x的方程x2﹣2mx+2n=0的根,则m﹣n的值为.解:∵2n(n≠0)是关于x的方程x2﹣2mx+2n=0的根,∴4n2﹣4mn+2n=0,∴4n﹣4m+2=0,∴m﹣n=.故答案是:.16.(2018•达州)若关于x的分式方程=2a无解,则a的值为1或.解:去分母得:x﹣3a=2a(x﹣3),整理得:(1﹣2a)x=﹣3a,当1﹣2a=0时,方程无解,故a=;当1﹣2a≠0时,x==3时,分式方程无解,则a=1,故关于x的分式方程=2a无解,则a的值为:1或.故答案为:1或.17.(2018•自贡)观察下列图中所示的一系列图形,它们是按一定规律排列的,依照此规律,第2018个图形共有6055个○.解:观察图形可知:第1个图形共有:1+1×3,第2个图形共有:1+2×3,第3个图形共有:1+3×3,…,第n个图形共有:1+3n,∴第2018个图形共有1+3×2018=6055,故答案为:6055.18.(2018•眉山)已知关于x的分式方程﹣2=有一个正数解,则k的取值范围为k<6且k≠3.解;﹣2=,方程两边都乘以(x﹣3),得x=2(x﹣3)+k,解得x=6﹣k≠3,关于x的方程程﹣2=有一个正数解,∴x=6﹣k>0,k<6,且k≠3,∴k的取值范围是k<6且k≠3.故答案为:k<6且k≠3.19.(2018•达州)已知:m2﹣2m﹣1=0,n2+2n﹣1=0且mn≠1,则的值为3.解:由n2+2n﹣1=0可知n≠0.∴1+﹣=0.∴﹣﹣1=0,又m2﹣2m﹣1=0,且mn≠1,即m≠.∴m,是方程x2﹣2x﹣1=0的两根.∴m+=2.∴=m+1+=2+1=3,故答案为:3.20.(2018•遂宁)A,B两市相距200千米,甲车从A市到B市,乙车从B市到A市,两车同时出发,已知甲车速度比乙车速度快15千米/小时,且甲车比乙车早半小时到达目的地.若设乙车的速度是x千米/小时,则根据题意,可列方程﹣=.解:设乙车的速度是x千米/小时,则根据题意,可列方程:﹣=.故答案为:﹣=.三.解答题(共16小题).(2018•攀枝花)解方程:﹣=1.解:去分母得:3(x﹣3)﹣2(2x+1)=6,去括号得:3x﹣9﹣4x﹣2=6,移项得:﹣x=17,系数化为1得:x=﹣17.22.(2018•遂宁)计算:()﹣1+(﹣1)0+2sin45°+|﹣2|.解:原式=3+1+2×+2﹣=4++2﹣=6.23.(2018•自贡)解不等式组:,并在数轴上表示其解集.解:解不等式①,得:x≤2;解不等式②,得:x>1,∴不等式组的解集为:1<x≤2.将其表示在数轴上,如图所示.24.(2018•遂宁)先化简,再求值•+.(其中x=1,y=2)解:当x=1,y=2时,原式=•+=+==﹣325.(2018•攀枝花)攀枝花市出租车的收费标准是:起步价5元(即行驶距离不超过2千米都需付5元车费),超过2千米以后,每增加1千米,加收1.8元(不足1千米按1千米计).某同学从家乘出租车到学校,付了车费24.8元.求该同学的家到学校的距离在什么范围?解:设该同学的家到学校的距离是x千米,依题意:24.8﹣1.8<5+1.8(x﹣2)≤24.8,解得:12<x≤13.故该同学的家到学校的距离在大于12小于等于13的范围.26.(2018•遂宁)已知关于x的一元二次方程x2﹣2x+a=0的两实数根x1,x2满足x1x2+x1+x2>0,求a的取值范围.解:∵该一元二次方程有两个实数根,∴△=(﹣2)2﹣4×1×a=4﹣4a≥0,解得:a≤1,由韦达定理可得x1x2=a,x1+x2=2,∵x1x2+x1+x2>0,∴a+2>0,解得:a>﹣2,∴﹣2<a≤1.27.(2018•宜宾)我市经济技术开发区某智能手机有限公司接到生产300万部智能手机的订单,为了尽快交货,增开了一条生产线,实际每月生产能力比原计划提高了50%,结果比原计划提前5个月完成交货,求每月实际生产智能手机多少万部.解:设原计划每月生产智能手机x万部,则实际每月生产智能手机(1+50%)x万部,根据题意得:﹣=5,解得:x=20,经检验,x=20是原方程的解,且符合题意,∴(1+50%)x=30.答:每月实际生产智能手机30万部.28.(2018•泸州)某图书馆计划选购甲、乙两种图书.已知甲图书每本价格是乙图书每本价格的2.5倍,用800元单独购买甲图书比用800元单独购买乙图书要少24本.(1)甲、乙两种图书每本价格分别为多少元?(2)如果该图书馆计划购买乙图书的本数比购买甲图书本数的2倍多8本,且用于购买甲、乙两种图书的总经费不超过1060元,那么该图书馆最多可以购买多少本乙图书?解:(1)设乙图书每本价格为x元,则甲图书每本价格是2.5x元,根据题意可得:﹣=24,解得:x=20,经检验得:x=20是原方程的根,则2.5x=50,答:乙图书每本价格为20元,则甲图书每本价格是50元;(2)设购买甲图书本数为x,则购买乙图书的本数为:2x+8,故50x+20(2x+8)≤1060,解得:x≤10,故2x+8≤28,答:该图书馆最多可以购买28本乙图书.29.(2018•绵阳)有大小两种货车,3辆大货车与4辆小货车一次可以运货18吨,2辆大货车与6辆小货车一次可以运货17吨.(1)请问1辆大货车和1辆小货车一次可以分别运货多少吨?(2)目前有33吨货物需要运输,货运公司拟安排大小货车共计10辆,全部货物一次运完.其中每辆大货车一次运货花费130元,每辆小货车一次运货花费100元,请问货运公司应如何安排车辆最节省费用?解:(1)设1辆大货车和1辆小货车一次可以分别运货x吨和y吨,根据题意可得:,解得:,答:1辆大货车和1辆小货车一次可以分别运货4吨和1.5吨;(2)设货运公司拟安排大货车m辆,则安排小货车(10﹣m)辆,根据题意可得:4m+1.5(10﹣m)≥33,解得:m≥7.2,令m=8,大货车运费高于小货车,故用大货车少费用就小则安排方案有:大货车8辆,小货车1辆,30.(2018•内江)某商场计划购进A,B两种型号的手机,已知每部A型号手机的进价比每部B型号手机进价多500元,每部A型号手机的售价是2500元,每部B型号手机的售价是00元.(1)若商场用50000元共购进A型号手机10部,B型号手机20部,求A、B两种型号的手机每部进价各是多少元?(2)为了满足市场需求,商场决定用不超过7.5万元采购A、B两种型号的手机共40部,且A型号手机的数量不少于B型号手机数量的2倍.①该商场有哪几种进货方式?②该商场选择哪种进货方式,获得的利润最大?解:(1)设A、B两种型号的手机每部进价各是x元、y元,根据题意得:,解得:,答:A、B两种型号的手机每部进价各是2000元、1500元;(2)①设A种型号的手机购进a部,则B种型号的手机购进(40﹣a)部,根据题意得:,解得:≤a≤30,∵a为解集内的正整数,∴a=27,28,29,30,∴有4种购机方案:方案一:A种型号的手机购进27部,则B种型号的手机购进13部;方案二:A种型号的手机购进28部,则B种型号的手机购进12部;方案三:A种型号的手机购进29部,则B种型号的手机购进11部;方案四:A种型号的手机购进30部,则B种型号的手机购进10部;②设A种型号的手机购进a部时,获得的利润为w元.根据题意,得w=500a+600(40﹣a)=﹣100a+24000,∵﹣10<0,∴w随a的增大而减小,∴当a=27时,能获得最大利润.此时w=﹣100×27+24000=300(元).因此,购进A种型号的手机27部,购进B种型号的手机13部时,获利最大.答:购进A种型号的手机27部,购进B种型号的手机13部时获利最大.31.(2018•乐山)已知关于x的一元二次方程mx2+(1﹣5m)x﹣5=0(m≠0).(1)求证:无论m为任何非零实数,此方程总有两个实数根;(2)若抛物线y=mx2+(1﹣5m)x﹣5=0与x轴交于A(x1,0)、B(x2,0)两点,且|x1﹣x2|=6,求m的值;(3)若m>0,点P(a,b)与Q(a+n,b)在(2)中的抛物线上(点P、Q不重合),求代数式4a2﹣n2+8n的值.(1)证明:由题意可得:△=(1﹣5m)2﹣4m×(﹣5)=1+25m2﹣10m+20m=25m2+10m+1=(5m+1)2≥0,故无论m为任何非零实数,此方程总有两个实数根;(2)解:mx2+(1﹣5m)x﹣5=0,解得:x1=﹣,x2=5,由|x1﹣x2|=6,得|﹣﹣5|=6,解得:m=1或m=﹣;(3)解:由(2)得,当m>0时,m=1,此时抛物线为y=x2﹣4x﹣5,其对称轴为:x=2,由题已知,P,Q关于x=2对称,∴=2,即2a=4﹣n,∴4a2﹣n2+8n=(4﹣n)2﹣n2+8n=16.32.(2018•南充)已知关于x的一元二次方程x2﹣(2m﹣2)x+(m2﹣2m)=0.(1)求证:方程有两个不相等的实数根.(2)如果方程的两实数根为x1,x2,且x12+x22=10,求m的值.解:(1)由题意可知:△=(2m﹣2)2﹣4(m2﹣2m)=4>0,∴方程有两个不相等的实数根.(2)∵x1+x2=2m﹣2,x1x2=m2﹣2m,∴+=(x1+x2)2﹣2x1x2=10,∴(2m﹣2)2﹣2(m2﹣2m)=10,∴m2﹣2m﹣3=0,∴m=﹣1或m=333.(2018•广安)某车行去年A型车的销售总额为6万元,今年每辆车的售价比去年减少400元.若卖出的数量相同,销售总额将比去年减少20%.(1)求今年A型车每辆车的售价.(2)该车行计划新进一批A型车和B型车共45辆,已知A、B型车的进货价格分别是1100元、1400元,今年B型车的销售价格是2000元,要求B型车的进货数量不超过A 型车数量的两倍,应如何进货才能使这批车获得最大利润,最大利润是多少?解:(1)设今年A型车每辆售价为x元,则去年每辆售价为(x+400)元,根据题意得:=,解得:x=1600,经检验,x=1600是原分式方程的解,∴今年A型车每辆车售价为1600元.(2)设今年新进A型车a辆,销售利润为y元,则新进B型车(45﹣a)辆,根据题意得:y=(1600﹣1100)a+(2000﹣1400)(45﹣a)=﹣100a+27000.∵B型车的进货数量不超过A型车数量的两倍,∴45﹣a≤2a,解得:a≥15.∵﹣100<0,∴y随a的增大而减小,∴当a=15时,y取最大值,最大值=﹣100×15+27000=25500,此时45﹣a=30.答:购进15辆A型车、30辆B型车时销售利润最大,最大利润是25500元.34.(2018•资阳)为了美化市容市貌,政府决定将城区旁边一块162亩的荒地改建为湿地公园,规划公园分为绿化区和休闲区两部分.(1)若休闲区面积是绿化区面积的20%,求改建后的绿化区和休闲区各有多少亩?(2)经预算,绿化区的改建费用平均每亩35000元,休闲区的改建费用平均每亩25000元,政府计划投入资金不超过550万元,那么绿化区的面积最多可以达到多少亩?解:(1)设改建后的绿化区面积为x亩.由题意:x+20%•x=162,解得x=135,162﹣135=27,答:改建后的绿化区面积为135亩和休闲区面积有27亩.(2)设绿化区的面积为m亩.由题意:35000m+25000(162﹣m)≤5500000,解得m≤145,答:绿化区的面积最多可以达到145亩.35.(2018•自贡)阅读以下材料:对数的创始人是苏格兰数学家纳皮尔(J.Nplcr,1550﹣1617年),纳皮尔发明对数是在指数书写方式之前,直到18世纪瑞士数学家欧拉(Evlcr,1707﹣1783年)才发现指数与对数之间的联系.对数的定义:一般地,若a x=N(a>0,a≠1),那么x叫做以a为底N的对数,记作:x=log a N.比如指数式24=16可以转化为4=log6,对数式2=log525可以转化为52=25.我们根据对数的定义可得到对数的一个性质:log a(M•N)=log a M+log a N(a>0,a≠1,M>0,N>0);理由如下:设log a M=m,log a N=n,则M=a m,N=a n∴M•N=a m•a n=a m+n,由对数的定义得m+n=log a(M•N)又∵m+n=log a M+log a N∴log a(M•N)=log a M+log a N解决以下问题:(1)将指数43=64转化为对数式3=log464;(2)证明log a=log a M﹣log a N(a>0,a≠1,M>0,N>0)(3)拓展运用:计算log32+log36﹣log34=1.解:(1)由题意可得,指数式43=64写成对数式为:3=log 464,故答案为:3=log 464;(2)设log a M=m ,log a N=n ,则M=a m ,N=a n ,∴==a m ﹣n ,由对数的定义得m ﹣n=log a ,又∵m ﹣n=log a M ﹣log a N ,∴log a =log a M ﹣log a N (a >0,a ≠1,M >0,N >0);(3)log 32+log 36﹣log 34,=log 3(2×6÷4),=log 33,=1,故答案为:1.36.(2018•南充)某销售商准备在南充采购一批丝绸,经调查,用10000元采购A 型丝绸的件数与用8000元采购B 型丝绸的件数相等,一件A 型丝绸进价比一件B 型丝绸进价多100元.(1)求一件A 型、B 型丝绸的进价分别为多少元?(2)若销售商购进A 型、B 型丝绸共50件,其中A 型的件数不大于B 型的件数,且不少于16件,设购进A 型丝绸m 件.①求m 的取值范围.②已知A 型的售价是800元/件,销售成本为2n 元/件;B 型的售价为600元/件,销售成本为n 元/件.如果50≤n ≤150,求销售这批丝绸的最大利润w (元)与n (元)的函数关系式(每件销售利润=售价﹣进价﹣销售成本).解:(1)设B 型丝绸的进价为x 元,则A 型丝绸的进价为(x +100)元根据题意得:解得400=x经检验,400=x 为原方程的解 500100=+x答:一件A 型、B 型丝绸的进价分别为500元,400元.(2)①根据题意得:∴m的取值范围为:16≤m≤25②设销售这批丝绸的利润为y根据题意得:y=(800﹣500﹣2n)m+(600﹣400﹣n)•(50﹣m)=(100﹣n)m+10000﹣50n∵50≤n≤150∴(Ⅰ)当50≤n<100时,100﹣n>0m=25时,销售这批丝绸的最大利润w=25(100﹣n)+10000﹣50n=﹣75n+12500(Ⅱ)当n=100时,100﹣n=0,销售这批丝绸的最大利润w=5000(Ⅲ)当100<n≤150时,100﹣n<0当m=16时,销售这批丝绸的最大利润w=﹣66n+11600。
2018年四川省中考数学真题汇编解析:数与式、方程不等式

2018年全国各地中考数学真题汇编(四川专版)数与式、方程不等式参考答案与试题解析一.选择题(共10小题)1.(2018•绵阳)在一次酒会上,每两人都只碰一次杯,如果一共碰杯55次,则参加酒会的人数为()A.9人B.10人C.11人D.12人解:设参加酒会的人数为x人,根据题意得:x(x﹣1)=55,整理,得:x2﹣x﹣110=0,解得:x1=11,x2=﹣10(不合题意,舍去).答:参加酒会的人数为11人.故选:C.2.(2018•乐山)方程组==x+y﹣4的解是()A.B.C.D.解:由题可得,,消去x,可得2(4﹣y)=3y,解得y=2,把y=2代入2x=3y,可得x=3,∴方程组的解为.故选:D.3.(2018•乐山)估计+1的值,应在()A.1和2之间B.2和3之间C.3和4之间D.4和5之间解:∵≈2.236,∴+1≈3.236,故选:C.4.(2018•南充)不等式x+1≥2x﹣1的解集在数轴上表示为()A.B.C.D.解:移项,得:x﹣2x≥﹣1﹣1,合并同类项,得:﹣x≥﹣2,系数化为1,得:x≤2,将不等式的解集表示在数轴上如下:,故选:B.5.(2018•绵阳)将全体正奇数排成一个三角形数阵:13 57 9 1113 15 17 1923 25 27 29…按照以上排列的规律,第25行第20个数是()A.639 B.637 C.635 D.633解:根据三角形数阵可知,第n行奇数的个数为n个,则前n﹣1行奇数的总个数为1+2+3+…+(n﹣1)=个,则第n行(n≥3)从左向右的第m数为为第+m奇数,即:1+2[+m﹣1]=n2﹣n+2m﹣1n=25,m=20,这个数为639,故选:A.6.(2018•眉山)若α,β是一元二次方程3x2+2x﹣9=0的两根,则+的值是()A.B.﹣C.﹣D.解:∵α、β是一元二次方程3x2+2x﹣9=0的两根,∴α+β=﹣,αβ=﹣3,∴+====﹣.故选:C.7.(2018•乐山)已知实数a、b满足a+b=2,ab=,则a﹣b=()A.1 B.﹣C.±1 D.±解:∵a+b=2,ab=,∴(a+b)2=4=a2+2ab+b2,∴a2+b2=,∴(a﹣b)2=a2﹣2ab+b2=1,∴a﹣b=±1,故选:C.8.(2018•眉山)已知关于x的不等式组仅有三个整数解,则a的取值范围是()A.≤a<1 B.≤a≤1 C.<a≤1 D.a<1解:由x>2a﹣3,由2x>3(x﹣2)+5,解得:2a﹣3<x≤1,由关于x的不等式组仅有三个整数:解得﹣2≤2a﹣3<﹣1,解得≤a<1,故选:A.9.(2018•南充)已知=3,则代数式的值是( )A .B .C .D .解:∵=3,∴=3,∴x ﹣y=﹣3xy ,则原式====, 故选:D .10.(2018•眉山)我市某楼盘准备以每平方6000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望,为了加快资金周转,房地产开发商对价格经过连续两次下调后,决定以每平方4860元的均价开盘销售,则平均每次下调的百分率是( ) A .8% B .9%C .10%D .11%解:设平均每次下调的百分率为x ,由题意,得 6000(1﹣x )2=4860,解得:x 1=0.1,x 2=1.9(舍去). 答:平均每次下调的百分率为10%. 故选:C .二.填空题(共10小题)11.(2018•自贡)分解因式:ax 2+2axy +ay 2= a (x +y )2 . 解:原式=a (x 2+2xy +y 2)…(提取公因式) =a (x +y )2.…(完全平方公式)12.(2018•成都)已知a >0,S 1=,S 2=﹣S 1﹣1,S 3=,S 4=﹣S 3﹣1,S 5=,…(即当n 为大于1的奇数时,S n=;当n为大于1的偶数时,S n=﹣S n﹣1﹣1),按此规律,S2018=﹣.解:S1=,S2=﹣S1﹣1=﹣﹣1=﹣,S3==﹣,S4=﹣S3﹣1=﹣1=﹣,S5==﹣(a+1),S6=﹣S5﹣1=(a+1)﹣1=a,S7==,…,∴S n的值每6个一循环.∵2018=336×6+2,∴S2018=S2=﹣.故答案为:﹣.13.(2018•自贡)六一儿童节,某幼儿园用100元钱给小朋友买了甲、乙两种不同的玩具共30个,单价分别为2元和4元,则该幼儿园购买了甲、乙两种玩具分别为10、20个.解:设甲玩具购买x个,乙玩具购买y个,由题意,得,解得,甲玩具购买10个,乙玩具购买20个,故答案为:10,20.14.(2018•绵阳)已知a>b>0,且++=0,则=.解:由题意得:2b(b﹣a)+a(b﹣a)+3ab=0,整理得:2()2+﹣1=0,解得=,∵a>b>0,∴=,故答案为.15.(2018•南充)若2n(n≠0)是关于x的方程x2﹣2mx+2n=0的根,则m﹣n的值为.解:∵2n(n≠0)是关于x的方程x2﹣2mx+2n=0的根,∴4n2﹣4mn+2n=0,∴4n﹣4m+2=0,∴m﹣n=.故答案是:.16.(2018•达州)若关于x的分式方程=2a无解,则a的值为1或.解:去分母得:x﹣3a=2a(x﹣3),整理得:(1﹣2a)x=﹣3a,当1﹣2a=0时,方程无解,故a=;当1﹣2a≠0时,x==3时,分式方程无解,则a=1,故关于x的分式方程=2a无解,则a的值为:1或.故答案为:1或.17.(2018•自贡)观察下列图中所示的一系列图形,它们是按一定规律排列的,依照此规律,第2018个图形共有6055个○.解:观察图形可知:第1个图形共有:1+1×3,第2个图形共有:1+2×3,第3个图形共有:1+3×3,…,第n个图形共有:1+3n,∴第2018个图形共有1+3×2018=6055,故答案为:6055.18.(2018•眉山)已知关于x的分式方程﹣2=有一个正数解,则k的取值范围为k<6且k≠3.解;﹣2=,方程两边都乘以(x﹣3),得x=2(x﹣3)+k,解得x=6﹣k≠3,关于x的方程程﹣2=有一个正数解,∴x=6﹣k>0,k<6,且k≠3,∴k的取值范围是k<6且k≠3.故答案为:k<6且k≠3.19.(2018•达州)已知:m2﹣2m﹣1=0,n2+2n﹣1=0且mn≠1,则的值为3.解:由n2+2n﹣1=0可知n≠0.∴1+﹣=0.∴﹣﹣1=0,又m2﹣2m﹣1=0,且mn≠1,即m≠.∴m,是方程x2﹣2x﹣1=0的两根.∴m+=2.∴=m+1+=2+1=3,故答案为:3.20.(2018•遂宁)A,B两市相距200千米,甲车从A市到B市,乙车从B市到A市,两车同时出发,已知甲车速度比乙车速度快15千米/小时,且甲车比乙车早半小时到达目的地.若设乙车的速度是x千米/小时,则根据题意,可列方程﹣=.解:设乙车的速度是x千米/小时,则根据题意,可列方程:﹣=.故答案为:﹣=.三.解答题(共16小题).(2018•攀枝花)解方程:﹣=1.解:去分母得:3(x﹣3)﹣2(2x+1)=6,去括号得:3x﹣9﹣4x﹣2=6,移项得:﹣x=17,系数化为1得:x=﹣17.22.(2018•遂宁)计算:()﹣1+(﹣1)0+2sin45°+|﹣2|.解:原式=3+1+2×+2﹣=4++2﹣=6.23.(2018•自贡)解不等式组:,并在数轴上表示其解集.解:解不等式①,得:x≤2;解不等式②,得:x>1,∴不等式组的解集为:1<x≤2.将其表示在数轴上,如图所示.24.(2018•遂宁)先化简,再求值•+.(其中x=1,y=2)解:当x=1,y=2时,原式=•+=+==﹣325.(2018•攀枝花)攀枝花市出租车的收费标准是:起步价5元(即行驶距离不超过2千米都需付5元车费),超过2千米以后,每增加1千米,加收1.8元(不足1千米按1千米计).某同学从家乘出租车到学校,付了车费24.8元.求该同学的家到学校的距离在什么范围?解:设该同学的家到学校的距离是x千米,依题意:24.8﹣1.8<5+1.8(x﹣2)≤24.8,解得:12<x≤13.故该同学的家到学校的距离在大于12小于等于13的范围.26.(2018•遂宁)已知关于x的一元二次方程x2﹣2x+a=0的两实数根x1,x2满足x1x2+x1+x2>0,求a的取值范围.解:∵该一元二次方程有两个实数根,∴△=(﹣2)2﹣4×1×a=4﹣4a≥0,解得:a≤1,由韦达定理可得x1x2=a,x1+x2=2,∵x1x2+x1+x2>0,∴a+2>0,解得:a>﹣2,∴﹣2<a≤1.27.(2018•宜宾)我市经济技术开发区某智能手机有限公司接到生产300万部智能手机的订单,为了尽快交货,增开了一条生产线,实际每月生产能力比原计划提高了50%,结果比原计划提前5个月完成交货,求每月实际生产智能手机多少万部.解:设原计划每月生产智能手机x万部,则实际每月生产智能手机(1+50%)x万部,根据题意得:﹣=5,解得:x=20,经检验,x=20是原方程的解,且符合题意,∴(1+50%)x=30.答:每月实际生产智能手机30万部.28.(2018•泸州)某图书馆计划选购甲、乙两种图书.已知甲图书每本价格是乙图书每本价格的2.5倍,用800元单独购买甲图书比用800元单独购买乙图书要少24本.(1)甲、乙两种图书每本价格分别为多少元?(2)如果该图书馆计划购买乙图书的本数比购买甲图书本数的2倍多8本,且用于购买甲、乙两种图书的总经费不超过1060元,那么该图书馆最多可以购买多少本乙图书?解:(1)设乙图书每本价格为x元,则甲图书每本价格是2.5x元,根据题意可得:﹣=24,解得:x=20,经检验得:x=20是原方程的根,则2.5x=50,答:乙图书每本价格为20元,则甲图书每本价格是50元;(2)设购买甲图书本数为x,则购买乙图书的本数为:2x+8,故50x+20(2x+8)≤1060,解得:x≤10,故2x+8≤28,答:该图书馆最多可以购买28本乙图书.29.(2018•绵阳)有大小两种货车,3辆大货车与4辆小货车一次可以运货18吨,2辆大货车与6辆小货车一次可以运货17吨.(1)请问1辆大货车和1辆小货车一次可以分别运货多少吨?(2)目前有33吨货物需要运输,货运公司拟安排大小货车共计10辆,全部货物一次运完.其中每辆大货车一次运货花费130元,每辆小货车一次运货花费100元,请问货运公司应如何安排车辆最节省费用?解:(1)设1辆大货车和1辆小货车一次可以分别运货x吨和y吨,根据题意可得:,解得:,答:1辆大货车和1辆小货车一次可以分别运货4吨和1.5吨;(2)设货运公司拟安排大货车m辆,则安排小货车(10﹣m)辆,根据题意可得:4m+1.5(10﹣m)≥33,解得:m≥7.2,令m=8,大货车运费高于小货车,故用大货车少费用就小则安排方案有:大货车8辆,小货车1辆,30.(2018•内江)某商场计划购进A,B两种型号的手机,已知每部A型号手机的进价比每部B 型号手机进价多500元,每部A型号手机的售价是2500元,每部B型号手机的售价是00元.(1)若商场用50000元共购进A型号手机10部,B型号手机20部,求A、B两种型号的手机每部进价各是多少元?(2)为了满足市场需求,商场决定用不超过7.5万元采购A、B两种型号的手机共40部,且A 型号手机的数量不少于B型号手机数量的2倍.①该商场有哪几种进货方式?②该商场选择哪种进货方式,获得的利润最大?解:(1)设A、B两种型号的手机每部进价各是x元、y元,根据题意得:,解得:,答:A、B两种型号的手机每部进价各是2000元、1500元;(2)①设A种型号的手机购进a部,则B种型号的手机购进(40﹣a)部,根据题意得:,解得:≤a≤30,∵a为解集内的正整数,∴a=27,28,29,30,∴有4种购机方案:方案一:A种型号的手机购进27部,则B种型号的手机购进13部;方案二:A种型号的手机购进28部,则B种型号的手机购进12部;方案三:A种型号的手机购进29部,则B种型号的手机购进11部;方案四:A种型号的手机购进30部,则B种型号的手机购进10部;②设A种型号的手机购进a部时,获得的利润为w元.根据题意,得w=500a+600(40﹣a)=﹣100a+24000,∵﹣10<0,∴w随a的增大而减小,∴当a=27时,能获得最大利润.此时w=﹣100×27+24000=300(元).因此,购进A种型号的手机27部,购进B种型号的手机13部时,获利最大.答:购进A种型号的手机27部,购进B种型号的手机13部时获利最大.31.(2018•乐山)已知关于x的一元二次方程mx2+(1﹣5m)x﹣5=0(m≠0).(1)求证:无论m为任何非零实数,此方程总有两个实数根;(2)若抛物线y=mx2+(1﹣5m)x﹣5=0与x轴交于A(x1,0)、B(x2,0)两点,且|x1﹣x2|=6,求m的值;(3)若m>0,点P(a,b)与Q(a+n,b)在(2)中的抛物线上(点P、Q不重合),求代数式4a2﹣n2+8n的值.(1)证明:由题意可得:△=(1﹣5m)2﹣4m×(﹣5)=1+25m2﹣10m+20m=25m2+10m+1=(5m+1)2≥0,故无论m为任何非零实数,此方程总有两个实数根;(2)解:mx2+(1﹣5m)x﹣5=0,解得:x1=﹣,x2=5,由|x1﹣x2|=6,得|﹣﹣5|=6,解得:m=1或m=﹣;(3)解:由(2)得,当m>0时,m=1,此时抛物线为y=x2﹣4x﹣5,其对称轴为:x=2,由题已知,P,Q关于x=2对称,∴=2,即2a=4﹣n,∴4a2﹣n2+8n=(4﹣n)2﹣n2+8n=16.32.(2018•南充)已知关于x的一元二次方程x2﹣(2m﹣2)x+(m2﹣2m)=0.(1)求证:方程有两个不相等的实数根.(2)如果方程的两实数根为x1,x2,且x12+x22=10,求m的值.解:(1)由题意可知:△=(2m﹣2)2﹣4(m2﹣2m)=4>0,∴方程有两个不相等的实数根.(2)∵x1+x2=2m﹣2,x1x2=m2﹣2m,∴+=(x1+x2)2﹣2x1x2=10,∴(2m﹣2)2﹣2(m2﹣2m)=10,∴m2﹣2m﹣3=0,∴m=﹣1或m=333.(2018•广安)某车行去年A型车的销售总额为6万元,今年每辆车的售价比去年减少400元.若卖出的数量相同,销售总额将比去年减少20%.(1)求今年A型车每辆车的售价.(2)该车行计划新进一批A型车和B型车共45辆,已知A、B型车的进货价格分别是1100元、1400元,今年B型车的销售价格是2000元,要求B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获得最大利润,最大利润是多少?解:(1)设今年A型车每辆售价为x元,则去年每辆售价为(x+400)元,根据题意得:=,解得:x=1600,经检验,x=1600是原分式方程的解,∴今年A型车每辆车售价为1600元.(2)设今年新进A型车a辆,销售利润为y元,则新进B型车(45﹣a)辆,根据题意得:y=(1600﹣1100)a+(2000﹣1400)(45﹣a)=﹣100a+27000.∵B型车的进货数量不超过A型车数量的两倍,∴45﹣a≤2a,解得:a≥15.∵﹣100<0,∴y随a的增大而减小,∴当a=15时,y取最大值,最大值=﹣100×15+27000=25500,此时45﹣a=30.答:购进15辆A型车、30辆B型车时销售利润最大,最大利润是25500元.34.(2018•资阳)为了美化市容市貌,政府决定将城区旁边一块162亩的荒地改建为湿地公园,规划公园分为绿化区和休闲区两部分.(1)若休闲区面积是绿化区面积的20%,求改建后的绿化区和休闲区各有多少亩?(2)经预算,绿化区的改建费用平均每亩35000元,休闲区的改建费用平均每亩25000元,政府计划投入资金不超过550万元,那么绿化区的面积最多可以达到多少亩?解:(1)设改建后的绿化区面积为x亩.由题意:x+20%•x=162,解得x=135,162﹣135=27,答:改建后的绿化区面积为135亩和休闲区面积有27亩.(2)设绿化区的面积为m亩.由题意:35000m+25000(162﹣m)≤5500000,解得m≤145,答:绿化区的面积最多可以达到145亩.35.(2018•自贡)阅读以下材料:对数的创始人是苏格兰数学家纳皮尔(J.Nplcr,1550﹣1617年),纳皮尔发明对数是在指数书写方式之前,直到18世纪瑞士数学家欧拉(Evlcr,1707﹣1783年)才发现指数与对数之间的联系.对数的定义:一般地,若a x=N(a>0,a≠1),那么x叫做以a为底N的对数,记作:x=log a N.比如指数式24=16可以转化为4=log6,对数式2=log525可以转化为52=25.我们根据对数的定义可得到对数的一个性质:log a(M•N)=log a M+log a N(a>0,a≠1,M>0,N >0);理由如下:设log a M=m,log a N=n,则M=a m,N=a n∴M•N=a m•a n=a m+n,由对数的定义得m+n=log a(M•N)又∵m+n=log a M+log a N∴log a(M•N)=log a M+log a N解决以下问题:(1)将指数43=64转化为对数式3=log464;(2)证明log a=log a M﹣log a N(a>0,a≠1,M>0,N>0)(3)拓展运用:计算log32+log36﹣log34=1.解:(1)由题意可得,指数式43=64写成对数式为:3=log464,故答案为:3=log464;(2)设log a M=m ,log a N=n ,则M=a m ,N=a n ,∴==a m ﹣n ,由对数的定义得m ﹣n=log a ,又∵m ﹣n=log a M ﹣log a N ,∴log a =log a M ﹣log a N (a >0,a ≠1,M >0,N >0);(3)log 32+log 36﹣log 34,=log 3(2×6÷4),=log 33,=1,故答案为:1.36.(2018•南充)某销售商准备在南充采购一批丝绸,经调查,用10000元采购A 型丝绸的件数与用8000元采购B 型丝绸的件数相等,一件A 型丝绸进价比一件B 型丝绸进价多100元. (1)求一件A 型、B 型丝绸的进价分别为多少元?(2)若销售商购进A 型、B 型丝绸共50件,其中A 型的件数不大于B 型的件数,且不少于16件,设购进A 型丝绸m 件.①求m 的取值范围.②已知A 型的售价是800元/件,销售成本为2n 元/件;B 型的售价为600元/件,销售成本为n 元/件.如果50≤n ≤150,求销售这批丝绸的最大利润w (元)与n (元)的函数关系式(每件销售利润=售价﹣进价﹣销售成本).解:(1)设B 型丝绸的进价为x 元,则A 型丝绸的进价为(x +100)元根据题意得:解得400=x经检验,400=x 为原方程的解 500100=+x答:一件A 型、B 型丝绸的进价分别为500元,400元.(2)①根据题意得:∴m 的取值范围为:16≤m ≤25②设销售这批丝绸的利润为y根据题意得:y=(800﹣500﹣2n )m +(600﹣400﹣n )•(50﹣m )=(100﹣n)m+10000﹣50n∵50≤n≤150∴(Ⅰ)当50≤n<100时,100﹣n>0m=25时,销售这批丝绸的最大利润w=25(100﹣n)+10000﹣50n=﹣75n+12500(Ⅱ)当n=100时,100﹣n=0,销售这批丝绸的最大利润w=5000(Ⅲ)当100<n≤150时,100﹣n<0当m=16时,销售这批丝绸的最大利润w=﹣66n+11600。
【最新】全国各地中考数学专题《精品选择》(含答案解析)

全国各地中考数学选择真题汇编(含答案)一、选择题1.已知全集U =R ,集合A ={x |0≤x ≤2},B ={x |x 2-x >0},则图中的阴影部分表示的集合为( )A .{x |x ≤1或x >2}B .{x |x <0或1<x <2}C .{x |1≤x <2}D .{x |1<x ≤2}答案 A解析 B ={x |x 2-x >0}={x |x >1或x <0},由题意可知阴影部分对应的集合为∁U (A ∩B )∩(A ∪B ), 而A ∩B ={x |1<x ≤2},A ∪B =R , 即∁U (A ∩B )={x |x ≤1或x >2},所以∁U (A ∩B )∩(A ∪B )={x |x ≤1或x >2},故选A. 2.3(lg5-1)3-(lg2-1)2等于( ) A .lg 25 B .1 C .-1 D .lg 52答案 C 解析3(lg5-1)3-(lg2-1)2=lg5-1-(1-lg2)=lg5+lg2-2=lg(5×2)-2=1-2=-1,故选C.3.若关于x 的不等式(ax -1)(x +1)<0(a ∈R )的解集为{x |-1<x <1},则a 的值是( ) A .-2 B .-1 C .0 D .1答案 D解析 由题意得(ax -1)(x +1)=0的两根为-1和1, ∴1a =1,得a =1.4.已知数列{a n }是公比为2的等比数列,若a 4=16,则S 4等于( ) A .15B .30C .31D .63 答案 B解析 由等比数列的通项公式a n =a 1q n -1得a 4=a 1q 3,a 1=a 4q 3=168=2,所以S 4=2×(1-24)1-2=30,故选B.5.不等式组⎩⎪⎨⎪⎧y ≤-x +2,y ≤x -1,y ≥0所表示的平面区域的面积为( )A .1B.12C.13D.14 答案 D解析 作出不等式组对应的区域为△BCD ,由题意知x B =1,x C =2.由⎩⎪⎨⎪⎧y =-x +2,y =x -1,得y D =12, 所以S △BCD =12×(x C -x B )×12=14. 6.“x =1”是“x 2=1”成立的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件答案 A解析 由x =1⇒x 2=1知,充分性成立, 由x 2=1⇒x =±1⇏x =1知,必要性不成立. 所以“x =1”是“x 2=1”成立的充分不必要条件.7.已知F 1,F 2分别为双曲线x 2a 2-y 2b 2=1(a >0,b >0)的左、右焦点,P 为双曲线右支上一点,满足∠PF 2F 1=π2,连接PF 1交y 轴于点Q ,若|QF 2|=2c ,则双曲线的离心率是( ) A. 2 B. 3 C .1+ 2 D .1+ 3答案 C解析 ∵PF 2⊥x 轴,∴|PF 2|=b 2a ,∴|PF 1|=2a +b 2a =a 2+c 2a ,∴a 2+c 2a =22c , 即a 2+c 2=22ac ,∴e 2-22e +1=0,∴e =1+2或e =2-1(舍).8.某几何体的三视图如图所示,则该几何体的体积为( )A .1B .2C .3D .4 答案 B解析 由三视图可知,该几何体是底面为直角梯形(其上、下底分别为1和2,且高为2),高为2的四棱锥,所以该几何体的体积V =13×1+22×2×2=2,故选B.9.若偶函数f (x )在区间[0,4]上单调递减,则有( )A .f (-1)>f ⎝ ⎛⎭⎪⎫π3>f (-π)B .f ⎝ ⎛⎭⎪⎫π3>f (-1)>f (-π)C .f (-π)>f (-1)>f ⎝ ⎛⎭⎪⎫π3D .f (-1)>f (-π)>f ⎝ ⎛⎭⎪⎫π3答案 A解析 由f (x )是偶函数,则f (-1)=f (1),f (-π)=f (π),又f (x )在区间[0,4]上单调递减,∴f (1)>f ⎝ ⎛⎭⎪⎫π3>f (π),即f (-1)>f ⎝ ⎛⎭⎪⎫π3>f (-π).10.若cos2α=13,则sin2αtan α的值为( ) A.23B.13C.25D.12 答案 A解析 由题意得sin2αtan α=2sin αcos α·sin αcos α=2sin 2α=1-cos2α=23,故选A.11.在等差数列{a n }中,已知a 1=1,a 7=-23,若数列⎩⎨⎧⎭⎬⎫1a n +1a n 的前n 项和为-1455,则n 等于( ) A .14 B .15 C .16 D .18答案 A解析 a 7=a 1+6d =-23,由a 1=1,得d =-4, a n =a 1+(n -1)d =-4n +5,∵1a n +1a n =1d ×⎝ ⎛⎭⎪⎫1a n -1a n +1=-14⎝ ⎛⎭⎪⎫1a n -1a n +1, 设⎩⎨⎧⎭⎬⎫1a n +1a n 的前n 项和为S n , ∴S n =-14⎝ ⎛⎭⎪⎫1a 1-1a 2+1a 2-1a 3+…+1a n -1a n +1=-14⎝ ⎛⎭⎪⎫1a 1-1a n +1=-14⎝ ⎛⎭⎪⎫1-1-4n +1=-1455, 解得n =14.12.在△ABC 中,角A ,B ,C 对应的边为a ,b ,c ,若三边a ,b ,c 成等差数列,B =30°,且△ABC 的面积为32,则b 的值是( ) A .1+ 3 B .2+ 3 C .3+ 3 D.3+33答案 A解析 ∵S △ABC =12ac sin B =32,且B =30°, ∴ac =6.又b 2=a 2+c 2-2ac cos B =a 2+c 2-3ac =(a +c )2-(2+3)ac , 即b 2=(a +c )2-(2+3)×6, 又a +c =2b ,∴b 2=4b 2-(12+63), ∴3b 2=12+63,∴b 2=4+23,b =1+ 3.13.圆C 1:(x -m )2+(y +2)2=9与圆C 2:(x +1)2+(y -m )2=4内切,则m 的值为( ) A .-2 B .-1 C .-2或-1 D .2或1 答案 C解析 由题意得两个圆的圆心坐标分别为(m ,-2),(-1,m ),半径分别为3,2,由两圆内切的条件得(m +1)2+(-2-m )2=3-2,解得m =-2或m =-1,故选C.14.平面α,β及直线l 满足:α⊥β,l ∥α,则一定有( ) A .l ∥β B .l ⊂β C .l 与β相交D .以上三种情况都有可能 答案 D解析 当α⊥β,l ∥α时,如图所示,l 与β可能平行、相交或在β内,故选D.15.设函数f (x )=⎩⎨⎧1-|x -1|,x <2,12f (x -2),x ≥2,则方程16f (x )-lg|x |=0的实根个数为( )A .8B .9C .10D .11 答案 C解析 方程16f (x )-lg|x |=0的实根个数等价于函数f (x )与函数g (x )=lg|x |16的交点的个数,在平面直角坐标系内画出函数f (x )及g (x )=lg|x |16的图象,由图易得两函数图象在(-1,0)内有1个交点,在(1,10)内有9个交点,所以两函数图象共有10个交点,即方程16f (x )-lg|x |=0的实根的个数为10,故选C.16.若关于x 的不等式3-|x -a |>x 2在(-∞,0)上有解,则实数a 的取值范围是( )A.⎝ ⎛⎭⎪⎫-134,3 B.⎝ ⎛⎭⎪⎫-3,134 C.⎝ ⎛⎭⎪⎫-∞,-134 D .(3,+∞)答案 A解析 由3-|x -a |>x 2,得|x -a |<3-x 2,则有3-x 2>0,在平面直角坐标系中画出函数y =3-x 2和y =|x -a |的图象,如图所示.当函数y =|x -a |的图象在x =a 左侧的部分经过点(0,3)时,可得a =3; 当函数y =|x -a |的图象在x =a 右侧的部分和函数y =3-x 2的图象相切时,方程组⎩⎪⎨⎪⎧y =x -a ,y =3-x 2有唯一解, 即x 2+x -a -3=0有唯一解,即Δ=1-4(-a -3)=0, 解得a =-134,综上所述,原不等式若有解,则实数a 的取值范围是⎝ ⎛⎭⎪⎫-134,3,故选A.17.设A ,B 是椭圆C :x 24+y 2k =1长轴的两个端点,若C 上存在点P 满足∠APB =120°,则k 的取值范围是( ) A.⎝ ⎛⎦⎥⎤0,43∪[12,+∞) B.⎝ ⎛⎦⎥⎤0,23∪[6,+∞)C.⎝ ⎛⎦⎥⎤0,23∪[12,+∞) D.⎝ ⎛⎦⎥⎤0,43∪[6,+∞) 答案 A解析 ①当0<k <4时,易知当点P 位于短轴的端点M 时,∠APB 取最大值,要使椭圆C 上存在点P 满足∠APB =120°,则∠AMB ≥120°,即∠AMO ≥60°,tan ∠AMO =2k≥tan60°, 解得0<k ≤43;②当k >4,即椭圆的焦点在y 轴上时,同理可得k ≥12. 综上,k 的取值范围是⎝ ⎛⎦⎥⎤0,43∪[12,+∞),故选A. 18.已知函数f (x )=|x 2-2ax +b |(x ∈R ),给出下列命题: ①f (x )必是偶函数;②当f (0)=f (2)时,f (x )的图象关于直线x =1对称; ③若a 2-b ≤0,则f (x )在[a ,+∞)上是增函数; ④若a >0,在[-a ,a ]上f (x )有最大值|a 2-b |. 其中正确的命题序号是( ) A .③ B .①④ C .②④ D .①②③答案 A解析 对于①,当且仅当a =0时,函数f (x )=|x 2-2ax +b |为偶函数,①错误;对于②,当a =0,b =-2时,满足f (0)=2=f (2),此时函数图象不关于直线x =1对称,②错误;对于③,当a 2-b ≤0时,(-2a )2-4b =4(a 2-b )≤0,所以f (x )=x 2-2ax +b ,则f (x )在[a ,+∞)上是增函数,③正确;对于④,当a=1,b=4时,满足a>0,此时f(x)=|x2-2x+4|在[-1,1]上的最大值为f(-1)=|(-1)2-2×(-1)+4|=7≠|12-4|,④错误.综上所述,正确结论的序号为③,故选A.选择试题二一、选择题1.设集合M={-1,0,1},N为自然数集,则M∩N等于()A.{-1,0} B.{-1}C.{0,1} D.{1}答案C2.已知A(1,1,1),B(3,3,3),点P在x轴上,且|P A|=|PB|,则P点坐标为()A.(6,0,0) B.(6,0,1)C.(0,0,6) D.(0,6,0)答案A解析∵点P在x轴上,∴设P(x,0,0),又∵|P A|=|PB|,∴(x-1)2+(0-1)2+(0-1)2=(x-3)2+(0-3)2+(0-3)2,解得x=6.故选A.3.在等差数列{a n}中,a1=2,a3+a5=10,则a7等于()A.5B.6C.8D.10答案C解析因为在等差数列{a n}中,a1=2,a3+a5=10,所以2a4=a3+a5=10,解得a 4=5,所以公差d =a 4-a 14-1=1.所以a 7=a 1+6d =2+6=8.故选C.4.若幂函数f (x )的图象过点(2,8),则f (3)的值为() A .6B .9C .16D .27 答案D解析设幂函数f (x )=x α,其图象过点(2,8),可得f (2)=2α=8,解得α=3,即f (x )=x 3,可得f (3)=27. 故选D.5.在锐角三角形ABC 中,角A ,B 所对的边长分别为a ,b .若2a sin B =3b ,则A 等于() A.π3 B.π4 C.π6 D.π12答案A解析因为在△ABC 中,2a sin B =3b ,所以由正弦定理a sin A =bsin B ,得2sin A sin B =3sin B , 由角A 是锐角三角形的内角知sin B ≠0,所以sin A =32.又△ABC 为锐角三角形,所以A =π3. 6.已知cos α=-12,且α是钝角,则tan α等于() A.3B.33C .-3D .-33 答案 C解析 ∵cos α=-12,且α为钝角,∴sin α=1-cos 2α=32,∴tan α=sin αcos α=- 3.7.已知b ,c 是平面α内的两条直线,则“直线a ⊥α”是“直线a ⊥b ,直线a ⊥c ”的() A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件答案A解析依题意,由a ⊥α,b ⊂α,c ⊂α,得a ⊥b ,a ⊥c ; 反过来,由a ⊥b ,a ⊥c 不能得出a ⊥α.因为直线b ,c 可能是平面α内的两条平行直线.综上所述,“直线a ⊥α”是“直线a ⊥b ,直线a ⊥c ”的充分不必要条件,故选A.8.已知实数x ,y 满足不等式组⎩⎪⎨⎪⎧2x -y ≥0,x +2y ≥0,3x +y -5≤0,则2x +y 的最大值是()A .0B .3C .4D .5 答案C解析在平面直角坐标系中画出题中的不等式组表示的平面区域为以(0,0),(1,2),(2,-1)为顶点的三角形区域(如图阴影部分,含边界),由图易得当目标函数z =2x +y 经过平面区域内的点(1,2)时,z =2x +y取得最大值z max=2×1+2=4,故选C.9.下列命题为真命题的是()A.平行于同一平面的两条直线平行B.与某一平面成等角的两条直线平行C.垂直于同一平面的两条直线平行D.垂直于同一条直线的两条直线平行答案C解析如图所示,A1C1∥平面ABCD,B1D1∥平面ABCD,但是A1C1∩B1D1=O1,所以A错;A1O,C1O与平面ABCD所成的角相等,但是A1O∩C1O=O,所以B错;D1A1⊥A1A,B1A1⊥A1A,但是B1A1∩D1A1=A1,所以D错;由线面垂直的性质定理知C正确.10.如图是一个几何体的三视图,则这个几何体是()A.圆锥B.棱柱C.圆柱D.棱锥答案 C11.若关于x的不等式|a-x|+|x-3|≤4在R上有解,则实数a的取值范围是()A.[-7,+∞) B.[-7,7]C .[-1,+∞)D .[-1,7]答案D解析因为不等式|a -x |+|x -3|≤4在R 上有解, 所以4≥(|a -x |+|x -3|)min =|a -3|, 解得-1≤a ≤7,故选D.12.已知正项等比数列{a n }的前n 项和为S n ,若S 3=2a 3-a 1,则该数列的公比为() A .2B.12C .4D.14 答案A解析设正项等比数列{a n }的公比为q >0,因为S 3=2a 3-a 1,所以2a 1+a 2=a 3,所以a 1(2+q )=a 1q 2,化为q 2-q -2=0,q >0,解得q =2.故选A.13.如图,在直三棱柱ABC -A 1B 1C 1中,∠ACB =90°,CA =CB =CC 1=1,则直线A 1B 与平面BB 1C 1C 所成角的正弦值为( )A.22B.155C.33D.63答案C解析连接BC 1,由A 1C 1⊥平面BB 1C 1C ,得∠A 1BC 1=θ是直线A 1B 与平面BB 1C 1C 所成的角,在Rt △A 1BC 1中,A 1C 1=1,BC 1=2,BA 1=3,sin θ=13=33.14.已知F 1,F 2为双曲线Ax 2-By 2=1的焦点,其顶点是线段F 1F 2的三等分点,则其渐近线的方程为( ) A .y =±22x B .y =±24xC .y =±xD .y =±22x 或y =±24x答案D解析由题意可知,双曲线焦点在x 轴或y 轴上. ∵2a =13·2c ,∴c 2=9a 2. 又∵c 2=a 2+b 2, ∴b 2=8a 2, 故b a =22,a b =24.∴渐近线方程为y =±22x 或y =±24x .15.已知函数f (x )的定义域为R ,若f (x +1)与f (x -1)都是奇函数,则一定有() A .f (x )为偶函数 B .f (x )为奇函数 C .f (x +2)为偶函数 D .f (x +3)为奇函数 答案D解析因为函数f (x +1),f (x -1)均为奇函数, 所以f (x +1)=-f (-x +1),f (x -1)=-f (-x -1), 则f (x +3)=f (x +2+1)=-f [-(x +2)+1] =-f (-x -1)=f (x -1)=f (x -2+1) =-f [-(x -2)+1]=-f (-x +3), 所以函数f (x +3)为奇函数,故选D.16.存在函数f (x )满足:对于任意的x ∈R 都有f (x 2+2x )=|x +a |,则a 等于( )A .-1B .1C .2D .4 答案 B解析 由题意不妨令x 2+2x =0,则x =0或x =-2, 所以f (0)=|0+a |=|-2+a |,解得a =1,故选B.17.已知Rt △AOB 的面积为1,O 为直角顶点,设向量a =OA→|OA →|,b =OB →|OB→|,OP →=a +2b ,则P A →·PB→的最大值为( ) A .1B .2C .3D .4 答案 A解析 以O 为原点,OA 所在直线为x 轴,OB 所在直线为y 轴,建立平面直角坐标系(图略).设A (m ,0),B (0,n ),则a =(1,0), b =(0,1),OP→=a +2b =(1,2), P A →=(m -1,-2),PB→=(-1,n -2), 因为Rt △AOB 的面积为1,即有mn =2,则P A →·PB →=1-m -2(n -2)=5-(m +2n )≤5-22mn =5-2×2=1, 当且仅当m =2n =2时,取得最大值1.18.过双曲线x 2a 2-y 2b 2=1(a >0,b >0)的右焦点F 2向其一条渐近线作垂线l ,垂足为P ,l 与另一条渐近线交于Q 点,若QF 2→=3PF 2→,则双曲线的离心率为( )A .2B.3C.43D.233 答案 B解析 由题意得直线F 2Q 的方程为y =-ab (x -c ),与直线y =b a x 联立,消去x 得y =-a b ⎝ ⎛⎭⎪⎫ab y -c ,解得y P =abc .与直线y =-b a x 联立,消去x 得y =-a b ⎝ ⎛⎭⎪⎫-a b y -c ,解得y Q =abcb 2-a2. 因为QF 2→=3PF 2→, 所以y Q =3y P ,即abc b 2-a 2=3abc ,结合b 2=c 2-a 2化简得c 2=3a 2, 所以双曲线的离心率e =ca =3,故选B.。
2022年全国中考数学真题分类汇编专题16:圆(附答案解析)
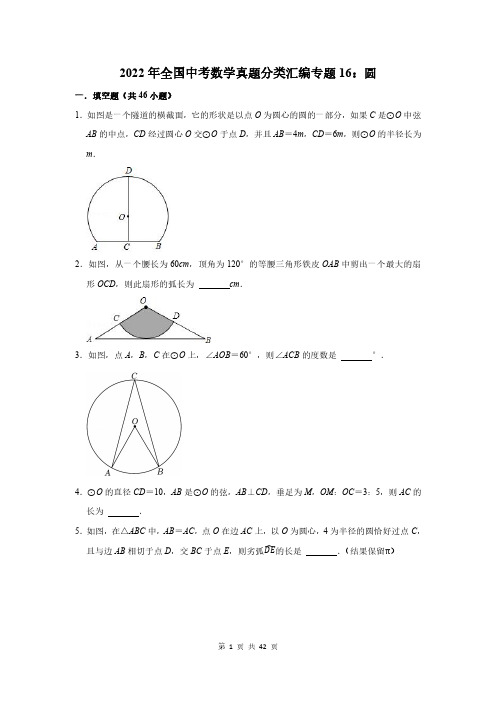
(结果保留π).
23.一个扇形的面积为 7πcm2,半径为 6cm,则此扇形的圆心角是
度.
24.如图,A、B、C 是⊙O 上的点,OC⊥AB,垂足为点 D,且 D 为 OC 的中点,若 OA=7,
则 BC 的长为
.
25.如图,正六边形 ABCDEF 和正五边形 AHIJK 内接于⊙O,且有公共顶点 A,则∠BOH
AC 于点 E,F.若 AB=2,∠BAD=60°,则图中阴影部分的面积为
.(结果不
取近似值)
第 10 页 共 42 页
第 11 页 共 42 页
2022 年全国中考数学真题分类汇编专题 16:圆
参考答案与试题解析
一.填空题(共 46 小题) 1.如图是一个隧道的横截面,它的形状是以点 O 为圆心的圆的一部分,如果 C 是⊙O 中弦
两点,AC=2,则 昀的长是
.
第 2 页 共 42 页
10.将等腰直角三角板与量角器按如图所示的方式摆放,使三角板的直角顶点与量角器的中
心 O 重合,且两条直角边分别与量角器边缘所在的弧交于 A、B 两点.若 OA=5 厘米,
则 t的长度为
厘米.(结果保留π)
11.如图,点 A.B,C 在⊙O 上,∠AOB=62°,则∠ACB=
中阴影部分的面积为(结果保留π)
.
31.如图,在⊙O 中,AB 是⊙O 的弦,⊙O 的半径为 3cm.C 为⊙O 上一点,∠ACB=60°,
则 AB 的长为
cm.
第 7 页 共 42 页
32.如图,△ABC 中,∠C=90°,AC=8,BC=6,O 为内心,过点 O 的直线分别与 AC、
AB 边相交于点 D、E.若 DE=CD+BE,则线段 CD 的长为
代数式及整式(46题)(原卷版)—2024年中考数学真题分类汇编(全国通用)

代数式及整式(46题)一、单选题1.(2024·辽宁·中考真题)下列计算正确的是( )A .2352a a a +=B .236a a a ×=C .()325a a =D .2(1)a a a a +=+2.(2024·江苏常州·中考真题)计算222a a -的结果是( )A .2B .2aC .23aD .42a 3.(2024·四川巴中·中考真题)下列运算正确的是( )A .33a b ab+=B .325a a a ×=C .()8240a a a a ÷=≠D .()222a b a b -=-4.(2024·四川雅安·中考真题)下列运算正确的是( )A .34a b ab +=B .()325a a =C .326a a a ×=D .54a a a ÷=5.(2024·四川资阳·中考真题)下列计算正确的是( )A .325a a a +=B .32a a a -=C .()325a a =D .523a a a ÷=6.(2024·湖北·中考真题)223x x ×的值是( )A .25xB .35xC .26xD .36x 7.(2024·湖北武汉·中考真题)下列计算正确的是( )A .236a a a ×=B .()1432a a =C .()2236a a =D .()2211a a +=+8.(2024·福建·中考真题)下列运算正确的是( )A .339a a a ×=B .422a a a ÷=C .()235a a =D .2222a a -=9.(2024·广东·中考真题)下列计算正确的是( )A .2510a a a ×=B .824a a a ÷=C .257a a a -+=D .()5210a a =10.(2024·云南·中考真题)按一定规律排列的代数式:2x ,23x ,34x ,45x ,56x ,L ,第n 个代数式是( )A .2n xB .()1n n x -C .1n nx +D .()1n n x +11.(2024·山东济宁·中考真题)如图,用大小相等的小正方形按照一定规律拼正方形.第一幅图有1个正方形,第二幅图有5个正方形,第三幅图有14个正方形……按照此规律,第六幅图中正方形的个数为( )A .90B .91C .92D .9312.(2024·甘肃兰州·中考真题)计算:22(1)2a a a --=( )A .aB .a -C .2aD .2a-13.(2024·四川成都·中考真题)下列计算正确的是( )A .()2233x x =B .336x y xy +=C .()222x y x y +=+D .()()2224x x x +-=-14.(2024·湖南长沙·中考真题)下列计算正确的是( )A .642x x x ÷=B =C .325()x x =D .222()x y x y +=+15.(2024·山东·中考真题)下列运算正确的是( )A .437a a a +=B .()2211a a -=-C .()2332a b a b =D .()2212a a a a +=+16.(2024·山东泰安·中考真题)下列运算正确的是( )A .22223x y xy x y-=-B .82224422x y x y x ÷=C .()()22x y x y x y ---=-D .()22346x y x y =17.(2024·四川·中考真题)下列计算正确的是( )A .()2222a a +=+B .2a a a +=C .23515a a a ×=D .()222a b a b +=+18.(2024·四川眉山·中考真题)如图,图1是北京国际数学家大会的会标,它取材于我国古代数学家赵爽的“弦图”,是由四个全等的直角三角形拼成.若图1中大正方形的面积为24,小正方形的面积为4,现将这四个直角三角形拼成图2,则图2中大正方形的面积为( )A .24B .36C .40D .4419.(2024·内蒙古呼伦贝尔·中考真题)下列计算正确的是( )A .()341226a a -=-B .253a a a -÷=C .111a a a a +-=D .()()2233a b a ab b a b +-+=+20.(2024·吉林长春·中考真题)下列运算一定正确的是( )A .236a a a ×=B .236a a a ×=C .()222ab a b =D .()235a a =21.(2024·青海·中考真题)计算1220x x -的结果是( )A .8xB .8x -C .8-D .2x 22.(2024·四川广安·中考真题)下列运算中,正确的是( )A .235a a a +=B .()32628a a -=-C .22(1)1a a -=-D .842a a a ÷=23.(2024·四川德阳·中考真题)下列计算正确的是( )A .236a a a ×=B .()a b a b--=-+C .()211a a a +=+D .222()a b a b +=+24.(2024·四川南充·中考真题)下列计算正确的是( )A .235a a a +=B .842a a a ÷=C .236a a a ×=D .()326327a a =25.(2024·四川泸州·中考真题)下列运算正确的是( )A .34325a a a +=B .236326a a a ×=C .()23624a a -=D .62344a a a ÷=26.(2024·四川达州·中考真题)下列计算正确的是( )A .235a a a +=B .()22224a a a +=++C .()3236928ab a b -=-D .1262a a a ÷=27.(2024·四川宜宾·中考真题)下列计算正确的是( )A .2a a a +=B .532a a -=C .2326x x x ×=D .32()()x x x-÷-=28.(2024·四川遂宁·中考真题)下列运算结果正确的是( )A .321a a -=B .236a a a ×=C .()44a a -=-D .()()2339a a a +-=-29.(2024·四川广安·中考真题)代数式3x -的意义可以是( )A .3-与x 的和B .3-与x 的差C .3-与x 的积D .3-与x 的商二、填空题30.(2024·四川雅安·中考真题)如图是1个纸杯和若干个叠放在一起的纸杯的示意图,在探究纸杯叠放在一起后的总高度H 与杯子数量n 的变化规律的活动中,我们可以获得以下数据(字母),请选用适当的字母表示H = .①杯子底部到杯沿底边的高h ;②杯口直径D ;③杯底直径d ;④杯沿高a .31.(2024·四川德阳·中考真题)若一个多项式加上234y xy +-,结果是2325xy y +-,则这个多项式为 .32.(2024·山东济宁·中考真题)已知2210a b -+=,则241b a +的值是 .33.(2024·四川广安·中考真题)若2230x x --=,则2241x x -+= .34.(2024·吉林长春·中考真题)单项式22a b -的次数是 .35.(2024·上海·中考真题)计算()()a b b a +-= .36.(2024·江苏苏州·中考真题)计算:32x x ×= .37.(2024·黑龙江大庆·中考真题)已知1a a +=,则221a a +的值是 .38.(2024·四川·中考真题)已知223x x +=,那么2245x x +-的值是 .39.(2024·山东泰安·中考真题)单项式23ab -的次数是 .40.(2024·四川乐山·中考真题)计算:2a a += .三、解答题41.(2024·江苏常州·中考真题)先化简,再求值:()()211x x x +-+,其中1x =.42.(2024·山东济宁·中考真题)先化简,再求值:(4)(2)(2)x y x x y x y -++-,其中12x =,2y =.43.(2024·重庆·中考真题)计算:(1)()()()312a a a a -+-+;(2)22241244x x x x -æö+÷ç÷--+èø.44.(2024·四川南充·中考真题)先化简,再求值:()23(2)3x x x x +-+÷,其中2 x =-.45.(2024·内蒙古通辽·中考真题)先化简,再求值:()()()()224+--+-a b a b a b a b ,其中2==a b .46.(2024·湖南长沙·中考真题)先化简,再求值:()()()2233m m m m m --++-,其中52m =.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018年中考数学真题汇编:圆(填空+选择46题)
一、选择题
1.已知的半径为,的半径为,圆心距,则与的位置关系是
()
A. 外离
B. 外切
C. 相交
D. 内切
【答案】C
2.
如图,为的直径,是的弦,,则的度数为()
A. B. C. D.
【答案】C
3.已知半径为5的⊙O是△ABC的外接圆,若∠ABC=25°,则劣弧的长为()
A. B. C. D.
【答案】C
4.
如图,在中,,的半径为3,则图中阴影部分的面积是()
A. B. C. D.
【答案】C
5.如图,AB是圆O的弦,OC⊥AB,交圆O于点C,连接OA,OB,BC,若∠ABC=20°,则∠AOB的度数是()
A.40°
B.50°
C.70°
D.80°
【答案】D
6.如图,蒙古包可近似看作由圆锥和圆柱组成,若用毛毡搭建一个底面圆面积为25πm2,圆柱高为3m,圆锥高为2m的蒙古包,则需要毛毡的面积是()
A.
B.40πm2
C.
D.55πm2
【答案】A
7.如图,从一块直径为的圆形铁皮上剪出一个圆心角为90°的扇形.则此扇形的面积为()
A. B. C. D.
【答案】A
8.用反证法证明时,假设结论“点在圆外”不成立,那么点与圆的位置关系只能是()
A. 点在圆内
B. 点在圆上
C. 点在圆心上
D. 点在圆上或圆内
【答案】D。
