第一节 定积分的概念和性质 定积分问题举例1
_定积分定义

( 3 ) 当 函 数 在 区 间 上 的 定 积 分 存 在 时 , f ( x ) [ a , b ]
称 在 区 间 上 可 积 . f ( x ) [ a , b ]
(4)函数 f ( x ) 在区间[a , b]上可积,则 f ( x ) 在区间[a , b]上一定有界。
三、存在定理
f ( x ) 在区间[a , b]上可积.
a x x x x b , 令 x x x ,任取 0 1 2 n i i i 1
[ x ] ,只要 max { x } 0 时 f ( i ) xi i i,x i 1 i
1 i n
b
n
总趋于确定的极限 I ,则称此极限 I 为函数 f ( x) 在区间
A ?
a b x
x b 所 围 成 .
o
解决步骤: 1) 分割.
在区间 [a,b]内插入若干个分点, a x0 x xn1 xn b, 1 x 2
把区间 [a, b] 分成n 个小区间 [ xi1, xi ] , 长度为 xi xi xi1;
y
在每个小区间 [x i 1, x i] 上任取一点 , i
f(x ) dx A 曲边梯形的面积 a
f(x ) dx A曲边梯形的面积 a
的负值
b
b
A1
A2
A3
A4
f ( x ) dx A A A A 1 2 3 4 a
b
几何意义:
它是介于 x 轴、函数 f (x)的图形及两条 直线 x a, x b之间的各部分面积的代 数和. 在x 轴上方的面积取正号; 在x 轴下方的面 积取负号.
高等数学 第5章 第一节 定积分的概念
定积分存在的两个充分条件:
定理1 设 f ( x) 在区间 [a, b]上连续, 则 f ( x)在区间 [a, b] 上可积. 定理2 设 f ( x)在区间 [a, b] 上有界, 且只有有限个间断点,则
f ( x)在区间 [a, b]上可积.
6
定积分的几何意义
y y f (x)
A
o xa xb x
lim
n
6n 2
3
10
1 i n
i
},
0,
n
A lim 0 i1
f ( i )xi
An
x xn1 nxn b
3
2. 变速直线运动的路程
设物体作直线运动,
已知速度 v v(t )是时间间隔 [T1 ,T2 ]上 的
连续函数, 且 v(t ) 0, 计算在这段时间内物体所经过的路程。
匀速直线运动:
路程=速度×时间.
(1) 分割
T1 t0 t1 ti1 ti tn T2 ,
v( i )
ti ti ti1
(i 1,2,, n)
(2) 近似代替
si v( i )t i
T1
i
T2
t t0 t1 t2 ti1 ti tn1 tn
(3) 求和 (4) 取极限
s
n i 1
s
i
n v(
i 1
i )t i
每 个小区间的长度 xi xi xi1 (i 1,2,n).
2
(2)近似代替
y Ai f (i )xi
(i 1,2,, n)
(3)求和
y f (x)
A1 A2
Ai
A
n i 1
Ai
n
第一节 定积分的概念和性质_1

∫a g( x)dx − ∫a f ( x)dx ≥ 0,
是 于
∫a f ( x)dx ≤ ∫a g( x)dx.
b
b
性质5的推论: 性质5的推论: (2) ) 证
∫a f ( x)dx ≤ ∫a
b
b
b
f ( x)dx. (a < b)
Q − f ( x) ≤ f ( x) ≤ f ( x) ,
3 当 数 ( ) 函 f (x) 在 间 a, b]上 定 分 在 , 区 [ 的 积 存 时
b
b
b
称 f (x)在 间 a, b]上 积 区 [ 可 .
存在定理
函 间 , 定理1 定理1 当 数 f (x)在区 [a, b]上连续时
称 f (x)在区 [a, b]上可积 间 .
[ 数 , 定理2 定理2 设函 f (x)在区间 a, b]上有界
y
y = f (x)
A=?
o
a b x
x = b所围 . 成
用矩形面积近似取代曲边梯形面积
y y
o
a
(四个小矩形) 四个小矩形)
b
x o
a
(九个小矩形) 九个小矩形)
b
x
显然,小矩形越多, 显然,小矩形越多,矩形总面积越接近 曲边梯形面积. 曲边梯形面积.
观察下列演示过程,注意当分割加细时, 观察下列演示过程,注意当分割加细时, 矩形面积和与曲边梯形面积的关系. 矩形面积和与曲边梯形面积的关系.
o a
x1
x i −1 i x i ξ
xn−1 b
x
为底, f 以[ xi−1, xi ]为底, (ξi ) 为高的小矩形面积为
Ai = f (ξi )∆xi
定积分的概念、性质

17
首页
上页
返回
下页
结束
铃
三、定积分的性质
•性 性质 质1 1 a b [ f ( x ) g ( x ) d ] a b f ( x x ) d a b g ( x x ) d . x 性 •性质 质2 2 a b k ( x ) d k f a b f ( x ) d x . x 性 •性质 质3 3 a b f ( x ) d a c f ( x ) x d c b f ( x ) x d . x •性 性质 质4 4 a b 1 d a b d b a . x x
上可积.
•定理2
如果函数f(x)在区间[a, b]上有界, 且只有有限个间断点,
则函数f(x)在区间[a, b]上可积.
9
首页
上页
返回
下页
结束
铃
二、定积分定义
定积分的定义
a b f ( x ) d l 0 i n 1 f ( i ) i x i . x m
例1 用定积分表示极限 lim1 n 1 i .
n n i1
n
解
lim 1 n
1
i
n
lim
1i 1
n n i1
n ni1
nn
xi
1
0 1xdx
0
i
i1 i
1x
nn
10
首页
上页
返回
下页
结束
铃
二、定积分定义
定积分的定义
a b f ( x ) d l 0 i n 1 f ( i ) i x i . x m
5-1 定积分的概念与性质

a x0 x1 x2
n
x n 1 x n b .
n
T1 t0 t1 t 2
T1
t n1 t n T2
T2 v(t )
2) 取近似. Ai f ( i )x i
2) 取近似. si v( i )t i
3) 求和. A A i f ( i )xi
b
(2) 定积分是一个数! 区间分法 被积函数 与 ξi的取法 无关 有关, (3) 定积分仅与 积分区间 积分变量记法 b b b a f ( x) d x f (t ) d t f (u ) d u
a
a
(三)可积条件
定理1 设f(x)在[a,b]上连续,则f(x)在[a,b]上可积.
4) 取极限. A lim f ( i )x i
0
i 1 n
i 1
4) 取极限.
不同点:背景不同
相同点:方法相同 数学形式相同
lim f ( i )x i
0
i 1
n
(二)定义
设函数 f ( x ) 在 [a , b] 上有界,在 [a , b] 中任意插入若干个分点 a x0 x1 x2 xn b , 把区间[a , b] 分成 n 个小区间
y
(1) xdx
0 5
o
y
(2)
a a
5
x
a 2 x 2 dx
a
o
a x
二、定积分的性质
约定
当a b时,
当a b时,
b
a b
f ( x )dx 0 f ( x )dx f ( x )dx
b
高数定积分概念与性质

2. 右矩形公式
ba n
( y0
y1
yn1)
ab f (x)dx y1x y2x ynx
ba n
(
y1
y2
yn
)
3. 梯形公式
ab f (x) dx
y
n1 i1
1[ 2
yi1
yi ]x
O a xi1xi
bx
b
n
a
1 2
i2xi
i2 n3
且只有有限个间断点
(证明略)
y
y x2
O
i 1x
n
n
i1
f
(i )xi
1 n3
n
i2
i1
1 n3
1 n(n 1)(2n 1) 注 6
注. 当n 较大时, 此值可作为
1 (1 1)(2 1) 6n n
01 x2 dx 的近似值
n k 0
nn 0
O12
nn
(n1) π π x
n
n1 1 x
n
思考: 如何用定积分表示下述极限
提示:
I lim 1 n sin k π π n π k 1 n n
lim 1 sin n π lim 1 sin (n 1) π
n n n n n
n
1
1
0 f (x) dx 0
1
1
即 0 x dx 0 ln (1 x) dx
作业
P235 *2 (2) ; 6 ; 7 ; 10 (3) , (4) ; 12(3) ; 13 (1) , (5)
定积分概念与性质(1)

b
[ f ( x) g( x)]dx
b
f ( x)dx
b
g( x)dx
a
a
a
b
推广
[ f1( x) f2 ( x) f2 ( x)]dx
a
b
b
b
f1( x)dx f2 ( x)dx fn ( x)dx
a
a
a
30
b
f ( x)dx
c
定理3. 如果函数F( x)是连续函数f ( x)
在区间[a, b]上的一个原函数,
b
则 f ( x)dx F(b) F(a)
a
证 已知F ( x)是 f ( x) 的一个原函数,
又
(
x)
x
a
f (t )dt 也是 f ( x)的一个原函数,
F ( x) ( x) C x [a,b]
7 0 定积分中值定理
设函数f ( x)在闭区间[a, b]上连续,
则在[a, b]上至少存在一个点,
b
使下列等式成立 f (x)dx f ( )(b a) a b a
证明: f ( x)在闭区间[a, b]连续,
一定存在最大值M与最小值m,
由7 0
m(b a)
2
x)
2 ( 2) 4
5
5
5 55
2
4
例4. 计算 dx 解 : 令x t 2 , 则dx 2tdt 0 1 x
当x 0时, t 0; 当x 4时, t 2;
4
2
dx 2t dt
0 1 x
1t
定积分概念与性质

第一节 定积分概念与性质教学目的:使学生了解定积分概念,掌握定积分的性质。
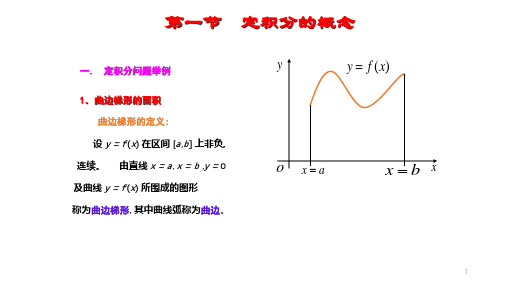
一、定积分问题举例1. 曲边梯形的面积曲边梯形: 设函数y =f (x )在区间[a , b ]上非负、连续. 由直线x =a 、x =b 、y =0及曲线y =f (x )所围成的图形称为曲边梯形, 其中曲线弧称为曲边. 求曲边梯形的面积的近似值:将曲边梯形分割成一些小的曲边梯形, 每个小曲边梯形都用一个等宽的小矩形代替, 每个小曲边梯形的面积都近似地等于小矩形的面积, 则所有小矩形面积的和就是曲边梯形面积的近似值. 具体方法是: 在区间[a , b ]中任意插入若干个分点a =x 0< x 1< x 2< × × ×< x n -1< x n =b ,把[a , b ]分成n 个小区间[x 0, x 1], [x 1, x 2], [x 2, x 3], × × × , [x n -1, x n ],它们的长度依次为D x 1= x 1-x 0 , D x 2= x 2-x 1 , × × × , D x n = x n -x n -1 .经过每一个分点作平行于y 轴的直线段, 把曲边梯形分成n 个窄曲边梯形. 在每个小区间 [x i -1, x i ]上任取一点x i , 以[x i -1, x i ]为底、f (x i )为高的窄矩形近似替代第i 个窄曲边梯形(i =1, 2, × × × , n ) , 把这样得到的n 个窄矩阵形面积之和作为所求曲边梯形面积A 的近似值, 即A »f (x 1)D x 1+ f (x 2)D x 2+× × ×+ f (x n )D x n ∑=∆=ni i i x f 1)(ξ.求曲边梯形的面积的精确值:显然, 分点越多、每个小曲边梯形越窄, 所求得的曲边梯形面积A 的近似值就越接近曲边梯形面积A 的精确值, 因此, 要求曲边梯形面积A 的精确值, 只需无限地增加分点, 使每个小曲边梯形的宽度趋于零. 记l=max{D x 1, D x 2,× × ×, D x n }, 于是, 上述增加分点, 使每个小曲边梯形的宽度趋于零, 相当于令l ®0. 所以曲边梯形的面积为∑=→∆=ni i i x f A 10)(lim ξλ.2. 变速直线运动的路程设物体作直线运动, 已知速度v =v (t )是时间间隔[T 1, T 2]上t 的连续函数, 且v (t )³0, 计算在这段时间内物体所经过的路程S . 求近似路程:我们把时间间隔[T 1, T 2]分成n 个小的时间间隔D t i , 在每个小的时间间隔D t i 内, 物体运动看成是均速的, 其速度近似为物体在时间间隔D t i 内某点x i 的速度v (t i ), 物体在时间间隔D t i 内 运动的距离近似为D S i = v (t i ) D t i . 把物体在每一小的时间间隔D t i 内 运动的距离加起来作为物体在时间间隔[T 1 , T 2]内所经过的路程S 的近似值. 具体做法是: 在时间间隔[T 1 , T 2]内任意插入若干个分点T 1=t 0< t 1< t 2<× × ×< t n -1< t n =T 2,把[T 1 , T 2]分成n 个小段[t 0, t 1], [t 1, t 2], × × ×, [t n -1, t n ] ,各小段时间的长依次为D t 1=t 1-t 0, D t 2=t 2-t 1,× × ×, D t n =t n -t n -1.相应地, 在各段时间内物体经过的路程依次为D S 1, D S 2, × × ×, D S n .在时间间隔[t i -1, t i ]上任取一个时刻t i (t i -1<t i < t i ), 以t i 时刻的速度v (t i )来代替[t i -1, t i ]上各个时刻的速度, 得到部分路程D S i 的近似值, 即D S i = v (t i ) D t i (i =1, 2, × × × , n ).于是这n 段部分路程的近似值之和就是所求变速直线运动路程S 的近似值, 即∑=∆≈ni i i t v S 1)(τ;求精确值:记l = max{D t 1, D t 2,× × ×, D t n }, 当l ®0时, 取上述和式的极限, 即得变速直线运动的路程∑=→∆=ni i i t v S 10)(lim τλ.设函数y =f (x )在区间[a , b ]上非负、连续. 求直线x =a 、x =b 、y =0 及曲线y =f (x )所围成的曲边梯形的面积.(1)用分点a =x 0<x 1<x 2< × × ×<x n -1<x n =b 把区间[a , b ]分成n 个小区间: [x 0, x 1], [x 1, x 2], [x 2, x 3], × × × , [x n -1, x n ], 记D x i =x i -x i -1 (i =1, 2, × × × , n ).(2)任取x i Î[x i -1, x i ], 以[x i -1, x i ]为底的小曲边梯形的面积可近似为i i x f ∆)(ξ (i =1, 2, × × × , n ); 所求曲边梯形面积A 的近似值为 ∑=∆≈ni i i x f A 1)(ξ.(3)记l =max{D x 1, D x 2,× × ×, D x n }, 所以曲边梯形面积的精确值为 ∑=→∆=ni i i x f A 10)(lim ξλ.设物体作直线运动, 已知速度v =v (t )是时间间隔[T 1, T 2]上t 的连续函数, 且v (t )³0, 计算在这段时间内物体所经过的路程S .(1)用分点T 1=t 0<t 1<t 2<× × ×<t n -1<t n =T 2把时间间隔[T 1 , T 2]分成n 个小时间段: [t 0, t 1], [t 1, t 2], × × ×, [t n -1, t n ] , 记D t i =t i -t i -1 (i =1, 2, × × × , n ).(2)任取t i Î[t i -1, t i ], 在时间段[t i -1, t i ]内物体所经过的路程可近似为v (t i )D t i(i =1, 2, × × × , n ); 所求路程S 的近似值为 ∑=∆≈ni i i t v S 1)(τ.(3)记l =max{D t 1, D t 2,× × ×, D t n }, 所求路程的精确值为 ∑=→∆=ni i i t v S 10)(lim τλ.二、定积分定义抛开上述问题的具体意义, 抓住它们在数量关系上共同的本质与特性加以概括, 就抽象出下述定积分的定义.定义 设函数f (x )在[a , b ]上有界, 在[a , b ]中任意插入若干个分点a =x 0< x 1< x 2< × × ×< x n -1< x n =b ,把区间[a , b ]分成n 个小区间[x 0, x 1], [x 1, x 2], × × ×, [x n -1, x n ] ,各小段区间的长依次为D x 1=x 1-x 0, D x 2=x 2-x 1,× × ×, D x n =x n -x n -1.在每个小区间[x i -1, x i ]上任取一个点x i (x i -1< x i < x i ), 作函数值f (x i )与小区间长度D x i 的乘积f (x i ) D x i (i =1, 2,× × ×, n ) , 并作出和∑=∆=ni i i x f S 1)(ξ.记l = max{D x 1, D x 2,× × ×, D x n }, 如果不论对[a , b ]怎样分法, 也不论在小区间[x i -1, x i ]上点x i 怎样取法, 只要当l ®0时, 和S 总趋于确定的极限I , 这时我们称这个极限I 为函数f (x )在区间[a , b ]上的定积分, 记作⎰ba dx x f )(, 即 ∑⎰=→∆=ni i i ba x f dx x f 10)(lim )(ξλ.其中f (x )叫做被积函数, f (x )dx 叫做被积表达式, x 叫做积分变量, a 叫做积分下限, b 叫做积分上限, [a , b ]叫做积分区间.定义 设函数f (x )在[a , b ]上有界, 用分点a =x 0<x 1<x 2< × × ×<x n -1<x n =b把[a , b ]分成n 个小区间: [x 0, x 1], [x 1, x 2], × × ×, [x n -1, x n ] , 记D x i =x i -x i -1(i =1, 2,× × ×, n ).任x i Î[x i -1, x i ] (i =1, 2,× × ×, n ), 作和∑=∆=ni i i x f S 1)(ξ.记l =max{D x 1, D x 2,× × ×, D x n }, 如果当l ®0时, 上述和式的极限存在, 且极限值与区间[a , b ]的分法和x i 的取法无关, 则称这个极限为函数f (x )在区间[a ,b ]上的定积分, 记作⎰badx x f )(,即 ∑⎰=→∆=ni i i bax f dx x f 1)(lim )(ξλ.根据定积分的定义, 曲边梯形的面积为⎰=ba dx x f A )(. 变速直线运动的路程为dt t v S TT )(21⎰=.说明:(1)定积分的值只与被积函数及积分区间有关, 而与积分变量的记法无关, 即⎰⎰⎰==ba ba ba du u f dt t f dx x f )()()(.(2)和∑=∆ni i i x f 1)(ξ通常称为f (x )的积分和.(3)如果函数f (x )在[a , b ]上的定积分存在, 我们就说f (x )在区间[a , b ]上可积. 函数f (x )在[a , b ]上满足什么条件时, f (x )在[a , b ]上可积呢? 定理1 设f (x )在区间[a , b ]上连续, 则f (x ) 在[a , b ]上可积.定理2 设f (x )在区间[a , b ]上有界, 且只有有限个间断点, 则f (x ) 在[a , b ]上可积. 定积分的几何意义:在区间[a , b ]上, 当f (x )³0时, 积分⎰ba dx x f )(在几何上表示由曲线y =f (x )、两条直线x =a 、x =b 与x 轴所围成的曲边梯形的面积; 当f (x )£0时, 由曲线y =f (x )、两条直线x =a 、x =b 与x 轴所围成的曲边梯形位于x 轴的下方, 定义分在几何上表示上述曲边梯形面积的负值;∑∑⎰--=∆--=∆==→=→ba ni i i n i i i badx x f x f x f dx x f )]([)]([lim )(lim )(1010ξξλλ.当f (x )既取得正值又取得负值时, 函数f (x )的图形某些部分在x 轴的上方, 而其它部分在x 轴的下方. 如果我们对面积赋以正负号, 在x 轴上方的图形面积赋以正号, 在x 轴下方的图形面积赋以负号, 则在一般情形下, 定积分⎰ba dx x f )(的几何意义为: 它是介于x 轴、函数f (x )的图形及两条直线x =a 、x =b 之间的各部分面积的代数和.用定积分的定义计算定积分:例1. 利用定义计算定积分dx x 210⎰.解 把区间[0, 1]分成n 等份, 分点为和小区间长度为n i x i =(i =1, 2,× × ×, n -1), n x i 1=∆(i =1, 2,× × ×, n ) .取n i i =ξ(i =1, 2,× × ×, n ), 作积分和 ∑∑∑===⋅=∆=∆ni ini i i ni i n ni x x f 121211)()(ξξ)12)(1(61113123++⋅==∑=n n n n i n ni )12)(11(61nn ++=.因为n 1=λ, 当l ®0时, n ®¥, 所以31)12)(11(61lim )(lim 10210=++=∆=∞→=→∑⎰n n x f dx x n n i i i ξλ.利定积分的几何意义求积分:例2. 用定积分的几何意义求⎰-10)1(dx x .解: 函数y =1-x 在区间[0, 1]上的定积分是以y =1-x 为曲边, 以区间[0, 1]为底的曲边梯形的面积. 因为以y =1-x 为曲边, 以区间[0, 1]为底的曲边梯形是一直角三角形, 其底边长及高均为1, 所以211121)1(10=⨯⨯=-⎰dx x .三、定积分的性质 两点规定:(1)当a =b 时, 0)(=⎰ba dx x f . (2)当a >b 时, ⎰⎰-=ab b a dx x f dx x f )()(.性质1 函数的和(差)的定积分等于它们的定积分的和(差) 即 ⎰⎰⎰±=±ba ba ba dx x g dx x f dx x g x f )()()]()([. 证明:⎰±b a dx x g x f )]()([∑=→∆±=ni i i i x g f 10)]()([lim ξξλ∑∑=→=→∆±∆=ni i i ni i i x g x f 1010)(lim )(lim ξξλλ⎰⎰±=ba ba dx x g dx x f )()(.性质2 被积函数的常数因子可以提到积分号外面 即 ⎰⎰=ba ba dx x f k dx x kf )()(.这是因为∑⎰=→∆=n i i i ba x kf dx x kf 10)(lim )(ξλ⎰∑=∆==→ba ni i i dx x f k x f k )()(lim 10ξλ.性质3 如果将积分区间分成两部分 则在整个区间上的定积分等于这两部分区间上定积分之和 即⎰⎰⎰+=bc ca ba dx x f dx x f dx x f )()()(.这个性质表明定积分对于积分区间具有可加性. 值得注意的是不论a ,b ,c 的相对位置如何总有等式 ⎰⎰⎰+=bc c a b a dx x f dx x f dx x f )()()( 成立. 例如, 当a <b <c 时, 由于 ⎰⎰⎰+=cb b ac a dx x f dx x f dx x f )()()(, 于是有⎰⎰⎰-=c b c a b a dx x f dx x f dx x f )()()(⎰⎰+=bc c a dx x f dx x f )()(. 性质4 如果在区间[a b ]上f (x )º1 则 a b dx dx ba ba -==⎰⎰1.性质5 如果在区间[a , b ]上 f (x )³0, 则 ⎰≥ba dx x f 0)((a <b ).推论1 如果在区间[a , b ]上 f (x )£ g (x ) 则 ⎰⎰≤ba ba dx x g dx x f )()((a <b ). 这是因为g (x )-f (x )³0, 从而⎰⎰⎰≥-=-b a ba b a dx x f x g dx x f dx x g 0)]()([)()(, 所以⎰⎰≤ba ba dx x g dx x f )()(.推论2 ⎰⎰≤ba ba dx x f dx x f |)(||)(|(a <b ).这是因为-|f (x )| £ f (x ) £ |f (x )|, 所以 ⎰⎰⎰≤≤-ba ba ba dx x f dx x f dx x f |)(|)(|)(|, 即 ⎰⎰≤ba ba dx x f dx x f |)(||)(|| .性质6 设M 及m 分别是函数f (x )在区间[a , b ]上的最大值及最小值, 则⎰-≤≤-ba ab M dx x f a b m )()()((a <b ).证明 因为 m £ f (x )£ M , 所以 ⎰⎰⎰≤≤ba ba ba Mdx dx x f mdx )(, 从而⎰-≤≤-ba ab M dx x f a b m )()()(.性质7 (定积分中值定理) 如果函数f (x )在闭区间[a , b ]上连续, 则在积分区间[a , b ]上至少存在一个点x , 使下式成立: ⎰-=ba ab f dx x f ))(()(ξ. 这个公式叫做积分中值公式. 证明 由性质6⎰-≤≤-ba ab M dx x f a b m )()()(,各项除以b -a 得⎰≤-≤ba M dx x f ab m )(1,再由连续函数的介值定理, 在[a , b ]上至少存在一点x , 使⎰-=ba dx x f ab f )(1)(ξ,于是两端乘以b -a 得中值公式 ⎰-=ba ab f dx x f ))(()(ξ. 积分中值公式的几何解释:应注意: 不论a <b 还是a >b , 积分中值公式都成立.第二节 微积分基本定理教学目的:使学生掌握变上限积分及其导数;使学生掌握牛顿—莱布尼兹公式(微积分基本定理,基本公式)一、变上限积分及其导数设函数f (x )在区间[a , b ]上连续, 并且设x 为[a , b ]上的一点.我们把函数f (x )在部分区间[a , x ]上的定积分 dx x f xa )(⎰称为积分上限的函数. 它是区间[a , b ]上的函数, 记为 (x )dx x f xa )(⎰=, 或 (x ) dt t f xa )(⎰.定理1 如果函数f (x )在区间[a , b ]上连续, 则函数 (x )dx x f xa )(⎰=在[a , b ]上具有导数, 并且它的导数为(x ))()(x f dt t f dxd xa ==⎰(a x <b ).简要证明 若x (a , b ), 取 x 使x x (a , b ). (x x ) (x )dt t f dt t f xa xx a )()(⎰⎰-=∆+dt t f dt t f dt t f xa xx x xa )()()(⎰⎰⎰-+=∆+x f dt t f x x x∆==⎰∆+)()(ξ,应用积分中值定理, 有 f ( ) x ,其中 在x 与x x 之间, x 0时, x . 于是 (x ))()(lim )(lim lim 00x f f f x xx x ===∆∆Φ=→→∆→∆ξξξ.若x a , 取 x >0, 则同理可证 (x ) f (a ); 若x b , 取 x <0, 则同理可证 (x ) f (b ).例1.求下列函数的导数:(1)⎰-=x dt t t y 02)3sin(; (2)⎰-=03)1tan(xdt t y ;(3)⎰+=3)1ln(x dt t y ; (4)⎰= xcos xsin 2dt e y t 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Ai f ( i )xi
曲边梯形面积的近似值为
A f ( i )xi
i 1 n
当分割无限加细,即小区间的最大长度
max{ x1 , x2 , xn }
趋近于零 ( 0) 时,
曲边梯形面积为 A lim f ( i )xi
0
i 1
n
实例2 (求变速直线运动的路程)
(1)分割
T1 t 0 t1 t 2 t n1 t n T2 t i t i t i 1 si v ( i )t i
部分路程值
某时刻的ቤተ መጻሕፍቲ ባይዱ度
(2)求和
s v ( i )t i
i 1
n
(3)取极限 max{t1 , t 2 ,, t n } 路程的精确值 s lim v ( i )t i
设某物体作直线运动,已知速度v v (t ) 是 时 间 间 隔 [T1 , T2 ] 上t 的 一 个 连 续 函 数 , 且
v ( t ) 0 ,求物体在这段时间内所经过的路程.
思路:把整段时间分割成若干小段,每小段上 速度看作不变,求出各小段的路程再相加,便 得到路程的近似值,最后通过对时间的无限细 分过程求得路程的精确值.
把区间 [a , b] 分成 n 个小区间 [ xi 1 , xi ], 长度为 xi xi xi 1 ;
y
在每个小区间 [ xi 1 , xi ] 上任取一点 i,
o a
x1
x i 1 x i
i
x n1 b
x
以 [ xi 1 , xi ]为底, ( i ) 为高的小矩形面积为 f
o
a
b
x
用矩形面积近似取代曲边梯形面积
y
y
o
a
(四个小矩形)
b
x o
a
(九个小矩形)
b
x
显然,小矩形越多,矩形总面积越接近 曲边梯形面积.
观察下列演示过程,注意当分割加细时, 矩形面积和与曲边梯形面积的关系.
播放
曲边梯形如图所示, 在区间 [a , b]内插入若干
个分点,a x0 x1 x2 xn1 xn b,
0
i 1 n
第一节 定积分的概念和性质
• • • • 一、定积分问题举例 二、定积分的定义 三、定积分的性质 四、小结
一、定积分问题举例
实例1 (求曲边梯形的面积)
y
曲边梯形由连续曲线
y f ( x ) ( f ( x ) 0) 、
x 轴与两条直线 x a 、
y f ( x)
A?
x b 所围成.
