2020年重庆中考几何第26题专题训练一(含答案解析)
2021年重庆中考数学第26题几何证明专题训练
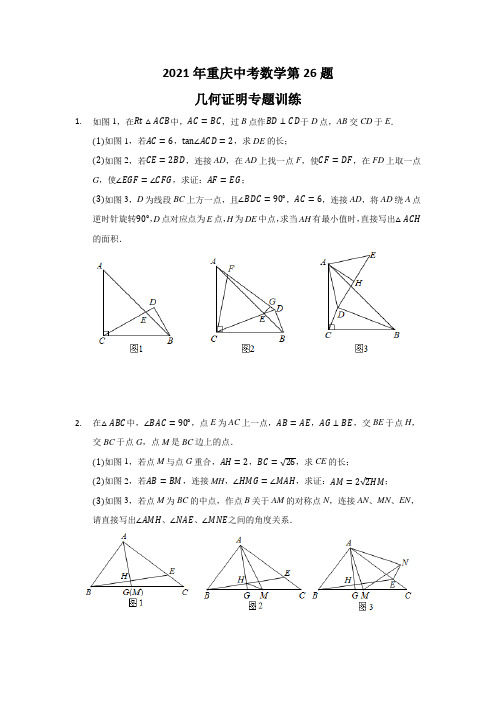
2021年重庆中考数学第26题几何证明专题训练1.如图1,在Rt△ACB中,AC=BC,过B点作BD⊥CD于D点,AB交CD于E.(1)如图1,若AC=6,tan∠ACD=2,求DE的长;(2)如图2,若CE=2BD,连接AD,在AD上找一点F,使CF=DF,在FD上取一点G,使∠EGF=∠CFG,求证:AF=EG;(3)如图3,D为线段BC上方一点,且∠BDC=90°,AC=6,连接AD,将AD绕A点逆时针旋转90°,D点对应点为E点,H为DE中点,求当AH有最小值时,直接写出△ACH 的面积.2.在△ABC中,∠BAC=90°,点E为AC上一点,AB=AE,AG⊥BE,交BE于点H,交BC于点G,点M是BC边上的点.(1)如图1,若点M与点G重合,AH=2,BC=√26,求CE的长;(2)如图2,若AB=BM,连接MH,∠HMG=∠MAH,求证:AM=2√2HM;(3)如图3,若点M为BC的中点,作点B关于AM的对称点N,连接AN、MN、EN,请直接写出∠AMH、∠NAE、∠MNE之间的角度关系.3.如图,在△ABC和△DEF中,AB=AC,DE=DF,∠BAC=∠EDF=120°,线段BC与EF相交于点O.(1)若点O恰好是线段BC与线段EF的中点.①如图1,当点D在线段BC上,A、F、O、E四点在同一条直线上时,已知BC=4√3,DE=√3,求AD的长;②如图2,连接AD,CF相交于点G,连接OG,BG,当BG⊥OG时,求证:BG=√3CG.2(2)若点D与点A重合,CF//AB,H、K分别为OC、AF的中点,连接HK,直接写出HKAE−OF 的值.AC,连接4.在△ABC和△AEF中,∠AFE=∠ABC=90°,∠AEF=∠ACB=30°,AE=12 EC,点G是EC中点,将△AEF绕点A顺时针旋转.(1)如图1,若E恰好在线段AC上,AB=2,连接FG,求FG的长度;(2)如图2,若点F恰好落在射线CE上,连接BG,证明:GB=√3AB+GC;2GC最大时,直接写出直线AB,(3)如图3,若AB=3,在△AEF旋转过程中,当GB−12AC,BG所围成三角形的面积.5.如图,四边形ABCD为正方形,△AEF为等腰直角三角形,∠AEF=90°,连接FC,G为FC的中点,连接GD,ED.(1)如图①,E在AB上,直接写出ED,GD的数量关系.(2)将图①中的△AEF绕点A逆时针旋转,其它条件不变,如图②,(1)中的结论是否成立?说明理由.(3)若AB=5,AE=1,将图①中的△AEF绕点A逆时针旋转一周,当E,F,C三点共线时,直接写出ED的长.6.如图1,在四边形ABCD中,AC交BD于点E,△ADE为等边三角形.(1)若点E为BD的中点,AD=4,CD=5,求△BCE的面积;(2)如图2,若BC=CD,点F为CD的中点,求证:AB=2AF;(3)如图3,若AB//CD,∠BAD=90°,点P为四边形ABCD内一点,且∠APD=90°,连接BP,取BP的中点Q,连接CQ.当AB=6√2,AD=4√2,tan∠ABC=2时,求CQ+√10BQ的最小值.107.已知△ABC中,∠ACB=90°,AC=2BC.(1)如图①,若AB=BD,AB⊥BD,求证:CD=√2AB;(2)如图②,若AB=AD,AB⊥AD,BC=1,求CD的长;(3)如图③,若AD=BD,AD⊥BD,AB=2√5,求CD的长.8.在△ABC中,∠ABM=45°,AM⊥BM,垂足为M,点C是BM延长线上一点,连接AC.(1)如图1,若AB=3√2,BC=5,求AC的长;(2)如图2,点D是线段AM上一点,MD=MC,点E是△ABC外一点,EC=AC,连接ED并延长交BC于点F,且点F是线段BC的中点,求证:∠BDF=∠CEF.9.在平行四边形ABCD中,对角线AC、BD交于点O,过点A作AE⊥BC于E,过点C作CF⊥CD交AE于点F,连接OF.以OF为直角边作Rt△OFG,其中∠OFG=90°,连接AG.(1)如图1,若∠EAB=30°,OA=2√3,AB=6,则求CE的长度;(2)如图2,若CF=CD,∠FGO=45°,求证:EC=√2AG+2EF;(3)如图3,动点P从点A运动到点D(不与点A、点D重合),连接FP,过点P作FP的垂线,又过点D作AD的垂线交FP的垂线于点Q,点A′是点A关于FP的对称点,连接A′Q.若AE=2EC,FG=2OF,EF=1,AG=√5,则在动点P的运动过程中,直接写出A′Q的最小值.10.在正方形ABCD中,E为边CD上一点(不与点C、D重合),垂直于BE的一条直线MN分别交BC、BE、AD于点M、P、N,正方形ABCD的边长为6.(1)如图1,当点M和点C重合时,若AN=4,求线段PM的长度;(2)如图2,当点M在边BC上时,判断线段AN、MB、EC之间的数量关系,并说明理由;(3)如图3,当垂足P在正方形ABCD的对角线AC上运动时,连接NB,将△BPN沿着BN翻折,点P落在点P′处,AB的中点为Q,直接写出P′Q的最小值.11.如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.(1)求∠CPE的度数;(2)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.12. 如图,在菱形ABCD 中,∠ABC =60°,分别过点B 作BC 的垂线,过点D 作CD 的垂线,两垂线相交于点E .(1)如图1,若AD =4,连接AE ,BD ,求三角形ADE 的面积;(2)如图2,点F 是DE 延长线上的一点,点G 为EB 延长线上的一点,且EF =BG ,连接BF ,DG ,DG 交FB 的延长线于点H ,连接AH ,试猜想线段AH ,BH ,HD 的数量关系并证明你的结论;(3)如图3,在(2)的条件下,在AH 上取得一点P ,使得HP =3AP ,已知Q 为直线ED 上一点,连接BQ ,连接QP ,当BQ +QP 最小时,直接写出S △QDC S 菱形ABCD 的值.13. 如图,已知△ABC 中,∠ABC =45°,CD 是边AB 上的高线,E 是AC 上一点,连接BE ,交CD 于点F .(1)如图1,若∠ABE =15°,BC =√3+1,求DF 的长;(2)如图2,若BF =AC ,过点D 作DG ⊥BE 于点G ,求证:BE =CE +2DG ;(3)如图3,若R 为射线BA 上的一个动点,以BR 为斜边向外作等腰直角△BRH ,M 为RH 的中点.在(2)的条件下,将△CEF 绕点C 旋转,得到△CE′F′,E ,F 的对应点分别为E′,F′,直线MF′与直线AB 交于点P ,tan∠ACD =13,直接写出当MF′取最小值时RMPF′的值.14. 如图△ABC 为等腰直角三角形,∠A =90°,D 、E 分别为AB 、AC 边上的点,连接DE ,以DE 为直角边向上作等腰直角三角形DEF ,连接BE 、BF .(1)如图1,当CE =AD 时,求证:BF ⊥BD ;(2)如图2,H 为BE 的中点,过点D 作DG ⊥BC 于点G ,连接GH.求证:BF =2HG ;(3)如图3,BE 与DF 交于点R ,延长BF 交AC 于点P ,∠APB 的角平分线交BE 于点Q.若点E 为AC 上靠近点A 的三等分点,且tan∠AED =67,请直接写出BR QR 的值.15. 如图,△ABC 是等边三角形,△BDE 是顶角为120°的等腰三角形,BD =DE ,连接CD ,AE .(1)如图1,连接AD ,若∠ABE =60°,AB =BE =√3,求CD 的长;(2)如图2,若点F 是AE 的中点,连接CF ,DF.求证:CD =2DF ;(3)如图3,在(2)的条件下,若AB =2√3,BD =2,将△BDE 绕点B 旋转,点H 是△AFC 内部的一点,当DF 最大时,请直接写出2HA +HF +√5HC 的最小值的平方.16.如图,点B,C,D在同一条直线上,△BCF和△ACD都是等腰直角三角形.连接AB,DF,延长DF交AB于点E.(1)如图1,若AD=BD,DE是△ABD的平分线,BC=1,求CD的长度;(2)如图2,连接CE,求证:DE=√2CE+AE;(3)如图3,改变△BCF的大小,始终保持点F在线段AC上(点F与点A,C不重合).将ED绕点E顺时针旋转90°得到EP.取AD的中点O,连接OP.当AC=2时,直接写出OP 长度的最大值.17.如图,已知△ABC为等腰直角三角形,AB=AC且∠CAB=90°,E为BC上一点,且BE=AC,过E作EF⊥BC且EF=EC,连接CF.(1)如图1,已知AB=2,连接AE、AF,求△AEF的面积;(2)如图2所示,D为AB上一点,连接DB,作∠DBH=45°交EF于H点,求证:CD=HF+√2CE;(3)已知△ABC面积为8+4√2,D为射线AC上一点,作∠DBH=45°,交射线EF于H,连接DH,点M为DH的中点,当CM有最小值时,请直接写出△CMD的面积.18.如图,Rt△ABC中,∠ABC=90°,AB=BC,点E是边BC上的一个动点,点D是射线AC上的一个动点;连接DE,以DE为斜边,在DE右侧作等腰Rt△DFE,再过点D 作DH⊥BC,交射线BC于点H.(1)如图1,若点F恰好落在线段AE上,且∠DEH=60°,CD=3√2,求出DF的长;(2)如图2,若点D在AC延长线上,此时,过F作FG⊥BC于点G,FG与AC边的交点记为M,当AE=DE时,求证:FM+√2MD=AB;(3)如图3,若AB=4√10,点D在AC延长线上运动,点E也随之运动,且始终满足AE=DE,作点E关于DF的对称点E′,连接CF、FE′、DE′,当CF取得最小值时,请直接写出此时四边形CFE′D的面积.19.如图1,在Rt△ABC中,∠BAC=90°,AB=AC,点D是BC边上一动点,连接AD,把AD绕点A顺时针旋转90°,得到AE,连接DE.(1)如图1所示,若BC=4,在D点运动过程中,当tan∠BDE=8时,求线段CD的长;11(2)如图2所示,点F是线段DE的中点,连接BF并延长交CA延长线于点M,连接DM,交AB于点N,连接CF,AF,当点N在线段CF上时,求证:AD+BF=CF;(3)如图3,若AB=2√3,将△ABC绕点A顺时针旋转得△AB′C′,连接CC′,P为线段CC′上一点,且CC′=√3PC′,连接BP,将BP绕点B顺时针旋转60°得到BQ,连接PQ,K 为PQ的中点,连接CK,请直接写出线段CK的最大值.20.在△ABC中,AC=BC,D为△ABC外一点,连接CD.(1)如图1,若∠ACB=60°,CD//AB,连接BD交AC于点E,且CD=2AB=2,求S△BCE.EC,(2)如图2,CE=CD,∠ECB=∠DCA,ED交AB于点F,FG垂直平分EC,且FG=12BF.M,N分别为AF,CD中点,连接MN,求证:MN=12(3)如图3,若∠ACB=90°,CD//AB,将AD绕着A点顺时针旋转60°得到AD′,连接DD′,BD′,且AC=√6,求BD′的最小值.21.已知,等腰直角△ABC中,AC=BC,∠ACB=90°,D为AB边上的一点,连接CD,以CD为斜边向右侧作直角△CDE,连接AE并延长交BC的延长线于点F.(1)如图1,当∠CDE=30°,AD=1,BD=3时,求线段DE的长;(2)如图2,当CE=DE时,求证:点E为线段AF的中点;(3)如图3,当点D与点A重合,AB=4时,过E作EG⊥BA交直线BA于点G,EH⊥BC交直线BC于点H,连接GH,求GH长度的最大值.22.如图,在锐角△ABC中,∠ACB=45°,点D是边BC上一动点,连接AD,将线段AD绕点A逆时针旋转90°得到线段AE,连接DE交AC于点F.(1)如图1,若∠ADC=60°,求证:DF=AF+EF;(2)如图2,在点D运动的过程中,当∠ADC是锐角时,点M在线段DC上,且AM=AD,连接ME,猜想线段ME,MD,AC之间存在的数量关系,并证明你猜想的结论;(3)在点D运动的过程中,当∠ADC是钝角时,点N是线段DE上一动点,连接CN,若AF=m,请直接用含m的代数式表示2CN+√2NE的最小值.CF=3523.如图1,在Rt△ABC与Rt△ABD中,∠ACB=∠ADB=90°,∠BAC=60°,CE⊥AB交AB于点E,AE=AD,点F在线段BD上,连接AF.(1)若AC=4,求线段BD的长;(2)如图2,若∠DAF=60°,点M为线段BF的中点,连接CM,证明:2CM=BF+√3AC;(3)如图3,在(2)的条件下,将△ADF绕点A旋转得△AD′F′,连接BF′,点M为线段BF′的中点,连接D′M,当D′M长度取最小时,在线段AB上有一动点N,连接MN,将线段MN绕点M逆时针旋转60°至MN′,连接D′N′,若AC=4,请直接写出(2MN′−√2D′N′)的最小值.。
重庆中考第26题专题专训(教师版)

重庆中考数学第26题专题专训1.如图1,在平面直角坐标系中,抛物线y=﹣x2﹣x﹣2与x轴交于A,B两点(点A 在点B的左侧),交y轴于点C.(1)求直线AC的解析式;(2)点P是直线AC上方抛物线上的一动点,过点P作PD⊥AC,垂足为D,当线段PD的长度最大时,点Q从点P出发,先以每秒1个单位的速度沿适当的路径运动到y轴上的点M处,再沿MC以每秒3个单位的速度运动到点C停止,当点Q在整个运动中所用时间t最少时,求点M的坐标;(3)如图2,将△BOC沿直线BC平移,平移后B,O,C三点的对应点分别是B′,O′,C′,点S是坐标平面内一点,若以A,C,O′,S为顶点的四边形是菱形,请直接写出所有符合条件的点S的坐标.解:(1)当y=0时,﹣x2﹣x﹣2=0,解这个方程,得:x1=﹣6,x2=﹣1,∴点A(﹣6,0),B(﹣1,0),当x=0时,y=﹣2,∴C(0,﹣2),设直线AC的解析式为:y=ax+b(a≠0),将点A(﹣6,0),C(0,﹣2)代入得:,∴,∴直线AC的解析式为:y=﹣x﹣2;(3分)(2)如图1,过点P作PE∥y轴交直线AC于点E,设P(a,﹣),则点E(a,﹣﹣2),∴PE=(﹣)﹣(﹣﹣2)=﹣﹣2a,∵AO=6,OC=2,∴AC===2,∵∠PDE=∠AOC=90°,∠PED=∠ACO,∴△PDE∽△AOC,∴=,∴PD=PE==﹣﹣,对称轴是:a=﹣3,∵﹣,∴当a=﹣3时,PD的长度最大,此时点P的坐标为(﹣3,2),如图1所示,在x轴上取点F(1,0),连接CF并延长,∴CF===3,∴sin∠OCF==,点M是y轴上一点,过点M作MH⊥CF于点H,由△CHM∽△COF,可知:=,∵t==PM+MH,如图2,当P、M、H在同一直线上时,t的值最小,此时,过P作PK⊥y轴于K,由△PKM∽△COF,可知:=2,∴KM=,∴M(0,),(7分)(3)如图3,当四边形ACSO'是菱形时,过S作SG⊥y轴于G,延长O'C'交x轴于H,∵四边形ACSO'是菱形,∴AO'=AC=SC,AO'∥SC,∴∠AMC=∠BCS,∴∠AO'H+∠MC'O'=∠BCO+∠OCS,∵∠MC'O'=∠BCO,∴∠AO'H=∠OCS,∵∠AHO'=∠CGS,∴△O'AH≌△CSG,∴AH=SG,O'H=CG,Rt△OCB中,sin∠OCB==,∴sin∠BC'H==,设BH=x,则BC'=3x,∴C'H=2x,∴AH=SG=5﹣x,∵O'C'=OC=2,∴C'H=OG=2x,由勾股定理得:AC2=O'A2,∴AO2+OC2=O'H2+AH2,∴=(5﹣x)2+(2+2x)2,解得:x=,当x=时,SG=5﹣x=,OG=2x=,当x=<0时,不符合题意,舍去,SG=5﹣x=,OG=2x=,此时S的坐标为:或;②如图4,过S作SH⊥AO于H,延长O'B'到y轴交于G,∵SE∥CF,EC∥SF,∴四边形SECF是平行四边形,∴∠ESF=∠ECF,∵四边形ASO'C是菱形,∴∠ASO'=∠ACO',∴∠ASH=∠O'CG,同理得:△ASH≌△O'CG,∴AH=O'G,SH=CG,sin∠GCB'==,设GB'=x,则CB'=3x,CG=2x,∴O'G=1+x,由勾股定理得:AC2=O'C2,∴62+(2)2=(2x)2+(x+1)2解得:x=,当x=时,SH=CG=2x=,OH=6﹣AH=6﹣O'G=5﹣x=,当x=<0时,不符合题意,舍去,此时,点S的坐标为:(,);③如图5,AC为对角线时,同理可得S(,)④如图6,过S作SE⊥x轴于E,延长B'O'交y轴于H,延长O'C'交x轴于G,设GB'=x,则CB'=3x,CG=2x,∴O'G=O'H=1+x,∵∠HO'D=∠O'DA=∠EAS,易得△SEA≌△CHO',同理可得S(,);⑤如图7,过S作SH⊥x轴于H,过O'作O'E⊥SH于E,延长C'O'交x轴于G,设OG=x,则BG=1+x,∵O'B'∥BG,∴,∴,∴C'G=2(1+x),∴O'G=C'G﹣C'O'=2x,∴AG=1+x,同理得:62+(2)2=(1+x)2+(2x)2,解得:x1=,x2=(舍),可得S;综上所述,S的坐标为:或或(,)或(,)或(,).(12分)2.在平面直角坐标系中,已知抛物线322+--=x x y 的图象交x 轴于A 、B 两点(点A 在点B 左侧),交y 轴于点C .(1)求直线AC 的解析式;(2)抛物线的对称轴交直线AC 于点E ,直线AC 上方的抛物线上有一动点P ,当△PEC 面积最大时,线段CE 在直线AC 上平移,记线段CE 平移 后为E C '',求E C P ''∆的周长最小值;(3)抛物线的顶点为D ,连接AD ,将线段AD 沿直线AC 平移,记线段AD 平移后为D A '',过点D '作x 轴的垂线交x 轴于点G ,当G D A ''∆ 为等腰三角形时,求A A '的长度.解:(1)抛物线y=﹣x 2﹣2x+3,∴A (﹣3,0),B (1,0),C (0,3),∴直线AC 的解析式 y=x+3; (2)∵对称轴为x=﹣1,∴E (﹣1,2),设P (m ,﹣m 2﹣2m+3), ∴S △PEC =﹣m 2﹣m=﹣(m+)2+,∴当m=﹣时,S △PEC 的有最大值, 即:P (﹣,),将线段PC 平移,使得C 与E 重合,得到线段P'E , ∴P'(﹣,),P''(﹣,),∴△PC'E'的周长的最小值为PP''+CE=+(3)∵抛物线y=﹣x 2﹣2x+3, ∴D (﹣1,4),设A'(﹣3+n ,n ),D'(﹣1+n ,4+n ),则G (﹣1+n ,0), ∴AA'=|n|, ∴A'D'2=20,A'G 2=n 2+4,D'G 2=n 2+8n+16,∵△A ′D ′G 为等腰三角形,①当A'D'=A'G时,∴20=n2+4,∴n=±4,∴AA'=4②当A'D'=D'G时,∴20=n2+8n+16,∴n=±2﹣4,∴AA'=2±4③当D'G=A'G时,∴n2+4=n2+8n+16,∴n=﹣,∴AA'=,即:AA′的长度为4或2或.3.如图,在平面直角坐标系中,抛物线y=﹣x2+x+3与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,连接BC,过点A作AD∥BC交y轴于点D.(1)求平行线AD、BC之间的距离;(2)如图1,点P为线段BC上方抛物线上的一动点,当△PCB的面积最大时,Q从点P出发,先沿适当的路径运动到直线BC上点M处,再沿垂直于直线BC的方向运动到直线AD上的点N处,最后沿适当的路径运动到点B处停止.当点Q的运动路径最短时,求点M的坐标及点Q经过的最短路径的长;(3)如图2,将抛物线以每秒个单位长度的速度沿射线AD方向平移,抛物线上的点A、C平移后的对应点分别记作A′、C′,当△A′C′B是以C′B为底边的等腰三角形时,将等腰△A′C′B 绕点D逆时针旋转一周,记旋转中的△A′C′B为△A″C″B′,若直线A″C″与y轴交于点K,直线A″C″与直线AD交于点I,当△DKI是以KI为底边的等腰三角形时,求出DK2的值.解:(1)如图1中,作AH⊥BC于H.对于抛物线y=﹣x2+x+3,令y=0,得到﹣x2+x+3=0,解得x=﹣或3,∴A(﹣,0),B(3,0),令x=0,得到y=3,∴C(0,3),∴OA=,OB=3,AB=4,OC=3,BC==3,∵S△ABC=•AB•CO=•BC•AH,∴AH==,∵AD∥BC,∴AD与BC之间的距离为.(2)如图2中,设P(m,﹣m2+m+3),S△PBC =S△POB+S△PCO﹣S△BOC=×3×(﹣m2+m+3)+×3×m﹣×3×3=﹣(m﹣)2+,∵﹣<0,∴m=时,△PBC的面积最大,此时P(,),作B关于直线AD的对称点B′交AD于K,连接PK交BC于M,作MN⊥AD于N,连接BN,则PM+MN+BN 的值最小.∵直线BC的解析式为y=﹣x+3,AD∥BC,∴直线AD的解析式为y=﹣x﹣1,∵BB′⊥BC,∴直线BB′的解析式为y=x﹣6,由,解得,∴K(,﹣),∴直线PK的解析式为y=﹣x+,由,解得,∴M(,),∴点Q经过的最短路径的长=PM+MN+BN=MN+(PM+MK)=MN+PK,∵MN=,PK==,∴点Q经过的最短路径的长为+.4. 抛物线y=﹣x2﹣x+与x轴交于点A,B(点A在点B的左边),与y轴交于点C,点D 是该抛物线的顶点.(1)如图1,连接CD,求线段CD的长;(2)如图2,点P是直线AC上方抛物线上一点,PF⊥x轴于点F,PF与线段AC交于点E;将线段OB沿x轴左右平移,线段OB的对应线段是O1B1,当PE+EC的值最大时,求四边形PO1B1C周长的最小值,并求出对应的点O1的坐标;(3)如图3,点H是线段AB的中点,连接CH,将△OBC沿直线CH翻折至△O2B2C的位置,再将△O 2B2C绕点B2旋转一周,在旋转过程中,点O2,C的对应点分别是点O3,C1,直线O3C1分别与直线AC,x轴交于点M,N.那么,在△O2B2C的整个旋转过程中,是否存在恰当的位置,使△AMN是以MN为腰的等腰三角形?若存在,请直接写出所有符合条件的线段O2M的长;若不存在,请说明理由.解:(1)如图1,过点D作DK⊥y轴于K,当x=0时,y=,∴C(0,),y=﹣x2﹣x+=﹣(x+)2+,∴D(﹣,),∴DK=,CK=﹣=,∴CD===;(4分)(2)在y=﹣x2﹣x+中,令y=0,则﹣x2﹣x+=0,解得:x1=﹣3,x2=,∴A(﹣3,0),B(,0),∵C(0,),易得直线AC的解析式为:y=,设E(x,),P(x,﹣x2﹣x+),∴PF=﹣x2﹣x+,EF=,Rt△ACO中,AO=3,OC=,∴AC=2,∴∠CAO=30°,∴AE=2EF=,∴PE+EC=(﹣x2﹣x+)﹣(x+)+(AC﹣AE),=﹣﹣x+[2﹣()],=﹣﹣x﹣x,=﹣(x+2)2+,(5分)∴当PE+EC的值最大时,x=﹣2,此时P(﹣2,),(6分)∴PC=2,∵O1B1=OB=,∴要使四边形PO1B1C周长的最小,即PO1+B1C的值最小,如图2,将点P向右平移个单位长度得点P1(﹣,),连接P1B1,则PO1=P1B1,再作点P1关于x轴的对称点P2(﹣,﹣),则P1B1=P2B1,∴PO1+B1C=P2B1+B1C,∴连接P2C与x轴的交点即为使PO1+B1C的值最小时的点B1,∴B 1(﹣,0),将B 1向左平移个单位长度即得点O 1,此时PO 1+B 1C=P 2C==,对应的点O 1的坐标为(﹣,0),(7分)∴四边形PO 1B 1C 周长的最小值为+3;(8分) (3)O 2M 的长度为或或2+或2.(12分)理由是:如图3,∵H 是AB 的中点,∴OH=,∵OC=,∴CH=BC=2,∴∠HCO=∠BCO=30°,∵∠ACO=60°,∴将CO 沿CH 对折后落在直线AC 上,即O2在AC 上, ∴∠B 2CA=∠CAB=30°, ∴B 2C ∥AB , ∴B 2(﹣2,),①如图4,AN=MN ,∴∠MAN=∠AMN=30°=∠O 2B 2O 3,由旋转得:∠CB 2C 1=∠O 2B 2O 3=30°,B 2C=B 2C 1, ∴∠B 2CC 1=∠B 2C 1C=75°,过C 1作C 1E ⊥B 2C 于E , ∵B 2C=B 2C 1=2,∴=B 2O 2,B 2E=,∵∠O 2MB 2=∠B 2MO 3=75°=∠B 2CC 1, ∠B 2O 2M=∠C 1EC=90°, ∴△C 1EC ≌△B 2O 2M , ∴O 2M=CE=B 2C ﹣B 2E=2﹣;②如图5,AM=MN ,此时M 与C 重合,O 2M=O 2C=,③如图6,AM=MN ,∵B 2C=B 2C 1=2=B 2H ,即N 和H 、C 1重合,∴∠CAO=∠AHM=∠MHO 2=30°,∴O 2M=AO 2=;④如图7,AN=MN ,过C 1作C 1E ⊥AC 于E , ∴∠NMA=∠NAM=30°,∵∠O 3C 1B 2=30°=∠O 3MA ,∴C 1B 2∥AC ,∴∠C 1B 2O 2=∠AO 2B 2=90°, ∵∠C 1EC=90°, ∴四边形C 1EO 2B 2是矩形, ∴EO 2=C 1B 2=2,,∴EM=,∴O 2M=EO 2+EM=2+, 综上所述,O 2M 的长是或或2+或2.5. 如图,在平面直角坐标系中,点A 在抛物线y=﹣x 2+4x 上,且横坐标为1,点B 与点A 关于抛物线的对称轴对称,直线AB 与y 轴交于点C ,点D 为抛物线的顶点,点E 的坐标为(1,1). (1)求线段AB 的长;(2)点P 为线段AB 上方抛物线上的任意一点,过点P 作AB 的垂线交AB 于点H ,点F 为y 轴上一点,当△PBE 的面积最大时,求PH+HF+FO 的最小值;(3)在(2)中,PH+HF+FO 取得最小值时,将△CFH 绕点C 顺时针旋转60°后得到△CF′H′,过点F'作CF′的垂线与直线AB 交于点Q ,点R 为抛物线对称轴上的一点,在平面直角坐标系中是否存在点S ,使以点D ,Q ,R ,S 为顶点的四边形为菱形,若存在,请直接写出点S 的坐标,若不存在,请说明理由.解:(1)由题意A (1,3),B (3,3), ∴AB=2.(2)如图1中,设P (m ,﹣m 2+4m ),作PN ∥y 轴J 交BE 于N .∵直线BE 的解析式为y=x , ∴N (m ,m ), ∴S △PEB =×2×(﹣m 2+3m )=﹣m 2+3m , ∴当m=时,△PEB 的面积最大,此时P (,),H (,3),∴PH=﹣3=,作直线OG 交AB 于G ,使得∠COG=30°,作HK ⊥OG 于K 交OC 于F , ∵FK=OF ,∴PH+HF+FO=PH+FH+FK=PH+HK ,此时PH+HF+OF 的值最小, ∵•HG•OC=•OG•HK,∴HK==+, ∴PH+HF+OF 的最小值为+. (3)如图2中,由题意CH=,CF=,QF=,CQ=1,∴Q (﹣1,3),D (2,4),DQ=,①当DQ 为菱形的边时,S 1(﹣1,3﹣),S 2(﹣1,3+),②当DQ 为对角线时,可得S 3(﹣1,8), ③当DR 为对角线时,可得S 4(5,3) 综上所述,满足条件的点S 坐标为(﹣1,3﹣)或(﹣1,3+)或(﹣1,8)或(5,3).6.如图1,在平面直角坐标系中,抛物线y=与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴交于点C ,抛物线的顶点为点D ,过点B 作BC 的垂线,交对称轴于点E .(1)求证:点E 与点D 关于x 轴对称;(2)点P 为第四象限内的抛物线上的一动点,当△PAE 的面积最大时,在对称轴上找一点M ,在y 轴上找一点N ,使得OM+MN+NP 最小,求此时点M 的坐标及OM+MN+NP 的最小值;(3)如图2,平移抛物线,使抛物线的顶点D 在射线AD 上移动,点D 平移后的对应点为D′,点A 的对应点A′,设抛物线的对称轴与x 轴交于点F ,将△FBC 沿BC 翻折,使点F 落在点F′处,在平面内找一点G ,若以F′、G 、D′、A′为顶点的四边形为菱形,求平移的距离.(1)证明:如图1中,令y=0,得到x2﹣x﹣3=0,解得x=﹣或3,∴A(﹣,0),B(3,0),令x=0,可得y=﹣3,∴C(0,﹣3),∵y=x2﹣x﹣3=(x﹣)2﹣4,∴顶点D(,﹣4),设对称轴与x轴交于F,则BF=2,∵△EFB∽△BOC,∴=,∴=,∴EF=4,∴E(,4),∴E、D关于x轴对称.(2)过点P作PQ∥y轴,交直线AE于点Q.∵yAE=x+2,∴设P(a,a2﹣a﹣3),Q(a,a+2),(0<a<3),7.如图1,在平面直角坐标系中,抛物线2y x x=-与x轴交于A、B两点(点A在点B 的左侧),与y轴交于点C.(1)求直线AC的解析式;(2)如图2,点E(a,b)是对称轴右侧抛物线上一点,过点E垂直于y轴的直线与AC交于点D(m,n).点P是x轴上的一点,点Q是该抛物线对称轴上的一点,当a m+最大时,求点E的坐标,并直接写出23EQ PQ PB++的最小值;(3)如图3,在(2)的条件下,连结OD,将△AOD沿x轴翻折得到△AOM,再将△AOM沿射线CB 的方向以每秒3个单位的速度沿平移,记平移后的△AOM为△A O M''',同时抛物线以每秒1个单位的速度沿x 轴正方向平移,点B 的对应点为B '.△A B M '''能否为等腰三角形?若能,请求出所有符合条件的点M '的坐标;若不能,请说明理由.8.如图1,在平面直角坐标系中,抛物线423412++-=x x y 与x 轴交于A 、B 两点(点A 在点B左侧),与y 轴交于点C .(1)求抛物线的对称轴及△ABC 的周长;(2)点D 是线段AC 的中点,过点D 作BC 的平行线,分别与x 轴、抛物线交于点E 、F ,点P 为直线BC 上方抛物线上的一动点,连接PD 交线段BC 于点G ,当四边形PGEF 面积最大时,点Q 从点P 出发沿适当的路径运动到x 轴上的点M 处,再沿射线DF 方向运动5个单位到点N 处,最后回到直线BC 上的点H 处停止,当点Q 的运动路径最短时,求点Q 的最短运动路径长及点H 的坐标;(3)如图2,将△AOC 绕点O 顺时针旋转至△A 1OC 1的位置,点A 、C 的对应点分别为点A 1、C 1,且点A 1落在线段AC 上,再将△A 1OC 1沿y 轴平移得△A 2O 1C 2,其中直线O 1C 2与x 轴交于点K ,点T 是抛物线对称轴上的动点,连接KT 、O 1T ,△O 1KT 能否成为以O 1K 为直角边的等腰直角三角形?若能,请直接写出所有符合条件的点T 的坐标;若不能,请说明理由.9.如图,在平面直角坐标系中,抛物线y=-x 2-3x+4交x 轴于A 、D 两点(点A 在点B 的左例), 交y 轴于点C,顶点为点D,连接BC,作直线AC.(1)求点D 的坐标和直线BC 的解析式;(2)若点P 为BC 上方抛物线上的一个动点,连接PC 、PB,过P 作PE ⊥y 轴于点E,当△PBC 面积最大时,将△PEC 绕平面内一点逆时针方向旋转90°后得到△111C E P .点P 、E 、C 的对应点分别是点1P 、1E 、1C ,当点C 1C 落在线段AC 上时,连接PP 1,求A C C P PP 111122++的最小值,并求出此时点1C 的坐标;(3)在(2)的条件下,将△111C E P 沿射线AC 以每秒2个单位长度的速度平移,记平移后的△111C E P 为△222C E P 点1P 、1E 、1C 的对应点分别是点2P 、2E ,C 2,设平移时间为秒,当△CD P2为等腰三角形时,求t 的值.10.如图,在平面直角坐标系中,抛物线)0≠(++=2a c bx ax y 交x 轴于A 、B 两点,交y 轴于点C ,AO=CO=4,BO=6,点D 是第四象限抛物线上一点,且点F 的纵坐标为-4.(1)求抛物线的解析式和直线CF 的解析式; (2)如图1,点P 是直线CF 上方抛物线上一点,点E 在直线CF 上,点E 的横坐标为3,当△PCF 的面积最大时,在y 轴有一动点M ,在x 轴有一动点N ,当PM+MN+NE 的值最小时,求出PM+MN+NE 的最小值.(3)如图2,点D 为线段BO 的中点,连接CD ,将C D O∆绕着点D 顺时针旋转α度得到对应''C DO ∆()0180α︒<<︒.设直线'C D 和直线''C O 分别与直线BC 交于H 、G 两点,当三角形C ′HG 是等腰三角形11.如图1,在平面直角坐标系中,抛物线c bx x y ++-=2的图像与x 轴交于点A 和点B (5,0),与y 轴交于点C ,点D (1,8)是抛物线上一点.(1)求抛物线和直线AD 的解析式;(2)点Q 是抛物线一象限内一动点,过点Q 作QN ∥AD 交BC 于N ,QG ⊥AB 交BC 与点M ,交AB 于点G (如图1),当QNM ∆的周长最大时,求QNM ∆周长的最大值;此时,在直线BC 上有两动点P 、H ,且PH=22(P 在H 的右边),K (2,0),当HK PQ -最大时求点P 的坐标(3)直线AD 与y 轴交于点F ,点E 是点C 关于对称轴的对称点,点P 是线段AE 上的一动点,将AFP ∆沿着FP 所在的直线翻折得到FP A '∆(点A 的对应点为点A ')(如图2),当FP A '∆与AED ∆重叠部分为直角三角形时,求AP 的长.(第26题1) (第26题2) (第26题备用图)13.如图1,在平面直角坐标系中,抛物线y=﹣x2﹣x﹣2与x轴交于A,B两点(点A 在点B的左侧),交y轴于点C.(1)求直线AC的解析式;(2)点P是直线AC上方抛物线上的一动点,过点P作PD⊥AC,垂足为D,当线段PD的长度最大时,点Q从点P出发,先以每秒1个单位的速度沿适当的路径运动到y轴上的点M处,再沿MC以每秒3个单位的速度运动到点C停止,当点Q在整个运动中所用时间t最少时,求点M的坐标;(3)如图2,将△BOC沿直线BC平移,平移后B,O,C三点的对应点分别是B′,O′,C′,点S是坐标平面内一点,若以A,C,O′,S为顶点的四边形是菱形,请直接写出所有符合条件的点S的坐标.解:(1)当y=0时,﹣x 2﹣x ﹣2=0,解这个方程,得:x 1=﹣6,x 2=﹣1, ∴点A (﹣6,0),B (﹣1,0), 当x=0时,y=﹣2,∴C (0,﹣2),设直线AC 的解析式为:y=ax+b (a ≠0), 将点A (﹣6,0),C (0,﹣2)代入得:, ∴,∴直线AC 的解析式为:y=﹣x ﹣2;(3分)(2)如图1,过点P 作PE ∥y 轴交直线AC 于点E , 设P (a ,﹣),则点E (a ,﹣﹣2), ∴PE=(﹣)﹣(﹣﹣2)=﹣﹣2a ,∵AO=6,OC=2, ∴AC===2,∵∠PDE=∠AOC=90°,∠PED=∠ACO , ∴△PDE ∽△AOC ,∴=, ∴PD=PE==﹣﹣,对称轴是:a=﹣3, ∵﹣,∴当a=﹣3时,PD 的长度最大,此时点P 的坐标为(﹣3,2),如图1所示,在x 轴上取点F (1,0),连接CF 并延长, ∴CF===3,∴sin ∠OCF==,点M 是y 轴上一点,过点M 作MH ⊥CF 于点H , 由△CHM ∽△COF ,可知:=,∵t==PM+MH,如图2,当P、M、H在同一直线上时,t的值最小,此时,过P作PK⊥y轴于K,由△PKM∽△COF,可知:=2,∴KM=,∴M(0,),(7分)(3)如图3,当四边形ACSO'是菱形时,过S作SG⊥y轴于G,延长O'C'交x轴于H,∵四边形ACSO'是菱形,∴AO'=AC=SC,AO'∥SC,∴∠AMC=∠BCS,∴∠AO'H+∠MC'O'=∠BCO+∠OCS,∵∠MC'O'=∠BCO,∴∠AO'H=∠OCS,∵∠AHO'=∠CGS,∴△O'AH≌△CSG,∴AH=SG,O'H=CG,Rt△OCB中,sin∠OCB==,∴sin∠BC'H==,设BH=x,则BC'=3x,∴C'H=2x,∴AH=SG=5﹣x,∵O'C'=OC=2,∴C'H=OG=2x,由勾股定理得:AC2=O'A2,∴AO2+OC2=O'H2+AH2,∴=(5﹣x)2+(2+2x)2,解得:x=,当x=时,SG=5﹣x=,OG=2x=,当x=<0时,不符合题意,舍去,SG=5﹣x=,OG=2x=,此时S的坐标为:或;②如图4,过S作SH⊥AO于H,延长O'B'到y轴交于G,∵SE∥CF,EC∥SF,∴四边形SECF是平行四边形,∴∠ESF=∠ECF,∵四边形ASO'C是菱形,∴∠ASO'=∠ACO',∴∠ASH=∠O'CG,同理得:△ASH≌△O'CG,∴AH=O'G,SH=CG,sin∠GCB'==,设GB'=x,则CB'=3x,CG=2x,∴O'G=1+x,由勾股定理得:AC2=O'C2,∴62+(2)2=(2x)2+(x+1)2解得:x=,当x=时,SH=CG=2x=,OH=6﹣AH=6﹣O'G=5﹣x=,当x=<0时,不符合题意,舍去,此时,点S的坐标为:(,);③如图5,AC为对角线时,同理可得S(,)④如图6,过S作SE⊥x轴于E,延长B'O'交y轴于H,延长O'C'交x轴于G,设GB'=x,则CB'=3x,CG=2x,∴O'G=O'H=1+x,∵∠HO'D=∠O'DA=∠EAS,易得△SEA≌△CHO',同理可得S(,);⑤如图7,过S作SH⊥x轴于H,过O'作O'E⊥SH于E,延长C'O'交x轴于G,设OG=x,则BG=1+x,∵O'B'∥BG,∴, ∴,∴C'G=2(1+x ),∴O'G=C'G ﹣C'O'=2x , ∴AG=1+x ,同理得:62+(2)2=(1+x )2+(2x )2, 解得:x 1=,x 2=(舍), 可得S ;综上所述,S 的坐标为:或或(,)或(,)或(,).(12分)。
2020重庆中考复习数学第26题专题训练六(含答案解析)

2020重庆中考复习数学第26题专题训练六 1、如图1,在△ABC中,∠BAC=90°,AC=2AB,D是线段AC中点,E是线段AD上一点,过点D作DF⊥BE交BE的延长钱于点F,连接AF,过点A作AG⊥AF于点A,交BF于点G(1)若∠ABE=∠C,BC=2,求AE的长;(2)若点E为AD中点,求证:GE﹣FE=FD;(3)如图2,连接BD,点N为BD中点,连接GN,若AD=GF,请直接写出NG、GE、EA的数量关系.4、已知△ABC中,点D为BC的中点,BD=AB,AD⊥BC.(1)如图1,求∠BAD的度数;(2)如图2,点E为BC上一点,点F为AC上一点,连接AE、BF交于点G,若∠AGF=60°,求证:BE=CF;(3)如图3,在(2)的条件下,点G为BF的中点,点H为AG上一点,延长BH交AC于点K,AK =HK,BM⊥AE交AE延长线于点M,BG=9,HM=10,求线段AG的长.5、已知△ABC中,∠B=60°,点D是AB边上的动点,过点D作DE∥BC交AC于点E,将△ADE沿DE折叠,点A对应点为F点.(1)如图1,当点F恰好落在BC边上,求证:△BDF是等边三角形;(2)如图2,当点F恰好落在△ABC内,且DF的延长线恰好经过点C,CF=EF,求∠A的大小;(3)如图3,当点F恰好落在△ABC外,DF交BC于点G,连接BF,若BF⊥AB,AB=9,求BG 的长.6、如图,在△ABC中,AB=AC,∠BAC=90°,D为BC边的中点,点E在直线BC上(不与点D重合),连接AE,过点C作直线AE的垂线,垂足为点F,交直线AD于点G,连接EG.(1)如图(1),当点E在线段BD上时,易证DE=DG,请直接写出三条线段BE,AB,EG之间的数量关系是 ;(2)如图(2),当点E在线段BC的延长线上时,请写出三条线段BE、AB、EG之间的数量关系,并证明你的结论;(3)若线段BC=2,当△AEG为等腰三角形时,请直接写出的值.7、如图,在△ABC中,∠BAC=90°,将△ABC沿AD翻折,点B恰好与点C重合,点E在AC边上,连接BE.(1)如图①,若点F是BE的中点,连接DF,且AF=5,AE=6,求DF的长;(2)如图②,若AF⊥BE于点F,并延长AF交BC于点G,当点E是AC的中点时,连接EG,求证:AG+EG=BE;(3)在(2)的条件下,连接DF,请直接写出∠DFG的度数.8、如图,在Rt△ABC中,AC=BC,∠ACB=90°,点D、E分别在AC、BC上,BD与AE交于点O,且CD=CE,若点F是BD的中点,连接CF,交AE于点G.(1)求证:CF⊥AE;(2)如图2,过点F作FM⊥BC,交AE的延长线于点M,垂足为H,连接CM,若CG=GM.①求证:CF=CM;②求的值.9、(1)【问题发现】如图1,在Rt△ABC中,AB=AC=4,∠BAC=90°,点D为AC的中点,过点A作BD的垂线,垂足为E,延长AE交BC于点F,求△ABF的面积.小明发现,过点C作AC的垂线,交AF的延长线于点G,构造出全等三角形,经过推理和计算,能够得到BF与CF的数量关系,从而使问题得到解决,请直接填空:= 2,△ABF的面积为 .(2)【类比探究】如图2,将(1)中的条件“点D为AC的中点”改为“点D为边AC上的一点,且满足CD=2AD”,其他条件不变,试求△ABF的面积,并写出推理过程.(3)【拓展迁移】如图3,在△ABC中,AB=AC=4,∠BAC=120°,点D为AC上一点,且满足CD =2AD,E为BD上一点,∠AEB=60°,延长AE交BC于F,请直接写出△ABF的面积.2020重庆中考复习数学第26题专题训练六参考答案 1、如图1,在△ABC中,∠BAC=90°,AC=2AB,D是线段AC中点,E是线段AD上一点,过点D作DF⊥BE交BE的延长钱于点F,连接AF,过点A作AG⊥AF于点A,交BF于点G(1)若∠ABE=∠C,BC=2,求AE的长;(2)若点E为AD中点,求证:GE﹣FE=FD;(3)如图2,连接BD,点N为BD中点,连接GN,若AD=GF,请直接写出NG、GE、EA的数量关系.解:(1)∵△ABC中,∠BAC=90°,AC=2AB,BC=2,∴由勾股定理可得AB=2,AC=4,∵∠ABE=∠C,∠BAE=∠CAB=90°,∴△BAE∽△CAB,∴AB2=AE×AC,即22=AE×4,解得AE=1,(2)证明:如图1,过A作AH⊥BF于H,则∠AHE=90°,∵DF⊥BE,∠BAC=90°,∠AEB=∠FED,∴∠ABG=∠ADF,∵AG⊥AF,∠BAC=90°,∴∠BAG=∠DAF,∵AC=2AB,D是线段AC中点,∴AB=AD,在△ABG和△ADF中,,∴△ABG≌△ADF(ASA),∴AG=AF,∴△AGF是等腰直角三角形,∴AH=GF=GH,∵点E为AD中点,∴AE=DE,在△AEH和△DEF中,,∴△AEH≌△DEF(AAS),∴EH=EF,AH=DF=GH,∵GE﹣HE=GH,∴GE﹣FE=FD;(3)NG、GE、EA的数量关系为:NG+GE=2AE.理由:如图2,连接AN,NF,由(2)可得,△AGF是等腰直角三角形,∵AB=AD,∠BAD=90°,N是BD的中点,∴∠DAN=45°=∠ADN,∴△ADN是等腰直角三角形,∵AD=GF,∴等腰Rt△AGF与等腰Rt△ADN全等,∴AG=AF=AN=ND,∵Rt△BDF中,N是BD的中点,∴NF=ND=BN,∴AN=NF=AF,即△ANF是等边三角形,∴∠NAF=∠ANF=60°,∵∠DAN=45°,△ABG≌△ADF,∴∠DAF=15°=∠BAG,∵∠ABN=∠BAN=45°,∴∠GAN=30°,∵∠AGF=45°,∴∠ABE=30°,∴Rt△ABE中,BE=2AE,∵∠ABN=45°,∴∠GBN=15°,由NF=ND=NB,可得∠FND=2∠GBN=30°,在△ANG和△NDF中,,∴△ANG≌△NDF(SAS),∴GN=FD=BG,∵BG+GE=BE=2AE,∴NG+GE=2AE.MDEFBACG解: (1)由E 为CR 中点可得AG 平分BAC ,过G 作GH AB ,则有GH=CG=1,故BG=2(2)延长FD 交AG 于点M ,易证:()BFD AMD AAS ,所以BF=AM再证:()BFC CEA AAS ,所以BF=CE=AM ,CF=AE∴CF-CE=AE-AM ,即EM=EF ∴EFM 为等腰直角三角形 ∴222EFFMDF(3)结论为:622BDEF4、(2017秋?许昌月考)已知△ABC中,点D为BC的中点,BD=AB,AD⊥BC.(1)如图1,求∠BAD的度数;(2)如图2,点E为BC上一点,点F为AC上一点,连接AE、BF交于点G,若∠AGF=60°,求证:BE=CF;(3)如图3,在(2)的条件下,点G为BF的中点,点H为AG上一点,延长BH交AC于点K,AK =HK,BM⊥AE交AE延长线于点M,BG=9,HM=10,求线段AG的长.解:(1)∵点D为BC的中点,AD⊥BC,∴AB=AC,BD=CD=BC,∵BD=AB,∴AB=BC=AC,∴△ABC是等边三角形,∴∠BAC=60°,∵AD⊥BC,∴∠BAD=∠BAC=30°;(2)由(1)知,△ABC是等边三角形,∴AB=BC,∠ABC=∠C=60°,∴∠ABF+∠CBF=60°,∵∠AGF=60°,∴∠BAE+∠ABF=60°,∴∠BAE=∠CBF,在△ABE和△BCF中,,∴△ABE≌△BCF(ASA),∴BE=CF,(3)如图,过F作FN⊥AE于N,过F作FD⊥BM,交BM的延长线于D,∵AM⊥BM,∴GM∥DF,∵BG=GF,∴BM=DM,∵∠AGF=60°,∴∠BGM=60°,∵BM⊥AE,∴∠BMG=90°,∴∠GBM=30°,在Rt△BMG中,MG=BG=,BM=DM=FN=,∵AK=HK,∴∠HAK=∠AHK=∠BHM,∵∠ANF=∠HMB=90°,∴△ANF≌△HMB,∴AN=HM=10,Rt△FGN中,∠NFG=∠GBM=30°,∴GN=GF=,∴AG=AN+NG=10+=14.5.5、(2019秋?中山市期末)已知△ABC中,∠B=60°,点D是AB边上的动点,过点D作DE∥BC交AC于点E,将△ADE沿DE折叠,点A对应点为F点.(1)如图1,当点F恰好落在BC边上,求证:△BDF是等边三角形;(2)如图2,当点F恰好落在△ABC内,且DF的延长线恰好经过点C,CF=EF,求∠A的大小;(3)如图3,当点F恰好落在△ABC外,DF交BC于点G,连接BF,若BF⊥AB,AB=9,求BG 的长.(1)证明:如图1,∵∠B=60°,DE∥BC,∴∠ADE=∠B=60°,∵△ADE沿DE折叠,点A对应点为F点,∴∠ADE=∠FDE=60°,∴∠BDF=60°,∴∠DFB=60°=∠B=∠BDF,∴△BDF是等边三角形;(2)解:∵∠B=60°,DE∥BC,∴∠ADE=∠B=60°,∵△ADE沿DE折叠,点A对应点为F点,∴∠ADE=∠FDE=60°,∠A=∠DFE,∴∠ADC=120°,∵CF=EF,∴∠FEC=∠FCE,设∠FEC=∠FCE=x,则∠A=∠DFE=∠FEC+∠FCE=2x,在△ADC中,∠A+∠ACD+∠ADC=180°,即2x+x+120°=180°,解得:x=20°,∴∠A=2x=40°;(3)解:同(1)得:∠BDF=60°,△BDG是等边三角形,∠ADE=∠B=60°,∴BG=BD,由折叠的性质得:AD=FD,∵BF⊥AB,∴∠BFD=90°﹣60°=30°,∴FD=2BD,∴AD=2BD,∵AD+BD=AB,∴2BD+BD=9,∴BD=3,∴BG=BD=3.6、(2018?连山区一模)如图,在△ABC中,AB=AC,∠BAC=90°,D为BC边的中点,点E在直线BC上(不与点D重合),连接AE,过点C作直线AE的垂线,垂足为点F,交直线AD于点G,连接EG.(1)如图(1),当点E在线段BD上时,易证DE=DG,请直接写出三条线段BE,AB,EG之间的数量关系是 AB﹣EG=BE;(2)如图(2),当点E在线段BC的延长线上时,请写出三条线段BE、AB、EG之间的数量关系,并证明你的结论;(3)若线段BC=2,当△AEG为等腰三角形时,请直接写出的值.解:(1)如图1中,结论:AB﹣EG=BE理由:∵AB=AC,∠BAC=90°,BD=DC,∴AD⊥BC,∠ABC=∠ACB=45°,AD=BD=DC,∴BD=AB,∵CF⊥AE,∴∠AFG=∠CDG=90°,∵∠AGF=∠CGD,∴∠FAG=∠GCD,∵∠ADE=∠CDG,∴△ADE≌△CDG,∴DE=DG,∴DE=EG,∵BE+ED=BD,∴BE+EG=AB,∴AB﹣EG=BE.(2)如图2中,结论:AB+EG=BE.理由:同法可证:△ADE≌△CDG,∴DE=DG,∴DE=EG,∵BE﹣ED=BD,∴BE+﹣EG=AB,∴AB+EG=BE.(3)①如图2中,当GA=GE时,DG=DE=2﹣2,EG=4﹣2,此时:==﹣1.②如图3中,当GA=GE时,设BD=AD=CD=a,则AB=AC=CE=a,DG=DE=a+a,EG=a+2a,∴==1+.③当点E与点C重合时,EG=AB,可得EG:AB=1,综上所述,的值为﹣1或1+或1.7、(2018?站前区校级一模)如图,在△ABC中,∠BAC=90°,将△ABC沿AD翻折,点B恰好与点C重合,点E在AC边上,连接BE.(1)如图①,若点F是BE的中点,连接DF,且AF=5,AE=6,求DF的长;(2)如图②,若AF⊥BE于点F,并延长AF交BC于点G,当点E是AC的中点时,连接EG,求证:AG+EG=BE;(3)在(2)的条件下,连接DF,请直接写出∠DFG的度数.解:(1)∵将△ABC沿AD翻折,点B恰好与点C重合,∴AB=AC,BD=CD,∠ADB=∠ADC=90°,且∠BAC=90°,∴△ABC是等腰直角三角形,∵点F是BE的中点,AF=5,∠BAC=90°,∴BE=10,∴AB===8,∴AC=8,∴EC=2,∵BD=CD,BF=EF,∴DF=EC=1,(2)如图②,过点C作CH⊥AC交AG的延长线于点H,∵AB=AC,∠BAC=90°,BD=CD,∴∠ABC=∠BAD=∠DAC=∠ACB=45°,∵∠BEA+∠CAH=90°,∠CAH+∠H=90°,∴∠H=∠BEA,且AB=AC,∠AFB=∠ACH=90°,∴△ABE≌△CAH(AAS)∴BE=AH,AE=CH,∠CAH=∠ABE,∵AE=CE,∴CE=CH,∵∠ACH=90°,∠ACB=45°,∴∠ACB=∠GCH,且CE=CH,CG=CG,∴△CEG≌△CHG(SAS)∴EG=GH,∵BE=AH=AG+GH,∴AG+EG=BE;(3)如图②,连接NG,∵∠ABC=∠BAD=∠DAC=∠ACB=45°,∴AD=BD=CD,∵∠BAN=∠ACG=45°,AB=AC,∠ABE=∠CAH,∴△ABN≌△CAG(ASA)∴AN=CG,∴AD﹣AN=CD﹣CG,∴DN=DG,∴∠DNG=45°∵∠NDG=∠NFG=90°,∴点N,点F,点G,点D四点共圆,∴∠DFG=∠DNG=45°.8、如图,在Rt△ABC中,AC=BC,∠ACB=90°,点D、E分别在AC、BC上,BD与AE交于点O,且CD=CE,若点F是BD的中点,连接CF,交AE于点G.(1)求证:CF⊥AE;(2)如图2,过点F作FM⊥BC,交AE的延长线于点M,垂足为H,连接CM,若CG=GM.①求证:CF=CM;②求的值.(1)证明:如图1中,∵AC=BC,∠ACE=∠BCD=90°,CE=CD,∴△ACE≌△BCD(SAS),∴∠CAE=∠CBD,∵DF=FB,∴CF=FD=FB,∴∠FCB=∠FBC,∴∠FCB=∠CAE,∵∠CAB+∠AEC=90°,∴∠AEC+∠FCB=90°,∴∠CGE=90°,∴CF⊥AE.(2)①证明:如图2中,∵FM⊥BC,∴∠FHC=∠CGE=∠MGF=90°,∴∠ECG+∠CEG=90°,∠ECG+∠CFH=90°,∴∠CEG=∠CFH,∵CG=GM,∴△CGE≌△MGF(AAS),∴CE=FM,EG=GF,∵CD=CE,∴CD=FM,∵∠FHB=∠ACB=90°,∴CD∥FM,∴四边形CDFM是平行四边形,∴CM=DF,∵CF=DF=FB,∴CM=CF.②连接EF,BM.设FG=EG=a,∵CM=BF,CM∥BF,∴FG∥BM,∴=,∵△CAE≌△CBD,∴∠CAE=∠CBD,∵∠CAB=∠CBA,∴∠OAB=∠OBA,∴OA=OB,∴=,易知OG=GF=EG=a,EF=EM=a,∴OM=2a+a,∴==.9、(2015?新乡二模)(1)【问题发现】如图1,在Rt△ABC中,AB=AC=4,∠BAC=90°,点D为AC的中点,过点A作BD的垂线,垂足为E,延长AE交BC于点F,求△ABF的面积.小明发现,过点C作AC的垂线,交AF的延长线于点G,构造出全等三角形,经过推理和计算,能够得到BF与CF的数量关系,从而使问题得到解决,请直接填空:= 2,△ABF的面积为 .(2)【类比探究】如图2,将(1)中的条件“点D为AC的中点”改为“点D为边AC上的一点,且满足CD=2AD”,其他条件不变,试求△ABF的面积,并写出推理过程.(3)【拓展迁移】如图3,在△ABC中,AB=AC=4,∠BAC=120°,点D为AC上一点,且满足CD =2AD,E为BD上一点,∠AEB=60°,延长AE交BC于F,请直接写出△ABF的面积.解:(1)如图1,过点C作AC的垂线,交AF的延长线于点G.∵∠BAC=90°,∴∠ABD+∠ADB=90°,∵AE⊥BD,∴∠DAE+∠ADB=90°,∴∠CAG=∠ABD,在△ACG和△BAD中,,∴△ACG≌△BAD(ASA),∴CG=AD=AC=,∵BA∥CG,∴△CFG∽△BFA,∴==,即BF=BC,BF:CF=2,∴△ABF的面积=××4×4=;故答案为2,.(2)如图2,过点C作AC的垂线,交AF的延长线于点H.∵∠BAC=90°∴∠ABD+∠ADB=90°,∵AE⊥BD,∴∠DAE+∠ADB=90°,∴∠CAG=∠ABD,在△ACG和△BAD中,,∴△ACH≌△BAD(ASA),∴CH=AD=AC=AB,∵BA∥CH,∴△CFH∽△BFA,∴==,即BF=BC,∴△ABF的面积=××4×4=6;(3)如图3中,作CH⊥BC交AF的延长线于H,AK⊥BC于K.∵AB=AC,∠BAC=120°,∴∠ABC=∠ACB=30°,∵∠BCH=90°,∴∠ACH=∠BAD=120°,∵∠ABD+∠ADB=180°﹣120°=60°,∠AEB=∠EAD+∠ADE=60°,∴∠ABD=∠CAH,∴△BAD≌△ACH(ASA),∴CH=AD∵AK⊥BC,∴BK=CK,在Rt△ACK中,∵AC=4,∠ACK=30°,∴AK=AC=2,CK=BK=2,∵AK∥CH,AD=CH=,∴FK:FC=AK:CH=2:=3:2,∴BF:BC=4:5,∴S△ABF=?S△ABC=××4×2=.。
2020重庆中考复习数学第26题专题训练六(含答案解析)

2020重庆中考复习数学第26题专题训练六1、如图1,在△ABC中,∠BAC=90°,AC=2AB,D是线段AC中点,E是线段AD上一点,过点D作DF⊥BE交BE的延长钱于点F,连接AF,过点A作AG⊥AF于点A,交BF于点G(1)若∠ABE=∠C,BC=2,求AE的长;(2)若点E为AD中点,求证:GE﹣FE=FD;(3)如图2,连接BD,点N为BD中点,连接GN,若AD=GF,请直接写出NG、GE、EA的数量关系.4、已知△ABC中,点D为BC的中点,BD=AB,AD⊥BC.(1)如图1,求∠BAD的度数;(2)如图2,点E为BC上一点,点F为AC上一点,连接AE、BF交于点G,若∠AGF=60°,求证:BE=CF;(3)如图3,在(2)的条件下,点G为BF的中点,点H为AG上一点,延长BH交AC于点K,AK =HK,BM⊥AE交AE延长线于点M,BG=9,HM=10,求线段AG的长.5、已知△ABC中,∠B=60°,点D是AB边上的动点,过点D作DE∥BC交AC于点E,将△ADE沿DE折叠,点A对应点为F点.(1)如图1,当点F恰好落在BC边上,求证:△BDF是等边三角形;(2)如图2,当点F恰好落在△ABC内,且DF的延长线恰好经过点C,CF=EF,求∠A的大小;(3)如图3,当点F恰好落在△ABC外,DF交BC于点G,连接BF,若BF⊥AB,AB=9,求BG 的长.6、如图,在△ABC中,AB=AC,∠BAC=90°,D为BC边的中点,点E在直线BC上(不与点D重合),连接AE,过点C作直线AE的垂线,垂足为点F,交直线AD于点G,连接EG.(1)如图(1),当点E在线段BD上时,易证DE=DG,请直接写出三条线段BE,AB,EG之间的数量关系是 ;(2)如图(2),当点E在线段BC的延长线上时,请写出三条线段BE、AB、EG之间的数量关系,并证明你的结论;(3)若线段BC=2,当△AEG为等腰三角形时,请直接写出的值.7、如图,在△ABC中,∠BAC=90°,将△ABC沿AD翻折,点B恰好与点C重合,点E在AC边上,连接BE.(1)如图①,若点F是BE的中点,连接DF,且AF=5,AE=6,求DF的长;(2)如图②,若AF⊥BE于点F,并延长AF交BC于点G,当点E是AC的中点时,连接EG,求证:AG+EG=BE;(3)在(2)的条件下,连接DF,请直接写出∠DFG的度数.8、如图,在Rt△ABC中,AC=BC,∠ACB=90°,点D、E分别在AC、BC上,BD与AE交于点O,且CD=CE,若点F是BD的中点,连接CF,交AE于点G.(1)求证:CF⊥AE;(2)如图2,过点F作FM⊥BC,交AE的延长线于点M,垂足为H,连接CM,若CG=GM.①求证:CF=CM;②求的值.9、(1)【问题发现】如图1,在Rt△ABC中,AB=AC=4,∠BAC=90°,点D为AC的中点,过点A作BD的垂线,垂足为E,延长AE交BC于点F,求△ABF的面积.小明发现,过点C作AC的垂线,交AF的延长线于点G,构造出全等三角形,经过推理和计算,能够得到BF与CF的数量关系,从而使问题得到解决,请直接填空:= 2,△ABF的面积为.(2)【类比探究】如图2,将(1)中的条件“点D为AC的中点”改为“点D为边AC上的一点,且满足CD=2AD”,其他条件不变,试求△ABF的面积,并写出推理过程.(3)【拓展迁移】如图3,在△ABC中,AB=AC=4,∠BAC=120°,点D为AC上一点,且满足CD =2AD,E为BD上一点,∠AEB=60°,延长AE交BC于F,请直接写出△ABF的面积.2020重庆中考复习数学第26题专题训练六参考答案1、如图1,在△ABC中,∠BAC=90°,AC=2AB,D是线段AC中点,E是线段AD上一点,过点D作DF⊥BE交BE的延长钱于点F,连接AF,过点A作AG⊥AF于点A,交BF于点G(1)若∠ABE=∠C,BC=2,求AE的长;(2)若点E为AD中点,求证:GE﹣FE=FD;(3)如图2,连接BD,点N为BD中点,连接GN,若AD=GF,请直接写出NG、GE、EA的数量关系.解:(1)∵△ABC中,∠BAC=90°,AC=2AB,BC=2,∴由勾股定理可得AB=2,AC=4,∵∠ABE=∠C,∠BAE=∠CAB=90°,∴△BAE∽△CAB,∴AB2=AE×AC,即22=AE×4,解得AE=1,(2)证明:如图1,过A作AH⊥BF于H,则∠AHE=90°,∵DF⊥BE,∠BAC=90°,∠AEB=∠FED,∴∠ABG=∠ADF,∵AG⊥AF,∠BAC=90°,∴∠BAG=∠DAF,∵AC=2AB,D是线段AC中点,∴AB=AD,在△ABG和△ADF中,,∴△ABG≌△ADF(ASA),∴AG=AF,∴△AGF是等腰直角三角形,∴AH=GF=GH,∵点E为AD中点,∴AE=DE,在△AEH和△DEF中,,∴△AEH≌△DEF(AAS),∴EH=EF,AH=DF=GH,∵GE﹣HE=GH,∴GE﹣FE=FD;(3)NG、GE、EA的数量关系为:NG+GE=2AE.理由:如图2,连接AN,NF,由(2)可得,△AGF是等腰直角三角形,∵AB=AD,∠BAD=90°,N是BD的中点,∴∠DAN=45°=∠ADN,∴△ADN是等腰直角三角形,∵AD=GF,∴等腰Rt△AGF与等腰Rt△ADN全等,∴AG=AF=AN=ND,∵Rt△BDF中,N是BD的中点,∴NF=ND=BN,∴AN=NF=AF,即△ANF是等边三角形,∴∠NAF=∠ANF=60°,∵∠DAN=45°,△ABG≌△ADF,∴∠DAF=15°=∠BAG,∵∠ABN=∠BAN=45°,∴∠GAN=30°,∵∠AGF=45°,∴∠ABE=30°,∴Rt△ABE中,BE=2AE,∵∠ABN=45°,∴∠GBN=15°,由NF=ND=NB,可得∠FND=2∠GBN=30°, 在△ANG和△NDF中,,∴△ANG≌△NDF(SAS),∴GN=FD=BG,∵BG+GE=BE=2AE,∴NG+GE=2AE.G解:(1)由E 为CR 中点可得AG平分BAC ∠,过G 作GH AB ⊥,则有GH=CG=1,故 (2)延长FD 交AG 于点M,易证:()BFD AMD AAS ∆≅∆,所以BF=AM 再证:()BFC CEA AAS∆≅∆,所以BF=CE=AM,CF=AE ∴CF-CE=AE-AM,即EM=EF ∴EFM ∆为等腰直角三角形∴2EF FM ==(3)结论为:2BD EF +=4、(2017秋•许昌月考)已知△ABC中,点D为BC的中点,BD=AB,AD⊥BC.(1)如图1,求∠BAD的度数;(2)如图2,点E为BC上一点,点F为AC上一点,连接AE、BF交于点G,若∠AGF=60°,求证:BE=CF;(3)如图3,在(2)的条件下,点G为BF的中点,点H为AG上一点,延长BH交AC于点K,AK =HK,BM⊥AE交AE延长线于点M,BG=9,HM=10,求线段AG的长.解:(1)∵点D为BC的中点,AD⊥BC,∴AB=AC,BD=CD=BC,∵BD=AB,∴AB=BC=AC,∴△ABC是等边三角形,∴∠BAC=60°,∵AD⊥BC,∴∠BAD=∠BAC=30°;(2)由(1)知,△ABC是等边三角形,∴AB=BC,∠ABC=∠C=60°,∴∠ABF+∠CBF=60°,∵∠AGF=60°,∴∠BAE+∠ABF=60°,∴∠BAE=∠CBF,在△ABE和△BCF中,,∴△ABE≌△BCF(ASA),∴BE=CF,(3)如图,过F作FN⊥AE于N,过F作FD⊥BM,交BM的延长线于D,∵AM⊥BM,∴GM∥DF,∵BG=GF,∴BM=DM,∵∠AGF=60°,∴∠BGM=60°,∵BM⊥AE,∴∠BMG=90°,∴∠GBM=30°,在Rt△BMG中,MG=BG=,BM=DM=FN=,∵AK=HK,∴∠HAK=∠AHK=∠BHM,∵∠ANF=∠HMB=90°,∴△ANF≌△HMB,∴AN=HM=10,Rt△FGN中,∠NFG=∠GBM=30°,∴GN=GF=,∴AG=AN+NG=10+=14.5.5、(2019秋•中山市期末)已知△ABC中,∠B=60°,点D是AB边上的动点,过点D作DE∥BC交AC于点E,将△ADE沿DE折叠,点A对应点为F点.(1)如图1,当点F恰好落在BC边上,求证:△BDF是等边三角形;(2)如图2,当点F恰好落在△ABC内,且DF的延长线恰好经过点C,CF=EF,求∠A的大小;(3)如图3,当点F恰好落在△ABC外,DF交BC于点G,连接BF,若BF⊥AB,AB=9,求BG 的长.(1)证明:如图1,∵∠B=60°,DE∥BC,∴∠ADE=∠B=60°,∵△ADE沿DE折叠,点A对应点为F点,∴∠ADE=∠FDE=60°,∴∠BDF=60°,∴∠DFB=60°=∠B=∠BDF,∴△BDF是等边三角形;(2)解:∵∠B=60°,DE∥BC,∴∠ADE=∠B=60°,∵△ADE沿DE折叠,点A对应点为F点,∴∠ADE=∠FDE=60°,∠A=∠DFE,∴∠ADC=120°,∵CF=EF,∴∠FEC=∠FCE,设∠FEC=∠FCE=x,则∠A=∠DFE=∠FEC+∠FCE=2x,在△ADC中,∠A+∠ACD+∠ADC=180°,即2x+x+120°=180°,解得:x=20°,∴∠A=2x=40°;(3)解:同(1)得:∠BDF=60°,△BDG是等边三角形,∠ADE=∠B=60°,∴BG=BD, 由折叠的性质得:AD=FD,∵BF⊥AB,∴∠BFD=90°﹣60°=30°,∴FD=2BD,∴AD=2BD,∵AD+BD=AB,∴2BD+BD=9,∴BD=3,∴BG=BD=3.6、(2018•连山区一模)如图,在△ABC中,AB=AC,∠BAC=90°,D为BC边的中点,点E在直线BC上(不与点D重合),连接AE,过点C作直线AE的垂线,垂足为点F,交直线AD于点G,连接EG. (1)如图(1),当点E在线段BD上时,易证DE=DG,请直接写出三条线段BE,AB,EG之间的数量关系是 AB﹣EG=BE;(2)如图(2),当点E在线段BC的延长线上时,请写出三条线段BE、AB、EG之间的数量关系,并证明你的结论;(3)若线段BC=2,当△AEG为等腰三角形时,请直接写出的值.解:(1)如图1中,结论:AB﹣EG=BE理由:∵AB=AC,∠BAC=90°,BD=DC,∴AD⊥BC,∠ABC=∠ACB=45°,AD=BD=DC,∴BD=AB,∵CF⊥AE,∴∠AFG=∠CDG=90°,∵∠AGF=∠CGD,∴∠F AG=∠GCD,∵∠ADE=∠CDG,∴△ADE≌△CDG,∴DE=DG,∴DE=EG,∵BE+ED=BD,∴BE+EG=AB,∴AB﹣EG=BE.(2)如图2中,结论:AB+EG=BE.理由:同法可证:△ADE≌△CDG,∴DE=DG,∴DE=EG,∵BE﹣ED=BD,∴BE+﹣EG=AB,∴AB+EG=BE.(3)①如图2中,当GA=GE时,DG=DE=2﹣2,EG=4﹣2,此时:==﹣1.②如图3中,当GA=GE时,设BD=AD=CD=a,则AB=AC=CE=a,DG=DE=a+a,EG=a+2a,∴==1+.③当点E与点C重合时,EG=AB,可得EG:AB=1,综上所述,的值为﹣1或1+或1.7、(2018•站前区校级一模)如图,在△ABC中,∠BAC=90°,将△ABC沿AD翻折,点B恰好与点C重合,点E在AC边上,连接BE.(1)如图①,若点F是BE的中点,连接DF,且AF=5,AE=6,求DF的长;(2)如图②,若AF⊥BE于点F,并延长AF交BC于点G,当点E是AC的中点时,连接EG,求证:AG+EG=BE;(3)在(2)的条件下,连接DF,请直接写出∠DFG的度数.解:(1)∵将△ABC沿AD翻折,点B恰好与点C重合,∴AB=AC,BD=CD,∠ADB=∠ADC=90°,且∠BAC=90°,∴△ABC是等腰直角三角形,∵点F是BE的中点,AF=5,∠BAC=90°,∴BE=10,∴AB===8,∴AC=8,∴EC=2,∵BD=CD,BF=EF,∴DF=EC=1,(2)如图②,过点C作CH⊥AC交AG的延长线于点H,∵AB=AC,∠BAC=90°,BD=CD,∴∠ABC=∠BAD=∠DAC=∠ACB=45°,∵∠BEA+∠CAH=90°,∠CAH+∠H=90°,∴∠H=∠BEA,且AB=AC,∠AFB=∠ACH=90°,∴△ABE≌△CAH(AAS)∴BE=AH,AE=CH,∠CAH=∠ABE,∵AE=CE,∴CE=CH,∵∠ACH=90°,∠ACB=45°,∴∠ACB=∠GCH,且CE=CH,CG=CG,∴△CEG≌△CHG(SAS)∴EG=GH,∵BE=AH=AG+GH,∴AG+EG=BE;(3)如图②,连接NG,∵∠ABC=∠BAD=∠DAC=∠ACB=45°,∴AD=BD=CD,∵∠BAN=∠ACG=45°,AB=AC,∠ABE=∠CAH,∴△ABN≌△CAG(ASA)∴AN=CG,∴AD﹣AN=CD﹣CG,∴DN=DG,∴∠DNG=45°∵∠NDG=∠NFG=90°,∴点N,点F,点G,点D四点共圆,∴∠DFG=∠DNG=45°.8、如图,在Rt△ABC中,AC=BC,∠ACB=90°,点D、E分别在AC、BC上,BD与AE交于点O,且CD=CE,若点F是BD的中点,连接CF,交AE于点G.(1)求证:CF⊥AE;(2)如图2,过点F作FM⊥BC,交AE的延长线于点M,垂足为H,连接CM,若CG=GM.①求证:CF=CM;②求的值.(1)证明:如图1中,∵AC=BC,∠ACE=∠BCD=90°,CE=CD,∴△ACE≌△BCD(SAS),∴∠CAE=∠CBD,∵DF=FB,∴CF=FD=FB,∴∠FCB=∠FBC,∴∠FCB=∠CAE,∵∠CAB+∠AEC=90°,∴∠AEC+∠FCB=90°,∴∠CGE=90°,∴CF⊥AE.(2)①证明:如图2中,∵FM⊥BC,∴∠FHC=∠CGE=∠MGF=90°,∴∠ECG+∠CEG=90°,∠ECG+∠CFH=90°, ∴∠CEG=∠CFH,∵CG=GM,∴△CGE≌△MGF(AAS),∴CE=FM,EG=GF,∵CD=CE,∴CD=FM,∵∠FHB=∠ACB=90°,∴CD∥FM,∴四边形CDFM是平行四边形,∴CM=DF,∵CF=DF=FB,∴CM=CF.②连接EF,BM.设FG=EG=a,∵CM=BF,CM∥BF,∴FG∥BM,∴=,∵△CAE≌△CBD,∴∠CAE=∠CBD,∵∠CAB=∠CBA,∴∠OAB=∠OBA,∴OA=OB,∴=,易知OG=GF=EG=a,EF=EM=a,∴OM=2a+a,∴==.9、(2015•新乡二模)(1)【问题发现】如图1,在Rt△ABC中,AB=AC=4,∠BAC=90°,点D为AC的中点,过点A作BD的垂线,垂足为E,延长AE交BC于点F,求△ABF的面积.小明发现,过点C作AC的垂线,交AF的延长线于点G,构造出全等三角形,经过推理和计算,能够得到BF与CF的数量关系,从而使问题得到解决,请直接填空:= 2,△ABF的面积为.(2)【类比探究】如图2,将(1)中的条件“点D为AC的中点”改为“点D为边AC上的一点,且满足CD=2AD”,其他条件不变,试求△ABF的面积,并写出推理过程.(3)【拓展迁移】如图3,在△ABC中,AB=AC=4,∠BAC=120°,点D为AC上一点,且满足CD =2AD,E为BD上一点,∠AEB=60°,延长AE交BC于F,请直接写出△ABF的面积.解:(1)如图1,过点C作AC的垂线,交AF的延长线于点G.∵∠BAC=90°,∴∠ABD+∠ADB=90°,∵AE⊥BD,∴∠DAE+∠ADB=90°,∴∠CAG=∠ABD,在△ACG和△BAD中,,∴△ACG≌△BAD(ASA),∴CG=AD=AC=,∵BA∥CG,∴△CFG∽△BF A,∴==,即BF=BC,BF:CF=2,∴△ABF的面积=××4×4=;故答案为2,.(2)如图2,过点C作AC的垂线,交AF的延长线于点H.∵∠BAC=90°∴∠ABD+∠ADB=90°,∵AE⊥BD,∴∠DAE+∠ADB=90°,∴∠CAG=∠ABD,在△ACG和△BAD中,,∴△ACH≌△BAD(ASA),∴CH=AD=AC=AB,∵BA∥CH,∴△CFH∽△BF A,∴==,即BF=BC,∴△ABF的面积=××4×4=6;(3)如图3中,作CH⊥BC交AF的延长线于H,AK⊥BC于K.∵AB=AC,∠BAC=120°,∴∠ABC=∠ACB=30°,∵∠BCH=90°,∴∠ACH=∠BAD=120°,∵∠ABD+∠ADB=180°﹣120°=60°,∠AEB=∠EAD+∠ADE=60°, ∴∠ABD=∠CAH,∴△BAD≌△ACH(ASA),∴CH=AD∵AK⊥BC,∴BK=CK,在Rt△ACK中,∵AC=4,∠ACK=30°,∴AK=AC=2,CK=BK=2,∵AK∥CH,AD=CH=,∴FK:FC=AK:CH=2:=3:2,∴BF:BC=4:5,∴S△ABF=•S△ABC=××4×2=.。
2021年重庆年中考26题三角形四边形几何综合专题(八中试题集)

2021年重庆年中考26题三角形四边形几何综合专题(八中试题集)1(八中2020级初三下定时训练九)在菱形ABCD中,∠ABC=60°,点M是对角线BD上一动点,将线段CM绕点C顺时针旋转120°到CN,连接DN,连接NM并延长,分别交AB、CD于点P、Q.(1)如图1,若CM⊥BD且PQ=4,求菱形ABCD的面积;(2)如图2,求证:PM=QN.2(八中2020级初三下定时训练五))已知:在△ABC中,∠C=90°,BC=AC.(1)如图1,若点D、E分别在BC、AC边上,且CD=CE,连接AD、BE,点O、M、N分别是AB、AD、BE 的中点.求证:△OMN是等腰直⻆三角形;(2)将图1中△CDE绕着点C顺时针旋转90°如图2,O、M、N分别为AB、AD、BE中点,则(1)中的结论是否成⽴,并说明理由;(3)如图3,将图1中△CDE绕着点C顺时针旋转,记旋转⻆为α(0<α<360°),O、M、N分别为AB、AD、BE中点,当MN=,请求出四边形ABED的⽴积.3(八中2020级初三下定时训练八)问题提出(1)如图①,在等腰Rt△ABC中,斜边AC=4,点D为AC上一点,连接BD,则BD的最小值为;问题探究(2)如图②,在△ABC中,AB=AC=5,BC=6,点M是BC上一点,且BM=4,点P是边AB上一动点,连接PM,将△BPM沿PM翻折得到△DPM,点D与点B对应,连接AD,求AD的最小值;问题解决(3)如图③,四边形ABCD是规划中的休闲广场示意图,其中∠BAD=∠ADC=135°,∠DCB=30°,AD=2km,AB=3km,点M是BC上一点,MC=4km.现计划在四边形ABCD内选取一点P,把△DCP建成商业活动区,其余部分建成景观绿化区.为方便进入商业区,需修建小路BP、MP,从实用和美观的角度,要求满足∠PMB=∠ABP,且景观绿化区面积足够大,即△DCP区域面积尽可能小.则在四边形ABCD内是否存在这样的点P?若存在,请求出△DCP面积的最小值;若不存在,请说明理由.4(八中2021级初三上第一次月考模拟)在矩形ABCD 中 ,点E 是BC 边上一点,连接AE ,点F 是CB 延长线上一点,点G 是矩形ABCD 外一点,连接GC ,GE ,GB ,GF ,GF ⊥GC ,CE 平分∠BGC ,∠GEF=45.(1)如图1,当∠EGC=15,BG=2时,求△CGF 的面积;(2)如图2,当矩形ABCD 是正方形,FB=CE 时,求证:FG ;(3)如图3,若线段PQ 在GE 上运动,PA =2BE =,3FB BE =,请直接写出线段FP+PQ+QC 的和的最小值以及此时△PBE 的面积。
专题26圆的有关计算(共52题)-2021年中考数学真题分项汇编(原卷版)【全国通用】(第01期)

2021年中考数学真题分项汇编【全国通用】(第01期)专题26圆的有关计算(共52题)一、单选题1.(2021·四川广元市·中考真题)如图,从一块直径是2的圆形铁片上剪出一个圆心角为90︒的扇形,将剪下来的扇形围成一个圆锥.那么这个圆锥的底面圆的半径是( )A .4πBC .12D .12.(2021·浙江衢州市·中考真题)已知扇形的半径为6,圆心角为150︒.则它的面积是( ) A .32π B .3π C .5π D .15π3.(2021·四川广安市·中考真题)如图,公园内有一个半径为18米的圆形草坪,从A 地走到B 地有观赏路(劣弧AB )和便民路(线段AB ).已知A 、B 是圆上的点,O 为圆心,120AOB ∠=︒,小强从A 走到B ,走便民路比走观赏路少走( )米.A .6π-B .6π-C .12π-D .12π-4.(2021·四川遂宁市·中考真题)如图,在△ABC 中,AB =AC ,以AB 为直径的△O 分别与BC ,AC 交于点D ,E ,过点D 作DF △AC ,垂足为点F ,若△O 的半径为△CDF =15°, 则阴影部分的面积为( )A .16π-B .16π-C .20π-D .20π-5.(2021·浙江中考真题)如图,已知在矩形ABCD 中,1,AB BC ==P 是AD 边上的一个动点,连结BP ,点C 关于直线BP 的对称点为1C ,当点P 运动时,点1C 也随之运动.若点P 从点A 运动到点D ,则线段1CC 扫过的区域的面积是( )A .πB .π+CD .2π6.(2021·山东枣庄市·中考真题)如图,正方形ABCD 的边长为2,O 为对角线的交点,点E 、F 分别为BC 、AD 的中点.以C 为圆心,2为半径作圆弧BD ,再分别以E 、F 为圆心,1为半径作圆弧BO 、OD ,则图中阴影部分的面积为( )A .π﹣1B .π﹣2C .π﹣3D .4﹣π7.(2021·青海中考真题)如图,一根5米长的绳子,一端拴在围墙墙角的柱子上,另一端拴着一只羊A (羊在草地上活动),那么羊在草地上的最大活动区域面积是( )平方米.A .17π12B .17π6C .25π4D .77π128.(2021·湖北荆州市·中考真题)如图,在菱形ABCD 中,60D ∠=︒,2AB =,以B 为圆心、BC 长为半径画AC ,点P 为菱形内一点,连接PA ,PB ,PC .当BPC △为等腰直角三角形时,图中阴影部分的面积为( )A .2132π-B .2132π-C .2πD .122π- 9.(2021·四川广元市·中考真题)如图,在边长为2的正方形ABCD 中,AE 是以BC 为直径的半圆的切线,则图中阴影部分的面积为( )A .32π+B .2π-C .1D .52π- 10.(2021·江苏苏州市·中考真题)如图,线段10AB =,点C 、D 在AB 上,1AC BD ==.已知点P 从点C 出发,以每秒1个单位长度的速度沿着AB 向点D 移动,到达点D 后停止移动,在点P 移动过程中作如下操作:先以点P 为圆心,PA 、PB 的长为半径分别作两个圆心角均为60°的扇形,再将两个扇形分别围成两个圆锥的侧面.设点P 的移动时间为(秒).两个圆锥的底面面积之和为S .则S 关于t 的函数图像大致是( )A.B.C.D.11.(2021·山东东营市·中考真题)已知某几何体的三视图如图所示,则该几何体的侧面展开图圆心角的度数为()A.214°B.215°C.216°D.217°12.(2021·四川成都市·中考真题)如图,正六边形ABCDEF的边长为6,以顶点A为圆心,AB的长为半径画圆,则图中阴影部分的面积为()A .4πB .6πC .8πD .12π13.(2021·云南中考真题)如图,等边ABC 的三个顶点都在O 上,AD 是O 的直径.若3OA =,则劣弧BD 的长是( )A .2πB .πC .32πD .2π14.(2021·湖北中考真题)用半径为30cm ,圆心角为120︒的扇形纸片恰好能围成一个圆锥的侧面,则这个圆锥底面半径为( )A .5cmB .10cmC .15cmD .20cm15.(2021·湖南张家界市·中考真题)如图,正方形ABCD 内的图形来自中国古代的太极图,正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称,设正方形ABCD 的面积为S ,黑色部分面积为1S ,则1:S S 的比值为( )A .8πB .4πC .14D .1216.(2021·河北中考真题)如图,点O 为正六边形ABCDEF 对角线FD 上一点,8AFO S =△,2CDO S =△,则ABCDEF S 正六边形的值是( )A .20B .30C .40D .随点O 位置而变化二、填空题 17.(2021·黑龙江绥化市·中考真题)边长为4cm 的正六边形,它的外接圆与内切圆半径的比值是_______. 18.(2021·上海中考真题)六个带30角的直角三角板拼成一个正六边形,直角三角板的最短边为1,求中间正六边形的面积_________.19.(2021·江西中考真题)如图,在边长为ABCDEF 中,连接BE ,CF ,其中点M ,N 分别为BE 和CF 上的动点,若以M ,N ,D 为顶点的三角形是等边三角形,且边长为整数,则该等边三角形的边长为______.20.(2021·重庆中考真题)如图,在菱形ABCD 中,对角线12AC =,16BD =,分别以点A ,B ,C ,D 为圆心,12AB 的长为半径画弧,与该菱形的边相交,则图中阴影部分的面积为__________.(结果保留π)21.(2021·四川凉山彝族自治州·中考真题)如图,将ABC 绕点C 顺时针旋转120︒得到''A B C .已知3,2AC BC ==,则线段AB 扫过的图形(阴影部分)的面积为__________________.22.(2021·浙江温州市·中考真题)若扇形的圆心角为30,半径为17,则扇形的弧长为______. 23.(2021·山东泰安市·中考真题)若ABC 为直角三角形,4AC BC ==,以BC 为直径画半圆如图所示,则阴影部分的面积为________.24.(2021·山东聊城市·中考真题)用一块弧长16πcm 的扇形铁片,做一个高为6cm 的圆锥形工件侧面(接缝忽略不计),那么这个扇形铁片的面积为_______cm 225.(2021·四川资阳市·中考真题)如图,在矩形ABCD 中,2cm,AB AD ==,以点B 为圆心,AB长为半径画弧,交CD 于点E ,则图中阴影部分的面积为_______2cm .26.(2021·江苏宿迁市·中考真题)已知圆锥的底面圆半径为4,侧面展开图扇形的圆心角为120°,则它的侧面展开图面积为_____________.27.(2021·湖北随州市·中考真题)如图,在Rt ABC 中,90C ∠=︒,30ABC ∠=︒,BC =,将ABC 绕点A 逆时针旋转角α(0180α︒<<︒)得到AB C ''△,并使点C '落在AB 边上,则点B 所经过的路径长为______.(结果保留π)28.(2021·湖南中考真题)如图,方老师用一张半径为18cm 的扇形纸板,做了一个圆锥形帽子(接缝忽略不计).如果圆锥形帽子的半径是10cm ,那么这张扇形纸板的面积是________2cm (结果用含π的式子表示).29.(2021·浙江嘉兴市·中考真题)如图,在ABC ∆中,30BAC ∠=︒,45ACB ∠=︒,2AB =,点P 从点A 出发沿AB 方向运动,到达点B 时停止运动,连结CP ,点A 关于直线CP 的对称点为'A ,连接A ′C ,'A P .在运动过程中,点'A 到直线AB 距离的最大值是_______;点P 到达点B 时,线段'A P 扫过的面积为___________.30.(2021·湖南衡阳市·中考真题)底面半径为3,母线长为4的圆锥的侧面积为__________.(结果保留π) 31.(2021·重庆中考真题)如图,矩形ABCD 的对角线AC ,BD 交于点O ,分别以点A ,C 为圆心,AO 长为半径画弧,分别交AB ,CD 于点E ,F .若BD =4,△CAB =36°,则图中阴影部分的面积为___________.(结果保留π).32.(2021·浙江宁波市·中考真题)抖空竹在我国有着悠久的历史,是国家级的非物质文化遗产之一.如示意图,,AC BD 分别与O 相切于点C ,D ,延长,AC BD 交于点P .若120P ∠=︒,O 的半径为6cm ,则图中CD 的长为________cm .(结果保留π)33.(2021·甘肃武威市·中考真题)如图,从一块直径为4dm 的圆形铁皮上剪出一个圆心角为90︒的扇形,则此扇形的面积为_____2dm .34.(2021·浙江台州市·中考真题)如图,将线段AB 绕点A 顺时针旋转30°,得到线段AC .若AB =12,则点B 经过的路径BC 长度为_____.(结果保留π)35.(2021·江苏无锡市·中考真题)用半径为50,圆心角为120°的扇形纸片围成一个圆锥的侧面,则这个圆锥的底面半径为________.36.(2021·广东中考真题)如图,等腰直角三角形ABC 中,90,4A BC ∠=︒=.分别以点B 、点C 为圆心,线段BC 长的一半为半径作圆弧,交AB 、BC 、AC 于点D 、E 、F ,则图中阴影部分的面积为____.37.(2021·黑龙江鹤岗市·中考真题)若一个圆锥的底面半径为1cm ,它的侧面展开图的圆心角为90︒,则这个圆锥的母线长为____ cm .38.(2021·湖南怀化市·中考真题)如图,在O 中,3OA =,45C ∠=︒,则图中阴影部分的面积是_________.(结果保留π)39.(2021·湖北十堰市·中考真题)如图,在边长为4的正方形ABCD 中,以AB 为直径的半圆交对角线AC 于点E ,以C 为圆心、BC 长为半径画弧交AC 于点F ,则图中阴影部分的面积是_________.40.(2021·湖南岳阳市·中考真题)如图,在Rt ABC 中,90C ∠=︒,AB 的垂直平分线分别交AB 、AC 于点D 、E ,8BE =,O 为BCE 的外接圆,过点E 作O 的切线EF 交AB 于点F ,则下列结论正确的是______.(写出所有正确结论的序号)△AE BE =;△AED CBD ∠=∠;△若40DBE ∠=︒,则DE 的长为89π;△DF EF EF BF=;△若6EF =,则 2.24CE =.41.(2021·吉林长春市·中考真题)如图是圆弧形状的铁轨示意图,半径OA 的长度为200米,圆心角90AOB ∠=︒,则这段铁轨的长度_____米,(铁轨的宽度忽略不计,结果保留π)42.(2021·湖北宜昌市·中考真题)“莱洛三角形”是工业生产中加工零件时广泛使用的一种图形.如图,以边长为2厘米的等边三角形ABC 的三个顶点为圆心,以边长为半径画弧,三段圆弧围成的图形就是“莱洛三角形”,该“莱洛三角形”的面积为____________平方厘米.(圆周率用π表示)三、解答题43.(2021·江苏扬州市·中考真题)如图,四边形ABCD 中,//AD BC ,90BAD ∠=︒,CB CD =,连接BD ,以点B 为圆心,BA 长为半径作B ,交BD 于点E .(1)试判断CD 与B 的位置关系,并说明理由;(2)若AB =60BCD ∠=︒,求图中阴影部分的面积.44.(2021·浙江丽水市·中考真题)如图,在ABC 中,AC BC =,以BC 为直径的半圆O 交AB 于点D ,过点D 作半圆O 的切线,交AC 于点E .(1)求证:2ACB ADE ∠=∠;(2)若3,DE AE ==CD 的长.45.(2021·湖北随州市·中考真题)等面积法是一种常用的、重要的数学解题方法.它是利用“同一个图形的面积相等”、“分割图形后各部分的面积之和等于原图形的面积”、“同底等高或等底同高的两个三角形面积相等”等性质解决有关数学问题,在解题中,灵活运用等面积法解决相关问题,可以使解题思路清晰,解题过程简便快捷.(1)在直角三角形中,两直角边长分别为3和4,则该直角三角形斜边上的高的长为_____,其内切圆的半径长为______;(2)△如图1,P 是边长为a 的正ABC 内任意一点,点O 为ABC 的中心,设点P 到ABC 各边距离分别为1h ,2h ,3h ,连接AP ,BP ,CP ,由等面积法,易知()123123ABC OAB h h h S a S ++==△△,可得123h h h ++=_____;(结果用含a 的式子表示)△如图2,P 是边长为a 的正五边形ABCDE 内任意一点,设点P 到五边形ABCDE 各边距离分别为1h ,2h ,3h ,4h ,5h ,参照△的探索过程,试用含a 的式子表示12345h h h h h ++++的值.(参考数据:8tan 3611≈°,11tan 548≈°)(3)△如图3,已知O 的半径为2,点A 为O 外一点,4OA =,AB 切O 于点B ,弦//BC OA ,连接AC ,则图中阴影部分的面积为______;(结果保留π)△如图4,现有六边形花坛ABCDEF ,由于修路等原因需将花坛进行改造.若要将花坛形状改造成五边形ABCDG ,其中点G 在AF 的延长线上,且要保证改造前后花坛的面积不变,试确定点G 的位置,并说明理由.46.(2021·浙江金华市·中考真题)在扇形AOB 中,半径6OA =,点P 在OA 上,连结PB ,将OBP 沿PB 折叠得到O BP '.(1)如图1,若75O ∠=︒,且BO '与AB 所在的圆相切于点B .△求APO ∠'的度数.△求AP 的长.(2)如图2,BO '与AB 相交于点D ,若点D 为AB 的中点,且//PD OB ,求AB 的长.47.(2021·湖南张家界市·中考真题)如图,在Rt AOB 中,90∠=︒ABO ,30OAB ∠=︒,以点O 为圆心,OB 为半径的圆交BO 的延长线于点C ,过点C 作OA 的平行线,交O 于点D ,连接AD .(1)求证:AD 为O 的切线;(2)若2OB =,求弧CD 的长.48.(2021·四川达州市·中考真题)如图,AB 是O 的直径,C 为O 上一点(C 不与点A ,B 重合)连接AC ,BC ,过点C 作CD AB ⊥,垂足为点D .将ACD ∆沿AC 翻折,点D 落在点E 处得ACE ∆,AE 交O 于点F .(1)求证:CE 是O 的切线;(2)若15BAC ∠=︒,2OA =,求阴影部分面积.49.(2021·湖南邵阳市·中考真题)某种冰激凌的外包装可以视为圆锥,它的底面圆直径ED 与母线AD 长之比为1:2.制作这种外包装需要用如图所示的等腰三角形材料,其中AB AC =,AD BC ⊥.将扇形AEF 围成圆锥时,AE ,AF 恰好重合.(1)求这种加工材料的顶角BAC ∠的大小(2)若圆锥底面圆的直径ED 为5cm ,求加工材料剩余部分(图中阴影部分)的面积.(结果保留π)50.(2021·湖北黄冈市·中考真题)如图,在Rt ABC △中,90ACB ∠=︒,O 与BC ,AC 分别相切于点E ,F ,BO 平分ABC ∠,连接OA .(1)求证:AB 是O 的切线;(2)若3BE AC ==,O 的半径是1,求图中阴影部分的面积.51.(2021·山东菏泽市·中考真题)在矩形ABCD 中,BC =,点E ,F 分别是边AD 、BC 上的动点,且AE CF =,连接EF ,将矩形ABCD 沿EF 折叠,点C 落在点G 处,点D 落在点H 处.(1)如图1,当EH 与线段BC 交于点P 时,求证:PE PF =;(2)如图2,当点P 在线段CB 的延长线上时,GH 交AB 于点M ,求证:点M 在线段EF 的垂直平分线上;(3)当5AB =时,在点E 由点A 移动到AD 中点的过程中,计算出点G 运动的路线长.52.(2021·江苏南京市·中考真题)在几何体表面上,蚂蚁怎样爬行路径最短?(1)如图△,圆锥的母线长为12cm ,B 为母线OC 的中点,点A 在底面圆周上,AC 的长为4cm π.在图△所示的圆锥的侧面展开图中画出蚂蚁从点A 爬行到点B 的最短路径,并标出它的长(结果保留根号).(2)图△中的几何体由底面半径相同的圆锥和圆柱组成.O是圆锥的顶点,点A在圆柱的底面圆周上.设圆锥的母线长为l,圆柱的高为h.△蚂蚁从点A爬行到点O的最短路径的长为________(用含l,h的代数式表示)..圆柱的侧面展开图如图△所示,在图中画出蚂蚁从点A △设AD的长为a,点B在母线OC上,OB b爬行到点B的最短路径的示意图,并写出求最短路径的长的思路.。
2020年重庆中考26题二次函数综合

二次函数二次函数压轴题总结:(凡解析几何问题,均是以几何性质探路,代数书写竣工。
) 已知、 y=322--x x (以下几种分类的函数解析式就是这个)1、和最小,差最大 在对称轴上找一点P ,使得PB+PC 的和最小,求出P 点坐标 在对称轴上找一点P ,使得PB-PC 的差最大,求出P 点坐标解决方案:识别模型,A 、若为过河问题模型,根据“异侧和最小,同侧差最大,根据问题同侧异侧相互转化”;B 、若有绝对值符号或不隶属于过河问题,可将问题形式平方,构建函数,转化为求函数最值问题(若表达式中含有根式等形式,可考虑用换元法求最值)。
2、求面积最大 连接AC,在第四象限抛物线上找一点P ,使得ACP ∆面积最大,求出P 坐标解决方案:熟悉基本图形的面积公式【或根据拼图思想,采用割补法求面积(注意不重不漏)。
】,根据问题,灵活选择面积公式,务必使表达式简单,变量的最值好求,讲变量的最值问题转化为:”定值+变量的最值“3、讨论直角三角 连接AC,在对称轴上找一点P ,使得ACP ∆为直角三角形,求出P 坐标或者在抛物线上求点P ,使△ACP 是以AC 为直角边的直角三角形.解决方案:此类问题是分类讨论思想能力的考察,由于直角三角形的”直角边“”和“斜边”不确定而展开讨论。
在不忘三角形满足三边关系的条件下,勿忘“等腰直角三角形”。
4、讨论等腰三角 连接AC,在对称轴上找一点P ,使得ACP ∆为等腰三角形,求出P 坐标 解决方案:分析同上4,在能组成△的大前提下,根据谁作为腰,谁作为底边展开讨论。
5、讨论平行四边形 1、点E 在抛物线的对称轴上,点F 在抛物线上,且以B ,A ,F ,E 四点为顶点的四 边形为平行四边形,求点F 的坐标解决方案:从平行四边形的性质入手,已知三点求另外一点,分析其位置情况(分别以3点中任一已知两点的线段为平行四边形的边或其对角线来展开所有的情况的讨论)。
6、相似三角形 问抛物线上是否存在一动点D ,使得△ABD ∽△ABC 。
最新重庆中考数学第26题专题训练

N MPCBA 1.如图,抛物线y=﹣x 2﹣2x+3 的图象与x 轴交于A 、B 两点(点A 在点B 的左边),与y 轴交于点C ,点D 为抛物线的顶点.(1)求A 、B 、C 的坐标;(2)点M 为线段AB 上一点(点M 不与点A 、B 重合),过点M 作x 轴的垂线,与直线AC 交于点E ,与抛物线交于点P ,过点P 作PQ ∥AB 交抛物线于点Q ,过点Q 作QN ⊥x 轴于点N .若点P 在点Q 左边,当矩形PQMN 的周长最大时,求△AEM 的面积;(3)在(2)的条件下,当矩形PMNQ 的周长最大时,连接DQ .过抛物线上一点F 作y轴的平行线,与直线AC 交于点G (点G 在点F 的上方).若FG=2DQ ,求点F 的坐标.2.如图,已知抛物线223y x x =-++与x 轴交于A 、B 两点(点A 在点B 的左边),与y 轴交于点C ,连接BC 。
(1)求A 、B 、C 三点的坐标;(2)若点P 为线段BC 上的一点(不与B 、C 重合),PM ∥y 轴,且PM 交抛物线于点M ,交x 轴于点N ,当△BCM 的面积最大时,求△BPN 的周长;(3)在(2)的条件下,当BCM 的面积最大时,在抛物线的对称轴上存在点Q ,使得△CNQ 为直角三角形,求点Q 的坐标。
3.如图,对称轴为直线x 1=-的抛物线()2y ax bx c a 0=++≠与x 轴相交于A 、B 两点,其中A 点的坐标为(-3,0)。
(1)求点B 的坐标;(2)已知a 1=,C 为抛物线与y 轴的交点。
①若点P 在抛物线上,且POC BOC S 4S ∆∆=,求点P 的坐标;②设点Q 是线段AC 上的动点,作QD ⊥x 轴交抛物线于点D ,求线段QD 长度的最大值。
4.如图,已知抛物线y=x 2+bx+c 的图象与x 轴的一个交点为B (5,0),另一个交点为A ,且与y 轴交于点C (0,5).(1)求直线BC与抛物线的解析式;(2)若点M是抛物线在x轴下方图象上的一动点,过点M作MN∥y轴交直线BC于点N,求MN的最大值;(3)在(2)的条件下,MN取得最大值时,若点P是抛物线在x轴下方图象上任意一点,以BC为边作平行四边形CBPQ,设平行四边形CBPQ的面积为S1,△ABN的面积为S2,且S1=6S2,求点P的坐标.5.如图1,在平面直角坐标系中,抛物线233334y x x=-++交x轴于A,B两点(点A在点B的左侧),交y轴于点W,顶点为C,抛物线的对称轴与x轴的交点为D。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020年中考几何题专题训练一答案解析\1、已知:在△ABC中,BC=2AC,∠DBC=∠ACB,BD=BC,CD交线段AB于点E.(1)如图1,当∠ACB=90°时,则线段DE、CE之间的数量关系为;(2)如图2,当∠ACB=120°时,求证:DE=3CE;(3)如图3,在(2)的条件下,点F是BC边的中点,连接DF,DF与AB交于G,△DKG和△DBG 关于直线DG对称(点B的对称点是点K,延长DK交AB于点H.若BH=10,求CE的长.2、(2016春•重庆校级期中)在△ABC中,AB=AC,D为射线BC上一点,DB=DA,E为射线AD上一点,且AE=CD,连接BE.(1)如图1,若∠ADB=120°,AC=2,求DE的长;(2)如图2,若BE=2CD,连接CE并延长交AB于点F,求证:CF=3EF;(3)如图3,若BE⊥AD,垂足为点E,猜想AE,BE,BD之间的数量关系,直接写出关系式.3、(2019秋•江岸区校级月考)在菱形ABCD中,∠ABC=60°(1)如图1,P是边BD延长线上一点,以AP为边向右作等边△APE,连接BE、CE.①求证:CE⊥AD;②若AB=,BE=,求AE的长;(2)如图2,P是边CD上一点,点D关于AP的对称点为E,连接BE并延长交AP的延长线于点F,连接DE、DF.若BE=11,DE=5,求△ADF的面积.4、(2016秋•南岗区校级月考)已知:如图,在等边△ABC中,点D是AC上任意一点,点E在BC延长线上,连接DB,使得BD=DE.(1)如图1,求证:AD=CE;(2)如图2,取BD的中点F,连接AE、AF.求证:∠CAE=∠BAF;(3)如图3,在(2)的条件下,过点F作AE的垂线,垂足为H,若AH=.求EH的长.5、已知,在Rt△ABC中,∠C=90°,AC=BC,点D在边BC上,连接AD,作DE⊥AD,且DE=AD,连接BE、AE,DE与AB交于点H,(1)如图1所示,求证:∠C=∠ABE;(2)如图2,把射线AD沿AB折叠,分别交BE、DE的延长线于点F、点G.若∠AEB=75°,求证:HG=2DH;(3)在(2)的条件下,若BE=3,求DH的长?6、如图,在△ABC中,∠ABC=90°,AB=BC,点D是△ABC内部一点,连接AD,BD和CD.(1)如图1,若∠BDC=90°,BD=1,CD=2,求AC的长.(2)如图2,若CD平分∠ACB,∠BDC=90°,过点B作BE∥AC交AD的延长线于点E,求证:AD =DE.(3)如图3,若CD=CB,∠BCD=30°,取线段AC的中点F,连接DF,求证:∠AFD=45°7、(2013•洪山区模拟)如图1,直角梯形ABCD中,BC=CD,AB∥CD,∠ABC=90°,点P为边AD上一点,BC=PB.(1)求证:∠CBP=2∠DCP;(2)如图2,若∠ABP的平分线交CP的延长线于点E,连接DE,求证:BE+DE=CE;(3)在(2)的条件下,若AB=1,BC=2,请直接写出线段CE的长度.8、(2016秋•松北区期末)如图,在△ABC中,∠ACB=60°,点D在射线BC上,AB=AD.(1)如图1,求证:BC+CD=AC;(2)如图2,取AB的中点F,延长CA至点E,连接BE、DE、EF,使得∠ABE=∠CAD,EF=AE,求证:∠BEF=2∠ABD;(3)如图3,在(2)的条件下,FG⊥BE于点G,FG=4,EF=,求△AED的面积.9、(2016•九龙坡区校级一模)已知,Rt△ABC中,∠ACB=90°,∠CAB=30°,分别以AB、AC为边,向Rt△ABC外作等边△ABD和等边△ACE(1)如图1,连接BE、CD,若BC=2,求BE的长;(2)如图2,连接DE交AB于点F,作BH⊥AD于H,连接FH.求证:BH=2FH;(3)如图3,取AB、CD得中点M、N,连接M、N,试探求MN和AE的数量关系,并直接写出结论.10、重庆八中初2020级九上期末11、重庆实验外国语学校初2020级九上期末12、重庆双福育才中学初2020级九上期末2020年中考几何题专题训练一答案解析\1、已知:在△ABC中,BC=2AC,∠DBC=∠ACB,BD=BC,CD交线段AB于点E.(1)如图1,当∠ACB=90°时,则线段DE、CE之间的数量关系为DE=2CE;(2)如图2,当∠ACB=120°时,求证:DE=3CE;(3)如图3,在(2)的条件下,点F是BC边的中点,连接DF,DF与AB交于G,△DKG和△DBG 关于直线DG对称(点B的对称点是点K,延长DK交AB于点H.若BH=10,求CE的长.(1)解:∵∠DBC=∠ACB=90°,∴∠DBC+∠ACB=180°,∴AC∥BD,∴∠DBE=∠CAE又∵∠DEB=∠AEC,∴△DBE∽△CAE,∴=,又∵BD=BC=2AC,∴DE=2CE;故答案为:DE=2CE.(2)证明:如图2,∵∠DBC=∠ACB=120°,BD=BC,∴∠D=∠BCD=30°,∴∠ACD=90°,过点B作BM⊥DC于M,则DM=MC,BM=BC,∵AC=BC,∴BM=AC,∵在△BME和△ACE中∴△BME≌△ACE(AAS),∴ME=CE=CM,∴DE=3EC;(3)解:如图,过点B作BM′⊥DC于点M′,过点F作FN⊥DB交DB的延长线于点N,设BF=a,∵∠DBF=120°,∴∠FBN=60°,∴FN=a,BN=a,∵DB=BC=2BF=2a,∴DN=DB+BN=a,∴DF===a,∵AC=BC,BF=BC,∴BF=AC,∴△BDF≌△BCA(SAS),∴∠BDF=∠CBA,又∵∠BFG=∠DFB,∴△FBG∽△FDB,∴==,∴BF2=FG×FD,∴a2=a×FG,∴FG=a,∴DG=DF﹣FG=a,BG==a,∵△DKG和△DBG关于直线DG对称,∴∠GDH=∠BDF,∴∠ABC=∠GDH,又∵∠BGF=∠DGH,∴△BGF∽△DGH,∴=,∴GH==a,∵BH=BG+GH=a=10,∴a=2;∴BC=2a=4,CM′=BC cos30°=2,∴DC=2CM′=4,∵DE=3EC,∴EC=DC=.2、(2016春•重庆校级期中)在△ABC中,AB=AC,D为射线BC上一点,DB=DA,E为射线AD上一点,且AE=CD,连接BE.(1)如图1,若∠ADB=120°,AC=2,求DE的长;(2)如图2,若BE=2CD,连接CE并延长交AB于点F,求证:CF=3EF;(3)如图3,若BE⊥AD,垂足为点E,猜想AE,BE,BD之间的数量关系,直接写出关系式.(1)解:∵DA=DB,∠ADB=120°,∴∠ABC=∠BAD=30°,∵AB=AC,∴∠ABC=∠C=30°,∴∠CAD=90°,在RtACD中,tan30°=,∴AD=2×=2,AE=CD=2AD=4 ∴DE=AE﹣AD=CD﹣AD=4﹣2=2;(2)证明:如图,过A作AG∥BC,∵DB=DA,AB=AC,∴∠BAD=∠ABC,∠ABC=∠ACB,∴∠BAD=∠ACB,∵AE=CD,在△ABE和△CAD中∴△ABE≌△CAD(SAS),∴BE=AD,∵BE=2CD,∴AD=2CD=2AE,∴AE=DE,∵AG∥BC,∴∠G=∠DCE,∠GAE=∠CDE,在△AGE和△DCE中∴△AGE≌△DCE(AAS),∴GE=CE,AG=CD=AE,∴△AGE为等腰三角形,∴∠GAF=∠ABC=∠BAD,∴F为GE的中点,∴CE=EG=2EF,∴CF=3EF;(3)如图3,取BE中点M,延长AM至N,使MN=AM,连接BN,EN,∴四边形ABNE是平行四边形,∴AE∥BN,∴∠NBC=∠D,BN=AE=CD,∵AB=AC,DB=DA,∴∠ABC=∠ACB=∠BAD,∴∠BAC=∠D=∠NBC,∵∠ABN=∠NBC+∠ABC,∠ACD=∠BAC+∠ABC,∴∠ABN=∠ACD,在△ABN和△ACD中∴△ABN≌△ACD(SAS),∴BD=AD=AN=2AM,∵BE⊥AD,∴AE2+ME2=AM2,∴AE2+(BE)2=(AN)2,∴AE2+BE2=BD2.3、(2019秋•江岸区校级月考)在菱形ABCD中,∠ABC=60°(1)如图1,P是边BD延长线上一点,以AP为边向右作等边△APE,连接BE、CE.①求证:CE⊥AD;②若AB=,BE=,求AE的长;(2)如图2,P是边CD上一点,点D关于AP的对称点为E,连接BE并延长交AP的延长线于点F,连接DE、DF.若BE=11,DE=5,求△ADF的面积.(1)①证明:在菱形ABCD中,∠ABC=60°,∴∠ADC=60°,且AB=BC=DA=DC,∴△ADC和△ABC是等边三角形,∴AB=AC,∠BAC=∠CAD=60°,又∵△APE是等边三角形,∴AE=AP,∠EAP=60°,∴∠BAC+∠CAP=∠PAE+∠CAP,即∠BAP=∠CAE,∴△BAP≌△CAE(SAS),∴∠ACE=∠ABP=∠ABC=30°,∵∠CAD=60°,∴∠ACE+∠CAD=90°,∴CE⊥AD;②解:如图1,设AC与BD交于点O,由①知,∠ACE=30°,且∠ACB=60°,∴∠ACE+∠ACB=∠BCE=90°,∵在Rt△BCE中,BC=AB=,BE=,∴CE==4,由①知,△BAP≌△CAE,∴BP=CE=4,在Rt△BOC中,∠ACB=60°,∴BO=BC=,CO=AO=BC=,∴OP=BP﹣BO=,∴在Rt△AOP中,AP===,∴AE=AP=;(2)解:如图2,连接AE,过点A作AH⊥BF于点H,∵点D关于AP的对称点为E,∴AP垂直平分DE,∴AD=AE,FD=FE,∴∠EAF=∠DAF=∠EAD,∠DFA=∠EFA=∠DFE,又∵在菱形ABCD中,AB=AD,∴AB=AE,∴AH垂直平分BE,∴EH=BH=BE=,∠BAH=∠EAH=∠BAE,∴∠HAF=∠EAH+∠EAF=∠BAD,∵∠ABC=60°,∴∠BAD=180°﹣∠ABC=120°,∴∠HAF=60°,∴∠AFH=90°﹣∠HAF=30°,∴∠DFE=60°,∴△DEF为等边三角形,∴EF=DE=5,∴HF=HE+EF=+5=,在Rt△AHF中,∠AFH=30°,∴AH=HF=,∴S△AEF=EF•AH=×5×=,∵AD=AE,FD=FE,AF=AF,∴△ADF≌△AEF(SSS),∴△ADF的面积为.4、(2016秋•南岗区校级月考)已知:如图,在等边△ABC中,点D是AC上任意一点,点E在BC延长线上,连接DB,使得BD=DE.(1)如图1,求证:AD=CE;(2)如图2,取BD的中点F,连接AE、AF.求证:∠CAE=∠BAF;(3)如图3,在(2)的条件下,过点F作AE的垂线,垂足为H,若AH=.求EH的长.解:(1)如图1,作DF∥AB,∵DF∥AB,∴,∵AC=BC,∴CF=CD,∴BF=AD,∵DF∥AB,∴∠DFC=60°,∴∠BFD=120°,∵BD=DE,∴∠E=∠DBE,在△BDF和△EDC中,,∴△BDF≌△EDC,(AAS)∴BF=CE,∴AD=CE,(2)如图2,过点B作BG∥AC交AF的延长线于G,∴∠G=∠DAF,∠CBG=∠ACB=60°,∴∠ABG=∠ABC+∠CBG=120°=∠ACE,∵点F是BD中点,∴BF=DF,在△BFG和△DFA中,,∴△BFG≌△DFA,∴BG=AD,由(1)知,AD=CE,∴BG=CE,在△ABG和△ACE中,,∴△ABG≌△ACE,∴∠BAF=CAE;(3)由(2)知,∠BAF=∠CAE,∴∠FAE=∠FAC+∠CAE=∠FAC+∠BAF=∠BAC=60°,∵FH⊥AE,∴∠AHF=90°,∴∠AFH=90°﹣∠FAE=30°,在Rt△AFH中,AH=,∴AF=2,由(2)知,△BFG≌△DFA,∴GF=AF=2,由(2)知,△ABG≌△ACE,∴AE=AG=2AF=4,∴EH=AE﹣AH=4﹣=3.5、已知,在Rt△ABC中,∠C=90°,AC=BC,点D在边BC上,连接AD,作DE⊥AD,且DE=AD,连接BE、AE,DE与AB交于点H,(1)如图1所示,求证:∠C=∠ABE;(2)如图2,把射线AD沿AB折叠,分别交BE、DE的延长线于点F、点G.若∠AEB=75°,求证:HG=2DH;(3)在(2)的条件下,若BE=3,求DH的长?证明:(1)如图1,过点E作EM⊥BC于M,∵∠ACB=90°,AD⊥DE∴∠ACB=∠ADE=90°∵∠ADB=∠ACB+∠DAC=∠ADE+∠EDB∴∠DAC=∠EDB,且∠ACD=∠EMD=90°,AD=DE ∴△ACD≌△DME(AAS)∴AC=DM,CD=EM∵AC=BC,∴BC=DM∴CD=BM∴BM=EM,且EM⊥BM∴∠EBM=45°∵∠C=90°,AC=BC∴∠ABC=∠BAC=45°∴∠ABE=180°﹣∠ABC﹣∠EBM=90°∴∠C=∠ABE(2)如图2,过点E作EM⊥BC于M,∵∠C=90°,AC=BC,∠ADE=90°,AD=DE∴∠CAB=∠DAE=∠AED=45°由(1)可知∠EBM=45°,∴∠CBE=135°,∵∠DAE+∠AEB+∠DBE+∠ADB=360°,且∠AEB=75°,∴∠ADB=105°∴∠ACD+∠CAD=∠ADB=105°∴∠CAD=15°∴∠DAB=30°∵把射线AD沿AB折叠,分别交BE、DE的延长线于点F、点G.∴∠DAB=∠BAG=30°∴∠DAG=60°,且∠ADE=90°∴∠G=30°=∠BAG∴AH=HG∵∠ADE=90°,∠DAH=30°∴AH=2DH∴HG=2DH(3)作EN平分∠DEB交BC于点N,∵EM=BM,∠EMB=90°∴BE=EM,且BE=3,∴EM=∵∠AEB=75°,∠AED=45°∴∠DEN=30°∵EN平分∠DEB∴∠DEN=15°∵∠EDM=∠CAD=15°∴∠DEN=∠EDB=15°,∴DN=EN,∠ENM=30°,且EM⊥BM∴NE=2EM=3,NM=EM=在Rt△DEM中,DE==3+3=AD∵∠DAH=30°,∠ADH=90°∴AD=DH=3+3∴DH=3+6、如图,在△ABC中,∠ABC=90°,AB=BC,点D是△ABC内部一点,连接AD,BD和CD.(1)如图1,若∠BDC=90°,BD=1,CD=2,求AC的长.(2)如图2,若CD平分∠ACB,∠BDC=90°,过点B作BE∥AC交AD的延长线于点E,求证:AD =DE.(3)如图3,若CD=CB,∠BCD=30°,取线段AC的中点F,连接DF,求证:∠AFD=45°解:(1)如图1,∵∠BDC=90°,BD=1,CD=2,∴BC===,∵AB=BC=,由勾股定理得:AC===;(2)如图2,延长BD交AC于P,∵DC平分∠ACB,∴∠BCD=∠ACD,∵∠BDC=90°,∴∠BDC=∠PDC=90°,∵CD=CD,∴△BDC≌△PDC,∴BD=PD,∵BE∥AC,∴∠E=∠EAC,∠EBD=∠DPA,∴△BDE≌△PDA,∴AD=DE;(3)如图3,以BD为边作等边三角形BDE,连接BF、CE,∴BD=DE=BE,∵AB=BC,F是AC的中点,∴BF⊥AC,∴∠AFB=90°,∵∠ABC=90°,∴BF=AF,∵CD=BC,∠BCD=30°,∴∠CBD=∠CDB=75°,∵CE=CE,∴△CEB≌△CED,∴∠BCE=∠DCE=15°,∵∠CBD=75°,∠DBE=60°,∴∠CBE=75°﹣60°=15°,∵∠ABC=90°,∴∠ABD=90°﹣75°=15°,∴∠ABD=∠CBE,∴△ABD≌△CBE,∴∠BAD=∠BCE=15°,∴∠ABD=∠BAD=15°,∴AD=BD,∵DF=DF,∴△ADF≌△BDF,∴∠AFD=∠BFD=∠AFB=×90°=45°.7、(2013•洪山区模拟)如图1,直角梯形ABCD中,BC=CD,AB∥CD,∠ABC=90°,点P为边AD上一点,BC=PB.(1)求证:∠CBP=2∠DCP;(2)如图2,若∠ABP的平分线交CP的延长线于点E,连接DE,求证:BE+DE=CE;(3)在(2)的条件下,若AB=1,BC=2,请直接写出线段CE的长度.解:(1)取CP的中点F,连接BF,如图1,∵BC=BP,BF是底边上的中点,∴∠CBF=∠PBF=∠CBP,BF⊥PC,∴∠CBF+∠BCF=90°,∵∠BCF+∠DCP=90°,∴∠DCP=∠CBF,∴∠CBP=2∠DCP;(2)过得C作CG⊥CE交EB的延长线于点G,连接BD,如图2,∵BC=CD,∠BCD=90°,∴∠CBD=45°,∵∠EBF=∠EBP+∠PBF=∠ABP+∠CBP=45°,∴∠BEF=180°﹣∠EBF﹣∠BFE=45°,∴△CEG是等腰直角三角形,∴EG=CE,CG=CE,∵∠ECG=90°=∠BCD,∴∠BCG=∠DCE,在△CBD和△CDE中∴△CBD≌△CDE(SAS),∴BG=DE,∴DE+BE=BG+BE=EG=CE;(3)CE=,理由如下;取CD的中点M,连接MF,设MF的延长线交直线AB与B′,如图2,∵F是PC的中点,∴FM∥AD,∵AB∥CD,∴四边形AB′MD是平行四边形,∴AB′=DM=1=AB,∴B′与B重合,即B、F、M在一条直线上,∴BM⊥CE,∵∠CBF=∠MBC,∴△BFC∽△BCM,∴=,即=,∴BF=2CF,∵∠BEF=45°,∠BFE=90°,∴EF=BF=2CF,∵CF=PF,∴CF=PF=PE,CE=3CF,∵S△BCM=CF•BM=BC•CM,∴CF===,∴CE=3CF=.8、(2016秋•松北区期末)如图,在△ABC中,∠ACB=60°,点D在射线BC上,AB=AD.(1)如图1,求证:BC+CD=AC;(2)如图2,取AB的中点F,延长CA至点E,连接BE、DE、EF,使得∠ABE=∠CAD,EF=AE,求证:∠BEF=2∠ABD;(3)如图3,在(2)的条件下,FG⊥BE于点G,FG=4,EF=,求△AED的面积.(1)证明:延长DB至E,使BE=CD,连接AE,∵AB=AD,∴∠ABD=∠ADB,∵∠ABE+∠ABD=180°,∠ADC+∠ADB=180°,∴∠ABE=∠ADC,在△ABE和△ADC中,,∴△ABE≌△ADC,∴∠C=∠E=60°,∴△AEC为等边三角形,∴AC=CE,∵BC+BE=CE,∴BC+CD=AC;(2)证明:∵AB=AD,∴∠ABD=∠ADB,∵∠CAD+∠ADB=∠ACB=60°,∠CAD=∠ABE,∴∠ABE+∠ABD=∠CAD+∠ADB=60°,∴△BEC为等边三角形,过点A作AN∥BC交EB于N,∴△ENA为等边三角形,∠NAB=∠ABD,∴AN=AE,∴BN=AC,∴∠NAB=∠ADC,在△BNA和△ACD中,,∴△BNA≌△ACD,∴AN=CD,∴CD=AE,延长EF至M使得EF=FM,连接BM,∴△AEF≌△BMF,∴AE=BM,AE∥BM,∴BM=CD,∠MBC=∠ECB=60°,∴∠EBM=∠EBC+∠MBC=120°,又∵∠ECD=∠EBM=120°,∴△BEM≌△CED,∴∠BEF=∠CED,∵EF=AE,∴∠EFA=∠EAF,∴∠BEF+∠EBF=∠ACB+∠ABD,∴∠BEF+60°﹣∠ABD=∠ABD+60°,∴∠BEF=2∠ABD∠CED=2∠ABD;(3)解:由(2)得,△EMD是等边三角形,∴,过点A作AP⊥DE于P,由(2)可证△EFG≌△EAP,∴AP=FG=4,∴S△AED=DE×AP=××4=37.9、(2016•九龙坡区校级一模)已知,Rt△ABC中,∠ACB=90°,∠CAB=30°,分别以AB、AC为边,向Rt△ABC外作等边△ABD和等边△ACE(1)如图1,连接BE、CD,若BC=2,求BE的长;(2)如图2,连接DE交AB于点F,作BH⊥AD于H,连接FH.求证:BH=2FH;(3)如图3,取AB、CD得中点M、N,连接M、N,试探求MN和AE的数量关系,并直接写出结论.解:(1)如图1,Rt△ABC中,∠CAB=30°,BC=2,∴AB=4,AC=2,∵△ACE是等边三角形,∴AE=AC=2,∠EAC=60°,∴∠EAB=60°+30°=90°,在Rt△EAB中,EB===2;(2)如图2,过E作EG∥BD,交BA的延长线于G,∴∠EGA=∠ABD,∵△ABD是等边三角形,∴∠ABD=60°,∴∠EGA=60°,Rt△AEG中,设AG=x,∴EG=2x,AE=x,∴AC=AE=BH=x,∵∠BDH=60°,∴BD=2x,∴EG=BD=2x,∵∠EFG=∠BFD,∴△EFG≌△DFB,∴EF=DF,等边△ABD中,∵BH⊥AD,∴AH=DH,∴FH是△AED的中位线,∴FH=AE=BH,∴BH=2FH;(3)如图3,连接BN,并延长交AD于H,∵∠CBA=60°=∠BAD,∴BC∥AD,∴∠BCN=∠NDH,∵CN=ND,∠CNB=∠DNH,∴△CNB≌△DNH,∴BN=NH,BC=DH,∵M是AB的中点,∴MN是△ABH的中位线,∴MN=AH,设BC=x,则DH=x,AB=AD=2x,∴AH=x,∴MN=x,Rt△ACB中,AC=2x,∴AE=2x,∴==,∴AE=4MN.10、重庆八中初2020级九上期末11、重庆实验外国语学校初2020级九上期末12、重庆双福育才中学初2020级九上期末。
