第一章 第三节
第一章第三节开集、闭集和博雷尔集

第三节 nR 中的开集、闭集和Borel 集一、nR 的几个基本概念度量空间:设X ≠∅,(,)d x y 是定义在X X ⨯(:d X X R ⨯→)上的一个二元实函数,若(,)d x y 满足:(1)非负性:对任意,x y X ∈,(,)0d x y ≥,且(,)0d x y x y =⇔=; (2)对称性:对任意,x y X ∈,(,)(,)d x y d y x =;(3)三角不等式:对任意,,x y z X ∈,(,)(,)(,)d x y d x z d y z ≤+, 则称(,)d x y 为,x y 之间的距离或度量,(),X d 称为距离(度量)空间.特别,取n X R =,(,)d x y =()()1212,,,,,,,n n x x x x y y y y ==,则(),X d 称为n 维欧式空间,仍记为nR .注:实变函数涉及的函数主要是nR 的点集上的实函数.集合的直径与有界集:设nE R ⊂,(){}diam sup ,,E d x y x y E =∈称为E 的直径;E 有界⇔0diam E ≤<+∞.E 有界的其他描述方法:如球覆盖和方覆盖.开球(球邻域)、闭球和球面:设0n x R ∈,0δ>,()(){}00,,n B x x R d x x δδ=∈<称为以0x 为心的开球(球邻域),简记为()0B x ; ()(){}00,,n B x x R d x x δδ=∈≤称为以0x 为心的闭球,简记为()0B x ; ()(){}00,,n S x x R d x x δδ=∈=称为以0x 为心的球面,简记为()0S x .n R 中的区间及区间的体积:设i I (1,2,,i n =)为R 上的n 个区间,则121ni n i I I I I =∏=⨯⨯⨯称为n R 上的区间;若iI (1,2,,i n =)都是开区间,则称1n i i I =∏为开区间;若i I (1,2,,i n =)都是闭区间,则称1ni i I =∏为闭区间;若i I (1,2,,i n =)都是同类的半开半闭区间,则称1ni i I =∏为半开半闭区间;设121ni n i I I I I =∏=⨯⨯⨯是nR 上的区间,则121nin i I I I I =∏称为1ni i I =∏的体积.二、开集、闭集的定义及基本性质1、开集的定义与性质:定义:设nG R ⊂,G 是开集是指对任意x G ∈,存在()B x G ⊂;易见,,n R ∅均为开集;()0B x 是开集;nR 上的开区间等都是开集.开集的性质:τ表示nR 中的开集全体,则 (1),n R τ∅∈;(2)对任意12,G G τ∈,总有12G G τ⋂∈,即τ对集合的有限交运算封闭; (3)对任意G ατ∈,α∈Λ,总有G αατ∈Λ∈,即τ对集合的任意并运算封闭.注:τ是nR 上的一个拓扑--------称为欧式拓扑. 2、闭集的定义与性质:定义:设nF R ⊂,F 是闭集是cF 是开集; 易见,开集和闭集在集合的余运算下是对偶的;,n R ∅均为闭集;()(){}00,cB x x d x x δ=>是闭集;()()(){}{}000,cS x B x x d x x δ=⋃>是闭集指对任意x G ∈,存在()B x G ⊂;闭集的性质:μ表示nR 中的闭集全体,则 (1),nR μ∅∈;(2)对任意12,F F μ∈,总有12F F μ⋃∈,即μ对集合的有限并运算封闭; (3)对任意F αμ∈,α∈Λ,总有F ααμ∈Λ∈,即μ对集合的任意交运算封闭.注意:一列开集的交不一定是开集;一列闭集的并不一定是闭集;τμ.三、开集、闭集的等价条件1、开集的等价条件1)点关于点集的一种分类关系(点集的内点、外点和边界点) 邻域的推广:设nx R ∈,若G 是开集,且x G ∈,则称G 为x 的一个邻域,\{}G x 为x 的一个去心邻域; 显然,()B x 就是x 的一个邻域,()\{}B x x 是x 的一个去心邻域. 点集的内点、外点和边界点: 设n x R ∈,nE R ⊂,(1)若存在x 的一个邻域G ,使得G E ⊂,则称x 为E 的内点,记0E 为E 的内点全体-------称为E 的内部(或内核或开核),显然0E E ⊂;(2)若存在x 的一个邻域G ,使得G E ⋂=∅,即cG E ⊂,则称x 为E 的外点,显然E 的外点一定不属于E ,其全体就是()c E;(3)若对x 的任意邻域G ,总有G E ⋂≠∅,cG E ⋂≠∅,则称x 为E 的边界点,记E ∂表示E 的边界点全体-----称为E 的边界.点关于点集的内点,外点和边界点关系是一个分类关系注:设nE R ⊂,则()n c R E E E=⋃∂⋃;记0E E E E E =⋃∂=⋃∂-----称为E 的闭包,则()()0c c E E =是闭集.()()0c c E E E∂=⋃是闭集.2)开集的等价条件 定理:设nE R ⊂,则 (1)0E 是开集;(2)E 是开集⇔0E E =.2、闭集的等价条件1)点列收敛设n k x R ∈,1,2,k =,0n x R ∈,若()0lim ,0k k d x x →∞=,则称{}k x 当k →∞时收敛于0x ,记为:0lim k k x x →∞=或0k x x →(k →∞).注:1)如何用邻域来反映点列收敛?2)点列收敛与坐标收敛有何关系?即,记()()00012012,,,,,,,k kk k n n x x x x x x x x ==,则0k x x →(k →∞)与0k i i x x →(k →∞)1,2,,i n =有何关系?2)点关于点集的另一种分类关系(点集的聚点、孤立点和外点) 设n x R ∈,nE R ⊂,(1)若对x 的任一个邻域G ,总有\{}G x E ⋂≠∅,则称x 为E 的聚点,记E '为E 的聚点全体-------称为E 的导集;(2)若存在x 的一个邻域G ,使得\{}G x E ⋂=∅,若x E ∈,即{}G E x ⋂=,则称x 为E 的孤立点,E 的孤立点全体所成的集称为E 的孤立点集,显然E 的孤立点集⊂E ;若x E ∉,即G E ⋂=∅,即cG E ⊂,则称x 为E 的外点,其全体就是()c E .点关于点集的聚点,孤立点和外点的关系也是一个分类关系 注:设nE R ⊂,则{}()0nc R E E E '=⋃⋃的孤立点全体,{}E E E E E ''=⋃=⋃的孤立点全体---------闭包的另一种表示.注:10孤立点集是至多可数集20聚点的等价条件:设nx R ∈,nE R ⊂,则下面的说法等价: (1)x 为E 的聚点;(2)对x 的任一球邻域(,)B x δ,总有(,)\{}B x x E δ⋂≠∅; (3)存在E 中一列彼此互异的点列{}k x ,使得k x x →(k →∞); (4)对x 的任一个邻域G ,总有G E ⋂为无限集. 证明:(1)⇒(2)显然;(2)⇒(3)只要δ取一列适当的趋于0的数列即可把满足要求的彼此互异的点列{}k x 取出来;(3)⇒(4)由极限定义的邻域形式即可; (4)⇒(1)显然. 注意:由等价形式立即可得,x 不是E 的聚点,即x E '∉⇔存在x 的一个邻域G ,使得G E ⋂为有限集. 30导集和闭包保持集合的有限并运算,但保持可数并运算;事实上,设有一列点集{}n E ,则()1212n n E E E E E E ''''⋃⋃⋃=⋃⋃⋃, ()1212n n E E E E E E ⋃⋃⋃=⋃⋃⋃,但11n n n n E E ∞∞=='⎛⎫'⊃ ⎪⎝⎭,11n n n n E E ∞∞==⊃. 证明?3)闭集的等价条件定理:设nE R ⊂,则下面的说法等价: (1)E 为闭集; (2)E E '⊂; (3)E E =;(4)对E 中的任意一列点{}k x ,若k x x →,则x E ∈. 证明 (1)⇒(2)对任意x E '∈,倘若x E ∉,即cx E ∈.因c E 为开集,存在()c B x E ⊂,从而()B x E ⋂=∅,这与x E '∈(x 为E 的聚点矛盾),故x E ∈.(2)⇒(3)显然,事实上,E EE E E E '⊂'=⋃=. (3)⇒(4)事实上,对E 中的点列{}k x ,k x x →,由聚点的等价条件,或者x E ∈或者x E E E '∈⊂=,即必有x E ∈.(4)⇒(1)反证法:倘若E 不是闭集,即cE 不是开集,则存在cx E ∈,使得对x 的任意球邻域(,)B x δ,都有(,)B x E δ⋂≠∅,于是,通过取δ为一列适当的趋于0的数列即可在E 中选取点列{}k x ,使得k x x →,从而x E ∈,这与cx E ∈矛盾,故E 必为闭集.注:利用上述等价条件可更为方便地判断一些集是闭集,例如,E '是闭集(因为易得()E E '''⊂);E 为有限点集,则E 为闭集(因为易得E E '=∅⊂);同理nE R ⊂整点集,则E 为闭集.四、聚点原理、Borel 有限覆盖定理和林德洛夫(Lindelof )至多可数覆盖定理聚点原理和有限覆盖定理是nR 中的两个基本定理,是nR 完备性的两种表现形式: 聚点原理:若nE R ⊂是有界无限点集,则E 至少有一个聚点(即E '≠∅); 致密性定理:若{}k x 是nR 中的有界无限点列,则{}k x 至少有一个收敛子列{}i k x ;Borel 有限覆盖定理:若nE R ⊂是有界闭集,ℑ为E 的一个开覆盖,则存在ℑ中的有限个开集,记为12,,,m G G G ,使得12m E G G G ⊂⋃⋃⋃.问题:若nE R ⊂不是有界闭集,则是否存在ℑ中的一列开集,记为12,,,,k G G G ,使得1k k E G ∞=⊂?林德洛夫(Lindelof )至多可数覆盖定理:若nE R ⊂,ℑ为E 的一个开覆盖,则存在ℑ中的一列开集,记为12,,,,k G G G ,使得1k k E G ∞=⊂.证明 对任意x E ∈,由ℑ为E 的一个开覆盖可得,存在开集x G ∈ℑ,使得x x G ∈.由有理点的稠密性,存在有理点x x q G ∈和有理正数x r ,使得(,)x x x x B q r G ∈⊂,显然{}(,)x x B q r x E ∈是至多可数集,且仍覆盖E ,记{}{}11(,)(,),,(,),k k xx x x x x B q r x E B q r B q r ∈=,则相应的开集12,,,,k x x x G G G 也覆盖E .注:试用林德洛夫至多可数覆盖定理证明:nR 任一个非空开集G 总可表示成至多可数个开区间的并集.五、几类与开集、闭集相关的集1、自密集和完全集 设nE R ⊂,自密集:若E E '⊂,则称E 是自密集(特点:E 没有孤立点). 例如,∅,n Q ,()cn Q(无理点集),nR ,开区间,闭区间,半开半闭区间,非空开集都是自密集.完全集:若E E '⊂且E E '⊂,即E E '=,则称E 是自密集(特点:E 没有孤立点的闭集). 例如,∅,nR ,闭区间都是完全集.思考:(1)非空有限点集一定不是自密集,更不是完全集; (2)有限个完全集的并仍是完全集; (3)一列完全集的并不一定是完全集; (4)完全集的交集不一定是完全集.记住一个结论:设E ≠∅是完全集,则E c =. 2、稠密集和疏朗集 设nE R ⊂,稠密集:若n E R =(即对任意n x R ∈以及x 的任意邻域G ,总有G E ⋂≠∅),则称E 在nR 中稠密,或E 是nR 中的稠密集.显然,E 是稠密集⇔对任意非空开集G ,G E ⋂≠∅(今后判断稠密集的常用方法).易见,nQ ,()cnQ (无理点集)均为n R 中的稠密集.疏朗集:若对任意的非空开集G ,总存在G 的非空开子集V G ⊂,使得V E ⋂=∅(即c V E ⊂),则称E 为疏朗集.易见,∅,有限点集,整点集都是疏朗集;疏朗集一定没有内点,但无内点的集并不一定是疏朗集.稠密集与疏朗集: 设nE R ⊂,(1)若E 为疏朗集,则cE 为稠密集,但反之不成立;证明 对任意非空开集G ,由E 为疏朗集可得,存在非空开子集V G ⊂,使得cV E ⊂,从而c V E G ⊂⋂,故c E G ⋂≠∅,即cE 为稠密集.反之,取n E Q =即可. (2)若E 为稠密开集,则cE 为疏朗闭集; 证明 显然,cE 为闭集,下证c E 为疏朗集.事实上,对任意非空开集G ,取V G E =⋂≠∅,显然V 为开集,cV E ⋂=∅,故c E 为疏朗集.综合(1)(2)得,(3)E 为稠密开集⇔cE 为疏朗闭集.3、三分Cantor 集三分Cantor 集构造图如图示,我们将[]01,中永远去不掉的点所成的集称为三分Cantor 集,记为P . 注:10P 的两种表示方法:[]12n=111P 0,1\(())n n n k n k F I -∞∞====;20 P 是闭集,完全集; 30 P 是疏朗集; 40 P c =; 50 mP 0=; 60nk=1P ∏称为nR中的Cantor 集,nk=1P c =∏.思考:(1)如何解释疏朗集不一定是至多可数集?(2)如何解释在[]01,去掉一个不可数集,不一定改变其长度?4、F σ型集、G δ型集和Borel 集1)F σ型集:若nE R ⊂能表示成可数个闭集的并,则称E 是F σ型集;G δ型集:若n E R ⊂能表示成可数个开集的交,则称E 是G δ型集.注:10 开集是G δ型集,闭集是F σ型集;20 问题:开集是F σ型集,闭集是G δ型集?可见,F σ型集和G δ型集都是比开集、闭集更广的两类集;30 至多可数个F σ型集的并仍为F σ型集,至多可数个G δ型集的交仍为G δ型集;40 F σ型集与G δ型集在余运算下相互转化;从而,nR 中至多可数集一定F σ型集,至多可数集的余集一定是G δ型集;50 问题:有理数集Q 是否G δ型集?无理数集c W Q =是否F σ型集?2)Borel 集记τ表示开集全体,则由τ生成的σ代数()στℜ称为Borel 体,其中的元素称为Borel 集. Borel 集一定是从开集出发经过至多可数次并、交、差、余运算得到的(Borel 集的结构). 易见,开集,闭集,F σ型集和G δ型集都是Borel 集.六、开集的结构开集的结构定理:(1)R 上的任一个非空开集总可表示称至多可数个互不相交的开区间的并;(2)nR (2n ≥)上的任一个非空开集总可表示成至多可数个互不相交的半开半闭区间的并.注:10(1)中构成R 中非空开集G 的互不相交的每个开区间(),αβ满足:(),G αβ⊂,且,G G αβ∉∉,它们都称为G 的构成区间.20 开集的结构定理的更一般的说法:(1)R 上的任一个开集或为∅,或总可表示称至多可数个互不相交的开区间的并;(2)nR (2n ≥)上的任一个开集或为∅,总可表示成至多可数个互不相交的半开半闭区间的并.七、点与集合间的距离,集合与集合间的距离1、点与集合间的距离,集合与集合间的距离的定义设nx R ∈,nE R ⊂,记(){},inf (,)inf (,)y Ed x E d x y y E d x y ∈∈=称为x 与E 间的距离;设12,n E E R ⊂,记(){}121212,,inf (,),inf(,)x E y E d E E d x y x E y E d x y ∈∈∈∈=称为1E 和2E 间的距离.注:由定义可得10 (){}{}122112,i n f (,)i n f(,)d E E d x E x E d y E y E=∈=∈; 事实上,对任意1x E ∈,2y E ∈,由定义,()()12,,d E E d x y ≤,()()2,,d x E d x y ≤对第一个不等式两边先对2y E ∈取下确界得,()()122,,d E E d x E ≤;再对1x E ∈取下确界得,(){}1221,inf (,)d E E d x E x E ≤∈.对第二个不等式两边同时对1x E ∈,2y E ∈取下确界得,{}()2112inf (,),d x E x E d E E ∈≤.综上所述,即得结论.20 若x E ∈,则(),0d x E =,反之不一定成立,如取0x =,(0,1)E =即可; 30 x E ∈⇔(),0d x E =;事实上,x E ∈⇔存在E 中的一列点{}k x ,使得k x x →,即(),0k d x x →⇔(),0d x E =.40 特别,若E 为闭集,则x E ∈⇔(),0d x E =;50 若12E E ⋂≠∅,则()12,0d E E =,反之不一定成立,如取1(0,1)E =,2(1,2)E =即可.引理((),d x E 在nR 上的连续性):设nE R ⊂,记()(),f x d x E =(nx R ∈),则()f x 在n R 上一致连续.事实上,对任意,nx y R ∈,z E ∈,由()()(),,,d x z d x y d y z ≤+,()()(),,,d y z d x y d x z ≤+对z E ∈取下确界可得()()(),f x f y d x y -≤,()()(),f y f x d x y -≤,即()()(),f x f y d x y -≤.2、距离可达到的条件(1)点到集合间的距离可达到的条件:设0n x R ∈,nE R ⊂为非空闭集,则存在0y E ∈,使得()()000,,d x y d x E =. (2)集合间的距离可达到的条件:设,nE F R ⊂均为非空闭集,且至少有一个有界,则存在0x E ∈,0y F ∈,使得 ()(),,d x y d E F =.思考:如何利用(1)和连续函数的最值性来证明?注:(2)中,n E F R ⊂都无界,结论不一定成立.3、闭集的分离性分离性定理:设,n E F R ⊂均为非空闭集,若E F ⋂=∅,则存在两个开集12,G G ,使得,1E G ⊂,2F G ⊂,且12G G ⋂=∅.4、闭集一定是G δ型集,开集一定是F σ型集先证一个结论:设n E R ⊂,0δ>,则{}()(,),n x R d x E U E δδ∈<为开集,且(),E U E δ⊂.再证结论:设n E R ⊂为闭集,取1n δ=(1,2,n =),则1,U E n ⎛⎫ ⎪⎝⎭为一列包含E 的开集,下证:11,n E U E n ∞=⎛⎫= ⎪⎝⎭.易见,11,n E U E n ∞=⎛⎫⊂ ⎪⎝⎭,反之,对任意11,n x U E n ∞=⎛⎫∈ ⎪⎝⎭有,1,x U E n ⎛⎫∈ ⎪⎝⎭,从而()1,0d x E n <→,所以(),0d x E =,注意到E 是闭集得,x E ∈,所以,11,n E U E n ∞=⎛⎫⊃ ⎪⎝⎭,故11,n E U E n ∞=⎛⎫= ⎪⎝⎭.。
第一章 绪论 第三节 文化市场营销研究

文化企业根据消费者需求 的差异性,把一个整体市 场划分为若干个消费者群 体,进而确定文化企业目 标市场的过程。
一、文化市场营销学的基本结构
(三)文化市场竞争者、文化市场消费者
文化消费者 是文化企业能否 获取竞争优势的最终决定者, 并且是文化企业竞争优势 唯一有效的 裁判和最终评判者。
1、产品能够满足 消费者的某种欲望; 2、产品的品质或 价格属性胜于竞争对手; 3、消费者愿意并 且有能力消费。
现代营销组织 建立在整体营销观念基础之上 成为整个文化企业经营运作的宗旨 文化企业才真正形成了 以整体营销为核心内容的 文化企业营销组织。
一、文化市场营销学的基本结构
(五)文化市场营销道德、文化企业社会责任
文化企业经营决策 对社会的影响或 文化企业履行 对社会所承担的义务, 主要包括 保护文化消费者权益, 保护社会利益与社会发展, 保护自然环境及 社会生态平衡。
文化消费者 对文化企业营销 决策的价值判断, 即判断文化企业 营销活动是否 符合广大文化消费者 及社会的利益, 能否给广大文化消费者 及社会带来 最大的幸福。
二、文化市场营销的基本框架(4c理论)
文化内容 文化行业的真正产品,创意、技术、 天赋、易变 文化产品的传输方式,即销售方式 (地点、方式) 消费者实际使用文化产品的具体形式
(一)文化市场营销学的研究原则
3、静态分析研究与 动态分析研究相结合
注重从整体与部分之间、 整体与外部环境的互相联 系中综合地、精确地考察 对象,从整体的联系和过 程的联系中认识对象,从 而达到最优化地分析和研 究问题。
文化市场营销是运动着 的文化现象和经济现象, 因而应该对文化市场作动 态的考察,用运动、发展 和变化的观点分析文化市 场营销问题。
2018版 思修 第一章第三节 创造有意义的人生

总之,大学生要加强人生观建设
(1) 正确看待人生
(2) 积极面对人生
(3) 勇于创造人生
假如生活欺骗了你
普希金
假如生活欺骗了你, 不要忧郁,也不要愤慨! 不顺心时暂且克制自己, 相信吧,快乐之日就会到来。
我们的心儿憧憬着未来, 现今总是令人悲哀! 一切都是暂时的,转瞬既逝, 而那逝去的将变为可爱。
一天忙碌为的饥,刚得饱来又思衣; 衣食刚得双足份,屋中缺少美貌妻; 有了娇妻并美妾,出入无轿少马骑; 骡马成群田万顷,无有官职怕受欺; 六品七品嫌官小,四品五品也嫌低; 当朝一品为宰相,又想面南做皇帝。
范 美 忠 的 极 端 个 人 主 义
范跑跑在其博客 中说:“只有为 了女儿我才可能 考虑牺牲自我, 其他人,哪怕是 我母亲,我也不 会管的。”
二、反对错误人生观
(一)反对拜金主义人生观 (二)反对享乐主义人生观 (三)反对个人主义人生观
12
坚决抵制各种错误人生观
反对拜金主义人生观 共性:认为金钱可以主宰一切,
把追求金钱作为人生至高理想。 大学生:傍大款,陪聊、陪玩、 陪游,甚至从事色情服务。采取 盗窃、抢劫等犯罪手段获取金钱 利益。
思考:金钱意识与 拜金主义的区别?
他眼中的人生……
也 不 愿 意 坐 在 自 行 车 后 面 笑 。
宁 愿 坐 在 宝 马 车 里 哭 ,
非诚勿扰 马诺
马诺
可以买到“房屋”,但买不到“家”; 可以买到“珠宝”,但买不到“美”;
可以买到“娱乐”,但买不到“愉快”;
可以买到“书籍”,但买不到“智慧”; 可以买到“谄媚”,但买不到“尊敬”; 可以买到“伙伴”,但买不到“朋友”; 可以买到“权势”,但买不到“威望”; 可以买到“服从”,但买不到“忠诚”; 可以买到“躯壳”,但买不到“灵魂”; 可以买到“小人之心”,但买不到“君子之 志”。
复变-积分变换课件第一章 第3节 二元实函数与复变函数

Re( z ) 当 z 0 时的极限 例2 证明函数 f ( z ) z 不存在.
证
令 z x iy, 则 f ( z )
u( x , y )
x , 2 2 x y
x , v ( x , y ) 0, 2 2 x y
当 z 沿直线 y kx 趋于零时, x x lim u( x , y ) lim 2 lim 2 2 2 x 0 x 0 x 0 x y x ( kx ) y kx y kx
例3 证:argz在原点及负实轴上不连续
y
证
t 0 t R t 0 t R
对z0=0,
o
lim arg( it ) / 2
x
lim arg( it ) / 2
arg z 不存在,故在z=0不连续 极限 lim z0
例3 证:argz在原点及负实轴上不连续
z z0 z z0
(1) lim[ f ( z ) g ( z )] A B;
z z0 z z0
(2) lim[ f ( z ) g ( z )] AB; f (z) A (3) lim ( B 0). z z0 g ( z ) B
与实变函数的极限运算法则类似.
z z0
说明 该定理将求复变函数 f ( z ) u( x , y ) iv ( x , y )
x x0 y y0
lim u( x , y ) u0 ,
x x0 y y0
lim v ( x , y ) v0 .
的极限问题, 转化为求两个二元实变 函数 u( x , y ) 和 v ( x , y ) 的极限问题.
{z x iy | 2 y xy c2 }
第一章 第三节 电子商务系统的组成和一般框架

议 网络层是指实现电子商务的最底层的基 础设施。它是信息传输系统,是实现电 子商务的基本保证。互联网是网络基础 设施中最重要的部分。
第三节 电子商务的系统组成和一般框架
三大支柱
国家政策及法律规范
开展商务活动时必须遵守有 关的法律、法规和相应的政 策。电子商务出现后,原有 的法律规范已经不适应新的 发展环境,需要制定新的法 律规范并形成一个成熟、统 一的法律体系,已成为世界 各国(地区)发展电子商务 活动的必然趋势。
技术标准和网络协议
技术标准定义了用户接口、传 输协议、信息发布标准等技术 细节,是信息发布和传递的基 础,是网络信息一致性的保证。
网络协议是计算机网络中为进 行数据交换而建立的规则、标 准或约定的集合。网络用户要 进行通信,就必须按照通信双 方预先约定好的规程进行。
物流体系构建
物流是电子商务的重要组成 部分,是信息流和资金流的 基础和载体。实体商品生产 和交换的全过程,都需要物 流活动的支持,需要高效、 合理、畅通的物流系统支撑。 物流业的发展壮大对电子商 务的快速发展起着重要的支 撑作用。
这些环境要素从整体上可分为网络层技术支持层服务支持层应用国家政策及法律规范技术标准和网络协议物流体系构建第三节电子商务系统的组成及一般框架网络层远程通信网有线电视网无线通信网互联网等技术支持层应用开发技术数据库技术文件管理技术服务支持层安全服务支付服务ca认证目录服务等应用层前端开发
电子商务系统的组成 及一般框架
互联网内容服务商(Internet Content Provider,ICP)
应用服务提供商(Application Service Provider,ASP)
第三节 电子商务系统的组成及一般框架
二、电子商务的一般框架
第一章 第三节 第二课时 地球自转的地理意义
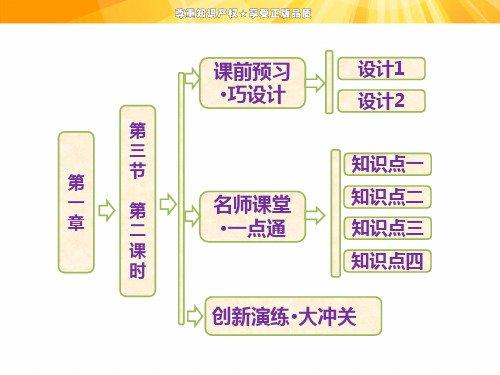
[答案] (1)略。 (4)C、D F、H
(2)晨
相互垂直
(3)昼
(5)B=H>D=E=F>A=C
1.读图(注:甲、乙、丙三图中,阴影区为黑夜,丙图 所示为北半球某地区),回答问题。
(1)各图中的晨线分别是:甲:弧______,乙:弧 ________,丙:弧________。 (2)赤道上晨线与昏线经度相距________度。 (3)晨昏线在一天中移动方向与地球自转方向________。 在一年中的________、________(节气)与经线重合。
国际日界线
自然日界线
示意图
相同点
都是经线,两侧日期都不一样(一般)
2.日期范围的界定 地球上新的一天开始于零时经线与180°经线重合时, 之后随零时经线西移,“今天”的范围逐渐扩大,“昨天” 的范围逐渐缩小。零时经线和国际日界线(180°经线)把 全球分为两个日期区,如下图所示:
快速确定地球上日期范围的方法 (1)由0时经线向东至日界线为今天(新的一天)的范围,由0时经 线向西至日界线为昨天(旧的一天)的范围,且两天的范围大小随着 地球自转不断变化。 ①当0时经线与180°经线重合时,全球属于同一日期(图a)。 ②当0时经线在东经度范围内时,地球上属于今天的范围 少于 一半(图b)。 ③当0时经线与0°经线重合时,全球平分成两个日期(图c)。 ④当0时经线在西经度范围内时,地球上属于今天的范围多于 一半(图d)。
(
)
A.172.5°E
C.165°E
B.170°E
D.172.Βιβλιοθήκη °W(4)四定值:即根据前面所确定的条件计算出所求时 间。如E点地方时为12:00+45°/15°=15:00,F点地 方时为24:00-45°/15°=21:00。
国际贸易实务与案列分析 第一章 第三节 FCA
?
CPT,CIP 与FCA的关系
? 学时:2-4课时
? 教学方式:PPT教学+案列分析讲授结合+情景模拟
2019/6/6
4.向承运人交货的贸易术语FCA
? Free Carrier(…named place):
卖方负责办理货物的出口手续,在指定 地点将货物交给买方指定的承运人,即 作为履行交货,卖方应承担承运人掌管 货物前的一切费用和风险。
? 相同:
? 风险、责任、费用划分的基本原则相同 ? 都是“凭单交货”,即卖方只要取得货运单据交给买方,就履行了交
货义务,可收取货款。
? 不同:
? 适用的运输方式不同:CIP组适用于各种方式及其组合;CIF组适用于 海运和内河运输
? 交货和风险的转移地点不同 ? 装卸费用不同 ? 交货时间不同:CIF组下取得正式提单日即是交货日;CIP组下货交承
CPT 注意事项
? 明确双方的责任和费用
? 明确装运期、装运地点和目的地 ? 由买方确定交货时间时,买方要及时通知卖方 ? 具体交货地点未确定,卖方可在最适合要求的地
点交货
? 风险划分与费用划分点分离 ? 风险划分是 交给承运人,费用是包含到目的港运费
CPT和CFR比较
? 相同:基本原则相同
? 风险划分点与责任划分点分离 ? 风险在交货地转移 ? 卖方订立运输合同,交付运费 ? 同属装运合同
FCA和FOB的比较
? 相同:买卖双方风险、责任、费用的划分的原则基
本相同。
? 不同:
? 风险:
? FOB下以船舷为界; ? FCA下以货交承运人为界
? 适用范围:
? FOB:海运、内河运输 ? FCA:各种运输方式和组合
第一章第三节+克莱姆法则
(16)
a11 ⋯ a1, j−1 b1 a1, j+1 ⋯ a1n ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯
行 Dj = ai1 ⋯ ai , j−1 bi ai , j+1 ⋯ a jn (第i行) ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯
an1 ⋯ an, j−1 bn an, j+1 ⋯ ann
(第j列) 列
3
( j = 1,2,⋯ , n)
λ x + y + z = 0, x + λ y + z = 0, x + y + λz = 0
有非零解, 有非零解 所以其系数行列式
λ
1 1
1
1 1 = 0,
λ
1
λ
∴ λ1 = −2 或 λ2 = 1.
即 (λ + 2)(λ − 1)2 = 0.
故 λ = −2 或 λ = 1 时, 所给齐次线性方程组有 非零解 .
(18)
定理三. 若齐次线性方程组(18)有非零解 则(18)的 有非零解,则 定理三 若齐次线性方程组 有非零解 的 系数行列式D=0. 系数行列式 证明: 反证. 证明 反证 由克莱姆法则知(18)只有零解 只有零解. 若 D≠0, 由克莱姆法则知 只有零解 矛盾! 证毕. 矛盾 证毕 ∴ D = 0.
返回
证明: 先验证(16)是(14)的解 即验证 的解, 证明 先验证 是 的解 即验证: D1 D2 Dn ai 1 + ai 2 + ⋯ + ain = bi ( i = 1,2,⋯, n.) D D D
D≠0
⇔
ai 1 D1 + ai 2 D2 + ⋯ + ain Dn ? Dbi . =
第1章 第3节 影响种群数量变化的因素
探究点一
探究点二
2.下图为某地东亚飞蝗种群数量变化示意图,下列叙述错误的是
()
A.为有效防治蝗灾,应在A点之前及时控制种群密度 B.A~B段,该种群的增长率与种群密度之间呈正相关 C.利用性引诱剂诱杀雄虫改变性别比例可防止C点出现 D.控制种群数量在D~E水平,有利于维持该地区生态系统的抵抗力 稳定性
探究点一
探究点二
种群研究的应用 情境导引
对种群的研究内容主要是什么?对于生产和生活的指导体现在哪 些方面? 1.大熊猫是我国特有的濒危保护动物,我国采取了建立保护区的方 式进行保护。请思考对大熊猫进行保护首先要研究的内容是什么? 提示:大熊猫种群的特征和影响数量变化的因素。 2.建立保护区的主要目的是什么?这样做有什么好处? 提示:减少人类的干扰。有利于提高环境容纳量,恢复大熊猫的种 群数量。
探究点一
探究点二
解析:图甲曲线的斜率代表种群的增长速率(即单位时间内种群个 体的增加数目),由题图曲线特征可以看出,在不同的时间点,曲线的 斜率不同,即种群的增长速率不同,A项错误;图乙中G点时种群的数 目不再变化,增长速率为0,B项错误;防治蝗灾应该在D点附近,超过 D点,蝗虫增长速率加快,灭虫效果差,C项错误;渔业捕捞应该在超过 K/2时进行,且每次捕捞后的剩余量应保持在E点左右,此时种群的 增长速率最快,D项正确。 答案:D
探究点一
探究点二
解析:从题中图的分析可知,未成熟个体从2月底到6月逐渐增多,从6 月到12月逐渐减少至12月变为0,而该动物个体从出生到性成熟需 要6个月,因此该种群出生时间大概为2月底到6月,到12月都成熟,表 明在后6个月内可能没有新的个体出生,9月份出生率可能为0,A项 错误;种群的数量2月底到6月逐渐增多,从6月到12月逐渐减少,B项 错误;该种群数量受气候、食物、行为调节等因素的影响,C项错误; 病原物和寄生物的致病力和传播速度是随着种群密度的增加而增 加的,种群密度越大,其抑制增长的作用力也就越强,D项正确。 答案:D
马克思主义基本原理概论 第一章 第三节
第一,要从实际出发,努力认识和把握 事物的发展规律。 第二,实践是发挥人的主观能动性的基 本途径。 第三,主观能动性的发挥,要依赖于一 定的物质条件和物质手段。
2、社会历史趋向与主体选择的关系
社会历史趋向属于历史决定论的内容,讲的是社会历 史规律的决定作用。主体选择讲的是历史主体在社会 历史发展中的能动性和选择性。历史发展的必然性, 规定了人们的活动要受规律性的制约,但不否认人在 可能的空间内的选择。 主体选择是在既定历史条件下对社会生活未来发展的 多种可能的方向、目标、方式的选择。在这当中,社 会生活未来发展存在着多种可能性是主体选择的客观 前提,主体利益和需要是选择的内在根据。马克思主 义历史决定论之所以强调社会历史规律的客观性,是 为了实现主体的正确选择,从而推动社会历史的前进。
第三,规律是事物的稳定联系。规律是变动 不居的现象中相对稳定和巩固的联系。规律 的稳定性突出地表现为它的重复性。就是说, 无论在什么地方、什么时候,只要具备了一 定的客观条件,就必然会表现出某种特定的 自然过程和规律,某种合乎规律的现象就必 定会重复出现。 第四,规律是客观的。客观性是规律的根本 特点,它不依赖于人的意识而存在。唯心主 义否认规律的客观性。人们在实践中可以发 现、认识和利用规律,但不能创造和消灭规 律。
自然规律可以完全相同的形式反复出现而社会规律则是历史的在不同社会国家民族以及不同的历史阶段具有不同的表现形二意识的能动作用辩证唯物主义认为
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三节 有机化合物的命名 [目标定位] 1.能说出简单有机物的习惯命名。2.能记住系统命名法的几个原则。3.能依据系统命名法的原则对烷烃、烯烃、炔烃、苯的简单同系物进行命名。4.能根据名称写出有机物的结构简式,并能判断所给有机物名称的正误。 一 烷烃的命名
1.烷基命名法 (1)烃分子失去一个氢原子所剩余的原子团叫烃基。 (2)甲烷分子失去一个H,得到—CH3,叫甲基;乙烷失去一个H,得到—CH2CH3,叫乙基。像这样由烷烃失去一个氢原子剩余的原子团叫烷基,烷基的组成通式为—CnH2n+1。 (3)丙烷分子失去一个氢原子后的烃基有两种,正丙基的的结构简式是—CH2CH2CH3、异丙基
的结构简式是。 2.烷烃习惯命名法 (1)根据烷烃分子里所含碳原子数目来命名,碳原子数加“烷”字,就是简单的烷烃的命名。 (2)碳原子数在十以内的,从一到十依次用甲、乙、丙、丁、戊、己、庚、辛、壬、癸来表示;碳原子数在十以上的用汉字数字表示;当碳原子数相同时,在(碳原子数)烷名前面加正、异、新等。 (3)分子式为C5H12的同分异构体有3种,写出它们的名称和结构简式。 ①正戊烷CH3CH2CH2CH2CH3;
②;
③。 (4)含碳原子数较多,结构复杂的烷烃采用系统命名法。 3.烷烃系统命名法 (1)分析下列烷烃的分子结构与其名称的对应关系,并填空: (2)总结烷烃系统命名法的步骤 ①选主链,称某烷。选定分子中最长的碳链为主链,按主链中碳原子数目称作“某烷”。 ②编序号,定支链。选主链中离支链最近的一端开始编号;当两个相同支链离两端主链相同时,从离第三个支链最近的一端开始编号,等近时按支链最简进行编号。 ③取代基写在前,注位置,短线连。先写取代基编号,再写取代基名称。 ④不同基团,简单在前、复杂在后、相同合并,最后写主链名称。
例如: 名称为3-甲基-4-乙基己烷。
烷烃的命名 (1)系统命名法书写顺序的规律 阿拉伯数字(用“,”隔开)-(汉字数字)支链名称、主链名称 ↓ ↓ (取代基位置) (取代基总数,若只有一个,则不用写) (2)烷烃命名的原则 ①选主链
最长:含碳原子数最多的碳链作主链最多:当有几条不同的碳链含碳原子数相同时,选择含支链最多的一条作为主链
②编序号
最近:从离支链最近的一端开始编号最简:若有两个不同支链且分别处于主链两端同等距离,则从简单的一端开始编号最小:取代基编号位次之和最小
(3)烷烃命名的注意事项 ①取代基的位号必须用阿拉伯数字表示。 ②相同取代基要合并,必须用中文数字表示其个数。 ③多个取代基位置间必须用逗号“,”分隔。 ④位置与名称间必须用短线“-”隔开。 ⑤若有多种取代基,必须简单写在前,复杂写在后。 1.用系统命名法命名下列烷烃。 (1)______________________________________________。 (2)________________________________________________。
(3)_____________________________________________。 (4)_______________________________________________。 (5)____________________________________。 答案 (1)2-甲基丁烷 (2)2,4-二甲基己烷 (3)2,5-二甲基-3-乙基己烷 (4)3,5-二甲基庚烷 (5)2,4-二甲基-3-乙基己烷 解析 烷烃命名必须按照三条原则进行:①选最长的碳链为主链,当最长的碳链不止一条时,应选取支链最多的为主链。②给主链编号时,应从距离取代基最近的一端开始编号,若两端距离取代基一样近,则按支链最简,并使全部取代基序号之和最小的一端来编号。③命名要规范。 2.下列烷烃的命名是否正确?若有错误,请加以改正。
(1)2-乙基丁烷
(2)3,4-二甲基戊烷
(3)1,2,4-三甲基丁烷 (4) 2,4-二甲基己烷 答案 (1)、(2)、(3)命名错误,正确的烷烃命名分别是(1)3-甲基戊烷,(2)2,3-二甲基戊烷,(3)3-甲基己烷。 (4)正确。 解析 (1)、(3)选错了主链,(1)中主链不是最长的,(3)中误把主链末端当成了取代基。
(2)是起点定错了,应是离支链最近的一端为起点:。 二 烯烃、炔烃的命名
1.写出下列较为简单的烯烃、炔烃的名称: (1)CH2===CH2乙烯;CH2===CH—CH3丙烯。 (2)CH≡CH乙炔;CH≡C—CH3丙炔。 2.分析下列二烯烃的分子结构与其名称的对应关系,并填空:
烯烃、炔烃的命名方法步骤 (1)选主链,定某烯(炔):将含双键或三键的最长碳链作为主链,称为“某烯”或“某炔”。 (2)近双(三)键,定位号:从距离双键或三键最近的一端给主链上的碳原子依次编号定位。 (3)标双(三)键,合并算:用阿拉伯数字标明双键或三键的位置(只需标明双键或三键碳原子编号较小的数字),用“二”“三”等表示双键或三键的个数。
3.某烯烃的结构简式为,有甲、乙、丙、丁四位同学分别将其命名为2-甲基-4-乙基-4-戊烯、2-异丁基-1-丁烯、2,4-二甲基-3-己烯、4-甲基-2-乙基-1-戊烯。下列对四位同学的命名判断正确的是( ) A.甲的命名主链选择是错误的 B.乙的命名编号是错误的 C.丙的命名主链选择是正确的 D.丁的命名是正确的 答案 D 解析 要注意烯烃的命名与烷烃的命名的不同之处:①烯烃中主链的选取必须包含双键在内,这样有可能主链并非是分子中最长的碳链;②对主链碳原子的编号是从离双键较近的一端开始,因而支链并不对编号起作用;③必须在书写名称时指出双键的位置。据此分析各位同学的命名,可以看出甲同学对主链碳原子编号错误,乙、丙同学的主链选择错误。
4.(1)有机物的系统命名是__________________。将其在催化剂存在下完全氢化,所得烷烃的系统命名是______。
(2)有机物的系统命名是________。将其在催化剂存在下完全氢化,所得烷烃的系统命名是________。 答案 (1)3-甲基-1-丁烯 2-甲基丁烷 (2)5,6-二甲基-3-乙基-1-庚炔 2,3-二甲基-5-乙基庚烷
解析 根据烯烃、炔烃的命名原则,选主链,编序号,具体编号如下:, ,然后再确定支链的位置,正确书写名称;当对烯烃、炔烃完全氢化后所得烷烃进行命名时,要注意主链及编号的变化。
三 苯的同系物的命名
1.苯的同系物的结构特征 (1)分子中含有一个苯环; (2)分子中侧链均为烷基。
如、、不是苯的同系物。 2.习惯命名法 以苯作为命名的母体,若氢原子被甲基取代叫甲苯;若氢原子被乙基取代叫乙苯;若两个氢原子被甲基取代叫二甲苯,二甲苯有邻、间、对三种不同的结构。 3.系统命名法 以二甲苯为例,若将苯环上的6个碳原子编号,以某个甲基所在的碳原子的位置为1号,选取最小位次号给另一个甲基编号。
1,2-二甲苯 1,3-二甲苯 1,4-二甲苯 苯的同系物的命名方法 (1)以苯作为母体,苯环侧链的烷基作为取代基,称为“某苯”。 (2)若苯环上有两个或两个以上的取代基时,则将苯环进行编号,编号时从小取代基开始,并沿使取代基位次和较小的方向进行。 注意:当苯环上含有不饱和烃基或虽为饱和基团但体积较大时,可将苯作为取代基。如
的名称为苯乙烯;的名称为苯乙炔。
5.苯有多种同系物,其中一种结构简式为 ,则它的名称为( ) A.2,4-二甲基-3-乙基苯 B.1,3-二甲基-2-乙基苯 C.1,5-二甲基-6-乙基苯 D.2-乙基-1,3-二甲基苯 答案 B 解析 苯的同系物命名时,将苯环进行编号,编号时从小的取代基开始,并且沿使取代基位
次和较小的方向进行,。因此命名为1,3-二甲基-2-乙基苯。 6.下列有机物命名是否正确?若不正确,请写出正确的名称。 (1)苯基甲烷________。 (2)二乙苯________。 (3)1,5-二甲基-6-乙基苯______。 答案 (1)甲苯 (2)邻二乙苯(或1,2-二乙苯) (3)1,3-二甲基-2-乙基苯 解析 苯的同系物命名时,以苯环为母体,侧链作取代基。编号时,将最简单的取代基所连的碳原子编为“1”号,然后按顺时针或逆时针编号,使取代基位置编号之和最小。
(1)有机物命名时选好主链是命名的最关键的一步,然后是编序号,就近、就简、最小是编序号时遵循的三条原则。同时书写要注意规范,数字与汉字之间用“-”隔开,数字之间用“,”隔开。 (2)烯烃、炔烃(或烃的衍生物)中都含有官能团,在命名时要注意到官能团对命名的影响,选择主链时要选择含有官能团的碳链为主链。
1.有机物(CH3CH2)2CHCH3的名称是( ) A.3-甲基戊烷 B.2-甲基戊烷 C.2-乙基戊烷 D.3-乙基丁烷 答案 A 解析 将该物质的结构简式变形为
。 2.下列选项中是3-甲基-2-戊烯的结构简式的是( )
