七年级数学几何图形单元测试题
人教版七年级上册数学《几何图形初步》单元检测题附答案
A.25°B.35°C.45°D.65°
8.∠1的补角是130°，∠2的余角是40°，则∠1与∠2的大小关系是( )
A.∠1>∠2B.∠1<∠2C.∠1＝∠2D.不能确定
9.下列说法中正确的是( )
A.8时45分，时针与分针的夹角是30°B.6时30分，时针与分针重合
C.3时30分，时针与分针的夹角是90°D.3时整，时针与分针的夹角是90°
10.将一副直角三角尺按如图所示的不同方式摆放,则图中 与 相等的是( )
A. B. C. D.
11.已知∠AOB＝20°，∠AOC＝4∠AOB，OD平分∠AOB，OM平分∠AOC，则∠MOD的度数是（ ）
A.20°或50°B.20°或60°C.30°或50°D.30°或60°
【点睛】本题是考查正方体 展开图，培养学生的观察能力、分析判断能力和空间想象能力．最好是动手操作一下，既可解决问题，又锻炼动手操作能力．
3.如图，下列说法中正确的是( )
A.OA的方向是北偏东20°B.OB的方向是北偏西65°
C.OC的方向是东南方向D.OD的方向是南偏西55°
【答案】D
【解析】
【分析】
A.①②B.②③C.④⑤D.①③④
【答案】C
【解析】
【分析】
根据线段的MN长度，及PM+PN的长度即可判断出P的位置．
【详解】∵MN=10cm，点P满足PM+PN=20cm，
∴点P不可能在线段MN上，而P的可能在直线MN上，可能在直线MN外．
故只有④⑤说法正确．
故选C．
【点睛】本题考查比较线段长度的知识，这类题目一般不能具体确定p的位置，只是可能不能说必然．
七年级数学上学期第四单元几何图形初步测试卷5套带答案
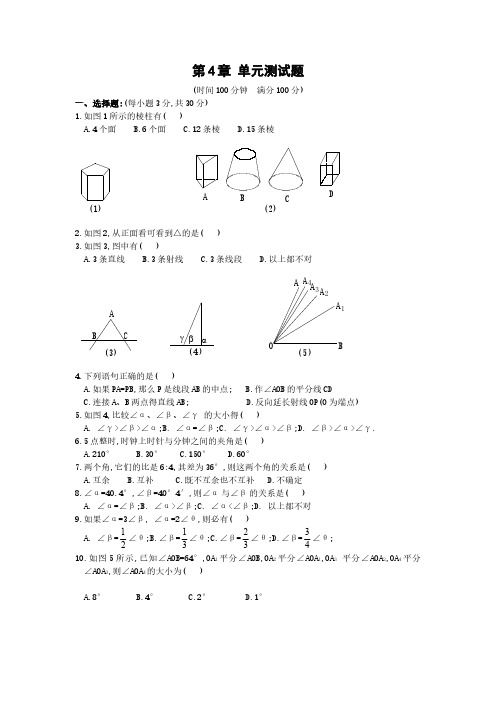
第4章 单元测试题(时间100分钟 满分100分)一、选择题:(每小题3分,共30分)1.如图1所示的棱柱有( )A.4个面B.6个面C.12条棱D.15条棱C(2)A DB2.如图2,从正面看可看到△的是( )3.如图3,图中有( )A.3条直线B.3条射线C.3条线段 D.以上都不对4.下列语句正确的是( )A.如果PA=PB,那么P是线段AB的中点;B.作∠AOB的平分线CDC.连接A、B两点得直线AB;D.反向延长射线OP(O为端点)5.如图4,比较∠α、∠β、∠γ 的大小得( )A. ∠γ>∠β>∠α;B. ∠α=∠β;C. ∠γ>∠α>∠β;D. ∠β>∠α>∠γ.6.5点整时,时钟上时针与分钟之间的夹角是( )A.210°B.30°C.150°D.60°7.两个角,它们的比是6:4,其差为36°,则这两个角的关系是( )A.互余B.互补C.既不互余也不互补D.不确定8.∠α=40.4°,∠β=40°4′,则∠α与∠β的关系是( )A. ∠α=∠β;B. ∠α>∠β;C. ∠α<∠β;D. 以上都不对9.如果∠α=3∠β, ∠α=2∠θ,则必有( )2310.如图5所示,已知∠AOB=64°,OA1平分∠AOB,OA2平分∠AOA1,OA3平分∠AOA2,OA4平分∠AOA3,则∠AOA4的大小为( )A.8°B.4°C.2°D.1°二、填空题:(每小题3分,共30分)11.已知线段AB=8cm,延长AB 至C,使AC=2AB,D 是AB 中点,则线段CD=______.12.如图,从城市A 到城市B 有三种不同的交通工作:汽车、火车、飞机,除去速度因素,坐飞机的时间最短是因为___________.13.57.32°=_______°_______′_______″;27°14′24″=_____°.14.已知∠a=36°42′15″,那么∠a 的余角等于________.15.∠1+∠2=180°,∠2+∠3=180°,根据________,得∠1=∠3.16.表示O 点南偏东15°方向和北偏东25°方向的两条射线组成的角等于____17.如图,∠AOC=90°,∠AOB=∠COD,则∠BOD=______°.航线铁路公路(6)A B18.102°43′32″+77°16′28″=________;98°12′25″÷5=_____.19.已知线段AB=acm,点A 1平分AB,A 2平分AA 1,A 3平分AA 2,……,____________cm.20.在平面上有任意四点,过其中任意两点画直线,能画_______条直线.三、解答题:(21、24、25、26每题6分,22、23题每题8分)21.根据下列语句画图:(1)画∠AOB=120°;(2)画∠AOB 的角平分线OC;(3)反向延长OC 得射线OD;(4)分别在射线OA、OB、OD 上画线段OE=OF=OG=2cm;(5)连接EF、EG、FG;(6)你能发现EF、EG、FG 有什么关系?∠EFG、∠EGF、∠GEF 有什么关系?22.已知线段AB=10cm,直线AB 上有一点C ,且BC=4cm,M 是线段AC 的中点,求AM 的长.23.如图,直线AB、CD 交于O 点,且∠BOC=80°,OE 平分∠BOC,OF 为OE 的反向延长线.(1)求∠2和∠3的度数.(2)OF平分∠AOD吗?为什么?24.一个角的补角与它的余角的度数之比是3:1,求这个角的度数.25.测量员沿着一块地的周围测绘.从A向东走600米到B,再从B向东南(∠ABC= 135°)走500米到C,再从C向西南(∠BCD=90°)走800米到D.用1厘米代表100米画图, 求DA的长(精确到10米)和DA的方向(精确到1°).北D CA B26.利用线段、角、三角形、圆等图形为你的学校设计一个校标,并简述你的设计思路.参考答案一、选择题1.D2.C3.C4.D5.C6.C7.B8.B9.C 10.B二、填空题11.12cm 12.两点之间,线段最短 13.57、19、12;27.2414. 53°17′45″ 15.同角的补角相等16.140° 17.90 18.180°;19°38′29″. 19. 20.1或4或6三、解答题21.(6)EF=EG=FG,∠EFG=∠EGF=∠FEG=60°22.AM=7cm或3cm23.(1)∠2=100°,∠3=40°;(2)∠AOF=40°,OF平分∠AOD24.设这个角为x0,( 180-x):(90-x)=3:1,x=45.第4章 单元测试题2检测时间：45分钟，满分：100分班级 学号 姓名 得分一、填空题：（每空2分，共46分）1．正方体有______条棱，_____个顶点， 个面.2．圆柱的侧面展开图是一个 ，圆锥的侧面展开图是一个 ，棱柱的侧面展开图是一个 。
人教版数学七年级上册第4章 几何图形初步单元测试(含答案)
七年级上册第4章单元测试一．选择题（共10小题）1．一个角的余角是44°，这个角的补角是（）A．134°B．136°C．156°D．146°2．下列图形能折叠成正方体的是（）A ．B ．C ．D ．3．下面各图是圆柱的展开图的是（）A ．B ．C ．D ．4．甲、乙两个城市，乙城市位于甲城市北偏东50°方向，距离为80km，那么甲城市位于乙城市（）A．南偏东50°方向，距离为80kmB．南偏西50°方向，距离为80kmC．南偏东40°方向，距离为80km第1页（共12页）D．南偏西40°方向，距离为80km5．有一个正六面体骰子放在桌面上，将骰子如图所示顺时针方向滚动，每滚动90°算一次，则滚动第2020次后，骰子朝下一面的数字是（）A．5B．4C．3D．26．下列各角中，（）是钝角．A ．周角B ．平角C．平角D ．平角7．小明家在学校的南偏西50°方向上，则学校在小明家（）上．A．南偏西50°B．西偏南50°C．北偏东50°D．北偏东40°8．下列度分秒运算中，正确的是（）A．48°39′+67°31′＝115°10′B．90°﹣70°39′＝20°21′C．21°17′×5＝185°5′D．180°÷7＝25°43′（精确到分）9．一个圆柱体切拼成一个近似长方体后（）A．表面积不变，体积变大B．表面积变大，体积不变C．表面积变小，体积不变D．表面积不变，体积不变10．下列语句中，正确的个数是（）第2页（共12页）①直线AB和直线BA是两条直线；②射线AB和射线BA是两条射线；③若∠1+∠2+∠3＝90°，则∠1、∠2、∠3互余；④一个角的余角比这个角的补角小；⑤一条射线就是一个周角；⑥两点之间，线段最短．A．1个B．2个C．3个D．4个二．填空题（共5小题）11．已知，∠A＝46°28'，则∠A 的余角＝．12．一个长方体的高是10cm，它的底面是边长为4cm的正方形，如果底面正方形的边长增加acm，则它的体积增加了cm3．13．已知如图，C是线段AB上的一点，N是线段BC的中点，若AB＝10，AC＝6，则AN＝．14．已知线段AB＝8cm．在直线AB上画线段AC＝5cm，则BC的长是cm．15．如图，将长方形ABCD纸片按如图所示的方式折叠，EF，EG为折痕，点A落在A'，点B落在B'，点A'，B'，E在同一直线上，则∠FEG＝度．三．解答题（共5小题）16．如图，CD是Rt△ABC斜边上的高，请找出图中各对互余的角．第3页（共12页）17．如图，是小明家和学校所在地的简单地图，已知OA＝2km，OB＝3.5km，OP＝4km，点C为OP的中点，回答下列问题：（1）图中到小明家距离相同的是哪些地方？（2）由图可知，公园在小明家东偏南30°方向2km处．请用方向与距离描述学校、商场、停车场相对于小明家的位置．18．如图，已知线段AB＝12 cm，点C为线段AB上的一动点，点D，E分别是AC和BC中点．（1）若点C恰好是AB的中点，则DE ＝cm；（2）若AC＝4 cm，求DE的长；（3）试说明无论AC取何值（不超过12 cm），DE的长不变．第4页（共12页）19．如图，已知射线OB平分∠AOC，∠AOC的余角比∠BOC小42°．（1）求∠AOB的度数：（2）过点O作射线OD，使得∠AOC＝4∠AOD，请你求出∠COD的度数．（3）在（2）的条件下，画∠AOD的角平分线OE，则∠BOE＝．20．如图，平面上有四个点A，B，C，D．（1）根据下列语句画图：Ⅰ、画射线DC；Ⅱ、画直线AC与线段BD相交于点F ；（2）图中以F为顶点的角中，请写出∠AFB的补角．第5页（共12页）参考答案一．选择题（共10小题）1．解：∵一个角的余角是44°，∴这个角的度数是：90°﹣44°＝46°，∴这个角的补角是：180°﹣46°＝134°．故选：A．2．解：A、能折叠成正方体，故此选项符合题意；B、出现了“凹”字格，不能折叠成正方体，故此选项不符合题意；C、折叠后有两个面重合，不能折叠成正方体，故此选项不符合题意；D、出现了“田”字格，不能折成正方体，故此选项不符合题意．故选：A．3．解：由图可知，该圆柱底面直径为6，高为4，所以该圆柱的底面周长（圆柱侧面展开得到的长方形的长）为：6×3.14＝18.84，故选：C．4．解：如图：第6页（共12页）∵乙城市位于甲城市北偏东50°方向，距离为80km，∴甲城市位于乙城市南偏西50°方向，距离为80km，故选：B．5．解：观察图形知道点数三和点数四相对，点数二和点数五相对且四次一循环，∵2020÷4＝505，∴滚动第2020次后与第一个相同，∴朝下的数字是3的对面4，故选：B．6．解：平角＝180°，钝角大于90°而小于180°，平角＝×180°＝120°，是钝角．故选：B．7．解：∵小明家在学校的南偏西50°方向上，∴学校在小明家北偏东50°方向上．故选：C．8．解：48°39'+67°31'＝115°70'＝116°10'，故A选项错误；90°﹣70°39'＝19°21'，故B选项错误；21°17'×5＝105°85'＝106°25'，故C选项错误；180°÷7＝25°43'，故D选项正确．故选：D．9．根据立体图形的切拼方法可知：圆柱体切拼成一个长方体后，体积大小不变，表面积增加了两个以圆柱的高和第7页（共12页）底面半径为边长的长方形的面积，所以表面积变大了．故选：B．10．解：①直线AB和直线BA是一条直线，原来的说法是错误的；②射线AB和射线BA是两条射线是正确的；③互余是指的两个角的关系，原来的说法是错误的；④一个角的余角比这个角的补角小是正确的；⑤周角的特点是两条边重合成射线．但不能说成周角是一条射线，原来的说法是错误的；⑥两点之间，线段最短是正确的．故正确的个数是3个．故选：C．二．填空题（共5小题）11．解：∵∠A＝46°28′，∴∠A的余角＝90°﹣46°28′＝43°32′．故答案为：43°32′．12．解：长方体原体积为：4×4×10＝160cm3．底面边长增加acm后，边长为（4+a）cm，体积为：10（4+a）2＝（10a2+80a+160）cm3．体积增加为：10a2+80a+160﹣160＝10a2+80a．故答案为：（10a2+80a）．13．解：∵AB＝10，AC＝6，∴CB＝10﹣6＝4，第8页（共12页）∵N是线段BC的中点，∴CN＝2，∴AN＝AC+CN＝6+2＝8．14．解：当C点在线段AB上时，BC＝AB﹣AC＝8﹣5＝3（cm）；当C点在线段BA的延长线上时，BC＝AB+AC＝8+5＝13（cm）．故BC的长为3或13cm．故答案为3或13．15．解：由折叠可得∠AEF＝∠A'EF，∠BEG＝∠B'EG，∵∠AEB＝180°，∴∠FEG＝∠A'EF+∠B'EG ＝∠AEB＝90°，故答案为90．三．解答题（共5小题）16．解：∵CD⊥AB，∴△ABC，△BCD是直角三角形，又∵△ABC是直角三角形，∴∠A与∠B，∠A与∠ACD，∠B与∠BCD互余（直角三角形的两个锐角互余），又∵∠ACB＝90°，∴∠ACD与∠BCD互余．∴图中互余的角有：∠A与∠B，∠A与∠ACD，∠B与∠BCD，∠ACD与∠BCD．17．解：（1）因为点C为OP的中点，第9页（共12页）所以OC＝2km，因为OA＝2km，所以可得出距小明家距离相同的是学校和公园；（2）由图可知，学校在小明家东偏北45°方向2km处，商场在小明家西偏北60°方向3.5km处，停车场在东偏南30°方向4km处．18．解：（1）∵点D，E分别是AC和BC的中点，∴DC ＝AC，CE ＝CB，∴DC+CE ＝（AC+CB）＝6cm；故答案为：6．（2）∵AC＝4cm，∴CD＝2cm，∵AB＝12cm，AC＝4cm，∴BC＝8cm，∴CE＝4cm，DE＝DC+CE＝6cm；（3）∵点D，E分别是AC和BC的中点，∴DC ＝AC，CE ＝CB，∴DC+CE ＝（AC+CB），即DE ＝AB＝6cm，故无论AC取何值（不超过12 cm），DE的长不变．第10页（共12页）19．解：（1）由射线OB平分∠AOC可得∠AOC＝2∠BOC，设∠BOC＝x，则∠AOC＝2x，依题意列方程90°﹣2x＝x﹣42°，解得：x＝44°，即∠AOB＝44°．（2）由（1）得，∠AOC＝88°，①当射线OD在∠AOC内部时，∠AOD＝22°，则∠COD＝∠AOC﹣∠AOD＝66°；②当射线OD在∠AOC外部时，∠AOD＝22°则∠COD＝∠AOC+∠AOD＝110°；（3）∵OE平分∠AOD，∴∠AOE ＝，当射线OD在∠AOC内部时，∠BOE＝∠AOB﹣∠AOE＝44°﹣11°＝33°；当射线OD在∠AOC外部时，∠BOE＝∠AOB+∠AOE＝44°+11°＝55°．∴∠BOE度数为33°或55°．故答案为：33°或55°20．解：（1）作图如下：第11页（共12页）（2）∠AFB的补角为∠BFC，∠AFD．第12页（共12页）。
人教版七年级上册数学第四章《几何图形》单元测试卷(Word版,含答案)
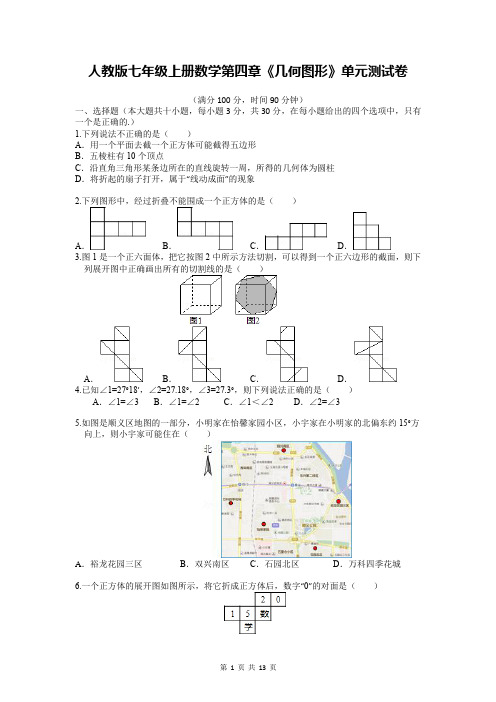
人教版七年级上册数学第四章《几何图形》单元测试卷（满分100分，时间90分钟）一、选择题（本大题共十小题，每小题3分，共30分，在每小题给出的四个选项中，只有一个是正确的.）1.下列说法不正确的是（）A．用一个平面去截一个正方体可能截得五边形B．五棱柱有10个顶点C．沿直角三角形某条边所在的直线旋转一周，所得的几何体为圆柱D．将折起的扇子打开，属于“线动成面”的现象2.下列图形中，经过折叠不能围成一个正方体的是（）A．B．C．D．3.图1是一个正六面体，把它按图2中所示方法切割，可以得到一个正六边形的截面，则下列展开图中正确画出所有的切割线的是（）A．B．C．D．4.已知∠1=27°18′，∠2=27.18°，∠3=27.3°，则下列说法正确的是（）A．∠1=∠3B．∠1=∠2C．∠1＜∠2D．∠2=∠35.如图是顺义区地图的一部分，小明家在怡馨家园小区，小宇家在小明家的北偏东约15°方向上，则小宇家可能住在（）A．裕龙花园三区B．双兴南区C．石园北区D．万科四季花城6.一个正方体的展开图如图所示，将它折成正方体后，数字“0”的对面是（）A．数B．5 C．1 D．学7.如图，∠AOB是一直角，∠AOC=40°，OD平分∠BOC，则∠AOD等于（）A．65°B．50°C．40°D．25°8.数学活动课上，四位同学围绕作图问题：“如图，已知直线l和直线l外一点P，用直尺和圆规作直线PQ，使PQ⊥l于点Q．”分别作出了下列四个图形，其中作法错误的为（）A．B．C．D．9.如图所示，一艘船从A点出发，沿东北方向航行至点B，再从B点出发沿南偏东15°方向航行至C点，则∠ABC的余角是（）A．15°B．30°C．45°D．75°10.某乡镇的4个村庄A,B,C,D恰好位于正方形的4个顶点上，为了解决农民出行难问题，镇政府决定修建连接各村庄的道路系统，使得每两个村庄都有直达的公路，设计人员给出了如下四个设计方案（实线表示连接的道路）在上述四个方案中最短的道路系统是方案（）A．一B．二C．三D．四二、填空题（本大题共10小题，每小题2分，共20分）11.有一正角锥的底面为正三角形.如果这个正角锥其中两个面的周长分别为27,15，则此正角锥所有边的长度和为.12.有3块积木，每一块的各面都涂上不同的颜色，3块的涂法完全相同，现把它们摆放成不同的位置（如图），请你根据图形判断涂成绿色一面的对面的颜色是.13.如图是一个立方体的平面展开图形，每个面上都有一个自然数，且相对的两个面上两数之和都相等，若13,9,3的对面的数分别是a,b,c，则a2+b2+c2﹣ab﹣ac﹣bc的值为.14.用一根长28分米的木条截开后刚好能搭一个长方体的架子，这个长方体的长、宽、高的长度都是整数分米，且都不相等，那么这个长方体的体积等于立方分米.15.经过A,B两点的直线上有一点C，AB=10，CB=6，D和E分别是AB,BC的中点，则DE 的长是.16.上午8：30钟表的时针和分针构成角的度数是.17.下列几何体属于柱体的有个.18.平面内不同的两点确定一条直线，不同的三点最多确定三条直线，平面内不同的七个点最多可确定条直线.19.用一个平面去截一个几何体，截面形状为三角形，则这个几何体可能为：①正方体；②圆柱；③圆锥；④正三棱柱（写出所有正确结果的序号）.20.已知一个圆柱的侧面展开图是如图所示的矩形，长为6π，宽为4π，那么这个圆柱底面圆的半径为.三、解答题（21 ~23题每题7分，25题8分，26题8分，27题8分）21.如图，点C在线段AB上，AC=6cm，MB=10cm，点M,N分别为AC,BC的中点．（1）求线段BC,MN的长；（2）若C在线段AB的延长线上，且满足AC﹣BC=bcm，M,N分别是线段AC,BC的中点，求MN的长度．22.如图是一个正方体的展开图，标注了字母“a”的面是正方体的正面，已知正方体相对两个面上的代数式的值相等．求a+的值．。
人教版七年级上册数学 第四章 几何图形初步 单元测试(含解析)
第四章几何图形初步单元测试一．选择题1．对如图所示几何体的认识正确的是（）A．棱柱的底面是四边形B．棱柱的侧面是三角形C．几何体是四棱柱D．棱柱的底面是三角形2．电视剧《西游记》中，孙悟空的“金箍棒”飞速旋转，形成一个圆面，是属于（）A．点动成线B．线动成面C．面动成体D．以上都不对3．下列说法正确的是（）A．延长直线AB到点CB．延长射线AB到点CC．延长线段AB到点CD．射线AB与射线BA是同一条射线4．如图，C为线段AD上一点，点B为CD的中点，且AD＝9，BD＝2．若点E在直线AD 上，且EA＝1，则BE的长为（）A．4B．6或8C．6D．85．下列说法正确的是（）A．两点之间的线段，叫做这两点之间的距离B．87'等于1.45°C．射线OA与射线AO表示的是同一条射线D．延长线段AB到点C，使AC＝BC6．线段AB＝9，点C在线段AB上，且有AC＝AB，M是AB的中点，则MC等于（）A．3B．C．D．7．某公司员工分别在A、B、C三个住宅区，A区有30人，B区有15人，C区有10人，三个区在一条直线上，位置如图所示，该公司的接送车打算在此间只设一个停靠点，为使所有员工步行到停靠点的路程之和最小，那么停靠点的位置应设在（）A．A区B．B区C．C区D．A、B两区之间8．如图，将一副三角板叠在一起使直角顶点重合于点O，（两块三角板可以在同一平面内自由转动），下列结论一定成立的是（）A．∠BOA＞∠DOC B．∠BOA﹣∠DOC＝90°C．∠BOA+∠DOC＝180°D．∠BOC≠∠DOA9．下列说法正确的是（）A．射线比直线短B．从同一点引出的两条射线所组成的图形叫做角C．若AP＝BP，则P是线段AB的中点D．两点之间的线段叫做这两点之间的距离10．如图，O在直线AB上，OC平分∠DOA（大于90°），OE平分∠DOB，OF⊥AB，则图中互余的角有（）对．A．6B．7C．8D．10二．填空题11．若一个六棱柱，则它有条棱，有个面．12．秒针旋转一周时，形成一个圆面，用数学知识可以理解为．13．已知点A、B、C在同一直线上，若AB＝10cm，AC＝16cm，点M、N分别是线段AB、AC中点，则线段MN的长是．14．如图，线段AB＝3，延长AB到点C，使BC＝2AB，则AC＝．15．如图，已知CD＝AD＝BC，E、F分别是AC、BC的中点，且BF＝40cm，则EF 的长度为cm．16．人们会把弯曲的河道改直，这样能够缩短航程．这样做的道理是．17．如图，有一种电子游戏，电子屏幕上有一条直线，在直线上有A，B，C，D四点，且AB＝BC＝CD，点P沿直线l从右向左移动，当出现点P与A，B，C，D四点中的至少两个点距离相等时，就会发出警报，则直线l上会发出警报的点P有个．18．如图，已知A、B是线段EF上两点，EA：AB：BF＝1：2：3，M、N分别为EA、BF 的中点，且MN＝8cm，则EF长为．19．如图，C、D是线段AB上的两点，E是AC的中点，F是BD的中点，若AB＝m，CD ＝n，则线段EF的长为．20．如图，射线OC，OD在∠AOB内，∠AOB和∠BOC互为补角，．若∠COD比∠BOD大m°（m＜30），则∠AOC＝°．（用含m的式子表示）三．解答题21．如图所示是一张铁皮．（1）计算该铁皮的面积；（2）它能否做成一个长方体盒子？若能，画出来，计算它的体积；若不能，说明理由．22．如图，线段AB＝20，BC＝15，点M是AC的中点．（1）求线段AM的长度；（2）在CB上取一点N，使得CN：NB＝2：3．求MN的长．23．如图，是小明家和学校所在地的简单地图，已知OA＝2km，OB＝3.5km，OP＝4km，点C为OP的中点，回答下列问题：（1）图中到小明家距离相同的是哪些地方？（2）由图可知，公园在小明家东偏南30°方向2km处．请用方向与距离描述学校、商场、停车场相对于小明家的位置．24．如图，在直线AD上任取一点O，过点O做射线OB，OE平分∠DOB，OC平分∠AOB，∠BOC＝26°时，求∠BOE的度数．25．如图，C是线段AB上一点，AC＝5cm，点p从点A出发沿AB以3cm/s的速度匀速向点B运动，点Q从点C出发沿CB以1cm/s的速度匀速向点B运动，两点同时出发，结果点P比点Q先到3s．（1）求AB的长；（2）设点P、Q出发时间为ts，①求点P与点Q重合时（未到达点B），t的值；②直接写出点P与点Q相距2cm时，t的值．26．线段与角的计算．（1）如图1，已知点C为AB上一点，AC＝15cm，CB＝AC，若D、E分别为AC、AB 的中点，求DE的长．（2）已知：如图2，∠AOB被分成∠AOC：∠COD：∠DOB＝2：3：4，OM平分∠AOC，ON平分∠DOB，且∠MON＝90°，求∠AOB的度数．参考答案1．解：如图所示的几何体是三棱柱，它有两个全等的三角形的底面，三个矩形的侧面，因此选项ABC均不符合题意，选项D符合题意；故选：D．2．解：孙悟空的“金箍棒”飞速旋转，形成一个圆面，是属于线动成面，故选：B．3．解：A、直线可以沿两个方向无限延伸，故不能说延长直线AB，故本选项不符合题意；B、射线可沿延伸方向无限延伸，故不能说延长射线AB，故本选项不符合题意；C、线段不能延伸，可以说延长线段AB到点C，故本选项符合题意；D、射线AB与射线BA不是同一条射线，故本选项不符合题意；故选：C．4．解：若E在线段DA的延长线，如图1，∵EA＝1，AD＝9，∴ED＝EA+AD＝1+9＝10，∵BD＝2，∴BE＝ED﹣BD＝10﹣2＝8，若E线段AD上，如图2，EA＝1，AD＝9，∴ED＝AD﹣EA＝9﹣1＝8，∵BD＝2，∴BE＝ED﹣BD＝8﹣2＝6，综上所述，BE的长为8或6．故选：B．5．解：A、应为：连结两点的线段的长度叫做这两点间的距离，故本选项错误；B、87'＝60'+27'＝1°+（）°＝1.45°，故本选项正确；C、射线OA的端点是点O，射线AO的端点是点A，所以，它们不是同一条射线，故本选项错误；D、延长线段AB到点C，则AC一定大于BC，不能使AC＝BC，故本选项错误．故选：B．6．解：∵AB＝9，∴AC＝AB＝3，∵M是AB的中点，∴AM＝AB＝∴MC＝AM﹣AC＝﹣3＝故选：B．7．解：∵当停靠点在A区时，所有员工步行到停靠点路程和是：15×100+10×300＝4500m，当停靠点在B区时，所有员工步行到停靠点路程和是：30×100+10×200＝5000m，当停靠点在C区时，所有员工步行到停靠点路程和是：30×300+15×200＝12000m，当停靠点在A、B区之间时，设在A区、B区之间时，设距离A区x米，则所有员工步行路程之和＝30x+15（100﹣x）+10（100+200﹣x），＝30x+1500﹣15x+3000﹣10x，＝5x+4500，∴当x＝0时，即在A区时，路程之和最小，为4500米；综上，当停靠点在A区时，所有员工步行到停靠点路程和最小，那么停靠点的位置应该在A区．故选：A．8．解：因为是直角三角板，所以∠AOC＝∠BOD＝90°，所以∠BOA+∠DOC＝∠AOC+∠BOC+∠DOC＝∠AOC＝∠BOD＝180°，故选：C．9．解：A．射线和直线不可以比较长短，原说法错误，故本选项不符合题意；B．从同一点引出的两条射线所组成的图形叫做角，原说法正确，故本选项符合题意；C．若点P在线段AB上，AP＝BP，则P是线段AB的中点，原说法错误，故本选项不符合题意；D．两点之间的线段的长度叫做这两点之间的距离，原说法错误，故本选项不符合题意；故选：B．10．解：∵OC平分∠DOA，∴∠AOC＝∠COD，∵OE平分∠DOB，∴∠DOE＝∠BOE，∴∠COE＝90°，∴∠AOC+∠BOE＝90°，∠AOC+∠DOE＝90°，∠COD+∠BOE＝90°，∠COD+∠DOE ＝90°，∠COF+∠EOF＝90°，∵OF⊥AB，∴∠AOC+∠COF＝90°，∠COD+∠COF＝90°，∠BOE+∠EOF＝90°，∠BOD+∠DOF ＝90°，∠DOE+∠EOF＝90°，∴互余的角有10对．故选：D．11．解：因为六棱柱上下两个底面是6边形，侧面是6个长方形，所以共有18条棱，8个面；故答案为18，8．12．解：根据点、线、面、体之间的关系可得，线动成面．13．解：（1）如图1，，∵AB＝10cm，点M是线段AB的中点，∴AM＝10÷2＝5（cm）；∵AC＝16cm，点N是线段AC的中点，∴AN＝16÷2＝8（cm），∴MN＝AM+AN＝5+8＝13（cm）（2）如图2，，∵AB＝10cm，点M是线段AB的中点，∴AM＝10÷2＝5（cm）；∵AC＝16cm，点N是线段AC的中点，∴AN＝16÷2＝8（cm），∴MN＝AN﹣AM＝8﹣5＝3（cm），综上，线段MN的长是13cm或3cm．故答案为：13cm或3cm．14．解：∵AB＝3，∴BC＝2AB＝6，∴AC＝AB+BC＝3+6＝9．故答案为：9．15．解：∵点F是BC的中点，且BF＝40cm，∴BC＝2BF＝80cm，∵CD＝AD＝BC，∴CD＝×80＝16cm，AD＝64cm，∴AC＝AD﹣CD＝48cm，∵E、F分别是AC、BC的中点，∴CE＝AC＝24cm，CF＝BF＝40cm，∴EF的长度为CE+CF＝64cm，故答案为：64．16．解：由线段的性质可知，把弯曲的河道改直，能够缩短航程，这样做根据的道理是两点之间线段最短，故答案为：两点之间线段最短．17．解：根据题意可知：当点P经过任意一条线段中点时会发出报警，∵图中共有线段DC、DB、DA、CB、CA、BA，∵BC和AD中点是同一个∴发出警报的可能最多有5个．故答案为5．18．解：∵EA：AB：BF＝1：2：3，可以设EA＝x，AB＝2x，BF＝3x，而M、N分别为EA、BF的中点，∴MA＝EA，NB＝BF，∴MN＝MA+AB+BN＝x+2x+x＝4x ∵MN＝8cm，∴4x＝8，∴x＝2，∴EF＝EA+AB+BF＝6x＝12，∴EF的长为12cm，故答案为：12cm．19．解：∵AB＝m，CD＝n．∴AB﹣CD＝m﹣n，∵E、F分别是AC、DB的中点，∴CE＝AC，DF＝DB，∴CE+DF＝（m﹣n），∴EF＝CE+DF+DC＝（m﹣n）+n＝m+n，故答案为：m+n．20．解：∵∠AOB和∠BOC互为补角，∴∠AOB+∠BOC＝180°，∵∠BOD＝，∴3∠BOD+∠BOC＝180°，即∠BOC＝180°﹣3∠BOD，∵∠COD+∠BOD＝∠BOC，∴180°﹣3∠BOD＝∠COD+∠BOD，∴∠COD+4∠BOD＝180°，∵∠COD比∠BOD大m°（m＜30），∴∠COD﹣∠BOD＝m°，∴∠BOD＝（）°，∠COD＝（）°∴∠BOC＝（）°，∴∠AOB＝180°﹣∠BOC＝（108﹣）°，∴∠AOC＝∠AOB﹣∠BOC＝（108﹣）°﹣（）°＝（36﹣m）°．故答案为（36﹣m）．21．解：（1）（1×3+2×3+1×2）×2＝22（m2），（2）根据棱柱的展开与折叠，可得可以折叠成长方体的盒子，其长、宽、高分别为3cm，2cm，1cm，因此体积为：1×2×3＝6（m3），22．解：（1）线段AB＝20，BC＝15，∴AC＝AB﹣BC＝20﹣15＝5．又∵点M是AC的中点．∴AM＝AC＝×5＝，即线段AM的长度是．（2）∵BC＝15，CN：NB＝2：3，∴CN＝BC＝×15＝6．又∵点M是AC的中点，AC＝5，∴MC＝AC＝，∴MN＝MC+NC＝，即MN的长度是．23．解：（1）因为点C为OP的中点，所以OC＝2km，因为OA＝2km，所以可得出距小明家距离相同的是学校和公园；（2）由图可知，学校在小明家东偏北45°方向2km处，商场在小明家西偏北60°方向3.5km处，停车场在东偏南30°方向4km处．24．解：∵OC平分∠AOB，∠BOC＝26°，∴∠AOB＝2∠BOC＝52°．∴∠BOD＝180°﹣52°＝128°．∵OE平分∠DOB，∴∠BOE＝∠DOB＝×128°＝64°．25．解：（1）设AB＝xcm，根据题意可得：（x﹣5）﹣＝3，解得：x＝12，答：AB的长为12cm；（2）①由题意可得：3t＝t+5，解得：t＝，故点P与点Q重合时（未到达点B），t的值为；②当点P追上点Q前相距2cm，由题意可得：3t+2＝t+5，解得：t＝，当追上后相距2cm，由题意可得：3t﹣2＝t+5，解得：t＝，总上所述：t＝或t＝．26．解：（1）∵AC＝15cm，CB＝AC，∴CB＝×15＝10（cm），∴AB＝15+10＝25（cm）．∵D，E分别为AC，AB的中点，∴AE＝BE＝AB＝12.5cm，DC＝AD＝AC＝7.5cm，∴DE＝AE﹣AD＝12.5﹣7.5＝5（cm）；（2）设∠AOC＝2x，∠COD＝3x，∠DOB＝4x，则∠AOB＝9x，∵OM平分∠AOC，ON平分∠DOB，∴∠MOC＝x，∠NOD＝2x，∴∠MON＝x+3x+2x＝6x，又∵∠MON＝90°，∴6x＝90°，∴x＝15°，∴∠AOB＝135°．。
2022-2023学年人教版七年级数学上册《第4章几何图形初步》单元达标测试题(附答案)
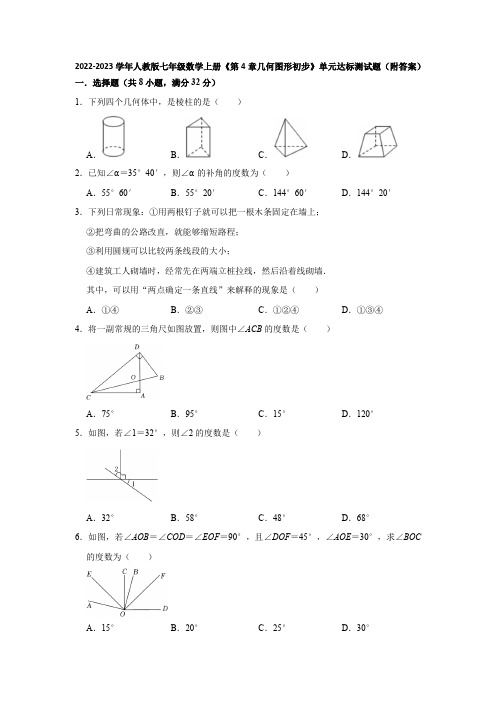
2022-2023学年人教版七年级数学上册《第4章几何图形初步》单元达标测试题（附答案）一．选择题（共8小题，满分32分）1．下列四个几何体中，是棱柱的是（）A．B．C．D．2．已知∠α＝35°40′，则∠α的补角的度数为（）A．55°60′B．55°20′C．144°60′D．144°20′3．下列日常现象：①用两根钉子就可以把一根木条固定在墙上；②把弯曲的公路改直，就能够缩短路程；③利用圆规可以比较两条线段的大小；④建筑工人砌墙时，经常先在两端立桩拉线，然后沿着线砌墙．其中，可以用“两点确定一条直线”来解释的现象是（）A．①④B．②③C．①②④D．①③④4．将一副常规的三角尺如图放置，则图中∠ACB的度数是（）A．75°B．95°C．15°D．120°5．如图，若∠1＝32°，则∠2的度数是（）A．32°B．58°C．48°D．68°6．如图，若∠AOB＝∠COD＝∠EOF＝90°，且∠DOF＝45°，∠AOE＝30°，求∠BOC 的度数为（）A．15°B．20°C．25°D．30°7．若∠1与∠2互为余角，∠1与∠3互为补角，则下列结论：①∠3﹣∠2＝90°；②∠3+∠2＝270°﹣2∠1；③∠3﹣∠1＝2∠2；④∠3＜∠1+∠2．其中正确的是（）A．①B．①②C．①②③D．①②③④8．如图，∠AOB与∠COB的度数分别记为m，n（m＞n），OM，ON分别是∠COB，∠AOC 的平分线，则∠MON的度数为（）A．B．C．D．二．填空题（共8小题，满分32分）9．如图，已知线段AB长度为x，CD长度为y，则图中所有线段的长度和为．10．点A，B，C是同一直线上的三个点，若AB＝7cm，BC＝5cm，则AC＝cm．11．（1）钟表上的时间是3时30分，此时时针与分针所成的夹角是度．（2）计算：24°24′＝°．（3）一个角是40°，则它的补角是度．12．如图是一个底面各边都相等的六棱柱，它的底面边长为2cm，高为5cm．这个棱柱共有条棱，个面，侧面积是cm2．13．在平整的地面上，有若干个完全相同的棱长为2cm的小正方体堆成一个几何体，如图所示：这个几何体露出的表面积是cm2．14．如图，将一个三角板60°角的顶点与另一个三角的直角顶点重合，∠1＝28°，∠2＝°．15．如图，已知点O是直线AB上的一点，∠COE＝120°，∠AOF＝∠AOE．（1）当∠BOE＝15°时，∠COA的度数为；（2）当∠FOE比∠BOE的余角大40°，∠COF的度数为．16．某天卢老师在数学课上，利用多媒体展示如下内容：如图，C为直线AB上一点，∠DCE 为直角，CF平分∠ACD，CH平分∠BCD，CG平分∠BCE，各学习小组经过讨论后得到以下结论：①∠ACF与∠BCH互余；②∠HCG＝45°；③∠ECF与∠GCH互补；④∠ACF﹣∠BCG＝45°．聪明的你认为哪些结论是正确的，请写出正确结论的序号．三．解答题（共7小题，满分56分）17．如图所示的是一个正方体的平面展开图，若将该展开图折叠成正方体后，相对面上的两个数字互为相反数，求2x+y﹣z的值．18．如图是一个食品包装盒的表面展开图．（1）该包装盒的几何体名称是；（2）根据图中所标尺寸，用a，b表示这个几何体的表面积S，并计算当a＝1，b＝4时，S的值．19．如图，C为线段AD上一点，点B为CD的中点，且AD＝9cm，BD＝2cm．（1）图中共有条线段．（2）求AC的长．（3）若点E在直线AD上，且EA＝3cm，求BE的长．20．如图，点C在线段AB上，点M，N分别为AC，BC的中点．（1）若AC＝6cm，MB＝10cm，求线段MN的长；（2）若C为线段AB上任一点，满足AC＝2acm，MB＝bcm，其它条件不变，你能猜想MN的长度吗？并说明理由；（3）若C在线段AB的延长线上，且满足AC＝xcm，BC＝ycm，M，N分别是线段AC，BC的中点，请画出图形，并用含x，y的式子表示MN的长度．21．如图1，∠AOC和∠BOD都是直角．（1）如果∠DOC＝35°，则∠AOB＝；（2）找出图1中一组相等的锐角为：；（3）若∠DOC变小，∠AOB将；（填变大、变小、或不变）（4）在图2中，利用能够画直角的工具在图2上再画一个与∠BOC相等的角．22．直观想象，逻辑推理已知点O为直线AB上一点．（1）如图1，过点O作射线OC，使∠AOC：∠BOC＝3：2，求∠AOC与∠BOC的度数；（2）如图2，射线OC为∠AOB内部任意一条射线，射线OD、OE分别是∠AOC、∠BOC 的角平分线，求∠DOE的度数，并写出简要的推理过程；（3）写出图2中所有互余的角和互补的角．23．如图，∠AOB＝m°，OC是∠AOB内的一条射线，OD、OE分别平分∠BOC、∠AOC．（1）若∠BOC＝90°，∠AOC＝30°，求∠DOE的度数；（2）试用含m的代数式表示∠DOE；（3）在图中，将OC反向延长，得到OP，OM、ON分别平分∠BOP、∠AOP．请将图补充完整，并用含m的代数式表示∠MON．参考答案一．选择题（共8小题，满分32分）1．解：选项A中的几何体是圆柱，因此选项A不符合题意；选项B中的几何体是三棱柱，因此选项B符合题意；选项C中的几何体是三棱锥，因此选项C不符合题意；选项D中的几何体是四棱台，因此选项D不符合题意；故选：B．2．解：∵∠α＝35°40′，∴∠α的补角的度数为180°﹣35°40′＝144°20′．故选：D．3．解：①④可以用“两点确定一条直线”来解释；②可以用“两点之间线段最短”来解释；③根据“作一条线段等于已知线段”的方法进行解释；故选：A．4．解：由题意得：∠ACD＝45°，∠BCD＝30°，则∠ACB＝∠ACD﹣∠BCD＝15°．故选：C．5．解：由图可得∠1+∠2+90°＝180°，∵∠1＝32°，∴∠2＝58°．故选：B．6．解：∵∠COD＝90°，∠DOF＝45°，∴∠COF＝45°，∵∠EOF＝90°，∴∠EOC＝45°，∵∠AOB＝90°，∴∠AOE+∠BOC＝45°，∵∠AOE＝30°，∴∠BOC＝15°，故选：A．7．解：根据题意得：（1）∠1+∠2＝90°，（2）∠1+∠3＝180°，∴（2）﹣（1）得，∠3﹣∠2＝90°，∴①正确；（1）+（2）得，∠1+∠2+∠1+∠3＝270°，∴∠3+∠2＝270°﹣2∠1，∴②正确；（2）﹣（1）×2得，∠3﹣∠1＝2∠2，∴③正确；∵（1）∠1+∠2＝90°，（2）∠1+∠3＝180°，∴2（∠1+∠2）＝180°，∴∠3＝180°﹣∠1＝2（∠1+∠2）﹣∠1＝∠1+2∠2，∴∠3＞∠1+∠2，∴④错误；故选：C．8．解：∵∠AOC＝∠AOB+∠BOC＝m+n，∵射线ON平分∠AOC，∴∠CON＝∠AOC＝（m+n），∵OM平分∠BOC，∴∠COM＝∠BOC＝n，∴∠MON＝∠CON﹣∠COM＝（m+n）﹣n＝m；故选：A．二．填空题（共8小题，满分32分）9．解：∵线段AB长度为x，∴AB＝AC+CD+DB＝x，又∵CD长度为y，∴AD+CB＝x+y，∴图中所有线段的长度和为：AB+AC+CD+DB+AD+CB＝x+x+x+y＝3x+y，故答案为：3x+y．10．解：①当点C在线段AB的延长线上时，AC＝AB+BC＝7+5＝12cm．②当点C在线段AB上时．AC＝AB﹣BC＝7﹣5＝2cm．故答案为：12或2．11．解：（1）3点30分时，时针与分针的较小夹角是2.5个大格，一个大格的度数是30°，所以30°×2.5＝75°；故答案为：75；（2）24°24′＝24.4°．故答案为：24.4；（3）由补角的性质，得40°角的补角是180°﹣40°＝140°，故答案为：140．12．解：六棱柱有18条棱，8个面，侧面积是2×6×5＝60cm2．故答案为：18，8，60．13．解：∵几何体露出的小正方体的面一共有32个，∴这个几何体露出的表面积为32×4＝128（cm2），故答案为：128．14．解：∵∠BAC＝60°，∠1＝28°，∴∠EAC＝∠BAC﹣∠1＝32°，∵∠DAE＝90°，∴∠2＝∠DAE﹣∠EAC＝58°．故答案为：58．15．解：（1）∵∠BOE＝15°，∠COE＝120°，∴∠COA＝180°﹣120°﹣15°＝45°．故答案为：45°．（2）由题意得，∠FOE＝90°﹣∠BOE+40°＝130°﹣∠BOE．∵∠AOF＝∠AOE，∴180°﹣∠BOF＝．∴180°﹣（∠EOF+∠BOE）＝60°﹣．∴180°﹣130°＝60°﹣．∴∠BOE＝30°．∴∠EOF＝90°﹣30°+40°＝100°．∴∠COF＝∠COE﹣∠EOF＝120°﹣100°＝20°．故答案为：20°．16．解：∵CF平分∠ACD，CH平分∠BCD，CG平分∠BCE，∴∠ACF＝∠FCD＝∠ACD，∠DCH＝∠HCB＝∠DCB，∠BCG＝∠ECG＝∠BCE，∵∠ACB＝180°，∠DCE＝90°，∴∠FCH＝90°，∠HCG＝45°，∠FCG＝135°∴∠ACF+∠BCH＝90°，故①②正确，∵∠ECF＝∠DCE+∠FCD＝90°+∠FCD，∠FCD+∠DCH＝90°，∴∠ECF+∠DCH＝180°，∵∠HCG≠∠DCH，∴∠ECF与∠GCH不互补，故③错误，∵∠ACD﹣∠BCE＝180°﹣∠DCB﹣∠BCE＝90°，∴∠ACF﹣∠BCG＝45°．故④正确．故答案为：①②④．三．解答题（共7小题，满分56分）17．解：由题意得：2与y，3与z，x与﹣2分别是相对面上的两个数，所以y＝﹣2，z＝﹣3，x＝2，则2x+y﹣z＝4﹣2+3＝5．18．解：（1）由展开图知，该包装盒的几何体为长方体，故答案为：长方体；（2）由题知，S＝2×2a×a+2×2a×b+2×a×b＝4a2+6ab，当a＝1，b＝4时，S＝4+6×4＝28．19．解：（1）以A为端点的线段为：AC，AB，AD；以C为端点的线段为：CB，CD；以B为端点的线段为：BD；共有3+2+1＝6（条）；故答案为：6．（2）∵点B为CD的中点，BD＝2cm．∴CD＝2BD＝2×2＝4（cm），∴AC＝AD﹣CD＝9﹣4＝5（cm），答：AC的长是5cm．（3）AB＝AC+BC＝7cm，EA＝3cm，当点E在线段AD上时，BE＝AB﹣AE＝7﹣3＝4（cm），当点E在线段DA的延长线上时，BE＝AB+AE＝7+3＝10（cm），答：BE的长是4或10cm．20．解：（1）∵M是AC的中点，∴MC＝AC＝3cm，∴BC＝MB﹣MC＝7cm，又∵N为BC的中点，∴CN＝BC＝3.5cm，∴MN＝MC+NC＝6.5cm；（2）∵点M、N分别是AC、BC的中点，AC＝2acm，MB＝bcm，∴AM＝AC＝a cm，AC+CB＝（a+b）cm，∴CM＝AC，CN＝BC，∴MN＝CM+CN＝AC+BC＝（AC+BC）＝（a+b）cm，即线段MN的长是（a+b）cm；（3）如图：MN＝（x﹣y）cm，理由是：∵点M、N分别是AC、BC的中点，AC﹣CB＝（x﹣y）cm，∴CM＝AC，CN＝BC，∴MN＝CM﹣CN＝AC﹣BC＝（AC﹣BC）＝（x﹣y）cm，即线段MN的长是（x﹣y）cm．21．解：（1）∵∠AOC＝∠DOB＝90°，∠DOC＝35°，∴∠COB＝∠BOD﹣∠DOC＝90°﹣35°＝55°，∴∠AOB＝∠AOC+∠COB＝90°+55°＝145°；故答案为：145°；（2）∵∠AOC＝∠DOB＝90°，∴∠AOD+∠COD＝∠BOC+∠COD＝90°，∴∠AOD＝∠BOC；故答案为：∠AOD＝∠BOC；（3）∵∠AOD+∠DOC+∠DOC+∠BOC＝∠AOB+∠COD＝∠AOC+∠BOD＝180°，∴∠AOB＝180°﹣∠DOC，∴∠DOC逐渐变小，∠AOB逐渐变大；故答案为：变大；（4）利用三角板画∠AOC＝∠BOD＝90°，则∠AOD＝∠BOC，理由如下：∵∠AOC＝∠DOB＝90°，∴∠AOD+∠COD＝∠BOC+∠COD＝90°，∴∠AOD＝∠BOC．22．解：（1）设∠AOC＝3x，∠BOC＝2x，∵∠AOC+∠BOC＝180°，∴3x+2x＝180°，∴x＝36°，∴∠AOC＝3×36°＝108°，∠BOC＝2×36°＝72°；（2）∵OD、OE分别是∠AOC、∠BOC的角平分线，∴∠DOC＝∠AOD＝，∠COE＝∠BOE＝∠BOC，∵∠AOC+∠BOC＝180°，∠DOE＝∠DOC+∠COE，∴∠DOE＝＝＝＝90°；（3）互余的角有，∠DOC与∠COE，∠AOD与∠COE，∠BOE与∠COD，∠BOE与∠AOD；互补的角有，∠AOD与∠BOD，∠AOC与∠BOC，∠AOE与∠BOE．23．解：（1）∵OD、OE分别平分∠BOC、∠AOC，∴∠DOE＝＝60°；（2）由（1）知，∠DOE＝＝＝；（3）补充图形如下：∵∠AOB＝m°，∴∠BOP+∠AOP＝360°﹣∠AOB＝360°﹣m°，∵OM、ON分别平分∠BOP、∠AOP，∴∠MON＝∠MOP+∠NOP＝＝．。
人教版数学七年级(上)第4章《几何图形初步》单元综合练习卷(含答案)
人教版数学七年级（上）第4章《几何图形初步》单元综合练习卷（含答案）一．选择题1．下列说法：①直线AB和直线BA是同一条直线；②平角是一条直线；③两点之间，线段最短；④如果AB=BC，则点B是线段AC的中点．其中正确的有（）A．1个B．2个C．3个D．4个2．下列四个图形中是如图展形图的立体图的是（）A．B．C．D．3．如图，若CB=4，DB=7，且D是AC的中点，则AC的长为（）A．3B．6C．9D．11 4．下列图形中不是正方体的平面展开图的是（）A．B．C．D．5．钟表在2点半时，其时针和分针所成的角是（）A．60°B．75°C．105°D．120°6．将一副三角板按如图所示的位置摆放，其中∠α和∠β一定互余的是（）A．B．C．D．第 1 页共33 页7．下列说法正确的有（）句．①两条射线组成的图形叫做角；②同角的补角相等；③若AC=BC，则C为线段AB的中点；④线段AB就是点A与点B之间的距离；⑤平面上有三点A、B、C，过其中两点的直线有三条或一条．A．0B．1C．2D．3 8．下列标注的图形名称与图形不相符的是（）A．球B．长方体C．圆柱D．圆锥9．点M在线段AB上，给出下列四个条件，其中不能判定点M是线段AB中点的是（）A．AM=BM B．AB=2AM C．BM=AB D．AM+BM=AB10．如图是小明画的正方体表面展开图，由7个相同的正方形组成．小颖认为小明画的不对，她剪去其中的一个正方形后，得到的平面图就可以折成一个正方体．小颖剪去的正方形的编号是（）A．7B．6C．5D．411．将一张长方形纸片按如图所示的方式折叠，EC，ED为折痕，折叠后点A′，B′，E在同一直线上，则∠CED的度数为（）第 2 页共33 页A．90°B．75°C．60°D．95°12．一个六棱柱模型如图所示，底面边长都是5cm，侧棱长为4cm，这个六棱柱的所有侧面的面积之和是（）A．20cm2B．60cm2C．120cm2D．240cm2二．填空题13．一个棱柱有20个顶点，每条侧棱长6cm，底面每条边长是2m，则所有侧棱长是．14．如图，若∠3：∠2=2：5，且∠2﹣∠1=12°，∠3等于．15．如图，点B、O、D在同一直线上，且OB平分∠AOC，若∠COD=150°，则∠AOC的度数是．16．已知线段AB，在AB的延长线上取一点C，使AC=2BC，若在AB的反向延长线上取一点D，使DA=2AB，那么线段AC是线段DB的倍．17．按照如图的平面展开图折叠成正方体后，相对面上的两个数都互为相反数，那么（a+b）c= ．第 3 页共33 页18．已知：如图，B，C两点把线段AD分成2：4：3三部分，M是AD的中点，CD=6cm，则线段MC的长为．三．解答题19．如图，已知A、O、B三点共线，∠AOD=42°，∠COB=90°．（1）求∠BOD的度数；（2）若OE平分∠BOD，求∠COE的度数．20．有一个养鱼专业户，在如图所示地形的两个池塘里养鱼，他每天早上要从住处P分别前往两个池塘投放鱼食，试问他怎样走才能以最短距离回到住地？（请用尺规作图，保留作图痕迹，不写作法）第 4 页共33 页21．将一个正方体木块涂成红色，然后如图把它的棱三等分，再沿等分线把正方体切开，可以得到27个小正方体．观察并回答下列问题：（1）其中三面涂色的小正方体有个，两面涂色的小正方体有个，各面都没有涂色的小正方体有个；（2）如果将这个正方体的棱n等分，所得的小正方体中三面涂色的有个，各面都没有涂色的有个；（3）如果要得到各面都没有涂色的小正方体125个，那么应该将此正方体的棱等分．22．已知，如图，点C在线段AB上，且AC=6cm，BC=14cm，点M、N分别是AC、BC的中点．（1）求线段MN的长度；（2）在（1）中，如果AC=acm，BC=bcm，其它条件不变，你能猜测出MN的长度吗？请说出你发现的结论，并说明理由．23．读句画图：如图，直线CD与直线AB相交于C，根据下列语句画图：（1）过点P作PQ∥CD，交AB于点Q；第 5 页共33 页（2）过点P作PR⊥CD，垂足为R．24．数学课上，李老师出示了如下框中的题目．如图1，在∠AOB的内部有一条射线OC把∠AOB分成两个角，射线OM、ON分别平分∠AOC、∠BOC，试探究∠MON与∠AOB之间的数量关系，并说明理由．小敏与同桌小聪讨论后，进行了如下解答：（1）特殊情况，探索结论：①请你在下表中填上当∠AOB为60°、90°、120°时∠MON的大小：②探索发现：无论∠AOB的度数是多少，∠MON与∠AOB的数量关系是不变的，请你直接写出结论：∠MON ∠AOB．（2）特例启发，解答题目：如图2，如果∠AOB=α，请你求∠MON的大小（用α表示）．（3）拓展结论，设计新题：如图3，把一张报纸的一角斜折过去，使A点落在E点处，BC为折痕，BD是∠EBM的平分线，求∠CBD的度数．第 6 页共33 页第7 页共33 页参考答案一．选择题1．解：①∵直线AB和直线BA是同一条直线，∴①正确；②∵角是角，线是线，∴平角是一条直线，∴②错误；③两点之间，线段最短，∴③正确；④∵如果A、B、C三点不共线，则AB=BC不能得出点B是线段AC的中点，∴④错误．故选：B．2．解：因为含小黑正方形的面不能与含大黑正方形的面相邻，两个小黑正方形不能在同一行，所以B，C不是左边展形图的立体图；两个小黑正方形在大黑正方形的对面”，那么A图中，正好是大黑正方形在上面，那么小黑正方形就在底面，A符合；故选：A．3．解：∵CB=4，DB=7，∴DC=DB﹣CB=7﹣4=3，∵D是AC的中点，∴AC=DC×2=3×2=6．故选：B．4．解：A、是正方体的展开图，不合题意；B、是正方体的展开图，不合题意；C、不能围成正方体，故此选项正确；D、是正方体的展开图，不合题意．故选：C．第8 页共33 页5．解：时针转过的角度是（2+）×30°=75°，分钟转过的角度是30×6°=180°，所以钟表在2点半时，其时针和分针所成的角是180°﹣75°=105°，故选：C．6．解：A、∠α与∠β不互余，故本选项错误；B、∠α与∠β互余，故本选项正确；C、∠α与∠β不互余，故本选项错误；D、∠α与∠β不互余，∠α和∠β互补，故本选项错误；故选：B．7．【解答】解：①由一个点出发的两条射线组成的图形叫角，故①错误；③若AC=BC，此时点C在线段AB的垂直平分线上，故③错误；④线段AB的长度是点A与点B之间的距离，故④错误；故选：C．8．解：长方体是立体图形，选项B中缺少遮挡的虚线，所以B图形名称与图形不相符．故选：B．9．解：A、由AM=BM可以判定点M是线段AB中点，所以此结论正确；B、由AB=2AM可以判定点M是线段AB中点，所以此结论正确；C、由BM=AB可以判定点M是线段AB中点，所以此结论正确；D、由AM+BM=AB不可以判定点M是线段AB中点，所以此结论不正确；因为本题选择不能判定点M是线段AB中点的说法，故选：D．10．解：根据只要有“田”字格的展开图都不是正方体的表面展开图，应剪去的小正方形的编号是5．故选：C．11．解：由题意知∠AEC=∠CEA′，∠DEB=∠DEB′，则∠A′EC=∠AEA′，∠B′DE=∠B′EB，第9 页共33 页所以∠CED=∠AEB=×180°=90°，故选：A．12．解：六棱柱的侧面积为：4×5×6=120（cm2）．故选：C．二．填空题（共6小题）13．解：∵一个棱柱有20个顶点，每条侧棱长6cm，∴底面为10边形，有10条侧棱，∴所有侧棱长的和是10×6=60cm，故答案为：60cm．14．解：∵∠3：∠2=2：5，设∠3=2x，∠2=5x，∵∠1+∠2+∠3=180°，∠2﹣∠1=12°，可得：5x﹣12°+5x+2x=180°，解得：x=16，所以∠3=2×16°=32°，故答案为：32°15．解：∵点B、O、D在同一直线上，∠COD=150°，∴∠COB=180°﹣150°=30°，∵OB平分∠AOC，∴∠AOC=2×30°=60°，故答案为：60°．16．解：如下图所示：设AB=1，则DA=2，AC=2，∴可得：DB=3，AC=2，∴可得线段AC是线段DB的倍．故答案为：．第10 页共33 页17．解：这是一个正方体的平面展开图，共有六个面，其中面“a”与面“﹣1”相对，面“c”与面“2”相对，“﹣3”与面“b”相对，∵相对面上的两个数都互为相反数，∴a=1，b=3，c=﹣2，则（a+b）c=（1+3）﹣2=．故答案为：．18．解：∵B，C两点把线段AD分成2：4：3三部分，∴设AB=2x，BC=4x，CD=3x，∵CD=6cm，即3x=6cm，解得x=2cm，∴AD=2x+4x+3x=9x=9×2=18cm，∵M是AD的中点，∴MD=AD=×18=9cm，∴MC=MD﹣CD=9﹣6=3cm．故答案为：3cm．三．解答题（共6小题）19．解：（1）∵A、O、B三点共线，∠AOD=42°，∴∠BOD=180°﹣∠AOD=138°；（2）∵∠COB=90°，∴∠AOC=90°，∵∠AOD=42°，∴∠COD=48°，∵OE平分∠BOD，∴∠DOE=∠BOD=69°，∴∠COE=69°﹣48°=21°．20．解：如图所示：PD→DE→EP才能以最短距离回到住地．第11 页共33 页21．解：（1）把正方体的棱三等分，然后沿等分线把正方体切开，得到27个小正方体．观察其中三面被涂色的有8个，两面涂色的有12个；各面都没有涂色的有1个，故答案为：8，12，1；（2）根据正方体的棱三等分时三面被涂色的有8个，有1个是各个面都没有涂色的，正方体的棱四等分时三面被涂色的有8个，有8个是各个面都没有涂色的，∴正方体的棱n等分时三面被涂色的有8个，有（n﹣2）3个是各个面都没有涂色的，故答案为：8，（n﹣2）3；（3）由（2）得将这个正方体的棱n等分，有（n﹣2）3个是各个面都没有涂色的，即（n﹣2）3=125，n﹣2=5，n=7，故答案为7．22．解：（1）∵AC=6cm，BC=14cm，点M、N分别是AC、BC的中点，∴MC=3cm，NC=7cm，∴MN=MC+NC=10cm；第12 页共33 页（2）MN=（a+b）cm．理由是：∵AC=acm，BC=bcm，点M、N分别是AC、BC的中点，∴MC=cm，NC=cm，∴MN=MC+NC=（a+b）cm．23．解：每对一问得（3分）如图，直线CD与直线AB相交于C，根据下列语句画图（1）过点P作PQ∥CD，交AB于点Q；（3分）（2）过点P作PR⊥CD，垂足为R．（6分）24．解：（1）①∵∠MOC=∠AOC，∠NOC=∠BOC，∴∠MON=∠MOC+∠NOC=∠AOC+∠BOC=∠AOB，当∠AOB=60°时，∠MON=×60°=30°，当∠AOB=90°时，∠MON=×90°=45°，当∠AOB=120°时，∠MON=×120°=60°；②由①知，∠MON=∠AOB，故答案为：①30°，45°，60°；②；第13 页共33 页（2）由（1）②知，∠MON=∠AOB，∴∠MON=α；（3）∵A点落在E点处，BC为折痕，∴∠CBA=∠CBE=∠ABE，∵D是∠EBM的平分线，∴∠EBD=∠DBM=∠MBE，∴∠CBE+∠EBD=（∠ABE+∠MBE）=∠ABM=×180°=90°．第14 页共33 页第 15 页 共 33 页人教版七年级上册第四章几何图形初步单元检测试题（含答案）一、单选题（共10题；共30分）1.如图，图中的长方形共有（ ）个．A. 9B. 8C. 5D. 4 2.如图所示几何图形中，是棱柱的是（ ）A. B. C. D.3.如图，是一个几何体的表面展开图，则该几何体是（ ） A. 正方体 B. 长方体 C. 三棱柱 D. 四棱锥4.如图，∠AOC ＞∠BOD ，则（ ）A. ∠AOB ＞∠CODB. ∠AOB=∠CODC. ∠AOB ＜∠CODD. 以上都有可能5.如图所示，∠AOC=∠BOD=90°，若∠AOB=150°，则∠DOC 的度数为（ ）A. 30°B. 40°C. 50°D. 60°6.如图，线段CD 在线段AB 上，且CD=2，若线段AB 的长度是一个正整数，则图中以A ，B ，C ，D 这四点中任意两点为端点的所有线段长度之和可能是（ ）A. 28B. 29C. 30D. 317.将一个圆分割成四个大小相同的扇形，则每个扇形的圆心角是（ ）度． A.45 B.60 C.90 D.1208.若∠AOB=90°，∠BOC=40°，则∠AOC 的度数为（ ）A. 50°B. 50° 或120°C. 50°或130°D. 130° 9.直棱柱的侧面都是（ ）A. 正方形B. 长方形C. 五边形D. 菱形 10.如果时钟上的时针、分针和秒针都是匀速地转动，那么从3时整（3:00）开始,在1分钟的时间内,3根针中,出现一根针与另外两根针所成的角相等的情况有 ( ) A. 1次 B. 2次 C. 3次 D. 4次二、填空题（共8题；共24分）11.已知∠α=36°14′25″，则∠α的余角的度数是________．12.如果一个六棱柱的一条侧棱长为5cm ，那么所有侧棱之和为________ cm13.（1）102°43′32″+77°16′28″=________；（2）98°12′25″÷5=________．14.如图，∠AOB 中，OD 是∠BOC 的平分线，OE 是∠AOC 的平分线，若∠AOB=135°，则∠EOD=________°．15.（1）32°43′30″=________°；（2）86.47°=________ °________′________″16.已知：点A、B、C在同一直线上，若AB=12cm，BC=4cm，且满足D、E分别是AB、BC的中点，则线段DE的长为________cm．17.用棱长是1cm的小正方体组成如图所示的几何体，把这个几何体放在桌子上，并把暴露.的面涂上颜色，那么涂颜色面的面积之和是________cm218.用平面截几何体可得到平面图形，在表示几何体的字母后填上它可截出的平面图形的号码．如A（1、5、6）；则B（________）；C（________）；D（________）；E（________）．三、解答题（共6题；共42分）19.如图，OC平分∠BOD，∠AOD=110°，∠COD=35°，求∠AOB的度数．20.直线AB、CD相交于点O，OE平分∠AOD，∠FOC=90°，∠1=40°，求∠2与∠3的度数。
七年级数学上册《第一章 基本的几何图形》单元测试卷及答案
七年级数学上册《第一章 基本的几何图形》单元测试卷及答案一、精心选一选（每小题3分，共30分）1.六棱柱由几个面围成（ ）A.6个B.7个C.8个D.9个2.下面形状的四张纸板，按图中线经过折叠可以围成一个直三棱柱的是（ ）3.下列说法错误的是（ ） A.若AP=BP,则点P 是线段的中点 B.若点C 在线段AB 上，则AB=AC+BCC.若AC+BC>AB,则点C 一定在线段AB 外D.两点之间，线段最短4.一个五棱锥的面数、棱数和顶点数分别是（ ）A.6,10,5B.6,10,6C.5,10,6D.5,6,55.下列平面展开图是由5个大小相同的正方形组成，其中沿正方形的边不能折成无盖小方盒的是（ ）6.在八面体顶点数V 、面数F 、棱数E 中，V+F -E=( )A.16B.6C.4D.2 7．如图，直线AB 、CD 相交于点O ，在这两条直线上，与点O 的距离为3cm 的点有（ ）A. 2个B.3个C.4个D.5个B A D CA B C DD B A8．如图所示，图中共有几条线段（ ）A. 4B. 5C. 10D.159.已知AB=21cm ，BC=9cm ，A 、B 、C 三点在同一条直线上，那么AC 等于（ ）A.30cmB. 15cmC. 30cm 或15cmD. 30cm 或12cm10.一个画家有14个边长为1cm 的正方体，他在地面上把它们摆成如图所示的形状，然后他们把露出的表面都涂上颜色，那么被涂上颜色的总面积是（ ）A.19cm 2B.21cm 2C.33cm 2D.34cm 2二、细心填一填（每小题3分，共30分）11.填名称：如图，图（1）是 ，图（2） ，图（3） 。
12.图甲能围成 ；图乙能围成 ；图丙能围成 。
13．写出你所熟悉的、由三个面围成的几何体的名称是14.直角三角形绕一条直角边旋转一周得到的几何体是15.如图，在正方形ABCD 中，点P 在对角线BD 上运动，当点P 运动到何处时，PA+PC 最小，在图中画出此时点P 的位置。
人教版数学七年级上册第4章《几何图形初步》单元同步检测试题(含答案)
第4章【几何图形初步】单元检测题题号一二三总分16 17 18 19 20分数一．选择题1．圣诞帽类似于几何体（）A．圆锥B．圆柱C．球D．棱柱2．如图，∠AOC＝90°，OC平分∠DOB，且∠DOC＝22°36′，∠BOA度数是（）A．67°64′B．57°64′C．67°24′D．68°24′3．如果一个正方体棱长扩大到原来的2倍，则表面积扩大到原来的（）A．2倍B．4倍C．8倍D．16倍4．如图是一个正方体的表面展开图，则这个正方体是（）A．B．C．D．5．如图，射线OA表示的方向是（）A．北偏东65°B．北偏西35°C．南偏东65°D．南偏西35°6．下列4个生产、生活现象中，可用“两点之间线段最短”来解释的是（）A．用两根钉子就可以把木条固定在墙上B．植树时，只要选出两棵树的位置，就能确定同一行树所在的直线C．把弯曲的公路改直，就能缩短路程D．砌墙时，经常在两个墙角的位置分别插一根木桩拉一条直的参照线7．在以下三个图形中，根据尺规作图的痕迹，不能判断射线AD平分∠BAC的是（）A．图2B．图1与图2C．图1与图3D．图2与图38．已知矩形两边长为2cm与3cm，绕长边旋转一周所得几何体的体积为（）A．3πcm3B．4πcm3C．12πcm3D．18πcm39．已知三条不同的射线OA、OB、OC，有下列条件，其中能确定OC平分∠AOB的有（）①∠AOC＝∠BOC②∠AOB＝2∠AOC③∠AOC+∠COB＝∠AOB④∠BOC＝∠AOBA．1个B．2个C．3个D．4个10．如图所示，在Rt△ABC中，∠C＝90°，按以下步骤作图：①以点A为圆心，以小于AC的长为半径作弧，分别交AC、AB于点M，N；②分别以点M，N为圆心，以大于MN的长为半径作弧，两弧相交于点O；③作射线OA，交BC于点E，若CE＝6，BE＝10．则AB的长为（）A．11B．12C．18D．20二．填空题11．若∠A＝25°，则它的补角是°．12．张雷同学从A地出发沿北偏东60°的方向行驶到B地，再由B地沿南偏西35°的方向行驶到C 地，则∠ABC＝度．13．一个直角三角形的两条直角边的长分别为3厘米和4厘米，绕它的直角边所在的直线旋转所形成几何体的体积是立方厘米．（结果保留π）14．已知点A、B、C在同一直线上，若AB＝10cm，AC＝16cm，点M、N分别是线段AB、AC中点，则线段MN的长是．15．已知△ABC，按以下步骤作图：①分别以B，C为圆心，以大于BC的长为半径作弧，两弧相交于两点M，N；②作直线MN交直线AB于点D，连接CD．若∠ABC＝40°，∠ACD＝30°，则∠BAC的度数为．三．解答题16．计算：（1）131°28′﹣51°32′15″（2）58°38′27″+47°42′40″（3）34°25′×3+35°42′17．如图，点B，D都在线段AC上，AB＝12，点D是线段AB的中点，BD＝3BC，求AC的长．18．如图，已知∠AOB＝128°，OC平分∠AOB，请你在∠COB内部画射线OD，使∠COD和∠AOC 互余，并求∠COD的度数．19．如图，在△ABC中，D是AB边上的一点．请用尺规作图法，在△ABC内，作出∠ADE，使∠ADE＝∠B，DE交AC于点E．（保留作图痕迹不写作法）20．在一个圆柱形水桶里，垂直放入一段半径是3cm的圆柱形钢材．如果把钢材全部侵入水中，桶里的水面上升10cm；如果再把钢材垂直露出水面6cm，桶里的水面下降4cm．（π取3.14）（1）整段钢材的体积是多少？（2）若把整段钢材全部用来锻造底面直径为2cm，高为3cm的圆锥形零件，一共可以锻造多少个这样的圆锥形零件？（假定锻造过程中无任何损耗）参考答案一．选择题1．解：圣诞帽的形状上面尖尖的，下面是圆形的，类似于圆锥体，故选：A．2．解：∵OC平分∠DOB，∴∠DOC＝∠BOC＝22°36′．∵∠AOC＝∠AOB+∠BOC＝90°，∴∠AOB＝∠AOC﹣∠BOC＝90°﹣22°36′＝67°24′．故选：C．3．解：设原来的正方体的棱长为a，则变化后的正方体的棱长为2a，原来的表面积：a×a×6＝6a2，变化后的表面积：2a×2a×6＝24a2，而24a2÷6a2＝4，故选：B．4．解：“面A“的字母与上面的“横线”方向不对，因此选项A不符合题意；有三个“空白”的面，其中的两个“空白”的面是对面，因此选项D不符合题意，由“面A”的对面和邻面是标有“横线”的面，因此选项C不符合题意；故选：B．5．解：射线OA表示的方向是南偏东65°，故选：C．6．解：A、用两根钉子就可以把木条固定在墙上，利用的是两点确定一条直线，故此选项不合题意；B、植树时，只要选出两棵树的位置，就能确定同一行树所在的直线，利用的是两点确定一条直线，故此选项不合题意；C、把弯曲的公路改直，就能缩短路程，可用“两点之间线段最短”来解释，符合题意；D、砌墙时，经常在两个墙角的位置分别插一根木桩拉一条直的参照线，利用的是两点确定一条直线，故此选项不合题意；故选：C．7．解：在图1中，利用基本作图可判断AD平分∠BAC；在图2中，利用基本作图得到D点为BC的中点，则AD为BC边上的中线；在图3中，利用作法得AE＝AF，AM＝AN，则可判断△ADM≌△ADN，所以∠AMD＝∠AND，则可判断△MDE≌△NDF，所以D点到AM和AN的距离相等，则可判断AD平分∠BAC．故选：A．8．解：将长方形纸片绕长边所在直线旋转一周，得到的几何体是底面半径为2cm，高为3cm的圆柱体，所以：体积为：π×22×3＝12π（cm3），故选：C．9．解：①由∠AOC＝∠BOC能确定OC平分∠AOB；②如图1，∠AOB＝2∠AOC所以不能确定OC平分∠AOB；③∠AOC+∠COB＝∠AOB不能确定OC平分∠AOB；④如图2，∠BOC＝∠AOB，不能确定OC平分∠AOB；所以只有①能确定OC平分∠AOB；故选：A．10．解：过点E作DE⊥AB于点D，由作图知AO平分∠BAC，∵∠C＝∠ADE＝90°，∴CE＝DE＝6，∵BE＝10，∴BD＝8，∵AD＝AC，CE＝DE，∴Rt△ACE≌Rt△ADE（HL），∴AC＝AD，设AC＝AD＝x，由AC2+BC2＝AB2得x2+162＝（x+8）2，解得：x＝12，即AC＝12，∴AB＝20，故选：D．二．填空题11．解：∵∠A＝25°，∴∠A的补角是180°﹣∠A＝180°﹣25°＝155°．故答案为：155．12．解：如图所示，∵AD∥BE，∠1＝60°，∴∠ABE＝∠DAB＝60°，又∵∠CBE＝35°，∴∠ABC＝60°﹣35°＝25°．故答案为：25．13．解：绕它的直角边所在的直线旋转所形成几何体是圆锥，①当绕它的直角边为3cm所在的直线旋转所形成几何体的的体积是：π×32×4＝12π，②当绕它的直角边为4cm所在的直线旋转所形成几何体的的体积是：π×42×3＝16π，故答案为：12π或16π．14．解：（1）如图1，，∵AB＝10cm，点M是线段AB的中点，∴AM＝10÷2＝5（cm）；∵AC＝16cm，点N是线段AC的中点，∴AN＝16÷2＝8（cm），∴MN＝AM+AN＝5+8＝13（cm）（2）如图2，，∵AB＝10cm，点M是线段AB的中点，∴AM＝10÷2＝5（cm）；∵AC＝16cm，点N是线段AC的中点，∴AN＝16÷2＝8（cm），∴MN＝AN﹣AM＝8﹣5＝3（cm），综上，线段MN的长是13cm或3cm．故答案为：13cm或3cm．15．解：由题意得，直线MN是线段BC的垂直平分线，∴BD＝CD，∴∠BCD＝∠B＝40°，∵∠ACD＝30°，如图1，∴∠ACB＝40°+30°＝70°，∴∠BAC＝180°﹣70°﹣40°＝70°；如图2，∴∠ACB＝40°﹣30°＝10°，∴∠BAC＝180°﹣10°﹣40°＝130°，综上所述，∠BAC的度数为70°或130°，故答案为：70°或130°．三．解答题16．解：（1）131°28′﹣51°32′15″＝79°55′45″；（2）58°38′27″+47°42′40″＝106°21′7″；（3）34°25′×3+35°42′＝103°15′+35°42′＝138°57′．17．解：∵AB＝12，点D是线段AB的中点，∴BD＝12÷2＝6；∵BD＝3BC，∴BC＝6÷3＝2，∴AC＝AB+BC＝12+2＝14．18．解：作OD⊥OA，则∠COD和∠AOC互余，如图所示．∵∠AOB＝128°，OC平分∠AOB，∴∠AOC＝∠AOB＝64°，∵∠COD和∠AOC互余，∴∠COD＝90°﹣∠AOC＝26°．19．解：如图，∠ADE即为所求．20．解：（1）整段钢材的高为：10×（6÷4）＝15（cm），整段钢材的体积为：3.14×32×15＝423.9（cm3），答：整段钢材的体积是423.9立方厘米；（2）每个圆锥形零件的体积为，锻造锥形零件的个数为：423.9÷3.14＝135（个）．答：一共可以锻造135个这样的圆锥形零件．。
人教版数学七年级上册 第4章几何图形初步单元测试题(一)
几何图形初步单元测试题（一）一．选择题1．下列说法正确的是（）A．射线比直线短B．从同一点引出的两条射线所组成的图形叫做角C．若AP＝BP，则P是线段AB的中点D．两点之间的线段叫做这两点之间的距离2．已知∠1和∠2互为余角，且∠2与∠3互补，∠1＝60°，则∠3为（）A．120°B．60°C．30°D．150°3．如图所示，截面的形状是（）A．长方形B．平行四边形C．梯形D．五边形4．如图，是一个正方体的一种平面展开图，正方体的每个面上都有一个汉字，那么在原正方体中和“培”字相对面的汉字是（）A．我B．爱C．北D．大5．若∠A＝38°15′，∠B＝38.15°，则（）A．∠A＞∠B B．∠A＜∠B C．∠A＝∠B D．无法确定6．下列图形能折叠成正方体的是（）A．B．C．D．7．如图所示的是正方形网格，则∠AOB___∠COD（）A．＞B．＜C．＝D．≥8．某镇初级中学在镇政府的南偏西60°方向上，且距离镇政府1500m，则如图所示的表示法正确的是（）A．B．C．D．9．下面各图是圆柱的展开图的是（）A．B．C．D．10．如图是株洲市的行政区域平面地图，下列说法明显错误的是（）A．炎陵位于株洲市区南偏东约35°的方向上B．醴陵位于攸县的北偏东约17°的方向上C．株洲县位于茶陵的南偏东约30°的方向上D．株洲市区位于攸县的北偏西约21°的方向上二．填空题11．钟表上的时间是3时20分，则此时时针与分针所成的夹角是度．12．一个直棱柱有八个面，所有侧棱长的和为36cm，则每条侧棱的长是cm．13．如图，是一个正方体的表面展开图，则原正方体中“人”字所在的面相对的面上标的字是．14．观察如图所示的长方体，用符号（“∥”或“⊥”）表示下列两棱的位置关系：AD BC，AB AA1，AB C1D1．15．如图，点A在点O的北偏西60°的方向上，点B在点O的南偏东20°的方向上，那么∠AOB的大小为°．三．解答题16．如图，点B，D都在线段AC上，AB＝12，点D是线段AB的中点，BD＝3BC，求AC 的长．17．如图，是一个正方体的六个面的展开图形（汉字和数字在正方体外部），回答下列问题：（1）“0”所对的面是．（2）若将其折叠成正方体，如果“7”所在的面在底面，“国”所在的面在后面，则上面是；前面是；右面是．（3）若将其折叠成正方体，“周”所在的面在前面，则上面不可能是．18．如图，在6×6的网格中，每个小正方形的边长为1，点A在格点（小正方形的顶点）上，试在各网格中画出顶点在格点上，面积为6，且符合相应条件的图形．19．将一副三角板中的含有60°角的三角板的顶点和另一块的45°角的顶点重合于一点O，绕着点O旋转60°的三角板，拼成如图的情况（OB在∠COD内部），请回答问题：（1）如图1放置，将含有60°角的一边与45°角的一边重合，求出此时∠AOD的度数．（2）绕着点O，转动三角板AOB，恰好是OB平分∠COD，此时∠AOD的度数应该是多少？（3）是否存在这种情况，∠AOC的度数恰好等于∠BOD度数的3倍．如果存在，请求出∠AOD的度数，如果不存在请说明理由．参考答案与试题解析一．选择题（共10小题）1．【解答】解：A．射线和直线不可以比较长短，原说法错误，故本选项不符合题意；B．从同一点引出的两条射线所组成的图形叫做角，原说法正确，故本选项符合题意；C．若点P在线段AB上，AP＝BP，则P是线段AB的中点，原说法错误，故本选项不符合题意；D．两点之间的线段的长度叫做这两点之间的距离，原说法错误，故本选项不符合题意；故选：B．2．【解答】解：∵∠1和∠2互为余角，∠1＝60°，∴∠2＝90°﹣∠1＝90°﹣60°＝30°，∵∠2与∠3互补，∴∠3＝180°﹣∠2＝180°﹣30°＝150°．故选：D．3．【解答】解；由于面与面相交成线，前后平行，上下面平行，可得截面的对边是平行的，因此是平行四边形，故选：B．4．【解答】解：这是一个正方体的平面展开图，共有六个面，其中面“培”与面“爱”相对．故选：B．5．【解答】解：∵∠A＝38°15′，∠B＝38.15°＝38°9′，∴∠A＞∠B．故选：A．6．【解答】解：A、能折叠成正方体，故此选项符合题意；B、出现了“凹”字格，不能折叠成正方体，故此选项不符合题意；C、折叠后有两个面重合，不能折叠成正方体，故此选项不符合题意；D、出现了“田”字格，不能折成正方体，故此选项不符合题意．故选：A．7．【解答】解：∵∠AOC＝∠BOD＝90°，∴∠AOB+∠BOC＝90°，∠COD+∠BOC＝90°，∴∠AOB＝∠COD．故选：C．8．【解答】解：A、镇初级中学在镇政府的南偏西60°方向上，且距离镇政府1500m，故本选项符合题意；B、镇初级中学在镇政府的南偏西30°方向上，且距离镇政府1500m，故本选项不符合题意；C、镇政府在镇初级中学的南偏西60°方向上，且距离镇政府1500m，故本选项不符合题意；D、镇政府在镇初级中学的南偏西30°方向上，且距离镇政府1500m，故本选项不符合题意．故选：A．9．【解答】解：由图可知，该圆柱底面直径为6，高为4，所以该圆柱的底面周长（圆柱侧面展开得到的长方形的长）为：6×3.14＝18.84，故选：C．10．【解答】解：A、炎陵位于株洲市区南偏东约35°的方向上，原说法正确，故本选项不符合题意；B、醴陵位于攸县的北偏东约17°的方向上，原说法正确，故本选项不符合题意；C、株洲县位于茶陵的北偏西约30°的方向上，原说法错误，故本选项符合题意；D、株洲市区位于攸县的北偏西约21°的方向上，原说法正确，故本选项不符合题意．故选：C．二．填空题（共5小题）11．【解答】解：∵钟表上的时间指示为3点20分，∴时针与分针所成的角是：30°×＝10°故答案是：10．12．【解答】解：∵一个直棱柱有八个面，∴这个直棱柱是六棱柱，因此每条侧棱的长为36÷6＝6（cm），故答案为：6．13．【解答】解：这是一个正方体的平面展开图，共有六个面，其中面“国”与面“伟”相对，面“梦”与面“的”相对，“人”与面“中”相对．故答案为：中．14．【解答】解：在平面A﹣B﹣C﹣D中，直线AD、BC无公共点，因此AD∥BC，在平面A﹣B﹣A1﹣B1中，直线AB、AA⊥相交成直角，因此AB⊥AA1，AB和C1D1是异面直线，根据异面直线的位置关系可得AB∥C1D1，故答案为：∥，⊥，∥．15．【解答】解：如图，∵点A在点O北偏西60°的方向上，∴OA与西方的夹角为90°﹣60°＝30°，又∵点B在点O的南偏东20°的方向上，∴∠AOB＝30°+90°+20°＝140°．故答案为：140．三．解答题（共4小题）16．【解答】解：∵AB＝12，点D是线段AB的中点，∴BD＝12÷2＝6；∵BD＝3BC，∴BC＝6÷3＝2，∴AC＝AB+BC＝12+2＝14．17．【解答】解：（1）“0”所对的面是建；故答案为：建；（2）如果“7”所在的面在底面，“国”所在的面在后面，则上面是周；前面是年；右面是建；故答案为：周，年，建；（3）将其折叠成正方体，“周”所在的面在前面，则上面不可能是7；故答案为：7。
第1章 基本的几何图形数学七年级上册-单元测试卷-青岛版(含答案)
第1章基本的几何图形数学七年级上册-单元测试卷-青岛版(含答案)一、单选题(共15题，共计45分)1、如图是正方体的表面展开图，则与“前”字相对的字是（）A.认B.真C.复D.习2、已知点A（-3，2），B（3，2），则A，B两点相距（）A.3个单位长度B.4个单位长度C.5个单位长度D.6个单位长度3、如果一个多面体的一个面是多边形，其余各面是有一个公共顶点的三角形，那么这个多面体叫做棱锥．如图是一个四棱柱和一个六棱锥，它们各有12条棱．下列棱柱中和九棱锥的棱数相等的是（）A.五棱柱B.六棱柱C.七棱柱D.八棱柱4、在数轴上有两个点A、B，点A表示-3，点B与点A相距5个单位长度，则点B表示的数为（）.A.-2或8B.2或-8C.-2D.-85、如图，从A到B有三条路径，最短的路径是②，理由是（）A.两点确定一条直线B.两点之间线段最短C.过一点有无数条直线 D.直线比曲线和折线短6、如图是一个正方体的表面展开图，若折叠成正方体后相对面上的两个数互为相反数，则的值分别为（）A. B. C. D.7、下列图形中，能通过折叠围成一个三棱柱的是（）A. B. C. D.8、直线a上有四个不同的点依次为A、B、C、D．那么到A、B、C、D的距离之和最小的点（）A.可以是直线AD外的某一点B.只是B点和C点C.只是线段AD的中点 D.有无数多个点9、两条相交直线与另一条直线在同一平面，它们的交点个数是（）A.1B.2C.3或2D.1或2或310、下列语句中表述正确的是（）A.延长直线ABB.延长线段ABC.作直线AB=BCD.延长射线OC11、下面的几何体，是由A、B、C、D中的哪个图旋转一周形成的( )A. B. C. D.12、下面是小明按照语句画出的四个图形：（1）直线EF经过点C；（2）点A在直线l外；（3）经过点O的三条线段a、b、c；（4）线段AB、CD相交于点B．他所画图形中，正确的个数是（）A.1B.2C.3D.413、数轴是一条( )A.射线B.直线C.线段D.以上都是14、如图，将正方体相邻的两个面上分别画出3×3的正方形网格，并分别用图形“”和“○”在网格内的交点处做上标记，则该正方体的表面展开图是（）A. B. C. D.15、如图，长方体的长为15，宽为10，高为20，点B离点C的距离为5，一只蚂蚁如果要沿着长方体的表面从点A爬到点B，需要爬行的最短距离是（）A.5B.25C.10 +5D.35二、填空题(共10题，共计30分)16、一块方形蛋糕，一刀切成相等的两块，两刀最多切成4块，试问：五刀最多可切成________块相等体积的蛋糕，十刀最多可切成________块（要求：竖切，不移动蛋糕）．17、从运动的观点看，点动成________，线动成________，面动成________．18、如图，一束光线从y轴上点A（0，1）发出，经过x轴上点C反射后，经过点B（6，2），则光线从A点到B点经过的路线的长度为________．19、修高速公路时，为减小成本尽可能要将弯曲的公路改直，数学依据是________.20、直线AB外有C、D两个点，由点A、B、C、D可确定的直线条数是________21、如图是正方体的展开图，则原正方体相对两个面上的数字和的最大值是________ ．22、如图，已知点在线段上，点、分别是线段、的中点，且，则图中共有________条线段，线段的长度＝________ ．23、我们知道平面内到两个定点距离之比为常数（常数大于零且不为1）的点轨迹是一个圆，那么在平面直角坐标系内到原点（0，0）和点（3，0）距离之比为2的圆的圆心坐标是________.24、如图，阴影部分扇形的面积占整个面积的15%，则此扇形的圆心角的度数是________．25、已知线段AB=8cm，在直线AB上有一点C，且BC=4cm，点M是线段AC的中点，线段AM 的长是________．三、解答题(共5题，共计25分)26、有一个长方形绕它的一边所在的直线旋转一周，得到的几何体是圆柱．现在有一个长为6cm，宽为5cm的长方形，分别绕它的长、宽所在直线旋转一周，得到不同的圆柱，它们的体积分别是多大？27、探究：有一弦长6cm，宽4cm的矩形纸板，现要求以其一组对边中点所在直线为轴，旋转180°，得到一个圆柱，现可按照两种方案进行操作：方案一：以较长的一组对边中点所在直线为轴旋转，如图①；方案二：以较短的一组对边中点所在直线为轴旋转，如图②．（1）请通过计算说明哪种方法构造的圆柱体积大；（2）如果该矩形的长宽分别是5cm和3cm呢？请通过计算说明哪种方法构造的圆柱体积大；（3）通过以上探究，你发现对于同一个矩形（不包括正方形），以其一组对边中点所在直线为轴旋转得到一个圆柱，怎样操作所得到的圆柱体积大（不必说明原因）？28、如图，把一个木制正方体的表面涂上颜色，然后将正方体的棱分成相等的四份，并做上标记，得到许多小正方体．问（1）有个小正方体；（2）有个小正方体只有两面涂有颜色（3）有个小正方体只有3面都涂了颜色．（4）有个小正方体6面都未涂色．29、如图是一个正方体的展开图，标注了字母A的面是正方体的正面，如果正方体的左面与右面所标注式子的值相等，求x的值．30、将一个圆分割成三个扇形，它们的圆心角的度数之比为2：3：4，求这三个扇形圆心角的度数．参考答案一、单选题(共15题，共计45分)1、B2、D3、B4、B5、B6、B7、C8、D9、D10、B11、A12、C13、B14、C二、填空题(共10题，共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题，共计25分)27、28、30、。
初一数学第一章基本的几何图形单元测试题
初一数学第一章基本的几何图形单元测试题一、选择题（每题3分，共45分）1、下列几何体属于柱体的个数是（）A. 3 B . 4 C . 5 D . 62、下列说法错误的是（）A、流星落下时在天空留下充满幻想的线条，说明点动成线；B汽车在雨中行驶，雨刷器来回摆动说明线动成面；C、旋转门旋转一周成为一个圆柱，说明面动成体；D面与面相交的地方是线，线有粗细之分4、如图是每个面上都有一个汉字的正方体的一种平面展开图，那么在原正方体中和“国” 字相对的面是（）A.中B .钓C .鱼D .岛5、如图，经过刨平的木板上的两个点，能弹出一条笔直的墨线，而且只能弹出一条墨线，能解释这一实际应用的数学知识是（）A.两点确定一条直线B .两点之间线段最短C.垂线段最短D .在同一平面内，过一点有且只有一条直线与已知直线垂直6、如图，在直线上依次有五个点A、B C、D E,则图中线段和射线条数依次分别为（）A. 4，2 B . 10，10 C . 10，20 D . 10，57、2015年8月12日济青高铁开工建设，建设中的济青高铁从济南出发，途径邹平-淄博- 潍坊-高密-胶州，最后到达青岛，若火车车票的价格由路程决定，则沿途总共有不同的票价（）种.A. 14 B . 15 C . 42 D . 21&下列语句正确的是（）A.画直线AB=10厘米B .若PA=PB则P是线段AB的中点；C•射线是直线的一半 D .延长线段AB到点C,使得BC=AB9、下列说法正确的是（）A、连接两点的线段叫两点间的距离；B延长射线MN到C; C、三条直线两两相交，有3个交点；D不在同一直线上的三点确定一个平面3、如图中是正方体的展开图的有（个A 2个B、3个C、4个D、5个中国的钓鱼岛（1）⑵⑶⑷⑸⑹（T）⑻/ 从lEffi看A.1、 共15分）且所有侧棱的和为40cn ,则每条侧棱长为2、 、填空题（每题3分， 一个棱柱有10个面，如图，为抄近路践踏草坪是一种不文明的现象，请你用数学知识解释出这一现象的原 cm.10、下列事实可以用“两点确定一条直线”来解释的有（ ）个①墙上钉木条至少要两颗钉子才能牢固；②农民拉绳播秧；③解放军叔叔打靶瞄准；④从 A 地到B 地架设电线，总是 尽可能沿着线段AB 架设.A. 1 B . 2 C . 3 D . 411、、将一个直角三角形绕它的最长边（斜边）旋转一周得到的几何体为（12、 已知AB=8cm BC=3cm 且A ，B ，C 三点在同一条直线上，则 AC=（ A. 11cm B . 5cm C . 8cm 或 3cm13、 观察图形，下列说法正确的个数是（（2）射线AC 和射线AD 是同一条射线 定有三个交点.A. 1个B . 2个C14、 点C 是线段AB 上一点，点D 是BC 的中点，若AD=5cm 则AC+A 等于（）A B 10cm C 、12cm D 、不确定15、 如图，一个几何体是由两个小正方体和一个圆锥构成，其主视图是（D . 5cm 或 11cm）（1）直线BA 和直线AB 是同一条直线（3） AB+B 8AD （4）三条直线两两相交时,.3个 D . 4个// :\、8cmA.C .D.因3、如图所示，以0为端点画六条射线OA OB OC OD OE OF,再从射线0A上某点开始按逆时针方向依次在射线上描点并连线，若将各条射线所描的点依次记为1，2，3，4，5，6, 7 , 8…后，那么所描的第2013个点在射线 __________ 上.4、从棱长为2的正方体毛坯的一角，挖去一个棱长为1的小正方体，得到一个如图所示的零件，则这个零件的表面积为_________________5、点与直线的位置关系是 __________ 和 _____________ ，平面内两条直线的位置关系是_________ 和_____________三、解答题（每题12分，共60分）1、如图，已知线段a,b,c,用圆规和直尺画线段，使它等于a+2b-c3、先阅读下面材料，然后解答问题：材料一：如图（1）,直线L上有A、A两个点，若在直线L上要确定一点P,且使点P到点A、A的距离之和最小，很明显点P的位置可取在A i和A之间的任何地方，此时距离之和为A到A的距离.如图（2）,直线L上依次有A、A A三个点，若在直线L上要确定一点P,且使点P到点A、A A的距离之和最小，不难判断，点P的位置应取在点A处，此时距离之和为A到A 的距离.（想一想，这是为什么）不难知道，如果直线L上依次有A、A、A、A四个点，同样要确定一点P,使它到各点的距离之和最小，则点P应取在点A和A之间的任何地方；如果直线L上依次有A、A A A A五个点，则相应点P的位置应取在点A的位置.---- * ---------A图⑴囹⑵问题一：若已知直线L上依次有点A、A A、…、人5共25个点，要确定一点P,使它到已知各点的距离之和最小，则点P的位置应取在_________________________ ;若已知直线L上依次有点A、A、A、…、A共50个点，要确定一点P,使它到已知各点的距离之和最小，则点P的位置应取在____________________ .4、十八世纪瑞士数学家欧拉证明了简单多面体中顶点数（V）、面数（F）、棱数（E）之间存在的一个有趣的关系式，被称为欧拉公式。
数学七年级上学期《几何图形初步》单元测试带答案
[解析]
试题分析：根据两点之间线段最短解答．
解：道理 ：两点之间线段最短．
故答案为两点之间线段最短．
考点：线段的性质：两点之间线段最短．
14.如图,B处在A处的南偏西45°方向,C处在A处的南偏东15°方向,C处在B处的北偏东85°方向,则∠A C B的度数为．
[答案]80°．
16如图所示,已知OA⊥OB,OC⊥OD,∠AOC︰∠BOD＝1︰2,则∠BOD＝________．
17.如图,M是线段A B的中点,N是线段B C的中点,A B=8Cm,B C=6Cm,则线段MN=______Cm．
18.上午10点30分,钟表上时针与分针所成的角是___________度.
三、计算题:
[解析]
试题分析：如图：
B处在A处的南偏西45°方向,C处在A处的南偏东15°方向,C处在B处的北偏东85°方向,
∴∠1=45°∠2=85°,∠3=15°,
由平行线的性质得∠5=∠1=45°．
由角 和差得
∠6=∠2-∠5=85°-45°=40°,
∠4=∠1+∠3=45°+15°=60°,
由三角形的内角和定理得∠A C B=180°-∠6-∠4=180°-40°-60°=80°,
(1)若∠AOD＝75°,求∠AOE的度数．
(2)若∠DOE＝54°,求∠EOC的度数．
27.已知∠AOB=100°,∠COD=40°,OE平分∠AOC,OF平分∠BOD.(本题中的角均为大于0°且小于等于180°的角).
(1)如图1,当OB、OC重合时,求∠EOF的度数；
(2)当∠COD从图1所示位置绕点O顺时针旋转n°(0＜n＜90)时,∠AOE﹣∠BOF的值是否为定值？若是定值,求出∠AOE﹣∠BOF的值；若不是,请说明理由.
七年级数学上册《几何图形初步》单元测试卷(含答案解析)
七年级数学上册《几何图形初步》单元测试卷（含答案解析）一、单选题（本大题共15小题，共45分）1.如图，将正方体的平面展开图重新折成正方体后，“奋”字对面的字是()A. 者B. 乐C. 的D. 园2.一枚六个面分别标有1−6个点的骰子，将它抛掷三次得到不同的结果，看到的情形如图所示，则图中写有“？”一面上的点数是()A. 6B. 2C. 3D. 13.已知图1的小正方形和图2中所有的小正方形都全等，将图1的小正方形安放在图2中的①、②、③、④的其中某一个位置，放置后所组成的图形是不能围成一个正方体的．那么安放的位置是()A. ①B. ②C. ③D. ④4.观察下图，把左边的图形绕着给定直线旋转一周后可能形成的几何体是()A. B.C. D.5.将一个直角三角形绕它的最长边(斜边)旋转一周得到的几何体为()A. B. C. D.6.已知A，B，C三点在同一条直线上，M，N分别为线段AB，BC的中点，且AB=80，BC=60，则MN的长为()A. 10B. 70C. 10或70D. 30或707.已知线段AB=8，延长线段AB至C，使得BC=12AB，延长线段BA至D，使得AD=14AB，则下列判断正确的是()A. BC=12AD B. BD=3BC C. BD=4AD D. AC=6AD8.下列作图语句中，正确的是()A. 画直线AB=6cmB. 延长线段AB到CC. 延长射线OA到BD. 作直线使之经过A，B，C三点9.如图给出的分别有射线，直线，线段，其中不能相交的图形是()A. B.C. D.10.如图，现实生活中有部分行人选择横穿马路而不走天桥或斑马线，用数学知识解释这一现象的原因，可以为()A. 过一点有无数条直线B. 两点之间线段的长度，叫做这两点之间的距离C. 两点确定一条直线D. 两点之间，线段最短11.若∠α=5.12°，则∠α用度、分、秒表示为()A. 5°12′B. 5°7′12′′C. 5°7′2′′D. 5°10′2′′12.下列图形中，能用∠α，∠O，∠AOB三种方式正确表示同一个角的图形是()A. B. C. D.13.按图1～图4的步骤作图，下列结论错误的是()∠AOB=∠AOP B. ∠AOP=∠BOPA. 12C. 2∠BOP=∠AOBD. ∠BOP=2∠AOP14.如图，OC是∠AOB的平分线，OD平分∠AOC，且∠COD=20°，则∠AOB=()A. 40°B. 50°C. 90°D. 80°15.如图，准确表示小岛A相对于灯塔O的位置是()A. 北偏东60°B. 距灯塔2km处C. 北偏东30°且距灯塔2km处D. 北偏东60°且距灯塔2km处二、填空题（本大题共5小题，共15分）16.如图，一个正方块的六个面分别标有A、B、C、D、E、F，从三个不同方向看到的情况如图所示，则A的对面应该是 ______.17.如图，已知点A、B、C、D、在同一条直线上，AB=5，AC=2，点D是线段BC的中点，则BD=______.18.时钟指示2点25分，它的时针与分针所成的锐角是 ______°.19.如图，点O在直线AE上，OC平分∠AOE，∠DOB是直角，若∠1=25°，那么∠AOB的度数是 ______°.20.在一次夏令营活动中，小明同学从营地A点出发，要到C地去，先沿北偏东70°方向走了500m到达B地，然后再沿北偏西20°方向走了500m到达目的地C，此时小明在营地A的______方向．三、解答题（本大题共5小题，共40分）21.如图所示的是一个长方体的表面展开图，每个面上都标注了字母(字母朝外)，回答下列问题：(1)如果面A在长方体的底部放置，那么哪一个面会在它的上面？(2)如果面F在前面，从左面看是面B，那么哪一个面会在上面？(3)从右面看是面C，面E在左面，那么哪一个面会在上面？22.如图，已知线段AB=14，AP=8，P是OB的中点，求AO的长．AC，D，E分别为AC，AB的中点，求线段DE的23.如图，点C是线段AB上一点，AC=12，CB=23长．24.如图∠AOC为直角，OC是∠BOD的平分线，且∠AOB=28°，求∠BOD的度数．25.如图，点A、O、B在同一条直线上，∠AOD=∠EOC=90°，∠BOC：∠AOE=4：1，求∠COD的度数．参考答案和解析1.【答案】B;【解析】解：由题意，将正方体的平面展开图重新折成正方体后，“斗”字对面的是“的”字，“奋”字对面的字是“乐”字，“者”字对面的是“园”字，故选：B.正方体的表面展开图，相对的面之间一定相隔一个正方形，根据这一特点作答．此题主要考查了正方体相对两个面上的文字，注意正方体的空间图形，从相对面入手，分析及解答问题．2.【答案】A;【解析】解：根据图形可知，与点数1相邻的面的点数有2、3、4、5，∴点数1与6是相对面，对比第一个和第三个图，可知写有“？”的面与点数1是相对面，故写有“？”一面上的点数是6.故选：A.根据与1个点数相邻的面的点数有2、3、4、5可知1个点数的对面是6个点数，再根据1与2、3相邻，从而得解．此题主要考查了正方体相对两个面上的文字，注意正方体的空间图形，从相邻的面上找出一个与另外4个相邻的数是解答该题的关键．3.【答案】A;【解析】解：将图1的正方形放在图2中的①的位置出现重叠的面，所以不能围成正方体．故选：A.由平面图形的折叠及正方体的表面展开图的特点解题．此题主要考查了展开图折叠成几何体，解题时勿忘记四棱柱的特征及正方体展开图的各种情形．注意：只要有“田”字格的展开图都不是正方体的表面展开图．4.【答案】D;【解析】根据面动成体的原理以及空间想象力即可解．考查学生立体图形的空间想象能力及分析问题，解决问题的能力．解：由图形可以看出，左边的长方形的竖直的两个边与已知的直线平行，因而这两条边旋转形成两个柱形表面，因而旋转一周后可能形成的立体图形是一个管状的物体．故选D．5.【答案】D;【解析】该题考查的是点线面的认识有关知识，根据面动成体的原理：一个直角三角形绕它的最长边旋转一周，得到的是两个同底且相连的圆锥．解：A.圆柱是由一长方形绕其一边长旋转而成的；B.圆锥是由一直角三角形绕其直角边旋转而成的；C.该几何体是由直角梯形绕其下底旋转而成的；D.该几何体是由直角三角形绕其斜边旋转而成的．故选D．6.【答案】C;【解析】解：(1)当C在线段AB延长线上时，如图1，∵M、N分别为AB、BC的中点，∴BM=12AB=40，BN=12BC=30；∴MN=BM+BN=40+30=70.(2)当C在AB上时，如图2，同理可知BM=40，BN=30，∴MN=BM−BN=40−30=10；所以MN=70或10，故选：C.根据题意画出图形，再根据图形求解即可．此题主要考查线段中点的定义，比较简单，注意有两种可能的情况；解答这类题目，应考虑周全，避免漏掉其中一种情况．【解析】解：如图所示：∵AB=8，BC=12AB，∴BC=4，∵AD=14AB，∴AD=2，∴AC=AB+BC=12，BD=AD+AB=10，∴BC=2AD，BD=2.5BC，BD=5AD，AC=6AD．故选：D．根据AB=8，由线段的倍分关系求出BC，AD的长，进一步得到AC，BD的长，依此即可求解．该题考查了两点之间的距离的应用，主要考查学生的理解能力和计算能力，解此题的关键是求出BC，AD，AC，BD的长．8.【答案】B;【解析】这道题主要考查的是直线、射线、线段的特点，掌握直线、射线、线段的特点是解答该题的关键．根据直线向两端无限延伸，两点确定一条直线，射线向一端无限延伸可判断A、C、D是否正确；根据线段的特点可判断B是否正确．解：A.直线向两端无限延伸，无限长，故A错误；B.正确；C. 因为射线无限长，故C错误；D.如果A、B、C三点不在同一直线上，不能作直线使之经过A，B，C三点，过D错误．故选B．9.【答案】B;【解析】解：A.由图中直线AB和射线CD的位置以及直线、射线的意义可得，直线AB与射线CD 能相交，因此A不符合题意；B. 由图中线段AB和线段CD的位置以及线段的意义可知，线段AB与线段CD不相交，故B符合题意；C. 由图中直线a和直线b的位置以及直线的意义可得，直线a与直线b能相交，因此C不符合题意；D. 由图中直线AB和直线CD的位置以及直线的意义可得，直线AB与直线CD能相交，因此D不符合题意；故选：B.根据直线、射线、线段的意义逐项进行判断即可．此题主要考查直线、射线、线段的意义，理解直线、射线、线段的意义是解决问题的关键．【解析】解：现实生活中有部分行人选择横穿马路而不走天桥或斑马线，用数学知识解释这一现象的原因，两点之间线段最短．故选：D.根据线段的性质，直线的性质，可得答案．此题主要考查了线段的性质，熟记性质并能灵活应用是解题关键．11.【答案】B;【解析】解：∠α=5.12°=5°+0.12×60′=5°+7′+0.2×60′′=5°7′12′′.故选：B.利用度分秒之间的换算关系进行计算即可求解．此题主要考查了度分秒的换算，关键是掌握1°=60′，1′=60′′.12.【答案】C;【解析】解：A、不能表示为∠O，故本选项错误；B、不能表示为∠O，故本选项错误；C、能用∠α，∠O，∠AOB三种方式表示，故本选项正确；D、不能表示为∠O，故本选项错误．故选：C.根据角的表示方法解答即可．此题主要考查了角的概念，主要考查了角的表示方法，同一个顶点处有不止一个角时，一定不能用一个大写字母表示角．13.【答案】D;【解析】解：∵OP是∠AOB的平分线，∴∠AOB=2∠AOP=2∠BOP，∠AOP=∠BOP=12∠AOB，∴选项A、B、C均正确，选项D错误．故选：D.根据角平分线的定义对各选项进行逐一分析即可．此题主要考查的是角平分线的定义．解答该题的关键是掌握角平分线的定义，即从一个角的顶点出发，把这个角分成相等的两个角的射线叫做这个角的平分线．14.【答案】D;【解析】解：∵OC是∠AOB的平分线，∴∠AOC=∠COB；∵OD是∠AOC的平分线，∴∠AOD=∠COD；∵∠COD=20°，∴∠AOC=40°，∴∠AOB=80°．故选D ．两次利用角平分线的性质计算．本题是角的平分线与对顶角的性质的考查，角平分线的性质是将两个角分成相等的两个角．15.【答案】D;【解析】解：由方向角的定义以及平面内位置的确定方法可知，小岛A 在灯塔O 的北偏东60°且距灯塔2km 处，故选：D.根据平面内，位置的表示方法以及方向角的定义可得答案．此题主要考查方向角，理解方向角的定义以及平面内位置的确定方法是解决问题的关键．16.【答案】C;【解析】解：由图可知，A 相邻的字母有D 、E 、B 、F ，所以A 对面的字母是C.故答案为：C.观察三个正方体，与A 相邻的字母有D 、E 、B 、F ，从而确定出A 对面的字母是C.此题主要考查了正方体相对两个面上的文字，仔细观察图形从相邻面考虑求解是解答该题的关键．17.【答案】32;【解析】解：∵AB =5，AC =2，∴BC =AB −AC =3，∵点D 是线段AC 的中点， ∴BD =12AC =32.故答案为：32. 先求出线段BC 的长，再由中点得出BD 的长．此题主要考查了两点间的距离，能计算出BC 的长是解答该题的关键．18.【答案】77.5;【解析】解：2时25分的时候，分针指向5，时针在2−3之间，周角为360°，平均分成12份，每格的度数为360°÷12=30°，时针1个小时走30°，每分钟走0.5°，25分钟走0.5°×25=12.5°，∴此时它的时针和分针所成的锐角为90°−12.5°=77.5°，故答案为：77.5.先计算出每个大格的度数是30°，再用90°减去时针走过的度数，即为时针和分针所成的锐角的度数．此题主要考查了钟面角，角度的计算，求出时针所走的度数是解答该题的关键．19.【答案】25;【解析】解：∵点O 在直线AE 上，∴∠AOE =180°.∵OC 平分∠AOE ，∴∠AOC=1∠AOE=90°.2∴∠AOB+∠BOC=90°.∵∠DOB是直角，∴∠DOB=∠BOC+∠COD=90°.∴∠AOB=∠1=25°.故答案为：25.∠AOE=90°.由∠DOB 由点O在直线AE上，得∠AOE=180°.由OC平分∠AOE，得∠AOC=12是直角，根据同角的余角相等得∠AOB=∠COD，从而解决此题．此题主要考查平角的定义、余角的性质以及角平分线的定义，熟练掌握平角的定义、余角的性质以及角平分线的定义是解决本题的关键．20.【答案】北偏东25°;【解析】解：∵小明A点沿北偏东70°的方向走到B，∴∠BAD=70°，∵B点沿北偏西20°的方向走到C，∴∠EBC=20°，又∵∠BAF=90°−∠DAB=90°−70°=20°，∴∠1=90°−20°=70°，∴∠ABC=180°−∠1−∠CBE=180°−70°−20°=90°.∴ΔABC是等腰直角三角形，∵AB=500m，BC=500m，∴∠CAB=45°，∴∠DAC=∠DAB−∠CAB=70°−45°=25°，∴小明在营地A的北偏东25°方向．故答案为：北偏东25°.先根据∠DAB=70°，∠CBE=20°判断出ΔABC的形状，求出∠DAC的度数即可．此题主要考查的是方向角的概念，解答此类题需要从运动的角度，再结合三角函数的知识求解．21.【答案】解：（1）根据“相间、Z端是对面”可知，“A”与“F”相对，“B”与“D”相对，“C”与“E“相对，所以面A在长方体的底部，那么F个面会在它的上面；（2）若面F在前面，左面是面B，则“A”在后面，“D”在右面，此时“C”在上面，“E”在下面，或“E”在上面，“C”在下面，答：如果面F在前面，从左面看是面B，那么“C”面或“E”面会在上面；（3）从右面看是面C，面E在左面，则“B”面或“D”面在上面．;【解析】根据长方体表面展开图的特征进行判断即可．此题主要考查长方体的展开与折叠，掌握长方体表面展开图的特征是解决问题的关键．22.【答案】解：因为AB=14，AP=8，所以BP=AB-AP=6．因为P是OB的中点，所以OP=BP=6，所以AO=AP-OP=8-6=2．;【解析】由线段的和差可求解BP的长，结合中点的定义可求OP的长，进而可求解．此题主要考查两点间的距离，求解OP的长是解答该题的关键．23.【答案】解：∵AC=12，CB=23AC，∴CB=AC+CB=20，∵D，E分别为AC，AB的中点，∴AD=12AC=6，AE=12AB=10，∴DE=AE-AD=10-6=4．;【解析】根据题意AC=12，CB=23AC，可得CB=AC+CB，由已知条件D，E分别为AC，AB的中点，AD=12AC，AE=12AB，即DE=AE−AD，代入计算即可得出答案．此题主要考查了两点间的距离，熟练应用两点间的距离计算方法进行求解是解决本题的关键．24.【答案】解：∵∠AOB=28°，∠AOC为直角，∴∠BOC=∠AOC-∠AOB=90°-28°=62°，∵OC是∠BOD的平分线，∴∠BOD=2∠BOC=124°．;【解析】首先由∠AOB=28°，∠AOC为直角，即可推出∠BOC=62°，然后根据角平分线的性质即可推出∠BOD=2∠BOC=124°．这道题主要考查角平分线的性质，角的计算，直角的定义，关键在于推出∠BOC的度数．25.【答案】解：设∠AOE=x，则∠BOC=4x．∵∠EOC=90°，∠EOC+∠AOE+∠BOC=180°，∴90°+x+4x=180°，∴x=18°．∴∠BOC=4x=72°．又∵∠AOD=90°，∴∠COD=180°-∠AOD-∠BOC=180°-90°-72°=18°．;【解析】根据补角的定义以及角的和差关系解决此题．此题主要考查补角的定义以及角的和差关系，熟练掌握补角的定义以及角的和差关系是解决本题额关键．。
人教版七年级上册数学第四章 几何图形初步单元测试卷附解析
人教版七年级上册数学第四章几何图形初步单元测试卷附解析一、单选题(共10题；共30分)1．（3分）下列图形沿着某一直线旋转180°后，一定能形成圆锥的是（）A．直角三角形B．等腰三角形C．矩形D．扇形2．（3分）以下哪个图形经过折叠可以得到正方体（）A．B．C．D．3．（3分）下列各图中直线的表示法正确的是（）.A．B．C．D．4．（3分）下列说法正确的是（）A．射线PA与射线AP是同一条射线B．射线OA的长度是12cmC．直线ab，cd相交于点MD．两点确定一条直线5．（3分）已知点A、B、C都是直线m上的点，且AB=5cm，BC=3cm，那么点A与点C之间的距离是（）A．8cm B．2cm或6cm C．8cm或2cm D．4cm6．（3分）下列角中，能用∠1，∠ACB，∠C三种方法表示同一个角的是（）A．B．C ．D ．7．（3分）下列图中的 ∠1 也可以用 ∠O 表示的是（ ）A ．B ．C ．D ．8．（3分）某测绘兴趣小组用测绘装置对一建筑的位置进行测量，测量前指针指向北偏东38°，测量后指针顺时针旋转了14周，则此时指针指向为（ ）A ．北偏西52°B ．南偏东52°C ．西偏南42°D ．东偏北42°9．（3分）已知∠1和∠2互为余角，且∠2与∠3互补，∠1＝60°，则∠3为（ ）A ．120°B ．60°C ．30°D ．150°10．（3分）如图，从点O 出发的5条射线，可以组成的锐角的个数是（ ）A ．8B ．9C ．10D ．11二、填空题(共5题；共15分)11．（3分）如图，D 是AC 的中点，CB ＝4cm ，DB ＝7cm ，则AB 的长为 cm ．12．（3分）已知线段AB=6cm ，点C 为直线AB 上一点，且BC=2cm ，则线段AC 的长是cm.13．（3分）将19.36°用度分秒表示为.14．（3分）钟表上显示8：30，时针与分针的夹角为。
七年级数学几何图形初步单元测试(二)(含答案)
几何图形初步单元测试（二）一、单选题(共12道，每道8分)1.下列说法中正确的是( )A.延长直线ABB.延长线段AB至点C，使AC=BCC.延长射线OAD.延长线段AB至点C，使BC=2AB答案：D解题思路：直线可向两个方向无限延伸，不可度量，所以不需延长，A选项错误；线段可以度量，可以延长，延长线段是有方向的，延长线段AB至点C，不论点C在什么位置，都有AC BC，如图，所以B选项错误；射线可向一个方向无限延伸，不可度量，可以反向延长，但不能延长，C选项错误；延长线段AB至点C，使BC=2AB，是可以做到的，D选项正确．故选D．试题难度：三颗星知识点：直线2.下列说法中错误的是( )A.角是由两条具有公共端点的射线组成的图形B.一条射线绕其端点旋转而成的图形叫做角C.大于直角的角不一定是钝角D.角的两边越长，表示的角就越大答案：D解题思路：角是由两条具有公共端点的射线组成的图形，两条射线的公共端点是这个角的顶点，角的两条边是两条射线，不可度量，与角的大小没有关系．角也可以看成是由一条射线绕着它的端点旋转而成的，因此选项A和选项B说法正确，选项D说法错误；根据角的分类，大于90°而小于180°的角是钝角，等于180°的角是平角，等于360°的角是周角，因此选项C说法正确．故选D．试题难度：三颗星知识点：角的分类3.下列现象中，能用“两点之间，线段最短”来解释的是( )A.墙上钉木条至少需要两颗钉子才能牢固B.把弯曲的公路改直，就能缩短路程C.植树时，只要定出两棵树的位置，就能确定同一行树所在的直线D.值日生摆课桌时，总是先把每一列最前和最后的课桌摆好，然后再依次摆中间的课桌，很快就能把课桌摆的整整齐齐答案：B解题思路：A选项是两点确定一条直线；B选项是两点之间，线段最短；C选项是两点确定一条直线；D选项是两点确定一条直线．故选B．试题难度：三颗星知识点：线段最短4.把用度分秒表示为( )A. B.C. D.答案：A解题思路：，故选A．试题难度：三颗星知识点：度分秒的换算5.下列各图经过折叠后能围成正方体的是( )A. B.C. D.答案：C解题思路：正方体有11种表面展开图，（1，4，1）型有6种，（2，3，1）型有3种，（2，2，2）型有1种，（3，3）型有1种．C选项中的是（2，3，1）型，因此经过折叠后能围成正方体．故选C．试题难度：三颗星知识点：正方体展开图6.有一正方体，六个面上分别写有数字1，2，3，4，5，6，有三个人从不同的角度观察的结果如图．如果记6的对面的数字为a，2的对面的数字为b，那么a+b的值为( )A.3B.7C.8D.11答案：B解题思路：本题通过相邻面确定相对面，正方体的每一个面与4个面相邻，1个面相对．比如本题，先找出现次数较多的，不妨先从数字1开始：从第一个图看出1与4，6相邻，从第二个图看出1与2，3相邻，所以1与2，3，4，6相邻，那么与5相对；同样的方法可以判断4与2相对，3与6相对，所以a=3，b=4，那么a+b=3+4=7．故选B．试题难度：三颗星知识点：正方体展开图——相对面、相邻面7.时钟的时针和分针夹角为90°的时刻是( )A.12:15B.3:00C.3:30D.11:45答案：B解题思路：3点整时，时针指向3，分针指向12.钟表上12个数字，每相邻两个数字之间的夹角为30°，故3点整时时针和分针的夹角正好是90°.故选B．试题难度：三颗星知识点：钟面角8.从三个不同方向看一个几何体如图所示，则这个几何体的表面积为（结果保留π）( )A.220πB.50π+120C.120πD.170π答案：D解题思路：由该几何体的三视图可知，该几何体是圆柱，且底面圆的直径为10，高为12，所以几何体的侧面积为，底面积为，表面积为．故选D．试题难度：三颗星知识点：几何体的三视图9.已知线段AB=8，延长AB到C，使BC=AB，则AC的长为( )A.8B.10C.12D.14答案：D解题思路：首先根据题意画出图形，然后设计算法求解．如图，∵，∴∴故选D．试题难度：三颗星知识点：线段的长10.如图，，，则∠AOB=( )A.30°B.40°C.45°D.48°答案：B解题思路：设，由，，得，．因为，所以，解得，即．故选B．试题难度：三颗星知识点：角的计算11.已知：如图，线段AB=12cm，C是线段AB的中点，求BC的长．解：如图，∵C是线段AB的中点∴_________________∵AB=12∴_________________即BC的长为6cm．①；②；③；④；⑤；⑥；⑦．以上空缺处正确的填写序号依次是( )A.①⑦B.②⑦C.④⑥D.①⑥答案：A解题思路：∵C是线段AB的中点∴∵∴答案为①⑦，故选A．试题难度：三颗星知识点：中点12.已知从点O出发的三条射线OA，OB，OC，若∠AOB=50°，∠AOC=30°，则∠BOC的度数为( )A.80°或20°B.40°或10°C.40°或20°D.80°或10°答案：A解题思路：根据题意，射线OC的位置不确定，有两种情况．①如图1，∵∠AOB=50°，∠AOC=30°∴∠BOC=∠AOB+∠AOC=50°+30°=80°②如图2，∵∠AOB=50°，∠AOC=30°∴∠BOC=∠AOB-∠AOC=50°-30°=20°综上，∠BOC的度数为80°或20°．故选A．试题难度：三颗星知识点：角度的计算。
人教版七年级数学上册《第4章几何图形初步》单元测试题人教版(有答案)
人教版七年级数学上册《第4章几何图形初步》单元测试题一．选择题（共10小题）1．如图，一个正方体有盖盒子（可密封）里装入六分之一高度的水，改变正方体盒子的放置方式，下列选项中不是盒子里的水能形成的几何体是（）A．正方体B．长方体C．三棱柱D．三棱锥2．下列说法中错误的是（）A．线段AB和射线AB都是直线的一部分B．直线AB和直线BA是同一条直线C．射线AB和射线BA是同一条射线D．线段AB和线段BA是同一条线段3．已知A、B、C三点，过其中任意两点画直线，一共可以画多少条直线（）A．1B．3C．3或1D．无数条4．图中下列从A到B的各条路线中最短的路线是（）A．A→C→G→E→B B．A→C→E→B C．A→D→G→E→B D．A→F→E→B 5．将一副直角三角尺按如下不同方式摆放，则图中锐角∠1与∠2互余的是（）A．B．C．D．6．下列图形中，不是正方体平面展开图的是（）A．B．C．D．7．“节日的焰火”可以说是（）A．面与面交于线B．点动成线C．面动成体D．线动成面8．将一张长方形纸片按如图所示的方式折叠，BD、BE为折痕，若∠ABE＝35°则∠DBC 为（）A．70°B．65°C．55°D．45°9．点C是线段AB的中点，点D是线段AC的三等分点．若线段AB＝12cm，则线段BD的长为（）A．10cm B．8cm C．10cm或8cm D．2cm或4cm 10．如图，已知轮船甲在A处沿北偏东65°的方向匀速航行，同时轮船乙在轮船甲的南偏东40°方向的点B处沿某一方向航行，速度与甲轮船的速度相同．若经过一段时间后，两艘轮船恰好相遇，则轮船乙的航行方向为（）A．北偏西40°B．北偏东40°C．北偏西35°D．北偏东35°二．填空题（共8小题）11．若∠A＝52°16'32''，则∠A的补角为．12．班数学活动小组的同学用纸板制作长方体包装盒，其平面展开图和相关尺寸如下，其中阴影部分为内部粘贴角料（单位：毫米），则此长方体包装盒的体积为立方毫米（用含x、y的式子表示）．13．如图，OC是∠AOB的平分线，∠BOD＝∠COD，∠BOD＝15°，则∠COD＝，∠BOC＝，∠AOB＝．14．如图，已知B处在A处的南偏西44°方向，C处在A处的正南方向，B处在C处的南偏西80°方向，则∠ABC的度数为．15．如图，若CB＝4cm，DB＝7cm，且D是AC的中点，则AC＝cm．16．点A，B，C在同一条直线上，AB＝1cm，BC＝3AB，则AC的长为．17．笔尖可以看作一个点，这个点在纸上运动时就形成了线，这可以说点动成线；汽车的雨刷在档风玻璃上画出一个扇面，这可以说．18．如图，点B是线段AC上一点，点O是线段AC的中点，且AB＝20，BC＝8．则线段OB的长为．三．解答题（共8小题）19．（1）如图，已知点C在线段AB上，AC＝8cm，BC＝6cm，M，N分别是AC，BC的中点，求线段MN的长度；（2）在（1）题中，如果AC＝acm，BC＝bcm，其他条件不变，求此时线段MN的长度．20．如图，点A，O，E在同一直线上，∠AOB＝40°，∠EOD＝25°，OD平分∠COE，（1）写出图中所有互补的角．（2）求∠COB的度数．21．有一个硬纸做成的礼品盒，用彩带扎住（如图），打结处用去的彩带长18厘米．（1）共需要彩带多少厘米？（2）做这样一个礼品盒至少要多少硬纸？（3）这个礼品盒的体积是多少？（π取3.14）22．如图，点B，D都在线段AC上，AB＝12，点D是线段AB的中点，BD＝3BC，求AC 的长．23．如图，是小明家和学校所在地的简单地图，已知OA＝2km，OB＝3.5km，OP＝4km，点C为OP的中点，回答下列问题：（1）图中到小明家距离相同的是哪些地方？（2）由图可知，公园在小明家东偏南30°方向2km处．请用方向与距离描述学校、商场、停车场相对于小明家的位置．24．下面是小王同学“过直线外一点作该直线的平行线”的尺规作图过程．已知：直线l及直线l外一点P．求作：直线PQ，使得PQ∥l．作法：如图，①在直线l外取一点A，作射线AP与直线l交于点B，②以A为圆心，AB为半径画弧与直线l交于点C，连接AC，③以A为圆心，AP为半径画弧与线段AC交于点Q，则直线PQ即为所求．根据小王设计的尺规作图过程，（1）使用直尺和圆规，补全图形；（保留作图痕迹）（2）完成下面的证明：证明：∵AB＝AC，∴∠ABC＝∠ACB，（）（填推理的依据）．∵AP＝，∴∠APQ＝∠AQP．∵∠ABC+∠ACB+∠A＝180°，∠APQ+∠AQP+∠A＝180°，∴∠APQ＝∠ABC．∴PQ∥BC（）（填推理的依据）．即PQ∥l．25．如图，已知点A为线段CB上的一点．（1）根据要求画出图形（不要求写法）：延长AB至点D，使BD＝AB；反向延长CA 至点E，使CE＝CA；（2）如果ED＝18，BD＝6，求CA的长参考答案与试题解析一．选择题（共10小题）1．解：根据题意可知，盒子里的水能形成的几何体是长方体，三棱柱，三棱锥；不可能是正方体．故选：A．2．解：A、线段AB和射线AB都是直线的一部分，正确，不合题意；B、直线AB和直线BA是同一条直线，正确，不符合题意；C、射线AB和射线BA不是同一条射线，错误，符合题意；D、线段AB和线段BA是同一条线段，正确，不合题意；故选：C．3．解：如图最多可以画3条直线，最少可以画1条直线；．故选：C．4．解：最短的路线是A→F→E→B．故选：D．5．解：∵∠1+∠2+90°＝180°，∴1+∠2＝90°，即∠1和∠2互余，因此A选项符合题意；选项B中的∠1＝∠2，因此选项B不符合题意；选项C中的∠1＝∠2＝135°，因此选项C不符合题意；可求出选项D中的∠1＝45°，∠2＝60°，因此选项D不符合题意；故选：A．6．解：根据正方体的展开图的特征可知，共有11种情况，可以分为“1﹣4﹣1型”6种，“2﹣3﹣1型”3种，“2﹣2﹣2型”1种，“3﹣3型”1种，没有“1﹣2﹣3型”的，因此选项B不是正方体平面展开图，故选：B．7．解：根据节日的焰火的火的运动路线，可以认为节日的焰火的火就是一个点，可知点动即可成线．故选：B．8．解：根据翻折的性质可知，∠ABE＝∠A′BE，∠DBC＝∠DBC′，又∵∠ABE+∠A′BE+∠DBC+∠DBC′＝180°，∴∠ABE+∠DBC＝90°，又∵∠ABE＝35°，∴∠DBC＝55°．故选：C．9．解：∵C是线段AB的中点，AB＝12cm，∴AC＝BC＝AB＝×12＝6（cm），点D是线段AC的三等分点，①当AD＝AC时，如图，BD＝BC+CD＝BC+AC＝6+4＝10（cm）；②当AD＝AC时，如图，BD＝BC+CD′＝BC+AC＝6+2＝8（cm）．所以线段BD的长为10cm或8cm，故选：C．10．解：设两船相遇于点C，如图，则△ABC是等腰三角形，即AC＝BC，也就是∠CAB＝∠B，根据题意得，∠B＝∠CAB＝180°﹣65°﹣40°＝75°，75°﹣40°＝35°，所以轮船乙的航行方向为北偏东35°．故选：D．二．填空题（共8小题）11．解：∵∠A＝52°16'32''，∴∠A的补角＝180°﹣52°16'32''＝127°43′28″，故答案为：127°43′28″．12．解：将展开图折叠，可得长、宽、高为y毫米、x毫米、65毫米的长方体，于是，体积为y•x×65＝65xy立方毫米，故答案为：65xy．13．解：∵∠BOD＝∠COD，∠BOD＝15°，∴∠COD＝3∠BOD＝3×15°＝45°，∠BOC＝∠COD﹣∠BOD＝45°﹣15°＝30°，∵OC是∠AOB的平分线，∴∠AOC＝∠BOC＝30°＝∠AOB，∴∠AOB＝60°，故答案为：45°，30°，60°．14．解：∵B处在A处的南偏西44°方向，C处在A处的正南方向，B处在C处的南偏西80°方向，∴∠ABC的度数为80°﹣44°＝36°，故答案为：36°．15．解：CD＝DB﹣BC＝7﹣4＝3cm，AC＝2CD＝2×3＝6cm．故答案为：6．16．解：AC的长度有两种情况：①点C在线段AB的延长线时，如图1所示：∵AC＝AB+BC，AB＝1cm，BC＝3cm，∴AC＝1+3＝4cm；②点C在线段AB的反向延长线时，如图2所示：∵AC＝BC﹣AB，AB＝1cm，BC＝3cm，∴AC＝3﹣1＝2cm；综合所述：AC的长为2cm或4ccm，故答案为2cm或4ccm．17．解：汽车的雨刷实际上是一条线，通过运动把玻璃上的雨水刷干净，所以应是线动成面．故答案为：线动成面．18．解：如图所示：∴AC＝AB+BC，AB＝20，BC＝8，∴AC＝20+8＝28，又∵点O是线段AC的中点，∴AO＝CO＝＝＝14，又∵OB＝OC﹣BC，∴OB＝14﹣8＝6，故答案为6．三．解答题（共7题）19．解：（1）∵AC＝8cm，点M是AC的中点，∴CM＝AC＝4cm，∵BC＝6cm，点N是BC的中点，∴CN＝BC＝3cm，∴MN＝CM+CN＝7cm，∴线段MN的长度为7cm；（2）∵点M、N分别是AC、BC的中点，∴CM＝AC，CN＝BC，∵AC＝acm，BC＝bcm，∴MN＝（AC+BC）＝cm．20．解：（1）∵点A，O，E在同一直线上，∴∠AOB+∠BOE＝180°，∠AOC+∠COE＝180°，∠AOD+∠DOE＝180°，∵OD平分∠COE，∴∠COD＝∠DOE，∴∠COD+∠AOD＝180°．∴图中所有互补的角有：∠AOB与∠BOE，∠AOC与∠COE，∠AOD与∠DOE，∠COD 与∠AOD．（2）因为∠EOD＝25°，OD平分∠COE，所以∠COE＝2∠EOD＝50°，所以∠COB＝180°﹣∠AOB﹣∠COE，＝180°﹣40°﹣50°＝90°．21．解：（1）50×4+20×4+18＝298（cm），（2）π×（）2×2+π×20×50＝200π+1000π＝1200π（cm2），（3）π×（）2×50＝5000π≈15700（cm3），答：做这样一个礼品盒共需要彩带298厘米；至少要1200π平方厘米的硬纸；这个礼品盒的体积约为15700立方厘米．22．解：∵AB＝12，点D是线段AB的中点，∴BD＝12÷2＝6；∵BD＝3BC，∴BC＝6÷3＝2，∴AC＝AB+BC＝12+2＝14．23．解：（1）因为点C为OP的中点，所以OC＝2km，因为OA＝2km，所以可得出距小明家距离相同的是学校和公园；（2）由图可知，学校在小明家东偏北45°方向2km处，商场在小明家西偏北60°方向3.5km处，停车场在东偏南30°方向4km处．24．解：（1）如图所示，直线PQ即为所求．（2）证明：∵AB＝AC，∴∠ABC＝∠ACB（等边对等角），∵AP＝AQ，∴∠APQ＝∠AQP．∵∠ABC+∠ACB+∠A＝180°，∠APQ+∠AQP+∠A＝180°，∴∠APQ＝∠ABC．∴PQ∥BC（同位角相等，两直线平行），即PQ∥l．故答案为：等边对等角；AQ；同位角相等，两直线平行．25．解：（1）画出的图形如图所示：（2）∵BD＝AB，BD＝6，∴AB＝6，∵ED＝18，∴AE＝ED﹣AB﹣BD＝18﹣6﹣6＝6，∵CE＝CA∴AC＝AE＝×6＝3．。
人教版七年级数学上册《第4章几何图形初步》单元测试含答案解析
《第4章几何图形初步》一、选择题1．分别从正面、左面和上面这三个方向看下面的四个几何体，得到如图所示的平面图形，那么这个几何体是（）A．B．C．D．2．从左面看图中四个几何体，得到的图形是四边形的几何体共有（）A．1个B．2个C．3个D．4个3．如图，四个图形是由立体图形展开得到的，相应的立体图形顺次是（）A．正方体、圆柱、三棱柱、圆锥B．正方体、圆锥、三棱柱、圆柱C．正方体、圆柱、三棱锥、圆锥D．正方体、圆柱、四棱柱、圆锥4．如图，对于直线AB，线段CD，射线EF，其中能相交的图是（）A．B．C． D．5．下面等式成立的是（）A．83.5°=83°50′B．37°12′36″=37.48°C．24°24′24″=24.44° D．41.25°=41°15′6．下列语句：①一条直线有且只有一条垂线；②不相等的两个角一定不是对顶角；③不在同一直线上的四个点可画6条直线；④如果两个角是邻补角，那么这两个角的平分线组成的图形是直角．其中错误的有（）A．1个B．2个C．3个D．4个7．如图，已知直线AB、CD相交于点O，OA平分∠EOC，∠EOC=110°，则∠BOD的度数是（）A．25° B．35° C．45° D．55°8．如图，∠1+∠2等于（）A．60° B．90° C．110°D．180°9．C是线段AB上一点，D是BC的中点，若AB=12cm，AC=2cm，则BD的长为（）A．3cm B．4cm C．5cm D．6cm10．甲乙两人各用一张正方形的纸片ABCD折出一个45°的角（如图），两人做法如下：甲：将纸片沿对角线AC折叠，使B点落在D点上，则∠1=45°；乙：将纸片沿AM、AN折叠，分别使B、D落在对角线AC上的一点P，则∠MAN=45°．对于两人的做法，下列判断正确的是（）A．甲乙都对 B．甲对乙错 C．甲错乙对 D．甲乙都错二、填空题11．如图，各图中的阴影部分绕着直线l旋转360°，所形成的立体图形分别是．12．如图，以图中A，B，C，D，E为端点的线段共有条．13．如图所示：把两块完全相同的直角三角板的直角顶点重合，如果∠AOD=128°，那么∠BOC= ．14．如图，直线AB，CD相交于点0，OE平分∠AOD，若∠BOC=80°，则∠AOE= °．15．如图是某几何体的平面展开图，则这个几何体是．16．如图绕着中心最小旋转能与自身重合．17．如图所示，一艘船从A点出发，沿东北方向航行至B，再从B点出发沿南偏东15°方向航行至C点，则∠ABC等于度．18．一个圆绕着它的直径只要旋转180度，就形成一个球体；半圆绕着直径旋转度，就可以形成一个球体．19．已知∠A=40°，则它的补角等于．20．两条直线相交有个交点，三条直线相交最多有个交点，最少有个交点．三、解答题（21、22、26、27小题各12分，23、24、25题各14分，共90分）21．如图，若CB=4cm，DB=7cm，且D是AC的中点，求线段DC和AB的长度．22．如图所示，直线AB、CD相交于O，OE平分∠AOD，∠FOC=90°，∠1=40°，求∠2和∠3的度数．23．已知：如图，∠AOB是直角，∠AOC=40°，ON是∠AOC的平分线，OM是∠BOC的平分线．（1）求∠MON的大小；（2）当锐角∠AOC的大小发生改变时，∠MON的大小是否发生改变？为什么？24．如图是一个正方体的平面展开图，标注了A字母的是正方体的正面，如果正方体的左面与右面标注的式子相等．（1）求x的值．（2）求正方体的上面和底面的数字和．25．如图，将书页一角斜折过去，使角的顶点A落在A′处，BC为折痕，BD平分∠A′BE，求∠CBD 的度数．26．如图，已知C是AB的中点，D是AC的中点，E是BC的中点．（1）若DE=9cm，求AB的长；（2）若CE=5cm，求DB的长．27．一个角的余角比它的补角的还少20°，求这个角．《第4章几何图形初步》参考答案与试题解析一、选择题1．分别从正面、左面和上面这三个方向看下面的四个几何体，得到如图所示的平面图形，那么这个几何体是（）A．B．C．D．【考点】由三视图判断几何体．【分析】由主视图和左视图可得此几何体为柱体，根据俯视图是三角形可判断出此几何体为三棱柱．【解答】解：∵主视图和左视图都是长方形，∴此几何体为柱体，∵俯视图是一个三角形，∴此几何体为三棱柱．故选C．【点评】本题主要考查了由三视图判断几何体，由主视图和左视图可得几何体是柱体，锥体还是球体，由俯视图可确定几何体的具体形状．2．从左面看图中四个几何体，得到的图形是四边形的几何体共有（）A．1个B．2个C．3个D．4个【考点】简单几何体的三视图．【分析】四个几何体的左视图：圆柱是矩形，圆锥是等腰三角形，球是圆，正方体是正方形，由此可确定答案．【解答】解：因为圆柱的左视图是矩形，圆锥的左视图是等腰三角形，球的左视图是圆，正方体的左视图是正方形，所以，左视图是四边形的几何体是圆柱和正方体；故选B．【点评】本题主要考查三视图的左视图的知识；考查了学生的空间想象能力，属于基础题．3．如图，四个图形是由立体图形展开得到的，相应的立体图形顺次是（）A．正方体、圆柱、三棱柱、圆锥B．正方体、圆锥、三棱柱、圆柱C．正方体、圆柱、三棱锥、圆锥D．正方体、圆柱、四棱柱、圆锥【考点】几何体的展开图．【分析】根据正方体、圆锥、三棱柱、圆柱及其表面展开图的特点解题．【解答】解：观察图形，由立体图形及其表面展开图的特点可知相应的立体图形顺次是正方体、圆柱、三棱柱、圆锥．故选A．【点评】可根据所给图形判断具体形状，也可根据所给几何体的面数进行判断．4．如图，对于直线AB，线段CD，射线EF，其中能相交的图是（）A．B．C． D．【考点】直线、射线、线段．【分析】根据直线、射线、线段的定义对各选项分析判断利用排除法求解．【解答】解：A、直线AB与线段CD不能相交，故本选项错误；B、直线AB与射线EF能够相交，故本选项正确；C、射线EF与线段CD不能相交，故本选项错误；D、直线AB与射线EF不能相交，故本选项错误．故选B．【点评】本题考查了直线、射线、线段，熟记定义并准确识图是解题的关键．5．下面等式成立的是（）A．83.5°=83°50′B．37°12′36″=37.48°C．24°24′24″=24.44° D．41.25°=41°15′【考点】度分秒的换算．【专题】计算题．【分析】进行度、分、秒的加法、减法计算，注意以60为进制．【解答】解：A、83.5°=83°50′，错误；B、37°12′=37.48°，错误；C、24°24′24″=24.44°，错误；D、41.25°=41°15′，正确．故选D．【点评】此类题是进行度、分、秒的加法、减法计算，相对比较简单，注意以60为进制即可．6．下列语句：①一条直线有且只有一条垂线；②不相等的两个角一定不是对顶角；③不在同一直线上的四个点可画6条直线；④如果两个角是邻补角，那么这两个角的平分线组成的图形是直角．其中错误的有（）A．1个B．2个C．3个D．4个【考点】垂线；直线、射线、线段；对顶角、邻补角．【分析】根据垂线的性质可得①错误；根据对顶角的性质可得②正确；根据两点确定一条直线可得③错误；根据邻补角互补可得④正确．【解答】解：①一条直线有且只有一条垂线，说法错误；②不相等的两个角一定不是对顶角，说法正确；③不在同一直线上的四个点可画6条直线，说法错误，应为4或6条；④如果两个角是邻补角，那么这两个角的平分线组成的图形是直角，说法正确．故选：B．【点评】此题主要考查了垂线、邻补角、对顶角，关键是熟练掌握课本知识．7．如图，已知直线AB、CD相交于点O，OA平分∠EOC，∠EOC=110°，则∠BOD的度数是（）A．25° B．35° C．45° D．55°【考点】角平分线的定义；对顶角、邻补角．【专题】计算题．【分析】根据角平分线的定义求出∠AOC的度数，再根据对顶角相等即可求解．【解答】解：∵OA平分∠EOC，∠EOC=110°，∴∠AOC=∠COE=55°，∴∠BOD=∠AOC=55°．故选D．【点评】本题主要考查了角平分线的定义以及对顶角相等的性质，认准图形是解题的关键．8．如图，∠1+∠2等于（）A．60° B．90° C．110°D．180°【考点】余角和补角．【专题】计算题．【分析】根据平角的定义得到∠1+90°+∠2=180°，即有∠1+∠2=90°．【解答】解：∵∠1+90°+∠2=180°，∴∠1+∠2=90°．故选B．【点评】本题考查了平角的定义：180°的角叫平角．9．C是线段AB上一点，D是BC的中点，若AB=12cm，AC=2cm，则BD的长为（）A．3cm B．4cm C．5cm D．6cm【考点】两点间的距离．【分析】先求出BC，再根据线段中点的定义解答．【解答】解：∵AB=12cm，AC=2cm，∴BC=AB﹣AC=12﹣2=10cm．∵D是BC的中点，∴BD=BC=×10=5cm．故选C．【点评】本题考查了两点间的距离，主要利用了线段中点的定义，熟记概念是解题的关键，作出图形更形象直观．10．甲乙两人各用一张正方形的纸片ABCD折出一个45°的角（如图），两人做法如下：甲：将纸片沿对角线AC折叠，使B点落在D点上，则∠1=45°；乙：将纸片沿AM、AN折叠，分别使B、D落在对角线AC上的一点P，则∠MAN=45°．对于两人的做法，下列判断正确的是（）A．甲乙都对 B．甲对乙错 C．甲错乙对 D．甲乙都错【考点】翻折变换（折叠问题）．【分析】甲沿正方形的对角线进行折叠，根据正方形对角线的性质，可得∠1=45°，故甲的做法是正确的；乙进行折叠后，可得两对等角，而四个角的和为90°，故∠MAN=45°是正确的，这样答案可得．【解答】解：∵AC为正方形的对角线，∴∠1=×90°=45°；∵AM、AN为折痕，∴∠2=∠3，4=∠5，又∵∠DAB=90°，∴∠3+∠4=×90°=45°．∴二者的做法都对．故选A．【点评】本题考查了图形的翻折问题；解答此类问题的关键是找着重合的角，结合直角进行求解．二、填空题11．如图，各图中的阴影部分绕着直线l旋转360°，所形成的立体图形分别是圆柱；圆锥；球．【考点】点、线、面、体．【分析】三角形旋转可得圆锥，长方形旋转得圆柱，半圆旋转得球，结合这些规律直接连线即可．【解答】解：根据分析可得：各图中的阴影图形绕着直线l旋转360°，各能形成圆柱、圆锥、球．故答案为：圆柱、圆锥、球．【点评】本题考查面动成体的知识，难度不大，熟记常见平面图形旋转可得到什么立体图形是解决本题的关键．12．如图，以图中A，B，C，D，E为端点的线段共有10 条．【考点】直线、射线、线段．【分析】分别写出各个线段即可得出答案．【解答】解：图中的线段有：线段AB，线段AC，线段AD，线段AE，线段BC，线段BD，线段BE，线段CD，线段CE，线段DE，线段共10条．故答案为：10．【点评】本题考查了直线上点与线段的数量关系，同学们可以记住公式：线段数=．13．如图所示：把两块完全相同的直角三角板的直角顶点重合，如果∠AOD=128°，那么∠BOC= 52°．【考点】角的计算．【专题】计算题．【分析】根据题意得到∠AOB=∠COD=90°，再计算∠BOD=∠AOD﹣90°=38°，然后根据∠BOC=∠COD ﹣∠BOD进行计算即可．【解答】解：∵∠AOB=∠COD=90°，而∠AOD=128°，∴∠BOD=∠AOD﹣90°=38°，∴∠BOC=∠COD﹣∠BOD=90°﹣38°=52°．故答案为52°．【点评】本题考查了角的计算：1直角=90°；1平角=180°．14．如图，直线AB，CD相交于点0，OE平分∠AOD，若∠BOC=80°，则∠AOE= 40 °．【考点】对顶角、邻补角；角平分线的定义．【分析】根据对顶角相等可得∠AOD=80°，再根据角平分线的性质可得∠AOE的度数．【解答】解：∵∠BOC=80°，∴∠AOD=80°，∵OE平分∠AOD，∴∠AOE=80°÷2=40°，故答案为：40．【点评】此题主要考查了角平分线定义，以及对顶角性质，关键是掌握对顶角相等，角平分线平分角．15．如图是某几何体的平面展开图，则这个几何体是三棱柱．【考点】几何体的展开图．【分析】侧面为三个长方形，底边为三角形，故原几何体为三棱柱．【解答】解：由几何体展开图可知，该几何体是三棱柱，故答案为：三棱柱．【点评】本题考查的是三棱柱的展开图，对三棱柱有充分的理解是解题的关键．16．如图绕着中心最小旋转90°能与自身重合．【考点】旋转对称图形．【分析】该图形被平分成四部分，因而每部分被分成的圆心角是90°，并且圆具有旋转不变性，因而旋转90°的整数倍，就可以与自身重合．【解答】解：该图形围绕自己的旋转中心，最少顺时针旋转360°÷4=90°后，能与其自身重合．【点评】本题考查旋转对称图形的概念：把一个图形绕着一个定点旋转一个角度后，与初始图形重合，这种图形叫做旋转对称图形，这个定点叫做旋转对称中心，旋转的角度叫做旋转角．17．如图所示，一艘船从A点出发，沿东北方向航行至B，再从B点出发沿南偏东15°方向航行至C点，则∠ABC等于60 度．【考点】方向角．【分析】根据南北方向是平行的得出∠ABF=45°，再和∠CBF相加即可得出答案．【解答】解：∵AE∥BF，∴∠ABF=∁EAB=45°，∴∠ABC=∠ABF+∠CBF=45°+15°=60°，故答案为：60．【点评】本题考查了方向角和角的有关计算的应用，主要考查学生的计算能力．18．一个圆绕着它的直径只要旋转180度，就形成一个球体；半圆绕着直径旋转360 度，就可以形成一个球体．【考点】点、线、面、体．【分析】一个半圆围绕直径旋转一周，根据面动成体的原理即可解．【解答】解：半圆绕它的直径旋转360度形成球．【点评】本题考查了平面图形与立体图形的联系，培养学生的观察能力和空间想象能力．19．已知∠A=40°，则它的补角等于140°．【考点】余角和补角．【专题】计算题．【分析】根据补角的和等于180°计算即可．【解答】解：∵∠A=40°，∴它的补角=180°﹣40°=140°．故答案为：140°．【点评】本题考查了补角的知识，熟记互为补角的两个角的和等于180°是解题的关键．20．两条直线相交有 1 个交点，三条直线相交最多有 3 个交点，最少有 1 个交点．【考点】直线、射线、线段．【分析】解析：两条直线相交有且只有1个交点；三条直线两两相交且不交于一点时，有3个交点；当三条直线交于同一点时，有1个交点．【解答】解：两条直线相交有1个交点，三条直线相交最多有3个交点，最少有1个交点．故答案为：1；3；1．【点评】本题考查了直线、射线、线段，主要利用了相交线的交点，是基础题．三、解答题（21、22、26、27小题各12分，23、24、25题各14分，共90分）21．如图，若CB=4cm，DB=7cm，且D是AC的中点，求线段DC和AB的长度．【考点】两点间的距离．【分析】根据线段的和差，CB、DB的长，可得DC的长，根据线段中点的性质，可得AD与DC的关系，根据线段的和差，可得答案．【解答】解：DC=DB﹣CB=7﹣4=3（cm）；D是AC的中点，AD=DC=3（cm），AB=AD+DB=3+7=10（cm）．【点评】本题考查了两点间的距离，线段的和差，线段中点的性质是解题关键．22．如图所示，直线AB、CD相交于O，OE平分∠AOD，∠FOC=90°，∠1=40°，求∠2和∠3的度数．【考点】对顶角、邻补角；角平分线的定义．【专题】计算题．【分析】由已知∠FOC=90°，∠1=40°结合平角的定义，可得∠3的度数，又因为∠3与∠AOD互为邻补角，可求出∠AOD的度数，又由OE平分∠AOD可求出∠2．【解答】解：∵∠FOC=90°，∠1=40°，AB为直线，∴∠3+∠FOC+∠1=180°，∴∠3=180°﹣90°﹣40°=50°．∠3与∠AOD互补，∴∠AOD=180°﹣∠3=130°，∵OE平分∠AOD，∴∠2=∠AOD=65°．【点评】本题主要考查邻补角的概念以及角平分线的定义．23．已知：如图，∠AOB是直角，∠AOC=40°，ON是∠AOC的平分线，OM是∠BOC的平分线．（1）求∠MON的大小；（2）当锐角∠AOC的大小发生改变时，∠MON的大小是否发生改变？为什么？【考点】角的计算；角平分线的定义．【专题】计算题．【分析】（1）根据∠AOB是直角，∠AOC=40°，可得∠AOB+∠AOC=90°+40°=130°，再利用OM是∠BOC的平分线，ON是∠AOC的平分线，即可求得答案．（2）根据∠MON=∠MOC﹣∠NOC，又利用∠AOB是直角，不改变，可得．【解答】解：（1）∵∠AOB是直角，∠AOC=40°，∴∠AOB+∠AOC=90°+40°=130°，∵OM是∠BOC的平分线，ON是∠AOC的平分线，∴，．∴∠MON=∠MOC﹣∠NOC=65°﹣20°=45°，（2）当锐角∠AOC的大小发生改变时，∠MON的大小不发生改变．∵=，又∠AOB是直角，不改变，∴．【点评】此题主要考查角的计算和角平分线的定义等知识点的理解和掌握，难度不大，属于基础题．24．如图是一个正方体的平面展开图，标注了A字母的是正方体的正面，如果正方体的左面与右面标注的式子相等．（1）求x的值．（2）求正方体的上面和底面的数字和．【考点】专题：正方体相对两个面上的文字．【分析】（1）正方体的表面展开图，相对的面之间一定相隔一个正方形确定出相对面，然后列出方程求解即可；（2）确定出上面和底面上的两个数字3和1，然后相加即可．【解答】解：正方体的表面展开图，相对的面之间一定相隔一个正方形，“A”与“﹣2”是相对面，“3”与“1”是相对面，“x”与“3x﹣2”是相对面，（1）∵正方体的左面与右面标注的式子相等，∴x=3x﹣2，解得x=1；（2）∵标注了A字母的是正方体的正面，左面与右面标注的式子相等，∴上面和底面上的两个数字3和1，∴3+1=4．【点评】本题主要考查了正方体相对两个面上的文字，注意正方体的空间图形，从相对面入手，分析及解答问题．25．如图，将书页一角斜折过去，使角的顶点A落在A′处，BC为折痕，BD平分∠A′BE，求∠CBD 的度数．【考点】角的计算；翻折变换（折叠问题）．【分析】根据翻折变换的性质可得∠ABC=∠A′BC，再根据角平分线的定义可得∠A′BD=∠EBD，再根据平角等于180°列式计算即可得解．【解答】解：由翻折的性质得，∠ABC=∠A′BC，∵BD平分∠A′BE，∴∠A′B D=∠EBD，∵∠ABC+∠A′BC+∠A′BD+∠EBD=180°，∴∠A′BC+∠A′BD=90°，即∠CBD=90°．【点评】本题考查了角的计算，主要利用了翻折变换的性质，角平分线的定义，熟记概念与性质是解题的关键．26．如图，已知C是AB的中点，D是AC的中点，E是BC的中点．（1）若DE=9cm，求AB的长；（2）若CE=5cm，求DB的长．【考点】比较线段的长短．【专题】计算题．【分析】（1）根据中点的概念，可以证明：AB=2DE，故AB的长可求；（2）由CE的长先求得BC的长，再根据C是AB的中点，D是AC的中点求得CD的长，最后即可求得BD的长．【解答】解：（1）∵D是AC的中点，E是BC的中点，∴AC=2CD，BC=2CE，∴AB=AC+BC=2DE=18cm；（2）∵E是BC的中点，∴BC=2CE=10cm，∵C是AB的中点，D是AC的中点，∴DC=AC=BC=5cm，∴DB=DC+CB=10+5=15cm．【点评】考查了线段的中点的概念．利用中点性质转化线段之间的倍分关系是解题的关键，灵活运用线段的和、差、倍、分转化线段之间的数量关系也是十分关键的一点．27．一个角的余角比它的补角的还少20°，求这个角．【考点】余角和补角．【专题】计算题．【分析】首先根据余角与补角的定义，设这个角为x，则它的余角为（90°﹣x），补角为（180°﹣x），再根据题中给出的等量关系列方程即可求解．【解答】解：设这个角为x，则它的余角为（90°﹣x），补角为（180°﹣x），根据题意可，得90°﹣x=（180°﹣x）﹣20°，解得x=75°．故答案为75°．【点评】此题综合考查余角与补角，属于基础题中较难的题，解答此类题一般先用未知数表示所求角的度数，再根据一个角的余角和补角列出代数式和方程求解．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
七年级数学单元测试题
一、精心选一选
1．下列说法中错误的是（）．
A．A、B两点之间的距离为3cm
B．A、B两点之间的距离为线段AB的长度
C．线段AB的中点C到A、B两点的距离相等
D．A、B两点之间的距离是线段AB
2．下列说法中，正确的个数有（）．
（1）射线AB和射线BA是同一条射线（2）延长射线MN到C
（3）延长线段MN到A使NA==2MN （4）连结两点的线段叫做两点间的距离
A．1 B．2 C．3 D．4
3．下列说法中，错误的是（）．
A．经过一点的直线可以有无数条 B．经过两点的直线只有一条
C．一条直线只能用一个字母表示 D．线段CD和线段DC是同一条线段
4．如图4,C是线段AB的中点，D是CB上一点，下列说法中错误的是（）．
A．CD=AC-BD B．CD=BC
C．CD=AB-BD D．CD=AD-BC
5.如果线段AB=13cm,MA+MB=17 cm,那么下面说法中正确的是( ).
A．M点在线段AB上
B．M点在直线AB上
C．M点在直线AB外
D．M点可能在直线AB上,也可能在直线AB外
6．下列图形中，能够相交的是( )．
7．已知点A、B、C都是直线l上的点，且AB=5cm，BC=3cm，那么点A与点C 之间的距离是（）.
A．8cm B．2cm C．8cm或2cm D．4cm
二、填空
8. 笔尖在纸上快速滑动写出了一个又一个字,这说明了_________;车轮旋转时,看起来像一个整体的圆面,这说明了_________;直角三角形绕它的直角边旋转一周,形成了一圆锥体,这说明了_____________.
9.如图,三棱锥有________个面,它们相交形成了________条棱, 这些棱相交形成了________个点.
0.如图5,各图中的阴影图形绕着直线I旋转360°,各能形成怎样的立体图形?
11．如图1-4，A，B，C，D是一直线上的四点，则 ______ ＋ ______ =AD
－AB，AB＋CD= ______ － ______ ．
12．如图1-5，OA反向延长得射线 ______ ，线段CD向 ______ 延长得直线CD．
13．四条直线两两相交，最多有 ______ 个交点．
14．经过同一平面内的A，B，C三点中的任意两点，可以作出 ______ 条直
线．
三．解答题
15、右面是一个正方体纸盒的展开图，请把－10，7，10，－2，－7，2分别
填入六个正方形，使得按虚线折成正方体后，相对面上的两数互为相反数。
16．读下面的语句，并按照这些语句画出图形．
（1）点P在直线AB上，但不在直线CD上。
（2）点Q既不在直线l1上，也不在直线l2上。
（3）直线a、b交于点，直线b、c交于点，直线c、a交于点。
（4）直线a、b、c两两相交。
（5）直线a和b相交于点P；点A在直线a上，但在直线b外．
17．过一点能确定几条直线？两点呢？三点呢？四点呢？
18．如图8，C为线段AB的中点，N为线段CB的中点，CN=1cm.求线段CB、线段AC、线段AB的长．
19. 如图4，AB=24cm，C、D点在线段AB上，且CD=10cm，M、N分别是AC、BD的中点，求线段MN的长．。