§2.3牛顿Newton法及其变形.doc
newton定理证法

newton定理证法牛顿定理证法牛顿定理证法是一种建立数学命题的证明方法,由英国数学家和物理学家艾萨克·牛顿发明。
该定理证法基于两个原理:1. 连续性原理:如果一个函数值在某区间内连续,则它在该区间内可取任一值。
2. 极限原理:如果一个函数值趋向于某个极限,且该函数在该点处连续,则该函数值等于该极限。
证明步骤1. 建立辅助函数:定义一个辅助函数,该函数与要证明的命题相关。
2. 证明辅助函数是连续的:通过求导或其他方法,证明辅助函数在相关区间内连续。
3. 证明辅助函数趋向于某个极限:证明辅助函数在相关区间内趋向于某个极限,并确定该极限。
4. 根据连续性原理,确定辅助函数值:根据辅助函数的连续性,可以断定辅助函数在相关区间内可以取任何值,包括极限值。
5. 根据极限原理,确定原命题:由于辅助函数的极限等于原命题,且辅助函数在相关区间内连续,因此根据极限原理,原命题也成立。
举例证明:对于任意正实数 x,存在实数 y,使得 y > 0 且 xy > 1。
辅助函数:定义辅助函数 f(x) = xy。
连续性:辅助函数 f(x) 是 x 和 y 的乘积,x 和 y 在正实数域内连续,因此 f(x) 在正实数域内连续。
极限:当 x 趋向于无穷大时,f(x) 趋向于无穷大。
因此,lim[x->∞] f(x) = ∞。
辅助函数值的确定:根据辅助函数的连续性,可以断定 f(x)可以取任何正值,包括无穷大。
原命题的确定:由于 f(x) 的极限等于无穷大,且 f(x) 在正实数域内连续,因此根据极限原理,存在 y > 0,使得 f(x) = xy > 1。
结论牛顿定理证法是一种有效的证明方法,用于建立连续函数的性质。
通过定义辅助函数并证明其连续性和极限,我们可以推出原命题的成立性。
牛顿(Newton)法

(2) 取初值 x 0 ∈ [ a , b ] ,使 f ( x 0 ) f " ( x 0 ) > 0
f " (ξ n ) (α − xn )2 , 故 α = xn+1 − 2 f ' ( xn ) xn+1 − α f "(ξn ) f "(α ) > 0(二阶收敛 )若 f " (α ) ≠ 0 → 2 = 2 f '( xn ) 2 f '(α ) = 0(大于二阶收敛 )若 f " (α ) = 0 xn − α
所以,此时Newton迭代法至少是二阶收敛的。 所以,此时Newton迭代法至少是二阶收敛的。 Newton迭代法至少是二阶收敛的
牛顿下山法 下山法——牛顿法的局部微调 牛顿法的局部微调 二. 牛顿下山法 牛顿法的
原理: 减小, 原理:若由 xk 得到的 xk+1 不能使 | f | 减小,则在 xk 和 xk+1 之间找一个更好的点 x k + 1 ,使得 f ( xk+1 ) < f ( xk ) 。 xk xk+1
]有单根α ] 设 f ( x ) = 0 在[a,b]有单根α,且 f ( x ) 在[a,b]上有 直到二阶的连续导数。 直到二阶的连续导数。
Newton迭 则 求 f ( x ) = 0的 单 根 α 的 Newton 迭 代 法 如 果 收 敛 , 其收敛至少是二阶的。
证明: 由定理2.3.1的证明有: 证明: 由定理2
牛顿(newton)插值法

牛顿(newton)插值法牛顿插值法是一种数值分析中的插值方法,它用于找到一个多项式函数,该函数会经过给定的一系列数据点。
该方法最初由英国数学家艾萨克·牛顿(Isaac Newton)发明并称为插值多项式,它也被称作差分插值法。
插值是数学和工程学中的一项重要任务,它是用于在给定数据点之间构建连续函数的一种数值方法。
插值方法通常涉及过渡从观察结果派生出抽象结果的过程,从而使得预测可能的结果取得更加准确。
下面介绍牛顿插值法的基本原理。
插值基础插值基础是插值方法中的一个重要概念。
在这里,我们将对牛顿插值法中用到的插值基础进行简要介绍。
一个插值基础是指一个已知数据点的集合,通常是一个 x 坐标和对应的 y 坐标。
每个插值基础一般定义为一个数据点的函数,该函数包含了给定点的所有信息并将这些信息用于构建连续函数。
在牛顿插值法中,我们使用差分来定义插值基础。
差分是指两个相邻数据点之间 y 坐标的差值。
具体来说,若给定以下节点:x0, y0x1, y1x2, y2...xn, yn我们则通过以下的 "+" 符号所示的不断进行差分的方式来构建一个插值基础:y0y1-y0…yn-yn-1 yn-yn-1 yn-yn-2 ... yn-y0上述图表所展示的差分的值即为定义插值基础的差商(divided difference)。
牛顿插值公式基于上述插值基础和差商,我们现在可以使用牛顿插值公式来实现插值。
具体来说,牛顿插值公式可以表示为:f(x) = y0 + d1*f[x0,x1] + d2*f[x0,x1,x2] + ... + dn*f[x0,x1,...,xn]其中 f(x) 是插值函数,x0, x1, ..., xn 是给定的节点,y0, y1, ..., yn 是对应的 y 值,f[x0,x1] 是差商 f(x0,...,x1) 的值,d1, d2, ..., dn 也是差商。
请注意,插值函数的次数最高为 n - 1,这意味着插值函数与插值基础的次数相同。
牛顿法和拟牛顿法

重置 否
x (1 ) = x ( n + 1 )
例4.13:用DFP方法求解 min 2 x + x − 4 x1 + 2
2 1 2 2
初始点x
(1)
2 1 0 = , H1 = 1 0 1
λ1 =
5 18
2 1
8 9 4 9
SQP方法
• 良好的性质 • 广泛应用 • 与Lagrange-Newton 法的关系
总结
简单的“拟”可以 是革命性的进步!
1 v
( k )T
q (k )
∆H k =
p
(k )
⋅p
( k )T (k )
p
( k )TΒιβλιοθήκη q−Hkq q
(k )
⋅q
( k )T
Hk
( k )T
Hkq
(k )
计 算 步 骤:
x (1 ) , ε > 0
H1 = I n , d (1) = −∇f ( x(1) ), k = 1
∇f ( x ( k ) ) < ε
p ( k ) := x ( k +1) − x ( k ) ⇓ q ( k ) := ∇f ( x ( k +1) ) − ∇f ( x ( k ) ) q
(k )
≈ ∇ f (x
2
( k +1)
)p
(k )
p ( k ) = H k + 1q ( k )
p ( k ) ≈ ∇ 2 f ( x ( k +1) ) −1 q ( k )
FletcherDavidon(1959), Fletcher-Powell(1963) DFP 方法
最优化理论方法——牛顿法
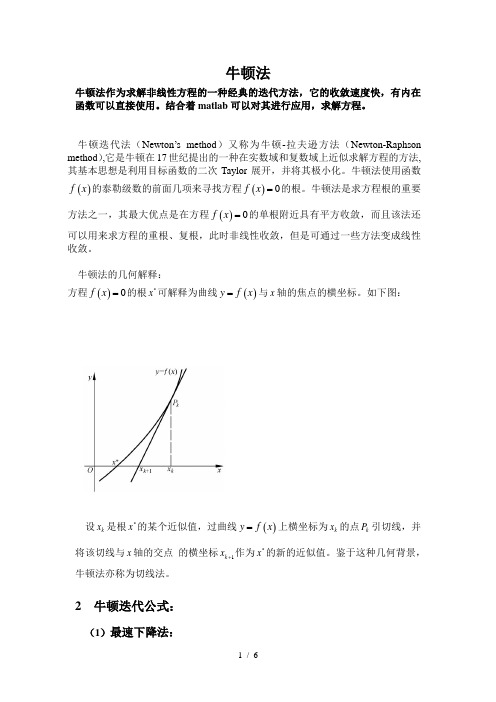
牛顿法牛顿法作为求解非线性方程的一种经典的迭代方法,它的收敛速度快,有内在函数可以直接使用。
结合着matlab 可以对其进行应用,求解方程。
牛顿迭代法(Newton ’s method )又称为牛顿-拉夫逊方法(Newton-Raphson method ),它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法,其基本思想是利用目标函数的二次Taylor 展开,并将其极小化。
牛顿法使用函数()f x 的泰勒级数的前面几项来寻找方程()0f x =的根。
牛顿法是求方程根的重要方法之一,其最大优点是在方程()0f x =的单根附近具有平方收敛,而且该法还可以用来求方程的重根、复根,此时非线性收敛,但是可通过一些方法变成线性收敛。
牛顿法的几何解释:方程()0f x =的根*x 可解释为曲线()y f x =与x 轴的焦点的横坐标。
如下图:设k x 是根*x 的某个近似值,过曲线()y f x =上横坐标为k x 的点k P 引切线,并将该切线与x 轴的交点 的横坐标1k x +作为*x 的新的近似值。
鉴于这种几何背景,牛顿法亦称为切线法。
2 牛顿迭代公式:(1)最速下降法:以负梯度方向作为极小化算法的下降方向,也称为梯度法。
设函数()f x 在k x 附近连续可微,且()0k k g f x =∇≠。
由泰勒展开式: ()()()()()Tk k k k fx f x x x f x x x ο=+-∇+- (*)可知,若记为k k x x d α-=,则满足0Tk k d g <的方向k d 是下降方向。
当α取定后,Tk k d g 的值越小,即T kk d g -的值越大,函数下降的越快。
由Cauchy-Schwartz 不等式:T k k kk d g d g ≤,故当且仅当k k d g =-时,Tk k d g 最小,从而称k g -是最速下降方向。
最速下降法的迭代格式为: 1k k k k x x g α+=-。
牛顿法原理

牛顿法原理
牛顿法是一种可以将非线性收敛到最小值的迭代法,是以传统意义上的函数最小值求解和极值求解具有重要意义的数值解法之一。
牛顿法(Newton's Method)或称牛顿迭代法,由英国数学家牛顿提出。
它是一种以逐步逼近的方式来求解极值,也就是最优求解法。
它可以帮助求解数学中连续函数极值及根的值,是近代数值分析的重要组成部分,也是当今最重要的最优方法之一。
牛顿法的基本思想是,如果一个连续函数的图像在某一点处有极值,那么该点处函数的导数为零,它即为函数的极值点。
根据这一思想,牛顿法寻找极值点,即就是不断从起点开始,计算梯度并根据梯度计算新的点,然后继续重复上面的步骤,直到收敛为止。
牛顿法的具体步骤有:
(1)确定变量的初始值,使用方程组求解;
(2)计算变量的一阶偏导数;
(3)根据一阶偏导数的函数值更新变量的值;
(4)用新值计算梯度,若精度满足要求,则可结束;若未满足要求,则重复步骤2和3。
在求解函数极值时,牛顿法优于迭代法。
牛顿法不仅使函数值逐渐收敛到极值,而且保持精度高。
其收敛速度快,收敛精度高,且稳定性好,而迭代法则收敛缓慢,而且收敛精度也不高。
总之,牛顿法是通过不断迭代计算求取函数极值的一种简便有效的求解方法,利用它求解特定类型函数的极值及其根可以弥补非线性方程其他求解方法的盲点,大大的提高了求解的效率。
牛顿定律PPT课件

同一性质的力; 4. 两个物体相互作用,可以接
触也可不接触。
弹性力
永磁体悬浮在超导体上方
磁场力
四、力的概念 力 一个物体所受的力必为其他物体所施予
▪ 自然界的四种基本力:
引力、电磁力、强相互作用和弱相互作用
1. 万有引力 两个物体之间的相互吸引力
F
各个力分别作用时所 产生的加速度的叠加
ai
Fi m
3. 第二定律 F m a 为瞬时关系 力与加速度同时存在、同时改变和同时消失
4. 第二定律表达 式为d矢2r量关系
F
i
Fi mdt2
y
解题时常用分量式
▪ 直角坐标系中的分量形式
m ax Fx
r
Fy
ay
a
F
Fx mxamdd2tx2
O
x
Fy may mdd2t2y 力和加速度的直角坐标分解
例题2-2 m1= 3 kg,m2= 2 kg,m1与m2间的静
摩擦系数0 = 0.3,m1与水平桌面间的滑动摩擦系 数 = 0.2, 受与水平面的夹角为30º的拉力F 作
用。求:(1)两物体不发生相对滑动时,拉力 F 与
系统的加速度 a 的关系,并考察 a = 0 时的情形;
(2)两物体不发生相对滑动时,系统的最大加速度
Fco3sm 01m s2ign 30 25
(2) 两物体无相对运动时,m2 受 m1的静摩擦力作 用,当加速度为最大时,摩擦力为最大静摩擦力,
取物体m2为研究对象,坐标系的选取与(1)相同。
根据牛顿第二定律列出m2的运动方程:
x 方向: y 方向:
Ffm2a F N 2m 2g0
牛顿-拉夫逊迭代法原理及其实现

牛顿迭代法(简写)就是一种近似求解实数域与复数域求解方程的数学方法。
那么这个方法是具体是什么原理呢?牛顿迭代如何迭代?直接看数学公式描述如何迭代不直观,先来看动图就很容易理解牛顿迭代法为什么叫迭代法以及怎样迭代的:牛顿迭代法是原理是根据一个初始点在该点做切线,切线与X轴相交得出下一个迭代点的坐标,再在处做切线,依次类推,直到求得满足精度的近似解为止。
由前面描述知道,牛顿迭代法是用来近似求解方程的,这里有两个点需要说明:•为啥要近似求解?很多方程可能无法直接求取其解•迭代法非常适合计算机编程实现,实际上计算机编程对于牛顿迭代法广为应用来看看,数学上如何描述的?其中为函数在处的一阶导数,也就是该点的切线。
来简单推一推上面公式的由来,直线函数方程为:知道一个直线的一个坐标点以及斜率则该直线的方程就很容易可以得知:那么该直线与轴的交点,就是y=0也即等式x 的解:啥时候停止迭代呢?1.计算出2.给出一个初始假定根值x0,利用上面迭代式子进行迭代3.计算绝对相对迭代近似误差4.将绝对相对近似误差与预定的相对误差容限进行比较。
如果,则迭代步骤2,否则停止算法。
另外,检查迭代次数是否已超过允许的最大迭代次数。
如果是这样,则需要终止算法并退出。
另一个终止条件是:如何编码呢?由于牛顿迭代法主要目的是解方程,当然也有可能用于某一个数学函数求极值,所以无法写出通用的代码,这里仅仅给出一个编代码的思路。
相信掌握了思路,对于各种实际应用应该能很快的写出符合实际应用的代码。
假定一函数为其波形图如下:其一阶导数为:那么对于该函数的根:从图上大致可以知道有两个根,如果直接解方程,则很难求出其根,可以编个代码试试:#include <stdio.h>#include <math.h>#include <stdlib.h>/*假定待求根函数如下*/#define F(x) (2*(x)*(x)-10*cos(x)+(x)-80)/*其一阶导数为*/#define DF(x) (4*(x)+10*sin(x)+1)float newton_rooting(float x0,float precision,float min_deltax,int max_iterations) {float xn,xn1,fn,fn1,dfn;float deltax;int step = 0;xn = x0;xn1 = x0;do{xn = xn1;fn = F(xn);dfn = DF(xn);/*判0*/if( fabs(dfn) <1e-6 ){if( fabs(fn)>precision )return NAN;elsereturn fn;}xn1 = xn - fn/dfn;fn1 = F(xn1);deltax = fabs(xn1-xn);step++;if( step>max_iterations ){if( fabs(fn1)<precision )return xn;elsereturn NAN;}}while( fabs(fn1)>precision || deltax>min_deltax );return xn1;}void main(){float root_guess = 23.0f;float precision = 0.00001f;float min_deltax = 0.001f;float root;int step = 7;root = newton_rooting( root_guess,precision,min_deltax,step );printf("根为: %f,函数值为:%f\n", root,F(root));root_guess = -23;root = newton_rooting( root_guess,precision,min_deltax,step );printf("根为: %f,函数值为:%f\n", root,F(root));}结果:根为: 6.457232, 函数值为:0.000004根为: -6.894969,函数值为:-0.000008函数值已经很接近于0了,如果还需要更为精确的值,则可以选择在此基础上进一步求解,比如利用二分法逼近。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.3 牛顿(Newton )法及其变形
一、Newton 迭代方法
牛顿迭代法计算公式的推导过程
设*x 是()0f x =的根,()f x 在*x 的邻域内具有二阶连续导数,在*x 的邻域内取一点0x ,使0()0f x '≠,则()f x 在*x 的邻域内连续,将它在0x 点二阶Taylor
展开得
2
0000000()()()()()()2!
()()()
f f x f x f x x x x x f x f x x x ξ'''=+-+-'≈+- 又()0f x =,则有
000()()()0f x f x x x '+-≈
故()0f x =的近似解000()()f x x x f x ≈-',记0100()()
f x x x f x =-' 类似,在点1x 处Taylor 展开,可得:
111()()
f x x x f x ≈-',记1211()()f x x x f x =-' 依次往下做,可得一般的迭代格式:
上述迭代格式称为求()0
f x=的解的牛顿迭代法。
几何意义
在点
00
(,())
x f x处作()
f x的切线,交x轴于一点,求该点的横坐标。
此切线方程为
000
()()()
y f x f x x x
'
-=-,
当0
y=时,得0
()
()
f x
x x
f x
=-
'
,正是
1
x的值。
类似地,在点(,())
k k
x f x作函数()
f x的切线,交x轴于一点,切线方程为
()()()
k k k
y f x f x x x
'
-=-,
当0
y=时,得
()
()
k
k
k
f x
x x
f x
=-
'
,正是
1
k
x
+
的值。
所以,牛顿迭代法又称为切线求根法。
例6用牛顿迭代法求方程x
x e-
=在0.5
x=附近的根。
解.将原方程化为()0
x
f x x e-
=-=,则牛顿迭代格式为
11k k x k k k x x e x x e
-+--=-+ 取00.5x =,迭代得
1230.566311 0.5671431, 0.5671433x x x === 与上一节例2-4相比,牛顿法的收敛速度快。
与埃特金法相当.
注意:牛顿法的几何意义说明了,迭代初值0x 必须足够接近*x ,否则可能不收敛或收敛与其它的根。
牛顿迭代法的流程图
二、Newton 迭代法的变形
牛顿法的优点:收敛速度快。
牛顿法的缺点:每次迭代要计算一次导数值'()k f x ,当()f x 表达式复杂或无明显表达式时求解困难。
简化的牛顿迭代法
1.主要思路:为了避免直接计算导数值,用某个定点上的值(或一常数M )取代()k f x ',如,令0()M f x '=,则牛顿迭代法的迭代格式变为:
称它为简化的牛顿迭代法。
只要M 选择得当,上式总是收敛的,不过其收敛速度降为线性 . 2.几何意义
其几何意义可描述为用平行线代替牛顿法中的切线。
过点(,())k k x f x ,斜率为0()f x '的直线与x 轴有一交点,下面求出该交点的横坐标。
该直线的方程为
0()()()k k y f x f x x x '-=-
当0y =时,即为直线与x 轴交点的横坐标值,也就是简化的牛顿迭代方法中的
1k x +的表达式:
10()()
k k k f x x x f x +=-'
3.优缺点
优点:计算简单。
缺点:没有充分利用()f x 本身的特性,收敛速度慢,收敛阶为1。
割线法
1. 双点割线法
(1)基本思想:利用一阶差商11
()()k k k k f x f x x x ----取代牛顿迭代法中的()k f x ',则有
111
()()()
k k k k k k k f x x x f x f x x x +--=--- , 即
上式称为双点割线法。
可以验证,在满足一定条件下,其收敛阶
(2) 几何意义
1k x +为过点11(,())k k x f x --与(,())k k x f x 的割线和x 轴交点的横坐标。
事实上,连接11(,())k k x f x --与(,())k k x f x ,得到一条直线,该直线的方程为:
11
()()()()k k k k k k f x f x y f x x x x x ----=-- 当0y =时,得到它与x 轴的交点的横坐标值,即1k x +:
111()()()()k k k k k k k f x x x x x f x f x +--=---,。
