2017年高考新课标全国3卷文科数学
2017年高考新课标3卷文科数学试题(解析版)

****
----
2017年普通高等学校招生全国统一考试
文科数学
(适用地区:云南、贵州、广西、四川)
第Ⅰ卷(选择题共60分)
一、选择题(本大题共12 个小题,每小题 5 分,共60 分.在每小题给出的四个选项中,只有一个选项
是符合题目要求的.)
1.已知集合A={1 ,2,3,4} ,B={2 ,4,6,8} ,则A∩B 中元素的个数为( )
A .1 B.2 C.3 D.4
[解析] 由题意可得A∩B={2 ,4} ,故选B.
答案: B
2.复平面内表示复数z=i(–2+i)的点位于( )
A .第一象限B.第二象限C.第三象限D.第四象限
[解析] 由题意z=-1-2i,故选B.
答案: B
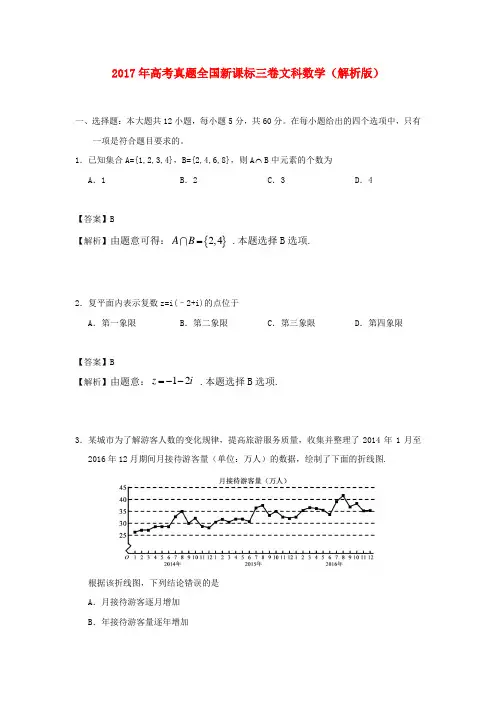
3.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014 年 1 月至2016 年12 月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.
根据该折线图,下列结论错误的是( )
A .月接待游客逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7,8 月
D.各年 1 月至 6 月的月接待游客量相对于7 月至12 月,波动性更小,变化比较平稳
[解析] 由折线图,7 月份后月接待游客量减少, A 错误,故选A.
答案: A
- 1 -。
2017年高考真题全国新课标三卷文科数学(解析版)
2017年高考真题全国新课标三卷文科数学(解析版)一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A={1,2,3,4},B={2,4,6,8},则A B 中元素的个数为 A .1B .2C .3D .4【答案】B【解析】由题意可得: .本题选择B 选项.2.复平面内表示复数z=i(–2+i)的点位于 A .第一象限B .第二象限C .第三象限D .第四象限【答案】B【解析】由题意: .本题选择B 选项.3.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是 A .月接待游客逐月增加 B .年接待游客量逐年增加⋂{}2,4A B =12z i =--C .各年的月接待游客量高峰期大致在7,8月D .各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳【答案】A【解析】由折线图,7月份后月接待游客量减少,A 错误;本题选择A 选项.4.已知,则= A .B .C .D .【答案】A【解析】 .本题选择A 选项.5.设x ,y 满足约束条件,则z =x -y 的取值范围是 A .[–3,0]B .[–3,2]C .[0,2]D .[0,3]【答案】B【解析】绘制不等式组表示的可行域,结合目标函数的几何意义可得函数在点处取得最小值 . 在点 处取得最大值 .本题选择B 选项.4sin cos 3αα-=sin 2α79-29-2979()2sin cos 17sin 22sin cos 19ααααα--===--326000x y x y +-≤⎧⎪≥⎨⎪≥⎩()0,3A 033z =-=-()2,0B 202z =-=6.函数f (x )=sin(x +)+cos(x −)的最大值为A .B .1C .D .【答案】A【解析】由诱导公式可得: , 则: ,函数的最大值为 .本题选择A 选项.153π6π653515cos cos sin 6233x x x ππππ⎡⎤⎛⎫⎛⎫⎛⎫-=-+=+ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦()16sin sin sin 53353f x x x x πππ⎛⎫⎛⎫⎛⎫=+++=+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭657.函数y =1+x +的部分图像大致为 A . B .C .D .【答案】D【解析】当时,,故排除A,C,当时,,故排除B,满足条件的只有D,故选D.8.执行下面的程序框图,为使输出S 的值小于91,则输入的正整数N 的最小值为A .5B .4C .3D .2【答案】D2sin xx 1x =()111sin12sin12f =++=+>x →+∞1y x →+【解析】若,第一次进入循环,成立,,成立,第二次进入循环,此时,不成立,所以输出成立,所以输入的正整数的最小值是2,故选D.9.已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为 A .B .C .D .【解析】如果,画出圆柱的轴截面,所以,那么圆柱的体积是,故选B.10.在正方体中,E 为棱CD 的中点,则A .B .C .D .2N =12≤100100,1010S M ==-=-2i =2≤101001090,110S M -=-==-=3i =2≤9091S =<N π3π4π2π411,2AC AB ==r BC ==223124V r h πππ⎛==⨯⨯= ⎝⎭1111ABCD A B C D -11A E DC ⊥1A E BD ⊥11A E BC ⊥1A E AC ⊥【答案】C11.已知椭圆C :,(a >b >0)的左、右顶点分别为A 1,A 2,且以线段A 1A 2为直径的圆与直线相切,则C 的离心率为ABCD .【答案】A【解析】以线段为直径的圆是,直线与圆相切,所以圆心到直线的距离,整理为,即,即 ,,故选A.12.已知函数有唯一零点,则a=A .B .C .D .1【答案】C22221x y a b+=20bx ay ab -+=1312A A 222x y a +=20bx ay ab -+=d a ==223a b =()22222323a a c a c =-⇒=2223c a =c e a ==211()2()x x f x x x a ee --+=-++12-1312二、填空题:本题共4小题,每小题5分,共20分。
2017年高考文科数学全国新课标3卷
绝密★启用前2017年普通高等学校招生全国统一考试(III卷)文科数学(适用地区:云南、广西、贵州、四川)注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效.3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A={1,2,3,4},B={2,4,6,8},则A∩B中元素的个数为A.1 B.2 C.3 D.42.复平面内表示复数z=i(﹣2+i)的点位于A.第一象限 B.第二象限 C.第三象限 D.第四象限3.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是A.月接待游客量逐月增加B.年接待游客量逐年增加C.各年的月接待游客量高峰期大致在7,8月D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳4.已知4sin cos3αα-=,则sin2α=A.﹣ B.﹣ C. D.5.设x,y满足约束条件则z=x﹣y的取值范围是A.[﹣3,0] B.[﹣3,2] C.[0,2] D.[0,3] 6.函数f(x)=sin(x+)+cos(x﹣)的最大值为A. B.1 C. D.7.函数y=1+x+的部分图象大致为A. B。
C。
D.8.执行如图的程序框图,为使输出S的值小于91,则输入的正整数N的最小值为A.5 B.4 C.3 D.29.已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为A.π B. C. D.10.在正方体ABCD﹣A1B1C1D1中,E为棱CD的中点,则A.A1E⊥DC1 B.A1E⊥BD C.A1E⊥BC1 D.A1E⊥AC 11.已知椭圆C:=1(a>b>0)的左、右顶点分别为A1,A2,且以线段A1A2为直径的圆与直线bx﹣ay+2ab=0相切,则C的离心率为A. B. C. D.12.已知函数f(x)=x2﹣2x+a(e x﹣1+e﹣x+1)有唯一零点,则a=A.﹣ B. C. D.1二、填空题:本题共4小题,每小题5分,共20分。
2017年全国3高考文科数学试题及答案-全国卷3

2017年普通高等学校招生全国统一考试(全国卷3)文科数学注意事项:1.答题前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A={1,2,3,4},B={2,4,6,8},则A B 中元素的个数为( )A .1B .2C .3D .42.复平面内表示复数(2)z i i =-+的点位于( ) A .第一象限B .第二象限C .第三象限D .第四象限3.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图. 根据该折线图,下列结论错误的是( ) A .月接待游客逐月增加 B .年接待游客量逐年增加C .各年的月接待游客量高峰期大致在7,8月D .各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳 4.已知4sin cos 3αα-=,则sin 2α=( ) A .79-B .29-C .29D .795.设,x y 满足约束条件326000x y x y +-≤⎧⎪≥⎨⎪≥⎩,则z x y =-的取值范围是( )A .[-3,0]B .[-3,2]C .[0,2]D .[0,3]6.函数1()sin()cos()536f x x x ππ=++-的最大值为( ) A .65 B .1 C .35D .157.函数2sin 1xy x x =++的部分图像大致为( ) A . B .C .D .8.执行右面的程序框图,为使输出S 的值小于91,则输入的正整数N 的最小值为( )A .5B .4C .3D .2 9.已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( ) A .πB .34π C .2πD .4π10.在正方体1111ABCD A B C D -中,E 为棱CD 的中点,则( )A .11A E DC ⊥B .1A E BD ⊥C .11A E BC ⊥D .1AE AC ⊥11.已知椭圆2222:1(0)x y C a b a b+=>>的左、右顶点分别为12,A A ,且以线段12A A 为直径的圆与直线20bx ay ab -+=相切,则C 的离心率为( )A BC .3D .1312.已知函数211()2()x x f x x x a ee --+=-++有唯一零点,则a =( )A .12-B .13C .12D .1二、填空题:本题共4小题,每小题5分,共20分。
2017高考全国3卷文科数学试题及标准答案

2017年普通高等学校招生全国统一考试(新课标Ⅲ)文科数学注意事项:1.答题前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A={1,2,3,4},B={2,4,6,8},则A⋂B中元素的个数为A.1ﻩﻩﻩﻩB.2ﻩﻩﻩC.3 ﻩﻩﻩD.42.复平面内表示复数z=i(–2+i)的点位于A.第一象限ﻩB.第二象限ﻩﻩC.第三象限ﻩD.第四象限3.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是A.月接待游客逐月增加B.年接待游客量逐年增加C.各年的月接待游客量高峰期大致在7,8月D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳4.已知4sin cos3αα-=,则sin2α=A.79-ﻩﻩﻩ B.29-ﻩﻩﻩC.29ﻩﻩD.795.设x,y满足约束条件3260x yxy+-≤⎧⎪≥⎨⎪≥⎩,则z=x-y的取值范围是A.[–3,0]ﻩﻩﻩB.[–3,2]ﻩﻩ C.[0,2] D.[0,3]6.函数f(x)=15sin(x+3π)+cos(x−6π)的最大值为A.65ﻩﻩB.1 ﻩﻩC.35ﻩﻩﻩD.157.函数y=1+x+2sin xx的部分图像大致为A.ﻩB.C.ﻩﻩD.8.执行下面的程序框图,为使输出S的值小于91,则输入的正整数N的最小值为A.5 ﻩﻩﻩB.4ﻩﻩﻩ C.3ﻩﻩD.2。
(完整版)2017年新课标3文科数学含答案

2017年普通高等学校招生全国统一考试(新课标Ⅲ)文科数学注意事项:1.答题前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A={1,2,3,4},B={2,4,6,8},则A⋂B中元素的个数为A.1 B.2 C.3 D.42.复平面内表示复数z=i(–2+i)的点位于A.第一象限B.第二象限C.第三象限D.第四象限3.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是A.月接待游客逐月增加B.年接待游客量逐年增加C.各年的月接待游客量高峰期大致在7,8月D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳4.已知4sin cos3αα-=,则sin2α=A .79-B .29-C .29D .795.设x ,y 满足约束条件326000x y x y +-≤⎧⎪≥⎨⎪≥⎩,则z =x -y 的取值范围是 A .[–3,0]B .[–3,2]C .[0,2]D .[0,3]6.函数f (x )=15sin(x +3π)+cos(x −6π)的最大值为A .65B .1C .35D .157.函数y =1+x +2sin xx的部分图像大致为A .B .C .D .8.执行下面的程序框图,为使输出S 的值小于91,则输入的正整数N 的最小值为A .5B .4C .3D .29.已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为 A .πB .3π4C .π2D .π410.在正方体1111ABCD A B C D -中,E 为棱CD 的中点,则A .11A E DC ⊥B .1A E BD ⊥C .11A E BC ⊥D .1AE AC ⊥11.已知椭圆C :22221x y a b+=,(a >b >0)的左、右顶点分别为A 1,A 2,且以线段A 1A 2为直径的圆与直线20bx ay ab -+=相切,则C 的离心率为AB C D .1312.已知函数211()2()x x f x x x a ee --+=-++有唯一零点,则a =A .12-B .13C .12D .1二、填空题:本题共4小题,每小题5分,共20分。
2017高考新课标全国3卷文科数学(word版可编辑修改)
2017高考新课标全国3卷文科数学(word版可编辑修改)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2017高考新课标全国3卷文科数学(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2017高考新课标全国3卷文科数学(word版可编辑修改)的全部内容。
2017年普通高等学校招生全国统一考试(新课标Ⅲ)文科数学一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A={1,2,3,4},B={2,4,6,8},则A B 中元素的个数为⋂A .1B .2C .3D .42.复平面内表示复数z=i(–2+i )的点位于A .第一象限B .第二象限C .第三象限D .第四象限3.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图。
根据该折线图,下列结论错误的是A .月接待游客逐月增加B .年接待游客量逐年增加C .各年的月接待游客量高峰期大致在7,8月D .各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳4.已知,则=4sin cos 3αα-=sin 2αA . B .C .D .79-29-29795.设x ,y 满足约束条件,则z =x -y 的取值范围是326000x y x y +-≤⎧⎪≥⎨⎪≥⎩A .[–3,0]B .[–3,2]C .[0,2]D .[0,3]6.函数f (x )=sin(x +)+cos (x −)的最大值为153π6πA .B .1C .D .6535157.函数y =1+x +的部分图像大致为2sin xx A . B .C .D .8.执行下面的程序框图,为使输出S 的值小于91,则输入的正整数N 的最小值为A .5B .4C .3D .29.已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为A .B .C .D .π3π4π2π410.在正方体中,E 为棱CD 的中点,则1111ABCD A B C D -A .B .C .D .11A E DC ⊥1A E BD⊥11A E BC ⊥1A E AC⊥11.已知椭圆C :,(a >b 〉0)的左、右顶点分别为A 1,A 2,且以线段A 1A 2为直径的圆22221x y a b+=与直线相切,则C 的离心率为20bx ay ab -+=A B C D .1312.已知函数有唯一零点,则a =211()2()x x f x x x a e e --+=-++A .B .C .D .112-1312二、填空题:本题共4小题,每小题5分,共20分。
2017年高考新课标3卷文科数学试题(解析版)
2017年普通高等学校招生全国统一考试文科数学(适用地区:云南、贵州、广西、四川)第Ⅰ卷(选择题共60分)一、选择题(本大题共12 个小题,每小题 5 分,共60 分.在每小题给出的四个选项中,只有一个选项是符合题目要求的.)1.已知集合A={1 ,2,3,4} ,B={2 ,4,6,8} ,则A∩B 中元素的个数为( )A .1 B.2 C.3 D.4[解析] 由题意可得A∩B={2 ,4} ,故选B.答案:B2.复平面内表示复数z=i(–2+i)的点位于( )A .第一象限B.第二象限C.第三象限D.第四象限[解析] 由题意z=-1-2i,故选B.答案:B3.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014 年1 月至2016 年12 月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是( )A .月接待游客逐月增加B.年接待游客量逐年增加C.各年的月接待游客量高峰期大致在7,8 月D.各年 1 月至6 月的月接待游客量相对于7 月至12 月,波动性更小,变化比较平稳[解析] 由折线图,7 月份后月接待游客量减少, A 错误,故选A.答案:A- 1 -4,则s in2α=( ) 4.已知sinα-cosα=3A .-79B.-2929C.D.792-1(sinα-cosα)[解析] sin2α=2sinαcosα==-1 79,故选A.答案:A3x+2y-6≤0x≥0,则z=x-y 的取值范围是( )5.设x,y 满足约束条件y≥0A .[–3,0] B.[–3,2] C.[0,2] D.[0,3][解析] 绘制不等式组表示的可行域,结合目标函数的几何意义可得函数在点A(0,3) 处取得最小值z =0-3=-3.在点B(2,0) 处取得最大值z=2-0=2,故选A.答案:B6.函数 f (x)=sin x+π+cos x-3π的最大值为()665 A .35B.1 C.15D.[解析] 由诱导公式可得cos x-π=cos6ππ-x+2 3π=sin x+,31π则f(x)=sin x+5 3 +sin x+π 66 π=sin x+,函数的最大值为,故选A.3 5 3 5答案:A7.函数y=1+x+s in x2 的部分图像大致为( ) x[解析] 当x=1 时,f(1)=1+1+sin1=2+sin1>2,故排除A,C,当x→+∞时,y→1+x,故排除B,D.D,故选满足条件的只有答案:D- 2 -8.执行下面的程序框图,为使输出S 的值小于91,则输入的正整数N的最小值为( ) A .5 B.4 C.3 D.2[解析] 若N=2,第一次进入循环,1≤2成立,S=100,M =-10010=-10,i=2≤2成立;第二次进入循环,此时S=100-10=90,M=--10=1,i=3≤2不成立,∴输出S=90<91 成立,∴输入的正整数N 10的最小值是2,故选D.答案:D9.已知圆柱的高为1,它的两个底面的圆周在直径为 2 的同一个球的球面上,则该圆柱的体积为( )3πA .πB.4πC.2πD.4[解析] 如果,画出圆柱的轴截面12,∴r=BC=AC=1,AB=3 32h=π×,那么圆柱的体积是V=πr2 22×1=3π,故选B.4答案:B10.在正方体ABCD -A1B1C1D1 中,E 为棱C D 的中点,则( )A .A1E⊥DC1 B.A1E⊥BD C.A1E⊥BC1 D.A1E⊥AC[解析] 根据三垂线逆定理,平面内的线垂直平面的斜线,那么也垂直斜线在平面内的射线.- 3 -对于C,若A1E⊥BC1,那么BC1⊥B1C,成立,反过来BC1⊥B1C 时,也能推出BC1⊥A1E,∴C 成立,对于D,若A1E⊥AC,则AE⊥AC,显然不成立,故选C.答案:C11.已知椭圆C:2 2x y2+2=1( a>b>0)的左、右顶点分别为A1、A2,且以线段A1A2 为直径的圆与直线bx a b-ay+2ab=0 相切,则 C 的离心率为( )A .63B.33C.23D.132+y2=a2,直线bx-ay+2ab=0 与圆相切,∴圆心到直线的距离 d[解析] 以线段A1A2 为直径的圆是x=2ab=a,整理为a2=3b2,即a2=3(a2-c2) 2a2=3c2,即2=3b2,即a2=3(a2-c2) 2a2=3c2,即2+b2a2c 2 c,e==2=a 3 a6,故选 A .3答案:A2-2x+a(e x-1+e-x+112.已知函数f(x)=x )有唯一零点,则a=( )A .-12 B.1 13 C.2 D.12-2x+a(e x-1+e-x+1[解析] 方法一:由条件,f(x)=x ),得:2-2(2-x)+a(e2-x-1+ e-(2-x)+1f(2-x)=(2-x) )2 1-x x-1=x -4x+4-4+2x+a(e +e)=x2-2x+a(e x -x+1)-1+e∴f(2-x)=f(x),即x=1为f(x)的对称轴,由题意,f(x)有唯一零点,∴f(x)的零点只能为x=1,1即f(1) =12-2·1+a(e1-1+e-1+1)=0,解得a=.22 x-1 -x+1 x-1 -x+1 x-1 -x+1 x-1方法二:x -2x=-a(e +e +e ,g′x()=e -e =e),设g(x)=e -2(x-1)-11 ex-1=x-1 ,e e当g′x()=0时,x=1,当x<1时,g′x()<0,函数单调递减,当x>1时,g′x()>0,函数单调递增,当x=1时,函数取得最小值g(1)=2,设h(x)=x2-2x,当x=1时,函数取得最小值-1;若-a>0,函数h( x)和ag(x)没有1交点,当-a<0时,-ag(1)=h(1)时,此时函数h(x)和ag(x)有一个交点,即-a×2=-1 a=,故选C.2 答案:C第Ⅱ卷(非选择题共90 分)本试卷包括必考题和选考题两部分.第13 题~第21 题为必考题,每个试题考生都必须作答.第22 题~第24 题为选考题,考生根据要求作答.- 4 -二、填空题(本大题共 4 小题,每小题 5 分,共20 分.)→13.已知向量 a→→=(-2,3),b =(3,m),且 a→⊥b ,则m=.[解析] 由题意可得-2×3+3m=0,∴m=2.答案:214.双曲线2x2-a2y 3=1(a>0)的一条渐近线方程为y=9 5x,则a=.3[解析] 由双曲线的标准方程可得渐近线方程为y=±x,结合题意可得a=5.a答案:515.△ABC 的内角A,B,C 的对边分别为a,b,c.已知C=60°,b=6,c=3,则A=.[解析] 由题意b=sinBc bsinC,即sinB==sinC c36×2=32,结合b<c 可得B=45°,则A=180°-B-C2=75°.答案:75°16.设函数f(x)=x+1,x≤0则满足f(x)+f(x-x,x>0212)>1 的x 的取值范围是.[解析] 方法一:∵f(x)=x+1,x≤0 1,f(x)+f x-x,x>02 212>1,即f x->1-f(x),由图象变换可画出y=f x-12与y=1-f(x)的图象如下:y1y f(x)21 1( , )4 41 1 x2 2y 1 f (x)12 由图可知,满足f x->1-f(x)的解为(-14,+∞).11 1 x+x-11方法二:由题意得,当x> 时,2 ;当0< x≤时,2 +1>1 恒成立,即x+2x-2>1 恒成立,即x>2 2 2 20< x≤12;当x≤0时x+1+x-12+1>1 x>-14,即-1 14< x≤0;综上x的取值范围是(-4,+∞).1答案:(-,+∞)4三、解答题(本大题共 6 小题,共70 分,解答应写出文字说明、证明过程或演算步骤.)第17~21 题为必考题,每个试题考生都必须作答.第22、23 题为选考题,考生根据要求作答.- 5 -(一)必考题:共60分.17.(本小题满分12 分)设数列{ a n} 满足a1+3a2+⋯+(2n-1)a n=2n.(1)求{ a n}的通项公式;(2)求数列a n2n+1的前n 项和.[解析] (1)∵a1+3a2+⋯+(2n-1)a n=2n,①∴n≥2时,a1+3a2+⋯+(2n-1)a n-1=2(n-1),②2①-②得,(2n-1)a n=2,a n=2n-1,又n=1 时,a1=2 适合上式,2∴a n=; 2n-1(2)由(1)a n=2n+12=(2n-1)(2n+1)1 1-,2n-1 2n+1a1 a2 a n 1 1 ∴S n=++⋯+=(1-)+( -3 5 2n+1 3 3 15)+⋯+(1 1 1-)=1-=2n-1 2n+1 2n+12n.2n+118.(本小题满分12 分)某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶 4 元,售价每瓶6 元,未售出的酸奶降价处理,以每瓶 2 元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500 瓶;如果最高气温位于区间[20,25),需求量为300 瓶;如果最高气温低于20,需求量为200 瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:最高气温[10,15) [15,20) [20,25) [25,30) [30,35) [35,40) 天数 2 16 36 25 7 4 以最高气温位于各区间的频率代替最高气温位于该区间的概率.(1)求六月份这种酸奶一天的需求量不超过300 瓶的概率;(2)设六月份一天销售这种酸奶的利润为Y(单位:元),当六月份这种酸奶一天的进货量为450 瓶时,写出Y 的所有可能值,并估计Y 大于零的概率.[解析] (1)需求量不超过300 瓶,即最高气温不高于25℃,从表中可知有54 天,∴所求概率为P=54 3=.90 5(2)Y 的可能值列表如下:最高气温[10,15) [15,20) [20,25) [25,30) [30,35) [35,40) Y -100 -100 300 900 900 900 低于20℃:y=200×6+250×2-450×4=-100;[20,25):y=300×6+150×2-450×4=300;不低于25℃:y=450×(6-4)=900,2 16 ∴Y 大于0 的概率为P=+=90 90 15.- 6 -19.(本小题满分 12 分)如图,四面体 ABCD 中,△ ABC 是正三角形, AD = CD .(1)证明: AC ⊥BD ;(2)已知△ ACD 是直角三角形, AB =BD .若 E 为棱B D 上与 D 不重合的点, 且 AE ⊥EC ,求四面体 ABCE 与四面体 ACDE 的体积比.[解析 ] (1)证明:取A C 中点 O ,连O D ,OB , ∵AD =CD ,O 为 AC 中点,∴ AC ⊥OD , 又∵△ ABC 是等边三角形,∴ AC ⊥ OB ,又∵ OB ∩OD =O ,∴ AC ⊥平面 OBD ,BD 平面 OBD , ∴AC ⊥BD ;(2)设A D =CD =2,∴ AC = 2 2,AB =CD =2 2,又∵ AB =BD ,∴ BD =2 2,∴△ ABD ≌ △ CBD ,∴ AE =EC , 又∵ AE ⊥EC ,AC =2 2,∴ AE =EC =2, 在△ ABD 中,设D E =x ,根据余弦定理cos ∠ ADB = AD 2+BD 2-AB 2 2AD ·BDAD=2+DE 2-AE 2 2AD ·DE= 2+(2 2)2-(2 2)22+x 2-22 2 2 = , 2×2×x 2×2×2 2解得 x = 2,∴点 E 是 BD 的中点,则V D -ACE =V B -ACE ,∴V D -ACE=1. V B -ACE-ACE2+mx –2 与 x 轴交于A ,B 两点,点 C 的坐标 20.(本小题满分 12 分)在直角坐标系x Oy 中,曲线 y =x为(0,1).当 m 变化时,解答下列问题:(1)能否出现A C ⊥BC 的情况?说明理由;(2)证明过A ,B ,C 三点的圆在 y 轴上截得的弦长为定值.2+mx -2=0 的根, [解析 ] (1)设A (x1,0),B(x 2,0),则x 1,x 2 是方程 x∴x 1+x 2=- m ,x 1x 2=- 2,→ →则A C ·BC= (-x 1,1) ·(-x 2,1)=x 1x 2+1=- 2+1=- 1≠0, ∴不会能否出现A C ⊥BC 的情况.(2)解法一:过A ,B ,C 三点的圆的圆心必在线段A B 垂直平分线上,设圆心E(x 0, y 0),- 7 -x1+x2则x0==-2 m,由|EA |=|EC|得2x1+x2-x1 2+y02=2x1+x222+(y0-1)2,1+x1x2化简得y0==-2 1 2 ,∴圆E 的方程为x+m22+y+122=-m22+-1-1-122,令x=0 得y1=1,y2=-2,∴过A,B,C 三点的圆在y 轴上截得的弦长为1-(-2)=3,∴过A,B,C 三点的圆在y 轴上截得的弦长为定值解法二:设过A,B,C 三点的圆与y 轴的另一个交点为D,由x1x2=-2 可知原点O 在圆内,由相交弦定理可得|OD ||OC |=|OA||OB|=|x1||x2|=2,又|OC |=1,∴|OD |=2,∴过A,B,C 三点的圆在y 轴上截得的弦长为|OC |+|OD |=3,为定值.2+(2a+1) x. 21.(本小题满分12 分)已知函数 f (x)=ln x+ax3-2. (1)讨论f( x)的单调性;(2)当a<0 时,证明f(x) ≤-4a[解析] (1) f′x()=2+(2a+1)x+12ax (2 ax+1)( x+1)=(x>0),x x当a≥0 时,f′x()≥,0则f(x )在(0,+∞)单调递增,当a<0 时,则f(x)在(0,- 1)单调递增,在(-1,+∞)单调递减. 2a 2a(2)由(1) 知,当a<0 时,f( x)max=f(-12a),1f(-)-(-2a 3+2)=ln(-4a1)+2a1+1,令y=ln t+1-t(t=-2a1>0),2a则y′=1t-1=0,解得t=1,∴y 在(0,1)单调递增,在(1,+∞)单调递减,3∴y max=y(1)=0,∴y≤0,即f (x)max≤-( +2),∴f( x) ≤-4a 3-2.4a(二)选考题:共10分.请考生在第22、23 题中任选一题作答,如果多做,则按所做的第一题计分.22.(本小题满分10 分)选修4―4坐标系与参数方程:在直角坐标系xOy 中,直线l1 的参数方程为x=2+ty=kt(t 为参数),直线l2 的参数方程为x=-2+mmky=(ml1 与l2 的交点为P,当k 变化时,P 的轨迹为曲线C.为参数).设(1)写出 C 的普通方程;(2)以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,设l3:ρ(cosθ+sinθ)-2=0,M 为l3 与C 的- 8 -交点,求M 的极径.[解析] (1)将参数方程转化为普通方程1l1:y=k(x-2)⋯⋯①;l2:y=(x+2)⋯⋯②k由①②消去k可得:x2-y2=4,即P的轨迹方程为x2-y2=4;(2)将参数方程转化为一般方程l3:x+y-2=0⋯⋯③联立l3和曲线C得x+y-2=0,解得2-y2=4x3 22x=,由2y=-2x=ρcosθ,解得ρ=5,y=ρsinθ即M的极半径是5.23.(本小题满分10 分)选修4— 5 不等式选讲:已知函数f( x)=|x+1|–|x–2|.(1)求不等式f(x) ≥1的解集;2(2)若不等式f(x) ≥x –x+m 的解集非空,求m 的取值范围.-3,x≤-12x-1,-1<x<2.由f (x) ≥1可得:[解析] (1) f( x)=|x+1|–|x–2|可等价为f(x)=3,x≥2①当x≤-1时显然不满足题意;②当-1< x<2时,2x-1≥1,解得x≥1;③当x≥2时,f(x)=3≥1恒成立.综上,f( x) ≥的1解集为{ x|x≥1}.2-x+m等价为f(x)-x2+x≥m,(2)不等式f(x) ≥x令g(x)=f( x)-x2+x,则g( x) ≥m解集非空只需要[g(x)] max≥m.-x2+x-3,x≤-1而g(x)=-x2+3x-1,-1<x<2.-x2+x+3,x≥2①当x≤-1时,[ g(x)]max=g(-1)=-3-1-1=-5;3②当-1< x<2时,[g(x)]max=g(2)=-322+3·3-1=-1=5;2 4③当x≥2时,[ g(x)] max=g(2)=-22+2+3=1.综上,[g( x)]max=5 5 ,故m≤.4 45∴m 的取值范围为(-∞,].4- 9 -。
2017年全国统一高考数学试卷(文科)(新课标ⅲ)(含解析版)
A. —6
5
5
3
B. 1
6
C. —3
5
D
1 _5
7. Cs 分)函数 y=l+x+兰坚-的部分图象大致为(
X2
C.
D.
8. Cs 分)执行如图的程序框图,为使输出 S 的值小千 91, 则输入的正整数 N 的最小值为(
A. 5
B. 4
C. 3
D. 2
9. cs 分)已知圆柱的高为 1, 它的两个底曲的圆周在直径为 2 的同一个球的球血上,则该圆柱的休
={ (5 分)设函数 f 16.
(x) x+l , x<o ,则满足 f (x) +f (x- 上) >1 的 x 的取值范围是
.
产, x >o
2
19. (12 分)如图四面体 ABCD 中,^ ABC 是正二伯形, AD=CD.
(1) 证明: AC 上 BD: (2) 已知^ ACD 是直伯二川形, AB=BD, 若 E 为棱 BD 上与 D 个重合的点,且 AE 上 EC, 求四面体 ABCE
7.【解答】解:函数y=l+x+兰坚一, 可知:f(x) =x+王坚-是奇函数, 所以函数的图象关千原点对称, 则函数y=l+x+主皿-的图象关千(O, 1) 对称, 当x➔o', f Cx) >o, 排除A、c, 当x=rr时,y=l顷, 排除B. 第4页(共9页)
故选:D. 【点评】本题考查函数 的图象的 判断,函数的奇偶性以及特殊点是常用方 法.
A
y
x 【点评】本题考查线线垂直的 判断,是中档题,斛题时要认真审题,注意向量法的合理运用.
【点评】本题考查曲圆柱 的体积的 求法,考查圆柱、球等基础知识,考查推理论证能力、运算求 解能 力、空间想象 能力,考查化归与转化思想,是中档题.
2017年高考数学全国卷3文(附参考答案及详解)
!#'$1;#
在直角坐标系 #6) 中#直 线:! 的 参 数 方 程 为 )'?;# $;为 参
,#' )$13#数%ຫໍສະໝຸດ 直线:$的参
数
方
程
为+ -)'
3 ?
#
$3 为 参 数 %!设:! 与:$
的交点为 *#当? 变化时#* 的轨迹为曲线&!
$!%写出 & 的普通方程*
$$%以坐标原点为极点## 轴正半轴为极轴建立极坐标 系#设:(&
!"
"#!$年普通高等学校招生全国统一考试全国卷*
!!)!解析5 $&!!#"#'#/"#"&!"#/#4#0"#6 $%"&!"#/"!
6 $%" 中元素的个数为"!
故选 )!
"!*!解析5 .&+%(",+&&(!("+#6 复 数.& (!("+所 对 应 的复平面内的点为 I%(!#("&#位于第三象限!
!!
年 普 通 高 等 学 校 招 生 全 国 统 一 考 试 数 学
!!请 考 生 在 第 $$$$( 题 中 任 选 一 题 作 答如 果 多 做则 按 所 做
的 第 一 题 计 分 !作 答 时 请 写 清 题 号 !
$$!$本 小 题 满 分 !# 分 %选 修 252&坐 标 系 与 参 数 方 程
排
除
选
项
%#*!
故选 .!
0!.!解析假设 -&"#程序执行过程如下'
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2017年普通高等学校招生全国统一考试(新课标Ⅲ)文科数学一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A={1,2,3,4},B={2,4,6,8},则A⋂B中元素的个数为A.1 B.2 C.3 D.42.复平面内表示复数z=i(–2+i)的点位于A.第一象限B.第二象限C.第三象限D.第四象限3.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是A.月接待游客逐月增加B.年接待游客量逐年增加C.各年的月接待游客量高峰期大致在7,8月D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳4.已知4sin cos3αα-=,则sin2α=A.79-B.29-C.29D.795.设x,y满足约束条件3260x yxy+-≤⎧⎪≥⎨⎪≥⎩,则z=x-y的取值范围是A.[–3,0] B.[–3,2] C.[0,2] D.[0,3]6.函数f (x )=15sin(x +3π)+cos(x −6π)的最大值为A .65B .1C .35D .157.函数y =1+x +2sin xx的部分图像大致为A .B .C .D .8.执行下面的程序框图,为使输出S 的值小于91,则输入的正整数N 的最小值为A .5B .4C .3D .29.已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为 A .πB .3π4C .π2D .π410.在正方体1111ABCD A B C D -中,E 为棱CD 的中点,则A .11A E DC ⊥B .1A E BD ⊥C .11A E BC ⊥D .1AE AC ⊥11.已知椭圆C :22221x y a b+=,(a >b >0)的左、右顶点分别为A 1,A 2,且以线段A 1A 2为直径的圆与直线20bx ay ab -+=相切,则C 的离心率为AB C .3D .1312.已知函数211()2()x x f x x x a ee --+=-++有唯一零点,则a =A .12-B .13C .12D .1二、填空题:本题共4小题,每小题5分,共20分。
13.已知向量(2,3),(3,)a b m =-=,且a ⊥b ,则m = .14.双曲线22219x y a -=(a >0)的一条渐近线方程为35y x =,则a = .15.△ABC 的内角A ,B ,C 的对边分别为a ,b ,c 。
已知C =60°,b ,c =3,则A =_________。
16.设函数10()20x x x f x x +≤⎧=⎨>⎩,,,,则满足1()()12f x f x +->的x 的取值范围是__________。
三、解答题:共70分。
解答应写出文字说明、证明过程或演算步骤。
第17~21题为必考题,每个试题考生都必须作答。
第22、23题为选考题,考生根据要求作答。
(一)必考题:共60分。
17.(12分)设数列{}n a 满足123(21)2n a a n a n +++-=.(1)求{}n a 的通项公式; (2)求数列21n a n ⎧⎫⎨⎬+⎩⎭的前n 项和.18.(12分)某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:以最高气温位于各区间的频率代替最高气温位于该区间的概率。
(1)求六月份这种酸奶一天的需求量不超过300瓶的概率;(2)设六月份一天销售这种酸奶的利润为Y(单位:元),当六月份这种酸奶一天的进货量为450瓶时,写出Y的所有可能值,并估计Y大于零的概率.19.(12分)如图,四面体ABCD中,△ABC是正三角形,AD=CD.(1)证明:AC⊥BD;(2)已知△ACD是直角三角形,AB=BD.若E为棱BD上与D不重合的点,且AE⊥EC,求四面体ABCE与四面体ACDE的体积比.20.(12分)在直角坐标系xOy中,曲线y=x2+mx–2与x轴交于A,B两点,点C的坐标为(0,1).当m变化时,解答下列问题:(1)能否出现AC⊥BC的情况?说明理由;(2)证明过A,B,C三点的圆在y轴上截得的弦长为定值.21.(12分)已知函数()f x=ln x+ax2+(2a+1)x.(1)讨论()f x的单调性;(2)当a﹤0时,证明3()24f xa≤--.(二)选考题:共10分。
请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分。
22.[选修4―4:坐标系与参数方程](10分)在直角坐标系xOy中,直线l1的参数方程为2+,,x ty kt=⎧⎨=⎩(t为参数),直线l2的参数方程为2,,x mmmyk=-+⎧⎪⎨=⎪⎩(为参数).设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.(1)写出C的普通方程;(2)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,设l3:ρ(cosθ+sinθ,M为l3与C的交点,求M的极径.23.[选修4—5:不等式选讲](10分)已知函数()f x=│x+1│–│x–2│.(1)求不等式()f x≥1的解集;(2)若不等式()f x≥x2–x +m的解集非空,求m的取值范围.2017年普通高等学校招生全国统一考试文科数学试题3答案一、选择题1.B2.C3.A4.A5.B6.A7.D8.D9.B 10.C 11.A 12.C二、填空题13. 2 14. 5 15. 75°16. (-,)三、解答题17.解:(1)因为+3+…+(2n-1)=2n,故当n≥2时,+3+…+(-3)=2(n-1)两式相减得(2n-1)=2所以=(n≥2)又因题设可得=2.从而{} 的通项公式为=.(2)记{}的前n项和为,由(1)知= = -.则= - +- +…+ - = .18.解:(1)这种酸奶一天的需求量不超过300瓶,当且仅当最高气温低于25,由表格数据知,最高气温低于25的频率为,所以这种酸奶一天的需求量不超过300瓶的概率估计值为0.6.(2)当这种酸奶一天的进货量为450瓶时,若最高气温不低于25,则Y=6450-4450=900;若最高气温位于区间[20,25),则Y=6300+2(450-300)-4450=300;若最高气温低于20,则Y=6200+2(450-200)-4450= -100.所以,Y的所有可能值为900,300,-100.Y大于零当且仅当最高气温不低于20,由表格数据知,最高气温不低于20的频率为,因此Y大于零的概率的估计值为0.8.19.解:(1)取A C的中点O连结DO,BO.因为AD=CD,所以AC⊥DO.又由于△ABC是正三角形,所以AC⊥BO.从而AC⊥平面DOB,故AC⊥BD.(2)连结EO.由(1)及题设知∠ADC=90°,所以DO=AO.在Rt△AOB中,.又AB=BD,所以,故∠DOB=90°.由题设知△AEC为直角三角形,所以.又△ABC是正三角形,且AB=BD,所以.故E为BD的中点,从而E到平面ABC的距离为D到平面ABC的距离的,四面体ABCE 的体积为四面体ABCD的体积的,即四面体ABCE与四面体ACDE的体积之比为1:1. 20.解:(1)不能出现AC⊥BC的情况,理由如下:设,,则满足所以.又C的坐标为(0,1),故AC的斜率与BC的斜率之积为,所以不能出现AC ⊥BC的情况.(2)BC的中点坐标为(),可得BC的中垂线方程为.由(1)可得,所以AB的中垂线方程为.联立又,可得所以过A、B、C三点的圆的圆心坐标为(),半径故圆在y轴上截得的弦长为,即过A、B、C三点的圆在y轴上的截得的弦长为定值.21.解:(1)f(x)的定义域为(0,+),.若a≥0,则当x∈(0,+)时,,故f(x)在(0,+)单调递增.若a<0,则当x∈时,;当x∈时,.故f(x)在单调递增,在单调递减.(2)由(1)知,当a<0时,f(x)在取得最大值,最大值为.所以等价于,即设g(x)=ln x-x+1,则当x∈(0,1)时,;当x∈(1,+)时,.所以g(x)在(0,1)单调递增,在(1,+)单调递减.故当x=1时,g(x)取得最大值,最大值为g(1)=0.所以当x>0时,g(x)≤0,.从而当a<0时,,即.22.解:(1)消去参数t得的普通方程:; 消去参数m得的普通方程:+2).设P(x,y),由题设得消去k得.所以C的普通方程为.(2)C的极坐标方程为联立得故,从而,.代入得=5,所以交点M的极径为.23.解:(1)当x<-1时,f(x)≥1无解;当时,由f(x)≥1得,2x-1≥1,解得1≤x≤2;当时,由f(x)≥1解得x>2.所以f(x)≥1的解集为{x|x≥1}.(2)由得m≤|x+1|-|x-2|-.而|x+1|-|x-2|-=≤,且当x=时,|x+1|-|x-2|-.故m的取值范围为(-].。
