小升初组合图形面积计算
小升初奥数数学:巧算表面积及复习资料

答:这27块长方体的表面积是18平 方分米.
第五章 图形与几何
第五章 图形与几何
第1课时 线与角 课时训练1 线与角 第2课时 平面图形 课时训练2 平面图形 第3课时 立体图形 课时训练3 立体图形 第4课时 图形与变换 课时训练4 图形与变换 第5课时 图形与位置 课时训练5 图形与位置 《图形与几何》达标检测
b
a
类型1:简单组合
例1、如图,在一 个棱长为5分米的 正方体上放一个 棱长为4分米的小 正方体,求这个 立体图形的表面 积。
解法(一)将棱长为4分米 的小正方体放上后,
总的表面积减少了小正方体 的两个面,
所以,这个立体图形的表面 积是
5×5×6+4×4×6- 4×4×2
=150+96-32
=214 (平方分米)
上下面
左右面
前后面
解:上下面的面积都是9平方厘米, 左右面的面积都是8平方厘米, 前后面的面积都是10平方厘米。 因此,这个立体图形的表面积是
(9+8+10)×2=54 (平方厘米)
上下面
左右面
前后面
【变式训练】
1、右图是16块棱长为2厘米的小正方 体堆成的,它的表面积是多少平方厘 米?
解:从上面和下面看到的面积 为2×9×(2×2)=72cm², 从正面和后面看面积为: 2×7×(2×2)=56cm², 从两个侧面看面积为: 2×7×(2×2)=68cm². 72+56+68=196cm². 答:它的表面积为196cm².
上下方向: 2个边长为2厘米的正方形的面积;
前后左右: 边长为2厘米的4个正方形的面积和 边长为1厘米的4个正方形的面积和 边长为0. 5厘米的4个正方形的面积和 边长为0.25厘米的4个正方形的面积和
小升初2019数学组合图形面积

图形练习专题【知识集锦】一、圆1、常见对称图形1)有1条对称轴的图形有:角、等腰三角形、等腰梯形、扇形、半圆2)有2条对称轴的图形是:长方形3)有3条对称轴的图形是:等边三角形4)有4条对称轴的图形是:正方形5)有无数条对称轴的图形是:圆、圆环2、半径、直径、周长、面积1)r扩大n倍,直径扩大n倍,周长扩大n倍,面积扩大n2倍.2)周长比=半径比=直径比,面积比=半径比2=直径比2=周长比2.3)圆周率的大小固定不变,它的大小跟圆的大小无关.3、半圆⎧+⎨⎩周长:圆周长的一半一条直径.面积:圆的面积的一半.注:1、周长相等的平面图形(长方形、正方形、圆)中,圆的面积最大,长方形的面积最小;面积相等的平面图形中,长方形周长最长,圆的周长最短.2、圆中剪一个最大的正方形,正方形的对角线长和圆的直径相等.(补充:正方形的面积等于对角线乘积的一半).------方中圆3、在长方形里剪一个最大的圆,圆的直径等于长方形的宽.4、几个直径和为n的圆的周长=直径为n的圆的周长.(即若大圆的直径等于几个小圆的直径之和,则大圆的周长就等于几个小圆的周长之和)如右图:二、求面积对于不规则阴影图形的面积计算问题,常见处理方式:1)将阴影部分自身分割成若干规则图形,分别算出每个规则图形再求和.2)若阴影部分自身不能分割成规则的图形,先算出含阴影的规则图形面积,再求出空白部分面积,然后用规则图形面积-空白部分面积.3)观察图形特征----对称拼合移补寻找隐藏条件----翻折旋转割补【例+练】一、判断题1、所有的半径都相等,所有的直径都相等.( )2、直径的长度是半径的2倍.( )3、圆是轴对称图形,对称轴是直径.( )4、一个圆的周长是r 厘米,半圆的周长就是2r 厘米.( ) 5、两条半径的长度等于一条直径的长度.( )6、半径2分米的圆的周长和面积一样大.( )7、r 2表示r ×2.( )二、填空题1、一个挂钟,时针长20厘米,经过一昼夜,时针扫过的面积是( )平方厘米.2、一种钟表的分针长6cm ,3小时分针尖端走过的距离是( ).3、两个连在一起的皮带轮,其中一个轮子的直径是6分米,当另一个轮子转一周时,它要转3周,另一个轮子的直径是( )分米.4、一台拖拉机,后轮直径是前轮的2倍,如后轮滚动6圈,前轮要滚动( )圈.5、一辆自行车车轮外直径为0.6米,小华骑自行车从家到学校,如果每分钟转动100周,小华每分钟走( )米.6、一条路长47.1米,小明在用路上滚铁环,铁环直径为30厘米,从路的一端滚到另一端,铁环要转( )圈.7、把一个圆形纸片剪成两个半圆,周长增加了10cm ,这个圆的面积是( ).8、一个圆剪拼成一个近似的长方形,长方形的周长是8.28,则圆的面积是( ).9、在一个正方形中画一个最大的圆,再在这个圆中画一个最大的正方形,由外到内的三个图形的面积比为( ).10、把一个正方体削成一个最大的圆,正方体与圆柱的体积比是( );把一个圆柱削成一个最大的长方体,长方体与圆柱的体积比是( ).11、把一个圆柱体沿高切成底面是若干相等的扇形的几何体,再拼成一个近似的长方体,若拼成的长方体前面与右侧面的面积和是103.5平方厘米,且原来圆柱高是5厘米,原来圆柱的体积是( ).12、如图,学校操场400米的跑道宽为1.2米,则相邻跑道起跑线相距( ).(第12题)(第13题)13、如图,正方形的面积为8cm2,圆的面积为().14、一个梯形的上底、下底与高的乘积分别为5、7cm,这个梯形的面积是()dm2.15、如图,一长方形被一条直线分成两个长方形,这两个长方形的宽的比为1:3,若阴影三角形面积为1平方厘米,则原长方形面积为()平方厘米.(第15题)(第16题)(第17题)16、如图,有三根直径都是2分米的圆柱形木材,想用一根绳子把它们捆成一捆,捆三圈最短需要()米长的绳子.(结果保留 )17、如图,一块长方形铁皮,利用图中的阴影部分刚好能做成一个油桶(接头处不计),这个油桶的容积是()平方厘米.三、选择1、两个大小不同的圆.如果这两个圆的半径都增加3厘米,那么,它们周长增加的部分相比,()A、大圆增加的多B、小圆增加的多C、增加的同样多D、无法比较2、两个大小不同的圆.如果这两个圆的半径都增加3厘米,那么,它们面积增加的部分相比,()A、大圆增加的多B、小圆增加的多C、增加的同样多D、无法比较3、直径为20厘米的圆的面积与两个直径为10厘米的圆的面积之和比较,()A、相等B、前者大C、后者大D、无法比较4、直径为20厘米的圆的周长与两个直径为10厘米的圆的周长之和比较,()A、相等B、前者大C、后者大D、无法比较5、如图,甲、乙、丙都是腰长为ɑ的等腰三角形,顶角分别是锐角、直角、钝角,比较三个图形的面积( )A、甲大B、乙大C、丙大D、相等四、计算下列各图阴影部分面积.四、解答题1、下图中阴影部分面积都是10cm2,求圆环的面积.2、如图,圆的周长为18.84厘米,圆的面积等于长方形的面积,求阴影部分的周长.3、如图,两个小圆和三个半圆的半径都是1厘米,阴影部分的面积是多少?4、下图是一个正三角形,以它每个顶点为圆心,以2cm为半径画弧,求阴影部分的面积.5、如图,一个直角三角形场地,设置为掷铅球的运动场,A、B为投掷点,空白区为投掷区,阴影部分为安全区,计算安全区的面积.(π取3,单位:米)6、下图中,直角三角形ABC周长24厘米,它的三条边长度比为3︰4︰5,求阴影部分的周长和面积各是多少?7、如图,求阴影部分的面积.8、如图,两个完全相同的直角梯形重叠在一起,求阴影部分的面积.9、如图,两个相同的直角三角形有一部分重叠在一起,阴影部分的面积是多少?10、已知半圆的直径为30厘米,求阴影部分的周长.11、一瓶装满的矿泉水,水瓶的内直径是8厘米。
数学(小升初) 组合图形周长、面积的计算

第2讲组合图形面积的计算一、计算公式例1、如图,正方形ABCD的边长为6厘米,△ABE、△ADF与四边形AECF的面积彼此相等,求三角形AEF的面积.例2、下图,求阴影部分的面积。
其他常用的基本方法有:一、相加法这种方法是将不规则图形分解转化成几个基本规则图形,分别计算它们的面积,然后相加求出整个图形的面积。
例如:求下图整个图形的面积二、相减法这方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差。
例如:下图,求阴影部分的面积。
一句话:正方形面积减去圆的面积即可。
三、直接求法这种方法是根据已知条件,从整体出发直接求出不规则图形面积。
例如:下图,求阴影部分的面积。
一句话:通过分析发现阴影部分就是一个底是2、高是4的三角形。
四、重新组合法这种方法是将不规则图形拆开,根据具体情况和计算上的需要,重新组合成一个新的图形,设法求出这个新图形面积即可。
例如:下图,求阴影部分的面积。
一句话:拆开图形,使阴影部分分布在正方形的4个角处,如下图。
五、辅助线法这种方法是根据具体情况在图形中添一条或若干条辅助线,使不规则图形转化成若干个基本规则图形,然后再采用相加、相减法解决即可例如:下图,若求阴影部分的面积。
六、割补法法这种方法是把原图形的一部分切割下来补在图形中的另一部分使之成为基本规则图形,从而使问题得到解决。
例如:求阴影部分的面积.七、平移法这种方法是将图形中某一部分切割下来平行移动到一恰当位置,使之组合成一个新的基本规则图形,便于求出面积。
例如:下图,求阴影部分的面积。
一句话:可先沿中间切开把左边正方形内的阴影部分平行移到右边正方形内,这样整个阴影部分恰是一个正方形。
八、旋转法这种方法是将图形中某一部分切割下来之后,使之沿某一点或某一轴旋转一定角度贴补在另一图形的一侧,从而组合成一个新的基本规则的图形,便于求出面积。
例如图(1),求阴影部分的面积。
一句话:左半图形绕B点逆时针方向旋转180°,使A与C重合,从而构成右图(2)的样子,此时阴影部分的面积可以看成半圆面积减去中间等腰直角三角形的面积.九、对称添补法这种方法是作出原图形的对称图形,从而得到一个新的基本规则图形.原来图形面积就是这个新图形面积的一半。
热点:关于不规则或组合立体图形的表面积和体积问题-2024年小升初数学(解析版)

热点:关于不规则或组合立体图形的表面积和体积问题一、计算题。
1求下图立体图形的表面积。
【答案】114.84dm2【分析】由图可知,圆柱的上底面刚好填补正方体的上底面被覆盖的部分面积,因此图中立体图形的表面积可以看作是一个正方体的表面积加上一个圆柱的侧面积;根据正方体的表面积=棱长×棱长×6,圆柱的侧面积=底面周长×高,代入相应数值计算即可解答。
【详解】4×4×6+3.14×2×3=16×6+6.28×3=96+18.84=114.84(dm2)因此这个立体图形的表面积是114.84dm2。
2如图下图,求组合体的表面积。
(单位:厘米;π取3.14)【答案】142.84平方厘米【分析】观察图形可知,组合体的表面积等于长方体的表面积加上圆柱体的侧面积,根据长方体的表面积公式:S=ab+ah+bh×2,圆柱体的侧面积公式:S=πdh,代入数据计算即可。
【详解】8×6+8×1+6×1×2+3.14×2×3=48+8+6×2+3.14×2×3=62×2+3.14×2×3=124+18.84=142.84(平方厘米)即组合体的表面积是142.84平方厘米。
3计算下面圆柱的表面积和体积。
(单位:厘米)【答案】表面积:734.76平方厘米;体积:571.48立方厘米【分析】表面积=大圆直径是20厘米,小圆直径是6厘米的圆环面积×2+底面直径是20厘米,高是2厘米的圆柱的侧面积+底面直径是6厘米,高是2厘米的圆柱的侧面积;根据圆环的面积公式:面积=π×(大圆半径2-小圆半径2),圆柱的侧面积公式:侧面积=底面周长×高,代入数据,即可解答;体积=底面直径是20厘米,高是2厘米的圆柱的体积-底面直径是6厘米,高是2厘米的圆柱的体积,根据圆柱的体积公式:体积=底面积×高,代入数据,即可解答。
小升初经典题型—小学平面几何图形的十大解法

几何图形的十大解法(30例)一、分割法例1:将两个相等的长方形重合在一起,求组合图形的面积。
(单位:厘米)2例2:下列两个正方形边长分别为8厘米和5厘米,求阴影部分面积。
例3:左图中两个正方形的边长分别为8厘米和6厘米。
求阴影部分面积。
二、添辅助线例1:已知正方形边长4厘米,A、B、C、D是正方形边上的中点,P是任意一点。
求阴影部分面积。
CPD BA例2:将下图平行四边形分成三角形和梯形两部分,它们面积相差40平方厘米,平行四边形底20.4厘米,高8厘米。
梯形下底是多少厘米?例3:平行四边形的面积是48平方厘米,BC分别是A 这个平行四边形相邻两条边的中点,连接A、B B、C得到4个三角形。
求阴影部分的面积。
C三、倍比法例1: A B 已知:OC=2AO,S ABO=2㎡,求梯形ABCDO 的面积。
D C例2:7.5 已知:S阴=8.75㎡,求下图梯形的面积。
2.5例3: A 下图AB是AD的3倍,AC是AE的5倍,D E 那么三角形ABC的面积是三角形ADE的多少倍?B C四、割补平移例1: A B 已知:S阴=20㎡, EF为中位线E F 求梯形ABCD的面积。
D C例2:10 求左图面积(单位:厘米)5510例3:把一个长方形的长和宽分别增加2厘米,面积增加24平方厘米。
求原长方形的周长。
2五、等量代换例已知:AB平行于EC,求阴影部分面积。
8E 10 D(单位:m)例2:下图两个正方形边长分别是6分米、4分米。
求阴影部分面积。
例3:已知三角形ABC的面积等于三角形AED的面积(形状大小都相同),它们重叠在一起,比较三角形BDF和三角形CEF的面积大小。
()A A 三角形DBF大B三角形CEF大D C C两个三角形一样大D无法比较B FE六、等腰直角三角形例1:已知长方形周长为22厘米,长7 厘米,求阴影部分面积。
45°例2:已知下列两个等腰直角三角形,直角边分别是10厘米和6厘米。
小升初专题之组合图形面积

一、几种常用求组合图形面积的方法: 1、旋转的思想方法。
将所给图形中的某一部分绕一个固定点旋转一定(或适当)的角度,变为较明显的简单而又直观的图形。
2.移动的思想方法。
A .点的移动:将图中的某一点看作一个“动点”沿直线移动,使原来分着的空白部分合并在一起变成一个简单明了的图形。
B .面的移动:将所给图形中的某个图形沿直线上下左右移动,把复杂的图形转化成简单的图形,使原来面积不等变成相等。
3.翻折的思想方法。
将所给图形的某一部分以某一直线为对称轴翻折,使原来复杂的图形变为直观图形。
【例题讲解】例1、如图,长方形的长是8厘米、宽是6厘米、A 和B 是宽的中点,求长方形内阴影部分的面积。
例2、下面的长方形是一块草坪,中间有两条宽1米的走道。
求植草的面积。
BB例3、下图是一块长方形草地。
长方形长16米、宽10米,中间有两条宽2米的道路,两条都是平行四边形。
求有草部分的面积。
【知识反馈】1、求图中阴影部分的面积。
(单位:厘米)2、梯形草坪(如下图),有一平形四边形人行道,求人行道的面积是多少平方米?80米50米16102203、一条白色的正方形手帕,它的边长是18厘米,手帕上横竖各有二道红条,如下图阴影所示部分,红条宽都是2厘米。
问:这条手帕白色部分的面积是多少?7、下图是一块长方形草地。
长方形长30米、宽15米,中间有两条宽3米的道路,一条是长方形,另一条是平行四边形。
求有草部分的面积。
8、如图,ABCD 是直角梯形,AD=4cm,BC=6cm,AB=3cm 求阴影部分的面积和。
(单位:厘米)3033DA 439、下图中,边长为10和15的两个正方形并放在一起,求三角形ABC (阴影部分)的面积。
(小升初培优讲义)专题27 组合图形的面积计算-六年级一轮复习(知识点精讲+达标检测)(教师版)
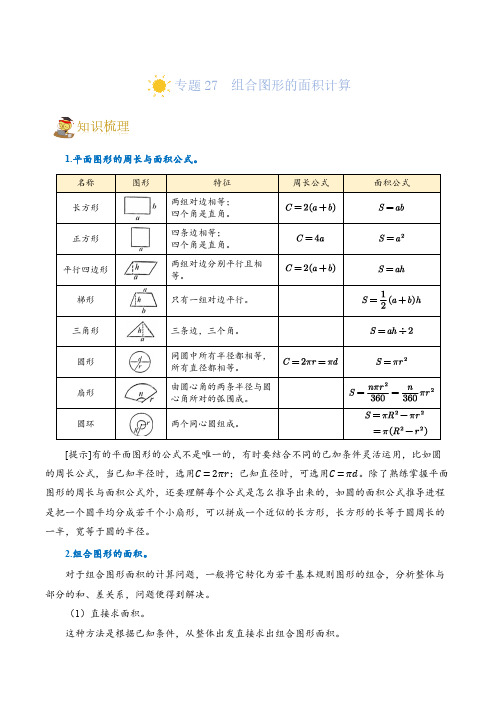
专题27 组合图形的面积计算知识梳理1.平面图形的周长与面积公式。
[提示]有的平面图形的公式不是唯一的,有时要结合不同的已加条件灵活运用,比如圆的周长公式,当已知半径时,选用C=2πr;已知直径时,可选用C=πd。
除了熟练掌握平面图形的周长与面积公式外,还要理解每个公式是怎么推导出来的,如圆的面积公式推导进程是把一个圆平均分成若干个小扇形,可以拼成一个近似的长方形,长方形的长等于圆周长的一半,宽等于圆的半径。
2.组合图形的面积。
对于组合图形面积的计算问题,一般将它转化为若干基本规则图形的组合,分析整体与部分的和、差关系,问题便得到解决。
(1)直接求面积。
这种方法是根据已知条件,从整体出发直接求出组合图形面积。
(2)相加、相减求面积。
这种方法是将组合图形分解转化成几个基本规则图形,分别计算它们的面积,然后相加或相减求出该图形的面积。
(3)等量代换求面积。
一个图形可以用与它相等的另一个图形替换,如果甲、乙大小相等,那么求出乙的大小,就知道甲的大小;两个图形同时增加或减少相同的面积,它们的差不变。
(4)借助辅助线求面积。
这种方法是根据具体情况在图形中添一条或若干条辅助线,使不规则图形转化成若干个基本规则图形,然后再采用相加、相减法求面积。
【例1】计算右面图形的面积。
(单位:厘米)【点拨分析】 求梯形的面积,必须知道上底、下底和高这三个条件。
从圆中可以看出,此梯形的高是6厘米,那么解题的关键就是求出上底和下底的长或求出它们的长度和。
在左边的直角三角形中,一个内角是45°,可知它是等腰直角三角形,所以高的左边部分与下底相等。
同样,右边的三角形也是一个等腰直角三角形,所以梯形的上底和高的右边部分相等。
这样就可推和梯形上、下底的长度和就是梯形高的长度6厘米。
【答 案】 6×6÷2=18(平方厘米)例题精讲1.计算下面图形的面积。
(单位:厘米)2.如图,长方形的面积是45平方米,求阴影部分的面积。
【小升初】小学数学《平面图形的测量专题课程》含答案
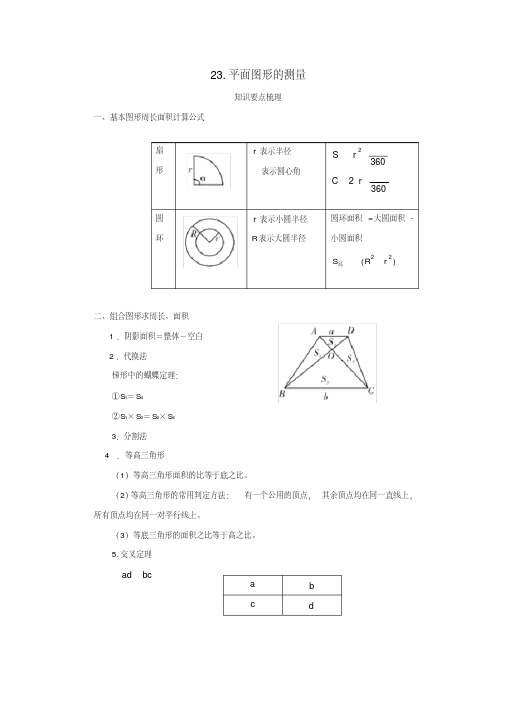
一、基本图形周长面积计算公式
知识要点梳理
扇
r 表示半径
S r2
360
形
表示圆心角
C 2r 360
圆
r 表示小圆半径
圆环面积 =大圆面积 -
环
R 表示大圆半径
小圆面积
S环
(R2 r 2 )
二、组合图形求周长、面积
1 .阴影面积=整体-空白
2 .代换法
梯形中的蝴蝶定理:
①S1= S4
小相同的小长方形,则图中阴影部分的面积是(
)。
3 .(西安高新某中入学 )某小区准备在长方形地块上种植花草,设
计图纸如图, BD、 CF 将长方形 ABCD分成四块,红色三角形面积是 8
平方厘米,黄色三角形面积是 12 平方厘米,问绿色四边形面积是(
)平方厘米。
4 .(江西某师大附中入学 )三角形 ABC的面积是 21 平方厘米,点
别等于大、小正方形的边长) ,则二者的面积相等,分别去掉公共部分(三角形
CFH),
那么剩余的部分的面积, 仍然相等, 即三角形 BCH和三角形 HFD的面积相等, 于是阴影
部分的面积就变成了大正方形的面积的一半,据此代入数据 100÷ 2=50(平方厘米)
答:三角形 BFD的面积为 50 平方厘米。
23.平图形的测量 25.12 3.12.56 3.14 0.86
二、 1.C B 2.C
三、 1. 【解析】阴影部分面积 =梯形 ABCD的面积 =(8-3
+8)
×5÷ 2=32.5
答: 阴影部分面积为 32.5 。
2. 【解析】阴影部分面积 =(16-2) ×(10-3)=98
( 米2) 答: 小草覆盖的面积是 98 平方米。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
组合图形1、求下列组合图形阴影部分的面积。
2、①求它的周长和面积。
(单位:厘米)②圆的周长是18.84cm,求阴影部分面积。
③长方形的面积和圆的面积相等,已知圆④求直角三角形中阴影部分的面积。
的半径是3cm,求阴影部分的周长和面积。
(单位:分米)
⑤下图中长方形长6cm,宽4cm,已知阴影⑥图中阴影①比阴影②面积小48平方厘米,
①比阴影②面积少3cm2,求EC的长。
⑦平行四边形的面积是30cm2,⑧一个圆的半径是4cm,求阴影部分面积。
求阴影部分的面积。
⑨已知AB=8cm,AD=12cm,三角形ABE和三角形ADF的面积,各占长方形ABCD的1/3,求三角形AEF的面积。
⑩梯形上底8cm,下底16cm,阴影⑾求阴影部分面积。
(单位:cm)
部分面积64cm2,求梯形面积。
⑿梯形面积是48平方厘米,阴影部分比空白⒀阴影部分比空白部分大6cm2,求S阴。
部分少12平方厘米,求阴影部分面积。
一、求出阴影部分面积:(6分)。
8
4 8m
4m
4、下图小正方形的边长分别是9厘米和5厘米,求阴影部分的面积(10分)
16、下图中阴影部分的面积是( )平方厘米。
25、如图(3),有两个边长是2厘米的正方形,其中一个正方形的一个顶点在另一个的中心上,并且两个涂色的三角形的面积相等。
问两个正方形不重合的部分面积的和是多少?
图(3)
20 20
A B
O
2、右图中阴影部分的面积为(单位:厘米)。
如图,等腰直角三角形ABC的面积是8平方厘米。
求阴影部分的面积。
(8分)
22. 求阴影部分的面积。
(单位:厘米)
D
A
C
450
6
3
5 5 4 4
1、求右图中阴影部分面积(单位:厘米)。
1. 下图是由正方形和半圆形组成的图形,其中P 点为半圆周的中点,Q 点为正方形一边的中点,
求阴影部分面积。
(单位:厘米)
1、下图中三角形的面积等于梯形的面积,求五边形的面积。
(单位:厘米)
16、下图中阴影部分的面积是( )平方厘米。
11、如图:阴影三角形的面积是 。
12、用一块面积为36平方厘米的圆形铝板下料,如图,裁出7个同样大小的圆铝板,
则余下的边角料的总面积是 平方厘米。
6
6
6
6
第11题
第12题
21、如图:直角梯形ABCD 的高AB 为10厘米,△AEO 与△BEO 的面积分别 为12平方厘米、18平方厘米,求梯形ABCD 的面积。
1、如图,长方形中,长和宽分别是6厘米和4厘米,阴影部分的面积和是10平方厘米,求四边形ABCD 的面积。
(1)如图所示是两个相同的直角梯形重叠在一起,求阴影部分的面积。
(单位:厘米)
A E
B D
C O H A E B C
D G F
1.求下图中阴影部分的面积(长度单位:厘米)
28、已知圆面积与长方形的面积相等(如下图),圆的周长是6.28厘米,求长方形的长。
