空间向量与立体几何教师版
空间向量1(教师)

第三章 空间向量与立体几何3.1 空间向量及其运算 3.1.1 空间向量及其加减法【考点同步解读】1.理解空间向量概念及其运算性质,掌握空间向量的几何表示法和字母表示法. 2.能够结合图形说明空间向量加减法及其运算律. 考点1:空间向量基本概念及理解例1:给出下列命题:①若空间向量a ,b 满足|a |=|b |,则a =b ;②若空间向量m ,n ,p 满足m =n ,n =p ,则m =p ; ③零向量没有方向;④若两个空间向量相等,则它们的起点相同,终点也相同. 其中假命题的个数是( ).A .1B .2C .3D .4正解:模相等的两个向量不一定相等,①错;|m |=|n |,|n |=|p |,所以|m |=|p |,又m 与n 同向,n 与p 同向,从而m 与p 同向,所以m =p ,②对;零向量方向任意,但并不是没有方向,③错;④错.C正解依据:(1)空间中的单位向量、向量的模、相等向量、相反向量等概念和平面向量中对应的概念完全一样.(2)两个向量的模相等,只是它们的长度相等,但它们的方向不一定相同. 考点2:空间向量加减法及运算律例2.如图,在正方体ABCD -A 1B 1C 1D 1中,M 、N 分别为AB 、B 1C的中点.用AB →、AD →、AA 1→表示向量MN →,则MN →=________. 正解:解析 MN →=MB →+BC →+CN →=12AB →+AD →+12(CB →+BB 1→) =12AB →+AD →+12(-AD →+AA 1→) =12AB →+12AD →+12AA 1→. 正解依据:(1)掌握好向量加、减法的三角形法则是解决这类问题的关键,灵活应用相反向量及两向量的和、差,可使这类题迅速获解,另外需注意零向量的书写要规范.(2)利用三角形法则和平行四边形法则进行向量的加法运算时,务必要注意和向量、差向量的方向,必要时可采用空间向量的自由平移获得更准确的结果. 考点3:对数函数的性质例4.已知点G 是△ABC 的重心,O 是空间任意一点,若OA →+OB →+OC →=λOG →,求λ的值. 正解:解 连结CG 并延长交AB 于D , 则D 为AB 中点,且CG =2GD ,∴OA →+OB →+OC →=OG →+GA →+OG →+GB →+OG →+GC →=3OG →+GA →+GB →+GC → =3OG →+2GD →+GC →=3OG →(→)-GC →+GC →=3OG →. ∴λ=3.正解依据:(1)根据向量加减运算的法则进行化简,注意向量的起点、终点;(2)几何与向量结合及数形结合是常见的数学方法. 【易错题纠正案】(不少于3道例题)例1 下列说法正确的是( A ).A .向量AB 与BA的长度相等B .将空间中所有的单位向量平移到同一起点,则它们的终点构成一个圆C .空间向量就是空间中的一条有向线段D .不相等的两个空间向量的模必不相等例2 在空间四边形ABCD 中,2AB +CA +BC -AD +BD=__________.答案:0例3 已知空间四边形ABCD ,连结,AC BD ,设,M G 分别是,BC CD 的中点,化简下列各表达式,并标出化简结果向量:(1)AB BC CD ++;(2)1()2AB BD BC ++ ;(3)1()2AG AB AC -+ .正解:解:如图,(1)AB BC CD AC CD AD ++=+=;(2)111()222AB BD BC AB BC BD ++=++AB BM MG AG =++= ; (3)1()2AG AB AC AG AM MG -+=-= .【高考试题链接】例1 (2011·上海高考理科·T17) 设12345,,,,A A A A A 是平面上给定的5个不同点,则使12345MA MA MA MA MA ++++ 0=成立的点M 的个数为( )(A )0. (B )1. (C )5. (D )10.正解:在平面中我们知道“三角形ABC 的重心G 满足:0GA GB GC ++=”则此题就能很快的答出,点M 即为这5个点的重心,即点M 只有一个点。
空间向量在立体几何中的应用教案(教师使用)

空间向量在立体几何中的应用(一)授课时间:2014年5月11日第7节课 授课班级:高二(9)班 授课教师:高志华教学目标 1、知识与技能(1) 进一步理解向量垂直的充要条件; (2)利用向量法证明线线、线面垂直;(3)利用向量解决立体几何问题,培养学生数形结合的思想方法; 2、过程与方法通过学生对空间几何图形的认识,建立恰当的空间直角坐标系,利用向量的坐标将几何问题代数化,提高学生应用知识的能力。
3、情感态度与价值观通过空间向量在立体几何中的应用,让学生感受数学、体会数学的美感, 从而激发学数学、用数学的热情。
教学重点建立恰当的空间直角坐标系,用向量法证明线线、线面垂直。
教学难点、关键建立恰当的空间直角坐标系,直线的方向向量; 正确写出空间向量的坐标。
教学方法启发式教学、讲练结合 教学媒体ppt 课件学法指导交流指导,渗透指导. 课型 新授课教学过程一、知识的复习与引人 自主学习1.若OP =x i +y j +z k ,那么(x ,y ,z )叫做向量OP 的坐标,也叫点P 的坐标.2. 如图,已知长方体D C B A ABCD ''''-的边长为AB=2,AD=2,1AA '=.以这个长方体的顶点A 为坐标原点,射线A A AD AB ',,分别为x 轴、y 轴、z 轴的正半轴,建立空间直角坐标系,试求长方体各个顶点及A C '中点G 的坐标.3.设a =(x 1,y 1,z 1),b =(x 2,y 2,z 2),那么b a ±=(x 1±x 2,y 1±y 2, ), a ⊥b ⇔ b a ∙=x 1x 2+y 1y 2+ =0.4.设M 1(x 1,y 1,z 1),M 2(x 2,y 2,z 2),则 12M M =(2121,x x y y --, ) [探究]1.直线的方向向量:直线的方向向量是指和这条直线平行(或重合)的非零向量,一条直线的方向向量有 个. 2.空间位置关系的向量表示位置关系向量表示直线l 1的方向向量为1l , 直线l 2的方向向量为2l , 直线a 的方向向量为a , 直线b 的方向向量为b .l 1⊥ l 21l ⊥2l ⇔l 1⊥αl 1⊥a ,l 1⊥b, ,a b αα⊂⊂,a ∩b=o ,[合作探究]二、新授课:利用空间向量证明线线垂直、线面垂直例1、如图,在棱长为2的正方体ABCD-A1B1C1D1中,M为BC的中点,N为AB的中点,P为BB1的中点.(Ⅰ)求证:BD1⊥B1C;(Ⅱ)求证:BD1⊥平面MNP.设计意图:使学生明确空间向量在证明线线垂直、线面垂直中的作用。
20学而思教材讲义高二数学秋季秋季 第12讲 空间向量与立体几何综合 教师版

当前形势空间向量与立体几何在近五年北京卷(理)考查14分高考要求内容要求层次具体要求A B C证明平行与垂直√运用向量的数量积证明直线与直线的平行与垂直直线的方向向量√灵活掌握共线向量性质平面的法向量√利用向量的数量积来计算平面的法向量线、面位置关系√运用空间向量的性质判断线面之间的平行与垂直线线、线面、面面的夹角√运用空间向量的数量积计算线线角线面角面面角北京高考解读2009年2010年(新课标)2011年(新课标)2012年(新课标)2013年(新课标)第16题14分第16题14分第16题14分第16题14分第17题14分新课标剖析满分晋级第12讲空间向量与立体几何综合立体几何9级点面距离与动点问题立体几何10级空间向量与立体几何综合立体几何11级折叠问题与最值问题考点1:空间向量的运算1.向量的加法、减法与数乘向量运算与平面向量类似; 2.空间向量的基本定理:共线向量定理:对空间两个向量a ,b (0b ≠),a b ∥的充要条件是存在实数x ,使a xb =.共面向量定理:如果两个向量a ,b 不共线,则向量c 与向量a ,b 共面的充要条件是,存在唯一的一对实数x ,y ,使c xa yb =+. 空间向量分解定理:如果三个向量a ,b ,c 不共面,那么对空间任一向量p ,存在唯一一个有序实数组x ,y ,z ,使p xa yb zc =++.表达式xa yb zc ++,叫做向量a ,b ,c 的线性表示式或线性组合.上述定理中,a ,b ,c 叫做空间的一个基底,记作{}a b c ,,,其中a b c ,,都叫做基向量. 由此定理知,空间任意三个不共面的向量都可以构成空间的一个基底. 四点共面定理:设点P 满足等式:OP xOA yOB zOC =++,其中x y z ∈R ,,,则P A B C ,,,四点共面的充要条件是1x y z ++=.<教师备案>四点共面定理的证明.充分性即证:若1x y z ++=,则P A B C ,,,四点共面,必要性即证:若P A B C ,,,四点共面,则有1x y z ++=. 先证充分性:∵1x y z ++=, ∴1z x y =--,∴(1)OP xOA yOB x y OC =++--()()x OA OC y OB OC OC =-+-+xCA yCB OC =++. 即CP xCA yCB =+,由共面向量定理知P A B C ,,,四点共面. 再证必要性:设x y z k ++=, 由条件OP xOA yOB zOC =++, 得:()OP xOA yOB k x y OC =++--()()x OA OC y OB OC kOC =-+-+()()(1)x OA OC y OB OC OC k OC =-+-++-,∴()()(1)OP OC x OA OC y OB OC k OC -=-+-+-, 即(1)CP xCA yCB k OC =++-,∵P A B C ,,,四点共面,而点O 为空间任意一点, ∴只能1k =,即1x y z ++=. 综上知,命题成立.知识点睛12.1空间向量的概念与运算3.两个向量的夹角:已知两个非零向量a b ,,在空间任取一点O ,作OA a =,OB b =,则AOB ∠叫做向量a 与b 的夹角,记作a b 〈〉,.通常规定0πa b 〈〉≤,≤. 在这个规定下,两个向量的夹角就被唯一确定了,并且a b b a 〈〉=〈〉,,. 如果90a b 〈〉=︒,,则称a 与b 互相垂直,记作a b ⊥. 4.两个向量的数量积:已知空间两个向量a ,b ,定义它们的数量积(或内积)为:cos a b a b a b ⋅=〈〉, 空间两个向量的数量积具有如下性质: ⑴ 0ab a b ⇔⋅=;⑵ 2a a a =⋅;⑶ ab a b ⋅≤.空间两个向量的数量积满足如下运算律:⑴ ()()a b a b λλ⋅=⋅;⑵ a b b a ⋅=⋅;⑶ ()a b c a c b c +⋅=⋅+⋅.<教师备案>空间向量的运算法则与平面向量大致一样,只不过是从二维平面转到三维空间.空间向量主要是用来解决立体几何问题.空间向量在暑期没有预习课程,只有这一讲同步讲义.提高班学案1【铺1】 ⑴ 给出下列命题:①两个空间向量相等,则它们起点相同,终点也相同;②若空间向量a ,b ,满足a b =,则a b =; ③在正方体1111ABCD A B C D -中,必有11AC A C =;④若空间向量m ,n ,p 满足m n =,n p =,则m p =; ⑤空间中任意两个单位向量必相等. 其中不正确的命题的个数是( )A .1B .2C .3D .4 ⑵ 如图所示,在平行六面体1111ABCD A B C D -中,M 为AC 与BD的交点,若11A B a =,11A D b =,1A A c =,则下列向量中与1B M 相等的是( ) A .111222a b c -++ B .111222a b c ++C .1122a b c -+D .1122a b c -++⑶ 设1e ,2e 是空间两个不共线的向量,已知122AB e ke =+,123CB e e =+,122CD e e =-,且A B D ,,三点共线,则k =__. ⑷ 若ABC △中,90C ∠=︒,()123A k -,,,()210B -,,,()402C k -,,,则k =__.【解析】 ⑴ C当两向量的起点相同,终点也相同时,这两个向量必相等;但两个向量相等,却不一定有起点相同,终点相同,故①错;根据向量相等的定义,不仅模相等,而且方向相同,故②经典精讲c b a MD 1C 1B 1A 1DCBA错;根据正方体1111ABCD A B C D -中,向量AC 与11A C 的方向相同,模也相等,应有11AC A C =,故③正确;命题④显然正确;空间中任意两个单位向量模均为1,但方向不一定相同,故不一定相等,故⑤错. ⑵ D∵()12AM AB AD =+,∴()12AM a b =+,又∵11B A a =-,1A A c =,1111B M B A A A AM =++,∴()1111222B M a c a b a b c =-+++=-++.⑶ 8-∵123CB e e =+,122CD e e =-,∴()()121212234BD CD CB e e e e e e =-=--+=-,∵A B D ,,三点共线,∴AB xBD =,∴()121212244e ke x e e xe xe +=-=-,∵1e ,2e 是不共线向量,∴24xk x =⎧⎨=-⎩,∴8k =-. ⑷ 10±()612CB k =-,,,()32CA k =--,,,则()()()263222200CB CA k k k ⋅=-⨯-++⨯-=-+=,∴10k =±.【例1】 ⑴已知A B C ,,三点不共线,对平面ABC 外的任一点O ,下列条件中能确定点M 与点 A B C ,,一定共面的是( )A .OM OA OB OC =++ B.2OM OA OB OC =--C.1123OM OA OB OC =++ D.111333OM OA OB OC =++⑵设a b ⊥,π3a c =,,π6b c =,,且1a =,2b =,3c =,则a b c ++=( )A .1763+ B.1743+ C.63D.932⑶若()213a x =,,,()129b y =-,,,如果a 与b 为共线向量,则( ) A .11x y ==,B.1122x y ==-, C.1362x y ==-, D.1362x y =-=,⑷已知空间三点()111A ,,,()104B -,,,()223C -,,,则向量AB 与CA 的夹角θ的大小是_______.【解析】 ⑴ D由向量四点共面的充要条件,只有D 选项中OA OB OC ,,系数和为1,所以选D ⑵ A∵2222ππ2221496cos 12cos 176336a b c a b c a b a c b c ++=+++⋅+⋅+⋅=++++=+∴1763a b c ++=+;⑶ C∵()213a x =,,与()129b y =-,,共线,故有213129x y ==-,∴1362x y ==-,.⑷ 120︒()213AB =--,,,()132CA =--,,,()()()()2113321cos 21414AB CA -⨯-+-⨯+⨯-==-⋅,,∴120AB CA θ==︒,.【例2】 ⑴如图所示,平行六面体1111ABCD A B C D -中,E ,F 分别在1B B 和1D D 上,且113BE BB =,123DF DD =,①证明1A E C F ,,,四点共面;②若1EF xAB y AD z AA =++,求x y z ++. F E ABC DA 1B 1C 1D 1⑵已知空间四边形OABC 中,AOB BOC AOC ∠=∠=∠,且OA OB OC ==,M N ,分别是OA BC ,的中点,G 是MN 的中点,求证:OG BC ⊥.【解析】 ⑴①∵11111233AC AB AD AA AB AD AA AA =++=+++111233AB AA AD AA ⎛⎫⎛⎫=+++ ⎪ ⎪⎝⎭⎝⎭AB BE AD DF =+++AE AF =+,∴1A E C F ,,,四点共面 ②()EF AF AE AD DF AB BE =-=+-+112133AD DD AB BB =+--113AB AD AA =-++,∴1113x y z =-==,,,∴13x y z ++=.⑵ 如图,连接ON ,设AOB BOC AOC θ∠=∠=∠=,OA a =,OB b =,OC c =,则a b c ==,又()12OG OM ON =+()111222OA OB OC ⎡⎤=++⎢⎥⎣⎦()14a b c =++,BC c b =-,所以()()14OG BC a b c c b ⋅=++⋅- ()2214a c ab bc b c b c =⋅-⋅+⋅-+-⋅()22221cos cos 04a a a a θθ=--+=, 所以OG BC ⊥.12.2平行垂直问题GN MO CBA考点2:用空间向量证明平行垂直1.直线的方向向量与平面的法向量的概念; 2.线、面平行与垂直:(设直线12l l ,的方向向量分别为12v v ,,平面αβ,的法向量分别为12n n ,) ⑴线线的平行关系:1l ∥2l (或1l 与2l 重合)1v ⇔∥2v ;线面的平行关系:1l ∥α或1l α⊂⇔存在实数x y ,,使1v xm yn =+110v n ⇔⋅=(其中m n ,为平面α内的两个不共线的向量) 面面的平行关系:α∥β(α,β重合)⇔1n ∥2n ; ⑵线线垂直:12l l 12120v v v v ⇔⇔⋅=;⑶线面垂直:1l α⊥11v n ⇔∥;⑷面面垂直:12120n n n n αβ⇔⇔⋅=;<教师备案>上面的证明线、面平行或垂直的结论不是绝对的,有其它的等价条件,需要灵活运用.一般来讲,证明平行或垂直用纯粹的立体几何更简便,涉及到稍微复杂的求角度时,适合用空间向量无脑算.提高班学案2【铺1】如图,四棱锥P ABCD -中,PA ⊥底面ABCD ,PC AD ⊥.底面ABCD 为梯形,AB DC ∥,AB BC ⊥.PA AB BC ==,点E 在棱PB 上,且2PE EB =.求证:PD ∥平面EAC .EDCBAP【解析】 证法一:以A 为原点、AB 、AP 所在直线分别为y 轴、z 轴,建立如图所示的空间直角坐标系.设PA AB BC a ===,则(000)A ,,,(00)B a ,,,(0)C a a ,,,(00)P a ,,,2033a a E ⎛⎫ ⎪⎝⎭,,.设(0)D a y ,,,则()PC a a a =-,,,(0)AD a y =,,, ∵PC AD ⊥,∴20PC AD a ay ⋅=+=,解得y a =-; 则有(0)D a a -,,,()PD a a a =--,,, 经典精讲知识点睛z yPEB A2033a a EA ⎛⎫=-- ⎪⎝⎭,,,33a a EC a ⎛⎫=- ⎪⎝⎭,,;∵2PD EA EC =+,PD ⊄平面EAC ,∴PD ∥平面EAC .(或者求出平面EAC 的法向量(112)n =-,,得出PD 与n 垂直也可证明结论) 证法二:AB BC =,AB BC ⊥,∴ABC △是等腰直角三角形;PA ⊥平面ABCD ⇒PA AD ⊥,又AD PC ⊥,∴AD ⊥平面PAC ;∴AD AC ⊥.又AB DC ∥,∴DAC △也是等腰直角三角形; ∴22DC AC AB ==.连接BD ,交AC 于点M ,则2DM DC MB AB==. 在BPD △中,2PE DMEB MB==,∴PD EM ∥.又PD ⊄平面EAC ,EM ⊂平面EAC , ∴PD ∥平面EAC .【例3】如图,四棱锥P ABCD -的底面是正方形,PA ⊥底面ABCD ,2PA =,45PDA ∠=︒,点E 、F 分别为棱AB 、PD 的中点.⑴求证:AF ∥平面PCE ;⑵求证:平面PCE ⊥平面PCD ;【追问】PC 上是否存在一点H ,使得AC ⊥面EFH ?【解析】 以A 为坐标原点,建立如图所示的坐标系A xyz -.⑴ ()002P ,,,()020D ,,,()200B ,,,()220C ,,, 则()011F ,,,()100E ,,, 于是,()011AF =,,,()102EP =-,,,()120EC =,, 因为()12AF EP EC =+,所以AF 与EP EC ,共面. 又AF ⊄面ECP ,所以AF ∥平面PCE .⑵ 因为()022PD =-,,,所以0AF PD ⋅=,即AF PD ⊥; 又()200DC =,,,所以0AF DC ⋅=,即AF DC ⊥. 于是AF ⊥面PCD ,由⑴AF ∥平面PCE , 则面PCE ⊥面PCD .【追问】设22H x x ⎛⎫- ⎪ ⎪⎝⎭,,,则()220AC =,,,()111EF =-,,,212EH x x ⎛⎫=- ⎪ ⎪⎝⎭,,, 易知0AC EF ⋅=,由()121202AC EH x x x ⋅=-+=⇒=.于是点112222H ⎛ ⎝⎭,,满足AC ⊥面EFH . MPEBA DP FEDBAHz yx P FE DCBAMz yxPED CB A 【点评】证明线面平行问题,可以有三个途径,一是在平面PCE 内找一向量与AF 共线;二是说明AF能用平面PCE 内的两不共线向量线性表示,三是证明AF 与平面的法向量垂直.证明面面垂直,也可以转化证明它们的法向量垂直,或者其中一个面的法向量平行于另一个面.尖子班学案1【拓2】 如图,正方形ABCD 所在平面与平面四边形ABEF 所在平面互相垂直,ABE △是等腰直角三角形,AB AE =,FA FE =,45AEF ∠=︒. ⑴求证:EF ⊥平面BCE ;⑵设线段CD 的中点为P ,在直线AE 上是否存在一点M ,使得∥PM 平面BCE ?若存在,请指出点M 的位置,并证明你的结论;若不存在,请说明理由;PFEDCBA【解析】 ⑴ ∵ABE △为等腰直角三角形,AB AE =,∴AE AB ⊥.又∵面ABEF ⊥平面ABCD ,AE ⊂平面ABEF ,平面ABEF 平面ABCD AB =,∴AE ⊥平面ABCD .∴AE AD ⊥.因此,AD ,AB ,AE 两两垂直,以A 为坐标原点,建立如图所示的直角坐标系A xyz -. 设1AB =,则1AE =,(010)B ,,,(100)D ,,,(001)E ,,,(110)C ,,.∵FA FE =,45AEF ∠=︒,∴90AFE ∠=︒.从而,11022F ⎛⎫- ⎪⎝⎭,,.∴11022EF ⎛⎫=-- ⎪⎝⎭,,,(011)BE =-,,,(100)BC =,,.110022EF BE ⋅=+-=,0EF BC ⋅=.∴EF BE ⊥,EF BC ⊥.∵BE ⊂平面BCE ,BC ⊂平面BCE ,BC BE B =,∴EF ⊥平面BCE .⑵ 存在点M ,当M 为AE 中点时,PM ∥平面BCE .设(00)M m ,,,1102P ⎛⎫ ⎪⎝⎭,,.从而112,,PM m ⎛⎫=-- ⎪⎝⎭, 由11111002222,,,,PM EF m m ⎛⎫⎛⎫⋅=--⋅--=⇒= ⎪ ⎪⎝⎭⎝⎭,即M 为AE 中点时,PM FE ⊥,又EF ⊥平面BCE ,直线PM 不在平面BCE 内, 故PM ∥平面BCE .目标班学案1【拓3】 如图,四棱锥S ABCD -的底面是正方形,每条侧棱的长都是底面边长的2倍,P 为侧棱SD 上的点. ⑴ 求证:AC SD ⊥;⑵ 若SD ⊥平面PAC ,侧棱SC 上是否存在一点E ,使得BE ∥平面PAC .若存在,求:SE EC 的值;若不存在,试说明理由.【解析】 ⑴ 连BD ,设AC 交BD 于O ,连接SO ,由题意知SO ⊥平面ABCD .以O 为坐标原点,OB ,OC ,OS 分别为x 轴、y 轴、z 轴正方向,建立坐标系O xyz -如图.设底面边长为a , 则高()222622SO aa a ⎛⎫=-= ⎪ ⎪⎝⎭. 于是600S a ⎛⎫ ⎪ ⎪⎝⎭,,,200D a ⎛⎫- ⎪ ⎪⎝⎭,,,200C a ⎛⎫ ⎪ ⎪⎝⎭,,, 200OC a ⎛⎫= ⎪ ⎪⎝⎭,,,260SD a a ⎛⎫=-- ⎪ ⎪⎝⎭,,, 0OC SD ⋅=,故OC SD ⊥.从而AC SD ⊥.⑵ 在棱SC 上存在一点E 使BE ∥平面PAC .由题设知,260DS a a ⎛⎫= ⎪ ⎪⎝⎭,,是平面PAC 的一个法向量, 设CE tCS =,则由260CS a a ⎛⎫=- ⎪ ⎪⎝⎭,,,200B a ⎛⎫ ⎪ ⎪⎝⎭,,,220BC a a ⎛⎫=- ⎪ ⎪⎝⎭,,可得: ()2261BE BC CE BC tCS a a t at ⎛⎫=+=+=-- ⎪ ⎪⎝⎭,,. 而22661003BE DS a a a at t ⎛⎫⋅=⇔⨯-+⨯=⇔= ⎪ ⎪⎝⎭. 即当21SE EC =∶∶时,BE DS ⊥.而BE 不在平面PAC 内,故BE ∥平面PAC .考点3:用空间向量求异面直线所成角和点面距离12.3角度与距离问题OPC BA Sx y z EPDBA S1.设直线12l l ,的方向向量分别为12v v ,,则12l l ,所成角θ满足:121212cos cos v v v v v v θ⋅=〈〉=,,π02θ⎡⎤∈⎢⎥⎣⎦, 2.空间中的点面距离⑴体积法⑵空间向量法:定点A 到平面α的距离,可设平面α的法向量为n ,面α内一点B ,则点A 到平面α的距离为AB n n⋅<教师备案>空间两条直线所成角的范围是π02⎡⎤⎢⎥⎣⎦,,异面直线所成角的范围是π02⎛⎤⎥⎝⎦,,而两个向量之间的夹角范围是[]0π,,这些是求空间中两条直线所成角时需要注意的地方.尖子班学案2【铺2】如图,正四棱锥P ABCD -的底面边长与侧面棱长都是2,M 是PC 的中点.⑴ 求异面直线AD 和BM 所成角的大小. ⑵ 求异面直线AM 和PD 所成角的余弦值. 【解析】 ⑴ 解法一:∵AD BC ∥,∴AD 和BM 所成的角就是BC 和BM 所成的角; ∵PBC △是正三角形,∴30MBC ∠=︒; ∴AD 和BM 所成的角为30︒. 解法二:设P 在底面的射影为O ,由于P ABCD -为正四棱锥, 所以O 为底面正方形的中心;以O 点为原点,DA 方向为x 轴正方向,DC 方向为y 轴正方向,OP 为z 轴建立如图所示的空间直角坐标系O xyz -; 由于四棱锥侧面都是边长为2的正三角形, ∴斜高3PH =,2PO =;∴(110)A -,,,(110)B ,,,(110)C -,,,(110)D --,,,()002P ,,;∴11222M ⎛⎫- ⎪ ⎪⎝⎭,,,(200)AD =-,,,31222BM ⎛⎫=-- ⎪ ⎪⎝⎭,,; ∴3cos 23AD BM AD BM AD BM⋅===⋅,; 经典精讲知识点睛Oz yxMPD BAH AB CDPM1第12讲·提高-尖子-目标·教师版∴向量AD 与向量BM 所成的角为30︒,即直线AD 和BM 所成的角为30︒. ⑵ 由⑴解法二得()112PD =---,,,33222AM ⎛⎫=- ⎪ ⎪⎝⎭,,;∴5cos AM PD AM PD AM PD⋅==-⋅,; 而直线AM 和PD 所成角只能在0︒至90︒之间,∴直线AM 和PD 所成角的余弦值为5.【例4】如图,在四棱锥O ABCD -中,底面ABCD 是边长为1的菱形,π4ABC ∠=,OA ⊥底面ABCD ,2OA =,M 为OA 的中点,N 为BC的中点.⑴ 证明:直线MN ∥平面OCD ;⑵ 求异面直线AB 与MD 所成角的大小; ⑶ 求点B 到平面OCD 的距离.【解析】 作AP CD ⊥于点P ,如图,分别以AB 、AP 、AO 所在直线为x 、y 、z 轴建立空间直角坐标系.()000A ,,,()100B ,,,220D ⎛⎫ ⎪ ⎪⎝⎭,,()002O ,,,()001M ,,,200P ⎛⎫ ⎪ ⎪⎝⎭,,2210C ⎛⎫- ⎪ ⎪⎝⎭,,2210N ⎛⎫- ⎪ ⎪⎝⎭,. ⑴ 2211MN ⎛⎫=-- ⎪ ⎪⎝⎭,,202OP ⎛⎫=- ⎪ ⎪⎝⎭,,222OD ⎛⎫=-- ⎪ ⎪⎝⎭,. 设平面OCD 的法向量为()n x y z =,,, 则00n OP n OD ⋅=⋅=,, 即2202220z y z ⎧-=⎪⎨⎪-=⎪⎩,,取2z =解得(042n =,,.∵(22110420MN n ⎛⎫⋅=--⋅= ⎪ ⎪⎝⎭,,,, ∴MN ∥平面OCD . ⑵ 设AB 与MD 所成的角为θ,∵()221001AB MD ⎛⎫==-- ⎪ ⎪⎝⎭,,,,, ∴1cos 2AB MDAB MD θ⋅==⋅,∴π3θ=,即AB 与MD 所成角的大小为π3.PNM O D CB AxyzNM ODCBA24 第12讲·提高-尖子-目标·教师版⑶ 设点B 到平面OCD 的距离为d ,则d 为OB 在平面OCD 的法向量(042n =,,上的投影的绝对值;由()102OB =-,,,得23OB n d n⋅==, 所以点B 到平面OCD 的距离为23.目标班学案2【拓3】 如图,已知棱锥S ABCD -的底面是边长为4的正方形,S 在底面的射影O 落在正方形ABCD内,且O 到AB 、AD 的距离分别是2、1.⑴ 求证:AB SC ⋅是定值;⑵ 已知P 是SC 的中点,且3SO =,问在棱SA 上是否存在一点Q ,使异面直线OP 与BQ 所成的角为90︒?若不存在,说明原因;若存在,则求AQ 的长.O SPCD 解析图xyzOD ABCPS【解析】 ⑴ 以点O 为坐标原点,OS 所在的直线为z 轴,过点O 且与AD 平行的直线为x 轴,过点O 且与AB 平行的直线为y 轴,建立如图的空间直角坐标系. 设高OS h =,则由已知得()()()000210230O A B -,,,,,,,,,()()23000C S h -,,,,,,()()04023AB SC h ==--,,,,,,则()()0243012AB SC h ⋅=⨯-+⨯+⨯-=,即AB SC ⋅是定值.⑵ 在棱SA 上任取一点()000Q x y z ,,,使01AQ AS λλ=,≤≤.由已知得()3333003112222S P OP ⎛⎫⎛⎫-=- ⎪ ⎪⎝⎭⎝⎭,,,,,,,,,()213AS =-,,. 由AQ AS λ=得()()00021213x y z λ-+=-,,,,, 从而022x λ=-,01y λ=-,03z λ=,()00023BQ x y z =--,,. 假设OP BQ ⊥,则0OP BQ ⋅=,即()()0003323022x y z --+-+=, ∴()()392400122λλλλ+-+=∈,,,∴34λ=. 故在棱SA 上存在点119244Q ⎛⎫- ⎪⎝⎭,,,使OP BQ ⊥.1第12讲·提高-尖子-目标·教师版此时()22233321314444AQ AS ==-++=.考点4:用空间向量求线面角设直线l 的方向向量为v ,平面α的法向量为n ,则l 与α所成角θ满足: sin cos v nv n v nθ⋅=〈〉=,(π02θ⎡⎤∈⎢⎥⎣⎦,);<教师备案> 用空间向量求角度时很多都不是直接求的角度本身的三角函数值,而是相关联的其它值,需要注意根据角度的范围定出所求角度的具体值.【例5】如图,已知点P 在正方体1111ABCD A B C D -的对角线1BD 上,60PDA ∠=︒. ⑴ 求DP 与1CC 所成角的大小; ⑵ 求DP 与平面11AA D D 所成角的大小.【解析】 如图,以D 为原点,DA 为单位长建立空间直角坐标系D xyz -.则(100)DA =,,,1(001)CC =,,.连结BD ,11B D . 在平面11BB D D 中,延长DP 交11B D 于H . 设(1)(0)DH m m m =>,,, 由已知60DH DA 〈〉=︒,, 由cos DA DH DA DH DA DH ⋅=〈〉, 可得2221m m =+.解得2m =,所以221DH ⎛⎫= ⎪ ⎪⎝⎭,,. ⑴ 因为1220011222cos 12DH CC ⨯+⨯+⨯〈〉==⨯,, 所以145DH CC 〈〉=︒,. 即DP 与1CC 所成的角为45︒.⑵ 平面11AA D D 的一个法向量是(010)DC =,,. 因为220110122cos 212DH DC ⨯+⨯+⨯〈〉==⨯,, 所以60DH DC 〈〉=︒,. 可得DP 与平面11AA D D 所成的角为30︒.经典精讲知识点睛D 1C 1B 1A 1D C BAPP D 1C 1B 1A 1D CB AH x y z24 第12讲·提高-尖子-目标·教师版尖子班学案3【拓2】 如图,在棱长为1的正方体1111ABCD A B C D -中,P 是侧棱1CC 上的一点,且CP m =,⑴试确定m ,使得直线AP 与平面11BDD B 所成角的正切值为32 ⑵在线段11A C 上是否存在一个定点Q ,使得对任意的m ,1D Q 在平面1APD 上的射影垂直于AP ?并证明你的结论.【解析】 ⑴ 建立如图所示的空间直角坐标系,则()100A ,,,()110B ,,, ()01P m ,,,()010C ,,,()000D ,,,()1111B ,,,()1001D ,,,所以()110BD =--,,,()1001BB =,,,()11AP m =-,,,()110AC =-,,,又由0AC BD ⋅=,10AC BB ⋅=知AC 为平面11BB D D 的一个法向量,设AP 与平面11BB D D 所成的角为θ,则2πsin cos 222AP AC AP AC mθθ⋅⎛⎫=-==⎪⎝⎭⨯⨯+, ()223222132m =⨯++,解得13m =,故当13m =时,直线AP 与平面11BDD B 所成的角的正切值为32⑵若在11A C 上存在这样的点Q ,设此点的横坐标为x ,则()11Q x x -,,,()110D Q x x =-,,,依题意,对任意的m 要使1D Q 在平面1APD 上的射影垂直于AP ,等价于()1110102D Q AP AP D Q x x x ⊥⇔⋅=⇔-+-=⇔=,即Q 为11A C 的中点时,满足题设要求.目标班学案3【拓3】如图所示,在直三棱柱111ABC A B C -中,1AB BB =,D 为AC 的中点,1AC ⊥平面1A BD .⑴ 求证:11B C ⊥平面11ABB A ;⑵ 设E 是1CC 的中点,试求出1A E 与平面1A BD 所成角的正弦值.E A 1B 1C 1ABCD【解析】 ⑴ 连接1AB ,∵1AB B B =,∴四边形11ABB A 为正方形,∴11A B AB ⊥.yz Q PD 1C 1B 1A 1DCBAz EC 1B 1A 1AB C D A 1B 1C 1D 11第12讲·提高-尖子-目标·教师版又∵1AC ⊥面1A BD ,∴11AC A B ⊥,∴1A B ⊥面11AB C , ∴111A B B C ⊥.又111BB B C ⊥,∴11B C ⊥平面11ABB A . ⑵ 在矩形11ACC A 中,由11AC A D ⊥可知11~A AD ACC △△,则11112CC CC AC AA AD AC==,故12AC AA =,从而AB BC =. 建立如图的空间直角坐标系,不妨设2AB =, 则()200A ,,,()1202A ,,,()1022C ,,,()021E ,,, 可得()1222AC =-,,,()1221A E =--,,. 由题意可知1AC 即为平面1A BD 的一个法向量, 设1A E 与平面1A BD 所成的角为θ, 则1111113sin cos 233AC A E AC A E AC A Eθ⋅====⨯⨯,.考点5:用空间向量求二面角设平面αβ,的法向量分别为12n n ,,则αβ,所成的二面角θ满足:121212cos cos n n n n n n θ⋅=〈〉=,(θ为平面α,β所生成的二面角,[]0πθ∈,)<教师备案> 利用空间向量求二面角的办法就是分别求出二面角的两个面所在平面的法向量,然后通过两个平面的法向量的夹角得到二面角的大小,要注意结合实际图形判断所求角是锐角还是钝角.【例6】如图,在三棱锥P ABC -中,PA PB =,PA PB ⊥, AB BC ⊥,30BAC ∠=︒,平面PAB ⊥平面ABC .⑴ 求证:PA ⊥平面PBC ;⑵ 求二面角P AC B --的余弦值;⑶ 求异面直线AB 和PC 所成角的余弦值.【追问】在线段PC 上有一点E ,PE PC λ=,求λ的值,使得二面角C AB E --的大小为60︒?【解析】 在平面PAB 中作PO AB ⊥于点O ,∵平面PAB ⊥平面ABC ,∴PO ⊥平面ABC .过点O 作BC 的平行线,交AC 于点D .经典精讲知识点睛PBA24 第12讲·提高-尖子-目标·教师版如图,以O 为原点,直线OD OB OP ,,分别为x 轴, y 轴,z 轴,建立空间直角坐标系.设6PA PB ==.∵PA PB ⊥, ∴233AB PO BO AO ===. ∵30AB BC BAC ⊥∠=︒,, ∴tan302BC AB =⋅︒=.∴()000O ,,,()030A ,,()030B ,, ()230C ,,,(003P ,,,()100.D ,, ⑴ ∵(033PA =-,,()200BC =,,, ∴0PA BC ⋅=,∴PA BC ⊥. 又∵PA PB ⊥, ∴PA ⊥平面PBC .⑵ 由⑴知,(003OP =,,为平面ABC 的一个法向量,设()n x y z =,,为平面PAC 的一个法向量,∵()2230AC =,,则3302230n PA y z n AC x y ⎧⋅=-=⎪⎨⋅=+=⎪⎩,令1y =得,31x z ==-,则()311n =--,,, ∴35cos 35n OP n OP n OP⋅-===⨯⨯,由图象知,二面角P AC B --为锐角,故二面角P AC B --5. ⑶ ∵()(0230233AB PC ==,,,,-,∴30cos AB PC AB PC AB PC⋅〈〉==,, ∴异面直线AB 和PC 30. 【追问】由PE PC λ=,可得点((2313E λλλ-,,,平面ABC 的法向量为()003OP =,, 可以算出平面ABE 的一个法向量为)()13102n λλ=--,,,于是11πcos 3OP n OP n ⋅=,解得13λ=(1-舍).提高班学案3【拓1】如图,在长方体1111ABCD A B C D -中,11AD AA ==,2AB =,点E 在棱AB 上移动.AE 等于何值时,二面角1D EC D --的大小为π4?PBOM DCxyz D 1C 1B 1A 11第12讲·提高-尖子-目标·教师版【解析】 以D 为坐标原点,直线DA ,DC ,1DD 分别为x ,y ,z 轴,建立空间直角坐标系,设AE x =,则()1101A ,,,()1001D ,,,()10E x ,,,()100A ,,,()020C ,,.由题意可知1DD 为平面ECD 的一个法向量,设平面1D EC 的法向量为()n a b c =,,,∵()120CE x =-,,,()1021D C =-,,,()1001DD =,,, ∴()120020.0b c n D C a b x n CE ⎧-=⋅=⎧⎪⎪⇒⎨⎨+-=⎪⋅=⎪⎩⎩,令1b =,得2c =,2a x =-, ∴()212n x =-,,. 依题意()121π22cos425n DD n DD x ⋅===⋅-+ ∴123x =+,223x =-∴23AE =1D EC D --的大小为π4.【备选】如图,在直三棱柱111ABC A B C -中,1AB =,13AC AA ==60ABC ∠=︒.⑴ 证明:1AB AC ⊥; ⑵ 求二面角1A ACB --的余弦值. 【解析】 方法一:⑴ ∵三棱柱111ABC A B C -为直三棱柱,∴1AB AA ⊥在ABC △中,1AB =,3AC ,60ABC ∠=︒, 由正弦定理得30ACB ∠=︒, ∴90BAC ∠=︒,即AB AC ⊥.∴AB ⊥平面11ACC A ,又1A C ⊂平面11ACC A ,∴1AB AC ⊥. ⑵ 如图,作1AD AC ⊥交1A C 于点D 点,连结BD , 由三垂线定理知1BD AC ⊥∴ADB ∠为二面角1A ACB --的平面角. 在1Rt AAC △中,113366AA AC AD AC ⋅⋅== 在Rt BAD △中,6tan AB ADB AD ∠==∴15cos ADB ∠=, 即二面角1A ACB --15. 方法二:⑴∵三棱柱111ABC A B C -为直三棱柱,∴1AA AB ⊥,1AA AC ⊥.在ABC △,1AB =,3AC =,60ABC ∠=︒,由正弦定理得30ACB ∠=︒,∴90BAC ∠=︒,即AB AC ⊥. 如图,建立空间直角坐标系,则(000)A ,,,(100)B ,,,()030C ,,(1003A ,,DCBA C 1B 1A 1CB AC 1B 1A 1AB C DA 1B 1C 1D 1Ez y x24 第12讲·提高-尖子-目标·教师版∴(100)AB =,,,()1033AC =-,,∵()11003030AB AC ⋅=⨯+⨯+⨯-= ∴1AB AC ⊥. ⑵ 如图可取(100)m AB ==,,为平面1AAC 的法向量, 设平面1A BC 的法向量为()n x y z =,,,则0BC n ⋅=,10A C n ⋅=,又()130BC =-,,,∴30330x y y z ⎧-+=⎪⎨-=⎪⎩∴3x y =,z y = 不妨取1y =,则()311n =,,()22222231101015cos 311100m n m n m n⋅⨯+⨯+⨯===⋅++⋅++,,结合图象知二面角1A ACB --为锐二面角, ∴二面角1A ACB --的余弦值为15.如图,在三棱柱111ABC A B C -中,AB AC ⊥,顶点1A 在底面ABC 上的射影恰为B 点,且12AB AC A B ===. ⑴ 分别求出1AA 与底面ABC 、棱BC 所成的角;⑵ 在棱11B C 上确定一点P ,使14AP =并求出二面角1P AB A --的平面角的余弦值.【解析】 ⑴ 因1A 在底面ABC 上的射影恰为B 点,则1A B ⊥底面ABC .所以1A AB ∠就是1AA 与底面ABC 所成的角.因112AB A B A B AB ==⊥,,故1π4A AB ∠=,即1AA 与底面ABC 所成的角是π4.如图,以A 为原点建立空间直角坐标系,则()200C ,,,()020B ,,,()1022A ,,,()1042B ,,,()1222C ,,,()1022AA =,,,()11220BC B C ==-,,,则1111cos 288AA BC AA BC AA BC⋅===-⨯⋅,,故1AA 与棱BC 所成的角是π3.⑵ 设()111220B P B C λλλ==-,,,则()2422P λλ-,,. 于是()2214424142AP λλλ=+-+=(32λ=舍去),则P 为棱11B C 的中点,其坐yzxC B AC 1B 1A 1Pyx A B CC 1B 1A 1A 1B 1C 1CBA1第12讲·提高-尖子-目标·教师版标为()132P ,,. 设平面PAB 的法向量为()1n x y z =,,,则11032022000n AP x y z x z y y n AB ⎧⋅=++==-⎧⎧⎪⇒⇒⎨⎨⎨==⋅=⎩⎩⎪⎩,,,, 不妨取1z =,得()1201n =-,,. 而平面1ABA 的法向量为()2100n =,,,则121212225cos 55n n n n n n ⋅-===-⋅,, 故二面角1P AB A --的平面角的余弦值是255.【演练1】⑴ 设空间四点O A B P ,,,满足OP mOA nOB =+,其中1m n +=,则( )A .P AB ∈ B .P AB ∉C .点P 不一定在直线AB 上D .以上都不对⑵ 已知a b ,是空间两个向量,若2a =,2b =,7a b -=,则cos a b =,_ 【解析】 ⑴ A已知1m n +=,则1m n =-,()1OP n OA nOB OA nOA nOB =-+=-+()OP OA n OB OA ⇒-=-AP nAB ⇒=,0AB ≠∵,AP ∴和AB 共线,即点A P B ,,共线 ⑵18将7a b -=化为()27a b -=,求得12a b ⋅=,再由cos a b a b a b ⋅=,求得1cos 8a b =,【演练2】在正方体1111ABCD A B C D -中,M 、N 分别为棱1AA 和1BB 的中点,则异面直线CM 与1D N夹角的正弦值为( )A .19B .459C .259D .23 实战演练24 第12讲·提高-尖子-目标·教师版NMA 1B 1C 1D 1AB CD解析图:zyxA 1B 1C 1D 1ABC DMN【解析】 B设正方体棱长为2,以D 为坐标原点,DA 为x 轴,DC 为y 轴,1DD 为z 轴建立空间直角坐标系,可知()221CM =-,,,()1221D N =-,,, 1111cos 999CM D N CM D N CM D N⋅===-⨯⨯,,∴145sin CM D N =,【演练3】三棱锥被平行于底面ABC 的平面所截得的几何体如图所示,截面为111A B C ,90BAC ∠=︒,1A A ⊥平面ABC ,13A A =1122AB AC AC ===,D 为BC 中点.⑴ 证明:平面1A AD ⊥平面11BCC B ; ⑵ 求二面角1A CC B --的余弦值.【解析】 ⑴ 如图,建立空间直角坐标系,则()()()000200020A B C ,,,,,,,,, ((11003013A C ,,,,,.∵D 为BC 的中点,∴D 点坐标为()110,,. ∴()()()1110003220AD AA BC ===-,,,,,,,,, ∵()1212000AD BC ⋅=⨯-+⨯+⨯=, ()10202300AA BC ⋅=⨯-+⨯+=.∴1BC AD BC AA ⊥⊥,,又1AA AD A =,∴BC ⊥平面1A AD ,又BC ⊂平面11BCC B ,∴平面1A AD ⊥平面11BCC B . ⑵ ∵AB ⊥平面11ACC A ,如图,可取()200m AB ==,,为平面11ACC A 的法向量, 设平面11BCC B 的法向量为()n x y z =,,,则0BC n ⋅=,10CC n ⋅=. ∵(1013CC =-,,,∴22030x y y z -+=⎧⎪⎨-=⎪⎩, 可取1y =,则311n ⎛= ⎝⎭,,. DABCA 1B 1C 1z yA 1B 1C 1ABDC1第12讲·提高-尖子-目标·教师版222222321010213cos 3200113m n ⨯+⨯+〈〉==⎛⎫++⋅++ ⎪ ⎪⎝⎭,. ∴二面角1A CC B --21.【演练4】如图,已知长方体1AC 中,112AB BC BB ===,,连接1B C ,过B 点作1B C 的垂线交1CC 于E ,交1B C 于F .⑴ 求证:1AC ⊥平面EBD ; ⑵ 求点A 到平面11A B C 的距离;⑶ 求直线ED 与平面11A B C 所成角的正弦值.【解析】 如图建立空间直角坐标系.∵1B BC BCE ∆∆∽,故2112BC CE BB ==; ⑴ ()()1000002A A ,,,,,, ()()()100010110B D C ,,,,,,,,,1112E ⎛⎫ ⎪⎝⎭,,,∴()111112011022AC BE DE ⎛⎫⎛⎫=-== ⎪ ⎪⎝⎭⎝⎭,,,,,,,, ∵()111011202AC BE ⋅=⨯+⨯+-⨯=, ()111110202AC DE ⋅=⨯+⨯+-⨯=. ∴1A C BE ⊥,1A C DE ⊥,即1AC BE ⊥,1AC DE ⊥, ∵BEDE E =,所以1A C ⊥平面EBD .⑵ 设平面11A B C 的一个法向量为()m x y z =,,由11(100)A B =,,,1(012)B C =-,,,而1110A B m B C m ⎧⋅=⎪⎨⋅=⎪⎩,∴02x y z =⎧⎨=⎩,令1z =,得()021m =,,;而()1002AA =,,, ∴所求的距离为12555AA m d m⋅===⑶ 由⑵知,()021m =,,;而1102ED ⎛⎫=-- ⎪⎝⎭,,, ∴设ED 与m 所成角为θ,则1cos 5m ED m EDθ⋅==-⋅所以直线ED 与平面11A B C 所成角的正弦值为15.【演练5】如图,已知长方体1111ABCD A B C D -中,2AB =,1BC =,12AA =,棱1DD 上是否存在点P ,使平面1APC ⊥平面1ACC ,证明你的结论.A 1D 1B 1C 1A BCD E F F E D 1C 1B 1A 1D CBA x y z24 第12讲·提高-尖子-目标·教师版【解析】 如图建立空间直角坐标系,则()100A ,,,()120B ,,,()020C ,,,()1022C ,,,假设P 点存在,且DP a =,则∵平面1APC ⊥平面1ACC ,()00P a ,,, 法一:∴在平面1ACC 中作1CH AC ⊥,垂足为H 1A H C ∵,, 三点共线,∴()11CH CA CC λλ=+-()()()1201002λλ=-+-,,,, ()222λλλ=--,,,1CH AC ⊥∵,()()12221220CH AC λλλ⋅=--⋅-=∴,,,,, 49λ=∴,4810999CH ⎛⎫=- ⎪⎝⎭∴,,,∵面1APC ⊥面1ACC ,1CH AC ⊥,CH ⊥∴面1APC CH AP ⇒⊥, ()4810100999CH AP a ⎛⎫⋅=-⋅-= ⎪⎝⎭∴,,,,,25a =∴,∴存在点2005P ⎛⎫ ⎪⎝⎭,,,使面1APC ⊥面1ACC .法二:()10,0,2CC =,()11,2,2AC =-,()1,0,AP a =-,设平面1ACC 的法向量为(),,m r s t =,平面1APC 的法向量为(),,n x y z =, 则1120220m CC t m AC r s t ⎧⋅==⎪⎨⋅=-++=⎪⎩,10220n AP x az n AC x y z ⎧⋅=-+=⎪⎨⋅=-++=⎪⎩ 即可取()2,1,0m =,2,,12a n a -⎛⎫= ⎪⎝⎭, 所以平面1ACC ⊥平面1APC ⇔0m n m n ⊥⇔⋅=,即2202a a -+=,解得25a =.∴存在点2005P ⎛⎫ ⎪⎝⎭,,,使平面1APC ⊥平面1ACC .在棱长为2的正方体1111ABCD A B C D -中,E 、F 、G 分别为AD 、1AA 、11A B 中点, ⑴ 求B 到平面EFG 的距离;⑵ 求二面角1G EF D --的余弦值.大千世界ABC DA 1B 1C 1D 1P zyxHP D 1C 1B 1A 1D C B AD 1C 1B 1A 1DCBAE FG1第12讲·提高-尖子-目标·教师版【解析】 以A 为原点,AB 、AD 、1AA 分别为x 、y 、z 轴建立如图所示的坐标系.则(010)E ,,,()200B ,,,(001)F ,,,(102)G ,,; 于是向量(011)FE =-,,,(101)FG =,,; 设面EFG 的法向量为()n x y z =,,,则0n FE n FG ⋅=⋅=, 即00y z x z -=⎧⎨+=⎩,于是可取(111)n =-,,; ⑴ (210)EB =-,,,设B 到面EFG 的距离为h ;则33n EB h n⋅===⑵ 平面11ADD A 的法向量可取成(100)m =,,;于是3cos 3m n m n m n⋅===, 由图象知二面角1G EF D --3G EA C D1B 1C D 1xy。
空间向量解立体几何第三讲教师版
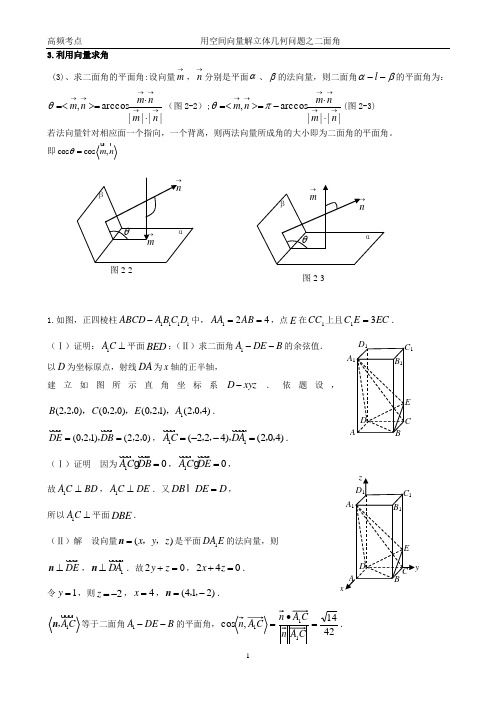
3.利用向量求角(3)、求二面角的平面角:设向量→m ,→n 分别是平面α、β的法向量,则二面角βα--l 的平面角为:||||arccos,→→→→→→⋅⋅>==<n m nm n m θ(图2-2);||||arccos,→→→→→→⋅⋅->==<n m nm n m πθ(图2-3)若法向量针对相应面一个指向,一个背离,则两法向量所成角的大小即为二面角的平面角。
即cos cos ,m n θ=1.如图,正四棱柱1111ABCD A BC D -中,124AA AB ==,点E 在1CC 上且EC E C 31=. (Ⅰ)证明:1AC ⊥平面BED ;(Ⅱ)求二面角1A DE B --的余弦值. 以D 为坐标原点,射线DA 为x 轴的正半轴, 建立如图所示直角坐标系D x y -.依题设,1(220)(020)(021)(204)B C E A ,,,,,,,,,,,. (021)(220)DE DB ==,,,,,,11(224)(204)AC DA =--= ,,,,,. (Ⅰ)证明 因为10AC DB = ,10AC DE =, 故1AC BD ⊥,1AC DE ⊥.又DB DE D = , 所以1AC ⊥平面DBE . (Ⅱ)解 设向量()x y z =,,n 是平面1DA E 的法向量,则DE ⊥ n ,1DA ⊥n .故20y z +=,240x z +=.令1y =,则2z =-,4x =,(412)=-,,n . 1AC ,n 等于二面角1A DEB --的平面角,4214==.图2-3AB CDEA 1B 1C 1D 12.如图,在直三棱柱111A B C ABC-中,AC AB ⊥,2==AC AB ,41=AA ,点D 是BC 的中点 (1)求异面直线B A 1与D C 1所成角的余弦值 (2)求平面1ADC 与1ABA 所成二面角的正弦值.解:(1)以{}1,,AA AC AB 为为单位正交基底建立空间直角坐标系xyz A -,则)0,0,0(A )0,0,2(B ,)0,2,0(C ,)4,0,0(1A ,)0,1,1(D ,)4,2,0(1C ∴)4,0,2(1-=A ,)4,1,1(1--=A [来源:学科网ZXXK]∴10103182018,cos 11==>=<D C B A ∴异面直线B A 1与D C 1所成角的余弦值为10103 (2))0,2,0(= 是平面1ABA 的的一个法向量设平面1ADC 的法向量为),,(z y x =,∵)0,1,1(=,)4,2,0(1=AC 由1,AC m AD m ⊥⊥ ∴⎩⎨⎧=+=+0420z y y x 取1=z ,得2,2=-=x y ,∴平面1ADC 的法向量为)1,2,2(-=设平面1ADC 与1ABA 所成二面角为θ∴32324,cos cos =⨯-==><=θ, 得35sin =θ2(1)证明:BC 1∥平面A 1CD ;(2)求二面角D -A 1C -E 的正弦值.解:(1)连结AC 1交A 1C 于点F ,则F 为AC 1中点. 又D 是AB 中点,连结DF ,则BC 1∥DF . 因为DF ⊂平面A 1CD ,BC 1平面A 1CD ,所以BC 1∥平面A 1CD . (2)由AC =CB =2AB 得,AC ⊥BC . 以C 为坐标原点,CA的方向为x 轴正方向,建立如图所示的空间直角坐标系C -xyz .设CA =2,则D (1,1,0),E (0,2,1),A 1(2,0,2),CD =(1,1,0),CE =(0,2,1),1CA=(2,0,2).设n =(x 1,y 1,z 1)是平面A 1CD 的法向量,则10,0,CD CA ⎧⋅=⎪⎨⋅=⎪⎩ n n 即11110,220.x y x z +=⎧⎨+=⎩可取n =(1,-1,-1).同理,设m 是平面A 1CE 的法向量,则10,0,CE CA ⎧⋅=⎪⎨⋅=⎪⎩m m 可取m =(2,1,-2). 从而cos 〈n ,m 〉=||||=·n m n m 故sin 〈n ,m 即二面角D -A 1C -E 的正弦值为3练2. 如图, 四棱柱ABCD -A 1B 1C 1D 1中, 侧棱A 1A ⊥底面ABCD , AB //DC , AB ⊥AD , AD = CD = 1, AA 1 = AB =2, E 为棱AA 1的中点. (Ⅰ) 证明B 1C 1⊥CE ;(Ⅱ) 求二面角B 1-CE -C 1的正弦值.(方法一)如图,以点A 为原点建立空间直角坐标系,依题意得A(0,0,0),B(0,0,2),C(1,0,1),B1(0,2,2),C 1(1,2,1),E(0,1,0).(Ⅰ)证明:易得11(1,0,1),BC =- (1,1,1)CE =--,于是110BC CE ⋅= ,所以11B C CE ⊥ .(Ⅱ)解:1(1,2,1)BC =--. 设平面1BCE D 法向量(,,)x y z =m , 则100B C CE ⎧⋅=⎪⎨⋅=⎪⎩m m ,即200x y z x y z --=⎧⎨-+-=⎩,消去x ,得20x y +=, 不妨设1z =,可得一个法向量为(3,2,1)=--m .由(Ⅰ),11B C CE ⊥,又111CC B C ⊥,可得11B C ⊥平面1CEC ,故11(1,0,1)BC =-为平面1CEC 的一个法向量.于是111111cos |B C B C B C ⋅===⋅m m,|m ||11sin 7B C = m,所以二面角B 1-CE -C 1的正弦值为7. (解法二)(Ⅰ)证明:因为侧棱1CC ⊥底面1111A B C D ,11B C ⊂平面1111A B C D .所以111CC BC ⊥.经计算可得1B E =,11B C =1EC 从而2221111B E B C EC =+.所以在△11B EC 中,111B C C E ⊥,又1CC ,1C E ⊂平面1CC E ,111CC C E C = ,所以11B C ⊥平面1CC E ,又CE ⊂平面1CC E ,故11B C CE ⊥.(Ⅱ)解:过1B 作1B G ⊥CE 于点G ,连接1C G .由(Ⅰ),11B C CE ⊥垂直,故CE ⊥平面11B C G ,得1CE C G ⊥,所以∠11B GC 为二面角B 1-CE -C 1的平面角.在△1CC E中,由1CE C E =12CC =,可得1C G =.在Rt △11B C G中,1B G =,所以11sin B GC ∠=,即二面角B 1-CE -C 1的正弦值为7. 3.如图, 四棱柱ABCD -A 1B 1C 1D 1的底面ABCD 是正方形, O 为底面中心, A 1O ⊥平面ABCD, 1AB AA =(Ⅰ) 证明: A 1C ⊥平面BB 1D 1D ;(Ⅱ) 求平面OCB 1与平面BB 1D 1D 的夹角θ的大小.1A【答案】解:(Ⅰ) BD O A ABCD BD ABCD O A ⊥∴⊂⊥11,,面且面 ;又因为,在正方形AB CD 中,BD C A AC A C A AC A BD A AC O A BD AC ⊥⊂⊥=⋂⊥11111,,故面且面所以;且. 在正方形AB CD 中,AO = 1 . .111=∆O A OA A RT 中,在O E C A OCE A E D B 1111111⊥为正方形,所以,则四边形的中点为设. [来源:学_科_网],所以由以上三点得且,面面又O O BD D D BB O D D BB BD =⋂⊂⊂111111E .E ,D D BB C A 111面⊥.(Ⅱ) 建立直角坐标系统,使用向量解题.以O 为原点,以OC 为X 轴正方向,以OB 为Y 轴正方向.则)1,0,1()1,1,1(),100(),001(,0,1,0111-=⇒A B A C B ,,,,)(.由(Ⅰ)知, 平面BB 1D 1D 的一个法向量.0,0,1),1,1,1(),1,0,1(111)(==-==OB A n 设平面OCB 1的法向量为,则0,0,2122=⋅=⋅n OB n n).1-,1,0(法向量2=n 为解得其中一个21221|||||,cos |cos 212111=⋅=⋅=><=n n n n θ. 所以,平面OCB 1与平面BB 1D 1D 的夹角θ为3π4.如图,四棱锥P ABCD -中,PA ,ABCD E BD ⊥平面为的中点, G PD 为的中点, 3,12DAB DCB EA EB AB PA ∆≅∆====,,连接CE 并延长交AD 于F . (1) 求证:AD CFG ⊥平面;(2) 求平面BCP 与平面DCP 的夹角的余弦值.【答案】解:(1)在ABD ∆中,因为E 是BD 的中点,所以1EA EB ED AB ====, 故,23BAD ABE AEB ππ∠=∠=∠=,因为DAB DCB ∆≅∆,所以EAB ECB ∆≅∆, 从而有FED FEA ∠=∠,故,EF AD AF FD ⊥=,又因为,PG GD =所以FG ∥PA . 又PA ⊥平面ABCD ,所以,GF AD ⊥故AD ⊥平面CFG .1A(3) 以点A 为坐标原点建立如图所示的坐标系,则3(0,0,0),(1,0,0),(22A B C D , (4)3(0,0,)2P ,故1333(0),(),(2222BC CP CD ==-=- ,设平面BCP 的法向量111(1,,)n y z = ,则111102233022y y z ⎧+=⎪⎪⎨⎪--+=⎪⎩ ,解得11323y z ⎧=-⎪⎪⎨⎪=⎪⎩,即12(1,)3n = .设平面DCP 的法向量222(1,,)n y z = ,则222302233022y y z ⎧-+=⎪⎪⎨⎪--+=⎪⎩,解得222y z ⎧=⎪⎨=⎪⎩,即2(1n =.从而平面B C P 与平面D C P 的夹角的余弦值为12124cos 4n n n n θ⋅=== 5.在如图所示的几何体中,四边形ABCD 是等腰梯形,AB ∥CD ,60,DAB FC ∠=⊥ 平面,,ABCD AE BD CB CD CF ⊥==.(Ⅰ)求证:BD ⊥平面AED ;(Ⅱ)求二面角F BD C --的余弦值. 【答案】(Ⅰ)证明:因为四边形ABCD 为等腰梯形,AB CD ,60DAB ∠= , 所以 120ADC BCD ∠=∠= . 又 CB CD =, 所以 30CDB ∠=因此 90ADB ∠= ,AD BD ⊥,又 AE BD ⊥,且AE AD A = ,,AE AD ⊂平面AED , 所以 BD ⊥平面AED . (Ⅱ)解法一:由(I )知AD BD ⊥,所以AC BC ⊥,又FC ⊥平面ABCD ,因此 ,,CA CB CF 两两垂直.以C 为坐标原点,分别以,,CA CB CF 所在的直 线为x 轴,y 轴,z 轴建立空间直角坐标系,不妨设1CB =,则,(0,0,0)C ,(0,1,0)B ,1(,,0)2D -,(0,0,1)F ,因此 3(,,0)2BD =- ,(0,1,1)BF =- .设平面BDF 的一个法向量为(,,)x y z =m ,则 0BD =⋅ m ,0BF =⋅m ,所以 x ==,取1z =,则 (=m .又平面BDC 的法向量可以取为(0,0,1)=n ,所以 cos ,||||<>===⋅m n m n m n ,所以二面角F BD C --.解法二:取BD 的中点G ,连结,CG FG ,由于CB CD =,所以CG BD ⊥. 又FC ⊥平面ABCD ,BD ⊂平面ABCD ,所以FC BD ⊥.由于FC CG C = ,,FC CG ⊂平面FCG ,所以BD ⊥平面FCG ,故BD FG ⊥. 所以FGC ∠为二面角F BD C --的平面角.在等腰三角形BCD 中,由于120BCD ∠= ,因此1CG CB =,又CB CF =,所以CF ,故 cos FGC ∠,因此 二面角F BD C --.。
空间向量解立体几何第二讲教师版

知识点4.利用空间向量解立体几何问题 1.利用向量证明平行(1)线线平行方法:→→→→→→=⇔≠a b a a b λ)0(//(2)线面平行方法:线垂直于平面的法向量或内外共线.在图2-1中,→m 向是平面α的法向量,→a 是直线a 的方向向量,证明平面的法向量与直线所在向量垂直(0=∙→→a m )。
(3)面面平行方法:一个平面的法向量垂直于另一个平面,在图2-2中, →m 向是平面α的法向量,→n 是平面β的法向量,证明两平面的法向量共线(→→=n m λ)。
2.利用向量证明垂直(1)线线垂直方法:0a b a b ⊥⇔⋅=(2)线面垂直方法:线垂直面内两相交直线或线平行面的法向量,在图2-3中,→m 向是平面α的法向量,→a 是直线a 的方向向量,证明平面的法向量与直线所在向量共线(→→=a m λ);或→a 垂直于面内两相交直线所在向量。
(3)面面垂直方法:两面的法向量垂直,在图2-4中,→m 是平面α的法向量,→n 是平面β的法向量,证明两平面的法向量垂直(0=∙→→n m )1. 如图,在四棱锥O ABCD -中,底面ABCD 四边长 为1的菱形,4ABC π∠=, OA ABCD ⊥底面, 2OA =,M 为OA 的中点,N 为BC 的中点→证明:直线MN OCD平面‖;解:作APCD ⊥于点P ,如图,分别以AB ,AP ,AO 所在直线为,,xy z 轴建立坐标系(0,0,0),(1,0,0),((0,0,2),(0,0,1),(1AB P D O M N, 证明(11),(0,2),(2)44222MN OP OD =--=-=--设平面OCD 的法向量为(,,)n xy z =,则0,0n OP n OD ==即 2022022y z x y z-=⎪⎪⎨⎪-+-=⎪⎩取z =,解得n =(11)(0,044MN n =--= ∵MN OCD ∴平面‖2.在正方体ABCD —A 1B 1C 1D 1中,E 、F 分别为BB 1、DC 的中点,求证:D 1F ⊥平面ADE . 解:如图所示,不妨设正方体的棱长为1,且设=i ,=j ,1DD =k , 以i 、j 、k 的坐标向量建立空间直角坐标系D —xy z , 则AD =(-1,0,0),F D 1=(0,21,-1),AD ·D 1=(-1,0,0)·(0,21,-1)=0,∴AD ⊥D 1F.又AE =(0,1,21),D 1=(0,21,-1), ∴AE ·F D 1=(0,1,21)·(0,21,-1)=21-21=0.∴A E ⊥D 1F ,又AE ∩AD =A , ∴D 1F ⊥平面AD E.练.已知P N M 、、分别是正方体1111D C B A ABCD -中的棱CDBC CC、、1的中点. 求证:⊥P A 1平面DMN .CA 13.利用向量求角(1)、求异面直线所成角:向量a 和b(或者说其补角)等于异面直线a 和b 的夹角:(设异面直线的夹角为θ)cos cos ,a b a b a bθ⋅==⋅(2)、求线面角:如图2-1-1,设→n 是平面α的法向量,AB 是平面α的一条斜线,α∈A ,则AB 与平面α所成的角为:(设直线AB 与面α的夹角为θ)|,cos |sin ><=→→AB n θ1.如图,在四棱锥ABCD P -中,底面ABCD 是矩形,⊥PA 底面,是的中点,已知,22=AD,2=PA ,求:异面直线BC 与AE 所成的角的大小。
2019-2020学年高中数学(苏教版 选修2-1)教师用书:第3章 空间向量与立体几何 3.1.5

3.1.5 空间向量的数量积1.理解空间向量的夹角的概念,理解空间向量的数量积的概念、性质和运算律.(重点) 2.掌握空间向量的数量积及应用.(重点、难点) 3.理解向量夹角与直线所成角的区别.(易错点)[基础·初探]教材整理1 空间向量的夹角阅读教材P 91~P 92上半部分,完成下列问题. a ,b 是空间两个非零向量,过空间任意一点O ,作OA→=a ,OB→=b ,则∠AOB 叫做向量a 与向量b 的夹角,记作〈a ,b 〉,a ,b的范围是[0,π],如果〈a ,b 〉=π2,则称a 与b 互相垂直,记作a ⊥b .如图3-1-25,在正方体ABCD -A 1B 1C 1D 1中,求向量BC1→与AC →夹角的大小.图3-1-25【解】 ∵AD1→=BC1→,∴∠CAD 1的大小就等于〈BC1→,AC →〉. ∵△ACD 1为正三角形,∴∠CAD 1=π3,∴〈BC1→,AC →〉=π3. ∴向量BC1→与AC →夹角的大小为π3. 教材整理2 空间向量的数量积阅读教材P 92例1以上的部分,完成下列问题. 1.数量积的定义设a ,b 是空间两个非零向量,我们把数量|a ||b |·cos 〈a ,b 〉叫做向量a ,b 的数量积,记作a ·b ,即a ·b =|a ||b |cos 〈a ,b 〉.规定:零向量与任一向量的数量积为0. 2.数量积的性质 (1)cosa ,b=a·b|a||b|(a ,b 是两个非零向量).(2)a ⊥b ⇔a·b =0(a ,b 是两个非零向量). (3)|a |2=a·a =a 2. 3.数量积的运算律 (1)a·b =b·a ;(2)(λa )·b =λ(a·b )(λ∈R ); (3)a ·(b +c )=a·b +a·c.1.判断(正确的打“√”,错误的打“×”) (1)若a·b =0,则a =0或b =0.( ) (2)在△ABC 中,〈AB →,BC →〉=∠B .( ) (3)两个向量的数量积是数量,而不是向量.( )(4)若a ,b 均为非零向量,则a·b =|a||b |是a 与b 共线的充要条件.( ) 【答案】 (1)× (2)× (3)√ (4)×2.已知|a |=2,|b |=22,a·b =-22,则a 与b 的夹角为________.【导学号:09390075】【解析】 cos 〈a ,b 〉=a·b |a||b|=-222×22=-22,又∵〈a ,b 〉∈[0,π],∴〈a ,b 〉=3π4.【答案】 3π4教材整理3 数量积的坐标表示阅读教材P 93~P 94例3以上的部分,完成下列问题. 1.若a =(x 1,y 1,z 1),b =(x 2,y 2,z 2),则 (1)a ·b =x 1x 2+y 1y 2+z 1z 2.(2)a ⊥b ⇔a ·b =0⇔x 1x 2+y 1y 2+z 1z 2=0(a ≠0,b ≠0). (3)|a |=a·a =x21+y21+z21. (4)cos 〈a ,b 〉=x1x2+y1y2+z1z2x21+y21+z21·x22+y22+z22(a ≠0,b ≠0).2.空间两点间距离公式设A (x 1,y 1,z 1),B (x 2,y 2,z 2),则AB =错误!.1.若a =(-1,0,2),b =(x ,y,1),且a ⊥b ,则x =______. 【解析】 ∵a ⊥b ,∴a·b =-x +2=0,解得x =2. 【答案】 22.与向量a =(1,2,2)方向相同的单位向量是________.【解析】 |a |=12+22+22=3,故与a 方向相同的单位向量是a |a|=13(1,2,2)=⎝ ⎛⎭⎪⎫13,23,23.【答案】 ⎝ ⎛⎭⎪⎫13,23,23[质疑·手记]预习完成后,请将你的疑问记录,并与“小伙伴们”探讨交流: 疑问1: 解惑: 疑问2: 解惑: 疑问3: 解惑:[小组合作型]已知长方体ABCD -A 1B 1C 1D 1中,AB =AA 1=2,AD =4,E 为侧面AA 1B 1B 的中心,F 为A 1D 1的中点.求下列向量的数量积.(1)BC →·ED1→; (2)BF →·AB1→.【精彩点拨】 法一(基向量法):BC →与ED1→,BF →与AB1→的夹角不易求,可考虑用向量AB →,AD →,AA1→表示向量BC →,ED1→,BF →,AB1→,再求结论即可.法二(坐标法):建系→求相关点坐标→向量坐标→数量积. 【自主解答】法一(基向量法):如图所示,设AB →=a ,AD →=b ,AA1→=c ,则|a |=|c |=2,|b |=4,a ·b =b ·c =c ·a =0.(1)BC →·ED1→=BC →·(EA1→+A1D1→)=b ·错误!=|b |2=42=16.(2)BF →·AB1→=(BA1→+A1F →)·(AB →+AA1→)=⎝ ⎛⎭⎪⎫c -a +12b ·(a +c )=|c |2-|a |2=22-22=0.法二(坐标法):以A 为原点建立空间直角坐标系,如图所示,则B (2,0,0),C (2,4,0),E (1,0,1),D 1(0,4,2),F (0,2,2),A (0,0,0),B 1(2,0,2),∴BC →=(0,4,0),ED1→=(-1,4,1),BF →=(-2,2,2),AB1→=(2,0,2), (1)BC →·ED1→=0×(-1)+4×4+0×1=16. (2)BF →·AB1→=-2×2+2×0+2×2=0.解决此类问题的常用方法1.基向量法:首先选取基向量,然后用基向量表示相关的向量,最后利用数量积的定义计算.注意:基向量的选取要合理,一般选模和夹角都确定的向量.2.坐标法:对于建系比较方便的题目,采用此法比较简单,只需建系后找出相关点的坐标,进而得向量的坐标,然后利用数量积的坐标公式计算即可.[再练一题]1.在上述例1中,求EF →·FC1→.【解】 法一:EF →·FC1→=错误!·错误!=错误!(-a +b +c )·错误! =-12|a |2+14|b |2=2.法二:以A 为原点建立空间直角坐标系,则E (1,0,1),F (0,2,2),C 1(2,4,2),∴EF →=(-1,2,1),FC1→=(2,2,0),∴EF →·FC1→=-1×2+2×2+1×0=2.如图3-1-26所示,在平行六面体ABCD -A ′B ′C ′D ′中,AB =4,AD =3,AA ′=5,∠BAD =90°,∠BAA ′=∠DAA ′=60°.(1)求AC ′的长;(2)求AC′→与AC →的夹角的余弦值.图3-1-26【精彩点拨】 求线段长,要利用向量的方法求解,关键是找到表示AC ′的基向量,只要模与夹角均可知,则问题可求解,求夹角问题则是向量数量积的逆用.【自主解答】 (1)∵AC′→=AB →+AD →+AA′→, ∴|AC′→|2=(AB →+AD →+AA′→)2 =|AB →|2+|AD →|2+|AA′→|2+2(AB →·AD →+AB →·AA′→+AD →·AA′→) =42+32+52+2(0+10+7.5)=85. ∴|AC′→|=85.(2)法一:设AC′→与AC →的夹角为θ,∵ABCD 是矩形,∴|AC →|=32+42=5. 由余弦定理可得cos θ=AC′2+AC2-CC′22AC′·AC =85+25-252·85·5=8510. 法二:设AB →=a ,AD →=b ,AA′→=c , 依题意得AC′→·AC →=(a +b +c )·(a +b ) =a 2+2a ·b +b 2+a ·c +b ·c=16+0+9+4×5×cos 60°+3×5×cos 60° =16+9+10+152=852,∴cos θ=AC′→·AC →|AC′→|·|AC →|=85285×5=8510.1.求两点间的距离或某线段的长度,就是把此线段用向量表示,然后用|a |2=a ·a ,即|a |=a·a 通过向量运算求|a |.2.对于空间向量a ,b ,有cos 〈a ,b 〉=a·b|a||b|.利用这一结论,可以较方便地求解异面直线所成角的问题,由于向量的夹角的取值范围为[0,π],而异面直线所成的角的取值范围为⎝ ⎛⎦⎥⎤0,π2,故〈a ,b 〉∈⎝ ⎛⎦⎥⎤0,π2时,它们相等;而当〈a ,b 〉∈⎝⎛⎭⎪⎫π2,π时,它们互补.[再练一题]2.如图3-1-27,正四面体ABCD 中,M ,N 分别为棱BC ,AB 的中点,设AB→=a ,AC→=b ,AD →=c .(1)用a ,b ,c 分别表示向量DM →,CN →; (2)求异面直线DM 与CN 所成角的余弦值.图3-1-27【解】 (1)DM →=12(DB →+DC →)=12[(AB →-AD →)+(AC →-AD →)] =12[(a -c )+(b -c )]=12(a +b -2c ), CN →=12(CB →+CA →)=12[(AB →-AC →)-AC →] =12[(a -b )-b ]=12(a -2b ).(2)设棱长为1,即|a |=|b |=|c |=1且〈a ,b 〉=〈b ,c 〉=〈c ,a 〉=π3,则|DM →|=|CN →|=32. 又DM →·CN →=14(a +b -2c )·(a -2b ) =14(a 2+a ·b -2a ·c -2a ·b -2b 2+4b ·c ) =-18,∴cos 〈DM →,CN →〉=DM →·CN →|DM →||CN →|=-1832×32=-16.∴异面直线DM 与CN 所成角的余弦值为16.已知(1)若a ∥b ,分别求λ与m 的值;(2)若|a |=5,且与c =(2,-2λ,-λ)垂直,求a .【精彩点拨】 利用向量平行、垂直、向量的模列方程组求解. 【自主解答】 (1)由a ∥b ,得 (λ+1,1,2λ)=k (6,2m -1,2), ∴错误!解得错误! ∴实数λ=15,m =3.(2)∵|a |=5,且a ⊥c , ∴错误!化简,得⎩⎨⎧5λ2+2λ=3,2-2λ2=0,解得λ=-1.因此,a =(0,1,-2).向量平行与垂直问题主要有两种题型1.平行与垂直的判断2.利用平行与垂直求参数或其他问题,即平行与垂直的应用.[再练一题]3.如图3-1-28所示,在直三棱柱ABC -A 1B 1C 1中,CA =CB =1,∠BCA =90°,棱AA 1=2,M 是A 1B 1的中点.求证:A 1B ⊥C 1M .图3-1-28【证明】 如图所示,以CA →,CB →,CC1→为正交基底,建立空间直角坐标系C -xyz .依题意得B (0,1,0),A 1(1,0,2),错误!,2),B 1(0,1,2),则M 错误!,错误!,2,于是错误!=(-1,1,-2),C1M →=⎝ ⎛⎭⎪⎫12,12,0,∴A1B →·C1M →=-12+12+0=0,∴A1B →⊥C1M →,故A 1B ⊥C 1M .[探究共研型]探究1 【提示】 对于三个不为0的实数a ,b ,c ,若ab =ac ,则b =c .对于三个非零向量a ,b ,c ,若a ·b =a ·c ,不能得出b =c ,即向量不能约分.如图,在三棱锥S -ABC 中,SC ⊥平面ABC ,则SC ⊥AC ,SC ⊥BC .设CS →=a ,CA →=b ,CB →=c ,则a ·b =a ·c =0,但b ≠c .探究2 数量积运算是否有除法?【提示】 数量积的运算不满足除法,即对于向量a ,b ,若a ·b =k ,不能得到a =k b ⎝ ⎛⎭⎪⎫或b =k a ,例如当非零向量a ,b 垂直时,a ·b =0,但a =0b 显然是没有意义的.探究3 数量积运算满足结合律吗?【提示】 由定义得(a ·b )c =(|a ||b |cos 〈a ,b 〉)c ,即(a ·b )c =λ1c ;a (b ·c )=a (|b ||c |cos 〈b ,c 〉),即a (b ·c )=λ2a ,因此,(a ·b )c 表示一个与c 共线的向量,而a (b ·c )表示一个与a 共线的向量,而a 与c 不一定共线,所以(a ·b )c =a (b ·c )不一定成立.如图3-1-29,已知正四面体OABC 的棱长为1.求: (1)OA →·OB →;(2)(OA →+OB →)·(CA →+CB →); (3)|OA →+OB →+OC →|.图3-1-29【精彩点拨】 在正四面体OABC 中,OA →,OB →,OC →的模和夹角都已知,因此可以先把相关向量用OA →,OB →,OC →线性表示,再结合空间向量数量积的运算律与运算性质求解即可.【自主解答】 在正四面体OABC 中,|OA →|=|OB →|=|OC →|=1, 〈OA →,OB →〉=〈OA →,OC →〉=〈OB →,OC →〉=60°.(1)OA →·OB →=|OA →||OB →|·cos ∠AOB =1×1×cos 60°=12. (2)(OA →+OB →)·(CA →+CB →)=(OA →+OB →)·(OA →-OC →+OB →-OC →) =(OA →+OB →)·(OA →+OB →-2OC →)=OA2→+2OA →·OB →-2OA →·OC →+OB →2-2OB →·OC →=12+2×12-2×1×1×cos 60°+12-2×1×1×cos 60° =1+1-1+1-1=1. (3)|OA →+OB →+OC →|=错误! =错误!=错误!. [再练一题]4.已知a +3b 与7a -5b 垂直,且a -4b 与7a -2b 垂直,则〈a ,b 〉=________.【导学号:09390076】【解析】 由条件知,(a +3b )·(7a -5b )=7|a |2+16a·b -15|b |2=0, 及(a -4b )·(7a -2b )=7|a |2+8|b |2-30a·b =0. 两式相减,得46a·b =23|b |2,∴a·b =12|b |2.代入上面两个式子中的任意一个,即可得到|a |=|b |. ∴cos 〈a ,b 〉=a·b |a||b|=12|b|2|b|2=12.∵〈a ,b 〉∈[0°,180°],∴〈a ,b 〉=60°. 【答案】 60°[构建·体系]1.已知向量a =(4,-2,-4),b =(6,-3,2),则(a +b )·(a -b )的值为________.【解析】 ∵a +b =(10,-5,-2),a -b =(-2,1,-6),∴(a +b )·(a -b )=-20-5+12=-13.【答案】 -132.已知向量a =(2,-3,0),b =(k,0,3).若a ,b 成120°的角,则k =________.【解析】 cos 〈a ,b 〉=a·b |a|·|b|=2k 139+k2=-12,得k =-39. 【答案】 -393.如图3-1-30,已知正三棱柱ABC -A 1B 1C 1的各条棱长都相等,M 是侧棱CC 1的中点,则异面直线AB 1和BM 所成的角的大小是________.图3-1-30【解析】 AB1→=AB →+BB1→,BM →=BC →+CM →,设棱长为1.又∵AB1→·BM →=(AB →+BB1→)(BC →+CM →)=AB →·BC →+BB1→·BC →+AB →·CM →+BB1→·CM →=-12+0+0+12=0,∴cos 〈AB1→,BM →〉=AB1→·BM →|AB1→|·|BM →|=0,∴AB1→⊥BM →,∴直线AB 1与BM 所成的角为90°.【答案】 90°4.已知正方形ABCD 的边长为2,E 为CD 的中点,则AE →·BD →=________.【解析】 ∵AE →=AD →+DE →=AD →+12AB →,BD →=AD →-AB →,∴AE →·BD →=⎝ ⎛⎭⎪⎫AD →+12AB →·(AD →-AB →)=AD →2-AD →·AB →+12AB →·AD →-12AB →2=4-0+0-2=2.【答案】 25.如图3-1-31所示,在空间四边形OABC 中,OA =8,AB =6,AC =4,BC =5,∠OAC =45°,∠OAB =60°,求OA 与BC 所成角的余弦值.图3-1-31【解】 由题意知BC →=AC →-AB →,∴OA →·BC →=OA →·AC →-OA →·AB →=|OA →||AC →|cos 〈OA →,AC →〉-|OA →||AB →|cos 〈OA →,AB →〉=8×4×cos 135°-8×6×cos 120°=24-162,∴cos 〈OA →,BC →〉=OA →·BC →|OA →||BC →|=24-1628×5=3-225,∴OA 与BC 所成角的余弦值为3-225.我还有这些不足:(1)(2)我的课下提升方案:(1)(2)。
空间向量与立体几何全章综合测试卷(基础篇)(教师版)

2
→
B. + +
→
→
→
→
→
→
1 → →
D. ( + ) +
2
→
→
→
【解题思路】根据图形可得11 = 111 = 1,进而利用空间向量的加减法运算可得1 = 11 +
→
→
11 + 1,得出结果.
→
→
→
→
→
→
→
→
→
【解答过程】解:由题意得,11 = 11,1 = 1,1 = 11 + 1 = 11 + 11 + 1 = 11
2 2
∥平面 α 或 l 在平面 α 内,B 错误;
→
对于 C,平面 α 的法向量为 = (1,1,1),和所有坐标轴相交,C 正确;
对于 D,原点 O 可以在平面 α 内,D 错误;
故选:C.
8.(5 分)(2024 春•天宁区校级期末)在四棱锥 P﹣ABCD 中,PA⊥平面 ABCD,底面 ABCD 为矩形,
【解题思路】先得到四面体 ABCD 为正四面体,再利用空间向量的数量积运算和线性运算求解即可.
【解答过程】解:∵四面体 ABCD,所有棱长均为 2,
∴四面体 ABCD 为正四面体,
∵E,F 分别为棱 AB,CD 的中点,
→
→
→
→
→
1 →
∴ ⋅ = ( + )•(−)
2
1→ → 1→2 1→ → 1→ →
→
∴ = (1,1,2),
由图可知,二面角 Q﹣PD﹣A 为锐角,设为 α,
→ →
空间向量与立体几何教案
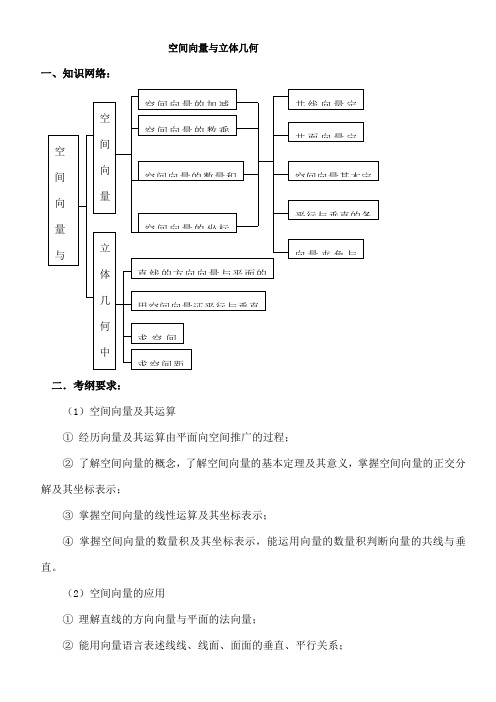
空间向量与立体几何一、知识网络:二.考纲要求:(1)空间向量及其运算① 经历向量及其运算由平面向空间推广的过程;② 了解空间向量的概念,了解空间向量的基本定理及其意义,掌握空间向量的正交分解及其坐标表示;③ 掌握空间向量的线性运算及其坐标表示;④ 掌握空间向量的数量积及其坐标表示,能运用向量的数量积判断向量的共线与垂直。
(2)空间向量的应用① 理解直线的方向向量与平面的法向量;② 能用向量语言表述线线、线面、面面的垂直、平行关系;③ 能用向量方法证明有关线、面位置关系的一些定理(包括三垂线定理);④ 能用向量方法解决线线、线面、面面的夹角的计算问题,体会向量方法在研究几何问题中的作用。
三、命题走向本章内容主要涉及空间向量的坐标及运算、空间向量的应用。
本章是立体几何的核心内容,高考对本章的考查形式为:以客观题形式考查空间向量的概念和运算,结合主观题借助空间向量求夹角和距离。
预测10年高考对本章内容的考查将侧重于向量的应用,尤其是求夹角、求距离,教材上淡化了利用空间关系找角、找距离这方面的讲解,加大了向量的应用,因此作为立体几何解答题,用向量法处理角和距离将是主要方法,在复习时应加大这方面的训练力度。
第一课时空间向量及其运算一、复习目标:1.理解空间向量的概念;掌握空间向量的加法、减法和数乘; 2.了解空间向量的基本定理;3.掌握空间向量的数量积的定义及其性质;理解空间向量的夹角的概念;掌握空间向量的数量积的概念、性质和运算律;了解空间向量的数量积的几何意义;能用向量的数量积判断向量的共线与垂直。
二、重难点:理解空间向量的概念;掌握空间向量的运算方法三、教学方法:探析类比归纳,讲练结合四、教学过程(一)、谈最新考纲要求及新课标高考命题考查情况,促使积极参与。
学生阅读复资P128页,教师点评,增强目标和参与意识。
(二)、知识梳理,方法定位。
(学生完成复资P128页填空题,教师准对问题讲评)。
1.空间向量的概念向量:在空间,我们把具有大小和方向的量叫做向量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第17讲:空间向量与立体几何一、 考纲点击1. 空间向量及其运算(1)掌握空间向量的线性运算及其坐标表示;(2)掌握空间向量的数量积及其坐标表示,能运用向量的数量积判断向量的共线与垂直。
2. 空间向量的应用(1)理解直线的方向向量与平面的法向量;(2)能用向量语言表述和证明直线与直线、直线与平面、平面与平面的垂直, 平行关系; (3)能用向量法解决直线与直线、直线与平面、平面与平面的夹角计算问题; (4)能用向量法解决空间距离问题。
二、 必备基础知识 1.空间向量的有关概念(1)空间向量:在空间中,具有大小和方向的量叫做空间向量。
(2)相等向量:方向相同且模相等的向量。
(3)共线向量:表示空间向量的有向线段所在的直线互相平行或重合的向量。
(4)共面向量:平行于同一个平面的向量。
2.空间向量的坐标表示及运算 (1)数量积的坐标运算设()111,,a x y z =,()222,,b x y z = ,则①()121212,,a b x x y y z z ±=+++②()111,,a x y z λλλλ=;③121212a b x x y y z z ⋅=++.(2)共线与垂直的坐标表示设()111,,a x y z =,()222,,b x y z =则 ①121212//,,a b a b x x y y z z λλλλ⇔=⇔===②12121200a b a b x x y y z z ⊥⇔⋅=⇔++=.(3)模、夹角和距离公式设()111,,a x y z =,()222,,b x y z =则a ==cos ,a b a b a b ⋅〈〉==若()111,,x y z A ,()222,,x y z B =,则d AB=AB =2.立体几何中的向量方法(1)直线的方向向量与平面的法向量的确定①直线的方向向量:l 是空间一直线,A ,B 是直线l 上任意两点,则称AB →为直线l 的方向向量,与AB →平行的任意非零向量也是直线l 的方向向量.②平面的法向量可利用方程组求出:设,a b是平面α内两不共线向量,n 为平面α的法向量,则求法向量的方程组为0n a n b ⎧⋅=⎪⎨⋅=⎪⎩ ,取其中一组坐标即可.(2)用向量法证明空间中的平行关系 ①线线平行:若空间不重合两条直线a ,b 的方向向量分别为a ,b ,则////a b a b ⇔⇔ ()a b R λλ=∈②线面平行:若直线a 的方向向量为a ,平面α的法向量为n ,且a α⊄,则////a a αα⇔ 0a n a n ⇔⊥⇔⋅=③面面平行若空间不重合的两个平面α,β的法向量分别为a ,b ,则////a b αβ⇔⇔a b λ= ,(3)用向量法证明空间中的垂直关系 ①线线垂直若空间不重合两条直线a ,b 的方向向量分别为a ,b ,则0a b a b a b ⊥⇔⊥⇔⋅=②线面垂直若直线a 的方向向量为a ,平面α的法向量为n ,且a α⊄,则//a a a n a n ααλ⊥⇔⊥⇔⇔=③面面垂直若空间不重合的两个平面α,β的法向量分别为a ,b ,则0a b a b αβ⊥⇔⊥⇔⋅=三、考点聚焦考点一 :空间向量概念及基本点、线、面间的位置关系的识别例1、如图,长方体''''ABCD A B C D -中,3AD =,5AB =,'3AA =,设E 为'DB 的中点,F为'BC 的中点,在给定的空间直角坐标系D xyz -下,试写出A B C D ,,,,'A ,'B ,'C ,'D ,E F ,各点的坐标。
例2、已知(2,3,1)a =--,(2,0,4)b = ,(4,6,2)c =-- ,则下列结论正确的是( ).A .////a c b c ,B .//a b a c ⊥ ,C .//a c a b ⊥ ,D .以上都不对 练习:1. 两不重合直线1l 和2l 的方向向量分别为121,012,0,()()2v v =-=-,,,则1l 与2l 的位置关系是( ).A .平行B .相交C .垂直D .不确定2. 已知平面α内有一个点2(1)1,M -,,平面α的一个法向量是,()636n -=,,则下列点P 中在平面α内的是( ).A .()2,3,3PB .()2,0,1P -C .()4,4,0P -D .()3,3,4P -3. 已知()2,2,1AB = ,()4,5,3AC =,则平面ABC 的单位法向量是4.已知点,,A B C ∈平面α,点P α∉,则0AP AB = ,且0AP AC = 是0AP BC =的( ).A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件考点二:用向量法证明平行关系例3、 如图,在正方体1111ABCD A BC D -中,E ,F 分别是棱BC ,11C D 的中点,求证:EF //平面11BB D D .考点三:用向量法证明垂直关系例4、已知正方体1111A B ABC C D D -中,E 为棱1CC 上的动点,(1)求证:1A E BD ⊥;(2)当E 恰为棱1CC 的中点时,求证:平面BD A 1⊥平面EBD ;(4)用向量法求空间角 ①异面直线夹角设异面直线a ,b 的夹角为θ,方向向量为a ,b,其夹角为ϕ,则有cos cos a b a bθϕ⋅==②线面角设直线l 的方向向量为l ,平面α的法向量为n,l 与α所成的角为θ,l 与n 的夹角为ϕ,则有sin cos l nl nθϕ⋅== .③二面角设1n ,2n 是二面角l αβ--的两个面α,β的法向量,则向量1n ,2n的夹角(或其补角)就是二面角的平面角的大小.若二面角l αβ--的平面角为θ,则1212cos n n n n θ⋅= .(5)用向量法求空间距离 ①点到点的距离点A 与点B 之间的距离可以转化为两点对应向量AB的模AB 计算.DA 1BCEAB 1C 1D 1②点到线的距离在直线l 上找一点P ,过定点A 且垂直于直线l 的向量为n,则定点A 到直线l 的距离为cos ,PA n d PA PA n n⋅=〈〉=③点到面距离点P 是平面α外一点,A 是平面α内的一定点,n为平面α的一个法向量,则点P 到平面α的距离为cos ,PA n d PA PA n n⋅=〈〉=考点一:求异面直线夹角例5、如图,在空间直角坐标系中有直三棱柱111ABC A B C -,12CA CC CB ==,则直线1BC 与直线1AB 夹角的余弦值为( ) (A )(B(C )(D ) 35例6、如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,底面ABCD 是菱形,2,60AB BAD =∠= 。
(Ⅰ)求证:BD ⊥平面;PAC(Ⅱ)若,PA AB =求PB 与AC 所成角的余弦值;考点二:线面角例7、【2016高考北京卷理第17题】(本小题14分)如图,在四棱锥P ABCD -中,平面PAD ⊥平面ABCD ,PA PD ⊥,PA PD =,AB AD ⊥,1AB =,2AD =,AC CD ==(1)求证:PD ⊥平面PAB ;(2)求直线PB 与平面PCD 所成角的正弦值;(3)在棱PA 上是否存在点M ,使得//BM 平面PCD ?若存在,求AMAP的值;若不存在,说明理由。
例8、【2015高考新课标1卷理第18题】如图,,四边形ABCD 为菱形,120ABC ∠=︒,E ,F 是平面ABCD同一侧的两点,BE ⊥平面ABCD ,DF ⊥平面ABCD ,2BE DF =,.AE EC ⊥ (Ⅰ)证明:平面AEC ⊥平面AFC ; (Ⅱ)求直线AE 与直线CF 所成角的余弦值。
考点三:二面角例10、【2016高考新课标2卷理第19题】如图,菱形ABCD 的对角线AC 与BD 交于点O ,5,6AB AC ==,点,E F 分别在AD CD ,上,54AE CF ==,EF 交于BD 于点H ,将△DEF 沿EF折到△D EF '的位置,OD '= (Ⅰ)证明:D H '⊥平面ABCD ; (Ⅱ)求二面角B D A C -'-的正弦值。
例11、【2014高考重庆卷理第19题】如题(19)图,四棱锥ABCD P -中,底面是以O 为中心的菱形,⊥PO 底面ABCD ,3,2π=∠=BAD AB ,M 为BC 上一点,且AP MP BM ⊥=,21。
(Ⅰ)求PO 的长;(Ⅱ)求二面角C PM A --的正弦值。
例12、【2014高考天津卷第17题】如图,在四棱锥P ABCD -中,PA ^底面ABCD ,AD AB ^,//AB DC ,2AD DC AP ===,1AB =,点E 为棱PC 的中点。
(Ⅰ)证明:BE DC ^;(Ⅱ)求直线BE 与平面PBD 所成角的正弦值;(Ⅲ)若F 为棱PC 上一点,满足BF AC ^,求二面角F AB P --的余弦值。
练习:1、【2013高考新课标1卷理第18题】如图,三棱柱111ABC A B C -中,1CA CB AB AA ==,, 160BAA ∠=︒。
(Ⅰ)证明1AB AC ⊥; (Ⅱ)若平面ABC ⊥平面11AA B B ,AB CB =,求直线1AC 与平面11BB C C 所成角的正弦值。
2、【2016高考新课标3卷理第19题】如图,四棱锥P ABC -中,PA ⊥地面ABCD ,AD BC ,3AB AD AC ===,4PA BC ==,M 为线段AD 上一点,2AM MD =,N 为PC 的中点。
(I )证明MN平面PAB ;(II )求直线AN 与平面PMN 所成角的正弦值。
3、【2014高考全国2卷理第18题】如图,四棱锥P ABCD -中,底面ABCD 为矩形,PA ⊥平面ABCD ,E 为PD 的中点。
(Ⅰ)证明:PB ∥平面AEC ;(Ⅱ)设二面角D AE C --为60°,1,AP AD ==E ACD -的体积。
4、【2014高考全国1卷第19题】如图,三棱柱111C B A ABC -中,侧面C C BB 11为菱形,C B AB 1⊥。
(Ⅰ)证明:1AC AB =;(Ⅱ)若1AC AB ⊥,︒=∠601CBB ,AB BC =,求二面角111C B A A --的余弦值。
5、【2013高考重庆理第19题】如图,四棱锥P ABCD -中,PA ABCD ⊥底面,2,4,3BC CD AC ACB ACD π===∠=∠=,F 为PC 的中点,AF PB ⊥.(1)求PA 的长; (2)求二面角B AF D --的正弦值.6、【2012高考新课标理第19题】如图,直三棱柱111ABC A B C -中,112AC BC AA ==,D 是棱1AA 的中点,1DC BD ⊥。
