beam188不能用于计算单轴对称截面梁的弯扭失稳问题(参考模板)
用beam188模拟梁和柱子,用solid45单元模拟基础

我现在有个问题:用beam188模拟梁和柱子,用solid45单元模拟基础。
采用cerig命令连接两种单元。
求解时总出错,请大侠帮忙看看。
命令流如下:/filename,lianxi/units,si/prep7et,1,beam188et,2,solid45sectype,1,beam,rectsecdata,0.55,0.55sectype,2,beam,rectsecdata,0.25,0.55r,1mp,ex,1,2.8e10mp,nuxy,1,0.2mp,dens,1,2500mp,ex,2,3.0e10mp,nuxy,2,0.2mp,dens,2,2500k,100,20,0,20k,1,0,0,0k,7,0,0,18kfill,1,7kgen,2,1,7,,6l,1,7l,8,14lsel,s,loc,z,0.01,18latt,1,1,1,,100,,1lesize,all,0.5lmesh,alllsel,u,,,alll,2,9lgen,6,3,,,,,3latt,1,1,1,,100,,2lesize,all,0.5lmesh,alllsel,u,,,allsave!基础/pnum,volu,1block,-0.6,0.6,-0.6,0.6,-1.0,0 vgen,2,1,,,6block,0.6,5.4,-0.6,0.6,-1.0,0 vglue,all!基础划分!Y 方向1vsel,s,loc,z,-1.0,-0.01vsel,r,loc,x,-0.6,0.6vsel,r,loc,y,-0.6,0.6vatt,2,,2aslvlslalesize,all,0.5mshape,0,3Dmshkey,1vmesh,allvsel,u,,,allallselvsel,s,loc,z,-1.0,-0.01vsel,r,loc,x,5.4,6.6vsel,r,loc,y,-0.6,0.6vatt,2,,2aslvlslalesize,all,0.5mshape,0,3Dmshkey,1vmesh,allvsel,u,,,allallselvsel,s,loc,z,-1.0,0vsel,r,loc,x,0.6,5.4vsel,r,loc,y,-0.6,0.6vatt,2,,2aslvlslalesize,all,0.5mshape,0,3Dmshkey,1vmesh,allvsel,u,,,allallsel/SOLantype,staticnlgeom,on !nropt,fulltime,1nsub,50outres,all,last!asel,s,loc,z,-1.0da,all,allasel,s,loc,x,-0.6asel,a,loc,x,6.6da,all,uxda,all,uyasel,s,loc,y,-0.6asel,a,loc,y,0.6da,all,uxda,all,uyallsel,allACEL,0,0,9.8nsel,s,loc,z,0nsel,r,loc,x,-0.6,0.6nsel,r,loc,y,-0.6,0.6 cerig,1,all,allnsel,s,loc,z,0nsel,r,loc,x,5.4,6.6nsel,r,loc,y,-0.6,0.6 cerig,74,all,all!在梁上施加线荷载7000N/m lsel,s,loc,z,3lsel,a,loc,z,6lsel,a,loc,z,9lsel,a,loc,z,12lsel,a,loc,z,15allsel,below,line sfbeam,all,1,pres,7000 allsel,allsolve2009-1-5 20:18 #4lsa512助理工程师精华0积分12帖子31水位39技术分0状态离线我用cerig命令建的刚性区域,出现下面警告Constraint equations may not be valid for elements that undergolarge deflections.请问高手这个警告可以忽略吗?ansys学习-beam188与189中的额外节点BEAM188和189是ANSYS从5.5版本开始起增加的新的梁单元,它的最大特点是支持梁截面形状显示,可以考虑剪切变形和翘曲,同时也支持大转动和大应变等非线性行为,而且也可以直接显示梁截面上的应力和变形。
梁等效计算长度系数确定及稳定设计

将上式分别对ab求偏导数可以得到因为ab不能同时为零所以方程式8有非零解即其系数行列式为零从而1荷载作用于梁的下翼缘荷载作用于梁的剪心面荷载作用于梁的上翼缘伸臂部分作用有均布荷载伸臂端部作用有集中荷载当荷载一定时式10中f等效计算长度系数计算公式确定对于双伸臂工字梁当引入等效计算长度系数11将式11变形为12则将k13这样双伸臂梁的等效计算长度系数即可以按照下面的公式进行计算14那么在每一种尺寸和荷载形式的组合下利用已经得到的k值和即可以计算出在该种情况下伸臂梁以集中荷载作用在双伸臂梁端部剪心面时为例计算结果列入表1中可以看出同时随着的变化而变化本文经过大量的反复试算选取了合适的基函数最后得到拟合公式为15采用类似的方法可以将双伸臂梁在4种荷载作用形式下的等效计算长度系数值的计算公式分别计算得出列入表2前面已经得到单伸臂梁的临界弯矩mcr的计算式11通常设计时采用整体稳定系数16其中17对双轴对称工字型截面式17可进一步简化为t双伸臂梁整体稳定设计步骤及相应设计公式首先由以下两式计算出双伸臂梁的为梁的伸臂段长度l为中间段长度
( θ1 ) z1 = 0 ( θ"1 ) ( 翘曲应力为 0 ) z1 = l1 = 0 GI k θ'1 - EI ω θ"'1 = Te ( 内外扭矩相等)
用 BEAM44,BEAM188,BEAM189 单元模拟线模型

7.3.3 用BEAM44,BEAM188,BEAM189 单元模拟线模型在用BEAM44、BEAM188、BEAM189 单元划分线实体前,要定义一些属性,包括:生成梁单元的材料设置属性点;要划分线的梁单元类型;以梁单元的轴向为基准的截面定位;参见《ANSYS Modeling and Meshing Guide》§7.5.2;生成梁单元的截面号。
使用LATT命令将这些属性与选择的线实体关联:命令:LATT,MAT,,TYPE,,KB,,SECIDGUI: Main Menu>Preprocessor>-Attributes-Define>Picked Lines其中:MAT--与所选择的尚未划分网格的线关联的材料号;TYPE--与所选择的尚未划分网格的线关联的类型号;KB--对应于模型中的关键点号。
所生成的梁单元的横截面按这样定向,梁的Z轴将位于由线的两端点和该关键点定义的平面;SECID--与SECTYPE命令定义的梁横截面相对应,截面号由SECNUM指定。
7.4 建立截面有两类梁截面:一般截面;自定义截面。
自定义截面可用标准的几何形状和单个材料来描述。
自定义截面可由任意几何形状定义,还可以包含若干各向同性材料。
7.4.1 使用梁工具生成通用横截面SECTYPE、SECDATA和SECOFFSET命令(Main Menu> Preprocessor>-Beam-Common Sectns),都与GUI上的梁工具(BEAM TOOL)关联。
梁工具的样式取决于所选择的梁横截面子形状:图7-3 梁工具对话框(包括子类型下拉框)梁工具的顶部,是截面形状号(以及截面名)[SECTYPE],中部是需要时定义截面偏移的信息[SECOFFSET],底部是截面几何形状信息[SECDATA]。
SECDATA命令定义的尺寸取决于所选子类型。
可以单击梁工具下的Help 按钮获取所选截面的帮助信息。
基于abaqus的钢梁特征值屈曲与失稳分析

目录:1. 绪论 (2)1.1背景 (2)1.2 钢梁稳定理论的发展状况 (2)2 . 稳定的概念 (3)3. 线性屈曲分析 (4)3.1 工程实例的简化 (4)3.2 有限元模型的建立 (4)3.2.1创建部件 (4)3.2.2创建材料和截面的属性 (6)3.2.3定义装配件 (7)3.2.4设置分析步 (7)3.2.5定义在载荷和边界条件 (8)3.2.6网格的划分 (9)3.2.7 提交分析作业 (9)3.2.8 模型数据的后处理 (10)3.2.9 数据分析总结 (12)4.结论 (12)基于abaqus的钢梁特征值屈曲与失稳分析摘要:钢结构的稳定性能是决定其承载力的一个特别重要的因素,稳定理论和设计方法需要完善。
近几十年以来,在研究发挥钢结构稳定性能的潜力和完善稳定计算的理论方面,国内外都取得了长足的进步。
例如完善钢结构的弹塑性稳定理论,研究有几何缺陷和残余应力的钢结构的实际受力性能和其极限荷载,用数值法来解决这类问题等都取得了不少研究成果。
在作理论分析的同时进行稳定性能的试验验证,以及将理论研究结果利用图表表示或深化为计算公式,从而将弹塑性稳定理论用于解决钢结构设计中的问题都取得了丰硕成果。
本文的主要内容是对现有失稳理论进行完善和发展及其总结,利用通用有限元abaqus软件,采用特征值的Lanczos方法及子空间迭代法对钢梁进行屈曲分析,文中总共给了10个特征向量,进而得出相应的模态分析变形图,最后把lanczos 方法及子空间迭代法进行了比较,提出一些新的问题。
关键词:有限元abaqus 失稳特征值屈曲分析1. 绪论1.1背景钢材具有强度高、质量轻、力学性能好的优点,是制造结构物的一种极好的建筑材料。
钢材与在建筑结构中应用广泛的钢筋混凝土结构相比,对于受力功能相同的构件,具有截面轮廓尺寸小、构件细长和板件薄柔的特点。
但是对于因受压、受弯和受剪等存在受压区域的构件和板件,如果技术上处理不当,可能使钢结构出现整体失稳或局部失稳。
梁模型有限元计算_ANSYS Workbench有限元分析实例详解(静力学)_[共7页]
![梁模型有限元计算_ANSYS Workbench有限元分析实例详解(静力学)_[共7页]](https://img.taocdn.com/s3/m/ba2491b227d3240c8547ef2c.png)
4.2 梁单元静力学分析当结构长度对横截面的比率超过10:1,沿长度方向的应力为主要分析对象,且横截面始终保持不变时,即应用梁单元。
梁单元可用于分析主要受侧向或横向载荷的结构,如建筑桁架、桥梁、螺栓等。
在WB中默认为铁摩辛柯(Timoshenko)梁单元,即Beam188和Beam189,可计算弯曲、轴向、扭转和横向剪切变形。
其中Beam188采用线性多项式作为形函数,Beam189采用二次多项式作为形函数,当WB的Mesh设置中Mesh-Element Midside Nodes为Dropped 时,即为Beam188;Mesh-Element Midside Nodes为Kept时,即为Beam189。
有限元对单元特性的描述包括单元形状、节点数目、自由度和形函数。
表4-2-1为Beam 单元的对比。
在WB中默认设置为二次单元。
一般来说,线性单元需要更多的网格数才能达到二次单元的精度。
选用二次单元可提高计算精度,这是因为二次单元的曲线或曲面边界能够更好地逼近结构的曲线和曲面边界,且二次插值函数可更高精度地逼近复杂场函数,所以当结构形状不规则、应力分布或变形很复杂时可以选用高阶单元。
但高阶单元的节点数较多,在网格数量相同的情况下由高阶单元组成的模型规模要大得多,计算内存消耗也多,因此,在使用时应权衡考虑计算精度和时间。
表4-2-1 Beam单元对比4.2.1 梁模型有限元计算用ProE建立一桁架模型,导入WB进行分析计算。
(1)ProE建模。
在草绘界面绘制一边长为30mm、40mm、50mm的三角形,然后选择投影命令将草绘图形投影到基准面上,另存为x_t文件(其他3D软件操作方法类似)。
(2)导入模型。
如图4-2-1所示,在Import设置中,Operation设为Add Frozen,Line Bodies 设为Yes。
– 65 –– 66 – 图4-2-1 Import ProE模型文件设置(3)梁截面赋值,并定义截面方向,最后用Form New Part将三根梁合并为一个部件,如图4-2-2所示。
悬臂梁的横向扭转屈曲例题

7.6 横向扭转屈曲分析实例(GUI方式)可以用 BEAM188 和 BEAM189 单元来模拟直梁的弯曲和剪切,也可以模拟梁的横向扭转屈曲。
为了建立这一模型,需要建立足够密的梁单元网格。
典型地,需要用一系列的梁单元来模拟一根直梁。
如图7-4 所示。
图7-4 悬臂梁的横向扭转屈曲悬臂梁的横向扭转屈曲,用60个 BEAM188 单元模拟(通过/ESHAPE显示)《ANSYS Structural Analysis Guide》§7 详细叙述了屈曲分析。
本例分析悬臂梁在末端承受横向载荷时的行为。
7.6.1 问题描述一根直的细长悬臂梁,一端固定一端自由。
在自由端施加载荷。
本模型做特征值屈曲分析,并进行非线性载荷和变形研究。
研究目标为确定梁发生支点失稳(标志为侧向的大位移)的临界载荷。
参见图7-5。
7.6.2 问题特性参数材料特性:杨氏模量=1.0X10e4 psi;泊松比=0.0。
几何特性:L=100 in;H=5 in;B=2 in。
载荷为:P=1 lb。
7.6.3 草图图7-5 梁的变形7.6.4 特征值屈曲和非线性破坏分析特征值屈曲分析是线性分析,通常仅适用于弹性结构。
通常在小于特征值屈曲分析得到的临界载荷之前发生材料屈服。
这种分析比完全非线性屈曲分析所需的求解时间要少。
用户还可以用弧长法做非线性载荷-位移研究,这时用弧长法确定临界载荷。
对于更一般的情况,需要进行破坏分析。
模型有缺陷时,必须做非线性破坏分析,因为完美模型不会表现出显著的屈曲。
可以通过使用特征值分析得到的特征向量,来加入缺陷。
求得的特征向量是对实际屈曲模态最接近的预测。
添加的缺陷与梁的典型厚度相比,应为小量。
缺陷删除了载荷-位移曲线的突变部分。
通常情况下,缺陷最大值为梁厚度的1%~10%。
UPGEOM命令在前一步分析的基础上添加位移,并把几何形状更新到变形后的形状。
7.6.5 设置分析名称和定义模型的几何实体1、选择菜单“Utility Menu>File>Change Title”。
ANSYS 中文帮助

压力3 压力4
Pseudo Node( Node(假节点) 1 温度 LBFE 1 2 2 3 3 4 4
file://C:\Documents and Settings\Administrator\Local Settings\Temp\...
2009-7-21
Beam3单元特性
页码,5/64
BEAM3项目和序号 目和序号表(KEYOPT(9) = 1)
Output Quantity Name (变量名) SDIR 轴向直接应力 命令输入项 ETABLE 和 ESOL命令输 Item LS LS LS LEPEL LEPEL LEPEL LEPTH LEPTH LEPTH LEPTH NMISC NMISC SMISC SMISC SMISC SMISC SMISC SMISC SMISC SMISC SMISC TEMP 温度 LBFE E 10 I 1 2 3 1 2 3 1 2 3 1 2 1 2 6 19 21 23 25 27 ILI 4 5 6 4 5 6 4 5 6 3 4 7 8 12 J 7 8 9 7 8 9 7 8 9 5 6 13 14 18 20 22 24 26 28
Output Quantity Name (变量名) SDIR 轴向直接应力 命令输入项 ETABLE 和 ESOL命令输 Item LS LS LS LEPEL LEPEL LEPEL LEPTH LEPTH LEPTH LEPTH NMISC NMISC SMISC SMISC SMISC SMISC SMISC SMISC SMISC SMISC SMISC E 7 I 1 2 3 1 2 3 1 2 3 1 2 1 2 6 13 15 17 19 21 J 4 5 6 4 5 6 4 5 6 3 4 7 8 12 14 16 18 20 22
ANSYS BEAM44单元详解
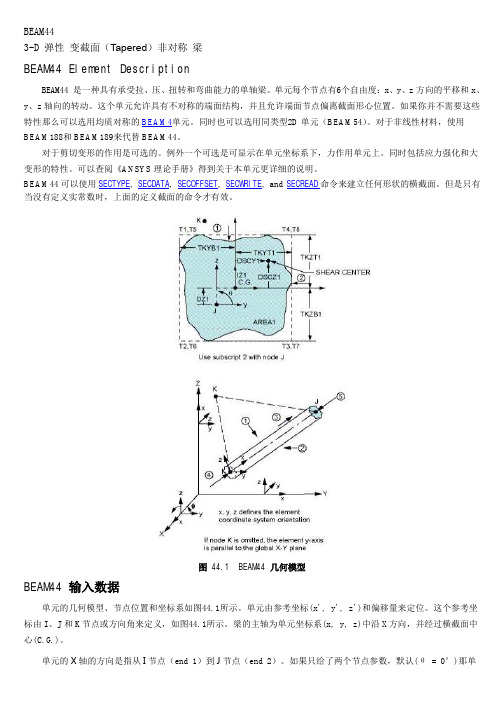
元 Y 轴的方向自动确定为平行于系统坐标系下的 X-Y 平面。有关示例见上图。当单元坐标的 X 轴平行于整体坐标系 下的 Z 轴(包括0.01%的偏差在内),单元 Y 轴的方向是平行于总体坐标系下的 Y 轴。用户可以通过给定 θ 角或定义 第三个节点的方法来控制单元的方向。如果前面的两个参数同时给定时,则以给定第三点的控制为准。第三点一经给 出就意味着定义了一个由 I,J,K 三点定义的平面且该平面包含了单元坐标的 X 与 Z 轴。当本单元用于大变形分析时, 那么给定的第三节点(K)或旋转角(θ)仅用来确定单元的初始状态。 (有关方向节点及单元划分的详细信息参见《实 体单元分网》及《ansys 建模与分网指南》。K 节点的只能生成可以查看 LMESH 和 LATT 命令描述。 用实常数来描述梁的横截面,需要定义面积、面积惯性矩、端点到形心的距离,形心的偏移,和剪切系数。IZ 和 IY 两个惯性矩是在单元主轴的侧面。截面 1(IX1)的扭转惯性矩如果没有特别说明,那其值就默认为在截面1的极惯 性矩(IZ1+IY1)。截面2 的转动惯性矩(IX2,IY2和 IZ2),如果空白,就默认为对应截面1的值。单元的扭转刚度随 着 IX 的值而减小。 偏移量常数(DX, DY, DZ)由截面中心位置相对节点位置来定义。沿着单元坐标系正向的位置为正。所有截面2 处 实常数(除了中心偏移实常数 DX, DY, 和 DZ)如果为0,则都默认为其对应截面 1 处的值。截面1节点的上层厚度(the "bottom" thicknesses),TKZT1 和 TKYT1,分别默认为截面1节点的下层厚度(the "bottom" thicknesses),TKZB1 and TKYB1。截面 2节点的上层厚度(the "bottom" thicknesses),TKZT2 和 TKYT2,也分别默认为截面 2节点的下 层厚度(the "bottom" thicknesses),TKZB2 and TKYB2。上层厚度为顶点到截面中心的距离,下层厚度为底点到截 面中心的距离。 剪切变形系数(SHEARZ 和 SHEARY)只有在考虑剪切变形时才使用。某个方向上剪切系数为0,一般用在忽略该方 向上的剪切变形。查看剪切变形细节。 如果没有实常数定义,使用 SECTYPE 和 SECDATA 命令来分别定义横截面(细节查看《ANSYS 结构分析指南》中的 梁分析和横截面)。注意使用 SECTYPE 和 SECDATA 命令建立的截面可以在同一个模型中被 BEAM44, BEAM188, 和 BEAM189中的任何组合使用。截面与单元用截面号(SECNUM)来关联,截面号是独立的单元属性。 KEYOPT(2)允许缩减质量矩阵(reduced mass matrix)表达(删除转动方向的自由度)。这个选项有助于改善在 分析细长杆在质量荷载(mass loading)下计算得到弯曲应力结果。 KEYOPT(7) 和 KEYOPT(8)允许在单元坐标系上节点上的单元节点约束释放。在做自由运动时,节点约束则不能释 放,同时将会有 pivot 警告和错误信息。同时,应力刚度矩阵的平移自由度上不能进行节点约束释放。作用在节点约 束释放方向上的荷载将被忽略。对于大变形,注意到单元的节点约束释放是沿着单元的方向,但是在节点耦合处不释 放。在没有节点约束释放的模型中添加柔性(低弹性模量)梁单元有助于提高解的稳定性。 剪切面积(ARES_ _)和扭转应力系数(TSF_) 在非零时,将起作用。剪切面积仅仅是为了计算剪切应力,一般小于 实际横截面的面积。扭惯性矩乘上扭转应力系数可计算得到扭转剪切应力。扭转剪切系数一般可在结构手册上查到。 对于圆截面,TSF=直径/(2*IX)。 对于有些梁的截面,剪切中心可以与形心不重合。非零的剪切中间偏移(DSC_ _)应该按图44.1“梁几何模型”所 示的输入。剪切中心偏移以形心沿单元坐标系正向为正。截面 2节点的偏移值如果为0,则默认为截面1节点的数值。 如图44.2“梁的应力输出”所示,如果从 Y1到 Z4的常数给定,梁每端可以输出给定点4个点的附加应力。 弹性基础刚度(EFS_)是基础产生单位法向变形所需的压力。当 EFS_为0时,可以忽略这个性能。单元的初始应变 (ISTRN) 通过 Δ/L 给定, 这里的 Δ 是单元长度 L (由节点 I 和 J 的坐标所决定) 与零应变时的长度之差。 参数 ADDMAS 要输入的值是每单位长度的附加质量。 “节点与单元荷载”一节对“单元荷载”有专门介绍。可以在本单元的表面施加面荷载,如上图中带圈数字所示, 其中箭头指向为面荷载作用正向。横向均布压力的单位为力每单位长度,端点作用的压力应以集中力的形式输入。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
beam188不能用于计算单轴对称截面梁的弯扭失稳问题?题:用beam188单元求单轴对称H型截面梁在纯弯作用下的线性屈曲特征值。
题目条件:截面高度:300mm上翼缘:150*12mm下翼缘:80*12mm腹板厚度:10mm构件长度:3000mm弹性模量:E=68000MPa泊松比:0.315两端铰接,简支,端部可自由翘曲打开Beam188的翘曲自由度计算结果:Mcr=50.17 kN*m根据经典弹性理论,βy=97.25mm(正值,由于上翼缘较大,受压),Mcr=85.93kN*m结果明显错误。
于是将上下翼缘颠倒,再计算之。
即:上翼缘:80*12mm下翼缘:150*12mm计算结果仍然是:Mcr=50.17 kN*m根据经典弹性理论,βy=-97.25mm(负值,由于上翼缘较小,受压),Mcr=29.22kN*m最后,经典弹性理论的计算公式中,直接取βy=0.0 mm(不考虑Wagnar效应),可得Mcr=50.11kN*m,这样才和Ansys计算结果相近。
结论:beam188不能用于计算单轴对称截面梁的弯扭失稳问题。
(也许我还没有找到某个开关,先暂时下此结论。
望有高手指教)再以板单元建立模型验证:单元采用SHELL63,上翼缘大时,得Mcr=50.12 kN*m颠倒过来,上翼缘小时,得Mcr=29.20 kN*m结论:板单元可以用于计算单轴对称截面梁的弯扭失稳问题。
也再次验证了beam188的计算错误。
2007-12-18 04:30 #1warsheep助理工程师精华 0积分 70帖子 33水位 70技术分 0忘了说明:Ansys版本为8.0支座位置位于截面形心上。
2007-12-18 10:12 #2wilsonweic助理工程师精华 0积分 70帖子 35水位 70技术分 0用beam188/189单元进行线性弯扭屈曲分析,结果不可靠。
除了你所说的单轴对称截面外,事实上,双轴对称截面梁的线性弯扭屈曲分析结果也不准确。
虽然所涉及的只是线性屈曲分析,但是,我们有理由怀疑,beam188/189非线性弯扭屈曲分析的结果也不一定准确。
条件允许的话,最好用壳单元分析结果进行校核。
我分别用beam188单元和shell181单元对两端简支和两端固支的双轴对称截面纯弯梁进行了特征值屈曲分析,分析结果与理论屈曲荷载进行了对比。
用beam188分析时,分别考虑了KEYOPT1=0和KEYOPT1=1两种情况。
结果显示shell181分析的结果与理论值吻合良好,而beam188分析的结果误差很大(见附件)。
相关的内容还可参见/viewthread ... mp;bpg=1&age=302007-12-18 18:26 #3mqiao助理工程师精华 0积分 69帖子 34水位 69技术分 0您说的有些道理,但部分观点不敢苟同。
经过对ansys的beam188单元刚度矩阵的研究,发现原因可能是beam188的几何刚度矩阵一项中只考虑了轴力的影响,而没有考虑和转角φ以及φ'所对应的弯矩和剪力的影响,梁单元的完整的几何刚度矩阵可参考《钢结构构件稳定理论于设计》(陈骥)p445。
让人郁闷的是,Ansys手册中没有给出beam188的几何刚度矩阵公式,只给出了一个beam4的几何刚度矩阵公式。
(Ansys theory Reference,式(3-60)),所以上述也仅仅是猜测而已。
但是,可以确定的是:beam188不能用于计算梁(主要是非双轴对称截面梁)的弯扭失稳,包括线性特征值分析和几何非线性分析。
另外经过我对大量算例的分析表明:对于双轴对称截面梁的弯扭屈曲,其计算结果和经典解接近。
(但长度很小时差别略大)对于轴心受压构件的弯曲屈曲,其计算结果和经典解接近。
对于轴压构件的弯扭屈曲,其计算结果和经典解接近。
其他有限元软件也有类似问题。
很不幸,我要算的梁太多了,如果全部用板单元恐怕要算到明年了。
只能自己编程序了。
郁闷中啊。
jxln兄,我的以上认识可能也有不妥,有空可相互探讨之,我的qq是1788382。
2007-12-19 00:03 #4710476703工程师精华 0积分 136帖子 38水位 79技术分 0jxln兄:我粗略研究了你的附件中的命令流,发现您的命令流其实是错误的。
您的命令流为:两端简支\beam188.c修改后的命令流为(修改处增加了注解):/prep7et,1,beam188,,,2,keyopt,1,1,1 !*******考虑翘曲自由度********mp,ex,1,2.06e11mp,prxy,1,0.3SECTYPE,1, BEAM, I, , 2!*******原有命令流截面划分过于粗糙******** SECOFFSET, CENTSECDATA,0.1,0.1,0.6,0.01,0.01,0.008,0,0,0,0secplot,1,1k,1,k,2,5,k,3,,-2,l,1,2latt,1,,1,,3,,1,lesize,all,,,20,lmesh,all/eshape,1,1,/rep/pnum,node,1/eshape,0,/replotsavefinish/solANTYPE,staticPSTRES,ONdk,1,ux,0dk,1,uy,0dk,1,uz,0dk,1,rotx,0dk,2,uy,0dk,2,uz,0dk,2,rotx,0 !*******重新设置了边界条件,主要是一端要可滑动********Fk,1,MZ,-1,Fk,2,MZ, 1, !*******主要错误:原有命令流中的弯矩施加到一端了,现改正之******** ftranSOLVEFINISHsave/SOLUTIONANTYPE,buckleBUCOPT,SUBSP,1MXPAND,1SOLVEFINISH/POST1SET,firstSET,LISTpldisp,1,最后得出的结果为58720(N.m),和经典解59007.25(N.m)是很接近的。
这正如我前文得出的结论,对于双轴对称截面,Ansys的分析勉强可以接受因为双轴对称截面的βy=0,φ'不会和弯曲M产生耦合(请参看弯扭屈曲经典微分方程)。
2007-12-19 09:31 #5小宝助理工程师精华 0积分 77帖子 38水位 77技术分 0算了,做人要厚道,既然要贴,就贴完整,把我分析的原因也贴出来。
以下文字基于《钢结构稳定理论与设计》(陈骥,科学出版社,2001)一书中第442页,附录《三、有限单元法求解受压和受弯构件的弯扭屈曲荷载》,本文的符号和公式均和该书相同。
以下简称该书为“陈骥书”先来将问题的表象:我进行了大量构件稳定问题的数值分析,包括弯曲屈曲和弯扭屈曲。
所有分析中均打开了翘曲自由度开关。
大量数值分析的结果表明:对轴压构件:弯曲屈曲和弯扭屈曲的分析结果和经典解一致。
对弯曲构件:双轴对称截面的梁的弯扭屈曲和经典解一致。
单轴对称截面梁的弯扭屈曲和经典解差别很大。
但是,在按经典弹性理论求Mcr时,若取βy=0,则得出的结果和Ansys 一致。
对压弯构件:双轴对称截面构件,无论弯曲还是弯扭均和经典解一致。
单轴对称截面压弯构件的分析结构和经典解差别很大。
弯矩越大,差别越大。
表象之要点:Ansys无法考虑βy的影响。
再来分析一下原因(Theory Reference中找不到beam188的单刚矩阵和几何刚度矩阵,故以下叙述仅为推断):首先:双轴对称截面梁的弯扭屈曲和经典解一致,说明beam188的单元刚度矩阵是正确的。
因为单元刚度矩阵中(见陈骥书p444,式3.8)没有βy。
其次:单轴对称截面梁的弯扭屈曲和经典解差别很大。
说明beam188的几何刚度矩阵是不正确的。
因为几何刚度矩阵中(见陈骥书p444,式3.9以及p450式3.30下面一段话)和βy有关。
再次:按经典弹性理论求Mcr时,若取βy=0,则得出的结果和Ansys一致。
这说明了什么呢?乖乖,原来是几何刚度矩阵中的2βy*Mx没放进去(注意:推断,仅仅是推断)。
结论: beam188的几何刚度矩阵有误。
或许也不能说人家有误,只是不适用于单轴对称梁的计算而已。
再结论:凡是βy不等于0的受弯、压弯构件不能用beam188来进行稳定分析。
但是轴压构件却可以用beam188来分析,因为轴压构件的M=0,压力P*i0^2在几何刚度矩阵中是主要项,βy几乎不起作用。
2007-12-19 18:07 #6wcysgc助理工程师精华 0积分 74帖子 37水位 74技术分 0最后再来研究Ansys中beam188的翘曲刚度开关的作用吧。
现象:用beam188分析构件时:对梁的弯扭稳定:考虑翘曲刚度得出的临界弯曲比不考虑翘曲刚度要大。
对轴压构件的弯扭稳定:考虑翘曲刚度得出的临界压力比不考虑翘曲刚度要大。
对轴压构件的弯曲稳定:考虑翘曲刚度得出的临界压力和不考虑翘曲刚度差不多。
原因(推断,还是推断而已):陈骥书p444页给出了单元刚度矩阵(式3.8),从刚度矩阵可以看出,和φ以及φ'对应的刚度有GIk和EIw。
对角元上,GIk和EIw均是正的。
这使我们容易推断出:beam188的翘曲刚度开关可能是将单元刚度矩阵中的EIw考虑进去。
显然,考虑了EIw将使单元刚度矩阵的特征值变大,因为对角元变大。
而在弯曲失稳中,扭转φ都不存在,因此考不考虑翘曲刚度对单元刚度矩阵没有影响。
结论:计算弯扭稳定问题,请打开beam188的翘曲自由度开关。
推论:构件端部的翘曲约束会使弯扭稳定临界荷载提高,但对弯曲稳定临界荷载无影响。
最后的请求:要是哪位大哥大姐知道某个开关,可以将βy考虑到几何刚度矩阵里面去,使beam188可以计算不对称截面梁的弯扭稳定,行行好告诉小弟我一声,以免去我编程之痛苦,我一定感激不尽,不尽感激啊!2007-12-19 21:18 #7ahhbck助理工程师精华 0积分 68帖子 34水位 68技术分 0ANSYS中的BEAM188,189分析单轴对称截面的平面外屈曲问题的确有问题,其中没有考虑2Mxbxu"t项的影响,包括ABAQUS中的B31OS,B32OS存在同样的问题。
可以参见Zhang L, Tong GSElastic buckling of inter-braced parallel beam systemsADVANCES IN STRUCTURAL ENGINEERING 7 (4): 371-382 AUG 2004上面有分析。
2007-12-20 00:41 #8sujiaquan助理工程师精华 0积分 69帖子 34水位 69技术分 0谢谢指点,EI检索里没有全文连接,我下载不到。
