2013年希望杯全国数学邀请赛答案
希望杯第4-13届小学六年级全国数学竞赛初赛复赛题及解答
2006年第四届小学“希望杯”全国数学邀请赛六年级第1试1．2006×2008×(12006×2007+12007×2008)＝________.2．900000－9＝________×99999.3． 1.•2×1.•2•4+ 1927＝________.4．如果a ＝20052006，b ＝20062007，c ＝20072008，那么a ，b ，c 中最大的是________，最小的是________.5．将某商品涨价25％，若涨价后销售金额与涨价前销售金额相同，则销售量减少了____％.6．小明和小刚各有玻璃弹球若干个。
小明对小刚说：“我若给你2个，我们的玻璃弹球将一样多。
”小刚说：“我若给你2个，我的弹球数量将是你的弹球数量的三分之一。
”小明和小刚共有玻璃弹球________个。
7．一次测验中，小明答错了10道题，小刚答错了8道题，小强答对的题的数量等于小明与小刚答对题的数量之和，且小强答错了3道题。
这次测验共有________道题。
8．一个两位数，加上它的个位数字的9倍，恰好等于100。
这个两位数的各位数字之和的五分之三是________。
9．将一个数A 的小数点向右移动两位，得到数B 。
那么B ＋A 是B －A 的_______倍.(结果写成分数形式) 10．用10根火柴棒首尾顺次连接接成一个三角形，能接成不同的三角形有________个。
11．希望小学举行运动会，全体运动员的编号是从1开始的连续整数，他们按左下图中实线所示，从第1珩第1列开始，按照编号从小到大的顺序排成一个方阵。
小明的编号是30，他排在第3行第6列，则运动员共有________人。
12．将长为5，宽为3，高为1的长方体木块的表面涂上漆，再切成15块棱长为l 的小正方体。
则三个面涂漆的小正方体有________块。
13．如下图中，∠AOB 的顶点0在直线l 上，已知图中所有小于平角的角之和是400度，则∠AOB ＝____度。
第十一届小学“希望杯”全国数学邀请赛五年级第1试题目及答案
第十一届小学“希望杯”全国数学邀请赛五年级第1试1.计算：5.62×49-5.62×39+43.8= 。
12.规定a△b=a÷(a+b),那么2△1.8=。
53.若干个数的平均数是2013，增加一个数后，平均数仍是2013，则增加的这个数是。
4.如果三位数3□2是4的倍数，那么□里能填的最小的数是，最大的数是。
5.观察下图，？代表的数是。
1 3 5 7 9 8 6 4 22 4 6 8 7 5 33 5 7 6 44 6 5？6.小明在计算一个整除的除法算式时，不小心将除数18看成15，得到的商是24，则正确的商是。
7.将100块糖分成5份，使每一份的数量依次多2，那么最少的一份有糖块，最多的一份有糖块。
8.一件商品，对原价打九折和打七折后的售价相差5.4，那么此商品的原价是元。
9.有26个连续的自然数，如果前13个数的和是247，那么，后13个数的和是。
10.在三位数253,257,523,527中，质数是。
11.14个棱长为1的正方体在地面上堆成如图1所示的几何体，将它的表面（包括与地面接触部分）染成红色，那么红色部分的面积是。
12.如图2，若梯形ABCD的上底AD长16厘米，高BD长21厘米，并且BD=3DE，则三角形ADE的面积是平方厘米，梯形的下底BC长厘米。
13.小丽将一些巧克力装入大，小两种礼盒中的一种礼盒内，如果每个小礼盒装5块巧克力，那么剩下10块；如果每个大礼盒装8块巧克力，那么少2块。
已知小礼盒比大礼盒多3个，则这些巧克力共有块。
14.从甲地到乙地，小张走完全程用2个小时，小李走完全程用1个小时。
如果小张和小李同时从甲地出发去乙地，后来，在某一时刻，小张未走的路程恰好是小李未走的路程的2倍，那么此时他们走了分钟。
15.有16盒饼干，其中15盒的重量（含盒子）相同，另有1盒少了几块，如果用天平称，那么至少称次就一定能找出这盒饼干。
16.编号1～10的10名篮球运动员轮流进行三人传球训练，第1轮由编号（1,2,3）的队员训练，然后依次是编号（4,5,6）（7,8,9）（10,1,2），…的队员训练，当再次轮到编号（1,2,3）的队员时，将要进行的是第轮训练。
2013希望杯六年级第二试
第十一届小学“希望杯”全国数学邀请赛六年级 第2试试题2013年4月14日 上午9:00-11:00一、填空题（每题5分，共60分）1. 计算：()()()()()3243542012201120132012÷⨯÷⨯÷⨯⨯÷⨯÷= 【解答】110062【解析】原式3452012201323420112012=⨯⨯⨯⨯⨯ 20132= 110062=2. 计算：11.53.1657.0512+++= 【解答】4165【解析】原式111.5357.05612=+++ 1.58.257.05=+++16.8=3. 地震时，震中同时向各个方向发出纵波和横波，传播速度分别是5.94千米/秒和3.87千米/秒。
某次地震，地震监测点的地震仪先接收到地震的纵波，11.5秒后接收到这个地震的横波，那么这次地震的震中距离地震监测点 千米。
（答案取整数）【解答】128【解析】设距离是x ，列方程得：11.53.87 5.94x x -=。
整理得：5.94 3.8711.5 3.87 5.94x x -=⨯⨯，解得：128x =。
4. 宏福超市购进一批食盐，第一个月售出这批食盐的40%，第二个月又售出120袋，这时已售出的和剩下的食盐的数量比是3:1，则宏福超市购进的这批食盐有 袋。
【解答】1200【解析】（1）已售出的占全部的：33134=+ （2）超市购进的这批食盐有：342040%12004⎛⎫÷-= ⎪⎝⎭（袋）。
5. 把一个自然数分解质因数，若所有质因数每个数位上的数字的和等于原数每个数位上的数字的和，则称这样的数为“史密斯数”。
如：27333,33327=⨯⨯++=+，即27是史密斯数。
那么，在4,32,58,65,94中，史密斯数有 个。
【解答】3【解析】（1）422,224,=⨯+=符合条件；（2）3222222,2222232=⨯⨯⨯⨯++++≠+，不符合条件。
2013年第24届希望杯全国数学邀请赛初一第2试试题(含答案word)
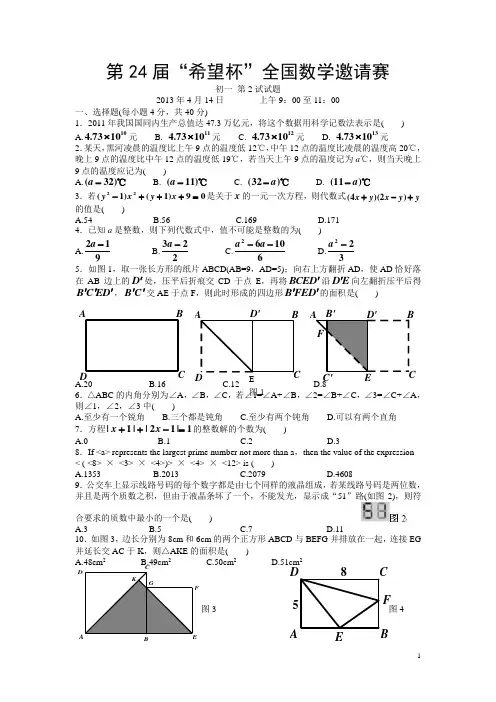
第24届“希望杯”全国数学邀请赛初一 第2试试题2013年4月14日 上午9：00至11：00一、选择题(每小题4分，共40分)1．2011年我国国同内生产总值达47.3万亿元，将这个数据用科学记数法表示是( )A.101073.4⨯元B. 111073.4⨯元C. 121073.4⨯元D. 131073.4⨯元2．某天，黑河凌晨的温度比上午9点的温度低12℃，中午12点的温度比凌晨的温度高20℃，晚上9点的温度比中午12点的温度低19℃，若当天上午9点的温度记为a ℃，则当天晚上9点的温度应记为( )A.℃)32(-aB. ℃)11(-aC. ℃)32(a -D. ℃)11(a -3．若09)1()1(22=+++-x y x y 是关于x 的一元一次方程，则代数式y y x y x +-+)2)(4(的值是( )A.54B.56C.169D.1714．已知a 是整数，则下列代数式中，值不可能是整数的为( ) A.912-a B.223-a C.61062--a a D.322-a 5．如图1，取一张长方形的纸片ABCD(AB=9，AD=5)；向右上方翻折AD ，使AD 恰好落在AB 边上的D '处，压平后折痕交CD 于点E ，再将D BCE '沿E D '向左翻折压平后得D E C B '''，C B ''交AE 于点F ，则此时形成的四边形D FE B ''的面积是( )A.20B.16C.12D.8 6．△ABC 的内角分别为∠A ，∠B ，∠C ，若∠1=∠A+∠B ，∠2=∠B+∠C ，∠3=∠C+∠A ，则∠1，∠2，∠3中( )A.至少有一个锐角B.三个都是钝角C.至少有两个钝角D.可以有两个直角7．方程1|12||1|=-++x x 的整数解的个数为( )A.0B.1C.2D.38．If <a> represents the largest prime number not more than a ，then the value of the expression < ( <8> × <3> × <4>)> × <4> × <12> is ( )A.1353B.2013C.2079D.46089．公交车上显示线路号码的每个数字都是由七个同样的液晶组成，若某线路号码是两位数，并且是两个质数之积，但由于液晶条坏了一个，不能发光，显示成“51”路(如图2)，则符合要求的质数中最小的一个是( )A.3B.5C.7D.1110．如图3，边长分别为8cm 和6cm 的两个正方形ABCD 与BEFG 并排放在一起，连接EG 并延长交AC 于K ，则△AKE 的面积是( )A.48cm 2B.49cm 2C.50cm 2D.51cm 2F B'D'A D'A D A D B C C B B C E 图1 KG F E D 8EC A F 图3 图4二、填空题(每小题4分，共40分)11．若a 表示x 与y 的和的平方，b 表示x 与y 的平方和，则当a=49，b=25时，xy=________；12．如图4，长方形ABCD 的长DC=8，宽AD=5，E 是AB 的中点，点F 在BC 上，已知△DEF 的面积为16，则点D 到直线EF 的距离为__________________13．若abc 都是质数，其中a 最小，且a+b+c=44，ab+3=c ，则ab+c=__________14．If a+3=b －9=c+6，then the value of 222)()()(a c c b b a -+-+- is ___________15．奇奇开车从北京去少林寺旅游，在高速公路和非高速公路上的行驶速度分别是120千米/时，60千米/时. 若奇奇驶完全用了6小时，其中在高速公路上行驶的路程是在非高速公路上行驶的路程的6倍，则全程长____________千米；16．如图5，在直角△ABC 的两直角边AC 、CB 上分别作正方形ACDE 和CBFG ，AF 交BC 于W ，连接GW ，若AC=14，BC=28，则__________=∆AGW S ；17．用2，0，1，3组成一个自然数，且每个数字至少用一次，其中可被225整除的最小的数是_________________.18．如图6，梯形ABCD 中，AD ∥BC ，BA=AD=DC ，BC=2AD ，若平行于底边的一条直线EF 把梯形分成周长相等的两部分，则___________=EF AE19．已知0≠abc ，若||4||3||2c c b b a a m ⨯⨯=，则__________122=++m m 20．在图7(1)中，对任意相邻的上下或左右两格中的数字同时加1或减2，这算作一次操作，经过若干次操作后，图7(1)能变为图7(2)，则图7(2)中A 格内的数是__________；(1) (2)三、解答题(每题都要写出推算过程)21．(本题满分10分)两个同样的圆柱形水池A 和B ，深度都是1.2米，1号抽水机18分钟可将A 池注满，2号抽水机24分钟可将A 池的满池水注入B 池，现在，若A 池中储有61池水，B 池没有水，同进打开1号，2号抽水机，当A 池水深0.6米时，同时关闭两个抽水机，求此时B 池的水深；F E B C 图5 图6 图722．(本题满分15分)如图8，E 、F 分别是平行四边形ABCD 的边AB 、BC 的中点，DE 与AF 交于点P ，点Q 在线段DE 上，且AQ ∥PC ，求梯形APCQ 的面积与平行四边形ABCD 的面积的比值；23．(本题满分15分)如图9，边长为1的等边三角形ABC 从图示的位置开始在数轴上顺时针无滑动地向右滚动，当三角形的一个顶点落在x =2013处时，三角形停止滚动.(1)落在x =2013处的点是三角形ABC 的哪个顶点？说明理由；(2)在滚动过程中，点A 走过的路程是多少？(3)若在滚动的过程中A 走过的路程是某个圆的周长，求这个圆的半径.B 图8图9。
历届(9—13届)希望杯五年级答案及解析
历届五年级希望杯答案及解析2010年第八届2011年第九届1、解：原式=1.25 ×31.3 ×3 ×8 = 100 ×93.9 = 9392、解：将循环节多写一次即可逐位比较3、解：十位数之前应该有1 + 2 + 3 +……+9 = 45位。
1位数有9位，10—19有20位，20—27有16位，所以十位数的开头应为28，为28293031324、解：从A到B一定会经过三步，第一步要从A走到中间，最后一步应该是从中间走到B，而第二步为从中间走到中间只能有一种走法。
从A到中间一条线上共有5种走法，从B到中间一条线上也有5种走法。
所以共有5 ×1 ×5 = 25种走法。
5、解：在3 ×4的长方形中有20个横平竖直的正方形。
斜着的有1 ×1正方形17个，2 ×2的正方形8个，还有1个3 ×3的大正方形。
共46个。
6、解：47 ÷b = c ……c ，即b ×c + c = 47，即c ×( b + 1 ) = 47，所以c一定是47的约数，c为47肯定不符合条件，所以c = 1，即除数是46，余数是1.7、解：能被90整除说明即能被9整除也能被10整除，被10整除说明最后一位是0，被9整除说明数字和应为9的倍数，即2 + 0 + 1 + 1 + a +0 是9的倍数，所以a = 5，即后两位是50.8、解：约数个数为奇数说明这个自然数为完全平方数，1000以内最大的完全平方数是31²= 9619、解：首先最下面的一个角肯定没有，最上面的中部也会少一部分，所以是丁。
10、解：一圈共400米，甲是乙速度的1.5倍，所以甲共走了240米，乙走了160米。
DE为60米，CE为40米。
SADE = 3000平方米，SBCE = 2000平方米，差为1000平方米。
11、解：弟弟如果不多跑半小时应比哥哥少跑80 ×30 — 900 = 1500米，所以哥哥共跑了1500 ÷（110—80）= 50分钟，共跑了50 ×110 = 5500米。
2013年希望杯数学竞赛试题答案
1、“a 的 3 倍与 b 的的和”用代数式表示为2、被 3 除商为 n 余 1 的数是3、某电影院第一排有x个座位，后面每一排都比前一排多2个座位，则第n排有个座位。
4、某市的出租车的起步价为5元（行驶不超过7千米），以后每增加1千米，加价1.5元，现在某人乘出租车行驶P千米的路程（P＞7）所需费用是（）A、5＋1.5PB、5＋1.5C、5－1.5PD、5＋1.5（P－7）5、用代数式表示（1）比a的倒数与b的倒数的和大1的数（2）与的和的20%（3）比x与y的积的倒数的4倍小3的数（4）a，b两数的平方和除以a，b两数的和的平方◆典例分析例：用代数式表示：（1）如果两数之和为20，其中一个数用字母表示，那么这两个数的积为。
（2）设为整数，则三个连续的偶数：。
（3）比的平方大的数。
（4）某产品的生产成品由元下降后是元（5）梯形的上底是，下底是上底的倍，高比上底小，则这个梯形的面积为。
解：（1）；（2），，；（3）；（4）；（5）。
评析：（1）根据两数之和为20，先表示出另一个数为，然后将两个数相乘，但要注意不能忘记在上加上括号；（2）首先是一个偶数的表示方法：，其次是相邻的两个偶数相差为2；（3）一是注意先读先写，二是“大”的意思用符号表示为“+”；（4）本例应注意避免将“由元下降”错误表示为“ ”。
正确理解是在元的基础上下降了5%x元，即；（5）先由题意分别表示下底= ，高= ，然后利用梯形面积公式列出式子：。
◆课下作业●拓展提高1、百货大楼进了一批花布，出售时要在进价的基础上加上一定的利润，其数量x与售价y之间的关系如下表：数量x（米）1 2 3 4 …售价y（元）8+0.3 16+0.6 24+0.9 32+1.2 …下列用数量x表示与售价y的公式中,正确的是( )A、 B、 C、 D、2、一台电视机成本a元，销售价比成本价增加，因库存积压，所以就按销售价的出售，那么每台实际售价为（）A、B、C、D、3、比和的差的一半大的数应表示为。
2013年希望杯六年级二试试题及标准答案
第十一届小学“希望杯”全国数学邀请赛六年级第２试试题2013年４月14日上午9:00-11:00一、填空题（每题5分，共60分)1．计算:()()()()()3243542012201120132012÷⨯÷⨯÷⨯⨯÷⨯÷=２．计算:11.5 3.1657.0512+++=3. 地震时，震中同时向各个方向发出纵波和横波，传播速度分别是5.9４千米/秒和3.87千米／秒。
某次地震，地震监测点的地震仪先接收到地震的纵波,11.5秒后接收到这个地震的横波,那么这次地震的震中距离地震监测点千米。
(答案取整数)４. 宏福超市购进一批食盐,第一个月售出这批食盐的40%，第二个月又售出１２０袋，这时已售出的和剩下的食盐的数量比是3:１,则宏福超市购进的这批食盐有袋。
5. 把一个自然数分解质因数,若所有质因数每个数位上的数字的和等于原数每个数位上的数字的和，则称这样的数为“史密斯数”。
如:27333,33327=⨯⨯++=+,即27是史密斯数。
那么，在4,３2,58,65，９４中,史密斯数有个。
6. 如图1,三个同心圆分别被直径AB，ＣD,EF,ＧＨ八等分,那么,图中阴影部分面积与非阴影部分面积之比是。
7. 有两列火车,车长分别时12５米和１1５米，车速分别是2２米/秒和18米/米,两车相向行驶，从两车车头相遇到车尾分别需要秒。
8. 老师让小明在10０米的环形跑道上按照如下的规律插上一些棋子做标记：从起点开始，沿着跑道每前进９０米就插上一面旗子，直到下一个90米的地方已经插有旗子为止,则小明要准备多少面旗子?9. 2013201320132013201312345++++除以5，余数是。
(注：2013a表示2013个a相乘）10．从1开始的n个连续的自然数，如果去掉其中的一个数后，余下各数的平均数是1527,那么去掉的数是。
1１. 若Ａ、B、C三种文具分别有３8个,７8个和1２8个，将每种文具都平均分给学生,分完后剩下2个A,6个Ｂ，20个C，则学生最多有人。
第四讲 2013小学“希望杯”全国数学邀请赛-赛前集训专题系列-4年级05-盈亏问题
2012小学“希望杯”全国数学邀请赛-赛前集训专题系列（四年级）专题之：盈亏问题【名师导航】：在生活中有这样一些问题：一定数量的物品分给一定数量的人，每人多一些，物品就不够；如果每人少一些，物品就有剩余。
盈亏问题就是在已知盈亏的情况下来确定物品总数和参加分配的人数。
解答盈亏问题的关键是弄清楚盈和亏两次分得差的关系。
此类问题常用比较法，最好把两次分配情况用简略的文字对齐罗列出来，这样便于比较分析。
其数量关系是：（1）（盈＋亏）÷两次分配差=份数，（大盈－小盈）÷两次分配差=份数（大亏－小亏）÷两次分配差=份数（2）每次分的数量×份数＋盈=总数量或每次分的数量×份数－亏=总数量非标准的盈亏问题都是由标准的盈亏问题演变过来的。
解答时一定要把两次分配方案进行比较，找到盈、亏的数量分别是多少？有些盈亏的量需转化后方可用公式直接解答。
【例题精讲】：例1、一个植树小组植树，如果每人栽6棵，还剩下14棵；如果每人栽8棵，就缺4棵。
这个植树小组多少人？一共有多少棵树？解答：每人栽6棵，多14棵------盈每人栽8棵，少4棵-------亏份数即总人数：（14＋4）÷（8－6）=9（人）总数量即总棵数：9×6＋14=68（棵）例2、学校将一批铅笔奖励给三好生，如果每人奖励9支，则缺45支；如果每人奖励7支，则缺7支。
三好生有多少人？铅笔有多少支？解答：每人9支，少45支----亏每人7支，少7支-----亏份数即总人数：（45―7）÷（9－7）=19（人）总数量即总支数：19×7－7=126（支）例3：有一些少先队员到山上去植树，如果每人植16棵，还有24棵没有植；如果每人植19棵，还有6棵没有植。
问有多少名少先队员？有多少棵树？解答：每人16棵，多24棵每人19棵，多6棵总人数：（24－6）÷（19－16）=6（名）总棵数：6×16＋24=120（棵））例4：学校给一批新入学的学生分配宿舍，如果每个房间住12人，则34人没有位置；如果每个房间住14人，则空出4个房间。
第八讲 2013小学“希望杯”全国数学邀请赛-赛前集训专题系列-4年级03-周期问题
2012小学“希望杯”全国数学邀请赛-赛前集训专题系列（四年级）专题三周期问题【名师导航】我们知道，每周七天，从星期一开始，依次为星期一，星期二，星期三，…，星期日。
一年有十二个月，从1月开始依次为1月，2月，3月，…，12月。
周周如此，年年一样。
生活中有许多类似这样重复出现的事物，这就是自然界常见的周期现象。
如果某一事物的变化具有周期性，那么该事物在经历一段变化后，又会呈现原来的状态。
我们把事物所经历的这一段，叫该事物变化的周期。
例如上面说到的星期的周期是7天，月份的周期是12个月。
再例如个位数字变化的周期是10，用动物记年的周期是12年等等。
在数学中，我们把与周期性有关的数学问题叫做周期问题，研究这一类问题主要是通过找规律，发现周期性，确定周期，然后把要求的问题和某一周期的变化相对应，以求得问题的解。
【例题精讲】例1.2003盏彩灯，按8盏红灯，5盏绿灯，12盏黄灯的顺序轮流排列挂在道路的旁边。
问最后一盏是什么颜色的灯，这2003盏灯中红灯、绿灯、黄灯各有多少盏？解：2003÷（8+5+12）=80…3，按彩灯排列的规律，最后一盏是红灯。
红灯有：8×80+3=643（盏）绿灯有：5×80=400（盏）黄灯有：12×80=960（盏）答：最的一盏灯是红灯，红灯有643盏，绿灯有400盏，黄灯有960盏。
例2.有4567个3连乘：3×3×3×…×3×3 它的积的个位数字是几？4567个3解：n个3相乘的个位数字是以“3、9、7、1”,四个数为一个周期循环的。
4567÷4=1141 (3)余数是3，所以4567个3连乘的个位数字是7。
例3.有一个一千位数，各位上的数字都是“1”。
这个一千位数除以7的余数是几？解：○1N个1除以7的余数是以“1、4、6、5、2、0”这六个数为一个周期循环的。
○2作有余除法：1000÷6=166 (4)○3余数是4，即在第167个周期的第四个数上，即余数是5.答：这个一千位数除以7的余数是5。
第24届希望杯全国数学竞赛八年级试题及答案
第24届“希望杯”全国数学邀请赛初二 第二试2013年4月15日 上午8：30至10：30一、 选择题（本大题共10小题，每小题4分，菜40分。
）以下每题的四个选项中，仅有一个是正确的，请将正确答案的英文字母写在每题后面的圆括号内。
1、红丝带是关注艾滋病防治问题的国际性标志，人胶将红丝带剪成小段，并用别针将折叠好的红丝带加紧在胸前，如图1所示，红丝带重叠部分形成的图形是（ ） （A ）正方形 （B ）矩形 C ）菱形 （D ）梯形2、设a 、b 、C 是不为零的实数，那么||||||a b cx a b c =+-的值有（ ） （A ）3种 （B ）4种 （C ）5种 （D ）6种3、ABC ∆的边长分别是21a m =-，21b m =+，()20c m m =>，则ABC ∆是（ ）（A ）等边三角形 （B ）钝角三角形 （C ）直角三角形 （D ）锐角三角形4、古人用天干和地支记序，其中天干有10个；甲乙丙丁戊己庚辛壬癸，地支有12个；子丑寅卯辰巳午未申酉戌亥，将天干的10个汉字和地支的12个汉字对应排列成如下两行； 甲乙丙丁戊己庚辛壬癸甲乙丙丁戊己庚辛壬癸甲乙丙丁…… 子丑寅卯辰巳午未申酉戌亥子丑寅卯辰巳午未申酉戌亥……从左向右数，第1列是甲子，第2列是乙丑，第3列是丙寅……，我国的农历纪年就是按这个顺序得来的，如公历2007年是农历丁亥年，那么从今年往后，农历纪年为甲亥年的那一年在公历中（ ）（A ）是2019年， （B ）是2031年， （C ）是2043年， （D ）没有对应的年号5、实数 a 、b 、m 、n 满足a<b, -1<n<m, 若1a mb M m +=+，1a nbN n+=+，则M 与N 的大小关系是（ ）（A ）M>N (B)M=N (C)M<N (D)无法确定的。
6、若干个正方形和等腰直角三角形拼接成如图2所示的图形，若最大的正方形的边长是7cm ，则正方形A 、B 、C 、D 的面积和是（ ）（A ）214cm （B ）242cm （C ）249cm （D ）264cm图27、已知关于x 的不等式组230320a x a x +>⎧⎨-≥⎩恰有3个整数解，则a 的取值范围是（ ）（A ）23≤a ≤32 (B)43≤a ≤32 (C)43＜a ≤32 (D)43≤a ＜328 、The number of intersection point of the graphs of function||k y x=and function (0)y kx k =≠ is( ) (A)0 (B)1 (C)2 (D)0 or 2.9、某医药研究所开发一种新药，成年人按规定的剂量限用，服药后每毫升血液中的含药量y （毫克）与时间t （小时）之间的函数关系近似满足如图3所示曲线，当每毫升血液中的含药量不少于0.25毫克时治疗有效，则服药一次治疗疾病有效的时间为（） （A ）16小时 （B ）7158小时 （C ）151516小时 （D ）17小时 )10、某公司组织员工一公园划船，报名人数不足50人，在安排乘船时发现，每只船坐6人，就剩下18人无船可乘；每只船坐10人，那么其余的船坐满后内参有一只船不空也不满，参加划船的员工共有（ ）（A ）48人 （B ）45人 （C ）44人 （D ）42人 二、填空题（本大题共10小题，每小题4分，共40分）11、已知a b c ⋅⋅o 为ABC ∆三边的长，则化简|a b c -+12、自从扫描隧道显微镜发明后，世界上便诞生了一间新科学，这就是“纳米技术”，已知1毫米微米，1微米纳米，那么2007纳米的长度用科学记数法表示为＿＿米。
【2013】希望杯竞赛数学试题详解(11-20题)
题11 使不等式x a xarccos 2>-的解是121≤<-x 的实数a 的取值范围是（ ） A 、21π-B 、3222π-C 、6522π-D 、π-21 （第十一届高二第一试第6题）解法1 由已知可知2arccos xx a ->的解集是⎥⎦⎤⎝⎛-121，.在此区间上函数()x x f x arccos 2-=是单调增的.因此a 的值应当满足关系,21a f =⎪⎭⎫⎝⎛-⎪⎭⎫⎝⎛--=∴-21arccos 221a .3222π-=选B. 解法2 原不等式同解于2arccos xa x <-，因为121≤<-x ，所以222,2x <≤ 23π-x arccos -<0≤，从而=∴≤-<-a x x ,2arccos 23222π3222π-.故选B. 评析 上述两种解法的实质是一回事.关于此题，刊物上有数篇文章的观点值得商榷，现摘其部分加以分析. 一篇文章认为：“由已知不等式得2arccos xa x <-，欲使其解为121≤<-x ，实际上是对⎥⎦⎤⎝⎛-∈121，x 的任何x ，2arccos xa x <-恒成立，而x y xarccos 2-=在⎥⎦⎤⎝⎛-121，上是增函数，所以当21-=x 时，=⎪⎭⎫⎝⎛--=-21arccos 221min y 3222π-.故选B.” 另一篇文章在介绍了“设(),n x f m ≤≤则()()()⇔<=>⇔>x f a n x f a x f a ;max()m x f a =<min ”后分析道：“令()x x f x arccos 2-=，当121≤<-x 时，()x f <-3222π2≤，又()x f a <，故2223a π≤-，选B. ” 还有一篇文章干脆将题目改为： 使不等式x a xarccos 2>-的解是121≤<-x 的实数a 的取值范围是（ ） A 、⎪⎭⎫⎝⎛-∞-21π， B 、⎪⎪⎭⎫⎝⎛-∞-3222π，C 、⎪⎪⎭⎫ ⎝⎛-∞-6522π， D 、⎪⎭⎫ ⎝⎛-∞-π21， 并作了如下解答：“由已知得2arccos xa x <-，记()x x f x arccos 2-=，因为x 在⎥⎦⎤⎝⎛-121，时，()x f 单调增，所以=⎪⎭⎫⎝⎛--=-21arccos 221min y 3222π-.因此，3222π-<a .选B.” 首先应当指出，第一、第三篇文章中说增函数()x x f x arccos 2-=在⎥⎦⎤⎝⎛-121，上的最小值是3222π-是明显错误的.这三篇文章共同的观点是“不等式x a xarccos 2>-的解是121≤<-x ”等价于“对⎥⎦⎤⎝⎛-∈121，x 的任何x ，2arccos xa x <-恒成立”.按此观点，应当有⎪⎭⎫⎝⎛-≤21f a ，题目就错了（选择支中没有正确答案），又怎么能选B 呢？第三篇文章也将题目改错了（选择支中同样没有正确答案）.问题的关键在于“不等式x a xarcco s 2>-的解是121≤<-x ”与“对⎥⎦⎤⎝⎛-∈121，x 的任何x ，2arccos x a x <-恒成立”到底是否等价.为说明这一问题，我们只要看一个简单的例子就能明白了. 不等式022≤+-a x x 的解集是[]3,1-，求a 的取值范围.如果认为它等价于“[]3,1-∈x 时，不等式022≤+-a x x 恒成立，求a 的取值范围”，就会这样解：由022≤+-a x x 得()2221122--=+-+-≤x x x x x a ，在[]3,1-上的最小值是()3,31312-≤∴-=--a 为所求.而事实上，38-<-，但0822≤--x x 的解集却不是[]3,1-，而是[]4,2-，可见两者并不等价.至此，我们可以得出结论：“关于x 的不等式()x f a >的解集是D ”与“D x ∈时，关于x 的不等式()x f a >恒成立”不一定是等价的.题12 已知b a ,是正数，并且1996199619981998b a b a+=+，求证222≤+b a .(第十届高一培训题第74题)证法1 若a 与b 中有一个等于1,那么另一个也等于1,此时,显然222≤+b a .若b a ≥且1≠b ,可将1996199619981998b a b a+=+改写为()()219962199611b b a a -=-,由此推得10<<b (若1>b ,则012<-a ,得1<a ,这与b a ≥矛盾),由此得,11199622⎪⎭⎫⎝⎛=--a b b a,111,10,10221996≤--∴≤⎪⎭⎫⎝⎛<≤<ba ab a b 得 222≤+b a . 证法2 ()()()1998199822199619961998219961996219982ab a b ab a a b a b b +-++=--+=()()221996199622.ab a b a b --- 与19961996b a -同号,∴ ()()22199619960,a b a b --≥()()()1998199822199619962.a b a b a b ∴+≥++ ∴>+=+,01996199619981998b a b a 222≤+b a .证法3 由1996199619981998b a b a+=+及+∈R b a ,,得()()19961996222219981998a b a b a b ab+++=+19981998199622199619981998199622199619981998199622199619981998.1b a b a b a b a b a b a b a b a b a b a --++++=++++= ()()2219961996,a b a b =---又22b a -与19961996b a -同号,()()22199619960,a b a b ∴---≤1996221996199819981,a b a b a b+∴≤∴+222≤+b a . 评析 解决本题的关键在于如何利用已知条件.证法1通过分类讨论证得222≤+b a ,较繁.由于1996199619981998b a b a+=+,故证法2作差()()()1996199622199819982b a b a b a ++-+,只要此差大于等于0命题便获证.而证法3将22b a +表示成()()199819982219961996ba b a b a+++①,便将问题转化成证①式小于等于2.证法2,3的作法既有技巧性,又有前瞻性,简洁明了.拓展 本题可作如下推广推广1 设R b a ∈,,且1996199619981998b a b a +=+,则222≤+b a .推广2 设R b a ∈,,且n n n n b a b a 222222+=+++,其中+∈N n ,则222≤+b a . 推广3 设R b a ∈,,且m m n m nm b a b a222222+=+++,其中+∈N n m ,,则.222≤+n n b a . 推广4 设R b a ∈,,且m m n m nm Bb Aa Bb Aa222222+=+++,其中+∈N n m ,,1,,≤+∈+B A R B A ,则122≤+n n Bb Aa ②.由于推广1，2，3都是推广4的特例，故下面证明推广4.证明 ⑴当0==b a 时，②式显然成立. ⑵当b a ,不全为零，有()()()()22222222m n m n m m n n A B Aa Bb Aa Bb Aa Bb ++++-++()()()222222222222.m n m n n m m n m m n n AB a a b a b b AB a b a b ++=--+=--m m b a 22- 与n n b a 22-同号，∴()()22220,m m n nAB a b a b--≥∴()()2222m nm nA B AaBb++++()()222222222222.0,m m n n m n m n m m n n Aa Bb Aa Bb Aa Bb Aa Bb Aa Bb A B ++≥+++=+>∴+≤+ .1≤即当b a ,不全为零时，②式也成立.综上，不等式②成立.推广5 设+∈R b a ,，且m m n m nm b a b a +=+++，其中0,,>∈mn Z n m ，则2≤+n n b a . 推广6 设+∈R b a ,，且m m n m nm b a b a+=+++，其中0,,>∈mn R n m ，则2≤+n n b a . 推广7 设+∈R b a ,，且m m n m nm Bb Aa Bb Aa+=+++，其中1,,,0,,≤+∈>∈+B A R B A mn R n m ，则1≤+nnBb Aa ③.由于推广5，6是推广7的特殊情形，故下面证明推广7.证明 ()()()()m nm n m m nn A B AaBb Aa Bb AaBb ++++-++()m n m n n m m n AB a a b a b b ++=--+()().0.m m n n AB a b a b mn =--> 由幂函数的性质，可知m m b a -与n n b a -同号，()()()()()()0,.m m n n m n m n m m n n AB a b a b A B Aa Bb Aa Bb Aa Bb ++∴--≥∴++≥++.1,0≤+≤+∴>+=+++B A Bb Aa Bb Aa Bb Aa n n m m n m n m 即不等式③成立.从变元个数进行推广可得推广8 设()k i R x i ,,2,1 =∈+，且m i ki nm iki x x 11=+=∑=∑，其中,0,,>∈mn R n m 则.1k x ni ki ≤∑=推广9 设()1,,,2,1,1≤∑=∈=+i k i i i A k i R A x ，且mi i ki nm ii ki x A x A 11=+=∑=∑，其中,0,,>∈mn R n m 则11≤∑=ki n ii xA ④.由于推广8是推广9的特例,故下面证明推广9. 证明 令1111k kk km nmn i i ii i i i i i i i A A xA x A x +====∆=-⋅∑∑∑∑1111k kkk m nmni j ji ij j i j i j A A x A x A x +=====-∑∑∑∑().11∑∑==-⋅=kj mi mj nj j i ki x x x A A 由下标的对称性,对换上式的下标,得()∑∑==-=∆kj mj m inij iki x xx A A 11..将上面两式相加,得()()112.kkmm n n ijij i j i j A A xx x x ==∆=--∑∑0>mn ,由幂函数性质知mj mi x x -与nj ni x x -同号,()()0,20,m m n n i j i j i j A A x x x x --≥∴∆≥即∑∑∑∑====+⋅≥∴≥∆k i k i ni i k i mi i ki n m iiix A x A xA A 1111,0,∑∑==+>=ki mi i ki nm ii x A x A 11,0111≤≤∴∑∑==ki i ki ni i A x A ,即不等式④成立.题13 设1x ，2x ，3x ，1y ，2y ，3y 是实数，且满足1232221≤++x x x ，证明不等式 )1)(1()1(2322212322212332211-++-++≥-++y y y x x x y x y x y x .（第十届高二第二试第22题）证法1 当1232221=++x x x 时，原不等式显然成立.当1232221<++x x x 时，可设()()22221231f t x x x t =++-2-()1122331x y x y x y t ++- ()2221231y y y +++-.易知右边()()221122x t y x t y =-+-()()22331x t y t +---.()()()()01233222211≥-+-+-=∴y x y x y x f .()t f 是开口向下的抛物线，()()()2222222112233123123414110t x y x y x y x x x y y y ∴∆=++--++-++-≥即)1)(1()1(2322212322212332211-++-++≥-++y y y x x x y x y x y x .综上，1232221≤++x x x 时，)1)(1()1(2322212322212332211-++-++≥-++y y y x x x y x y x y x .证法2，()3,2,1,=∈+i R y x i i ，1232221≤++x x x ，∴当1232221>++y y y 时，0)1)(1(232221232221≤-++-++y y y x x x ，又0)1(2332211≥-++y x y x y x ，∴求证的不等式成立.当1232221≤++y y y 时，=-++-++)1)(1(232221232221y y y x x x()()()()=⎥⎦⎤⎢⎣⎡---+---≤------223222123222123222123222121111y y y x x x y y y x x x()2222222233112211223311222x y x y x y x y x y x y ⎡⎤⎛⎫⎛⎫⎛⎫+++---≤---=⎢⎥ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎣⎦2332211)1(-++y x y x y x .综上，在题设条件下，总有)1)(1()1(2322212322212332211-++-++≥-++y y y x x x y x y x y x .证法3 设1232221-++=x x x a ，1122332(1)b x y x y x y =-++-，1232221-++=y y y c ，则由1232221≤++x x x 知0≤a ，从而()222123112233121a b c x x x x y x y x y ++=++--++-21y + 22231y y ++-()()()0233222211≥-+-+-=y x y x y x .()()()0444424222≥++-=---=+--c b a a ac ab a b a ac b,()22420b ac a b -≥+≥，042≥-∴ac b ，即)1)(1()1(2322212322212332211-++-++≥-++y y y x x x y x y x y x .证法4 设()321,,x x x a =，()321,,y y y b = ，则 ()()332211321321,,,,y x y x y x y y y x x x b a ++==⋅，又θcos ⋅⋅=⋅b a b a θcos 232221232221⋅++⋅++=y y y x x x . 22222211223312312311cos x y x y x y x x x y y y θ∴++-=-++⋅++⋅≥01cos 1232221232221232221232221≥++⋅++-≥⋅++⋅++-y y y x x x y y y x x x θ22222222112233123123(1)(1)x y x y x y x x x y y y ∴++-≥-++++ 222222123123(1)(1)x x x y y y ≥++-++-.证法5 记()321,,x x x A =，()321,,y y y B =，()0,0,0O 为坐标原点，则由OB OA AB -≥, 得()()()222222222112233123123x y x y x y x x x y y y -+-+-≥++-++，整理得 ()222222112233123123110x y x y x y x x x y y y -++≥-++⋅++≥，01123222123222133221≥++++-≥-++∴y y y x x x y x y x y x ，()22222222222222112233123123123123(1)1(1)(1)x y x y x y x x xy y yx x x y y y ∴++-≥-++++≥++-++-.评析 这是一个条件不等式的证明问题.由求证式是ac b ≥2的形式自然联想到二次函数的判别式，构造一个什么样的二次函数是关键.当然是构造()()()()11212322213322112232221-+++-++--++=y y y t y x y x y x t x x x t f ，但只有当01232221≠-++x x x 时，()t f 才是二次函数，故证法1又分01232221=-++x x x 与01232221≠-++x x x 两类情形分别证明.很显然，等价转化思想、分类讨论思想是证法1的精髓.证法2直接运用基本不等式证明.证法3通过换元后证明042≥-ac b （即求证式），技巧性很强，一般不易想到，读者可细心体会其思路是如何形成的.证法4由求证式中的232221x x x ++,232221y y y ++及332211y x y x y x ++联想到空间向量的模及数量积，因而构造向量解决问题.证法5则从几何角度出发，利用OB OA AB -≥使问题轻松得证.五种证法，从多角度展示了本压轴题的丰富内涵.拓展 本题可作如下推广：推广 1 若()21,1,2,,,1ni i ii x y R i n x=∈=≤∑ ，则⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-≥⎪⎭⎫ ⎝⎛-∑∑∑===111121221n i i n i i n i i i y x y x . 推广 2 若()0,,,2,1,≥=∈m n i R y x i i ，∑=≤ni im x12，则⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-≥⎪⎭⎫ ⎝⎛-∑∑∑===m y m x m y x n i i n i i n i i i 121221. 两个推广的证明留给读者.题14 已知0x y z >、、，并且2222222111x y z x y z ++=+++， 求证：2222222111x y z x y z ++≤+++.（第一届备选题）证法1 令tan ,tan ,tan x y z αβγ===，且,,αβγ为锐角，则题设可化为222sin sin sin 2αβγ++=，即222c o sc o sc o s 1αβγ++=.由柯西不等式知221=⨯=()()222222sin sin sin cos cos cos αβγαβγ++++()()221sin cos sin cos sin cos sin 2sin 2sin 22ααββγγαβγ⎡⎤≥++=++⎢⎥⎣⎦. ()1sin 2sin 2sin 222αβγ∴++≤.由万能公式得222tan tan tan 21tan 1tan 1tan αβγαβγ++≤+++,即2222.111x y zx y z ++≤+++证法2 构造二次函数()222222222111111111x yz f t t t t x x yy z z ⎛⎫⎛⎫⎛⎫ ⎪=-+-+- ⎪ ⎪ ⎪++++++⎝⎭⎝⎭⎝⎭22222221112111111x y z t t x y z x y z ⎛⎫⎛⎫=++-++ ⎪ ⎪++++++⎝⎭⎝⎭ 222222111x y z x y z ⎛⎫+++ ⎪+++⎝⎭.()0f t ≥ ，当且仅当,x y z ==取t x y z ===时取等号，0∴∆≤，即222222222222211144111111111x y z x y z x y z x y z x y z ⎛⎫⎛⎫⎛⎫++-++++ ⎪ ⎪ ⎪+++++++++⎝⎭⎝⎭⎝⎭≤，2222222221111,1,1,111111x y z x x y y z z =-=-=-++++++ 又2222222221112,1,111111x y z x y z x y z++=∴++=++++++ 222244120111x y z x y z ⎛⎫∴++-⨯⨯≤ ⎪+++⎝⎭， 故2222111x y zx y z ++≤+++.（当且仅当2x y z ===时取等号） 证法3 2222222111x y z x y z ++=+++，即2221111112111x y z ⎛⎫⎛⎫⎛⎫-+-+-= ⎪ ⎪ ⎪+++⎝⎭⎝⎭⎝⎭，即2221111,111x y z ++=+++于是2222222222222111111111111x y z xy z x y z x y z x y z ⎛⎫⎛⎫⎛⎫++++≥++ ⎪ ⎪ ⎪+++++++++⎝⎭⎝⎭⎝⎭, 即2222111x y zx y z++≤+++. 证法4 令222222,,,111x y z X Y Z x y z===+++则2X Y Z ++=，且 222,,111X Y Zx y z X Y Z ===---，所以2222111x y z x y z ⎛⎫++ ⎪+++⎝⎭2X Y Z x y z ⎛⎫=++ ⎪⎝⎭22222222233111X Y Z X Y Z X Y Z x y z X Y Z ⎛⎫⎪⎛⎫≤++=++ ⎪ ⎪⎝⎭ ⎪⎝---⎭()()2223X Y Z X Y Z ⎡⎤=++-++⎣⎦ ()221132322 2.33X Y Z ⎡⎤⎛⎫≤-++=-⨯= ⎪⎢⎥⎣⎦⎝⎭所以2222111x y z x y z ++≤+++. 证法5 设222222222,,,111x a y b z cx a b c y a b c z a b c===+++++++++ 则222222,,,a b c x y z b c a a c b a b c===+-+-+-左边=222222111111x y z x x y y z z+++++ ()()()()()()()()()()()22222122222222362621 2.33b c a c a b a b c a b c a b c a b c a b c a b a c b c b a c a b ca b c a b a c b c b a c a b cab bc ca a b c a b ca b c a b c a b c ⎛⎫+-+-+-=++ ⎪ ⎪++⎝⎭=+-++-++-++≤+-++-++-++=++-++++≤++-++=++证法6 ()222222222222;1111x x xx xxx +≥=++++ 同理222222222222;22.111111y y z zy y y z z z +≥+≥++++++三式相加得2222222221112111111x y z x y z x y z ⎛⎫+++++ ⎪++++++⎝⎭22222,111x y z x y z ⎛⎫≥++ ⎪+++⎝⎭即22222122.111x y z x y z ⎛⎫+⨯≥++ ⎪+++⎝⎭故2222.111x y zx y z ++≤+++ 证法7 2222111x y z x y z ⎛⎫++ ⎪+++⎝⎭2222222222222222111111111111.111111x y z x x y y z z x y z x y z x y z ⎛⎫ ⎪=++ ⎪++++++⎝⎭⎛⎫⎛⎫≤++++ ⎪ ⎪++++++⎝⎭⎝⎭由已知，易知2222222221111,2,111111x y z x y z x y z++=++=++++++ 22222222, 2.111111x y z x y zx y z x y z ⎛⎫∴++≤∴++≤ ⎪++++++⎝⎭证法8 由已知，易知2221111.111x y z ++=+++ 设222111,,,111a b cx a b c y a b c z a b c===+++++++++ 则,,.b c c a a bx y z a b c+++=== 所以222111x y z a b c b c a c a bx y z a b c+++++++=+++++ ()()2.a b c b c c a a b a b c+++++++≤=++证法9 由2222222,111x y z x y z++=+++易得2221111111x y z ++=+++，于是 2222222222222221112111111111y x z y x y z x z x y zx y z ⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪+++⎝⎭⎝⎭⎝⎭=++=++++++++ 22222222222222111. 2.111111111111x y z x y z x y z x y z x y z x y z x y z⎛⎫++ ⎪+++⎛⎫⎝⎭≥=++∴++≤ ⎪++++++⎝⎭+++++ 证法10 由2222222,111x y z x y z ++=+++易得2221111111x y z ++=+++. ()2222222112112,1112221x x x x x x x +=≤=+++++同理，()()2222211211,,12122121y z y z y z =+=+++++ 22222231111312 2.1112211122x y z x y z x y z ⎛⎫⎛⎫∴++≤+++=+= ⎪ ⎪++++++⎝⎭⎝⎭2222.111x y zx y z ∴++≤+++ 证法11 由已知，易得2221111111x y z++=+++.构造空间向量 222111,,,111a x y z ⎛⎫= ⎪ ⎪+++⎝⎭ 222222,,,111x y z b x y z ⎛⎫= ⎪ ⎪+++⎝⎭2222222cos ,.111x y z a b a b a b a b a b x y z θ⎛⎫=≤∴≤++ ⎪+++⎝⎭2222222222111111111x y z x x y y z z ⎛⎫=++ ⎪ ⎪++++++⎝⎭ 222222111111x y z ⎡⎤⎛⎫⎛⎫⎛⎫⎢⎥≤++ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪+++⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦222222222111x y z x y z ⎡⎤⎛⎫⎛⎫⎛⎫⎢⎥++ ⎪⎪⎪ ⎪ ⎪ ⎪⎢⎥+++⎝⎭⎝⎭⎝⎭⎣⎦122,=⨯= 2222.111x y zx y z ∴++≤+++ 评析 条件不等式证明的关键在于如何利用条件，而当条件难以直接利用或条件式显得相当复杂时，通常应当将条件适当转化，证法1、4、5、8正是通过不同形式的换元，使得问题变得简单易证的.灵活（变形）应用基本不等式（证法6、证法10），柯西不等式（证法3、7），以及一些重要的结论（证法9）也是证明不等式的常用方法.证法2、11分别构造函数、向量加以证明，很富创新性，同时也应纳入我们正常思考的范围.拓展 本赛题可推广为：命题1 若12,,,0,n x x x >…且()22113,1ni i ix n n x ==-≥+∑ 则21 1.1nii ix n x =≤-+∑ 证明 设tan ,1,2,,,0,2i i i x i n παα==<<…则有2222221111tan 1,sin 1,cos 1.11tan nn n ni i i i i i i i i i x n n x αααα======-∴=-=++∑∑∑∑22111tan sin cos .11tan nn ni ii i i i i i ix x αααα=====++∑∑∑ 由柯西不等式得22111sin cos sin cos nn n i i i i i i i αααα===⎛⎫⎛⎫≤ ⎪⎪⎝⎭⎝⎭∑∑∑()11 1.n n =-=-21 1.1nii ix n x =∴≤-+∑命题2 若12,,,0,n x x x >…且()221,1ni i ix k k x ==≥+∑为常数,n 3,0<k<n 则()21.1nii ix k n k x =≤-+∑ 命题3 若12,,,0,n x x x >…且()221,,1mni mi ix k k n m R x ==<∈+∑ 则()21.1mni mi ix k n k x =≤-+∑ 命题2、3的证明与命题1相仿.命题4 设12,,,0,n x x x >…且221ni i ix k s x ==+∑（,,s k 为正常数3,n ≥ 0k n <<），则()21.nii ik n k x s x s =-≤+∑ 证明 将题设化为221,1i n i ix s k x s ==+∑作变换()221,2,,i i x t i n s ==…，则题设化为221.1ni i i t k t ==+∑由命题2得()21,1ni i it k n k t =≤-+∑即()21,1in i ix s k n k x s=≤-+∑化简得()()2211,.nni ii i i ik n k x x s k n k s x s x s==-≤-∴≤++∑∑ 进一步发散思维，还可得到：命题5 设12,,,0,n x x x >…且2211ni i ix k x ==+∑(),3,0,k n k n ≥<<为常数则21.ni i knx n k=≥-∑ 证明 设tan ,i i x α=且i α为锐角()1,2,,i n =….则题设可化为21sin,ni i k α==∑由此得21cos .ni i n k α==-∑由柯西不等式得22222211111cos cos ,cos cos nnn i i i i i i i n αααα===⎡⎤⎛⎫≥=⎢⎥ ⎪⎝⎭⎣⎦∑∑∑ 即222211sec ,tan ,nn i i i i n n n n k n k αα==≥+≥--∑∑221tan ,ni i n kn n n k n k α=∴≥-=--∑即21.ni i kn x n k=≥-∑ 仿命题4的证法可将命题5推广为：命题6 设12,,,0,n x x x >…且221ni i ix k s x ==+∑（,,s k 为正常数3,n ≥ 0k n <<），则21.ni i sknx n k=≥-∑ 对本赛题的条件再联想，又可推出命题7 设12,,,0,n x x x >…且()221131ni i ix n n x ==-≥+∑,则()211.n ni i x n =≥-∏ 证明 设tan ,i i x α=且i α为锐角()1,2,,i n =….则题设可化为21sin1,ni i n α==-∑由此得21cos 1.ni i α==∑2222221211121cos cos cos cos cos cos 1n n n n αααααα---+++≤-……221cos sin ,11n n n n αα-==--即()222211211cos cos cos sin n n n n αααα---≤…，同理可得 ()22222112211cos cos cos cos sin n n n n n ααααα----≤…，…()22221211cos cos cos sin n n n αααα--≤3….以上n 个式子相乘，得()()()22212121cos cos cos sin sin sin ,nn n n αααααα-≤… ∴有()21tan 1,nnn i n α=≥-∏即()211.nn i i x n =≥-∏仿命题4的证法又可将命题7推广为：命题8 设12,,,0,n x x x >…且()2211,3ni i ix n s n s x ==-≥+∑为常数， 则()211.nnii xs n =≥-⎡⎤⎣⎦∏命题8又可推广为：命题9 设12,,,0,n x x x >…且()113,2,1kni ki ix n n k N k n x ==-≥∈≤≤+∑且 则()11nnki i x n =≥-∏.证明 题设可化为11 1.1nki ix ==+∑作变换1,1i k i a x =+则题设化为11,ni i a ==∑且111,ki i i i a x a a -=-= 2311111,k na a a a x a a +++-∴==… ()11123231111,kn kn n n a a a a a a x a a -⎡⎤-⎛⎫+++=≥⎢⎥ ⎪⎢⎥⎝⎭⎣⎦……即有()1123111,kn n n a a a x a -⎡⎤-≥⎢⎥⎢⎥⎣⎦…同理可得()1113221,kn nn a a a x a -⎡⎤-≥⎢⎥⎢⎥⎣⎦……, ()111211kn n n n n a a a x a --⎡⎤-≥⎢⎥⎢⎥⎣⎦… .以上n 个式子相乘，得()11nnki i x n =≥-∏.仿命题4的证法，命题9可进一步推广为：命题10 设12,,,0,n x x x > (11)ni ki ix n s x ==-+∑ (),2,s k N k n ∈≤<为正常数且()11.nnki i x s n ==-⎡⎤⎣⎦∏则题15 求所有的正实数a ，使得对任意实数x 都有22sin 22cos ≤+xxaa（第十一届高二第二试第23题）解法1 原不等式即222s i n 2s i n 21≤+-x x a a ①.设t a x=2sin2，则化为021≤-+-t at ，其中],1[2s i n 22a a t x ∈=（当1>a ），]1,[2s i n 22a a t x ∈=（当10<<a ）.①式即022≤+-a t t .设a t t t f +-=2)(2，由于)(t f 在1与2a 之间恒小于或等于零，所以0)1(≤f 且0)(2≤a f ，即⎪⎩⎪⎨⎧>≤+-≤002124a a a a a ，解之，得1215≤≤-a 为所求. 解法2 ∵0>a ，∴22222c o s22s i n12s in 2s i n 2s i2si n2x x xx xx a aaaaa aa-+=+=+≥，又22si n22co s≤+x x a a ，∴1≤a .设)1(2sin 22≤≤=t a a t x ，记t tat f +=)(.依题意，2()f t ≥恒成立，∴max )(2t f ≥.t tat f +=)(在区间],[2a a 上单调递减；在区间]1,[a 上单调递增.而1)1(1)(22+=≥+=a f a a a f ，∴2m a x 1)(a a t f +=（当2a t =时取最大值）,故212≤+a a，解得1215≤≤-a 为所求. 解法3 原不等式即222sin2sin 21≤+-xxa a.令x a t 2sin 2=，则2≤+t ta①. (1)若1=a ，则1=t ，①式显然成立.(2)若1>a ，则2sin202a aa x≤≤，即21a t ≤≤，即①式对任意],1[2a t ∈恒成立由函数t t a y +=的图象（图1）及21a a <<，可得211≤+a ，且222≤+aaa ,但这与1>a 矛盾. （3）若10<<a ，则0s i n 222a a a x≤≤，即12≤≤t a .由函数t ta y +=的图象（图2）及12<<a a ，yO12a a a 2ta t y += 图 2xyO1 2a a a 2t a t y +=(1>a )图1(10<<a )x可得222≤+a a a 且211≤+a ，即0)1)(1(2≤-+-a a a 且1≤a ，又10<<a ，解得1215<≤-a . 综合（1）、（2）、（3），可得1215≤≤-a 为所求. 评析 解决本题的关键是如何由22sin22cos ≤+xx a a 对任意实数x 恒成立，得到关于a 的不等式.由于x x 2sin 212cos -=，故原不等式即222sin2sin 21≤+-xx a a ，亦即222sin2sin 2≤+xxa aa .令x a t 2sin 2=，则原不等式就是2≤+t t a.至此，若去分母，便将原问题转化为二次不等式恒成立的问题；若不去分母，应当有max )(2t t a +≥，可通过函数t tat f +=)(的最大值解决问题.解法1运用函数思想，把二次不等式022≤+-a t t 恒成立问题转化成二次函数a t t t f +-=2)(2的图象恒不在x 轴上方的问题，从而得到关于a 的不等式组，求出了a 的范围.解法2则由a aaxx22s i n 22c o s ≥+及22sin 22cos ≤+xxaa，得1≤a 从而得12≤≤t a .再由函数t tat f +=)(在],[2a a 上单调减，在]1,[a 上单调增，求出了)(t f 的最大值21a a +，由2)(≤t f 恒成立，得212≤+a a，求出了a 的范围.解法3则直接根据函数t tat f +=)(的图象，分1=a ，1>a ，10<<a 三种情形讨论，直观地求出了a 的范围.三种解法，道出了解决恒成立问题中求参数的三种方法：解法1为函数法；解法2为最值法；解法3为图象法.当然，解决恒成立问题决不仅仅是这三种方法，比如，还有分离参数法，变更主元法，运用补集思想等.题16 函数()()122222>-+-=x x x x x f 的最小值为 ( ) A 、-1 B 、1 C 、-2 D 、2（第七届高一培训题第2题）解法1 ()()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+-=11121x x x f .因为两个互为倒数的数，在它们等于1±时，其和可以取到绝对值的最小值.即当11±=-x ，即2=x 或0=x 时，()x f 的绝对值最小.又1x >，故2x =时，()f x 的绝对值最小.又()0>x f ，∴()()12min ==f x f .选B .解法2 因为1>x ，联想到1sec ≥θ，于是令θ2sec =x ，⎪⎭⎫ ⎝⎛∈2,0πθ，则θ2tan 1=-x . ()()()()1tan 1tan 221tan 1tan 21tan 21tan 12111222222=⋅⋅≥⎪⎭⎫ ⎝⎛+=+=-+-=-+-=θθθθθθx x x x x x f ，当且仅当θθ22tan 1tan =，即2=x 时，()1min =x f .故选B . 解法3 设()()1222>+-=x x x x ϕ，()()122>-=x x x g .()()()()02442222222≥-=+-=--+-=-x x x x x x x g x ϕ ，()()0>≥∴x g x ϕ.()()1≥∴x g x ϕ，即()1,f x ≥∴()1min =x f .故选B .解法4 ()()()()11211222222>-+-=-+-=x x x x x x x f .由此联想到万能公式: 22tan2sin 1tan 2ααα=+，故令02tan 1>=-αx ，则()()21tan 120sin 2tan 2f xg αααα+===>， 0sin >∴α.又1sin 1≤≤-α，1sin 0≤<α,1sin 1≥α,即()1≥x f .()1min =∴x f .故选B .解法5 1>x ，01>-∴x ，()()()()()11212121212112112=-⋅-≥-+-=-+-=x x x x x x x f 当且仅当()12121-=-x x ，即2=x 时取等号.()1min =∴x f .故选B . 解法6 1>x ，()()()11222222222222222≥+--=--+-=-+-=∴x x x x x x x x x f ，当2=x 时取等号.故选B .解法7 由22222-+-=x x x y 去分母并整理，得()022222=+++-y x y x .R x ∈ ，()()0224222≥+-+=∆∴y y ，即012≥-y ，1-≤∴y 或1≥y .1>x ，()()()012112>-+-==∴x x x f y ，1≥∴y .当1=y 时，由222212-+-=x x x ，解得()+∞∈=,12x ，()1min =∴x f .故选B .评析 解法1、6、7都是运用高一知识解决问题的，其余解法都用到了不等式知识，以解法5、6最简捷.解法7运用的是判别式法.运用此法是有前提的，如果将题中限制条件“1>x ”去掉，此法总能解决问题.但有了“1>x ”的限制，此法就不一定能奏效.只有当1=y 时求出的x 的值在1>x 的范围内时，1才是最小值，否则1就不是最小值，应当另寻他法加以解决.事实上，若将此题改为“求函数()()322222≥-+-=x x x x x f 的最小值，”此法就失灵了.因为1=y 时， [)+∞∉=,32x .故y 取不到1，也就谈不上1min =y 了.若用不等式知识解：()()()221122112221221x x x x y x x x -+-+-===+---，3≥x ，01>-∴x ，()1121212=-⋅-≥∴x x y ，当且仅当()12121-=-x x ，即2=x 时取等号，但[)+∞∉,32，故y 取不到1，同样不能解决问题.此时我们可利用函数单调性解：设213x x <≤，则()()222222222222112121-+---+-=-x x x x x x x f x f ()()()()()()1121221222112222121---+---+-=x x x x x x x x()()()()()()()()()[]()()112112112212121212121212121212212221221--+--=---+--=--+--=x x x x x x x x x x x x x x x x x x x x x x x x x x .213x x <≤ ，021<-∴x x ,()02121>+-x x x x ,011>-∴x ，012>-x ， ()()021<-∴x f x f ，()()21x f x f <，已知函数是[)+∞,3的单调增函数.()45232232332min=-⨯+⨯-==∴f y .拓展 本题的函数模型实际就是()()0,0>>+=k x xkx x f ，容易证明，该函数在(0,]k 上单调递减，在[,)k +∞上单调递增.于是关于其最值，我们有下面的定理 已知函数()()0,0>>+=k x xkx x f ，则 ⑴当()k m m x ≤<≥0时，()x f 有最小值k 2；⑵当k n x <≤<0时，()x f 有最小值()n f ；⑶当k p x >≥时，()x f 有最小值()p f ；⑷当()r k q r x q <<≤≤时，()x f 有最小值k 2，且有最大值()(){}r f q f ,max .例如，函数()x x x f 4+=在[)+∞,1上有最小值442=；在(]1,0上有最小值()51411=+=f ；在[)+∞,3上有最小值()3133433=+=f ；在[]3,1上有最小值442=，最大值()(){}5313,5max 3,1max =⎭⎬⎫⎩⎨⎧=f f .题17 已知,,x y z R +∈，且1231x y z++=，则23y z x ++的最小值是 （ ）A 、5B 、6C 、8D 、9（第十一届高二第二试第9题、高二培训题第14题） 解法1 ,,x y z R +∈ ，且1231x y z ++=，1232323y z y z x x x y z ⎛⎫⎛⎫∴++=++++ ⎪ ⎪⎝⎭⎝⎭2323332229,2332y x z x z y x y x z y z ⎛⎫⎛⎫⎛⎫=++++++≥+++= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭当且仅当3,6,9x y z ===时取等号．故选D ．解法2 由,0a x >时有2a xx a+≥，可知 12313691112222,33369923x y z y z x x y z x y z ⎛⎫⎛⎫⎛⎫=++=++≥-+-+-=-++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭923y z x ∴++≥，当且仅当369,,369x y zx y z ===，即3,6,9x y z ===时取等号．故选D ． 解法3 33123123339232323y z y z y z x x x x y z x y z ⎛⎫⎛⎫++=++++≥⋅⋅⋅⋅⋅⋅⋅=⎪ ⎪⎝⎭⎝⎭，当且仅当 12313x y z ===，即3,6,9x y z ===时取等号．故选D ． 解法4 由柯西不等式，1232323y z y z x x x y z ⎛⎫⎛⎫++=++++ ⎪ ⎪⎝⎭⎝⎭2123923y z x x y z ⎛⎫≥⋅+⋅+⋅= ⎪ ⎪⎝⎭，当且仅当3,6,9x y z ===时取等号．故选D ． 解法5 利用“三个正数的算术平均值不小于它们的调和平均值”，立得32331233y zx x y z++≥=++，923y z x ∴++≥．当且仅当3,6,9x y z ===时取等号．故选D ．解法6 若α、β、γ是长方体一条对角线与相邻三棱所成的角，则222coscos cos 1αβγ++=．,,x y z R +∈ ，且1231x y z++=，故不妨设2222222212,,a b x a b c y a b c==++++22223c z a b c =++（其中a 、b 、c 是长方体的长宽高）．则222222222222222222222222323y z a b c a b c a b c b a c a c b x a b c a b a c b c ++++++++=++=++++++≥3+2+2+2=9，当且仅当a b c ==，即3,6,9x y z ===时取等号．故选D ．解法7 构造二次函数222123()23y z f t t x t t x y z ⎛⎫⎛⎫⎛⎫=-+-+- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ 21232(111)23y z t t x x y z ⎛⎫⎛⎫=++-+++++ ⎪ ⎪⎝⎭⎝⎭，()0,0f t ≥∴∆≤ ，即212364023y z x x y z ⎛⎫⎛⎫-++++≤ ⎪ ⎪⎝⎭⎝⎭，又1231,923y z x x y z ++=∴++≥．故选D ．解法8 设123123,,m m m x y z ===，则123123111,,,1,23y z x m m m m m m ===++= 123123123111111()923y z x m m m m m m m m m ⎛⎫∴++=++=++++≥ ⎪⎝⎭．故选D ． 评析 解法1、2、3、4、5、8都是利用一些重要的基本不等式解决问题的．解法6、解法7分别通过构造长方体、函数将原问题转化，根据图形特征解决问题．根据解法2的思路，很容易得下面的错误解法：123123,,,,,,,,,2(1),2(2),2(3),2323y z y z x y z R x R x x y z x y z++∈∴∈∴+≥+≥+≥ 1231232226615,23y z x x y z x y z ⎛⎫⎛⎫⎛⎫⎛⎫∴++≥-+-+-=-++=-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭min 523y z x ⎛⎫∴++= ⎪⎝⎭．故选A ．错误原因就在于（1）、（2）、（3）式取等号的条件分别是1,2,3x y z ===，而此时1233x y z++=，与已知矛盾．故23y zx ++取不到5． 拓展 本题可作如下推广：推广1 若,,i i i x a R a +∈为常数(1,2,,)i n = ，且12121n na a a x x x +++= ， 则21212min n n x x x n a a a ⎛⎫+++=⎪⎝⎭ ．证明121212121212n n n n n n x x a x x x x a a a a a a a a x x x ⎛⎫⎛⎫+++=++++++ ⎪⎪⎝⎭⎝⎭212121212n n nn n nx x x a a a n n n a a a x x x ≥⋅⋅⋅= ，当且仅当12121n n a a a x x x n ==== 时取等号．21212min n n x x x n a a a ⎛⎫∴+++= ⎪⎝⎭ ．推广2 若,,i i i x a R a +∈为常数(1,2,,)i n = ，且1212n na a a k x x x +++= ， 则21212min n n x x x n a a a k ⎛⎫+++= ⎪⎝⎭ ．证明121212121n n n n x x x x x xk a a a k a a a ⎛⎫+++=⋅+++⋅ ⎪⎝⎭121212121n n n n x a x x a a k a a a x x x ⎛⎫⎛⎫=⋅++++++ ⎪⎪⎝⎭⎝⎭ 2121212121n n n n n n x x x a a a n n n k a a a x x x k≥⋅⋅⋅⋅=，当且仅当1212n n a a a k x x x n ==== 时取等号．21212min n n x x x n a a a k ⎛⎫∴+++=⎪⎝⎭ ． 推广3 若,,i i i x a R a +∈为常数(1,2,,)i n = ，且1212n na a a k x x x +++= ， 则212min 121()()n n x x x a a a k+++=+++ ． 证明 1212,n na a a k x x x +++=∴运用柯西不等式有 121212121211()()n n n n n a a a x x x x x x k x x x k k x x x ⎛⎫+++=⋅+++⋅=++++++ ⎪⎝⎭ 221212121211()n nn n a a a x x x a a a k x x x k⎛⎫≥⋅+⋅++⋅=+++ ⎪ ⎪⎝⎭， 当且仅当121212n n na a a x x x x x x ===，即1212n na a ax x x === 时取等号． 212min 121()()n n x x x a a a k∴+++=+++ . 根据推广1、2，立得本题所求最小值为9．由1231x y z ++=，得111123y zx ++=．根据推广3， 21(111)9231y z x ++≥++=，当且仅当11123y z x==，即3,6,9x y z ===时取等号．min 923y z x ⎛⎫∴++= ⎪⎝⎭．故选D ．再看一例：例 已知,,x y z R +∈，且2475x y z++=，求274y x z ++的最小值．解 由2475x y z ++=，得41495274y x z ++=．根据推广3，2127(4149)2045y x z ++≥++=．当且仅当4149274y x z ==，即2,8x z y ===时取等号．min27204y x z ⎛⎫∴++= ⎪⎝⎭． 题18 设b a y x ,,,为正实数，b a ,为常数，且1=+ybx a ,则y x +的最小值为_______. （第十一届高二培训题第36题）解法1 设⎪⎪⎩⎪⎪⎨⎧==,sin ,cos 22ααyb xa则=+=+αα22csc secb a y x αα22cot tan b a b a +++ab b a 2++≥，当αα22cot tan b a =，即4tan baα=时取等号， ab b a y x 2)(min ++=+∴.解法2 ()22ab a y b xa yb x x y x y a b a b a b a bx y xy x y⎛⎫+=++=+++≥++⋅=++ ⎪⎝⎭, 当且仅当ay bx x y=时取等号,ab b a y x 2)(min ++=+∴. 解法3 令(,),,,a b m x y n x y ⎛⎫== ⎪ ⎪⎝⎭则222,m n a b m n m n ⋅=+⋅≥⋅ ，()(a b x y a x y ⎛⎫∴++≥+⎪⎝⎭2)b ，即ab b a y x 2++≥+，当且仅当m、→n 共线，即当(,),a b x y x y λ⎛⎫= ⎪ ⎪⎝⎭，亦即bay x=时取等号，ab b a y x 2)(min ++=+∴. 解法422()()2a b a b x y x y xy ab a b a bx y xy ⎛⎫⎛⎫+=++≥⋅+⋅=+=++ ⎪ ⎪⎪⎝⎭⎝⎭, 当且仅当yb y x a x =，即b ay x =22时取等号，ab b a y x 2)(min ++=+∴.解法5 设k y x =+，即x k y -=，代入1=+ybx a ，得0)(2=+--+ka x k a b x ， +∈R x ，由0≥∆，得b a k +≥ab 2+或ab b a k 2-+≤（舍去）．由0=∆，求得)(b a a x +=，)(b a b x k y +=-=，bay x=∴时，ab b a y x 2)(min ++=+. 解法6 +∈R b a y x ,,,且1=+yb x a ⇒10<<x a ，10<<y b⇒0>>a x ，0>>b y ,故设μ+=a x ，ν+=b y )0,(>νμ代入1=+ybx a ，得ab =μν（定值），ab b a b a b a y x 22++=++≥+++=+∴μννμ，当且仅当ab ==νμ，即baab b ab a y x =++=时取等号，ab b a y x 2)(min ++=+∴. 解法7 由解法6知0>>a x ，0>>b y ，记y x k +=①，由1=+ybx a ，得a x bx y -=，代入①可得+-+-=ax aba x k )(ab b a b a 2)(++≥+，当且仅当 ⎪⎩⎪⎨⎧>--=-0a x a x ab a x ，即x a ab =+时取等号，此时ab b y +=， ∴当bay x=时 ，ab b a y x 2)(min ++=+.。
2013年第11届小学“希望杯”全国数学邀请赛试卷(五年级第2试)
2013年第11届小学“希望杯”全国数学邀请赛试卷（五年级第2试）一、填空题1．（3分）请在横线上方填入一个数，使等式成立：5×4÷_________=0.8．2．（3分）两个自然数的和与差的积是37，那么，这两个自然数的积是_________．3．（3分）180的因数共有_________个．4．（3分）数字1～9的排列如图所示，沿着图中的连接线将全部的数字各取一遍（每个数字只能经过一次），组成一个九位数，例如，123654789，按此取法取得的数中，最小的是_________最大的是_________．5．（3分）若32只兔子可换4只羊，9只羊可换3头猪，6头猪可换2头牛，那么5头牛可换_________只兔子．6．（3分）包含数字0的四位自然数共有_________个．7．（3分）养殖场将一批鸡蛋装入包装盒，每盒30枚，恰好全部装完，后来重新包装，使每个包装盒中装入36枚鸡蛋，最后也恰好全部装完，并节约了24个包装盒，则这批鸡蛋有_________枚．8．（3分）一只蜘蛛有8条腿，一只蜻蜓有6条腿，如果蜘蛛、蜻蜓共有腿450条，蜘蛛的只数是蜻蜓只数的3倍，那么蜘蛛有_________只．9．（3分）甲乙两桶中共装有26升水，先将乙桶中的一半倒入甲桶，再将甲桶中一半倒入乙桶，然后，从乙桶中取5升水倒入甲桶，整个过程中无水溢出．这时，甲桶中的水比乙桶中的水多2升，则最初甲桶中有水_________升．10．（3分）如图，若△ABC的面积是24，D、E、F分别是BC、AD、AB的中点，则△BEF的面积是_________．11．（3分）数一堆贝壳，若4个4个地数，则剩1个；若5个5个地数，则剩2个；若6个6个地数，则剩3个，由以上情况可推知，这堆贝壳至少有_________个．12．（3分）一个长方形形状的玻璃缸，不计玻璃的厚度，量得长54厘米，宽24厘米，高20厘米，缸内水深12厘米，将一块正方体形状的石块放入玻璃缸中，水面升高至16厘米，则石块的体积是_________立方厘米．二、解答题:每题都要写出推算过程．13．小明绕操场跑一圈5分钟，妈妈绕操场跑一圈用3分钟．（1）如果小明和妈妈从同一起点同时同向出发，几分钟后两人再次同时到达起点？此时妈妈和小明各跑了几圈？（2）如果小明和妈妈从同一起点同时同向出发，几分钟后妈妈第一次追上小明？（3）如果小明和妈妈从同一起点同时反向出发，几分钟后两人第四次相遇？14．有一批货物，用28辆货车一次运走，货车有载重8吨的和载重5吨的两种，若所有货车都满载，且载重8吨的货车运送货物的总重量比载重5吨的货车运送货物的总重量多3吨．则这批货物共有多少吨？15．图是一块宅基地的平面图，其中相邻的两条线段都互相垂直．求：（1）这块宅基地的周长；（2）这块宅基地的面积．16．两个不同的三位自然数和除以7都余3，求和的和．2013年第11届小学“希望杯”全国数学邀请赛试卷（五年级第2试）参考答案与试题解析一、填空题1．（3分）请在横线上方填入一个数，使等式成立：5×4÷25=0.8．2．（3分）两个自然数的和与差的积是37，那么，这两个自然数的积是342．3．（3分）180的因数共有18个．4．（3分）数字1～9的排列如图所示，沿着图中的连接线将全部的数字各取一遍（每个数字只能经过一次），组成一个九位数，例如，123654789，按此取法取得的数中，最小的是123547896最大的是987563214．5．（3分）若32只兔子可换4只羊，9只羊可换3头猪，6头猪可换2头牛，那么5头牛可换360只兔子．6．（3分）包含数字0的四位自然数共有2439个．7．（3分）养殖场将一批鸡蛋装入包装盒，每盒30枚，恰好全部装完，后来重新包装，使每个包装盒中装入36枚鸡蛋，最后也恰好全部装完，并节约了24个包装盒，则这批鸡蛋有4320枚．8．（3分）一只蜘蛛有8条腿，一只蜻蜓有6条腿，如果蜘蛛、蜻蜓共有腿450条，蜘蛛的只数是蜻蜓只数的3倍，那么蜘蛛有45只．9．（3分）甲乙两桶中共装有26升水，先将乙桶中的一半倒入甲桶，再将甲桶中一半倒入乙桶，然后，从乙桶中取5升水倒入甲桶，整个过程中无水溢出．这时，甲桶中的水比乙桶中的水多2升，则最初甲桶中有水10升．10．（3分）如图，若△ABC的面积是24，D、E、F分别是BC、AD、AB的中点，则△BEF的面积是3．三角形三角形=××三角形三角形三角形××=11．（3分）数一堆贝壳，若4个4个地数，则剩1个；若5个5个地数，则剩2个；若6个6个地数，则剩3个，由以上情况可推知，这堆贝壳至少有57个．12．（3分）一个长方形形状的玻璃缸，不计玻璃的厚度，量得长54厘米，宽24厘米，高20厘米，缸内水深12厘米，将一块正方体形状的石块放入玻璃缸中，水面升高至16厘米，则石块的体积是5832立方厘米．二、解答题:每题都要写出推算过程．13．小明绕操场跑一圈5分钟，妈妈绕操场跑一圈用3分钟．（1）如果小明和妈妈从同一起点同时同向出发，几分钟后两人再次同时到达起点？此时妈妈和小明各跑了几圈？（2）如果小明和妈妈从同一起点同时同向出发，几分钟后妈妈第一次追上小明？（3）如果小明和妈妈从同一起点同时反向出发，几分钟后两人第四次相遇？，，妈妈每分钟比小明多跑一周的﹣（﹣，则第四相遇时两人共行了（）（﹣（+14．有一批货物，用28辆货车一次运走，货车有载重8吨的和载重5吨的两种，若所有货车都满载，且载重8吨的货车运送货物的总重量比载重5吨的货车运送货物的总重量多3吨．则这批货物共有多少吨？15．图是一块宅基地的平面图，其中相邻的两条线段都互相垂直．求：（1）这块宅基地的周长；（2）这块宅基地的面积．16．两个不同的三位自然数和除以7都余3，求和的和．是数符合，然后再求它们的和即可．+=108+801=909。
2013年第11届小学“希望杯”全国数学邀请赛试卷(五年级第1试)
2013年第11届小学“希望杯”全国数学邀请赛试卷（五年级第1试）一、以下每题6分，共120分．1．（6分）计算：5.62×49﹣5.62×39+43.8=_________．2．（6分）规定a△b=a÷（a+b），那么，2△1.8=_________．3．（6分）若干个数的平均数是2013，增加一个数后，平均数仍为2013，则增加的这个数是_________．4．（6分）如果三位数3□2是4的倍数，那么□里能填的最小的数是_________，最大的数是_________．6．（6分）小明在计算一个整除的除法算式时，不小心将除数18看成15，得到的商是24，则正确的商是_________．7．（6分）将100块糖分成5份，使每一份数量依次多2，那么最少的一份有糖_________块，最多的一份有糖_________块．8．（6分）一件商品，对原价打九折和打七折后的售价相差5.4元，那么此商品的原价是_________元．9．（6分）有26个连续的自然数，如果前13个数的和是247，那么后13个数的和是_________．10．（6分）在三位数253，257，523，527中，质数是_________．11．（6分）14个棱长为1的正方体在地面上堆成如图所示的几何体，将它的表面（包括与地面接触部分）染成红色，那么红色部分的面积是_________．12．（6分）如图所示，若梯形ABCD的上底AD长16厘米，高BD长21厘米，并且BD=3DE，则三角形ADE的面积是_________平方厘米，梯形的下底BC长_________厘米．13．（6分）小丽将一些巧克力装入大，小两种礼盒中的一种礼盒内，如果每个小礼盒装5块巧克力，那么剩下10块；如果每个大礼盒装8块巧克力，那么少2块，已知大礼盒比小礼盒少3个，则这些巧克力共有_________块．14．（6分）从甲地到乙地，小张走完全程要2小时，小李走完全程要1小时，如果小张和小李同时从甲地出发去乙地，后来，在某一时刻，小张未走的路程恰好是小李为走的路程的2倍，那么此时他们走了_________分钟．15．（6分）有16盒饼干，期中15盒的重量（含盒子）相同，另有1盒少了几块，如果用天平称，那么至少称_________次就一定能找出这盒饼干．16．（6分）编号为1～10的10名篮球运动员轮流进行三人传球训练，第1轮由编号（1，2，3）的队员训练，然后，依次是编号（4，5，6）（7，8，9）（，10，1，2），…队员训练．当再次轮到编号（1，2，3）的队员时，将要进行的是第_________轮训练．17．（6分）将一个胶质的正方体扩大成另一个正方体，使新正方体的表面积是原正方体表面积的4倍，则新正方体的棱长是原正方体棱长的_________倍，体积是原正方体体积的_________倍．18．（6分）将55株杜鹃分成株数相同的若干份，32株月季也分成株数相同的若干份，然后将两种花逐份间隔，排成一列，并且两端都种杜鹃，如图所示，那么．每份杜鹃有_________株，每份月季有_________株．19．（6分）从1分，2分，5分硬币各有5枚的一堆硬币中取出一些，合成1角，共有不同的取法_________种．20．（6分）将1到2013中的偶数排成一列，然后按每组1，2，3，4，1，2，3，4，…个数的规律分组如下（每个括号为一组）：（2）（4，6）（8，10，12），（14，16，18，20），（22），（24，26），…则最后一个括号内的各数之和是_________．二、附加题（每题10分）21．（10分）将1，2，3，4，5，6随意填入图中的小圆圈内，将相邻两数相乘，再将所得的6个乘积相加，则得到的和最小是_________．22．（10分）如图，5个等腰直角三角形叠放在一起，它们的斜边都在一条直线上，已知最小的等腰直角三角形的斜边长是4厘米，其余等腰三角形的斜边依次多4厘米，则图中阴影部分的面积_________是平方厘米．2013年第11届小学“希望杯”全国数学邀请赛试卷（五年级第1试）参考答案与试题解析一、以下每题6分，共120分．1．（6分）计算：5.62×49﹣5.62×39+43.8=100．2．（6分）规定a△b=a÷（a+b），那么，2△1.8=．2△+1.8故答案为：3．（6分）若干个数的平均数是2013，增加一个数后，平均数仍为2013，则增加的这个数是2013．4．（6分）如果三位数3□2是4的倍数，那么□里能填的最小的数是1，最大的数是9．6．（6分）小明在计算一个整除的除法算式时，不小心将除数18看成15，得到的商是24，则正确的商是20．7．（6分）将100块糖分成5份，使每一份数量依次多2，那么最少的一份有糖16块，最多的一份有糖24块．8．（6分）一件商品，对原价打九折和打七折后的售价相差5.4元，那么此商品的原价是27元．9．（6分）有26个连续的自然数，如果前13个数的和是247，那么后13个数的和是416．10．（6分）在三位数253，257，523，527中，质数是523、257．11．（6分）14个棱长为1的正方体在地面上堆成如图所示的几何体，将它的表面（包括与地面接触部分）染成红色，那么红色部分的面积是42．12．（6分）如图所示，若梯形ABCD的上底AD长16厘米，高BD长21厘米，并且BD=3DE，则三角形ADE的面积是56平方厘米，梯形的下底BC长32厘米．13．（6分）小丽将一些巧克力装入大，小两种礼盒中的一种礼盒内，如果每个小礼盒装5块巧克力，那么剩下10块；如果每个大礼盒装8块巧克力，那么少2块，已知大礼盒比小礼盒少3个，则这些巧克力共有70块．14．（6分）从甲地到乙地，小张走完全程要2小时，小李走完全程要1小时，如果小张和小李同时从甲地出发去乙地，后来，在某一时刻，小张未走的路程恰好是小李为走的路程的2倍，那么此时他们走了24分钟．、，以小张未走的路程恰好是小李为走的路程的=15．（6分）有16盒饼干，期中15盒的重量（含盒子）相同，另有1盒少了几块，如果用天平称，那么至少称3次就一定能找出这盒饼干．16．（6分）编号为1～10的10名篮球运动员轮流进行三人传球训练，第1轮由编号（1，2，3）的队员训练，然后，依次是编号（4，5，6）（7，8，9）（，10，1，2），…队员训练．当再次轮到编号（1，2，3）的队员时，将要进行的是第11轮训练．17．（6分）将一个胶质的正方体扩大成另一个正方体，使新正方体的表面积是原正方体表面积的4倍，则新正方体的棱长是原正方体棱长的2倍，体积是原正方体体积的8倍．18．（6分）将55株杜鹃分成株数相同的若干份，32株月季也分成株数相同的若干份，然后将两种花逐份间隔，排成一列，并且两端都种杜鹃，如图所示，那么．每份杜鹃有11株，每份月季有8株．19．（6分）从1分，2分，5分硬币各有5枚的一堆硬币中取出一些，合成1角，共有不同的取法7种．20．（6分）将1到2013中的偶数排成一列，然后按每组1，2，3，4，1，2，3，4，…个数的规律分组如下（每个括号为一组）：（2）（4，6）（8，10，12），（14，16，18，20），（22），（24，26），…则最后一个括号内的各数之和是6030．二、附加题（每题10分）21．（10分）将1，2，3，4，5，6随意填入图中的小圆圈内，将相邻两数相乘，再将所得的6个乘积相加，则得到的和最小是58．22．（10分）如图，5个等腰直角三角形叠放在一起，它们的斜边都在一条直线上，已知最小的等腰直角三角形的斜边长是4厘米，其余等腰三角形的斜边依次多4厘米，则图中阴影部分的面积60是平方厘米．。
第11~13届小学四年级奥数
第十一届小学“希望杯”全国数学邀请赛四年级 第Ⅰ试试题2013年3月17日 上午8:30至10:00以下每题6分，共120分1．计算：4×37×25= 。
2．某种速印机每小时可以印3600张纸，那么印240张纸需要 分钟。
3．若三个连续奇数的和是111，则其中最小的奇数是 。
4．一个数除以3余2，除以4余3，除以5余4，则这样的数中最小的是 。
5．图1是一个5×5的网格，每个小方格的面积都是1，阴影部分是类似数字“2”的图形，那么阴影部分的面积是 。
6．将两个长4厘米、宽2厘米的长方形拼在一起（彼此不重叠），组成一个新长方形，则新长方形的周长是 厘米，或 厘米。
7．今年，小明12岁，爸爸40岁，在小明 岁的时候，爸爸的年龄是小明的5倍。
8．商店按每个60元购进了50个足球，全部售出后获利1950元，则每个足球的售价是 元。
9．如图2，将数字4，5，6填入正方体的展开图中，使正方形相对的两个面内数字的和都相等，则A 处应该填 ，B 处应该填 ，C 处应该填 。
10．从九位数798056132中任意划去4个数字，使剩下的5个数字顺次组成5位数，则所得五位数最大的是 ，最小的是 。
11．如图3，在一大一小两个正方形拼成的图形中，阴影部分的面积是50平方厘米，则小正方形的面积是 平方厘米。
12．2013的质因数中，最大的质因数与最小的质因数的乘积是 。
13．从边长为5的正方形纸片的四个角剪掉四个小长方形后得到图4，得到新图形的周长是 。
图1图2图3图6图4图514．喜羊羊打开一本书，发现左右两页的页码数的乘积是420，则这两页的页码数的和是。
15．将1到16这16个自然数排成如图5的形状，如果每条斜线是的4个数的和相等，那么a－b－c+d+e+f－g= 。
16．行驶在索马里海域的商船发现在它北偏西60°方向50海里处有一海盗船，于是商船向在它南偏西60°方向50海里处的护航舰呼救，此时，护航舰在海盗船的正（填东、西、南、北）方向海里处。
2013年希望杯全国数学邀请赛一试参考答案及评分标准
第11届小学“希望杯”全国数学邀请赛第1试
参考答案及评分标准
评分标准：第1~20题，每题6分（其中，第6、10、16题，每空3分；第9、19题，每空2分）；
附加题，每题10分。
五年级
评分标准：第1~20题，每题6分（其中，第4，7，12，17，18题，每空3分）；附加题，每题10分。
六年级
评分标准：第1~20题，每题6分（其中，第4，7，13，17题，每空3分）；
附加题，每题10分（其中，附加题2，每空5分）。
参考答案及评分标准
评分标准：第1~20题，每题4分；
第21~25题，每题8分，每空4分（其中，第25题，两空答案可交换）；
附加题，每题10分（其中，附加题2，每空5分）。
初中二年级
第1~20题，每题4分；
第21~25题，每题8分，每空4分（其中，第22，23题，两空答案可交换）；
附加题，每题10分。
参考答案及评分标准
评分标准：第1~20题，每题4分（其中，第16题，写出一个解析式得2分）；
第21~25题，每题8分，每空4分（其中，第21，22，25题，每空4分；第24题，前两空
每空3分，最后一空2分）；
附加题，每题10分，每空5分。
参考答案及评分标准
第1~20题，每题4分；
第21~25题，每题8分，每空4分;
附加题，每题10分（其中，附加题1，答对一种情况得3分，答对两种情况得6分）。
第24届中学“希望杯”全国数学邀请赛第1试
参考答案及评分标准
高中二年级
第1~20题，每题4分；
第21~25题，每题8分，每空4分;
附加题，每题10分.。
第二十四届希望杯全国数学邀请赛初二试题(第1试)及答案
第二十四届“希望杯”全国数学邀请赛初二 第1试试题2013年3月17日 上午8：30至10：00一、选择题(每小题4分，共40分) 1．有下列五个等式： 13+=x y ①；1y22-=x ②；x y =③；||x y =④；x y =||⑤； 其中，表示“y是x 的函数”的有( )A ．1个B ．2个C ．3个D ．4个2．点),7(m -和点),8(n -都在直线62--=x y 上，则m 和n 的大小关系是( ) A ．m>n B ．m<n C ．m=n D ．不能确定 3．下列命题中，正确的是( )A ．若0>a ，则aa 1> B ．若2a a >，则1>aC ．若10<<a ，则2a a >D ．若a a =||，则0>a 4．若定义运算“⊗”：a b b a =⊗，如82233==⊗，则213⊗等于( )A ．81B ．8C ．61D ．235．以下关于平行四边形的判定中，不正确的是( ) A ．两组对角分别相等的四边形是平行四边形； B ．两组对边分别相等的四边形是平行四边形； C ．对角线相等的四边形是平行四边形；D ．一组对边平行且相等的四边形是平行四边形；6．用一根长为a ，并且没有伸缩性的线围成面积为S 的等边三角形．在这个等边三角形内任取一点P ，则点P 到等边三角形三条边的距离之和为( )A ．aS 2 B ．aS 4 C ．aS 6 D ．aS 87．若199199<<-x ，且100-=x m 的值为整数，则m 的值为( ) A ．100个 B ．101个 C ．201个 D ．203个 8．已知32+=x ，且)86(148+=+y x x ，则y 的值是( )A ．10B ．15C ．20D ．309．If a right triangle has edge lengths b a -，a ，and b a + (a and b are both positive integers)，then the perimeter of the triangle might be ( ) A ．60 B ．70 C ．80 D ．9010．小王与小李约定下午3点在学校门口见面，他们在早上8点将自己的手表对准．小王于下午3点到达学校门口，可是小李还没有到，原来小李的手表比正确时间每小时慢4分钟．如果小李按他自己的手表在3点到达，则小王还需要等( )(正确时间) A ．26分钟 B ．28分钟 C ．30分钟 D ．32分钟 二、A 组填空题(每小题4分，共40分) 11．若125512=+x ，则____________)2(2012=-+xx ．12．计算：___________1222222201120122013=------ ．13．用边长为1cm 的小正方形在桌面上摆放成 如图1所示的塔状图形，则第n 次所摆图形的周长是______________cm(用关于n 的代数式表示)14．有两个函数b ax y +=和5+=cx y ，第1次第2次 第3次图1学生甲求出它们图象的交点的正确坐标)2,3(-，学生乙因抄错c 而得出交点坐标⎪⎭⎫⎝⎛41,43，则函数b ax y +=的解析式是_____________；15．如图2，三个正比例函数的图象分别对应解析式：ax y =①，bx y =②，cx y =③，若将a ，b ，c 从小到大排列，则应当是_____________．16．如图3，在正方形ABCD 中，E 、G 、F 分别是AB 、AD 、BC 边上的点，若BE=2AE ，AG=1，BF=2，∠GEF=90°，则GF 的长是_______________．17．一个三角形的三条边的长分别是3，5，7，另一个三角形的三条边的长分别是3，23-x ，12-x ．若这两个三角形全等，则x 的值是___________．18．有甲、乙、丙三种商品，购甲3件，乙7件，丙1件，需3．15元；购甲4件，乙10件，丙1件，需4．20元．若购甲、乙、丙各1件，则需______________元．19．设a ，b 是实数，且a b b a -=+-+11111，则baa b +++++1111的值是____________． 20．将不大于20的正偶数分成两组，使得第一组中数的乘积能被第二组中数的乘积整除．则商的最小值是__________________． 三、B 组填空题(每小题8分，共40分) 21．数学老师用10道题作为一次课堂练习，课代表将全班同学的答题情况绘制成条形统计图，如图4所示．观察此图可知，每位同学答对的题的个数组成 的样本众数是______，中位数是_______．22．方程3||12||=+-x x 的解 是__________或__________．23．若关于x 的方程234222+=-+-x x mx x 有增根，则_______=m 或________． 24．Let 20131=⎪⎭⎫ ⎝⎛+x y x ，x and y are both positive integers ，then the largest value ofy x + is ____________，the smallest value of y x + is _________．25．已知0=++c b a ，c b a ≥≥，0≠a ，则ac 的最大值是____________，最小值是___________．附加题(每小题10分，共20分) 1．A 商品的单价是50元，B 商品的单价是60元，几所学校各付款1220元购买这两种商品，任意2所学校购买的A 商品的数量都不同．则参加这次采购的学校最多有________所． 2．十进制数中，右边的数友比左边的数友大的数叫做上升数，如134，258．那么三位数中的上升数有_________个；在三位上升数中，3的倍数有___________个．F 图2 图3 答对题数5 图4答案：一、选择题(每小题4分，共40)二、A 组填空题(每小题4分，共40分)11．1- 12．1 13．4n 14．1+-=x y 15．c<a<b 16．10 17．3 18．1.05 19．3 20．7三、B 组填空题(每小题8分，共40分)21．8， 9 22．234=-=x x 或 23．46-或 24．2013，507 25．21-，2-附加题(每小题10分，共20分)1．4 2．84，30。
2013新希望杯-详解
2013新希望杯-详解由dictator2002制作2013年第九届新希望杯五年级决赛考试时间60分钟，总分120分一、选择题（本大题共6小题，每题4分，共24分）题1.在期末考试中，方方五科的总分是445分，除数学外的四科平均分是87.25分，方方的数学是___________．A、95分B、96分C、97分D、98分题2.王伯去水果店买水果，如果买4千克梨和7千克苹果，要付款84元；如果买4.5千克梨和7千克苹果，要付款87.5元。
那么买1千克梨要付款___________．A、3.5元B、5元C、6元D、7元题3.下表中的数是按规律排列的，其中第2行第4列是9，那么第9行第9列是___________．12345635791113581114172071115192327A、99B、95C、89D、87题4.布袋中的球大小相同，其中黄球和红球各有9个，蓝球有4个，绿球有3个，从布袋中摸出m个球，为保证摸出的球中至少有5个球颜色相同，m最小是___________．A、15B、16C、17D、18题5.如图，3个长方形与1个直角三角形的面积已知，那么阴影长方形和阴影三角形的面积之和为___________．14303642A、56.1B、60.4C、68.2D、78.6题6.在有10个不同因数的自然数中，最小的两个数的和是___________．A、92B、128C、210D、560由dictator2002制作二、填空题（本大题共10小题，每题5分，共50分）题7.计算：92.0122.0132.0122.01332492.0122.0133242.0122.01 3____题8.李某以17元/个的进价购买一批玩具，再以35元/个售出。
当卖了一半时，除去购进这批玩具的全部成本外还获得了200元的利润。
李某卖完这批玩具共可获得利润_______元题9.在循环小数0.425871??中，从小数点后第m位开始到第n 位止的所有数字之和为2013，当m取最小值时，n?______．题10.如图，一个圆周上有9个位置，依次编号为1~9号。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
一、填空题。
（，每题2分，共24分）
1、一个数亿位上是最大的一位数、千万位上是6，万位上是最小的合数，千位上是最小的质数，其余数位上是0，这个数是（），四舍五入到亿位记作（）亿。
2、一批货物按2:3:5分配给甲、乙、丙三个商店。
( )商店分得这批货物的1/2，乙商店分得这批货物的( )%。
3、（）÷（）= 15（）= 0.6 = （）: 15=( )%
4、12小时12分=（）小时112 公顷=（）平方米
5、六年级一班男生人数的正好和女生的相等，男生和女生的人数比是（）：（），已知男生32人，女生（）人。
6、在12 、13 、14 、15 、16 这五个数中，选出其中的四个数，写出一个比例式：
（）。
7、正方体棱长的总和是48厘米，它的表面积是（）平方厘米，体积是（
）立方厘
8、一本故事书有300页，小明第一天看了这本书的20%，第二天接着看，小明第二天要从第（）页开始看。
9、在一幅表示某学校学生人数的条形统计图中，纵轴“5格”表示一年级有250人，那么五年级有300人，在纵轴上应该用（）格表示。
10、一辆汽车从甲地开往乙地用15小时，返回时这辆汽车每小时行全程的112 ，这辆汽车往返时间比是（），往返速度比是（）。
11、线段比例尺02505007501000千米改写成数字比例尺是（），在这幅图上量得北京到上海的距离是 4.2厘米，北京到上海的实际距离是（）千米
12、如右图所示，把底面直径是8厘米，高是20厘米
的圆柱切成若干等分，拼成一个近似的长方体。
这个近似长方体的表面积是( )
平方厘米，体积是( )立方厘米。
二、判断题。
（每题2分，共10分）
1、王师傅生产110个零件，其中100个是合格产品，合格率是100%。
（）
（）
2、一个圆柱体的铁块重60克，从这个圆柱体上截下一个最大的圆锥体，剩下部分的铁块
的重量是20克。
（）
3、如果x×2/3＝y×3/4，那么x:y＝2/3:3/4。
（）
4、工作时间一定，制造每个零件的时间和零件个数成正比例。
（）
5、一个圆柱形的底面积扩大3倍，高不变，体积也扩大3倍。
( )
三、选择题。
（每题2分，共12分）
1、小明有若干张10元、5元的纸币，这两种纸币的张数相同，那么王小明可能有（）元钱。
①50 ②51 ③75 ④100
2、估计与288.9×1.756的积最接近的数是（）。
①400 ②500 ③600 ④1000
3、一个长方形的框架，如果把它拉成一个平行四边形，它的周长和面积（）。
①周长不变，面积变大②周长不变，面积也不变
③周长变小，面积变小④周长不变，面积变小
4、把一张正方形的纸连续对折4次，折后的每一小块占这张正方形纸的（）。
①14 ②18 ③116 ④132
5、下列各数量关系中，成正比例关系的有（）。
①路程一定，时间和速度。
②圆的半径和它的面积。
③运送一批货物，运走的吨数和剩下的吨数。
④买同样的书，应付的钱数与所买的本数。
6、有一个棱长是4厘米的正方体，从它的一个顶点处挖去一个棱长是1厘米的正方体后，剩下物体表面积和原来的表面积相比较，（）。
①大了②小了③不变④无法确定
四、计算。
（共27分）
1、直接写出得数。
（每题0.5分，共4分）
1787－998＝58 ＋0.25＝1021 ×35 ＝21÷37 ＝
59 ×15 ÷59 ×15 = 18 ÷18 ÷18 ＝111 ×12.1－1= 35 ＋25 ÷15 =
2、用递等式计算。
（每题2.5分，共10分）
①987＋104×65－1747 ②3763 ÷7 ＋17 ×2663
③( 79 ＋421 －37 )×6.3 ④15÷〔( 57 －12 )÷328 〕－0.5
3、求未知数X。
（每題2分，共6分）
0.4 X－0.4×10.8 =20 13 X＋34 X =1348 56 : X = 34 : 25
4、画出面积相等的长方形、三角形、平行四边形和梯形各一个。
（4分）
5、如右图，直角梯形中，高是5厘米，下底是14厘米，求阴影部分的面积？（3分）
五、解决问题。
（27分）
1、只列综合算式，不必解答。
（每小题2分，共6分）
①某一天，李叔叔上午工作4小时，下午工作3小时，共加工零件1400个。
如果李叔叔每小时生产的零件个数是不变的，那么李叔叔上午生产多少个零件？
长江机床厂五月份生产机床650台，比四月份多生产机床150台。
五月份增产百分之几？
③在一张比例尺是5：1的零件设计图上，量得某个零件的长度是6厘米，这个零件的实际长度是多少厘米？
2、小星生日那天，妈妈给小星买了一套衣服和一双运动鞋共用去540元，已知一套衣服的价钱是一双运动鞋的1.7倍，一套衣服和一双运动鞋的价钱各是多少元？（用方程方法解决问题）（5分）
3、李师傅计划加工2620个零件，已经加工了5天，每天加工260个，剩下的要4天完成，平均每天加工多少个零件？(用算术、方程两种方法解答) （5分）
4一个圆锥形麦堆，底面周长12.56米，高1.5米，每立方米小麦重735千克，这堆小麦重多少千克？（保留整千克）
5、李老师带240元钱去买一批笔记本。
在甲商店，看到一种标价为8元的笔记本，李老师感到很满意，问营业员怎么买？营业员说：“买十本送一本”。
到了乙商店，看到同样的笔记本，营业员介绍说：“每本8元，十本起，可打九折”。
根据以上信息请你算一下，李老师到那家商店购买合算，为什么？（6分）
文章来源。