语音信号滤波去噪——使用双线性变换法设计的切比雪夫II型滤波器
基于语音信号去噪处理的IIR滤波器设计

摘要语音信号是我们日常生活中最常见的一种信号,本课程设计主要使用Matlab软件进行一个数字带通IIR滤波器的设计,使之可以对加噪的语音信号进行滤波去噪处理。
文中主要介绍了利用双线性变换法设计切比雪夫Ⅰ型带通数字滤波器的实现方法,并对所设计IIR带通滤波器滤波结果进行信号谱对比和分析,并与预计的仿真结果进行比较说明。
关键词:Matlab ;IIR滤波器;切比雪夫Ⅰ;双线性变换目录前言 (1)第1章滤波器原理综述 (2)1.1滤波器的定义 (2)1.2滤波器的分类 (2)1.3滤波器的原理与设计 (3)第2章 IIR数字滤波器设计原理 (5)2.1 IIR数字滤波器简介 (5)2.2 IIR数字滤波器的主要技术指标 (5)2.3 IIR数字滤波器的设计过程 (6)2.4 双线性变换法设计IIR数字滤波器 (7)第3章IIR数字带通滤波器设计与仿真结果分析 (11)3.1滤波器参数设置 (11)3.2程序设计流程框图 (12)3.3仿真与结果分析 (13)总结 (16)参考文献 (17)附录 (18)致谢 (21)前言滤波技术是信号分析、处理技术的重要分支。
无论是信号的获取、传输,还是信号的处理和交换都离不开滤波技术,它对信号安全可靠和有效灵活地传输是至关重要的。
随着信息时代和数字世界的到来, 数字信号处理已成为当今一门极其重要的学科和技术领域。
目前数字信号处理在通信、语音、图像、自动控制、雷达、军事、航空航天、医疗和家用电器等众多领域得到了广泛的应用,在所有的电子系统和各类控制系统中,数字滤波器的优劣直接决定产品的优劣。
数字滤波器(DF,Digital Filter), 根据其单位冲激响应函数的时域特性可分为两类: 无限冲激响应 IIR(Infinite Impulse Response)滤波器和有限冲激响应 FIR(Finite Impulse Response)滤波器。
与 FIR 滤波器相比,IIR 的实现采用的是递归结构, 极点须在单位圆内, 在相同设计指标下, 实现 IIR滤波器的阶次较低, 即所用的存储单元少, 从而经济效率高,在不要求严格线性相位的情况下,IIR滤波器的应用相当广泛。
切比雪夫Ⅰ型滤波器和切比雪夫Ⅱ型滤波器的对比
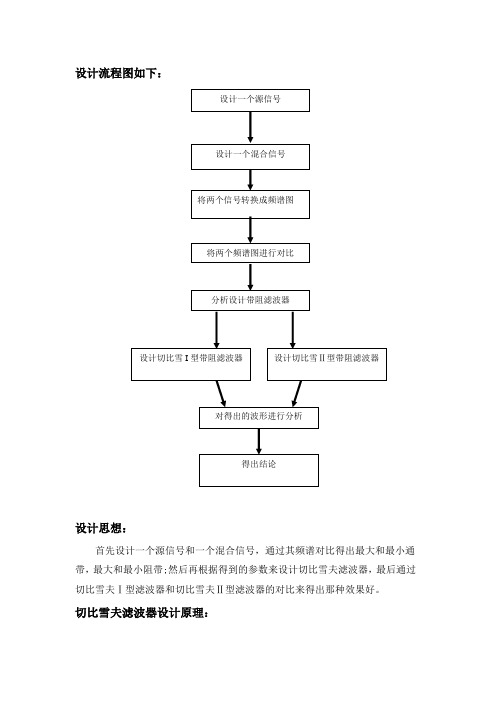
设计流程图如下:设计思想:首先设计一个源信号和一个混合信号,通过其频谱对比得出最大和最小通带,最大和最小阻带;然后再根据得到的参数来设计切比雪夫滤波器,最后通过切比雪夫Ⅰ型滤波器和切比雪夫Ⅱ型滤波器的对比来得出那种效果好。
切比雪夫滤波器设计原理:切比雪夫滤波器的振幅具有等波纹特性,它有两种形式:1)振幅特性在通带内是等波纹的、在阻带内是单调的切比雪夫I 型滤波器;2)振幅特性在通带内是单调的、在阻带内是等波纹的切比雪夫II型滤波器,采用何种形式的切比雪夫滤波器取决于实际用途.切比雪夫滤波器的设计方法就是将逼近精确度均匀分布在整个通带内,或者均匀分布在整个阻带内,或者均匀分布在两者之内,这样就可以使滤波器阶数大大降低。
切比雪夫I型滤波器平方幅度响应函数表示为:2)(ΩjG=[1+2εC2N(Ω)]2/1-其中ε<1(正数),它与通带波纹有关,ε越大,波纹也越大;CN(Ω) 是切比雪夫多项式,它被定义为:CN (Ω)=cos(Narccos(Ω)),Ω≤1, CN(Ω)=cosh(Narcosh(Ω)),Ω>1. 而切比雪夫II型滤波器平方幅度响应函数表示为:)(ΩjG2={1+2ε{ C2N(Ω)/[2N(Ω/cΩ)]2}}1-其中ε<1(正数),表示波纹变化情况;cΩ为截止频率;N为滤波器的阶次,也是CN (NΩΩ/)的阶次。
源信号编码及其图形:t=-1:0.01:1y=(cos(2*pi*10*t)+cos(2*pi*40*t)); N=length(y);fx=fft(y);df=100/N;n=0:N/2;f=n*df;subplot(2,1,1);plot(f,abs(fx(n+1))*2/N); grid;title('源波形频谱')图(一)混合信号编码及其图形:t=-1:0.01:1;X=(cos(2*pi*10*t)+cos(2*pi*25*t)+cos(2*pi*40*t));N=length(X);fx=fft(X);df=100/N;n=0:N/2;f=n*df;subplot(2,1,2);plot(f,abs(fx(n+1))*2/N); grid;title('混合波形频谱')图(二)从图(一)和图(二)对比可以得出:为了能达到和满足我们的要求,我们取以下的参数,最大通带wp2:0.5,最小通带wp1:0.05,最大阻带w s2:0.3,最小阻带ws1:0.1。
双线性变换法设计数字切比雪夫带通IIR滤波器

摘要在进行DSP系统设计时,往往先采用MATLAB软件等对算法进行仿真,确定最佳算法和参数。
利用MATLAB勺信号处理工具箱可以直接设计数字滤波器,也可以建立模拟原型,离散化设计数字滤波器。
本文介绍了IIR数字带通滤波器的设计原理、步骤以及在MATLAB中勺实现方法,并能应用到实际勺信号处理中。
关键词:IIR 数字滤波器,数字信号处理(DSP), MATLAB仿真AbstractWhen the DSP system is designed, we often simulate the algorithm and decide the best algorithm and parameters on the MATLAB software. We can design a digital filter either using the MATLAB Toolbox directly or creating a analog filter prototype and scatering the digital filter. This paper introduces the design principle of IIR digital bandpass filter, the steps as well as the methods in MATLAB ,and it also can be applied to the actual signal processing.Key words: IIR digital filters, Digital signal processing (DSP), MATLAB, Simulation目录摘要 (I)ABSTRACT (II)1 绪论 (1)2 IIR 数字滤波器设计的原理与方法 (1)2.1 IIR 数字滤波器设计的原理 (1)2.2 IIR 数字滤波器设计的基本方法 (3)3 IIR 带通滤波器的MATLAB设计 (3)3.1IIR 带通滤波器的设计流程 (4)3.2IIR 带通滤波器的设计步骤 (5)4 IIR 带通滤波器的仿真结果及波形 (8)5 IIR 带通滤波器的仿真结果分析 (9)6 总结 (11)参考文献 (13)附录:原程序 (14)Matlab 课程设计——双线性变换法设计数字切比雪夫带通IIR 滤波器1 绪论在现代通信系统中,由于信号中经常混有各种复杂成分,所以很多信号的处理和分析都是基于滤波器而进行的。
语音信号滤波去噪--使用双线性变换法设计的级联型椭圆滤波器.

语音信号滤波去噪——使用双线性变换法设计的级联型椭圆滤波器学生姓名:Su 指导老师:摘要本课程设计主要内容是利用双线性变换法设计一个级联型的椭圆IIR滤波器,对一段含噪语音信号进行滤波去噪处理并根据滤波前后的波形和频谱分析滤波性能。
本课程设计仿真平台为MATLAB7.0,开发工具是M语言编程。
首先在windows下用录音机工具录制一段语音信号,并人为加入一单频噪声,然后对信号进行频谱分析以确定所加噪声频率,并设计滤波器进行滤波去噪处理,最后比较滤波前后的波形和频谱并进行分析。
由分析结果可知,滤波器后的语音信号与原始信号基本一致,即设计的IIR滤波器能够去除信号中所加单频噪声,达到了设计目的。
关键词滤波去噪;IIR椭圆滤波器;双线性变换法;级联型;MATLAB1 引言信号处理是科学研究和工程技术许多领域都需要进行的一个重要环节,传统上对信号的处理大都采用模拟系统实现。
随着人们对信号处理要求的日益提高,以及模拟信号处理中一些不可克服的缺点,对信号的许多处理而采用数字的方法进行。
数字信号处理系统无论在性能、可靠性、体积、耗电量、成本等诸多方面都比模拟信号处理系统优越的多,使得许多以往采用模拟信号处理的系统越来越多地被数字处理系统所代替,数字信号处理技术在通信、语音、图像、自动控制、雷达、军事、航空航天、医疗和家用电器等众多领域得到了广泛的应用。
滤波器是一种用来消除干扰杂讯的器件,凡是可以使信号中特定的频率成分通过,而极大地衰减或抑制其他频率成分的装置或系统称之为滤波器。
在数字信号处理中,数字滤波器设计在电子工程、应用数学和计算机科学领域都是非常重要的内容。
设计滤波器的方法有多种,在各种滤波器中,椭圆滤波器相比其他类型的滤波器,在阶数相同的条件下有着最小的通带和阻带波动,它在通带和阻带的波动相同。
本课程设计主要解决在含噪情况下对语音信号的滤波去噪处理,处理时采用的是利用双线性变换法设计的级联型的椭圆IIR滤波器。
IIR滤波器语音去噪处理

课程设计(论文)题目基于IIR数字滤波器的有噪语音信号的处理课程设计(论文)任务书学院:电气工程学院题目:基于IIR数字滤波器的有噪语音信号的处理起止时间:2016年10月25日至16年11月20日学生姓名:专业班级:指导教师:教研室主任:院长:2016年 11 月 20 日语音信号的时频分析加噪后的语音信号及其频谱分析验证所设计的滤波器比较滤波前后语音信号的波形及频谱滤波器处理结果的分析5. 课题结论6. 参考文献7. 谢辞8. 附录附录1:IIR数字滤波器的主要程序附录2:比较滤波前后语音信号的波形及频谱三、课程设计(论文)基本要求(1)技术要求:编制 Matlab 程序,完成以下功能,产生系统输入信号;根据系统差分方程求解单位脉冲响应序列;根据输入信号求解输出响应;用实验方法检查系统是否稳定;绘制相关信号的波形。
(2)工作要求:简述离散系统时域分析和判断系统稳定性方法;完成所给设计实验,并对结果进行分析和解释;打印程序清单和要求画出的信号波形;写出本次课程设计的收获和体会;列出参考文献。
四、课程设计(论文)进度安排课程设计进度(时间)安排如下:1. 2016年10月25日—2016年10月31日理解课程设计题目的设计要求,查阅相关资料;2. 2016年11月1日—2016年11月8日完成各部分程序代码及系统调试;3. 2016年11月9日—2016年12月11日完成课程设计初稿;4. 2016年11月12日—2016年11月24日完成完整的课程设计报告;5. 2016年11月20日上交课程设计作品并答辩。
五、主要参考文献[1].高西全,丁玉美.数字信号处理[M].北京:西安电子科技大学出版社,2008[2].刘泉,阙大顺.数字信号处理原理与实现[M].北京:电子工业出版社,2005[3].张磊,毕靖,郭莲英.MATLAB实用教程[M].北京:人民邮电出版社,2008[4].张威.MATLAB基础与编程入门[M].西安:西安电子科技大学出版社,2006[5].周利清,苏菲.数字信号处理基础[M].北京:北京邮电大学出版社,2005指导老师:(签名)年月日摘要:滤波器设计在数字信号处理中占有极其重要的地位,IIR滤波器是滤波器设计的重要组成部分。
结合双线性变换法设计一个数字切比雪夫带通IIR滤波器。要点

课程设计任务书学生姓名:蒋立豪专业班级:通信1303指导教师:魏勤工作单位:信息工程学院题目:利用MATLAB仿真软件系统结合双线性变换法设计一个数字切比雪夫带通IIR滤波器。
初始条件:1 MATLAB编程的基础知识2《信号与系统》滤波器的相关知识3《数字信号处理》的相关知识要求完成的主要任务:(包括课程设计工作量及技术要求,以及说明书撰写等具体要求)1、课程设计工作量:1周。
2、技术要求:1)设计一个数字滤波器,要求运用切比雪夫原理和双线性变换法2)具有带通的功能,能够滤除小频率的信号和大频率的信号3)能够让频带内的信号通过4) 确定设计方案,按功能模块的设计程序,写出总体程序,并阐述基本原理。
5) 查阅至少5篇参考文献。
按《武汉理工大学课程设计工作规范》要求撰写设计报告书。
全文用A4纸打印,图纸应符合绘图规范。
时间安排:序阶段内容所需时间号1 方案设计1天2 软件设计2天3 系统调试1天4 答辩1天合计5天指导教师签名:年月日系主任(或责任教师)签名:年月日摘要面对庞杂繁多的原始信号, 如何提取所需信号、抑制不需要的信号这就需要使用滤波器。
滤波器的作用主要是选择所需频带的信号内容而抑制不需要的其他频带的信号内容。
数字滤波器因其精度高、可靠性好、灵活性大等优点, 在语音信号处理、信号频谱估计、信号去噪、无线通信中的数字变频以及图像处理等工程实际应用中都很广泛。
MATLAB是“矩证实验室”(MATrix LABoratoy)的缩写,它是一种以钜阵运算为基础的交互式程序语言,专门针对科学﹑工程计算机绘图的需求。
与其他计算机语言相比,其特点是简洁和智能化,适应科技专业人员的思维方式和书写习惯,使得编程和调试效率大大提高本次课程设计将完成一个数字切比雪夫带通IIR滤波器的设计,利用双线性变换和无限冲激响应IIR原理完成设计,并利用MATLAB进行仿真。
关键字:滤波器、数字信号处理、噪声、IIR、带通、MATLABAbstractFaced with a huge variety of original signal, how to extract the desired signal, suppress the signal does not need to use the filter. The function of the filter is to select the signal content of the desired frequency band and suppress the signal content of the other frequency band which is not needed. Digital filter because of the advantage of its high accuracy, good reliability and great flexibility, in speech signal processing, signal spectrum estimation, signal to noise, wireless communication in the digital frequency conversion and image processing etc. in actual engineering application is very widespread.Matlab is the abbreviation of "moment of laboratory medicine" (matrix LABoratoy) it is a kind of to huge operational matrices based interactive programming language, specifically for the needs of science and engineering computer graphics. Compared with other computer languages, it is characterized by its simplicity and intelligence, the way of thinking and writing habits, which makes the programming and debugging efficiency greatly improved.The curriculum design will be completed a digital Chebyshev bandpass IIR filter design, using bilinear transform and infinite impulse response IIR principle of the completion of design, and is simulated with MATLAB.Keywords: filter, digital signal processing, noise, IIR, band-pass, MATLAB目录摘要 (I)ABSTRACT (II)1 前言 (1)2数字滤波器 (2)2.1 数字滤波器介绍 (2)2.2 IIR数字滤波器 (3)2.2.1 IIR数字滤波器的特点 (3)2.2.2 IIR数字滤波器与FIR数字滤波器的区别 (4)3切比雪夫滤波器 (4)3.1概述 (4)3.2切比雪夫滤波器的种类 (5)4双线性变换法 (8)5 IIR数字滤波器设计原理与方法 (12)5.1IIR数字滤波器设计原理 (12)5.2IIR数字滤波器设计的基本方法 (14)6 IIR带通滤波器的MATLAB 设计 (16)6.1IIR带通滤波器的设计步骤 (16)6.2IIR带通滤波器设计 (16)6.4仿真结果 (20)6.4.1滤波器性能仿真 (20)6.4.2滤波器性能验证 (21)7. 用FDATOOL设计数字滤波器 (26)8 总结与体会 (30)9 致谢 (32)参考文献 (33)附录:源程序 (34)1 前言在现代通信系统中,由于信号中经常混有各种复杂成分,所以很多信号的处理和分析都是基于滤波器而进行的。
MATLAB结合双线性变换法设计一个数字切比雪夫带阻IIR滤波器

课程设计题目Matlab课程设计——利用MATLAB 结合双线性变换法设计一个数字切比雪夫带阻IIR滤波器学院信息工程学院专业通信工程班级通信0803姓名王欢指导教师魏洪涛学号:01208103408142011 年1月月14日日武汉理工大学《Matlab课程设计》报告课程设计任务书学生姓名:王欢专业班级:通信0803指导教师:魏洪涛工作单位:信息工程学院题目: Matlab课程设计——利用MATLAB仿真软件系统结合双线性变换法设计一个数字切比雪夫带阻IIR滤波器。
初始条件:Matlab基础知识、计算机要求完成的主要任务:1.方案的理论设计2.方案的安装、调试3.设计报告的撰写时间安排:指导教师签名: 2010 年 1月日系主任(或责任教师)签名: 2010 年 1月日目录摘要 (3)ABSTRACT (4)1 数字滤波器 (5)1.1概述 (5)1.2特点 (6)1.3分类 (6)1.4设计原理 (6)2 双线性变换法 (8)2.1简介 (8)2.2对比 (11)2.2.1优点 (11)2.2.2缺点 (12)3 切比雪夫滤波器 (13)3.1概述 (13)3.2切比雪夫滤波器的种类 (13)3.2.1 I型切比雪夫滤波器 (13)3.2.2 II型切比雪夫滤波器 (13)3.3特点 (13)4 用MATLAB实现切比雪夫IIR带阻滤波器 (14)4.1程序流程图 (14)4.2MATLAB程序代码 (15)4.3仿真结果 (16)5 学习小结 (17)6 参考文献 (17)摘要随着信息时代和数字世界的到来,数字信号处理已成为当今一门极其重要的学科和技术领域。
目前数字信号处理在通信、语音、图像、自动控制、雷达、军事、航空航天、医疗和家用电器等众多领域得到了广泛的应用。
在数字信号处理中起着重要的作用并已获得广泛应用的是数字滤波器(DF,Digital Filter)。
数字滤波器是一种用来过滤时间离散信号的数字系统,通过对抽样数据进行数学处理来达到频域滤波的目的。
切比雪夫II型带通IIR数字滤波器设计

切比雪夫II 型带通IIR 数字滤波器设计1.设计思路(1) 数字—模拟指标转换。
利用双线性变换的频率预畸变公式2tan 2ωT =Ω,把所要求的数字滤波器)(z H 数字频率指标转换为相应的模拟滤波器)(s H 的模拟频率指标。
(2) 低通模拟指标转换。
将模拟滤波器)(s H 的频率指标归一化原型低通滤波器)(p H LP 的频率指标。
(3) 模拟滤波器的设计,得到低通滤波器的归一化传输函数)(p H LP 。
(4) 模拟频率变换,将模拟低通滤波器归一化传输函数)(p H LP 转换成所需要的模拟滤波器传输函数)(z H 。
(5) 模拟—数字滤波器变换。
利用双线性变换得到所要求的数字滤波器传输函数11112)()(--+-==z z T s s H Z H 。
2.设计要求及方案设计一带通切比雪夫II 型IIR 滤波器,要求如下:通带上下边沿频率分别为300 Hz 和400 Hz ,通带最大衰减dB p3=α,阻带上下边沿频率分别为200Hz 和500 Hz ,阻带最小衰减 dB s 18=α,采样频率Hz f s 2000=。
2.1带通滤波器的边缘频率为Hz f p 3001=,Hz f p 4002= Hz f s 2001=,Hz f s 5002=给定的系统取样频率为Hz f s 2000=,相应的数字频率为ππω3.0211=⨯=sp p f f ππω4.0222=⨯=sp p f fππω2.02=⨯=s sl sl f f ππω5.0222=⨯=ss s f f2.2采用双线性变换,以获得相应的模拟带通滤波器的边缘频率s rad f p s p /1.20382tan211==Ωω s rad f p s p /2.29062tan222==Ωωs rad f s s s /7.12992tan211==Ωω s rad f s s s /0.40002tan222==Ωωs rad B p p /1.86812=Ω-Ω=2.3归一化低通滤波器的技术指标1=p λ 11.31212≈Ω-ΩΩ-Ω=p p s s s λ通带最大衰减dB p3=α阻带最小衰减 dB s 18=αss s B s p w p 1001200002202+=Ω+=λ 用MTALAB 算法设计归一化切比雪夫II 型低通模拟滤波器>> [N2,wp2]=cheb2ord(wp,ws,Rp,As,'s'); %Chebyshev Ⅱ型滤波器参数计算(模拟域); >> [B2,A2]=cheby2(N2,Rp,wp2,'s'); %计算H(s)的系数B 和A ;>> [Z,P,K]=cheby2(N2,As,wp2,'s'); %构造Chebyshev Ⅱ型滤波器(零极点模型) >> subplot(2,2,1);>> [Z,P,K]=cheby2(N2,As,wp2,'s'); %构造Chebyshev Ⅱ型滤波器(零极点模型) >> [H,W]=zp2tf(Z,P,K); %将零极点模型转化成传递函数的模型 >> figure(1);>> [P,Q]=freqs(H,W); %在Figure1上显示滤波器的幅频响应及相频响应>> figure(2); >> subplot(2,2,1);>> fk=0:12000/512:12000;wk=2*pi*fk; %在Figure2上显示幅频特性曲线>> Hk=freqs(B2,A2,wk);>> plot(fk/1000,20*log10(abs(Hk)));grid on >> xlabel('Frequency(Hz)') >> ylabel('Magnitude Response')2.4将)(p H LP 转化为带通滤波器的系统sB s p LP w pp H s H 202)()(Ω+==λ2.5用双线性变换法将)(s H 转换成数字滤波器)(z H ,即1112)()(-+-==z z s s H Z H()()()()()()()()()()()()()()()⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+-+++-+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-+++-∙⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+-+++-+⎪⎪⎪⎪⎪⎭⎫⎝⎛-+++-+-+++-=--------------------6359.011219001148720.0112190011411949.111219001143331.01121900114)5389.01121900114(442.21111212111211112121112111121zz z z z z z z z z z zz z z z z z zz3.利用MATLAB 一步编写切比雪夫II 型带通数字滤波器Matlab 总程序如下:>> W1=300;W2=400;rp=3;rs=18;Fs=2000; >> WP=[200,300];WS=[50,450];>> [N,Wn]=cheb2ord(WP/(Fs/2),WS/(Fs/2),rp,rs);>> [P,Q]=cheby2(N,rp,Wn,'bandpass'); %创建Chebyshev 带通滤波器 >> ylabel('幅度'); >> figure(1);>> freqz(P,Q); %显示产生滤波器的幅频及相频曲线 >> [H,W]=freqz(P,Q); >> figure(2);>> plot(W*Fs/(2*pi),abs(H));grid; >> xlabel('频率/Hz');>> ylabel('幅度')>> title('数字滤波器幅频响应|H(ejOmega)| ');仿真出的幅频特性曲线如下图1.1所示:图1.1:幅频特性曲线相频特性及幅度特性曲线如下图1.2所示:图1.2:相频特性及幅度特性曲线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课程设计任务书语音信号滤波去噪——使用脉冲响应不变法设计的巴特沃斯滤波器摘要本课程设计主要运用麦克风采集一段语音信号,绘制波形并观察其频谱,给定相应技术指标,用脉冲响应不变法设计的一个满足指标的巴特沃斯IIR滤波器,对该语音信号进行滤波去噪处理,比较滤波前后的波形和频谱并进行分析,根据结果和学过的理论得出合理的结论。
关键词课程设计;滤波去噪;巴特沃斯滤波器;脉冲响应不变法;MATLAB1 引言本课程设计主要利用麦克风采集一段8000Hz,8k的单声道语音信号,并绘制波形观察其频谱,再用MATLAB利用脉冲响应不变法设计一个巴特沃斯滤波器,将该语音信号进行滤波去噪处理。
1.1 课程设计目的《数字信号处理》课程设计是在学生完成数字信号处理和MATLAB的结合后的基本实验以后开设的。
本课程设计的目的是为了让学生综合数字信号处理和MATLAB并实现一个较为完整的小型滤波系统。
这一点与验证性的基本实验有本质性的区别。
开设课程设计环节的主要目的是通过系统设计、软件仿真、程序安排与调试、写实习报告等步骤,使学生初步掌握工程设计的具体步骤和方法,提高分析问题和解决问题的能力,提高实际应用水平。
1.2课程设计的要求(1)滤波器指标必须符合工程设计。
(2)设计完后应检查其频率响应曲线是否满足指标。
(3)处理结果和分析结论应该一致,而且应符合理论。
(4)独立完成课程设计并按要求编写课程设计报告。
2 设计原理用麦克风采集一段语音信号,绘制波形并观察其频谱,给定相应技术指标,用脉冲响应不变法设计的一个满足指标的巴特沃斯IIR滤波器,对该语音信号进行滤波去噪处理,比较滤波前后的波形和频谱并进行分析。
2.1 IIR滤波器I IR滤波器设计方法有间接法和直接法,间接法是借助于模拟滤波器的设计方法进行的。
其设计步骤是:先设计过渡模拟滤波器得到系统函数H(s),然后将H(s)按某种方法转换成数字滤波器的系统函数H(z)。
FIR滤波器比鞥采用间接法,常用的方法有窗函数法、频率采样发和切比雪夫等波纹逼近法。
对于线性相位滤波器,经常采用FIR 滤波器。
对于数字高通、带通滤波器的设计,通用方法为双线性变换法。
可以借助于模拟滤波器的频率转换设计一个所需类型的过渡模拟滤波器,再经过双线性变换将其转换策划那个所需的数字滤波器。
具体设计步骤如下:(1)确定所需类型数字滤波器的技术指标。
(2)将所需类型数字滤波器的边界频率转换成相应的模拟滤波器的边界频率,转换公式为Ω=2/T tan(0.5ω)(3)将相应类型的模拟滤波器技术指标转换成模拟低通滤波器技术指标。
(4)设计模拟低通滤波器。
(5)通过频率变换将模拟低通转换成相应类型的过渡模拟滤波器。
(6)采用双线性变换法将相应类型的过渡模拟滤波器转换成所需类型的数字滤波器。
我们知道,脉冲响应不变法的主要缺点是会产生频谱混叠现象,使数字滤波器的频响偏离模拟滤波器的频响特性。
为了克服之一缺点,可以采用双线性变换法。
下面我们总结一下利用模拟滤波器设计IIR数字低通滤波器的步骤:(1)确定数字低通滤波器的技术指标:通带边界频率、通带最大衰减,阻带截止频率、阻带最小衰减。
(2)将数字低通滤波器的技术指标转换成相应的模拟低通滤波器的技术指标。
(3)按照模拟低通滤波器的技术指标设计及过渡模拟低通滤波器。
(4)用双线性变换法,模拟滤波器系统函数转换成数字低通滤波器系统函数。
设IIR滤波器的输入序列为,则IIR滤波器的输入序列和输出序列之间的关系可用下列方程式表示:(2-1)其中和是滤波器的系数,且中至少有一个非零。
与上述差分方程对应的传递函数为:(2-2) 由传递函数可以发现无限长单位冲激响应滤波器有如下特点:(1)单位冲激响应是无限长的。
(2)系统传递函数在有限z平面上有极点存在。
(3)结构上存在着输出到输入的反馈,也就是结构上是递归型的。
设是某个模拟滤波器的频率响应,那么低通滤波器在幅度平方响应上的技术指标给出为:(2-3)(2-4)式中是通带波纹参数,是通带截止频率以rad/s(弧度每秒)计,A是阻带衰减参数,以及是阻带截止频率以rad/s计。
(2-5)(2-6)参数和A是分别与以dB计的参数和有关的,这些关系是(2-7)(2-8)波纹和的绝对标尺是通过下式与和A有关的:利用幅度平方响应给出的模拟滤波器要求(2-1)和(2-2)式不包含任何相位信息。
现在,为了求s域的系统函数,考虑那么有(2-12)或者有(2-9)因此,幅度平方函数的零点和极点相对于轴是以镜像对称方式分布的【2】。
接下来,我们根据语音信号的特点给出有关滤波器的技术指标:低通滤波器的性能指标:fp=1200Hz,fs=1200Hz,ft=8000Hz, As=20db ,Ap=1dB2.2 巴特沃斯滤波器MATLAB信号处理工具箱函数buttp buttor butter是巴特沃斯滤波器设计函数,其有5种调用格式,本课程设计中用到的是[N,wc]=butter(N,wc,Rp,As,’s’),该格式用于计算巴特沃斯模拟滤波器的阶数N和3dB截止频率wc。
函数butter,cheby1和ellip设计IIR滤波器时都是默认的双线性变换法,所以在设计滤波器时只需要代入相应的实现函数即可。
下面我们设计的IIR数字滤波器的主要程序:wp=2*pi*Fp/Ft;ws=2*pi*Fs/Ft;fp=2*Ft*tan(wp/2);fs=2*Ft*tan(ws/2);[n,wn]=buttord(wp,ws,Ap,As,'s');[b,a]=butter(n,wn,'s');[num,den]=bilinear(b,a,1);[h,w]=freqz(num,den);3.设计步骤3.1设计流程图语音信号滤波去噪——使用脉冲不变响应法设计的巴特沃斯滤波器的设计流程如图2所示:图1 脉冲响应不变法巴特沃斯滤波器对语音信号去噪流程图3.2语言信号的采集图3是基于PC机的语音信号采集过程:通过计算机录音系统录制1秒:图2 语音采集过程图3 录音过程截图3.3语音信号的频谱分析3.4滤波器设计将数字滤波器的设计指标设为通带截止频率fb=1100HZ,阻带频率fc=1200HZ,通带波纹Ap=1dB,阻带波纹As=20dB,要求确定H(z)。
设计程序如下:Fp=1200;Ft=8000;As=20;Ap=1;wp=2*pi*Fp/Ft;ws=2*pi*Fs/Ft;fp=2*Ft*tan(wp/2);fs=2*Ft*tan(ws/2);[n,wn]=buttord(wp,ws,Ap,As,'s');[b,a]=butter(n,wn,'s');[num,den]=bilinear(b,a,1);[h,w]=freqz(num,den);Buttor波形如下图5:图5 IIR低通滤波器3.5 信号滤波过程[y,fs,nbits]=wavread('3333.wav');%载入波形N=length(y)%计算输入波形长度Y=fft(y,N);%进行快速傅里叶变换sound(y);%播放声音figure(4);%时域图figure(5);plot(abs(Y));%滤波前频谱图Fp=1200;%阻带截止频率Fs=1100;%通带截止频率Ft=8000;%采集频率As=20;%通带波纹Ap=1Ap=1;%阻带波纹As=20wp=2*pi*Fp/Ft;ws=2*pi*Fs/Ft;fp=2*Ft*tan(wp/2);fs=2*Ft*tan(ws/2);[n,wn]=buttord(wp,ws,Ap,As,'s'); %求低通滤波器的阶数和截止频率[b,a]=butter(n,wn,'s'); %求S域的频率响应的参数[num,den]=bilinear(b,a,1); %双线性变换实现S域到Z域的变换[h,w]=freqz(num,den); %根据参数求出频率响应figure(3)plot(w*8000*0.5/pi,abs(h));z=filter(num,den,y);sound(z);m=z; %求滤波后的信号figure(1)subplot(2,2,3);plot(abs(m),'r');title('滤波后信号的频谱');grid;subplot(2,2,4);plot(z,'b');title('滤波后的信号波形');grid;subplot(2,2,2);plot(y,'b');title('滤波前信号的波形');grid;subplot(2,2,1);plot(abs(Y),'r');title('滤波前信号的频谱');grid;figure(2);p=angle(m);q=angle(Y);subplot(2,1,1);plot(q,'b');title('滤波前相位');grid;subplot(2,1,2);plot(p,'b');title('滤波后相位');grid;所得波形为:图6.1滤波前后的时域对比波形和滤波前后频域频谱图图6.2滤波前后相位比较图3.5结果分析由图6.1中滤波前后波形比较可看出,经过滤波后的波形比原波形的振幅有所减小,去除了很多由于噪声所产生的干扰;从滤波前后的频谱比较可以看出经过滤波后除了原本的声音外,中间由于噪声产生的频谱波形已经滤除;由图6.2滤波前后相位比较图可看出由于经过滤波,相位变得稀疏;经过MATLAB仿真,听滤波前后的声音,可以听出有明显的滤波效果。
因此利用脉冲响应不变法设计的巴特沃斯滤波器已经达到了设计的要求。
4.出现的问题及解决方法在这次的课程设计中我们设计的滤波器对语音信号的滤噪处理或多或少会因为我们的疏忽或者实践能力不够还是会遇到问题的,当遇到问题时我们不但运用自己学到的知识还得到同学和老师的帮助将其解决,不断完善和修改。
设计中出现的问题及解决方法如下:(1)设计的滤波器达不到要求,因为在采集语音信号时,录音机的音频格式应该是PCM 8000kHz,8位,单声道。
若由非人发出的声音可能会被滤波器滤去,且声音文件最好在一秒左右。
(2)在运用Matlab设计滤波器时,当编辑完前面两条程序时无法放出声音,后来发现我们应当把采集的语音信号wav文件放到Matlab的work文件夹中。
(3)还要在滤波器性能曲线的wc处画一根竖线,这样更方便看出结果,其中wc 处线的确定还需计算出wb/pi的值。
