自动控制原理实验报告——合肥工业大学
自动控制原理的实训报告

一、实训目的本次实训旨在通过实际操作和实验,加深对自动控制原理的理解,掌握控制系统分析和设计的基本方法,提高动手能力和分析问题、解决问题的能力。
通过实训,使学生能够:1. 理解自动控制系统的基本组成和原理;2. 掌握典型控制系统的时域响应和频域响应分析方法;3. 学会使用实验设备进行控制系统实验,并能够分析实验结果;4. 培养团队协作和沟通能力。
二、实训仪器与设备1. 自动控制原理实验台;2. 信号发生器;3. 数据采集器;4. 计算机;5. 控制系统模拟软件。
三、实训内容1. 控制系统结构分析通过实验台搭建一个典型的控制系统,分析其结构,包括各个环节的功能和相互关系。
2. 时域响应实验对搭建的控制系统进行阶跃响应实验,记录并分析系统的输出波形,计算超调量、上升时间、调节时间等性能指标。
3. 频域响应实验对搭建的控制系统进行频率特性实验,记录并分析系统的幅频特性、相频特性,绘制Bode图。
4. 控制系统设计根据实验结果,对控制系统进行设计,包括PID参数整定、控制器设计等。
四、实验过程1. 搭建控制系统根据实验要求,搭建一个典型的控制系统,包括控制器、执行器、被控对象等环节。
2. 进行阶跃响应实验使用信号发生器产生阶跃信号,输入到控制系统中,记录输出波形,并计算超调量、上升时间、调节时间等性能指标。
3. 进行频率特性实验使用信号发生器产生不同频率的正弦信号,输入到控制系统中,记录输出波形,并绘制Bode图。
4. 控制系统设计根据实验结果,对控制系统进行设计,包括PID参数整定、控制器设计等。
五、实验结果与分析1. 阶跃响应实验通过阶跃响应实验,可以分析系统的稳定性和动态性能。
例如,超调量反映了系统的振荡程度,上升时间反映了系统的响应速度,调节时间反映了系统达到稳态所需的时间。
2. 频率特性实验通过频率特性实验,可以分析系统的频率响应特性。
例如,幅频特性反映了系统对不同频率信号的放大倍数,相频特性反映了系统对不同频率信号的相位延迟。
自动控制原理实验报告

自动控制原理实验报告一、实验目的。
本实验旨在通过实际操作,加深对自动控制原理的理解,掌握PID控制器的调节方法,并验证PID控制器的性能。
二、实验原理。
PID控制器是一种常见的控制器,它由比例环节(P)、积分环节(I)和微分环节(D)三部分组成。
比例环节的作用是根据偏差的大小来调节控制量的大小;积分环节的作用是根据偏差的累积值来调节控制量的大小;微分环节的作用是根据偏差的变化率来调节控制量的大小。
PID控制器通过这三个环节的协同作用,可以实现对被控对象的精确控制。
三、实验装置。
本次实验所使用的实验装置包括PID控制器、被控对象、传感器、执行机构等。
四、实验步骤。
1. 将PID控制器与被控对象连接好,并接通电源。
2. 调节PID控制器的参数,使其逐渐接近理想状态。
3. 对被控对象施加不同的输入信号,观察PID控制器对输出信号的调节情况。
4. 根据实验结果,对PID控制器的参数进行调整,以达到最佳控制效果。
五、实验结果与分析。
经过实验,我们发现当PID控制器的比例系数较大时,控制效果会更为迅速,但会引起超调;当积分系数较大时,可以有效消除稳态误差,但会引起响应速度变慢;当微分系数较大时,可以有效抑制超调,但会引起控制系统的抖动。
因此,在实际应用中,需要根据被控对象的特性和控制要求,合理调节PID控制器的参数。
六、实验总结。
通过本次实验,我们深刻理解了PID控制器的工作原理和调节方法,加深了对自动控制原理的认识。
同时,我们也意识到在实际应用中,需要根据具体情况对PID控制器的参数进行调整,以实现最佳的控制效果。
七、实验心得。
本次实验不仅让我们在理论知识的基础上得到了实践锻炼,更重要的是让我们意识到掌握自动控制原理是非常重要的。
只有通过实际操作,我们才能更好地理解和掌握知识,提高自己的实际动手能力和解决问题的能力。
八、参考文献。
[1] 《自动控制原理》,XXX,XXX出版社,2010年。
[2] 《PID控制器调节方法》,XXX,XXX期刊,2008年。
自动控制原理实验报告

自动控制原理实验报告实验目的,通过本次实验,掌握自动控制原理的基本概念和实验操作方法,加深对自动控制原理的理解和应用。
实验仪器与设备,本次实验所需仪器设备包括PID控制器、温度传感器、电磁阀、水槽、水泵等。
实验原理,PID控制器是一种广泛应用的自动控制设备,它通过对比设定值和实际值,根据比例、积分、微分三个控制参数对控制对象进行调节,以实现对控制对象的精确控制。
实验步骤:1. 将温度传感器插入水槽中,保证传感器与水温充分接触;2. 将水泵接通,使水槽内的水开始循环;3. 设置PID控制器的参数,包括比例系数、积分时间、微分时间等;4. 通过调节PID控制器的参数,使得水槽中的水温稳定在设定的目标温度;5. 观察记录PID控制器的输出信号和水温的变化情况;6. 分析实验结果,总结PID控制器的控制特性。
实验结果与分析:经过实验操作,我们成功地将水槽中的水温控制在了设定的目标温度范围内。
在调节PID控制器参数的过程中,我们发现比例系数的调节对控制效果有着明显的影响,适当增大比例系数可以缩小温度偏差,但过大的比例系数也会导致控制系统的超调现象;积分时间的调节可以消除静差,但过大的积分时间会导致控制系统的超调和振荡;微分时间的调节可以抑制控制系统的振荡,但过大的微分时间也会使控制系统的响应变慢。
结论:通过本次实验,我们深入理解了PID控制器的工作原理和调节方法,掌握了自动控制原理的基本概念和实验操作方法。
我们通过实验操作和数据分析,加深了对自动控制原理的理解和应用。
总结:自动控制原理是现代控制工程中的重要内容,PID控制器作为一种经典的控制方法,具有广泛的应用前景。
通过本次实验,我们不仅学习了自动控制原理的基本知识,还掌握了PID控制器的调节方法和控制特性。
这对我们今后的学习和工作都具有重要的意义。
合肥工业大学自动控制理论综合实验倒立摆实验报告

合肥工业大学自动控制理论综合实验倒立摆实验报告————————————————————————————————作者: ————————————————————————————————日期:1、把上述参数代入,求解系统的实际模型;a)摆杆角度和小车位移之间的传递函数;M=1.096;m=0.109;b=0.1;l=0.25;I=0.0034;g=9.8;n1=[m*l 00];d1=[I+m*l^20-m*g*l];Phi1=tf(n1,d1)返回:Transfer function:0.02725 s^2--------------------0.01021 s^2- 0.2671b)摆杆角度和小车加速度之间的传递函数;继续输入:n2=[m*l];d2=d1; Phi2=tf(n2,d2)返回:Transfer function:0.02725--------------------0.01021 s^2 - 0.2671c)摆杆角度和小车所受外界作用力的传递函数;继续输入:q=(M+m)*(I+m*l^2)-(m*l)^2;n3=[m*l/q 0 0];d3=[1 b*(I+m*l^2)/q -(M+m)*m*g*l/q -b*m*g*l/q 0];Phi3=tf(n3,d3)返回:Transfer function:2.357 s^2---------------------------------------s^4+ 0.08832 s^3 - 27.83 s^2 - 2.309 sd)以外界作用力作为输入的系统状态方程;继续输入:q2=(I*(M+m)+M*m*l^2);A1=[0 1 0 0;0-(I+m*l^2)*b/q2m^2*g*l^2/q2 0;0 001;0 -m*l*b/q2m*g*l*(M+m)/q20];B1=[0;(I+m*l^2)/q2;0;m*l/q2];C1=[1 0 0 0;0 0 1 0];D1=[0;0];sys1=ss(A1,B1,C1,D1)返回:a =x1 x2 x3 x4x1 0 1 0 0x2 0-0.08832 0.6293 0x3 0 00 1x4 0-0.2357 27.830b=u1x1 0x2 0.8832x3 0x4 2.357c =x1 x2 x3 x4y1 1 0 0 0y2 0 0 1 0d =u1y1 0y2 0e)以小车加速度作为输入的系统状态方程;继续输入:A2=[0 1 0 0;0 0 00;0 0 0 1;0 0 3/(4*l)0];B2=[0;1;0;3/(4*l)];C2=C1;D2=D1;sys2=ss(A2,B2,C2,D2)返回:a=x1 x2x3 x4x10 100x2 00 0 0x300 0 1x400 3 0b =u1x1 0x2 1x3 0x43c=x1 x2 x3x4y110 00y200 1 0d=u1y10y2 02、根据倒立摆系统数学模型(以小车的加速度为输入的模型,即sys2),判断开环系统的稳定性、可控性和可观性;稳定性:继续输入:eig(A2)返回:ans =1.7321-1.7321有一个位于正实轴的根和两个位于原点的根,表明系统是不稳定的。
自控原理实验报告

一、实验目的1. 理解并掌握自动控制原理的基本概念和基本分析方法。
2. 掌握典型环节的数学模型及其在控制系统中的应用。
3. 熟悉控制系统的时间响应和频率响应分析方法。
4. 培养实验操作技能和数据处理能力。
二、实验原理自动控制原理是研究控制系统动态性能和稳定性的一门学科。
本实验主要涉及以下几个方面:1. 典型环节:比例环节、积分环节、微分环节、惯性环节等。
2. 控制系统:开环控制系统和闭环控制系统。
3. 时间响应:阶跃响应、斜坡响应、正弦响应等。
4. 频率响应:幅频特性、相频特性等。
三、实验内容1. 典型环节的阶跃响应- 比例环节- 积分环节- 比例积分环节- 比例微分环节- 比例积分微分环节2. 典型环节的频率响应- 幅频特性- 相频特性3. 二阶系统的阶跃响应- 上升时间- 调节时间- 超调量- 峰值时间4. 线性系统的稳态误差分析- 偶然误差- 稳态误差四、实验步骤1. 典型环节的阶跃响应- 搭建比例环节、积分环节、比例积分环节、比例微分环节、比例积分微分环节的实验电路。
- 使用示波器观察并记录各个环节的阶跃响应曲线。
- 分析并比较各个环节的阶跃响应曲线,得出结论。
2. 典型环节的频率响应- 搭建比例环节、积分环节、比例积分环节、比例微分环节、比例积分微分环节的实验电路。
- 使用频率响应分析仪测量各个环节的幅频特性和相频特性。
- 分析并比较各个环节的频率响应特性,得出结论。
3. 二阶系统的阶跃响应- 搭建二阶系统的实验电路。
- 使用示波器观察并记录二阶系统的阶跃响应曲线。
- 计算并分析二阶系统的上升时间、调节时间、超调量、峰值时间等性能指标。
4. 线性系统的稳态误差分析- 搭建线性系统的实验电路。
- 使用示波器观察并记录系统的稳态响应曲线。
- 计算并分析系统的稳态误差。
五、实验数据记录与分析1. 典型环节的阶跃响应- 比例环节:K=1,阶跃响应曲线如图1所示。
- 积分环节:K=1,阶跃响应曲线如图2所示。
自控原理课程实验报告

一、实验目的1. 理解并掌握自动控制原理的基本概念和基本分析方法。
2. 熟悉自动控制系统的典型环节,包括比例环节、积分环节、比例积分环节、惯性环节、比例微分环节和比例积分微分环节。
3. 通过实验,验证自动控制理论在实践中的应用,提高分析问题和解决问题的能力。
二、实验原理自动控制原理是研究自动控制系统动态和稳态性能的学科。
本实验主要围绕以下几个方面展开:1. 典型环节:通过搭建模拟电路,研究典型环节的阶跃响应、频率响应等特性。
2. 系统校正:通过在系统中加入校正环节,改善系统的性能,使其满足设计要求。
3. 系统仿真:利用MATLAB等仿真软件,对自动控制系统进行建模和仿真,分析系统的动态和稳态性能。
三、实验内容1. 典型环节实验(1)比例环节:搭建比例环节模拟电路,观察其阶跃响应,分析比例系数对系统性能的影响。
(2)积分环节:搭建积分环节模拟电路,观察其阶跃响应,分析积分时间常数对系统性能的影响。
(3)比例积分环节:搭建比例积分环节模拟电路,观察其阶跃响应,分析比例系数和积分时间常数对系统性能的影响。
(4)惯性环节:搭建惯性环节模拟电路,观察其阶跃响应,分析时间常数对系统性能的影响。
(5)比例微分环节:搭建比例微分环节模拟电路,观察其阶跃响应,分析比例系数和微分时间常数对系统性能的影响。
(6)比例积分微分环节:搭建比例积分微分环节模拟电路,观察其阶跃响应,分析比例系数、积分时间常数和微分时间常数对系统性能的影响。
2. 系统校正实验(1)串联校正:在系统中加入串联校正环节,改善系统的性能,使其满足设计要求。
(2)反馈校正:在系统中加入反馈校正环节,改善系统的性能,使其满足设计要求。
3. 系统仿真实验(1)利用MATLAB等仿真软件,对自动控制系统进行建模和仿真,分析系统的动态和稳态性能。
(2)根据仿真结果,优化系统参数,提高系统性能。
四、实验步骤1. 搭建模拟电路:根据实验内容,搭建相应的模拟电路,并连接好测试设备。
合肥工业大学自动控制控制理论综合实验球杆实验报告
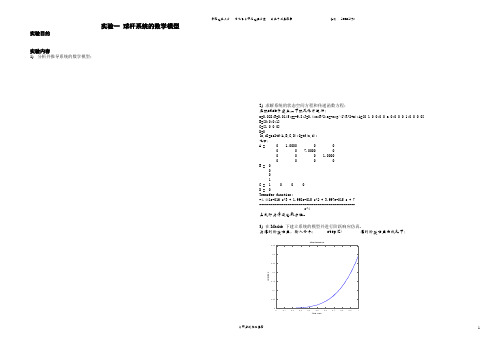
实验一 球杆系统的数学模型实验目的实验内容1) 分析并推导系统的数学模型;2) 求解系统的状态空间方程和传递函数方程; 在matlab 中建立一下m 文件并运行:m=0.028;R=0.0145;g=-9.8;J=0.4*m*R^2;a=-m*g/(J/R^2+m);A=[0 1 0 0;0 0 a 0;0 0 0 1;0 0 0 0] B=[0;0;0;1] C=[1 0 0 0] D=0[n,d]=ss2tf(A,B,C,D);G=tf(n,d); 返回:A = 0 1.0000 0 0 0 0 7.0000 0 0 0 0 1.0000 0 0 0 0B = 0 0 0 1C = 1 0 0 0D = 0Transfer function:-4.441e-016 s^3 + 1.998e-015 s^2 + 3.997e-015 s + 7 --------------------------------------------------- s^4上式即为传递函数方程。
3) 在Matlab 下建立系统的模型并进行阶跃响应仿真。
为得到阶跃响应,输入命令: step(G) 得到阶跃响应曲线如下:Step ResponseTime (sec)A m p l i t u d e实验二球杆系统的数字P 控制器设计实验目的实验原理实验内容:1. 在matlab下仿真比例控制时系统的响应情况。
在matlab中建立m文件并运行:m = 0.028;R = 0.0145;g = -9.8;L = 0.40;d = 0.045;J = 0.4*m*R^2;K = (m*g*d)/(L*(J/R^2+m)); %simplifies input num = [-K];den = [1 0 0];ball=tf(num,den)kp = 1;sys_cl=feedback(kp*ball,1) %建立闭环系统step(0.25*sys_cl) %阶跃响应05101520253035400.050.10.150.20.250.30.350.40.450.5Step ResponseTime (sec)Amplitude2.进入BallBeamControl 应用控制程序进行实时控制;实验三 球杆系统的数字PD 控制器设计实验目的实验原理:实验内容:1、 在matlab 中仿真PD 控制器下球杆系统的响应情况。
自动控制原理实验报告——合肥工业大学

实验步骤:注:‘S ST’不能用“短路套”短接!(1)将信号发生器(B1)中的阶跃输出0/+5V作为系统的输入信号(Ui)。
(2)安置短路套、联线,构造模拟电路:(a)安置短路套(b)测孔联线(3)虚拟示波器(B3)的联接:示波器输入端CH1接到A6单元信号输出端OUT(Uo)。
注:CH1选‘X1’档,CH2置‘0’ 档。
(4)运行、观察、记录:按下信号发生器(B1)阶跃信号按钮时(0→+5V阶跃),用示波器观测A6输出端(Uo)的实际响应曲线Uo(t),且将结果记下。
改变比例参数(改变运算模拟单元A1的反馈电阻R1),重新观测结果,其实际阶跃响应曲线见表1-1-1。
当R1=200K的电路与相应曲线当R1=100K的电路与相应曲线2.观察惯性环节的阶跃响应曲线典型惯性环节模似电路如图1-1-2所示。
该环节在A1单元中分别选取反馈电容C =1uf、2uf来改变时间常数。
实验步骤:注:‘S ST’不能用“短路套”短接!(1)将信号发生器(B1)中的阶跃输出0/+5V作为系统的信号输入(Ui)。
(2)安置短路套、联线,构造模拟电路:(a)安置短路套(b)测孔联线(3)虚拟示波器(B3)的联接:示波器输入端CH1接到A6单元信号输出端OUT (Uo)。
注:CH1选‘X1’档,CH2置‘0’ 档。
(4)运行、观察、记录:按下信号发生器(B1)阶跃信号按钮时(0→+5V阶跃),用示波器观测A6输出端(Uo)的实际响应曲线Uo(t),且将结果记下。
改变时间常数(改变运算模拟单元A1的反馈反馈电容C),重新观测结果,其实际阶跃响应曲线见表1-1-1。
下图为实验电路以及示波器显示的波形C =1uf时的电路图与相应曲线示波器显示:当C =1uf时的电路图与相应曲线示波器显示:3.观察积分环节的阶跃响应曲线典型积分环节模似电路如图1-1-3所示。
该环节在A1单元中分别选取反馈电容C=1uf、2uf来改变时间常数。
实验步骤:(1)为了避免积分饱和,将函数发生器(B5)所产生的周期性方波信号(OUT),代替信号发生器(B1)中的阶跃输出0/+5V作为系统的信号输入(Ui):a.将函数发生器(B5)中的插针‘S ST’用短路套短接。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验一典型环节的模拟研究
一、实验要求
了解和掌握各典型环节的传递函数及模拟电路图,观察和分析各典型环节的响应曲线。
二、实验原理(典型环节的方块图及传递函数)
三.实验内容及步骤
在实验中欲观测实验结果时,可用普通示波器,也可选用本实验机配套的虚拟示波器。
如果选用虚拟示波器,只要运行LCAACT程序,选择自动控制菜单下的典型环节的模拟研究实验项目,再选择开始实验,就会弹出虚拟示波器的界面,点击开始即可使用本实验机配套的虚拟示波器(B3)单元的CH1测孔测量波形。
具体用法参见用户手册中的示波器部分。
1.观察比例环节的阶跃响应曲线
典型比例环节模似电路如图1-1-1所示。
该环节在A1单元中分别选取反馈电阻R1=100K、200K来改变比例参数。
实验步骤:注:‘S ST’不能用“短路套”短接!
(1)将信号发生器(B1)中的阶跃输出0/+5V作为系统的输入信号(Ui)。
(2)安置短路套、联线,构造模拟电路:
(a)安置短路套
(b)测孔联线
(3)虚拟示波器(B3)的联接:示波器输入端CH1接到A6单元信号输出端OUT (Uo)。
注:CH1选‘X1’档,CH2置‘0’档。
(4)运行、观察、记录:
按下信号发生器(B1)阶跃信号按钮时(0→+5V阶跃),用示波器观测A6输出端(Uo)的实际响应曲线Uo(t),且将结果记下。
改变比例参数(改变运算模拟单元A1的反馈电阻R1),重新观测结果,其实际阶跃响应曲线见表1-1-1。
当R1=200K的电路与相应曲线
当R1=100K的电路与相应曲线
2.观察惯性环节的阶跃响应曲线
典型惯性环节模似电路如图1-1-2所示。
该环节在A1单元中分别选取反馈电容C =1uf、2uf来改变时间常数。
实验步骤:注:‘S ST’不能用“短路套”短接!
(1)将信号发生器(B1)中的阶跃输出0/+5V作为系统的信号输入(Ui)。
(2)安置短路套、联线,构造模拟电路:
(a)安置短路套
(b)测孔联线
(3)虚拟示波器(B3)的联接:示波器输入端CH1接到A6单元信号输出端OUT (Uo)。
注:CH1选‘X1’档,CH2置‘0’档。
(4)运行、观察、记录:
按下信号发生器(B1)阶跃信号按钮时(0→+5V阶跃),用示波器观测A6输出端(Uo)的实际响应曲线Uo(t),且将结果记下。
改变时间常数(改变运算模拟单元A1的反馈反馈电容C),重新观测结果,其实际阶跃响应曲线见表1-1-1。
下图为实验电路以及示波器显示的波形
C =1uf时的电路图与相应曲线示波器显示:
当C =1uf时的电路图与相应曲线示波器显示:
3.观察积分环节的阶跃响应曲线
典型积分环节模似电路如图1-1-3所示。
该环节在A1单元中分别选取反馈电容C=1uf、2uf来改变时间常数。
实验步骤:
(1)为了避免积分饱和,将函数发生器(B5)所产生的周期性方波信号(OUT),代替信号发生器(B1)中的阶跃输出0/+5V作为系统的信号输入(Ui):
a.将函数发生器(B5)中的插针‘S ST’用短路套短接。
b.将S1拨动开关置于最上档(阶跃信号)。
c.信号周期由拨动开关S2和“调频”旋钮调节,信号幅度由“调幅”旋钮调节,
以信号幅值小,信号周期较长比较适宜(频率在0.3Hz左右,幅度在1V左右)。
(2)安置短路套、联线,构造模拟电路:
(a)安置短路套
(b)测孔联线
(3)虚拟示波器(B3)的联接:示波器输入端CH1接到A6单元信号输出端OUT (Uo)。
注:CH1选‘X1’档,CH2置‘0’档。
(4)运行、观察、记录:
按下信号发生器(B1)阶跃信号按钮时(0→+5V阶跃),用示波器观测A6输出端(Uo)的实际响应曲线Uo(t),且将结果记下。
改变时间常数(改变运算模拟单元A1的反馈反馈电容C),重新观测结果,其实际阶跃响应曲线见表1-1-1。
下图为实验电路以及示波器显示的波形
实验4,用‘扫频法’测量系统的对数幅频曲线和相频曲线幅频曲线
相频曲线
二、MATLAB语言与控制系统仿真
实验任务:
⏹4-11
⏹绘制(a)(b)的根轨迹图
⏹绘制(a)(b)的单位阶跃响应图,分析比例-微分校正器的作用
⏹5-4
⏹绘制(1)(3)的奈氏图
⏹绘制(2)(4)的伯特图
MATLAB 函数说明:
⏹根轨迹
⏹rlocus( )
⏹格式1:rlocus(num,den)
⏹num和den是系统开环传函G K(s)分子和分母多项式的系数。
⏹功能:绘制系统根轨迹。
⏹频率法
⏹nyquist( )
⏹格式:nyquist(num,den)
⏹num和den是开环传递函数的分子和分母多项式的系数。
⏹功能:绘制系统的乃氏曲线。
⏹bode( )
⏹格式:bode(num,den)
⏹num和den是开环传递函数的分子和分母多项式的系数。
⏹功能:绘制系统的bode图。
4-11(A)
实验程序:
根轨迹图:
rlocus( [5],[5,1,0])
4-11(B)
rlocus( [4,5],[5,5,5])
5-4(1)奈氏图
nyquist([2],[16,10,1])
(2)伯特图bode([50],[6,7,7,1,0,0])
(3)奈氏图nyquist([10,2],[1,0.1,0,0])
(4)伯特图bode([8,0.8],[1,5,30,29,25,0])。
