混合像元组分信息的盲分解方法.pdf
混合像元分解法操作步骤

混合像元分解法操作步骤1.数据准备-获取多光谱图像数据,可以使用航空或卫星遥感数据。
- 准备高分辨率的真实地物标记(Ground Truth),用于评估分解结果的准确性。
2.选择变量-选择用于混合像元分解的变量,一般是多光谱图像的波段数据。
-可以利用统计学方法、专家知识或试错法来选择最适合的变量。
3.确定光谱参考-选择用于确定混合像元分解的光谱参考数据。
-光谱参考可以是单一的像素或像元组合。
-光谱参考应该具有代表性,并且包含不同地物的特征光谱。
4.混合像元分解-使用混合像元分解模型来计算每个像素的混合成分比例。
-混合像元分解模型通常假设图像中的每个像素是由多个地物的混合成分组成,并输出每个地物的比例。
- 常用的混合像元分解模型包括Spectral Mixture Analysis(SMA)和Linear Spectral Mixture Analysis(LSMA)等。
5.分解结果评估-使用真实地物标记来评估混合像元分解的准确性。
-可以使用混合像元分解的结果与真实地物标记进行对比,计算混淆矩阵或其他评估指标。
-可以根据评估结果来调整或优化混合像元分解模型的参数。
6.结果解释-根据混合像元分解得到的地物比例,进行图像分类、植被指数计算等应用。
-可以通过阈值或其他分类方法将分解得到的比例转化为具体的地物类别。
-可以根据混合像元分解的结果进行地物变化检测、遥感图像解译等分析。
7.结果可视化-可以使用各种图像处理软件将混合像元分解的结果可视化。
-可以使用颜色编码、图形绘制等方法将混合像元分解的结果与原始图像进行对比。
-可以生成分类图像或指数图像等用于进一步分析或展示的结果。
总之,混合像元分解法是一种通过对多光谱图像像素进行分解来获取地物混合成分比例的方法。
它具有广泛的应用前景,并可以通过合理的参数选择和模型优化来提高分解结果的精度和准确性。
常见混合像元分解方法简介二

端元就相当于一个像素里的亚像元,只包含一种地物的光谱信息,根据多光谱或高光谱的高光谱分辨率可以提取出来。
端元只包含一种地物信息,一般的像元都为混合像元,包括多种地物,在进行混合像元分解的时候,可以对一个像元中包括的几种端元进行定量描述,求得每个像元中几种端元在这个像元中的面积百分比,即端元的丰度。
混合像元分解(2011-06-10 14:46:57)转载▼分类:ENVI/IDL学习标签:杂谈混合像元是指在一个像元内存在有不同类型的地物,主要出现在地类的边界处。
混合像元的存在是影响识别分类精度的主要因素之一,特别是对线状地类和细小地物的分类识别影响较为突出,在土地利用遥感动态监测工作中,经常遇到混合像元的难题,解决这一问题的关键在于通过一定方法找出组成混合像元的各种典型地物的比例。
线性混合像元分解由于线性模型是应用最广泛,也是研究最多的算法,下面重点介绍基于线性模型的混合像元分解算法。
一般而言,混合像元分解算法包括数据降维、端元选取和反演三个步骤。
1.数据降维尽管数据降维不是混合像元分解算法的一个必需步骤,但由于大多数算法都将其作为一个流程,我们也将其当作一个步骤。
常用的降维算法有主成分分析(Principle Component Analysis,PCA)、最大噪声比变换(Maximum Noise Fraction,MNF)和奇异值分解(Singular Value Decomposition,SVD)。
(1) 主成分分析:遥感图像各波段之间经常是高度相关的,因此所有的波段参加分析是不必要的。
PCA就是一种去除波段之间相关性的变换。
PCA通过对原数据进行线性变换,获得新的一组变量,即主成分。
其中前几个主成分包含了原数据主要方差,同时各个主成分之间是不相关的。
(2) 最大噪声比变换:最大噪声比变换(Maximum Noise Fraction,MNF)[24]由Green等(1989)提出,该变换通过引入噪声协方差矩阵以实现对噪声比率的估计。
混合像元分析

x
A
xB
xC
yA yB yC
0 0 0
S ' 1.5 1.5 0
0 2 2
y
SABC A
A(1,1)
SABC C
C(5,4)
B(5,1)
SABC B
x
统计方法
• 盲信号分离
实验情况
• 下面的端元提取实验针对Cuprite区域的AVIRIS数据进行,这里我们 将选取其中短波红外的50个连续的波段(1978-2478nm)进行算法的 验证
Kaolinite Calcite
由我们的算 法从Cuprite 区域的AVI RIS数据中获 取的端元光
谱(带点的曲 线)与USGS 光谱库中相应 的光谱曲线 的对比情况
混合像元分解
• 基本概念
混合像元分解
• 无约束最小二乘 • 和为1约束最小二乘 • 非负约束最小二乘 • 全约束最小二乘 • OSP • 端元投影向量 • 几何法 • 统计法
元
假
设
误差目标 投影算子 体积约束
体积目标 最大体积 误差约束
纯 像 选择端元 元 假 设
几何优化模型(GOM)
• 单变量目标函数
GOM
• GOM的解(梯度下降法)
GOM-基础知识
• 行列式的导数
W W W 1 T
W
• 三角形面积
1 1 1
S ABC
1 2
det
无约束最小二乘
• 最小二乘的基本原理 y=ax+b x=a’y+b’
• 线性混合模型的无约束最小二乘解
混合像元分解及其应用(ENVI操作文本)讲解
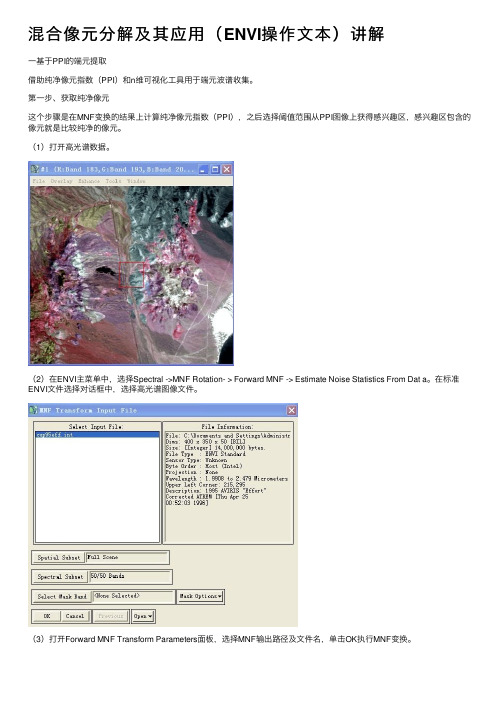
混合像元分解及其应⽤(ENVI操作⽂本)讲解⼀基于PPI的端元提取借助纯净像元指数(PPI)和n维可视化⼯具⽤于端元波谱收集。
第⼀步、获取纯净像元这个步骤是在MNF变换的结果上计算纯净像元指数(PPI),之后选择阈值范围从PPI图像上获得感兴趣区,感兴趣区包含的像元就是⽐较纯净的像元。
(1)打开⾼光谱数据。
(2)在ENVI主菜单中,选择Spectral ->MNF Rotation- > Forward MNF -> Estimate Noise Statistics From Dat a。
在标准ENVI⽂件选择对话框中,选择⾼光谱图像⽂件。
(3)打开Forward MNF Transform Parameters⾯板,选择MNF输出路径及⽂件名,单击OK执⾏MNF变换。
(4)在波段列表中输出MNF影像及特征曲线值。
从图中可以看出,⼤约20个波段以后的MNF的特征值很⼩(5)MNF变换后,在ENVI主菜单中,选择 Spectral-> Pixel Purity Index->[FAST] New Output Band。
在打开的Pixel Purity Index Input File对话框中,选择MNF变换结果,单击Spectral Subset按钮,选择前⾯10个波段(MNF后⾯波段基本为噪声),单击OK。
(6)在Display窗⼝中显⽰PPI结果。
选择Overlay->Region of Interest,在ROI Tool ⾯板中,选择Options->Band Threshold to ROI,选择PPI图像作为输⼊波段,单击OK,打开Band Threshold to ROI ⾯板(图14.19)。
Min Thresh Value:10,Max Thresh Value:空(PPI图像最⼤值),其他默认设置,单击OK计算感兴趣区,得到的感兴趣区显⽰在Display窗⼝中。
混合像元分解算法的比较和改进

1本科毕业设计(论文) GRADUATION DESIGN(THESIS)题目混合像元分解算法的比较学生姓名吴洋指导教师杨敏华学院地球科学与信息物理学院专业班级测绘1103班本科生院制2015年6月混合像元分解算法的比较摘要高光谱遥感在当今社会的各个领域都有着比较普遍的应用和广阔的前景。
它所得到的高光谱影像数据具有波段多、数据大、分辨率高的特点[1],不过高光谱遥感数据同时还存在着光谱分辨率高而空间分辨率低的问题。
因为在高光谱遥感影像中普遍存在混合像元,且它并不是纯像元,而是各个端元按照一定的比例组合而成的[2],所以混合像元的出现不仅让我们在直接进行像元的分类上受到了阻碍,也给高光谱遥感数据分类精度的提高带来了困扰[3]。
现如今,为了解决混合像元带来的问题,提升高光谱遥感影像在应用上的精度,科研人员已经发现了许多不同类型的混合像元分解算法。
本论文为混合像元分解端元提取算法的比较,就是围绕混合像元分解的问题,通过分析当前国内外几个比较典型且常用的混合像元技术的原理和算法,得到它们各自的优缺点。
本文总结了高光谱图像数据的特点,高光谱遥感影像数据降维、端元提取和丰度估计的算法。
其中在数据降维算法上我们介绍了主成分分析法(PCA),在端元提取算法上介绍了像元纯度指数算法(PPI)、内部最大体积法(N-FINDR)和顶点成分分析法(VCA),在丰度估计算法中也主要介绍了最小二乘法。
最后实验重点总结PPI、N-FINDR 和VCA三种混合像元分解算法操作的步骤和结果,并将结果进行比较。
关键词:高光谱遥感,混合像元分解,端元提取算法The Comparison of Endmember Extractionof Unmixing AlgorithmAbstractHyperspectral remote sensing has been used widely in every research field and also have broad prospects.The hyperspectral image data it receives has features of multi-band,large data and high resolution[1].However,remote sensing data also have high spectral resolution and low spatial resolution.Because the hyperspectral remote sensing has mixed pixel prevalently,and it is a combination of various endmember in accordance with a certain proportion rather than pure pixel[2].So the appearance of mixed pixel is not only hindered in our classification but also difficult to improve our accuracy of classification[3].Nowadays,in order to solve the problem brought by mixed pixel and enhance the accuracy of hyperspectral remote sensing image in the application,researchers have already found large different types of decomposition algorithm of mixed pixels.This paper is the comparison of endmember extraction of unmixing algorithm,which center on the unmixing problem,by analyzing several current typical and common hyperspectral imaging technique principle and algorithm, to get their own advantages and disadvantages.This paper describes the characteristics of hyperspectral image data,the algorithms of data reduction of hyperspectral remote sensing image,endmember extraction and abundance estimation.Wherein the article,we introduced the Principal Component Analysis(PCA)in the data reduction,the Pixel Purity Index(PPI),N-FINDR and Vertex Component Analysis (VCA)in the endmember extraction algorithm.And in the abundance estimation algorithm, we also introduced the Least Squares Method.Finally,we focus on three unmixing algorithm operation steps and results,and the results were compared.Keyword:Hyperspectral remote sensing,Unmixing pixel,Endmember Extraction algorithm目录第1章绪论 (1)1.1论文概况 (1)1.2研究背景和建设意义 (1)1.2.1研究背景 (1)1.2.2混合像元分解技术介绍和研究现状 (2)1.3课题主要任务及论文结构 (4)第2章混合像元分解算法介绍 (5)2.1高光谱遥感数据 (5)2.1.1高光谱遥感数据特性 (5)2.2数据降维 (6)2.2.1主成分分析算法介绍 (6)2.3端元提取算法 (7)2.3.1像元纯度指数 (8)2.3.2N-FINDR (9)2.3.3顶点成分分析 (10)2.3.4端元提取算法之间比较 (11)2.4丰度估计算法介绍 (12)2.4.1非负约束最小二乘法 (13)2.4.2和为一限制性最小二乘法 (14)2.4.3四种形式最小二乘法优缺点比较 (15)第3章混合像元分解的程序操作 (16)3.1高光谱遥感影像来源及预处理 (16)3.1.1高光谱遥感影像来源 (16)3.1.2高光谱遥感数据预处理 (16)3.1.3像元纯度指数提取端元 (18)3.1.4N-FINDR提取端元结果 (19)3.1.5结论 (21)第4章总结与展望 (23)4.1总结 (23)4.2展望 (23)致谢 (24)参考文献 (25)第1章绪论1.1论文概况本论文为混合像元分解算法比较和改进的设计,为计算机程序编辑和软件操作论文。
混合像元分解

混合像元分解
混合像元分解(MixedPixelDecomposition,MPD)是一种不需要任何理论假设的半监督算法,用于自动地从复杂的观测图像中分解出多个不同的像元组。
MPD是计算机视觉和图像处理领域的一个关键技术,它支持多种现代视觉任务,包括目标检测、跟踪、语义分割、深度学习等。
MPD技术应用于图像处理,首先要建立一个模型,该模型由不同的像元组成,比如彩色图像的RGB通道,使用MPD技术,可以将彩色图像分解成RGB三个通道,也可以分解成更多的像元,比如灰度、噪声、亮度、颜色等像元。
使用MPD技术可以方便地处理复杂的图像,将它们分解成可操作的不同像元集。
MPD技术采用半监督学习方法,把原始图像分解成不同的像元,可以是灰度、噪声、亮度、颜色等像元,这样就可以很容易地提取,保存和操作不同的像元,MPD技术的优点是不需要任何理论假设,只要输入输入完整的图像,就可以得到准确的结果。
MPD技术的基本流程是:输入原始图像,通过全局优化算法,得到混合像元,然后使用机器学习模型,学习每个混合像元的结构,最终得到像元分解的结果。
MPD技术的应用非常广泛,可以应用在图像分类和识别、目标检测、图像处理领域,深度学习、自然语言处理等领域。
比如在目标检测任务中,可以使用MPD技术训练的模型来识别目标物体或背景中的特征;在图像处理领域,可以用MPD技术来分离图像中的不同像元,
从而得到更高质量的图像;在深度学习和自然语言处理领域,MPD技术也可以用来提取文本特征和语义信息。
总之,MPD是一种非常有用的技术,可以应用于图像处理、目标检测、深度学习、自然语言处理等领域,可以有效处理复杂的图像信息,提取出单像素或多像素的信息,以及文本特征和语义信息等,为图像分析和处理提供了可靠的基础。
常见混合像元分解方法简介二

端元就相当于一个像素里的亚像元,只包含一种地物的光谱信息,根据多光谱或高光谱的高光谱分辨率可以提取出来。
端元只包含一种地物信息,一般的像元都为混合像元,包括多种地物,在进行混合像元分解的时候,可以对一个像元中包括的几种端元进行定量描述,求得每个像元中几种端元在这个像元中的面积百分比,即端元的丰度。
混合像元分解(2011-06-10 14:46:57)转载▼分类:ENVI/IDL学习标签:杂谈混合像元是指在一个像元内存在有不同类型的地物,主要出现在地类的边界处。
混合像元的存在是影响识别分类精度的主要因素之一,特别是对线状地类和细小地物的分类识别影响较为突出,在土地利用遥感动态监测工作中,经常遇到混合像元的难题,解决这一问题的关键在于通过一定方法找出组成混合像元的各种典型地物的比例。
线性混合像元分解由于线性模型是应用最广泛,也是研究最多的算法,下面重点介绍基于线性模型的混合像元分解算法。
一般而言,混合像元分解算法包括数据降维、端元选取和反演三个步骤。
1.数据降维尽管数据降维不是混合像元分解算法的一个必需步骤,但由于大多数算法都将其作为一个流程,我们也将其当作一个步骤。
常用的降维算法有主成分分析(Principle Component Analysis,PCA)、最大噪声比变换(Maximum Noise Fraction,MNF)和奇异值分解(Singular Value Decomposition,SVD)。
(1) 主成分分析:遥感图像各波段之间经常是高度相关的,因此所有的波段参加分析是不必要的。
PCA就是一种去除波段之间相关性的变换。
PCA通过对原数据进行线性变换,获得新的一组变量,即主成分。
其中前几个主成分包含了原数据主要方差,同时各个主成分之间是不相关的。
(2) 最大噪声比变换:最大噪声比变换(Maximum Noise Fraction,MNF)[24]由Green等(1989)提出,该变换通过引入噪声协方差矩阵以实现对噪声比率的估计。
常见混合像元分解方法简介

常见混合像元分解方法(2021-04-20 20:35:42)转载▼分类:遥感技术标签:混合像元亚像元分解方法线性波谱别离教育常见的混合像元分解方法,主要包括线性波谱别离(Linear Spectral Unmixing )、匹配滤波(MF )、混合调谐匹配滤波(MTMF〕、最小能量约束(CEM〕、自适应一致估计〔ACE〕、正交子空间投影(OSP)等。
下面分别对几种分类方法原理一一说明。
(1)线性波段预测(Linear Band Prediction)线性波段预测法〔LS-Fit〕使用一个最小方框〔least squares〕拟合技术来进展线性波段预测,它可以用于在数据集中找出异常波谱响应区。
LS-Fit先计算出输入数据的协方差,用它对所选的波段进展预测模拟,预测值作为预测波段线性组的一个增加值。
还计算实际波段和模拟波段之间的残差,并输出为一幅图像,残差大的像元〔无论正负〕表示出现了不可预测的特征〔比方一个吸收波段〕。
(2)线性波谱别离(Linear Spectral Unmixing )Linear Spectral Unmixing可以根据物质的波谱特征,获取多光谱或高光谱图像中物质的丰度信息,即混合像元分解过程。
假设图像中每个像元的反射率为像元中每种物质的反射率或者端元波谱的线性组合。
例如:像元中的25%为物质A,25%为物质B,50%为物质C,那么该像元的波谱就是三种物质波谱的一个加权平均值,等于,线性波谱别离解决了像元中每个端元波谱的权重问题。
线性波谱别离结果是一系列端元波谱的灰度图像〔丰度图像〕,图像的像元值表示端元波谱在这个像元波谱中占的比重。
比方端元波谱A的丰度图像中一个像元值为,那么表示这个像元中端元波谱A占了45%。
丰度图像中也可能出现负值和大于1的值,这可能是选择的端元波谱没有明显的特征,或者在分析中缺少一种或者多种端元波谱。
(3)匹配滤波(Matched Filtering )使用匹配滤波〔MF〕工具使用局部分离获取端元波谱的丰度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
@ @ !
" 卷 ! 第 # 期 !$ % % "年#月 !第!
!+ 盲分 解 方 法 " 是 6 0 / 3 :7 / 3 . 0 77 9 9 B . 8 / 4 3 A A$ Y V 近年来发展 起 来 的 一 种 信 号 盲 分 离 技 术 已得到广泛应用
% ’ &E( % % %E!’
!在信
(’ 的公式可以表达 % 为
9 = >AaG
=eaG ! - )Aae ,
$ " (
论问题 ! 至今还没 有 得 到 妥 善 解 决 % 而 这 正 是 盲 分 解要回答的问题 %
# # ! ’ ( ( ’ " # 收稿 !% # # ! ’ # " ’ ( ) 收修改稿 !% 批准号 #! 和国家重点基础研究发展规划 " 编号 # 资助项目 $ $ # ! # ( # " ) a % # # # # $ $ @ # # ! " 国家自然科学基金 " # ’ . / 0 b . 3 = B 6 . 35 X 25 9 : 25 ; 3 !!!, !2 1 V
@ @ &
A A分解得到的组分信 !! 其中 !;Aae 和 "eaG 是 + 息矩阵和 权 重 矩 阵 !1 为 任 意 的 常 系 数 对 角 矩 阵 % 此式表明盲分解可 以 保 持 组 分 的 波 形 不 变 ! 但 幅 度 可以取任意值 % 这种 模 糊 特 性 对 于 定 量 遥 感 来 说 是 致命的 ! 所以能否克服这一不确定 性 是 + A A能否用 于遥感定量 分 析 的 关 键 问 题 % 应 用 公 式 " 进行混 %$ 合像元盲分解 ! 并令 ;Aae -)Aae "10( ! 因此 !
B 与. 空间的某一基矢量相一致 % 因此实施盲分解 的 对 象 必 须 满 足 以 下 几 个 前 提
条件 #" $权重系 数 矩 阵 ) 必 须 为 常 系 数 矩 阵 ! 即 ( 物理过程可以用线性 方 程 组 来 表 达 (" %$各 组 分 信 息必须完全满 足 统 计 独 立 的 条 件 (" "$各 组 分 信 息 的概率密度函数应 是 非 a . 2 7 7分 布 ! 最 多 只 允 许 有 一个独立成分拥有 a . 2 7 7型概率密度函数 5 无论主成分分析 还 是 盲 分 解 的 目 的 都 是 对 传 感 器测量 的 信 息 矩 阵 进 行 线 性 变 换 以 便 获 得 组 分 信 息 5主成分分析是以 ) 方差" 二 阶 矩$ 极 大* 作 为 选 取独立矢量的判 别 标 准 ! 其 分 解 结 果 很 难 有 明 确 的 物理意义 5而 + " A A 方法用 c 2 B 8 @$@# 作 为 选 取 独 立矢量的判别标准 ! 可 以 直 接 获 得 彼 此 统 计 独 立 的 组分信息 5 高阶矩信息为 + A A 提供了 必要 的补充 信 息来源 ! 这就是 + A A 拥有盲分解特性的内在原因 5
’! 盲分解概念及其在定量遥感应用中的应用 价值
!! 从混 合像元中 分解出 组分 信息是 遥 感 反演 的 重 要内容 % 许多 遥 感 物 理 过 程 可 用 线 性 方 程 组 来 描 述 ! 可表达为 <$) .% 一般来 说 !< 为 传 感 器 测 量 的信息矩 阵 !. 为 混 合 像 元 各 组 分 的 信 息 矩 阵 !) 为各组分的权重矩阵 % 如果 ) 已知 ! 通过 .$)’(<! 可分解得到组分信 息 % 盲 分 解 就 是 要 在 仅 知 道 矩 阵
,
/! 作物播种面积和长势信息的 P + + 分解
通过对作物播种 面 积 和 长 势 信 息 实 施 同 步 盲 分 解方法的数值实验 ! 本文试图表 明 + A A 是遥 感信息 反演的可行方法 之 一 5 在 我 国 黄 河 以 北 地 区 与 冬 小 麦同期生长的作物 很 少 ! 黄 河 以 南 同 期 生 长 的 作 物 主要为油菜 ! 通 过 对 地 面 样 地 光 谱 测 量 ! 土 壤 + 冬 小麦与油菜地的 # / N 值随时间地变化规律如图 ( 所 示 5 作物长势地好坏表现在其 # / N 值随时间的变化
件 ! 其中的二 个 条 件 对 于 作 物 长 势 监 测 很 容 易 满 足 5 至于概率密度函 数 的 类 型 问 题 可 以 通 过 四 阶 矩 来判定 5 土壤的 # / N 值随时间的变化曲线是一条统 " 计意义上的直线 ! 根 据 计 算 c 近 似 为 零! 因 2 B 8 @$ 此满足 a . 2 7 7分 布 5 而 冬 小 麦 和 油 菜 # / N的 c 2 B 8 " $ ! ! 值 均 小 于 零 为 亚 分 布 因 此 可 以 满 足 a . 2 7 7 @ + A A 分解的条件 5 根据实 际 情 况 ! 选 择 固 定 点 " 算法 $ b / [ 9 :V 4 / 3 8 $ 对" 式 进 行 混 合 像 元 分 解5 固 定 点 算 法 基 于 互 信 ( 息极小与负熵极大 的 等 效 性 ! 利 用 牛 顿 迭 代 算 法 进
( "&( &’ 行快速稳健的迭代计算 % 5 计算步骤如下 #
4 6 ‘ -
* 6 ‘ ! 1‘ ‘
" $ "
其中 4 * 6 6 ‘ 为矩阵 )A ae 的元素 ! ‘ 为矩阵;A ae 的元素 %
(! 实施盲分解的前提条件和判别准则
若对 传 感 器 测 量 的 信 息 矩 阵 < 进 行 线 性 变 换 !
A< $A) .! 如 果 A $)’( ! 则 .$A< ! 由 于 ) 未 知 ! 所以不可能 有同时获 得 ) 和. 的解 析 方 法 %然
而可以根据传感器测量的信息矩阵 < 的 高 阶 统计 特 征同时给出) 和. 的估计值 % 信息论认为各组分 之 间 彼 此 信 息 独 立 的 充 要 条
&#! 第!
@ @ "
混合像元组分信息的盲分解方法 "
% 范闻捷(! 徐希孺(! (5北京大学遥感与地理信息系统研究所 ! 北京 ( # # > $ (( %5北京师范大学遥感与地理信息系统研究中心 ! 北京 ( # # > $ &
摘要 !! 从混合像元中分解组分 信 息 是 遥 感 反 演 的 重 要 内 容 5 若 遥 感 物 理 过 程 可 用 线 性 方 程 组 表 达 ! 遥感测量信息矩阵就等于权 重 矩 阵 乘 以 混 合 像 元 的 组 分 信 息 矩 阵 ! 一 般 认 为 ! 求 解 组 分 信 息 矩阵的前提是权重矩阵已知 5 利 用 盲 分 解 方 法 则 无 需 已 知 权 重 矩 阵 ! 直 接 将 矩 阵 分 解 5 其 原 理 是 利用了遥感可测信息矩阵大量 样 本 的 统 计 特 性 ! 获 得 分 解 所 需 的 附 加 信 息 ! 给 出 组 分 信 息 矩 阵 和 权重矩阵的估计值 5 但盲分解方 法 仅 可 以 复 原 组 分 信 息 的 波 形 ! 不 能 确 定 幅 度 5 为 得 到 混 合 像 元 的定量组分信息 ! 文中选择作物 E 土 壤 混 合 像 元 为 主 要 研 究 对 象 进 行 盲 分 解 研 究 ! 解 决 了 盲 分 解 的幅度不确定性 ! 并通过数值模拟 和 应 用 实 验 验 证 了 该 方 法 5 研 究 表 明 盲 分 解 可 以 成 为 遥 感 混 合 像元信息分解的有效工具之一 ! 具有良好的应用前景 5 关键词 !! 混合像元 ! 组分信息 ! 盲分解
9 = > / N 值!可 AaG 代表 A 个混合像元 G 个时相 的 #
以通过遥感手段获得 %)Aae 描述了每 个像元 内e 个 组分所占的面积比例 ! =eaG 为每个组分的# / N 值在
G 个时相内随时间的变化规律 % 传统的混合像元 分 解 方 法 是 利 用 主 成 分 分 析 方
法" ! K * I$
号处理 + 图像信息压 缩 以 及 遥 感 图 像 处 理 等 领 域 中 5 由于 盲 分 解 组 分 波 谱 振 幅 的 不确定性 ! 它还没 能 应 用 于 定 量 遥 感 研 究 中 ! 本 文 以同步反演作物播种面积和长势 为 例 ! 研 究 + A A方 法的适用条件 ! 力图 解 决 盲 分 解 方 法 本 身 存 在 的 不 确定性问题 ! 提供 一 个 具 有 盲 分 解 性 质 的 ! 遥 感 混 合像元信息分解方 法 ! 并 通 过 数 值 模 拟 和 应 用 实 验 验证该方法的可行性 5
< 的条件下 ! 同步获 得 矩 阵 ) 和.% 这 是 一 个 具 有 挑战性的问题 %
以作物 估 产 为 例 ! 要 想 实 现 大 面 积 作 物 估 产 ! 需要同步获取作物 的 播 种 面 积 和 单 位 面 积 长 势 5 如 果把单位面积的长 势 用 垂 直 植 被 指 数 " 随时间 # / N$ 的变化趋势来表达 ! 作 物 估 产 的 遥 感 混 合 像 元 分 解
图 ’! 小麦 ’ 油菜和土壤的 9 = > 值随时间变化
/2 ’!P + + 分解的幅度不确定性问题 $ 若将 " 式展开为 (
( " =eaG ! 9 = @AaG - ; 10 ,1, Aa e, e G -) Aa e, a $ " %
" 卷 ! 第 # 期 !$ % % "年#月 !第!
9 = >AaG - ;,? $ ;,@,@’( ,? !
此处 ; 为特 征 矢 量 矩 阵 !? 为 相 应 的 负 载 矩 阵 !G 为转换矩阵 !@0( 为 它 的 逆 矩 阵 %K * I 分解中每个 特征矢量其实只 代 表 方 差 取 极 大 的 方 向 ! 并 没 有 任 何物理意义 % 若 令 )Aae -;,@ 则 =eaG -@’( ,?% 要获得有意义的独立 成 分 !)Aae 必 须 已 知 ! 才 能 计 算 =eaG % 反 之 亦 然 %)Aae 与 =eaG 都 是 遥 感 作 物 估 产的未知关键参 数 % 能 否 在 仅 知 道 9 = > A aG 条 件 下 ! 同时获知 )Aae 和 =eaG ! 这 是 遥 感 估 产 中 的 基 本 理
