Statistical Table T-test F-test 的表格
Excel 数据分析工具一览表
Excel 数据分析工具一览表1.“F - 检验：双样本方差分析”分析工具此分析工具可以进行双样本F - 检验，用来比较两个样本总体的方差。
例如，可以对参加游泳比赛的两个队的时间记分进行F- 检验，查看二者的样本方差是否不同。
2.“t - 检验：成对双样本均值分析”分析工具此分析工具及其公式可以进行成对双样本进行t - 检验，用来确定样本均值是否不等。
此t -检验并不假设两个总体的方差是相等的。
当样本中出现自然配对的观察值时，可以使用此成对检验，例如对一个样本组进行了两次检验，抽取实验前的一次和实验后的一次。
3.“t - 检验：双样本等方差假设”分析工具此分析工具可以进行双样本t - 检验。
此t- 检验先假设两个数据集的方差相等，故也称作齐次方差t - 检验。
可以使用t - 检验来确定两个样本均值实际上是否相等。
4.“t - 检验：双样本异方差假设”分析工具此分析工具及其公式可以进行双样本t –检验。
此t - 检验先假设两个数据集的方差不等，故也称作异方差t - 检验。
可以使用t - 检验来确定两个样本均值实际上是否相等。
当进行分析的样本组不同时，可使用此检验。
如果某一样本组在某次处理前后都进行了检验，则应使用“成对检验”。
5.“z - 检验：双样本均值分析”分析工具此分析工具可以进行方差已知的双样本均值z-检验。
此工具用于检验两个总体均值之间存在差异的假设。
例如，可以使用此检验来确定两种汽车模型性能之间的差异情况。
6.“抽样分析”分析工具此分析工具以输入区域为总体构造总体的一个样本。
当总体太大而不能进行处理或绘制时，可以选用具有代表性的样本。
如果确认输入区域中的数据是周期性的，还可以对一个周期中特定时间段中的数值进行采样。
例如，如果输入区域包含季度销售量数据，以四为周期进行取样，将在输出区域中生成某个季度的样本。
7.“傅立叶分析”分析工具此分析工具可以解决线性系统问题，并能通过快速傅立叶变换（FFT）分析周期性的数据。
stata的f检验命令
stata的f检验命令文章标题：深入解析Stata中的F检验命令摘要：本文将对Stata中的F检验命令进行深入研究和解析，从基本概念到实际应用，为读者提供详细的指导和理解。
我们将从什么是F检验开始，逐步介绍其原理、应用场景以及如何在Stata中进行操作。
通过本文的阅读，读者将能够更好地理解F检验的背景和原理，并能熟练地在Stata中运用F检验命令进行数据分析。
1. 什么是F检验1.1 F检验的基本概念1.2 F检验的假设检验原理1.3 F统计量的计算方法2. F检验的应用场景2.1 单因素方差分析中的F检验2.2 多元回归分析中的F检验2.3 重复测量设计中的F检验3. 在Stata中使用F检验命令3.1 数据导入与准备3.2 单因素方差分析中的F检验3.3 多元回归分析中的F检验3.4 重复测量设计中的F检验4. F检验结果的解读与可视化分析4.1 F统计量的解读4.2 P值的解读4.3 效应量的计算与解读4.4 结果的可视化分析5. F检验的局限性和注意事项5.1 数据正态性的检验前提5.2 样本容量对F检验的影响5.3 其他相关统计检验的补充6. 对F检验的观点和理解6.1 F检验在统计学中的重要性6.2 F检验在实际数据分析中的应用6.3 F检验的局限性和替代方法结论：通过本文的阅读和学习，读者对Stata中的F检验命令的相关知识和应用方法应具有一定的了解。
我们也要认识到F检验的局限性，并在实际数据分析中综合应用其他统计方法以获得更准确和全面的结论。
希望本文能够为读者提供有价值的参考和帮助。
1. F检验在多元回归分析中的应用多元回归分析是一种用于研究多个自变量对因变量的影响的统计方法。
在进行多元回归分析时，需要对自变量的整体影响进行评估，而F检验则提供了一种评估自变量整体影响是否显著的方法。
F检验在多元回归分析中的应用非常广泛。
它可以用来判断模型整体的显著性，即自变量是否对因变量的解释具有统计学意义。
f statistic计算公式
f statistic计算公式F-statistic是统计分析中常用的重要指标，它可以用来分析两个或者多个样本均值之间的差异情况。
F-statistic包含两个参数，分别为F统计量和自由度，它们共同决定结果的可靠性。
F-statistic 计算公式如下：F-Statistics = (概率统计:/求和组内方差X自由度1) / (概率统计:/求和组间方差X自由度2)其中，概率统计可以定义为平均值的差值的绝对值的平方，也可以定义为协方差的绝对值的平方，而求和组内方差和求和组间方差就是组内方差和组间方差。
自由度1和自由度2则是代表F-statistic统计检验最多可以比较几组样本的变量值，其计算方式如下：自由度1：自由度1 = 样本总数 - 组数自由度2：自由度2 = 组数 -1F-statistic的结果可以用来判断两个或者多个样本均值之间的差异究竟有多大。
当多个样本均值之间的差异较大时，F-statistic值一般会非常大；当多个样本均值之间的差异较小时，F-statistic值一般会较小；当多个样本均值差异接近零时，F-statistic值则会接近零。
因此，F-statistic检验可以作为社会科学研究中常用的统计数据，来判断不同群体是否存在显著的差异。
此外，F-statistic还可以用于判断不同模型的差异性，如某一模型的拟合程度会比另一种模型的拟合程度好。
这一F-statistic用于比较多个模型时经常被称为F比较统计量，它可以明确表明拟合好的模型和不太拟合的模型之间的差异。
总之，F-statistic是一种在社会科学研究中常常被用于测量群体差异的统计量，在多个样本均值之间的差异分析中具有重要的作用。
通过F-statistic公式的求解，可以得出F-statistic的值，它可以用来衡量两个或者多个样本均值之间的显著性差异，从而帮助人们判断研究结果的可靠性。
另外，F-statistic甚至可以帮助我们定量地分析不同模型间的差异性，从而更好地进行特定研究。
如何使用FTEST和TTEST函数进行假设检验
如何使用FTEST和TTEST函数进行假设检验在统计学中，假设检验是一种重要的方法，用来验证关于总体参数的假设。
FTEST函数和TTEST函数是Excel中相关的函数，可以帮助我们进行假设检验。
本文将详细介绍如何使用FTEST和TTEST函数进行假设检验，并给出相应的示例。
一、FTEST函数的使用FTEST函数用来比较两个总体的方差是否相等。
它的语法为：FTEST(array1, array2)。
其中，array1和array2分别代表两个样本的数据范围或者数据数组。
下面以一个例子来说明FTEST函数的使用。
例：某公司开发了两种不同的产品A和B，想要比较这两种产品的质量差异是否显著。
我们分别随机抽取了30个A产品和30个B产品，并记录了每个产品的质量指标数据。
现在，我们要使用FTEST函数来进行假设检验。
步骤1：打开Excel，并将A产品的质量指标数据放在A列，将B产品的质量指标数据放在B列。
步骤2：在C列输入FTEST函数的公式：=FTEST(A1:A30, B1:B30)。
步骤3：按下Enter键，即可得到FTEST函数的返回值，该返回值为两个样本的方差比。
为0.05），判断两个样本的方差是否显著不同。
如果返回值小于设定的显著性水平，则可以拒绝原假设，即两个样本的方差不相等。
二、TTEST函数的使用TTEST函数用来比较两个总体的均值是否相等。
它的语法为：TTEST(array1, array2, tails, type)。
其中，array1和array2分别代表两个样本的数据范围或者数据数组；tails代表检验类型，1代表双尾检验，2代表单尾检验；type代表配对数据假设检验还是不配对数据假设检验，0代表配对数据，1代表不配对数据。
下面以一个例子来说明TTEST函数的使用。
例：某公司开发了一种新的药物，想要比较该药物的疗效是否显著。
我们随机选择了30名患者，将其分成两组，一组使用新药物治疗，另一组使用传统药物治疗，并记录了两组患者的治疗时间数据。
Statistical Table T-test F-test 的表格
Appendix2Tables of statistical distributionsTable A2.1Normal critical values for different values ofαα0.40.250.20.150.10.050.0250.010.0050.001Zα.2533.6745.84161.03641.28161.64491.96002.32632.57583.0902Source:Biometrika Tables for Statisticians(1966),volume1,3rd edn.Reprinted withpermission of Oxford University Press.616Appendixes617 Table A2.2Critical values of Student’s t-distribution for different probability levels,αand degrees of freedom,να0.40.250.150.10.050.0250.010.0050.0010.0005ν10.3249 1.0000 1.9626 3.0777 6.313812.706231.820563.6567318.3087636.6189 20.28870.8165 1.3862 1.8856 2.9200 4.3027 6.96469.924822.327131.5991 30.27670.7649 1.2498 1.6377 2.3534 3.1824 4.5407 5.840910.214512.9240 40.27070.7407 1.1896 1.5332 2.1318 2.7764 3.7469 4.60417.17328.6103 50.26720.7267 1.1558 1.4759 2.0150 2.5706 3.3649 4.0321 5.8934 6.8688 60.26480.7176 1.1342 1.4398 1.9432 2.4469 3.1427 3.7074 5.2076 5.9588 70.26320.7111 1.1192 1.4149 1.8946 2.3646 2.9980 3.4995 4.7853 5.4079 80.26190.7064 1.1081 1.3968 1.8595 2.3060 2.8965 3.3554 4.5008 5.0413 90.26100.7027 1.0997 1.3830 1.8331 2.2622 2.8214 3.2498 4.2968 4.7809 100.26020.6998 1.0931 1.3722 1.8125 2.2281 2.7638 3.1693 4.1437 4.5869 110.25960.6974 1.0877 1.3634 1.7959 2.2010 2.7181 3.1058 4.0247 4.4370 120.25900.6955 1.0832 1.3562 1.7823 2.1788 2.6810 3.0545 3.9296 4.3178 130.25860.6938 1.0795 1.3502 1.7709 2.1604 2.6503 3.0123 3.8520 4.2208 140.25820.6924 1.0763 1.3450 1.7613 2.1448 2.6245 2.9768 3.7874 4.1405 150.25790.6912 1.0735 1.3406 1.7531 2.1314 2.6025 2.9467 3.7328 4.0728 160.25760.6901 1.0711 1.3368 1.7459 2.1199 2.5835 2.9208 3.6862 4.0150 170.25730.6892 1.0690 1.3334 1.7396 2.1098 2.5669 2.8982 3.6458 3.9651 180.25710.6884 1.0672 1.3304 1.7341 2.1009 2.5524 2.8784 3.6105 3.9216 190.25690.6876 1.0655 1.3277 1.7291 2.0930 2.5395 2.8609 3.5794 3.8834 200.25670.6870 1.0640 1.3253 1.7247 2.0860 2.5280 2.8453 3.5518 3.8495 210.25660.6864 1.0627 1.3232 1.7207 2.0796 2.5176 2.8314 3.5272 3.8193 220.25640.6858 1.0614 1.3212 1.7171 2.0739 2.5083 2.8188 3.5050 3.7921 230.25630.6853 1.0603 1.3195 1.7139 2.0687 2.4999 2.8073 3.4850 3.7676 240.25620.6848 1.0593 1.3178 1.7109 2.0639 2.4922 2.7969 3.4668 3.7454 250.25610.6844 1.0584 1.3163 1.7081 2.0595 2.4851 2.7874 3.4502 3.7251 260.25600.6840 1.0575 1.3150 1.7056 2.0555 2.4786 2.7787 3.4350 3.7066 270.25590.6837 1.0567 1.3137 1.7033 2.0518 2.4727 2.7707 3.4210 3.6896 280.25580.6834 1.0560 1.3125 1.7011 2.0484 2.4671 2.7633 3.4082 3.6739 290.25570.6830 1.0553 1.3114 1.6991 2.0452 2.4620 2.7564 3.3962 3.6594 300.25560.6828 1.0547 1.3104 1.6973 2.0423 2.4573 2.7500 3.3852 3.6460 350.25530.6816 1.0520 1.3062 1.6896 2.0301 2.4377 2.7238 3.3400 3.5911 400.25500.6807 1.0500 1.3031 1.6839 2.0211 2.4233 2.7045 3.3069 3.5510 450.25490.6800 1.0485 1.3006 1.6794 2.0141 2.4121 2.6896 3.2815 3.5203 500.25470.6794 1.0473 1.2987 1.6759 2.0086 2.4033 2.6778 3.2614 3.4960 600.25450.6786 1.0455 1.2958 1.6706 2.0003 2.3901 2.6603 3.2317 3.4602 700.25430.6780 1.0442 1.2938 1.6669 1.9944 2.3808 2.6479 3.2108 3.4350 800.25420.6776 1.0432 1.2922 1.6641 1.9901 2.3739 2.6387 3.1953 3.4163 900.25410.6772 1.0424 1.2910 1.6620 1.9867 2.3685 2.6316 3.1833 3.4019 1000.25400.6770 1.0418 1.2901 1.6602 1.9840 2.3642 2.6259 3.1737 3.3905 1200.25390.6765 1.0409 1.2886 1.6577 1.9799 2.3578 2.6174 3.1595 3.3735 1500.25380.6761 1.0400 1.2872 1.6551 1.9759 2.3515 2.6090 3.1455 3.3566 2000.25370.6757 1.0391 1.2858 1.6525 1.9719 2.3451 2.6006 3.1315 3.3398 3000.25360.6753 1.0382 1.2844 1.6499 1.9679 2.3388 2.5923 3.1176 3.3233∞0.25330.6745 1.0364 1.2816 1.6449 1.9600 2.3263 2.5758 3.0902 3.2905 Source:Biometrika Tables for Statisticians(1966),volume1,3rd edn.Reprinted withpermission of Oxford University Press.T a b l e A 2.3U p p e r 5%c r i t i c a l v a l u e s f o r F -d i s t r i b u t i o nD e g r e e s o f f r e e d o m f o r n u m e r a t o r (m )1234567891012152024304060120∞D e g r e e s o f F r e e d o m f o r d e n o m i n a t o r (T −k )1161200216225230234237239241242244246248249250251252253254218.519.019.219.219.319.319.419.419.419.419.419.419.419.519.519.519.519.519.5310.19.559.289.129.018.948.898.858.818.798.748.708.668.648.628.598.578.558.5347.716.946.596.396.266.166.096.046.005.965.915.865.805.775.755.725.695.665.6356.615.795.415.195.054.954.884.824.774.744.684.624.564.534.504.464.434.404.3765.995.144.764.534.394.284.214.154.104.064.003.943.873.843.813.773.743.703.6775.594.744.354.123.973.873.793.733.683.643.573.513.443.413.383.343.303.273.2385.324.464.073.843.693.583.503.443.393.353.283.223.153.123.083.043.012.972.9395.124.263.863.633.483.373.293.233.183.143.073.012.942.902.862.832.792.752.71104.964.103.713.483.333.223.143.073.022.982.912.852.772.742.702.662.622.582.54114.843.983.593.363.203.093.012.952.902.852.792.722.652.612.572.532.492.452.40124.753.893.493.263.113.002.912.852.802.752.692.622.542.512.472.432.382.342.30134.673.813.413.183.032.922.832.772.712.672.602.532.462.422.382.342.302.252.21144.603.743.343.112.962.852.762.702.652.602.532.462.392.352.312.272.222.182.13154.543.683.293.062.902.792.712.642.592.542.482.402:332.292.252.202.162.112.07164.493.633.243.012.852.742.662.592.542.492.422.352.282.242.192.152.112.062.01174.453.593.202.962.812.702.612.552.492.452.382.312.232.192.152.102.062.011.96184.413.553.162.932.772.662.582.512.462.412.342.272.192.152.112.062.021.971.92194.383.523.132.902.742.632.542.482.422.382.312.232.162.112.072.031.981.931.88204.353.493.102.872.712.602.512.452.392.352.282.202.122.082.041.991.951.901.84214.323.473.072.842.682.572.492.422.372.322.252.182.102.052.011.961.921.871.81224.303.443.052.822.662.552.462.402.342.302.232.152.072.031.981.941.891.841.78234.283.423.032.802.642.532.442.372.322.272.202.132.052.011.961.911.861.811.76244.263.403.012.782.622.512.422.362.302.252.182.112.031.981.941.891.841.791.73254.243.392.992.762.602.492.402.342.282.242.162.092.011.961.921.871.821.771.71304.173.322.922.692.532.422.332.272.212.162.092.011.931.891.841.791.741.681.62404.083.232.842.612.452.342.252.182.122.08.2.001.921.841.791.741.691.641.581.51604.003.152.762.532.372.252.172.102.041.991.921.841.751.701.651.591.531.471.391203.923.072.682.452.292.182.092.021.961.911.831.751.661.611.551.501.431.351.25∞3.843.002.602.372.212.102.011.941.881.831.751.671.571.521.461.391.321.221.00S o u r c e :B i o m e t r i k a T a b l e s f o r S t a t i s t i c i a n s (1966),v o l u m e 1,3r d e d n .R e p r i n t e d w i t h p e r m i s s i o n o f O x f o r d U n i v e r s i t y P r e s s .T a b l e A 2.4U p p e r 1%c r i t i c a l v a l u e s f o r F -d i s t r i b u t i o nD e g r e e s o f f r e e d o m f o r n u m e r a t o r (m )1234567891012152024304060120∞D e g r e e s o f F r e e d o m f o r d e n o m i n a t o r (T −k )14,0525,0005,4035,6255,7645,8595,9285,9826,0236,0566,1066,1576,2096,2356,2616,2876,3136,3396,366298.599.099.299.399.399.399.499.499.499.499.499.499.599.599.599.599.599.599.5334.130.829.528.728.227.927.727.527.327.227.126.926.726.626.526.426.426.226.1421.218.016.716.015.515.215.014.814.714.514.414.214.013.913.813.713.713.613.5516.313.312.111.411.010.710.510.310.210.19.899.729.559.479.389.299.209.119.02613.710.99.789.158.758.478.268.107.987.877.727.567.407.317.237.147.066.976.88712.29.558.457.857.467.196.996.846.726.626.476.316.166.075.995.915.825.745.65811.38.657.597.016.636.376.186.035.915.815.675.525.365.285.205.125.034.954.86910.68.026.996.426.065.805.615.475.355.265.114.964.814.734.654.574.484.404.311010.07.566.555.995.645.395.205.064.944.854.714.564.414.334.254.174.084.003.91119.657.216.225.675.325.074.894.744.634.544.404.254.104.023.943.863.783.693.60129.336.935.955.415.064.824.644.504.394.304.164.013.863.783.703.623.543.453.36139.076.705.745.214.864.624.444.304.194.103.963.823.663.593.513.433.343.253.17148.866.515.565.044.704.464.284.144.033.943.803.663.513.433.353.273.183.093.00158.686.365.424.894.564.324.144.003.893.803.673.523.373.293.213.133.052.962.87168.536.235.294.774.444.204.033.893.783.693.553.413.263.183.103.022.932.842.75178.406.115.194.674.344.103.933.793.683.593.463.313.163.083.002.922.832.752.65188.296.015.094.584.254.013.843.713.603.513.373.233.083.002.922.842.752.662.57198.195.935.014.504.173.943.773.633.523.433.303.153.002.922.842.762.672.582.49208.105.854.944.434.103.873.703.563.463.373.233.092.942.862.782.692.612.522.42218.025.784.874.374.043.813.643.513.403.313.173.032.882.802.722.642.552.462.36227.955.724.824.313.993.763.593.453.353.263.122.982.832.752.672.582.502.402.31237.885.664.764.263.943.713.543.413.303.213.072.932.782.702.622.542.452.352.26247.825.614.724.223.903.673.503.363.263.173.032.892.742.662.582.492.402.312.21257.775.574.684.183.863.633.463.323.223.132.992.852.702.622.532.452.362.272.17307.565.394.514.023.703.473.303.173.072.982.842.702.552.472.392.302.212.112.01407.315.184.313.833.513.293.122.992.892.802.662.522.372.292.202.112.021.921.80607.084.984.133.653.343.122.952.822.722.632.502.352.202.122.031.941.841.731.601206.854.793.953.483.172.962.792.662.562.472.342.192.031.951.861.761.661.531.38∞6.634.613.783.323.022.802.642.512.412.322.182.041.881.791.701.591.471.321.00S o u r c e :B i o m e t r i k a T a b l e s f o r S t a t i s t i c i a n s (1966),v o l u m e 1,3r d e d n .R e p r i n t e d w i t h p e r m i s s i o n o f O x f o r d U n i v e r s i t y P r e s s .T a b l e A 2.5C h i -s q u a r e d c r i t i c a l v a l u e s f o r d i f f e r e n t v a l u e s o f αa n d d e g r e e s o f f r e e d o m ,υυ0.9950.9900.9750.9500.9000.7500.5000.2500.1000.0500.0250.0100.00510.000040.000160.000980.003930.015790.10150.45491.3232.7063.8415.0246.6357.87920.010030.020100.050650.10260.21070.57541.3862.7734.6055.9917.3789.21010.59730.071720.11480.21580.35180.58441.2132.3664.1086.2517.8159.34811.34512.83840.20700.29710.48440.71071.0641.9233.3575.3857.7799.48811.14313.27714.86050.41170.55430.83121.1451.6102.6754.3516.6269.23611.07012.83315.08616.75060.67570.87211.2371.6352.2043.4555.3487.84110.64512.59214.44916.81218.54870.98931.2391.6902.1672.8334.2556.3469.03712.01714.06716.01318.47520.27881.3441.6462.1802.7333.4905.0717.34410.21913.36215.50717.53520.09021.95591.7352.0882.7003.3254.1685.8998.34311.38914.68416.91919.02321.66623.589102.1562.5583.2473.9404.8656.7379.34212.54915.98718.30720.48323.20925.188112.6033.0533.8164.5755.5787.58410.34113.70117.27519.67521.92024.72526.757123.0743.5714.4045.2266.3048.43811.34014.84518.5421.02623.33726.21728.300133.5654.1075.0095.8927.0419.29912.34015.98419.81222.36224.73627.68829.819144.0754.6605.6296.5717.79010.16513.33917.11721.06423.68526.11929.14131.319154.6015.2296.2627.2618.54711.03614.33918.24522.30724.99627.48830.57832.801165.1425.8126.9087.9629.31211.91215.33819.36923.54226.29628.84532.00034.267175.6976.4087.5648.67210.08512.79216.33820.48924.76927.58730.19133.40935.718186.2657.0158.2319.39010.86513.67517.33821.60525.98928.86931.52634.80537.156196.8447.6338.90710.11711.65114.56218.33822.71827.20430.14332.85236.19138.582207.4348.2609.59110.85112.44315.45219.33723.82828.41231.41034.17037.56639.997218.0348.89710.28311.59113.24016.34420.33724.93529.61532.67035.47938.93241.401228.6439.54210.98212.33814.04117.24021.33726.03930.81333.92436.78140.28942.796239.26010.19611.68813.09014.84818.13722.33727.14132.00735.17238.07641.63844.181249.88610.85612.40113.84815.65919.03723.33728.24133.19636.41539.36442.08045.5582510.52011.52413.12014.61116.47319.93924.33729.33934.38237.65240.64644.31446.9282611.16012.19813.84415.37917.29220.84325.33630.43435.56338.88541.92345.64248.2902711.80812.87914.57316.15118.11421.74926.33631.52836.74140.11343.19446.96349.6452812.46113.56515.30816.92818.93922.65727.33632.62037.91641.33744.46148.27850.9932913.12114.25616.04717.70819.76823.56728.33633.71139.08742.55745.72249.58852.3363013.78714.95416.79118.49320.59924.47829.33634.80040.25643.77346.97950.89253.6723517.19218.50920.56922.46524.79729.05434.33640.22346.05949.80253.20357.34260.2754020.70722.16424.43326.50929.05033.66039.33545.61651.80555.75859.34263.69166.7664524.31125.90128.36630.61233.35038.29144.33550.98557.50561.65665.41069.95773.1665027.99129.70732.35734.76437.68942.94249.33556.33463.16767.50571.42076.15479.4905531.73533.57136.39838.95842.06047.61154.33561.66568.79673.31177.38182.29285.7496035.53537.48540.48243.15846.45952.29459.33566.98174.39779.08283.29885.37991.9527043.27545.44248.75851.73955.32961.69869.33477.57785.52790.53195.023100.425104.2158051.17253.54057.15360.39164.27871.14479.33488.13096.578101.879106.629112.329116.3219059.19661.75465.64769.12673.29180.62589.33498.650107.565113.145118.136124.116128.29910067.32870.06574.22277.92982.35890.13399.334109.141118.498124.342129.561135.807140.16912083.82986.90991.56895.705100.627109.224119.335130.051140.228146.565152.214158.963163.670150109.122112.655117.980122.692126.278137.987149.334161.258172.577179.579185.803193.219198.380200152.224156.421162.724168.279174.825156.175199.334213.099226.018233.993241.060249.455255.281250196.145200.929208.095214.392221.809234.580249.334264.694279.947287.889295.691304.948311.361S o u r c e :B i o m e t r i k a T a b l e s f o r S t a t i s t i c i a n s (1966),v o l u m e 1,3r d e d n .R e p r i n t e d w i t h p e r m i s s i o n o f O x f o r d U n i v e r s i t y P r e s s .622AppendixesTable A2.6Lower and upper1%critical values for Durbin–Watson statistick =1k =2k =3k =4k =5 T d L d U d L d U d L d U d L d U d L d U150.81 1.070.70 1.250.59 1.460.49 1.700.39 1.96160.84 1.090.74 1.250.63 1.440.53 1.660.44 1.90170.87 1.100.77 1.250.67 1.430.57 1.630.48 1.85180.90 1.120.80 1.260.71 1.420.61 1.600.52 1.80190.93 1.130.83 1.260.74 1.410.65 1.580.56 1.77200.95 1.150.86 1.270.77 1.410.68 1.570.60 1.74210.97 1.160.89 1.270.80 1.410.72 1.550.63 1.7122 1.00 1.170.91 1.280.83 1.400.75 1.540.66 1.6923 1.02 1.190.94 1.290.86 1.400.77 1.530.70 1.6724 1.04 1.200.96 1.300.88 1.410.80 1.530.72 1.6625 1.05 1.210.98 1.300.90 1.410.83 1.520.75 1.6526 1.07 1.22 1.00 1.310.93 1.410.85 1.520.78 1.6427 1.09 1.23 1.02 1.320.95 1.410.88 1.510.81 1.6328 1.10 1.24 1.04 1.320.97 1.410.90 1.510.83 1.6229 1.12 1.25 1.05 1.330.99 1.420.92 1.510.85 1.6130 1.13 1.26 1.07 1.34 1.01 1.420.94 1.510.88 1.6131 1.15 1.27 1.08 1.34 1.02 1.420.96 1.510.90 1.6032 1.16 1.28 1.10 1.35 1.04 1.430.98 1.510.92 1.6033 1.17 1.29 1.11 1.36 1.05 1.43 1.00 1.510.94 1.5934 1.18 1.30 1.13 1.36 1.07 1.43 1.01 1.510.95 1.5935 1.19 1.31 1.14 1.37 1.08 1.44 1.03 1.510.97 1.5936 1.21 1.32 1.15 1.38 1.10 1.44 1.04 1.510.99 1.5937 1.22 1.32 1.16 1.38 1.11 1.45 1.06 1.51 1.00 1.5938 1.23 1.33 1.18 1.39 1.12 1.45 1.07 1.52 1.02 1.5839 1.24 1.34 1.19 1.39 1.14 1.45 1.09 1.52 1.03 1.5840 1.25 1.34 1.20 1.40 1.15 1.46 1.10 1.52 1.05 1.5845 1.29 1.38 1.24 1.42 1.20 1.48 1.16 1.53 1.11 1.5850 1.32 1.40 1.28 1.45 1.24 1.49 1.20 1.54 1.16 1.5955 1.36 1.43 1.32 1.47 1.28 1.51 1.25 1.55 1.21 1.5960 1.38 1.45 1.35 1.48 1.32 1.52 1.28 1.56 1.25 1.6065 1.41 1.47 1.38 1.50 1.35 1.53 1.31 1.57 1.28 1.6170 1.43 1.49 1.40 1.52 1.37 1.55 1.34 1.58 1.31 1.6175 1.45 1.50 1.42 1.53 1.39 1.56 1.37 1.59 1.34 1.6280 1.47 1.52 1.44 1.54 1.42 1.57 1.39 1.60 1.36 1.6285 1.48 1.53 1.46 1.55 1.43 1.58 1.41 1.60 1.39 1.6390 1.50 1.54 1.47 1.56 1.45 1.59 1.43 1.61 1.41 1.6495 1.51 1.55 1.49 1.57 1.47 1.60 1.45 1.62 1.42 1.64100 1.52 1.56 1.50 1.58 1.48 1.60 1.46 1.63 1.44 1.65Note:T,number of observations;k ,number of explanatory variables(excluding aconstant term).Source:Durbin,J.and Watson,G.S.(1951)Testing for serial correlation in leastsquares regression II Biometrika,38(1--2),159--177.Reprinted with the permission ofOxford University Press.Appendixes623Table A2.7Dickey–Fuller critical values for different significance levels,αSample size T0.010.0250.050.10τ25−2.66−2.26−1.95−1.6050−2.62−2.25−1.95−1.61100−2.60−2.24−1.95−1.61250−2.58−2.23−1.95−1.62500−2.58−2.23−1.95−1.62∞−2.58−2.23−1.95−1.62τμ25−3.75−3.33−3.00−2.6350−3.58−3.22−2.93−2.60100−3.51−3.17−2.89−2.58250−3.46−3.14−2.88−2.57500−3.44−3.13−2.87−2.57∞−3.43−3.12−2.86−2.57ττ25−4.38−3.95−3.60−3.2450−4.15−3.80−3.50−3.18100−4.04−3.73−3.45−3.15250−3.99−3.69−3.43−3.13500−3.98−3.68−3.42−3.13∞−3.96−3.66−3.41−3.12Source:Fuller(1976).Reprinted with the permission of John Wiley&Sons.624AppendixesTable A2.8Critical values for the Engle–Granger cointegration test on regression residuals with no constant in test regressionNumber of variables Samplein system size T0.010.050.1050−4.32−3.67−3.28 2100−4.07−3.37−3.03200−4.00−3.37−3.0250−4.84−4.11−3.73 3100−4.45−3.93−3.59200−4.35−3.78−3.4750−4.94−4.35−4.02 4100−4.75−4.22−3.89200−4.70−4.18−3.8950−5.41−4.76−4.42 5100−5.18−4.58−4.26200−5.02−4.48−4.18 Source:Engle and Yoo(1987).Reprinted with the permission of Elsevier Science.Appendixes625 Table A2.9Quantiles of the asymptotic distribution of the Johansen cointegration rank test statistics(constant in cointegrating vectors only)p−r50%80%90%95%97.5%99%Mean Varλmax1 3.40 5.917.529.2410.8012.97 4.037.0728.2711.5413.7515.6717.6320.208.8613.08313.4717.4019.7722.0024.0726.8114.0219.24418.7022.9525.5628.1430.3233.2419.2323.83523.7828.7631.6634.4036.9039.7924.4829.26629.0834.2537.4540.3043.2246.8229.7234.63734.7340.1343.2546.4548.9951.9135.1838.35839.7045.5348.9152.0054.7157.9540.3541.98944.9750.7354.3557.4260.5063.7145.5544.131050.2156.5260.2563.5766.2469.9450.8249.281155.7062.3866.0269.7472.6476.6356.3354.99λTrace1 3.40 5.917.529.2410.8012.97 4.037.07211.2515.2517.8519.9622.0524.6011.9118.94323.2828.7532.0034.9137.6141.0723.8437.98438.8445.6549.6553.1256.0660.1639.5059.42558.4666.9171.8676.0780.0684.4559.1691.65681.9091.5797.18102.14106.74111.0182.49126.947109.17120.35126.58131.70136.49143.09109.75167.918139.83152.56159.48165.58171.28177.20140.57208.099174.88198.08196.37202.92208.81215.74175.44257.8410212.93228.08236.54244.15251.30257.68213.53317.2411254.84272.82282.45291.40298.31307.64256.15413.35Source:Osterwald-Lenum(1992,table1∗).Reprinted with the permission of BlackwellPublishers.626AppendixesTable A2.10Quantiles of the asymptotic distribution of the Johansen cointegration rank test statistics(constant,i.e.a drift only in VAR and in cointegrating vector)p−r50%80%90%95%97.5%99%Mean Varλmax10.44 1.66 2.69 3.76 4.95 6.650.99 2.042 6.8510.0412.0714.0716.0518.637.4712.42312.3416.2018.6020.9723.0925.5212.8818.67417.6621.9824.7327.0728.9832.2418.2623.47523.0527.8530.9033.4635.7138.7723.6728.82628.4533.6736.7639.3741.8645.1029.0633.57733.8339.1242.3245.2847.9651.5734.3737.41839.2945.0548.3351.4254.2957.6939.8542.90944.5850.5553.9857.1259.3362.8045.1044.931049.6655.9759.6262.8165.4469.0950.2949.411154.9961.5565.3868.8372.1175.9555.6354.92λTrace10.44 1.66 2.69 3.76 4.95 6.650.99 2.0427.5511.0713.3315.4117.5220.048.2314.38318.7023.6426.7929.6832.5635.6519.3232.43433.6040.1543.9547.2150.3554.4634.2452.75552.3060.2964.8468.5271.8076.0752.9579.25675.2684.5789.4894.1598.33103.1875.74114.657101.22112.30118.50124.24128.45133.57101.91158.788131.62143.97150.53156.00161.32168.36132.09201.829165.11178.90186.39192.89198.82204.95165.90246.4510202.58217.81225.85233.13239.46247.18203.39300.8011243.90260.82269.96277.71284.87293.44244.66379.56Source:Osterwald-Lenum(1992,table1).Reprinted with the permission of BlackwellPublishers.Appendixes627 Table A2.11Quantiles of the asymptotic distribution of the Johansen cointegration rank test statistics(constant in cointegrating vector and VAR,trend incointegrating vector)p−r50%80%90%95%97.5%99%Mean Varλmax1 5.558.6510.4912.2514.2116.26 6.2210.11210.9014.7016.8518.9621.1423.6511.5116.38316.2420.4523.1125.5427.6830.3416.8222.01421.5026.3029.1231.4633.6036.6522.0827.74526.7231.7234.7537.5240.0142.3627.3231.36632.0137.5040.9143.9746.8449.5132.6837.91737.5743.1146.3249.4251.9454.7138.0639.74842.7248.5652.1655.5058.0862.4643.3444.83948.1754.3457.8761.2964.1267.8848.7449.201053.2159.4963.1866.2369.5673.7353.7452.641158.5464.9769.2672.7275.7279.2359.1556.97λTrace1 5.558.6510.4912.2514.2116.26 6.2210.11215.5920.1922.7625.3227.7530.4516.2024.90329.5335.5639.0642.4445.4248.4530.1545.68447.1754.8059.1462.9966.2570.0547.7974.48568.6477.8383.2087.3191.0696.5869.35106.56694.05104.73110.42114.90119.29124.7594.67143.337122.87134.57141.01146.76152.52158.49123.51182.858155.40169.10176.67182.82187.91196.08156.41234.119192.37207.25215.17222.21228.05234.41193.03288.3010231.59247.91256.72263.42270.33279.07232.25345.2311276.34294.12303.13310.81318.02327.45276.88416.98Source:Osterwald-Lenum(1992,table2∗).Reprinted with the permission of BlackwellPublishers.。
统计学常用表格
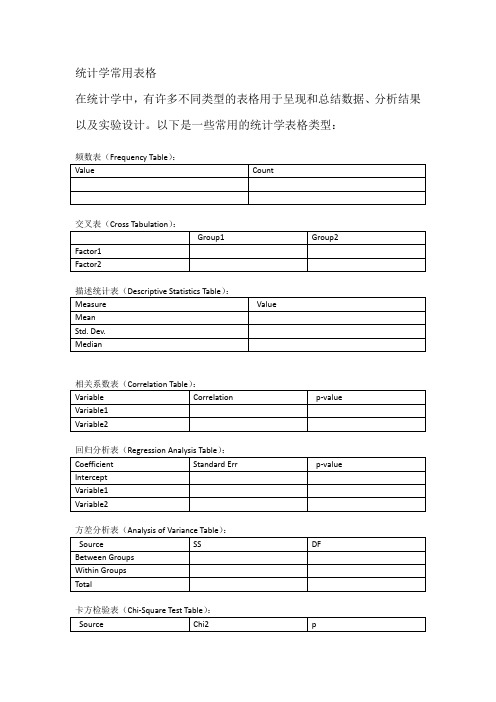
统计学常用表格在统计学中，有许多不同类型的表格用于呈现和总结数据、分析结果以及实验设计。
以下是一些常用的统计学表格类型：交叉表（Cross Tabulation）：实验设计表（Experimental Design Table）：说明：统计学表格类型：1.频数表（Frequency Table）：描述变量各个取值的出现频率。
2.交叉表（Cross Tabulation）：将两个或多个变量的频数列在一个表格中，用于观察它们之间的关系。
3.描述统计表（Descriptive Statistics Table）：包括均值、中位数、标准差等描述性统计指标，用于概括数据分布的特征。
4.相关系数表（Correlation Table）：展示变量之间的相关关系，通常包括皮尔逊相关系数或斯皮尔曼等级相关系数。
5.回归分析表（Regression Analysis Table）：呈现回归模型的系数、标准误差、t统计量等信息。
6.方差分析表（Analysis of Variance Table）：用于展示方差分析的结果，包括组间方差、组内方差、F统计量等。
7.卡方检验表（Chi-Square Test Table）：展示卡方检验的结果，通常用于分析分类变量之间的关联。
8.生存分析表（Survival Analysis Table）：包括生存曲线、中位生存时间等，用于描述时间至事件发生的分布。
9.混淆矩阵（Confusion Matrix）：用于评估分类模型的性能，特别是在分类问题中。
10.ANOVA表（ANOVA Table）：用于分析方差，通常与方差分析一起使用，包括平方和、自由度、均方等。
11.正态性检验表（Normality Test Table）：用于检验数据是否符合正态分布。
12.实验设计表（Experimental Design Table）：描述实验设计中的因子水平、处理组合以及实验结果。
f检验表完整版
f检验表完整版一、F检验的概述1.F检验的定义F检验，又称F分布检验，是一种用于比较两个样本均值是否显著不同的统计方法。
它是由英国统计学家威廉·戈塞特（William Gosset）在20世纪初发现的，主要用于方差分析、独立性检验和拟合优度检验等。
2.F检验的应用场景F检验广泛应用于以下场景：（1）方差分析：在实验设计中，比较多个实验组与对照组的均值差异是否显著。
（2）独立性检验：检验两个分类变量之间是否存在显著关联。
（3）拟合优度检验：评估线性回归模型的拟合效果，检验观测值与预测值之间的差异是否显著。
二、F检验的计算过程1.总体方差的计算总体方差（σ）表示所有观测值与总体均值之间的差异平方和的平均值。
计算公式为：σ= Σ（xi - μ）/ n其中，xi为每个观测值，μ为总体均值，n为样本数量。
2.样本方差的计算样本方差（S）表示样本中每个观测值与样本均值之间的差异平方和的平均值。
计算公式为：S = Σ（xi - x）/ (n - 1)其中，xi为每个观测值，x为样本均值，n为样本数量。
3.F值的计算F值是用来比较总体方差与样本方差的比值。
计算公式为：F = (Σ（xi - μ）/ σ) / (Σ（xi - x）/ S)4.F检验的判断标准当F值大于临界值时，认为两个样本的均值存在显著差异。
临界值的确定取决于显著性水平和自由度。
自由度等于样本数量减去1。
三、F检验的优缺点1.优点（1）F检验具有较强的推断能力，可以较为准确地判断均值差异。
（2）适用范围广泛，可以应用于多种统计分析场景。
2.缺点（1）对样本数量有一定要求，当样本数量较小（如n < 30）时，F检验的准确性降低。
（2）对总体分布有一定要求，当总体分布与假设不符时，F检验的结果可能出现偏差。
四、F检验在实际应用中的案例分析1.案例介绍某研究者想要探究不同教学方法对学生数学成绩的影响，随机抽取了两个班级进行实验。
实验结束后，分别计算出两个班级的数学成绩均值，分别为70和80。
f critical value表
f critical value表临界值表是在统计学中常用的表格之一，用于帮助确定假设检验的结果是否显著。
该表格记录了在给定的显著性水平下，不同自由度条件下的临界值。
本文将对临界值表进行详细介绍，包括其定义、用途、计算方法等方面，以期能够对读者提供清晰明了的理解。
第一部分：定义临界值表是一个统计学工具，用于确定统计显著性检验中的拒绝域。
在统计推断中，我们常常会根据样本数据来推断总体的参数，然后再进行统计检验。
在进行统计检验时，我们会设置一个显著性水平α，并将给定的统计量与临界值进行比较，以判断原假设是否可接受或拒绝。
临界值是样本观测值在假设检验中应达到的临界点，该观测值与临界值的比较可以帮助我们确定是否能够拒绝原假设。
临界值表通常是一个以显著性水平α和自由度为两个参数的表格。
在统计学中，自由度是指样本数据中可以自由变化的部分的个数。
临界值表根据不同的显著性水平和自由度条件，提供了相应的临界值。
第二部分：用途临界值表在统计学中起到了至关重要的作用。
它为统计推断提供了一种明确的参考标准，使我们能够对假设检验结果进行客观、科学的判断。
临界值表的应用涉及到很多领域，包括医学、社会科学、自然科学等等。
以下是临界值表在常见的统计检验中的应用举例：1.单样本t检验：用于比较一个样本的均值与总体均值是否有显著差异。
2.两样本t检验：用于比较两个独立样本的均值是否有显著差异。
3.方差分析：用于比较多个样本均值之间是否存在显著差异。
4.相关分析：用于分析两个变量之间的相关性是否显著。
在以上的各种统计分析中，临界值表起到了决策的作用。
根据计算出的统计量，我们可以在临界值表中查找相应的临界值，如果统计量超过了临界值，那么我们就可以拒绝原假设，否则我们接受原假设。
第三部分：计算方法临界值的计算是基于概率分布的性质进行的。
不同的统计量的分布可能会有所不同，因此根据不同的统计量，我们需要使用不同的概率分布进行计算。
常见的统计量及其相应的概率分布包括：1. t分布：用于单样本t检验和两样本t检验。
计量经济学查表值
计量经济学查表值
计量经济学是应用数学和统计学方法研究经济学问题的学科。
在实际研究过程中，经常需要查找一些数值表格以便进行数据分析和模型建立。
下面是一些常见的计量经济学查表值：
1. t分布表，用于计算t统计量的p值和置信区间。
2. F分布表，用于计算F统计量的p值和置信区间。
3. 卡方分布表，用于计算卡方统计量的p值和置信区间。
4. 标准正态分布表，用于计算标准正态分布的累积概率和反函数值。
5. t检验临界值表，用于计算两个样本之间的t检验临界值。
6. F检验临界值表，用于计算方差分析和回归分析中F检验的临界值。
7. Durbin-Watson统计量表，用于计算回归分析中的自相关性。
8. Breusch-Pagan检验表，用于检验方差齐性。
以上是一些常见的计量经济学查表值，研究者们可以根据自身的研究需求进行选择和使用。
- 1 -。
r语言 卡方检验非四格表形式
r语言卡方检验非四格表形式全文共四篇示例，供读者参考第一篇示例：卡方检验是统计学中常用的假设检验方法，用于判断观察到的频数与期望频数之间的差异是否显著。
在传统的卡方检验中，我们通常会使用四格表形式的数据进行分析，但是在实际应用中，有时候数据的形式并不总是四格表，可能是二格表、三格表甚至是更多格表。
本文将着重介绍在R语言中如何进行卡方检验非四格表形式的数据分析。
在R语言中，进行卡方检验非四格表形式的数据分析可以使用chisq.test()函数。
该函数可以接受一个矩阵作为输入参数，矩阵中每一行代表一个类别，每一列代表一个水平，矩阵中的值为频数。
如果有一个二格表形式的数据，可以将其转换为一个矩阵，然后使用chisq.test()函数进行卡方检验。
下面以一个实例来说明如何在R语言中进行卡方检验非四格表形式的数据分析。
假设有一组数据如下所示：```Rdata <- matrix(c(20, 30, 10, 40), nrow = 2, byrow = TRUE)rownames(data) <- c("A", "B")colnames(data) <- c("X", "Y")```上述代码中，我们创建了一个二格表形式的数据，其中行代表两个类别，列代表两个水平，值为频数。
接下来，我们可以使用chisq.test()函数对这组数据进行卡方检验：```Rresult <- chisq.test(data)print(result)```运行上面的代码后，我们就可以得到卡方检验的结果，包括卡方统计量、自由度和p值等信息。
通过检查p值是否小于显著性水平，我们可以判断观察到的频数与期望频数之间的差异是否显著。
R语言提供了强大的工具和函数来进行卡方检验非四格表形式的数据分析。
通过掌握这些方法，我们能够更灵活地应对不同形式的数据，并进行准确的统计推断。
Excel中的数据分析工具假设检验和方差分析
Excel中的数据分析工具假设检验和方差分析Excel中的数据分析工具——假设检验和方差分析数据分析在现代社会中扮演着重要的角色，而Excel作为一款常用的办公软件，在数据分析方面具有强大的功能和工具。
本文将重点介绍Excel中的数据分析工具——假设检验和方差分析。
一、假设检验假设检验是一种统计方法，用于确定一个样本是否代表着整个总体的特征。
它通过对样本数据进行分析，来推断和判断总体的参数。
Excel提供了多种假设检验的方法，常用的有t检验和z检验。
1. t检验t检验用于对一个总体或两个总体的均值是否存在显著差异进行判断。
在Excel中，可以通过T.TEST()函数进行t检验的计算。
该函数的语法为：T.TEST(array1, array2, tails, type)。
其中，array1和array2分别表示两个样本的数据范围，tails表示尾部情况（单尾或双尾），type表示两个样本是否具有相等的方差。
2. z检验z检验用于判断一个样本均值和总体均值的显著性差异。
在Excel 中，可以通过Z.TEST()函数进行z检验的计算。
该函数的语法为：Z.TEST(array, x, sigma)。
其中，array表示样本数据范围，x表示总体均值的猜测值，sigma表示总体标准差。
二、方差分析方差分析是一种用于分析多个样本之间差异性的统计方法。
它可以用于判断一个因素是否对样本产生了显著影响。
Excel中提供了ANOVA()函数来进行方差分析的计算。
方差分析可以分为单因素方差分析和双因素方差分析两种情况。
1. 单因素方差分析单因素方差分析用于对一个因素（变量）的多个水平（组别）之间的差异进行比较。
在Excel中，可以通过使用ANOVA()函数进行单因素方差分析的计算。
该函数的语法为：ANOVA(data, group)。
其中，data表示包含多个组别数据的范围，group表示包含组别标识的范围。
2. 双因素方差分析双因素方差分析用于分析两个因素（变量）对样本数据的影响。
stata制作表格的操作命令
在Stata中制作表格的命令有很多种，以下是几种常用的操作命令：
stataesttab：这是Stata中常用的制作表格的命令之一，可以将Stata的数据集输出为各种格式的表格，包括LaTeX、HTML、Excel等。
基本语法为：stataesttab [varlist] [using filename] [using filename2] ...，其中varlist是要输出的变量列表，using filename是输出文件名。
tabout：这个命令可以很方便地生成频数和交叉列联表格，并输出到Word、Excel等文件中。
estimates table：这个命令可以将多个回归结果合并到一张表格中，非常方便进行结果汇总和比较。
collapse：这个命令可以将数据按照某个变量进行汇总，例如计算平均值、总和等。
egen：这个命令可以生成新的变量，例如计算行内最大值、行内平均值等。
以上表格制作命令只是Stata的一部分功能，更多高级的功能和操作请查阅Stata官方文档或咨询专业人士。
stata表格解读
解读Stata表格需要根据具体的问题和经济背景进行分析。
以下是一些常见的经济角度问题和相应的解读方法：1. 回归模型输出表格：- 系数（Coefficients）：回归模型中的系数表示不同自变量对因变量的影响。
通过系数的正负和显著性水平可以判断变量之间的关系。
- 标准误（Standard Errors）：标准误用于衡量估计系数的精度。
较小的标准误意味着估计系数的可靠性更高。
- t值（t-values）：t值是系数除以其标准误的结果。
较大的t值说明估计系数与零偏离得更远，表明该变量的影响在统计上是显著的。
- P值（P-values）：P值表示观察到的样本结果与原假设之间的差异。
较小的P值意味着观察到的结果对于原假设的拒绝更具有统计显著性。
2. 描述统计表格：- 均值（Mean）：均值是样本数据的平均值，用于描述数据的集中趋势。
- 标准差（Standard Deviation）：标准差测量数据的离散程度。
较大的标准差表明数据的变异性较高。
- 最小值（Minimum）和最大值（Maximum）：这些值表示数据的范围，有助于了解数据的分布范围。
- 百分位数（Percentiles）：百分位数显示了数据中特定百分比的观察值的位置，可用于了解数据分布的形状。
3. 面板数据表格：- 固定效应（Fixed Effects）：面板数据通常包含固定效应，即个体或单位之间的不可观测差异。
固定效应可以通过控制面板数据中个体固定特征的影响，以获得更准确的估计结果。
- 随机效应（Random Effects）：面板数据还可以包含随机效应，也称为单位特异性误差。
随机效应可以帮助解释个体或单位之间的随机差异，例如企业之间的管理差异。
- 滞后效应（Lagged Effects）：面板数据还可以用于估计滞后效应，即一个变量对于未来时间点的影响。
滞后效应可以解释变量之间的时序关系。
通过综合考虑这些指标，结合经济理论和问题背景进行分析，可以更好地解读Stata表格并回答特定的经济问题。
stata组间系数差异检验命令
stata组间系数差异检验命令Stata是一个非常强大的统计分析软件，在数据分析中有着广泛的应用。
在实际的数据分析中，经常需要进行组间系数差异检验，以比较不同组之间的差异。
本文将介绍Stata中的组间系数差异检验命令，帮助读者更好地进行数据分析。
一、什么是组间系数差异检验组间系数差异检验是一种比较不同组之间差异的方法。
在数据分析中，我们经常需要比较不同组之间的差异，例如比较两个不同的治疗方法的疗效、比较不同地区的经济发展水平等。
通过组间系数差异检验，我们可以得到不同组之间的差异情况，从而更好地进行数据分析和决策。
二、Stata中的组间系数差异检验命令Stata中提供了多种组间系数差异检验命令，包括t检验、方差分析、卡方检验等。
下面我们将介绍几种常用的命令。
1、t检验t检验是一种常用的组间系数差异检验方法，用于比较两个样本之间的差异。
在Stata中，可以使用如下命令进行t检验：ttest var1==var2其中，var1和var2表示要比较的两个变量。
该命令将计算两个变量的均值差异，并输出t值、p值和置信区间等结果。
2、方差分析方差分析是一种比较多个样本之间差异的方法，可以同时比较多个因素对结果的影响。
在Stata中，可以使用如下命令进行方差分析： anova var1 var2 var3, by(group)其中，var1、var2和var3表示要比较的变量，group表示分组变量。
该命令将计算不同组之间的差异，并输出方差分析表和F值等结果。
3、卡方检验卡方检验是一种用于比较两个或多个分类变量之间差异的方法。
在Stata中，可以使用如下命令进行卡方检验：tab var1 var2, chi2其中，var1和var2表示要比较的两个分类变量，chi2表示进行卡方检验。
该命令将计算两个变量之间的卡方值和p值等结果。
三、实例演示为了更好地理解Stata中的组间系数差异检验命令，下面我们将以一个实例进行演示。
MSA组间均方缩写
MSA组间均方缩写
“MS”（均方），分别表示MSA（组间均方或组间方差），MSE（组内均方）。
“F”：检验统计量值F=MSA/MSE（服从F分布）。
Fcrit：自由度为（3，19）的F的上α分位点值。
P-value：P值，小于α表示落在了拒绝域内。
SUMMARY表展示了各组样本的描述统计量。
方差分析表：
“组间”表示不同行业间，
“组内”表示同一行业间的不同公司，
“SS”（平方和），第一个是SSA（组间平方和），第二个是SSE （组内平方和）。
“df”：分别表示组间自由度、组内自由度。
使用Excel进行单方差分析
首先在Excel中添加加载项【数据分析】。
【数据】选项卡，【分析】，【数据分析】对话框，选择“方差分析：单因素方差分析”，在对话框设置中依次选择数据区域、第一行是否有标志、α值等，【确定】。
F-test,T-test
2
Version01_100407
你应该知道的几个统计学定义
3
Version01_100407
假设验证 (Hypothesis Test)
1) 假设验证的概念 · 用 Sample调查对 样品总体的品质特性，推定母集体的品质特性 · 假设验证是对于母集体设定某个假设，对于母数检讨并确认事前 设定的假设在给定的确率范围内是否正确.
全部测量值与组间变异betweengroupvariation各组的均数与总均数间的差异组间变异随机误差处理因素效应组内变异withingroupvariation组的每个测量值与该组均数的差异22version01100407内容用离均差平方和sumdeviationsfrommeanss反映变异的大小ssssss随机误差组间变异ss随机误差23version01100407均方差meansquarems变异程度除与离均差平方和的大小有关外还与其自由度有关由于各部分自由度不相等因此各部分离均差平方和不能直接比较须将各部分离均差平方和除以相应自由度其比值称为均方差简称均方meansquarems
不拒绝H0，表示拒绝总体均数相等的证据不足 ————>分析终止。
拒绝H0，接受H1, 表示总体均数不全相等 哪两两均数之间相等？哪两两均数之间不等？ ————>需要进一步作多重比较
28
Version01_100407
内容
29
Version01_100407
内容
30
Version01_100407
解题：
1. 建立假设
Ho : a b
=（8.44-7.88）/ （1.4/35^1/2)=1.08
Excel中自动完成方差齐性与非齐性t检验
１、缺失值处理缺失值是数据分析中一个非常常见的现象，出现的主要原因有：设备故障、拒绝回答、测验时走神等，对此应对缺失值的进行检测，ＳＰＳＳ默认缺失值以黑点表示，可以通过快速浏览数据列表发现，记录下缺失值所在的变量即数据的列。
缺失值的处理方式有以下三种：（1）剔除有缺失值的观测单位，即删除ＳＰＳＳ数据列表中缺失值所在的数据行。
在ＳＰＳＳ的统计分析程序中，打开ｏｐｔｉｏｎｓ按钮，便会出现缺失值的处理栏，可分别选择下列选项：“剔除正在分析的变量中带缺失值的观察单位”、“剔除所有分析变量中带缺失值的观察单位”。
虽然这种做法可以为执行许多统计分析命令扫清障碍，但要求每一步统计分析都联系于特定的有效样本容量，而样本容量不能稳定会给整个分析带来不便。
（2）对缺失值进行估计后补上。
主要有两种方法：一是根据文献报道等知识经验进行估计；二是用ＳＰＳＳ提供的工具进行估计。
在“ｔｒａｎｓｆｏｒｍ”菜单下的“ｒｅｐｌａｃｅｍｉｓｓｉｎｇｖａｌｕｅｓ”列出了５种替代的方法：１）ｓｅｒｉｅｓｍｅａｎ：以列的算术平均值进行替代；２）ｍｅａｎｏｆｎｅａｒｌｙｐｏｉｎｔ：以缺失值邻近点的算术平均值进行替代；３）Ｍｅｄｉａｎｏｆｎｅａｒｌｙｐｏｉｎｔ：以缺失值临近点的中位数替代；４）ｌｉｎｅａｒｉｎｔｅｒｐｏｌａｔｉｏｎ：根据缺失值前后的２个观察值进行线性内查法估计和替代；５）ｌｉｎｅａｒｔｒｅｎｄａｔｐｏｉｎｔ：用线形回归法进行估计和替代。
（3）将缺失值作为常数值，如：作为“０”。
２、奇异值和极端值的处理奇异值和极端值是指各变量中与整体数据相距太远的极值，由于它的夸大作用，常常会歪曲统计结果，导致犯一类和二类错误。
导致奇异值和极端值的原因：（１）数据输入时出错；（２）在不同数据格式之间进行转换时，缺失值处的数码代号被当成了实际观测值；（３）出现奇异值的样本并非属于所要考察的总体；（４）考察的样本相对于正态分布有比较多的极值。
奇异值和极端值的检测：在描述统计分析菜单下，点击Ｅｘｐｌｏｒｅ（探索性分析）对话框后把变量选入Ｖａｒｉａｂｌｅｓ框中，单击统计量选择描述统计量，单击图可以选择箱形图、茎叶图、直方图与正态检验的Ｑ－Ｑ图等检测有无极端值和奇异值。
统计表英语缩写
在统计和数据分析领域，有许多常见的英语缩写用于表示各种统计表和相关的概念。
以下是一些常见的统计表和相关概念的英语缩写及其解释：
1.ANOVA：Analysis of Variance，方差分析。
用于比较
两个或两个以上组之间的平均值差异。
2.Chi-Square：卡方检验。
常用于比较实际观测频数与期
望频数之间的差异，常用于检验分类变量。
3.DF：Degrees of Freedom，自由度。
在统计检验中，
用于计算统计量的自由变动的样本点的数量。
4.F-Test：F检验。
一种统计检验方法，常用于检验两个
或两个以上总体的方差是否相等，或检验回归模型的显
著性。
5.P-Value：概率值。
在假设检验中，观察到的统计量值
（或更极端值）出现的概率，用于决定是否拒绝原假设。
6.R-Square：决定系数。
在回归分析中，表示模型解释
的变异与总变异的比例。
7.SD：Standard Deviation，标准差。
表示数据的离散程
度。
8.T-Test：T检验。
一种统计检验方法，常用于比较两组
数据的均值，或检验单个样本的均值是否与某个特定值
有显著差异。
9.Z-Score：Z分数。
表示一个数值在分布中的相对位置，
常用于将不同分布的数据标准化。
f检验表完整版
f检验表完整版摘要：一、F检验表简介1.F检验表的定义2.F检验表的作用二、F检验表的使用方法1.F检验表的构成2.如何选择合适的F检验表3.F检验表的使用步骤三、F检验表的应用领域1.在学术研究中的应用2.在实际生活中的应用四、F检验表的优缺点1.F检验表的优点2.F检验表的缺点五、结论正文：F检验表是一种用于检验数据之间是否存在显著差异的统计工具。
通过对数据进行F检验，我们可以判断不同样本的均值是否存在显著差异，从而为后续的实验设计和数据分析提供依据。
一、F检验表简介F检验表是一种统计工具，用于帮助研究者分析数据，判断不同样本之间是否存在显著差异。
F检验表主要应用于方差分析（ANOVA）中，通过对数据进行检验，我们可以得到F值和相应的p值。
若p值小于预先设定的显著性水平（通常为0.05），则认为样本之间存在显著差异；反之，则认为样本之间不存在显著差异。
二、F检验表的使用方法1.F检验表的构成：F检验表通常包括行和列。
行表示不同样本的自由度（df），列表示不同的显著性水平（α）。
在表格中，我们会找到对应的F值和p 值。
2.如何选择合适的F检验表：选择F检验表时，需要根据实际的研究设计和数据情况，选择适当的显著性水平和自由度组合。
一般来说，显著性水平α越小，检验的敏感性越高，但相应的犯错误的概率也越大；自由度df越大，所需的样本量越大，但检验的准确性也越高。
3.F检验表的使用步骤：（1）确定研究问题和研究假设；（2）收集数据，并计算出样本的均值和标准差；（3）确定显著性水平和自由度；（4）查找F检验表，找到对应的F值和p值；（5）比较计算得到的F值和p值与表格中的值，判断样本之间是否存在显著差异。
三、F检验表的应用领域F检验表广泛应用于学术研究和实际生活中。
在学术研究中，例如心理学、教育学、生物学等领域，研究者需要对实验数据进行分析，判断不同实验组之间的处理效果是否存在显著差异。
在实际生活中，例如市场调查、产品比较等场景，也需要使用F检验表来分析数据，从而为决策提供依据。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
Appendix2Tables of statistical distributionsTable A2.1Normal critical values for different values ofαα0.40.250.20.150.10.050.0250.010.0050.001Zα.2533.6745.84161.03641.28161.64491.96002.32632.57583.0902Source:Biometrika Tables for Statisticians(1966),volume1,3rd edn.Reprinted withpermission of Oxford University Press.616Appendixes617 Table A2.2Critical values of Student’s t-distribution for different probability levels,αand degrees of freedom,να0.40.250.150.10.050.0250.010.0050.0010.0005ν10.3249 1.0000 1.9626 3.0777 6.313812.706231.820563.6567318.3087636.6189 20.28870.8165 1.3862 1.8856 2.9200 4.3027 6.96469.924822.327131.5991 30.27670.7649 1.2498 1.6377 2.3534 3.1824 4.5407 5.840910.214512.9240 40.27070.7407 1.1896 1.5332 2.1318 2.7764 3.7469 4.60417.17328.6103 50.26720.7267 1.1558 1.4759 2.0150 2.5706 3.3649 4.0321 5.8934 6.8688 60.26480.7176 1.1342 1.4398 1.9432 2.4469 3.1427 3.7074 5.2076 5.9588 70.26320.7111 1.1192 1.4149 1.8946 2.3646 2.9980 3.4995 4.7853 5.4079 80.26190.7064 1.1081 1.3968 1.8595 2.3060 2.8965 3.3554 4.5008 5.0413 90.26100.7027 1.0997 1.3830 1.8331 2.2622 2.8214 3.2498 4.2968 4.7809 100.26020.6998 1.0931 1.3722 1.8125 2.2281 2.7638 3.1693 4.1437 4.5869 110.25960.6974 1.0877 1.3634 1.7959 2.2010 2.7181 3.1058 4.0247 4.4370 120.25900.6955 1.0832 1.3562 1.7823 2.1788 2.6810 3.0545 3.9296 4.3178 130.25860.6938 1.0795 1.3502 1.7709 2.1604 2.6503 3.0123 3.8520 4.2208 140.25820.6924 1.0763 1.3450 1.7613 2.1448 2.6245 2.9768 3.7874 4.1405 150.25790.6912 1.0735 1.3406 1.7531 2.1314 2.6025 2.9467 3.7328 4.0728 160.25760.6901 1.0711 1.3368 1.7459 2.1199 2.5835 2.9208 3.6862 4.0150 170.25730.6892 1.0690 1.3334 1.7396 2.1098 2.5669 2.8982 3.6458 3.9651 180.25710.6884 1.0672 1.3304 1.7341 2.1009 2.5524 2.8784 3.6105 3.9216 190.25690.6876 1.0655 1.3277 1.7291 2.0930 2.5395 2.8609 3.5794 3.8834 200.25670.6870 1.0640 1.3253 1.7247 2.0860 2.5280 2.8453 3.5518 3.8495 210.25660.6864 1.0627 1.3232 1.7207 2.0796 2.5176 2.8314 3.5272 3.8193 220.25640.6858 1.0614 1.3212 1.7171 2.0739 2.5083 2.8188 3.5050 3.7921 230.25630.6853 1.0603 1.3195 1.7139 2.0687 2.4999 2.8073 3.4850 3.7676 240.25620.6848 1.0593 1.3178 1.7109 2.0639 2.4922 2.7969 3.4668 3.7454 250.25610.6844 1.0584 1.3163 1.7081 2.0595 2.4851 2.7874 3.4502 3.7251 260.25600.6840 1.0575 1.3150 1.7056 2.0555 2.4786 2.7787 3.4350 3.7066 270.25590.6837 1.0567 1.3137 1.7033 2.0518 2.4727 2.7707 3.4210 3.6896 280.25580.6834 1.0560 1.3125 1.7011 2.0484 2.4671 2.7633 3.4082 3.6739 290.25570.6830 1.0553 1.3114 1.6991 2.0452 2.4620 2.7564 3.3962 3.6594 300.25560.6828 1.0547 1.3104 1.6973 2.0423 2.4573 2.7500 3.3852 3.6460 350.25530.6816 1.0520 1.3062 1.6896 2.0301 2.4377 2.7238 3.3400 3.5911 400.25500.6807 1.0500 1.3031 1.6839 2.0211 2.4233 2.7045 3.3069 3.5510 450.25490.6800 1.0485 1.3006 1.6794 2.0141 2.4121 2.6896 3.2815 3.5203 500.25470.6794 1.0473 1.2987 1.6759 2.0086 2.4033 2.6778 3.2614 3.4960 600.25450.6786 1.0455 1.2958 1.6706 2.0003 2.3901 2.6603 3.2317 3.4602 700.25430.6780 1.0442 1.2938 1.6669 1.9944 2.3808 2.6479 3.2108 3.4350 800.25420.6776 1.0432 1.2922 1.6641 1.9901 2.3739 2.6387 3.1953 3.4163 900.25410.6772 1.0424 1.2910 1.6620 1.9867 2.3685 2.6316 3.1833 3.4019 1000.25400.6770 1.0418 1.2901 1.6602 1.9840 2.3642 2.6259 3.1737 3.3905 1200.25390.6765 1.0409 1.2886 1.6577 1.9799 2.3578 2.6174 3.1595 3.3735 1500.25380.6761 1.0400 1.2872 1.6551 1.9759 2.3515 2.6090 3.1455 3.3566 2000.25370.6757 1.0391 1.2858 1.6525 1.9719 2.3451 2.6006 3.1315 3.3398 3000.25360.6753 1.0382 1.2844 1.6499 1.9679 2.3388 2.5923 3.1176 3.3233∞0.25330.6745 1.0364 1.2816 1.6449 1.9600 2.3263 2.5758 3.0902 3.2905 Source:Biometrika Tables for Statisticians(1966),volume1,3rd edn.Reprinted withpermission of Oxford University Press.T a b l e A 2.3U p p e r 5%c r i t i c a l v a l u e s f o r F -d i s t r i b u t i o nD e g r e e s o f f r e e d o m f o r n u m e r a t o r (m )1234567891012152024304060120∞D e g r e e s o f F r e e d o m f o r d e n o m i n a t o r (T −k )1161200216225230234237239241242244246248249250251252253254218.519.019.219.219.319.319.419.419.419.419.419.419.419.519.519.519.519.519.5310.19.559.289.129.018.948.898.858.818.798.748.708.668.648.628.598.578.558.5347.716.946.596.396.266.166.096.046.005.965.915.865.805.775.755.725.695.665.6356.615.795.415.195.054.954.884.824.774.744.684.624.564.534.504.464.434.404.3765.995.144.764.534.394.284.214.154.104.064.003.943.873.843.813.773.743.703.6775.594.744.354.123.973.873.793.733.683.643.573.513.443.413.383.343.303.273.2385.324.464.073.843.693.583.503.443.393.353.283.223.153.123.083.043.012.972.9395.124.263.863.633.483.373.293.233.183.143.073.012.942.902.862.832.792.752.71104.964.103.713.483.333.223.143.073.022.982.912.852.772.742.702.662.622.582.54114.843.983.593.363.203.093.012.952.902.852.792.722.652.612.572.532.492.452.40124.753.893.493.263.113.002.912.852.802.752.692.622.542.512.472.432.382.342.30134.673.813.413.183.032.922.832.772.712.672.602.532.462.422.382.342.302.252.21144.603.743.343.112.962.852.762.702.652.602.532.462.392.352.312.272.222.182.13154.543.683.293.062.902.792.712.642.592.542.482.402:332.292.252.202.162.112.07164.493.633.243.012.852.742.662.592.542.492.422.352.282.242.192.152.112.062.01174.453.593.202.962.812.702.612.552.492.452.382.312.232.192.152.102.062.011.96184.413.553.162.932.772.662.582.512.462.412.342.272.192.152.112.062.021.971.92194.383.523.132.902.742.632.542.482.422.382.312.232.162.112.072.031.981.931.88204.353.493.102.872.712.602.512.452.392.352.282.202.122.082.041.991.951.901.84214.323.473.072.842.682.572.492.422.372.322.252.182.102.052.011.961.921.871.81224.303.443.052.822.662.552.462.402.342.302.232.152.072.031.981.941.891.841.78234.283.423.032.802.642.532.442.372.322.272.202.132.052.011.961.911.861.811.76244.263.403.012.782.622.512.422.362.302.252.182.112.031.981.941.891.841.791.73254.243.392.992.762.602.492.402.342.282.242.162.092.011.961.921.871.821.771.71304.173.322.922.692.532.422.332.272.212.162.092.011.931.891.841.791.741.681.62404.083.232.842.612.452.342.252.182.122.08.2.001.921.841.791.741.691.641.581.51604.003.152.762.532.372.252.172.102.041.991.921.841.751.701.651.591.531.471.391203.923.072.682.452.292.182.092.021.961.911.831.751.661.611.551.501.431.351.25∞3.843.002.602.372.212.102.011.941.881.831.751.671.571.521.461.391.321.221.00S o u r c e :B i o m e t r i k a T a b l e s f o r S t a t i s t i c i a n s (1966),v o l u m e 1,3r d e d n .R e p r i n t e d w i t h p e r m i s s i o n o f O x f o r d U n i v e r s i t y P r e s s .T a b l e A 2.4U p p e r 1%c r i t i c a l v a l u e s f o r F -d i s t r i b u t i o nD e g r e e s o f f r e e d o m f o r n u m e r a t o r (m )1234567891012152024304060120∞D e g r e e s o f F r e e d o m f o r d e n o m i n a t o r (T −k )14,0525,0005,4035,6255,7645,8595,9285,9826,0236,0566,1066,1576,2096,2356,2616,2876,3136,3396,366298.599.099.299.399.399.399.499.499.499.499.499.499.599.599.599.599.599.599.5334.130.829.528.728.227.927.727.527.327.227.126.926.726.626.526.426.426.226.1421.218.016.716.015.515.215.014.814.714.514.414.214.013.913.813.713.713.613.5516.313.312.111.411.010.710.510.310.210.19.899.729.559.479.389.299.209.119.02613.710.99.789.158.758.478.268.107.987.877.727.567.407.317.237.147.066.976.88712.29.558.457.857.467.196.996.846.726.626.476.316.166.075.995.915.825.745.65811.38.657.597.016.636.376.186.035.915.815.675.525.365.285.205.125.034.954.86910.68.026.996.426.065.805.615.475.355.265.114.964.814.734.654.574.484.404.311010.07.566.555.995.645.395.205.064.944.854.714.564.414.334.254.174.084.003.91119.657.216.225.675.325.074.894.744.634.544.404.254.104.023.943.863.783.693.60129.336.935.955.415.064.824.644.504.394.304.164.013.863.783.703.623.543.453.36139.076.705.745.214.864.624.444.304.194.103.963.823.663.593.513.433.343.253.17148.866.515.565.044.704.464.284.144.033.943.803.663.513.433.353.273.183.093.00158.686.365.424.894.564.324.144.003.893.803.673.523.373.293.213.133.052.962.87168.536.235.294.774.444.204.033.893.783.693.553.413.263.183.103.022.932.842.75178.406.115.194.674.344.103.933.793.683.593.463.313.163.083.002.922.832.752.65188.296.015.094.584.254.013.843.713.603.513.373.233.083.002.922.842.752.662.57198.195.935.014.504.173.943.773.633.523.433.303.153.002.922.842.762.672.582.49208.105.854.944.434.103.873.703.563.463.373.233.092.942.862.782.692.612.522.42218.025.784.874.374.043.813.643.513.403.313.173.032.882.802.722.642.552.462.36227.955.724.824.313.993.763.593.453.353.263.122.982.832.752.672.582.502.402.31237.885.664.764.263.943.713.543.413.303.213.072.932.782.702.622.542.452.352.26247.825.614.724.223.903.673.503.363.263.173.032.892.742.662.582.492.402.312.21257.775.574.684.183.863.633.463.323.223.132.992.852.702.622.532.452.362.272.17307.565.394.514.023.703.473.303.173.072.982.842.702.552.472.392.302.212.112.01407.315.184.313.833.513.293.122.992.892.802.662.522.372.292.202.112.021.921.80607.084.984.133.653.343.122.952.822.722.632.502.352.202.122.031.941.841.731.601206.854.793.953.483.172.962.792.662.562.472.342.192.031.951.861.761.661.531.38∞6.634.613.783.323.022.802.642.512.412.322.182.041.881.791.701.591.471.321.00S o u r c e :B i o m e t r i k a T a b l e s f o r S t a t i s t i c i a n s (1966),v o l u m e 1,3r d e d n .R e p r i n t e d w i t h p e r m i s s i o n o f O x f o r d U n i v e r s i t y P r e s s .T a b l e A 2.5C h i -s q u a r e d c r i t i c a l v a l u e s f o r d i f f e r e n t v a l u e s o f αa n d d e g r e e s o f f r e e d o m ,υυ0.9950.9900.9750.9500.9000.7500.5000.2500.1000.0500.0250.0100.00510.000040.000160.000980.003930.015790.10150.45491.3232.7063.8415.0246.6357.87920.010030.020100.050650.10260.21070.57541.3862.7734.6055.9917.3789.21010.59730.071720.11480.21580.35180.58441.2132.3664.1086.2517.8159.34811.34512.83840.20700.29710.48440.71071.0641.9233.3575.3857.7799.48811.14313.27714.86050.41170.55430.83121.1451.6102.6754.3516.6269.23611.07012.83315.08616.75060.67570.87211.2371.6352.2043.4555.3487.84110.64512.59214.44916.81218.54870.98931.2391.6902.1672.8334.2556.3469.03712.01714.06716.01318.47520.27881.3441.6462.1802.7333.4905.0717.34410.21913.36215.50717.53520.09021.95591.7352.0882.7003.3254.1685.8998.34311.38914.68416.91919.02321.66623.589102.1562.5583.2473.9404.8656.7379.34212.54915.98718.30720.48323.20925.188112.6033.0533.8164.5755.5787.58410.34113.70117.27519.67521.92024.72526.757123.0743.5714.4045.2266.3048.43811.34014.84518.5421.02623.33726.21728.300133.5654.1075.0095.8927.0419.29912.34015.98419.81222.36224.73627.68829.819144.0754.6605.6296.5717.79010.16513.33917.11721.06423.68526.11929.14131.319154.6015.2296.2627.2618.54711.03614.33918.24522.30724.99627.48830.57832.801165.1425.8126.9087.9629.31211.91215.33819.36923.54226.29628.84532.00034.267175.6976.4087.5648.67210.08512.79216.33820.48924.76927.58730.19133.40935.718186.2657.0158.2319.39010.86513.67517.33821.60525.98928.86931.52634.80537.156196.8447.6338.90710.11711.65114.56218.33822.71827.20430.14332.85236.19138.582207.4348.2609.59110.85112.44315.45219.33723.82828.41231.41034.17037.56639.997218.0348.89710.28311.59113.24016.34420.33724.93529.61532.67035.47938.93241.401228.6439.54210.98212.33814.04117.24021.33726.03930.81333.92436.78140.28942.796239.26010.19611.68813.09014.84818.13722.33727.14132.00735.17238.07641.63844.181249.88610.85612.40113.84815.65919.03723.33728.24133.19636.41539.36442.08045.5582510.52011.52413.12014.61116.47319.93924.33729.33934.38237.65240.64644.31446.9282611.16012.19813.84415.37917.29220.84325.33630.43435.56338.88541.92345.64248.2902711.80812.87914.57316.15118.11421.74926.33631.52836.74140.11343.19446.96349.6452812.46113.56515.30816.92818.93922.65727.33632.62037.91641.33744.46148.27850.9932913.12114.25616.04717.70819.76823.56728.33633.71139.08742.55745.72249.58852.3363013.78714.95416.79118.49320.59924.47829.33634.80040.25643.77346.97950.89253.6723517.19218.50920.56922.46524.79729.05434.33640.22346.05949.80253.20357.34260.2754020.70722.16424.43326.50929.05033.66039.33545.61651.80555.75859.34263.69166.7664524.31125.90128.36630.61233.35038.29144.33550.98557.50561.65665.41069.95773.1665027.99129.70732.35734.76437.68942.94249.33556.33463.16767.50571.42076.15479.4905531.73533.57136.39838.95842.06047.61154.33561.66568.79673.31177.38182.29285.7496035.53537.48540.48243.15846.45952.29459.33566.98174.39779.08283.29885.37991.9527043.27545.44248.75851.73955.32961.69869.33477.57785.52790.53195.023100.425104.2158051.17253.54057.15360.39164.27871.14479.33488.13096.578101.879106.629112.329116.3219059.19661.75465.64769.12673.29180.62589.33498.650107.565113.145118.136124.116128.29910067.32870.06574.22277.92982.35890.13399.334109.141118.498124.342129.561135.807140.16912083.82986.90991.56895.705100.627109.224119.335130.051140.228146.565152.214158.963163.670150109.122112.655117.980122.692126.278137.987149.334161.258172.577179.579185.803193.219198.380200152.224156.421162.724168.279174.825156.175199.334213.099226.018233.993241.060249.455255.281250196.145200.929208.095214.392221.809234.580249.334264.694279.947287.889295.691304.948311.361S o u r c e :B i o m e t r i k a T a b l e s f o r S t a t i s t i c i a n s (1966),v o l u m e 1,3r d e d n .R e p r i n t e d w i t h p e r m i s s i o n o f O x f o r d U n i v e r s i t y P r e s s .622AppendixesTable A2.6Lower and upper1%critical values for Durbin–Watson statistick =1k =2k =3k =4k =5 T d L d U d L d U d L d U d L d U d L d U150.81 1.070.70 1.250.59 1.460.49 1.700.39 1.96160.84 1.090.74 1.250.63 1.440.53 1.660.44 1.90170.87 1.100.77 1.250.67 1.430.57 1.630.48 1.85180.90 1.120.80 1.260.71 1.420.61 1.600.52 1.80190.93 1.130.83 1.260.74 1.410.65 1.580.56 1.77200.95 1.150.86 1.270.77 1.410.68 1.570.60 1.74210.97 1.160.89 1.270.80 1.410.72 1.550.63 1.7122 1.00 1.170.91 1.280.83 1.400.75 1.540.66 1.6923 1.02 1.190.94 1.290.86 1.400.77 1.530.70 1.6724 1.04 1.200.96 1.300.88 1.410.80 1.530.72 1.6625 1.05 1.210.98 1.300.90 1.410.83 1.520.75 1.6526 1.07 1.22 1.00 1.310.93 1.410.85 1.520.78 1.6427 1.09 1.23 1.02 1.320.95 1.410.88 1.510.81 1.6328 1.10 1.24 1.04 1.320.97 1.410.90 1.510.83 1.6229 1.12 1.25 1.05 1.330.99 1.420.92 1.510.85 1.6130 1.13 1.26 1.07 1.34 1.01 1.420.94 1.510.88 1.6131 1.15 1.27 1.08 1.34 1.02 1.420.96 1.510.90 1.6032 1.16 1.28 1.10 1.35 1.04 1.430.98 1.510.92 1.6033 1.17 1.29 1.11 1.36 1.05 1.43 1.00 1.510.94 1.5934 1.18 1.30 1.13 1.36 1.07 1.43 1.01 1.510.95 1.5935 1.19 1.31 1.14 1.37 1.08 1.44 1.03 1.510.97 1.5936 1.21 1.32 1.15 1.38 1.10 1.44 1.04 1.510.99 1.5937 1.22 1.32 1.16 1.38 1.11 1.45 1.06 1.51 1.00 1.5938 1.23 1.33 1.18 1.39 1.12 1.45 1.07 1.52 1.02 1.5839 1.24 1.34 1.19 1.39 1.14 1.45 1.09 1.52 1.03 1.5840 1.25 1.34 1.20 1.40 1.15 1.46 1.10 1.52 1.05 1.5845 1.29 1.38 1.24 1.42 1.20 1.48 1.16 1.53 1.11 1.5850 1.32 1.40 1.28 1.45 1.24 1.49 1.20 1.54 1.16 1.5955 1.36 1.43 1.32 1.47 1.28 1.51 1.25 1.55 1.21 1.5960 1.38 1.45 1.35 1.48 1.32 1.52 1.28 1.56 1.25 1.6065 1.41 1.47 1.38 1.50 1.35 1.53 1.31 1.57 1.28 1.6170 1.43 1.49 1.40 1.52 1.37 1.55 1.34 1.58 1.31 1.6175 1.45 1.50 1.42 1.53 1.39 1.56 1.37 1.59 1.34 1.6280 1.47 1.52 1.44 1.54 1.42 1.57 1.39 1.60 1.36 1.6285 1.48 1.53 1.46 1.55 1.43 1.58 1.41 1.60 1.39 1.6390 1.50 1.54 1.47 1.56 1.45 1.59 1.43 1.61 1.41 1.6495 1.51 1.55 1.49 1.57 1.47 1.60 1.45 1.62 1.42 1.64100 1.52 1.56 1.50 1.58 1.48 1.60 1.46 1.63 1.44 1.65Note:T,number of observations;k ,number of explanatory variables(excluding aconstant term).Source:Durbin,J.and Watson,G.S.(1951)Testing for serial correlation in leastsquares regression II Biometrika,38(1--2),159--177.Reprinted with the permission ofOxford University Press.Appendixes623Table A2.7Dickey–Fuller critical values for different significance levels,αSample size T0.010.0250.050.10τ25−2.66−2.26−1.95−1.6050−2.62−2.25−1.95−1.61100−2.60−2.24−1.95−1.61250−2.58−2.23−1.95−1.62500−2.58−2.23−1.95−1.62∞−2.58−2.23−1.95−1.62τμ25−3.75−3.33−3.00−2.6350−3.58−3.22−2.93−2.60100−3.51−3.17−2.89−2.58250−3.46−3.14−2.88−2.57500−3.44−3.13−2.87−2.57∞−3.43−3.12−2.86−2.57ττ25−4.38−3.95−3.60−3.2450−4.15−3.80−3.50−3.18100−4.04−3.73−3.45−3.15250−3.99−3.69−3.43−3.13500−3.98−3.68−3.42−3.13∞−3.96−3.66−3.41−3.12Source:Fuller(1976).Reprinted with the permission of John Wiley&Sons.624AppendixesTable A2.8Critical values for the Engle–Granger cointegration test on regression residuals with no constant in test regressionNumber of variables Samplein system size T0.010.050.1050−4.32−3.67−3.28 2100−4.07−3.37−3.03200−4.00−3.37−3.0250−4.84−4.11−3.73 3100−4.45−3.93−3.59200−4.35−3.78−3.4750−4.94−4.35−4.02 4100−4.75−4.22−3.89200−4.70−4.18−3.8950−5.41−4.76−4.42 5100−5.18−4.58−4.26200−5.02−4.48−4.18 Source:Engle and Yoo(1987).Reprinted with the permission of Elsevier Science.Appendixes625 Table A2.9Quantiles of the asymptotic distribution of the Johansen cointegration rank test statistics(constant in cointegrating vectors only)p−r50%80%90%95%97.5%99%Mean Varλmax1 3.40 5.917.529.2410.8012.97 4.037.0728.2711.5413.7515.6717.6320.208.8613.08313.4717.4019.7722.0024.0726.8114.0219.24418.7022.9525.5628.1430.3233.2419.2323.83523.7828.7631.6634.4036.9039.7924.4829.26629.0834.2537.4540.3043.2246.8229.7234.63734.7340.1343.2546.4548.9951.9135.1838.35839.7045.5348.9152.0054.7157.9540.3541.98944.9750.7354.3557.4260.5063.7145.5544.131050.2156.5260.2563.5766.2469.9450.8249.281155.7062.3866.0269.7472.6476.6356.3354.99λTrace1 3.40 5.917.529.2410.8012.97 4.037.07211.2515.2517.8519.9622.0524.6011.9118.94323.2828.7532.0034.9137.6141.0723.8437.98438.8445.6549.6553.1256.0660.1639.5059.42558.4666.9171.8676.0780.0684.4559.1691.65681.9091.5797.18102.14106.74111.0182.49126.947109.17120.35126.58131.70136.49143.09109.75167.918139.83152.56159.48165.58171.28177.20140.57208.099174.88198.08196.37202.92208.81215.74175.44257.8410212.93228.08236.54244.15251.30257.68213.53317.2411254.84272.82282.45291.40298.31307.64256.15413.35Source:Osterwald-Lenum(1992,table1∗).Reprinted with the permission of BlackwellPublishers.626AppendixesTable A2.10Quantiles of the asymptotic distribution of the Johansen cointegration rank test statistics(constant,i.e.a drift only in VAR and in cointegrating vector)p−r50%80%90%95%97.5%99%Mean Varλmax10.44 1.66 2.69 3.76 4.95 6.650.99 2.042 6.8510.0412.0714.0716.0518.637.4712.42312.3416.2018.6020.9723.0925.5212.8818.67417.6621.9824.7327.0728.9832.2418.2623.47523.0527.8530.9033.4635.7138.7723.6728.82628.4533.6736.7639.3741.8645.1029.0633.57733.8339.1242.3245.2847.9651.5734.3737.41839.2945.0548.3351.4254.2957.6939.8542.90944.5850.5553.9857.1259.3362.8045.1044.931049.6655.9759.6262.8165.4469.0950.2949.411154.9961.5565.3868.8372.1175.9555.6354.92λTrace10.44 1.66 2.69 3.76 4.95 6.650.99 2.0427.5511.0713.3315.4117.5220.048.2314.38318.7023.6426.7929.6832.5635.6519.3232.43433.6040.1543.9547.2150.3554.4634.2452.75552.3060.2964.8468.5271.8076.0752.9579.25675.2684.5789.4894.1598.33103.1875.74114.657101.22112.30118.50124.24128.45133.57101.91158.788131.62143.97150.53156.00161.32168.36132.09201.829165.11178.90186.39192.89198.82204.95165.90246.4510202.58217.81225.85233.13239.46247.18203.39300.8011243.90260.82269.96277.71284.87293.44244.66379.56Source:Osterwald-Lenum(1992,table1).Reprinted with the permission of BlackwellPublishers.Appendixes627 Table A2.11Quantiles of the asymptotic distribution of the Johansen cointegration rank test statistics(constant in cointegrating vector and VAR,trend incointegrating vector)p−r50%80%90%95%97.5%99%Mean Varλmax1 5.558.6510.4912.2514.2116.26 6.2210.11210.9014.7016.8518.9621.1423.6511.5116.38316.2420.4523.1125.5427.6830.3416.8222.01421.5026.3029.1231.4633.6036.6522.0827.74526.7231.7234.7537.5240.0142.3627.3231.36632.0137.5040.9143.9746.8449.5132.6837.91737.5743.1146.3249.4251.9454.7138.0639.74842.7248.5652.1655.5058.0862.4643.3444.83948.1754.3457.8761.2964.1267.8848.7449.201053.2159.4963.1866.2369.5673.7353.7452.641158.5464.9769.2672.7275.7279.2359.1556.97λTrace1 5.558.6510.4912.2514.2116.26 6.2210.11215.5920.1922.7625.3227.7530.4516.2024.90329.5335.5639.0642.4445.4248.4530.1545.68447.1754.8059.1462.9966.2570.0547.7974.48568.6477.8383.2087.3191.0696.5869.35106.56694.05104.73110.42114.90119.29124.7594.67143.337122.87134.57141.01146.76152.52158.49123.51182.858155.40169.10176.67182.82187.91196.08156.41234.119192.37207.25215.17222.21228.05234.41193.03288.3010231.59247.91256.72263.42270.33279.07232.25345.2311276.34294.12303.13310.81318.02327.45276.88416.98Source:Osterwald-Lenum(1992,table2∗).Reprinted with the permission of BlackwellPublishers.。