高中数学第四章导数应用41函数的单调性与极值利用导数求最值素材北师大版1-1.
高中数学 第四章 导数应用 4.1.2 函数的极值课件7 北师大版选修1-1

K12课件
9
(1)如图是函数 y f x 的图象,试找出函数 y f x的
极值点,并指出哪些是极大值点,哪些是极小值点?
y
x3
a x1 o x2 x4 x5
yy ff' xx x6 b x
答:
(1). x1,x3,x5,x6是函数y=f(x)的极值点,其中x1,x5是 函数y=f(x)的极大值点,x3,x6函数y=f(x)的极小值点。
hx
K12课件
8
(1)极值是一个局部概念。由定义,极值只是某个 点的函数值与它附近点的函数值比较是最大或最小, 并不意味着它在函数的整个定义域内最大或最小。
(2)函数的极值不是唯一的。即一个函数在某区间 上或定义域内极大值或极小值可以不止一个。
(3)极大值与极小值之间无确定的大小关系。即一个 函数的极大值未必大于极小值。
的附近,当 t a 时,函数h(t)单调递 增, h(t) 0 ;当 t a 时,函数h(t)单调递 减, h(t) 0
K12课件
5
f (b) 0
y
f (x) 0 f (x) 0 f (x) 0
ao
f
(a)
b
(0图一)
问题导航:
x
y f x
(1)函数 y f x在点 a, b的函数值与这些点附近的
观察图形并回答以下问题。 h' a 0
h
单调递增
单调递减
h(t) 0
h(t(1)当t=a时,高台跳水运动员距水面的高度最 大,那么函数在t=a处的导数是多少呢? (2)在点t=a附近的图象有什么特点?
2018-2019学年高中数学 第四章 导数应用 4.1.2 函数的极值优质课件 北师大版选修1-1

x
(-∞, 0)
0
(0,25)
2 5
(25,+ ∞)
f′(x) + 不存在 -
0
+
极小值
f(x)
↗
极大值 0
↘
-3 32520
↗
所以函数在 x=0 处有极大值,f(x)极大值=f(0)=0.
3 在 x=25处有极小值,f(x)极小值=f(25)=-3 2520.
(4)定义在[a,b]上的连续函数 f(x)若有极值 f(x0),则 x0∈(a, b).( √ )
2.已知函数 y=f(x)的导函数 y=f′(x)的图像如图,则( A )
A.函数 f(x)有 1 个极大值点,1 个极小值点 B.函数 f(x)有 2 个极大值点,2 个极小值点 C.函数 f(x)有 3 个极大值点,1 个极小值点 D.函数 f(x)有 1 个极大值点,3 个极小值点 解析:由 y=f′(x)图像可知 x2 为 f(x)的极大值点,x3 为 f(x)的 极小值点,x1 和 x4 不是 f(x)的极值点.
(2)P83 例 3.通过本例学习,掌握求可导函数极值的方法和步 骤.
1. 函数的极值的概念 如图 1 所示,在包含 x0 的一个区间(a,b)内,函数 y=f(x)在任 何一点的函数值都小于或等于 x0 点的函数值,称点 x0 为函数
y=f(x)的___极__大__值__点____,其函数值 f(x0)为函数的 ___极__大__值______.
3.可导函数的极值与导数的关系
(1)
x
(a,x0)
x0
f′(x)
+
0
y=f(x)
增加↗ 极大值
(2)
高中数学第四章导数应用4.1.2函数的极值课件北师大版选修1_1

x (-∞,-1) -1 (-1,3) 3
f′(x)
+
0
-
0
Байду номын сангаас
(3,+∞) +
f(x)
增加
极大值 减少 极小值 增加
因此,当 x=-1 时函数取得极大值,且极大值为 f(-1)=10; 当 x=3 时函数取得极小值,且极小值为 f(3)=-22.
(2)函数
f(x)=lnx
x的定义域为(0,+∞),且
2.在包含 x0 的一个区间(a,b)内,函数 y=f(x)在任何一点的函数值都大于 或等于 x0 点的函数值,______为函数 y=f(x)的________,其函数值________为 函数的极小值.
3.函数的________与________统称为极值,________与________统称为极 值点.
图(1)
图(2)
研究函数的零点个数可转化为其图像与 x 轴交点个数问题,也可转化为较熟 悉的两个函数图像的交点问题.用导数可求出函数的单调区间和极值,可以画出 函数草图,通过数形结合来确定交点个数.
[再练一题] 3.若函数 f(x)=exx+a(x>0)的图像与 x 轴恰有一个交点,求 a 的值.
[小组合作型]
求函数的极值
求下列函数的极值. (1)f(x)=x3-3x2-9x+5; (2)f(x)=lnx x. 【精彩点拨】 求导 → 求导函数的零点 → 列表得单调性、极值
【自主解答】 (1)f′(x)=3x2-6x-9.
解方程 3x2-6x-9=0,得 x1=-1,x2=3.
当 x 变化时,f′(x)与 f(x)的变化情况如下表:
[构建·体系]
1.函数 y=f(x)的定义域为(a,b),y=f′(x)的图像如图 4-1-4,则函数 y=f(x)
高中数学第四章导数应用4.1函数的单调性与极值4.1.1导数与函数的单调性导学案北师大版选修1-1
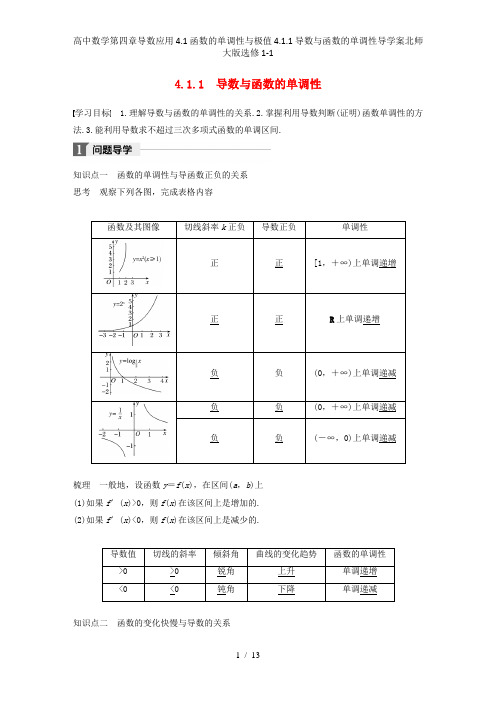
4.1.1 导数与函数的单调性学习目标 1.理解导数与函数的单调性的关系.2.掌握利用导数判断(证明)函数单调性的方.法.3.能利用导数求不超过三次多项式函数的单调区间思考观察下列各图,完成表格内容函数及其图像切线斜率k正负导数正负单调性正正[1,+∞)上单调递增正正R上单调递增负负(0,+∞)上单调递减负负(0,+∞)上单调递减负负(-∞,0)上单调递减梳理一般地,设函数y=f(x),在区间(a,b)上(1)如果f′(x)>0,则f(x)在该区间上是增加的.(2)如果f′(x)<0,则f(x)在该区间上是减少的.导数值切线的斜率倾斜角曲线的变化趋势函数的单调性>0>0锐角上升单调递增<0<0钝角下降单调递减知识点二函数的变化快慢与导数的关系思考我们知道导数的符号反映函数y=f(x)的增减情况,怎样反映函数y=f(x)增减的快慢呢?能否从导数的角度解释变化的快慢呢?答案如图所示,函数y=f(x)在(0,b)或(a,0)内导数的绝对值较大,图像“陡峭”,在(b,+∞)或(-∞,a)内导数的绝对值较小,图像“平缓”.梳理一般地,如果一个函数在某一范围内导数的绝对值较大,那么函数在这个范围内变化得快,这时,函数的图像就比较“陡峭”(向上或向下);反之,函数的图像就“平缓”一些.类型一原函数与导函数的关系例1 已知函数y=f(x)的图像如图所示,则函数y=f′(x)的图像可能是图中的( )答案 C解析由函数y=f(x)的图像的增减变化趋势判断函数y=f′(x)的正、负情况如下表:x (-1,b)(b,a)(a,1)f(x)↘↗↘f′(x)-+-由表可知函数y=f′(x)的图像,当x∈(-1,b)时,函数图像在x轴下方;当x∈(b,a)时,函数图像在x轴上方;当x∈(a,1)时,函数图像在x轴下方.故选C.反思与感悟(1)对于原函数图像,要看其在哪个区间内单调递增,则在此区间内导数值大于零.在哪个区间内单调递减,则在此区间内导数值小于零.根据导数值的正负可判定导函数图像.(2)对于导函数的图像可确定原函数的增减区间及增减快慢.跟踪训练 1 已知y =f ′(x )的图像如图所示,则y =f (x )的图像最有可能是如图所示的( )答案 C解析 由f ′(x )>0(f ′(x )<0)的分界点判断原函数在此分界点两侧的图像的上升和下降趋势.由已知可得x 的取值范围和f ′(x )的正、负,f (x )的增减变化情况如下表所示:x (-∞,0)(0,2) (2,+∞)f ′(x ) + - + f (x )↗↘↗由表可知f (x )在(-∞,0)上是增加的,在(0,2)上是减少的,在(2,+∞)上是增加的,满足条件的只有C ,故选C.类型二 单调区间的求解及单调性证明 命题角度1 求函数的单调区间 例2 求f (x )=3x 2-2ln x 的单调区间. 解 f (x )=3x 2-2ln x 的定义域为(0,+∞). f ′(x )=6x -2x =23x 2-1x=23x -13x +1x, 由x >0,解f ′(x )>0,得x >33. 由x <0,解f ′(x )<0,得0<x <33. ∴函数f (x )=3x 2-2ln x 的单调递增区间为(33,+∞), 单调递减区间为(0,33). 反思与感悟 求函数y =f (x )的单调区间的步骤(1)确定函数y =f (x )的定义域.(2)求导数y ′=f ′(x ).(3)解不等式f ′(x )>0,函数在定义域内的解集上为增函数. (4)解不等式f ′(x )<0,函数在定义域内的解集上为减函数. 跟踪训练2 求函数f (x )=exx -2的单调区间.解 函数f (x )的定义域为(-∞,2)∪(2,+∞). f ′(x )=exx -2-e x x -22=e x x -3x -22.因为x ∈(-∞,2)∪(2,+∞),所以e x>0,(x -2)2>0. 由f ′(x )>0,得x >3,所以函数f (x )的单调递增区间为(3,+∞); 由f ′(x )<0,得x <3.又函数f (x )的定义域为(-∞,2)∪(2,+∞), 所以函数f (x )的单调递减区间为(-∞,2)和(2,3).命题角度2 证明函数的单调性例3 证明函数f (x )=ln xx在区间(0,2)上是单调递增函数.证明 由题意,得f ′(x )=1x·x -ln xx2=1-ln x x2. ∵0<x <2,∴ln x <ln 2<1,1-ln x >0, ∴f ′(x )=1-ln xx2>0. 根据导数与函数单调性的关系,可得函数f (x )=ln x x在区间(0,2)上是单调递增函数.反思与感悟 利用导数证明不等式的一般步骤 (1)构造函数:F (x )=f (x )-g (x ). (2)求导:F ′(x )=f ′(x )-g ′(x ). (3)判断函数的单调性.(4)若F (x )在区间上的最小值大于等于0,则f (x )≥g (x );若F (x )在区间上的最大值小于等于0,则f (x )≤g (x ).跟踪训练3 证明:函数f (x )=sin x x 在区间⎝ ⎛⎭⎪⎫π2,π上是减少的.证明 f ′(x )=x cos x -sin x x 2,又x ∈⎝ ⎛⎭⎪⎫π2,π, 则cos x <0,所以x cos x -sin x <0,所以f ′(x )<0,所以f (x )在⎝ ⎛⎭⎪⎫π2,π上是减少的.类型三 含参数函数的单调性例4 若函数f (x )=kx -ln x 在区间(1,+∞)上是增加的,则k 的取值范围是________. 答案 [1,+∞)解析 由于f ′(x )=k -1x ,f (x )=kx -ln x 在区间(1,+∞)上单调递增⇔f ′(x )=k -1x≥0在(1,+∞)上恒成立.由于k ≥1x ,而0<1x<1,所以k ≥1.即k 的取值范围为[1,+∞). 引申探究试求函数f (x )=kx -ln x 的单调区间. 解 f (x )=kx -ln x 的定义域为(0,+∞),f ′(x )=k -1x,当k ≤0时,函数的单调递减区间为(0,+∞);当k >0时,函数的单调递增区间为(1k ,+∞),单调递减区间为(0,1k).反思与感悟 (1)讨论含有参数的函数的单调性,通常归结为求含参数不等式的解集的问题,而对含有参数的不等式要针对具体情况进行讨论,但始终注意定义域对单调性的影响以及分类讨论的标准.(2)利用导数法解决取值范围问题的两个基本思路①将问题转化为不等式在某区间上的恒成立问题,即f ′(x )≥0(或f ′(x )≤0)恒成立,利用分离参数或函数性质求解参数范围,然后检验参数取“=”时是否满足题意;②先令f ′(x )>0(或f ′(x )<0),求出参数的取值范围后,再验证参数取“=”时f (x )是否满足题意.(3)恒成立问题的重要思路 ①m ≥f (x )恒成立⇒m ≥f (x )max ; ②m ≤f (x )恒成立⇒m ≤f (x )min .跟踪训练4 已知函数f (x )=x 2+2a ln x . (1)试讨论函数f (x )的单调区间;(2)若函数g (x )=2x+f (x )在[1,2]上是减函数,求实数a 的取值范围.解 (1)f ′(x )=2x +2a x =2x 2+2ax,函数f (x )的定义域为(0,+∞).①当a ≥0时,f ′(x )>0,f (x )的单调递增区间为(0,+∞);②当a <0时,f ′(x )=2x +-ax --ax,当x 变化时,f ′(x ),f (x )的变化情况如下表:x (0,-a )-a (-a ,+∞)f ′(x ) - 0+ f (x )递减递增由上表可知,函数f (x )的单调递减区间是(0,-a ); 单调递增区间是(-a ,+∞).(2)由g (x )=2x +x 2+2a ln x ,得g ′(x )=-2x 2+2x +2ax,由已知函数g (x )为[1,2]上的单调减函数, 则g ′(x )≤0在[1,2]上恒成立, 即-2x 2+2x +2ax≤0在[1,2]上恒成立,即a ≤1x-x 2在[1,2]上恒成立.令h (x )=1x-x 2,则h ′(x )=-1x 2-2x =-(1x2+2x )<0,x ∈[1,2],所以h (x )在[1,2]上为减函数,h (x )min =h (2)=-72,所以a ≤-72.故实数a 的取值范围为{a |a ≤-72}.1.f (x )=(x -3)e x的单调递增区间是( ) A.(-∞,2)B.(0,3)C.(1,4)D.(2,+∞)答案 D解析 f ′(x )=e x+(x -3)·e x=(x -2)e x>0, 解得x >2.∴f (x )的单调递增区间是(2,+∞).2.函数y =f (x )在定义域(-32,3)内可导,其图像如图所示,记y =f (x )的导函数为y =f ′(x ),则不等式f ′(x )≤0的解集是( )A.[-13,1]∪[2,3)B.[-1,12]∪[43,83]C.(-32,12)∪[1,2]D.(-32,-1)∪[12,43]∪[83,3]答案 A解析 求f ′(x )≤0的解集,即求函数f (x )在(-32,3)上的单调减区间.由题干图像可知y=f (x )的单调减区间为[-13,1],[2,3).3.若函数f (x )=x 3+2x 2+mx +1在(-∞,+∞)上是增加的,则m 的取值范围是( ) A.m ≥43B.m >43C.m ≤43D.m <43答案 A解析 ∵函数f (x )=x 3+2x 2+mx +1在(-∞,+∞)上是增加的, ∴f ′(x )=3x 2+4x +m ≥0在R 上恒成立, 则判别式Δ=16-12m ≤0,即m ≥43.4.若函数y =f (x )=a (x 3-x )的单调减区间为⎝ ⎛⎭⎪⎫-33,33,则a 的取值范围是________. 答案 (0,+∞)解析 f ′(x )=a (3x 2-1)=3a (x +33)(x -33), 令f ′(x )<0,由已知得-33<x <33, 故a >0.5.已知a >0且a ≠1,证明:函数y =a x-x ln a 在(-∞,0)上是减少的. 证明 y ′=a xln a -ln a =ln a (a x-1), 当a >1时,因为ln a >0,a x<1,所以y ′<0,即y 在(-∞,0)上是减少的; 当0<a <1时,因为ln a <0,a x >1, 所以y ′<0,即y 在(-∞,0)上是减少的. 综上,函数y =a x-x ln a 在(-∞,0)上是减少的.1.导数的符号反映了函数在某个区间上的单调性,导数绝对值的大小反映了函数在某个区间或某点附近变化的快慢程度.2.利用导数求函数f (x )的单调区间的一般步骤: (1)确定函数f (x )的定义域; (2)求导数f ′(x );(3)在函数f (x )的定义域内解不等式f ′(x )>0和f ′(x )<0; (4)根据(3)的结果确定函数f (x )的单调区间.40分钟课时作业一、选择题1.函数y =x cos x -sin x 在下面哪个区间内是增函数( ) A.(π2,3π2)B.(π,2π)C.(3π2,5π2)D.(2π,3π)答案 B解析 y ′=cos x -x sin x -cos x =-x sin x , 若y =f (x )在某区间内是增函数, 只需在此区间内y ′>0恒成立即可, ∴只有选项B 符合题意,当x ∈(π,2π)时,y ′>0恒成立.2.下列函数中,在(0,+∞)上是增函数的是( )A.y =sin xB.y =x e xC.y =x 3-x D.y =ln x -x答案 B解析 显然y =sin x 在(0,+∞)上既有增又有减,故排除A ;对于函数y =x e x ,因为e x恒大于零,易知y =x e x在(0,+∞)内为增函数; 对于C ,y ′=3x 2-1=3(x +33)(x -33), 故函数在(-∞,-33),(33,+∞)上为增函数, 在(-33,33)上为减函数;对于D ,y ′=1x-1 (x >0). 故函数在(1,+∞)上为减函数,在(0,1)上为增函数.故选B.3.设函数f (x )在定义域内可导,y =f (x )的图像如图所示,则导函数f ′(x )的图像可能是( )答案 C解析 原函数的单调性是当x <0时,f (x )单调递增; 当x >0时,f (x )的单调性变化依次为增、减、增,故当x <0时,f ′(x )>0;当x >0时,f ′(x )的符号变化依次为+,-,+.故选C. 4.函数f (x )=ax 3-x 在R 上为减函数,则( ) A.a ≤0 B.a <1 C.a <2 D.a ≤13答案 A解析 f ′(x )=3ax 2-1,由题意知,对∀x ∈R ,3ax 2-1≤0,当a >0时,显然不合题意, 当a ≤0时,成立.故a ≤0.5.函数f (x )的导函数为f ′(x ),若y =f ′(x )的图像如图所示,则f (x )的解析式可能是( )A.y =x 2-2x B.y =13x 3+x 2C.y =x 2+2xD.y =13x 3-x 2答案 B解析 由题图知f ′(x )=0时,x 1=-2,x 2=0,由此可知B 正确.6.已知函数f (x )在定义域R 上为增函数,且f (x )<0,则g (x )=x 2f (x )在(-∞,0)内的单调情况一定是( ) A.单调递减 B.单调递增 C.先增后减 D.先减后增答案 B解析 因为函数f (x )在定义域R 上为增函数, 所以f ′(x )≥0.又因为g ′(x )=2xf (x )+x 2f ′(x ), 所以当x ∈(-∞,0)时,g ′(x )>0恒成立, 所以g (x )=x 2f (x )在(-∞,0)内单调递增.7.函数f (x )=sin x +2xf ′(π3),f ′(x )为f (x )的导函数,令a =-12,b =log 32,则下列关系正确的是( ) A.f (a )>f (b ) B.f (a )<f (b ) C.f (a )=f (b ) D.f (|a |)<f (b )答案 A解析 ∵f ′(x )=cos x +2f ′(π3),∴f ′(π3)=cos π3+2f ′(π3),解得f ′(π3)=-12,∴f (x )=sin x -x ,由f ′(x )=cos x -1≤0知函数f (x )为减函数,而-12<log 32,则f (-12)>f (log 32),即f (a )>f (b ).二、填空题 8.已知函数f (x )=k ex -1-x +12x 2(k 为常数),曲线y =f (x )在点(0,f (0))处的切线与x 轴平行,则f (x )的单调递减区间为____________. 答案 (-∞,0) 解析 f ′(x )=k ex -1-1+x ,∵曲线y =f (x )在点(0,f (0))处的切线与x 轴平行, ∴f ′(0)=k ·e -1-1=0,解得k =e , 故f ′(x )=e x+x -1. 令f ′(x )<0,解得x <0,故f (x )的单调递减区间为(-∞,0).9.若函数f (x )=2x 3-3mx 2+6x 在区间(2,+∞)上为增函数,则实数m 的取值范围为__________. 答案 (-∞,52]解析 ∵f ′(x )=6x 2-6mx +6, 当x ∈(2,+∞)时,f ′(x )≥0恒成立, 即x 2-mx +1≥0恒成立,∴m ≤x +1x恒成立.令g (x )=x +1x ,g ′(x )=1-1x2,∴当x >2时,g ′(x )>0,即g (x )在(2,+∞)上是增加的, ∴m ≤2+12=52.10.函数f (x )的图像如图所示,f ′(x )为函数f (x )的导函数,则不等式f ′xx<0的解集为________.答案 (-3,-1)∪(0,1)解析 由题图知,当x ∈(-∞,-3)∪(-1,1)时,f ′(x )<0,当x ∈(-3,-1)∪(1,+∞)时,f ′(x )>0, 故不等式f ′xx<0的解集为(-3,-1)∪(0,1). 11.如果函数y =f (x )=2x 2-ln x 在定义域内的一个子区间(k -1,k +1)上不是单调函数,那么实数k 的取值范围是________. 答案 [1,32)解析 y =f (x )的定义域为(0,+∞), f ′(x )=4x -1x =4x 2-1x =2x +12x -1x,由f ′(x )>0,得x >12,f (x )的增区间是(12,+∞),由f ′(x )<0,得0<x <12,f (x )的减区间是(0,12),由题意知⎩⎪⎨⎪⎧k -1<12<k +1,k -1≥0,即⎩⎪⎨⎪⎧k -1<12,k +1>12,k -1≥0,得1≤k <32.三、解答题12.若函数f (x )=13x 3-12ax 2+(a -1)x +1在区间(1,4)内为减函数,在区间(6,+∞)内为增函数,试求实数a 的取值范围.解 f ′(x )=x 2-ax +a -1=(x -1)[x -(a -1)], 令f ′(x )=0,得x 1=1,x 2=a -1. 因为f (x )在(1,4)内为减函数, 所以当x ∈(1,4)时,f ′(x )≤0; 因为f (x )在(6,+∞)内为增函数, 所以当x ∈(6,+∞)时,f ′(x )≥0. 所以4≤a -1≤6,解得5≤a ≤7. 所以实数a 的取值范围为[5,7].13.已知二次函数h (x )=ax 2+bx +2,其导函数y =h ′(x )的图像如图,f (x )=6ln x +h (x ).(1)求函数f (x )的解析式;(2)若函数f (x )在区间(1,m +12)上是单调函数,求实数m 的取值范围.解 (1)由已知,h ′(x )=2ax +b ,其图像为直线,且过(0,-8),(4,0)两点, 把两点坐标代入h ′(x )=2ax +b ,∴⎩⎪⎨⎪⎧8a +b =0,b =-8, 解得⎩⎪⎨⎪⎧a =1,b =-8,∴h (x )=x 2-8x +2,h ′(x )=2x -8, ∴f (x )=6ln x +x 2-8x +2. (2)f ′(x )=6x+2x -8=2x -1x -3x(x >0).当x 变化时,f ′(x ),f (x )的变化情况如下表:x (0,1) 1 (1,3) 3 (3,+∞)f ′(x ) + 0- 0+ f (x )↗↘↗∴f (x )的单调递增区间为(0,1)和(3,+∞),f (x )的单调递减区间为(1,3).要使函数f (x )在区间(1,m +12)上是单调函数,则⎩⎪⎨⎪⎧1<m +12,m +12≤3,解得12<m ≤52.即实数m 的取值范围为(12,52].。
高二数学-1第四章 第1节 函数的单调性与极值北师大版选修知识精讲

高二数学-1第四章第1节函数的单调性与极值北师大版选修1【本讲教育信息】一、教学内容第四章第1节函数的单调性与极值二、教学目标1、理解可导函数的单调性与其导数的关系;2、理解并掌握极值的概念。
了解可导函数在某点取得极值的必要条件和充分必要条件。
3、能利用函数导数判断简单函数的单调性,会求简单的函数的单调区间和极值。
三、教学重、难点函数的单调性与其导数的关系的理解、极值的概念的理解是教学的重点,判断函数的单调性,求函数的极值是教学的难点。
四、知识要点分析:(一)函数的单调性与函数的导数的关系函数。
某个区间内,函数f (x )的导数f '(x )>0,则在这个区间上f (x )单调递增。
某个区间内,函数f (x )的导数f '(x )<0,则在这个区间上f (x )单调递减。
反之,某个区间内,函数f (x )单调递增,则在这个区间上f (x )的导数f '(x )≥0; 某个区间内,函数f (x )单调递减,则在这个区间上f (x )的导数f '(x )≤0 例如函数f (x )=x 3,在R 上单调递增,其导函数在R 上,f '(x )≥0.(二)求可导函数y=f (x )的单调区间的步骤:(1)确定函数定义域(2)求f '(x )并将f '(x )通分或分解因式,将之化为乘积或商的形式。
(3)解不等式f '(x )≥0(或f '(x )≤0) (4)确认并写出单调区间(三)极值的定义:一般地,设函数)(x f y =在0x x =及其附近有定义,如果)(0x f 的值比0x 附近所有各点的函数值都大,我们说 f (0x )是函数)(x f y =的一个极大值;如果)(0x f 的值比0x 附近所有各点的函数值都小,我们说f (0x )是函数)(x f y =的一个极小值。
极大值与极小值统称极值。
取得极值的点称为极值点,极值点是自变量的值,极值指的是函数值。
高中数学 第四章 导数应用 4.1.2 函数的极值课件 北师大版选修1-1.ppt

[再练一题] 1.求函数 f(x)=x22+x 1-2 的极值.
【导学号:63470080】
【解】 函数的定义域为 R.
f′(x)=2x2x+2+11-24x2=-2x-x21+1x+2 1.
令 f′(x)=0,得 x=-1 或 x=1.
列表:
x (-∞,-1) -1 (-1,1) 1 (1,+∞)
f′(x)=1-xl2n
x .
令 f′(x)=0,得 x=e.
当 x 变化时,f′(x)与 f(x)的变化情况如下表:
x (0,e) e (e,+∞)
f′(x) +
0
-
f(x) 增加 极大值 减少
故当 x=e 时函数取得极大值,且极大值为 f(e)=1e.
求函数 y=fx的极值点的步骤: 1求出导数 f′x. 2解方程 f′x=0. 3对于方程 f′x=0 的每一个解 x0,分析 f′x在 x0 左、右两侧的符号 即 fx的单调性,确定极值点: ①若 f′x在 x0 两侧的符号“左正右负”,则 x0 为极大值点; ②若 f′x在 x0 两侧的符号“左负右正”,则 x0 为极小值点.
【答案】 D
教材整理 2 函数极值的判定 阅读教材 P84 至 P85“例 3”以上部分,完成下列问题. 1.单调性判别 (1)如果函数 y=f(x)在区间(a,x0)上是________,在区间(x0,b)上是________, 则 x0 是极大值点,f(x0)是极大值. (2)如果函数 y=f(x)在区间(a,x0)上是________,在区间(x0,b)上是________, 则 x0 是极小值点,f(x0)是极小值.
4.极值是函数在一个适当区间内的________性质,函数的某些极大值有时 候比其他极大值小,有时候可能比一些极小值还小.
高中数学第四章导数应用1函数的单调性与极值1.2函数的极值课件北师大版选修1-1

-1a,且极大值为ln-1a-1.
对于含参数函数的极值,若参数对函数的单调性(即导数的正负)有影响,需对参数分类 讨论.
3.已知函数f(x)=x-2x+a(2-ln x)(a>0),求函数f(x)的单调区间与极值点. 解析:f(x)的定义域是(0,+∞),f′(x)=1+x22-ax=x2-xa2x+2. 设g(x)=x2-ax+2,对于二次方程g(x)=0, 判别式Δ=a2-8. ①当Δ=a2-8<0,即0<a<2 2 时,对一切x>0都有f′(x)>0,此时f(x)在(0,+∞)上是 增函数,无极值点. ②当Δ=a2-8=0,即a=2 2 时,仅对x= 2 有f′(x)=0,对其余的x>0都有 f′(x)>0,此时f(x)在(0,+∞)上也是增函数,无极值点.
[解析] 由已知得f(x)的定义域为{x|x>0}, f′(x)=2ax+2x=2axx2+1. ①当a>0时,f′(x)>0, ∴y=f(x)为(0,+∞)上的增函数, 此时f(x)无极值.
②当a<0时, 令f′(x)=0可得:2axx2+1=0, 即ax2+1=0, ∴x2=-1a, ∴x= -1a或- -1a. 又∵- -1a∉(0,+∞), ∴x= -1a.
= 33时,f(x)取得极小值.从而f(x)的极小值点为x= 33,无极大值点,选B. 答案:B
4.函数y=2x3-15x2+36x-24的极大值为________,极小值为________. 解析:y′=6x2-30x+36,即y′=6(x-2)(x-3),令y′=0,得x=2或x=3, 经判断极大值为f(2)=4,极小值为f(3)=3. 答案:4 3
2.在f(x0)存在时,f′(x0)=0只是函数f(x)在x0处有极值的必要不充分条件,必须 再加上在x0左右两侧导数的符号相反,才能断定函数在x0处取得极值,反映在解题 上,错误判断极值点或漏掉极值点是经常出现的错误.
高中数学第四章导数应用4.1.2函数的极值课件北师大版选修1-1

4.求可导函数 y=f(x)极值点的步骤 (1)确定函数的定义区间,求导数 f′(x). (2)求 f(x)的拐点,即求方程 f′(x)=0 的根. (3)利用 f′(x)与 f(x)随 x 的变化情况表,根据极值点左右两侧 单调性的变化情况求极值.
1.判断正误(正确的打“√”,错误的打“×”) (1)导数值为 0 的点一定是函数的极值点.( × ) (2)在可导函数的极值点处,切线与 x 轴平行.( × ) 1 (3)函数 f(x)= 无极值.( √ ) x (4)定义在[a,b]上的连续函数 f(x)若有极值 f(x0),则 x0∈(a, b).( √ )
2.已知函数 y=f(x)的导函数 y=f′(x)的图像如图,则( A )
A.函数 f(x)有 1 个极大值点,1 个极小值点 B.函数 f(x)有 2 个极大值点,2 个极小值点 C.函数 f(x)有 3 个极大值点,1 个极小值点 D.函数 f(x)有 1 个极大值点,3 个极小值点 解析:由 y=f′(x)图像可知 x2 为 f(x)的极大值点,x3 为 f(x)的
1 - e 4.设函数 f(x)=xln x,则 f(x)的极小值为________ .
解析:f(x)的定义域为(0,+∞),f′(x)=ln x+1, 1 1 令 f′(x)=0 即 ln x+1=0 得 x= , 当 x∈(0, )时, f′(x)<0, e e 1 1 1 1 1 当 x∈e,+∞时,f′(x)>0,故当 x= 时,fe = ln = e e e 1 - 为 f(x)的极小值. e
极小值 ____________ .
极值 , 极大值与极小值统称为___________ 极大值点与极小值点统 极值点 . 称为________
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
利用导数求最值导数是研究数学和其他自然科学的基础,是研究客观事物变化率和优化问题的有利工具,研究导数,有利于对数学的本质和价值的认识。
导数的工具性已渗透到数学的很多分支,在函数的研究中得到充分的体现,主要涉及到研究曲线的切线问题、函数的单调性、函数的极值、最值等。
下面就利用导数求最值作一阐述,供参考。
一、函数的最大值与最小值在闭区间[b a ,]上连续,在(b a ,)内可导,)(x f 在[b a ,]上求最大值与最小值的步骤:先求 )(x f 在(b a ,)内的极值;再将)(x f 的各极值与)(a f 、)(b f 比较,其中最大的一个是最大值,最小的一个是最小值。
求可导函数极值的步骤:首先:求导数)('x f ;再求导数)('x f =0的根;最后:检查)('x f 在方程根左右的值的符号,如果左正右负,那么)(x f 在这个根处取极大值;如果左负右正,那么)(x f 在这个根处取极小值。
二、利用导数求最值例1、设0>x ,求32)1(32)1(211ln -+--+x x x x 的最小值。
解:设32)1(32)1(211ln )(-+--+=x x x x x f ,则2222)1(2)1()1(1)1(2)1(11)(-+---=-+---='x x x xx x x x x f⎪⎭⎫⎝⎛+--=⎥⎦⎤⎢⎣⎡-+--=⎥⎦⎤⎢⎣⎡-+--=2222212)1()1(21)1()1(211)1(x x x x x x x x x x.12)1(23xx x +-= 令0)(='x f ,由0>x ,解得1=x 。
列表:由表可知,当1=x 时,)(x f 有最小值1。
评注:利用导数求最值,先确定函数的极值是关键,同时,最值通常应在极值及端点处取得。
当函数f (x )为连续函数且在[]b a ,上单调时,其最大值、最小值在端点处取得;当连续函数f (x )在(a ,b )内只有一个可疑点时,若在这一点处f (x )有极大(小)值,则可以判定f (x )在该点处取得最大(小)值,这里(a ,b )也可以是无穷区间。
练习1:已知a ≥ 0,函数f (x )=(x 2-2ax )e x,当x 为何值时,f (x )取得最小值?并证明你的结论; 三、利用导数求最值的运用 (一)求函数的值域例2 、求函数x x x x f --++=4325)(的值域.解:由⎩⎨⎧≥-≥+0403x x 得)(x f 的定义域为43≤≤-x 。
因为0421315)4()32()5()(>++++='--'++'='='x x x x x x f y ,所以)(x f 在[]4,3-上单调递增,故当3-=x 时,4,715=--=x y 最小时,7220+=最大y 。
所以值域为[]7220,715+--。
评注:求函数的值域转化为求)(x f 在闭区间[]4,3-上的最大值和最小值的问题,考虑其单调性易求值域,必须注意函数的定义域。
练习2:已知x ,y 为正实数,且满足关系式04222=+-y x x ,求xy 的最大值。
(二)利用最值求参数的值(或范围) 例3、设132<<a ,函数)11(23)(23≤≤-+-=x b ax x x f 的最大值为1,最小值为26-,求a ,b 的值。
解:)(333)('2a x x ax x x f -=-=,当x 变化时,)(),('x f x f 变化情况列表如下:当x=0时,f (x )取极大值b ,而)()0(a f f >,)1()1(f f <-,故需比较f (0)与f (1)的大小。
∵0123)1()0(>-=-a f f ,∴f (x )最大值为f (0)=b=1。
又0)2()1(21)23(21)()1(23<-+=--=--a a a a a f f 。
∴)1()(min -=f x f ,∴2623123-=-=+--a b a ,∴1,36==b a 。
评注:这是一道求函数的最值的逆向思维问题。
本题的关键是比较极值和端点处的函数值的大小,列表解题一目了然,从而确定出a ,b 的值。
(三)利用最值研究恒成立问题 例4、设函数,5x 2x 21x )x (f 23+--=若对于任意]2,1[x -∈都有m )x (f <成立,求实数m 的取值范围。
解: ,2x x 3)x (f 2--='令,0)x (f ='得32x -=或1x =。
∵当32x -<或1x >时,,0)x (f >'∴)x (f y =在)32,(--∞ 和),1(∞+ 上为增函数, 在)1,32( -上为减函数,∴)x (f 在32x -=处有极大值,在1x =处有极小值。
极大值为27225)32(f =-, 而7)2(f =, ∴)x (f 在]2,1[ -上的最大值为7。
若对于任意x ]2,1[ -∈都有m )x (f <成立, 得m 的范围 7m >。
评注:利用最值可以研究一类恒成立问题,一般地,f(x)≥a 对x ∈R 恒成立⇔ f(x)的最小值≥a 成立;f(x)≤a 对x ∈R 恒成立⇔f(x)的最大值≤a 成立。
练习2:已知函数32()f x x ax bx c =+++在23x =-与x =1时都取得极值。
⑴求a 、b 的值;⑵若对2[1,2],()x f x c ∈- 恒成立,求c 的取值范围。
四、利用最值证明不等式例5、已知)0()(3≠++=a d cx ax x f 是R 上的奇函数,当x=1时,f(x)取得极值-2。
(1)求 f(x)的单调区间和极大值;(2)对任意)1,1(,21-∈x x ,求证:不等式4)()(21<-x f x f 恒成立。
解:(1)∵f(x)是奇函数,R x ∈, ∴f(0)=0, ∴d=0因此c ax x f cx ax x f +=+=2'33)(,)( 由条件f(1)=-2为f(x)的极值,∴f ,(1)=0,∴⎩⎨⎧=+-=+032c a c a ,解之得:a=1,c=-3则33)(,3)(2'3-=-=x x f x x x f , 令0)('=x f ,得1±=x∴f(x)的单调减区间是[-1,1],f(x)的单调增区间是(][)∞+-∞-,和11,当x=-1时,f(x)有极大值2。
(2)证明:由(1)知f(x)在[-1,1]上是减函数,且f(x)在[-1,1]上有最大值f(-1)=2,有最小值f(1)=-2∴对任意)1,1(,21-∈x x , 恒有4)1()1()()(21=--<-f f x f x f评注:本题(2)借助于最值证明不等式,最值的研究利用了导数法,同时对于可导函数,某点为极值点的必要条件是这点的导数为0;某一点是极值点的充分条件是在这点两侧的导数异号。
此外,函数的极值点也可能是不可导点。
附练习答案:1、解:(1)对函数f (x )求导数,得 f′(x )=(x 2-2ax )e x+(2x -2a )e x=[x 2+2(1-a )x-2a ]e x。
令f′(x )=0,得[x 2+2(1-a )x-2a ]e x=0,从而x 2+2(1-a )x -2a =0。
解得2111a a x +--=2211a a x ++-=,其中x 1<x 2。
当x 变化时,f′(x ),f (x )的变化如下表: x (-∞ ,x 1 )x 1 ( x 1 , x 2)x 2 (x 2 ,+∞)f ′(x ) +0 — 0 + f (x )极大值极小值当f (x )在x =x 1处取到极大值,在x =x 2处取到极小值.当a≥0时,x 1<-1,x 2 ≥0,f (x )在(x 1,x 2)为减函数,在(x 2,+∞)为增函数. 而当x <0时,f (x )=x (x -2a )e x>0; 当x =0时,f (x )=0. 所以当211a a x ++-=时,f (x )取得最小值。
2、解:由题意,)20(2212≤<-=x x x x xy ,设f (x ))20(2212≤<-=x x x x 。
当20<<x 时,222)23()('x x x x x f --=,令0)('=x f ,得23=x 或x=0(舍去)。
当x 在(]2,0内变化时,y /,y 有如下变化情况:由上表可知,当x=23时,f (x )最大值为833,亦即xy 的最大值为833。
3、解:⑴1,22a b =-=-; ⑵令32321()22g x x ax bx x x x =++=--,故对任意2[1,2],()x g x c c ∈-- 恒成立。
∵2()32(1)(2)g x x x x x '=--=-+,列表知对任意[1,2]x ∈-,y =()g x 的最大值为g(2)=2,∴2<c 2-c ,得c <-1或c >2。
