小学奥数几何图形经典方法
奥数解谜立体几何中的难题

奥数解谜立体几何中的难题立体几何是奥数中的一个重要分支,它与点、线、面相比,更加复杂和有趣。
解决立体几何难题需要学生具备良好的想象力、逻辑思维和空间想象能力。
本文将重点探讨奥数解谜立体几何中的一些难题,以及解决这些难题的方法。
第一部分:平面与立体的关系在立体几何中,我们经常需要将二维平面转化为三维立体,并理解它们之间的关系。
其中一个经典的难题是给定一个底面视图和一个侧面视图,要求确定对应的立体图形。
解决这个难题可以按照以下步骤进行:1. 观察底面视图和侧面视图,找出每个图形的特点和规律;2. 根据底面视图中的点、线、面的位置,将其转化为立体中的点、线、面;3. 根据侧面视图中的高度信息,确定立体图形的高度;4. 综合底面和侧面的信息,确定立体图形的形状和大小。
第二部分:直方体的拼装问题直方体是解谜立体几何中常见的图形。
一个常见的难题是给定一些尺寸相同的立方体块,要求用这些块拼出一个大的立方体。
解决这个难题可以按照以下步骤进行:1. 观察每个立方体块的形状和特点,找出它们之间的联系;2. 根据大立方体的尺寸确定需要多少个立方体块;3. 将每个立方体块按照规律进行拼装,注意保持块与块之间的相邻面接触。
第三部分:平行四边形的性质在立体几何中,平行四边形是常见的一个图形。
一个经典的难题是给定一个平行四边形,要求根据已有信息计算出其他未知的性质。
解决这个难题可以按照以下步骤进行:1. 观察平行四边形的特点,如平行边、角的性质等;2. 利用平行四边形的性质求解已知信息;3. 根据已知信息推导出其他未知的性质。
第四部分:圆锥体与圆台的体积计算圆锥体和圆台是奥数解谜立体几何中的另一个重要内容。
一个常见的难题是给定一个圆锥体或圆台,要求计算其体积。
解决这个难题可以按照以下步骤进行:1. 观察圆锥体或圆台的特点,了解它们的形状和性质;2. 根据已知信息计算出底面的面积和高度;3. 根据体积的计算公式,将已知信息代入计算。
六年级奥数平面几何常用技巧

平面几何常用技巧【加油站】常有正多边形:正三正方形正五边正六正八边形正十边形正十二角形形边形边形图形内角和每个内角【加油站】正十二边形的做法:一、做正六边形二、以正六边形每边为边长向外做六个正方形三、依次连接正方形外面的十二个极点。
则所构成的是正十二边形。
【例 1】(★★★)125 平方厘米,那么【例 2】(★★★)1 厘米,空白部分是等边以下列图,正八边形中的阴影部分面积是以下列图,一个正十二边形的边长是正八边形的面积是多少?三角形,一共有 12 个.请算出阴影部分的面积.1cm1【例 3】(★★★★)如右图,正十二边形和中心白色的正六边形的边长均为 12,图中阴影部分的面积 _________。
【例 5】(★★★★)如图,三角形 ABC 是等腰直角三角形, P 是三角形外的一点,其中 AP = 10 厘米,∠BPC =90°,求四边形 ABPC 的面积.QDBCP 【例 4】(★★★)依照图中的样子,在一平行四边形纸片上割去了甲、乙两个直角三角形.已知甲三角形两条直角边分别为 2 和 4,乙三角形两条直角边分别为 3 和 6,求图中阴影部分的面积.甲43乙6【例 6】(★★★)以下列图的四边形 ABCD 中,∠A=∠C=45°∠ABC=105 °, AB= CD =10 厘米,连接对角线,∠ABD =30°.求四边形 ABCD 的面积.CDA2【例 7】 (★★)6 厘米,小正方形边长是 4 厘米,两块阴【例 8】(★★★)华杯赛复赛试题10 厘米, 则阴影部分的面积为多少如图,大正方形边长是右图中的正方形的边长为影的面积差是多少?平方厘米?【本讲总结】一、特别图形的性质二、割补法、差不变:化不可以求为可求三、平移、旋转、对称:动向几何——改变地址不改变形状重点例题:例 3、例 4、例 5 、例 6、例 83。
小学数学几何图形学习技巧归纳

小学数学几何图形学习技巧归纳无论是在小学阶段还是在更高年级的学习中,几何图形都是数学学科中非常重要的一部分。
几何图形不仅帮助我们认识和理解空间,还能提高我们的空间想象力和问题解决能力。
在小学数学几何图形学习中,掌握一些技巧和归纳总结将会对学习产生积极的影响。
本文将为您介绍一些小学数学几何图形学习的技巧和归纳。
首先,我们需要掌握常见的几何图形。
在小学阶段,常见的几何图形包括线段、直线、射线、角、三角形、四边形、圆等。
了解这些几何图形的定义和性质非常重要。
线段是由两个端点确定的一段直线段,直线是连续的、无限延伸的线段,射线是由一个端点和一个方向确定的一段直线。
角是由两条射线共享一个端点形成的图形,三角形是由三条线段围成的图形,四边形是由四条线段围成的图形,圆是由一条曲线和圆心确定的图形。
通过掌握这些基本几何图形的定义,可以在学习中更好地理解和运用。
其次,我们需要学会通过观察和比较来归纳总结几何图形的性质。
比较不同几何图形的性质,可以帮助我们发现它们之间的共同点和特征。
例如,观察三角形的边和角可以发现,等边三角形的三条边相等,等腰三角形的两边相等,直角三角形的一个角为90度。
通过观察和比较,我们可以归纳出三角形的性质。
类似地,我们还可以比较四边形、圆等几何图形的性质,通过归纳总结形成对它们的深入理解。
再次,我们需要练习几何图形的画法和测量。
在学习几何图形的过程中,绘制图形是非常重要的一部分。
通过练习画图,可以提高我们对几何图形的认识和理解。
绘制图形时,我们需要掌握一些基本的画法和测量技巧。
例如,当我们需要画一个等边三角形时,可以使用直尺和量角器来辅助绘制。
对于圆的绘制,可以使用罗盘或者定圆规来帮助画出一个完美的圆。
通过练习几何图形的画法和测量,我们可以提高我们的技能和创造力。
此外,我们还需要学会运用几何图形解决问题。
几何图形不仅是一种美丽的图形表达方式,它们也是解决实际问题的有力工具。
在学习中,我们经常会遇到需要运用几何图形解决问题的情况。
2019-2020学年小学平面几何图形的十大解法.doc

几何图形的十大解法(30例)一、分割法例1:将两个相等的长方形重合在一起,求组合图形的面积。
(单位:厘米)2例2:下列两个正方形边长分别为8厘米和5厘米,求阴影部分面积。
例3:左图中两个正方形的边长分别为8厘米和6厘米。
求阴影部分面积。
二、添辅助线例1:已知正方形边长4厘米,A、B、C、D是正方形边上的中点,P是任意一点。
求阴影部分面积。
CPD BA例2:将下图平行四边形分成三角形和梯形两部分,它们面积相差40平方厘米,平行四边形底20.4厘米,高8厘米。
梯形下底是多少厘米?例3:平行四边形的面积是48平方厘米,BC分别是A 这个平行四边形相邻两条边的中点,连接A、B B、C得到4个三角形。
求阴影部分的面积。
C三、倍比法例1: A B 已知:OC=2AO,S ABO=2㎡,求梯形ABCD O 的面积。
D C例2:7.5 已知:S阴=8.75㎡,求下图梯形的面积。
2.5例3: A 下图AB是AD的3倍,AC是AE的5倍,D E 那么三角形ABC的面积是三角形ADE的多少倍?B C四、割补平移例1: A B 已知:S阴=20㎡,EF为中位线E F 求梯形ABCD的面积。
D C例2:10 求左图面积(单位:厘米)5510例3:把一个长方形的长和宽分别增加2a 2 厘米,面积增加24平方厘米。
求原长方形的周长。
五、等量代换例已知:AB平行于EC,求阴影部分面积。
C8E 10 D(单位:m)例2:下图两个正方形边长分别是6分米、4分米。
求阴影部分面积。
例3AED的面积(形状大小都相同),BDF和三角形CEF的面积大小。
()A A 三角形DBF大B三角形CEF大D C C两个三角形一样大D无法比较B FE六、等腰直角三角形例1:已知长方形周长为22厘米,长7 厘米,求阴影部分面积。
45°例2:已知下列两个等腰直角三角形,直角边分别是10厘米和6厘米。
求阴影部分的面积。
2例3:下图长方形长9厘米,宽6厘米,求阴影部分A B 面积。
几何图形的九大解法
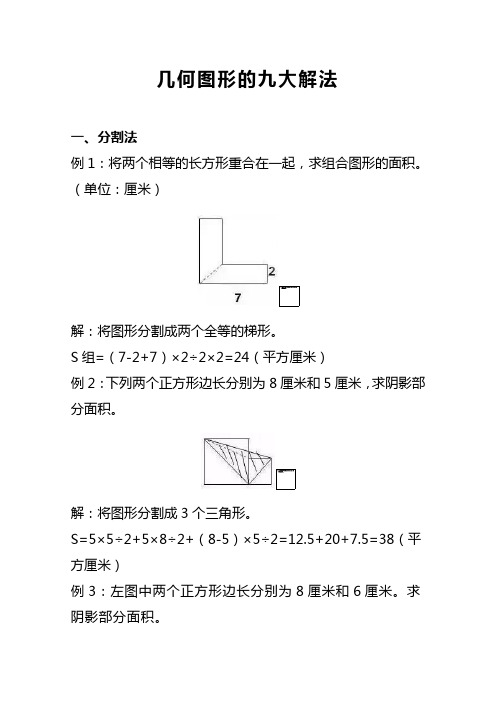
几何图形的九大解法一、分割法例1:将两个相等的长方形重合在一起,求组合图形的面积。
(单位:厘米)解:将图形分割成两个全等的梯形。
S组=(7-2+7)×2÷2×2=24(平方厘米)例2:下列两个正方形边长分别为8厘米和5厘米,求阴影部分面积。
解:将图形分割成3个三角形。
S=5×5÷2+5×8÷2+(8-5)×5÷2=12.5+20+7.5=38(平方厘米)例3:左图中两个正方形边长分别为8厘米和6厘米。
求阴影部分面积。
解:将阴影部分分割成两个三角形。
S阴=8×(8+6)÷2+8×6÷2=56+24=80(平方厘米)二、添辅助线例1:已知正方形边长4厘米,A、B、C、D是正方形边上的中点,P是任意一点。
求阴影部分面积。
解:从P点向4个定点添辅助线,由此看出,阴影部分面积和空白部分面积相等。
S阴=4×4÷2=8(平方厘米)例2:将下图平行四边形分成三角形和梯形两部分,它们面积相差40平方厘米,平行四边形底20.4厘米,高8厘米。
梯形下底是多少厘米?解:因为添一条辅助线平行于三角形一条边,发现40平方厘米是一个平行四边形。
所以梯形下底:40÷8=5(厘米)例3:平行四边形的面积是48平方厘米,BC分别是这个平行四边形相邻两条边的中点,连接A、B、C得到4个三角形。
求阴影部分的面积。
解:如果连接平行四边形各条边上的中点,可以看出空白部分占了整个平行四边形的八分之五,阴影部分占了八分之三。
S阴=48÷8×3=18(平方厘米)三、倍比法例1:已知OC=2AO,SABO=2㎡,求梯形ABCD的面积。
解:因为OC=2AO,所以SBOC=2×2=4(㎡)SDOC=4×2=8(㎡)SABCD=2+4×2+8=18(㎡)例2:已知S阴=8.75㎡,求下图梯形的面积。
小学奥数经典专题点拨:几何图形计数

几何图形的计数【点与线的计数】例1如图5.45,每相邻的三个圆点组成一个小三角形,问:图中是这样的小三解形个数多还是圆点的个数多?(全国第二届“华杯赛”决赛试题)讲析:可用“分组对应法”来计数。
将每一排三角形个数与它的下行线进行对应比较。
第一排三角形有1个,其下行线有2点;第二排三角形有3个,其下行线有3点;第三排三角形有5个,其下行线有4点;以后每排三角形个数都比它的下行线上的点多。
所以是小三角形个数多。
例2直线m上有4个点,直线n上有5个点。
以这些点为顶点可以组成多少个三角形?(如图5.46)(哈尔滨市第十一届小学数学竞赛试题)讲析:本题只要数出各直线上有多少条线段,问题就好解决了。
直线n 上有5个点,这5点共可以组成4+3+3++2+1+1==10(条)线段。
以这些线段分别为底边,m 上的点为顶点,共可以组成4×1×100=40(个)三角形。
同理,m 上4个点可以组成6条线段。
以它们为底边,以n 上的点为顶点可以组成6×5×5==30(个)三角形。
所以,一共可以组成70个三角形。
【长方形与三角形的计数】例1图5.47中的正方形被分成9个相同的小正方形,个相同的小正方形,它们一共有它们一共有16个顶点,个顶点,以其中不在一条直线上的以其中不在一条直线上的3点为顶点,点为顶点,可以构成三角形。
可以构成三角形。
可以构成三角形。
在这些在这些三角形中,与阴影三角形有同样大小面积的有多少个?(全国第三届“华杯赛”复赛试题)为3的三角形,或者高为2,底为3的三角形,都符合要求。
①底边长为2,高为3的三角形有2×4×4×4×4×4==32(个); ②高为2,底边长为3的三角形有8×2×2==16(个)。
所以,包括图中阴影部分三角形共有48个。
例2 图5.48中共有_中共有_______个三角形。
三年级奥数:图形规律

三年级奥数:图形规律知识定位找规律是解决数学问题的一种重要的手段,而规律的找寻既需要敏锐的观察力,又需要严密的逻辑推理能力.知识梳理一般地说,在观察图形变化规律时,应抓住一下几点来考虑问题:(1)图形数量的变化;(2)图形形状的变化;(3)图形大小的变化;(4)图形颜色的变化;(5)图形位置的变化;(6)图形繁简的变化.对于较复杂的图形,也可分为几部分来分别考虑,总而言之,只要全面观察,勤于思考就一定能抓住规律,解决问题.关于解决图形规律问题的常用方法:1、从图形数量、位置变化出发观察思考几何图形的规律2、从图形形状、大小变化发现寻找图形的变化规律3、掌握寻找复杂图形变化规律的方法图形规律问题的分类:1、从图形形状、大小、颜色变化发现寻找图形的变化规律2、从图形数量、位置变化出发观察思考几何图形的规律3、复杂图形变化规律竞赛考点挖掘1.从图形形状、大小、颜色变化发现寻找图形的变化规律题目2.从图形数量、位置变化出发观察思考几何图形的规律题目3.复杂图形变化规律题目例题精讲【题目】请找出下面哪个图形与其他图形不一样.【题目】根据左边图形的关系,画出右边图形的另一半.(1)(2)(3)【题目】在下面图形中找出一个与众不同的.【题目】按照下列图形的变化规律,空白处应是什么样的图形??【题目】如图,根据图中已知3个方格表中阴影的规律,在空白的方格表中也填上相应的阴影.【题目】观察图形变化规律,在右边补上一幅,使它成为一个完整系列【题目】观察图中所给出图形的变化规律,然后在空白处填画上所缺的图形.【题目】请观察下图中已有的几个图形,并按规律填出空白处的图形.【题目】下图中的图形是按一定规律排列的,请仔细观察,并在“?”处填上适当的图形.【题目】观察下列各组图的变化规律,并在“?”处画出相关的图形. (1)(2)【题目】观察下图中的点群,请回答:(1) 方框内的点群包含多少个点? (2) 推测第10个点群中包含多少个点? (3) 前10个点群中,所有点的总数是多少????ihgfedcba【题目】仔细观察下图中图形的变化规律,并在“?”处填入合适的图形.【题目】将“猫”“狗”“兔”“鸡”“猴”“虎”六个动物名称分别写在六个正方体的六个面上,从下面三种不同摆法中,判断这个正方体上哪些动物名名称分别写在相对面上.edcba??【题目】图10—1是由9个小人排列的方阵,但有一个小人没有到位,请你从下面图10—2中的6个小人中,选一位小人放到问号的位置,你认为最合适的人选是几号?【题目】四个小动物排座位,一开始,小鼠坐在第1号位子上,小猴坐在第2号,小兔坐在第3号,小猫坐在第4号.以后它们不停地交换位子,第一次上下两排交换.第二次是在第一次交换后左右两列交换,第三次再上下两排交换,第四次再左右两列交换…这样一直换下去.问:第十次交换位子后,小兔坐在第几号位子上?习题演练【题目】顺序观察给出图形的变化,按照这种变化规律,在空格中填上应有的图形【题目】根据下列图形的变化规律,接着画下去.【题目】请找出下面哪个图形与其他图形不一样【题目】观察图形变化规律,在右边再补上一幅,使它们成为一个完整的系列.【题目】仔细观察下列图形的变化,请先回答:(1)在方框(4)中应画出怎样的图形?(2)再按(1)、(2)、(3)、……的顺序数下去,第(10)个方框是怎样的图形?。
小升初经典题型—小学平面几何图形的十大解法

几何图形的十大解法(30例)一、分割法例1:将两个相等的长方形重合在一起,求组合图形的面积。
(单位:厘米)2例2:下列两个正方形边长分别为8厘米和5厘米,求阴影部分面积。
例3:左图中两个正方形的边长分别为8厘米和6厘米。
求阴影部分面积。
二、添辅助线例1:已知正方形边长4厘米,A、B、C、D是正方形边上的中点,P是任意一点。
求阴影部分面积。
CPD BA例2:将下图平行四边形分成三角形和梯形两部分,它们面积相差40平方厘米,平行四边形底20.4厘米,高8厘米。
梯形下底是多少厘米?例3:平行四边形的面积是48平方厘米,BC分别是A 这个平行四边形相邻两条边的中点,连接A、B B、C得到4个三角形。
求阴影部分的面积。
C三、倍比法例1: A B 已知:OC=2AO,S ABO=2㎡,求梯形ABCDO 的面积。
D C例2:7.5 已知:S阴=8.75㎡,求下图梯形的面积。
2.5例3: A 下图AB是AD的3倍,AC是AE的5倍,D E 那么三角形ABC的面积是三角形ADE的多少倍?B C四、割补平移例1: A B 已知:S阴=20㎡, EF为中位线E F 求梯形ABCD的面积。
D C例2:10 求左图面积(单位:厘米)5510例3:把一个长方形的长和宽分别增加2厘米,面积增加24平方厘米。
求原长方形的周长。
2五、等量代换例已知:AB平行于EC,求阴影部分面积。
8E 10 D(单位:m)例2:下图两个正方形边长分别是6分米、4分米。
求阴影部分面积。
例3:已知三角形ABC的面积等于三角形AED的面积(形状大小都相同),它们重叠在一起,比较三角形BDF和三角形CEF的面积大小。
()A A 三角形DBF大B三角形CEF大D C C两个三角形一样大D无法比较B FE六、等腰直角三角形例1:已知长方形周长为22厘米,长7 厘米,求阴影部分面积。
45°例2:已知下列两个等腰直角三角形,直角边分别是10厘米和6厘米。
