山东建筑大学2009~2010学年第1学期
山东建筑大学概率论历年试题汇总

山东建筑大学历年概率论试题汇总···········································································································装 订线··································································································山东建筑大学试卷 共 3 页 第 1 页2009至2010第 1 学期 课程名称 概率论与数理统计 试卷 (A ) 专业: 理工科各专业考试性质: 闭卷 考试时间 120 分钟 题号 一 二 三 总分 分数一、 填空题(每题3分,共24分)1、 掷两颗骰子,已知两颗骰子的点数之和为6,则其中有一颗为1点的概率为______.2、 若()0.4P A =,7.0)(=⋃B A P ,A 和B 独立,则()P B = 。
山东建筑大学(亲民版)公共选修课课程类别查询 (1)

山东建筑大学2010-2011-2选修课开课清单[带分类]课程名称授课教师开课院系课程分类学分地球科学导论田洪水土木工程学院自然科学与工程类2道路与桥梁工程概论范伟土木工程学院自然科学与工程类2高层建筑与地基基础肖俊华土木工程学院自然科学与工程类2工程质量与事故处理吕丛军土木工程学院自然科学与工程类2地震漫谈张华英土木工程学院自然科学与工程类2建筑结构工程设计案例刘之春土木工程学院自然科学与工程类2现代建筑结构赏析雷淑忠土木工程学院自然科学与工程类2珠宝玉石鉴赏吕明英土木工程学院自然科学与工程类2环境与健康张彦浩市政与环境工程学院自然科学与工程类2生态危机下的濒危物种祁峰市政与环境工程学院自然科学与工程类2循环经济与可持续发展王金鹤市政与环境工程学院自然科学与工程类2当代环境热点问题张桂芹市政与环境工程学院自然科学与工程类2人类活动引起的全球气候变化探秘张桂芹市政与环境工程学院自然科学与工程类2环境保护与探索盖磊市政与环境工程学院自然科学与工程类2 CAD2008的入门与环境工程实训孙翠珍市政与环境工程学院自然科学与工程类2环境学概论朱丽市政与环境工程学院自然科学与工程类2地质灾害安克锐市政与环境工程学院自然科学与工程类2人类免疫与健康张金凤市政与环境工程学院自然科学与工程类2生命科学导论张维建市政与环境工程学院自然科学与工程类2思维导图与潜能开发吕志杰机电工程学院自然科学与工程类2机器人大赛知识与评析李云江机电工程学院自然科学与工程类2机器人概论李云江机电工程学院自然科学与工程类2 Delphi工程应用程序设计基础王忠雷机电工程学院自然科学与工程类2创新思维方法与训练王日君机电工程学院自然科学与工程类2现代技术创新方法陈继文机电工程学院自然科学与工程类2CAXA实体设计刘辉机电工程学院自然科学与工程类2 SolidWorks产品设计张蔚波机电工程学院自然科学与工程类2电子设计与制作A苗松池信息与电气工程学院自然科学与工程类2建筑电气概论李明信息与电气工程学院自然科学与工程类2建筑电气施工与预算袁丽卿信息与电气工程学院自然科学与工程类2三维产品造型及渲染唐炳涛材料科学与工程学院自然科学与工程类2数学实验葛倩理学院自然科学与工程类2 Excel工程应用实践赵全斌土木工程学院自然科学与工程类2英语写作蔡修凯土木工程学院外语与计算机类2CAD基础田蕴艺术学院外语与计算机类2德语入门李兆东机电工程学院外语与计算机类2 Photoshopcs图像处理刘建华机电工程学院外语与计算机类2网络攻击透视与防范程钢机电工程学院外语与计算机类23DS-MAX三维建模基础段辉机电工程学院外语与计算机类2多媒体设计与制作姜洪奎机电工程学院外语与计算机类2低碳经济2 1同宿舍一起选一样的。
山东建筑大学全校课表

JZ0512
2
32 32
00GIS原理源自 应用JZ05162
32 20
0
12
园林植物 与应用
JZ0522
2
32 32
0
0
城市绿地
系统规划概 JZ0531 2 32 32 0 0
论
建筑经济 GL0504 1 16 16 0 0
城市社会 调查方法
JZ0122
1
16 16
0
0
城市物理 环境
JZ0124
1
16 16
大学英语 一级
WY3001
5
72 48
0
24
大学英语 二级
WY3002 4.5 72
48
0
24
大学英语 三级
WY3003 4.5 72
48
0
24
大学英语 四级
WY3004 4.5 72
48
0
24
场地与建 筑群设计
JZ0104
7
112 112
0
0
城市公共 空间规划原 JZ0108 1 16 16 0 0 理
毛泽东思 想和中国特 色社会主义 FZ4003 3 48 48 0 0 理论体系概 论
计算机文 公共必修课 化基础
JS0001
3
48 24
0
24
大学体育1 TY0001 2 32 32 0 0
大学体育2 TY0002 2 32 32 0 0
大学体育3 TY0003 2 32 32 0 0
大学体育4 TY0004 2 32 32 0 0
指导2
工程地质 与水文地质
HJ0144 1.5 24
24
山东建筑大学结构力学A2试卷
山东建筑大学试卷
2011 至 2012 学年第 1 学期
考试时间: 120 分钟
课程名称: 结构力学 A2 (A√、B)卷 考试形式:(闭卷、√开卷)
年级: 2009 专业: 土木工程、交通工程 ;层次:(√本、专科)
题号 一 二 三 四 五
总分
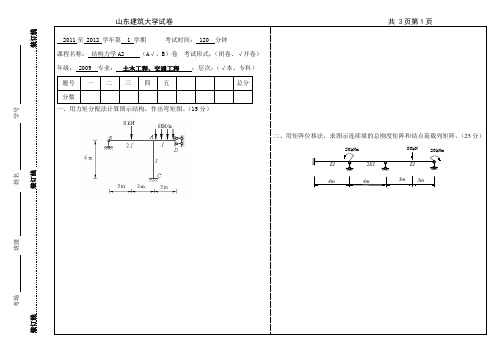
分数 一、用力矩分配法计算图示结构,作出弯矩图。(15 分)
共 3 页第 1 页
学号
二、用矩阵位移法,求图示连续梁的总刚度矩阵和结点荷载列矩阵。(25 分)
20kNm
80kN 20kNm
EI
2EI
EI
4m
4m
3m 3m
姓名 装订线
班级
考场 装订线
姓名 装订线
学号
装订线
装订线
山东建筑大学试卷
共 3 页第 2 页
三、图示结构,已知 M=1t,EI=7200kNm2,θ=2.5rad/s,求自振园频率,和平稳阶 段质点的最大位移(忽略杆件轴向变形)。(20 分)
2sinθt MMEI Nhomakorabea6m
EI
6m
山东建筑大学试卷
共 3 页第 3 页
装订线
四、图示结构,刚性竖杆具有分布质量 m ,弹性横杆抗弯刚度 EI 相同,并 五、图示梁的截面极限弯矩为 Mu 。试求梁的极限荷载 Pu。(20 分) 忽略质量,试确定自振圆频率和相关主振型。(20 分)
学号
姓名 装订线
装订线
山东建筑大学选课课程表
交际与沟通 AutoCAD计算机二维三维绘图实战 AUTOCAD工程师级教程 大学生职业素养 电子设计自动化(EDA) 计算生物学导论 手机游戏开发 《大学生心理健康与生命教育》 数学实验 大学生职业生涯规划理论与实践 绿色建筑思维与行动 战略管理与职业规划 《西方文学经典鉴赏》 商业经济学 证券投资基础知识 电子商务概论 大学生婚恋指导 证券投资技术分析 供应链物流管理 新制度经济学 OFFICE办公软件高级应用 交谊舞 篮球 篮球 篮球
曹萍 张彦浩 祁峰 王金鹤 张桂芹 张桂芹 盖磊 孙翠珍 朱丽 安克锐 张金凤 张维建 祁峰 刘雷 盖磊 王金鹤 赵增文 王静(环 境学院) 胡文军
48 49 50 51 52 53 54 55 56 57 58 机电学院 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73
吕志杰 李云江 李云江 李兆东 刘建华 王忠雷 程钢 段辉 姜洪奎 姜洪奎 汤爱君 王芳 李锦 王日君 何东 陈继文 刘辉 张蔚波 武藤素直 贾德芳 闫法义 刘娜(机电 学院) 何ห้องสมุดไป่ตู้ 刘援朝 刘刚 李跃军
32 32 32 32 32 32 32 32 32 32 32 32 32 32 32 32 32 32 48 32 32 32 32 32 32 32
GXJD0001 GXJD0002 GXJD0003 GXJD0004 GXJD0005 GXJD0006 GXJD0007 GXJD0008 GXJD0009 GXJD0010 GXJD0011 GXJD0012 GXJD0013 GXJD0014 GXJD0015 GXJD0016 GXJD0017 GXJD0018 GXJD0019 GXJD0020 GXJD0021 GXJD0022 GXJD0023 GXJS0001 GXJS0002 GXJS0003
山东建筑大学2014~2015校历
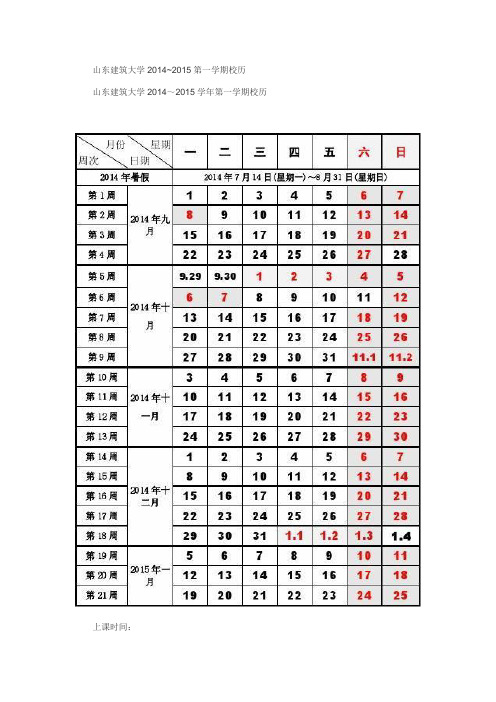
山东建筑大学2014~2015第一学期校历
山东建筑大学2014~2015学年第一学期校历
上课时间:
第1节7:50-8:35;第2节8:40-9:25;第3节9:40-10:25;第4节10:30-11:15;第5节11:20-12:05;第6节13:40-14:25;第7节14:30-15:15;第8节15:30-16:15;第9节16:20-17:05。
第10节18:40-19:25;第11节19:30-20:1
节假日教学工作安排
1. 教职工8月29日(星期五)上班;
2. 学生8月30日(星期六) 、8月31日(星期日)报到,领取教材;
3. 9月1日(星期一)正式开学上课,本学期教学周共21周;
4. 9月6日(星期六)~8日(星期一,中秋节)放假、公休,停课;
5. 9月28日(星期日)上班,按课程表安排正常上课;
6. 10月1日(星期三)~10月7日(星期二)放假、调休,停课;
7. 10月11日(星期六)上班,按星期一课表上课;
8. 2014年元旦期间放假调休及课程调整方案另行通知;
9. 2015年1月26日(星期一,农历腊月初七)开始寒假。
关于表彰20082009学年第一学期

关于表彰2008/2009学年第一学期文明班级标兵、文明班级、优秀学生干部三好学生、优秀团员、全优生的决定经各班级、团支部、学生会评选申报,学生处团委、教务处审查通过,学院决定对先进班级和优秀个人进行表彰。
一、授予以下15个班级“文明班级标兵”荣誉称号集控062班继电061班热动072班集控073班集控075班继电071班通信071班电化071班电化072班热动081班热动083班热动084班热动085班检测081班电化081班二、授予以下22个班级“文明班级”荣誉称号计算机045班热动063班集控061班集控063班集控064班供热071班热动071班计算机071班发电071班发电072班集控071班集控072班集控074班集控076班供热081班继电081班通信081班检测082班集控082班集控083班发电085班热动086班三、授予刘佳等 113名学生“优秀学生干部”荣誉称号;四、授予邱坤等252名学生“三好学生”荣誉称号;五、授予牟建鹏等 252名学生“优秀团员”荣誉称号六、授予以下26名学生“全优生”荣誉称号。
发电061班王雷震发电062班曹莹静发电065班梁柱峰周红威热动061班贺宇辰陈晓丛热动063班李盛秋通信061班顾海超发电071班祖家伟陈雅静发电072班张健发电073班任志强热动071班靳魁王辉贾晓东热动072班丁钾沨安林伟唐伟计算机072班王丽伟供热071班刘杰通信071班高鑫杨忠野发电084班许冠楠发电085班车克妍热动085班田明明供电081班徐菲菲学院希望受表彰的先进集体和优秀个人要珍惜荣誉、再接再励,同时也希望广大同学以他们为榜样,勇于进取、刻苦钻研,努力提高技能,不断完善自我,为学院的发展、为个人的进步付出努力、做出贡献。
哈尔滨电力职业技术学院二〇〇九年三月二十七日关于表彰“优秀团员”的决定经各班团支部评选申报,团委审查通过,党委批准,授予牟建鹏等 252名学生2008/2009学年第一学期“优秀团员”荣誉称号。
山东建筑大学2007-2008(1)概率论与数理统计试题(A卷)解答

1 3
(B)
2 5
(C)
1 5
( D)
4 15
二.填空题(每小题 3 分,共 15 分) 1. 一个均匀骰子,掷一次,朝上那面点数不小于 2 的概率是___5/6_____. 2. 射击两次,事件 Ai 表示第 i 次命中目标(i=1,2) ,则事件“至多命中一次”可表示为
A1 A2
.
3. 设 P ( A) 0.5, P ( B ) 0.6, P ( A B ) 0.9 , 则 P(B-A)=___0.4_______. 4. 设随机变量 X~N(0,1) ,φ(x)为其分布函数,则φ(x)+φ(-x)=___1____. 5. 设 X 与 Y 相互独立,且 D(X)=3,D(Y)=5,则 D(2X-Y+1)=_17___. 三.解答下列各题(每小题 6 分,共 30 分) 1. 一口袋装有 4 只白球, 5 只红球. 从袋中任取一只球后, 放回去, 再从中任取一只球. 求下列事 件的概率: 1) 取出两只都是红球; 2) 取出的是一只白球, 一只红球. 解:以 A 表示事件“取出两只都是红球” ,以 B 表示“取出的是一只白球, 一只红球” 。 由于是有放回取球,因而样本点总数 n=9×9=81。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。2 分 有利于事件 A 的样本点数 k1=5×5=25 事件 A 发生的概率为 P(A)=k1/n=25/81。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。4 分 有利于事件 B 的样本点数 k2=2×4×5=40 事件 B 发生的概率为 P(B)=k1/n=40/81。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。6 分 2. 有两个口袋,甲袋中盛有 2 个白球,1 个黑球;乙袋中盛有 1 个白球,2 个黑球。由甲袋中任 取一球放入乙袋,再从乙袋任取一球,求从乙袋中取得白球的概率。 解:以 A 表示 “从乙袋中取得白球” ,以 B1、B2 分别表示从甲袋中取得白球、黑球。 由于 B1∪B2=Ω, 可用全概率公式 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。2 分 P(A)=P(B1)×P(A|B1)+P(B2)×P(A|B2) =2/3×2/4+1/3×1/4 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。4 分 =5/12 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。6 分
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
山东建筑大学2010~2011学年第1学期
函授专升本科2010 年级土木工程、工程造价专业自学周
历
课程名称:线性代数与概率论
教材名称1:线性代数出版社同济大学出版社主编同大函授数学教研室版本: 2010 年 5 月第 3 版
教材名称2:概率论出版社高教大学出版社主编同大数学教研室
版本: 1982 年 10 月第 1 版
面授学时:18;自学学时:88;实验学时:0 ;指导/制定教师:岳修奎第1页共4
说明:线性代数部分重点是教材前三章;概率论部分重点是教材后六章
附件:
测验作业1: 线性代数部分测验作业
一、填空
1.行列式 x
A 2
214
101||=中元素x 的代数余子式值为 。
2. 设A 是一个三阶方阵, 且5||=A , 则|3A|= .
3.⎪⎪⎭⎫
⎝⎛+=⎪⎪⎭⎫
⎝⎛-=01224,01224
212
1x x B x x A ,若A=B ,则x 1= ,x 2= 。
4.设向量()0,3,5,1),9,5,5,
2(--==βα,若βγα=+,则=γ .
5.⎪⎪⎭
⎫ ⎝
⎛
=⎪⎪⎭⎫ ⎝⎛3
1021。
6.⎪⎪⎪⎭
⎫ ⎝⎛
=⎪⎪⎪⎭⎫ ⎝⎛--1
200020003。
7.设A ,B 为3阶方阵,且|A |=9,|B|=3,则|-2AB -1|=_____________.
8.设A 是秩为3的5×6矩阵,则齐次线性方程组A X =O 的解集合中线性无关的解向量个数为_____________.
9. 的根为x
x f 2
3
132
3
1
1)(--= 10. 线性方程组Ax=b ,其增广矩阵
A -
经初等变换化为阶梯形矩阵
,201000
11002110
1321
⎥⎥⎥⎥⎦
⎤
⎢⎢⎢
⎢⎣⎡--→t s
A 则
(1)S._________,t.__________时 AX=b 无解 (2)S.__________,t.___________时AX=b 有无穷多解 (3)S.__________,t.___________时AX=b 有唯一解
二、设⎪⎪⎪⎭
⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛--=212131121,111111111B A ,计算|)2(|T
A A
B -
三、解方程组⎪⎩⎪
⎨⎧=+---=-+-=-+-4
223123204321
43214321x x x x x x x x x x x x
四、求方程组⎪⎩⎪
⎨⎧=+--=-+-=+--0
32030
4321
43214321x x x x x x x x x x x x 的基础解和通解。
五、解矩阵方程⎪⎪⎭
⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛12643152X
测验作业2:概率论部分测验作业
一、5个白球,3个黑球,连续不放回地取两球,求都是白球的概率。
二、甲、乙独立地向一目标射击,命中的概率分别为21,P P , (1)甲中乙不中的概率,(2)甲乙恰有一人命中的概率
三、两台机床加工同样的零件,第一台出现废品的概率为0.03,第二台出现废品的概率为0.02,已知第一台加工的零件比第二台加工的零件多一倍,加工出来的零件放在一起,求:任意取出的零件是合格品(A )的概率.
四、零件出现次品的概率为0.04,如果生产这种零件4件,求至多一件次品的概率。
五、电话交换台每分钟的呼叫次数X服从参数为4泊松分布,求 (1) 每分钟的恰有8次呼叫的概率. (2) 每分钟呼叫次数大于8的概率. 六、设离散型随机变量X 的概率函数为
求X Y 4=和2
X Z =的概率函数。
七、已知随机变量X 的概率密度为⎩
⎨⎧≤≤=其他010)(x kx
x p ,
求(1)常数k ;(2)数学期望()X E ;(3)方差)(X D
八、的概率密度,求若σ
μ
σμ-=
X Y N X ),(~2
九、一口袋中装有4只球,依次标有数字1, 1, 2, 3 .从袋中任取两次,每次一只,取后不放回, 以X ,Y 分别记第一次,第二次得的球上标有的数字,求(1)(X ,Y )的联合概率函数;(2)关于X 、Y 的边缘分布;(3)X 、Y 是否独立?。
