八年级数学上册 平方差公式导学案2
八年级数学上册14.2.1平方差公式导学案新版新人教版2

14.2.1平方差公式(一)【学习目标】:1.会推导平方差公式,并能运用公式进行简单的运算.2.培养学生观察、归纳、概括的能力.3.在探索平方差公式的过程中,培养符号感和推理能力.【学习重点】掌握平方差公式的推导和应用.【学习难点】理解平方差公式的结构特征,灵活应用平方差公式一.自主学习1.多项式与多项式相乘:多项式与多项式相乘,先用一个多项式的________乘另一个多项式的__________,再把所得的积________。
符号表示:(m+b)(n+a)=-------------2.计算⑴(5+2)(5-2)= 【__×__+__× __】+【__×__+__×〔__〕】 = __- __= __⑵(a+3)×(a-3)=二.合作交流探究与展示:1. 计算下列多项式的积.(1)(x+1)(x-1 )(2)(m+2)(m-2)(3)(2x+1)(2x-1)从刚才的运算我发现:等号的一边:两个数的和与差的积,等号的另一边:是这两个数的平方差2.提出问题:观察上述算式,你发现什么规律?运算出结果后,你又发现什么规律?等号的一边:两个数的和与差的积,等号的另一边:是这两个数的平方差得到结论:。
(文字叙述)(a+b)(a-b)=a2-ab+ab-b2=a2-b2.即(a+b)(a-b)=a2-b2运用平方差公式计算1.(1)(3x+2)(3x—2)(2)(b+2a)(2a—b)(3)(—x+2y)(—x—2y)2.用简便方法计算(1)102×98 (2)(y+2)(y —2)—(y —1)(y+5)三、当堂检测:(1、2、3题为必做题;4、5、题为选做题)1、参照平方差公式“(a+b )(a -b )= a 2-b 2”填空(1)(t+s)(t-s)= (2) (3m+2n)(3m-2n)=2、. .下列哪些多项式相乘可以用平方差公式?)32)(32(b a b a -+ )32)(32(b a b a -+- )32)(32(b a b a +-+-)32)(32(b a b a --- ))((c b a c b a +-++ ))((c b a c b a -+--3、用平方差公式计算:(1).()()m n m n +- (2).(2)(2)x y x y -+ (3). (5)(5)x x ---+(4). 11(3)(3)33m n m n -+-- (5). 2211(7)(7)22x y x y -+4、计算 20012 -199925、已知228,4x y x y -=+=,求x-y 的值2019-2020学年初二下学期期末数学模拟试卷一、选择题(每题只有一个答案正确)1.若直线y =kx+k+1经过点(m ,n+3)和(m+1,2n ﹣1),且0<k <2,则n 的值可以是( ) A .4 B .5 C .6 D .72.如图,Rt △ABC 中,∠ACB=90°,若AB=15,则正方形ADEC 和正方形BCFG 的面积之和为( )A .150B .200C .225D .无法计算3.菱形ABCD 对角线交于O 点,E ,F 分别是AD 、CD 的中点,连结EF ,若EF=3,OB=4,则菱形面积( )A .24B .20C .12D .64.已知点A (-5,y 1)、B (-2,y 2)都在直线y=-12x 上,则y 1与y 2的关系是( ) A .12y y ≤ B .12y y = C .12y y <D .12y y > 5.甲、乙两车从A 地出发,沿同一路线驶向B 地.甲车先出发匀速驶向B 地,40min 后,乙车出发,匀速行驶一段时间后,在途中的货站装货耗时半小时.由于满载货物,为了行驶安全,速度减少了50km /h ,结果与甲车同时到达B 地.甲乙两车距A 地的路程y (km )与乙车行驶时间x (h )之间的函数图象如图所示,则下列说法中正确的有( )① 4.5a =;②甲的速度是60km /h ;③乙出发80min 追上甲;④乙刚到达货站时,甲距B 地180km .A .4个B .3个C .2个D .1个6.勾股定理是“人类最伟大的十个科学发现之一”.中国对勾股定理的证明最早出现在对《周髀算经》的注解中,它表现了我国古人对数学的钻研精神和聪明才智,是我国古代数学的骄傲.在《周髀算经》注解中证明勾股定理的是我国古代数学家( )A .祖冲之B .杨辉C .刘徽D .赵爽7.如图,点A 是反比例函数6y x =-(x <0)的图象上的一点,过点A 作平行四边形ABCD ,使B 、C 在x 轴上,点D 在y 轴上,则平行四边形ABCD 的面积为( )A .1B .3C .6D .128.已知12x <≤ ,则23(2)x x -+-的值为( )A .2 x - 5B .—2C .5 - 2 xD .29.如图,△ABC 中,∠B=55°,∠C=30°,分别以点A 和点C 为圆心,大于12AC 的长为半径画弧,两弧相交于点M ,N 作直线MN ,交BC 于点D ,连结AD ,则∠BAD 的度数为( )A .65°B .60°C .55°D .45°10.若b >0,则一次函数y=﹣x+b 的图象大致是( )A .B .C .D .二、填空题11.如图 ,D 为△ABC 的 AC 边上的一点,∠A =∠DBC =36°,∠C =72°,则图中 共有等腰三角形____个.12.如图,平行四边形ABCD 的周长为36,对角线AC ,BD 相交于点O .点E 是CD 的中点,BD =10,则DOE 的周长为_____.13.如图,在正方形ABCD中,延长BC至E,使CE=CA,则∠E的度数是_____.14.我们把顺次连接任意一个四边形各边中点所得的四边形叫做中点四边形,如果四边形ABCD的中点四边形是矩形,则对角线AC_____BD.15.若y与x的函数关系式为y=2x-2,当x=2时,y的值为_______.16.已知实数a、b在数轴上的位置如图所示,则化简222a b b a+--的结果为________()17.如图,直线 y=x+1 与 y 轴交于点 A1,以 OA1为边,在 y 轴右侧作正方形 OA1B1C1,延长 C1B1交直线y=x+1 于点 A2,再以 C1A2为边作正方形,…,这些正方形与直线 y=x+1 的交点分别为 A1,A2,A3,…,A n,则点 B n的坐标为_______.三、解答题18.如图,已知,直线y=2x+3与直线y=-2x-1,求ΔABC的面积.19.(6分)在边长为1个单位长度的正方形网格中建立如图所示的平面直角坐标系,△ABC的顶点都在格点上,请解答下列问题:(1)①作出△ABC 向左平移4个单位长度后得到的△A 1B 1C 1, 并写出点C 1的坐标;②作出△ABC 关于原点O 对称的△A 2B 2C 2, 并写出点C 2的坐标;(2)已知△ABC 关于直线l 对称的△A 3B 3C 3的顶点A 3的坐标为(-4,-2),请直接写出直线l 的函数解析式.20.(6分)计算:20122(21)(2019)16π-+---- 21.(6分)如图,E 为正方形ABCD 内一点,点F 在CD 边上,且∠BEF =90°,EF =2BE .点G 为EF 的中点,点H 为DG 的中点,连接EH 并延长到点P ,使得PH =EH ,连接DP .(1)依题意补全图形;(2)求证:DP =BE ;(3)连接EC ,CP ,猜想线段EC 和CP 的数量关系并证明.22.(8分)如图,菱形ABCD 中,E 是AB 的中点,DE AB ⊥,2AE =.(1)求对角线AC ,BD 的长;(2)求菱形ABCD 的面积.23.(8分)如图,点、分别在矩形的边、上,把这个矩形沿折叠后,点恰好落在边上的点处,且. (1)求证:; (2)连接、,试证明:.24.(10分)如图,在梯形ABCD AD //BC 中,,AB CD =,过点D DE BC 作⊥,垂足为E ,并延长DE F 至,使EF DE =,联结BF CD AC 、、.(1)求证:四边形ABFC 是平行四边形。
人教版八年级数学上册14.2.1平方差公式导学案

人教版义务教育课程标准实验教科书八年级上册14.2.1《平方差公式》导学案一、学习目标1.会推导平方差公式,并能运用公式进行简单的运算.2.培养学生观察、归纳、概括的能力.3.在探索平方差公式的过程中,培养符号感和推理能力.4.在计算过程中发现规律,并能用符号表示,从而体会数学的简捷美二、预习内容阅读课本P107 ~108 页,思考下列问题:1、平方差公式的内容是什么?2、 计算下列多项式的积,你能发现什么规律?(1)、(a+5)(b-2)= (2)、(x-3)(x+5)=(3)、(x+2)(x-2)= (4)、(2x+y)(2x-y)=3、课本P108页例1例2你能独立解答吗?三、探究学习1、趣味思考:有一个边长为a(a ﹥1)米的正方形,现在将其中一组对边增加5米,另一组对边减少5米,形成一个长方形。
请想一想:这时面积是增大,减小,还是不变。
2、几何验证:(1)请表示图(1)中阴影部分的面积.(2)将阴影部分拼成了一个长方形(图2),这个长方形的长和宽分别是多少?你能表示出它的面积吗?(3)比较前两问的结果,你有什么发现? ab bb a b -a b a b -ab四、巩固测评1、口答下列各题:(l)(-a+b)(a+b)=_________(2)(a-b)(b+a)= __________(3)(-a-b)(-a+b)=________(4)(a-b)(-a-b)=2、应用平方差公式计算。
1、(a+3b) (a-3b)2、(3+2a) (-3+2a)3、(-2+x) (-2-x)4、51×495、(-2x2-y)(-2x2+y)6、(3x+4)(3x-4)-(2x+3)(3x-2)3、[想一想]下列两个多项式相乘,哪些可以用平方差公式?哪些不能用?(1)(2x-3y)(3y-2x)(2)(-2x+3y)(2x+3y)(3)(2x-3y)(2x-3y)(4)(4)(2x+3y)(2x-3y)五、学习心得。
新人教版八年级数学上册《平方差公式》导学案
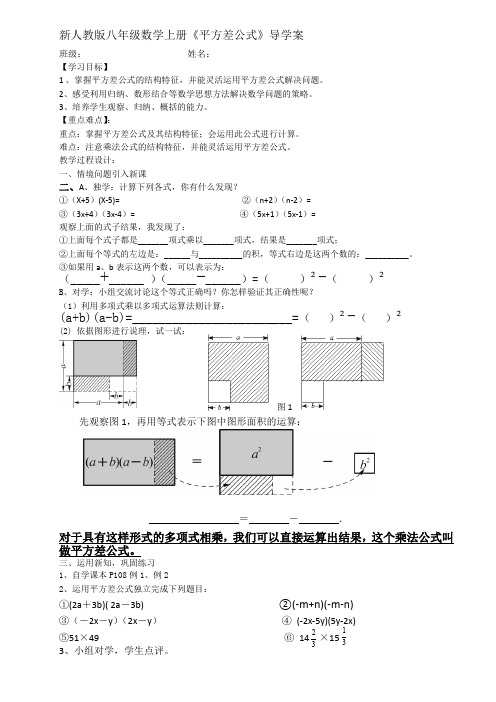
新人教版八年级数学上册《平方差公式》导学案班级: 姓名:【学习目标】1 、掌握平方差公式的结构特征,并能灵活运用平方差公式解决问题。
2、感受利用归纳、数形结合等数学思想方法解决数学问题的策略。
3、培养学生观察、归纳、概括的能力。
【重点难点】:重点:掌握平方差公式及其结构特征;会运用此公式进行计算。
难点:注意乘法公式的结构特征,并能灵活运用平方差公式。
教学过程设计:一、情境问题引入新课二、A 、独学:计算下列各式,你有什么发现?①(X+5)(X-5)= ②(n+2)(n-2)=③(3x+4)(3x-4)= ④(5x+1)(5x-1)=观察上面的式子结果,我发现了:①上面每个式子都是_______项式乘以_______项式,结果是_______项式;②上面每个等式的左边是:______与__________的积,等式右边是这两个数的:__________。
③如果用a 、b 表示这两个数,可以表示为:(_____+______ )(_____-______)=( )²-( )²B 、对学:小组交流讨论这个等式正确吗?你怎样验证其正确性呢?(1)利用多项式乘以多项式运算法则计算:(a+b)(a-b)=________________________=( )²-( )²(2) 依据图形进行说理,试一试:先观察图1,再用等式表示下图中图形面积的运算:_________________ = - .对于具有这样形式的多项式相乘,我们可以直接运算出结果,这个乘法公式叫做平方差公式。
三、运用新知,巩固练习1、自学课本P108例1、例22、运用平方差公式独立完成下列题目:①(2a +3b)( 2a -3b) ②(-m+n)(-m-n)③(-2x -y )(2x -y ) ④ (-2x-5y)(5y-2x)⑤51×49 ⑥ 14 ×15 3、小组对学,学生点评。
平方差公式(2)导学案

樊城区中学八年级数学学科课堂设计活页第周第课时上课时间:年月日星期:备课组长签字:蹲点领导签字:班级:小组:姓名:一、导学创设情境,引导学生探究新知二、独学:认真阅读课本,独立完成“独学”中的题目。
在探索练习的指引下,自主的完成有关的练习,并在练习中发现幂的乘方的法则,从猜测到探索到理解法则的实际意义从而从本质上认识、学习幂的乘方的来历。
进一步体会幂的意义。
三、互学找出自己不明白的问题,先对学,再群学。
充分在小组内展示自己,课题:平方差公式(2)课型:自学+展示+评学(新授课)设计人:复备人:学习目标:1、能经历探索平方差公式的过程.2、会推导平方差公式,并能运用公式进行简单的运算.3、体味科学的思想方法,接受数学文化的熏陶,激发探索创新精神.对照答案,提出疑惑,小组内讨论解决。
小组解决不了的问题,写在各小组展示的黑板上,在大展示的时候解决。
四、评学积极发表自己的不同看法和解法,大胆质疑,认真倾听。
做每一步运算时都要自觉地注意有理有据,也就是避免知识上的混淆及符号等错误.一、明确目标,创设情境你能快速准确求(y+2)(y-2)-(-y-1)(-y+1)结果是多少吗?二、独学(独立思考,挖掘潜能。
)1.你能用简便方法计算下列各题吗?(1)2001×1999 (2)998×10022.计算下列多项式的积.(1)(x+1)(x-1)(2)(m+2)(m-2)(3)(2x+1)(2x-1)(4)(x+5y)(x-5y)结论:两个数的和与这两个数的__________的积,等于这两个数的___________.即:(a+b)(a-b)=a2-b2运算形式:运算方法:三、互学(交流展示,释疑解惑)例1:运用平方差公式计算:(1)(3x+2)(3x-2)(2)(b+2a)(2a-b)(3)(-x+2y)(-x-2y)例2:计算:(1)102×98 (2)(y+2)(y-2)-(y-1)(y+5)计算:(1)(a+b)(-b+a)(2)(-a-b)(a-b)(3)(3a+2b)(3a-2b)四、评学(学以致用,能力提升。
八年级数学上册《14.2.1 平方差公式》 精品导学案 新人教版

【学习目标】1.经历探索平方差公式的过程,会运用平方差公式。
2.在探索平方差公式的过程中,发展学生的符号感和推理能力。
学习重点:会运用平方差公式。
学习难点:会运用平方差公式。
【知识准备】1.单乘单法则:2.单乘多法则:3.多乘多法则:【自习自疑文】一、预习与新知(阅读教材P107-P108内容,并思考回答下列问题)1.计算下面各式(1)(x+3)(x-3) (2)(-2a-2)(2a-2)平方差公式:二、预习评估1.计算下列各题。
(1)(x+1)(x-1) (2)(a+2)(a-2)我想问:请你将预习中遇见的问题和疑问写下来,等待课堂上与同学、老师共同探究解决。
等级 组长(或家长)签字【自主探究文】【探究一】 验证平方差公式请用剪刀从边长为a 的正方形纸板上,剪下一个边长为b 的小正方形(如图1),然后拼成如图2的长方形,你能根据图中的面积说明平方差公式吗?【探究二】平方差公式的直接应用: ①(a-2b 2)(a+2b 2)② (3x+2y)(2y-3x)③(m-3n)(-m-3n)【探究三】灵活运用平方差公式2111(1)()()()242y y y -++ 2(2)201120092010⨯- (3)911101⨯⨯【探究四】a-b=10b-c=15c+a=20.a-c)(a+c)已知,,求(的值。
【自测自结文】1. 下列各式哪些可用平方差公式计算?能用的请在括号内写出结果,不能的化×. (1)(2)(2)a b b a -+ ( )(2)(1)(2)x x ++( ) (3)()()x y x y ---+ ( ) (4)(5)(5)a a --+( ) (5)(23)(32)x y x y +- ( ) (6)()()a b b a --( )2. 直接写出结果:(1)(23)(23)x y x y +-= (2)22(51)(51)xx -+=(3)22(34)(34)b ab a +-= (4)=+-+)2)(2(b a a b(5))(221(y x +-)22441y x -=3.利用平方差公式计算:(1)(ab+1)(-ab+1) (2)(-2xy+z)(-2xy-z)4.如果(2a+2b+1)(2a+2b-1)=63,那么a+b 的值等于多少?【自我小结】通过本节课的学习,你有哪些收获?还有哪些困惑呢?教师个人研修总结在新课改的形式下,如何激发教师的教研热情,提升教师的教研能力和学校整体的教研实效,是摆在每一个学校面前的一项重要的“校本工程”。
八年级数学上册14.2.1平方差公式导学案(新版)新人教版

八年级数学上册14.2.1平方差公式导学案(新版)新人教版14、2、1 平方差公式学习目标1、探索平方差公式2、会推导平方差公式,并能运用公式进行简单的运算、3、在计算过程中发现规律,并能用符号表示,从而体会数学的简洁美、学习重点:平方差公式的应用学习难点:灵活应用平方差公式【学前准备】1、计算:(1)(2)(3)(4)【导入】【自主学习,合作交流】1、算算下面的题,写出步骤及结果,看看结果有什么规律?(1)(2)(3)(4)(5)(a –b)(a+b)(6)(a+b)(a –b)2、看看结果是什么?运用平方差公式计算:(通过自学你能学会吗?)(1);(2);(3)、计算(注意:只有符合公式要求的乘法,才能运用公式简化运算)(1)10298 (2)【精讲点拔】这个公式叫做(乘法的)平方差公式、(其实可以表示任意数,也可以表示任意单项式、多项式)、(x+2y1)(xy+1)思考?:你能根据图中的面积说明平方差公式吗?【本节小结】【当堂测试】1、下面各式的计算对不对?如果不对,应怎样改正?(1)( )(2)、( )2、运用平方差公式计算:(1)(2)纠错栏(3)(4)【课后作业】Ⅰ必做题1、计算:(1)20011999 (2)(a2+1)(a-1)(a+1)(3)(x-3)(x2+9)(x+3)(4)(-2b-5)(2b-5)(5)(xy+1)(xy-1)(6)9981002Ⅱ选做题1、若()=,则括号内应填入的代数式是()A、B、C、D、2、计算:(1)(2)【评价】准确程度评价优良中差书写整洁程度评价优良中差【课后反思】。
人教版数学八年级上册导学案:14.2.1平方差公式(二)

B、
C、
D、
(3)、计算 的结果是()
A、 B、-
C、 D、
(4)、已知 =4,则 的值是()
A、4 B、8 C、16 D、12
(5)已知x+y=5,xy=7,则 的值是()
A、18 B、11 C、39 D、44
(6)、边长为a的正方形,其边长减少b以后所得的正方形面积比原来正方形面积少 ( )
A、 B、 C、 D、
3、填空。
(1)、 。
(2)、 ( ) =( )
(3)、若 =9, =5,则xy=。
(4)、9 +( )+ =
=
4、计算。
1、 (2)、
3、 (4)、
5、 (6)、
例1、计算:
例2、1、先化简再求值 ,其中x=1,y=3.
2、计算
主备人:审核人: 时间:编号
(三)巩固提高
1、下列各式中,能够成立的等式是
课题:完全平方公式课型:质疑拓展提升课
学习目标:1、复习完全平方公式和添括号法则的应用。
2、敢于面对数学活动中的困难,并有独立克服困难的能力,树立学习数学的自信心。
3、培养分析问题和解决问题的思想,总结、归纳问题的能力。学习环节
学习重点:完全平方公式和添括号法则的应用
学习难点:灵活运用完全平方公式和添括号法则解题。
A. B.
C. D.
2、下列式子:①
② ③ ④ 中正确的是
A.① B.①② C.①②③ D.④
3、
A. B.
C. D.
4、若 ,则M为( ).
A. B. C. D.
5、已知 ,则下列等式成立的是 ( )
① ②
③ ④
A.① B.①② C.①②③ D.①②③④
平方差公式-八年级上数学导学案

平方差公式-八年级上数学导学案(总1页)-CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面,使用请直接删除14.2.1平方差公式(一)学习目标1.熟练掌握平方差公式,并能运用公式进行计算.2.在计算过程中发现规律,并能用符号表示,从而体会数学的简捷美. 3.在探索平方差公式的过程中,明确平方差公式的结构特征并培养符号感.重点: 1.平方差公式的推导和应用;2.掌握公式的结构特征及正确运用公式;难点:理解平方差公式的结构特征,灵活应用平方差公式;预习案使用说明学法指导诵读教材P107-P108的内容,熟记基础知识.完成下面的问题教材助读1.旧知回顾多项式与多项式相乘,先用_____________________乘另一个多项式的每一项,再把__________________.计算:(第一组)(1) (x+3)(x−3) (2) (1+2a)(1−2a)(3) (x+4y)(x−4y)(4) (y+5z)(y−5z)第二组 (用多项式与多项式相乘的法则计算)(1)(x+y)(x-y)(2)(y+x)(x-y)(3)(-x-y)(-x+y)(4)(x-y)(-x-y)2.平方差公式: __________________________文字叙述:两个数的____与________________,等于________探究案探究点一1.用多项式与多项式相乘的法则计算:(1)(2)(3)像这样具有特殊形式的多项式相乘,我们能否找到一个一般性的公式,并加以熟记,遇到相同形式的多项式相乘时,直接把结果写出来呢?2.公式的推导探究点二例1 运用平方差公式计算:(1)(3x+2)(3x-2)(2)(-x+2y)(-x-2y)(3)(b+2a)(2a-b)(4)(x2 - y2) (y2+x2)探究点三计算:(1)(b+2)(b−2) (2)(a +2b)(a−2b) 11+-x x()()22+-m m()() 2121+-x x()()(3)(−3x+2)(−3x−2) (4)(−3x+y)(3x+y)(5)(−4a+3)(−4a−3) (6)(y−x)(−x−y)探究点四例2 利用平方差公式计算(1)102×98 (2)51×49当堂检测1.下列各式运算正确的是( )A.(a-2)(2+a)=a2-2B.(x+2)(2x-2)=2x2-4C.(-a-b)(a+b)=a2-b2D.(ab-3)(ab+3)=a2b2-92.计算:(1)(x+6)(x-6) (2)(5x+2)(5x-2)(3)(3y+2x)(2x-3y)(4)(-5m-n)(5m-n)3。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《平方差公式》
学习目标
(一)知识点
1.经历探索平方差公式的过程. 2.会推导平方差公式,并能运用公式进行简单的运算.(二)能力要求
1.在探索平方差公式的过程中培养符号感和推理能力。
2.培养学生观察、归纳、概括的能力.
(三)情感与价值观要求在计算过程中发现规律,并能用符号表示,从而体会数学的简捷美.学习重点:平方差公式的推导和应用.
学习难点:理解平方差公式的结构特征,灵活应用平方差公式
I.探究一:你能用简便的方法计算:(提示:把数化成整百,整千的运算,从而使运算简单)
(1)2001×1999 (2)998×1002
(1)2001×1999=(2000+1)(2000-1)=20002-1×2000+1×2000+1×(-1) =20002-1
=4000000-1
=3999999.
2001×1999=20002-12
(2)998×1002=(1000-2)(1000+2)=10002+1000×2+(-2)×1000+(-2)×2 =10002-22
=1000000-4
=1999996.
998×1002=10002-22
它们积的结果都是两个数的平方差,那么其他满足这个特点的运算是否也有这个规律呢?我们继续进行探索.
II.探究二:
(1)(x+1)(x-1)(2)(m+2)(m-2)(3)(2x+1)(2x-1)
(4)(n+3m)(n-3m)(6)(x+2y(x-2y)
①上面的算式具有怎样的特点:每个因式都是两项,它们都是两个数的和与差的积;.
②计算上面多项式的积
③通过运算发现规律,并用语言叙述:
两个数的和与这两个数的差的积,等于这两个数的平方差.
④你能用字母表示这个规律吗
(a+b)(a-b)=a2-b2.其中a、b表示任意数,也可以表示任意的单项式、多项式。
III. 练习巩固:
1.判断下列计算是否正确;不正确给予改正:
(1)(a+2)(a+3)=a2-6×(2)(m+n)(n+m)= m2-n2
(3)(2a-8)(2a+8)=4a2-64 对 (4) (2m+n)(2m-n)=2m2-n2 ×
(5)(-3x+y)(3x-y)=9x2-y2×
公式的结构特征:左边的两个多项式中有一项相同,有一项互为相反数,积的结果为相同项的平方减去互为相反数项的平方的差
2.(课时学案)填空:(1)(x+2)(x-2)= ()2-()2
(2)(5a+2b)()= 25a-4b2 (3)()(a-1)= 1-a2
认清公式:在等号左边的两个括号内分别没有符号变化的是a,变号的是b
IV.例1:运用平方差公式计算:
(1)(3x+2)(3x-2)(2)(b+2a)(2a-b)
(3)(-x+2y)(-x-2y)(4)(a5-b2)(a5+b2)
(5)(a+2b+2c)(a+2b-2c)(6)(a-b)(a+b)(a2+b2)
注:(1)公式中的字母a、b可以表示数,也可以是表示数的单项式、多项式即整式.(2)要符合公式的结构特征才能运用平方差公式.
(3)有些多项式与多项式的乘法表面上不能应用公式,•但通过加法或乘法的交换律、结合律适当变形实质上能应用公式.
(4)运算的最后结果应该是最简才行
例2:计算:
(1)102×98 (2)(y+2)(y-2)-(y-1)(y+5)
(1)102×98=(100+2)(100-2)
=1002-22
=10000-4
=9996
(2)(y+2)(y-2)-(y-1)(y+5)
=y2-22-(y2+5y-y-5)
=y2-4-y2-4y+5
=-4y+1.
只有符合公式要求的乘法才能用平方差简化运算,其余的运算仍按乘法法则进行
V.探究三: (课时学案探究二)怎样用图中的面积的集合意义来解释平方差公式?(书152思考)
附加:下列哪些多项式相乘可以用平方差公式?
)32)(32(b a b a -+ )32)(32(b a b a -+- )32)(32(b a b a +-+- )32)(32(b a b a --- ))((c b a c b a +-++ ))((c b a c b a -+-- 认清公式:在等号左边的两个括号内分别没有符号变化的集团是a ,变号的是b 计算:22)7()5(--+m m
课后反思:你学会了什么:
还有哪些不懂:
课后作业: 课时学案课后巩固。
