第23章 图形的旋转单元测试题(人教版)
人教版九年级数学上册第23章《图形的旋转》单元检测题

15.
解析:连接
所以∠
∠
由旋转的性质知, ,所 以 △
∠
∠
,所以
, ,所 以
.
16. (3, 4) 解析:两个点关于原点对称时, 它们的横、 纵坐标符号分别相反, 所以点 的
坐标为 (3, 4) .
17.2 解析:∵ 点
与点
关于原点对称,∴ b 3, a 1 ,∴
a b 2.
18.( , ) 解析:将点
第二十三章 《旋转》检测题 附答案
一 、选择题 (每小题 3 分,共 30 分)
1( 2014 ·长沙中考)下列四个圆形图案中,分别以它们所在圆的圆心为
旋转中心,顺时针旋转 120°后,能与原图形完全重合的是 (
)
2. 下列图形中,是中心对称图形的有(
)
第 9 题图
10.如图所示,在正方形网格中,将△
3.A 解析:本题考查了矩形的性质、 对顶角和四边形的内角和 .如图所示,设 BC 与 C′D′ 交于点 E.
45
点 O 的纵坐标为
.
3
因为∠ D′AD+∠BAD′=90,°所以∠ BAD′=90-°α. 因为∠ 1=110°,所以∠ BED′=110°. 在四边形 ABED′中, 因为∠ BAD′∠+B+∠BED′∠+D′=360,°
代入 y x 3 ,得 n 6 ,∴ 对称点 为(
).
19.(1)6,135° (2)证明: AOA1
OA1B1 90 ,
∵∠ ACB =90°,∴∠ BCD =90°-∠ ACD =∠ FCE . 在△ BCD 和△ FCE 中,
CB CF , BCD FCE ,
CD CE ,
∴△ BCD ≌△ FCE . (2)解:由( 1)可知△ BCD≌△ FCE ,∴ ∠ BDC=∠ E. ∵ EF ∥CD ,∴ ∠E=180°-∠ DCE =90°,∴ ∠ BDC=90°.
人教版九年级数学上册第23章《图形的旋转》测试题附答案

第3题图ED C BA 第4题图O D CBA 第5题AB 旋转测试题附答案一、 选择题:1.一个图形经过旋转变化后,发生改变的是 .A.旋转中心B.旋转角度C.图形的形状D.图形的位置 2.下列图形中绕某个旋转180°后能与自身重合的有 .①正方形; ②长方形; ③等边三角形; ④线段; ⑤角; ⑥平行四边形 A. 5个 B. 2个 C. 3个 D. 4个3.如图所示,△ABC 中,AC =5,中线AD =7,△EDC 是由△ADB 旋转180°所得,则AB 边的取值范围是 .A. 1<AB <29B. 4<AB <24C. 5<AB <19D. 9<AB <194.如图,已知△OAB 绕点O 沿逆时针方向旋转80°到△OCD 的位置,且∠A =110°,∠D =40°,则∠AOD 的度数为 .A. 30°B. 40°C. 50°D. 60°5.将方格纸中的图形(如图所示)绕点O 沿顺时针方向旋转90°后,得到的图形是6.下列图形中,是中心对称图形而不是轴对称图形的是 . A.等边三角形 B.矩形 C.平行四边形 D.菱形7.点A (-3,2)关于x 轴的对称点为点B ,点B 关于原点的对称点为C ,则点C 的坐标是 .A.(3,2)B.(-3,2)C.(3,-2)D.(-2,3) 8.已知点A 的坐标为(a ,b ),O 为原点,连结OA ,将线段OA 绕点O 按逆时针方向旋转90°得OA 1,则点A 1的坐标为 .A.(-a ,b )B.(a ,-b )C.(-b ,a )D.(b ,-a ) 9.如图,△ABC 为等腰三角形,AB =AC ,∠A =38°,现将△ABC 绕点旋转,使BC 的对应边落在AC 上,则其旋转角为 .A. 38°B. 52°C. 71°D. 81°10.如图所示,在直角三角形ABC 中,∠C =90°,AC =6,BC =8,将△ABC 绕点B 旋转90°,得到关于点A 的对称点D ,则AD 的长是 .第9题图EDCBA 第10题图CBA第16题图C /B /()A /C B A 第17题图B /A /C B AB. 10C. 10D. 20A. 2011.平面直角坐标系中有一图案,如果将图案中各点的横、纵坐标都乘以-1,所得图案与原图案相比 .A.向下平移了一个单位长度B.向左平移了一个单位长度C.关于坐标轴成轴对称D.关于坐标原点成中心对称12.在正方形ABCD 中,E 是CD 上一点,F 是BC 上一点,且EF =BF +DE ,则∠EAF 的度数是 .A. 30°B. 60°C. 45°D. 小于60° 二、填空题:13.线段的对称中心是 ,平行四边形的对称中心是 ,圆的对称中心是 .14.已知A 、B 、O 三点不在同一直线上,A 、A /关于点O 对称,B 、B /关于点O 对称,那么线段AB 与A /B /的关系是 .16.如图在Rt △ABC 中,∠C =90°,∠A =60°,AC =3cm ,将△ABC 绕B 点旋转到 △A /B /C /的位置且使A 、B 、C /三点在同一直线上,则A 点经过的最短路线长是 cm.17.如图,将Rt △ABC 绕C 点逆时针旋转得到△A /B /,若∠A /CB =160°,则此图形旋转角是 度.18.若矩形ABCD 的对称中心恰为原点O ,且点B 坐标为(-2,-3), 则点D 坐标为 .19.点(1,-3)绕原点顺时针旋转90°得到的点的坐标是 ;直线y =-3x 绕原点顺时针旋转90°得到的直线的解析式为 . 20.阅读课题学习:“如果一个图形绕着某点O 旋转α后所得的图形与原图形重合,则称此图形关于点O 有角α的旋转对称。
人教版九年级数学上册第23章《图形的旋转》单元测试题

第二十三章旋转单元测试题一、选择题1、以下说法中正确的选项是()A 、会重合的图形必定是轴对称图形;B 、两个成中心对称的图形的对称点连线必过对称中心C 、中心对称图形必定是会重合的图形;D、两个会重合的三角形必定对于某一点成中心对称2、在图形旋转中,以下说法错误的选项是()A、图形上的每一个点到旋转中心的距离相等B 、图形上每一点挪动的角度都同样C、图形上可能存在不动的点D、图形上随意两点的连结线段与旋转后对应两点的连结线段相等3、如下图的图中,既是轴对称又是中心对称图形的是()(A)( B )( C )( D ) 4、将一张正方形纸片沿右图中虚线剪开后,能拼成以下四个图形,则此中是中心对称图形的是()5、以下用英文字母设计的五个图案中既是轴对称图形,又是中心对称图形的有()(A)0 个(B)1 个(C)2个(D)3 个6、以下图形中,中心对称图形的个数是A.1 个B.2 个C.3 个D.4 个二、填空题7、以下图形中,旋转60 度后能够和原图形重合的是()A 、正六边形B、正五边形C、正方形D、正三角形ADOB C图15-3-38、如图 15-3-3 所示,△OA B 绕点 O 旋转 180°获得△ OCD ,连结 AD、BC,获得四边形 ABCD ,则 AB________CD(填地点关系);与△ AOD成中心对称的是__________由此可获得AD______ BC (填地点关系)。
9、如图: P 是等边ABC内的一点,把ABP经过旋转分别获得BQC和ACR。
A( 1)指出旋转中心是、旋转方向是旋转角度是。
( 2) ACR能否能够直接经过把BQC旋转获得?R ( 3)若 PA=5, PC=4, PB=3,则△ PQC是什么三角形?说明原因。
PB CQ10、假如正方形 CDEF旋转后能与正方形 ABCD重合,平面上能够作为旋转中心的点共有 ______个,并指AD E那么图形所在的出B FC11、现实生活中有好多图形中都有圆的影子,它们看上去特别美丽,这是由于圆不单是轴对称图形,仍是中心对称图形。
人教版九年级数学上册《第23章旋转》单元测试题含答案

九年级数学二十三章测试题题号一二三合计得分一、选择题(每小题4分,共40分)1.在平面内将一个图形绕一个定点沿某个方向转动一个角度这样的图形运动称为旋转.下列图形中不能由一个图形通过旋转而构成的是( C )2.下列图形中,为中心对称图形的是(B)3.下列图形中是轴对称图形,但不是中心对称图形的是(B)4.下列图标中,既是轴对称图形,又是中心对称图形的是(D)5.将点P(-2,3)向右平移3个单位长度得到点P1,则点P1关于原点的对称点的坐标是(C)时间:120分钟满分:150分A.(-5,-3) B.(1,-3) C.(-1,-3) D.(5,-3)6.如下所示的4组图形中,左边图形与右边图形成中心对称的有(C)A.1组B.2组C.3组D.4组7.已知a<0,则点P(-a2,-a+1)关于原点对称的点在(D)A.第一象限B.第二象限C.第三象限D.第四象限8.如图,在Rt△ABC中,∠BAC=90°.将Rt△ABC绕点C按逆时针方向旋转48°得到Rt△A′B′C,点A在边B′C上,则∠B′的大小为(A)A.42° B.48°C.52° D.58°9.如图,在方格纸中的△ABC经过变换得到△DEF,正确的变换是(D)A.把△ABC向右平移6格B.把△ABC向右平移4格,再向上平移1格C.把△ABC绕着点A顺时针旋转90°,再向右平移6格D.把△ABC绕着点A逆时针旋转90°,再向右平移6格,第10题图)10.如图,在△ABO中,AB⊥OB,OB=3,AB=1,将△ABO绕O点旋转90°后得到△A1B1O,则点A1的坐标是(B)A.(-1,3) B.(-1,3) 或(1,-3)C.(-1,-3) D.(-1,3)或(-3,-1)二、填空题(每小题4分,共24分)11.将如图所示的图案绕其中心旋转n°时与原图案完全重合,那么n的最小值是__120__.12.如图,大圆的面积为4π,大圆的两条直径互相垂直,则图中阴影部分的面积的和为__π__.,第11题图),第12题图),第13题图),第14题图),第16题图)13.如图,将△ABC绕A逆时针旋转得到△ADE,点C和点E是对应点,若∠CAE=90°,AB=1,则BD=__2__.14.如图,在△ABC中,∠CAB=70°,将△ABC绕点A逆时针旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′的度数是__40°__.15.已知点A(m,m+1)在直线y=12x+1上,则点A关于原点的对称点的坐标是__(0,-1)__.16.如图,将一张直角三角板纸片ABC沿中位线DE剪开后,在平面上将△BDE绕着CB的中点D逆时针旋转180°,点E到了点E′位置,则四边形ACE′E 的形状是__平行四边形__.三、解答题(本大题共8小题,共86分)17.(8分)如图,△ABC中,∠B=10° ,∠ACB=20°,AB=4,△ABC 逆时针旋转一定角度后与△ADE重合,且点C恰好成为AD的中点.(1)指出旋转中心,并求出旋转的度数;(2)求出∠BAE的度数和AE的长.解:(1)旋转中心是点A ,∵∠CAB =180°-∠B -∠ACB =150°,∴旋转角是150°.(2)∠BAE =360°-150°×2=60°,由旋转的性质得△ABC ≌△ADE , ∴AB =AD ,AE =AC ,又∵点C 是AD 的中点,∴AC =12AD =12AB =12×4=2,∴AE =2.18.(8分)如图,D 是△ABC 的边BC 的中点,连接AD 并延长到点E ,使DE =AD ,连接BE.(1)图中哪两个图形成中心对称?(2)若△ADC 的面积为4,求△ABE 的面积.解:(1)△ADC 与△EDB 成中心对称;(2)∵△ADC 与△EDB 关于点D 中心对称,∴△ADC ≌△EDB ,∴S △ADC =S △EDB =4,∵D 是BC 中点,∴BD =CD ,∴S △ABD =S △ACD =4,∴S △ABE =S △ABD +S △BED =8.19.(8分)如图,在边长为1的正方形网格中,△ABC 的顶点均在格点上.(1)画出△ABC关于原点成中心对称的△A′B′C′,并直接写出△A′B′C′各顶点的坐标;(2)连接BC′,B′C,求四边形BCB′C′的面积.解:(1)如图,△A′B′C′即为所求,A′(4,0),B′(3,3),C′(1,3).(2)∵B′(3,3),C′(1,3),∴B′C′∥x轴,B′C′=2,∵B(-3,-3),C(-1,-3),∴BC∥x轴,BC=2,∴BC∥B′C′,BC=B′C′,∴四边形BCB′C′是平行四边形,∴S BCB′C′=2×6=12.20.(12分)如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5)(每个方格的边长均为1个单位长度).(1)请画出△A1B1C1,使△A1B1C1与△ABC关于x轴对称;(2)将△ABC绕点O逆时针旋转90°,画出旋转后得到的△A2B2C2,并直接写出点B2,C2的坐标;(3)若点P(a,b)是△ABC内任意一点,试写出将△ABC绕点O逆时针旋转90°后点P的对应点P2的坐标.解:(1)如图,△A1B1C1即为所求;(2)如图,△A2B2C2即为所求,B2的坐标是(-2,4),C2的坐标是(-5,3);(3)点P2的坐标是(-b,a).21.(12分)如图,四边形ABCD是正方形,E,F分别是DC和CB的延长线上的点,且DE=BF,连接AE,AF,EF.(1)求证:△ADE≌△ABF;(2)填空:△ABF可以由△ADE绕旋转中心__A__点,按顺时针方向旋转__90__度得到;(3)若BC=8,DE=2,求△AEF的面积.解:(1)∵四边形ABCD是正方形,∴AD=AB,∠D=∠ABC=90°,而F是CB的延长线上的点,∴∠ABF=∠D=90°.又∵AB=AD,DE=BF,∴△ADE≌△ABF(SAS);(3)∵BC=8,∴AD=8,在Rt△ADE中,DE=2,AD=8,∴AE=AD2+DE2=217,∵△ABF可以由△ADE绕旋转中心A点,按顺时针方向旋转90°得到,∴AE=AF,∠EAF=90°.∴△AEF的面积=12AE2=12×4×17=34.22.(12分)如图,在Rt△OAB中,∠OAB=90°,OA=AB=6.(1)请你画出将△OAB绕点O沿逆时针方向旋转90°得到的△OA1B1;(2)线段OA1的长度是________,∠AOB1的度数是________;(3)连接AA1,求证:四边形OAA1B1是平行四边形.(1)解:△OA1B1如图所示.(2)解:根据旋转的性质知,OA1=OA=6.∵将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1,∴∠BOB1=90°.∵在Rt△OAB中,∠OAB=90°,OA=AB=6,∴∠BOA=∠OBA=45°,∴∠AOB1=∠BOB1+∠BOA=90°+45°=135°,即∠AOB1的度数是135°.(3)证明:根据旋转的性质知,△OA1B1≌△OAB,则∠OA1B1=∠OAB=90°,A1B1=AB,∵将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1,∴∠A1OA =90°,∴∠OA1B1=∠A1OA,∴A1B1∥OA.又∵OA=AB,∴A1B1=OA,∴四边形OAA1B1是平行四边形.23.(12分)如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,点D刚好落在AB边上.(1)求n的值;(2)若F是DE的中点,判断四边形ACFD的形状,并说明理由.解:(1)由旋转的性质可知,CA=CD.∵∠ACB=90°,∠B=30°,∴∠A=60°.∴△ACD为等边三角形.∴∠ACD=60°,即n=60;(2)四边形ACFD是菱形.理由:∵F是DE的中点,∴CF=12DE=DF.∵∠EDC=∠A=60°,∴△FCD为等边三角形,∴CF=DF=CD.∵△ACD为等边三角形,∴AC=AD=CD.∴AC=AD=DF=CF,∴四边形ACFD是菱形.24.(14分)在同一平面内,△ABC和△ABD如图①放置,其中AB=BD.小明做了如下操作:将△ABC绕着边AC的中点旋转180°得到△CEA,将△ABD绕着边AD的中点旋转180°得到△DFA,如图②,请完成下列问题:(1)试猜想四边形ABDF是什么特殊四边形,并说明理由;(2)连接EF,CD,如图③,求证:四边形CDFE是平行四边形.(1)解:四边形ABDF是菱形,理由如下:∵△ABD绕边AD的中点旋转180°得△DFA,∴△ABD≌△DFA,又∵AB =BD,∴AB=DF=BD=AF,∴四边形ABDF是菱形;(2)证明:∵四边形ABDF是菱形,∴AB∥DF,AB=DF,∵△ABC绕边AC的中点旋转180°得△CEA,∴△ABC≌△CEA,∴AB=EC,AE=BC,∴四边形ABCE是平行四边形,∴AB=CE,AB∥CE,又∵AB∥DF,AB=DF,∴EC∥DF,EC=DF,∴四边形CDFE是平行四边形.。
人教版九年级上册数学 第二十三章 旋转 单元综合测试(含解析)
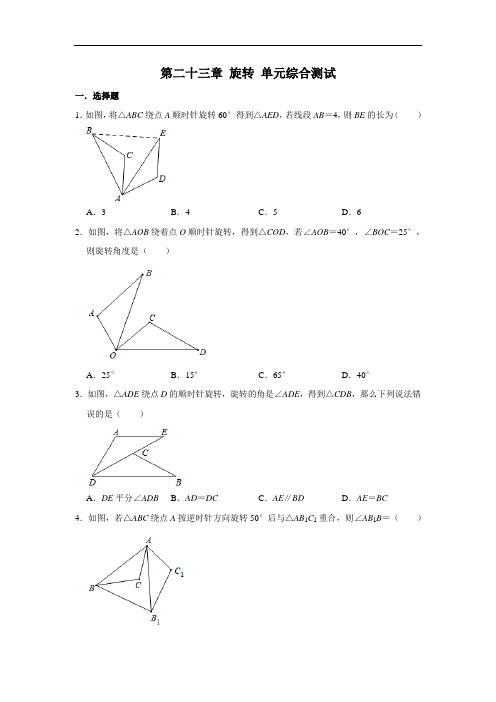
第二十三章旋转单元综合测试一.选择题1.如图,将△ABC绕点A顺时针旋转60°得到△AED,若线段AB=4,则BE的长为()A.3B.4C.5D.62.如图,将△AOB绕着点O顺时针旋转,得到△COD,若∠AOB=40°,∠BOC=25°,则旋转角度是()A.25°B.15°C.65°D.40°3.如图,△ADE绕点D的顺时针旋转,旋转的角是∠ADE,得到△CDB,那么下列说法错误的是()A.DE平分∠ADB B.AD=DC C.AE∥BD D.AE=BC4.如图,若△ABC绕点A按逆时针方向旋转50°后与△AB1C1重合,则∠AB1B=()A.50°B.55°C.60°D.65°5.下列图案中,既是中心对称图形又是轴对称图形的是()A.B.C.D.6.如图,将△ABC绕点C(0,)旋转180°得到△A'B'C,设点A的坐标为(a,b),则点A'的坐标为()A.(﹣a,﹣b)B.(a,﹣b+2)C.(﹣a,﹣b+)D.(﹣a,﹣b+2)7.如图,将等边△AOB放在平面直角坐标系中,点A的坐标为(0,4),点B在第一象限,将等边△AOB绕点O顺时针旋转180°得到△A′OB′,则点B的对应点B′的坐标是()A.B.C.D.(0,﹣4)8.如图,在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°得到△BAE,连接ED,若BC=8,BD=7,则△AED的周长是()A.15B.14C.13D.129.如图,CD是△ABC的边AB上的中线,将线段AD绕点D顺时针旋转90°后,点A的对应点E恰好落在AC边上,若AD=,BC=,则AC的长为()A.B.3C.2D.410.在平面直角坐标系xOy中,点A(4,3),点B为x轴正半轴上一点,将△AOB绕其一顶点旋转180°,连接其余四个顶点得到一个四边形,若该四边形是一个轴对称图形,则满足条件的点有()A.5个B.4个C.3个D.2个二.填空题11.如图,四角星的顶点是一个正方形的四个顶点,将这个四角星绕其中心旋转,当第一次与自身重合时,其旋转角的大小是度.12.一副三角尺按如图的位置摆放(顶点C与F重合,边CA与边FE叠合,顶点B、C、D 在一条直线上).将三角尺DEF绕着点F按顺时针方向旋转n°后(0<n<180),如果EF⊥AB,那么n的值是.13.如图,在Rt△ABC,∠B=90°,∠ACB=50°.将Rt△ABC在平面内绕点A逆时针旋转到△AB'C'的位置,连接CC'.若AB∥CC',则旋转角的度数为°.14.如图,在正方形ABCD中,AB=4,点M在CD边上,且DM=1,△AEM与△ADM关于AM所在直线对称,将△ADM按顺时针方向绕点A旋转90°得到△ABF,连接EF,则线段EF的长为.15.已知点A(x﹣2,3)与B(x+4,y﹣5)关于原点对称,则xy的值是.16.如图,△ABC和△DEC关于点C成中心对称,若AC=1,AB=2,∠BAC=90°,则AE的长是.17.已知点P(a﹣3,2﹣a)关于原点对称的点在第四象限,则a的取值范围是.18.用四块大正方形地砖和一块小正方形地砖拼成如图所示的实线图案,每块大正方形地砖面积为a,小正方形地砖面积为b,依次连接四块大正方形地砖的中心得到正方形ABCD.则正方形ABCD的面积为.(用含a,b的代数式表示)19.在平面直角坐标系中,△OAB的位置如图所示,将△OAB绕点O顺时针旋转90°得△OA1B1;再将△OA1B1绕点O顺时针旋转90°得△OA2B2;再将△OA2B2绕点O顺时针旋转90°得△OA3B3;……依此类推,第2020次旋转得到△OA2020B2020,则项点A的对应点A2020的坐标是.三.解答题20.在平面直角坐标系中,已知点P(a,﹣1),请解答下列问题:(1)若点P在第三象限,则a的取值范围为;(2)若点P在y轴上,则a的值为;(3)当a=2时,点P关于y轴对称的点的坐标为点P关于原点对称的点的坐标为.21.如图,在△ABC中,AB=BC,∠ABC=120°,点D在边AC上,且线段BD绕着点B 按逆时针方向旋转120°能与BE重合,点F是ED与AB的交点.(1)求证:AE=CD;(2)若∠DBC=45°,求∠BFE的度数.22.如图所示,把△ABC绕点A旋转至△ADE位置,延长BC交AD于F,交DE于G,若∠CAD=10°,∠D=25°,∠EAB=120°,求∠DFB的度数.23.已知点A(﹣1,3a﹣1)与点B(2b+1,﹣2)关于x轴对称,点C(a+2,b)与点D 关于原点对称.(1)求点A、B、C、D的坐标;(2)顺次联结点A、D、B、C,求所得图形的面积.24.如图,正△ABC与正△A1B1C1关于某点中心对称,已知A,A1,B三点的坐标分别是(0,4),(0,3),(0,2).(1)求对称中心的坐标;(2)写出顶点C,C1的坐标.25.如图,在△ABC中,AB=AC,△ABC与△DEC关于点C成中心对称,连接AE、BD.(1)线段AE、BD具有怎样的位置关系和大小关系?说明你的理由.(2)如果△ABC的面积为5cm2,求四边形ABDE的面积.(3)当∠ACB为多少度时,四边形ABDE为矩形?说明你的理由.参考答案1.解:∵△ABC绕点A顺时针旋转60°得到△AED,∴AB=AE,∠BAE=60°,∴△AEB是等边三角形,∴BE=AB,∵AB=4,∴BE=4.故选:B.2.解:∵∠AOB=40°,∠BOC=25°,∴∠AOC=65°,∵将△AOB绕着点O顺时针旋转,得到△COD,∴旋转角为∠AOC=65°,故选:C.3.解:将△ADE绕点D顺时针旋转,得到△CDB,∴∠ADE=∠CDB,AD=CD,AE=BC,故A、B、D选项正确;∵∠B=∠E,但∠B不一定等于∠BDC,∴BD不一定平行于AE,故C选项错误;故选:C.4.解:∵△ABC绕点A按逆时针方向旋转50°后与△AB1C1重合,∴AB=AB1,∠BAB1=50°,∴∠AB1B=(180°﹣50°)=65°.故选:D.5.解:A、是轴对称图形,不是中心对称图形,不符合题意;B、既不是轴对称图形,也不是中心对称图形,不符合题意;C、不是轴对称图形,是中心对称图形,不符合题意;D、既是轴对称图形,又是中心对称图形,符合题意.故选:D.6.解:将点A的坐标为(a,b)向下平移个单位,得到对应点坐标为(a,b),再将其绕原点旋转180°可得对称点坐标为(﹣a,﹣b+),然后再向上平移个单位可得点A'的坐标为(﹣a,﹣b+2),故选:D.7.解:作BH⊥y轴于H,如图,∵△OAB为等边三角形,∴OH=AH=2,∠BOA=60°,∴BH=OH=2,∴B点坐标为(2,2),∵等边△AOB绕点O顺时针旋转180°得到△A′OB′,∴点B′的坐标是(﹣2,﹣2).故选:C.8.解:∵将△BCD绕点B逆时针旋转60°得到△BAE,∴BD=BE,∠DBE=60°,CD=AE,∴△DBE是等边三角形,∴BD=DE=7,∴△AED的周长=AE+AD+DE=CD+AD+DE=8+7=15,故选:A.9.解:如图,连接BE,∵CD是△ABC的边AB上的中线,∴AD=BD,∵将线段AD绕点D顺时针旋转90°,∴AD=DE,∠ADE=90°,∴∠A=45°,AE=AD=2,AD=DE=BD,∴∠AEB=90°,∴∠A=∠ABE=45°,∴AE=BE=2,∴EC===1,∴AC=AE+EC=3,故选:B.10.解:观察图象可知,满足条件的点B有5个.故选:A.11.解:该图形被平分成四部分,旋转90°的整数倍,就可以与自身重合,故当此图案第一次与自身重合时,其旋转角的大小为90°.故答案为:90.12.解:如图1,延长EF交AB于H,∵EF⊥AB,∠A=45°,∴∠ACH=45°,∴∠ACE=135°,∴n=135;如图2,∵EF⊥AB,∠A=45°,∴∠ACE=45°,∴n=360﹣45=315,∵0<n<180,∴n=315不合题意舍去,故答案为:135.13.解:∵AB∥CC',∴∠ABC+∠C′CB=180°,而∠B=90°,∴∠C′CB=90°,∴∠ACC′=90°﹣∠ACB=90°﹣50°=40°,∵Rt△ABC在平面内绕点A逆时针旋转到△AB'C'的位置,∴AC=AC′,∠C′AC等于旋转角,∴∠AC′C=∠ACC′=40°,∴∠C′AC=180°﹣40°﹣40°=100°,即旋转角为100°.故答案为100.14.解:如图,连接BM.∵△AEM与△ADM关于AM所在的直线对称,∴AE=AD,∠MAD=∠MAE.∵△ADM按照顺时针方向绕点A旋转90°得到△ABF,∴AF=AM,∠F AB=∠MAD.∴∠F AB=∠MAE,∴∠F AB+∠BAE=∠BAE+∠MAE.∴∠F AE=∠MAB.∴△F AE≌△MAB(SAS).∴EF=BM.∵四边形ABCD是正方形,∴BC=CD=AB=4.∵DM=1,∴CM=3.∴在Rt△BCM中,BM==5,∴EF=5,故答案为:5.15.解:∵点A(x﹣2,3)与B(x+4,y﹣5)关于原点对称,∴x﹣2+x+4=0,3+y﹣5=0,解得:x=﹣1,y=2,则xy的值是:﹣2.故答案为:﹣2.16.解:∵△DEC与△ABC关于点C成中心对称,∴△ABC≌△DEC,∴AB=DE=2,AC=DC=1,∠D=∠BAC=90°,∴AD=2,∵∠D=90°,∴AE==2,故答案为2.17.解:∵点P(a﹣3,2﹣a)关于原点对称的点在第四象限,∴点P(a﹣3,2﹣a)在第二象限,,解得:a<2.∴故答案为:a<2.18.解:如图,连接DK,DN,∵∠KDN=∠MDT=90°,∴∠KDM=∠NDT,∵DK=DN,∠DKM=∠DNT=45°,∴△DKM≌△DNT(ASA),∴S△DKM=S△DNT,∴S四边形DMNT=S△DKN=a,∴正方形ABCD的面积=4×a+b=a+b.故答案为(a+b).19.解:将△OAB绕点O顺时针旋转90°得△OA1B1;此时,点A1的坐标为(2,﹣1);再将△OA1B1绕点O顺时针旋转90°得△OA2B2;此时,点A2的坐标为(﹣1,2);再将△OA2B2绕点O顺时针旋转90°得△OA3B3;此时,点A3的坐标为(﹣2,1);再将△OA3B3绕点O顺时针旋转90°得△OA4B4;此时,点A4的坐标为(1,2);∴每旋转4次一个循环,∵2020÷4=505,∴第2020次旋转得到△OA2020B2020,则顶点A的对应点A2020的坐标与点A4的坐标相同,为(1,2);故答案为:(1,2).20.解:(1)∵点P(a,﹣1),点P在第三象限,∴a<0;故答案为:a<0;(2)∵点P(a,﹣1),点P在y轴上,∴a=0;故答案为:0;(3)当a=2时,点P(a,﹣1)的坐标为:(2,﹣1)关于y轴对称的点的坐标为:(﹣2,﹣1),点P关于原点对称的点的坐标为:(﹣2,1).故答案为:(﹣2,﹣1),(﹣2,1).21.(1)证明:∵线段BD绕着点B按逆时针方向旋转120°能与BE重合,∴BD=BE,∠EBD=120°,∵AB=BC,∠ABC=120°,∴∠ABD+∠DBC=∠ABD+∠ABE=120°,∴∠DBC=∠ABE,∴△ABE≌△CBD(SAS),∴AE=CD;(2)解:由(1)知∠DBC=∠ABE=45°,BD=BE,∠EBD=120°,∴∠BED=∠BDE=(180°﹣120°)=30°,∴∠BFE=180°﹣∠BED﹣∠ABE=180°﹣30°﹣45°=105°.22.解:由旋转可知:△ABC≌△ADE,∵∠D=25°,∴∠B=∠D=25°,∠EAD=∠CAB,∵∠EAB=∠EAD+∠CAD+∠CAB=120°,∠CAD=10°,∴∠CAB=(120°﹣10°)÷2=55°,∴∠F AB=∠CAB+∠CAD=55°+10°=65°,∵∠DFB是△ABF的外角,∴∠DFB=∠B+∠F AB,∴∠DFB=25°+65°=90°.23.解:(1)∵点A(﹣1,3a﹣1)与点B(2b+1,﹣2)关于x轴对称,∴2b+1=﹣1,3a﹣1=2,解得a=1,b=﹣1,∴点A(﹣1,2),B(﹣1,﹣2),C(3,﹣1),∵点C(a+2,b)与点D关于原点对称,∴点D(﹣3,1);(2)如图所示:四边形ADBC的面积为:.24.解:(1)∵A,A1,B三点的坐标分别是(0,4),(0,3),(0,2),所以对称中心的坐标为(0,2.5);(2)等边三角形的边长为4﹣2=2,所以点C的坐标为(,3),点C1的坐标(,2).25.解:(1)∵△ABC与△DEC关于点C成中心对称,∴AC=CD,BC=CE,∴四边形ABDE是平行四边形,∴AE与BD平行且相等;(2)∵四边形ABDE是平行四边形,∴S△ABC=S△BCD=S△CDE=S△ACE,∵△ABC的面积为5cm2,∴四边形ABDE的面积=4×5=20cm2;(3)∠ACB=60°时,四边形ABDE为矩形.理由如下:∵AB=AC,∠ACB=60°,∴△ABC是等边三角形,∴AC=BC,∵四边形ABDE是平行四边形,∴AD=2AC,BE=2BC,∴AD=BE,∴四边形ABDE为矩形.。
人教版九年级数学上册 第23章 旋转 单元测试卷

第23章旋转一.选择题(共10小题,满分30分,每小题3分)1.时钟上的分针匀速旋转一周需要60min,则经过5min,分针旋转了()A.10°B.20°C.30°D.60°2.将图中可爱的“小鸭子”图片按顺时针方向旋转90°后得到的图片是()A.B.C.D.3.香港特别行政区的区徽中间紫金花图案如图所示,则至少需要旋转()和原图案重合.A.72°B.60°C.36°D.18°4.下列四张扑克牌图案,属于中心对称图形的是()A.B.C.D.5.下列图形中,中心对称图形有()A.1个B.2个C.3个D.4个6.在平面直角坐标系中,点M(1,﹣2)与点N关于原点对称,则点N的坐标为()A.(﹣2,1)B.(1,﹣2)C.(2,﹣1)D.(﹣1,2)7.在中国集邮总公司设计的2017年纪特邮票首日纪念戳图案中,可以看作中心对称图形的是()A.千里江山图B.京津冀协同发展C.内蒙古自治区成立七十周年D.河北雄安新区建立纪念8.如图所示的图案分别是大众、奥迪、奔驰、三菱汽车的车标,其中,可以看作由“基本图案”经过平移得到的是()A.B.C.D.9.如图,在方格纸中,选择标有序号①②③④中的一个小正方形涂黑,不能与图中阴影部分构成轴对称图形的是()A.①B.②C.③D.④10.如图,将等边三角形OAB放在平面直角坐标系中,A点坐标(1,0),将△OAB绕点O逆时针旋转60°,则旋转后点B的对应点B′的坐标为()A.(﹣,)B.(﹣1,)C.(﹣,)D.(﹣,)二.填空题(共7小题,满分28分,每小题4分)11.如图,香港特别行政区区徽由五个相同的花瓣组成,它是以一个花瓣为“基本图案”通过连续四次旋转所组成,这四次旋转中,旋转角度最小是度.12.在平面直角坐标系中,点A(0,1)关于原点对称的点是.13.把一个正六边形绕着其对称中心旋转一定的角度,要使旋转后的图形与原来的图形重合,那么旋转的角度至少是°.14.如图,把△ABC绕着点A顺时针方向旋转角度α(0°<α<90°),得到△AB'C',若B',C,C'三点在同一条直线上,∠B'CB=46°,则α的度数是.15.若点A(m,7)与点B(﹣4,n)关于原点成中心对称,则m+n=.16.如图,Rt△ABC中,∠ABC=90°,AB=BC=2,将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,那么BM的长是.17.如图,在平面直角坐标系xOy中,△DEF可以看作是△ABC经过若干次图形的变化(平移、轴对称、旋转)得到的,写出一种由△ABC得到△DEF的过程:.三.解答题(共8小题,满分62分)18.(6分)请在如图四个3×3的正方形网格中,画出与格点三角形(阴影部分)成轴对称且以格点为顶点的三角形,并将所画三角形涂上阴影.(注:所画的四个图不能重复)19.(6分)如图,∠ACD=90°,AC=DC,MN是过点A的直线,DB⊥MN于点B,连接BC.(1)当MN绕A旋转到如图1位置时,线段AB、BC、BD之间满足怎样的数量关系,请写出你的猜想,并证明你的猜想.(2)MN在绕点A旋转过程中,当∠BCD=30°,BD=时,则CB=.20.(6分)如图,在平面直角坐标系中,△ABC的三个顶点分别是A(1,3),B(4,4),C(2,1).(1)把△ABC向左平移4个单位后得到对应的△A1B1C1,请画出平移后的△A1B1C1;(2)把△ABC绕原点O旋转180°后得到对应的△A2B2C2,请画出旋转后的△A2B2C2;(3)观察图形可知,△A1B1C1与△A2B2C2关于点(,)中心对称.21.(8分)如图,在边长为1个单位长度的小正方形组成的网格中,点A、B、C都是格点.(1)将△ABC向左平移6个单位长度得到△A1B1C1;(2)将△ABC绕点O按逆时针方向旋转180°得到△A2B2C2,请画出△A2B2C2;(3)若点B的坐标为(3,3);写出△A1B1C1与△A2B2C2的对称中心的坐标.22.(8分)已知点P(x,y)的坐标满足方程(x+3)2+=0,求点P分别关于x轴,y轴以及原点的对称点坐标.23.(8分)将两块全等的含30°角的直角三角板按图1的方式放置,已知∠BAC=∠B1A1C =30°,AB=2BC.(1)固定三角板A1B1C,然后将三角板ABC绕点C顺时针方向旋转至图2所示的位置,AB与A1C、A1B1分别交于点D、E,AC与A1B1交于点F.①填空:当旋转角等于20°时,∠BCB1=度;②当旋转角等于多少度时,AB与A1B1垂直?请说明理由.(2)将图2中的三角板ABC绕点C顺时针方向旋转至图3所示的位置,使AB∥CB1,AB与A1C交于点D,试说明A1D=CD.24.(10分)将Rt△ABC绕点直角顶点C逆时针旋转90°后得到△A'B'C,A'B'的延长线与AB交于点D,连接DC.①求证:AB⊥A'D;②求∠A'DC的度数.25.(10分)已知,△ABC中,AB=AC,点E是边AC上一点,过点E作EF∥BC交AB 于点F.(1)如图①,求证:AE=AF;(2)如图②,将△AEF绕点A逆时针旋转α(0°<α<144°)得到△AE′F′.连接CE′、BF′.①若BF′=6,求CE′的长;②若∠EBC=∠BAC=36°,在图②的旋转过程中,当CE′∥AB时,直接写出旋转角α的大小.参考答案一.选择题(共10小题,满分30分,每小题3分)1.解:根据题意知,分针旋转一周(360°)需要60min,则分针每分钟旋转=6°,∴经过5min,分针旋转了5×6=30°,故选:C.2.解:如图所示:“小鸭子”图片按顺时针方向旋转90°后得到的图片是:.故选:C.3.解:观察图形可知,中心角是由五个相同的角组成,∴旋转角度是360°÷5=72°,∴这四次旋转中,旋转角度最小是72°,故选:A.4.解:A、是中心对称图形,符合题意;B、不是中心对称图形,不符合题意;C、不是中心对称图形,不符合题意;D、不是中心对称图形,不符合题意.故选:A.5.解:第一个图形是中心对称图形;第二个图形不是中心对称图形;第三个图形是中心对称图形;第四个图形不是中心对称图形.故共2个中心对称图形.故选:B.6.解:∵点M(1,﹣2)与点N关于原点对称,点N的坐标为(﹣1,2),故选:D.7.解:A选项是轴对称图形,不是中心对称图形,故本选项错误;B选项不是中心对称图形,故本选项错误;C选项为中心对称图形,故本选项正确;D选项不是中心对称图形,故本选项错误.故选:C.8.解:观察图形可知,图案B可以看作由“基本图案”经过平移得到.故选:B.9.解:选择标有序号①②③④中的一个小正方形涂黑,不能与图中阴影部分构成轴对称图形的是:④.故选:D.10.解:如图,故点B作BH⊥OA于H,设BB′交y轴于J.∵A(1,0),∴OA=1,∵△AOB是等边三角形,BH⊥OA,∴OH=AH=OA=,BH=OH=,∴B(,),∵∠AOB=∠BOB′=60°,∠JOA=90°,∴∠BOJ=∠JOB′=30°,∵OB=OB′,∴BB′⊥OJ,∴BJ=JB′,∴B,B′关于y轴对称,∴B′(﹣,),故选:A.二.填空题(共7小题,满分28分,每小题4分)11.解:观察图形可知,中心角是由五个相同的角组成,∴旋转角度是360°÷5=72°,∴这四次旋转中,旋转角度最小是72°.12.解:点(0,1)关于原点O对称的点是(0,﹣1),故答案为:(0,﹣1).13.解:正六边形旋转最小的角度,360°÷6=60°,故答案为:60°14.解:由题意可得:AC=AC′,∠C'=∠ACB,∴∠ACC'=∠C',∵把△ABC绕着点A顺时针方向旋转α,得到△AB′C′,点C刚好落在边B′C′上,∴∠B'CB+∠ACB=∠C'+∠CAC′,∠B'CB=∠CAC'=46°.故答案为:46°.15.解:∵点A(m,7)与点B(﹣4,n)关于原点成中心对称,∴m=4,n=﹣7,∴m+n=﹣3.故答案为:﹣3.16.解:如图,连接AM,由题意得:CA=CM,∠ACM=60°,∴△ACM为等边三角形,∴AM=CM,∠MAC=∠MCA=∠AMC=60°;∵∠ABC=90°,AB=BC=2,∴AC=CM=2,∵AB=BC,CM=AM,∴BM垂直平分AC,∴BO=AC=,OM=CM•sin60°=,∴BM=BO+OM=+,故答案为:+.17.解:△ABC绕C点逆时针旋转90°,并向左平移2个单位得到△DEF;故答案为:△ABC绕C点逆时针旋转90°,并向左平移2个单位得到△DEF 三.解答题(共8小题,满分62分)18.解:如图所示:.19.解:(1)BD+AB=CB理由如下:如图,过点C作CE⊥CB于点C,与MN交于点E∵∠ACB+∠BCD=90°,∠ACB+∠ACE=90°,∴∠BCD=∠ACE∵DB⊥MN∴∠ABC+∠CBD=90°,∵CE⊥CB∴∠ABC+∠CEA=90°,∴∠CBD=∠CEA.又∵AC=DC,∴△ACE≌△DCB(AAS),∴AE=DB,CE=CB,∴△ECB为等腰直角三角形,∴BE=CB.又∵BE=AE+AB,∴BE=BD+AB,∴BD+AB=CB(2)若点B在CD上方,连接AD,过点D作DF⊥BC于点F,∵AC=CD,∠ACD=90°,∴∠CAD=∠ADC=45°,∵∠ACD=∠ABD=90°,∴点A,点C,点D,点B四点共圆,∴∠CAD=∠CBD=45°,且CF⊥BC ∴∠FBD=∠FDB=45°,且BD=∴BF=DF=1,∵∠BCD=30°,DF⊥BC∴CF=DF=∴BC=CF+BF=+1当点B在CD的下方,同理可得DF=BF=1,CF=∴BC=﹣1故答案为:+1或﹣120.解:(1)如图所示,△A1B1C1即为所求;(2)如图所示,△A2B2C2即为所求;(3)由图可得,△A1B1C1与△A2B2C2关于点(﹣2,0)中心对称.故答案为:﹣2,0.21.解:(1)如图,△A1B1C1即为所求;(2)如图,△A2B2C2即为所求;(3)C1C2与x轴的交点即为△A1B1C1与△A2B2C2的对称中心,所以对称中心的坐标为(﹣2,0).故答案为:(﹣2,0).22.解:由题意,得x+3=0,y+4=0,解得x=﹣3,y=﹣4,P点的坐标为(﹣3,﹣4),点P关于x轴,y轴以及原点的对称点坐标分别为(﹣3,4),(3,﹣4),(3,4).23.解:(1)①∵将三角板ABC绕点C顺时针方向旋转至图2所示的位置,∴∠A1CA=20°∴∠ACB1=70°,∴∠BCB1=∠ACB+∠ACB1=160°;故答案为160;②当旋转角等于30°时,AB与A1B1垂直.理由如下:当AB与A1B1垂直时,∠A1ED=90°,∴∠A1DE=90°﹣∠A1=90°﹣30°=60°,∴∠BDC=60°,∵∠B=60°,∴∠A1CB=180°﹣∠BDC﹣∠B=60°,∴∠ACA1=90°﹣∠A1CB=30°;即旋转角等于30°时,AB与A1B1垂直;(2)∵AB∥CB1,∠ACB1=90°,∴∠ADC=90°,在Rt△ADC中,∠A=30°,∴CD=AC,∵图2中的三角板ABC绕点C顺时针方向旋转至图3所示的位置,∴AC=A1C,∴CD=A1C,∴A1D=CD.24.解:(1)∵将Rt△ABC绕点直角顶点C逆时针旋转90°后得到△A'B'C,∴∠A=∠A',∠B=∠A'B'C,BC=B'C,AC=A'C',∵∠A+∠B=90°,∴∠A'+∠B=90°∴∠A'DB=90°,∴AB⊥A'D(2)如图,过点C作CE⊥A'D于E,CF⊥AB于F,∵∠A'=∠A,A'C=AC,∠A'EC=∠AFC=90°,∴△A'EC≌△AFC(AAS)∴CE=CF,且CE⊥A'D,CF⊥AB,∴∠CDF=∠CDE,且∠A'DB=90°,∴∠A'DC=45°25.(1)证明:∵AB=AC,∴∠ABC=∠ACB,∵EF∥BC,∴∠AFE=∠ABC,∠AEF=∠ACB,∴∠AFE=∠AEF,∴AE=AF.(2)解:①由旋转的性质得,∠E′AC=∠F′AB,AE′=AF′,在△CAE′和△BAF′中,,∴△CAE′≌△BAF′(SAS),∴CE′=BF′=6;②由(1)可知AE=AF,所以,在△AEF绕点A逆时针旋转过程中,点E经过的路径(圆弧)与过点C且与AB 平行的直线l相交于点M、N,如图,①当点E的像E′与点M重合时,四边形ABCM是等腰梯形,所以,∠BAM=∠ABC=72°,又∵∠BAC=36°,∴α=∠CAM=36°;②当点E的像E′与点N重合时,∵CE′∥AB,∴∠AMN=∠BAM=72°,∵AM=AN,∴∠ANM=∠AMN=72°,∴∠MAN=180°﹣72°×2=36°,∴α=∠CAN=∠CAM+∠MAN=36°+36°=72°,综上所述,当旋转角α为36°或72°.。
人教版九年级数学上册《第23章旋转》单元测试卷含答案
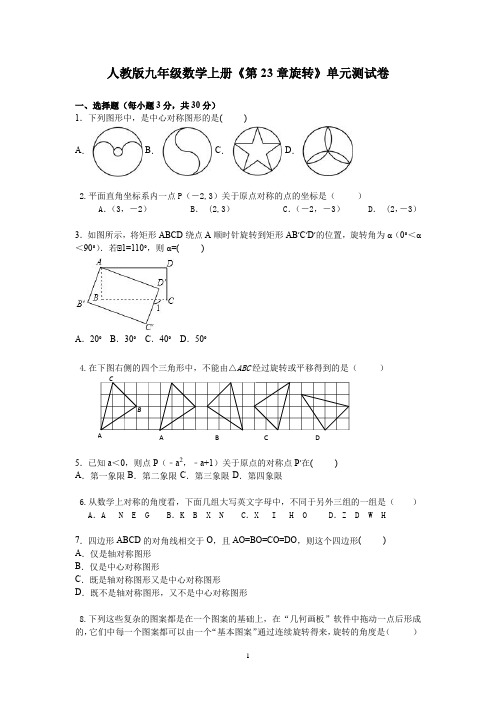
人教版九年级数学上册《第23章旋转》单元测试卷一、选择题(每小题3分,共30分)1.下列图形中,是中心对称图形的是( )A .B .C .D .2.平面直角坐标系内一点P (-2,3)关于原点对称的点的坐标是( )A .(3,-2)B . (2,3)C .(-2,-3)D . (2,-3)3.如图所示,将矩形ABCD 绕点A 顺时针旋转到矩形AB ′C ′D ′的位置,旋转角为α(0°<α<90°).若∠1=110°,则α=( )A .20°B .30°C .40°D .50°4.在下图右侧的四个三角形中,不能由△ABC 经过旋转或平移得到的是( )5.已知a <0,则点P (﹣a 2,﹣a+1)关于原点的对称点P ′在( )A .第一象限B .第二象限C .第三象限D .第四象限6.从数学上对称的角度看,下面几组大写英文字母中,不同于另外三组的一组是( )A .A N E GB .K B X NC .X I H OD .Z D W H7.四边形ABCD 的对角线相交于O ,且AO=BO=CO=DO ,则这个四边形( ) A .仅是轴对称图形B .仅是中心对称图形C .既是轴对称图形又是中心对称图形D .既不是轴对称图形,又不是中心对称图形8.下列这些复杂的图案都是在一个图案的基础上,在“几何画板”软件中拖动一点后形成的,它们中每一个图案都可以由一个“基本图案”通过连续旋转得来,旋转的角度是( )A B CA B C DA.︒30 B.︒9045 C.︒60 D.︒9.下列命题正确的个数是( )(1)成中心对称的两个三角形是全等三角形;(2)两个全等三角形必定关于某一点成中心对称;(3)两个三角形对应点的连线都经过同一点,则这两个三角形关于该点成中心对称;(4)成中心对称的两个三角形,对称点的连线都经过对称中心.A.1B.2C.3D.410.如图,在正方形网格中,将∠ABC绕点A旋转后得到∠ADE,则下列旋转方式中,符合题意的是( )A.顺时针旋转90°B.逆时针旋转90°C.顺时针旋转45°D.逆时针旋转45°二、填空题(每小题3分,共24分)11.如图,在6×4方格纸中,格点三角形甲经过旋转后得到格点三角形乙,则其旋转中心是( )A.点M B.格点N C.格点P D.格点Q12.已知a<0,则点P(a2,-a+3)关于原点的对称点P1在第________象限.13.如图4,△COD是△AOB绕点O顺时针方向旋转40°后所得的图形,点C恰好在AB上,∠AOD=90°,则∠D的度数是.14.如图5,在两个同心圆中,三条直径把大圆分成相等的六部分,若大圆的半径为2,则图中阴影部分的面积是__________.15.如图6,四边形ABCD中,∠BAD=∠C=90º,AB=AD,AE⊥BC于E,若线段AE=5,则S四A边形ABCD=.16.如图,设P是等边三角形ABC内任意一点,∠ACP′是由∠ABP旋转得到的,则PA__________PB+PC(选填“>”、“=”、“<”)17.已知点P(﹣b,2)与点Q(3,2a)关于原点对称,则a+b的值是__________.18.直线y=x+3上有一点P(3,n),则点P关于原点的对称点P′为__________.三、解答题(共66分)19.如图,在Rt∠OAB中,∠OAB=90°,OA=AB=6,将∠OAB绕点O沿逆时针方向旋转90°得到∠OA1B1.(1)线段OA1的长是__________,∠AOB1的度数是__________;(2)连接AA1,求证:四边形OAA1B1是平行四边形;(3)求四边形OAA1B1的面积.20.(9分)如图10,E、F分别是正方形ABCD的边CD、DA上一点,且CE+AF=EF,请你用旋转的方法求∠EBF的大小.21.(9分)已知正方形ABCD和正方形AEFG有一个公共点A,点G、E分别在线段AD、AB上. (1)如图11(1), 连接DF、BF,若将正方形AEFG绕点A按顺时针方向旋转,判断命题:“在旋转的过程中,线段DF与BF的长始终相等”是否正确,若正确请说明理由,若不正确请举反例说明;(2)若将正方形AEFG绕点A按顺时针方向旋转, 连接DG,在旋转的过程中,你能否找到一条线段的长与线段DG的长始终相等?并以图11(2)为例说明理由.图1022.如图,在Rt∠ABC中,∠ACB=90°,点D、F分别在AB、AC上,CF=CB,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CE,连接EF.(1)求证:∠BCD∠∠FCE;(2)若EF∠CD,求∠BDC的度数.23.如图,将正方形ABCD中的∠ABD绕对称中心O旋转至∠GEF的位置,EF交AB于M,GF交BD于N.请猜想BM与FN有怎样的数量关系?并证明你的结论.24.如图,∠ABC是直角三角形,延长AB到点E,使BE=BC,在BC上取一点F,使BF=AB,连接EF,∠ABC旋转后能与∠FBE重合,请回答:(1)旋转中心是哪一点?(2)旋转了多少度?(3)AC与EF的关系如何?答案:一、选择题(每小题3分,共30分)1.B 2.D 3.A 4.B 5.D 6.D 7.C 8.C 9.B 10.B二、填空题(每小题3分,共24分)11.B12.故答案为15°.13.故答案为:4.14.故填空答案:4π.15.∠PA <PB+PC .16.故答案为:(3,﹣4).17.故答案为:2.18.故答案为:(﹣3,﹣6).三、解答题(共66分)19.(1)解:因为,∠OAB=90°,OA=AB ,所以,∠OAB 为等腰直角三角形,即∠AOB=45°,根据旋转的性质,对应点到旋转中心的距离相等,即OA 1=OA=6,对应角∠A 1OB 1=∠AOB=45°,旋转角∠AOA 1=90°,所以,∠AOB 1的度数是90°+45°=135°.(2)证明:∠∠AOA 1=∠OA 1B 1=90°,∠OA ∠A 1B 1,又∠OA=AB=A 1B 1,∠四边形OAA 1B 1是平行四边形.(3)解:∠OAA 1B 1的面积=6×6=36.20.解:将△BCE 以B 为旋转中心,逆时针旋转90º,使BC 落在BA 边上,得△BAM ,则∠MBE=90º,AM=CE,BM=BE,因为CE +AF =EF ,所以MF =EF ,又BF=BF,所以△FBM ≌△FBE,所以∠MBF=∠EBF, 所以∠EBF=ºº190452⨯= 21.解:(1)解:(1)不正确.若在正方形GAEF 绕点A 顺时针旋转45°,这时点F 落在线段AB 或AB 的延长线上.(或将正方形GAEF 绕点A 顺时针旋转,使得点F 落在线段AB 或AB 的延长线上).如图:设AD=a ,AG=b ,则22a 2b +a ,2b|<a ,∴DF >BF ,即此时DF ≠BF ;(2)连接BE ,则DG=BE .如图,(2)连接BE ,则DG=BE .如图,∵四边形ABCD 是正方形,∴AD=AB ,∵四边形GAEF 是正方形,∴AG=AE ,又∠DAG+∠GAB=90°,∠BAE+∠GAB=90°,∴∠DAG=∠BAE,∴△DAG≌△BAE,∴DG=BE.∵四边形ABCD是正方形,∴AD=AB,∵四边形GAEF是正方形,∴AG=AE,又∠DAG+∠GAB=90°,∠BAE+∠GAB=90°,∴∠DAG=∠BAE,∴△DAG≌△BAE,∴DG=BE.22.(1)证明:∠将线段CD绕点C按顺时针方向旋转90°后得CE,∠CD=CE,∠DCE=90°,∠∠ACB=90°,∠∠BCD=90°﹣∠ACD=∠FCE,在∠BCD和∠FCE中,,∠∠BCD∠∠FCE(SAS).(2)解:由(1)可知∠BCD∠∠FCE,∠∠BDC=∠E,∠BCD=∠FCE,∠∠DCE=∠DCA+∠FCE=∠DCA+∠BCD=∠ACB=90°,∠EF∠CD,∠∠E=180°﹣∠DCE=90°,∠∠BDC=90°.23.解:猜想:BM=FN.证明:在正方形ABCD中,BD为对角线,O为对称中心,∠BO=DO,∠BDA=∠DBA=45°,∠∠GEF为∠ABD绕O点旋转所得,∠FO=DO,∠F=∠BDA,∠OB=OF,∠OBM=∠OFN,在∠OMB和∠ONF中,∠∠OBM∠∠OFN,∠BM=FN.24.解:(1)∠BC=BE,BA=BF,∠BC和BE,BA和BF为对应边,∠∠ABC旋转后能与∠FBE重合,∠旋转中心为点B;(2)∠∠ABC=90°,而∠ABC旋转后能与∠FBE重合,∠∠ABF等于旋转角,∠旋转了90度;(3)AC=EF,AC∠EF.理由如下:∠∠ABC绕点B顺时针旋转90°后能与∠FBE重合,∠EF=AC,EF与AC成90°的角,即AC∠EF.。
九年级数学上册《第二十三章 旋转》单元测试卷及答案-人教版

九年级数学上册《第二十三章 旋转》单元测试卷及答案-人教版一、选择题1.如图,将ABC 绕点A 顺时针旋转60︒得到AED (点B 旋转至点E ,点C 旋转至点D ),若线段4AB =,则BE 的长为( )A .4B .5C .6D .72.古典园林中的花窗通常利用对称构图,体现对称美.下面四个花窗图案,既是轴对称图形又是中心对称图形的是( )A .B .C .D .3.下列图形既是轴对称图形,又是中心对称图形的是( )A .等边三角形B .等腰三角形C .平行四边形D .菱形4.若点()2A a -,,()3B b ,关于原点成中心对称,则a ,b 的值分别为( ) A .3a =和2b =- B .3a =-和2b =- C .3a =和2b =D .3a =-和2b =5.下列大学校微可以看成是由图案自身的一部分经平移后得到的为( )A .B .C .D .6.如图,在正方形ABCD 中,点E ,F 分别在BC ,CD 上,连接AE ,AF ,EF ,45EAF ∠=︒若αBAE ∠=,则FEC ∠一定等于( )A .2αB .902α︒-C .45α︒-D .90α︒-7.如图,在平面直角坐标系中,点A 的坐标是()23-,,将线段OA 绕点O 顺时针旋转90︒得到线段OB ,则点B 的坐标为( )A .()23,B .()32,C .()32--,D .()23-,8.如图,以平行四边形ABCD 对角线的交点O 为原点.平行于BC 边的直线为x 轴,建立如图所示的平面直角坐标系.若D 点坐标为()53,.则B 点坐标为( )A .()43--,B .()35--,C .()53--,D .()34--,9.下面四个图案中,不能由基本图案(图中阴影部分)旋转得到的是( )A .B .C .D .10.如图,在 33⨯ 的正方形网格中两个小正方形被涂黑,再将图中其余小正方形任意一个涂黑,使得整个图形(包括网格)构成一个轴对称图形,那么涂法共有( )A .4种B .5种C .6种D .7种二、填空题11.如图,将ABC 绕着点A 逆时针旋转得到ADE ,使得点B 的对应点D 落在边AC 的延长线上若8AB =,5AE =则线段CD 的长为 .12.在①平行四边形、②正方形、③等边三角形、④等腰梯形、⑤圆、⑥正八边形这些图形中,既是轴对称图形又是中心对称图形的是 (填序号).13.在直角坐标系中,点(4,5)绕原点O 逆时针方向旋转90°,得到的点的坐标是 .14.把18个边长都为1的等边三角形如图拼接成平行四边形,且其中6个涂上了阴影,现在,可以旋转、翻折或平移某一个阴影等边三角形到某一个空白的等边三角形处,使新构成的阴影部分图案是轴对称图形,共可得 种轴对称图形.三、解答题15.如图,点E ,F 分别在正方形ABCD 的边BC ,CD 上,且45EAF ∠=︒.把ADF 绕点A 顺时针旋转90︒得到ABG .求证:AGE AFE ≌.16.如图所示,正方形网格中,ABC 为格点三角形(即三角形的顶点都在格点上).( 1 )把ABC 沿BA 方向平移后,点A 移到点1A ,在网格中画出平移后得到的111A B C ; ( 2 )把111A B C 绕点1A 按逆时针方向旋转90︒,在网格中画出旋转后的122A B C .17.ABC 在平面直角坐标系xoy 中的位置如图所示.( 1 )作ABC 关于点C 成中心对称的111A B C .( 2 )将111A B C 向右平移3个单位,作出平移后的222A B C .( 3 )在x 轴上求作一点P ,使12PA PC +的值最小,并求出点P 的坐标.18.如果点 (11)P x y --,在第二象限,那么点 (11)Q x y --, 关于原点的对称点 M 在第几象限?19.如图是4×4的正方形网格,请选取一个白色的正方形并涂上阴影,使图中阴影部分是一个中心对称图形.四、综合题20.如图1,一大一小两个等腰直角三角形叠放在一起,M ,N 分别是斜边DE ,AB 的中点24DE AB ==,(1)将CDE绕顶点C旋转一周,请直接写出点M,N距离的最大值和最小值;(2)将CDE绕顶点C逆时针旋转120 (如图2),求MN的长.21.知识背景:过中心对称图形的对称中心的任意一条直线都将其分成全等的两个部分.(1)如图①,直线EF经过平行四边形ABCD对角线的交点O,则S四边形AEFB S四边形DEFC(填“>”“<”“=”);(2)如图②,两个矩形如图所示摆放,O为小矩形对角线的交点,求作过点O的直线将整个图形分成面积相等的两部分;(3)八个大小相同的正方形如图③所示摆放,求作直线将整个图形分成面积相等的两部分(用两种方法分割).22.阅读材料:课堂上,老师设计了一个活动:将一个4×4的正方形网格沿着网格线划分成两部分(分别用阴影和空白表示),使得这两部分图形是全等的,请同学们尝试给出划分的方法.约定:如果两位同学的划分结果经过旋转、翻折后能够重合,那么就认为他们的划分方法相同.小方、小易和小红分别对网格进行了划分,结果如图①、图②、图③所示.小方说:“我们三个人的划分方法都是正确的.但是将小红的整个图形(图③)逆时针旋转90°后得到的划分方法与我的划分方法(图①)是一样的,应该认为是同一种方法,而小易的划分方法与我的不同.”老师说:“小方说得对.”完成下列问题:(1)图④的划分方法是否正确?(2)判断图⑤的划分方法与图②小易的划分方法是否相同,并说明你的理由.(3)请你再想出一种与已有方法不同的划分方法,使之满足上述条件,并在图⑥中画出来.参考答案与解析1.【答案】A【解析】【解答】解:由旋转的性质得:60BAE AE AB ∠=︒=,ABE ∴是等边三角形4BE AB ∴==故答案为:A.【分析】由旋转的性质得∠BAE=60°,AE=AB ,根据有一个角是60°的等腰三角形是等边三角形得∠ABE 是等边三角形,进而根据等边三角形的三边相等得BE=AB=4.2.【答案】C【解析】【解答】解:A 、是轴对称图形,不是中心对称图形,故此选项不符合题意;B 、即不是轴对称图形,也不是中心对称图形,故此选项不符合题意;C 、即是轴对称图形,也是中心对称图形,故此选项符合题意;D 、是轴对称图形,不是中心对称图形,故此选项不符合题意. 故答案为:C.【分析】把一个平面图形,沿着某一条直线折叠,直线两旁的部分能完全重合的平面图形就是轴对称图形;把一个平面图形,沿着某一点旋转180°后,能与自身重合的图形就是中心对称图形,根据定义即可一一判断得出答案.3.【答案】D【解析】【解答】解:A 、等边三角形是轴对称图形,不是中心对称图形,故不符合题意;B 、等腰三角形是轴对称图形,不是中心对称图形,故不符合题意;C 、平行四边形是中心对称图形,不是轴对称图形,故不符合题意;D 、菱形既是轴对称图形,又是中心对称图形,故符合题意; 故答案为:D.【分析】中心对称图形:把一个图形绕着某一点旋转180°后,旋转后的图形能够与原来的图形重合,轴对称图形:一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形,据此逐项判断即可.4.【答案】D【解析】【解答】解:∵A (a ,-2)、B (3,b )关于原点成中心对称∴a=-3,b=2. 故答案为:D.【分析】关于原点对称的点:横、纵坐标均互为相反数,据此解答.5.【答案】C【解析】【解答】解:A 、是一个轴对称图形,不能由平移得到,故此选项错误,不符合题意;B 、是一个轴对称图形,不能由平移得到,故此选项错误,不符合题意;C 、图案是由自身一部分沿着直线平移后得到的, 故此选项正确,符合题意;D 、此图案不能由平移得到,故此选项错误,不符合题意. 故答案为:C.【分析】根据平移不会改变图形的方向、形状及大小,只会改变图形的位置,即可一一判断得出答案.6.【答案】A【解析】【解答】解:将∠FDA 绕点A 逆时针旋转90°到∠HBA ,如图所示:∵四边形ABCD 为正方形∴∠C=∠D=∠DAB=∠ABC=90°,AB=AD由旋转可知AF=AH ,∠ABH=90°,∠HAF=90°,∠AHB=∠AFD ,∠FAD=∠HAB ∵45EAF ∠=︒ αBAE ∠= ∴∠FAD=45°-α ∴∠FAD=∠HAB=45°-α∴∠AHB=∠AFD=45°+α,∠HAE=45° ∴∠AEH∠∠AEF (SAS ) ∴∠AHB=∠AFE=45°+α ∴∠EFD=90°+2α ∵∠EFD 为∠CEF 的外角 ∴∠EFD=∠C+∠CEF ∴2FEC α∠= 故答案为:A【分析】将∠FDA 绕点A 逆时针旋转90°到∠HBA ,先根据正方形性质得到∠C=∠D=∠DAB=∠ABC=90°,AB=AD ,再根据旋转的性质得到AF=AH ,∠ABH=90°,∠HAF=90° ∠AHB=∠AFD ,∠FAD=∠HAB ,进而得到∠AHB=∠AFD=45°+α,∠HAE=45°,再根据三角形全等的判定与性质结合外角的性质即可求解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第23章 图形的旋转单元测试题
一、选择题:(每题3分,共36分)
1、在右边四个图形中,既是轴对称图形又是中心对称图形的是( ) A .①②③④ B .③ C .①③ D .①③④
2、如图,该图形围绕自己的旋转中心,按下列角度旋转后,不能..与其自身重合的是( ) A.72° B.108° C.144° D.216°
3、如图,将正方形图案绕中心O 旋转180°后,得到的图案是( )
第3题 第2题
4、已知点A 关于原点对称点的坐标为(a,b ),那么点A 关于y 轴对称点的坐标是( ) A.(a,-b ) B.(-a,b ) C.(-a,-b ) D.(a,b )
5、如图,已知□ABCD 的两条对角线AC 与BD 交于平面直角坐标系的原点,点A 的坐标为(-2,3),则点C
的坐标为( )
A .(-3,2) B.(-2,-3) C.(3,-2) D.(2,-3) 6、在下图右侧的四个三角形中,不能由△ABC 经过旋转或平移得到的是( )
第5题
7、如图,将三角尺ABC (其中∠ABC =60°,∠C =90°)绕B 点按顺时针方向转动一个角度到A 1BC 1的位置,使得点A ,B ,C 1在同一条直线上,那么这个角度等于( ).
A .120° B.90° C.60° D.30°
8、如图,△OAB 绕点O 逆时针旋转80°到△OCD 的位置,已知∠AOB =45°,则∠AOD 等于( ) A.55° B.45° C.40° D.35°
9、已知点A 的坐标为(a,b),O 为坐标原点,连结OA ,将线段OA 绕点O 按逆时针方向旋转90°得OA 1,则点A 1的坐标为( ).
A.(-a,b) B .(a,-b) C .(-b,a) D .(b,-a)
A
B
C
A
B
C
D
(第9题)
1
A 1
A
(第11题) A
B
C
E
F
P′
P
C
B
A
A
P
C
B
P '
第10题
第7题 第8题 10、△ABC 在如图所示的平面直角坐标系中,将△ABC 向右平移3个单位长度后得△A 1B 1C 1再将△A 1B 1C 1绕点O 旋转180°后得到△A 2B 2C 2,则下列说法正确的是( ) A. A 1的坐标为(3,1)
B .S 四边形ABB1A1=3 C.B 2C=22 D .∠A
C 2O=45°
11、如图,直线y=-3
4x+4与x 轴、y 轴分别交于A 、B 两点,把△AOB 绕点A 顺时针旋转90°后得到△AO /B /
,则点B /
的坐标是( ).
A . (3,4)
B . (4,5)
C . (7,4)
D . (7,3)
第12题
12、右边有两个边长为4cm 的正方形,其中一个正方形的顶点在另一个正方形的中心上,那么图中阴影部分的面积是( ) cm 2
. A.4
B.8
C.16
D.无法确定
二、填空题(每题3分,共24分)
13、若点(a,4)与(3,b)关于原点对称,则a+b= .
14、如图,在平面内将Rt △ABC 绕着直角顶点C 逆时针旋转90°得到Rt △EFC .若AB=5,BC=1,则线段BE 的长为 .
15、如图,P 是正△ABC 内的一点,若将△PAC 绕点A 逆时针旋转到△P /
AB ,则∠PAP /
的度数为 .
第14题 第15题 第16题 第17题
O M 22
16.如图△ABC 是等腰直角三角形,BC 是斜边,P 为△ABC 内一点,将△ABP 绕点A 逆时针旋转后与△ACP /
重合,如果AP=3,那么线段PP /
的长等于____________.
17、如图,把三角形△ABC 绕着点C 顺时针旋转35°,得到△A /B /C ,A /B /交AC 于点D ,若∠A /DC=900
,则∠A 的度数是__________。
18、如图是4×4正方形网格,请在其中选取一个白色的单位正方形并涂黑,使图中黑色部分是一个中心对称图形.
19、如图用等腰直角三角板画∠AOB=45°,并将三角板沿OB 方向平移到如图所示的虚线处后绕点M 逆时针方向旋转22°,则三角板的斜边与射线OA 的夹角α为______.
第18题 第19题 第20题
20、将直角边长为5cm 的等腰直角△ABC 绕点A 逆时针旋转15°后得到△AB /C /
,则图中阴影部分的面积是 cm 2
. 三 解答题(共50分)
21、(本题9分). △ABC 在平面直角坐标系中的位置如图所示,将△ABC 沿y 轴向下平移2个单位得到△A 1B 1C 1,再将△A 1B 1C 1绕点O 旋转180°得到△A 2B 2C 2. 请依次画出△A 1B 1C 1和△A 2B 2C 2.
22、(本题8分)如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC 的顶点均在格点上,点B 的坐标为(1,0). (1)画出△ABC 关于x 轴对称的△A 1B 1C 1;
(2)画出将△ABC 绕原点O 按逆时针方向旋转90°所得的△A 2B 2C 2; (3)△A 1B 1C 1与△A 2B 2C 2成轴对称吗?若成轴对称,画出所有的对称轴; (4)△A 1B 1C 1与△A 2B 2C 2
B '
D
C A
B
G
H
F E (第
24
B
图①
图②
图③
23、(本题9分)如图,把一个直角三角尺ACB 绕着30•°角的顶点B 顺时针旋转,使得点A 与CB 的延长线上的点E 重合.
(1)三角尺旋转了多少度?
(2)连结CD ,试判断△CBD 的形状; (3)求∠BDC 的度数.
24、(12分)把正方形ABCD 绕着点A ,按顺时针方向旋转得到正方形AEFG ,边FG 与BC 交于点H (如图). (1)试问线段HG 与线段HB 相等吗?请先观察猜想,然后再证明你的猜想. (2)若正方形的边长为2cm ,重叠部分(四边形ABHG )的面积为3
34cm 2
,求旋转的角度.
25、(本题12分)一位同学拿了两块45°三角尺△MNK ,△ACB 做了一个探究活动:将△MNK 的直角顶点M 放在△ACB 的斜边AB 的中点处,设AC=BC=4.
(1)如图①,两三角尺的重叠部分为△ACM ,则重叠部分的面积为 ,周长为 . (2
)将图①中的△MNK 绕顶点M 逆时针旋转45°,得到图26②,此时重叠部分的面积为 ,
A
B
C
D
O
110
α
周长为 .
(3)如果将△MN 绕M 旋转到不同于图①和图②的图形,如图③,请你猜想此时重叠部分的面积为 .
(4)在图③情况下,若AD=1,求出重叠部分图形的周长.
26、如图,点O 是等边△ABC 内一点,∠AOB=110°, ∠BOC=α.将△BOC 绕点C 按顺时针方向旋转60°得△ADC ,连接OD .
(1)求证:△COD 是等边三角形;
(2)当α=150°时,试判断△AOD 的形状,并说明理由; (3)探究:当α为多少度时,△AOD 是等腰三角形?。
