框架柱正截面受弯承载力及抗震验算Nmin
第三章 钢筋混凝土受弯构件正截面承载力计算

第三章钢筋混凝土受弯构件正截面承载力计算受弯构件(bendingmember)是指截面上通常有弯矩和剪力共同作用而轴力可以忽视不计的构件。
钢筋混凝土受弯构件的主要形式是板(Slab)和梁(beam),它们是组成工程结构的基本构件,在桥梁工程中应用很广。
在荷载作用下,受弯构件的截面将承受弯矩M和V的作用。
因此设计受弯构件时,一般应满意下列两方面的要求:(1)由于弯矩M的作用,构件可能沿弯矩最大的截面发生破坏,当受弯构件沿弯矩最大的截面发生破坏时,破坏截面与构件轴线垂直,称为正截面破坏。
故需进行正截面承载力计算。
(2)由于弯矩M和剪力V的共同作用,构件可能沿剪力最大或弯矩和努力都较大的截面破坏,破坏截面与构件的轴线斜交,称为沿斜截面破坏,故需进行斜截面承载力计算。
为了保证梁正截面具有足够的承载力,在设计时除了适当的选用材料和截面尺寸外,必需在梁的受拉区配置足够数量的纵向钢筋,以承受因弯矩作用而产生的拉力;为了防止梁的斜截面破坏,必需在梁中设置肯定数量的箍筋和弯起钢筋,以承受由于剪力作用而产生的拉力。
第一节受弯构件的截面形式与构造一、钢筋混凝土板的构造板是在两个方向上(长、宽)尺度很大,而在另一方向上(厚度)尺寸相对较小的构件。
钢筋混凝土板可分为整体现浇板和预制板。
在施工场地现场搭支架、立模板、配置钢筋,然后就地浇筑混凝土的板称为整体现浇板。
通常这种板的截面宽度较大,在计算中常取单位宽度的矩形截面进行计算。
预制板是在预制厂和施工场地现场预先制好的板,板宽度一般掌握在Inl左右,由于施工条件好,预制板不仅能采纳矩形实心板,还能采纳矩形空心板,以减轻板的自重。
板的厚度h由截面上的最大弯矩和板的刚度要求打算,但是为了保证施工质量及耐久性的要求,《大路桥规》规定了各种板的最小厚度;行车道板厚度不小于IOOmm人行道板厚度,就地浇注的混凝土板不宜小于80mm,预制不宜小于60mm。
空心板桥的顶板和底板厚度,均不宜小于80mm。
--框架柱设计-受剪承载力验算

梁柱强剪弱弯调整比较
框架梁强剪弱弯调整
梁左右两端弯矩
用组合弯矩设计值直 接进行调整 强柱弱梁调整
用调整后的增大了的
梁的净跨
l Mb M br Vb Vb VGb ln
框架柱强剪弱弯调整
柱上下两端调整 后的弯矩设计值
弯矩设计值进一步进 行强剪弱弯调整。 柱的净高 Vc:柱端剪力增大系数。一级为1.4,二级为1.2,三 / 四级为1.1。
柱中箍筋的体积配筋率-定义
柱的箍筋体积配箍率v 按下式计算:
v
式中 k
lk 算 l1、l 2
k lk
l1l2 s
—箍筋单肢截面面积; —对应于 k 的箍筋单肢总长度,重叠段按一肢计
—柱核芯混凝土面积的两个边长; s —箍筋间距
当柱的纵向钢筋每边 4根及4根以上时,宜采用井字形箍 A sv na sv 筋 比较:梁的箍筋配股率是面 梁: v a sv 单肢截面积 bs bs 积配筋率。柱是体积配筋率
例题-剪力设计值强剪弱弯调整
9度和一级框架结构尚应符合:
t b Vc 1.2( M cua M cua ) / Hn
(6 13b)
按实配纵筋取矩得到,方法与梁相同
第三步-1:构造要求-箍筋肢距与复合箍筋
必须设置复合箍筋的情况:
1.
2.
柱短边尺寸> 400mm,且纵筋多于3根 柱短边尺寸≤400mm,且纵筋多于4根
c c 框架柱的剪跨比 M /(V hc 0 )
本例题中剪跨比:
剪跨比 2时: V 1 Nhomakorabea RE0.20 c f cbh0
REV 0.20 c f cbh0
结构设计指导书

结构设计指导书第一部分结构计算一、框架结构体系及其布置1.1、框架结构组成框架结构是由梁、柱、节点及基础组成的结构形式,横梁和立柱通过节点连为一体,形成承重结构,将荷载传至基础。
1.2、框架结构种类根据施工方法的不同,分为整体式、装配式和装配整体式三种。
本次设计采用整体式框架结构。
1.3、框架结构布置横向承重框架、纵向承重框架、纵横双向承重框架。
1.4变形缝的设置1、沉降缝设置沉降缝是为了避免地基不均匀沉降在房屋构件中引起裂缝。
房屋扩建时,新建部分与原有建筑结合处也可设置沉降缝分开。
沉降缝将建筑物从基础至屋顶全部分开,各部分能够自由沉降。
2、伸缩缝设置伸缩缝是为了避免温度应力和混凝土收缩应力而使房屋产生裂缝。
伸缩缝仅将上部结构从基础顶面断开,基础不断开。
3、防震缝当房屋平面复杂、立面高差悬殊、各部分质量和刚度截然不同时,应设置防震缝。
对有抗震设防要求的房屋,其沉降缝和伸缩缝均应符合防震缝要求,并尽可能三缝合并设置。
1.5、结构布置应注意的几个原则1、满足使用要求、尽可能的与建筑设计的划分一致。
2、柱网的布置应规则整齐且每个楼层的柱网尺寸应相同,构件类型应尽可能的少。
3、变形缝的设置应满足有关的规范要求。
4、满足施工简便、经济合理的要求。
二、框架梁、柱截面尺寸2.1梁、柱截面形状采用矩形、T型、圆形等截面形式。
2.2梁、柱截面尺寸:以矩形截面选择为例。
1、梁截面尺寸一般取:h=(1/8~1/12)l,b=(1/2~1/3)h。
2、柱截面尺寸柱截面高度可取:h=(1/15~1/20)H,柱截面宽度可取:b=(1~2/3)h。
并按下述方法进行初步验算。
①框架柱承受竖向荷载为主时,可先按负荷面积估算出柱轴力,再按轴心受压柱验算。
考虑到弯矩影响,适当将柱轴力乘以1.2~1.4的放大系数。
②λ框架柱截面高度不宜小于400mm,宽度不宜小于350mm。
为避免发生剪切破坏,柱净高与截面长边之比宜大于4。
3、梁截面惯性矩I0——为梁矩形截面部分的截面惯性矩。
受弯构件正截面受弯承载力计算

受弯构件正截面受弯承载力计算受弯构件是指在受外力作用下,其截面产生弯曲变形的结构元素。
在计算受弯构件的正截面受弯承载力时,一般可以采用弯剪理论或变形分离理论。
弯剪理论是指受弯构件的弯曲变形和剪切变形是相互耦合的,即在计算截面受弯承载力时考虑弯曲破坏和剪切破坏的综合影响。
变形分离理论是指将受弯构件的弯曲变形和剪切变形分开计算,即先计算弯曲破坏时的承载力,再计算剪切破坏时的承载力,最后取两者中较小的值作为截面受弯承载力。
无论采用哪种理论,计算截面受弯承载力的步骤大致相同,包括以下几个方面:1.确定受弯构件的截面形状、尺寸和材料特性。
这些参数是计算受弯承载力的基本数据,需要根据实际情况进行确定。
2.计算受弯构件的惯性矩和截面模数。
惯性矩和截面模数是描述截面抗弯刚度的重要参数,可以通过数学公式或截面性质手册中的查表获得。
3.计算受弯构件的弯矩和剪力。
弯矩和剪力是受弯构件所受外力的作用结果,可以通过等距剪力图法、弯矩分布图法或有限元分析等方法进行计算。
4.判定截面的受弯破坏形式。
根据弯剪理论或变形分离理论,判定截面在受弯作用下的破坏形式,即是由弯曲破坏控制还是由剪切破坏控制。
5.计算截面受弯承载力。
根据受弯构件截面的受弯破坏形式,分别应用弯剪理论或变形分离理论计算截面受弯承载力。
6.比较计算结果与设计要求。
将计算得到的截面受弯承载力与设计要求进行比较,确保受弯构件的受弯性能满足结构设计的要求。
总之,在计算受弯构件的正截面受弯承载力时,需要综合考虑弯剪理论和变形分离理论,通过确定截面形状、尺寸和材料特性,计算惯性矩和截面模数,计算弯矩和剪力,判定受弯破坏形式,计算截面受弯承载力,并与设计要求进行比较,以保证结构的安全和可靠性。
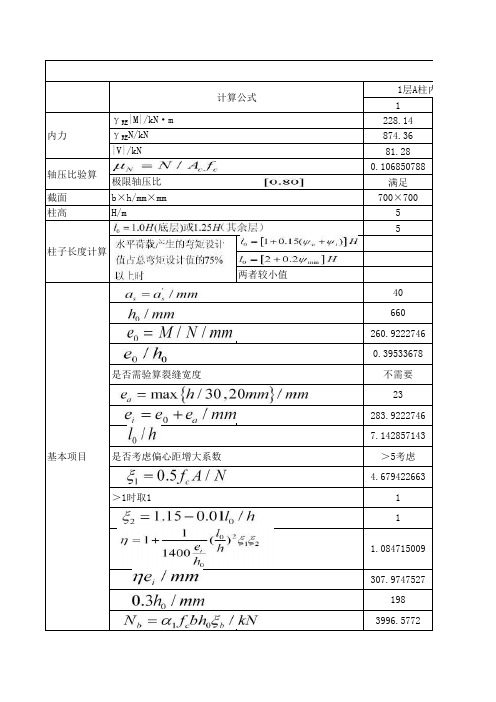
柱抗震正截面受弯承载力计算
-3488.5972 39.98805823
609.2055
1850.7355Байду номын сангаас
-803.0672
-48.3372 -132.93377
-125.5781131 -105.6102812 -126.7209682
大偏压 0.518 547.9880582 43.45423439 80 0.121212121 -1350.613917
40 660 164.8302603 0.249742819 不需要 23 187.8302603 5.714285714 >5考虑 11.4131496 1 1 1.081954771 203.2238463 198 3996.5772
计算公式 γ 内力 γ
RE|M|/kN·m REN/kN
1层A柱内力组合 1 228.14 874.36 81.28 0.106850788 满足 700×700 5 5
|V|/kN 轴压比验算 截面 柱高 极限轴压比 b×h/mm×mm H/m
柱子长度计算 两者较小值 40 660 260.9222746 0.39533678 是否需验算裂缝宽度 不需要 23 283.9222746 7.142857143 基本项目 是否考虑偏心距增大系数 >5考虑 4.679422663 >1时取1 1 1 1.084715009 307.9747527 198 3996.5772
0.125139332
0.121212121
-1541.883876 -419.6448232 -2006.848275 -1465.770159
980 3920
980 3920
980 3920
980 3920
980 3920
受弯正截面承载力计算

受弯正截面承载力计算
首先,对于抗弯能力的计算,需要考虑材料的截面特性,如截面形状、尺寸和材料的强度。
根据梁的受弯分析原理,材料在截面的上、下表面受
到不同的应力分布。
最大应力出现在截面的最远纤维上,称为最外纤维。
最外纤维的应力可以通过式子σ=My/I来计算,其中M是弯矩,y是距离
最外纤维距离,I是惯性矩。
弯矩的大小可以通过受力平衡和几何原理计算。
弯矩的计算方法有多种,例如对简单支座梁、跨越悬臂壁架梁等不同
受力条件下的梁都有相应的计算方法。
然后,需要考虑稳定性的计算。
稳定性主要是指截面在受弯加载时是
否会产生局部屈曲或整体屈曲。
局部屈曲主要发生在截面的一部分,例如
腹板的局部屈曲,而整体屈曲则是整个截面都发生屈曲。
对于不同截面形
状和材料,局部屈曲和整体屈曲的计算方法略有不同。
在计算受弯正截面承载力时,还需要考虑截面的边界条件,例如支座
和跨距。
这些边界条件对承载力的影响需要根据具体的受力情况进行考虑。
此外,还需要根据设计要求和规范要求,在承载力计算中引入安全系数。
总之,计算受弯正截面承载力需要综合考虑材料的抗弯能力和稳定性。
通过正确的弯矩计算和边界条件的考虑,可以得到准确的承载力计算结果。
为了确保结构的安全性,还需要根据设计要求和规范要求引入适当的安全
系数。
不同材料和截面形状的承载力计算方法略有差异,需要根据具体情
况进行。
框架 柱正截面受弯承载力计算
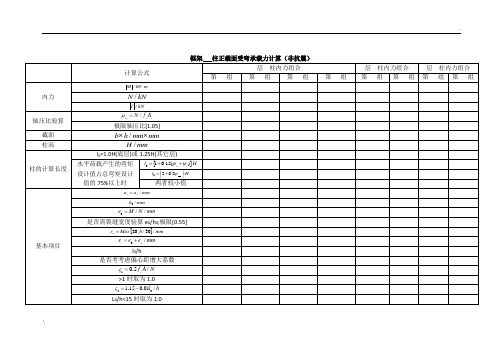
计算公式
层柱内力组合
层柱内力组合
层柱内力组合
第组
第组
第组
第组
第组
第组
第组
第组
内力
轴压比验算
极限轴压比[1.05]
截面
柱高
柱的计算长度
l0=1.0H(底层)或1.25H(其它层)
水平荷载产生的弯矩设计值占总弯矩设计值的75%以上时
两者较小值
基本项目
是否需裂缝宽度验算e0/h0;极限[0.55]
l0/h
是否考考虑偏心距增大系数
>1时取为1.0
L0/h<15时取为1.0
续表
计算公式
层柱内力组合
层柱内力组合
层柱内力组合
第组
第组
第组
第组
第组
第组
第组
第组
基本项目
大小偏心受压的判定
类型
大偏心受压的计算
X<2as’时取为2 as’
小偏心受பைடு நூலகம்的计算
单侧
双侧
实配钢筋/mm2
单侧
单侧
总配筋率
框架梁柱截面抗震承载力验算

表4-3 现浇钢筋混凝土结构高层建筑适用的高宽比
结构体系
非抗震设计
抗震设防烈度 6度、7度 8度 9度
框架
5
板柱-抗震墙
6
框架-抗震墙、抗震墙
7
框架-核心筒
8
筒中筒
8
4
32
5
4—
6
54
7
64
8
75
4.2.2 抗震等级的划分*
抗震等级是多层和高层钢筋混凝土结构、构件进行抗
震级造考,设措虑为具计施建有的要此筑不标求,重同准。我要和的国性要抗抗震求类震设。别设同计、一计计设结算规防构(范烈体抗和度系弯高,、、层不抗结规同剪构的等程类抗)综型震和合及等构 房屋高度等因素,对钢筋混凝土结构划分了不 同的抗震等级。表4-5,表4-6。
表4-1 多层及A级高度钢筋混凝土高层建筑结构的最大适用高度
结构体系
非抗震设计 6度
框架
70
60
框架-抗震墙
150
130
全部落地
抗震墙
150
140
抗震墙
部分框支
抗震墙
130
120
框架-核心筒
160
150
筒体
筒中筒
200
180
板柱-抗震墙
110
80
抗震设防烈度
8度
7度
9度
0.2g
0.3g
50
45
35
应避免
侧移刚度沿竖向变化不均匀
3.防震缝的设置
结构类型
防震缝最小宽度要求
设防烈度
框架结构
框架-抗震墙结构 抗震墙结构
高度
6
78
9
