10-4 二重积分应用
二重积分的计算方法及应用

二重积分的计算方法及应用二重积分是微积分中重要的计算方法之一,它用于计算二元函数在平面区域上的累积效应。
本文将介绍二重积分的计算方法和其在实际问题中的应用。
一、二重积分的计算方法1. 矩形区域上的二重积分计算当被积函数在矩形区域上有明显的解析表达式时,可以使用矩形区域的特点进行计算。
首先,将矩形区域划分成小矩形,计算每个小矩形上函数值的加权累计,然后将这些小矩形的累加值相加得到最终结果。
2. 极坐标下的二重积分计算在某些情况下,函数的表达式在直角坐标下很难处理,但在极坐标下却具有较简单的形式。
对于极坐标下的二重积分计算,我们需要根据被积函数的性质选择适当的极坐标变换,并利用极坐标系下的面积微元进行计算。
3. 变量替换法变量替换是一种常用的二重积分计算方法。
通过引入新的变量替换原有的积分变量,可以简化被积函数的形式,使问题变得更易处理。
变量替换法的关键在于选择合适的变换关系,并确定新的积分范围。
4. 利用对称性简化计算当被积函数具有一定的对称性时,我们可以利用对称性简化计算。
例如,如果被积函数关于某个坐标轴对称,可以将积分区域关于对称轴进行映射,再利用对称性将两边的积分结果相等。
二、二重积分的应用1. 物理学中的应用二重积分在物理学中有广泛的应用。
例如,通过对平面区域上的力场进行二重积分计算,可以求解物体的质心、转动惯量等物理量。
二重积分还可以用于计算电场、磁场等物理场的分布情况。
2. 统计学中的应用统计学中的某些问题可以通过二重积分来求解。
例如,在概率密度函数已知的情况下,可以通过二重积分计算随机变量落在某一区域内的概率。
这在统计推断和假设检验中有着重要的应用。
3. 经济学中的应用在经济学中,二重积分可以用于计算产量、收入、消费等指标。
通过对经济模型中的生产函数或效用函数进行二重积分计算,可以分析经济变量之间的相互作用关系。
4. 工程学中的应用工程学中常常需要对平面区域上的物理量进行计算和分析。
10-4重积分的应用

四川大学数学学院 邓瑾
小块, 将 Ω 分成 n 小块 在第 k 块上任取一点 (ξk ,ηk ,ζk ), 的质点, 将第 k 块看作质量集中于点 (ξk ,ηk ,ζk ) 的质点 此质点 系的质心坐标就近似该物体的质心坐标. 例如, 系的质心坐标就近似该物体的质心坐标 例如
x≈
∑ξ ρ(ξ ,η ,ζ
Ω
o x
y
= ρ ∫∫∫ ( r2 sin2 φ cos2 θ + r2 sin2 φ sin2 θ)
Ω
⋅r2 sinϕdrd d ϕ θ
球体的质量 4 3 M = πa ρ 3
= ρ ∫ dθ ∫ sin ϕdϕ ∫ r dr
3 4 0 0 0
z
dIz = (x + y )ρ (x, y, z)dv
2 2
Ω
的转动惯量: 因此物体 对 z 轴 的转动惯量
o x
y
Iz = ∫∫∫ (x + y )ρ (x, y, z)dxdydz
2 2 Ω
18
四川大学数学学院 邓瑾
类似可得: 类似可得 对 x 轴的转动惯量
Ix = ∫∫∫ ( y + z ) ρ (x, y, z)dxdydz
A= ∫∫
= ∫∫
D
1+ zx2 + zy2 dxdy
1+ x2 + y2 dxdy
R 0
D
= ∫ dθ ∫
0
2π
1+ r r dr
2
3 2 2 2 = π [(1+ R ) −1)] 3
9
四川大学数学学院 邓瑾
的球的表面积. 例4. 计算半径为 a 的球的表面积 方法1 利用球坐标方程. 解: 方法 利用球坐标方程 设球面方程为 r = a 球面面积元素为
二重积分计算及其应用(已处理)

二重积分计算及其应用包头师范学院本科毕业论文题目:二重积分的计算及其应用学生姓名:学院:数学科学院专业:数学与应用数学班级:08本一班指导教师: 讲师二 ? 一二年五月二重积分计算及其应用内容摘要在二重积分的计算中,由于计算和函数比较繁杂,因此按照二重积分的定义计算二重积分有很大的局限性。
常用方法是化简二重积分为两次定积分或累次积分,又因为二重积分的计算与被积函数和积分区域有关。
掌握二重积分计算和它的性质的基础上,讨论如何利用函数的奇偶性与区域的对称性,探讨如何利用二重积分的性质解决二重积分的计算中的证明不等式、确定积分值的符号、估计积分之值、求极限等问题。
对于这些问题我们可以利用二重积分的性质和函数的奇偶性与区域的对称性来解决问题,试图找到一些简便方法,简化二重积分的计算。
关于二重积分的应用它可以求曲面面积以外,二重积分在物理学当中的应用也极其广泛,尤其是在平面薄板当中巧妙而简练的利用二重积分来解决平面薄板的重心坐标、转动惯量以及对质点的引力等问题,二重积分的应用在物理学当中是一种不可忽视的知识。
关键词:二重积分; 直角坐标; 极坐标系; 曲面面积;平面薄片Abstract In the calculation of double integrals, due to the complex calculations and comparison functions, in accordance with the definition of double integral calculation of double integrals have a lot of limitations. A common approach to simplification double integrals are definite integral and repeated integral as twice, because the calculationof double integrals with integrand and integral region. Mastering double integral calculation and on the basis of its nature, discusses how to use functions of symmetry of parity with regional, nature of the discussion on how to use double integral to prove inequality solving double integral calculation, identifying symbols, estimated value of the integral, the integral values for limit and so on. These questions we can use the double integral and parity of the nature and functions of symmetry to solving problems of the region, trying to find some easy way to simplify the calculation of double integrals. But also concise and clear to problem conclusion. On the application of double integral it can be found outside of the surface area of, and applications of double integrals in physics are very widely, especially in a flat sheet, ingenious and simple to use double integral to solving Planar sheet of Barycentric coordinates, moments of inertia and gravitational energy of the particle, and other issues, applications of double integrals in physics is a knowledge that cannot be neglected.Key words: double integral;Cartesian; polar; surface area; flat blades目录内容摘要 (2)关键词 (2)引言 (7)二重积分的定义 (8)二. 二重积分的计算 (8)(一)直角坐标系下二重积分的计算 (8)(二)极坐标系下二重积分的计算 (9)三.利用函数的奇偶性与区域的对称性计算二重积分 (9)(一)计算二重积分,设区域D关于轴对称 (9)若函数关于是奇函数 (9)若函数关于是偶函数 (9)(二)计算二重积分,设区域D关于轴对称 (10)若函数关于是奇函数 (10)若函数关于是偶函数 (10)(三)计算二重积分,设区域D关于轴和轴都对称,同时也是关于,对称的 (10)四.二重积分的性质 (13)五.应用二重积分的性质解题 (14)(一)证明不等式 (14)(二)确定积分值的符号 (14)(三)估计积分之值 (15)(四)求极限 (16)六.二重积分的应用 (17)(一)曲面的面积 (17)1.曲面由显函数给出的情形 (17)2.曲面由参数方程给出的情形 (18)(二)平面薄片的重心 (19)(三)平面薄片的转动惯量 (20)(四)平面薄片对质点的引力 (21)结语 (23)参考文献 (24)引言在二重积分的计算中,由于计算和函数比较繁杂,因此按照二重积分的定义计算二重积分有很大的局限性。
二重积分应用

二重积分应用1、定积分的元素法就如第六章中所述,许多求总量的问题可以用定积分的元素法来处理,这个元素法也可以推广到二重积分,如果所求的某个量对于闭区域来说具有可加性,并且在闭区域内取任意小区域σd时,相应的部分可以用σdx,在σd内,,,(来表示,其中yf)yx这个σd,(成为总量的元素。
f)yx2、曲面的面积的投影,函数在D上具有连续的偏导数,我们要计算曲面的面积A。
γσcos d dA =),(),(11cos 22y x f y x f y x ++=γ.既得:σd y x f y x f dA y x ),(),(122++=dxdyy x f y x f A d y x D),(),(122++=∫∫3、在xoy 平面内有n 个质点,它们分别位于:,,……上,质量分别为:,,……),(11y x ),(22y x ),(33y x ),(n n y x 1m 2m 3m n m法向量的方向余弦则该质点系的重心坐标为:∑∑====n i ini iiymx mMM x 11∑∑====n i ini iixmy mMM y 11∑==ni iiyx mM1∑==ni iixy mM1称作该质点对于y 轴和x 轴的静矩。
若其面密度为:),(y x ρ对X 轴和Y 轴的静矩元素为:σρd y x y dM x ),(=σρd y x x dM y ),(=重心坐标为:∫∫∫∫==DDyd y x d y x x MM x σρσρ),(),(∫∫∫∫==DD xd y x d y x y MM y σρσρ),(),(4、 形心如果薄片是均匀的,即其线密度是常数,则这时的重心坐标为:∫∫==Dyxd AMM x σ1∫∫==Dx yd AM M y σ1把均匀薄片的重心,称作这个平面薄片所占平面图形的行心。
5、 平面薄片的转动惯量在xoy 平面内有n 个质点,它们分别位于:,,……上,质量分别为:,,……),(11y x ),(22y x ),(y x ),(y x m m 3m n m该质点系对于x 轴和y 轴的转动惯量为:i ni i x m y I ∑==12ini i x m y I ∑==12σρd y x y dI x ),(2= σρd y x x dI Y ),(2=6、 平面薄片对质点的吸引力设有一薄片,占有xoy 平面内的闭区域D ,在(x,y )处的面密度为),(y x ρ,且),(y x ρ在D 内连续,现要计算该薄片利用元素法求引力},,{Z Y X F F F F =面积元素σρd y x ),(引力为:2),(r d y x GF σρ=方向为:}0,0,0{a y x n −−−=则引力在三个坐标轴的投影的元素为:r xr d y x G dF x •=2),(σρ ryr d y x G dF y •=2),(σρ ra r d y x G dF z )0(),(2−•=σρ 则可得引力的坐标表达式:r x r d y x G F Dx •=∫∫2),(σρ r y r d y x G F Dy •=∫∫2),(σρ r a r d y x G F Dz −•=∫∫2),(σρ其中:222a y x r ++=7、 附加知识1) 圆的极坐标方程: ① 中心在C(a,0),半径为ar =2acos θ② 中心在(a,π/2),半径为a r =2asin θ ③ 中心在极点,半径为a r=a2) 圆的参数方程x=acos θ y=asin θ3)θθ2cos 22cos 1=+ θθ2sin 22cos 1=−4) 扇形面积公式:θ221r s =.5) 弧长的公式:θr L =6) 球的体积公式:334r V π=。
二重积分的计算与应用

二重积分的计算与应用在微积分中,二重积分是一种对二维平面上的函数进行求和的数学工具。
它广泛应用于物理、经济学、工程学以及其他领域。
本文将介绍二重积分的计算方法以及其在实际问题中的应用。
一、二重积分的计算方法二重积分可以通过多种方法进行计算,包括直接计算、极坐标变换和换元积分等方法。
1. 直接计算直接计算是最常用的方法之一,它将二重积分分解为两个一元积分的乘积。
假设要计算的函数为f(x, y),定义在区域D上,可以将二重积分表示为:∬D f(x, y) dA其中dA表示面积元素。
可以通过将区域D划分为小的面积元素,并在每个面积元素上进行函数值的计算,然后对所有面积元素求和,最终得到二重积分的结果。
2. 极坐标变换极坐标变换是一种常用的简化二重积分计算的方法,特别适用于具有旋转对称性的函数。
通过将直角坐标系下的变量x和y表示为极坐标下的变量r和θ,可以将二重积分转化为极坐标下的形式。
例如,对于函数f(x, y),可以进行如下的极坐标变换:x = rcosθy = rsinθ同时,面积元素dA可以表示为:dA = rdrdθ将函数f(x, y)和面积元素dA用极坐标形式表示后,就可以将二重积分转化为对r和θ的一元积分进行计算。
3. 换元积分换元积分是一种将二重积分转化为更简单形式的计算方法。
通过选择适当的变量替换,可以减小积分的难度。
例如,当被积函数具有形如f(x, y) = g(x + y)的形式时,可以进行变量替换u = x + y,将二重积分转化为对u的一元积分进行计算。
二、二重积分在实际问题中的应用二重积分在各个领域中都有广泛的应用,下面将介绍二重积分在物理学和经济学中的一些具体应用。
1. 物理学中的应用在物理学中,二重积分可以应用于计算质心、质量、转动惯量等物理量。
例如,计算平面上杂质浓度分布可以利用二重积分来求解。
通过将杂质浓度表示为函数f(x, y),然后计算其在给定区域上的二重积分,就可以得到平均浓度。
二重积分的计算方法与应用

二重积分的计算方法与应用二重积分是微积分中的一个重要概念,用于计算平面区域上的某一函数在该区域上的总体积量。
在本文中,我们将介绍二重积分的计算方法与应用。
首先,我们将讨论二重积分的基本概念和计算方法。
假设有一个平面区域D,可以用一个闭合曲线C来描述。
我们将函数f(x, y)定义在区域D内的每一个点上,并且假设f(x, y)在D上连续。
那么在D上的二重积分可以表示为:∬D f(x, y) dA其中,dA表示面积元素,其大小等于dxdy。
要计算二重积分,我们可以将区域D划分成许多小的面积元素,然后对每个面积元素上的函数值进行加权求和。
通常可以使用二重积分的累次积分形式来计算,可以按顺序进行x方向的积分,然后再进行y方向的积分。
在具体计算二重积分时,可以根据问题的特点选择不同的计算方法。
下面介绍常见的二重积分计算方法:1. 矩形坐标系下的二重积分:在矩形坐标系下,将区域D投影到xy平面上,可以得到一个矩形R。
这时,二重积分可以转化为对两个变量的累次积分,其中外层积分表示对x的积分,内层积分表示对y的积分。
通过对x和y的积分限进行适当选择,可以将二重积分转化为两个定积分的计算。
2. 极坐标系下的二重积分:在某些问题中,使用极坐标系进行二重积分计算可以更加简洁。
通过将区域D在极坐标系下的表示,可以将二重积分转化为对极坐标下的两个变量的累次积分。
在计算时,可以通过选择适当的极坐标系下的积分限来简化计算过程。
3. 对称性的利用:在某些问题中,可以利用区域D的对称性简化二重积分的计算。
通过观察函数f(x, y)的对称性,可以改变积分限或者变量的顺序,从而简化计算的过程。
接下来,我们将讨论二重积分在实际问题中的应用。
1. 面积与质量:二重积分可以用来计算平面区域的面积。
将函数f(x, y)设为1,即可得到区域D的面积。
此外,如果区域D上的密度函数为ρ(x, y),那么通过计算二重积分∬D ρ(x, y) dA,可以得到区域D的质量。
二重积分计算及应用

一、利用直角坐标系计算二重积分 二、利用极坐标计算二重积分 三、二重积分的应用
一、利用直角坐标系计算二重积分
X -型区域 积分区域为: 积分区域为: a ≤ x ≤ b, ϕ 1 ( x ) ≤ y ≤ ϕ 2 ( x ).
y = ϕ 2 ( x) y = ϕ 2 ( x)
D
y = ϕ1 ( x )
2
π
∵ I1 < I < I 2 , ∴
π
4
(1 − e
− R2
) < (∫ e
R 0
− x2
dx ) <
2
π
4
(1 − e
−2 R2
);
当 R → +∞ 时, I1 →
π
4
, I2 →
π
4
,
故当 R → +∞ 时,I →
+∞ 0
π
4
, 即 (∫
+∞ 0
e
− x2
dx ) =
2
π
4
,
所求广义积分 ∫
D3
D1
D2
∫∫ = ∫∫ + ∫∫ + ∫∫ .
D D1 D2 D3
例1 改变积分 ∫ dx ∫
1 0
1− x 0
f ( x , y )dy的次序.
y = 1− x
解 积分区域如图 原式= 原式= ∫0 dy ∫
1 1− y 0
f ( x , y )dx .
例2 改变积分
∫ dx ∫0
1 0
2 x− x2
S = {( x , y ) | 0 ≤ x ≤ R,0 ≤ y ≤ R}
经典高等数学课件D10-4重积分的应用
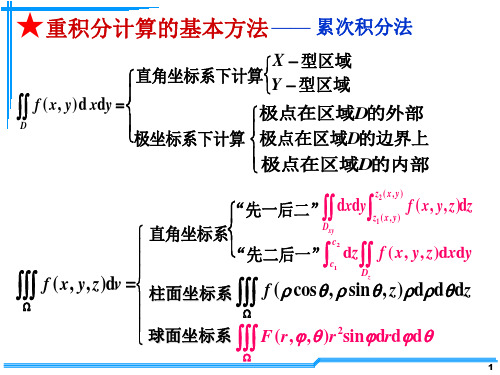
x 2 y 2 a 2 .由
z x , x a2 x2 y2
得 1 (
z y , 2 2 2 y a x y
z 2 z 2 a ) ( ) . x y a2 x2 y2
12
A上
D
a a x y a
2 2 2
dxdy D : x 2 y 2 a 2 .
设曲面S的方程为z 如图, 设小区域
z
z f ( x, y )
f ( x, y ),
M
o
曲面S在xoy面上的投影为区 域D,
sS d
d
( x, y)
点(x,y) d, d D, 以 为S上过点M(x,y,z)的切平面, d
的边界为准线, 母线平行于z轴的 截切平面 小柱面, 截曲面S为 dS, 为 dA, 则有 dA dS.
C2 D
7 所求质心是(0, ). 3
o
x
17
推广: 占有空间有界闭区域, 在点( x, y, z )处的密度为 ( x, y, z )
(假定 ( x, y, z )在上连续)的物体的质心坐标(x , y , z )为:
1 x x ( x, y, z )dv , M 1 y y ( x, y, z )dv , M 1 z z ( x, y, z )dv , M
D
D
y
( x, y)
又M ( x , y )d , 则薄片的质心坐标为:
D
o
d
x
m yi x ( x , yxi mi )d i y ( x, y )d M xM i 1 y M M i 1 y ,, y x n D y n x x D . MM M M ( x , m)d m y i i ( x, y )d
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
y 2 ( x )
X型区域
D
y 1 ( x )
a
b
D : a x b, 1 ( x ) y 2 ( x ).
b
f ( x , y )dxdy dx a (x) D
1
2 (x)
f(x , y )dy
Y型区域
d
x 1 ( y )
D : c y d , 1 ( y ) x 2 ( y ).
d
D
x 2 ( y )
c
f ( x , y )dxdy dy c ( y) D
1
2 ( y)
f ( x , y )dx
1
二重积分在极坐标下的计算公式
f ( x , y )dxdy f ( r cos , r sin )rdrd D D
把定积分的元素法推广到二重积分的应用中. 若要计算的某个量U对于闭区域D具有可加性 (即当闭区域D分成许多小闭区域时,所求量U相应 地分成许多部分量,且U等于部分量之和),并且 在闭区域D内任取一个直径很小的闭区域 d 时, 相应地部分量可近似地表示为 f ( x , y )d 的形式, f ( x, y )d (x , y ) 内.这个 d 其中 在 称为所求量 U dU 的元素,记为 ,所求量的积分表达式为
2 1
例2. 计算二重积分
(1) I sgn( y x 2 )d xd y, D : 1 x 1, 0 y 1 D
(2) I ( x 2 y 2 2 xy 2) d xd y, 其中D 为圆域
D
在第一象限部分.
解: (1) 作辅助线 y x 把与D 分成
所以形心在x a 上,
即
x a ,
y( x ) 1 1 2 a y ydxdy dx ydy 0 AD A 0
1 2 a a 2 5 2 3 [ y( x )] dx [1 cos t ] dt . 2 0 6 a 6 6 0
) . 所求形心坐标为 ( a, 5 6
积分域分块要少, 二次积分易算. 3. 掌握确定积分限的方法 图示法 列不等式法
3
二重积分计算的基本技巧
1. 交换积分顺序的方法 2. 利用对称性或重心公式简化计算 3. 消去被积函数绝对值符号
分块积分法
利用对称性
4
例1. 计算二重积分 I ( x x ye
2 D
x2 y2
) d xd y , 其中:
18
平面薄片的重心
( x, y)
设 xoy平面上有 n个质点,它们分别位于
( x1 , y1 ),( x2 , y2 ),, ( xn , yn )处,质量分别
为 m1 , m2 ,, mn .则该质点系的重心的坐标为
x
My M
mi xi
i 1 n
n
mi
i 1
,
Mx y M
8 4
(b 3 a 3 ) (b 2 a 2 )
b 2 ba a 2 . 2(b a )
23
例4. 计算二重积分 线
D D
其中D 是由曲
所围成的平面域 .
解: I 5 x d xd y 3 y d xd y
积分区域 ( x 1) 2 ( y 2) 2 32
2 2
D
16
被积函数:z a 2 x 2 y 2 D1 : 0 ,0 r a cos
V1 2 d
0
a cos
2
D
0
a 2 r 2 rdr
3 2 a cos
1 2 1 2 2 2 2 2 2 2 d a r d (r ) a r d 0 2 0 2 0 3 0 3 1 2 2 2 2 2 2 2 3 a3 3 a a cos a d 2 1 sin d 2 0 3 3 3 0
( x1 , y1 ) , ( x2 , y2 ) , , ( xn , yn ) 处 , 质 量 分 别 为 m1 , m2 ,, mn .则该质点系对于 x 轴和 y 轴的转动
惯量依次为
I x m i yi
i 1
n
2
,
I y mi xi
i 1
n
2
.
25
设有一平面薄片,占有 xoy面上的闭区域 D , 在点( x , y )处的面密度为 ( x , y ),假定 ( x , y )在 D 上连续,平面薄片对于 x 轴和 y 轴 的转动惯量为
(1) D为圆域 (2) D由直线 围成 .
x2 y2
解: (1) 利用对称性.
I x d x d y x ye
2 D
D
d xd y
1 2 2 ( x y ) d xd y 0 2 D 1 3 1 2 d r d r 0 4 2 0
y
a cos
3 a 2 a3 3 2 2 d sin d 0 3 2 3 3 0 a 3 (6 8) V 4V1 9
a 3 (3 4) 18
17
二重积分的物理上应用
一、平面薄片的重心 二、平面薄片的转动惯量 三、空间中物体的引力
f ( r cos , r sin )rdr .
r ( )
D
o
A
D
0
0
适用范围:被积函数形如 f ( x y )
2 2
o
2
或积分区域为圆形,扇形或圆环形。
二重积分计算的基本方法 —— 二次积分法
1. 选择合适的坐标系 使积分域多为坐标线围成; 被积函数用此坐标表示简洁.
2. 选择易计算的积分序
4 y
11 543 15
10
例4 证明:
0
a
a
d y e
0
y
m(a x )
f ( x )d x (a x )e m ( a x ) f ( x )d x
0
a
y
证明: 左端积分区域如图, 交换积分顺序.
a
D
yx
0
d y e
0 a x
y
m(a x )
f ( x )d x
22
例3 求位于两圆 r a cos , r b cos (0 a b ) y 之间的均匀薄片的重心 .
解
薄片关于 x 轴对称
则 y 0,
o
2 0
a
b x
x
xd
D
d
D
2 d
b cos
a cos
r cos rdr
D
解
先求区域 D 的面积 A,
y( x )
0 t 2 , 0 x 2a
D
a
2a
A
ห้องสมุดไป่ตู้
2 a
0
y( x )dx a(1 cos t )d[a( t sin t )]
0
2
a 2 (1 cos t ) 2 dt 3a 2 .
0
21
2
由于区域关于直线x a 对称 ,
2
D1 , D2 两部分, 则
I d xd y
D1
1 1 1 x
1 D1 1
y
D2
d xd y
x2 0
o D2
1 x
d x 2 d y d x
1
1
2 dy 3
7
I ( x 2 y 2 2 xy 2) d xd y 其中D 为圆域
r 1 ( )
r 2 ( )
D
o
A
( ) ( ) d 0 f ( r cos , r sin )rdr. 2 d ( ) f (r cos , r sin )rdr.
1
d
2 ( )
D ( x y )d s
D2 D1
4 2 o D1 D 2 D 4 6
y 2 2x
x
( x y )d s ( x y )d s
d y y 2
6
2
4
12 y
( x y) d x d y 2 ( x y) d x y
4
2
2
a a
b
b
D
1 2
D[ f
2
( x) f ( y )] dxd y
2
a xb D: a y b
1 b 2 a
dy
b 2 b b 2 f ( x ) dx dx f ( y ) d y a a a
b a b f 2 ( x)d x b f 2 ( y )d y 利用 2 a a
a b b a y
x
y x
D
dy ( x y )n 2 f ( y )dx
1 n1 b f ( y )dy[ ( x y ) ]y a n1 1 b n1 (b y ) f ( y )dy. a n1
b
a
a
b
13
第九章 重积分
二重积分的应用
14
问题的提出
D
在第一象限部分.
y 1
作辅助线 y x 将D 分成
