(广西地区)2017版中考数学总复习第一篇考点聚焦第一章数与式考点跟踪突破4二次根式及其运算
2017广西南宁中考数学试题及答案解析
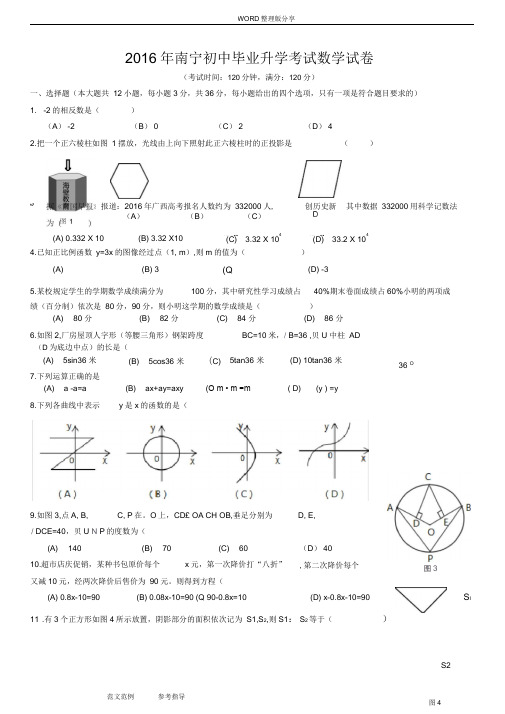
S22016年南宁初中毕业升学考试数学试卷(考试时间:120分钟,满分:120分)一、选择题(本大题共 12小题,每小题3分,共36分,每小题给出的四个选项,只有一项是符合题目要求的) 1.-2的相反数是() (A ) -2(B ) 0(C ) 2(D ) 42.把一个正六棱柱如图 1摆放,光线由上向下照射此正六棱柱时的正投影是()4.已知正比例函数 y=3x 的图像经过点(1, m ),则m 的值为()绩(百分制)依次是 80分,90分,则小明这学期的数学成绩是()(D 为底边中点)的长是(7.下列运算正确的是11 .有3个正方形如图4所示放置,阴影部分的面积依次记为 S1,S 2,则S1: S 2等于( )报道:2016年广西高考报名人数约为 332000人,(A ) (B ) (C )(A) 0.332 X 10(B) 3.32 X10,一、 一 _ _一4(C) 3.32 X 10其中数据 332000用科学记数法,—、 一 _ _一4(D) 33.2 X 10(A)(B) 3(Q(D) -35.某校规定学生的学期数学成绩满分为100分,其中研究性学习成绩占40%期末卷面成绩占60%小明的两项成 (A) 80 分 (B) 82 分(C) 84 分(D) 86 分6.如图2,厂房屋顶人字形(等腰三角形)钢架跨度BC=10米,/ B=36 ,贝U 中柱 AD(A) 5sin36 米 (B) 5cos36 米 (C) 5tan36 米(D) 10tan36 米 36 O(A) a -a=a (B) ax+ay=axy (O m • m =m( D)(y ) =y/ DCE=40,贝U N P 的度数为((A) 140(B) 70(C) 6010.超市店庆促销,某种书包原价每个x 元,第一次降价打“八折”(D ) 40 ,第二次降价每个又减10元,经两次降价后售价为 90元。
则得到方程((A) 0.8x-10=90(B) 0.08x-10=90 (Q 90-0.8x=10(D) x-0.8x-10=903创历史新y 是x 的函数的是(8.下列各曲线中表示9.如图3,点A, B, C, P 在。
2017年广西省桂林市中考数学(word版,有解析)

2017年广西省桂林市中考数学试题参考答案与试题解析一、选择题(本大题共12小题,每小题3分,共36分)1.2017的绝对值是()A.2017 B.﹣2017 C.0 D.1 2017【解析】根据将绝对值的意义,得2017的绝对值等于2017,故选A.2.4的算术平方根是()A.4 B.2 C.﹣2 D.±2【解析】4的算术平方根是2.故选B.3.一组数据2,3,5,7,8的平均数是()A.2 B.3 C.4 D.5【解析】数据2,3,5,7,8的平均数=235785++++=5.故选D.4.如图所示的几何体的主视图是()A.B.C.D.【解析】根据圆锥的摆放位置,可知从正面看圆锥所得的图形是三角形,故该圆锥的主视图是三角形,故选A.5.下列图形中不是中心对称图形的是()A.B.C.D.【解析】根据中心对称图形的概念:把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,易得B是中心对称图形,A,C,D不是中心对称图形.故选B.6.用科学记数法表示数57 000 000为()A.57×106B.5.7×106C.5.7×107D.0.57×108【解析】用科学记数法表示数57 000 000为5.7×107,故选:C.7.(3分)下列计算正确的是()A.a3÷a3=a B.(x2)3=x5C.m2•m4=m6D.2a+4a=8a【解析】A、a3÷a3=1,故本选项错误;B、(x2)3=x6,故本选项错误;C、m2•m4= m2+4=m6,故本选项正确;D、2a+4a=6a,故本选项错误.故选C.8.(3分)如图,直线a,b被直线c所截,下列条件能判断a∥b的是()A .∠1=∠2B .∠1=∠4C .∠3+∠4=180°D .∠2=30°,∠4=35°【解析】解:∵∠1=∠4,∴a ∥b (同位角相等两直线平行).故选B .9.(3分)下列命题是真命题的是( )A .相等的角是对顶角B .若实数a ,b 满足a 2=b 2,则a=bC .若实数a ,b 满足a <0,b <0,则ab <0D .角的平分线上的点到角的两边的距离相等【解析】A 、是假命题,例如,角平分线把角分成的两个角相等,但它们不是对顶角,故本选项错误;B 、是假命题,结论应为a=b 或a=﹣b ,故本选项错误;C 、是假命题,结论应为ab >0,故本选项错误;D 、是真命题,故本选项正确.故选D .10.若分式242x x -+的值为0,则x 的值为( ) A .﹣2 B .0 C .2 D .±2【解析】由题意可知,x 2-4=0,且x+2≠0.解得x=2.故选C.11.一次函数y=﹣x+1(0≤x ≤10)与反比例函数y=1x(﹣10≤x <0)在同一平面直角坐标系中的图象如图所示,点(x 1,y 1),(x 2,y 2)是图象上两个不同的点,若y 1=y 2,则x 1+x 2的取值范围是( )A .﹣8910≤x ≤1 B .﹣8910≤x ≤899 C .﹣899≤x ≤8910 D .1≤x ≤8910【解析】当x=﹣10时,y=1x =﹣110; 当x=10时,y=﹣x+1=﹣9,∴﹣9≤y 1=y 2≤﹣110. 设x 1<x 2,则y 2=﹣x 2+1,y 1=11x , ∴x 2=1﹣y 2,x 1=11y ,∴x 1+x 2=1﹣y 2+11y . 设x=1﹣y+1y (﹣9≤y ≤﹣110),﹣9≤y m <y n ≤﹣110, 则x n ﹣x m =y m ﹣y n +1n y ﹣1m y =(y m ﹣y n )(1+1m ny y )<0,∴x=1﹣y+1y中x 值随y 值的增大而减小, ∴1﹣(﹣110)﹣10=﹣8910≤x ≤1﹣(﹣9)﹣19=899. 故选B .12.如图,在菱形ABCD 中,∠ABC=60°,AB=4,点E 是AB 边上的动点,过点B 作直线CE 的垂线,垂足为F ,当点E 从点A 运动到点B 时,点F 的运动路径长为( )A .3B .23C .23πD .43π 【解析】如图,连接AC 、BD 交于点G ,连接OG .∵BF ⊥CE ,∴∠BFC=90°,∴点F 的运动轨迹在以边长为直径的⊙O 上.当点E 从点A 运动到点B 时,点F 的运动路径长为, ∵四边形ABCD 是菱形,∴AB=BC=CD=AD=4.∵∠ABC=60°,∴∠BCG=60°,∴∠BOG=120°, ∴的长= =43π, 故选D .二、填空题(本大题共6小题,每小题3分,共18分)13.分解因式:x 2﹣x= .【解析】x 2﹣x=x (x ﹣1).故答案为:x (x ﹣1).14.如图,点D 是线段AB 的中点,点C 是线段AD 的中点,若CD=1,则AB= .【解析】∵点C 是线段AD 的中点,CD=1,∴AD=1×2=2.∵点D 是线段AB 的中点,∴AB=2×2=4.故答案为4.15.分式212a b 与21ab 的最简公分母是 . 【解析】212a b 与21ab 的分母分别是2a 2b ,ab 2,故最简公分母是2a 2b 2; 故答案是2a 2b 2.16.一个不透明的口袋中有6个完全相同的小球,把它们分别标号为1,2,3,4,5,6,从中随机摸取一个小球,取出的小球标号恰好是偶数的概率是.【解答】解:∵共有6个完全相同的小球,其中偶数有2,4,6,共3个,∴从中随机摸取一个小球,取出的小球标号恰好是偶数的概率是36=12;故答案为12.17.(3分)如图,在矩形ABCD中,对角线AC,BD交于点O,过点A作EA⊥CA交DB的延长线于点E,若AB=3,BC=4,则AOAE的值为.【解析】如图,作BH⊥OA于H.∵四边形ABCD为矩形,∴OA=OC=OB,∠ABC=90°,在Rt△ABC中,AC==5,∴AO=OB=52,∵12BH•AC=12AB•BC,∴BH==125.在Rt△OBH中,OH===,∵EA⊥CA,∴BH∥AE,∴△OBH∽△OEA,∴BH OH AE OA=,∴710125OA OHAE BH===724.故答案为724.18.如图,第一个图形中有1个点,第二个图形中有4个点,第三个图形中有13个点,…,按此规律,第n个图形中有个点.【解析】第一个图形中有1个点,即1=12(31﹣1);第二个图形中有4个点,即4=12(32﹣1)第三个图形中有13个点,即13=12(32﹣1),…按此规律,第n个图形中有12(3n﹣1)个点,故答案为12(3n﹣1).三、解答题(本大题共8小题,共66分)19.(6分)计算:(﹣2017)0﹣sin30°+8+2﹣1.【解】原式=1﹣12+22+12=1+22.20.(6分)解二元一次方程组:.【解】②﹣①,得3x=6,解得x=2,把x=2代入①,得y=﹣1,∴原方程组的解为.21.(8分)某校为了解学生的每周平均课外阅读时间,在本校随机抽取若干名学生进行调查,并将调查结果绘制成如下不完整的统计图表,请根据图表中所给的信息,解答下列问题:组别阅读时间t(单位:小时)频数(人数)A 0≤t<1 8B 1≤t<2 20C 2≤t<3 24D 3≤t<4 mE 4≤t<5 8F t≥5 4(1)图表中的m= ,n= ;(2)扇形统计图中F组所对应的圆心角为度;(3)该校共有学生1500名,请估计该校有多少名学生的每周平均课外阅读时间不低于3小时?【解】(1)m=8÷10%×20%=16,n=24÷(8÷10%)×100=30;(2)扇形统计图中F组所对应的圆心角为:360°×=18°;(3)由题意得,每周平均课外阅读时间不低于3小时的学生数为1500×(20%+10%+5%)=525名.故答案为:16,30,18.22.(8分)如图,在网格中,每个小正方形的边长均为1个单位长度,我们将小正方形的顶点叫做格点,线段AB的端点均在格点上.(1)将线段AB向右平移3个单位长度,得到线段A′B′,画出平移后的线段并连接AB′和A′B,两线段相交于点O;(2)求证:△AOB≌△B′OA′.【解】(1)如图所示:(2)证明:∵AB∥A′B′,∴∠A=∠B′,∠B=∠A′在△AOB和△B′OA′中,,∴△AOB≌△B′OA′.23.(8分)“C919”大型客机首飞成功,激发了同学们对航空科技的兴趣,如图是某校航模兴趣小组获得的一张数据不完整的航模飞机机翼图纸,图中AB∥CD,AM∥BN∥ED,AE⊥DE,请根据图中数据,求出线段BE和CD的长.(sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,结果保留小数点后一位)【解】∵BN∥ED,∴∠NBD=∠BDE=37°.∵AE⊥DE,∴∠E=90°,∴BE=DE•tan∠BDE≈18.75(cm).如图,过C作AE的垂线,垂足为F.∵∠FCA=∠CAM=45°,∴AF=FC=25cm.∵CD∥AE,∴四边形CDEF为矩形,∴CD=EF,∵AE=AB+EB=35.75(cm),∴CD=EF=AE﹣AF≈10.8(cm),答:线段BE的长约等于18.8cm,线段CD的长约等于10.8cm.24.(8分)为进一步促进义务教育均恒发展,某市加大了基础教育经费的投入,已知2015年该市投入基础教育经费5000万元,2017年投入基础教育经费7200万元.(1)求该市这两年投入基础教育经费的年平均增长率;(2)如果按(1)中基础教育经费投入的年平均增长率计算,该市计划2018年用不超过当年基础教育经费的5%购买电脑和实物投影仪共1500台,调配给农村学校,若购买一台电脑需3500元,购买一台实物投影需2000元,则最多可购买电脑多少台?【解】(1)设该市这两年投入基础教育经费的年平均增长率为x,根据题意,得5000(1+x)2=7200,解得x1=0.2=20%,x2=﹣2.2(舍去).答:该市这两年投入基础教育经费的年平均增长率为20%.(2)2018年投入基础教育经费为7200×(1+20%)=8640(万元),设购买电脑m台,则购买实物投影仪(1500﹣m)台,根据题意得:3500m+2000(1500﹣m)≤86 400 000×5%,解得m≤880.答:2018年最多可购买电脑880台.25.(10分)已知:如图,在△ABC中,AB=BC=10,以AB为直径作⊙O分别交AC,BC于点D,E,连接DE和DB,过点E作EF⊥AB,垂足为F,交BD于点P.(1)求证:AD=DE;(2)若CE=2,求线段CD的长;(3)在(2)的条件下,求△DPE的面积.(1)证明:∵AB是⊙O的直径,∴∠ADB=90°.∵AB=BC,∴D是AC的中点,∠ABD=∠CBD,∴AD=DE.(2)解:∵四边形ABED内接于⊙O,∴∠CED=∠CAB,∵∠C=∠C,∴△CED∽△CAB,∴CE CD CA CB=.∵AB=BC=10,CE=2,D是AC的中点,∴CD=10. (3)解:如图,延长EF交⊙O于M.在Rt△ABD中,AD=10,AB=10,∴BD=310.∵EM⊥AB,AB是⊙O的直径,∴,∴∠BEP=∠EDB,∴△BPE∽△BED,∴BD BEBE BP=,∴BP=321015,∴DP=BD﹣BP=1310 15,∴S△DPE:S△BPE=DP:BP=13:32,∵S△BCD=12×10×310=15,S△BDE:S△BCD=BE:BC=4:5,∴S△BDE=12,∴S△DPE=52 15.26.(12分)已知抛物线y1=ax2+bx﹣4(a≠0)与x轴交于点A(﹣1,0)和点B(4,0).(1)求抛物线y1的函数解析式;(2)如图,将抛物线y1沿x轴翻折得到抛物线y2,抛物线y2与y轴交于点C,点D是线段BC上的一个动点,过点D作DE∥y轴交抛物线y1于点E,求线段DE的长度的最大值;(3)在(2)的条件下,当线段DE处于长度最大值位置时,作线段BC的垂直平分线交DE于点F,垂足为H,点P是抛物线y2上一动点,⊙P与直线BC相切,且S⊙P:S△DFH=2π,求满足条件的所有点P的坐标.【解】(1)将点A(﹣1,0)和点B(4,0)代入y1=ax2+bx﹣4,得a=1,b=﹣3,∴抛物线y1的函数解析式为y1=x2﹣3x﹣4.(2)由对称性可知,抛物线y2的函数解析式为:y2=﹣x2+3x+4,∴C(0,4),设直线BC的解析式为:y=kx+q,把B(4,0),C(0,4)代入得,k=﹣1,q=4,∴直线BC的解析式为:y=﹣x+4.设D(m,﹣m+4),E(m,m2﹣3m﹣4),其中0≤m≤4,∴DE=﹣m+4﹣(m2﹣3m﹣4)=﹣(m﹣1)2+9,∵0≤m≤4,∴当m=1时,DE max=9;此时,D(1,3),E(1,﹣6).(3)如图,由题意可知,△BOC是等腰直角三角形,∴线段BC的垂直平分线为y=x,由(2)知,直线DE的解析式为x=1,∴F(1,1).∵H是BC的中点,∴H(2,2),∴DH=2,FH=2,∴S△DFH=1.设⊙P的半径为r,∵S⊙P:S△DFH=2π,∴r=2,∵⊙P与直线BC相切,∴点P在与直线BC平行且距离为2的直线上,∴点P在直线y=﹣x+2或y=﹣x+6的直线上,∵点P在抛物线y2=﹣x2+3x+4上,∴﹣x+2=﹣x2+3x+4,解得x1=2+6,x2=2﹣6;﹣x+6=﹣x2+3x+4,解得x3=2+2,x4=2﹣2,∴符合条件的点P的坐标有4个,分别是(2+6,﹣6),(2﹣6,6),(2+2,4﹣2),(2﹣2,4+2).。
广西贵港市2017届中考数学总复习第一单元数与式(课件 练习 单元测试)

有一个内角是60°的菱形
版权所有-
AC
3 BD
较长的对角线是较短对角线的 3 倍
版权所有-
菱形的判定方法
版权所有-
菱形的判定方法
1.一组邻边相等的平行四边形是菱形. 2.对角线互相垂直平分的四边形是菱形.
平 行 四 边 形的 判 别 方 法
1.两组对边分别平行的四边形是平行四边形
2.一组对边平行且相等的四边形是平行四边形 3.两组对边分别相等的四边形是平行四边形 4.对角线互相平分的四边形是平行四边形
版权所有-
中位线的性质
∵点D、E分别是AB、AC的中点
1 ∴DE∥BC,且DE= BC 2
与平行四边形相比,特殊在哪?
对角线相等、含有90°的内角
版权所有-
矩形的判定方法
1.一个角是直角的平行四边形是矩形.
2.三个内角是直角的四边形是矩形.
3.对角线相等且互相平分的四边形是矩形.
对角线相等的平行四边形是矩形.
版权所有-
先证平行四边形,再找特殊之处
版权所有-
特殊的平行四边形
版权所有-
平行四边形
四边形ABCD,有以下四个关系: ①AB=CD; ②AD=BC;
③AB∥CD;
④∠A=∠C
任意取两个作为条件,能够得出这个四
边形ABCD是平行四边形的概率为_____.
版权所有-
版权所有-
对角线垂直、邻边相等
菱形的对角线互相垂直平分, 且每一条对角线平分一组对角.
版权所有-
菱形的面积=底×高 菱形的面积=对角线乘积的一半
版权所有-
有一个内角是60°的菱形
版权所有-
则图形为菱形;
2017年广西省中考数学科目考试说明

2017年广西省中考数学科目考试说明导读:广西省2017年数学科目说明已经公布,主要在知识与技能、数学思考、问题解决、情感态度等方面对学生进行全面的考查,具体内容请看如下信息。
想了解更多相关信息请持续关注我们!一、考试性质初中毕业升学考试是义务教育阶段的终结性考试,目的是全面、准确地反映初中毕业生在学科学习目标方面所达到的水平。
该考试具有两考合一的功能,考试结果既是衡量初中毕业要求的主要依据,也是普通高中阶段学校招生的重要依据之一,还可以作为衡量义务教育质量的重要依据。
二、命题指导思想以党的十八大、十八届三中、四中、五中全会精神为指导,坚持有利于全面贯彻国家教育方针,坚持有利于体现素质教育导向、促进学生的全面发展,进一步推进数学学科教学改革的实施,全面提高数学学科的教育教学质量;坚持有利于建立科学的数学教学评估体系,为高中阶段综合评价、择优录取提供依据;数学学科考试结合北部湾四市同城初中数学教学实际,考查学生数学基本知识与技能、逻辑思维、问题解决的发展情况,以及学生在情感态度和价值观方面的发展状况。
三、命题基本原则(一)导向性原则。
以社会主义核心价值体系为导向,坚持以学生为本,全面、公正、客观、准确地评价学生的学习水平,充分发挥考试的甄别、激励、选拔等评价功能。
引导教师转变教学方式,提高教学能力。
促进学生改进学习方式,着眼长远发展;有利于初高中教学衔接,为学生在高中阶段的学习与发展打好基础。
(二)基础性原则。
以《全日制义务教育数学课程标准》(2011年版)和现行教材为依据,结合学生的实际,加强对学生必备的初中数学基础知识、基本技能、基本数学思想方法和基本数学活动的考查。
体现基础性、教育公平和均衡发展要求。
(三)科学性原则。
严格按照规定的程序和要求组织命题,试题内容科学,符合考生的认知水平,难易适当;试卷结构科学、合理,形式规范,具有较高信度、效度和良好的区分度。
(四)能力立意原则。
在考查学生理解和掌握必要的数学基础知识与技能的基础上,考查学生运用数学知识、方法和技能分析问题、解决问题的能力,并联系社会生活实际和科技发展的问题情景,考查应用意识和创新意识。
(广西地区)中考数学总复习 第一篇 考点聚焦 第一章 数与式 考点跟踪突破2 整式(含因式分解)-人

考点跟踪突破2 整式(含因式分解)一、选择题1.(2016·某某)下列运算正确的是( C )A .a 2-a =aB .ax +ay =axyC .m 2·m 4=m 6 D. (y 3)2=y 52.(2016·某某)已知x -2y =3,那么代数式3-2x +4y 的值是( A )A .-3B .0C .6D .93.(2015·某某)下列各式的变形中,正确的是( A )A .(-x -y )(-x +y )=x 2-y 2B.1x -x =1-x xC .x 2-4x +3=(x -2)2+1D .x ÷(x 2+x )=1x+1 4.(2015·贵港)下列因式分解错误的是( C )A .2a -2b =2(a -b )B .x 2-9=(x +3)(x -3)C .a 2+4a -4=(a +2)2D .-x 2-x +2=-(x -1)(x +2)5.(2016·某某)小红要购买珠子串成一条手链,黑色珠子每个a 元,白色珠子每个b 元,要串成如图所示的手链,小红购买珠子应该花费( A )A .(3a +4b )元B .(4a +3b )元C .4(a +b )元D .3(a +b )元6.(2016·贺州)n 是整数,式子18[1-(-1)n ](n 2-1)计算的结果( C ) A .是0 B .总是奇数C .总是偶数D .可能是奇数也可能是偶数二、填空题7.(2016·某某)若a m =2,a n =8,则a m +n =__16__.8.(2016·某某)若mn =m +3,则2mn +3m -5mn +10=__1__.9.(2016·某某)一个矩形的面积为a 2+2a ,若一边长为a ,则另一边长为__a +2__.10.(2016·某某)对于实数a ,b ,定义运算“*”为a*b =⎩⎪⎨⎪⎧a 2-ab (a ≥b ),a -b (a<b ),例如:因为4>2,所以4*2=42-4×2=8,则(-3)*(-2)=__-1__.11.(2016·某某)观察下列各式的规律:(a -b)(a +b)=a 2-b 2(a -b)(a 2+ab +b 2)=a 3-b 3(a -b)(a 3+a 2b +ab 2+b 3)=a 4-b 4…可得到(a -b)(a2016+a 2015b +…+ab 2015+b 2016)=__a 2017-b 2017__. 三、解答题12.(2016·某某)化简:(a 2b -2ab 2-b 3)÷b -(a -b)2.解:原式=-2b 213.分解因式:(1)(2015·某某)3x 2-27;解:原式=3(x2-9)=3(x+3)(x-3)(2)4+12(x-y)+9(x-y)2;解:原式=[2+3(x-y)]2=(3x-3y+2)2(3)8(x2-2y2)-x(7x+y)+xy.解:原式=8x2-16y2-7x2-xy+xy=x2-16y2=(x+4y)(x-4y)14.(2016·襄阳)先化简,再求值:(2x+1)(2x-1)-(x+1)(3x-2),其中x=2-1.解:(2x+1)(2x-1)-(x+1)(3x-2)=4x2-1-(3x2+3x-2x-2)=4x2-1-3x2-x+2=x2-x+1,把x=2-1代入得:原式=(2-1)2-(2-1)+1=3-22-2+2=5-3215.(2015·某某)设y=ax,若代数式(x+y)(x-2y)+3y(x+y)化简的结果为x2,请你求出满足条件的a值.解:原式=(x+y)(x-2y)+3y(x+y)=(x+y)2,当y=ax,代入原式得(1+a)2x2=x2,即(1+a)2=1,解得:a=-2或016.(2016·达州)已知x ,y 满足方程组⎩⎪⎨⎪⎧x -5y =-2,2x +5y =-1,求代数式(x -y)2-(x +2y)(x -2y)的值.解:原式=(x 2-2xy +y 2)-(x 2-4y 2)=x 2-2xy +y 2-x 2+4y 2=-2xy +5y 2,方程组⎩⎪⎨⎪⎧x -5y =-2①,2x +5y =-1②①+②得:3x =-3,即x =-1,把x =-1代入①得:y =15,则原式=25+15=35。
(广西地区)2017版中考数学总复习第二篇专题聚焦跟踪汇总

专题跟踪突破11二次函数综合题(针对广西中考压轴题)1 . (2016 •百色)正方形OABO的边长为4,对角线相交于点P,抛物线L经过0, P, A 三点,点E 是正方形内的抛物线上的动点.(1)建立适当的平面直角坐标系,①直接写出0, P, A三点坐标;②求抛物线L的解析式;(2)求厶OAE M^ OCE面积之和的最大值.解:(1)以0点为原点,线段0A所在的直线为x轴,线段0C所在的直线为y轴建立直角坐标系,如图所示.①•••正方形0ABC勺边长为4,对角线相交于点P,.••点0的坐标为(0, 0),点A的坐标为(4, 0),点P的坐标为(2, 2).②设抛物线L的解析式为y = ax2+ bx + c,c,•••抛物线L经过0, P, A三点,.••有0= 16a+ 4b+ c,解得2= 4a+ 2b+ c,1a=-2 1抛物线L的解析式为y =—^x2+ 2x (2):点E是正方形内的抛物线上的b= 2, 2c = 0一一1 2 1 1动点,•设点E 的坐标为(m —尹+ 2n)(0v m< 4), • &。
人片&0CE= ^0A- y e+^0C- X E=—m+ 4n^2n=—(n—3)2+ 9,二当n= 3 时,△ 0AE W^ 0CE面积之和最大,最大值为922. (2016 •河池)在平面直角坐标系中,抛物线 y =— x - 2x + 3与x 轴交于A , B 两点(A 在B 的左侧),与y 轴交于点C,顶点为D.(1) 请直接写出点 A, C ,D 的坐标;(2)如图1,在x 轴上找一点E ,使得△ CDE 的周长最小,求点 E 的坐标;(3)如图2,F 为直线AC 上的动点,在抛物线上是否存在点P,使得△ AFP 为等腰直角三角形?若存在,求出点 P 的坐标;若不存在,请说明理由.解:(1)A ( — 3,0),C (0,3),D ( — 1,4) (2)如解图甲,作点 C 关于x 轴的对称点为 点M 贝U MO ,— 3),连接DM 与 x 轴的交点即为点 E,连接CE 此时△ CDE 勺周长最小•设DIM 勺解析式为 y = kx + b (k z 0),将 D — 1,4),M (0,— 3)代入 y = kx + b ,得*-k + b = 4, b =— 3,解得<k=— 7, 直线DM 的解析式为:y =— 7x — 3,令y = 0,则y =— 7x — 3= 0,解得x =b =— 3,—3,二点 E 的坐标为(一7, 0) (3)存在•由(1)知,OA = 0(= 3,Z AO = 90°,.・./ CAB= 45°,如解图乙,①当/ AFF = 90°时,即/ AFP = 90°,点P 既在x 轴上,又在抛物线上, 则点R 与点B 重合,点P 1的坐标为(1, 0);②当/ FAF = 90°时,即/F 2AP = 90°,则/ F 2A0 =45°,设AP 与y 轴的交点为点 N,「. OA= ON= 3,贝U N (0,— 3),易求AP 的解析式为:yy = — x — 3,x =— 3,x = 2,=—x — 3,联立方程组2解得或T A — 3, 0) ,••• P 2(2,y = — x — 2x + 3, l y = 0,(y = — 5,—5);③当/ APF = 90°时,即/ APF 3= 90°,点P s 既在x 轴上,又在抛物线上,则点R 与点B 重合,点P 3的坐标为(1, 0).综上所述,抛物线上存在点P,使得△ AFP 为等腰直角三为点D, E.(1)直接写出点A , C, D 的坐标;3. (2016•桂林)如图,已知开口向下的抛物线 2y 1 = ax — 2ax + 1 过点 A(m, 1),与 y 轴 交于点C,顶点为B ,将抛物线y 1绕点C 旋转180 后得到抛物线y 2,点A, B 的对应点分别 角形,其坐标为(2)当四边形ABDE是矩形时,求a的值及抛物线y的解析式;⑶在⑵ 的条件下,连接DC,线段DC上的动点P从点D出发,以每秒1个单位长度的速度运动到点 C 停止,在点P 运动的过程中,过点 P 作直线I 丄x 轴,将矩形ABDE 沿直线I 折叠,设矩形折叠后相互重合部分面积为 S 平方单位,点P 的运动时间为t 秒,求S 与t 的 函数关系.备用图2 2解:(1)由题意得:将 A ( m 1)代入 y i = ax -2ax + 1 得:am —2am^ 1 = 1,解得 m = 2,m = 0(舍),••• A (2, 1), C (0, 1), Q — 2, 1) (2)如图 1,由(1)知:耳 1, 1 — a ),过点 B 作 BM 丄y 轴,若四边形 ABD 助矩形,贝U BC= CD •- B M+ C M^ B C= C D,「. 12+ ( — a ) 2= 22,• a =±3,v y 1抛物线开口向下,• a = — 3,v 甲由如绕点C 旋转180°得到,则顶点E ( — 1, 1— 3),•设 y 2 = k (x + 1)2+ 1— 3,则 k = 3, • y 2= 3x 2 + 2 3x +1 (3)如图 1,当 O w t w 1 时,贝U DI t ,构建直角厶 BQD 得 BQ= •. 3, DQ= 3,贝U BD= 2 3, BDQ= 30°, • PH=^t , PG^^3t ,• S = 2(P® PH x DF ^233t 2;如图 2,当 1v t w 2 时,EG= E ' G=t — 1) ,E ' F = 2( t — 1) ,S 不重合=233(t — 1)2,S = S + S 2— S 不重合=—>1 BB2亠 — 4f 3+ 3 t― ~3~ ;综上所述:2(O w t w 1)或 S =—(1)求抛物线的解析式及点C 的坐标;(2) 求证:△ ABC 是直角三角形;(3) 若点N 为x 轴上的一个动点,过点N 作MN 丄x 轴与抛物线交于点 M,则是否存在以0, M, N 为顶点的三角形与△ ABC 相似?若存在,请求出点 N 的坐标;若不存在,请说明理由.2解:(1) •••顶点坐标为(1, 1),•设抛物线解析式为 y = a (x — 1) + 1,又抛物线过原点,• 0 = a (0— 1)2+ 1,解得 a =— 1,二抛物线解析式为 y =— (x — 1)2+ 1,即卩 y = — x 2+ 2x ,联4. (2016 •南宁)如图,已知抛物线经过原点 于B , C 两点.0,顶点为A(1 , 1),且与直线y = x — 2交立抛物线和直线解析式可得y = — x + 2x , y = x — 2,x = 2, x =—1, 解得y = 0或仁—3, • B (2, 0) , q — 1,—BE= OB OE= 2+ 1= 3, EC= 3,「./ ABO=Z CBO= 45°,即/ ABG= 90°,「仏 ABC 是直角三角形(3)假设存在满足条件的点 N,设 N (x , 0),贝U Mx ,— x 2 + 2x ) ,「.0N = |x| , MN= | — x 2 + 2x|,由(2)在 Rt △ ABD 和 Rt △ CE 沖,可分别求得 AB= 2, BC= 3 2,v MNLx 轴于点 N t十 ~, MN O 也MN ON _「MN ON 」…•••/ABC=Z MN = 90°,「.当厶ABC 和厶MNO 相似时有 忑=Be 或阿忑,①当 荷BC 时,贝U1 1 5 7 5 7 x 丰0,二| — x + 2| = 3,即一x + 2=± 3,解得x = 3或x = 3 此时N 点坐标为(3,0)或(3,0);x + 2=± 3,解得x = 5或x =— 1,此时N 点坐标为(—1, 0)或(5, 0),综上可知,存在满足条件的N 点,其坐标为 百,0)或(5 6 7, 0)或(—1 , 0)或(5, 0)解:(1)y =— x 2+ 2x + 3 (2) • C (0, 3), B (3, 0),•直线 BC 解析式为 y = — x + 3,v22y = — x + 2x + 3= — (x — 1) + 4,「.顶点坐标为(1, 4),•对于直线 BC y = — x + 1,当 x = 1时,y= 2;将抛物线l 向下平移h 个单位长度,•当 h = 2时,抛物线顶点落在 BC 上;当 h = 4时,抛物线顶点落在 OB 上,•将抛物线I 向下平移h 个单位长度,使平移后所得抛物 线的顶点落在△ OBC 内(包括△ OB®边界),则2< h w 4 (3)设P (m — m i + 2m B 3), Q — 3,5 (2016 •玉林)如图,抛物线I : y = ax 2+ bx + c 与x 轴交于 A, B(3 , 0)两点(A 在B 的 左侧),与y 轴交于点C(0, 3),已知对称轴x = 1.(1) 求抛物线I 的解析式;(2) 将抛物线I 向下平移h 个单位长度,使平移后所得抛物线的顶点落在△ OBC 内(包括△ OBC 的边界),求h 的取值范围;(3) 设点P 是抛物线I 上任一点,点 Q 在直线l : x =— 3 上, △ PBQ 能否成为以点 P 为直3)| — x 2 + 2x| 3役,即|x|-| — x + 2| = 3|x| ,•••当x = 0时,M O, N 不能构成三角形,②当舉AB 时,则有2上爲纽=凶2,即|x|-| — x + 2| = 3|x| ,• | — x + 2| = 3,即一(2)如图,分别过n),①当P点在x轴上方时,过P点作PM垂直于y轴,交I于M点,过B点作BN垂直于MP 的延长线于N点,如图所示:••• B(3, 0) , △ PBQ是以点P为直角顶点的等腰直角三角形,•••/ BPQ= 90°, BP= PQ 则/ PMO Z BNP= 90°,/ MPQ=/ NBP 在厶PQM和厶BPN 中,PMQ:/ BNPMPQ:/ BPN PQI WA BNPAAS , • PM= BN •/ PM= BN=- m i+ 2m^3 ,根据B点坐标PQ= BP,2可得PN= 3- m,且PM F PN= 6,•—m i+ 2m n 3+ 3- mi= 6,解得mi= 1 或m= 0 , • F( 1 , 4)或P(0 , 3);②当P点在x轴下方时,过P点作PM垂直于I于M点,过B点作BN垂直于MP的延长线于N 点,同理可得厶PQI W^ BPN •- PM= BN •- PM= 6- (3- m) = 3+ m BN= m-2m2-3,则3 + m= m- 2m- 3,解得m=-^I-9) •综上可得,符合条件的点(3- _33 33-9)( 2 ,2 )•P 的坐标是(1, 4) , (0 , 3), (3+ 33 (2。
(广西地区)2017版中考英语总复习第一轮课本考点聚焦考点跟踪突破21九上Modules9-10外研版

考点跟踪突破21 九年级(上)Modules 9~10一、单项选择。
1.—The traffic is too busy.We have to drive slowly.—I think more new roads __A__ in our city.(2016,贺州)A.should be built B.should builtC.have built D.build2.—What kind of TV show do you prefer?—I like the ones __C__ make me laugh.(2016,玉林)A.who B.whom C.that D.what3.The environment here becomes better and better.__A__ birds are coming back.(2016,重庆)A.Thousands of B.Thousand ofC.Thousands D.Thousand4.Life is __A__ the unexpected.Whatever we do,try our best.(2016,烟台) A.full of B.proud ofC.instead of D.because of5.It is said that the project connecting mainland and Hong Kong __D__ soon.(2016,潍坊)A.is completed B.has completedC.will complete D.will be completed6.—Could you please __C__ me your notebook,Grace?—Certainly.Here you are.(2016,烟台)A.borrow B.to borrow C.lend D.to lend7.My parents don't allow me __B__ late.(2016,南充)A.stay up B.to stay upC.stays up D.staying up8.Today,WeChat (微信) becomes very popular,and more and more people like to use it to __B__ each other.(2016,菏泽)A.depend on B.communicate withC.believe in9.Don't make me __A__ this or that when I am busy.A.do B.done C.to do D.doing10.They __A__ a notice to tell the students about the changed meeting time.A.put up B.put on C.put away D.put out11.Here is the book.First __B__ it and then tell me what you think of it.A.look into B.look throughC.look up D.look after12.—A new park __B__ in our home town next year.—Really? Our home town must be more beautiful.(2017,桂林预测)A. will buildB. will be builtC. is built二、根据句意及汉语或首字母提示填写单词。
(广西地区)2017版中考数学总复习 第二篇 专题聚焦 跟踪突破3 动点或最值问题

专题跟踪突破3 动点或最值问题(针对广西中考动点或最值问题)一、选择题1.(2016·百色)如图,正△ABC 的边长为2,过点B 的直线l ⊥AB ,且△ABC 与△A ′BC ′关于直线l 对称,D 为线段BC ′上一动点,则AD +CD 的最小值是( A )A .4B .3 2C .2 3D .2+ 32.(2016·包头)如图,直线y =23x +4与x 轴、y 轴分别交于点A 和点B ,点C ,D 分别为线段AB ,OB 的中点,点P 为OA 上一动点,PC +PD 值最小时点P 的坐标为( C )A .(-3,0)B .(-6,0)C .(-32,0)D .(-52,0),第2题图),第4题图)3.(2016·呼和浩特)已知a ≥2,m 2-2am +2=0,n 2-2an +2=0,则(m -1)2+(n -1)2的最小值是( A )A .6B .3C .-3D .0解析:∵m 2-2am +2=0,n 2-2an +2=0,∴m ,n 是关于x 的方程x 2-2ax +2=0的两个根,∴m +n =2a ,mn =2,∴(m -1)2+(n -1)2=m 2-2m +1+n 2-2n +1=(m +n )2-2mn -2(m +n )+2=4a 2-4-4a +2=4(a -12)2-3,∵a ≥2,∴当a =2时,(m -1)2+(n -1)2有最小值,∴(m -1)2+(n -1)2的最小值=4(a -12)2-3=4(2-12)2-3=6,故选A4.(2016·苏州)矩形OABC 在平面直角坐标系中的位置如图所示,点B 的坐标为(3,4),D 是OA 的中点,点E 在AB 上,当△CDE 的周长最小时,点E 的坐标为( B )A .(3,1)B .(3,43)C .(3,53) D .(3,2)5.(2016·西宁)如图,在△ABC 中,∠B =90°,tan C =34,AB =6 cm .动点P 从点A 开始沿边AB 向点B 以1 cm /s 的速度移动,动点Q 从点B 开始沿边BC 向点C 以2 cm /s 的速度移动.若P ,Q 两点分别从A ,B 两点同时出发,在运动过程中,△PBQ 的最大面积是( C )A .18 cm 2B .12 cm 2C .9 cm 2D .3 cm 2,第5题图) ,第6题图)6.(2016·温州)如图,在△ABC 中,∠ACB =90°,AC =4,BC =2.P 是AB 边上一动点,PD ⊥AC 于点D ,点E 在P 的右侧,且PE =1,连接CE.P 从点A 出发,沿AB 方向运动,当E 到达点B 时,P 停止运动.在整个运动过程中,图中阴影部分面积S 1+S 2的大小变化情况是( C )A .一直减小B .一直不变C .先减小后增大D .先增大后减小解析:在Rt △ABC 中,∵∠ACB =90°,AC =4,BC =2,∴AB =AC 2+BC 2=42+22=25,设PD =x ,AB 边上的高为h ,h =AC ·BC AB =455,∵PD ∥BC ,∴PD BC =ADAC ,∴AD =2x ,AP=5x ,∴S 1+S 2=12·2x ·x +12(25-1-5x )·455=x 2-2x +4-255=(x -1)2+3-255,∴当0<x <1时,S 1+S 2的值随x 的增大而减小,当1≤x ≤2时,S 1+S 2的值随x 的增大而增大.故选C二、填空题7.如图,正方形ABCD 的边长是8,P 是CD 上的一点,且PD 的长为2,M 是其对角线AC 上的一个动点,则DM +MP 的最小值是___10__.8.(2016·眉山)如图,已知点A 是双曲线y =6x在第三象限分支上的一个动点,连接AO 并延长交另一分支于点B ,以AB 为边作等边三角形ABC ,点C 在第四象限内,且随着点A的运动,点C 的位置也在不断变化,但点C 始终在双曲线y =kx 上运动,则k 的值是__.解析:∵双曲线y =6x的图象关于原点对称,∴点A 与点B 关于原点对称,∴OA =OB ,连接OC ,如图所示,∵△ABC 是等边三角形,OA =OB ,∴OC ⊥AB ,∠BAC =60°,∴tan ∠OAC =OCOA=3,∴OC =3OA ,过点A 作AE ⊥y 轴,垂足为E ,过点C 作CF ⊥y 轴,垂足为F ,∵AE ⊥OE ,CF ⊥OF ,OC ⊥OA ,∴∠AEO =∠OFC ,∠AOE =90°-∠FOC =∠OCF ,∴△OFC ∽△AEO ,相似比OC OA =3,∴面积比S △OFCS △AEO=3,∵点A 在第一象限,设点A 坐标为(a ,b ),∵点A 在双曲线y =6x 上,∴S △AEO =12ab =62,∴S △OFC =12FC ·OF =362,∴设点C 坐标为(x ,y ),∵点C 在双曲线y =kx上,∴k =xy ,∵点C 在第四象限,∴FC =x ,OF =-y.∴FC ·OF=x ·(-y )=-xy =36,∴k =xy =-36,故答案为-36,第8题图) ,第9题图)9.(2016·沈阳)如图,在Rt △ABC 中,∠A =90°,AB =AC ,BC =20,DE 是△ABC 的中位线,点M 是边BC 上一点,BM =3,点N 是线段MC 上的一个动点,连接DN ,ME ,DN 与ME 相交于点O.若△OMN 是直角三角形,则DO 的长是__256或5013__.解析:如图,作EF ⊥BC 于F ,DN ′⊥BC 于N ′交EM 于点O ′,此时∠MN ′O ′=90°,∵DE 是△ABC 中位线,∴DE ∥BC ,DE =12BC =10,∵DN ′∥EF ,∴四边形DEFN ′是平行四边形,∵∠EFN ′=90°,∴四边形DEFN ′是矩形,∴EF =DN ′,DE =FN ′=10,∵AB =AC ,∠A =90°,∴∠B =∠C =45°,∴BN ′=DN ′=EF =FC =5,∴ED MN ′=DO ′O ′N ′,∴102=DO ′5-DO ′,∴DO ′=256.当∠MON =90°时,∵△DOE ∽△EFM ,∴DO EF =ED EM ,∵EM =EF 2+MF 2=13,∴DO =5013,故答案为256或501310.(2016·咸宁)如图,边长为4的正方形ABCD 内接于点O ,点E 是AB ︵上的一动点(不与A ,B 重合),点F 是BC ︵上的一点,连接OE ,OF ,分别与AB ,BC 交于点G ,H ,且∠EOF =90°,有以下结论:①AE ︵=BF ︵;②△OGH 是等腰直角三角形;③四边形OGBH 的面积随着点E 位置的变化而变化; ④△GBH 周长的最小值为4+ 2.其中正确的是__①②__.(把你认为正确结论的序号都填上),答图1) ,答图2)解析:①如答图1所示, ∵∠BOE +∠BOF =90°,∠COF +∠BOF =90°,∴∠BOE =∠COF ,在△BOE 与△COF 中,⎩⎪⎨⎪⎧OB =OC ,∠BOE =∠COF ,OE =OF ,∴△BOE ≌△COF (SAS ),∴BE =CF ,∴AE ︵=BF ︵,①正确;②∵BE =CF ,∴∠BOG =∠COH ,∴△BOG ≌△COH (ASA ),∴OG =OH ,∠COH +∠BOF=90°,∴∠GOH =90°,OG =OH ,∴△OGH 是等腰直角三角形,②正确;③如答图2所示, ∵△HOM ≌△GON ,∴四边形OGBH 的面积始终等于正方形ONBM 的面积,③错误;④∵△BOG ≌△COH ,∴BG =CH ,∴BG +BH =BC =4,设BG =x ,则BH =4-x ,则GH =BG 2+BH 2=x 2+(4-x )2,∴其最小值为22,④错误.故答案为①② 三、解答题11.如图,抛物线y =12x 2+bx -2与x 轴交于A ,B 两点,与y 轴交于C 点,且A(-1,0).(1)求抛物线的解析式及顶点D 的坐标;(2)点M 是x 轴上的一个动点,当△DCM 的周长最小时,求点M 的坐标.解:(1)∵点A (-1,0)在抛物线y =12x 2+bx -2上,∴12×(-1)2+b ×(-1)-2=0,解得b =-32,∴抛物线的解析式为y =12x 2-32x -2,∵y =12x 2-32x -2=12(x -32)2-258,∴顶点D 的坐标为(32,-258)(2)作出点C 关于x 轴的对称点C ′,则C ′(0,2),连接C ′D 交x 轴于点M ,根据轴对称性及两点之间线段最短可知,CD 一定,当MC +MD 的值最小时,△CDM 的周长最小,设直线C ′D 的解析式为y =ax +b (a ≠0),则⎩⎪⎨⎪⎧b =2,32a +b =-258,解得a =-4112,b =2,∴y C ′D =-4112x +2,当y =0时,-4112x +2=0,则x =2441,∴M (2441,0)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
考点跟踪突破4 二次根式及其运算
一、选择题
1.(2016·宁波)使二次根式x -1有意义的x 的取值范围是( D )
A .x ≠1
B .x >1
C .x ≤1
D .x ≥1
2.(2016·淮安)估计7+1的值( C )
A .在1和2之间
B .在2和3之间
C .在3和4之间
D .在4和5之间
3.(2016·自贡)下列根式中,不是最简二次根式的是( B ) A.10 B.8
C. 6
D. 2
4.(2015·荆门)当1<a <2时,代数式(a -2)2+|1-a|的值是( B )
A .-1
B .1
C .2a -3
D .3-2a
5.已知y =2x -5+5-2x -3,则2xy 的值为( A )
A .-15
B .15
C .-152 D.152
6.(2015·钦州)对于任意的正数m ,n 定义运算※为:m ※n =⎩⎨⎧m -n (m ≥n ),m +n (m<n ),计算(3※2)×(8※12)的结果为( B )
A .2-4 6
B .2
C .2 5
D .20
二、填空题
7.(2016·自贡)若代数式x -1x
有意义,则x 的取值范围是__x ≥1__. 8.(2016·聊城)计算:27·
83÷12=__12__. 9.(2015·自贡)若两个连续整数x ,y 满足x <5+1<y ,则x +y 的值是__7__.
10.(2016·天津)计算(5+3)(5-3)的结果等于__2__.
11.(2015·黔西南)已知x =
5-12,则x 2+x +1=__2__. 三、解答题
12.计算: (1)|22-3|-8+18; 解:原式=3-2
(2)48÷3-12×12+24; 解:原式=4+6
(3)(2016·盐城)(3-7)(3+7)+2(2-2);
解:原式=22
(4)(2-3)2 016·(2+3)2 017-2|-
32|-(-2)0. 解:原式=[(2-3)(2+3)]
2 016·(2+3)-3-1=2+3-3-1=1
13.(2016·烟台)先化简,再求值:(x 2-y x -x -1)÷x 2-y 2
x 2-2xy +y
2,其中x =2,y = 6. 解:(x 2-y x -x -1)÷x 2-y 2x 2-2xy +y 2=(x 2-y x -x 2x -x x )×(x -y )2(x +y )(x -y )=-y -x x ×x -y x +y =-x -y x ,把x =2,y =6代入得:原式=-2-62
=-1+3
14.已知x =3+1,y =3-1,求代数式x 2-y 2
的值.
解:原式=(x +y )(x -y ),∵x =3+1,y =3-1,∴原式=(3+1+3-1)(3+1-3+1)=23×2=43
15.已知x ,y 为实数,且满足1+x -(y -1)1-y =0,求x 2 017-y 2 016的值.
解:∵1+x -(y -1)1-y =0,∴1+x +(1-y )1-y =0,∴x +1=0,y -1=0,
解得x =-1,y =1,∴x 2 017-y 2 016=(-1)2017-12016=-1-1=-2
16.观察下面的变形规律: 12+1
=2-1, 13+2=3-2, 14+3=4-3, 15+4=5-4, …
解答下面的问题:
(1)若n 为正整数,请你猜想1n +1+n
=; (2)计算:
(12+1+13+2+14+3+…+12016+2015
)×(2016+1) 解:(2)原式=[(2-1)+(3-2)+(4-3)+…+(2016-2015)](2016+1)=(2016-1)(2016+1)=(2016)2-12=2015。
