七年级数学生活中的立体图形练习题
七年级数学上册“生活中的立体图形”能力训练题

华师七年级上册 4.1生活中的立体图形【知识技能天地】一、判断题1.柱体的上、下两个面一样大.………………………………………………..()2.圆柱的侧面展开图是长方形.………………………………………………()3.球体不是多面体.……………………………………………………………()4.圆锥是多面体.………………………………………………………………..()5.长方体是多面体.……………………………………………………………..()6.柱体都是多面体.……………………………………………………………..()二、选择题:1、如图,下列图形()柱体.2、下面给出的图形中,绕虚线旋转一周能形成圆锥的是()3、如下图,下列图形中有十四棱的是()二、填空题。
1、一个多面体有12条棱,6个顶点,则这个多面体是体。
2、把下列图形的名称填在括号内:3、长方体有个顶点,经过每个顶点有条棱,共有条棱。
4、一个七棱柱共有个面,条棱,个顶点,形状和面积完全相同的只有个面.5、如图4-5是一些具体的图形—三棱镜、方砖、帆布帐篷、笔筒、铅锤、粮囤、天文台,图4-6中是一些立体图形,找出与图4-6立体图形。
三、连线题:把图形与对应的图形名称用线连接起来。
四、解答题:1、将图4-8中的几何体进行分类,并说明理由。
2、图中的的几何体由几个面围成,面与面相交成几条线?它们是直的还是曲的?【探究创新乐园】3、三棱柱有9条棱,6个顶点,5个面;三棱锥有6条棱,4个顶点,4个面;四棱柱有12个棱,8个顶点,6个面;四棱锥有8条棱,5个顶点,5个面,等等,问能否组成一个有24条棱,10个面,15个顶点的多面体?请简要说明理由?4、若一个简单的多面体的每个面都是三角形,其顶点数为V,棱数为E,面数为F,则F=2V-4成立吗,若成立,说明理由;若不成立,请举出反例。
【数学生活实践】将一个圆柱体的面包切3刀,能将面包切成6块吗?能将面包切成7块吗?能将面包切成8块吗?如果能,请画图说明如何切法。
七年级数学生活中的立体图形1

[填空题]合成塔环隙主气流的作用是保持合成塔壳体()。 [多选]某建筑公司承建写字楼工程,根据我国《建筑法》和《建设工程安全生产管理条例》投保了建筑职工意外伤害保险。该险种承保的范围包括()。A.工程本身受损B.施工用设施受损C.被保险人从事建筑施工时由于操作不当受伤害致残D.被保险人在施工现场被高空坠物砸死E.场地清理费 [单选,A1型题]严重胸腹联合损伤后,必须首先处理的是()。A.呼吸骤停B.闭合性液气胸C.急性弥漫性腹膜炎D.粉碎性胸腰椎骨折E.轻度血压下降 [单选]贫液流量通过()调节的。A.FV-0703B.FV-0704C.FV-0705D.FV-0707 [单选]胡萝卜素是合成视紫红质的主要物顶,因此食用胡萝卜可以()。A、降低血液汞浓度B、预防对视网膜的伤害C、降低血压D、降低血脂 [单选]硝石不宜与下列哪些药物混放()。A.朴硝B.青盐C.硇砂D.雄黄、硫黄E.蒲黄 [单选]事业单位年终结账时,下列项目中不应转入“结余分配”科目的是()。A."事业结余"科目借方余额B."事业结余"科目贷方余额C."经营结余"科目借方余额D."经营结余"科目贷方余额 [单选]假定甲公司本年盈余Байду номын сангаас110万元,某股东持有10000股普通股(占总股数的1%),目前每股市价为22元。股票股利发放率为10%,假设市盈率不变,则下列表述中,不正确的是()。A、发放股票股利之后每股收益为1元B、发放股票股利之后每股价格为20元C、发放股票股利之后该股东持股比例为 [单选,A2型题,A1/A2型题]选择氢原子核作为人体磁共振成像的原子核的理由是()A.1H是人体中最多的原子核B.1H约占人体中总原子核数的2/3以上C.1H的磁化率在人体磁性原子核中是最高的D.以上都是E.以上都不是 [判断题]气体发生器的作用是,车辆发生碰撞时,将碰撞信号输送给气囊控制单元。()A.正确B.错误 [名词解释]地球化学旋回 [单选]关于阴道正确的是().A.上端包绕子宫颈,下端开口于阴道前庭前部B.阴道壁仅由黏膜与弹力纤维构成C.后穹隆顶端与子宫直肠陷凹贴近.后者是腹腔最低部分D.后壁短于前壁E.黏膜由复层鳞状上皮细胞所覆盖,有腺体 [单选]1915年在经济学领域,明确提出将企业的流通活动分为创造需求的活动和物流活动的是()A.阿齐•箫B.美国物流管理协会C.琼西•贝克D.美国国防部 [单选,A1型题]医疗机构从业人员违反本规范的,视情节轻重给予处罚,其中不正确的是()A.批评教育、通报批评、取消当年评优评职资格B.卫生行政部门依法给予警告、暂停执业或吊销执业证书C.纪检监察部门按照党纪政纪案件的调查处理程序办理D.缓聘、解职待聘、解聘E.涉嫌犯罪的,移 [多选]下列属于火焰切割的是()。A.液化石油气切割B.氢氧元切割C.氧熔剂切割D.激光切割 [判断题]硬膜外导管消毒时,常选用甲醛蒸气消毒法。A.正确B.错误 [填空题]()是面向家庭客户提供的集固定电话、手机和增值业务于一体的融合套餐,套餐内成员用户统一账户缴费,固话、手机共享时长。 [单选]()是涉烟情报分析的基础的思维方法。A、辩证思维方法B、灵感思维方法C、逻辑思维方法D、数据整合方法 [多选]以下几种机关之间,因工作需要往来公文,可以使用函的有()。A.省财政厅与省经贸委B.××大学与市劳动局C.省教委与省人民政府D.县公安局与乡人民政府 [问答题,简答题]机泵启动前的准备? [单选]教育部先后于1999年和2002年分别颁布了《关于加强中小学心理健康教育的若干意见》与《中小学心理健康教育指导纲要》两个重要文件,对中小学心理健康教育的目的、任务、方法、形式和具体内容都作出了明确的规定。根据文件精神和当前中小学实际,你认为下列论述正确的是:() [单选,A2型题,A1/A2型题]MRI与CT相比较不具有优势的是()A.中枢神经系统疾病B.对纵隔及肺门淋巴结肿大,占位性病变的诊断C.肺内病变如钙化及小病灶D.半月板损伤E.关节软骨的变性与坏死 [问答题,简答题]稀土元素在矿物中是如何赋存的?主要矿物有几种?具有实际利用价值的矿物有几种?请举三种最著名的矿物名称。 [单选]在OSI模型中,传输层为第()层A.3B.4C.6D.7 [单选,A2型题,A1/A2型题]正常人心脏的起搏点为()A.窦房结B.房室结C.结间束D.希氏束E.蒲肯野纤维 [单选,A2型题,A1/A2型题]下列疾病需采用严密隔离的是()A.疟疾B.破伤风C.霍乱D.肺结核E.新生儿脓疱疮 [单选,A1型题]暑湿感冒,暑热偏盛,热盛烦渴者,治疗方剂宜首选()。A.新加香薷饮B.黄连香薷饮C.藿朴夏苓饮D.三物香薷饮E.藿香正气散 [填空题]有机化合物一般是指组成里含()的化合物。 [单选,A2型题,A1/A2型题]VEP的作用有()A.协助诊断多发性硬化B.昏迷及脑死亡预后判断C.评估视力D.判定视网膜病变E.诊断听神经瘤一后颅凹瘤 [单选]患者眼前闪光,视力减退1周。结合超声声像图,最可能的诊断是()A.局限性脉络膜脱离B.局限性视网膜脱离C.完全性视网膜脱离D.玻璃体后脱离E.以上均不对 [单选,A2型题,A1/A2型题]妇女一生中最后一次行经后,停闭1年以上,称()A.绝经期B.绝经C.绝经前期D.绝经后期E.围绝经期 [单选]石油中的铁、镍、铜、钒、砷等微量元素通常只占石油总含量的()%左右。A、1B、3C、5D、7 [单选]配送网络的处理对象是()A.商流B.信息流C.物流D.资金流 [单选]下列哪种农药属于杀虫剂()A、乐果B、大隆C、百菌清D、2.4-滴 [单选]下列选项中,属于催化裂化反应的是()。A、烷烃脱氢生成烯烃B、烃类分解为甲烷和碳C、烯烃加氢D、烯烃叠合 [单选]项目投资估算所在的阶段是()。A.设计阶段B.决策阶段C.招标阶段D.施工阶段 [问答题,简答题]打磨的作用与要求? [单选]深龋患者激发痛较重,洞底软龋能够彻底去净,治疗方法应选择()A.双层垫底,一次完成充填治疗B.局麻后开髓失活,行牙髓治疗C.先做安抚疗法,待一到二周复诊时症状消除后,再以双层垫底充填D.施行活髓切除术E.间接盖髓、双层垫底一次完成充填治疗 [多选]下列有关计算加油站销售收入的公式中,正确的有()。A.销售收入=不含税销售收入÷(1+增值税税率)B.销售收入=含税销售收入÷(1+增值税税率)C.销售收入=含税销售单价×销售总量D.销售收入=不含税销售单价×销售总量 [单选]直流母线的正、负极色漆规定为()。A.蓝、白B.红、白C.红、蓝D.黑、白
生活中的立体图形课后题(题目+答案)

【采分点】面的个数(4分)
【采分点】判断平曲面(2分)
【题干】2.你认为生活中有哪些几何体可以由平面图形旋转而得到?你能想象它们是由什么平面图形旋转而成的吗?举例说明.
【答案】比如:篮球是由圆旋转而成;圆锥形的沙堆是由三角形旋转而成;水杯是由四边形旋转而成的;易拉罐是由矩形旋转而成的;.
【答案】(1)圆柱体和长方体(2)圆柱体(3)圆柱体和圆锥(4)长方体和球
【采分点】每幅图(1.5分)
【题干】6.圆柱和棱柱有很多相同点,下面的这个几何体也有这样的相同点吗?
【答案】有,上下底面相同且平行;侧面展开是矩形.
【采分点】有(2分)
【采分点】相同点(4分)
【大题】习题1.2(每小题6分)
【题干】1.图中的棱柱,圆锥分别是由几个面围成的?他们分别是平的还是曲的?
【采分点】正确举例3个(6分)
【题干】3.下列几何体可以由平面图形绕其中一条直线旋转一周得到吗?
【答案】(1)(3)(4)可以由平面图形绕其中一条直线旋转一周得到
【采分点】(1)(3)(4)(6分)
【小题】(2)这个六棱柱的所有侧面的面积之和是多少?
【答案】侧面积之和:5×4×6=120cm2
【采分点】120cm2(4分)
【问答题】
【题干】3.将下列几何体分类,并说明理由.
正方体长方体球圆柱圆锥四棱柱三棱柱
【答案】这些几何体分别是正方体、长方体、球、圆柱、圆锥、四棱柱、三棱柱
可以分为柱体、锥体、球体三类;
【综合题】
【题干】2.一个六棱柱模型如图所示,它的底面边长都是5cm,侧棱长4cm观察这个模型,回答下列问题:
生活中的立体图形(分层练习)-2023-2024学年七年级数学上册基础知识专项突破讲与练(北师大版)
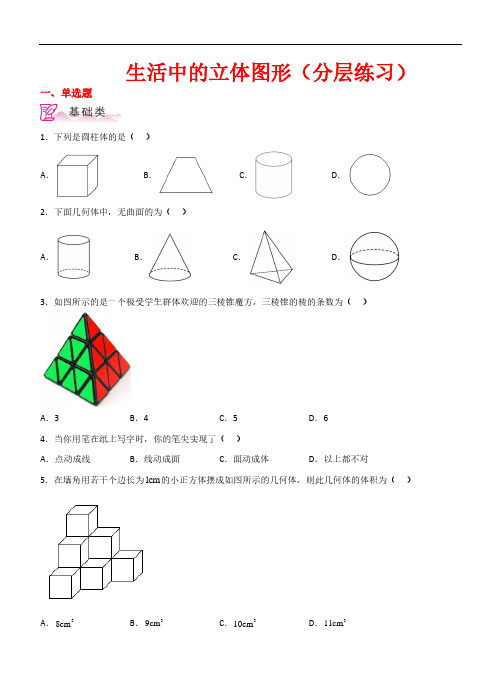
生活中的立体图形(分层练习)一、单选题1.下列是圆柱体的是( )A .B .C .D .2.下面几何体中,无曲面的为( )A .B .C .D .3.如图所示的是一个极受学生群体欢迎的三棱锥魔方,三棱锥的棱的条数为( )A .3B .4C .5D .64.当你用笔在纸上写字时,你的笔尖实现了( )A .点动成线B .线动成面C .面动成体D .以上都不对5.在墙角用若干个边长为1cm 的小正方体摆成如图所示的几何体,则此几何体的体积为( )A .38cmB .39cmC .310cmD .311cm6.下列几何体是棱锥的是().A.B.C.D.7.把14个棱长为1分米的正方体摆成如图所示的形式,然后把露出的表面都涂上颜色,则被涂上颜色的部分面积为()A.33平方分米B.24平方分米C.21平方分米D.42平方分米8.正方体切去一个块,可得到如图几何体,这个几何体有()条棱.A.10B.11C.12D.139.你见过一种折叠灯笼吗?它看起来是平面的,可是提起来后却变成了美丽的灯笼,这个过程可近似地用哪个数学原理来解释()A.点动成线B.线动成面C.面动成体D.面与面相交的地方是线10.下面几何体可以由平面图形绕某条直线旋转一周得到的是()A.B.C.D.11.下列说法不正确的是( )A .长方体是四棱柱B .八棱柱有8个面C .六棱柱有12个顶点D .经过棱柱的每个顶点有3条棱12.下列几何体中,由曲面和平面围成的是( )A .三棱柱B .圆锥C .球体D .正方体13.物理实验室有高度同为10cm 的圆柱形容器A 和B (如图),它们的底面半径分别为2cm 和4cm ,用一水龙头单独向A 注水,3分钟后可以注满容器.在实验室课上,某同学将两容器在它们高度的一半用一个细水管连通(连接细管的容积忽略不计),仍用该水龙头向A 注水,问6分钟后容器A 中水的高度是( )cm .(注:若圆柱体底面半径为r ,高为h ,体积为V ,则2V r h π=)A .6B .5C .4D .314.棱长为3英寸的正方体是由27个单位小正方体组成的,其中有21个红色小正方体,6个白色小正方体,若让大正方体的表面尽可能少地出现白色,则大正方体表面积中白色部分占整个正方体表面积的( )A .554B .19C .527D .2915.将一个棱长为3的正方体的表面涂上颜色,分割成棱长为1的小正方体(如图).设其中一面、两面、三面涂色的小正方体的个数分别为为1x 、2x 、3x ,则1x 、2x 、3x 之间的关系为( )A .1x -2x +3x =1B .1x +2x -3x =1C .1x -2x +3x =2D .1x +2x -3x =2二、填空题16.如图,这个几何体的名称为______________.17.一个长方体的表面积是40平方厘米,把这个长方体平均分成两个相等的正方体,每个正方体的表面积是_____平方厘米.18.若一个棱柱有12个顶点,且所有侧棱长的和为30cm,则每条侧棱长为________cm.19.如图,将此长方形绕虚线旋转一周,得到的是圆柱体,其体积是______.(结果保留 )20.已知一个边长分别为7cm和8cm的长方形,若绕着该长方形的一条边所在的直线旋转一周得到的几何体的体积最小是________.21.如图所示的立体图形的名称是_____.22.如图,有一内部装有水的直圆柱形水桶,桶高20cm;另有一直圆柱形的实心铁柱,柱高30cm,直立放置于水桶底面上,此时水桶内的水面高度为12cm.若水桶的底面直径为20cm,铁柱的底面直径为10cm现将铁柱取出,则水桶内的水面高度变为________.(不计桶的厚度及水的损失)23.若一个棱柱有9个面,则它是_______棱柱.24.一个长方体的所有棱长之和是180cm,则相交于一个顶点的三条棱的长度和是______cm.25.图中的大矩形长8厘米、宽6厘米,小矩形长4厘米、宽3厘米,以长边中点连线(图中的虚线)为轴,将图中的阴影部分旋转一周得到的几何体的表面积为________平方厘米.26.圆柱、圆锥、球的共同点是_____________________________;27.用8个棱长3厘米的立方体拼成一个长方体,其中表面积最小的长方体的面积为______平方厘米.28.分别写出下列各立体图形的名称:① ______ ② ______ ③ ______.29.一个棱柱的面数为14,棱数是36,则其顶点数为________.30.已知一个直角三角形的两直角边分别是6cm,8cm.将这个直角三角形绕它的一直角边所在直线旋转一周,可以得到一个圆锥,则这个圆锥的体积是___cm3.(结果用π表示)三、解答题31.如图所示,是我们熟悉的三棱柱、五棱柱和六棱柱.(1)填写下表:(2) 设n 棱柱(n 为正整数,且3n ≥)的顶点数为a 、棱数为b 、面数为c ,根据表中数据猜想a c b +−=________.32.如图是一张长方形纸片,AB 长为a ,BC 长为b .(1)若将此长方形纸片绕它的一边所在直线旋转一周,则形成的几何体是 .(2)若将这个长方形纸片绕AB 边所在直旋转一周形成的几何体的体积.(结果保留π)33.综合与实践新年晚会是我们最欢乐的时候,会场上,悬挂着五彩缤纷的小装饰,其中有各种各样的立体图形.下面是常见的一些多面体:操作探究:(1)通过数上面图形中每个多面体的顶点数(V)、面数(F)和棱数(E),填写下表中空缺的部分:通过填表发现:顶点数(V)、面数(F)和棱数(E)之间的数量关系是,这就是伟大的数学家欧拉(L.Euler,1707—1783)证明的这一个关系式.我们把它称为欧拉公式;探究应用:(2)已知一个棱柱只有七个面,则这个棱柱是棱柱;(3)已知一个多面体只有8个顶点,并且过每个顶点都有3条棱,求这个多面体的面数.34.探究:有一长9cm,宽6cm的长方形纸板,现要求以其一组对边中点所在直线为轴,旋转180 ,得到一个圆柱,现可按照两种方案进行操作:方案一:以较长的一组对边中点所在直线为轴旋转,如图①;方案二:以较短的一组对边中点所在直线为轴旋转,如图②.(1)请通过计算说明哪种方案构造的圆柱体积大;(2)若将此长方形绕着它的其中一条边所在的直线为轴旋转360°,则得到的圆柱体积为多少?35.如图1至图3是将正方体截去一部分后得到的多面体.(1)根据要求填写表格:(2)猜想三个数量间有何关系;(3)根据猜想计算,若一个多面体有顶点数2018个,棱数4036条,试求出它的面数.36.一位父亲有一块正方形的土地,他把其中的14留给自己,其余的平均分给他的四个儿子,如下图所示,他想使每个儿子获得的土地面积相等,形状相同,这位父亲应该怎么分?试画出示意图,并加以说明.参考答案1.C【分析】根据圆柱的特征:圆柱由侧面和上下两个底面组成,圆柱的侧面是曲面,上下两个面是完全相等的两个圆;由此选择即可.【详解】A .是长方体,不符合题意;B .是梯形,不符合题意;C .是圆柱体,符合题意;D .是圆,不符合题意,故选C .【点拨】本题考查的圆柱的定义,关键点在于:圆柱的侧面是光滑的曲面,且上下底面是完全相等的两个圆.2.C【分析】根据棱锥,棱柱没有曲面可得答案.【详解】解:圆,圆锥,球都有曲面,三棱锥没有曲面,故选C【点拨】本题考查的是简单几何体的认识,熟记各几何体的特点是解本题的关键.3.D【分析】根据三棱锥的特点进行解答即可.【详解】解:三棱锥的棱的条数为6,故D 正确.故选:D .【点拨】本题主要考查了三棱锥的特点,解题的关键是熟练掌握n 棱锥有2n 条棱,()1n +个面,()1n +个顶点.4.A【分析】笔尖点在纸上是一个点,写字滑动笔尖就是一条直线,即点动成线.【详解】解:当你用笔在纸上写字时,你的笔尖实现了点动成线,故选:A.【点拨】本题考查了点动成线,理解点动成线是解题关键.5.C【分析】最下层是6个小正方体,第二层是3个小正方体,最上一层是1个小正方体据此加起来即可;【详解】解:(1)6+3+1=10(个),∵每个小正方体的边长为1cm∴每个小正方体的体积为31cm,∴10个小正方体的体积为310cm故选:C.【点拨】此题主要考查了图形的计数方法及求几何体的体积,计数时要注意分层计数,做到不重不漏是解题的关键.6.A【分析】根据棱锥的定义判定,即可.【详解】A、属于棱锥,符合题意;B、是圆柱,不符合题意;C、是圆锥,不符合题意;D、是棱柱,不符合题意.故选:A.【点拨】本题考查棱锥的知识,解题的关键是理解棱锥的定义:如果一个多面体的一个面是多边形,其余各面是有一个公共顶点的三角形,那么这个多面体叫棱锥.7.A【分析】把每一层的面积求出,相加即可得出答案.【详解】棱长为1分米的正方体每个面的面积为1平方分米,最上层,侧面积为4平方分米,上表面积为1平方分米,总面积为415+=(平方分米),中间一层,侧面积为248⨯=(平方分米),上表面积为413−=(平方分米),总面积为8311+=(平方分米),最下层,侧面积为3412⨯=(平方分米),上表面积为945−=(平方分米),总面积为12517+=(平方分米),5111733++=(平方分米),∴被涂上颜色的部分面积为33平方分米.故选:A .【点拨】本题考查几何体的表面积,分别把每层的面积求出来是解题的关键.8.C【分析】根据几何体分别求出上面、侧面及下面的棱即可得解.【详解】解:由题意可知上面有3条棱,侧面有5条棱,下面有4条棱,∴这个几何体有35412++=条棱,故选:C .【点拨】本题主要考查了几何体,按位置的不同数出几何体的棱是解题的关键.9.C【分析】根据点、线、面、体相关的知识进行解答即可.【详解】解:由平面图形变成立体图形的过程是面动成体,故选:C .【点拨】本题考查了根据点、线、面、体的相关知识,解题的关键在于掌握几何变换之间的关系.10.B【分析】根据平面图形旋转的特点即可得.【详解】解:∵平面图形绕某条直线旋转一周得到的几何体必有曲面,且矩形沿其一条边旋转得到圆柱体, ∴选项B 符合题意,【点拨】本题考查了平面图形旋转后所得的立体图形,熟练掌握平面图形绕某条直线旋转一周得到的几何体必有曲面是解题关键.11.B【分析】根据四、六、八棱柱的特点可得答案.【详解】解:A 、长方体是四棱柱,选项说法正确,不符合题意;B 、八棱柱有8+2=10个面,选项说法错误,符合题意;C 、六棱柱有2×6=12个顶点,选项说法正确,不符合题意;D 、经过棱柱的每个顶点有3条棱,选项说法正确,不符合题意;故选:B .【点拨】此题主要考查了认识立体图形,关键是认识常见的立体图形,掌握棱柱、棱锥、圆柱、圆锥的特点.12.B【分析】三棱柱由平面组成、圆锥由曲面和平面组成、球体由曲面组成、正方体由平面组成,结合各图形的特点可得出答案.【详解】解:三棱柱由平面组成、圆锥由曲面和平面组成、球体由曲面组成、正方体由平面组成; 故选:B【点拨】此题考查了认识立体图形的知识,熟练掌握是解题的关键.13.B【分析】3分钟后可以注满容器A ,可以算出水的流速,从而可以得出6分钟内水龙头的出水量,然后得出答案.【详解】解:3分钟后可以注满容器A ,A 容器的体积为22321040cm V r h πππ==⨯⨯=.则6分钟的注入水量为380cm π,设6分钟后容器A 中水的高度是cm x ,当5x <时,22520ππ⨯⨯=,注入水量20V π<.当5x =时,2225452080100πππππ⨯⨯+⨯⨯=+=,注入水量20100V ππ≤≤.当510x <≤时,2221041040160200πππππ⨯⨯+⨯⨯=+=,注入水量100200V ππ<≤故选:B .【点拨】本题考查了认识立体图形,解题关键是要读懂题目的意思,也考查了同学们的物理知识和分类讨14.A【分析】想使大正方体的表面尽可能少的出现白色,可将8个红色单位正方体放在大正方体的8个顶点处,每个棱上放2个,剩下1个放在外层,再根据大正方体的表面积54,用1减去红色部分占整个表面积的多少即可求得结果.【详解】解:根据题意:大正方体的表面尽可能少的出现白色,将8个红色单位正方体放在大正方体的8个顶点处,每个棱的中间放1个,剩下1个放在外层, ∵大正方体的表面积为263⨯=54∴红色部分占整个表面积的831221495454⨯+⨯+=, ∴白色部分占整个表面积的14955454−=. 故选:A .【点拨】本题考查了几何体的表面积,解决本题的关键是21个红色小正方体的摆放问题.15.C【详解】分析:如下图所示,只有1个面被涂色的小正方体共有6个,有两个面被涂色的小正方体共有12个,有三个面被涂色的小正方体共有8个,即1236128x x x ===,,,将所得结果代入各选项检验即可作出判断.详解:如下图所示,由图可知:只有1个面被涂色的小正方体共有6个,有两个面被涂色的小正方体共有12个,有三个面被涂色的小正方体共有8个,∴1236128x x x ===,,,∴12361282x x x −+=−+=,即A 中结论错误,C 中结论正确;123612810x x x +−=+−=,即B 和D 中结论都是错误的.故选C.16.圆锥【分析】根据常见图形的名称可直接得到答案.【详解】解:根据图形可得该几何体的名称为:圆锥,故答案为:圆锥.【点拨】本题考查常见的几何体,解题的关键是熟练掌握常见体的名称.17.24【分析】把一个长方体平均分开,正好成为两个相同的正方体,即长方体的表面积相当于一个正方体的10个面的面积和,先求出正方体的一个面的面积,即可得解. 【详解】解:一个长方体的表面积是40平方厘米,把这个长方体平均分成两个相等的正方体, ∴正方体的一个面的面积为:40(662)4÷+−=(平方厘米);∴每个正方体的表面积是:4624⨯=(平方厘米);故答案为:24.【点拨】此题考查了长方体与正方体表面积的计算,长方体与两个相同正方体的表面积之间的关系是解答此题的关键.18.5【分析】根据棱柱的概念和定义,可知12个顶点的棱柱是六棱柱,进而可得出答案.【详解】解:根据一个棱柱有12个顶点,所以它是六棱柱,即有6条侧棱,又因为所有侧棱长的和是30cm ,所以每条侧棱长是3066cm ÷=.故答案为:5.【点拨】本题考查了棱柱的知识,掌握棱柱是几棱柱,它就有几个侧面,并且就有几条侧棱是关键. 19.16π【分析】将长方形旋转可得出圆柱体,根据圆柱体积公式即可求出该圆柱的体积.【详解】解:将此长方形绕虚线旋转一周,得到的是圆柱体,其体积为:222416V r h πππ==⨯⨯=.故答案为圆柱;16π.【点拨】本题考查了圆柱体的形成,牢记圆柱的体积公式是解题的关键.20.3392πcm即可,再比较大小.【详解】解:绕长方形的一边旋转一周,会得到一个圆柱体,该边为圆柱体的高,另一边为底面半径. 圆柱体积为底面积⨯高,底面为圆,圆的面积为2=πS r ,绕长度为7的边旋转时,底面半径为8,223ππ87448πcm V r h ==⨯⨯=;绕长度为8的边旋转时,底面半径为7,223ππ78392πcm V r h ==⨯⨯=448>392,所以体积最小为3392πcm .故答案为:3392πcm【点拨】本题主要考查圆柱的体积问题,注意分情况讨论是解题的关键.21.三棱柱【分析】根据三棱柱的形状即可得出答案.【详解】解:∵该立体图形上面和底面都是三角形,且有三条棱,∴它的名称是三棱柱,故答案为:三棱柱.【点拨】本题主要考查立体图形的名称,关键是要牢记三棱柱的形状.22.9cm【分析】先求出取出铁柱前水的体积,然后根据取出后水柱的底面积为整个圆形水桶的底面积求出此时的水面高度即可. 【详解】铁柱取出前,水的体积为:22320101212900cm 22V πππ⎛⎫⎛⎫=⨯−⨯= ⎪ ⎪⎝⎭⎝⎭, 铁柱取出后,水铺满整个圆桶地面,即此时水柱的底面积等于圆桶的底面积,∴此时水面高度为:29009cm 202h ππ==⎛⎫ ⎪⎝⎭,故答案为:9cm .【点拨】本题考查圆柱体的体积计算,准确分析变化前后对应圆柱体的底面积是解题关键.23.七【分析】根据n 棱柱的特点,由n 个侧面和两个底面构成,可判断.【详解】由题意可知:9-2=7.故答案为:七.24.45【分析】根据长方体有12条棱,分别是4条高,4条长,4条宽,相交于一个顶点的是一条长,一条宽,一条高,即可进行解答.【详解】解:()180445cm ÷=,故答案为:45.【点拨】本题主要考查了长方体的棱,解题的关键是掌握长方体有12条棱,分别是4条高,4条长,4条宽.25.92π【详解】矩形旋转后形成圆柱,根据题意求出大圆柱的侧面积和小圆柱的侧面积,再加上大圆柱的上下两圆的面积,即可得出答案.【分析】解:由题意可得:大圆柱的侧面积为:8648p p ⨯⨯=(平方厘米);小圆柱的侧面积为:4312p p ⨯⨯=(平方厘米);大圆柱上下圆的面积为:22432p p ⨯=(平方厘米), ∴几何体的表面积为:48123292p p p p ++=(平方厘米). 故答案为:92π.【点拨】本题考查圆柱的表面积计算,难度不大,关键是根据线动成面的知识得出旋转后的图形.26.都有一个面是曲面【分析】根据圆柱、圆锥、球的概念和特性即可解答.【详解】圆柱、圆锥、球的共同点是:都有一个面是曲面.故答案为都有一个面是曲面.【点拨】本题考查几何体的面的组成情况.注意面有平面和曲面之分.27.216【分析】用8个棱长3厘米的立方体拼成一个长方体,有3种不同的拼组方法:(1)1×8排列;(2)2×4排列;(3)2×2×2排列,由此利用长方体的表面积公式分别求出它们的表面积即可解决问题.【详解】(1)1×8排列,表面积为:(3×24+3×24+3×3)×2,=153×2,=306(平方厘米);(2)2×4排列,表面积为:(3×12+6×12+3×6)×2,=126×2,=252(平方厘米);6×6×6=216(平方厘米),答:表面积最小的是216平方厘米.故答案为:216.【点拨】本题考查了长方体的表面积公式的计算应用,抓住8个小正方体拼组长方体的特点,得出3种不同的拼组方法是解决本题的关键.28. 圆锥 五棱柱 三棱锥【详解】根据几何体的形状,可知①是圆锥,②是五棱柱,③是三棱锥,由此填空即可.故答案为圆锥,五棱柱,三棱锥.29.24【分析】利用简单多面体的顶点数V ,面数F 及棱数E 之间的关系为:V+F -E=2,这个公式叫做欧拉公式,公式描述了简单多面体顶点数、面数、棱数特有的规律,进而得出答案.【详解】∵简单多面体的顶点数V ,面数F 及棱数E 之间的关系为:V+F -E=2,一个棱柱的面数为14,棱数为36,∴ 顶点数为:V+14-36=2,解得:V=24.故答案为:24.【点拨】本题考查了欧拉公式,正确记忆公式是解题的关键;30.128π或96π8cm ,高为6cm 的一个圆锥;如果以这个直角形的长直角边为轴,旋转后所组成的图形是一个底面半径为6cm ,高为6cm 的圆锥.根据圆锥的体积公式213V r h π=即可求出圆锥的体积. 【详解】解:分两种情况: ①2118664612833πππ⨯⨯⨯=⨯⨯⨯=cm 3; ②211683689633πππ⨯⨯⨯=⨯⨯⨯=cm 3. ∴这个圆锥的体积是128π或96π立方厘米.故答案为:128π或96π.【点拨】本题考查的是将一个简单图形绕一轴旋转一周所组成的图形是什么图形,即面动成体,解题的关键是掌握圆锥的体积计算公式.(2)2【分析】(1)根据所给的图形,数一数直接得出结果;(2)把(1)中的结果代入a c b +−,即可发现规律.【详解】(1)根据图形,可以得出三棱柱有6个顶点,5个面,9条棱;五棱柱有10个顶点,7个面,15条棱;六棱柱有12个顶点,8个面,18条棱;故答案为:6,5,9;10,7,15;12,8,18.(2)三棱柱:6a =,9b =,5c =,∴6592a c b +−=+−=;五棱柱:10a =,15b =,7c =,∴107152a c b +−=+−=;六棱柱: 12a =,18b =,8c =,∴128182a c b +−=+−=;猜想:2a c b +−=.【点拨】本题主要考查了几何体的结构特征,根据所给的材料,仔细观察图形,找出一般规律是解本题的关键.32.(1)圆柱(2)2ab π【分析】(1(2)根据题意可得,圆柱的底面半径为b,高为a,再根据圆柱的体积公式进行计算即可解答.【详解】(1)若将此长方形纸片绕它的一边所在直线旋转一周,则形成的几何体是圆柱,故答案为:圆柱;(2)由题意得:223(cm )b a ab ππ⨯⨯=,∴形成的几何体的体积2ab π.【点拨】本题考查了点、线、面、体,熟练掌握圆柱的特征,以及圆柱的体积计算公式是解题的关键.33.(1)表见解析,2V F E +−=(2)五(3)6(2)根据棱柱的定义进行解答即可;(3)由(1)得出的规律进行解答即可.【详解】(1)解:填表如下:顶点数(V )、面数(F )和棱数(E )之间的数量关系是2V F E +−=,故答案为:2V F E +−=;(2)解:一个棱柱只有七个面,必有2个底面,∴有72=5−个侧面,∴这个棱柱是五棱柱,故答案为:五;(3)解:由题意得:棱的总条数为83122⨯=(条), 由2V F E +−=可得8122F +−=,解得:6F =,故该多面体的面数为6.【点拨】本题考查了多面体与棱柱的认识,点线面体的相关概念,正确看出图形中各量之间的关系是解题的关键.34.(1)方案一构造的圆柱的体积大,见解析(2)324π(cm 3)【分析】(1)分别按方案一,方案二转法,根据体积公式找出半径与高,代入计算即可;(2)分两种情况,按长方形长边所在的直线为轴旋转360°,绕长方形的短边所在的直线为轴旋转360°,确定半径与高代入体积公式计算即可.方案二:23981p p ´´=(cm 3),∵121.581p p >,∴方案一构造的圆柱的体积大;(2)以较短一条边所在的直线为轴旋转360︒,其体积为:296486p p ´´=(cm 3),以较长一条边所在的直线为轴旋转360︒,其体积为:269324p p ´´=(cm 3).【点拨】本题考查基本图形旋转得到的体积问题,掌握解决旋转半径与圆柱体的高是解题关键.35.(1)见解析;(2)2f v e +−=;(3)2020【分析】(1)根据图形数出即可.(2)根据(1)中结果得出2f v e +−=.(3)代入2f v e +−=求出即可.【详解】解:(1)(2)猜想:2f v e +−=;(3)2018v =,4036e =,2f v e +−=201840362f ∴+−=,2020f =,即它的面数是2020.【点拨】本题考查了截一个几何体,图形的变化类的应用,关键是能根据(1)中的结果得出规律.36.见解析.【详解】【分析】父亲和四个儿子分割一个正方形,父亲留14,则所剩三个小正方形每一个再分割为四个小正方形,并且让出一个,土地面积就会相等.【详解】解:如答图,父亲和四个儿子分割一个正方形,父亲留14,则所剩三个小正方形每一个再分割为四个小正方形,并且让出一个,土地面积就会相等.所让的三个小正方形必有一条棱重合才能为一体,故如图所分就会形状相同.【点拨】本题考核知识点:正方形的分割.解题关键点:根据实际对图形进行合理分割.。
2019-2020年七年级数学上册4.1生活中的立体图形4.1.1认识立体图形跟踪训练含解析新版华东师大版

2019-2020年七年级数学上册4.1生活中的立体图形4.1.1认识立体图形跟踪训练含解析新版华东师大版一.选择题(共9小题)1.如果一个多面体的一个面是多边形,其余各面是有一个公共顶点的三角形,那么这个多面体叫做棱锥.如图是一个四棱柱和一个六棱锥,它们各有12条棱.下列棱柱中和九棱锥的棱数相等的是()A.五棱柱B.六棱柱C.七棱柱D.八棱柱2.如图的长方体是由A,B,C,D四个选项中所示的四个几何体拼接而成的,而且这四个几何体都是由4个同样大小的小正方体组成的,那么长方体中,第四部分所对应的几何体应是()A.B.C.D.3.如图,在长方体ABCD﹣EFGH中,与棱AD平行的平面共有()A.1个B.2个C.3个D.4个4.直四棱柱,长方体和正方体之间的包含关系是()A. B C. D.5.下列物体的形状类似于球体的是()A.茶杯B.羽毛球C.乒乓球D.白炽灯泡6.由棱长为1的小正方体组成新的大正方体,如果不允许切割,至少要几个小正方体()A.4个B.8个C.16个D.27个7.如图,正方体ABCD﹣A′B′C′D′中,面ABB′A′上△AOA′的实际图形是()A.B.C.D.8.如图,立体图形由小正方体组成,这个立体图形有小正方体()A.9个B.10个C.11个D.12个9.下列立体图形中,是多面体的是()A.B. C.D.二.填空题(共6小题)10.如图,在长方体ABCD﹣EFGH中,与平面ADHE垂直的棱共有_________ 条.11.如图,在长方体中,面ABCD与面_________ 平行.12.圆柱上下两个面是_________ 的圆形;圆锥的底面是一个_________ 形,侧面是一个_________ 面.13.从棱长为4a的正方体中,挖去一个棱长为2a的小正方体,则该几何体的体积是_________ .14.下列说法中正确的有_________ 个.①棱锥的底面边数和侧面数相等;②正方体和长方体是特殊的四棱柱,也是特殊的四面体;③长方体是四棱柱,四棱柱也是长方体.15.如图,在每个几何体下面写出它们的名称_________ .三.解答题(共6小题)16.如图是由一个正方体和一个长方体组成的组合体.(1)请你用代数式表示这个组合体的体积;(2)请你说出它是几次几项式.17.如图,画出8个立体图形,请你找出与图②具有相同特征的图形,并说出相同的特征是什么?18.观察图中的圆柱和棱柱,通过想象回答下列问题:(1)该圆柱和棱柱各由几个面组成?这些面是平面还是曲面?(2)该圆柱的侧面与底面相交形成几条线?这些线是直线还是曲线?(3)该棱柱的侧面与下底面相交形成几条线?(4)该棱柱共有几个顶点?经过一个顶点有几条棱?19.观察如图所示的直四棱柱.(1)它有几个面?几个底面?底面与侧面分别是什么图形?(2)侧面的个数与底面多边形的边数有什么关系?(3)若底面的周长为20cm,侧棱长为8cm,则它的侧面积为多少?20.将下列几何体与它的名称连接起来.21.一位画家有若干个边长为1cm的正方体,他在地面上把它们摆成如图(三层)的形式,然后,他把露出的表面都涂上颜色.(1)图中的正方体一共有多少个?(2)一点颜色都没涂上颜色的正方体有多少个?(3)如果画家摆按此方式摆成七层,那又要多少个正方体?同样涂上颜色,又有多少个正方体没有涂上一点颜色?第四章图形的认识4.1.1认识立体图形参考答案与试题解析一.选择题(共10小题)1.如果一个多面体的一个面是多边形,其余各面是有一个公共顶点的三角形,那么这个多面体叫做棱锥.如图是一个四棱柱和一个六棱锥,它们各有12条棱.下列棱柱中和九棱锥的棱数相等的是()A.五棱柱B.六棱柱C.七棱柱D.八棱柱考点:认识立体图形.专题:几何图形问题.分析:根据棱锥的特点可得九棱锥侧面有9条棱,底面是九边形,也有9条棱,共9+9=18条棱,然后分析四个选项中的棱柱棱的条数可得答案.解答:解:九棱锥侧面有9条棱,底面是九边形,也有9条棱,共9+9=18条棱,A、五棱柱共15条棱,故A误;B、六棱柱共18条棱,故B正确;C、七棱柱共21条棱,故C错误;D、八棱柱共24条棱,故D错误;故选:B.点评:此题主要考查了认识立体图形,关键是掌握棱柱和棱锥的形状.2如图的长方体是由A,B,C,D四个选项中所示的四个几何体拼接而成的,而且这四个几何体都是由4个同样大小的小正方体组成的,那么长方体中,第四部分所对应的几何体应是()A.B.C.D.考点:认识立体图形.分析:观察长方体,可知第四部分所对应的几何体在长方体中,前面有一个正方体,后面有三个正方体,前面一个正方体在后面三个正方体的中间.解答:解:由长方体和第一、二、三部分所对应的几何体可知,第四部分所对应的几何体一排有一个正方体,一排有三个正方体,前面一个正方体在后面三个正方体的中间.故选A.点评:本题考查了认识立体图形,找到长方体中,第四部分所对应的几何体的形状是解题的关键.3.如图,在长方体ABCD﹣EFGH中,与棱AD平行的平面共有()A.1个B.2个C.3个D.4个考点:认识立体图形.分析:根据图示,我们可以看出,与AD相交的面有前面、后面、左面、下面四个面,只有上面和右面与其平行,解答即可.解答:解:观察可知,AD平行的平面有BCGF、EFGH两个面,故选B.点评:正确理解平行的概念是解题的关键.4.直四棱柱,长方体和正方体之间的包含关系是()A B. C.D.考点:认识立体图形.分析:根据正方体,长方体,直四棱柱的概念和定义即可解.解答:解:正方体是特殊的长方体,长方体又是特殊的直四棱柱故选:A.点评:本题考查了直四棱柱,长方体和正方体之间的包含关系.5.下列物体的形状类似于球体的是()A.茶杯B.羽毛球C.乒乓球D.白炽灯泡考点:认识立体图形.分析:根据球的形状与特点即可解答.解答:解:根据日常生活常识可知乒乓球是球体.故选:C.点评:熟练掌握常见立体图形的特征,是解决此类问题的关键.6.由棱长为1的小正方体组成新的大正方体,如果不允许切割,至少要几个小正方体()A.4个B.8个C.16个D.27个考点:认识立体图形.专题:压轴题.分析:本题要求所得到的正方体最小,则每条棱是由两条小正方体的边组成.解答:解:根据以上分析要组成新的正方体至少要2×2×2=8个.故选B.点评:本题主要考查空间想象能力,解决的关键是要能想象出正方体的形状.7.如图,正方体ABCD﹣A′B′C′D′中,面ABB′A′上△AOA′的实际图形是()A.B.C.D.考点:认识立体图形.分析:结合正方体的特点,根据围成正方体6个面都是正方形,再由正方形的性质判断△AOA′的实际图形.解答:解:因为围成正方体6个面都是正方形,且正方形的对角线垂直平分,所以△AOA′是等腰直角三角形.故选B.点评:本题考查了立体图形的认识,属于基础题型.解题的关键是熟记正方体和正方形的性质.8.如图,立体图形由小正方体组成,这个立体图形有小正方体()A.9个B.10个C.11个D.12个考点:认识立体图形.分析:仔细观察图,从左向右依次相加即解.注意被挡住的一个.解答:解:这个立体图形有小正方体5+2+1+3=11个.故选:C.点评:解决此类问题,注意不要忽略了被挡住的小正方体.9.下列立体图形中,是多面体的是()A.B. C. D.考点:认识立体图形.分析:多面体指四个或四个以上多边形所围成的立体图形.解答:解:A、只有一个面是曲面;B、有6个面故是多面体;C、有3个面,一个曲面两个平面;D、有2个面,一个曲面,一个平面.故选B.点评:本题考查的是多面体的定义,关键点在于:多面体指四个或四个以上多边形所围成的立体图形.二.填空题(共6小题)10.如图,在长方体ABCD﹣EFGH中,与平面ADHE垂直的棱共有 4 条.考点:认识立体图形.分析:在长方体,棱与面之间的关系有平行和垂直两种.解答:解:与平面ADHE垂直的棱有:AB,DC,HG,EF.共4条.故答案为4.点评:本题考查的知识点为:与一个平面内的一条直线垂直的直线就与这个平面垂直.11.如图,在长方体中,面ABCD与面A1B1C1D1平行.考点:认识立体图形.分析:根据图形可直接得到答案.解答:解:根据图形可得面ABCD与面A1B1C1D1平行,故答案为:A1B1C1D1.点评:此题主要考查了认识立体图形,题目比较简单.12.圆柱上下两个面是相等的圆形;圆锥的底面是一个圆形,侧面是一个扇形面.考点:认识立体图形.分析:根据圆柱和圆锥的特征,即可进行解答.解答:解:由圆柱和圆锥的特征可以得知:圆柱的底面都是圆,并且大小一样,侧面是曲面;圆锥的底面也是圆形,侧面是扇形面,则圆柱上下两个面是相等的圆形;圆锥的底面是一个圆形,侧面是一个扇形面.故答案为:相等;圆;扇形.点评:此题考查了对圆柱体和圆锥体的认识,正确记忆重点图形的形状是解题关键.13.从棱长为4a的正方体中,挖去一个棱长为2a的小正方体,则该几何体的体积是56a .考点:认识立体图形.分析:根据正方体的体积减去正方体的体积,可得答案.解答:解:V=(4a)3﹣(2a)3=64a3﹣8a3=56a3,故答案为:56a3.点评:本题考查了认识立体图形,利用了正方体的体积.14.下列说法中正确的有 1 个.①棱锥的底面边数和侧面数相等;②正方体和长方体是特殊的四棱柱,也是特殊的四面体;③长方体是四棱柱,四棱柱也是长方体.考点:认识立体图形.分析:根据棱锥的特点,可判断①;根据长方体的特点,可判断②③.解答:解:①棱锥的底面边数和侧面数相等,故①说法正确;②正方体和长方体是特殊的四棱柱,也是特殊的六面体,故②说法错误;③长方体是四棱柱,四棱柱不一定是长方体,故③说法错误;故答案为:1.点评:本题考查了认识立体图形,利用了长方体和四棱柱的关系.15.如图,在每个几何体下面写出它们的名称长方体、圆柱、三棱锥.考点:认识立体图形.分析:根据所给图形的特征进行判断.解答:解:从左向右三个几何体的名称是:长方体、圆柱、三棱锥.故答案为长方体、圆柱、三棱锥.点评:熟记常见立体图形的特征,是解决此类问题的关键,此题属于简单题型.三.解答题(共6小题)16.如图是由一个正方体和一个长方体组成的组合体.(1)请你用代数式表示这个组合体的体积;(2)请你说出它是几次几项式.考点:认识立体图形;多项式.分析:(1)根据正方体的体积公式,长方体的体积公式,可得组合体的体积;(2)根据多项式的项与次数,可得多项式的表示方法.解答:解;(1)由题意,得这个组合体的体积是:a3+a2b;(2)a3+a2b是三次二项式.点评:本题考查了认识立体图形,利用了正方体的体积公式,长方体的体积公式.17.如图,画出8个立体图形,请你找出与图②具有相同特征的图形,并说出相同的特征是什么?考点:认识立体图形.分析:根据立体图形的特点从形状的特征考虑.解答:解:图④、⑦与图②,相同的特征是:它们都是锥体.点评:本题考查了认识立体图形,题目简单但不容易解答,需熟悉立体图形的特点,找出与题目已经提供的特征不相同的共同特征.18.观察图中的圆柱和棱柱,通过想象回答下列问题:(1)该圆柱和棱柱各由几个面组成?这些面是平面还是曲面?(2)该圆柱的侧面与底面相交形成几条线?这些线是直线还是曲线?(3)该棱柱的侧面与下底面相交形成几条线?(4)该棱柱共有几个顶点?经过一个顶点有几条棱?考点:认识立体图形.分析:根据立体图形可得圆柱有3个面,六棱柱有8个面,圆柱的侧面与底面相交形成曲线,棱柱的侧面与下底面相交形成6条线.解答:解:(1)圆柱有3个面,上下底为平面,侧面为曲面;六棱柱有8个面,都是平面;(2)圆柱的侧面与底面相交形成2条线,是曲线;(3)该棱柱的侧面与下底面相交形成6条线;(4)棱柱共有12个顶点,经过一个顶点有3条棱.点评:此题主要考查了认识立体图形,根据图形的形状进行解答即可.19.观察如图所示的直四棱柱.(1)它有几个面?几个底面?底面与侧面分别是什么图形?(2)侧面的个数与底面多边形的边数有什么关系?(3)若底面的周长为20cm,侧棱长为8cm,则它的侧面积为多少?考点:认识立体图形;几何体的表面积.分析:(1)(2)(3)根据直四棱柱的特征直接解答即可.(4)根据棱柱的侧面积公式:底面周长×高,进行计算.解答:解:(1)它有6个面, 2个底面,底面是梯形,侧面是长方形;(2)侧面的个数与底面多边形的边数相等都为4;(3)它的侧面积为20×8=160cm2.点评:本题考查了立体图形.解题时勿忘记四棱柱的特征及展开图的特征.四棱柱是由四个长方形的侧面和上下两个底面组成.20.将下列几何体与它的名称连接起来.考点:认识立体图形.分析:根据常见立体图形的特征直接连线即可.注意正确区分各个几何体的特征.解答:解:如图所示:点评:考查了认识立体图形,熟记常见立体图形的特征是解决此类问题的关键.此题属于简单题型.21.一位画家有若干个边长为1cm的正方体,他在地面上把它们摆成如图(三层)的形式,然后,他把露出的表面都涂上颜色.(1)图中的正方体一共有多少个?(2)一点颜色都没涂上颜色的正方体有多少个?(3)如果画家摆按此方式摆成七层,那又要多少个正方体?同样涂上颜色,又有多少个正方体没有涂上一点颜色?考点:认识立体图形.分析:(1)图中的正方体一共的个数=三层的个数的和;(2)观察图形可知最底层正中间一个没涂上颜色;(3)观察图形可知最底层有72个正方体,第2层有62个正方体,第3层有52个正方体,第4层有42个正方体,第5层有32个正方体,第6层有22个正方体,第7层有12个正方体,相加即可求出摆成七层的正方体一共的个数;没有涂上一点颜色的正方体第5层有12个正方体,第4层有22个正方体,第3层有32个正方体,第4层有42个正方体,最底层有52个正方体,相加即可求出.解答:解:(1)图中的正方体一共有1+4+9=14个;(2)一点颜色都没涂上颜色的正方体有1个;(3)七层的正方体一共的个数12+22+32+42+52+62+72=140个;没有涂上一点颜色的正方体12+22+32+42+52=55个.答:(1)图中的正方体一共有14个.(2)一点颜色都没涂上颜色的正方体有1个.(3)如果画家摆按此方式摆成七层,要140个正方体,同样涂上颜色,有55个正方体没有涂上一点颜色.点评:本题考查学生对简单几何图形的掌握情况,既避免了单纯依靠公式机械计算的做法,又体现了数学知识在现实生活、甚至娱乐中的运用,体现了数学学科的基础性.2019-2020年七年级数学上册4.1生活中的立体图形4.1.2跟踪训练含解析新版华东师大版一.选择题(共8小题)1.如图所示,将平面图形绕轴旋转一周,得到的几何体是()A.球B.圆柱C.半球D.圆锥2.将一个长方形绕它的一条边旋转一周,所得的几何体是()A.圆柱B.三棱柱C.长方体D.圆锥3.小军将一个直角三角板(如图)绕它的一条直角边所在的直线旋转一周形成一个几何体,将这个几何体的侧面展开得到的大致图形是()A.B.C.D.4.将如图放置的含30°角的直角三角形,绕点A旋转90°所得的图形是()A. B.C.D.5.图中的几何体,由两个正方体组合而成,大正方体的棱长为a,小正方体的棱长是b,则这个几何体的表面积等于()A.6a2+4b2B.6a2+6b2C.5a2+6b2D.6(a+b)(a﹣b)6.李强同学用棱长为l的正方体在桌面上堆成如图所示的图形,然后把露出的表面都染成红色,则表面被他染成红色的面积为()A.37 B.33 C.24 D.217.正四面体的顶点数和棱数分别是()A.3,4 B.3,6 C.4,4 D.4,68.一个画家有14个边长为1m的正方体,他在地面上把它们摆成如下图的形状,然后他把露出的表面都涂上颜色,那么被涂上颜色的总面积为()A.19m2B.21m2C.33m2D.34m2二.填空题(共6小题)9.5个棱长为1的正方体组成,如图的几何体,该几何体的表面积是_________ .10.如图,正方形ABCD的边长为3cm,以直线AB为轴,将正方形旋转一周,所得几何体的主视图的面积是_________ .11.矩形绕其一边旋转一周形成的几何体叫_________ ,直角三角形绕其中一条直角边旋转一周形成的几何体叫_________ .12.如图所示的图形可以被折成一个长方体,则该长方体的表面积为_________ cm2.13.长方体有_________ 个顶点,_________ 条棱,_________ 个面.14.把一块学生使用的三角板以一条直角边为轴旋转成的形状是_________ 形状.三.解答题(共6小题)15.将下列平面图形绕直线AB旋转一周,所得的几何体分别是什么?16.一个长方形的两边分别是2cm、3cm,若将这个长方形绕一边所在直线旋转一周后是一个什么几何体?请求出这个几何体的底面积和侧面积.17.如图,上面的平面图形绕轴旋转一周,可以得出下面的立方图形,请你把有对应关系的平面图形与立体图形连接起来.18.如图,一个棱长为10cm的正方体,在它的一个角上挖掉一个棱长是2cm的正方体,求出剩余部分的表面积和体积.19.棱长为a的正方体摆放成如图的形状:(1)试求其表面积(含底面);(2)若如此摆放10层,其表面积是多少?若如此摆放n层呢?20.下列各图是棱长为1cm的小正方体摆成的,如图①中,共有1个小正方体,从正面看有1个正方形,表面积为6cm2;如图②中,共有4个小正方体,从正面看有3个正方形,表面积为18cm2;如图③,共有10个小正方体,从正面看有6个正方形,表面积为36cm2;…(1)第6个图中,共有多少个小正方体?从正面看有多少个正方形?表面积是多少?(2)第n个图形中,从正面看有多少个正方形?表面积是多少?第四章图形的初步认识4.1.2参考答案与试题解析一.选择题(共8小题)1.如图所示,将平面图形绕轴旋转一周,得到的几何体是()A.球B.圆柱C.半球D.圆锥考点:点、线、面、体.分析:根据半圆绕直径旋转一周,结合几何体的特点可得答案.解答:解:将平面图形绕轴旋转一周,得到的几何体是球,故选:A.点评:本题考查了点、线、面、体,半圆绕直径旋转一周得到的几何体是球.2.将一个长方形绕它的一条边旋转一周,所得的几何体是()A.圆柱B.三棱柱C.长方体D.圆锥考点:点、线、面、体.分析:一个长方形围绕它的一条边为中为对称轴旋转一周,根据面动成体的原理即可解.解答:解:一个长方形绕着它的一条边旋转一周,围成一个光滑的曲面是圆柱体.故选A.点评:本题考查了平面图形旋转可以得到立体图形,体现了面动成体的运动观点.3.小军将一个直角三角板(如图)绕它的一条直角边所在的直线旋转一周形成一个几何体,将这个几何体的侧面展开得到的大致图形是()A.B.C.D.考点:点、线、面、体.分析:先根据面动成体得到圆锥,进而可知其侧面展开图是扇形.解答:解:直角三角板(如图)绕它的一条直角边所在的直线旋转一周形成一个圆锥,那么它的侧面展开得到的图形是扇形.故选:D.点评:主要考查了圆锥的侧面展开图和面动成体的道理.4.将如图放置的含30°角的直角三角形,绕点A旋转90°所得的图形是()A. B.C.D.考点:点、线、面、体.分析:图形的旋转关键是对应点的旋转,根据三角形其他两点绕点A旋转90°的位置,即可得出所得的图形的位置.解答:解:根据三角形其他两点绕点A旋转90°的位置,即可得出所得的图形的位置如图所示:故选:C.点评:此题主要考查了图形绕点旋转:考查学生图形的空间想象能力及分析问题,解决问题的能力.5.图中的几何体,由两个正方体组合而成,大正方体的棱长为a,小正方体的棱长是b,则这个几何体的表面积等于()A.6a2+4b2B.6a2+6b2C.5a2+6b2D.6(a+b)(a﹣b)考点:几何体的表面积;整式的混合运算.分析:分大正方体的表面积为六个正方形的面积减去重叠部分小正方形的面积,小正方体的五个表面的面积,然后根据正方形的面积公式列式进行计算即可得解.解答:解:∵大正方体的棱长为a,小正方体的棱长是b,∴大正方体的表面积为6a2﹣b2,小正方体可看见的面的面积为5b2,所以,这个几何体的表面积等于6a2﹣b2+5b2=6a2+4b2.故选A.点评:本题考查了几何体的表面积,以及整式的加减运算,要注意重叠部分的面积为小正方形的面积,需要在大正方体与小正方体分别减去一次.6.李强同学用棱长为l的正方体在桌面上堆成如图所示的图形,然后把露出的表面都染成红色,则表面被他染成红色的面积为()A.37 B.33 C.24 D.21考点:几何体的表面积.专题:压轴题.分析:此题可根据表面积的计算分层计算得出红色部分的面积再相加.解答:解:根据题意得:第一层露出的表面积为:1×1×6﹣1×1=5;第二层露出的表面积为:1×1×6×4﹣1×1×13=11;第,三层露出的表面积为:1×1×6×9﹣1×1×37=17.所以红色部分的面积为:5+11+17=33.故选B.点评:此题考查的知识点是几何体的表面积,关键是在计算表面积时减去不露的或重叠的面积.7.正四面体的顶点数和棱数分别是()A.3,4 B.3,6 C.4,4 D.4,6考点:欧拉公式.分析:正四面体也就是正三棱锥,根据三棱锥的侧面是三个三角形围成和底面是一个三角形的特征,可以判断它的顶点数和棱数.解答:解:正四面体的顶点数和棱数分别是4,6.故选D.点评:掌握三棱锥的侧面是三个三角形围成和底面是一个三角形的特征,即三棱锥共有4个面,三个侧面,一个底面.8.一个画家有14个边长为1m的正方体,他在地面上把它们摆成如下图的形状,然后他把露出的表面都涂上颜色,那么被涂上颜色的总面积为()A.19m2B.21m2C.33m2D.34m2考点:几何体的表面积.专题:压轴题.分析:解此类题首先要计算表面积即从上面看到的面积+四个侧面看到的面积.解答:解:根据分析其表面积=4×(1+2+3)+9=33m2,即涂上颜色的为33m2.故选C.点评:本题的难点在于理解露出的表面的算法.二.填空题(共6小题)9.5个棱长为1的正方体组成,如图的几何体,该几何体的表面积是22 .考点:几何体的表面积.分析:先根据正方体的棱长为1,求出1个正方形的面积为1,再根据该几何体的表面有22个正方形构成,即可得出答案.解答:解:∵正方体的棱长为1,∴1个正方形的面积为1,∵该几何体的表面有22个正方形构成,∴该几何体的表面积22.故答案为:22.点评:此题考查了几何体的表面积,解决这类题的关键是找出该几何体的表面有多少个正方形构成.10.如图,正方形ABCD的边长为3cm,以直线AB为轴,将正方形旋转一周,所得几何体的主视图的面积是18cm2.考点:点、线、面、体;简单几何体的三视图.分析:首先根据题意可得将正方形旋转一周可得圆柱体,圆柱的高为3cm,底面直径为6cm,再找出主视图的形状可得答案.解答:解:直线AB为轴,将正方形旋转一周可得圆柱体,圆柱的高为3cm,底面直径为6cm,几何体的主视图是长6cm,宽3cm的矩形,因此面积为:6×3=18(cm2),故答案为:18cm2.点评:此题主要考查了点、线、面、体,以及三视图,关键是掌握主视图是从几何体的正面看所得到的图形.11.矩形绕其一边旋转一周形成的几何体叫圆柱,直角三角形绕其中一条直角边旋转一周形成的几何体叫圆锥.考点:点、线、面、体.分析:根据线动成面的知识可判断矩形及三角形旋转后的图形.解答:解:长方形绕它的一边旋转一周可形成圆柱,直角三角形绕它的直角边旋转一周可形成圆锥.故答案为圆柱,圆锥.点评:本题考查线动成面的知识,难度不大,解决本题的关键是掌握各种面动成体的特征.12.如图所示的图形可以被折成一个长方体,则该长方体的表面积为88 cm2.考点:几何体的表面积;展开图折叠成几何体.专题:计算题;几何图形问题.分析:由图形可知,这是一个长方体图形的展开图,先得出长方体的长、宽、高,根据长方体的表面积计算公式即可求解.解答:解:长方体的表面积是:2×(6×4+6×2+4×2)=88m2.故答案为:88.点评:本题考查了几何体的展开图和表面积,长方体的表面积=2(长×宽+长×高+宽×高).13.长方体有8 个顶点,12 条棱, 6 个面.考点:欧拉公式.。
第1章《丰富的图形世界》同步练习及答案— 生活中的立体图形(2)

精品"正版〞资料系列,由本公司独创 .旨在将"人教版〞、〞苏教版"、〞北师大版"、〞华师大版"等涵盖几乎所有版本的教材教案、课件、导学案及同步练习和检测题分享给需要的朋友 .本资源创作于2021年8月,是当前最|新版本的教材资源 .包含本课对应内容,是您备课、上课、课后练习以及寒暑假预习的最|正确选择 .北师大版七年级|数学上册第1章<丰富的图形世|界>同步练习及答案 -1.1生活中的立体图形 (2 )生活中的立体图形一.填空题:1.立体图形的各个面都是__________的面 ,这样的立体图形称为多面体.;2.图形是由________ ,_________ ,________构成的;3.物体的形状似于圆柱的有________________ ,类似于圆锥的有_____________________ ,类似于球的有__________________; (各举一例 )4.围成几何体的侧面中 ,至|少有一个是曲面的是______________; (举一例 )5.正方体有_____个顶点 ,经过每个顶点有_________条棱 ,这些棱都____________;6.圆柱、圆锥、球的共同点是_____________________________;7.假设我们把笔尖看作一个点,当笔尖在纸上移动时,就能画出线,说明了______________,时钟秒针旋转时 ,形成一个圆面 ,这说明了_______________ ,三角板绕它的一条直角边旋转一周 ,形成一个圆锥体 ,这说明了___________________;8.圆可以分割成_____ 个扇形 ,每个扇形都是由___________________;9.从一个七边形的某个顶点出发 ,分别连结这个点与其余各顶点 ,可以把七边形分割成__________个三角形;10.在乒乓球、橄榄球、足球、羽毛球、冰球中 ,是球体的有;11.将以下几何体分类 ,柱体有: ,锥体有 (填序号 ) ;12.长方体由_______________个面_______________条棱_______________个顶点;13.半圆面绕直径旋转一周形成__________;A B C D 二.选择题14.观察以下图 ,请把左边的图形绕着给定的直线旋转一周后可能形成的几何体选出来( )15.从一个十边形的某个点出发 ,分别连接这个顶点与其余各顶点 ,可以把这个多边形分割成三角形( )(A ) 10个 (B ) 9个 (C ) 8个 (D ) 7个 16.如图的几何体是下面 ( )平面图形绕轴旋转一周得到的( )(A ) (B ) (C ) (D )18.下面图形不能围成封闭几何体的是( )(A ) (B ) (C ) (D )三.解答题:19.指出以下平面图形是什么几何体的展开图:B20. ⑴.下面这些根本图形和你很熟悉 ,试一试在括号里写出它们的名称. A C( ) ( ) ( ) ( ) ( ) ⑵. 将这些几何体分类 ,并写出分类的理由.平面内的立体图形一.填空题:1.围成球的面有个;2.圆柱有_____ 个面组成 ,这些面相交共得____ 条线 ,圆锥的侧面展开图是____ ;3.圆锥是由_ __个面围成 ,其中__ _个平面 ,___ _个曲面 ,圆锥的侧面与底面相交成条线 ,是线;4.圆柱的外表展开图是________________________ (用语言描述);5.图形所表示的各个局部不在同一个平面内 ,这样的图形称为图形;6.图形所表示的各个局部都在同一个平面内 ,称为图形;二.选择题:7.圆锥的侧面展开图是 ( ) (A ) 长方形 (B ) 正方形 (C ) 圆 (D ) 扇形8.将半圆绕它的直径旋转一周形成的几何体是( )(A ) 圆柱 (B ) 圆锥 (C ) 球 (D ) 正方体9.如下图的图形绕虚线旋转一周 ,所形成的几何体是 ( ) ( )10.以下立体图形中是棱柱的有( )(A ) ①⑤ (B ) ①②③ (C ) ①②④⑤ (D ) ①②⑤11.以下说法中,正确的选项是( )(A ) 正方体不是棱柱 (B )圆锥是由3个面围成(C )正方体的各条棱都相等(D )棱柱的各条棱都相等12.将一个直角三角形绕它的最|长边旋转一周,得到的几何体是(A ) (B ) (C ) (D )13.按组成面的平或曲划分,与圆锥为同一类几何体的是( )(A ) 正方体 (B ) 长方体 (C ) 球 (D ) 棱柱14,沿着虚线旋转一周得到的图形为(A ) (B ) (C ) (D )15.一个正方体锯掉一个角后,顶点的个数是( )(A ) 7个 (B ) 8个 (C ) 9个 (D ) 7个或8个或9个或10个三、解答题16.请写出以下几何体的名称( ) ( ) ( ) ( )( ) ( ) ( ) ( )17.如图 ,第二行的图形绕点划线旋转一周 ,便形成第|一行的某个图形(几何体) ,将对应的两个图形用线联结起来.参考答案一、1.平;2.点、线、面;3.略;4.略;5.8 ,3 ,相等;6.都有一个面是曲面;7.点动成线 ,线动成面 ,面动成体;8.无数 ,一条弧和两条半径组成的;9.5;10.乒乓球、足球;11. (1 ) (2 ) (3 ) , (5 ) (6 );12.6 ,12 ,8;13.球体;二、14.D;15.C;16.B; 17.A;三、18.长方体 (四棱柱 ) ,圆锥 ,圆柱;19. (1 ) (从左至|右 )球、圆柱、圆锥、长方体、三棱柱;(2 )按面分:曲面:球、圆柱、圆锥;平面:长方体、三棱柱;按柱体分:圆柱、长方体、三棱柱;球;圆锥;参考答案一、1.一个;2.三 ,二 ,扇形;3.二 ,一 ,一 ,一 ,曲;4.由一个长方形和两个相等的圆形组成;5.平面;6.立体;二、7.D;8.C;9.B;10.A;11.C;12.D;13.C;14.C;15.D;三、16.略;17.略;以下为赠送内容别想一下造出大海,必须先由小河川开始 .成功不是只有将来才有,而是从决定做的那一刻起,持续积累而成!人假设软弱就是自己最|大的敌人,人假设勇敢就是自己最|好的朋友 .成功就是每天进步一点点!如果要挖井,就要挖到水出为止 .即使爬到最|高的山上,一次也只能脚踏实地地迈一步 .今天拼搏努力,他日谁与争锋 .在你不害怕的时候去斗牛,这不算什么;在你害怕的时候不去斗牛,这没什么了不起;只有在你害怕的时候还去斗牛才是真正的了不起 .行动不一定带来快乐,但无行动决无快乐 .只有一条路不能选择- -那就是放弃之路;只有一条路不能拒绝| - -那就是成长之路 .坚韧是成功的一大要素,只要在门上敲得够久够大声,终会把人唤醒的 .只要我努力过,尽力过,哪怕我失败了,我也能拍着胸膛说:"我问心无愧 ."用今天的泪播种,收获明天的微笑 .人生重要的不是所站的位置,而是所朝的方向 .弱者只有千难万难,而勇者那么能披荆斩棘;愚者只有声声哀叹,智者却有千路万路 .坚持不懈,直到成功!最|淡的墨水也胜过最|强的记忆 .凑合凑合,自己负责 .有志者自有千计万计,无志者只感千难万难 .我中|考,我自信!我尽力我无悔!听从命运安排的是凡人;主宰自己命运的才是强者;没有主见的是盲从,三思而行的是智者 .相信自己能突破重围 .努力造就实力,态度决定高度 .把自己当傻瓜,不懂就问,你会学的更多 .人的活动如果没有理想的鼓舞,就会变得空虚而渺小 .安乐给人予舒适,却又给人予早逝;劳作给人予磨砺,却能给人予长久 .眉毛上的汗水和眉毛下的泪水,你必须选择一样!假设不给自己设限,那么人生中就没有限制你发挥的藩篱 .相信自己我能行!任何业绩的质变都来自于量变的积累 .明天的希望,让我们忘了今天的痛苦 .世|界上最|重要的事情,不在于我们身在何处,而在于我们朝着什么方向走 .爱拼才会赢努力拼搏,青春无悔!。
【红对勾45分钟】-xxx七年级数学上册 1.1 生活中的立体图形课时作业 (新版)北师大版

1.1 生活中的立体图形
1.如图甲所示,将三角形绕虚线旋转一周,可以得到图乙所示的立体图形的是( )
2.下列几何体中,由4个面围成的几何体是( )
3.在下列立体图形中,面数相同的是( )
A.(1)(2) B.(1)(3) C.(2)(3) D.(3)(4) 4.以下四种说法:
(1)正方形绕着它的一边旋转一周,能够形成圆柱;
(2)梯形绕着它的下底边旋转一周,能够形成圆柱;
(3)直角梯形绕着垂直于底边的腰旋转一周,能够形成圆锥;
(4)直角三角形绕着一条直角边旋转一周能够形成圆锥.
其中正确的说法为( )
A.(1)(2) B.(1)(3) C.(1)(4) D.(2)(3)
5.如图所示:
(1)这个棱柱的底面是________形.
(2)这个棱柱有________个侧面,侧面的形状是________边形.
(3)侧面的个数与底面的边数____.
(4)这个棱柱有________条侧棱,一共有________条棱.
(5)如果CC′=3 cm,那么BB′=________cm.
6.如图,请将几何体进行分类,并说明理由.
7.在横线上写出图中的几何体的名称.
8.如图中的图形绕虚线旋转一周,可以形成怎样的几何体?连一连,并说明名称.。
七年级数学生活中的立体图形练习题

第一章丰富的图形世界一.填空题1.立体图形的各个面都是__________的面,这样的立体图形称为多面体.2.图形是由________,__________,____________构成的.3.物体的形状似于圆柱的有________________;类似于圆锥的有_____________________;类似于球的有__________________.4.围成几何体的侧面中,至少有一个是曲面的是______________.5.正方体有_____个顶点,经过每个顶点有_________条棱,这些棱都____________.6.圆柱,圆锥,球的共同点是_____________________________.7.假如我们把笔尖看作一个点,当笔尖在纸上移动时,就能画出线,说明了______________,时钟秒针旋转时,形成一个圆面,这说明了_______________,三角板绕它的一条直角边旋转一周,形成一个圆锥体,这说明了___________________.8.圆可以分割成_____个扇形,每个扇形都是由___________________.9.从一个七边形的某个顶点出发,分别连结这个点与其余各顶点,可以把七边形分割成__________个三角形.二.选择题10. 从一个十边形的某个点出发,分别连接这个顶点与其余各顶点,可以把这个多边形分割成( )个三角形A. 10B. 9C. 8D. 711. 图1-1是由( )图形饶虚线旋转一周形成的A B C D 图1-113.图1-2绕虚线旋转一周形成的图形是 ( )图1-2A B C D14.图1-3这个美丽的图案是由我们所熟悉的( )图形组成A.三角形和扇形B圆和四边形 C.圆和三角形D圆和扇形15.下面全由圆形组成的图案是( )A B C D三.解答题16.请观察丰富多彩的生活世界,有哪些物体的形状与下列几何体类似?(1)六面体(2)圆柱(3)圆锥(4)棱锥17.请写出下列几何体的名称( ) ( ) ( )( ) ( ) ( )18.请说出生活中至少4个规则的物体,并说出和它们类似的立体图形?19.动手做一做.将一个长方体切去一部分,看一看剩余的部分是几面体呢?四.开放创新提高题20.如图1-4,一长方体土地,用两条直线把它分成形状相同,大小相等的四块,你能做到吗,能用不同的方法完成这个任务吗?21.一个圆绕着它的直径的直线旋转一周就形成球体,那么现有一个长方形(如图1-5)你有几种方法使它类似于圆柱的几何体?请你画出这些立体圆形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章丰富的图形世界
一.填空题
1.立体图形的各个面都是__________的面,这样的立体图形称为多面体.
2.图形是由________,__________,____________构成的.
3.物体的形状似于圆柱的有________________;类似于圆锥的有_____________________;
类似于球的有__________________.
4.围成几何体的侧面中,至少有一个是曲面的是______________.
5.正方体有_____个顶点,经过每个顶点有_________条棱,这些棱都____________.
6.圆柱,圆锥,球的共同点是_____________________________.
7.假如我们把笔尖看作一个点,当笔尖在纸上移动时,就能画出线,说明了______________,
时钟秒针旋转时,形成一个圆面,这说明了_______________,三角板绕它的一条直角边旋转一周,形成一个圆锥体,这说明了___________________.
8.圆可以分割成_____个扇形,每个扇形都是由___________________.
9.从一个七边形的某个顶点出发,分别连结这个点与其余各顶点,可以把七边形分割成___
_______个三角形.
二.选择题
10. 从一个十边形的某个点出发,分别连接这个顶点与其余各顶点,可以把这个多边形分割成( )个三角形
A. 10
B. 9
C. 8
D. 7
11. 图1-1是由( )图形饶虚线旋转一周形成的
A B C D 图1-1
13.图1-2绕虚线旋转一周形成的图形是 ( )
图1-2
A B C D
14.图1-3这个美丽的图案是由我们所熟悉的( )图形组成
A.三角形和扇形B圆和四边形 C.圆和三角形D圆和扇形
15.下面全由圆形组成的图案是( )
A B C D
三.解答题
16.请观察丰富多彩的生活世界,有哪些物体的形状与下列几何体类似?
(1)六面体(2)圆柱(3)圆锥(4)棱锥
17.请写出下列几何体的名称
( ) ( ) ( )
( ) ( ) ( )
18.请说出生活中至少4个规则的物体,并说出和它们类似的立体图形?
19.动手做一做.
将一个长方体切去一部分,看一看剩余的部分是几面体呢?
四.开放创新提高题
20.如图1-4,一长方体土地,用两条直线把它分成形状相同,大小相等的四块,你能做到吗,能用不同的方法完成这个任务吗?
21.一个圆绕着它的直径的直线旋转一周就形成球体,那么现有一个长方形(如图1-5)你有几种方法使它类似于圆柱的几何体?请你画出这些立体圆形。
