第二讲——1
《多媒体技术》 第二讲 多媒体数据压缩技术(第1—2节)课堂笔记及练习题

多媒体技术第二讲多媒体数据压缩技术(第1—2节)课堂笔记及练习题主题:第二讲多媒体数据压缩技术(第1—2节)学习时间: 4月4日--4月10日内容:第二讲多媒体数据压缩技术第一节多媒体数据和信息转换一、多媒体间的信息转换为了便于交流信息,需要对不同的媒体信息进行转换。
下表是部分媒体之间说明:*易**较困难***很困难二、多媒体数据文件格式多媒体文件的格式很多,下表介绍常用文件格式的特点和应用场合。
三、多媒体数据的信息冗余多媒体计算机系统主要采用数字化方式,对声音、文字、图形、图像、视频等媒体进行处理。
数字化处理的主要问题是巨大的数据量。
一般来说,多媒体数据中存在以下种类的数据冗余:1)空间冗余:一些相关性的成像结构在数字化图像中就表现为空间冗余。
2)时间冗余:两幅相邻的图像之间有较大的相关性,这反映为时间冗余。
3)信息熵冗余(编码冗余):信息熵是指一组数据所携带的信息量。
如果图像中平均每个像素使用的比特数大于该图像的信息熵,则图像中存在冗余,这种冗余称为信息熵冗余。
4)结构冗余:有些图像从大域上看存在着非常强的纹理结构,例如布纹图像和草席图像,我们说它们在结构上存在冗余。
5)知识冗余:有许多图像的理解与某些基础知识有较大的相关性。
这类规律性的结构可由先验知识和背景知识得到,我们称此类冗余为知识冗余。
6)视觉冗余:人类视觉系统对于图像场的任何变化,并不是都能感知的。
这类冗余我们称为视觉冗余。
7)其他冗余:例如由图像的空间非定常特性所带来的冗余。
以上所讲的是多媒体数据的信息冗余。
设法去掉信号数据中的冗余,就是数据压缩。
第二节常用的数据压缩技术一、数据压缩编码方法1)根据解码后数据与原始数据是否完全一致来进行分类:① 可逆编码(无失真编码),如Huffman编码、算术编码、行程长度编码等。
② 不可逆编码(有失真编码),常用的有变换编码和预测编码。
2)根据压缩的原理进行划分:① 预测编码:它是利用空间中相邻数据的相关性,利用过去和现在出现过的点的数据情况来预测未来点的数据。
高中数学人教A版选修4-4第二讲 一 1. 参数方程的概念 课件

[解] 法一:设 P 点的坐标为(x,y),过
P 点作 x 轴的垂线交 x 轴于 Q.如图所示,则 Rt△OAB≌Rt△QBP.
∴xy==bascions
θ, θ.
这就是所求的轨迹方程.
9.如图所示,OA是圆C的直径,且OA=2a, 射线OB与圆交于Q点,和经过A点的切线 交于B点,作PQ⊥OA,PB∥OA,试求点P 的轨迹方程.
解:设 P(x,y)是轨迹上任意一点,取∠DOQ=θ, 由 PQ⊥OA,PB∥OA,得 x=OD=OQcosθ=OAcos2θ= 2acos2θ,y=AB=OAtan θ=2atan θ. 所以 P 点轨迹的参数方程为xy==22aatcaons2θθ,, θ∈-π2,π2.
解析:x轴上的点横坐标可取任意实数,纵坐标为0.
答案:D
2.若点P(4,a)在曲线x=2t , (t为参数)上,则a等于(
)
y=2 t
A.4
B.4 2
C.8
D.1
解析:根据题意,将点P坐标代入曲线方程中得
4=2t , a=2 t
⇒ta==84,2.
答案:B
3.在方程
参数方程是曲线方程的另一种表达形式,点与曲线 位置关系的判断,与平面直角坐标方程下的判断方法是 一致的.
1.已知点 M(2,-2)在曲线 C:x=t+1t , (t 为参数)上, y=-2
则其对应的参数 t 的值为________. 解:由 t+1t =2 知 t=1. 答案:1
2.已知某条曲线 C 的参数方程为xy==a1t+2 2t, (其中 t 为参数, a∈R).点 M(5,4)在该曲线上,求常数 a.
五年级数学思维训练第2讲行程问题1相遇问题

第2讲行程问题(1)——相遇问题学法指导:相遇问题是指两个人或车辆(物体……)各按一定的速度从两地同时出发,沿着同一条道路相向而行,并由各种条件的变化而产生的一类应用题。
基本数量关系是:速度和×相遇时间=相遇路程相遇路程÷速度和=相遇时间相遇路程÷相遇时间=速度和【例题1】一列客车和一列货车同时从甲、乙两个城市相对开出,已知货车每小时行45千米,客车每小时比货车多行10千米,两车开出后5小时相遇,问:甲、乙两城市间的铁路长有多少千米?【练习1】1.甲、乙两艘轮船分别从两个码头同时出发相向而行,甲船每小时行38海里,乙船每小时行28海里。
两船行驶4小时后,还相距67海里。
两个码头相距多少海里?2.肯德基快餐店到王叔叔家的距离为1500米,肯德基外送员给王叔叔送汉堡,王叔叔因着急出门打算自己去店里取汉堡,他们同时出发,外送员每分钟比王叔叔多走4米,30分钟后两人相遇,那么王叔叔的速度是每分钟走多少米?3.已知在同一条铁路线上依次有三个站点北京、郑州、长沙。
北京到郑州的距离为695km,北京到长沙为1560km。
一列慢车以每小时100千米的速度从北京开往长沙,同时一列快车以每小时160千米的速度从长沙开往北京,如果不考虑中间停车等问题,两车相遇时哪列车已经过了郑州?(单位:千米)【例题2】甲、乙两辆汽车同时从东、西两地相向开出,甲车每小时行60千米,乙车每小时行48千米,两车在离两地中点30千米处第一次相遇。
那么东、西两地相距多少千米?【练习2】1.甲、乙两个工程队分别从道路的东、西两端同时开工修路。
甲队每天修路20米,乙队每天修路25米。
开工若干天后,两队在离这条路的中点50米的地方会合。
这条马路的长度是多少米?2.快车和慢车同时从A、B两地相对开出,快车每小时行70千米,慢车每小时行55千米,当快车到达A、B两地中点时,与慢车还相距90千米,求A、B两地间的路程长多少千米?3.快车和慢车两车同时从A、B两地出发,相向而行,快车每小时行60千米,经过4小时,快车已驶过中点16千米,这时与慢车还相距24千米。
第二讲 公文文体1-通知

② 事项
• 即通知的主体,要写明它的具体内 容,包括工作任务、原则规定、基 本措施、执行要求、注意事项等, 内容繁简不一。
事项的结构形式
• 一是只用一两句概括性的语句; • 二是条目式,即将内容分项列条,每 条前面加提示语或序号; • 三是分部组合式,即将内容分为若干 部分或层次,各自说明一个方面。
(2)主送机关
• 主送机关较多时,要按从大到小、 先主后次顺序排列,可用概称,例 如“各区、县、局”; • 向社会公布的通知可以省略主送机 关。
(3)正文
正文结构
: 缘由+事项+结尾
① 缘由
• 在开头先简要交代发出通知的原因、 依据或目的、意义。 • 缘由的最后通常用“特作如下通 知:”、“现通知如下:”提领 下文。
例:
• 《北京市人民政府转发国务院关于进 一步加强质量管理工作决定的通知》 • 《国务院办公厅转发建设部关于进一 步清理整顿房地产开发公司意见的通知》
转发性通知图示
上级(同级或不相隶属)机关
决定 /意见/通知(被转发公文)
本机关
加 按 语 转 发
通知
下级机关
(4)知照性通知
• 不仅可用于上级机关对下级机 关、平级机关及机关内部,还 可用于不相隶属机关之间沟通 情况,告知需知晓、办理的有 关事项。
【例7】
国务院关于香港特区政府王永平等3人职务任免的通知
香港特别行政区政府: 依照《中华人民共和国香港特别行政区基本法》 有关规定,根据香港特别行政区行政长官曾荫权 的提名和建议,国务院2006年1月24日决定:任 命王永平为工商及科技局局长、俞宗怡为公务员 事务局局长;免去曾俊华的工商及科技局局长职 务、王永平的公务员事务局局长职务。 国务院 二○○六年一月二十四日
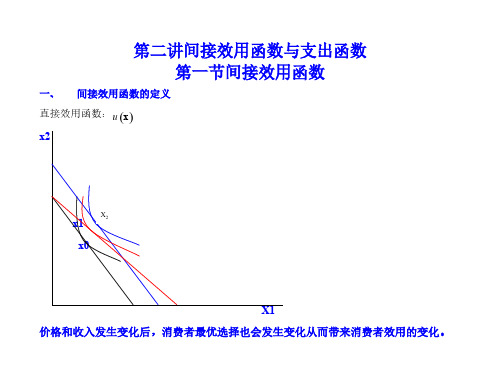
第二讲间接效用函数与支出函数 第一节间接效用函数 间接效用函数的定义
x1*
y 2p1
2 2*0.5
2
税收总量=2*0.25=0.5。与所得税相同。
v (.) y y
22 =1.41
2p1 2p2 2 * 0.5 2 *1
商品税带来的效用损失大于所得税。
为什么?
第二节支出函数 一、 支出函数的定义
y
y
0
0
4.间接效用函数v p, y关于价格 p 递减
设 x*i 0, 用与(3)同样的方法可证:
v(p, pi
y)
L(x*, *)
pi
* x *i
〈0
5、间接效用函数v p, y在p, y上拟凸
定义 A1.27:一个函数 f : D ? 是拟凸函数,当且仅当对于所
有 X1, X2 D ,有: f (Xt ) max[ f (X1), f (X2 )] 。即凸组合的函
x
px,
x
x
x
?
n
,u
x
u,u
?
两元空间支出最小化:
ep,u p1x1h p1, p2,u p2x2h p1, p2,u
min x1, x2
p1x1
p1,
p2 , u
p2
x2
p1,
p2 , u
,
s.t., u x1, x2 u
x2
p0 p0 p1
X0
X1
p1
希克斯需求函数(补偿需求函数,或实际收入不变的需求函数)
第二讲间接效用函数与支出函数 第一节间接效用函数
一、 间接效用函数的定义
直接效用函数:u x
x2
X2
第二讲 多项式理论1

(一)解析式的定义和恒等
1、定义:用运算符号把数、表示数的字母连 接而成的式子叫做解析式。
说明: 1、在研究解析式恒等时,一定要清楚他 们在什么范围内讨论。(公共定义域) 2、解析式的恒等变形,可能引起定义域 的变化。
(二)一元多项式理论
1、一元多项式的标准形式
多项式理论是方程理论、函数理论、不等 式理论的基础。
4
2
...
( iy ) n!
n
...
3
(1 [1
2
y
...) i ( y
4
y
2n
y
5
...)
2! y y
3
4! y ... ( 1 ) y
5 n
3! x
5! ...] x
2 n 1
2! i[ y
4! ... ( 1 )
第二讲 多项式理论
题记: 克莱因评价高斯在数学中的地位:“我们会 得出这样一个数学场景,如果把18世纪的数学界 想象成为一系列高山峻岭,那么最后一个令人肃 然起敬的峰巅便是高斯,如果把18世纪的数学界 想象成为一条条江河,那么源头便是高斯,他是 那样一个广大丰富的区域中充满了生命的新元 素。”
初等代数研究
分解因式中的两个有用的结论:
对称、轮换多项式
主要内容:
1、对称多项式的定义;
2、对称多项式的形式; 3、基本对称函数与根与系数的关系; 4、轮换多项式的定义与因式分解;
5、用基本对称函数表示对称多项式。
定义分析: 1、一个置换实际上是指一个排列;
2、置换的总数共有n!种。
判断下列多项式是否是对称多项式
(4)轮换多项式的因式分解(因式定理)
第二讲 社会主义从理论到实践的初步探索1

第二讲
列宁的社会主义理论和实践
垄断资本主义的形成和发展 列宁的一国胜利论 十月革命的胜利 列宁对社会主义道路的探索 列宁对社会主义认识的深化
思考题
列宁的“一国胜利论”的立论依据是什么? 如何理解经济文化相对落后国家赢得社会主 义革命的胜利,体现了历史发展进程中的必 然性和偶然性、普遍性和特殊性的统一。 简要评述“战时共产主义政策”。 “新经济政策“的主要内容及其启示。
经济的不平衡:指各个企业、各个生产 部门、 各个国家之间经济发展速度不 同。 政治发展不平衡:一些国家已建立了 较完备的议会民主政治,而另一些国 家还保留有浓厚的封建、 军事色彩。
资本主义统治最薄弱环节的标志 资本主义统治最薄弱环节的标志 最薄弱环节
统治阶级遇到政治经济危机,不可能 照旧不变地维持自己的统治; 被统治阶级的贫困和苦难异常加剧, 已经不能照旧生存下去; 群众的积极性大大提高,已表现为革 命行动。
新经济政策的意义
建设社会主义是一个长期实践探 索的过程,绝不是伟大思想家预 言的产物。“对俄国来说,根据 书本争论社会主义纲领的时代已 经过去了,我深信已经一去不复 返了。今天只能根据经验来谈论 社会主义。”
新经济政策的意义
经济文化比较落后的国பைடு நூலகம்,在 取得社会主义革命胜利后,不 能直接过渡到社会主义,而必 须走迂回曲折的道路。即利用 资本主义走向社会主义。
垄断资本主义的形成和发展
在19世纪最后30年间,资本主义国家发 生了以电力的广泛应用为特征的第二次 产业革命。这次产业革命不仅推动了社 会生产力的巨大发展,也影响着资本主 义生产关系的变化,即造成了以自由竞 争为特征的资本主义向以垄断为特征的 资本主义(帝国主义)的过渡。
小学奥数知识讲解-第二讲 一半问题1

第二讲一半问题
知识要点:小朋友,你知道吗?一些问题分成同样多的两份,其中一份就是总数的一半.已知一半求总数,只要用一半数再加一半数就是总数.当出现连续几次一半,要仔细分辨,正确计算总数.
[ 例1 ] 爸爸买了一些草莓,小名吃了一半后,还剩下6个,爸爸买了多少个草莓?
分析:根据题意,爸爸买了一些草莓,吃了一半,剩下6个与吃了的同样多,说明吃了的一半也是6个.因而原来一共有6+6=12(个).
草莓总数
所以,爸爸买了12个草莓.
[ 例2] 爸爸买了一些草莓,小名吃了一半后,还剩下6个,爸爸买了多少个草莓?
分析:根据题意,爸爸买了一些草莓,吃了一半,剩下6个与吃了[ 例3 ] 玲玲有12本书,?
分析:根据题意,爸爸买了一些草莓,吃了一半,剩下6个与吃了。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• This enabling manufacturers to integrate
– millions of such circuits on a single silicon chip
– the Italian mathematician Leonardo Pisano, • better known as Fibonacci.
5
Why Bit?
• Using decimal notation is natural for tenfingered humans
• But binary values work better when building machines
– Sometimes, they can behave in unexpected way
13
‘int’ is not integer
• Overflow
– 200*300*400*500 = -884,901,888 – Product of a set of positive numbers yielded a negative result
0 1 1 0 0 1 1
(0) (1) (1) (0) (0) (1) (1)
11
Group bits as numbers Three encodings
• Unsigned encoding
– Representing numbers greater than or equal to 0 – Using traditional binary representation
12
Group bits as numbers Understanding numbers
• Machine representation of numbers are not same as
– Integers and real numbers
• They are finite approximations to integers and real numbers
• • • •
Base-10 Has been in use for over 1000 years Developed in India Improved by Arab mathematicians in the 12th century • Brought to the West in the 13th century by
8
Group Bits
• In isolation, a single bit is not very useful
• In English, there are 26(or 52) characters in its alphabet. They are not useful either in isolation • However, there are plenty of words in its vocabulary. How is this achieved? • Similarly, we are able to represent the elements of any finite set by using bits (instead of bit)
A^B = 1 when either A=1 or B=1, but not both
~ 0 1 1 0
^ 0 1 0 0 1 1 1 0
22
General Boolean Algebras
• Operate on Bit Vectors
– Operations applied bitwise
01101001 & 01010101 01000001 01101001 | 01010101 01111101 01101001 ^ 01010101 00111100 ~ 01010101 10101010
‘float’ is not real number
• Product of a set of positive numbers is positive
• Overflow and Underflow • Associativity does not hold
– (3.14+1e20)-1e20 = 0.0 – 3.14+(1e20-1e20) = 3.14
• Commutativity & Associativity remain
– – – – (500 * 400) * (300 * 200) ((500 * 400) * 300) * 200 ((200 * 500) * 300) * 400 400 * (200 * (300 * 500))
14
9
Group Bits
• To do this, we
– first group bits together – then apply some interpretation to the different possible bit patterns • that gives meaning to each patterns
Hexadecimal
19
Bit Level Operations
20
Boolean Algebra
• Developed by George Boole in 19th Century
– Algebraic representation of logic • Encode “True” as 1 • Encode “False” as 0
– 2.1.1,2.1.2,2.1.7~2.1.10
2
Outline(cont.)
• Conversions
– Signed vs. unsigned
• Suggested reading
– Chap 2.2.1 – 2.2.4
3
Why Bit?
• Modern computers store and process
– Information represented as two-valued signals – These lowly binary digits are bits
• Bits form the basis of the digital revolution
4
The Decimal Representation
15
Hexadecimal
• Base 16 number representation
• Use characters „0‟ to „9‟ and „A‟ to „F‟ • Write FA1D37B16 in C as
– 0xFA1D37B or – 0xfcimal
21
Boolean Algebra
And
A&B = 1 when both A=1 and B=1
Or
A|B = 1 when either A=1 or B=1
& 0 1 0 0 0 1 0 1
Not
~A = 1 when A=0
| 0 1 0 0 1 1 1 1
Exclusive-Or (Xor)
17
Hexadecimal vs. Binary
0x173A4C Hexadecimal 1 7 3 A 4 C Binary 0001 0111 0011 1010 0100 1100 1111001010110110110011 Binary 11 1100 1010 1101 1011 0011 Hexadecimal 3 C A D B 3 0x3CADB3
– A high or low voltage on a wire – A magnetic domain oriented clockwise or counterclockwise.
7
Why Bit?
• The electronic circuitry is very simple and reliable for
– that store and process information
6
Why Bit?
• Two-valued signals can readily be
– represented, stored, and transmitted,
• Examples
– The presence or absence of a hole in a punched card
24
Data Size
C Declaration char short int int long int Typical 32-bit 1 2 4 4 Compaq Alpha 1 2 4 8
• 8-bit chunks are organized as a byte
– Dr. Werner Buchholz in July 1956 – during the early design phase for the IBM Stretch computer
10
Value of Bits
Bits Value Value Bits 01010 0*24+1*23+0*22+1*21+0*20 = 10 102(1100110) 102 = 51*2 + 51 = 25*2 + 25 = 12*2 + 12 = 6*2 + 6 = 3*2 + 3 = 1*2 + 1 = 0*2 +
Representation and Manipulation Information (1)
